Abstract
Traumatic brain injury such as that developed as a consequence of blast is a complex injury with a broad range of symptoms and disabilities. Computational models of brain biomechanics hold promise for illuminating the mechanics of traumatic brain injury (TBI) and for developing preventive devices. However, reliable material parameters are needed for models to be predictive. Unfortunately, the properties of human brain tissue are difficult to measure, and the bulk modulus of brain tissue in particular is not well-characterized. Thus, a wide range of bulk modulus values are used in computational models of brain biomechanics, spanning up to three orders of magnitude in the differences between values. However, the sensitivity of these variations on computational predictions is not known. In this work, we study the sensitivity of a 3D computational human head model to various bulk modulus values. A subject-specific human head model was constructed from T1-weighted MRI images at 2 mm3 voxel resolution. Diffusion tensor imaging provided data on spatial distribution and orientation of axonal fiber-bundles for modeling white-matter anisotropy. Non-injurious, full-field brain deformations in a human volunteer were used to assess the simulated predictions. The comparison suggests that a bulk modulus value on the order of GPa gives the best agreement with experimentally measured in vivo deformation in the human brain. Further, simulations of injurious loading suggest that bulk modulus values on the order of GPa provide the closest match with the clinical findings in terms of predicated injured regions and extent of injury.
Keywords: Brain bulk modulus, computational head model, in vivo brain deformation, comparison of strain fields, prediction of injury
1. Introduction
Traumatic brain injury (TBI) has been a major public health concern worldwide. In the United States alone, an average of 1.7 million Americans sustain a TBI per year, leading to 52,000 deaths, 275,000 hospitalizations, and 1.36 million emergency department visits [1]; of these, an estimated 124,000 experience the onset of long-term disability. TBI is largely caused by falls, motor vehicle crashes, sports collisions, blast and firearm assaults [1], but the precise mechanisms associated with the injury remain a matter of intense study [2,3]. Computational models hold promise to determine severity and locations of injury, either a priori or post-injury, in patient-specific human heads. This simulation capability is even more important in reliably and consistently predicting TBI as injury-causing deformations cannot be generated in live humans. As a result, computational models of the head have become increasingly elaborate, in terms of anatomical details and constitutive response [4–6]. However, efforts in regards to reliable material parameters are still ongoing.
Much of the brain characterization literature has focused on shear properties [7], with little attention on bulk properties (Table 1a). Instead, the brain tissue is often assumed to be incompressible, or nearly so. As a consequence, a wide range of bulk modulus values, spanning up to three orders of magnitude difference, are used in computational head models of brain biomechanics (Table 1b). Most of these values were chosen in an ad-hoc manner to mimic near incompressibility, with the aim of achieving numerical stability and convergence. However, the influence of such computational adjustments on computational predictions, especially on shearing deformations within the brain, has not been investigated.
Table 1.
Summary of bulk modulus values of brain in the literature
| (a) Experimentally measured bulk modulus values | |||
|---|---|---|---|
| Source | Bulk modulus value | Frequency/strain rate* | Method of obtaining bulk modulus value |
| McElhaney et al. (1973) [75] | 2.06 GPa | 0–100 Hz (102 s−1) | hydrodynamic compression tests on human and monkey brains within 10 hours of post mortem |
| Stalnaker (1969) [64] | 2.10 GPa (human) 2.08 GPa (monkey) |
0–100 Hz (102 s−1) | hydrodynamic compression tests on human and monkey brains within 10 hours of post mortem |
| Etoh et al. (1994) [65] | 2.7 GPa | 1.7 MHz (106 s−1) | ultrasonic testing of bovine gray matter |
| (b) Values of bulk modulus used in computational head models | ||
|---|---|---|
| Source | Bulk modulus value | Remarks regarding choice of bulk modulus value |
| Ruan et al. (1994) [25] | 21.9 to 219 MPa | by fitting the results of computational model to intracranial pressure measurements in post mortem human subjects |
| Claessens et al. (1997) [8] | 0.83 to 83.3 MPa | rationale for choice not stated |
| El Sayed et al. (2008) [9] | 2.19 MPa | rationale for choice not stated |
| Zoghi-Moghadam and Sadegh (2009) [11] | 50 MPa | rationale for choice not stated |
| Giordano and Kleiven (2014) [10,5] | 50 MPa | bulk modulus is lowered with respect to the acknowledged value of 2 GPa to account for numerical stability |
| Ji et al. (2015) [12] | 219 MPa | rationale for choice not stated |
| Takhounts et al. (2003, 2008) [13,14] | 560 MPa | bulk modulus was chosen to simulate near incompressibility |
| Sahoo et al. (2014) [15] | 1.125 GPa | rationale for choice not stated |
| Kleiven and Hardy (2002) [16] | 2.1 GPa | based on the experimental works of Stalnaker [64] and McElhaney et al. [75] |
| Horgan and Gilchrist (2004) [17], Zhang et al. (2004) [18], Mao et al. (2013) [4], Sarvghad-Moghaddam et al. (2015) [11] | 2.19 GPa | rationale for choice not stated |
| Taylor and Ford (2009) [23] | 2.37 GPa | by citing Zhang et al. [76] |
Since frequencies are reported in aforementioned papers, approximate strain rate is stated in the brackets
Wave propagation within the human head plays an important role in intracranial dynamics and deep brain injuries. Interestingly, shear wave speeds within the brain are orders of magnitude smaller than the bulk and longitudinal wave speeds due to the large difference between shear and bulk moduli. One consequence of this significant difference in wave speeds is that there is a timescale separation [6] that is developed in terms of potential injury-causing mechanisms in the brain. This timescale separation is particularly apparent in the case of blast loading. For example, consider a blast wave incident on the head, with a typical blast wave speed in air; the entire head observes the passage of the wave over and around the head within a time on the order of a few milliseconds. This fluid-structure boundary condition generates a pressure [27,28] and shear waves [29] within the brain. A pressure wave within the brain traverses the brain quickly (wave speed ~1000 m/sec) and establishes a pressure field inside the brain within less than a millisecond. However, the shear waves in the brain generated by the blast loading boundary condition move much more slowly (wave speed ~1 m/sec), and the shear fields that develop the rotational motions of the brain are established much later, after timeframes of over ten milliseconds. Numerous recent investigations elude to rotational-acceleration-induced brain injuries as a result of blast load [30,31]. Since these rotational motions can lead to mild TBI through deep brain injuries in the white matter, it is important to understand such deformations and motions while studying TBI under blast. Thus, in this manuscript, we focus on the effects of rotational loading and shear wave propagation within the head. Further, we focus on shear strains as opposed to intracranial pressure, since intracranial pressure does not provide a significant constraint on the material properties [32,26]. Also, brain being much compliant in shear, larger deformations are sustained in shear and hence the brain is more prone to injury under shear.
The goal of this work is to study sensitivity of brain (shear) deformations to various values of bulk modulus. We perform three-dimensional (3D) head simulations under mild rotational accelerations and compare model response against non-injurious, full-field brain deformations in a human volunteer. We use this validated model to assess sensitivity of model response to bulk modulus values for both non-injurious and injurious loading. Simulations are performed until 100 ms in order to fully capture the effects of shear wave propagation [33,6], which are often neglected in computational simulations of the head in studying blast. The manuscript is organized as follows. In section 2, we briefly describe mild acceleration experiments on human volunteers, followed by detailed description of the 3D head model including descriptions of geometry and constitutive models, solution scheme, and loading and boundary conditions. In section 3, computational results from the 3D head model are presented and compared with experimentally obtained non-injurious brain deformations in human volunteers. Later in this section, results of injurious loading are presented. Specific observations regarding sensitivity of brain deformations to various brain bulk modulus values are also made for both non-injurious and injurious loading. Key conclusions of this work are summarized in section 4.
2. Methods
2.1 Head rotation experiments in human volunteers
Mild head rotation experiments were performed with healthy human subjects with the objective of obtaining full-field, in vivo deformations in the brain. Human volunteers were recruited by the Center for Neuroscience and Regenerative Medicine (CNRM) under the CNS Institutional Review Board at the National Institutes of Health. Dynamic motions during head rotation were captured using tagged Magnetic Resonance Imaging (tagged-MRI) [36,37]. Full-field brain deformations were obtained from these tagged-MRI images using the harmonic phase (HARP) method [36]. This data was used to validate a computational model of a human head. Note that, there is a one-to-one correspondence between the experiment and the model in terms of morphology and fiber orientation of the brain tissue, loading conditions, and measured deformations. Additional details of these experiments are available in [38] and avoided here for brevity.
2.2 Computational modeling of human head
2.2.1 Construction of Subject-specific 3D head model
A 3D human head model was created from MRI images of a human volunteer (age: 22 years). T1-weighted MRI images were segmented into different substructures (Fig. 1b), namely, white matter, grey matter, caudate, putamen, thalamus, ventricles, and cerebrospinal fluid (CSF). A topology-preserving, atlas-based technique described in Bazin et al. [39] was used for the segmentation. In addition to these segmented structures, an approximate, artificial “skull” was generated by dilation of a brain mask. Stiff membranes of the falx and tentorium were also added to the head model. The falx and tentorium in the MRI images of the human volunteer were unclear due to insufficient contrast, so these structures were segmented from MRI images of a post-mortem human subject (PMHS) and incorporated into the head model.
Figure 1.
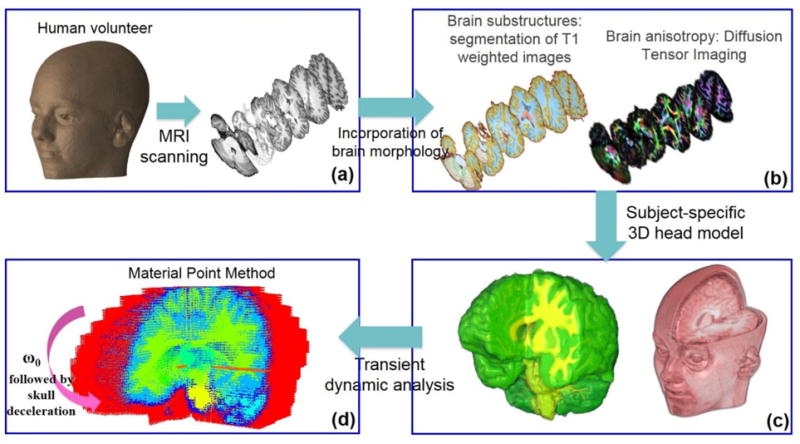
3D computational human head model. The model was constructed from the T1 and diffusion MRI images of a human volunteer. T1-weighted images were used to segment brain tissue into different substructures (a). Diffusion images provided information on fiber orientation and fractional anisotropy of the brain tissue (b). Individual images were stacked together to generate a 3D model (c). Resulting model was subjected to mild angular acceleration and solved using Material Point Method (MPM) (d).
2.2.2 Constitutive Modeling
The white matter of the brain consists of fiber bundles and shows anisotropic response in shear [40,41]. On the other hand, the grey matter contains the cell bodies and shows isotropic response [41,42]. White matter shear anisotropy was modeled using the Holzapfel-Gasser-Ogden (HGO) strain energy function (1) [43,44]. All other substructures of the head, with the exception of the CSF, were modeled using an isotropic limit of the HGO model [41,42]. In (1), the first two terms account for shear behavior while the third term accounts for volumetric behavior. A form of volumetric strain energy was chosen such that it satisfies all the physical requirements for a volumetric strain energy function, as described in Doll and Schweizerhof [45].
| (1) |
with
| (2) |
where μ is the shear modulus of the isotropic matrix, k1 is the stiffness of the fibers, k2 is the dimensionless material parameter that controls the nonlinearity of the anisotropic response, K is the effective bulk modulus, J is the volume change ratio, and κ is the structural parameter that defines the degree of fiber dispersion. In the current work, it was assumed that only a single family of fibers existed in the material, and the original HGO model is reduced accordingly while arriving at a form presented in equation 1.
The modified invariants, and , are defined as,
| (3) |
| (4) |
where is the deviatoric component of the right Cauchy–Green deformation tensor and α0 is a unit vector representing the fiber direction in the undeformed configuration. The fiber direction after deformation is given by the unit vector α. The fiber stretch, λ, is then defined as,
| (5) |
Because α is a unit vector,
| (6) |
The fiber orientation map and Fractional Anisotropy (FA) map from the DTI provide the information on fiber alignment and fiber dispersion, respectively, for each voxel (Fig. 1b). The fiber dispersion parameter κ can be related to FA from DTI using a following relation [44],
| (7) |
The lower limit of κ = 0 represents perfectly aligned fibers, whereas the upper limit of κ = 1/3 represents randomly oriented fibers. In this work, both fiber direction and fractional anisotropy are incorporated based on DTI data for this particular human volunteer. In addition to anisotropy, the constitutive model also incorporates the viscoelasticity in shear using a quasilinear viscoelastic function [46]. The shear relaxation is defined using a Prony series,
| (8) |
| (9) |
where μ0 is the instantaneous shear modulus, gi are constant parameters, and τi are relaxation time constants.
The CSF was modeled using the Tait equation of state [48], given by,
| (10) |
where, P is the pressure, K is the bulk modulus, and ρ is the density. The subscript 0 indicates values at zero pressure or initial density. For fluids similar in composition and viscosity to that of water, the value of the constant n is 7.15 [48]. The Tait equation of state is commonly used to model fluids under large pressure variations.
Constitutive model parameters
In these simulations, we use a baseline bulk modulus value based on our own measurements on human tissue samples (Ramesh, unpublished work). We obtain a dynamic bulk modulus value of 1.46 GPa for the human cerebrum and a bulk modulus value of 1.19 GPa for the human cerebellum, at a strain rate of ~103 s−1. These values are consistent with values reported in the literature (Table 1). The anisotropic properties and viscoelastic properties are based on Velardi et al. [40] and Lee et al. [49], respectively. All of the material properties used in the simulations are tabulated in Table 2 [48–51,40].
Table 2.
Material properties of head constituents
| Substructure | Properties |
|---|---|
| White Matter | G0 = 1520 Pa; G∞ = 286 Pa; g1 = 0.81; τ1 = 2 sec k1 = 121 Pa; k2 = 0.0001; fractional anisotropy (κ) and fiber direction (α, unit vector) for each material point from DTI |
| Grey Matter | G0 = 2750 Pa; G∞ = 385 Pa; g1 = 0.625; g2 = 0.055; g3 = 0.182; τ1 = 2 sec; τ2 = 11 sec; τ3 = 47.5 sec |
| Caudate, Putamen | G0 = 700 Pa; G∞ = 110 Pa; g1 = 0.61; g2 = 0.135; g3 = 0.103; τ1 = 1.45 sec; τ2 = 10 sec; τ3 = 110 sec |
| Thalamus | G0 = 6700 Pa; G∞ = 943 Pa; g1 = 0.81; τ1 = 2 sec |
| Common properties for brain substructures | ρ = 1040 kg/m3; Kcerebrum = 1.46 GPa; Kcerebellum = 1.19 GPa |
| Falx, Tentorium | ρ = 1133 kg/m3; E = 60.67 MPa; ν = 0.45 |
| Skull | ρ = 2070 kg/m3; E = 8 GPa; ν = 0.22 |
| Ventricles, Cerebrospinal fluid (CSF) | ρ = 1004 kg/m3; K = 1.46 GPa; n = 7.15; μ = 1.002e-3 Pa-sec |
2.2.3 Solution Scheme
The material point method (MPM) [52–54] was used for transient, dynamic analysis of a human head subjected to rotational acceleration. The MPM approach incorporates salient features of both Lagrangian and Eulerian formulations. In this technique, the material points are used to represent a material continuum, and a background grid is used to solve governing equations of elastodynamics. The grid (mesh) is held fixed and is used to determine spatial gradients. The updated field variable advects material points in and out of a grid cell. Boundary conditions are applied on the grid nodes that are populated by material points. Constitutive equations are used to update stress using a finite deformation framework to handle large deformations. The background mesh in MPM does not encounter any mesh-degeneration, and thus provides stable and efficient numerical solution despite material points undergoing very large deformations. MPM assumes no-slip contact between various interfaces. In this work, we have used the public domain Uintah MPM package to perform high-performance simulations on a parallel computing cluster. The segmented MRI images in the form of voxels were imported in MPM. Simulations were performed with a background mesh size of 2 mm3. A mesh convergence study was conducted to arrive at this mesh size. Less than 5% change in field variables (i.e., stresses and strains) was used as a convergence criterion.
The capability of MPM for handling large deformation problems in soft materials has already been demonstrated [55,56]. In this work, we use MPM over conventional FEM for several reasons listed here: (a) In MPM, confirming meshes are not required, thus one can directly import voxelated information from MRI images and explicit meshing is not required. Hence, the cost associated with developing subject-specific head models in MPM is minimal. Developing subject-specific head models using conventical FEM can be time consuming and costly. (b) In MPM, as the background grid is fixed, it does not suffer from the excessive distortion limits and associated errors. (c) MPM can handle a very large ratio between the bulk modulus and the shear modulus of the brain tissue with minimal volumetric locking artifacts. Note that, modeling the entire blast event including fluid-structure interaction is not fully developed and validated in the current Uintah MPM framework. Thus, in this work we do not explicitly simulate the blast event. Efforts will be made in the future to fully develop this capability in the Uintah MPM framework.
2.2.4 Pressure Stabilization
A numerical artifact known as volumetric locking is typical in simulations of nearly incompressible materials undergoing deformation. Locking refers to the build-up of fictitious stiffness due to the element’s inability to reproduce correct deformation mode shapes. Locking can result in poor kinematics and erroneous pressures and subsequent strains. Due to the many orders of magnitude difference between the shear modulus (~1–3 kPa) and bulk modulus (~1–2 GPa) of the brain tissue, volumetric locking can generally occur in the computations of the brain dynamics. Some finite element procedures rely on the use of reduced integration techniques in order to circumvent locking. However, use of reduced integration can result in spurious singular or hourglass modes. In MPM, volumetric locking is addressed by Mast et al. [57]. They provide a generalized solution to regularize volumetric and deviatoric parts of stress. In this work, we use the simplest scheme of volumetric averaging of a kinematic variable over a certain length to alleviate effects of volumetric locking. In our computations, we average the Jacobian measure for material points belonging to a background cell (Fig. 2). The Jacobian, is defined for an individual material point, because material points “carry” with them all the field variables in MPM. The deformation gradient for each material point is scaled based on the average value of the Jacobian for the cell (equation 11).
| (11) |
where,
: old deformation gradient at a given time
: new deformation gradient after stabilization
Jmp: Jacobian for a material point
Jcell: average Jacobian for the
Figure 2.
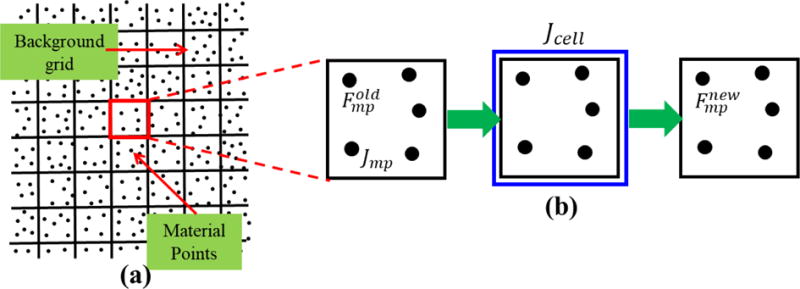
Cell-averaging-based approach for stabilization. (a) Material point and background cell configuration in MPM (b) the Jacobian for the cell is determined by averaging the Jacobian for each material point within a cell. Old deformation gradient is scaled based on the Jacobian for the cell to obtain new deformation gradient for each material point.
As shown by Mast et al. [57], use of this pressure stabilization technique reduces the numerical artifacts associated with the orders of magnitude difference between the normal and shear components of stress values.
2.2.5 Loading and Boundary Condition
Simulations are exact replicates of head rotation experiments in human volunteers described in section 2.1. The MPM head model was subjected to an angular deceleration history obtained from head-rotation experiments [38]. The head initially rotates with finite velocity (Fig. 1d) ω0 and then decelerates according to the deceleration history shown as in Fig. 3, resembling a half sinusoidal wave. Note that magnitude and duration of the loading pulse are different for injurious loading (Fig. 7a); however, the shape and loading direction remain the same. The head/neck is free at the bottom as dictated by the experiment.
Figure 3.
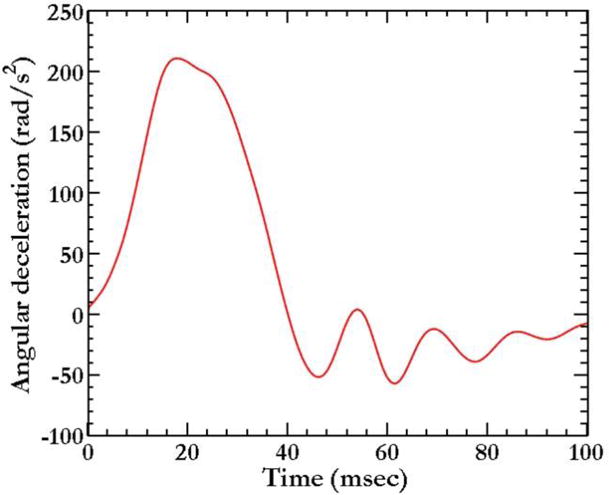
Deceleration-time history for head deceleration
Figure 7.
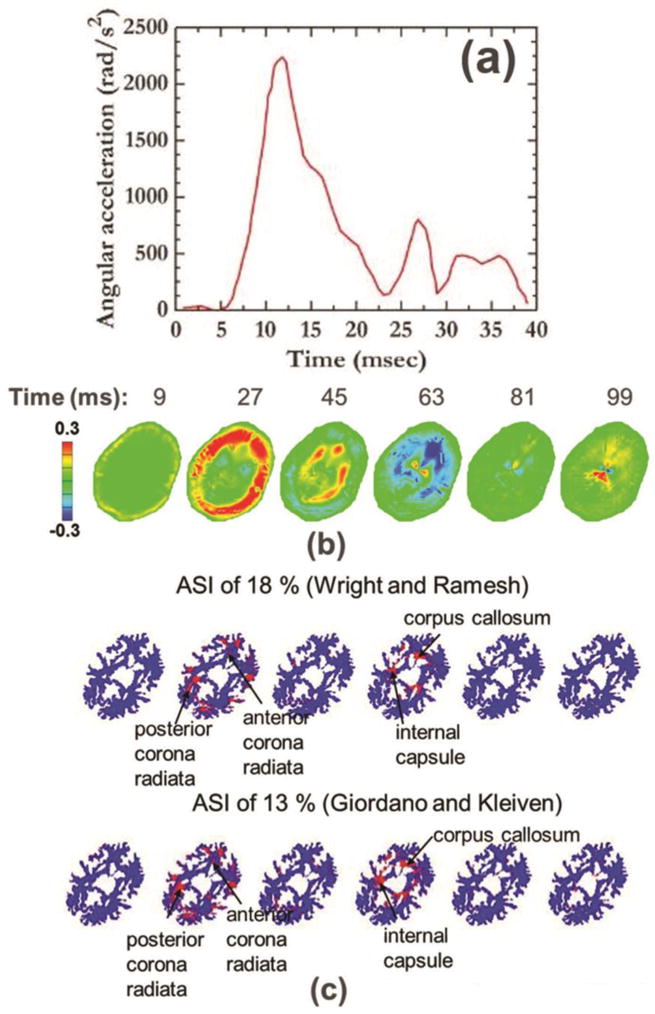
Simulations of injurious loading that resulted in definitive concussion. (a) Input acceleration for injurious loading. (b) Radial-circumferential shear strain shear strain (Ert) pattern in the brain for injurious loading. (c) Regions of white matter fiber tracts exceeding axonal strain injury criterion. Injured regions are marked in red.
2.3. Quantitative comparison between the simulations and the experiment
We use the following measures to compare brain deformations from the simulations with the experiment: (a) peak values, (b) area-fraction distribution, and (c) correlation score. Out of these measures, the first measure takes into account peak values at discrete spatial points; whereas the latter two measures take into account full-field spatial information. For area fraction measure, we consider 2D sections along the axial plane for comparison of the model with the experiments. The area-fraction, ϕ, for a given 2D section that has a shear strain, E, within the specified range m to n, is defined as:
| (12) |
Area fraction measure presented above tend to integrate out the heterogeneity of the strain field distribution. A more robust way to compare full-field 3D data between the model and the experiment is to use statistical measures that take into account point-wise spatial variations between the model and the experiment. Here, we use two such measures, namely, root mean square error (RMSE) and correlation score (CS) for model evaluation. RMSE and CS are defined as,
| (13) |
| (14) |
Where, NISE is the normalized integral square error, which is defined as,
| (15) |
Variables P and O represent spatially varying simulated (predicted) dataset and experimentally measured (observed) dataset, respectively. CS has a range from 0 to 100. For CS, the validity rating in terms of a qualitative index (such as excellent, unacceptable) is available in the literature [58]. The qualitative index is categorized into five classifications as: Excellent: 86 ≤ CS ≤ 100; Good: 65 ≤ CS <86; Fair: 44 ≤ CS <65; Marginal: 26 ≤ CS < 44; Unacceptable: 0 ≤ CS <26.
3. Results and Discussion
3.1 Validation of model against human volunteer data
We validate the computational head model against full-field brain deformations [59,60,37] obtained in a human volunteer [38]. The experiments were performed with spatial and temporal resolutions of 8 mm and 18 ms, respectively, to obtain spatial displacements [38]. This information was used to calculate shear strains throughout the head. Shear strains from the simulation were then compared with the experimentally obtained shear strains. Even though simulations were run with a much finer resolution of 2 mm3, simulation results were coarsened to match the experimentally tagged-MRI resolution of 8 mm3. In this way, comparisons are made at the same length scale. The qualitative comparison of radial-circumferential shear strain (Ert) is shown in Fig. 4. From Fig. 4, it is evident that the computational model is able to capture the overall dynamics and the magnitudes of the experimentally observed shear strain fields in the human brain. The agreement between the experiment and simulation is less definitive at t = 63 ms, likely due to the fact that viscoelastic time constants that are used in this work are not comprehensive. In both experiments and simulations, a shear wave starts to propagate from the outer boundary towards the inside. Peak shear occurs at 45 ms and, as time proceeds, shearing in other directions (sign change) starts due to the reflection of waves from the center. Note that, entire wave propagation dynamics plays out in 100 ms, thus the shear wave propagation within the brain has a timescale of ~100 ms.
Figure 4.
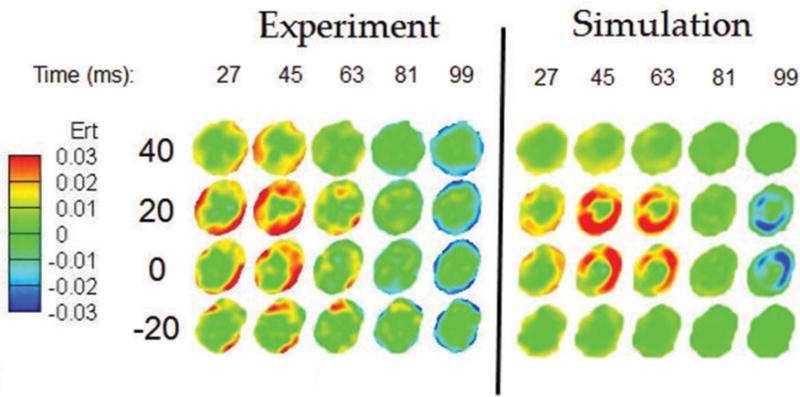
Qualitative comparison of radial-circumferential shear strain (Ert) between the experiment and the simulation. Simulation results are based on baseline bulk modulus value on the order of 109 Pa.
More robust quantitative comparisons in terms of peak radial-circumferential shear strain (Ert) and correlation score are shown in Table 3 and 4, respectively, and quantitative comparison in terms of area fraction distribution of shear strain is shown in Fig. 5. The comparison between experiment and simulation is reasonable using each of these quantitative measures.
Table 3.
Comparison of peak radial-circumferential shear strain (Ert) between the experiment and the simulation. Simulation results are based on baseline bulk modulus value on the order of 109 Pa
| Peak positive shear strain (Ert) | % difference with respect to experimental value | Peak negative shear strain (Ert) | % difference with respect to experimental value | |
|---|---|---|---|---|
| Experiment | 0.060 | – | 0.018 | – |
| Simulation | 0.064 | 6.67 | 0.020 | 11.11 |
Table 4.
Comparison of model performance between the experiment and the simulation using root mean square error (RMSE) and correlation score (CS) measures. Simulation results are based on a baseline bulk modulus value on the order of 109 Pa.
| Radial-circumferential shear strain (Ert) | |||
|---|---|---|---|
| Time | Root mean square error (RMSE) %, Ert | Correlation score (CS), Ert | Performance rating in terms of qualitative Index [58] |
| t = 27 | 0.88 | 86.70 | Excellent |
| t = 45 | 0.83 | 91.20 | Excellent |
| t = 63 | 1.25 | 62.36 | Fair |
| t = 81 | 0.96 | 78.90 | Good |
| t = 99 | 1.03 | 72.55 | Good |
Figure 5.
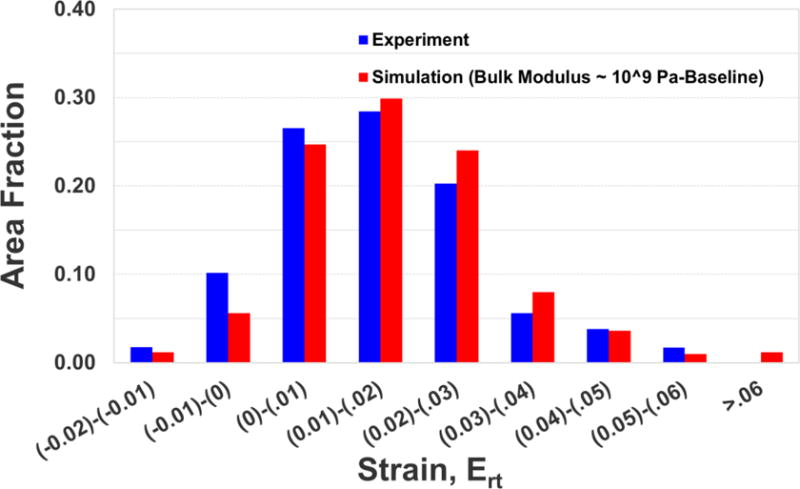
Quantitative comparison in terms of area fraction distribution of radial-circumferential shear strain (Ert) between the experiment and the simulation. A representative result for a midaxial slice (z = 0) at a representative time (t = 45 ms) is shown. This trend extends throughout the head.
3.2. Sensitivity of simulations to bulk modulus
We use quantitative measures described in section 2.3 to study the sensitivity of brain deformations to various values of bulk modulus. Bulk modulus values are changed by orders of magnitude to cover all the values typically used in computational simulations of brain biomechanics. Table 5 tabulates peak radial-circumferential shear strain (Ert) from the simulations as the bulk modulus value is changed with order of differences in the magnitude from 1010 Pa to 106 Pa. Peak radial-circumferential shear strain (Ert) from the experiment is also tabulated. As indicated in the table, bulk modulus on the order of 1010 Pa under-predict the measured magnitude of peak shear strain, whereas bulk modulus on the order of 108 Pa or lower over-predict the measured magnitude of peak shear strain. To quantify the differences in distributions of strains, the area fraction distribution is plotted in Fig. 6, and again it is apparent that the best overall comparison with experiment is obtained with simulations using the GPa bulk modulus. Table 6 tabulates root mean square error (RMSE) and correlation score (CS) along with the qualitative rating for various bulk modulus values. Best model performance is obtained for a bulk modulus value of 109 Pa. These results suggest that a realistic bulk modulus value on the order of GPa is necessary to reproduce the experimentally observed shear deformations in the brain. This is especially important because shear and rotation-related injury modes and the axonal-injury criteria based on strain measures [44,10,12] are now widely accepted.
Table 5.
Sensitivity of model response, based on peak shear strain (Ert) to brain bulk modulus values
| Bulk Modulus | Peak positive strain | % difference with respect to experimental value | Peak negative strain | % difference with respect to experimental value |
|---|---|---|---|---|
| Experiment | 0.060 | – | 0.018 | – |
| 1010 | 0.049 | −18.33 | 0.014 | −22.22 |
| 109 | 0.064 | 6.67 | 0.020 | 11.11 |
| 108 | 0.084 | 40.00 | 0.038 | 111.11 |
| 107 | 0.097 | 61.67 | 0.046 | 155.56 |
| 106 | 0.107 | 78.33 | 0.052 | 188.89 |
Figure 6.
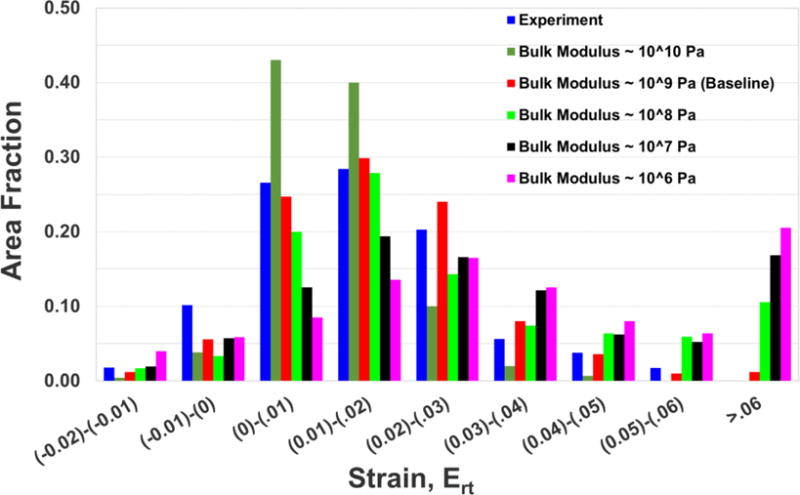
Sensitivity of model response based on area fraction distribution of radial-circumferential shear strain (Ert) to various bulk modulus values. A representative result for a midaxial slice (z = 0) at a representative time (t = 45 ms) is shown. This trend extends throughout the head.
Table 6.
Sensitivity of model response, based on root mean square error (RMSE) and correlation score (CS) measures, to brain bulk modulus values. Representative result at t = 45 ms is shown.
| Radial-circumferential shear strain (Ert) | |||
|---|---|---|---|
| Bulk Modulus | Root mean square error (RMSE) % | Correlation score (CS) | Performance rating in terms of qualitative Index [58] |
| 1010 | 1.40 | 60.82 | Fair |
| 109 | 0.83 | 91.20 | Excellent |
| 108 | 2.1 | 52.73 | Fair |
| 107 | 3.32 | 42.30 | Marginal |
| 106 | 3.97 | 33.54 | Marginal |
3.3 Dynamic brain deformations during injury-causing loading
In the earlier sections, we have focused on studying the sensitivity of brain deformations to values of bulk modulus for mild rotational loading. However, it is also important to understand how bulk modulus values affect the prediction of injury and injured regions. Thus, the head model presented above is further used to simulate injurious loading that resulted in definitive concussion during collegiate football impacts [67]. Figure 7a shows loading pulse for injurious loading [67,63]. Figure 7b shows the shear strain in the brain for injurious loading for a specific 2D slice (z = 0) and for the baseline bulk modulus value on the order of 109. Peak radial-circumferential shear strains on the order of ±30% are seen for this loading. Further, overall wave propagation dynamics is similar to the non-injurious case.
Injured regions within the brain are quantified using axonal strain injury criterion, as recent investigations suggest that axonal strain is the best predictor of mild traumatic brain injuries [44,10,12]. We use white matter axonal strain injury threshold values of 18% and 13% based on the works of Wright and Ramesh [44] and Giordano and Kleiven [10], respectively. Using these thresholds, the white matter regions that would be injured, are shown in Fig. 7c. Notable damage regions include the corpus callosum, corticospinal tract, cingulum, corona radiata, and internal capsule. The injured regions found in this work are consistent with DTI findings in blast TBI patients. Ivanov et al. [68] collected DTI data in Iraq and Afghanistan veterans scanned on an average of 3.7 years after trauma exposure. They found DTI abnormalities in several white matter (WM) regions including the corpus callosum, the corticospinal tract, the internal capsule, and the cingulum. Mac Donald et al. [69–71] collected DTI data in service members deployed to the combat operations in Iraq and Afghanistan. Data was collected in acute/sub-acute stages and during one-year and five-year follow ups. They found DTI abnormalities in several white matter regions including internal and external capsules, longitudinal fasciculus, corpus callosum, and right middle frontal gyrus white matter.
Sensitivity of injury to the value of bulk modulus
Table 7 tabulates total cumulative injury (damage) in the white matter of the brain for various bulk modulus values. Cumulative injury is based on the entire volume of the brain and for the entire simulation time of 100 ms. The total volume of the injured regions increases as the bulk modulus is decreased. As a consequence, many white matter regions indicate damage for bulk modulus values of 108 or smaller. However, clinical evidence [72,73,68,71,74] does not support WM damage over such a large volume and a large number of regions.
Table 7.
Cumulative injury in white matter of a brain for various bulk modulus values
4. Conclusions
Computational models of brain biomechanics hold promise for overall management of TBI, including their use in diagnostics and prevention of injury. However, models have predictive value only if they are able to capture the biomechanics of the brain as both a material and a structure. Even though significant progress has been made in terms of accurately incorporating the morphology and constitutive relationships of the brain, the understanding regarding accurate material parameters is uncertain. One such parameter is a bulk modulus of the brain tissue; bulk modulus values spanning up to three orders of magnitude differences have been used in the computational models. However, their sensitivity to model predictions is not known. In this work, we have studied the sensitivity of brain deformations to bulk modulus values using a subject-specific computational head model. The model incorporated detailed morphology of the brain tissue, including anisotropy of the white matter. The model was validated against sub-injurious brain deformations in a living human volunteer. Simulation results show that a bulk modulus on the order of GPa gave the best agreement with experimental data from tagged MRI. A bulk modulus value of 1010 Pa underestimated magnitudes of peak strains and distribution of area fractions. On the other hand, bulk moduli of 108 Pa and lower overestimated the magnitudes of the peak strains and the distribution of area fractions. Further, based on statistical measures such as RMSE and CS, the simulations with a bulk modulus value of 109 Pa gave the best overall agreement with respect to the experimentally measured deformations. The model was further used to simulate injurious loading that results in a definitive concussion. For the injury simulations, a bulk modulus value on the order of 109 Pa provided the results that are consistent with clinical findings of injury. These results underscore the importance of using accurate bulk modulus values in computational head models.
Acknowledgments
The authors acknowledge funding from the National Institute of Neurological Disorders and Strokes, National Institutes of Health (Project # R01NS055951). The authors also thank Andy Knutsen and Dzung Pham from the Henry Jackson Foundation for sharing tagged-MRI experimental data from Knutsen et al., J. Biomechanics (2014). The numerical technique to circumvent locking in Uintah MPM package (uintah.utah.edu) was implemented by James Guilkey of the University of Utah, and we express our appreciation for his help and that of Rebecca Brannon with Uintah.
Footnotes
Author Disclosure Statement
No competing financial interests exist.
References
- 1.Faul M, Xu L, Wald MM, Coronado V. Traumatic brain injury in the United States. National Center for Injury Prevention and Control, Centers for Disease Control and Prevention; Atlanta, GA: 2010. [Google Scholar]
- 2.Goriely A, Geers MG, Holzapfel GA, Jayamohan J, Jérusalem A, Sivaloganathan S, Squier W, van Dommelen JA, Waters S, Kuhl E. Mechanics of the brain: perspectives, challenges, and opportunities. Biomechanics and modeling in mechanobiology. 2015;14(5):931–965. doi: 10.1007/s10237-015-0662-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Meaney DF, Morrison B, Bass CD. The Mechanics of Traumatic Brain Injury: A Review of What We Know and What We Need to Know for Reducing Its Societal Burden. Journal of biomechanical engineering. 2014;136(2):021008. doi: 10.1115/1.4026364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mao H, Zhang L, Jiang B, Genthikatti VV, Jin X, Zhu F, Makwana R, Gill A, Jandir G, Singh A, Yang KH. Development of a finite element human head model partially validated with thirty five experimental cases. Journal of biomechanical engineering. 2013;135(11):111002. doi: 10.1115/1.4025101. [DOI] [PubMed] [Google Scholar]
- 5.Giordano C, Cloots R, Van Dommelen J, Kleiven S. The influence of anisotropy on brain injury prediction. Journal of biomechanics. 2014;47(5):1052–1059. doi: 10.1016/j.jbiomech.2013.12.036. [DOI] [PubMed] [Google Scholar]
- 6.Ganpule S, Daphalapurkar NP, Ramesh KT, Knutsen AK, Pham DL, Bayly PV, Prince JL. A Three-Dimensional Computational Human Head Model That Captures Live Human Brain Dynamics. Journal of Neurotrauma. 2017;34(13):2154–2166. doi: 10.1089/neu.2016.4744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chatelin S, Constantinesco A, Willinger R. Fifty years of brain tissue mechanical testing: From in vitro to in vivo investigations. Biorheology. 2010;47(5–6):255–276. doi: 10.3233/BIR-2010-0576. [DOI] [PubMed] [Google Scholar]
- 8.Claessens M, Sauren F, Wismans J. Modeling of the human head under impact conditions: a parametric study. SAE Technical Paper. 1997;973338 doi: 10.4271/973338. [DOI] [Google Scholar]
- 9.El Sayed T, Mota A, Fraternali F, Ortiz M. Biomechanics of traumatic brain injury. Computer Methods in Applied Mechanics and Engineering. 2008;197(51–52):4692–4701. doi: 10.1016/j.cma.2008.06.006. [DOI] [Google Scholar]
- 10.Giordano C, Kleiven S. Evaluation of axonal strain as a predictor for mild traumatic brain injuries using finite element modeling. Stapp car crash journal. 2014;58:29. doi: 10.4271/2014-22-0002. [DOI] [PubMed] [Google Scholar]
- 11.Zoghi-Moghadam M, Sadegh AM. Global/local head models to analyse cerebral blood vessel rupture leading to ASDH and SAH. Computer Methods in Biomechanics and Biomedical Engineering. 2009;12(1):1–12. doi: 10.1080/10255840802020420. [DOI] [PubMed] [Google Scholar]
- 12.Ji S, Zhao W, Ford JC, Beckwith JG, Bolander RP, Greenwald RM, Flashman LA, Paulsen KD, McAllister TW. Group-wise evaluation and comparison of white matter fiber strain and maximum principal strain in sports-related concussion. Journal of neurotrauma. 2015;32(7):441–454. doi: 10.1089/neu.2013.3268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Takhounts EG, Ridella SA, Hasija V, Tannous RE, Campbell JQ, Malone D, Danelson K, Stitzel J, Rowson S, Duma S. Investigation of Traumatic Brain Injuries Using the Next Generation of Simulated Injury Monitor (SIMon) Finite Element Head Model. Stapp Car Crash Journal. 2008;52:1–31. doi: 10.4271/2008-22-0001. [DOI] [PubMed] [Google Scholar]
- 14.Takhounts EG, Eppinger RH, Campbell JQ, Tannous RE, Power ED, Shook LS. On the development of the SIMon Finite Element Head Model. Stapp Car Crash Journal. 2003;47:107–133. doi: 10.4271/2003-22-0007. [DOI] [PubMed] [Google Scholar]
- 15.Sahoo D, Deck C, Willinger R. Development and validation of an advanced anisotropic visco-hyperelastic human brain FE model. Journal of the Mechanical Behavior of Biomedical Materials. 2014;33:24–42. doi: 10.1016/j.jmbbm.2013.08.022. [DOI] [PubMed] [Google Scholar]
- 16.Kleiven S, Hardy WN. Correlation of an FE model of the human head with local brain motion: Consequences for injury prediction. Stapp Car Crash Journal. 2002;46:123–144. doi: 10.4271/2002-22-0007. [DOI] [PubMed] [Google Scholar]
- 17.Horgan TJ, Gilchrist MD. Influence of FE model variability in predicting brain motion and intracranial pressure changes in head impact simulations. International Journal of Crashworthiness. 2004;9(4):401–418. doi: 10.1533/ijcr.2004.0299. [DOI] [Google Scholar]
- 18.Zhang L, Yang KH, King AI. A proposed injury threshold for mild traumatic brain injury. Journal of biomechanical engineering. 2004;126(2):226–236. doi: 10.1115/1.1691446. [DOI] [PubMed] [Google Scholar]
- 19.Moore DF, Jerusalem A, Nyein M, Noels L, Jaffee MS, Radovitzky RA. Computational biology - Modeling of primary blast effects on the central nervous system. Neuroimage. 2009;47:T10–T20. doi: 10.1016/j.neuroimage.2009.02.019. [DOI] [PubMed] [Google Scholar]
- 20.Sarvghad-Moghaddam H, Rezaei A, Ziejewski M, Karami G. Evaluation of brain tissue responses because of the underwash overpressure of helmet and faceshield under blast loading. International journal for numerical methods in biomedical engineering. 2017;33(1) doi: 10.1002/cnm.2782. [DOI] [PubMed] [Google Scholar]
- 21.Sarvghad-Moghaddam H, Jazi MS, Rezaei A, Karami G, Ziejewski M. Examination of the protective roles of helmet/faceshield and directionality for human head under blast waves. Computer methods in biomechanics and biomedical engineering. 2015;18(16):1846–1855. doi: 10.1080/10255842.2014.977878. [DOI] [PubMed] [Google Scholar]
- 22.Kraft RH, McKee PJ, Dagro AM, Grafton ST. Combining the Finite Element Method with Structural Connectome-based Analysis for Modeling Neurotrauma: Connectome Neurotrauma Mechanics. PLOS Computational Biology. 2012;8(8):e1002619. doi: 10.1371/journal.pcbi.1002619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Taylor PA, Ford CC. Simulation of Blast-Induced Early-Time Intracranial Wave Physics leading to Traumatic Brain Injury. Journal of Biomechanical Engineering. 2009;131(6):061007. doi: 10.1115/1.3118765. [DOI] [PubMed] [Google Scholar]
- 24.Nahum AM, Smith R, Ward CC. (SAE Technical Paper (Paper No. 770922)).Intracranial pressure dynamics during head impact. 1977 doi: 10.4271/770922. [DOI] [Google Scholar]
- 25.Ruan JS, Khalil T, King AI. Dynamic response of the human head to impact by three-dimensional finite element analysis. Journal of Biomechanical Engineering, Transactions of the ASME. 1994;116(1):44–50. doi: 10.1115/1.2895703. [DOI] [PubMed] [Google Scholar]
- 26.Horgan T, Gilchrist MD. The creation of three-dimensional finite element models for simulating head impact biomechanics. International Journal of Crashworthiness. 2003;8(4):353–366. doi: 10.1533/ijcr.2003.0243. [DOI] [Google Scholar]
- 27.Ganpule S, Alai A, Plougonven E, Chandra N. Mechanics of blast loading on the head models in the study of traumatic brain injury using experimental and computational approaches. Biomechanics and modeling in mechanobiology. 2013;12(3):511–531. doi: 10.1007/s10237-012-0421-8. [DOI] [PubMed] [Google Scholar]
- 28.Nyein MK, Jason AM, Yu L, Pita CM, Joannopoulos JD, Moore DF, Radovitzky RA. In silico investigation of intracranial blast mitigation with relevance to military traumatic brain injury. Proceedings of the National Academy of Sciences. 2010;107(48):20703–20708. doi: 10.1073/pnas.1014786107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chen Y, Ostoja-Starzewski M. MRI-based finite element modeling of head trauma: spherically focusing shear waves. Acta Mechanica. 2010;213(1–2):155–167. doi: 10.1007/s00707-009-0274-0. [DOI] [Google Scholar]
- 30.Chandra N, Sundaramurthy A, Gupta RK. Validation of Laboratory Animal and Surrogate Human Models in Primary Blast Injury Studies. Milit Med. 2017;182 doi: 10.7205/MILMED-D-16-00144. [DOI] [PubMed] [Google Scholar]
- 31.Goldstein LE, Fisher AM, Tagge CA, Zhang XL, Velisek L, Sullivan JA, Upreti C, Kracht JM, Ericsson M, Wojnarowicz MW. Chronic traumatic encephalopathy in blast-exposed military veterans and a blast neurotrauma mouse model. Science translational medicine. 2012;4(134):134ra160–134ra160. doi: 10.1126/scitranslmed.3003716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bayly PV, Clayton EH, Genin GM. Quantitative imaging methods for the development and validation of brain biomechanics models. Annual review of biomedical engineering. 2012;14(369) doi: 10.1146/annurev-bioeng-071811-150032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bayly PV, Cohen TS, Leister EP, Ajo D, Leuthardt EC, Genin GM. Deformation of the human brain induced by mild acceleration. J Neurotrauma. 2005;22(8):845–856. doi: 10.1089/neu.2005.22.845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Saraf H, Ramesh K, Lennon A, Merkle A, Roberts J. Mechanical properties of soft human tissues under dynamic loading. Journal of Biomechanics. 2007;40(9):1960–1967. doi: 10.1016/j.jbiomech.2006.09.021. [DOI] [PubMed] [Google Scholar]
- 35.Feng R, Ramesh K. On the compressibility of elastohydrodynamic lubricants. Journal of tribology. 1993;115(3):557–559. doi: 10.1115/1.2921674. [DOI] [Google Scholar]
- 36.Osman NF, McVeigh ER, Prince JL. Imaging heart motion using harmonic phase MRI. IEEE Trans Med Imaging. 2000;19(3):186–202. doi: 10.1109/42.845177. [DOI] [PubMed] [Google Scholar]
- 37.Bayly P, Cohen T, Leister E, Ajo D, Leuthardt E, Genin G. Deformation of the human brain induced by mild acceleration. Journal of Neurotrauma. 2005;22(8):845–856. doi: 10.1089/neu.2005.22.845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Knutsen AK, Magrath E, McEntee JE, Xing F, Prince JL, Bayly PV, Butman JA, Pham DL. Improved measurement of brain deformation during mild head acceleration using a novel tagged MRI sequence. Journal of biomechanics. 2014;47(14):3475–3481. doi: 10.1016/j.jbiomech.2014.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bazin PL, Pham DL. Homeomorphic brain image segmentation with topological and statistical atlases. Medical image analysis. 2008;12(5):616–625. doi: 10.1016/j.media.2008.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Velardi F, Fraternali F, Angelillo M. Anisotropic constitutive equations and experimental tensile behavior of brain tissue. Biomechanics and modeling in mechanobiology. 2006;5(1):53–61. doi: 10.1007/s10237-005-0007-9. [DOI] [PubMed] [Google Scholar]
- 41.Feng Y, Okamoto RJ, Namani R, Genin GM, Bayly PV. Measurements of mechanical anisotropy in brain tissue and implications for transversely isotropic material models of white matter. Journal of the mechanical behavior of biomedical materials. 2013;23:117–132. doi: 10.1016/j.jmbbm.2013.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Prange MT, Margulies SS. Regional, directional, and age-dependent properties of the brain undergoing large deformation. Journal of Biomechanical Engineering-Transactions of the Asme. 2002;124(2):244–252. doi: 10.1115/1.1449907. [DOI] [PubMed] [Google Scholar]
- 43.Gasser TC, Ogden RW, Holzapfel GA. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. Journal of the royal society interface. 2006;3(6):15–35. doi: 10.1098/rsif.2005.0073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wright RM, Post A, Hoshizaki B, Ramesh KT. A multiscale computational approach to estimating axonal damage under inertial loading of the head. Journal of neurotrauma. 2013;30(2):102–118. doi: 10.1089/neu.2012.2418. [DOI] [PubMed] [Google Scholar]
- 45.Doll S, Schweizerhof K. On the development of volumetric strain energy functions. Journal of applied mechanics. 1999;67(1):17–21. doi: 10.1115/1.321146. [DOI] [Google Scholar]
- 46.Fung Y-c. Biomechanics: Mechanical Properties of Living Tissues. Springer Science & Business Media; 2013. [DOI] [Google Scholar]
- 47.Weiss J, Puso M. Finite Element Implementation of Anisotropic Quasi-linear Viscoelasticty using a Discrete Spectrum Approximation. Journal of Biomech Engng. 1998;120:62–70. doi: 10.1115/1.2834308. [DOI] [PubMed] [Google Scholar]
- 48.Cole RH, Weller R. Underwater explosions. Physics Today. 1948;1:35. doi: 10.1063/1.3066176. [DOI] [Google Scholar]
- 49.Lee S, King M, Sun J, Xie H, Subhash G, Sarntinoranont M. Measurement of viscoelastic properties in multiple anatomical regions of acute rat brain tissue slices. Journal of the mechanical behavior of biomedical materials. 2014;29:213–224. doi: 10.1016/j.jmbbm.2013.08.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.McElhaney JH, Fogle JL, Melvin JW, Haynes RR, Roberts VL, Alem NM. Mechanical properties of cranial bone. Journal of Biomechanics. 1970;3(5):495–511. doi: 10.1016/0021-9290(70)90059-X. [DOI] [PubMed] [Google Scholar]
- 51.McElhaney JH, Melvin JW, Roberts VL, Portnoy HD. Dynamic Characteristics of the Tissues of the Head. In: Kenedi RM, editor. Perspectives in Biomedical Engineering: Proceedings of a Symposium organised in association with the Biological Engineering Society and held in the University of Strathclyde; Glasgow. June 1972; London: Palgrave Macmillan UK; 1973. pp. 215–222. [DOI] [Google Scholar]
- 52.Sulsky D, Zhou SJ, Schreyer HL. Application of a particle-in-cell method to solid mechanics. Computer Physics Communications. 1995;87(1–2):236–252. doi: 10.1016/0010-4655(94)00170-7. [DOI] [Google Scholar]
- 53.Daphalapurkar N, Hanan J, Phelps N, Bale H, Lu H. Tomography and simulation of microstructure evolution of a closed-cell polymer foam in compression. Mechanics of advanced materials and structures. 2008;15(8):594–611. doi: 10.1080/15376490802470523. [DOI] [Google Scholar]
- 54.Sadeghirad A, Brannon RM, Burghardt J. A convected particle domain interpolation technique to extend applicability of the material point method for problems involving massive deformations. International Journal for Numerical Methods in Engineering. 2011;86(12):1435–1456. doi: 10.1002/nme.3110. [DOI] [Google Scholar]
- 55.Ganpule S, Daphalapurkar NP, Ramesh KT. Shear wave propagation in soft materials with application to modeling traumatic brain injury. (Paper B-08-671).Proceedings of 17th US National Congress on Theoretical and Applied Mechanics. 2014 [Google Scholar]
- 56.Kamojjala K, Brannon R, Sadeghirad A, Guilkey J. Verification tests in solid mechanics. Engineering with Computers. 2015;31(2):193–213. doi: 10.1007/s00366-013-0342-x. [DOI] [Google Scholar]
- 57.Mast C, Mackenzie-Helnwein P, Arduino P, Miller G, Shin W. Mitigating kinematic locking in the material point method. Journal of Computational Physics. 2012;231(16):5351–5373. doi: 10.1016/j.jcp.2012.04.032. [DOI] [Google Scholar]
- 58.Kimpara H, Nakahira Y, Iwamoto M, Miki K, Ichihara K, Kawano S, Taguchi T. Investigation of anteroposterior head-neck responses during severe frontal impacts using a brain-spinal cord complex FE model. Stapp Car Crash J. 2006;50:509–544. doi: 10.4271/2006-22-0019. [DOI] [PubMed] [Google Scholar]
- 59.Margulies SS, Thibault LE, Gennarelli TA. Physical model simulations of brain injury in the primate. Journal of biomechanics. 1990;23(8):823–836. doi: 10.1016/0021-9290(90)90029-3. [DOI] [PubMed] [Google Scholar]
- 60.Graham D, Adams JH, Nicoll J, Maxwell W, Gennarelli T. The nature, distribution and causes of traumatic brain injury. Brain Pathology. 1995;5(4):397–406. doi: 10.1111/j.1750-3639.1995.tb00618.x. [DOI] [PubMed] [Google Scholar]
- 61.Brands DD, Bovendeerd PP, Wismans JJ. On the potential importance of non-linear viscoelastic material modelling for numerical prediction of brain tissue response: test and application. Stapp Car Crash Journal. 2002;46(1):103. doi: 10.4271/2002-22-0006. [DOI] [PubMed] [Google Scholar]
- 62.DiMasi FP, Eppinger RH, Bandak FA. Computational analysis of head impact response under car crash loadings. SAE Technical Paper. 1995;952718 doi: 10.4271/952718. [DOI] [Google Scholar]
- 63.Rowson S, Beckwith JG, Chu JJ, Leonard DS, Greenwald RM, Duma SM. A Six Degree of Freedom Head Acceleration Measurement Device for Use in Football. Journal of Applied Biomechanics. 2011;27(1):8–14. doi: 10.1123/jab.27.1.8. [DOI] [PubMed] [Google Scholar]
- 64.Stalnaker RL. PhD dissertation. West Virginia University; 1969. Mechanical Properties of the Head. [Google Scholar]
- 65.Etoh A, Mitaku S, Yamamoto J, Okano K. Ultrasonic absorption anomaly of brain tissue. Japanese journal of applied physics. 1994;33(5S):2874. doi: 10.1143/JJAP.33.2874. [DOI] [Google Scholar]
- 66.Cui S, Li H, Li X, Ruan J. Effects of the Variation in Brain Tissue Mechanical Properties on the Intracranial Response of a 6-Year-Old Child. Computational and Mathematical Methods in Medicine. 2015;10(2015) doi: 10.1155/2015/529729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Rowson S, Duma SM, Beckwith JG, Chu JJ, Greenwald RM, Crisco JJ, Brolinson GP, Duhaime AC, McAllister TW, Maerlender AC. Rotational Head Kinematics in Football Impacts: An Injury Risk Function for Concussion. Annals of Biomedical Engineering. 2012;40(1):1–13. doi: 10.1007/s10439-011-0392-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Ivanov I, Fernandez C, Mitsis EM, Dickstein DL, Wong E, Tang CY, Simantov J, Bang C, Moshier E, Sano M, Elder GA, Hazlett EA. Blast Exposure, White Matter Integrity, and Cognitive Function in Iraq and Afghanistan Combat Veterans. Frontiers in Neurology. 2017;8:127. doi: 10.3389/fneur.2017.00127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Mac Donald CL, Barber J, Andre J, Evans N, Panks C, Sun S, Zalewski K, Sanders RE, Temkin N. 5-Year imaging sequelae of concussive blast injury and relation to early clinical outcome. NeuroImage: Clinical. 2017;14:371–378. doi: 10.1016/j.nicl.2017.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Adam O, Mac Donald CL, Rivet D, Ritter J, May T, Barefield M, Duckworth J, LaBarge D, Asher D, Drinkwine B. Clinical and imaging assessment of acute combat mild traumatic brain injury in Afghanistan. Neurology. 2015;85(3):219–227. doi: 10.1212/WNL.0000000000001758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Mac Donald CL, Johnson AM, Cooper D, Nelson EC, Werner NJ, Shimony JS, Snyder AZ, Raichle ME, Witherow JR, Fang R. Detection of blast-related traumatic brain injury in US military personnel. New England Journal of Medicine. 2011;364(22):2091–2100. doi: 10.1056/NEJMoa1008069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Eierud C, Craddock RC, Fletcher S, Aulakh M, King-Casas B, Kuehl D, LaConte SM. Neuroimaging after mild traumatic brain injury: Review and meta-analysis. NeuroImage: Clinical. 2014;4:283–294. doi: 10.1016/j.nicl.2013.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Herweh C, Hess K, Meyding-Lamadé U, Bartsch AJ, Stippich C, Jost J, Friedmann-Bette B, Heiland S, Bendszus M, Hähnel S. Reduced white matter integrity in amateur boxers. Neuroradiology. 2016:1–10. doi: 10.1007/s00234-016-1705-y. [DOI] [PubMed] [Google Scholar]
- 74.Meier TB, Bergamino M, Bellgowan PS, Teague TK, Ling JM, Jeromin A, Mayer AR. Longitudinal assessment of white matter abnormalities following sports-related concussion. Human Brain Mapping. 2016;37(2):833–845. doi: 10.1002/hbm.23072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.McElhaney J, Melvin JW, Roberts VL, Portnoy HD. Dynamic characteristics of the tissues of the head. Perspectives in Biomedical Engineering. 1973:215–222. doi: 10.1007/978-1-349-01604-4_34. [DOI] [Google Scholar]
- 76.Zhang LY, Yang KH, King AI. Comparison of brain responses between frontal and lateral impacts by finite element modeling. Journal of Neurotrauma. 2004;18(1):21–30. doi: 10.1089/089771501750055749. [DOI] [PubMed] [Google Scholar]


