A two-stage design for phase II trials with time-to-event endpoint using restricted follow-up

Abstract

In phase II oncology trials, the use of new cytostatic drugs raises some questions regarding the endpoint. Time-to-event endpoints such as Progression-Free Survival have been recommended and led to new designs. In 2003, Case and Morgan proposed a design based on the comparison of the cumulative hazards at a clinically relevant timepoint. In 2013, Kwak proposed a design based on the one-sample log-rank test. If all the patients are followed from their entry time to the analysis date, the Kwak and Jung’s design leads to a smaller sample size as compared to the Case-Morgan’s design. However, the Case and Morgan’s design requires less information since it only needs to follow every patient during a fixed interval of time. We propose a trade-off between these two approaches that corresponds to an adaptation of Kwak and Jung’s design when the follow-up is expected to be restricted. Our proposal is based on the one-sample log-rank test as the Kwak and Jung’s design but it uses the same follow-up information as the Case-Morgan’s design. Simulation study shows that our proposal allows reducing the sample size as compared to the Case-Morgan’s design (median difference of 23% [15%-33%]). Type I and type II error rates are close to their nominal rates planned in the protocol. A real phase II clinical trial in cervical cancer illustrated the interest of this new design. Thus, our proposal can be recommended as an alternative to the Kwak’s design when patients’ follow-up is restricted.

1. Introduction

Up to now, Phase II oncology trial designs are mainly relying upon response-based endpoints. However, since the inception of cytostatic therapies, the Progression Free Survival is nowadays strongly recommended for evaluating these new drugs [1]. This problematic has led to the development of new phase II designs that represent new alternatives to the classical phase II response-based design. Several designs have been recently proposed by Sun et al. [2], Case and Morgan [3], Huang et al. [4], Wu [5], Kwak and Jung [6] and Whitehead [7].

In this paper, we focus our research on the two designs developed by Case and Morgan [3](referred to herein as CM), and Kwak and Jung [6], (referred to herein as KJ). Both proposals are single-arm two-stage phase II design and rely on comparing the cumulative hazard function of an experimental treatment to an historical one. Both procedures assume that there is no lost to follow-up patient. The CM design compares the cumulative hazard rates [8] at a clinically meaningful timepoint and requires each patient to be followed until this timepoint unless an event occurs before. The KJ design which relies on the one-sample log-rank test [9], [10], compares the cumulative hazard rate over a defined period. Calculation of the stopping rules for the KJ design is based on an expected number of events which places strong constraints on obtaining an adequate follow-up over a large window of time. The failure to achieve such requirement leads to deviation from the original design.

However, in real practice, follow-up information is easier to obtain during the early period of the trial, due to the tight clinical monitoring, as compared to the late period. When the accrual duration is long, the update of the patient status at the date of analysis may be challenging whereas obtaining the status of each included patients within a restricted window of time is more realistic.

To take into account this practical problem while keeping the core features of the KJ design, we propose a modified KJ design that considers a predefined window of time for which a complete follow-up is expected. This new proposal is called the restricted-Kwak and Jung's design (referred to herein as r-KJ).

In Section 2, we recall the main features of the CM and KJ designs and present our proposed r-KJ design. In Section 3, a simulation study compares the properties of the r-KJ to the CM design. In Section 4, a phase II trial planned at the Institut Curie illustrates the use of r-KJ design. Finally, we discuss our results and give practical advices for using the r-KJ design.

2. Methods

2.1. Notations and background

For each patient $i$, $i=1,\dots n$, let denote $A_i$ the accrual time and $T_i$ the failure time.

We denote $DA$ the calendar time of analysis. Let denote $C_i=DA-A_i$ the administrative censoring time (i.e. the time elapsed between the inclusion date and the date of analysis) and $C_i^{\ast }$ the censoring times that reflects the amount of follow-up information required by the design. We denote $F\left(t\right)$, $G\left(t,DA\right)$ and $G^{\ast }\left(t\right)$ the survival functions of $T_i$, $C_i$ and $C_i^{\ast }$, respectively. The functions $\overline{F}\left(t\right)$, $\overline{G}\left(t,DA\right)$ and ${\overline{G}}^{\ast }\left(t\right)$ denote the corresponding cumulative density functions. Due to censoring mechanisms, we observe the pair of random variables $({\text{X}}_{\text{i}},{\text{δ}}_{\text{i}})$, where $X_i=min\left(T_i,C_{i,}{C}_i^{\ast }\right)$ and ${\text{δ}}_{\text{i }}$ denotes the event indicator taking 1 if an event is observed and 0 otherwise. We assume that the censoring times are independent and non-informative.

The instantaneous hazard function of T is noted $\text{λ}\left(t\right)$ and defined as: $\text{λ}\left(t\right)=-\frac{\partial \text{ln}\left[F\left(t\right)\right]}{\partial t}$ and the cumulative hazard function $\text{Λ}\left(t\right)$ is such as: $\text{Λ}\left(\text{t}\right)=\underset{0}{\overset{\text{t}}{\int }}\text{λ}\left(\text{u}\right)\text{du}$. Let ${\text{N}}_{\text{i}}\left(\text{t},\text{DA}\right)=\text{I}\left\{{\text{X}}_{\text{i}}\le \text{t}\right\}$ and ${\text{Y}}_{\text{i}}\left(\text{t},\text{DA}\right)=\text{I}\left\{{\text{X}}_{\text{i}}\ge \text{t}\right\}$ be the event and at-risk processes, respectively. Here $\text{Λ}\left(t\right)$ is the cumulative hazard function of the experimental therapy, ${\text{Λ}}_0\left(t\right)$ is a pre-specified (null) reference cumulative hazard function and ${\text{Λ}}_1\left(t\right)$ the desired target cumulative hazard function. Here ${\text{Λ}}_0\left(\text{t}\right)$ is the cumulative hazard function of the historical data that can either be the Nelson-Aalen estimate or a model based estimate from previous data (previous study or meta-analyses). In the following, $F_0$ and $F_1$ are the survival functions of the failure times under the null and the alternatives hypotheses.

Let ${\text{DA}}_1$ and ${\text{DA}}_2$ be the date of analysis at first and second stage respectively. We denote ${\text{t}}_{\text{a}}$ the accrual duration for including the total sample size for the two stages.

A two stage design will be defined by the quadruplet $\left(n_1,c_1,n_2,c_2\right)$ where $n_1$ and $n_2$ are the total number of patients included at stage 1 and 2 respectively and $c_1$ and $c_2$ are futility boundaries for the first and the final analyses. If, we assume that the accrual rate is known, we have the following quadruplet $\left(D{A}_1,c_1,t_a,c_2\right)$.

In the following, we briefly recall the main features of CM ad KJ designs.

2.2. Case and Morgan's design

In 2003, Case and Morgan [3] have proposed a two-stage design based on the comparison of the cumulative hazards at a clinically meaningful time point (denoted $x_0$). This design relies upon the test proposed by Lin et al. [8] where the null and alternative hypotheses are:

$$H_0:\text{Λ}\left(x_0\right)\ge {\text{Λ}}_0\left(x_0\right)vs{H}_1:\text{Λ}\left(x_0\right)\le {\text{Λ}}_1\left(x_0\right)$$

For the CM design, each patient is followed for $x_0$ (months). According to our notations, here $C_i^{\ast }=x_0$ for all $i$. The authors have provided an optimal allocation of accrual and follow-up to maintain type I and II error rates with or without suspending inclusion during the interim analysis.

2.3. Kwak and Jung's design

In 2013, Kwak and Jung [6] have proposed a one-sample log-rank test for phase II clinical trials allowing to compare the whole survival curves where the null and alternative hypotheses are:

$$H_0:\text{Λ}\left(t\right)\ge {\text{Λ}}_0\left(t\right)vs{H}_1:\text{Λ}\left(t\right)\le {\text{Λ}}_1\left(t\right)\mathrm{for}t>0.$$

It is worth noting that for the KJ design the null and the alternative hypothesis were expressed in terms of instantaneous hazard, but can obviously be re-expressed in term of cumulative hazard function. Indeed, hazard rate ordering implies stochastic ordering of the cumulative hazard function but not vice-versa. . Kwak and Jung's design compares the whole observed survival curve to an historical survival curve. Thus, it focuses on differences over survival curves rather than on survival probabilities computed at a unique timepoint as in the CM design. Kwak and Jung provided an optimal two-stage design which minimizes the expected sample size if the new drug has low efficacy and meets the requirements for the planned type I and type II error rates.

In the KJ procedure, from the null and alternatives hypotheses, the expected number of event is calculated which leads to a defined period for which we assume a complete follow-up of the patients. According to our notations and for the sake of simplicity, this assumption corresponds to $C_i^{\ast }=+\infty \text{.}$ After design specification data will be censored at the study duration, $C_i^{\ast }=D{A}_2$. If this follow-up is not guaranteed, the performance of the design can be altered.

As explained in the introduction, this practical problem prompted us to develop the restricted KJ design, presented just below, that considers a predefined window of time for which a complete follow-up is expected.

2.4. The proposed method: the restricted Kwak and Jung's design

Following the work of Kwak and Jung, we propose to re-design their strategy in considering a restricted window of monitoring time whose upper boundary corresponds to the clinically meaningful timepoint denoted ${\text{x}}_0$. Thus, the value of ${\text{C}}_{\text{i}}^{\text{*}}$ is fixed to ${\text{x}}_0$. Consequently, the survival function of ${\text{C}}_{\text{i}}^{\text{*}}$ is ${\text{G}}^{\text{*}}\left(\text{t}\right)=\text{I}\left\{{\text{x}}_0\ge \text{t}\right\}$.

Single stage restricted Kwak and Jung's design:

Let $\mathit{W}$ be the counting process of the one-sample logrank test at the calendar time of analysis $DA$,

$$W=\frac{1}{\sqrt{n_{single}}}\sum _{i=1}^{n_{single}}\underset{0}{\overset{\infty }{\int }}\left[d{N}_i\left(t,DA\right)-Y_i\left(t,DA\right)d{\text{Λ}}_0\left(t\right)\right]$$

Under $H_0$, for n large, $W$ is approximately normal with mean 0 and its variance can be consistently estimated by ${\hat{\sigma }}^2=\frac{1}{n_{single}}\sum _{i=1}^{n_{single}}\underset{0}{\overset{\infty }{\int }}{Y}_i\left(t,DA\right)d{\text{Λ}}_0\left(t\right)$. We reject $H_0$ with one-sided type I error rate $\alpha$ if $Z=\frac{W}{{\hat{\sigma }}^2}<z_{1-\alpha /2}$. Here $z_{1-\alpha }$ denotes the $1-\alpha$ -100^th percentile of the standard normal distribution. We calculate the required sample size $n_{single}$ for a specified power under a specific alternative hypothesis ${\text{H}}_1:\text{Λ}\left(\text{t}\right)={\text{Λ}}_1\left(\text{t}\right)$. Under ${\text{H}}_1$ $n_{single}^{-1}\sum _{\text{i}=1}^{\text{n}}{\text{Y}}_{\text{i}}\left(\text{t},\text{DA}\right)$ uniformly converge to ${\text{F}}_1\left(\text{t}\right)\text{G}\left(\text{t},\text{DA}\right)\text{I}\left\{{\text{x}}_0\ge \text{t}\right\}$ [6], [11].

Thus, ${\widehat{\text{σ}}}^2$ converge to

$${\text{σ}}_{\text{0}}^2=\underset{0}{\overset{{\text{x}}_0}{\int }}{\text{F}}_1\left(\text{t}\right)\text{G}\left(\text{t},\text{DA}\right){\text{dΛ}}_0\left(\text{t}\right)$$

From expression of $\text{W}$ introduced by Jung [12], under ${\text{H}}_1$, we state that $\text{W}$ is approximately Gaussian with mean $\sqrt{{\text{n}}_{\text{single}}}\text{ω}$,

$$\sqrt{{\text{n}}_{\text{single}}}\text{ω}=\sqrt{{\text{n}}_{\text{single}}}\underset{0}{\overset{{\text{x}}_0}{\int }}{\text{F}}_1\left(\text{t}\right)\text{G}\left(\text{t},\text{DA}\right)\left({\text{dΛ}}_1\left(\text{t}\right)-{\text{dΛ}}_0\left(\text{t}\right)\right)\text{.}$$

Kwak and Jung assume that ${\text{Λ}}_1\left(\text{t}\right)$ and ${\text{Λ}}_0\left(\text{t}\right)$ are close and considered that under ${\text{H}}_1$, the variance of $\text{W}$ can be approached by:

$${\text{σ}}_1^2=\underset{0}{\overset{{\text{x}}_0}{\int }}\text{G}\left(\text{t},\text{DA}\right)\breve{\text{F}}\left(\text{t}\right)\text{d}\breve{\text{Λ}}\left(\text{t}\right)\text{,}$$

where $\breve{\text{Λ}}\left(\text{t}\right)=\frac{{\text{Λ}}_0\left(\text{t}\right)+{\text{Λ}}_1\left(\text{t}\right)}{2}$ and $\breve{\text{F}}\left(\text{t}\right)=\text{exp}\left(-\breve{\text{Λ}}\left(\text{t}\right)\right)$. $\check{F\left(t\right)}$ is the survival function corresponding to the “averaged” hazard function $\check{\lambda }\left(t\right)=\frac{{\lambda }_0\left(t\right)+{\lambda }_1\left(t\right)}{2}$. Indeed, to calculate a sample size, Kwak and Jung [6] have considered an “averaged” alternative hypothesis for computing variances.

Thus, the power function is defined by $1-\beta =P\left(\frac{W}{\hat{\sigma }}<-z_{1-\alpha }|H_1\right)=P\left(\frac{W-\sqrt{n}\omega }{{\sigma }_1}<\frac{-{\sigma }_0{z}_{1-\alpha }-\sqrt{n}\omega }{{\sigma }_1}\right)$.

By solving this equation, we obtain

$$n_{single}=\frac{{\left({\sigma }_0{z}_{1-\alpha }+{\sigma }_1{z}_{1-\beta }\right)}^2}{{\omega }^2}\text{.}$$

2.4.1. Two-stage restricted Kwak and Jung's design

Let $W_1$ and $W_2$ be the two counting processes of the one-sample logrank test for the two stages at the respective calendar time of analysis $D{A}_1$ and $D{A}_2$ such as:

$$\begin{gathered} W_1=\frac{1}{\sqrt{n_1}}\sum _{i=1}^{n_1}\underset{0}{\overset{\infty }{\int }}\left[d{N}_i\left(t,D{A}_1\right)-Y_i\left(t,D{A}_1\right)d{\text{Λ}}_0\left(t\right)\right] \\ \mathrm{and} \\ {W}_2=\frac{1}{\sqrt{n_2}}\sum _{i=1}^{n_2}\underset{0}{\overset{\infty }{\int }}\left[d{N}_i\left(t,D{A}_2\right)-Y_i\left(t,D{A}_2\right)d{\text{Λ}}_0\left(t\right)\right]\text{.} \end{gathered}$$

For large $n_1$ and $n_2$, the joint distribution of $\left(W_1,W_2\right)$ under $H_0$ is approximately a bivariate normal with mean vector zero and approximated variance covariance matrix such as [13]:

$$\begin{gathered} {\hat{\sigma }}_{01}^2=\frac{1}{n_1}\sum _{i=1}^{n_1}\underset{0}{\overset{\infty }{\int }}{Y}_i\left(t,D{A}_1\right)d{\text{Λ}}_0\left(t\right) \\ \mathrm{and} \\ {\hat{\sigma }}_{02}^2=\frac{1}{n_2}\sum _{i=1}^{n_2}\underset{0}{\overset{\infty }{\int }}{Y}_i\left(t,D{A}_2\right)d{\text{Λ}}_0\left(t\right),\text{and}cov\left(W_1,W_2\right)={\hat{\sigma }}_{01}^2 \end{gathered}$$

The correlation coefficient between $W_1$ and $W_2$ is such as $\hat{\rho }=\frac{{\hat{\sigma }}_{01}}{{\hat{\sigma }}_{02}}$ .

Algorithm to build the r-KJ design, type I error rate function and power function are similar to the KJ design [6]. Limits of ${\hat{\sigma }}_{01}^2$ and ${\hat{\sigma }}_{02}^2$ and the distribution of $W_1$ and $W_2$ under the null and the alternative hypotheses are adapted as presented below.

Under $H_1$ $n^{-1}\sum _{i=1}^n{Y}_i\left(t,DA\right)$ uniformly converges to $P\left(\left\{X\ge t\right\}|H_1\right)=F_1\left(t\right)G\left(t,DA\right)I\left\{x_0\ge t\right\}$.

Then, the limits of ${\hat{\sigma }}_{01}^2$ and ${\hat{\sigma }}_{02}^2$ and the distributions of $W_1$ and $W_2$ under the null and the alternative hypotheses can be derived.

Under $H_0$, $E_{H_0}\left(W_1\right)=E_{H_0}\left(W_2\right)=0$ and ${\hat{\sigma }}_{01}^2$ and ${\hat{\sigma }}_{02}^2$ respectively converge to

$v_1=-\underset{0}{\overset{x_0}{\int }}G\left(t,D{A}_1\right)d{F}_0\left(t\right)$ and $v_2=-\underset{0}{\overset{x_0}{\int }}G\left(t,D{A}_2\right)d{F}_0\left(t\right)\text{.}$

So, $corr\left(W_1,W_2\right)$ is given by ${\rho }_0=\sqrt{v_1/v_2}$.

Under $H_1$, we have $E_{H_1}\left(W_1\right)=\sqrt{n_1}{\omega }_1$ and $E_{H_1}\left(W_2\right)=\sqrt{n}{\omega }_2$ with

${\omega }_1=\underset{0}{\overset{x_0}{\int }}G\left(t,D{A}_1\right)F_1\left(t\right)d\left\{{\text{Λ}}_1\left(t\right)-{\text{Λ}}_0\left(t\right)\right\}$ and ${\omega }_2=\underset{0}{\overset{x_0}{\int }}G\left(t,D{A}_2\right)F_1\left(t\right)d\left\{{\text{Λ}}_1\left(t\right)-{\text{Λ}}_0\left(t\right)\right\}$.

Under $H_1$, ${\hat{\sigma }}_{01}^2$ and ${\hat{\sigma }}_{02}^2$ respectively converge to

${\sigma }_{01}^2=\underset{0}{\overset{x_0}{\int }}G\left(t,D{A}_1\right)F_1\left(t\right){\text{dΛ}}_0\left(t\right)$ and ${\sigma }_{02}^2=\underset{0}{\overset{x_0}{\int }}G\left(t,D{A}_2\right)F_1\left(t\right){\text{dΛ}}_0\left(t\right)$.

Moreover, the variances of $W_1$ and $W_2$ are respectively approximated by

$${\sigma }_{11}^2=\underset{0}{\overset{x_0}{\int }}G\left(t,D{A}_1\right)\check{F\left(t\right)}\text{d}\check{\text{Λ}}\left(t\right)$$

and

$${\sigma }_{12}^2=\underset{0}{\overset{x_0}{\int }}G\left(t,D{A}_2\right)\check{F\left(t\right)}\text{d}\check{\text{Λ}}\left(t\right)\text{.}$$

Finally, $corr\left(W_1,W_2\right)$ is given by ${\rho }_1={\sigma }_{11}/{\sigma }_{12}$.

2.4.2. Practical rules and sample size calculation

Here, we give the practical rules for designing a r-KJ design. From the specified values $\left({\text{Λ}}_0\left(t\right),{\text{Λ}}_1\left(t\right),\alpha ,\beta ,x_0,rate\right)$ where $rate$ denoted the inclusion rate, we can establish a restricted Kwak and Jung's design with quadruplet $\left(n_1,c_1,n_2,c_2\right)$. Using the inclusion rate, calendar times and accrual duration $t_a$ could then be derived by $t_a=\frac{n_2}{rate};D{A}_1=\frac{n_1}{rate}$ and $D{A}_2=t_a+x_0$ and the restricted Kwak and Jung's design takes place as follows:

2.4.2.1. At stage 1

At $D{A}_1$, each patient is followed until an event occurred before $x_0$. A patient who is free of event before $x_0$ is followed until $D{A}_1$ or censored at $x_0$ depending whose time is the smallest. At $D{A}_1\text{,}$ $X_i$ is the minimum between $T_i$, $x_0$ and $D{A}_1-A_i$. The test statistic $Z_1=\raisebox{1ex}{$W_1$}\!\left/ \!\raisebox{-1ex}{${\hat{\sigma }}_{01}$}\right.$ is calculated and compared to the stopping boundary $c_1$. If $Z_1>c_1$, then trial is stopped for futility. Otherwise, inclusions continue until $n_2$ patients are included.

2.4.2.2. At stage 2

At $D{A}_2$, each patient is followed until an event occurred before $x_0$ or being censored at $x_0$. Then the test statistic $Z_2=\raisebox{1ex}{$W_2$}\!\left/ \!\raisebox{-1ex}{${\hat{\sigma }}_{02}$}\right.$ is calculated and compared to the stopping boundary $c_2$. If $Z_2>c_2$, we conclude to the inefficacy of treatment. If $Z_2\le c_2$ we conclude that the treatment is promising.

Stage 2 conclusion can also be reached by calculating the p-value in order to take into account the observed correlation between $Z_1$ and $Z_2$. Computation of the p-value is the same as the Kwak and Jung's design:

$$p-value=P\left(Z_1\le c_1\cap Z_2\le z\right)=\underset{-\infty }{\overset{z}{\int }}\varphi \left(u\right)\text{Φ}\left(\frac{c_1-\hat{\rho }u}{\sqrt{1-{\hat{\rho }}^2}}\right)du$$

where $\left(Z_1,Z_2\right)$ is bivariate Gaussian vector with means 0, variance of 1 and correlation coefficient $\hat{\rho }$ equals to $\raisebox{1ex}{${\hat{\sigma }}_{01}$}\!\left/ \!\raisebox{-1ex}{${\hat{\sigma }}_{02}$}\right.$ and $z$ is the observed value of $Z_2\text{.}$

2.4.3. Sample size calculation and futility boundaries determination

An iterative algorithm has been implemented to determined $\left(n_1,c_1,n_2,c_2\right)$.

• Step 1: From $\left({\text{Λ}}_0\left(t\right),{\text{Λ}}_1\left(t\right),\alpha ,\beta ,x_0,rate\right)$, determine the sample size for single stage r-KJ design.

• Step 2: Initiate the algorithm with $n_1=n_2=n_{single}$ , and $c_1=0.25$. Various value of $\left(n_1,c_1,n_2\right)$ will be tested until reaching convergence of the value.

• Step 3: Find $c_2$ satisfying:

$$\alpha =\underset{-\infty }{\overset{c_2}{\int }}\varphi \left(z\right)\text{Φ}\left(\frac{c_1-{\rho }_{0}z}{\sqrt{1-{\rho }_0^2}}\right)dz$$

• Step 4: Calculate the power of the design $\left(n_1,c_1,n_2,c_2\right)$ using the following expression:

$$power=\underset{-\infty }{\overset{\overline{c_2}}{\int }}\varphi \left(z\right)\text{Φ}\left(\frac{\overline{c_1}-{\rho }_{1}z}{\sqrt{1-{\rho }_1^2}}\right)dz$$

with $\overline{c_1}=\frac{{\sigma }_{01}}{{\sigma }_{11}}\left(c_1-\frac{{\omega }_1\sqrt{n_1}}{{\sigma }_{01}}\right)$ and $\overline{c_2}=\frac{{\sigma }_{02}}{{\sigma }_{12}}\left(c_2-\frac{{\omega }_2\sqrt{n_2}}{{\sigma }_{02}}\right)$.

• Step 5: If power is less than $1-\beta$, then $\left(n_1,c_1,n_2,c_2\right)$ is left and a new triplet $\left(n_1,c_1,n_2\right)$ is tested by repeating step 3 to 5. Otherwise, $\left(n_1,c_1,n_2,c_2\right)$ is selected.

For each selected candidate, the probability of early termination (PET) and the number of included patient under $H_0$ is calculated. The r-KJ design is those which minimize $\text{E}\left(\text{n}|{\text{H}}_0\right)={\text{n}}_1+(1-\text{PET})\left({\text{n}}_2-{\text{n}}_1\right)$.

2.4.4. Sample size under uniform accrual and exponential survival assumptions

For sample size calculation, we assume that the failure time distribution is exponential with hazard rate ${\lambda }_0$ under $H_0$ and ${\lambda }_1$ under $H_1$. Hazard ratio is given by: $HR=\raisebox{1ex}{${\lambda }_0$}\!\left/ \!\raisebox{-1ex}{${\lambda }_1$}\right.$. Accrual is supposed to be uniform between 0 and $t_a$ and censoring is fixed at $x_0$.

Under these assumptions, we have derived the expressions of $v_1,v_2,{\sigma }_{11}^2,{\sigma }_{12}^2,{\sigma }_{01}^2,{\sigma }_{02}^2,{\omega }_1$ and ${\omega }_2$ in Appendix A.

The above procedure has been implemented in R and the function to implement the r-KJ design is available in Supplementary Material.

2.5. Simulation protocol

Here, we compared our restricted Kwak and Jung design to the CM design since both designs use the same follow-up information. The comparison with the original KJ design would be irrelevant since for a fixed sample size it would require, for each patient except the last included patient, a longer period of follow-up.

To assess the performance of our procedure, we conducted a simulation study where the scenarios explored the impact of the following parameters: $F_0\left(\text{t}\right),HR,\text{ α},\text{β},x_0,rate$.

The historical distribution of survival times was an exponential distribution with rate ${\lambda }_0$, that was computed for obtaining survival rates at $x_0$ of $\left\{70\%,50\%,35\%,15\%\right\}$, the hazard ratio $\left(HR\right)$ of $\left\{2,1.75,1.5\right\}$, the type I error rate $\left(\alpha \right)$ of $\left\{0.05,0.1\right\}$, the type II error rate $\left(\beta \right)$ of $\left\{0.05,0.1\right\}$, an accrual rate $\left(rate\right)$ of $\left\{15,30,50\right\}$ and a timepoint of $x_0$ fixed at 1.

For each of the 144 configurations, sample size and stopping boundaries at each stage were determined based on the Case and Morgan design and the restricted Kwak and Jung's design using the parameters $F_0\left(\text{t}\right),HR,\text{α},\text{β},x_0,rate\text{.}$

For each patient of each simulated trials, accrual time $A_i$ and failure time $T_i$ were generated independently. As required by these design, censoring time for each patient was fixed to $x_0$. Failure times were generated from an exponential distribution and accrual times from an uniform distribution. For each configuration, 10,000 trials were simulated.

The r-KJ designs were compared to CM designs by several criteria: the sample size required by each design, the probability of early termination (denoted $PET$), the stopping probability for efficacy. This last criterion under the null and the alternative hypotheses corresponded respectively to the type I and type II error rates of the design. We also considered the final number of subjects required under the null or the alternative hypotheses (it is denoted $n$ and it corresponds to $n_1$ if the trial stops early and to $n_2$ if the trial goes to the second stage).

3. Results

The CM design required to include more patients than the r-KJ design (see Table 1): the median difference between the sample sizes of the two designs was of 23% (15%–33%) on the 144 studied configurations.

Table 1.

Case and Morgan's designs and restricted Kwak and Jung's designs.

$x_0=1,HR=2$
$F_0\left(x_0\right)$	$\alpha$	1-$\beta$	$rate$	Restricted Kwak and Jung							Case and Morgan
				$n_{single}$	$n_1$	$c_1$	$n_2$	$c_2$	$E\left(n|H_0\right)$	$PET$	$n_1$	$c_1$	$n_2$	$c_2$	$E\left(n|H_0\right)$	$PET$
0.5	0.05	0.9	15	51	33	−0.06	53	−1.63	42.33	0.52	35	0.29	71	1.64	48.72	0.61
0.5	0.05	0.95	15	62	42	−0.07	65	−1.63	52.56	0.53	44	0.28	88	1.64	60.92	0.61
0.5	0.05	0.9	30	51	35	0.08	53	−1.62	44.59	0.47	43	0.04	67	1.64	54.41	0.52
0.5	0.05	0.95	30	62	44	0.06	65	−1.63	54.76	0.48	51	0.11	85	1.64	66.44	0.54
0.5	0.05	0.9	50	51	38	0.42	52	−1.63	46.97	0.34	55	−0.90	62	1.64	60.63	0.18
0.5	0.05	0.95	50	62	48	0.28	64	−1.63	57.49	0.39	62	−0.28	81	1.64	73.37	0.39
0.35	0.05	0.9	15	36	24	0.00	37	−1.63	30.44	0.50	28	0.18	50	1.64	37.07	0.57
0.35	0.05	0.95	15	44	30	−0.03	46	−1.63	37.56	0.51	34	0.22	63	1.64	45.89	0.59
0.35	0.05	0.9	30	36	27	0.21	37	−1.63	32.54	0.42	36	−0.25	47	1.64	42.51	0.40
0.35	0.05	0.95	30	44	33	0.21	45	−1.63	39.70	0.41	42	−0.09	60	1.64	51.39	0.46
0.35	0.05	0.9	50	36	26	0.61	37	−1.63	33.98	0.27	a	a	a	a	a	a
0.35	0.05	0.95	50	44	34	0.54	45	−1.63	41.64	0.30	53	−1.07	57	1.64	56.36	0.14

$\alpha$: type I error rate and 1-$\beta$: power. $PET$: Probability of early termination and $\text{E}\left(\text{n}|{\text{H}}_0\right)={\text{n}}_1+(1-\text{PET})\left({\text{n}}_2-{\text{n}}_1\right)$.

^aNo Case and Morgan‘s design could be found because with this accrual rate each selected design allow to include every patients before the interim analysis.

The mean number of patients included under $H_0$ was higher with the CM design than with the restricted r-KJ design. The median difference was of 17%, but it ranged from 2% to 34% depending of the configuration.

Probability of early stopping was similar for the two designs. In our 144 configurations, there was no difference of probability of early termination in medians. That is to say, there was an equal proportion of discrepancy in favor of one of the two designs.

Type I and type II error rate were respected in most configurations. Nevertheless, simulation study showed that Case and Morgan's design was conservative and over-powered. Although deviations of type I and type II error rates were small, they were statistically significant. (see Table 2). Simulations show that the r-KJ design was also conservative and over-powered although deviations from nominal type I and type II error rate are smaller than performance obtained with CM design. These results are similar with the other configurations (data not shown) although the over-power of the r-KJ design decreased when sample size increased.

Table 2.

Stopping probabilities for efficacy and its 95% confidence interval under the null and the alternative hypotheses of the Case and Morgan's design and the Kwak and Jung's design.

$F_0\left(x_0\right)$	$\alpha$	1-$\beta$	$rate$	Restricted Kwak and Jung				Case and Morgan
				Single stage design		Two-stage design
				$H_0$	$H_1$	$H_0$	$H_1$	$H_0$	$H_1$
0.5	0.05	0.9	15	0.047 [0.043; 0.051]	0.917 [0.911; 0.922]	0.039 [0.035; 0.043]	0.917 [0.911; 0.922]	0.043 [0.039; 0.047]	0.958 [0.954; 0.962]
0.5	0.05	0.95	15	0.042 [0.038; 0.046]	0.953 [0.948; 0.957]	0.040 [0.036; 0.044]	0.959 [0.955; 0.963]	0.051 [0.047; 0.056]	0.985 [0.983; 0.987]
0.5	0.05	0.9	30	0.041 [0.037; 0.045]	0.912 [0.906; 0.918]	0.043 [0.039; 0.047]	0.919 [0.914; 0.924]	0.043 [0.039; 0.047]	0.954 [0.950; 0.958]
0.5	0.05	0.95	30	0.043 [0.039; 0.047]	0.954 [0.950; 0.958]	0.041 [0.037; 0.045]	0.964 [0.960; 0.967]	0.042 [0.038; 0.046]	0.983 [0.980; 0.985]
0.5	0.05	0.9	50	0.040 [0.037; 0.044]	0.915 [0.909; 0.920]	0.040 [0.036; 0.044]	0.921 [0.915; 0.926]	0.049 [0.045; 0.053]	0.959 [0.955; 0.963]
0.5	0.05	0.95	50	0.042 [0.038; 0.046]	0.953 [0.948; 0.957]	0.044 [0.040; 0.048]	0.963 [0.959; 0.967]	0.035 [0.031; 0.038]	0.980 [0.977; 0.983]
0.35	0.05	0.9	15	0.043 [0.039; 0.047]	0.904 [0.898; 0.909]	0.041 [0.037; 0.045]	0.900 [0.894; 0.906]	0.038 [0.034; 0.041]	0.946 [0.941; 0.950]
0.35	0.05	0.95	15	0.041 [0.037; 0.045]	0.947 [0.942; 0.951]	0.040 [0.036; 0.044]	0.949 [0.944; 0.95]	0.043 [0.039; 0.047]	0.977 [0.974; 0.980]
0.35	0.05	0.9	30	0.045 [0.041; 0.050]	0.898 [0.891; 0.903]	0.043 [0.039; 0.047]	0.899 [0.892; 0.90]	0.061 [0.056; 0.066]	0.960 [0.956; 0.964]
0.35	0.05	0.95	30	0.043 [0.039; 0.047]	0.948 [0.943; 0.952]	0.040 [0.036; 0.044]	0.950 [0.945; 0.954]	0.038 [0.034; 0.042]	0.976 [0.973; 0.979]
0.35	0.05	0.9	50	0.038 [0.034; 0.042]	0.903 [0.897; 0.908]	0.038 [0.034; 0.042]	0.901 [0.894; 0.906]	a	a
0.35	0.05	0.95	50	0.044 [0.040; 0.048]	0.946 [0.941; 0.950]	0.036 [0.032; 0.040]	0.947 [0.942; 0.951]	0.061 [0.056; 0.066]	0.985 [0.982; 0.987]

^aNo CM design could be found because with this accrual rate each selected design allow to include every patients before the interim analysis.

The r-KJ design allowed including less patients as compared to the CM design. In our 144 configurations, the number of included patients to conclude to the null hypothesis was 18% (4%–34%) less than with the CM design (see Table 3). Under the alternative hypothesis, the median relative difference was 22% (15–33). Whatever the investigated configuration, the r-KJ design allowed to include less patients as compared to the CM design. The minimum was of 4% (see Table 3).

Table 3.

Comparison of Case and Morgan's design and two-stage restricted Kwak and Jung's design regarding the number of included patient at the end of the trial under the null and the alternative hypothesis.

$x_0=1,HR=2$
$F_0\left(x_0\right)$	$\alpha$	1-$\beta$	$rate$	$\frac{n_{CM}-n_{r-KJ}}{n_{CM}}|H_0$	$\frac{n_{CM}-n_{r-KJ}}{n_{CM}}|H_1$
0.5	0.05	0.9	15	0.155	0.249
0.5	0.05	0.95	15	0.158	0.260
0.5	0.05	0.9	30	0.202	0.209
0.5	0.05	0.95	30	0.185	0.234
0.5	0.05	0.9	50	0.222	0.164
0.5	0.05	0.95	50	0.222	0.210
0.35	0.05	0.9	15	0.214	0.257
0.35	0.05	0.95	15	0.205	0.268
0.35	0.05	0.9	30	0.242	0.214
0.35	0.05	0.95	30	0.241	0.250
0.35	0.05	0.9	50	a	a
0.35	0.05	0.95	50	0.263	0.212

^aNo CM design could be found because with this accrual rate each selected design allow to include every patients before the interim analysis.

3.1. Real clinical example

The trial presented in this work was an open phase II randomized non comparative trial, conducted at the Institut Curie, which included patients with IB2 to III stage of cervix cancer. This trial aimed to evaluate the efficacy of the association of a targeted therapy with a standard radio-chemotherapy (Cisplatine plus pelvic irradiation). The primary endpoint was the disease-free survival (DFS) at 24 months. The trial was planned in 2007. The first patient was included in 2008 and results were published in 2015 [14]. The two treatment arms were planned with the same hypotheses. The original design was a one-stage Fleming design and DFS rates were analyzed as a binary endpoint. They planned the trial with an historical DFS rate at 24 months of 50% and they expected to have a DFS rate at 24 months of 75% with the new treatment with an expected inclusion rate of 2 patients by month.

Here, we suppose that we would like to design a r-KJ trial with the same assumptions and a type I error rate of 7% and a power of 94.5%. Under an exponential distribution, these values correspond to an hazard ratio of $2.409$. For a two-stage r-KJ design, we need to include 28 patients at the first stage and 38 patients at the second stage. Analyses have to be performed at 14 and 43 (19 + 24) months after the first inclusion for the first and the second stage respectively. One-sample log-rank test statistics have to be compared to the stopping boundary $c_1$ and $c_2$ which were fixed to 0.77 and −1.46 respectively. Each patient has to be followed 24 months. Here, we assume no loss to follow-up and the follow-up information is restricted to the first 24 months for every patient.

It is worth noting that the CM design could not be planned here because the clinical timepoint is too late compared to the duration accrual. The CM design requires that the interim analysis being performed when at least one patient has reached the minimum follow-up (here 24 months). At 24 months, every patient would be included; no CM designs could be found satisfying all constraints of the design. An optimal Kwak and Jung design could have been planned but this design would have required that every patient being followed 24 months after the last inclusion which seemed unrealistic. In this practical case, a restricted Kwak and Jung's design is a good option since it uses realistic follow-up information.

3.1.1. Trial results

In total, 78 patients were included in the trial. 40 patients were randomized in the experimental arm and 38 patients were randomized in the standard arm. Among the 40 patients randomized in the experimental arm, two patients withdrew their consent few days after inclusion. Thus, 38 patients by arm are analyzed (see Table 4).

Table 4.

Conclusions of the trial.

		Restricted Kwak and Jung
		N	Test statistics	Stopping boundary	Decision
Stage 1	Experimental arm	21	1.51	0.77	→Stop inclusion
	Standard arm	20	−1.13	0.77	→Proceed to stage 2
Stage 2	Experimental Arm
	Standard arm	38	−2.75	−1.46	→Reject ${\text{H}}_0$

According to the boundaries computed above, the first analysis would take place at 14 months after the first inclusion: no patient has reached 24 months of follow-up. At the first stage, the test statistics of experimental and standard arm would be equals to 1.51 and −1.13 respectively. In experimental arm, test statistic would be higher than the stopping boundary $c_1$: the null hypothesis would not be rejected and inclusion would be stopped. To the contrary, in the standard arm the null hypothesis would be rejected leading to move forward to the second stage. At second stage, in the standard arm, test statistic would be −2.75 and would be less than $c_2$. The null hypothesis would have been rejected.

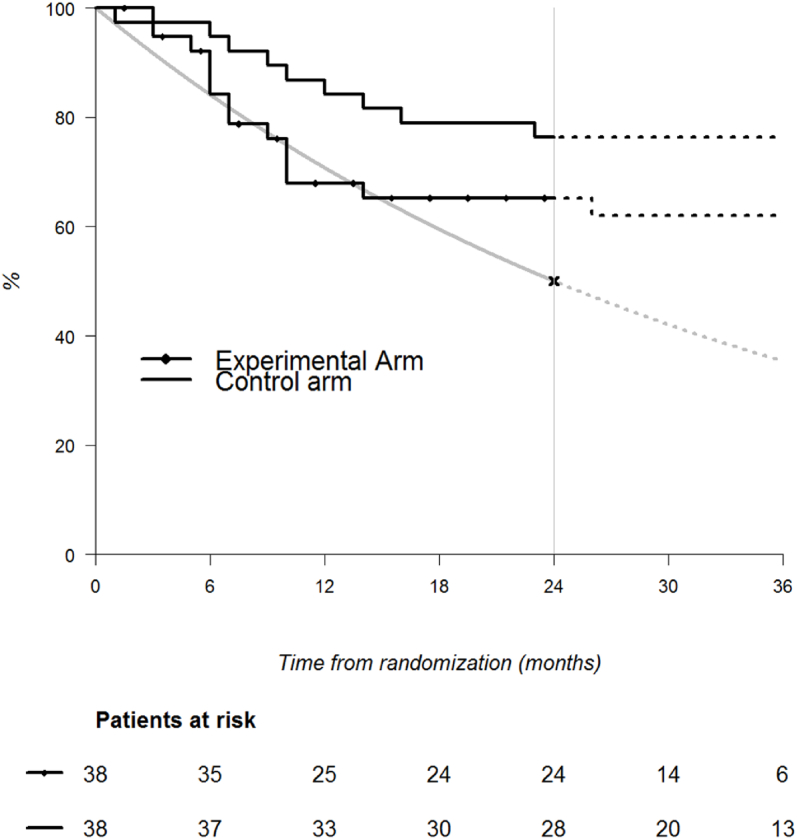
It is worth noting that the stopping rules and sample sizes were computed under historical rates that could be seriously questioned (see Fig. 1). Fig. 1 shows that disease-free survival of patients randomized in the experimental arm (green curve) is compatible to the null hypothesis (represented by the red curve) at least until 18 months of follow-up. The disease-free survival of patient randomized in the standard arm (blue curve) is higher than the null hypothesis (as the statistical rules suggest). The restricted Kwak and Jung's design allows coherence between statistical rules and graphical representation which is very important when communicating the results.

Fig. 1.

Disease-free survival (DFS) of 76 patients included in the trial. Grey curve is the historical DFS modeled by an exponential survival with a median DFS at 24 months.

4. Discussion

In recent years, new sequential designs for phase II trial with time-to-event endpoint have been proposed such as the Case-Morgan and Kwak-Jung designs. The KJ design focuses on the survival distributions whereas the CM considers only survival probabilities at a particular timepoint. However, the KJ design assumes that the investigator is able to provide complete follow-up for all enrolled patients which may be challenging in many cases.

In this article, we present the restricted KJ design which is a new two-stage design for phase II trials with time-to-event endpoint restricted to a predefined window of time over which we expect an adequate follow-up. We provide the general formulas for computing the stopping boundaries and sample sizes for pre-specified null and hypotheses and error rates.

From the simulations, we show that for a wide variety of configuration the r-KJ design is better than the CM design as it requires fewer patients for the same follow-up information. Both designs use the same window of time but the first one compares the entire survival curves whereas the second is limited to a punctual comparison. With equivalent follow-up information, the r-KJ design shows better operating characteristics than the Case and Morgan's design.

Simulations results show that the r-KJ design is conservative but power gains are nevertheless preserved. The conservativeness and under-power of the one-sample log-rank test have already been documented by Wu [5]. Using the estimate of the variance proposed by Kwak and Jung [6] leads to an under-estimation which impacts the performances of the test. To improve the type I error rate control, we may use the exact estimate of the variance under the null hypothesis as proposed by Wu [5]. This modification can be implemented but requires further works for being fully evaluated. The r-KJ design, just like the KJ design, is a non-parametric design but sample size calculations are provided under exponential survival which can be a limitation of their uses. However, a current work is to develop sample size formulation under Weibull survival to help to the diffusion of these designs.

The use of the r-KJ designs in a real phase II cancer clinical trial highlights its practical interest in situations where the clinical timepoint is late and accrual rate is relatively high. Requiring a complete follow-up in such trials can be unrealistic due to financial or management constraints. Thus, a KJ design is expected to deviate from the planned constraints due to the incomplete follow-up. In our phase II cancer clinical trial with a long term endpoint, complete follow-up is extremely difficult to obtain and loss of power could be feared. Thus, a restricted Kwak and Jung's design represents a perfect alternative to the classical Kwak and Jung's design. It is worth noting that our phase II clinical trial also emphasizes the need of randomized phase II trial when the efficacy of the historical treatment is unknown. Randomized phase II trial could be used to check the null hypothesis of historical survival [15], [16]. All previously discussed designs (CM, KJ, r-KJ) are well-suited to parallel randomized non-comparative randomized trial. It is also worth noting that since both designs require the specification of a survival curve and an accrual rate, any misspecification will lead to alter performances. Moreover, the KJ designs require providing the whole historical curve that could be particularly challenging. Influence of misspecifications of this is a topic for further works.

In summary, we recommend the use of our restricted Kwak and Jung's design when the investigator is expecting to have adequate follow-up over a specified window of time.

Formatting of funding source

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Appendix A.

For sample size calculation, we assume that the failure time distribution is exponential with hazard rate ${\lambda }_0$ under $H_0$ and ${\lambda }_1$ under $H_1$. Hazard ratio is given by: $HR=\raisebox{1ex}{${\lambda }_0$}\!\left/ \!\raisebox{-1ex}{${\lambda }_1$}\right.$. Accrual is supposed to be uniform between 0 and $t_a$ and censoring is fixed at $x_0$. So, survival functions $F\left(t\right)$, $G\left(t,DA\right)$ and $G^{\ast }\left(t\right)$ are the following:

$$F\left(t\right)=\text{exp}(-\lambda t)$$

$$G\left(t,DA\right)=\{\begin{array}{cc}0,& DA<t\\ \frac{DA-t}{t_a},& DA-t_a\le t\le DA\\ 1,& t<DA-t_a\end{array}$$

$$G^{\ast }\left(t\right)=I\left\{x_0\ge t\right\}$$

Under these assumptions, we have:

$$v_1=\{\begin{array}{c}\frac{1}{t_a}\left[D{A}_1+\frac{exp\left(-{\lambda }_{0}D{A}_1\right)}{{\lambda }_0}-\frac{1}{{\lambda }_0}\right]\text{,}D{A}_1<x_0\\ \frac{1}{t_a}\left[D{A}_1-\frac{1}{{\lambda }_0}+exp\left(-{\lambda }_0{x}_0\right)\left(x_0-t_a+\frac{1}{{\lambda }_0}\right)\right],D{A}_1\ge x_0\end{array}$$

$$v_2=1-exp\left(-{\lambda }_0{x}_0\right)$$

$${\sigma }_{11}^2=\{\begin{array}{c}\frac{1}{t_a}\left[D{A}_1+\frac{exp\left(-\check{\lambda }D{A}_1\right)}{\check{\lambda }}-\frac{1}{\check{\lambda }}\right],D{A}_1<x_0\\ \frac{1}{t_a}\left[D{A}_1\left(1-exp\left(-\check{\lambda }{x}_0\right)\right)+x_{0}exp\left(-\check{\lambda }{x}_0\right)+\frac{exp\left(-\check{\lambda }{x}_0\right)}{\check{\lambda }}-\frac{1}{\check{\lambda }}\right],D{A}_1\ge x_0\end{array}$$

$${\sigma }_{12}^2=1-exp\left(-\check{\lambda }{x}_0\right)$$

$${\sigma }_{01}^2=\{\begin{array}{c}\frac{HR}{t_a}\left[D{A}_1+\frac{exp\left(-{\lambda }_{1}D{A}_1\right)}{{\lambda }_1}-\frac{1}{{\lambda }_1}\right],D{A}_1<x_0\\ \frac{HR}{t_a}\left[D{A}_1\left(1-exp\left(-{\lambda }_1{x}_0\right)\right)+x_{0}exp\left(-{\lambda }_1{x}_0\right)+\frac{exp\left(-{\lambda }_1{x}_0\right)}{{\lambda }_1}-\frac{1}{{\lambda }_1}\right],D{A}_1\ge x_0\end{array}$$

$${\sigma }_{02}^2=HR\left[1-exp\left(-{\lambda }_1{x}_0\right)\right]$$

$${\omega }_1=\{\begin{array}{c}\frac{\left({\lambda }_1-{\lambda }_0\right)}{{\lambda }_1{t}_a}\left[D{A}_1+\frac{exp\left(-{\lambda }_{1}D{A}_1\right)}{{\lambda }_1}-\frac{1}{{\lambda }_1}\right],D{A}_1<x_0\\ \frac{\left({\lambda }_1-{\lambda }_0\right)}{{\lambda }_1{t}_a}\left[D{A}_1\left(1-exp\left(-{\lambda }_1{x}_0\right)\right)+x_{0}exp\left(-{\lambda }_1{x}_0\right)+\frac{exp\left(-{\lambda }_1{x}_0\right)}{{\lambda }_1}-\frac{1}{{\lambda }_1}\right],D{A}_1\ge x_0\end{array}$$

$${\omega }_2=\left(1-HR\right)\left[1-exp\left(-{\lambda }_1{x}_0\right)\right]\text{.}$$

Appendix B. Supplementary data

The following is the supplementary data related to this article: