Accelerated discovery of metallic glasses through iteration of machine learning and high-throughput experiments

Coupling artificial intelligence with high-throughput experimentation accelerates discovery of amorphous alloys.

Abstract

With more than a hundred elements in the periodic table, a large number of potential new materials exist to address the technological and societal challenges we face today; however, without some guidance, searching through this vast combinatorial space is frustratingly slow and expensive, especially for materials strongly influenced by processing. We train a machine learning (ML) model on previously reported observations, parameters from physiochemical theories, and make it synthesis method–dependent to guide high-throughput (HiTp) experiments to find a new system of metallic glasses in the Co-V-Zr ternary. Experimental observations are in good agreement with the predictions of the model, but there are quantitative discrepancies in the precise compositions predicted. We use these discrepancies to retrain the ML model. The refined model has significantly improved accuracy not only for the Co-V-Zr system but also across all other available validation data. We then use the refined model to guide the discovery of metallic glasses in two additional previously unreported ternaries. Although our approach of iterative use of ML and HiTp experiments has guided us to rapid discovery of three new glass-forming systems, it has also provided us with a quantitatively accurate, synthesis method–sensitive predictor for metallic glasses that improves performance with use and thus promises to greatly accelerate discovery of many new metallic glasses. We believe that this discovery paradigm is applicable to a wider range of materials and should prove equally powerful for other materials and properties that are synthesis path–dependent and that current physiochemical theories find challenging to predict.

INTRODUCTION

Some technologically important materials are kinetically stabilized. One such metastable class of materials is amorphous alloys of metals, namely, metallic glasses (MGs) (1). The lack of crystalline order in MG significantly alters the properties of these materials, thus enabling novel and improved functionalities. For example, the absence of deformation pathways based on gliding dislocations leads to exceptional yield strength and wear resistance (2, 3). Some MGs have enhanced corrosion resistance because of their ability to rapidly form protective films on the surface (4). MGs are therefore very promising candidates for structural applications, especially for high-cycle use in chemically harsh environments. Other MGs, such as the well-known Metglas system of alloys (5), exhibit high magnetic permeability, making them attractive for electromagnetic shielding.

Recent reports estimate upward of several million MGs, with a large fraction of them occurring in the multi-elemental composition space (6). However, less than a few thousand have been discovered in the last 50 years. The search for new MGs is challenging because they often contain three or more elements, and the nonequilibrium nature of the system implies that processing parameters (most commonly cooling rates, but in some cases enhanced surface diffusion) strongly influence formability. The vastness of the combined composition-processing space makes searches based on serial trial-and-error experimentation difficult and expensive; even rapid parallel synthesis combined with high-throughput characterization (HiTp experimentation) (7) can stall without additional guidance. For instance, even an aggressive rate of synthesizing and fully characterizing one ternary per day would take more than 10 years of HiTp experimentations to search just the ternary combinatorial space encompassed by 30 common elements for MGs.

Traditionally, new MG formers have been identified using empirical rules (8), for instance, Turnbull’s observation that MGs form near deep eutectics (9). More recently, several theories, based on a variety of factors including thermodynamic parameters (6, 10, 11), geometric factors (12), and atomic number fractions (13), lend a more fundamental understanding of the glass-forming ability (GFA). Although these theories work well for some MG compositions, no universal predictor of GFA is currently available. Furthermore, there is no obvious way to easily incorporate processing conditions or quickly improve these models from failed predictions.

Here, we demonstrate an alternate strategy that overcomes these limitations. We use machine learning (ML) iteratively with HiTp experiments (14–16) to guide the search for new MGs. ML approaches are well suited to this problem because they can (i) begin with a heterogeneous and sparse data set, (ii) operate with less than perfect understanding of the underlying physics but still take physiochemical parameters to accelerate learning, and (iii) progressively improve by simply adding more observations to the training set. In particular, the ability of ML to find patterns in observed data makes it possible to model relationships that are as yet unexplained by physiochemical theories (PCTs) (for example, the relationship between synthesis method and GFA, as will be shown below). However, there is a problem in training an ML model solely on previous MG experiments; the MG literature tends to report successful materials, but examples of unsuccessful materials are particularly valuable in improving ML models (17). Because HiTp methods test large numbers of materials rapidly, they simultaneously discover and report a large number of successful and unsuccessful materials, thereby providing a much wider variation of properties and very high quality data for ML studies.

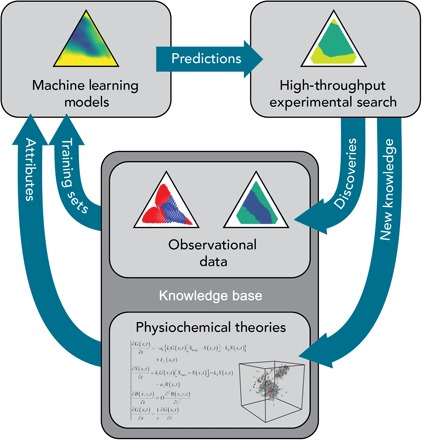
This paper highlights an emerging paradigm of data-driven discoveries for rapid and guided discovery of materials, whose functionality depends not only on chemical composition but also on synthesis. The paradigm is depicted schematically in Fig. 1. The paper begins by constructing an ML model based on known discoveries and predicts high likelihood of finding MG in the Co-V-Zr ternary, which we subsequently validate by HiTp experimentation. The results of HiTp experimentation are used to train a greatly improved “second-generation” ML model. We demonstrate that this refined ML/HiTp model successfully predicts GFA in three new ternary composition spaces, where no experimental observations exist. This paper illustrates how ML and HiTp experimentation can be used in an iterative/feedback loop to easily accelerate discoveries of new MG systems by more than two orders of magnitude as compared to traditional search approaches relied upon for the last 50 years.

Fig. 1. Schematic depiction of a paradigm for rapid and guided discovery of materials through iterative combination of ML with HiTp experimentation.

RESULTS AND DISCUSSION

First-generation predictions

We began the search for new MGs by training an ML model on reports of GFA in 6780 melt-spinning experiments at 5313 unique compositions, extracted from the Landolt-Börnstein (LB) handbook (18). This data set contains a large fraction of MG-forming experiments performed over the last 50 years. If there were multiple experiments at a composition, then it lists whether any of them resulted in a fully amorphous alloy. The data set samples a large number of elements (51) and contains many examples of metal-metal and metal-metalloid glasses. It is, however, biased toward experiments that report amorphous samples (71% of samples are “amorphous”). It contains 315 binary systems (25% of all possible binaries of the 51 elements) and 293 different ternary systems, but the ternaries are covered very sparsely with a median number of 8 observations per ternary. In addition, nearly 50% of the total training data come from only 38 ternaries, with the Al-La-Ni ternary contributing nearly 4% of the observations (225 training entries). As we will demonstrate, even this relatively small and biased data set is very useful in guiding a subsequent generation of successful experiments.

We trained an ML model to predict MGs on the melt-spun MG data in the LB handbook. When there were multiple experiments reported for the same composition, we assigned a label of “glass-forming” to that alloy if any one of the experiments reported a glass formation. We based our starting ML model on the model described by Ward et al. (19). We used the same features and a similar data set as Ward et al. (we removed Ag-Fe-Cu data, which were actually from sputtering experiments) but retuned the parameters of the ML algorithm and used a single model for the entire data set rather than the two separate models used by Ward et al. (The use of a single model facilitates automated model tuning.) We used the random forest algorithm (20) as implemented in Weka (21), and selected the optimal number of attributes assessed at each split by identifying which number yielded the highest accuracy in 10-fold cross-validation. Henceforth, we will call this the “melt-spun” model.

Because our eventual goal is to predict new MG compositions in ternaries outside our training set, we evaluate its performance using a specially designed cross-validation test where we iteratively exclude from the training set all of the compositions from a ternary and use the excluded ternary for validation. We call this approach “grouping” (see Materials and Methods for details). To concisely summarize the prediction performance of the models, we constructed receiver operating characteristic (ROC) curves, which evaluate the performance of a model in a way that takes the uncertainty of each prediction into account [see the study of Obuchowski (22) for details on use of ROC curves for assessing performance of binary classification models]. Figure 2A shows the ROC curve for the melt-spun model cross-validated against the melt-spun observations from the LB handbook. (The orange dashed lines show the ROC curve for random guesses and therefore for a model with no predictive performance.) The deviation of the curve toward the upper left corner from the random guess baseline indicates enhancement in prediction accuracy. We find strong classification performance (the area under the ROC curve shown in Fig. 2A is 0.88), which suggests that this model would be useful in predicting glasses capable of being produced by melt spinning.

Fig. 2. Performance and predictions of ML models for MG formation.

(A) ROC curve for the model that predicts melt-spun GFA cross-validated against melt-spun observations from the LB handbook. (B) ROC curve from the melt-spun (blue curve) and stacked (pink curve) model cross-validated against observations of MGs in the LB handbook, synthesized by sputtering. Predictions of the GFL for compositions in Co-V-Zr synthesized by melt spinning (C) and sputter co-deposition (D).

Synthesis method dependence

Diffusion kinetics plays a critical role in stabilizing glasses. Different synthesis methods, therefore, can alter the GFA noticeably. For example, materials synthesized by physical vapor deposition, such as magnetron co-sputtering, impart enhanced mobility to the surface layers, achieving local atom conformations that are very difficult to reach by melt spinning. Several recent experimental reports (23) show that sputter syntheses often naturally form ultrastable glasses, which molecular dynamics simulations (24) suggest would require thousands of years of annealing if synthesized by melt quenching.

We therefore needed to know whether the predictions of our model (melt-spun model) were sensitive to synthesis methods (particularly if sputtered synthesis was different from melt spinning). To that end, we extracted an additional 411 observations at 387 unique alloy compositions synthesized by sputtering from the LB handbook (18). (Notice that this is even a smaller training set than that for the melt-spinning model.) The sputtering data set also contains examples of metal-metal and metal-metalloid glasses but contains fewer elements than the melt-spinning data set (29 instead of 51). The sputtering data set also has a more equitable split between amorphous and non-amorphous entries, with 66% of the entries being amorphous.

We assessed the performance of the melt-spun model to predict MGs synthesized by sputtering with a similar grouping cross-validation test described above, but against the 411 observations in the LB handbook of alloys synthesized by sputtering. The ROC curve, shown as the blue curve in Fig. 2B, suggests that its performance is significantly poorer in predicting sputtered synthesized MGs. It appears, perhaps not surprisingly, that the synthesis method has significant influence on glass-forming likelihood (GFL; see Materials and Methods for details).

To make the model sensitive and accurate to synthesis methods, we tested three different approaches: In the first approach, we added synthesis method as an attribute in training; in the second approach, we trained separate models for each synthesis method; and finally, we used the classification scores from the melt-spun ML model as an input to train a new model on sputtering data. The last approach, in effect, assesses how well melt-spinning GFL corresponds to sputter-deposited GFL. We call it the “stacked” approach. The cross-validation tests (see the Supplementary Materials for details) show that all three approaches improve the accuracy of synthesis-dependent predictions, but the stacked approach shows the most improvement, especially for MG formation by sputtered co-deposition. (We will call the stacked approach ML model for sputtered synthesis just the stacked model.)

The ROC curve for the stacked model, the pink curve in Fig. 2B, is noticeably different from the ROC curve for the melt-spun model cross-validated against the same data set, indicating that there is sufficient difference between GFA by melt spinning versus sputtering to justify two separate ML models. Furthermore, we also noticed that the performance of the stacked model has markedly improved at the high false-positive rate (FPR), as indicated by flatter slope of the tangent to the curve, suggesting that the model is much better at predicting compositions unlikely to form glasses by sputtering.

We then used both the melt-spinning and stacked models to search for new MG compositions in ternaries composed of 24 nonpoisonous and inexpensive metals and metalloids [with Herfindahl-Hirschman index <6000 (25)]: B, Mg, Al, Ca, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Ge, Sr, Zr, Nb, Mo, In, Sn, Si, Ba, and Ta. We searched 2024 ternaries (24 choose 3), and for each ternary, we considered compositions on a 2 atomic % (at %) grid, corresponding to 1326 compositions per ternary, for a total of 2.38 million unique alloys. From these 2.38 million compositions, we selected alloys with a predicted GFL greater than 95%. From this list, we removed alloys that were compositionally close to known MGs. We rejected alloys where the sum of the absolute difference in atom fractions of each element—L₁ compositional distance—is less than 10 at % from known MGs. For the stacked model, these two filters reduced 2.38 million possibilities to 92,700 MG candidates (~3.5% of the search space, and thus an acceleration of more than 20 in search speed) in 385 different ternary systems.

We made a list of ternaries predicted to contain a large number of as-yet-unexplored glass-forming alloys—large glass-forming region (GFR)—and found, for either synthesis method, Co-V-Zr near the top of the list (see Fig. 2, C and D). [The purple region denotes high GFL (>95%), yellow denotes low GFL, and green and blue denote intermediate GFL.] Comparison of the two GFL maps indicates that the synthesis methods have a strong influence in stabilizing glasses, as also suggested by the ROC curves (in Fig. 2B), but neither method is necessarily better than the other for all compositions. For example, for Co-V-Zr, the models predict that melt spinning will stabilize glasses in Zr-rich compositions, whereas synthesis by sputtered co-deposition will extend GFL deeper into the V-rich region.

Comparison with PCTs

Several recent PCTs for MG also suggest that the Co-V-Zr ternary contains as-yet-undiscovered glasses. Here, we consider two such theories and apply them to the Co-V-Zr ternary.

The first theory, developed by Yang and Zhang (10), uses the ratio of the entropy and the enthalpy of mixing of the liquid phase (Ω, a thermodynamic parameter; δ, a parameter that captures the structural stability as the mean square deviation of the atomic size of elements). Figure 3A shows the prediction of Yang and Zhang’s approach for the Co-V-Zr ternary. The prediction not only covers the known MGs on the Co-Zr binary and the Co-rich region of the ternary but also predicts high likelihood of forming MG in the center of the ternary.

Fig. 3. Comparison of the first-generation ML model and PCTs.

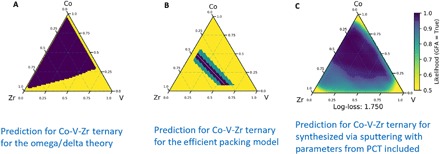
(A) Prediction of high GFL based on the theories of Yang and Zhang (10). (B) Prediction of GFL based on efficient packing model (12). The white line is the ideal packing prediction, the purple band shows 1% deviation from ideal packing, and the green band shows 2% deviation from ideal packing. (C) Prediction of GFL from ML model with incorporation of the two PCTs (stacked + PCT).

The second theory is a structure-only approach based on the concept of efficient packing of atoms in materials. This geometric model (12) uses a “hard sphere” approximation and calculates the composition range, where every atom in a given atom’s first coordination shell touches the central atom and its nearest neighbours; hence, every atom is simultaneously efficiently packed, forming a highly stable short-range cluster. The compositions that form efficiently packed clusters tend to form stable MGs. Figure 3B shows the predictions of this approach for the Co-V-Zr ternary (see the Supplementary Materials for details of the two physiochemical models).

Although both models have overlapping regions of predictions, the predictions differ from each other and provide no obvious path to reconcile them into a single model with improved agreement with each other. ML, on the other hand, allows inclusion of any inputs, including parameters from these theories, into a training set to create a unified model.

We retrained the sputter co-deposition ML model by including parameters from the thermodynamic model of Yang and Zhang and quantities related to the efficiently packed clusters as attributes. The predictions for the Co-V-Zr ternary modified with inclusion of the two theories are shown in Fig. 3C. (Henceforth, we will call this the “first-generation ML model for sputtered synthesis” or just the “first-generation model.”) Inclusion of PCT into the ML predictions for Co-V-Zr does not significantly alter the shape of the GFR, which is perhaps unsurprising given the general agreement between both theories and our original model.

To further understand the influence of theories on the results of our predictions, we investigated the most important features and model performance before and after adding the PCT-related features. We evaluated the importance of features by first eliminating features that have Kendall rank correlation coefficients above 90% with another feature, and then used recursive feature elimination to identify the 20 features with the highest random forest feature importance scores. The top features in the model did not significantly change whether PCT was included or not. The top four features for the models with and without PCTs are the variance in covalent radii, variance in electronegativity, GFL from melt spinning, and the mean number of unfilled valence orbitals. The only PCT-related feature that appears in the top 20 is the Ω parameter from Yang and Zhang. The effect of new features on predicted GFL for systems is also subtle. Only 6% of the predicted GFLs for the 2.4 million candidate alloys changed by more than 10% upon addition of the theories. Nevertheless, we find that adding PCTs to our model leads to a small improvement in accuracy, as measured in the grouping test (from 75.9 to 76.8%). We speculate that majority of the physiochemical insights from the two theories considered here are already coded into the model through other attributes. However, as newer theories emerge, including attributes from them into the ML model is a very fruitful pathway for rapid enhancement in predictive accuracy.

All four models, the two ML models for two different synthesis methods and the predictions of the two PCTs, despite large differences between them, predict high likelihood of finding a large GFR in the middle of the Co-V-Zr ternary. MGs were first reported in the Co-rich region of the Co-V-Zr ternary more than 30 years ago (see fig. S6) (26–28). Sputtered glasses in the Co-Zr binary were also reported more than 30 years ago and are promising candidates for magnetic shielding technologies (29). More recently, doping of V into Co-Zr was explored to create high-energy product rare earth–free permanent magnets by devitrification (30). All these reports are at the edges of the ternary, however, and the large central portion of the ternary still remains experimentally unexplored.

HiTp experimentation

Quantitative validation of the ML and physiochemical MG models to accurately predict the GFR in even a single ternary system requires synthesis and characterization of at least around 50 to 100, and ideally a few hundred different compositions. Traditional experimental methods are too expensive and slow. Therefore, we applied the “fail fast” experimental approach of massively parallel synthesis and rapid characterization. We selected “combinatorial magnetron co-sputtering” for parallel synthesis because it can cover large regions of the ternary phase diagram in a single deposition (31) and has the added advantage, in contrast to layer-by-layer deposition techniques, of providing excellent atomic mixing.

We also needed a rapid and nondestructive method to identify glasses. We used the full width at half maximum (FWHM) of the first sharp diffraction peak (FSDP) from synchrotron-based HiTp x-ray diffraction (XRD) measurements to decide whether the material was amorphous (a glass). The XRD data collection was integrated with on-the-fly data analysis (32), which allowed us to characterize more than a thousand compositions and accurately assess the MG-forming regions in a ternary in less than a day. Here, we define FWHM of FSDP of 0.57 Å⁻¹, the FWHM of FSDP for amorphous silica (33), a prototypical glass, as the threshold to classify our experimental FWHM observations into labels for glass formation. We report both FWHM and categorical (glass/not glass) labels.

Although a large fraction of reports in the MG literature use XRD and widths of the diffraction peaks to classify materials as glasses, we were unable to find a consensus threshold for the width of the diffraction peak for glass formation. Several published reports have classified glass formation with narrower peak widths than that for amorphous silica, and thus have used a less stringent threshold than we have here. Some have only reported qualitative classifier, such as “broad diffraction peak(s),” to label glass formation. The lack of a consistent classification threshold in literature (and consequently in the LB database) lends a certain amount of uncertainty to the labels on which we train our models. The uncertainty in the labels is particularly critical in determining the boundary of the GFR (glass/not glass boundary) and ultimately puts a limit on how accurate these models can ever become. We hope that this publication will motivate the MG community to strive for a consensus on the peak width threshold for classifying glasses and, even better, to incentivize inclusion of FWHM of the FSDP for MG discoveries in publications and databases. Publication of both observational information (FWHM) and a domain experts’ label is invaluable in concisely capturing community knowledge and quantifying label “fuzziness” by determining the maximum expectation envelope. Furthermore, large and easily available data sets of FWHM of FSDP will allow transition from categorical (glass/not glass) ML models to regression ML models trained to predict a continuous variable (FWHM instead of GFL), and thus make them easier to compare to experimental observations.

A new discovery

For ease of comparison, in Fig. 4A, we again show the prediction of the first-generation model for the Co-V-Zr ternary (repeat of Fig. 3C). Figure 4B shows the FWHM of the FSDP for the sputtered co-deposited Co-V-Zr ternary extracted from the HiTp experimental observations, and Fig. 4C shows the GFR labeled on the threshold derived from amorphous silica (discussed above) (see the Supplementary Materials for details). Figure 4 highlights two very important results: (i) the discovery of a large region of new MGs in the previously unexplored ternary through ML-guided HiTp experiments, and (ii) the remarkable agreement between ML predictions and experiments, especially when we consider that these predictions were generated from a small, biased, and sparsely distributed training set of MG observations.

Fig. 4. Comparison of new HiTp experimental results with the first-generation predictions.

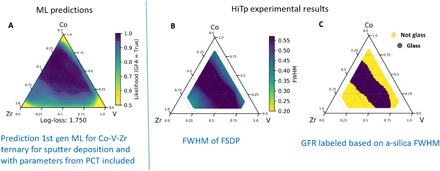
(A) Prediction of GFL for sputter co-deposition from ML model with incorporation of PCTs. (B) FWHM of the FSDP measured in HiTp XRD experiments. (C) Map of the GFR based on a glass formation threshold determined based on the FWHM of FSDP of amorphous silica (a-silica) in XRD measurements (see text for details).

Both the ML model and the HiTp observations indicate that the Co-V-Zr system has a large and previously undiscovered GFR. The ML model predicts that less than 50% of the alloys in this system have high likelihood of forming glasses, whereas our measurements find 54% of the ternary to be amorphous. The predicted and observed GFR in the Co-V-Zr system forms a wide band extending from the Co-Zr binary through the center of the ternary. The experimentally measured GFR starts on the Co-Zr binary spans, a region approximately bound by Co₅₀Zr₅₀ to Co₇₅Zr₂₅, and continues along a line where Co is mostly replaced with V. The width of the band decreases slightly as more V is added. The ML model predicts a similar band, but it is a little wider and shifted closer to the Co-rich end of the ternary, where there are known melt-spinning glasses. Overall, we find strong qualitative agreement between our ML predictions and experimental findings.

To quantify the agreement between the predictions of ML models and experimental observations, we use a log-loss measure. We use log-loss measure because it includes confidence of the prediction in weighing accuracy. It tolerates false predictions if they are slightly wrong but penalizes them heavily if they are very wrong (see Materials and Methods for details). The log-loss measure for each ML model is listed below the GFL map for that model. Quantifying the agreement of the model with experimental prediction (by log-loss measure) allows estimation of influence various inputs have on glass formation. For example, log-loss measure suggests that inclusion of PCTs in the ML model for the sputtered co-deposited Co-V-Zr model improves accuracy of the predictions by a factor of 2 (log-loss of 3.56 versus 1.75).

Finally, careful analysis of the FWHM of the FSDP reveals that the material in the center ridge of the Co-V-Zr ternary is nearly twice as disordered as the material at the boundaries (measured as structural correlation length, or 1/FWHM). This ridge of high GFR, though broader, is similar to the prediction of the efficient packing model (Fig. 3B), suggesting that the concept of efficiently packed clusters captures some of the essence of glass formation in the Co-V-Zr system. The narrowness of the predicted GFR in the efficient packing model is because it is calculated on the basis of a 2% deviation from the ideal packing ratios. As the radius ratios deviate further from ideal packing, atomic diffusion and crystallization rates increase, lowering the ability to form a glass. Implications of our discovery of new MG systems reported here and other physiochemical insights into the formation and stability of efficiently packed clusters will be explored in detail elsewhere.

The experimentally observed GFR, shown in Fig. 4C, also overlaps predictions of some of the melt-spun alloys with high GFL (in Fig. 2C). Full validation of melt-spinning predictions is beyond the scope of the current work, but we selected a few alloy compositions along the center of the GFR band (with the broadest FSDP) to test for GFL by melt spinning by casting in water-cooled 10:1 copper wedge mold. Preliminary analysis of the casted wedges shows fully glassy material up to 200 μm, suggesting that these compositions will be MGs if they were melt spun. (These casted MGs are still undergoing further characterization and analysis, and the detailed results on them will be published elsewhere.) In summary, through ML-guided experiments, we have rapidly discovered a large new region of MGs with high GFA in a previously unexplored ternary.

Improving the ML model

Our next step was to explore whether we can make the ML predictions even more accurate and thereby further accelerate discoveries. The natural way to improve an ML model is to incorporate more labeled observations in the training set.

However, combining HiTp observations with observations from the LB data set poses an inherent challenge. We have more than 1000 unique new observations from a single HiTp experiment, that is, more than one-sixth the size of the entire LB data set is all concentrated in just one ternary. To balance this large asymmetry, we “down-sampled” the HiTp observations to reflect the additional information they provided to the original LB data set. (Note that this asymmetry will become progressively less severe as results of glass formation, from more ternaries, from HiTp experiments become available.) We randomly selected 70 observations from the Co-V-Zr ternary so that it contained approximately the same number of entries as the most densely sampled ternary in the LB sputtering data set (Mg-Ti-Al with 65 entries). However, note that the down-sampled HiTp data set contains much higher fraction of negative observations than any of the ternaries in the LB data set and is therefore of much higher quality for learning. After down-sampling the HiTp data, retraining the model requires no tweaking or retuning but simply adding the new data to the training set—a process that is completely automated and allows instantaneous update of the model as soon as new data are acquired. The automated and rapid iterative update of the model further accelerates the process of discovery. The updated model retrained on the HiTp experiments on the Co-V-Zr ternary constitutes the second iteration of the discovery cycle depicted in Fig. 1, and we call the resultant predictions the second-generation ML model.

The predictions of the second-generation model for Co-V-Zr are shown in Fig. 5A. The excellent agreement with the experimental observations (shown in Fig. 4C), reflected in more than sixfold improvement in prediction accuracy (measured as reduction in the log-loss value from 1.75 to 0.28), is not surprising given that our training set now includes Co-V-Zr data. The (marked) improvement in the prediction accuracy for Co-V-Zr is necessary but not sufficient to ascertain whether the model on the whole has become more accurate over a larger combinatorial space after the second iteration.

Fig. 5. Higher-generation ML models.

(A) Revised predictions for Co-V-Zr ternary. (B) Predictions of ternaries with the largest as-yet-unexplored GFR. (C) Comparison of the ROC curves for first-, second-, and third-generation models cross-validated against all available sputtered co-deposited synthesis data (LB + HiTp).

The question is how much has the second-generation model improved at predicting clusters of high GFL (≥95%) region (that is, GFR) in yet to be measured ternaries. To identify the potential new ternaries to further validate the second-generation model, we ranked the ternaries in the decreasing area of the GFR. The bold black curve in Fig. 5B shows such a ranking on a semi-log plot. The blue curve in Fig. 5B shows the fraction of each ternary of likely glass formers that has yet to be experimentally examined. From the list, we selected two candidates with large predicted and unexplored GFR, that is, high on both the black and the blue curves, namely, Co-Ti-Zr and Co-Fe-Zr. We also selected one candidate ternary predicted not to have any glass-forming alloys: Fe-Ti-Nb. We chose the Fe-Ti-Nb ternary also because, although its three elements are neighbors of Co-V-Zr in the periodic table, the ML model predicts it to have very poor GFA, suggesting a very high and still incompletely understood variability in GFA across the periodic table. The first two columns (A1 to A3 and B1 to B3) of Fig. 6 show the prediction of the first- and second-generation ML model, respectively. The third column (C1 to C3) shows the FWHM of the FSDP for these three ternaries extracted from HiTp experiments, and the last column (D1 to D3) shows the map of GFR for each of the three ternaries derived from the glass/no-glass threshold based on amorphous silica FWHM. Figure 6 shows that the experimental observations, for all three ternaries, are in good agreement with the prediction for both generations of ML models, although the agreements with the second-generation model are significantly better. The second-generation model improves prediction accuracy (as measured by log-loss value) by three to four times for the glass-forming ternaries. Log-loss measure decreases from 1.58 to 0.39 for Co-Ti-Zr and from 1.70 to 0.49 for Co-Fe-Zr from the first-generation to the second-generation model. For the non–glass-forming ternary, Fe-Ti-Nb, the second-generation model improves prediction accuracy by 60% (the log-loss value decreases from 2.37 to 1.48). Iteration of ML with HiTp experimentation has made the second-generation ML model a much improved predictor of MGs in ternaries produced by sputtering. It has also guided us to discover two new glass-forming ternaries with significantly large GFR.

Fig. 6. Comparison of first- and second-generation predictions with HiTp experimental results for Co-Ti-Zr (first row), Co-Fe-Zr (second row), and Fe-Ti-Nb (third row) ternary.

(A1 to A3) Prediction of GFL from the first-generation ML model. (B1 to B3) Revised predictions from the second-generation ML model. (C1 to C3) HiTp experimental map of the FWHM of the FSDP in XRD measurements. (D1 to D3) Experimental map of the GFR derived after application of the glass formation threshold based on amorphous silica applied to data in (C1) to (C3). Purple, glass; yellow, not glass.

One obvious trend highlighted by Fig. 5B is that only approximately 8% of the ternaries, and even a fewer fraction of alloys, are predicted to form glasses. (The model predicts that only 20,104 alloys out of 2.38 million composition search space, that is, ~0.8%, are likely to form glasses.) The second-generation model predicts occurrence of glasses to be much rarer than the first-generation model (8% versus 18% of ternaries and 0.8% versus 3.4% of the compositions). The rareness of MGs implies that without guidance, only a very small fraction of experiments would lead to the desired outcome, making discoveries very expensive. Leveraging the predictions of the ML model highlights a pathway for improving the rate of successful discoveries by over an order of magnitude on top of the orders of magnitude acceleration possible from HiTp experimentation. The models predict that glass-forming alloys are clustered into a small number of ternaries rather than randomly dispersed throughout the composition space. Clustering of MGs in a composition space suggests that searching the broad swaths of compositions in a single ternary for MGs rather than a small number of compositions in many different ternaries is likely to be far more effective for finding new MGs; HiTp experimentation, where an entire ternary (or at least a very large fraction of a ternary) is synthesized in parallel and rapidly characterized, seems particularly well suited for accelerated discoveries. For example, searching 2.4 million alloy compositions for MGs by traditional methods (serial experimentation), with even an aggressive search protocol of synthesis and characterization of 5 alloys a day, operating 365 days a year, would take over a millennium (1300 years) to complete. In the course of this work, we were able to synthesize and screen a ternary (~1000 alloy compositions) in a day, resulting in a 100-fold acceleration. But even with HiTp experimental searches, glass formation in ternary alloys is still sufficiently rare that, without guidance provided by the ML models, discovering all potential MG formers in ternaries composed of 30 common elements could easily take decades. But with a predictive model with a precision of ~80%, such as that of the ML models developed here, experiments can be directed to ternaries predicted to have at least a few alloys with high GFA, and a further 10-fold increase in the rate of discoveries can be easily achieved (see the Supplementary Materials for details of the estimate of increase in the rate of success). Therefore, by combining ML and HiTp experimentation, we believe that a focused and guided search can discover most ternary MGs composed of nontoxic and earth-abundant elements in a just few years.

A more detailed analysis of the GFR ranking of the ternaries (Fig. 5B) highlights other curious trends. For example, several, but not all, Co-Zr–containing ternaries are predicted to contain alloy compositions with high GFA. The model predicts the following trend with decreasing GFR in Co-Zr-X ternaries, where X goes from V, Ti, Fe, Mn, Ta, Nb, Al, Si, B, Zn, etc. (Less than 2% of compositions in Co-Zr-B are predicted to be glass-forming.) To better understand this trend, we estimated liquidus surfaces for the four ternaries investigated in detail here. Liquidus surfaces are known for a several ternary systems but not for the four ternaries investigated here. We estimate them from known binary and ternary phase equilibria data, but note that there is a high degree of uncertainty in some of the composition spaces. The relationship between the liquidus, FWHM, and GFR, shown in fig. S7, suggests a strong correlation between glass formation and the C15 (MgCu₂ prototype) Lave and B2 liquidus phase fields common to all four systems. These results indicate that these particular ordered phases are difficult to crystallize quickly, resulting in glass formation. For instance, for the Co-Zr–containing ternaries, despite the ZrCo₂ C15 Lave phase having a high melting point relative to surrounding phases, the exceptional correlation between the GFR and the ZrCo₂ liquidus phase field as it extends into the ternary composition space suggests a high kinetic barrier to crystallization. These correlations further suggest that large mismatch in ionic sizes and the presence of larger atoms in these structures, such as Zr, hinders crystallization more so. Extending this argument further, relatively small size difference between the constituent atoms, as is the case for the Fe-Ti-Nb ternary system, appears to lower the resistance to crystallization, resulting in poorer GFA. It is also worth noting that liquidus regions relating to the primary crystallization of solid solution regions exhibit negligible to near-zero glass formation, which aligns well with the lattice destabilization model outlined by Laws et al. (12). The Co-Zr glass-forming ternaries can also be understood in the framework of the efficient packing model (12), whereby the atomic size ratio of Co to Zr is almost topologically ideal for efficient atomic packing within this composition space and is also likely in part responsible for extended glass formation in these particular systems. Fully understanding the role the third element plays in the ternary systems to either enhance or suppress this propensity could lead to further new insights. For example, Fe and Co are similar in size and appear to easily substitute for each other, giving rise to a pseudo-binary glass-forming band in the ternary. Therefore, although our search approach is not built on any deep physiochemical foundations, we believe that a reliable ML model which predicts GFL in as-yet-unexplored ternaries could lead to new insights and deeper physiochemical understanding when combined with HiTp experimentation that assess glass formation in the whole ternary composition space. It opens the possibility for virtual experimentation and exploration. We are beginning to use the predictions of the ML models as highlighted above to explore these trends further. Results of these explorations will be published elsewhere.

Following the discovery paradigm outlined here, observations for the three new ternaries (Co-Ti-Zr, Co-Fe-Zr, and Fe-Ti-Nb) were added to the ML model for the third iteration (third-generation ML model). To understand how each generation of the ML model performs, we tested them in a grouping cross-validation against all the sputtered data we have (that is, 411 observations from the LB handbook plus 70 randomly picked observations from each of the four HiTp data sets discussed here). Again, the model was not tweaked or retuned in any way but only retrained with additional data from these three ternaries. We find, as seen in Fig. 5C, that the performance of the model improves systematically between each generation (the area under the ROC curve increases from 0.66 to 0.80). The improvement from the first generation to the second generation is over the entire prediction range, but it is particularly large at high FPR. The near-perfect performance of the model at the highest FPR (indicated by a flat slope of the tangent to the curve) suggests that the second-generation model has learned with near perfection to predict compositions unable to form glasses. A cursory observation appears to show marginal improvement from the second generation to the third generation, but the improvements are significant if one focuses on where they occur. The third-generation model still has near-perfect accuracy on predicting alloys with low GFL, but now it has become much better at predicting glass-forming alloys as well (improvements at the left, low FPR region of the ROC curve). We emphasize that these increases in accuracies indicate improved performance not only on the systems we assessed in this work but also for all ternaries for which there are experimental data. The generalizability/universality of our model is improving as we perform more HiTp experiments and feed their results back into the ML model.

Moving forward, we are faced with two complementary choices. The second- and third-generation ML models, as seen above, have become sufficiently reliable, though still not perfect, predictors for glass formation. The first choice is then to use these models, even if they are not completely accurate in their predictions, to quickly guide toward rapid discoveries of new MGs. The model will slowly improve as more observations are included in the training set. The second choice is to investigate strengths and weaknesses of the current model and then to search for unexplored ternaries that would have the highest likelihood of improving the prediction accuracy of the model. In the beginning, the second strategy may appear unproductive as it focuses on high uncertainty predictions and will often lead to exploration of ternaries with few alloys with high GFL, but it would allow the model to evolve far more quickly toward a highly accurate predictor of MGs and, in the long run, would result in more discoveries than the first strategy. Consequently, an active learning approach that balances these two strategies might be the optimal use of HiTp experimentation to guide to new undiscovered MGs and lead to more reliable models for predicting MGs (34). The more reliable model with higher accuracy will be eventually needed to guide the search for MGs into more complex composition spaces (quaternary and higher-order systems) and more nuanced synthesis conditions.

CONCLUSIONS

In conclusion, we show that iterative application of ML modeling and HiTp experimentation is a very powerful paradigm to find new MGs. We used it here to discover three new ternaries with large GFRs. We further show that even when the first-generation ML predictions are not significantly more accurate than predictions of PCTs, they rapidly surpass them with additional observations and can capture nuances that are harder to predict otherwise. We believe that this paradigm of data-driven discovery can be easily extended to accelerate the search for a wide range of technologically important materials, from high-entropy alloys to catalysts. It is particularly attractive for materials for which fully predictive PCTs have yet to be developed, and synthesis methods and other complex parameters (such as morphology, microstructure, and substrate interaction) play a large role in determining their properties and performance.

MATERIALS AND METHODS

Experimental design

The objective of this work was to combine supervised ML, rapid parallel synthesis, and HiTp characterization to accelerate material discovery.

Supervised ML modeling

We used four different ML models in this study: (i) a retuned version of the Ward 2016 model (19), (ii) a model trained on sputtering data from the literature, (iii) a model where we added PCTs into the representation, and (iv) a model trained on sputtering data from the literature plus the Co-V-Zr data generated in this work. All models were trained using Magpie (19, 35), and the software, data sets, and input files necessary for recreation are available on GitHub (https://github.com/fang-ren/Discover_MG_CoVZr).

The revised Ward 2016 model was trained on the melt-spinning GFA of metal alloys collected using the set of “general purpose” attributes proposed by Ward et al. as the representation (19). The differences between this model and the one created by Ward et al. in 2016 are as follows: (i) the elimination of Ag-Cu-Fe data from the training set (Ag-Cu-Fe data in the LB database were synthesized by sputtering, not melt-spinning, and erroneously included in the 2016 data set), (ii) retuning of the ML algorithm, and (iii) using a single model for the entire data set, rather than two separate models, to facilitate automated model tuning. Ward et al. used two different models: one for alloys that contain only metallic elements and the other alloys that contain at least one nonmetal or metalloid. Each ML model was trained using a random forest algorithm, as implemented in Weka (21, 36). Full details of the model and a web interface for using it for arbitrary compositions are available at oqmd.org/static/analytics/composition.html.

The sputtering GFA model was trained using the same attributes and ML algorithm as model (i), but was trained on data describing GFA measured using sputtering experiments. In total, our sputtering data set includes 411 entries at 393 different compositions, which were all collected from the LB handbook (18). We used the same strategy to select a single entry for each composition as with the melt-spinning data set (that is, reporting glassy if any entry reported glass formation). To make the model sensitive to synthesis methods, we tried three different approaches (described in the Supplementary Materials) but finally chose a stacked approach where we use the label (that is, “glass” or “not glass”) predicted by model (i) and the likelihood as an additional attribute in training. We also reoptimized the hyperparameters for random forest using the same technique as model (i).

The PCT-enhanced model used the same training set as model (ii) but included attributes derived from two different theories for glass formation: the thermodynamic theory of Yang and Zhang (10) and the structural theory of Laws et al. (12). Complete details of the attributes created based on these theories are available in the Supplementary Materials. We also used random forest as the ML algorithm for this model and determined the optimal set of hyperparameters for random forest using the same strategy as for models (i) and (ii).

The sputtering model with HiTp data for Co-V-Zr, Co-Ti-Zr, Co-Fe-Zr, and Fe-Ti-Nb was trained first by including the down-sampled Co-V-Zr data generated in this work through HiTp experimentation to the training set for model (iii) for the second-generation ML model, and again retrained by including down-sampled HiTp data for the additional three ternaries for the third-generation model. Full details of the model and a web interface for using it for arbitrary compositions are available at oqmd.org/static/analytics/composition.html.

Thin-film alloy deposition

Each ternary was divided into three combinatorial composition spreads (libraries). Each library was deposited on a 76.2-mm Si wafer using an AJA sputtering system at room temperature with a substrate-target distance of 11.3 to 12.0 cm and a base pressure of less than 1 × 10⁻⁸ torr. Alloys were co-deposited using single-element targets onto 76.2-mm Si to form 100-nm-thick films. The single-element targets were calibrated by controlling the deposition rate at various gun powers and gun tilts and fitted to the in-house sputter model. The exact deposition parameters are included in the Supplementary Materials. The precision of composition calculated by the in-house sputter model is also included in the Supplementary Materials. The ternary system was synthesized using a deposition rate less than 0.07 Å/s for each element. The film thickness was quantified by a quartz crystal monitor within the deposition chamber and then modeled based on the procedure described by Bunn et al. (31).

XRD and XRF measurements

Two-dimensional (2D) XRD patterns were collected on the combinatorial libraries at the HiTp XRD facility at Beamline 1-5 at Stanford Synchrotron Radiation Lightsource. A MarCCD detector was used for data collection. A 12.7-keV x-ray beam was collimated to 0.3 mm × 0.3 mm for the measurements. The libraries were scanned with a grazing incidence angle of 3° or 4° to minimize the diffraction from the silicon substrate. The grazing incidence geometry resulted in an approximately 3-mm probe footprint on the library. The libraries were scanned with a 3-mm spacing.

Simultaneously with XRD data collection, a fluorescence detector (Vortex, SNTUS-178-1113) was used to collect (partial and relative) composition maps. The x-ray fluorescence (XRF) system was not calibrated to provide absolute compositions. It was also unable to map certain elements (for example, Zr) because of the incidence x-ray energy. The main goal for the XRF analysis was to provide orientation and rotation registration. The orientation and rotation information thus obtained was fed into an in-house model that generated composition maps associated with the XRD maps. The chemical compositions predicted by the in-house model were then validated by wavelength-dispersive spectroscopic (WDS) analysis on a few selected regions of the combinatorial libraries (for example, Co- and V-rich regions of the C-V-Zr system).

XRD data processing

By using LaB₆ powder as a standard material, we extracted the geometric parameters of the 2D detector including the sample-to-detector distance, the direct beam position on the detector, and the tilting and rotation of the detector. These parameters were used to transform raw images to calibrated Q-χ images in diffraction coordinates, and then integrated and normalized to obtain 1D spectra. The details for XRD data processing can be found elsewhere (32). The backgrounds were found by fitting a spline subtracted function on a few manually selected data points on the 1D spectra. Because most of the spectra have the FSDP located between 2.49 and 3.15 Å⁻¹ in Q, and two small peaks centered at about 1.9 and 3.4 Å⁻¹ in Q are known to be from the silicon substrate, the FWHM of FSDP was extracted by fitting a Gaussian and Lorentzian sum function using three predefined peaks on the background subtracted spectra.

Ternary plotting

The ternary plots in this paper were made by modifying the Python package “python-ternary” (37).

Statistical analysis

Glass-forming likelihood

The GFL was defined as the confidence that an alloy will form a glass, as predicted by the ML model. Here, we select a threshold GFL of 95% to define “high-confidence” predictions for MGs and color them purple in the prediction ternaries. At this threshold, the FPR of the model (that is, the fraction of non-glasses predicted as glasses) is only 1%. At a 50% GFL, where the model predicts glass and non-glass with equal likelihood, the FPR is 24%, which suggests that selecting 50% as the threshold for predicting a material to be glass-forming would lead to many false positives.

Two sets of statistical accuracies were used to assess ML predictions. The first was used to test the prediction accuracy of the model for the entire data set, and the second was used to test the prediction accuracy of the model for individual ternaries.

ROC curves

We performed a specialized cross-validation test, which we call grouping cross-validation to assess the prediction performance of the model against the entire data set. In grouping cross-validation, we iteratively withheld each ternary system present in our data set to use as a test set. This test was designed to evaluate the ability of each model to predict the GFA of systems not included in the training set and thereby approximate how this model is used in practice. We performed three grouping cross-validation tests: We compared the performance of a model trained on only melt-spinning data (tested against only melt-spun observation from the LB handbook), compared the performance of the melt-spun model and the stacked model against sputtering data from the LB handbook, and finally tested the performance of the first-generation (trained on sputtering only data from the LB handbook), second-generation (trained on sputtering data from the LB handbook plus down-sampled Co-V-Zr HiTp data), and third-generation (trained on sputtering data from the LB handbook plus down-sampled Co-V-Zr, Fe-Ti-Nb, Co-Fe-Zr, and Co-Ti-Zr HiTp data) model against the entire sputtering data set (LB handbook entries plus observations from all four HiTp ternaries investigated here).

Log-loss accuracy

We use log-loss to measure the accuracy of the ML predictions in a ternary. The log-loss accuracy is a metric for measuring the performance of a classification model that takes the “certainty” of each prediction into account. It is computed using the following relationship

$$\text{Log}‐\text{loss} =\frac{1}{\mathit{N}}{\displaystyle \sum _{\mathit{n}=1}^{\mathit{N}}}{\mathit{y}}_{\mathit{n}}\text{Log}({\widehat{\mathit{y}}}_{\mathit{n}})+(1-{\mathit{y}}_{\mathit{n}})\text{Log}(1-{\widehat{\mathit{y}}}_{\mathit{n}})$$

where N is the number of entries, y_n is the true value of prediction (here, 0 is defined as “glassy” and 1 as “crystalline”), and ${\widehat{\mathit{y}}}_{\mathit{n}}$ is the predicted class, which ranges from 0 (100% confidence in glassy) to 1 (100% confidence in crystalline). Smaller values of log-loss are better, and the optimal value is 0. For reference, the log-loss of the Ward 2016 model in cross-validation (that is, averaged over all materials in the training set) is 0.246.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/4/eaaq1566/DC1

ML models

HiTp experiments

Published data on Co-V-Zr

Correlation between the liquidus surfaces, FWHM of FSDP, and GFR

Estimation of the rate of success for discovering new MGs

fig. S1. Performance of four approaches of including synthesis method into an ML model on a cross-validation test.

fig. S2. Prediction of GFR by two physiochemical models.

fig. S3. Elemental gun configuration on AJA ATC Orion 5 sputtering system.

fig. S4. Accuracy of composition calculated by the in-house sputter model.

fig. S5. Experimental determination of glass formation in Co-V-Zr ternary.

fig. S6. Published reports of MGs in Co-V-Zr ternary.

fig. S7. Correlation between the liquidus surfaces, FWHM of FSDP, and GFR.

table S1. Sputtering parameters for all samples.

References (38, 39)