Experimental signatures of spin superfluid ground state in canted antiferromagnet Cr₂O₃ via nonlocal spin transport

We report direct experimental signatures for the spin superfluid ground state in canted antiferromagnets via nonlocal spin transport.

Abstract

Spin superfluid is a novel emerging quantum matter arising from the Bose-Einstein condensate (BEC) of spin-1 bosons. We demonstrate the spin superfluid ground state in canted antiferromagnetic Cr₂O₃ thin film at low temperatures via nonlocal spin transport. A large enhancement of the nonlocal spin signal is observed below ~20 K, and it saturates from ~5 down to 2 K. We show that the spins can propagate over very long distances (~20 μm) in such spin superfluid ground state and that the nonlocal spin signal decreases very slowly as the spacing increases with an inverse relationship, which is consistent with theoretical prediction. Furthermore, spin superfluidity has been investigated in the canted antiferromagnetic phase of the (11$\overline{2}$0)-oriented Cr₂O₃ film, where the magnetic field dependence of the associated critical temperature follows a ²/₃ power law near the critical point. The experimental demonstration of the spin superfluid ground state in canted antiferromagnet will be extremely important for the fundamental physics on the BEC of spin-1 bosons and paves the way for future spin supercurrent devices, such as spin-Josephson junctions.

INTRODUCTION

The Bose-Einstein condensate (BEC) refers to the quantum state of matter when a large fraction of bosons occupy in the lowest accessible quantum state and has been observed in liquid helium (⁴He), cold gases, polaritons, photons, etc. (1–6). Recently, this concept has been much more general, for example, the BEC of spin-1 bosons and the spin superfluid (7–14). To achieve this spin superfluid state, a great deal of effort has been made. For example, microwave pumping has been used to generate the BEC of magnons and supercurrent at room temperature (9, 14). However, because the condensed magnons are inherently thermal excitations, the spin superfluidity is not the ground state and, thus, occurs only in a very short time scale (microseconds). Theoretically, the spin transport in spin superfluid has been recently proposed for ferromagnetic graphene and the ν = 0 quantum Hall state of graphene (15–17), ferromagnetic materials (18–20), and antiferromagnetic insulators (21–23). Besides, recent progresses of BEC in quantum magnets exhibit a thermodynamic ground state at low temperatures inferred from magnetization and heat capacity measurements (7, 8, 10, 11, 13), where the condensing spin-1 bosons can be regarded as the mapping of the spin ground state onto a lattice of bosons (13). However, despite the enormous effort in this field, the direct experimental observation of real spin transport in the spin superfluid ground state has been lacking.

We report the experimental observation of long-distance spin transport in the spin superfluid ground state in canted antiferromagnetic Cr₂O₃ thin films at low temperatures, which provides the direct experimental evidence of the spin superfluid ground state in canted antiferromagnet.

RESULTS AND DISCUSSION

The high-quality Cr₂O₃ thin films are grown on (0001)-oriented Al₂O₃ substrates via pulsed laser deposition (PLD) (see Materials and Methods). The spin configurations on the Cr atoms (Cr³⁺, s = ³/₂) are illustrated in Fig. 1A, which shows that the spins are aligned along the crystal’s [0001] orientation. The spin transport in the spin superfluid state is performed using the nonlocal geometry, as shown in Fig. 1 (B and C, inset). The spins are injected into the antiferromagnetic Cr₂O₃ thin films from the local Joule heating on the Pt strip via spin Seebeck effect (24–26). Then, the spin information transports in the spin superfluid state, which can propagate to the right Pt electrode and be detected by voltage measurement across the Pt strip via the inverse spin Hall effect using standard low-frequency lock-in technique (see Materials and Methods). Because the spins are injected by thermal heating via spin Seebeck effect and detected via inverse spin Hall effect, the nonlocal spin signal is probed by measuring the second harmonic nonlocal resistance (R_2ϖ).

Fig. 1. The nonlocal spin transport in the spin superfluid ground state of the canted antiferromagnetic Cr₂O₃ thin film.

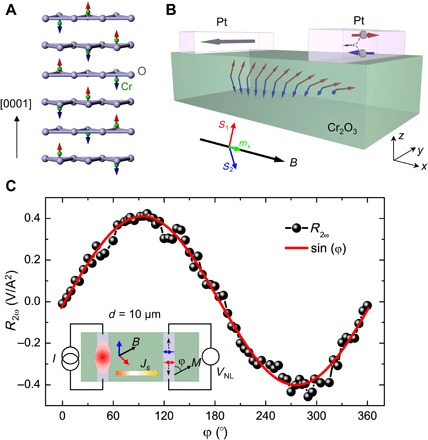
(A) The spin structure of single crystalline antiferromagnetic (0001)-oriented Cr₂O₃ thin film. Up (red arrows) and down (blue arrows) spins of the Cr³⁺ ions are aligned parallel the crystal’s [0001] orientation. (B) Schematic of the nonlocal spin transport geometry for the spin transport measurement in the spin superfluid state. The canted magnetization direction is controlled by the external magnetic field (B) along the x direction. In such canted antiferromagnetic configuration, the spin component (S_y + iS_z) that is perpendicular to the magnetic field direction becomes coherent in the spin superfluid state. (C) The second harmonic resistance in the nonlocal geometry measured on the nonlocal device as a function of the in-plane magnetic field angle at 2 K and 9 T. The spins are injected at the left Pt strip via the spin Seebeck effect. The collective spin transport in the spin superfluid ground state is probed at the right Pt strip via the inverse spin Hall effect. The nonlocal device is fabricated on the ~19-nm Cr₂O₃ thin film, and the spacing between two Pt strips (d) is 10 μm. The red curve is a sin (φ) fit for the experimental data (solid balls).

Figure 1C shows the R_2ϖ as a function of the magnetic field angle (φ) measured on the nonlocal device on the ~19-nm Cr₂O₃ thin film with a spacing (d) of 10 μm between the two Pt strips. During the measurement, the temperature is 2 K, and the in-plane static magnetic field is 9 T. The in-plane magnetic field is used to generate a canted antiferromagnetic phase, as shown in Fig. 1B. The effective spins are detected via the inverse spin Hall effect of Pt, and the second harmonic nonlocal resistance is expected to be proportional to sin (φ) (25)

$${\mathit{R}}_{2\mathrm{\varpi }}=\frac{1}{2}{\mathit{R}}_{\text{NL}} \text{sin}(\mathrm{\varphi })$$ (1)

where the R_NL is the nonlocal spin signal. The red solid line is a fitting curve based on Eq. 1, from which R_NL is determined to be 0.79 ± 0.02 V/A². Figure 2A shows typical representative R_2ϖ curves on this device (d = 10 μm) as a function of the magnetic field angle (φ) in 9 T at 2, 5, 10, 15, and 30 K, respectively. The nonlocal spin signal as a function of the temperature from 2 to 110 K is summarized in Fig. 2B. No clear nonlocal spin signal is observable when the temperature is higher than 110 K. At ~60 K, a modest enhancement of the nonlocal spin signal is observed (section S3 and fig. S8). When the temperature further decreases to ~20 K, the nonlocal spin signal starts to increase dramatically. From 20 to 5 K, a large enhancement of the nonlocal spin signal is observed. Furthermore, the nonlocal spin signal exhibits a saturation feature when the temperature decreases from ~5 down to 2 K. These low-temperature behaviors cannot be attributed to the thermally excited incoherent magnons, the population of which decreases as the temperature decreases below the Néel temperature (27–30).

Fig. 2. Temperature dependence of the nonlocal spin transport in the canted antiferromagnetic (0001)-oriented Cr₂O₃ thin film.

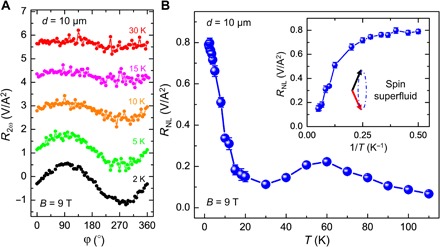
(A) The second harmonic resistance in the nonlocal geometry measured as a function of the in-plane rotation angle under the magnetic field of 9 T at 2, 5, 10, 15, and 30 K. (B) The nonlocal spin signal as a function of the temperature (T). Inset: The nonlocal spin signal as a function of 1/T. At low temperatures, in the spin superfluid ground state, the transverse spin component (S_y + iS_z) that is perpendicular to the magnetic field direction becomes coherent.

We attribute the observation of the low-temperature enhancement and the saturation of the nonlocal spin signal to the spin superfluid ground state in a canted antiferromagnet, as depicted in Fig. 1B. In such a spin superfluid ground state, the spin-1 bosons exhibit the BEC at low temperatures, as previously found for the content of BEC in quantum magnets (13). This spin superfluid ground state is totally different from the magnon BEC, where the magnons are inherently excitations and have a finite lifetime, and thereby, the spin supercurrent and magnon BEC only occur in very short time scales (9, 14), whereas the BEC in our case is a thermodynamic ground state, for which the spin Hamiltonian originally has the U(1) spin-rotational symmetry around the magnetic field direction (x direction). On lowering temperature, the U(1) symmetry is spontaneously broken by the canted antiferromagnetic order, where a free U(1) processional motion of the antiferromagnetic moment within the y-z plane leads to a spin supercurrent of the x component of the spin density (Fig. 1B). That is, the spin component in the y-z plane (S_y + iS_z) acquires a phase rigidity in the spin superfluid state, which results in a spin analog of the superconducting effect. Despite the injected magnons by the thermal method being usually incoherent, a BEC condensation from incoherent magnons could happen via magnon scatterings (9, 31, 32). The detailed condensation of the incoherent magnons into the spin superfluid state needs future studies. The nonlocal spin signal versus the inverse of temperature is plotted in Fig. 2B (inset). Furthermore, this saturation feature below ~5 K agrees well with the theoretical calculation of nonlocal spin signal in the spin superfluid ground state below a critical temperature (15).

Theoretically, the spin superfluid density is expected to show no variation or very slow decaying in the presence of the spin-orbit interaction or magnetic damping (13, 15, 22). To verify this property, we study the nonlocal spin transport as a function of the spacing between the two Pt strips. To avoid the thermal effect close to the spin injector (33), we purposely vary the spacing from 2 to 20 μm that is significantly longer than the width of the Pt strip (300 nm). Figure 3A shows the temperature dependence of the nonlocal spin signal for several typical spacing of 2, 8, 14, and 20 μm. Similar to the feature observed on the 10-μm device discussed earlier, the nonlocal spin signals of all the devices exhibit a large enhancement around ~20 K and saturate below the temperature of ~5 K. Figure 3B shows the spacing dependence of the nonlocal spin signals at 2 and 10 K under the magnetic field of 9 T. The nonlocal spin signal exhibits a very slow decrease as the spacing increases from 2 up to 20 μm, which is quite different from previous results on the ferrimagnetic insulator yttrium iron garnet (YIG), where the nonlocal spin signal exponentially decays as a function of the spacing (25, 30, 33). Whereas, in our case, for the spin superfluid ground state, the nonlocal spin signal is shown to be inversely proportional to the spacing. This observation agrees well with the theoretical calculation (red dashed lines in Fig. 3B) for spin superfluidity in the presence of the magnetic damping (22)

$${\mathit{R}}_{\text{NL}}={\mathit{R}}_{\text{NL}}^{\mathit{d}=0}\frac{{\mathit{L}}_{\mathrm{\alpha }}}{\mathit{d}+{\mathit{L}}_{\mathrm{\alpha }}}$$ (2)

where ${\mathit{R}}_{\text{NL}}^{\mathit{d}=0}$ is related to the spin-dependent chemical potential at the spin injector and the spin mixing conductance (g^↑↓) at the interfaces between Pt and Cr₂O₃ and L_α = ℏg^↑↓/2παS, where ℏ is the reduced Planck constant, α is the magnetic damping, and S is the saturated spin density in the spin superfluid state. L_α is obtained to be 16.3 ± 1.1 μm at 2 K and 13.3 ± 2.5 μm at 10 K based on the best fitting (red lines in Fig. 3B). As the temperature increases, L_α decreases, and a transition from spin superfluid transport to thermally generated incoherent magnon transport is observed (section S2 and fig. S5). For example, at 80 K, the nonlocal spin signal decays rapidly as a function of spacing, which is very similar to incoherent magnon diffusion in YIG reported previously (25, 30).

Fig. 3. Spacing dependence of the nonlocal spin transport in spin superfluid ground state.

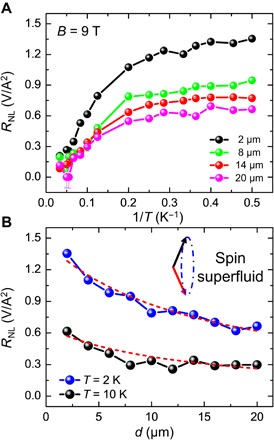
(A) The nonlocal spin signal as a function of 1/T for the spacing between the two Pt strips (d) of 2, 8, 14, and 20 μm. These results are obtained under the in-plane magnetic field of 9 T. (B) The nonlocal spin signal at 2 and 10 K in the spin superfluid ground state as a function of the spacing between the two Pt strips. The red dashed lines are the fitting curves based on spin superfluid model using the Eq. 2.

Because the spin component in the y-z plane (S_y + iS_z) acquires a free U(1) processional motion of the antiferromagnetic moment within the y-z plane, the canted antiferromagnet rotation around the [0001] direction is more favorable. Hence, we investigate the spin superfluid ground state in the (11$\overline{2}$0)-oriented Cr₂O₃ films, of which the spins on Cr atoms are aligned along the [0001] orientation and in the film plane. Figure 4A shows the schematic spin configurations of the (11$\overline{2}$0)-oriented Cr₂O₃ films epitaxially grown on (11$\overline{2}$0)-Al₂O₃ (see Materials and Methods). When the in-plane magnetic field is larger than the spin flop field, a free U(1) processional motion of the antiferromagnetic moment within the y-z plane leads to a spin supercurrent of the x component of the spin density, giving rise to the appurtenance of the nonlocal spin signal, as shown in Fig. 4B. The saturation of the nonlocal spin signal at low temperature and the spacing dependence of the nonlocal spin signal at 2 and 10 K (section S6 and figs. S13 and S14) are consistent with the spin superfluid model (15, 22). Furthermore, as the spin analog of the superconducting effect, the spin superfluid ground state exhibits a critical temperature (T_C), indicated by the rapid increase of the nonlocal spin signal, as shown in Fig. 4C (inset). The T_C versus the in-plane magnetic field is shown in Fig. 4C. The best fit of the boundary of the spin superfluid phase gives a power law with an exponent of 0.65: T_C ~ (B − 3.5)^0.65, as indicated by the red line. The magnetic field dependence of the associated critical temperature follows a ²/₃ power law, suggesting that the transition shares the similar feature as a BEC transition of spin-1 bosons expected theoretically (10, 13).

Fig. 4. Spin superfluid ground state in the canted antiferromagnet (11$\overline{2}$0)-oriented Cr₂O₃.

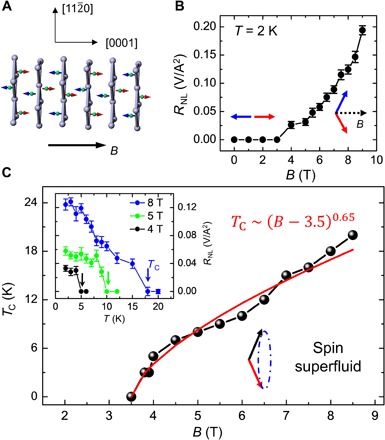
(A) The spin structure of single crystalline antiferromagnetic (11$\overline{2}$0)-oriented Cr₂O₃ thin film. Up (red arrows) and down (blue arrows) spins of the Cr³⁺ ions are aligned in the film plane. (B) The nonlocal spin signal at 2 K as a function of the magnetic field. The nonlocal spin signal is observed when the magnetic field is higher than the spin flop field. (C) The critical temperature as a function of the magnetic field. Red line presents the best fitting curve, which follows a relationship of T_C ~ (B − 3.5)^0.65.

CONCLUSION

In summary, our experiments demonstrate the spin superfluid ground state in canted antiferromagnetic Cr₂O₃ thin films at low temperatures. Our discovery of the long-distance spin transport in superfluid ground state provides an ideal platform for the fundamental physics on the BEC of spin-1 bosons and is extremely important for the development of future spin supercurrent–based applications (15, 34).

MATERIALS AND METHODS

(0001)-Oriented Cr₂O₃ film growth and characterization

Antiferromagnetic insulating (0001)-oriented Cr₂O₃ thin films were epitaxially grown on (0001)-oriented Al₂O₃ substrates via PLD with a base pressure of 2 × 10⁻⁸ mbar. Before the growth of Cr₂O₃ thin films, the Al₂O₃ substrates were subsequently cleaned in a mixture (H₂O₂/NH₄OH/H₂O = 1:1:50) for 1 min, isopropyl alcohol for 1 min, and deionized water for 1 min, and then annealed at 1000°C for 2 hours in an oxygen gas–filled furnace. Then, the Al₂O₃ substrates were loaded into the PLD chamber, and the substrate temperature was increased to 500°C with a rate of 20°C/min in the oxygen partial pressure of 0.03 mbar. The Cr₂O₃ films were deposited from a Cr₂O₃ target with a laser power of (8.0 ± 0.2) mJ and a frequency of 8 Hz. Reflection high-energy electron diffraction (RHEED) was used to monitor the growth of the antiferromagnetic Cr₂O₃ film (fig. S1, A and B). The Cr₂O₃ growth rate was ~0.15 nm/min, inferred from the oscillations of the RHEED intensity during the growth. Atomically flat surfaces were achieved, as evidenced by atomic force microscopy (fig. S1, C and D). The root mean square (RMS) roughness of the (0001)-oriented Al₂O₃ substrate and the ~19-nm Cr₂O₃ film were 0.12 and 0.17 nm, respectively. The thickness of the Cr₂O₃ thin film was estimated to be ~19 nm from both the growth rate and the x-ray diffraction (XRD) after the film growth (fig. S1E).

(11$\overline{2}$0)-Oriented Cr₂O₃ film growth and characterization

(11$\overline{2}$0)-Oriented Cr₂O₃ films were grown on the (11$\overline{2}$0)-oriented Al₂O₃ substrates following the same recipe as (0001)-oriented Cr₂O₃ thin films, except that the (11$\overline{2}$0)-oriented Al₂O₃ substrates were annealed at 1350°C for 2 hours in an oxygen gas–filled furnace before the growth. Figure S2 (A and B) shows the typical RHEED patterns. Atomically flat surfaces were also achieved on (11$\overline{2}$0)-oriented films (fig. S2, C and D), and the RMS roughness of the Al₂O₃ substrate and the ~18 nm Cr₂O₃ film were 0.08 and 0.14 nm, respectively. Figure S2E shows the XRD result of this Cr₂O₃ film.

Nonlocal device fabrication

The nonlocal devices were fabricated using standard e-beam lithography followed by Pt metal deposition with the growth rate of 0.6 Å/s using the dc sputtering system in Ar plasma with a base pressure lower than 8 × 10⁻⁷ mbar. Then, the devices were formed after a lift-off process in acetone. As shown in fig. S3, one long Pt strip (width, 300 nm; length, 100 μm) was used for spin injection via the spin Seebeck effect, and the other one was used for spin detection via the inverse spin Hall effect. The thickness of the Pt strips is ~8 nm, measured by atomic force microscopy. The optical image of the nonlocal device discussed in the main text (d = 10 μm) is shown in fig. S3.

Nonlocal spin transport measurements

The nonlocal spin transport measurements were carried out via standard low-frequency lock-in technique, as illustrated in fig. S3. The ac current (I_AC = 500 μA unless noted otherwise) with a frequency of 7 Hz was applied using Keithley current source (K6221), and the second harmonic voltage was measured using Signal Recovery lock-in amplifier (SR830). The second harmonic resistance (R_2ϖ) was calculated from the second harmonic voltage (V_2ϖ) based on the equation ${\mathit{R}}_{2\mathrm{\varpi }}=\sqrt{2}{\mathit{V}}_{2\mathrm{\varpi }}/{{\mathit{I}}_{\text{AC}}}^2$. During the measurement, the nonlocal devices were rotated in-plane under static magnetic fields in the Physical Property Measurement System (Quantum Design). A low-noise voltage preamplifier (SR560) was used to enhance the signal-to-noise ratio.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/4/eaat1098/DC1

section S1. First and second harmonic results on (0001)-oriented Cr₂O₃ thin film

section S2. Comparison of low-temperature and high-temperature results on (0001)-oriented Cr₂O₃ thin film

section S3. Mechanism for the modest enhancement of the nonlocal spin signal at ~60 K

section S4. Supporting results on extra samples: 6- and 45-nm (0001)-oriented Cr₂O₃ films

section S5. First and second harmonic results on (11$\overline{2}$0)-oriented Cr₂O₃ thin film

section S6. Temperature and spacing dependence of the nonlocal spin transport on (11$\overline{2}$0)-oriented Cr₂O₃ thin film

section S7. Magnetic field dependence of the nonlocal spin transport on (0001)-oriented Cr₂O₃ thin film

fig. S1. RHEED and XRD of the (0001)-oriented Cr₂O₃ thin film (~19 nm) on the (0001)-oriented Al₂O₃ substrate.

fig. S2. RHEED and XRD of the ($11\overline{2}0$)-oriented Cr₂O₃ thin film (~18 nm) on the ($11\overline{2}0$)-oriented Al₂O₃ substrate.

fig. S3. The typical optical image of the nonlocal device and the nonlocal measurement.

fig. S4. The first and second harmonic nonlocal resistance on the ~19-nm (0001)-oriented Cr₂O₃ film.

fig. S5. The transition from spin transport via spin superfluid to that via thermally generated incoherent magnons.

fig. S6. Current dependence of the nonlocal spin transport on the ~19-nm (0001)-oriented Cr₂O₃ film.

fig. S7. The exchange bias between 2-nm Py and the ~19-nm (0001)-oriented film.

fig. S8. Thermal conductivity (κ) measured by the 3ω method for the (0001)-oriented Cr₂O₃ film.

fig. S9. The nonlocal spin transport on the ~6-nm (0001)-oriented Cr₂O₃ film.

fig. 10. The nonlocal spin transport on the ~45-nm (0001)-oriented Cr₂O₃ film.

fig. S11. Temperature dependence of the nonlocal spin transport for (0001)-oriented Cr₂O₃ films with various thicknesses.

fig. S12. The first and second harmonic nonlocal resistance on the ~18-nm ($11\overline{2}0$)-oriented Cr₂O₃ film.

fig. S13. The nonlocal spin transport on the ~18-nm ($11\overline{2}0$)-oriented Cr₂O₃ film.

fig. S14. Current dependence of the nonlocal spin transport on the ~18-nm ($11\overline{2}0$)-oriented Cr₂O₃ film.

fig. S15. Magnetic field dependence of nonlocal spin transport on the ~19-nm (0001)-oriented Cr₂O₃ film.

References (35–39)