Parenchymal strain heterogeneity during oscillatory ventilation: why two frequencies are better than one

Abstract

High-frequency oscillatory ventilation (HFOV) relies on low tidal volumes cycled at supraphysiological rates, producing fundamentally different mechanisms for gas transport and exchange compared with conventional mechanical ventilation. Despite the appeal of using low tidal volumes to mitigate the risks of ventilator-induced lung injury, HFOV has not improved mortality for most clinical indications. This may be due to nonuniform and frequency-dependent distribution of flow throughout the lung. The goal of this study was to compare parenchymal strain heterogeneity during eucapnic HFOV when using oscillatory waveforms that consisted of either a single discrete frequency or two simultaneous frequencies. We utilized a three-dimensional, anatomically structured canine lung model for simulating frequency-dependent ventilation distribution. Gas transport was simulated via direct alveolar ventilation, advective mixing at bifurcations, turbulent and oscillatory dispersion, and molecular diffusion. Volume amplitudes at each oscillatory frequency were iteratively optimized to attain eucapnia. Ventilation using single-frequency HFOV demonstrated increasing heterogeneity of acinar flow and CO₂ elimination with frequency for frequencies greater than the resonant frequency. For certain pairs of frequencies, a linear combination of the two corresponding ventilation distributions yielded reduced acinar strain heterogeneity compared with either frequency alone. Our model demonstrates that superposition of two simultaneous oscillatory frequencies can achieve more uniform ventilation distribution, and therefore lessen the potential for ventilator-induced lung injury, compared with traditional single-frequency HFOV.

NEW & NOTEWORTHY In this study, we simulated oscillatory ventilation with multiple simultaneous frequencies using a computational lung model that includes distributed flow and gas transport. A mechanism of benefit was identified by which ventilation with two simultaneous frequencies results in reduced acinar strain heterogeneity compared with either frequency alone. This finding suggests the possibility of tuning the spectral content of ventilator waveforms according to patient-specific mechanical heterogeneity.

INTRODUCTION

High-frequency oscillatory ventilation (HFOV) relies on low tidal volumes cycled at supraphysiological rates, which produce fundamentally different mechanisms for gas transport compared with conventional mechanical ventilation. Despite the appeal of using low tidal volumes to mitigate the risks of ventilator-induced lung injury (VILI) in conditions such as the acute respiratory distress syndrome, HFOV has not improved mortality in most clinical applications (8, 22, 23, 38). The nonsuperiority of HFOV over conventional mechanical ventilation may be due to its tendency to distribute flow throughout the lung in a nonuniform and frequency-dependent manner, especially in the presence of lung tissue mechanical heterogeneity (4, 6). Reductions in prescribed tidal volume during HFOV may therefore be counterbalanced by increased strain heterogeneity (13). That is, oscillatory ventilation at a single discrete frequency may result in some lung regions being underventilated and predisposed to atelectrauma, whereas other regions are overventilated and subject to volutrauma (3). VILI has also been associated with increased strain rate (26) and mechanical power (11), which depend on both frequency and amplitude of oscillatory stretch and therefore may be regionally amplified during heterogeneous ventilation. Thus maldistribution of oscillatory flow may increase the risk for worsening VILI. Furthermore, heterogeneous distribution of flow may contribute to ventilation-perfusion mismatching and inefficient gas exchange (13).

In a previous study of HFOV in preterm lambs (16), we demonstrated that oscillation with multiple simultaneous frequencies resulted in improved gas exchange and lung recruitment at lower distending pressures compared with more traditional “single-frequency” oscillatory ventilation. We hypothesized that these short-term physiological improvements resulted from a more even distribution of ventilation throughout the heterogeneous surfactant-deficient lung. We further conjectured that during “multifrequency” oscillatory ventilation (MFOV), flow oscillations are distributed throughout the injured lung in accordance with local mechanical properties of the parenchyma and air-liquid interface. Thus particular regions of the lung may be preferentially ventilated by some frequencies yet simultaneously reject other frequencies (4, 13). Such a mechanical filtering effect during MFOV waveform may maximize the participation of various lung regions in gas exchange despite different “preferred” frequencies within each region. As a result, MFOV may produce more efficient CO₂ elimination compared with traditional single-frequency oscillatory ventilation along with a possible reduction in net parenchymal strain heterogeneity and less potential for VILI.

In this study, we hypothesized that oscillatory ventilation with two simultaneous frequencies results in more uniform parenchymal strain distribution compared with oscillation with either frequency alone, with a reduction in peak strains required to maintain eucapnic CO₂ elimination. To test this hypothesis, we relied on our (13) previously published computational model of the canine lung, which allowed for simulated gas transport via direct alveolar ventilation, mixing at bifurcations, turbulent and oscillatory dispersion, as well as molecular diffusion. We compared the distributions of parenchymal strain during traditional single-frequency HFOV and then selected candidate pairs of frequencies for dual-frequency oscillatory ventilation based on a ventilation distribution similarity index. Finally, we assessed whether such a similarity index can be an appropriate criterion for selecting complementary frequencies during dual-frequency oscillatory ventilation.

METHODS

Model Overview

A complete description of our computational lung model can be found in Herrmann et al. (13). Briefly, the model structure is based on a 3-dimensional central airway tree, segmented from a computed tomographic image of a supine dog. Peripheral airways with diameters <2 mm were generated using a space-filling algorithm (34). The model consisted of 40,085 cylindrical airway segments in total, with 19,932 viscoelastic acini. Each airway segment was characterized by a unique length l and diameter d, with luminal volume given by:

$${\text{V}}_{\text{seg}}=\frac{1}{4}\pi d^{2}l.$$ (1)

Regional pleural pressure was assumed to vary with gravity according to the hydrostatic weight of the lung in a supine orientation by 0.25 cmH₂O per centimeter lung height (19, 21), with an average value of −5 cmH₂O. Acinar viscoelasticity was determined according to a second-order polynomial function of local transpulmonary pressure (4, 6, 18). Longitudinal and shunt impedances for each airway segment accounted for pressure losses associated with oscillatory flow, isothermal gas compression, as well as soft tissue and cartilaginous viscoelasticity (17). Flow oscillations delivered at the trachea were distributed throughout the lung periphery using a recursive flow-dividing scheme, according to the local input impedance at each node in the tree (6). Flow in each segment was characterized as laminar or turbulent according to the Reynolds number Re (31):

$$\text{Re}=\frac{{\overline{U}}_{\text{RMS}}d}{\nu },$$ (2)

where Ū_RMS is the root mean square of the time-varying mean axial velocity and ν is kinematic viscosity of the gas. The transition from laminar to turbulent oscillatory flow was assumed to occur at the critical Reynolds number Re_crit = 30 (14, 31).

Gas transport mechanisms.

The transport of CO₂ throughout the airway network was solved as a steady-state problem, being time-averaged throughout the oscillatory ventilation cycle and with total CO₂ elimination equal to metabolic CO₂ production (13). The molar flux of CO₂ through each airway segment was driven by a concentration gradient and characterized by its effective diffusivity D_eff:

$$D_{\text{eff}}=\{\begin{array}{lll}{D}_{\text{mol}}+{\displaystyle \sum }_{k=1}^K{D}_{\text{dis}}^{\text{lam}}\left(f_k\right)\hfill & ,\hfill & \text{Re}<{\text{Re}}_{\text{crit}}\hfill \\ D_{\text{mol}}+D_{\text{dis}}^{\text{tur}}\hfill & ,\hfill & \text{Re}\ge {\text{Re}}_{\text{crit}}\hfill \end{array},$$ (3)

where K is number of distinct oscillation frequencies in multifrequency waveform. During laminar oscillatory flow at multiple frequencies (i.e., Re < Re_crit), D_eff is equal to the sum of its molecular diffusivity D_mol and the laminar dispersion coefficients $D_{\text{dis}}^{\text{lam}}$ computed at each discrete frequency f_k (appendix a). However, during turbulent oscillatory flow, D_eff is equal to the sum of D_mol and the frequency-independent dispersion coefficient $D_{\text{dis}}^{\text{tur}}$ (9, 35) of the form:

$$D_{\text{dis}}^{\text{tur}}=0.7{\overline{U}}_{\text{RMS}}d.$$ (4)

Equation 4 is consistent with previous computational studies (9, 30) based on theoretical (35) and experimental results (29). Oscillatory flows were assumed to be either fully laminar or fully turbulent, ignoring transitional flows. The resulting CO₂ transport resistance due to diffusion and dispersion is given by:

$$R_T^{\text{diff}}=\frac{4\mathcal{R}Tl}{\pi d^2{D}_{\text{eff}}},$$ (5)

where $\mathcal{R}$ is the universal gas constant and T is absolute temperature of the gas.

In our (13) previous model of convective gas transport, we described the linear transport resistance due to gas mixing ($R_T^{\text{mix}}$) during repeated division and recombination of oscillatory flow past airway bifurcations during oscillation at a single discrete frequency. With this approach, $R_T^{\text{mix}}$ is characterized by the oscillation frequency, f, and the mixing volume, V_mix, which quantifies the volume of gas that passes completely through an airway during each period of oscillation. However, during oscillation with multiple simultaneous frequencies, V_mix is computed over one period of the fundamental frequency (f₀) of the broadband flow waveform:

$${\text{V}}_{\text{mix}}=\underset{0}{\overset{1/f_0}{{\displaystyle \int }}}{\dot{\mathrm{V}}}_{\text{mix}}\left(t\right)\text{d}t,$$ (6)

where V̇_mix is the flow contributing to V_mix, given by:

$${\dot{\mathrm{V}}}_{\text{mix}}\left(t\right)=\{\begin{array}{ccc}\dot{\mathrm{V}}\left(t\right)& ,& \left[\dot{\mathrm{V}}\left(t\right)>0\right]\text{\hspace{0.17em}and\hspace{0.17em}}\left[\mathrm{V}\left(t\right)>{\text{V}}_{\text{seg}}\right]\\ 0& ,& \text{otherwise}\end{array}.$$ (7)

V̇(t) is the time-varying flow in an airway segment, V_seg is the lumenal volume of the airway segment, and V(t) is the time integral of flow:

$$\mathrm{V}\left(t\right)=\underset{0}{\overset{t}{{\displaystyle \int }}}\dot{\mathrm{V}}\left(\tau \right)\text{d}\tau .$$ (8)

In practice, V_mix may be computed using numerical integration techniques (15). An example flow waveform through a hypothetical airway segment of 70-ml volume, along with the corresponding V̇_mix and V_mix for the segment, is shown in Fig. 1. For the special case of single-frequency oscillation, this numerical computation of V_mix is consistent with the analytical expression for V_mix in our (13) previous model. The resulting gas transport resistance due to mixing, $R_T^{\text{mix}}$, is then given by:

$$R_T^{\text{mix}}=\frac{\mathcal{R}T}{f_0{\text{V}}_{\text{mix}}}.$$ (9)

The total transport resistance, $R_T^{\text{tot}}$, in each airway segment is given by the parallel combination of diffusive/dispersive and mixing resistances:

$$R_T^{\text{tot}}={\left(\frac{1}{R_T^{\text{diff}}}+\frac{1}{R_T^{\text{mix}}}\right)}^{-1}.$$ (10)

$R_T^{\text{tot}}$ describes the relationship between CO₂ molar flux through an airway segment and CO₂ partial pressure difference across the airway segment. Combining the transport resistances of all airways in the model yields a system of equations describing the relationship between acinar CO₂ partial pressure P_nCO₂ and acinar CO₂ molar flux due to diffusion, dispersion, and mixing Ṁ_nCO₂:

$${\mathit{R}}_{\mathbf{T}}\dot{\mathit{M}}\mathbf{C}{\mathbf{O}}_2=\Delta \mathbf{P}\mathbf{C}{\mathbf{O}}_2,$$ (11)

where R_T is a full matrix of transport resistances, ṀCO₂ is a vector of acinar CO₂ molar fluxes, and ΔPCO₂ is a vector of CO₂ partial pressure differentials between acini and airway opening (13). After solving Eq. 11 to obtain ṀCO₂, acinar CO₂ elimination due to diffusion, dispersion, and mixing, ${\dot{\mathrm{V}}}_n^{\text{DDM}}{\text{CO}}_2$, is computed as:

$${\dot{\mathrm{V}}}_n^{\text{DDM}}{\text{CO}}_2=\frac{\mathcal{R}T}{{\text{P}}_{\text{atm}}}{\dot{M}}_n{\text{CO}}_2,$$ (12)

where P_atm is atmospheric pressure. During ventilation with large tidal volumes, gas transport occurs primarily via direct ventilation, whereby fresh gas is advected directly between the airway opening and acini. Under such circumstances, CO₂ elimination from the nth acinus due to convective ventilation, ${\dot{\mathrm{V}}}_n^{\text{DAV}}{\text{CO}}_2$, is determined by the rate of fresh gas delivery:

$${\dot{\mathrm{V}}}_n^{\text{DAV}}{\text{CO}}_2=\frac{{\text{P}}_n{\text{CO}}_2}{863}{\displaystyle \sum }_{k=1}^K{f}_k·\left|{\mathrm{V}}_{\text{F},n}\left(f_k\right)\right|,$$ (13)

where P_nCO₂ is the CO₂ partial pressure of the nth acinus, 863 is a conversion factor between partial pressure in millimeters of mercury and gas volume fraction (13), and V_F,n(f_k) is the fresh gas delivered to the nth acinus per oscillation at the kth frequency:

$$\left|{\mathrm{V}}_{\text{F},n}\left(f_k\right)\right|={\displaystyle \sum }_{k=1}^K\max \left(\begin{array}{cc}0,& \frac{\left|{\dot{\mathrm{V}}}_n\left(f_k\right)\right|}{\pi f_k}-\left|{\mathrm{V}}_{\text{D},n}^{}\left(f_k\right)\right|\end{array}\right),$$ (14)

where max( ) denotes the maximum of the enclosed argument, and |V̇_n(f_k)| and |V_D,n(f_k)| are the magnitudes of oscillatory flow and dead space delivered at the kth frequency, respectively (13). Total CO₂ elimination for each acinus, V̇_nCO₂, is computed as the sum of ${\dot{\mathrm{V}}}_n^{\text{DDM}}{\text{CO}}_2$ and ${\dot{\mathrm{V}}}_n^{\text{DAV}}{\text{CO}}_2$. Total CO₂ elimination for the entire lung model, V̇_totCO₂, is then the sum of V̇_nCO₂ across all acini:

Fig. 1.

Illustration of method for computing V_mix during ventilation with multiple frequencies of oscillation. In this example, 2 frequencies are used, 3 and 7 Hz, such that f₀ = 1 Hz. The shading indicates where the conditions of V̇(t) > 0 (light and dark) and V(t) > V_seg (dark) are satisfied. V_mix can be calculated from the sum of flow integrals indicated by dark shading for which both conditions are satisfied. Equivalently, V_mix can be calculated from the sum of the lengths of the dark lines denoting the local maxima of V(t) − V_seg.

$${\dot{\mathrm{V}}}_{\text{tot}}{\text{CO}}_2={\displaystyle \sum }_{n=1}^N\left({\dot{\mathrm{V}}}_n^{\text{DDM}}{\text{CO}}_2+{\dot{\mathrm{V}}}_n^{\text{DAV}}{\text{CO}}_2\right).$$ (15)

Figure 2 illustrates which of the modeled gas transport mechanisms dominates overall gas transport during eucapnic single-frequency ventilation between 0.3 and 26 Hz. Direct acinar ventilation accounts for the majority of total respiratory gas exchange at low frequencies (i.e., <2 Hz) yet is entirely absent at high frequencies (i.e., >5 Hz). The greatest contribution to the overall rate of gas transport in individual airways derives from the transport mechanism describing bifurcation mixing due to the repetitive division and recombination of gases. The contribution of turbulent mixing to gas transport in individual airways increases at higher frequencies, dominating in the larger central airways during delivery of small volume amplitudes at high instantaneous flow rates. This behavior is consistent with the analysis of bifurcating flow regimes by Jan et al. (14) as well as the numerical simulations performed by Choi et al. (5).

Fig. 2.

Airway segments and acini labeled according to gas transport mechanisms. A: decision trees used for labeling airway segments according to the dominant gas transport mechanism contributing to the overall rate of gas transport within each individual airway. Acini are labeled if fresh gas is advected via bulk flow directly into the acinar space. B: airways and acini colored according to gas transport mechanisms during eucapnic ventilation at various frequencies using the tidal volumes indicated in milliliters. Acini that do not receive fresh gas ventilation are not shown. Gravitational direction (g) is indicated for a supine orientation.

Comparison of Single-Frequency and Dual-Frequency Oscillation

To identify plausible candidate frequency pairs for dual-frequency simulations, each combination of two distinct oscillatory frequencies was considered by taking the inner product between their respective normalized acinar flow distributions:

$$S_{\dot{\mathrm{V}}}\left(f_1,f_2\right)=\frac{{\displaystyle \sum }_{n=1}^N\left|{\dot{\mathrm{V}}}_n\left(f_1\right)\right|\left|{\dot{\mathrm{V}}}_n\left(f_2\right)\right|}{\sqrt{{\displaystyle \sum }_{n=1}^N{\left|{\dot{\mathrm{V}}}_n\left(f_1\right)\right|}^2}\sqrt{{\displaystyle \sum }_{n=1}^N{\left|{\dot{\mathrm{V}}}_n\left(f_2\right)\right|}^2}},$$ (16)

where S_V̇, the value of the inner product, quantifies the ventilation distribution similarity. Thus S_V̇ = 1 implies two identical distributions, whereas S_V̇ = 0 implies two orthogonal distributions. Figure 3 shows a schematic lung with three mechanically heterogeneous compartments as a simplified example of quantifying ventilation distribution similarity.

Fig. 3.

Two examples of ventilation distribution similarity (S_V̇) and correlation coefficient (r) in a schematic lung with three mechanically heterogeneous compartments. The frequency-dependent fraction of oscillatory flow received by each compartment is indicated for two frequencies, f₁ and f₂. In the case of similar distributions (A), the central compartment receives the greatest proportion of oscillatory flow at both frequencies, and the corresponding value of S_V̇ is close to unity, whereas r is close to +1. In the case of dissimilar distributions (B), the compartments underventilated at f₁ are overventilated at f₂ and vice versa; thus the value of S_V̇ is close to 0, and r is close to −1. See main text for definitions of S_V̇ and r.

Figure 4A shows the contours of S_V̇ for each permutation of two frequencies from 0.2 to 40 Hz, spaced over 0.2-Hz intervals. Identifying pairs of frequencies with the lowest degree of similarity (i.e., the smallest values of S_V̇) reveals the most complementary pairs, i.e., those pairs that are most able to compensate for each other’s respective underventilated and overventilated regions. Alternatively, the Pearson correlation coefficient (r) between normalized acinar flow distributions for each frequency pair can also be used to identify complementary distributions. Positive values of r correspond to similar distributions, such that acini tend to receive either above-average or below-average amounts of flow at both frequencies. By contrast, negative values of r correspond to dissimilar distributions, such that acini tend to receive above-average flow at one frequency yet below-average at the other. Figure 4B shows the contours of r for each permutation of two frequencies between 0.2 and 40 Hz. Identifying pairs of frequencies with the most negative correlation coefficients reveals the most complementary pairs.

Fig. 4.

Contours of ventilation distribution similarity (S_V̇; A) and correlation coefficient (r; B) in the canine lung model for pairs of frequencies between 0.1 and 40 Hz. The line of identity (dotted line) represents comparisons between each frequency and itself such that S_V̇(f₁,f₁) = 1 and r(f₁,f₁) = +1. The contours of S_V̇ are symmetric about the line of identity such that S_V̇(f₁,f₂) = S_V̇(f₂,f₁) and r(f₁,f₂) = r(f₂,f₁). Symbols correspond to frequency pairs selected for further examination: 12 and 26 Hz (○) 0.3 and 12 Hz (△). See main text for definitions of S_V̇ and r.

Based on the contour maps shown in Fig. 4, we selected a pair of frequencies representing a low value of S_V̇ (i.e., dissimilar ventilation distributions) for simulation of gas transport. We selected the local minimum of the S_V̇ contour map corresponding to 12 and 26 Hz. For comparison, another pair of frequencies with a high value of S_V̇ was also selected for simulation, at 0.3 and 12 Hz. For each pair of frequencies, multiple waveforms were constructed to define flow at the airway opening (V̇_ao) according to the following template:

$${\dot{V}}_{\text{ao}}\left(t\right)={\text{Ψ}}_{\text{euc}}\left[\beta \sin \left(2\pi f_{1}t\right)+\left(1-\beta \right)\sin \left(2\pi f_{2}t+\varphi \right)\right],$$ (17)

where β is a scaling factor adjusting the relative contributions of f₁ vs. f₂ such that 0 ≤ β ≤ 1, ϕ is the relative phase offset between the flow oscillations such that 0 ≤ ϕ ≤ 2π, and Ψ_euc > 0 is a scaling factor used to adjust the flow amplitudes delivered by the MFOV waveform. For any combination of f₁, f₂, β, and ϕ, the corresponding value of Ψ_euc was iteratively optimized to attain eucapnic CO₂ elimination, which was approximated according to the assumed weight of the animal (13). For simplicity, the value of ϕ was constrained to be 0 for all simulations.

Following the determination of eucapnic scaling, the distribution of peak acinar volumetric strain (ε_V,n) was computed by calculating the range of time-varying acinar volume, V_n(t), divided by the minimum value (min):

$${\epsilon }_{\text{V},n}=\frac{\max \left[{\text{V}}_n\left(t\right)\right]-\min \left[{\text{V}}_n\left(t\right)\right]}{\min \left[{\text{V}}_n\left(t\right)\right]}.$$ (18)

The distribution of acinar root-mean-square volume (V_RMS,n) was also used to assess distributed ventilation heterogeneity:

$${\text{V}}_{\text{RMS},n}=\sqrt{f_0\underset{0}{\overset{1/f_0}{{\displaystyle \int }}}{\left[{\text{V}}_n\left(t\right)-{\overline{\mathrm{V}}}_n\right]}^2\text{d}t},$$ (19)

where V̄_n is time-averaged acinar volume given by:

$${\overline{\mathrm{V}}}_n=f_0\underset{0}{\overset{1/f_0}{{\displaystyle \int }}}{\text{V}}_n\left(t\right)\text{d}t.$$ (20)

The values of V_RMS,n and V̄_n in Eqs. 19 and 20 were numerically approximated using trapezoidal integration (15).

Simulations

The recursive algorithms for computing and storing impedances and determining advective flow division throughout the tree were written in C++. Computation time for generating advective flow distribution at each distinct f was ~3 s on a 64-bit computer with an Intel Core i7-950 processor operating at 3.07 GHz with 12-GB random-access memory. The gas transport model was written and executed in MATLAB (version R2016a; The MathWorks, Natick, MA). Total computation time for each distinct dual-frequency simulation was ~70 s.¹

RESULTS

Two pairs of frequencies were selected for gas transport simulations based on ventilation distribution similarity (S_V̇) and correlation coefficient (r), as indicated by the symbols on the contour maps of Fig. 4. The frequency pair with similar distributions was chosen at 0.3 and 12 Hz, with S_V̇ = 0.98 and r = +0.69. The pair with dissimilar distributions was chosen at 12 and 26 Hz, with S_V̇ = 0.85 and r = −0.64. Figure 5 shows the anatomic distributions of acini receiving relatively more or less oscillatory flow at 0.3, 12, and 26 Hz compared with a perfectly uniform distribution. Acinar flow magnitudes were normalized relative to their corresponding values for a symmetric, homogeneous lung with rigid airway walls and no gas compression (6). Figure 6 shows scatterplots comparing normalized ventilation distributions between frequencies for both selected frequency pairs. The dissimilar distributions at 12 and 26 Hz exhibit a majority of acini (72.7%) that are preferentially ventilated by only one frequency or the other, whereas the similar distributions at 0.3 and 12 Hz exhibit only a minority of acini (17.3%) with the same complementary behavior.

Fig. 5.

Acini labeled according to relative share of delivered oscillatory flow during 0.3-, 12-, and 26-Hz ventilation. Acinar flow is normalized by the flow amplitude delivered at the trachea divided by the total number of acini such that values above or below 1 represent, respectively, acini receiving more (red) or less (blue) than their respective shares of uniformly distributed flow. Note that color bars are scaled differently for each frequency to emphasize the regional distributions of relative over- and underventilation. Various view angles are provided, with gravitational direction (g) indicated for a supine orientation (directed downward, out of the page, or upward).

Fig. 6.

Scatterplots comparing normalized acinar flow distributions at 2 frequencies, where each point represents a single acinus, and horizontal or vertical position correspond to normalized flow amplitude in each acinus at either frequency. Two examples are shown: similar distributions at 0.3 vs. 12 Hz with S_V̇ = 0.98 and r = +0.69 (A) and dissimilar distributions at 12 vs. 26 Hz with S_V̇ = 0.85 and r = −0.64 (B). The 4 quadrants delineate acini that receive either above-average (i.e., >1.0) or below-average (i.e., <1.0) amounts of oscillatory flow at 1 or both frequencies.

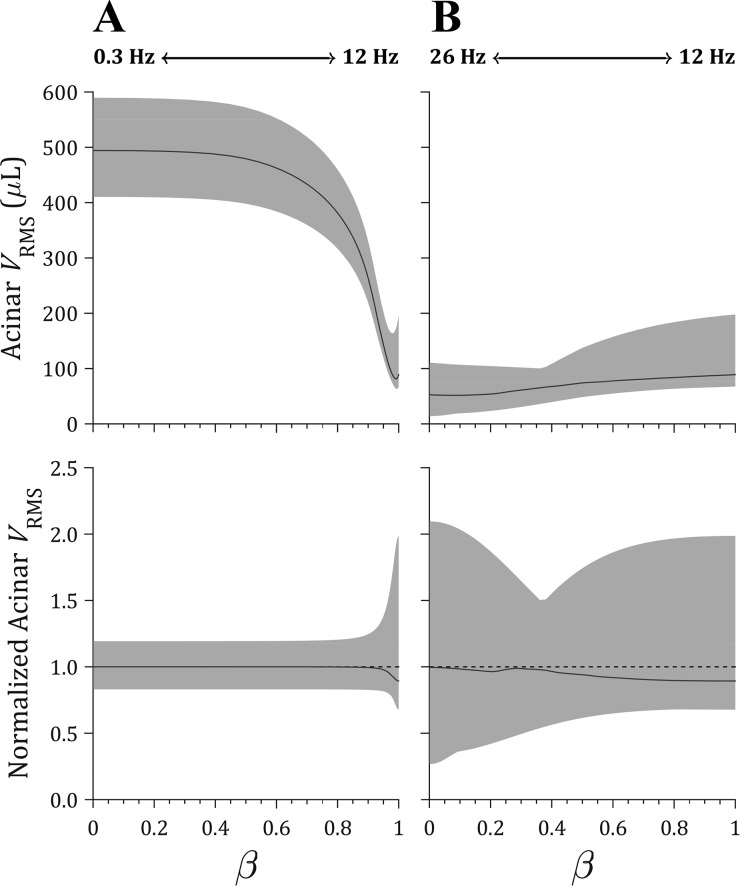
Figure 7 shows the required eucapnic flow scaling for dual-frequency waveforms constructed from various linear combinations of each frequency in the selected frequency pairs, according to Eq. 17. For all values of β, values of Ψ_euc were iteratively adjusted to achieve total CO₂ elimination within 0.3% error of the predicted metabolic CO₂ production of 1.93 × 10⁻³ l/s for a 25-kg dog. Figure 8 shows the resulting distributions of acinar peak volumetric strain (ε_V,n), and Fig. 9 shows distributions of acinar root-mean-square volume (V_RMS,n). Comparing distributed ventilation using oscillations at only a single frequency (i.e., at β = 0 or β = 1 only), 0.3-Hz ventilation produced the least heterogeneity in both strain and V_RMS but also the largest magnitudes of strain compared with either 12 or 26 Hz. For example, the range of ε_V,n, reported as median (minimum, maximum), was 15.5% (12.3%, 19.4%) during single-frequency ventilation at 0.3 Hz compared with 2.8% (6.5%, 2.1%) at 12 Hz or 1.6% (0.5%, 3.4%) at 26 Hz. For the dual-frequency waveforms constructed using 0.3 and 12 Hz, no improvement in ventilation heterogeneity was observed for any linear combination of the two frequencies compared with either single frequency alone (i.e., 0 < β < 1 compared with β = 0 or β = 1). However, for waveforms using 12- and 26-Hz oscillations, an optimal value of β = 0.4 was found to provide the greatest reduction in the difference between the maximum and minimum values of normalized acinar strain and V_RMS. Specifically, at β = 0.4, the range of normalized strain was reduced by 50.8% compared with 26 Hz (β = 0) and 37.2% compared with 12 Hz (β = 1).

Fig. 7.

Eucapnic flow scaling (Ψ_euc) for dual-frequency waveforms constructed according to Eq. 17 using 0 ≤ β ≤ 1 to scale the contribution of each frequency, using oscillations at either 0.3 and 12 Hz (A) or 12 and 26 Hz (B). Each point represents a single simulation. Corresponding volume waveforms at the airway opening are shown for each frequency pair at select values of β.

Fig. 8.

Distributions of acinar peak volumetric strain (ε_V) for dual-frequency waveforms constructed according to Eq. 17 using 0 ≤ β ≤ 1 to scale the contribution of each frequency, using oscillations at either 0.3 and 12 Hz (A) or 12 and 26 Hz (B). Distributions are represented by the median (solid line) and full range between minimum and maximum value (shaded region). Normalized distributions are shown with the mean value normalized to unity (dotted line).

Fig. 9.

Distributions of acinar root-mean-square volume (V_RMS) for dual-frequency waveforms constructed according to Eq. 17 using 0 ≤ β ≤ 1 to scale the contribution of each frequency using oscillations at either 0.3 and 12 Hz (A) or 12 and 26 Hz (B). Distributions are represented by the median (solid line) and full range between minimum and maximum value (shaded region). Normalized distributions are shown with the mean value normalized to unity (dotted line).

DISCUSSION

In this study, we extended an existing computational model of distributed flow and gas transport (13) to simulate ventilation heterogeneity during oscillatory ventilation with either a single frequency or two frequencies delivered simultaneously. By choosing pairs of frequencies with complementary ventilation distributions, we demonstrated that regional underventilation at one frequency may be compensated by regional overventilation at the other frequency. Thus an optimal linear combination of two frequencies can be identified that yields the least amount of parenchymal strain heterogeneity compared with either single frequency alone (Figs. 8B and 9B). However, for a pair of oscillatory frequencies yielding similar ventilation distributions, no linear combination was found to reduce ventilation heterogeneity (Figs. 8A and 9A). This finding suggests that it is possible to optimize the spectral content of oscillatory waveforms to achieve substantial reductions in ventilation heterogeneity and parenchymal strain.

In these simulations of eucapnic oscillatory ventilation in a canine lung, low frequencies produced the lowest degree of ventilation heterogeneity yet the largest magnitudes of regional strain. However, increasing oscillatory frequency resulted in reduced regional strain but increased strain heterogeneity, especially for frequencies greater than the resonant frequency of this model, f_res = 7.5 Hz (13). The resonant frequency indicates the transition from flows dominated by elastic forces (f < f_res) to flows dominated by inertial forces (f > f_res; Refs. 4, 6). Thus high-frequency oscillatory ventilation (HFOV) may reduce parenchymal strain yet increase both strain rate and strain heterogeneity compared with conventional mechanical ventilation (20, 25, 26). This trade-off may in part explain the nonsuperiority of HFOV over conventional mechanical ventilation in patients with mechanically heterogeneous lungs (8, 22, 38).

Our computational model highlights a means by which both parenchymal strain and strain heterogeneity may be minimized. If multiple frequencies are delivered simultaneously, the respective contributions of each frequency to the combined distribution of parenchymal strain may be tuned toward a particular objective, e.g., minimizing strain heterogeneity. By extending this concept of dual-frequency oscillation to the more general case of three of more frequencies (16), one may further exploit frequency-dependent ventilation distribution to mitigate adverse consequences of parenchymal strain heterogeneity. This proposed mechanism of benefit may in part explain improvements in oxygenation and gas exchange reported during experimental use of multifrequency oscillatory ventilation in surfactant-deficient preterm lungs (16). These findings are also relevant to high-frequency percussive ventilation, which involves high-frequency oscillations superimposed on conventional mechanical ventilation waveforms (1, 7, 28). Large reductions in parenchymal strain at lower frequencies may be achieved during high-frequency percussive ventilation by supplementary gas transport using a relatively small contribution of superimposed high-frequency oscillation.

Two criteria were proposed to evaluate candidate frequency pairs in this study: the ventilation distribution similarity (S_V̇) and the correlation coefficient (r). As shown in Fig. 4, S_V̇ and r demonstrate close agreement with each other over the range of frequencies from 0.1 to 30 Hz, suggesting that the outcome of candidate frequency pair selection may not be specific to the particular criterion used for evaluation.

Although peak acinar volumetric strain and specific ventilation are typically used to assess regional ventilation heterogeneity during tidal breathing (2, 27), these metrics may not be directly applicable during oscillation with two or more frequencies, since the corresponding regional volume fluctuations will not oscillate between a consistent minimum and maximum. Rather, parenchymal strain may exhibit various local minima and maxima. Thus ventilation heterogeneity during multifrequency oscillation may be more appropriately characterized by the root-mean-square of regional volume fluctuations (V_RMS; Ref. 16). V_RMS describes the variance of regional distension about a mean lung volume, which is proportional to volume amplitude during single-frequency oscillatory ventilation yet also accounts for oscillation at multiple distinct frequencies. In Figs. 8 and 9, the distributions of peak acinar volumetric strain (ε_V,n) and V_RMS,n exhibited close agreement, suggesting that the analysis of ventilation heterogeneity is not sensitive to the choice of either metric.

Limitations

The modeling assumptions and validation for the single-frequency gas transport model have been presented in our (13) previous study. Additional comparison with distributed strain measured on the pleural surface of excised canine lungs is provided in appendix b. Our currently proposed extension to accommodate two frequencies of oscillations simultaneously has been derived using a similar conceptual framework. However, to our knowledge, no robust experimental data are available to validate these model simulations. Specific or quantitative predictions based on this model should therefore be treated with appropriate caution. Particularly, our simulations assume that the mechanical behavior of the lung is linear and time-invariant. Thus superposition of two sinusoidal oscillations at the airway opening results in a simple linear combination of the respective flow distributions at each frequency. However, nonlinear mechanical properties of an actual mammalian lung may lead to unpredictable distortion and interaction of superimposed oscillations (32, 33, 39). Experimental imaging techniques such as frequency-selective computed tomography (12) or optical coherence tomography (24) may be used to assess further the extent of nonlinear mechanical behavior during multifrequency oscillation in situ.

This particular analysis of simulated multifrequency oscillation examined only two specific pairs of frequencies, to establish the feasibility of using a multifrequency approach to reduce parenchymal strain heterogeneity compared with single-frequency oscillation in a computational model. Furthermore, the simulations were performed using a model of healthy canine lungs, with all mechanical heterogeneity derived only from gravitational gradients in transpulmonary pressure and airway network asymmetries. Nonetheless, this healthy model exhibited substantial ventilation heterogeneity at high frequencies (10, 20), indicating that exploiting frequency-dependent ventilation heterogeneity may be possible even within lungs with homogeneous tissue compliance. The particular distribution of regional strain may be appreciably altered under injured conditions (13), yet the rationale for applying a multifrequency approach remains the same (16). The results of these simulations warrant further investigation, involving optimization of the spectral content in oscillatory waveforms using a larger number of distinct frequencies. Such an optimization procedure may involve an evaluation of the ventilation distribution similarity, similar to that presented in Fig. 4. However, the prospect of translating these computational modeling results into a practical in vivo approach for identification of optimal frequencies presents several considerable technical challenges, not the least of which is noninvasive quantification of frequency-dependent ventilation heterogeneity (10, 27).

Conclusion

Although high-frequency oscillatory ventilation achieves CO₂ elimination with reduced parenchymal strain compared with conventional mechanical ventilation, increased strain heterogeneity during HFOV may be injurious to the lung. Heterogeneity of regional mechanical properties and airway network asymmetry result in frequency-dependent distributions of oscillatory flow, especially at high frequencies. Such frequency-dependent heterogeneity in ventilation may be exploited by combining multiple simultaneous frequencies of oscillation. Dual-frequency oscillatory ventilation may provide more uniform ventilation throughout the heterogeneous lung, such that regional maldistribution of parenchymal strain can be minimized by using oscillatory frequencies with dissimilar ventilation distributions. This unique oscillatory modality may thus have utility for the treatment of patients with heterogeneous lung injury by minimizing the extremes of cyclic parenchymal strain and reducing the risk of ventilator-induced lung injury.

GRANTS

This work was supported in part by the Medical Technologies Centre of Research Excellence at the University of Auckland (M. H. Tawhai), National Heart, Lung, and Blood Institute Grants UM1-HL-108724, R01-HL-112986, and R01-HL-126838 (D. W. Kaczka), and the University of Iowa, Department of Anesthesia (D. W. Kaczka and J. Herrmann) and by the Office of the Assistant Secretary of Defense for Health Affairs through the Peer Reviewed Medical Research Program under Award no. W81XWH-16-1-0434 (D. W. Kaczka).

DISCLAIMERS

Opinions, interpretations, conclusions, and recommendations are those of the authors and are not necessarily endorsed by the U.S. Department of Defense.

DISCLOSURES

D. W. Kaczka and J. Herrmann are coinventors on a pending patent involving multifrequency oscillatory ventilation (MFOV). In addition, they are cofounders and shareholders of OscillaVent, Inc.

AUTHOR CONTRIBUTIONS

J.H., M.H.T., and D.W.K. conceived and designed research; J.H. and M.H.T. performed experiments; J.H., M.H.T., and D.W.K. analyzed data; J.H., M.H.T., and D.W.K. interpreted results of experiments; J.H. and D.W.K. prepared figures; J.H. and D.W.K. drafted manuscript; J.H., M.H.T., and D.W.K. edited and revised manuscript; J.H., M.H.T., and D.W.K. approved final version of manuscript.

APPENDIX A: LAMINAR OSCILLATORY DISPERSION

In this analysis of laminar oscillatory dispersion during flow with multiple simultaneous frequencies, we follow the reasoning and nomenclature of Watson (37). Consider multifrequency oscillatory flow in a tube with velocity profile:

$$w\left(x,y,t\right)={\displaystyle \sum }_{k=1}^K\mathfrak{N}\mathfrak{e}\left[F_k\left(x,y\right)e^{j{\omega }_{k}t}\right],$$ (A1)

where k denotes the angular oscillation frequencies ω_k = 2πf_k from 1 to K, j is the unit imaginary number, and F_k = F_k(x,y) is velocity amplitude distribution over the cross-section in the x–y plane, which is periodic in time t. The operator $\mathfrak{N}\mathfrak{e}[\cdots ]$ denotes the real part of the complex-valued argument within the brackets. The concentration profile of a contaminant species contained in the carrier gas will then be of the form (37):

$$\theta \left(x,y,z,t\right)=-\gamma z+{\displaystyle \sum }_{k=1}^K\mathfrak{N}\mathfrak{e}\left[\gamma G_k\left(x,y\right)e^{j{\omega }_{k}t}\right],$$ (A2)

where z is the axial direction, γ is a constant corresponding to a linear concentration gradient in the axial direction, and G_k = G_k(x,y) is the modulated amplitude distribution over the cross-section in the x–y plane and is periodic in time t with angular frequency ω_k, such that the concentration amplitude distribution is given by γG_k. The rate of molar flux of the contaminant has advective and diffusive terms integrated over the cross-section S is given by (37):

$$\underset{S}{\overset{}{{\displaystyle \iint }}}\left(w\theta -D_{\text{mol}}\frac{\partial \theta }{\partial z}\right)\text{d}x\text{d}y,$$ (A3)

where D_mol is molecular diffusivity and ∂ indicates partial derivative. This expands to:

$$\underset{S}{\overset{}{{\displaystyle \iint }}}\left(\gamma D_{\text{mol}}+\frac{1}{2}\left[{\displaystyle \sum }_{k=1}^K\left(F_k{e}^{j{\omega }_{k}t}+F_k^{*}{e}^{-j{\omega }_{k}t}\right)\right]\times \left\{-\gamma z+\frac{1}{2}\gamma \left[{\displaystyle \sum }_{k=1}^K\left(G_k{e}^{j{\omega }_{k}t}+G_k^{*}{e}^{-j{\omega }_{k}t}\right)\right]\right\}\right)\text{d}x\text{d}y,$$ (A4)

where the asterisks denote complex conjugates. The expansion of the product produces oscillatory terms (i.e., terms preceding $e^{j{\omega }_{k}t}{e}^{j{\omega }_{k}t}=e^{2j{\omega }_{k}t}$ or preceding $e^{j{\omega }_{k}t}{e}^{-j{\omega }_{i}t}=e^{j\left({\omega }_k-{\omega }_i\right)t}$ with i ≠ k) and steady terms (i.e., terms preceding $e^{j{\omega }_{k}t}{e}^{-j{\omega }_{k}t}$ = 1). The mean rate of flux, averaged over time, is:

$$\underset{S}{\overset{}{{\displaystyle \iint }}}\left\{\gamma D_{\text{mol}}+\frac{1}{4}\gamma \left[{\displaystyle \sum }_{k=1}^K\left(F_k{G}_k^{*}+F_k^{*}{G}_k\right)\right]\right\}\text{d}x\text{d}y,$$ (A5)

wherein all oscillatory terms are reduced to 0 in the time-averaging, and only the steady terms remain (37). The effective diffusivity is:

$$D_{\text{eff}}=D_{\text{mol}}\left(1+R_D\right),$$ (A6)

where R_D is the relative increase in diffusivity compared with molecular diffusivity, given by:

$$R_D=\frac{1}{4D_{\text{mol}}{A}_S}\underset{S}{\overset{}{{\displaystyle \iint }}}\left[{\displaystyle \sum }_{k=1}^K\left(F_k{G}_k^{*}+F_k^{*}{G}_k\right)\right]\text{d}x\text{d}y,$$ (A7)

which rearranges to:

$$R_D={\displaystyle \sum }_{k=1}^K\left[\frac{1}{4D_{\text{mol}}{A}_S}\underset{S}{\overset{}{{\displaystyle \iint }}}\left(F_k{G}_k^{*}+F_k^{*}{G}_k\right)\text{d}x\text{d}y\right],$$ (A8)

where A_S is the area of the cross-section S, and the term inside the summation is identical to the relative increase in diffusivity for any individual frequency of oscillation (37). Thus the effective diffusivity is given by:

$$D_{\text{eff}}=D_{\text{mol}}+{\displaystyle \sum }_{k=1}^K{D}_{\text{dis}}^{\text{lam}}\left(f_k\right).$$ (A9)

Equation A9 relies on the reduction of time-averaged oscillatory terms to 0 over a long period of oscillation, i.e., the elimination of $e^{2j{\omega }_{k}t}$ and $e^{j\left({\omega }_k-{\omega }_i\right)t}$ terms in the transition from Eq. A4 to A5. Therefore, this model of dispersion during simultaneous multiple frequencies may not apply when the beat frequency (i.e., the difference between any 2 frequencies) is small.

APPENDIX B: COMPARISON WITH EXPERIMENTAL STRAIN MEASUREMENTS

In our (13) previous work, we demonstrated that the tidal volume required for eucapnic ventilation during single-frequency oscillatory ventilation was consistent with the experimental findings of Venegas et al. (36). The distribution of volumetric strain within lungs in vivo is difficult to quantify experimentally, especially during rapid motion such as during high-frequency oscillatory ventilation. Lehr et al. (20) used stroboscopic photography to capture time-varying motion of grid points marked on the pleural surface of an excised canine lung. They reported area strain measurements during oscillations at 1, 15, and 30 Hz. We may compare our simulated distributions of volumetric strain to the area strain distributions reported by Lehr et al. (20) by first adjusting the simulated volume oscillations to achieve the same ratio of volume amplitude to total lung volume. Lehr et al. (20) reported using 100-ml volume oscillations applied to a lung of total volume 1,320 ml, expecting volumetric strains of ~7.6%. Assuming isotropic expansion and contraction, they expected the corresponding area strains to be two-thirds of the volumetric strain, or ~5.1%. Figure A1 shows the mean and standard deviation of pleural surface area strain amplitudes and phases reported by Lehr et al. (20) as well as the equivalent acinar area strain amplitudes and phases computed from our simulations (assuming isotropic deformation). Both acinar strain amplitude heterogeneity and phase heterogeneity increase at high oscillation frequencies above resonant frequency (7.5 Hz in our model). This trend is also consistent with increasing heterogeneity in alveolar pressure amplitudes and phases measured by Fredberg et al. (10), although pressure measurements alone cannot be used to infer volumetric strain.

Fig. A1.

Comparison between experimental and simulated acinar area strains. Experimental data for pleural surface area strain reported by Lehr et al. (20) is indicated by mean (○) and standard deviation (error bars) at 1, 15, and 30 Hz. Equivalent area strain for our model assuming isotropic deformation during simulated ventilation is shown as mean (dashed gray line) and standard deviation (solid gray lines). A: area strain amplitude is reported during oscillation using a constant ratio of 7.6% oscillatory volume amplitude relative to total lung volume (see main text for additional experimental details). B: area strain phase is reported relative to volume phase measured at the airway opening. deg, Degrees.