Potential for noninvasive assessment of lung inhomogeneity using highly precise, highly time-resolved measurements of gas exchange

Abstract

Inhomogeneity in the lung impairs gas exchange and can be an early marker of lung disease. We hypothesized that highly precise measurements of gas exchange contain sufficient information to quantify many aspects of the inhomogeneity noninvasively. Our aim was to explore whether one parameterization of lung inhomogeneity could both fit such data and provide reliable parameter estimates. A mathematical model of gas exchange in an inhomogeneous lung was developed, containing inhomogeneity parameters for compliance, vascular conductance, and dead space, all relative to lung volume. Inputs were respiratory flow, cardiac output, and the inspiratory and pulmonary arterial gas compositions. Outputs were expiratory and pulmonary venous gas compositions. All values were specified every 10 ms. Some parameters were set to physiologically plausible values. To estimate the remaining unknown parameters and inputs, the model was embedded within a nonlinear estimation routine to minimize the deviations between model and data for CO₂, O₂, and N₂ flows during expiration. Three groups, each of six individuals, were studied: young (20–30 yr); old (70–80 yr); and patients with mild to moderate chronic obstructive pulmonary disease (COPD). Each participant undertook a 15-min measurement protocol six times. For all parameters reflecting inhomogeneity, highly significant differences were found between the three participant groups (P < 0.001, ANOVA). Intraclass correlation coefficients were 0.96, 0.99, and 0.94 for the parameters reflecting inhomogeneity in deadspace, compliance, and vascular conductance, respectively. We conclude that, for the particular participants selected, highly repeatable estimates for parameters reflecting inhomogeneity could be obtained from noninvasive measurements of respiratory gas exchange.

NEW & NOTEWORTHY This study describes a new method, based on highly precise measures of gas exchange, that quantifies three distributions that are intrinsic to the lung. These distributions represent three fundamentally different types of inhomogeneity that together give rise to ventilation-perfusion mismatch and result in impaired gas exchange. The measurement technique has potentially broad clinical applicability because it is simple for both patient and operator, it does not involve ionizing radiation, and it is completely noninvasive.

INTRODUCTION

Inhomogeneities in gas exchange within the lung occur physiologically through, for example, small-scale variations in specific ventilation of lung units, the effects of gravity on lung expansion, and the effects of different dead space-to-alveolar volume ratios between hilar and peripheral lung units. Inhomogeneities also arise pathologically, and the consequent alveolar ventilation-perfusion (V̇_A:Q̇) mismatch is a very common cause of respiratory failure. Furthermore, because pathological change within the lung tends not to affect all lung units equally (13), changes in the degree of inhomogeneity in the lung may provide a sensitive early indicator of disease. Despite these considerations, no simple, noninvasive technique to assess inhomogeneity has become part of a standard lung function test.

This study seeks to explore the possibility that, if measured with sufficient accuracy, there is enough information contained within the way that expiratory gases emerge from the lungs during steady breathing and during a subsequent period of inert gas washout to infer much of the form and degree of inhomogeneity present within the lung.

There are many factors that influence the form of the expiratory profiles for CO₂, O₂, and N₂, and because of this, it is impossible to devise a process by which parameters reflecting different aspects of lung inhomogeneity can be calculated directly from the profiles. Instead, the approach we adopt is to devise a model of gas exchange in the lung that represents different aspects of inhomogeneity through a set of parameter values. This model is then nested within a nonlinear least-squares estimation routine to determine the model parameters that best approximate the manner in which CO₂, O₂, and N₂ emerge during expiration over the course of the experimental period.

Pure shunt and lung units with very low V̇_A:Q̇ do not contribute to the signal in the expired gas because there is either no, or very little, gas flow associated with these (31). However, the magnitude of these components can be determined from the difference between the (systemic) arterial saturation predicted by the model and that recorded experimentally by pulse oximetry.

The methods section describes the development of the model and estimation process. It also describes the experimental technique that provides the highly accurate measurements of CO₂ and O₂ flow at the mouth. Testing of the process is undertaken using both synthetic data and data from a human study. The human study involves three groups of participants: healthy young individuals, healthy older individuals, and individuals with chronic obstructive pulmonary disease (COPD). A particular focus of the human study is to determine the reproducibility of the results from test to test.

METHODS

Protocol and Experimental Approach

The experimental protocol adopted was to collect data during 10 min of air breathing followed by 5 min of pure oxygen breathing to wash out the nitrogen in the lungs. In order to provide gas exchange data of sufficient accuracy to recover parameters reflecting inhomogeneity, we used the recently described technique of in-airway molecular flow sensing (MFS) (7). In brief, this uses laser absorption spectroscopy to measure the concentration of O₂, CO₂, and water vapor every 10 ms within the airway. The balance gas (mostly N₂) can then be calculated by subtraction. The advantages of this technique are that it is fast, highly linear, and the measurements take place within the airway. This last feature means that the measurements are made with no time delay, enabling them to be accurately aligned with measurements of respiratory flow, and that they are made under the same physicochemical conditions (temperature, pressure) as the measurement of flow. The inclusion of water vapor along with O₂ and CO₂ within the gas analyses enables an accurate calculation every 10 ms of the density and viscosity of the gas, which in turn allows a much greater accuracy of flow measurement than when these physical properties are unknown.

Parameterization of Inhomogeneity

Inhomogeneity is often considered through its effects on the V̇_A:Q̇ distribution in the lung. However, there are some limitations to this approach. First, neither V̇_A nor Q̇ are strictly variables that are intrinsic to the lung because both are principally determined by metabolic rate. Second, the V̇_A:Q̇ ratio gives no information on the distribution of either quantity with respect to the volume of the lungs. Third, the V̇_A:Q̇ ratio does not discriminate between differences in V̇_A that arise through differences in overall ventilation to different parts of the lung, and those that arise through differences in dead space. To address these issues, we prefer to consider inhomogeneity as arising from a set of different distributions, all relative to alveolar volume (as we now describe).

A perfectly homogeneous lung may be thought of as a single (well-mixed) alveolar volume that exchanges with blood flowing through the lung, and that is connected to the atmosphere via a dead space. Using this concept, one way to approach inhomogeneity is to consider the overall lung as composed of a set of small homogeneous lung units, but each having different amounts of ventilation, blood flow, and dead space (Fig. 1A). Thus, to model inhomogeneity within the lung, we construct a lung of total alveolar volume V_A,tot from a set of N lung units (with index i), each with the same fractional alveolar volume, $F_{{\text{V}}_{\text{A}}}^i$, at functional residual capacity (N.B., this equal volume definition of lung units does not equate to approximately equal numbers of acini in each unit because, physically, the lung is more compressed at its base than at its apex). These units differ in their fractional share, $F_{{\text{C}}_{\text{L}}}^i$, of total lung compliance, C_L,tot; their fractional share, $F_{{\text{C}}_{\text{d}}}^i$, of total pulmonary vascular conductance, C_d,tot; and their fractional share, $F_{{\text{V}}_{\text{D}}}^i$, of total dead space, V_D,tot (Fig. 1A). Note that differences in these quantities between model lung units will include those that arise because of differences in compression between the lung units—thus the measures of inhomogeneity will include any physiological inhomogeneity arising through gravitational effects. The use of fractional lung compliance and fractional pulmonary vascular conductance in preference to ventilation and perfusion is to ensure that the model of lung inhomogeneity is constructed from properties that are intrinsic to the lung. Total ventilation and perfusion then become inputs to the model.

Fig. 1.

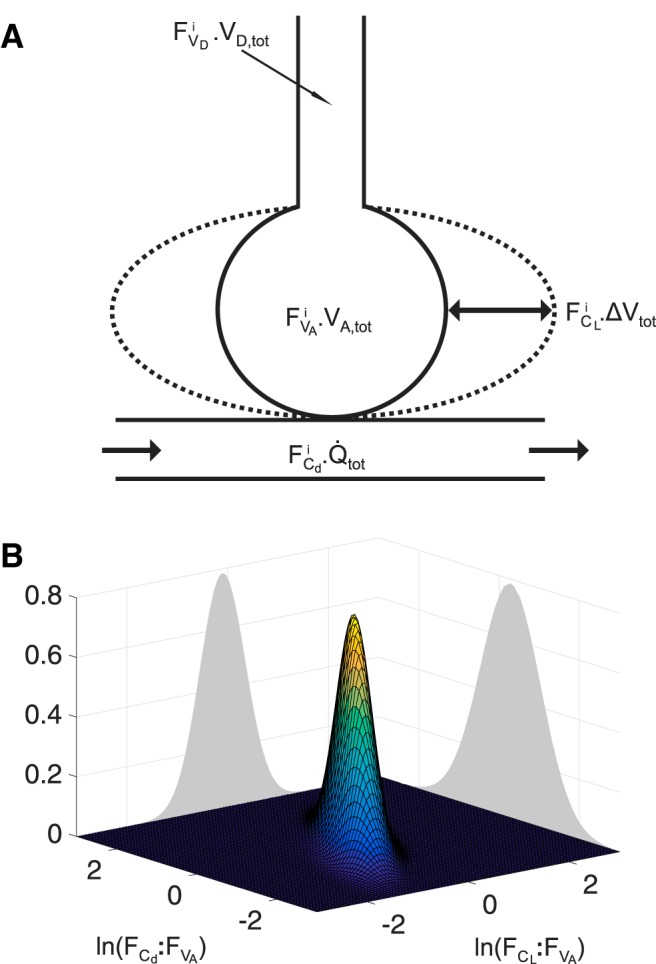
Model of lung inhomogeneity. A: schematic for a single lung unit (index i) of the model. ΔV_tot is change in total lung volume from functional residual capacity; Q̇_tot is the total pulmonary flow; other symbols are as defined in Table 1. B: illustration of the continuous bivariate log normal distribution for the fractional lung compliance–fractional alveolar volume ratio ($\ln \left[F_{{\text{C}}_{\text{L}}}(x,y):F_{{\text{V}}_{\text{A}}}(x,y)\right]$, or $\ln \left({\text{C}}_{\text{L}}^{\text{*}}\right)$ where ${\text{C}}_{\text{L}}^{\text{*}}$ is the standardized lung compliance) and fractional lung vascular conductance–fractional alveolar volume ratio ($\ln \left[F_{{\text{C}}_{\text{d}}}(x,y):F_{{\text{V}}_{\text{A}}}(x,y)\right]$, or $\ln \left({\text{C}}_{\text{d}}^{*}\right)$ where ${\text{C}}_{\text{d}}^{*}$ is the standardized lung vascular conductance).

In a real lung, the distributions of $F_{{\text{C}}_{\text{L}}}^i$, $F_{{\text{C}}_{\text{d}}}^i$, and $F_{{\text{V}}_{\text{D}}}^i$ relative to $F_{{\text{V}}_{\text{A}}}^i$ are likely to be quite complex. We cannot hope to recover their precise form, but instead aim to recover an approximation of the variance for each of these distributions. To make progress, we assume that the (continuous) distributions $F_{{\text{C}}_{\text{L}}}$:$F_{{\text{V}}_{\text{A}}}$ and $F_{{\text{C}}_{\text{d}}}$:$F_{{\text{V}}_{\text{A}}}$ follow a bivariate log-normal form (Fig. 1B) with correlation ρ (2, 3, 35), and that $F_{{\text{V}}_{\text{D}}}$:$F_{{\text{V}}_{\text{A}}}$ follows an independent normal distribution. Here, it is important to recognize that it is not necessary for these distributions to replicate faithfully the distributions within a real lung, but only that the assumed distributions allow the model to fit the data well (i.e., as if the data came from such a model), and for the parameters obtained to be a reasonable representation of the underlying variance within the real lung. We define the values for each of these ratios at each point of the lung as the standardized lung compliance, ${\text{C}}_{\text{L}}^{*}$, the standardized vascular conductance, ${\text{C}}_{\text{d}}^{*}$, and the standardized dead space, ${\text{V}}_{\text{D}}^{\text{*}}$, respectively. This gives our three primary parameters reflecting inhomogeneity in the lung as the standard deviation for the logarithm of ${\text{C}}_{\text{L}}^{*}$, ${\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}$, the standard deviation for the logarithm of ${\text{C}}_{\text{d}}^{*}$, ${\sigma }_{\ln {\text{C}}_{\text{d}}^{\text{*}}}$, and the standard deviation for ${\text{V}}_{\text{D}}^{\text{*}}$, ${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$, respectively. The parameters for the lung model and their relation to the discretized lung units are given in Table 1.

Table 1.

Parameters of the lung inhomogeneity model

Parameter	Definition (Units)
VD,tot	Dead space volume (liters, BTPS)
${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$= SD[$F_{{\text{V}}_{\text{D}}}^i$:$F_{{\text{V}}_{\text{A}}}^i$]	Standard deviation for the standardized dead space, ${\text{V}}_{\text{D}}^{\text{*}}$, equivalent to the standard deviation for the ratio between fractional dead space, $F_{{\text{V}}_{\text{D}}}^i$, and fractional alveolar volume, $F_{{\text{V}}_{\text{A}}}^i$, of the lung units (Note: $\Sigma F_{{\text{V}}_{\text{D}}}^i$ = 1 and $\Sigma F_{{\text{V}}_{\text{A}}}^i$ = 1).
VA,tot	Alveolar volume at functional residual capacity (liters, BTPS)
${\lambda }_{\text{T},{\text{CO}}_{\text{2}}}$	Fraction of additional apparent alveolar volume (defined at functional residual capacity) arising through the solubility of CO2 in lung tissue
${\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}=\text{SD}\left[\text{ln}(F_{{\text{C}}_{\text{L}}}^i:F_{{\text{V}}_{\text{A}}}^i)\right]$	Standard deviation for the natural logarithm of the standardized lung compliance, equivalent to the standard deviation for the natural logarithm of the ratio between fractional lung compliance, $F_{{\text{C}}_{\text{L}}}^i$, and fractional alveolar volume of the lung units (Note: $\Sigma {F_{{\text{C}}_{\mathrm{L}}}^i}_{}$ = 1 and $\Sigma {F_{{\text{V}}_{\mathrm{A}}}^i}_{}$= 1).
${\sigma }_{\ln {\mathrm{C}}_{\text{d}}^{*}}=\text{SD}\left[\text{ln}(F_{{\text{C}}_{\text{d}}}^i:F_{{\text{V}}_{\text{A}}}^i)\right]$	Standard deviation for the natural logarithm of the standardized lung vascular conductance, ${\text{C}}_{\text{d}}^{*}$, equivalent to the standard deviation for the natural logarithm of the ratio between fractional lung vascular conductance, $F_{{\text{C}}_{\text{d}}}^i$, and fractional alveolar volume of the lung units (Note: $\Sigma {F_{{\text{C}}_{\mathrm{d}}}^i}_{}$ = 1 and $\Sigma {F_{{\mathrm{V}}_{\mathrm{A}}}^i}_{}$= 1).
$\rho =\text{corr}\left[\text{ln}\left(F_{{\text{C}}_{\text{L}}}^i:F_{{\text{V}}_{\text{A}}}^i\right),\text{ln}\left(F_{{\text{C}}_{\text{d}}}^i:F_{{\text{V}}_{\text{A}}}^i\right)\right]$	Correlation between distributions for the natural logarithm of the standardized lung compliance and the natural logarithm of the standardized lung vascular conductance

i is the index number for the N lung units of the model, SD[] is the standard deviation; ln() is the natural logarithm, and corr[ , ] is the correlation.

Governing Equations for Model of Lung Inhomogeneity

The mathematical derivation of the values for $F_{{\text{V}}_{\text{A}}}^i$, $F_{{\text{V}}_{\text{D}}}^i$, $F_{{\text{C}}_{\text{L}}}^i$, $F_{{\text{C}}_{\text{d}}}^i$ for each lung unit in terms of the parameter values for ${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$, ${\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}$, ${\sigma }_{\ln {\text{C}}_{\text{d}}^{\text{*}}}$, and ρ is detailed in the appendix. Given these, the governing equations for each lung unit are derived by applying conservation of mass for each gas present and assuming that the exchange between the gas and blood phase within each lung unit reaches equilibrium. The quantity of gas species g (where g may be N₂, O₂, or CO₂) in lung unit i is the sum of both undissolved gas and gas dissolved in tissue. The rate of change of this quantity is given by the net flux of that gas species entering the lung unit via either the airways or the bloodstream. For inspiration we have:

$$\frac{\text{d}}{\text{d}t}\left[F_{\text{g}}^i(t)\left({\text{V}}^i(t)+{\lambda }_{\text{T},\text{g}}{F}_{{\text{V}}_{\text{A}}}^i{\text{V}}_{\text{A,tot}}\right)\right]=F_{\text{I},\text{g}}^i(t)F_{\text{I},{\dot{\mathrm{V}}}_{\text{M}}}^i{F}_{\text{I},{\dot{\mathrm{V}}}_{\text{M}}}^i{\dot{\mathrm{V}}}_{\text{M}}(t)+F_{C_{\text{d}}}^i{\dot{\mathrm{Q}}}_{\text{tot}}\left[C_{\overline{\mathrm{v}},\text{g}}(t)-C_{\text{c}\prime ,\text{g}}^i(t)\right],$$ (1)

where $F_{\text{g}}^i(t)$ is the fractional concentration of gas g in lung unit i at time t, Vⁱ(t) is the volume of lung unit i at time t, λ_T,g is the fraction of additional apparent alveolar volume (at functional residual capacity) arising through gas g physically dissolving in the lung tissue, $F_{\text{I},\text{g}}^i(t)$ is the fractional concentration of gas g inspired into the alveolar volume of lung unit i from the connected personal dead space lung unit, $F_{\text{I},{\dot{\mathrm{V}}}_{\text{M}}}^i$ is the fraction of the flow measured at the mouth that enters lung unit i during inspiration, V̇_M(t) is the total respiratory flow of gas [measured by the in-airway molecular flow sensing device (MFS)], Q̇_tot is the pulmonary blood flow, $C_{\overline{\mathrm{v}},\text{g}}(t)$ is the mixed venous (pulmonary arterial) gas concentration of species g entering the lung units, and $C_{\mathrm{c\prime },\mathrm{g}}^i(t)$ is the end-capillary blood gas concentration of species g leaving lung unit i.

For expiration, where the flux due to ventilation is leaving [V̇_M(t) is negative] rather than entering the lung unit, Eq. 1 becomes (10, 11):

$$\frac{\text{d}}{\text{d}t}\left[F_{\text{g}}^i(t)\left({\text{V}}^i(t)+{\lambda }_{\text{T},\text{g}}{F}_{{\text{V}}_{\text{A}}}^i{\text{V}}_{\text{A,tot}}\right)\right]=F_{\text{g}}^i(t)F_{\text{E},{\dot{\mathrm{V}}}_{\text{M}}}^{\mathit{i}}{\dot{\mathrm{V}}}_{\text{M}}(t)+F_{{\text{C}}_{\text{d}}}^i{\dot{\mathrm{Q}}}_{\text{tot}}\left[C_{\overline{\mathrm{v}},\text{g}}(t)-C_{\text{c}\prime ,\text{g}}^i(t)\right],$$ (2)

where $F_{\text{E},{\dot{\mathrm{V}}}_{\text{M}}}^i,$ is the fraction of the flow at the mouth leaving lung unit i.

When combined with the constraint that $F_{{\text{CO}}_{\text{2}}}$+$F_{{\text{N}}_{\text{2}}}$+$F_{{\text{O}}_{\text{2}}}$= 1, Eqs. 1 and 2 may be solved numerically for $F_{\text{g}}^i(t)$ and Vⁱ(t), subject to knowledge of the other terms in the equation. The remainder of this section on modeling inhomogeneity in the lung describes how values for these other terms are obtained.

First, N₂ and O₂ are sufficiently insoluble in lung tissue that we can set ${\lambda }_{\text{T},{\text{N}}_{\text{2}}}$ = ${\lambda }_{\text{T},{\text{O}}_{\text{2}}}$ = 0. For CO₂ the dissolved phase is significant and ${\lambda }_{\text{T},{\text{CO}}_{\text{2}}}$ either needs to be estimated from the data or a value taken from the literature. Second, as we assume gas exchange with the blood reaches equilibrium, $C_{\mathrm{c\prime },{\text{CO}}_{\text{2}}}^i(t)$ and $C_{\mathrm{c\prime },{\text{O}}_{\text{2}}}^i(t)$ may be calculated from $F_{{\text{CO}}_{\text{2}}}^i$ and $F_{{\text{O}}_{\text{2}}}^i$ using a model of CO₂ and O₂ carriage by blood (19). $C_{\mathrm{c\prime },{\text{N}}_{\text{2}}}^i(t)$ may be calculated from $F_{{\text{N}}_{\text{2}}}^i$ using the solubility of N₂ in blood. Third, Q̇_tot is an unmeasured input to the model, and therefore either a constant value has to be estimated from the data as effectively a parameter of the model, or alternatively an assumed value used that is based on metabolic rate. Fourth, values for the volumes, V_A,tot and V_D,tot (used in the calculation of $F_{\text{I},\text{g}}^i$ below), are estimated from the data as parameters of the model. Calculation of the remaining terms is more involved, and they have their own subsections below.

Calculation of $F_{\mathit{\text{I}},\text{g}}^i(t)$.

Values for $F_{\text{I},\text{g}}^i(t)$ are not the same as the gas fractions recorded experimentally at time t because the values are necessarily delayed by transit through the dead space associated with the lung unit. Plug flow, which describes the situation when the gas fronts that enter the dead space propagate through the dead space unaltered, is the simplest flow pattern to model, and this has been used successfully by others (34). We use the method of characteristics to calculate the appropriate delay from the experimentally measured flow pattern (18), and thus obtain $F_{\text{I},\text{g}}^i(t)$ from the inspired gas fractions recorded by the MFS at time t. It is important to note that this technique is also required to reconstitute the bulk expired gas composition from the values for $F_{\text{g}}^i$ as this gas leaves the alveolar units at time t.

At the end of expiration, there will be gas that has left the alveolar volume but has not left the dead space. In the model, the dead space is personal to the lung unit, but in a real lung the branching nature of the conducting airways causes gas from one lung unit progressively to mix with gas from other lung units as it moves along the airway. To approximate this process in the model, we run a partial mixing algorithm at the end of each expiration. This algorithm calculates the unique CO₂, O₂, and N₂ concentrations at the mouth that both preserve mass balance for these gases in the airway and, at the same time, allow a linear concentration gradient along the airway for each gas species between the lung unit and mouth. It is these linear concentration gradients that reenter the lung units during the first part of expiration. Note that a similar algorithm is not required at the end of inspiration, because inspiration does not generate mixing within the airways.

Calculation of $F_{\mathit{\text{I}},{\dot{V}}_{\mathit{\text{M}}}}^i$ and $F_{\mathit{\text{E}},{\dot{V}}_{\mathit{\text{M}}}}^i$.

The values for $F_{\text{I},{\dot{\mathrm{V}}}_{\text{M}}}^i$ and $F_{\text{E},{\dot{\mathrm{V}}}_{\text{M}}}^i$ for each lung unit are closely approximated by their values for $F_{{\text{C}}_{\text{L}}}^i$, and some authors have assumed equivalence (4). However, different lung units will have different respiratory quotients; thus, for example, a unit with a low respiratory quotient will need to inspire a little more gas and breathe out a little less gas to compensate for the stoichiometry between O₂ uptake and CO₂ output, as compared with a unit with a high respiratory quotient. We adopted a recursive approach to address this issue, where values for $F_{\text{I},{\dot{\mathrm{V}}}_{\text{M}}}^i$ and $F_{\text{E},{\dot{\mathrm{V}}}_{\text{M}}}^i$ were initially set to the values for $F_{{\text{C}}_{\text{L}}}^i$, and then adjusted on each successive breath for the error on the previous breath, as follows:

$$F_{\text{I},{\dot{\mathrm{V}}}_{\text{M}}}^i(m+1)=F_{\text{I},{\dot{\mathrm{V}}}_{\text{M}}}^i(m)-\frac{\left[{\text{V}}^i(t_{\text{I}}^m)-{\text{V}}^i(t_0^m)\right]-F_{{\text{C}}_{\text{L}}}^i{\sum }^i\left[{\text{V}}^i(t_{\text{I}}^m)-{\text{V}}^i(t_0^m)\right]}{{\displaystyle {\int }_{t_0^m}^{t_{\text{I}}^m}{\dot{\mathrm{V}}}_{\text{M}}}(t)\text{d}t}$$ (3)

and

$$F_{\text{E},{\dot{\mathrm{V}}}_{\text{M}}}^i(m+1)=F_{\text{E},{\dot{\mathrm{V}}}_{\text{M}}}^i(m)-\frac{\left[{\text{V}}^i(t_{\text{I}}^m)-{\text{V}}^i(t_{\text{E}}^m)\right]-F_{{\text{C}}_{\text{L}}}^i{\sum }^i\left[{\text{V}}^i(t_{\text{I}}^m)-{\text{V}}^i(t_{\text{E}}^m)\right]}{{\displaystyle {\int }_{t_{\text{E}}^m}^{t_{\text{I}}^m}{\dot{\mathrm{V}}}_{\text{M}}}(t)\text{d}t},$$ (4)

where $t_0^m$, $t_{\text{I}}^m$, and $t_{\text{E}}^m$ are the times for the start of the breath, the end of inspiration, and the end of expiration for the mth breath, respectively.

Calculation of $C_{\overline{v},\mathit{\text{g}}}(t)$.

During the air-breathing phase of our measurement protocol, these values will be relatively stable. Although they are unmeasured inputs to the model, constant values for $C_{\overline{\mathrm{v}},{\text{CO}}_{\text{2}}}(t)$ and $C_{\overline{\mathrm{v}},{\text{O}}_{\text{2}}}(t)$ (with or without the addition of trend terms to allow for gradual drift during the experiment) can be estimated as part of the overall parameter recovery process. A value for $C_{\overline{\mathrm{v}},{\text{N}}_{\text{2}}}(t)$ was set to approximate the value for the pulmonary venous concentration for N₂ leaving the lung so as to reflect the absence of net exchange of N₂ during the air-breathing phase.

During the pure oxygen-breathing phase, the concentrations of both N₂ and O₂ in the pulmonary venous blood change substantially, and so models for recirculation must be employed to calculate the effects on $C_{\overline{\mathrm{v}},{\text{N}}_{\text{2}}}(t)$ and $C_{\overline{\mathrm{v}},{\text{O}}_{\text{2}}}(t)$. To model the body’s N₂ stores, we adopt the model and parameters of Baker and Farmery (1) for the inert gas stores of the body. This model requires a systemic arterial input for N₂ content and provides a systemic venous output that may be used for $C_{\overline{\mathrm{v}},{\text{N}}_{\text{2}}}(t)$.

Unlike N₂, O₂ is consumed by the body and also stored through binding to heme proteins. For these reasons the model of Baker and Farmery (1) together with its parameters cannot be used. Thus for the O₂ stores we assume a single effective O₂ storage compartment (${\text{V}}_{\text{B},{\text{O}}_{\text{2}}}$) which gives rise to a governing differential equation for $C_{\overline{\mathrm{v}},{\text{O}}_{\text{2}}}$ during the high O₂ breathing period of the form

$$\frac{\text{d}{C}_{\overline{\mathrm{v}},{\text{O}}_{\text{2}}}}{\text{d}t}=\frac{1}{{\text{V}}_{{\text{B,O}}_{\text{2}}}}\left[{\dot{\mathrm{Q}}}_{\text{tot}}\left({\sum }^i{\displaystyle F_{C_{\text{d}}}^i}{C}_{\mathrm{c\prime },{\text{O}}_{\text{2}}}^i(t)-C_{\overline{\mathrm{v}},{\text{O}}_2}(t)\right)-{\dot{\mathrm{V}}}_{{\text{O}}_{\text{2}}}\right],$$ (5)

where ${\dot{\mathrm{V}}}_{{\text{O}}_{\text{2}}}$ is the body’s oxygen consumption and is assumed to be the average of that determined during the air-breathing period.

This approach adds another parameter, ${\text{V}}_{{\text{B,O}}_{\text{2}}}$, that requires estimation. If ${\text{V}}_{{\text{B,O}}_{\text{2}}}$ is chosen at too large a value, then $C_{\overline{\mathrm{v}},{\text{O}}_{\text{2}}}$ will rise too slowly during the high O₂ breathing period, the O₂ uptake from gas to blood will be too large, and as a consequence the lung volume of the model will shrink over the high O₂ breathing period. If ${\text{V}}_{{\text{B,O}}_{\text{2}}}$ is chosen at too small a value, then the converse will be true, and the lung volume of the model will rise over this period. We use this feature to determine an effective value for ${\text{V}}_{{\text{B,O}}_{\text{2}}}$ that minimizes the drift in the lung volume of the model over the period of high O₂ breathing.

This section completes the calculation for the terms required to integrate numerically Eq. 1 and Eq. 2 and so run the model.

Shunt.

Shunt and very low V̇_A:Q̇ contribute very little to the expired gas composition and consequently this aspect of inhomogeneity cannot be recovered from information within the expired gas profile. However, very low V̇_A:Q̇ and shunt will lower the oxygen saturation of arterial blood below that predicted from the model for pulmonary venous blood. As such, the shunt fraction, $F_{{\dot{\mathrm{Q}}}_s}$, may be estimated using one further experimental measurement:

$$F_{{\dot{\mathrm{Q}}}_s}=1-\frac{({\text{S}}_{\text{a},{\text{O}}_{\text{2}}}-{\text{S}}_{\overline{\mathrm{v}},{\text{O}}_{\text{2}}})}{({\text{S}}_{\overline{\mathrm{c}\prime },{\text{O}}_{\text{2}}}-{\text{S}}_{\overline{\mathrm{v}},{\text{O}}_{\text{2}}})}$$ (6)

where ${\mathrm{S}}_{\mathrm{a}\mathrm{,}{\mathrm{O}}_{\mathrm{2}}}$ is the arterial O₂ saturation and is measured by pulse oximetry, ${\text{S}}_{\overline{\mathrm{v}},{\text{O}}_{\text{2}}}$ is the mixed-venous O₂ saturation and ${\text{S}}_{\overline{\mathrm{c}\prime },{\text{O}}_{\text{2}}}$ is the mixed, end-pulmonary capillary O₂ saturation.

Parameter Recovery

Parameter estimates and estimates for any unknown model inputs were obtained by minimizing the sum of squared differences (the objective or cost function) between the values for the gas flows for each of the gas species output by the model every 10 ms during expiration and those recorded experimentally. The model used had 125 lung units. During air breathing, the CO₂ and O₂ flow differences were used in the cost function, and during pure O₂ breathing the N₂ flow differences were used. The cost function, R, may be written

$$\mathrm{R}\hspace{0.17em}={\displaystyle \sum _{\text{air\hspace{0.17em}breathing}}{\dot{\mathrm{V}}}_{\text{M}}}{\left(t_n\right)}^2\left[{\left(F_{\text{M},{\text{CO}}_{\text{2}}}(t_n)-F_{\text{S},{\text{CO}}_{\text{2}}}(t_n)\right)}^2+{\left(F_{\text{M},{\text{O}}_{\text{2}}}(t_n)-F_{\text{S},{\text{O}}_{\text{2}}}(t_n)\right)}^2\right]+{\displaystyle \sum _{{\text{O}}_{\text{2}}\text{\hspace{0.17em}breathing}}{\dot{\mathrm{V}}}_{\text{M}}}{\left(t_n\right)}^2{\left(F_{\text{M},{\text{N}}_{\text{2}}}(t_n)-F_{\text{S},{\text{N}}_{\text{2}}}(t_n)\right)}^2,$$ (7)

where t_n are times at which measurements are taken with the MFS and F_M,g and F_S,g are the measured and simulated fractions at the MFS, respectively.

The “air breathing period” for the cost function is defined as the 5 min of normal breathing immediately preceding the high O₂ breathing phase. The first 2 min of normal breathing are discarded to allow the subject to adjust to breathing on the MFS, and the following 3 min allow the model to settle into a quasi-steady state.

The minimization problem was solved in MATLAB (Mathworks) using the function fmincon, implemented in parallel. It took ∼5 h to perform a minimization using a single node of the Arcus Phase B high-performance computer at Oxford (23). For each experimental data set, the fitting procedure was repeated at least four times from different, randomized starting points to check that the same minimum would be found. If this were not the case, then additional randomized starting points would be used as a practical check to ensure that the minimum associated with the best fit (smallest residuals) had been found.

Generation of Synthetic Data

Synthetic data were generated by setting lung parameters (V_A,tot, V_D,tot, ${\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}$, ${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$, ${\sigma }_{\ln {\text{C}}_{\text{d}}^{\text{*}}}$, ρ, and ${\lambda }_{{\text{T,CO}}_{\text{2}}}$), systemic inputs (Q̇_tot, $C_{\overline{\mathrm{v}},{\text{CO}}_{\text{2}}}$, and $C_{\overline{\mathrm{v}},{\text{O}}_{\text{2}}}$), and ${\text{V}}_{\text{B},{\text{O}}_{\text{2}}}$ to physiologically plausible values (the systemic inputs were assumed not to vary over time during the air-breathing component of the simulation). The model was driven using experimentally recorded respiratory flow and inspiratory gas compositions. The outputs were the expiratory flow composition and the pulmonary venous composition. Simulations were normally conducted using a model of 125 lung units, but in some cases simulations were performed using a model with 343 lung units or 729 lung units.

Synthetic data were generated “noise free”, and also with two different noise models to reflect the measurement error associated with standard equipment (24) and the measurement error associated with the MFS device used in this study (7). Four different types of “noise” were added to the signals: random sensor error was simulated with a Gaussian measurement error incorporated into the flow signal; the finite response time of the gas analyzers was reflected by incorporating first-order dynamics into the measured gas fractions; temporal misalignment of the flow and gas fractions was simulated by shifting the flow and gas fraction time series relative to each other; and errors in recorded volumes were simulated by adding a Gaussian random walk into the time series for flow at the MFS.

Human Studies

To explore the reproducibility of parameter recovery, a human study was conducted involving 6 young (20–30 yr) healthy participants, 6 older (70–80 yr) healthy participants and 6 participants with mild or moderate COPD. The participants’ physical characteristics are given in Table 2. For each participant, three repeats of the measurement protocol—10 min of breathing air followed by 5 min of breathing pure O₂—were conducted on each of two days. Experimental data were collected using the highly precise MFS device (7) and arterial O₂ saturation was recorded using a pulse oximeter. The experimental work was conducted in accordance with the general ethical principles of the Declaration of Helsinki, ethics approval was obtained from the Scotland A Research Ethics Committee, and all participants provided written informed consent prior to study.

Table 2.

Participant characteristics

Subject	Sex	Height /m	Weight /kg	Age /yr	FRC /liters	FEV1 /%pred,	FVC /%pred	FEV1/FVC /%	Vt /liters (BTPS)	RR /min−1
Young #1	F	1.80	63	23	n.a.	n.a.	n.a.	n.a.	0.76	13.1
Young #2	F	1.71	65	22	2.71	118	121	85	1.06	10.8
Young #3	F	1.80	66	24	3.38	91	103	77	1.05	9.5
Young #4	F	1.73	55	23	3.75	119	115	90	0.83	16.3
Young #5	M	1.93	83	20	3.91	96	119	67	1.38	9.4
Young #6	M	1.77	78	20	4.80	154	150	87	1.52	8.4
Old #1	F	1.58	53	72	3.10	107	123	72	1.14	6.1
Old #2	F	1.60	50	71	3.02	97	116	69	0.83	10.3
Old #3	M	1.69	72	79	3.48	62	76	61	1.30	9.4
Old #4	F	1.65	49	71	3.94	119	125	79	0.90	9.8
Old #5	M	1.76	80	76	5.05	125	141	67	1.63	5.7
Old #6	M	1.85	69	70	5.36	111	122	69	1.42	7.6
COPD #1	F	1.62	72	67	3.46	78	117	56	0.92	13.2
COPD #2	M	1.65	72	67	5.04	36	92	30	0.95	20.0
COPD #3	F	1.62	71	66	3.33	76	124	51	0.99	8.8
COPD #4	F	1.63	76	74	4.50	47	84	48	0.79	16.0
COPD #5	M	1.63	85	72	4.30	74	116	49	1.10	14.3
COPD #6	M	1.78	101	63	5.08	75	112	52	2.22	7.9

FRC is the functional residual capacity, FEV₁ is the forced expiratory volume in 1 s, FVC is the forced vital capacity, Vt is tidal volume of spontaneous breathing, and RR is respiratory rate.

A summary of the assumptions made in the construction of the model, in the estimation of the parameters, and in the experimental work is given in Table 3.

Table 3.

Key assumptions made during the modeling, the parameter estimation, and the physiological measurement aspects of the study

Assumption	Note
Modeling assumptions
“Plug flow” in airways	Flat convection profile—no diffusive mixing
Complete alveolar mixing	No mixed convection–diffusion problem at boundary between airways and alveolar volumes
Complete equilibration between alveolar gas and blood in pulmonary capillaries
Constant compliances for each lung unit throughout breath
Constant vascular conductances for each lung unit throughout breath
Airways treated as independent for each lung unit apart from modeling a partial mixing of gas in airways at the end of each expiration	For gas completely transiting the airways in a constant compliance lung model, for every bifurcating airway model there exists an equivalent “parallel” model of the airways
Distribution of compliance and vascular conductance across lung units may be modeled with a bivariate log-normal distribution
Distribution of dead space across lung units may be modeled with a normal distribution
Distribution of dead space is uncorrelated with distributions for either compliance or vascular conductance
Assumptions associated with parameter estimation
${\lambda }_{\text{T},{\text{CO}}_{\text{2}}}$ assumed constant at 0.4	Not recoverable from human data. Sensitivity analysis revealed all estimated parameter values were insensitive to value chosen for ${\lambda }_{\text{T},{\text{CO}}_{\text{2}}}$.
ρ assumed constant at 0.8	Not recoverable from human data. Sensitivity analysis revealed all estimated parameter values were insensitive to value chosen for ρ except ${\sigma }_{\ln {\mathrm{C}}_{\text{d}}^{\text{*}}}$. An estimate for the upper limit of uncertainty in ${\sigma }_{\ln {\text{C}}_{\text{d}}^{\text{*}}}$ induced by uncertainty in ρ is ± 6%.
Q̇tot assumed constant to give a ~25% difference in hemoglobin saturation between pulmonary venous and pulmonary arterial blood	Not recoverable from human data. Sensitivity analysis revealed all estimated parameter values were insensitive to Q̇tot except ${\sigma }_{\ln {\mathrm{C}}_{\text{d}}^{\text{*}}}$. An estimate for the upper limit of uncertainty in ${\sigma }_{\ln {\text{C}}_{\text{d}}^{\text{*}}}$ induced by uncertainty in Q̇tot is ± 5%.
Global minimum found by nonlinear least-squares estimation algorithm	If four repeats of the estimation algorithm from different starting points identified the existence of more than one solution point (minimum), then algorithm repeated from further starting points until lowest minimum clearly identified
Physiological assumptions during measurement
Constant physiological state	Pulmonary blood flow and metabolic rate remain constant over the measurement period.

RESULTS

Results Obtained Using Synthetic Data

The first question to be addressed was whether the fitting procedure could retrieve all parameter values from the noise-free simulations, and therefore whether all parameters were formally identifiable in the absence of noise. This was the case. The fitting procedure was able to converge on the underlying parameter values for the lung parameters (V_A,tot, V_D,tot, ${\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}$, ${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$, ${\sigma }_{\ln {\text{C}}_{\text{d}}^{\text{*}}}$, ρ, and ${\lambda }_{\text{T},{\text{CO}}_{\text{2}}}$) and the systemic inputs (Q̇_tot, $C_{\overline{\mathrm{v}},{\text{CO}}_{\text{2}}}$, and $C_{\overline{\mathrm{v}},{\text{O}}_{\text{2}}}$) from different randomized starting points. As a further confirmatory step, we examined the variation in cost function that occurred on a surface around the solution point for every possible pairing of two parameters. In all cases, there was a unique minimum at the true value of the parameters. We also noted that the position for the minima for those parameters associated with the airways (V_A,tot, V_D,tot, ${\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}$, and ${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$) appeared virtually unaffected by the values assumed for the other parameters of the model.

We next determined whether the fitting procedure could retrieve parameter values in the presence of a noise model designed to reflect the errors associated with standard equipment (24). Of the 10 synthetic data sets used, 8 failed to converge. For the 2 that did converge, the parameter values were not close to the values used to generate the synthetic data set.

Next, we explored the fitting procedure in the presence of a noise model designed to reflect the errors associated with the MFS device (7) used in the human studies below. The fitting routine successfully converged on a parameter set for all 10 data sets employed. The estimates obtained for the airway parameters (V_A,tot, V_D,tot, ${\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}$, and ${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$) were all close to the values used when generating the synthetic datasets. Estimates for $C_{\overline{\mathrm{v}},{\text{CO}}_{\text{2}}},\hspace{0.17em}{C}_{\overline{\mathrm{v}},{\text{O}}_{\text{2}}}$ could also be obtained. However, this was generally not the case for the other parameters, where the standard deviation for the recovered parameters could be a large fraction of the true underlying value (for example, 60% for ${\lambda }_{\text{T},{\text{CO}}_{\text{2}}}$). Better estimates for some of these parameters could be obtained if others were fixed to physiologically reasonable values.

The above findings dictated the recovery procedure adopted for the human studies presented below. In this procedure, the parameters V_A,tot, V_D,tot, ${\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}$, ${\sigma }_{\ln {\text{C}}_{\text{d}}^{*}}$, and ${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$ were estimated together with the unknown inputs, $C_{\overline{\mathrm{v}},{\text{CO}}_{\text{2}}}(t)$ and $C_{\overline{\mathrm{v}},{\text{O}}_{\text{2}}}(t)$, each as a constant value plus linear trend term. Q̇_tot, ρ, and ${\lambda }_{\text{T},{\text{CO}}_{\text{2}}}$ were assumed. Specifically, Q̇_tot was set to give an arteriovenous difference in oxygen saturation across the pulmonary circulation of ∼25% [equivalent to a difference of 50 ml (STPD) per liter for O₂ in blood with normal hemoglobin], ρ = 0.8 (2, 3, 16, 17, 30), and ${\lambda }_{\text{T},{\text{CO}}_{\text{2}}}$ = 0.4 (8, 9, 21, 28, 29). These three assumptions were subjected to a sensitivity analysis using human data, as described below.

Finally, in the simulation studies above, the data used were all generated using a model of 125 lung units, and the same sized model was used for parameter recovery. To check that 125 lung units for the size of the recovery model was adequate, we also simulated data using 343 lung units and 729 lung units. In both cases, accurate recovery of parameter values could be obtained using the 125 lung unit model, indicating that it was adequate.

Human Studies

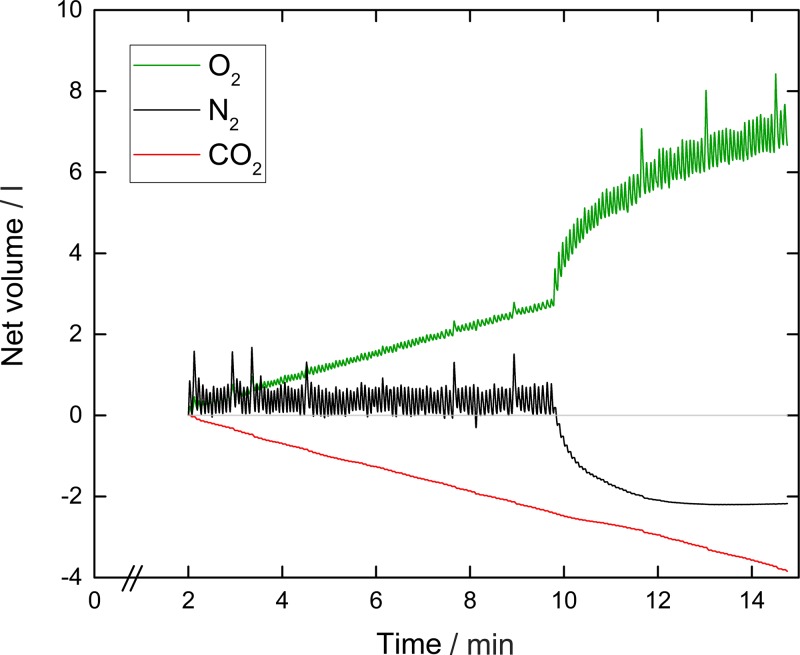
An example experimental record for a young healthy participant using the MFS technique is shown in Fig. 2. Note the stability of the N₂ record during the air-breathing phase, and the slopes of the CO₂ and O₂ records associated with CO₂ excretion and O₂ uptake, respectively.

Fig. 2.

Example record of a lung inhomogeneity test conducted using in-airway molecular flow sensing. Shown are the tidal flows for oxygen, carbon dioxide, and nitrogen. The upward trend for oxygen indicates oxygen consumption, and the downward trend for carbon dioxide indicates carbon dioxide production. The absence of any trend in the nitrogen record reflects the lack of any net uptake or production of nitrogen apart from the washout period which begins at ∼10 min, when the inspirate is changed from air to 100% oxygen. Although not visible, data are recorded every 10 ms.

An example of the model fit to the data is shown for one young healthy participant in Fig. 3. Figure 3A illustrates the experimental and model outputs for the mixed expired N₂ fraction ($F_{{\text{N}}_{\text{2}}}$) over the entire course of a measurement period. The fit of the model is extremely good. Figure 3 also illustrates expiratory profiles for representative breaths during air breathing (Fig. 3B), near the start of the N₂ washout (Fig. 3C), and midway through the N₂ washout (Fig. 3D). The model describes the within-breath morphology of these expiratory profiles well, and this was typical. Figure 4 illustrates, for one participant from each group, the fit of the model to the data during the N₂ washout phase in a format similar to that used in clinical studies. The progressive fall in N₂ fraction is well described by the model which is also capable of generating the positive slopes observed in the N₂ record during phase III of expiration. The mean squared error for the residuals for each participant is given in Table 4. The values are larger for the participants with COPD than for the healthy participants, but the absolute values for all are small, suggesting a good fit of the model to the data.

Fig. 3.

Illustration of the fit of the lung inhomogeneity model to the data for one participant. A: mixed expired nitrogen values (one per breath) over the entire course of the inhomogeneity measurement. The quality of the fit is such that the data essentially overlap the model output throughout the entire nitrogen washout phase. B–D: fit of the model to the data for single breaths (expirations) sampled from the air-breathing phase (B), near the start of the nitrogen washout phase (C), and midway through the nitrogen washout phase (D). In each plot, measured data are shown with an unbroken line, and simulated data are shown with a broken line. The model output closely reproduces the form of the expiratory profile in each case.

Fig. 4.

Example records for the first section of the nitrogen washout phase of the experimental protocol. A–C: end-tidal N₂ fractions ($F_{\text{ET},{\text{N}}_{\text{2}}}$) plotted against lung turnover. D–F: the normalized slope of the N₂ record during phase III of expiration. A, D: young healthy participant. B, E: old participant. C, F: participant with COPD.

Table 4.

Primary parameters of the model

Subject	VD,tot /liters	${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$	VA,tot /liters	${\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}$	${\sigma }_{\ln {\text{C}}_{\text{d}}^{\text{*}}}$	$\Delta {\text{SpO}}_2$ /%	MSE /10−6
Young #1	0.157 ± 0.007	0.44 ± 0.01	2.39 ± 0.05	0.32 ± 0.02	0.45 ± 0.21	0.6 ± 1.0	1.13
Young #2	0.154 ± 0.008	0.50 ± 0.06	2.73 ± 0.10	0.40 ± 0.01	0.62 ± 0.25	−0.1 ± 0.5	2.75
Young #3	0.166 ± 0.006	0.37 ± 0.03	3.25 ± 0.22	0.43 ± 0.03	0.87 ± 0.13	0.9 ± 1.4	1.84
Young #4	0.176 ± 0.014	0.43 ± 0.01	3.18 ± 0.12	0.35 ± 0.02	0.54 ± 0.29	−1.1 ± 0.7	3.39
Young #5	0.199 ± 0.009	0.38 ± 0.03	4.37 ± 0.25	0.35 ± 0.04	0.53 ± 0.17	0.3 ± 0.9	2.30
Young #6	0.224 ± 0.012	0.34 ± 0.03	4.49 ± 0.11	0.41 ± 0.03	0.70 ± 0.11	0.2 ± 0.6	3.16
Mean	0.179	0.41	3.40	0.38	0.62	–0.1	2.43
CoV	5%	7%	4%	7%	34%
Old #1	0.198 ± 0.009	0.30 ± 0.03	2.88 ± 0.10	0.56 ± 0.05	0.92 ± 0.13	−0.6 ± 0.8	1.43
Old #2	0.192 ± 0.007	0.39 ± 0.05	2.96 ± 0.20	0.38 ± 0.03	0.65 ± 0.17	−0.4 ± 0.5	1.75
Old #3	0.288 ± 0.023	0.25 ± 0.07	3.48 ± 0.12	0.63 ± 0.04	1.04 ± 0.12	−1.9 ± 0.5	4.29
Old #4	0.224 ± 0.010	0.44 ± 0.04	3.83 ± 0.08	0.40 ± 0.02	0.78 ± 0.12	−1.0 ± 0.9	2.24
Old #5	0.309 ± 0.012	0.20 ± 0.05	4.98 ± 0.29	0.56 ± 0.05	1.01 ± 0.09	−1.4 ± 0.4	3.38
Old #6	0.360 ± 0.019	0.33 ± 0.03	6.34 ± 0.17	0.57 ± 0.02	1.01 ± 0.07	−0.2 ± 0.2	5.81
Mean	0.262	0.32	4.08	0.52	0.90	–0.9	3.33
CoV	5%	16%	4%	7%	14%
COPD #1	0.246 ± 0.019	0.42 ± 0.12	2.35 ± 0.23	0.86 ± 0.14	0.87 ± 0.22	−1.0 ± 1.1	7.07
COPD #2	0.394 ± 0.030	0.42 ± 0.16	2.60 ± 0.11	0.83 ± 0.05	1.19 ± 0.39	−1.5 ± 1.2	8.30
COPD #3	0.226 ± 0.015	0.47 ± 0.02	2.66 ± 0.09	0.73 ± 0.04	1.36 ± 0.37	−0.6 ± 0.6	3.59
COPD #4	0.270 ± 0.031	0.55 ± 0.02	3.14 ± 0.20	0.88 ± 0.05	1.50 ± 0.39	−1.0 ± 0.7	7.85
COPD #5	0.344 ± 0.006	0.38 ± 0.01	3.91 ± 0.18	0.71 ± 0.02	1.38 ± 0.07	−2.3 ± 0.8	7.89
COPD #6	0.497 ± 0.083	0.65 ± 0.05	5.38 ± 1.57	0.94 ± 0.13	1.72 ± 0.21	0.0 ± 0.9	13.6
Mean	0.330	0.48	3.34	0.82	1.34	–1.1	8.05
CoV	9%	14%	10%	8%	21%
Analysis of variance
F ratio (BG:WG)	6.0*	5.5*	0.8	43.2***	17.6***	4.8*	26.3***
F ratio (BP:WP)	48.5***	13.2***	42.8***	12.2***	5.2***	4.7***	1.2
ICC	0.99	0.95	0.98	0.99	0.94	0.87

$\Delta {\text{SpO}}_2$ is the difference between pulse oximeter measurements of arterial oxygen saturation during air breathing and calculated pulmonary mixed venous oxygen concentration from the model. MSE is mean squared error. Other parameters are as defined in Table 1. CoV, coefficient of variation; F ratio (BG:WG) is the variance ratio for the between-group to within-group comparison; F ratio (BP:WP) is the variance ratio for the between-participant to within-participant comparison. ICC is the intraclass correlation coefficient. Errors shown are for  ±  1SD.

^*P < 0.05;

^***P < 0.001.

Of the 108 tests conducted (18 participants, 6 repeats on each), only four fits failed to converge (possibly due to experimental errors providing inadequate data). A further three fits were rejected on grounds of the model predicting air-breathing pulmonary venous oxygen saturations that were more than 3% below the value measured with the pulse oximeter. This left 101 tests for further analysis. For almost all experimental data sets, the same minimum was found when starting the minimization procedure from a number of different starting points. For a few data sets, different minima could be found, but repeating the fitting process from further randomized starting points always allowed a dominant minimum to be found which also had the smallest least-squares error.

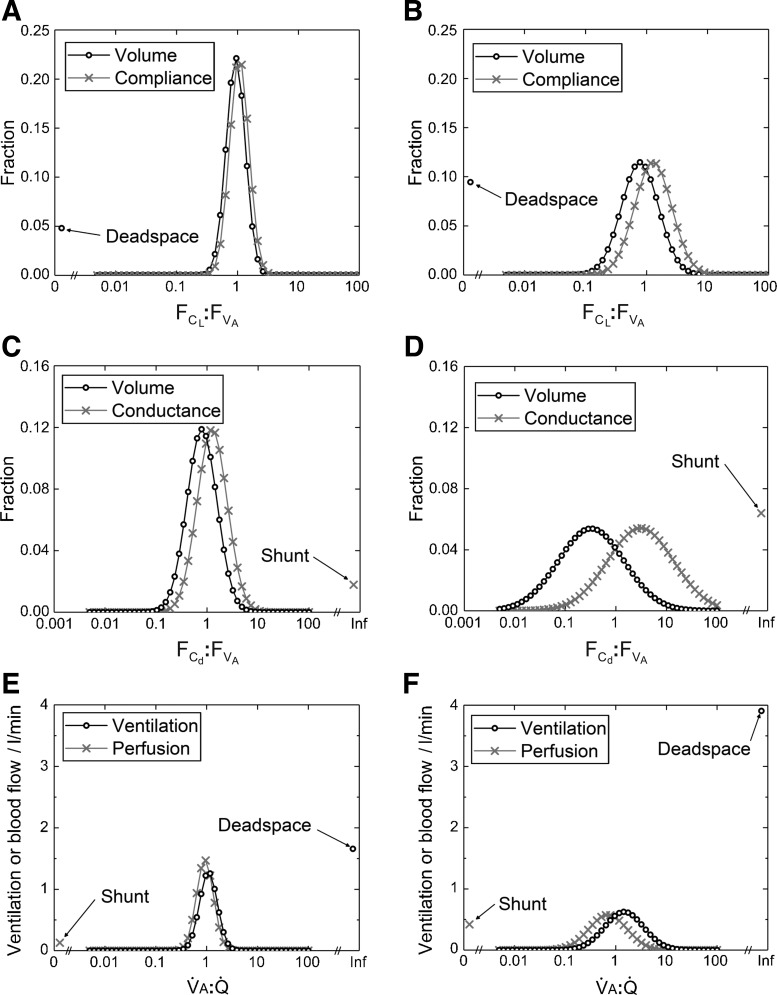
Figures 5 and 6 illustrate different distributions for the lung, as determined by fitting the model to one record from a young healthy participant (left plots), and one from a participant with COPD (right plots). The top and middle plots in Fig. 5, illustrate the distributions for $\ln \left(F_{{\text{C}}_{\text{L}}}:F_{{\text{V}}_{\text{A}}}\right)$ and $\ln \left(F_{{\text{C}}_{\text{d}}}:F_{{\text{V}}_{\text{A}}}\right)$, and the plots in Fig. 6 illustrate the distributions for $\left(F_{{\text{V}}_{\text{D}}}{\text{V}}_{\text{D,tot}}\right)$:$\left(F_{{\text{V}}_{\text{A}}}{\text{V}}_{\text{A,tot}}\right)$. In each case, the distribution is markedly wider for the participant with COPD. The bottom plots in Fig. 5 illustrate the classical ventilation-to-perfusion (V̇_A:Q̇) distribution which is calculated directly from the model once the values for the primary model parameters have been estimated. Here, the alveolar ventilation was calculated as the average volume of fresh gas entering each lung unit per minute over the air-breathing phase of the data collection period. Again, the distribution is clearly wider for the participant with COPD, and is associated with an increased dead space ventilation and a modest increase in shunt.

Fig. 5.

Example distributions recovered by fitting the lung inhomogeneity model to the data. A, C, and E: distributions recovered from healthy participant. B, D, and F: distributions recovered from a participant with COPD. A and B: distributions for the fractional lung compliance to fractional alveolar volume ratio ($F_{{\text{C}}_{\text{L}}}$:$F_{{\text{V}}_{\text{A}}}$); the volume distribution is identically that for ${\text{C}}_{\text{L}}^{\text{*}}$. C and D: distributions for fractional vascular conductance to fractional alveolar volume ratio ($F_{{\text{C}}_{\text{d}}}$:$F_{{\text{V}}_{\text{A}}}$); the volume distribution is identically that for ${\text{C}}_{\text{d}}^{*}$. E and F: distributions for alveolar ventilation to perfusion (V̇_A:Q̇), as calculated from the model parameters. In all cases, the distributions are wider for the participant with COPD compared with the healthy young participant. The distributions have been illustrated in a discretized form, with 50 points evenly spaced on a logarithmic scale from 0.005 to 100.

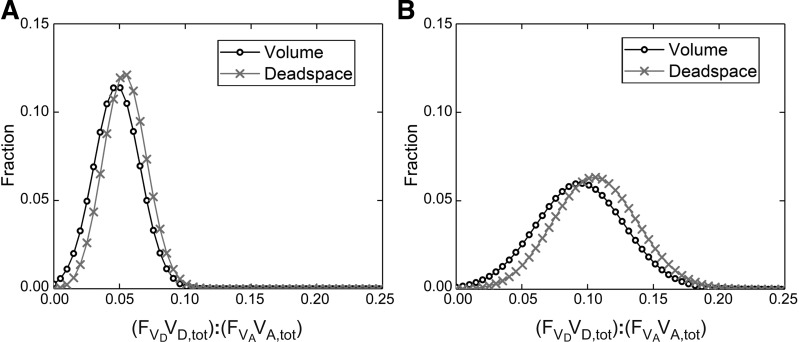
Fig. 6.

Example distribution for the dead space-to-alveolar volume ratio, ($F_{{\text{V}}_{\text{D}}}$V_D,tot):($F_{{\text{V}}_{\text{A}}}$V_A,tot). A: healthy young participant. B: participant with COPD. The volume distributions shown are identically those for (V_D,tot/V_A,tot)${\text{V}}_{\text{D}}^{\text{*}}$, where ${\text{V}}_{\text{D}}^{\text{*}}$ is the standardized dead space. Note that the mean value for this distribution in the participant with COPD is around double that of the healthy young participant and that the distribution is substantially wider. The distributions have been illustrated in a discretized form, with 50 points evenly spaced on a scale from 0 to 0.25.

For each participant, mean values and standard deviations for the primary model parameters are given in Table 4, and those for selected, secondary parameters calculated from the model are given in Table 5. The derived parameters include alternative presentations for V_D,tot and ${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$ where V_D,tot has been scaled relative to V_A,tot (as illustrated in Fig. 6). Of particular note is that the standard deviation for this distribution [(V_D,tot/V_A,tot)${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$] appears to be little affected by ageing as compared with COPD. The derived parameters also include estimates for the standard deviation for the natural logarithm of the V̇_A:Q̇ distribution, LogSDV̇ and LogSDQ̇, as estimated from the alveolar ventilation and perfusion distributions within the lung model, respectively. Calculation of these allows comparison with previous work concerning the V̇_A:Q̇ distribution (Table 6). Also shown are the differences in saturation between the pulse oximeter and model under air-breathing conditions (Table 4) and the corresponding calculated shunt (Table 5). Overall, these values were small for our participants.

Table 5.

Selected parameters derived from model fits

Subject	VD,tot/VA,tot	(VD,tot/VA,tot)${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$	LogSDV̇	LogSDQ̇	Shunt /%
Young #1	0.066 ± 0.004	0.029 ± 0.001	0.35 ± 0.08	0.38 ± 0.05	0.8 ± 1.5
Young #2	0.056 ± 0.002	0.028 ± 0.003	0.42 ± 0.08	0.42 ± 0.05	1.2 ± 1.3
Young #3	0.051 ± 0.005	0.019 ± 0.001	0.52 ± 0.09	0.49 ± 0.07	0.4 ± 1.1
Young #4	0.055 ± 0.004	0.024 ± 0.002	0.41 ± 0.13	0.42 ± 0.08	4.9 ± 2.9
Young #5	0.046 ± 0.003	0.017 ± 0.002	0.33 ± 0.08	0.33 ± 0.07	0.9 ± 1.5
Young #6	0.050 ± 0.003	0.017 ± 0.001	0.41 ± 0.07	0.39 ± 0.06	0.3 ± 0.9
Mean	0.054	0.022	0.41	0.40	1.5
CoV	7%	7%	22%	16%
Old #1	0.069 ± 0.003	0.021 ± 0.003	0.53 ± 0.07	0.52 ± 0.06	3.2 ± 2.6
Old #2	0.065 ± 0.004	0.025 ± 0.003	0.42 ± 0.08	0.44 ± 0.07	1.9 ± 1.8
Old #3	0.083 ± 0.007	0.021 ± 0.007	0.60 ± 0.06	0.64 ± 0.03	8.2 ± 2.3
Old #4	0.058 ± 0.003	0.026 ± 0.002	0.49 ± 0.09	0.53 ± 0.05	4.7 ± 3.5
Old #5	0.062 ± 0.003	0.013 ± 0.003	0.58 ± 0.05	0.54 ± 0.04	5.9 ± 1.7
Old #6	0.057 ± 0.004	0.019 ± 0.003	0.59 ± 0.04	0.65 ± 0.05	0.9 ± 0.7
Mean	0.066	0.021	0.53	0.55	4.1
CoV	6%	17%	13%	9%
COPD #1	0.105 ± 0.008	0.044 ± 0.013	0.64 ± 0.07	1.26 ± 0.34	4.7 ± 3.8
COPD #2	0.152 ± 0.011	0.064 ± 0.027	0.75 ± 0.18	1.34 ± 0.20	6.8 ± 5.3
COPD #3	0.085 ± 0.004	0.040 ± 0.003	0.85 ± 0.23	0.84 ± 0.06	2.7 ± 2.3
COPD #4	0.086 ± 0.012	0.047 ± 0.006	0.92 ± 0.24	1.10 ± 0.07	4.3 ± 2.9
COPD #5	0.088 ± 0.004	0.033 ± 0.001	0.81 ± 0.05	0.89 ± 0.03	9.7 ± 3.5
COPD #6	0.096 ± 0.014	0.061 ± 0.006	1.02 ± 0.17	0.92 ± 0.13	1.4 ± 2.7
Mean	0.102	0.048	0.83	1.06	5.0
CoV	9%	17%	19%	12%
Analysis of variance
F ratio (BG:WG)	17.1***	22.8***	30.5***	42.6***	2.9
F ratio (BP:WP)	30.2***	7.5***	3.7***	7.6***	5.5***
ICC	0.99	0.96	0.95	0.98	0.86

LogSDV̇ and LogSDQ̇ are estimates for the standard deviation for the natural logarithm of the ventilation–perfusion (V̇_A:Q̇) distribution, as estimated from the alveolar ventilation and perfusion distributions within the lung model, respectively. Other parameters are as defined in Table 1. CoV, coefficient of variation; F ratio (BG:WG) is the variance ratio for the between-group to within-group comparison; F ratio (BP:WP) is the variance ratio for the between-participant to within-participant comparison. ICC is the intraclass correlation coefficient. Errors shown are for  ±  1SD.

^***P < 0.001.

Table 6.

Comparison of studies reporting widths for the ventilation-to-perfusion distribution in humans

	Young		Older		COPD
	LogSDV̇	LogSDQ̇	LogSDV̇	LogSDQ̇	LogSDV̇	LogSDQ̇
Present study (n = 6)	0.41	0.40	0.53	0.55	0.83	1.06
Wagner et al. (32) (n = 4 or 5)	0.35	0.43	0.44	0.76
Wagner et al. (33) (n = 23)					1.27	1.12
Rodríguez-Roisin et al. (25) (n = 150)					0.88	0.92
Beck et al. (3) (n = 7)	←0.84→

LogSDV̇ and LogSDQ̇ are standard deviations for the natural logarithm of the ventilation–perfusion (V̇_A:Q̇) distribution, as estimated from the alveolar ventilation and perfusion distributions, respectively; n is the number of participants. Young participants for present study were 20–24 yr old; older participants were 70–79 yr old. Young participants for Wagner et al. (32) were 21–24 yr old; older participants were 39–60 yr old. Age range for participants for Beck et al. (3) is unknown, and their technique does not distinguish between LogSDV̇ and LogSDQ̇.

An important feature of the results is that the within-participant standard deviations and coefficients of variation for the parameters in Tables 4 and 5 are generally small and the intraclass correlation coefficients are high. This demonstrates that the results are highly repeatable from test to test for a given participant. The one exception to this among the primary parameters is ${\sigma }_{\ln {\text{C}}_{\text{d}}^{\text{*}}}$, where the coefficients of variation are higher. This is particularly so for the young participants, presumably because their lower absolute values for ${\sigma }_{\ln {\text{C}}_{\text{d}}^{*}}$ lessens the parameter’s influence on their overall lung function.

Tables 4 and 5 also illustrate for each parameter the variance ratios for the between-group versus within-group comparison and for the between-participant (within-group) versus within-participant comparison, as estimated using analysis of variance. These variance ratios were generally large. The between-participant (within-group) comparisons were highly significant (P < 0.001) for all parameters. The between-group comparisons were significant for all parameters except alveolar volume, where there were large variations within each group, and shunt.

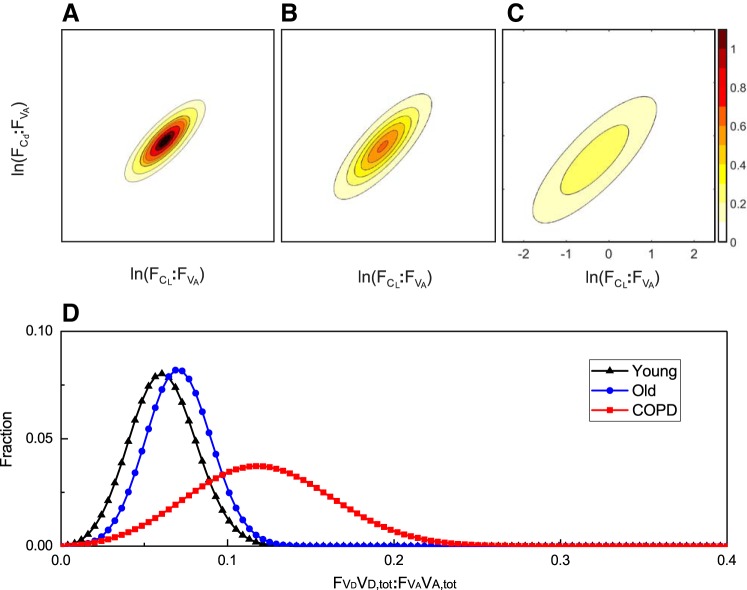
Figure 7 illustrates, for each participant group, the overall mean bivariate log normal distributions for ${\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}$ and ${\sigma }_{\ln {\text{C}}_{\text{d}}^{*}}$ as contour plots, and the normal distributions for (V_D,tot/V_A,tot)${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$. With the exception of the comparison between young and old for (V_D,tot/V_A,tot)${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$, these plots illustrate the very marked differences for these distributions between the groups.

Fig. 7.

Distributions associated with the mean lung parameters from the 3 groups of participants. A–C: contour plots for the bivariate log normal distributions for the young group (A), the old group (B), and the COPD group (C). Contour intervals are values for the probability density function. D: normal distributions for the dead space relative to alveolar volume at FRC for all 3 groups. These distributions have been illustrated in a discretized form, with 100 points evenly spaced on a scale from 0 to 0.4.

Data from the young healthy participants were subjected to a detailed sensitivity analysis to determine the likely influence of the assumed parameter values of the model (Q̇_tot, ρ, ${\lambda }_{\text{T},{\text{CO}}_{\text{2}}}$) on those estimated in the recovery process. For each data set, parameters were recovered with Q̇_tot set to give an arteriovenous O₂ difference of 40, 50, or 60 ml/l, with ρ set to 0.65, 0.8, or 0.95, and with ${\lambda }_{\text{T},{\text{CO}}_{\text{2}}}$ set to 0.25, 0.40, or 0.55, giving a matrix of 27 parameter estimates from each data set. The sensitivity (%) of the fitted parameter value to the assumed parameter value was calculated as the fractional change in the fitted parameter value relative to the fractional change in the assumed parameter value. For the airway parameters (V_A,tot, V_D,tot, ${\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}$, ${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$), these sensitivities were very low—always less than 10%, and usually less than 5%. However, for ${\sigma }_{\ln {\text{C}}_{\text{d}}^{*}}$ this was not the case: Q̇_tot had a relative influence of 20% and ρ a relative influence of 50%, with smaller values for Q̇_tot, and larger values for ρ, being associated with smaller values for ${\sigma }_{\ln {\text{C}}_{\text{d}}^{\text{*}}}$.

DISCUSSION

This study has explored the conjecture that, if measured with sufficient accuracy, there is enough information contained within the way that expiratory gases emerge from a lung during steady breathing and during a subsequent period of inert gas washout to infer much of the form and degree of inhomogeneity present within the lung. The study has required the development of a new model of inhomogeneity of gas exchange within the lung. It has also required highly accurate measures of gas exchange that have only recently become available. We have shown that, by fitting parameters of the model to the experimental gas exchange data, it is possible to recover parameters reflecting a number of different aspects of inhomogeneity in gas exchange.

Formal support for our conjecture is provided through the synthetic data study. In particular, we demonstrated that the underlying values for the parameters reflecting inhomogeneity that were used to generate the synthetic gas exchange data could be recovered from those gas exchange data. However, the original reasoning behind our conjecture was intuitive and was as follows. First, the shape of a multibreath N₂ washout gives a measure of the spread of the alveolar ventilation to volume ratio, V̇_A:V_A, across the lung. [Changes in the shape of a multibreath inert gas washout form the basis of the lung clearance index (24).] Second, the profiles by which ${\text{CO}}_2$ and ${\text{O}}_2$ emerge during expiration give an overall indication of the anatomic dead space, V_D, and the distribution of the anatomic dead space to volume ratio, V_D:V_A, across the lung. Third, V̇_A:Q̇ mismatch generates a far greater range of values for alveolar Po₂ across the lung than it does for alveolar Pco₂ (because of dissimilarities between the dissociation curves for ${\text{O}}_{\text{2}}$ and ${\text{CO}}_{\text{2}}$ in blood). In a lung with a single common dead space—where the expired gas profile would resemble a step function—this aspect of lung function is not necessarily detectable from the expiratory profiles at the mouth. However, in a lung with a distributed dead space—where the expired gas profile is more sigmoidal in shape—alveolar gas from lung units with high ventilations relative to dead space/lung volume will arrive at the mouth earlier than gas from units with low ventilations. For a lung where the blood flow to a lung unit is positively correlated with ventilation to that unit, then this also results in alveolar gas from lung units with high blood flows arriving at the mouth earlier (on average) than gas from units with low blood flows. Together, these features provide a sequential addition of alveolar gas to phase II of expiration from the lung units, with gas arriving (on average) earlier from units with high blood flow than from those with low blood flow. As the lung units with high blood flow on average have low V̇_A:Q̇ ratios (the variance for blood flow being greater than the variance for ventilation), this will generate an asymmetry between the Pco₂ and Po₂ profiles during phase II of expiration that would not be present in a lung without V̇_A:Q̇ mismatch. Thus features relating to all the proposed aspects of inhomogeneity in our model should be present within the expiratory gas profile.

Our model of inhomogeneity is relatively simple but as judged from the residuals, it nevertheless describes well the data gathered from young healthy participants, older healthy participants, and participants with mild to moderate COPD. Whether this will be true for more severe COPD or other respiratory diseases remains to be determined. The parameter values obtained were very repeatable from test to test, and are clearly different between different individuals and between the different groups. This suggests that our methodology is not especially sensitive to moment-to-moment variations in an individual’s physiology, and that reliable values may be obtained from a single experimental procedure. Both of these features would seem prerequisites for utility. Finally, our model makes an important conceptual distinction between parameters that reflect intrinsic properties of the lung, i.e., anatomical dead space, alveolar volume, and the distributions for anatomical dead space, compliance, and vascular conductance, and those that reflect extrinsic factors, such as total ventilation, total pulmonary blood flow, and metabolic rate, that also influence the effects of lung inhomogeneity on gas exchange.

A major biological novelty of our model is that it partitions unevenness in alveolar ventilation within the lung into a component that arises from uneven inflation of the lung and a second component that arises from differences in anatomic dead space between lung units. Although this study is primarily concerned with method development, a surprise to the authors was the large increase in anatomic dead space (as distinct from the increase in purely physiological dead space that arises through the increase in V̇_A:Q̇ mismatch) relative to alveolar volume recorded in the patients with COPD. We now suspect that this may arise from the pathological process of centrilobular emphysema that occurs in patients with COPD (13). In functional terms, this process may be carving out additional dead space beyond the terminal bronchiole as respiratory bronchioles and alveolar ducts are progressively destroyed from the central region of the acinus. If so, then part of the recognized apparent increase in dead space in COPD may be genuinely anatomical rather than simply physiological in nature.

A comparison of parameter values between the young and the old illustrates the importance of aging within the lung—something that has long been known, and is recognized by the enormous effort that has been made to generate accurate age- (and sex-, and ethnic-) specific reference values for spirometry (22). Although we have only studied a small number of participants, one striking exception appears to be [(V_D,tot/V_A,tot)${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$], where the difference between the young and old participants is minimal, but the gap between the healthy participants and those with COPD is very large. One possible interpretation is that, in COPD, some acini are much more affected than others (13), and therefore that emphysematous progression in COPD occurs as much by progressive recruitment of more acini into the disease process as by progressively worsening disease within each acinus. If so, then a parameter that is measuring inhomogeneity between acini should be highly sensitive to even small amounts of lung damage, far more so than one that is simply registering mean progression of disease. Thus it is possible that (V_D,tot/V_A,tot)${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$ has the potential to fulfill the role of a long sought-after marker of early lung damage that occurs before a diagnosis of COPD can be made (36).

As noted above, an essential prerequisite to this work has been the recent development of the experimental technique of MFS (7). This technique has reduced the error between inspiratory and expiratory molecular flow measurements from around 1 in 20 molecules to less than 1 in 500 molecules. The importance of this was demonstrated in the simulation studies, where the parameter recovery algorithm generally failed to converge for data generated using a noise model that reflects current equipment guidelines (24). Effectively, the additional precision associated with the MFS technique allows signals in the data associated with inhomogeneity to rise above the noise. This precision also allows the direct integration of flow in the lung model to proceed without too much gain or loss of lung volume over time. If, at rest, we assume that the volume of gas breathed in or out over 1 min is approximately double FRC, then a 5% error between inspiratory and expiratory flow would cause the lung volume to shrink or expand by 10%/min, whereas the corresponding value for a 0.2% error is a shrinkage or expansion of 0.4%/min.

Our approach has significant practical advantages over other methods of assessing inhomogeneity in the lung. The test is relatively simple for the patient to undertake; it is noninvasive, unlike the multiple inert gas elimination technique (MIGET) (31, 32); it does not require ionizing radiation, unlike CT and PET; it does not require expensive scanners and reagents, unlike hyperpolarized He and Xe MRI; and it is sufficiently simple to conduct that it could be implemented by any standard lung function testing laboratory.

The use of a bivariate (log) normal distribution in our model bears some similarity to the models of Wilson and Beck (35) and Beck et al. (3), where this distribution was used for ventilation and perfusion in the lung. However, these studies modeled dead space as one single volume and were only concerned with single values for gas exchange for each breath. A unique feature of the present model is that the distribution for dead space enables it to describe the profile of CO₂, O₂, and N₂ exchange during each expiration. The parameter recovery routine fits the molar flow of the gases every 10 ms ensuring that this information is not lost.

Our approach to assessing inhomogeneity in the lung differs substantially from MIGET (31–33). First, MIGET is concerned with steady-state concentrations and fluxes. Therefore it cannot provide information for distributions relating to lung volume. Second, MIGET uses inert gases with solubility ranges that greatly exceed the range for apparent solubility associated with O₂ and CO₂. Therefore it can explore V̇_A:Q̇ distributions over a wider range than is possible with the present technique. Third, MIGET constrains distributions to be smooth and can recover distributions with more than one maximum, although there has been considerable debate over exactly how much detail within the underlying distribution can be recovered (15). Our technique constrains the distributions to be (log) normal, and hence also unimodal. As MIGET has shown that the distribution for V̇_A:Q̇ may be bi- or even trimodal, this is one area where our model may be underparameterized. However, as units with very high or very low V̇_A:Q̇ cannot influence the exchange of CO₂ and O₂ to a very great degree, we suspect (although do not know) that such units will appear within our model as additional dead space or shunt, respectively. Finally, MIGET has a very complex protocol and requires the volunteer to have a systemic arterial catheter in place. The present test is noninvasive, easy for volunteers to undertake, and lasts 15 min.

Table 6 compares data from this study for the V̇_A:Q̇ distribution with those from other studies. There is good agreement with data from MIGET (32) for both young and older healthy participants. For participants with COPD, the widths reported in the literature from MIGET are themselves somewhat variable (25, 33). This is not especially surprising given the heterogeneity of the disease and the variations in severity that will have been present between patients. The results from our study are consistent with the range of values reported. The results obtained by Beck et al. (3) for healthy individuals using their technique are less consistent with either MIGET or the current findings.

Clinical approaches to assessing airways inhomogeneity using lung washout studies have been summarized in a recent consensus statement (24). This statement recognizes the significant difficulties caused by the limited accuracy of existing technologies. Clinical indexes include the lung clearance index (LCI) and the variation in slope of the nitrogen record in phase III of expiration over the course of a nitrogen washout. Although the nitrogen washout phase of our protocol was not conducted with a controlled tidal volume as normally applied to clinical washout studies, we nevertheless present examples for the data and model fit in Fig. 4 in a manner suitable for comparison with the existing washout literature. A particular feature to note is that our model of inhomogeneity is capable of generating a slope in the nitrogen record during phase III of expiration in the absence of any diffusional limitation within the model. It is important to recognize that the LCI and the slope of the nitrogen record in phase III of expiration are essentially empirical descriptions of parts of the results from particular tests, rather than parameters of a structural model relating to different aspects of inhomogeneity within the lung. With that caveat, however, it is clear that the LCI is becoming increasingly important for monitoring disease progression in cystic fibrosis (14). The present study suggests many ways in which the LCI could be improved. For example, MFS technology (7) can provide far greater accuracy of measurement, and estimable parameters within models of lung inhomogeneity can provide far greater insight into the underlying nature of airway inhomogeneity as well as ensuring that the information content within the whole data set can be exploited.

For completeness, it should also be noted that other MRI approaches to imaging inhomogeneity are under development. In particular, the technique of arterial spin labeling to provide measures of regional blood flow (6) and the technique of oxygen enhanced proton MRI to measure specific ventilation (26) have recently been combined in humans to produce a map of V̇_A:Q̇ in a sagittal lung section (27).

There remain a number of shortcomings associated with our measurements of lung heterogeneity. First, the recovered values for ${\sigma }_{\ln {\text{C}}_{\text{d}}^{\text{*}}}$ were less precise than those for the other parameters. This is not surprising as, unlike the other estimated parameters, ${\sigma }_{\ln {\text{C}}_{\text{d}}^{*}}$ relates to perfusion, and so its recovery has to depend on more subtle features within the gas phase.

A second caveat is that, in the presence of experimental variability, the fitting process was not usually able to converge on a unique set of parameters if estimates were sought for all of the parameters of the model. Consequently, we fixed ${\lambda }_{\text{T},{\text{CO}}_{\text{2}}}$, ρ, and Q̇_tot at physiologically plausible values and used the fitting process to estimate values for the remaining subset of the parameters. To explore the significance of fixing these three parameters on the estimates for the other parameters, a sensitivity analysis was undertaken. This sensitivity analysis revealed that the choice of value for ${\lambda }_{\text{T},{\text{CO}}_{\text{2}}}$ had essentially no effect on the value for any other parameter estimate. This is unsurprising as the experimental protocol did not involve varying the alveolar Pco₂, and so the amount of CO₂ stored in the lung tissue will have remained almost constant. The analysis also revealed that the parameter estimates for V_A,tot, V_D,tot, ${\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}$, and ${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$ were essentially independent of the choice of value for ρ and Q̇_tot. However, the estimate for ${\sigma }_{\ln {\text{C}}_{\text{d}}^{\text{*}}}$ was significantly influenced by the choice of value for both Q̇_tot and ρ, with ${\sigma }_{\ln {\text{C}}_{\text{d}}^{\text{*}}}$ changing by 0.2% for every 1% change in Q̇_tot and by 0.5% for every 1% change in ρ. The assumed value for Q̇_tot was based on metabolic rate, but could still be inaccurate by perhaps  ± 25%. Thus, fixing the value for Q̇_tot introduces an uncertainty of  ± 5% into the estimate for ${\sigma }_{\ln {\text{C}}_{\text{d}}^{*}}$ (0.2 of 25%). For ρ, there is a mathematical upper bound for its value of 1. Although not used in the modeling process, there is also effectively a lower bound to ρ. Values below this bound cause the model to generate infeasible values for pulmonary venous oxygen saturation that are below the recorded arterial oxygen saturation by more than the intrinsic error of the pulse oximeter (typically, 1–2% in this region). This lower bound appears generally to be quite high, at around 0.65–0.7. We assumed a value for ρ of 0.8, and we think it unlikely that this value is wrong by more than 0.1 or 12% (at least, in lungs that are not very badly diseased). Therefore we estimate that fixing the value of ρ introduces a further additional uncertainty to the estimated value for ${\sigma }_{\ln {\text{C}}_{\text{d}}^{\text{*}}}$ of  ± 6%.

A third caveat relates to the use of pure O₂ to generate the N₂ washout from the lung. First, it means that the breaths used to fit the washout data are not the same as those used to fit the steady-state expiratory profiles for CO₂ and O₂. Second, pure O₂ reduces cardiac output and vasodilates the pulmonary vasculature, and so the properties of the lung may differ between the air-breathing and pure oxygen-breathing periods. This may be less important than it first appears because the model-fitting process uses only the residuals for N₂ during the washout phase. Third, breathing pure O₂ causes significant amounts of O₂ physically to dissolve in the blood, and the subsequent effects on mixed-venous composition add complexity and uncertainty to the overall model.

Some of these limitations could be addressed by further engineering the MFS system so that it can track tracer gas flows added to the inspirate. In particular, a soluble tracer gas would allow measurement of pulmonary blood flow, and an insoluble tracer gas would allow the wash-in/washout data to be obtained contemporaneously with the “air” breathing data. This would both remove the need to assume a cardiac output and remove the need for the period of high O₂ breathing.

To conclude, in a small group of participants, we have confirmed our hypothesis that it is possible to extract measures of lung inhomogeneity from highly precise measurements of respiratory gas exchange coupled with noninvasive measurements of arterial saturation. This has required not only the new technique of molecular flow sensing to provide experimental data of sufficient accuracy, but also the development of an entirely new physiological model of inhomogeneity of gas exchange within the lungs. The method should be practical within a clinical setting and should provide information on a number of distributions intrinsic to the lung. For the particular participants selected, most parameter estimates were highly repeatable from test to test. The hope for the future is that the approach may provide quantitative information that is useful for the early detection of disease, for monitoring the progression of disease, for monitoring therapeutic effect, and for stratifying heterogeneous diseases such as COPD. Of course, much remains unknown, including how broadly the approach can be applied across different forms of respiratory disease. To answer these questions will require detailed and extensive clinical study.

GRANTS

This work was supported by the National Institute for Health Research (NIHR) Biomedical Research Centre, based at Oxford University Hospitals NHS Trust, Oxford. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health. J. E. Mountain and N. M. J. Smith were supported by Engineering and Physical Sciences Research Council-funded Systems Biology Doctoral Training Centre studentships.

DISCLOSURES

Oxford University Innovation, a wholly owned subsidiary of the University of Oxford, holds/has filed patents relating to this work. J.E.M., D.P.O’N., L.C., J.H.C., G.A.D.R., G.H., J.P.W., and P.A.R. have an interest in one or more of these patents/filings.

AUTHOR CONTRIBUTIONS

J.E.M., P.S., D.P.O'N., L.C., J.H.C., G.A.D.R., and G.H. performed experiments; J.E.M., J.P.W., and P.A.R. analyzed data; J.E.M., J.P.W., and P.A.R. interpreted results of experiments; J.E.M. and N.M.J.S. prepared figures; J.E.M., D.P.O'N., N.M.J.S., and P.A.R. drafted manuscript; J.E.M., P.S., D.P.O'N., N.M.J.S., L.C., J.H.C., G.A.D.R., G.H., J.P.W., and P.A.R. approved final version of manuscript; D.P.O'N., N.M.J.S., G.A.D.R., and P.A.R. edited and revised manuscript; P.A.R. conceived and designed research.

APPENDIX

This appendix is concerned with the calculation of the fractional shares of alveolar volume, lung compliance, lung vascular conductance, and dead space ($F_{{\text{V}}_{\text{A}}}^i$, $F_{{\text{C}}_{\text{L}}}^i$, $F_{{\text{C}}_{\text{d}}}^i$, and $F_{{\text{V}}_{\text{D}}}^i$respectively) for each lung unit of the model in terms of our fundamental measures of inhomogeneity ${\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}$, ${\sigma }_{\ln {\text{C}}_{\text{d}}^{\text{*}}}$, and ${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$ together with ρ. The underlying assumptions are that the (continuous) distributions $F_{{\text{C}}_{\text{L}}}$:$F_{{\text{V}}_{\text{A}}}$ and $F_{{\text{C}}_{\text{d}}}$:$F_{{\text{V}}_{\text{A}}}$ follow a bivariate log-normal form (Fig. 1B) with correlation ρ (2, 3, 35), and that $F_{{\text{V}}_{\text{D}}}$:$F_{{\text{V}}_{\text{A}}}$ follows an independent normal distribution.

For ease of notation we define the continuous variables x and y as

$$x=\ln \left(\frac{F_{{\text{C}}_{\text{L}}}(x,y)}{F_{{\text{V}}_{\text{A}}}(x,y)}\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}y=\ln \left(\frac{F_{{\text{C}}_{\text{d}}}(x,y)}{F_{{\text{V}}_{\text{A}}}(x,y)}\right),$$ (A1)

where the following are probability density functions for fractional compliance, $F_{{\text{C}}_{\text{L}}}(x,y)$, fractional pulmonary vascular conductance, $F_{{\text{C}}_{\text{d}}}(x,y)$, and fractional alveolar volume at FRC, $F_{{\text{V}}_{\text{A}}}(x,y)$.

Using the notation of linear algebra, we may write the bivariate distribution for ${\text{V}}_{\text{A}}(x,y)$ as

$${\text{V}}_{\text{A}}(x)=\frac{1}{2\pi {\left|\Sigma \right|}^{\frac{1}{2}}}\exp \left[-\frac{1}{2}{\left(x-\mathbf{\text{μ}}\right)}^{\text{T}}{\Sigma }^{-1}\left(x-\mathbf{\text{μ}}\right)\right],$$ (A2)

where

$$x=\left(\begin{array}{c}x\\ y\end{array}\right),\hspace{0.17em}\mathbf{\text{\hspace{0.17em}μ}}=\left(\begin{array}{c}\overline{x}\\ \overline{y}\end{array}\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Sigma =\left(\begin{array}{cc}{\left({\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}\right)}^2& \rho {\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}{\sigma }_{\ln {\text{C}}_{\text{d}}^{*}}\\ \rho {\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}{\sigma }_{\ln {\text{C}}_{\text{d}}^{*}}& {\left({\sigma }_{\ln {\text{C}}_{\text{d}}^{*}}\right)}^2\end{array}\right),$$ (A3)

ρ is the correlation between the two distributions, and x̄ and ȳ are the means of x and y.

The equidensity contours for this distribution are ellipsoids, where the directions of the principal axes are the eigenvectors of the covariance matrix Σ, and the squared relative lengths are given by the eigenvalues (12). We can undertake an eigendecomposition of Σ to provide these values as follows:

$$\Sigma =U\Lambda U^{\text{T}}=\left(U{\Lambda }^{\frac{1}{2}}\right){\left(U{\Lambda }^{\frac{1}{2}}\right)}^{\text{T}},$$ (A4)

where Λ is a diagonal matrix with, as $0\le \rho \le 1$, positive entries on the diagonal and U is chosen as a rotation matrix (columns are unit eigenvectors). Thus any specific distribution may be generated by scaling the standard normal distribution (zero mean, unit variance, and zero correlation by Λ^1/2, rotating by U, and translating by μ. Values for the elements of μ may be obtained by noting that $F_{{\text{V}}_{\text{A}}}(x,y)$ integrates over the x,y plane to 1, and, therefore, using Eqs. A1 and A2, that $\overline{x}=-{\left({\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}\right)}^2/2$, and $\overline{y}=-{\left({\sigma }_{\ln {\text{C}}_{\text{d}}^{\text{*}}}\right)}^2/2$.

From these results, we can now define a change of variables that works in the opposite direction and maps our specific distribution onto the standard normal distribution as follows

$$s=\left(\begin{array}{c}s\\ t\end{array}\right)={\left(U{\Lambda }^{\frac{1}{2}}\right)}^{-1}\left(x-\mathbf{\text{μ}}\right),$$ (A5)

and Eq. A2 becomes

$$F_{{\text{V}}_{\text{A}}}(s)=\frac{1}{2\pi }\exp \left(-\frac{1}{2}{s}^{\text{T}}s\right)$$ (A6)

or equivalently,

$$F_{{\text{V}}_{\text{A}}}(s,t)=\frac{1}{2\pi }\exp \left(\frac{-s^2}{2}\right)\exp \left(\frac{-t^2}{2}\right).$$ (A7)

We can now discretize $F_{{\text{V}}_{\text{A}}}$(s,t) into N_s lung units in the s direction, and N_t lung units in the t direction. We can ensure that each has an equal fraction of the alveolar volume at FRC [i.e., $F_{{\text{V}}_{\text{A}}jk}$ = 1/(N_sN_t)] by ensuring that the points are evenly spaced on the cumulative distribution function for the standard normal distribution. This results in N_s + 1 points s₀,s₁,…, $s_{N_s}$, such that s₀ = −∞, $s_{N_s}$ = ∞, and s_j+1 > s_j, and N_t + 1 points t₀,t₁,…, $t_{N_t}$, such that t₀ = −∞, $t_{N_t}$ = ∞, and t_k+1 > t_k.

Changing the variables of Eq. A1 using Eq. A5 we can now calculate the fractional compliance and fractional vascular conductance associated with each of these lung units

$$F_{{\text{C}}_{\text{L}}jk}={\displaystyle {\int }_{t_{k-1}}^{t_k}{\displaystyle {\int }_{s_{j-1}}^{s_j}\exp }}\left(\overline{x}+J_{11}s+J_{12}t\right)F_{{\text{V}}_{\text{A}}}(s,t)\text{d}s\text{d}t,$$ (A8)

$$F_{{\text{C}}_{\text{d}}jk}={\displaystyle {\int }_{t_{k-1}}^{t_k}{\displaystyle {\int }_{s_{j-1}}^{s_j}\exp }}\left(\overline{y}+J_{21}s+J_{22}t\right)F_{{\text{V}}_{\text{A}}}(s,t)\text{d}s\text{d}t,$$ (A9)

where J₁₁, J₁₂, J₂₁, and J₂₂ are the elements of UΛ^1/2. For efficient computation, these equations may be factorized into the product of two line integrals.

The total volume of dead space associated with each of the N_sN_t unique pairs of compliance–volume and vascular conductance–volume ratios is assumed to be equal. However, alveolar units with the same compliance–volume and vascular conductance–volume ratios may be located in different regions of the lung, and thus they will be associated with different volumes of dead space. We assume that rather than forming a single compartment, this dead space is distributed according to a normal distribution. This distribution is discretized into N_d lung units of equal alveolar volume for each pair of compliance–volume and vascular conductance–volume ratios. This is done in a manner analogous to that used above for the bimodal distribution. Thus the total number of lung units, N, becomes N_sN_tN_d. As each of the N_sN_t lung units, denoted with indexes jk, is split into N_d lung units, we introduce a third index, m. Thus we have

$$F_{{\text{V}}_{\text{D}}jkm}=\frac{1}{N_s{N}_t}{\displaystyle {\int }_{z_{m-1}}^{z_m}\frac{z}{\sqrt{2\pi }{\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}}}\exp \left(\frac{-{\left(z-1\right)}^2}{2{({\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}})}^2}\right)\text{d}z,$$ (A10)

where the integration limits z_m have been chosen so that the fractional alveolar volume of lung unit jkm is 1/(N_sN_tN_d).

Finally, we note that in the discretization of the continuous distribution above, each lung unit has three indexes, j, k, and m. We can, however, label each lung unit with a single index i, where

$$i=j+N_s\left(k-1\right)+N_s{N}_t\left(m-1\right),$$ (A11)

for j = 1,2,…,N_s, k = 1,2,…,N_t, m = 1,2,…N_d. For the process of fitting our model to the data, we chose N_s = N_t = N_d = 5, and this provides 125 lung units that are indexed by i.

This completes the calculation of the values for $F_{{\text{V}}_{\text{A}}}^i$, $F_{{\text{V}}_{\text{D}}}^i$, $F_{{\text{C}}_{\text{L}}}^i$, $F_{{\text{C}}_{\text{d}}}^i$ for each lung unit of the model.

Glossary

${\text{C}}_{\text{L}}^{\text{*}}$

Standardized lung compliance, defined for a lung unit as the ratio of the fractional lung compliance to fractional alveolar volume (at functional residual capacity)

C_L,tot

Total lung compliance

$C_{\mathrm{c\prime },\text{g}}^i$

Blood gas content of gas g leaving lung unit i

$C_{\overline{\mathrm{c}\prime },\text{g}}$

Mixed pulmonary venous blood gas content of gas g

${\mathrm{C}}_{\text{d}}^{*}$

Standardized lung vascular conductance, defined for a lung unit as the ratio of the fractional lung vascular conductance to fractional alveolar volume (at functional residual capacity)

C_d,tot

Total pulmonary vascular conductance

$C_{\overline{\mathrm{v}},\text{g}}$

Systemic mixed venous (or pulmonary arterial) blood gas content of gas g

COPD

Chronic obstructive pulmonary disease

$F_{{\text{C}}_{\text{L}}}^i$

Fractional share of total lung compliance of lung unit i

$F_{{\mathrm{C}}_{\text{d}}}^i$

Fractional share of total pulmonary vascular conductance of lung unit i

$F_{\text{E},{\dot{\mathrm{V}}}_{\text{M}}}^i$

Fraction of total respiratory flow leaving lung unit i during expiration

$F_{\text{I},\text{g}}^i$

Fractional concentration of gas g inspired into lung unit i

$F_{\text{I},{\dot{\mathrm{V}}}_{\text{M}}}^i$

Fraction of total respiratory flow entering lung unit i during inspiration

F_M,g

Measured fractional concentration of gas g at apparatus measurement plane

$F_{{\dot{\mathrm{Q}}}_{\text{S}}}$

Shunt fraction

F_S,g

Simulated fractional concentration of gas g, at apparatus measurement plane

$F_{{\text{V}}_{\text{A}}}^i$

Fractional share of alveolar volume of lung unit i

$F_{{\text{V}}_{\text{D}}}^i$

Fractional share of dead space volume of lung unit i

$F_{\text{g}}^i$

Fractional concentration of gas g, in lung unit i

J_m,n

Element m,n of the Jacobian matrix of first-order partial derivatives of the coordinate transformation

LogSDQ̇

Standard deviation for the natural logarithm of V̇_A:Q̇ distribution estimated from the perfusion distribution

LogSDV̇

Standard deviation for the natural logarithm of V̇_A:Q̇ distribution estimated from the alveolar ventilation distribution

MFS

Molecular flow sensor

P_g

Partial pressure of gas g

Q̇

Perfusion

Q̇_tot

Total pulmonary flow (equal to cardiac output less shunt)

Vⁱ

Volume of lung unit i

V_A,tot

Total alveolar volume at functional residual capacity

${\text{V}}_{\text{B},{\text{O}}_{\text{2}}}$

Effective volume of body oxygen stores

${\text{V}}_{\text{D}}^{\text{*}}$

Standardized dead space, defined for a lung unit as the ratio of the fractional dead space to fractional alveolar volume (at functional residual capacity)

V_D,tot

Total dead space volume

V̇_A

Alveolar ventilation

V̇_M

Total respiratory flow

V̇_o2

Oxygen consumption of the body

${\mathrm{S}}_{\mathrm{a}\mathrm{,}{\mathrm{O}}_{\mathrm{2}}}$

Arterial O₂ saturation

${\text{S}}_{\overline{\mathrm{c}\prime },{\text{O}}_{\text{2}}}$

Mixed, end-pulmonary capillary O₂ saturation

${\text{S}}_{\overline{\mathrm{v}},{\text{O}}_{\text{2}}}$

Mixed-venous (pulmonary arterial) O₂ saturation

ΔV_tot

Change in total lung volume from functional residual capacity

λ_T,g

Fraction of additional apparent alveolar volume (defined at functional residual capacity) arising through solubility of gas g, in lung tissue

ρ

Coefficient of correlation between the (log) distributions for standardized lung compliance and standardized lung vascular conductance

${\sigma }_{{\text{V}}_{\text{D}}^{\text{*}}}$

Standard deviation for the normal distribution for standardized dead space

${\sigma }_{\ln {\text{C}}_{\text{L}}^{\text{*}}}$

Standard deviation for the log (to base e) normal distribution of standardized lung compliance

${\sigma }_{\ln {\mathrm{C}}_{\text{d}}^{*}}$

Standard deviation for the log (to base e) normal distribution for standardized vascular conductance