Model of a bilateral Brown-type central pattern generator for symmetric and asymmetric locomotion

Abstract

The coordinated activity of muscles is produced in part by spinal rhythmogenic neural circuits, termed central pattern generators (CPGs). A classical CPG model is a system of coupled oscillators that transform locomotor drive into coordinated and gait-specific patterns of muscle recruitment. The network properties of this conceptual model can be simulated by a system of ordinary differential equations with a physiologically inspired coupling locus of interactions capturing the timing relationship for bilateral coordination of limbs in locomotion. Whereas most similar models are solved numerically, it is intriguing to have a full analytical description of this plausible CPG architecture to illuminate the functionality within this structure and to expand it to include steering control. Here, we provided a closed-form analytical solution contrasted against the previous numerical method. The evaluation time of the analytical solution was decreased by an order of magnitude when compared with the numerical approach (relative errors, <0.01%). The analytical solution tested and supported the previous finding that the input to the model can be expressed in units of the desired limb locomotor speed. Furthermore, we performed parametric sensitivity analysis in the context of controlling steering and documented two possible mechanisms associated with either an external drive or intrinsic CPG parameters. The results identify specific propriospinal pathways that may be associated with adaptations within the CPG structure. The model offered several network configurations that may generate the same behavioral outcomes.

NEW & NOTEWORTHY Using a simple process of leaky integration, we developed an analytical solution to a robust model of spinal pattern generation. We analyzed the ability of this neural element to exert locomotor control of the signal associated with limb speeds and tested the ability of this simple structure to embed steering control using the velocity signal in the model’s inputs or within the internal connectivity of its elements.

INTRODUCTION

Specialized neural elements in the spinal cord, known as the central pattern generators (CPGs), contribute to the generation of periodic coordinated patterns of locomotor activity (Grillner and Zangger 1975). Discovered in deafferented preparations, CPGs do not require sensory signals to produce locomotor behavior; however, their pattern is greatly influenced by sensory and descending inputs (Prochazka and Ellaway 2012; Yakovenko 2011). Specifically, the direct electrical stimulation of a brain stem structure called the mesencephalic locomotor region (MLR), even in decerebrated animals, produces oscillations in the CPGs and subsequent locomotor behavior (Grillner and Wallén 1985). This locomotor behavior is characterized by the complex coordinated actions of multiple muscle groups. It is remarkable that a change in either the magnitude or frequency of MLR stimulation can generate all appropriate modifications of these patterns. This increase in stimulation expresses a full repertoire of gaits with continuous transitions, such as from walking to trotting or galloping in over-the-ground locomotion (Shik et al. 1966), or transitioning from slow walking to swimming in amphibians (Cabelguen et al. 2003), which is faster than the walking mode of locomotion. Thus increasing stimulation input current corresponds to an increase in locomotor velocity.

Many CPG models were developed over the last century (Barnett and Cymbalyuk 2014a; Bashor 1998; Markin et al. 2010; Rybak et al. 2006; Taga et al. 1991; Yakovenko et al. 2005; Verzár 1923). Simulated model structure and its parameters are usually derived from observing the motor output patterns or their changes in response to external inputs or naturally occurring variations. These models give rise to the mechanistic descriptions that capture biological organization and the processes; however, they generally start as phenomenological or statistical representations of observed phase variations or timing in the recorded muscle activity. For example, both the limb-based Brown’s CPG (Brown 1911) and the joint-based Grillner’s CPG (Grillner 1981) are similarly founded on the observations of multiple representative electromyographic profiles providing insight into the functional organization of this circuitry.

The idea of a CPG as a distributed mechanism that integrates convergent inputs (Grillner and Wallén 1985) has been supported by both computational and experimental studies. Using calcium imaging, the spatiotemporal activity of rhythmogenic circuitry was found to be functionally distributed with motoneurons in the rostral lumbar and sacral segments of the spinal cord (Bonnot et al. 2002; O’Donovan et al. 2005). The spatiotemporal distribution of neural activity throughout the lumbar enlargement with descending control and sensory inputs intact was visualized by combining the anatomical location of the motoneurons with information about their activity during normal locomotion (Yakovenko et al. 2002). This was also supported by observations of independent and coupled recruitment of flexor and extensor rhythmogenic spinal circuits using selective optogenetic approaches (Hägglund et al. 2013). The rhythmogenesis in only flexors or only extensors observed with optogenetics supports the computational observation of a switchlike transition between flexors and extensors (or more precisely, limb protractors and retractors), which identifies them as distinct network elements (Yakovenko et al. 2002). This bilateral, switchlike activation of the motor pools spanning the full rostocaudal extent of the lumbosacral enlargement is likely associated with distributed rhythm-generating networks responsible for this activity.

The integration of feedforward predictions and sensory feedback about ongoing execution is the optimal solution for generating robust control of complex body morphology (Kuo 2002). Over the course of evolution, the process of optimization within control pathways has likely been concerned with the optimization of locomotion, as this is a central behavior that is essential for animal survival (Yakovenko 2011). One engineering solution to the problem of computing predictive commands for complex systems is the use of inverse models (Smith 1957; Wolpert and Ghahramani 2000). The complex transformation from muscle activations into movement kinematics could be internalized for inverse solutions that generate appropriate output for the desired kinematic input. It is then not surprising that dedicated rhythmogenic networks for locomotion may be embedding the dynamics of body-ground interactions to solve the problems of intra- and interlimb coordination (Full and Koditschek 1999; Taga et al. 1991). The accuracy of these embedded neural calculations of musculoskeletal transformation may be fine-tuned by experience (Bhushan and Shadmehr 1999; Ijspeert et al. 2013; Kawato 1999; Wolpert et al. 1998). It is important to acknowledge that sensory feedback pathways may also shape the final output of motor pathways and compensate for dynamics during locomotion. In addition, there is considerable evidence that CPGs integrate sensory inputs together with supraspinal commands to generate changes in the timing and magnitude of locomotor activity (Ijspeert 2008; Yakovenko 2011). The inputs from descending pathways may also be phasically modulated by supraspinal interactions to provide appropriate locomotor synergistic coupling, e.g., by the phasic modulation from cerebellum (Arshavsky and Orlovsky 1986) receiving sensory feedback about ongoing phasic activity via ascending tracts. The theoretical details of interactions between multiple descending pathways on the spinal pattern-generating circuitry remains to be unknown.

CPG models offer a unique research opportunity to understand the interplay between these neural directives and biomechanical constraints that govern a complex dynamic task. To this extent, we have previously used inverse solutions of a CPG model to infer the nature of descending inputs (Yakovenko 2011). The surprising result of these simulations was that the input to the CPG was the speed of each limb. Described mathematically as a system of differential equations (Cymbalyuk et al. 2002; Matsuoka 1985; Rybak et al. 2006; Schöner et al. 1990; Wallén et al. 1992; Yakovenko 2011), CPG models are hard, even impossible, to solve analytically in the form of known functions and variables. Still, analytical expressions have several advantages over numerical models. Unlike numerical solutions that often suffer from the accumulating errors and inversely related computational load, the analytical solutions are precise within assumptions taken during their derivation. Even though they are also evaluated, their formulation is more efficient and faster than the approximate numerical solutions.

In this study, we developed a method to obtain an analytical solution to one of the simplest implementations of a locomotor CPG using a rate network with continuous variables, not spikes. We used this analytical expression to further test the ability of this circuitry to embed the regulation of phases appropriate for different speeds and control steering with asymmetric gaits. While the identification of pattern-generating elements is a considerable challenge in experimental techniques, the function of distributed elements of a CPG can be probed with computational methods that allow us to monitor and manipulate any part of the circuit. We tested two hypotheses in this study: 1) the exact analytical solution exists for a bilateral CPG model implemented with a leaky integration process; and 2) the intrinsic circuit redundancy in a CPG can accommodate the expression of asymmetric gait. The function of embedding the asymmetric representations of gait may be relevant for understanding steering and short- and long-term adaptations within spinal systems.

METHODS

Model description.

Whereas a few CPG models of neural activity consider specific ion dynamics using the Hodgkin-Huxley formulation (Cymbalyuk et al. 2002; Rybak et al. 2006), our model captures gross CPG network dynamics, described by T. G. Brown (Brown 1911), in a form of gated leaky integration. We expressed the input-output relationship using coupled leaky integrators formulated as a system of ordinary differential equations (ODEs). The system of ODEs can be expressed in matrix form (Eq. 1), with ipsilateral antagonism expressed as abrupt, non-overlapping state transitions. The state transitions of coupled reciprocal integrators may require complex handling. An event associated with any given state value (x_i) crossing 1 (detected at machine precision) triggers the resetting of the state to 0 and the start of integration for the ipsilateral antagonist. Small perturbations at the transition points could lead to instability. We have solved this problem by allowing only the switching of reciprocal states initiated by the transition from 1 to 0. The reversal of integration to 0 or negative values does not initiate the integration in the reciprocal state in this model. In Fig. 1, for example, if the left flexor (x₁) reaches 1, it resets to 0 and turns off, while the left extensor (x₂) switches on.

$$\dot{x}=U_0+G_{u}u+G_{l}x+Gx$$ (1)

where x = (x₁, x₂, x₃, x₄)^T is state vector; U₀ is constant input from intrinsic connections; G_u is extrinsic input gains; u is extrinsic inputs; G_l is leak gains; and G is weights for connections between integrators (r_ff, r_fe, r_ef, and r_ee weights in Fig. 1).

Fig. 1.

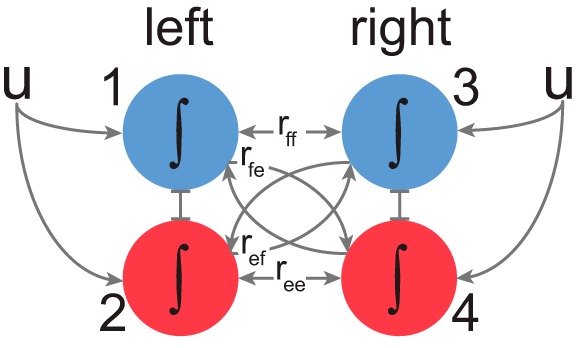
Schematic of the bilateral locomotor CPG model. The oscillatory behavior in each half-center (marked 1–4) was generated through an intrinsic, leaky integrate-to-threshold resetting. This process was also under regulation from intrinsic inputs governed by parameters (r_ff, r_fe, r_ef, r_ee). The flexor half-centers (blue) were reciprocally connected to extensor half-centers (red). See Eqs. 1 and 2 for details.

To simplify model parameter space, the parameters were coupled assuming symmetric organization across the midline, as seen in Eq. 2. Additionally, the connection between flexors (r_ff) was removed for simulations of walking behavior, where swing phases do not overlap.

$$U_0=\left(\begin{array}{c}\begin{array}{c}{u}_{0f}\\ u_{0e}\end{array}\\ \begin{array}{c}{u}_{0f}\\ u_{oe}\end{array}\end{array}\right),G_u=\left(\begin{array}{c}\begin{array}{c}{g}_{uf}\\ g_{ue}\end{array}\\ \begin{array}{c}{g}_{uf}\\ g_{ue}\end{array}\end{array}\right),G_l=\left(\begin{array}{c}\begin{array}{c}{g}_{lf}\\ g_{le}\end{array}\\ \begin{array}{c}{g}_{lf}\\ g_{le}\end{array}\end{array}\right)\cdot I,G=\left(\begin{array}{cc}\begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}0& r_{ef}\\ r_{fe}& r_{ee}\end{array}\\ \begin{array}{cc}0& r_{ef}\\ r_{fe}& r_{ee}\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\end{array}\right)$$ (2)

We used the fixed-step fourth-order Runge-Kutta method with 10⁻³-s precision for forward numerical integration.

The bilateral CPG model produces flexor (swing) and extensor (stance) phases for two limbs in relation to extrinsic input and intrinsic structure. To obtain these phases, Eq. 1 needs to be integrated in time between the state changes. Numerical integration was previously used (Yakovenko 2011) to generate swing and stance periods. The same transition points can be calculated analytically by transforming Eq. 1 into a matrix Cauchy problem and solving a transcendental equation for time of phase change of individual integrators:

$$z_1\cdot \cosh \left(q\tau \right)+z_2\cdot \frac{\sinh \left(q\tau \right)}{q}=z_3\cdot e^{-s\tau }$$ (3)

where z₁ and z₂ are terms describing interactions between internal structure of the system and input (U₀ and u); z₃ represents the terms with inverse leaks and external inputs; s represents general system leakage; and q corresponds to the internal structure of the model (for the detailed description of these terms, see appendix below).

Using this equation, the periods of activity of flexors and extensors during a step cycle were obtained with an iterative algorithm that was sequentially estimating state changes of each integrator until a full step was completed. The appendix (below) provides the details of derivation for Eq. 3.

Cost function.

The CPG model can generate multiple locomotor behaviors as a function of extrinsic inputs and intrinsic interactions (Yakovenko 2011). Given a desired behavior, e.g., stereotypical symmetric walking (Halbertsma 1983), the appropriate CPG parameters were found by optimizing the cost function (J_c) (Eq. 4) that expressed the goodness of fit between target (experimental) and simulated patterns. In the symmetric model, we optimized for six different speeds, from 0.1 to 1.5 m/s (dashed lines in Fig. 2), that were generated with six values of u (evenly distributed between 0.1 and 1.5 arbitrary units). Figure 2 shows the quality of simulated solutions for symmetric walking over a full range of walking speeds.

$$J_c=k_{1}H+k_{2}M+k_{3}O+k_{4}C$$ (4)

where H is the squared difference of simulated and experimental stance and swing periods. The experimental periods were calculated using a best-fit formula obtained empirically with 1% average error (see Fig. 6 and Table 2 in Halbertsma 1983). M is the squared difference of simulated and desired speed ranges that promotes the converging on nontrivial solutions. O is the cost associated with the erroneous coactivation of contralateral flexors. C is the degree of asymmetricity between the simulated speeds of the left and right limbs. All function components were normalized to the domain between 0 and 1 and relative weights (k₁, k₂, k₃, k₄) = (1, 0.7, 2, 0.4). C and M components were removed in simulations intended to produce asymmetric gait (see Figs. 6 and 7 in results).

Fig. 2.

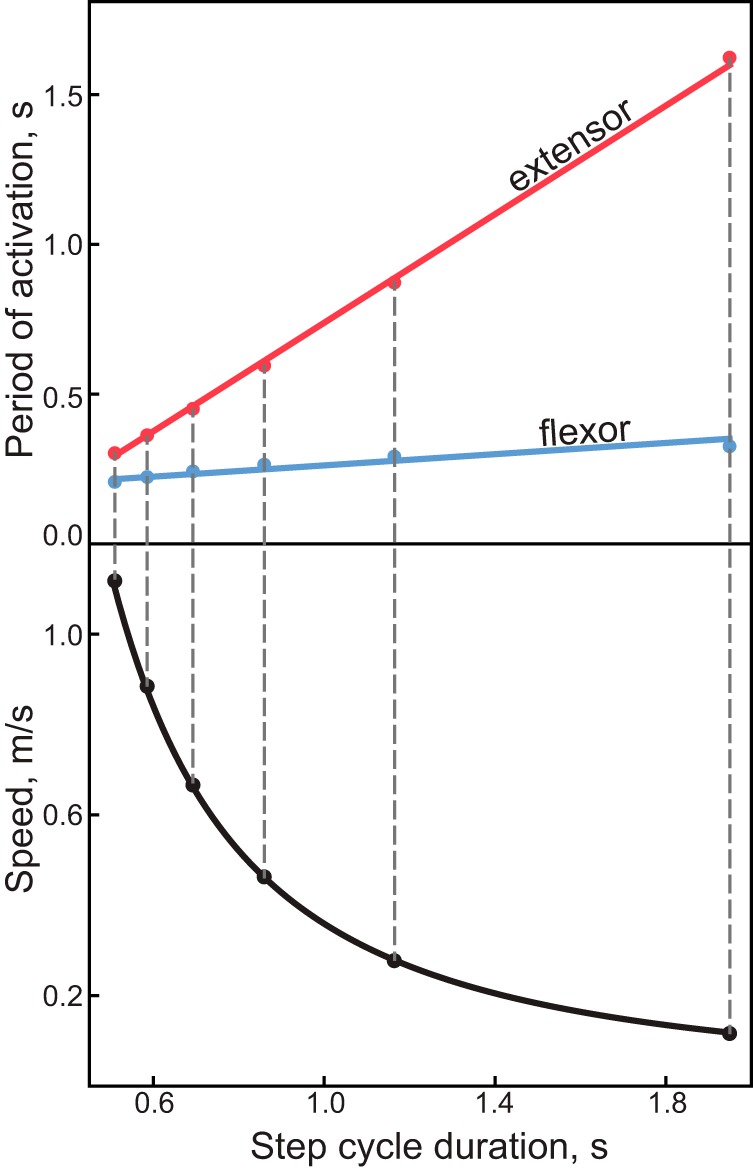
Experimental and simulated locomotor phase duration characteristic. Top: the relationship between the locomotor phase and step cycle duration is shown with points representing the superimposed numerical and analytical solutions for flexor (blue) and extensor (red) phases (Halbertsma 1983). Bottom: the corresponding simulated speed (●) is plotted as a function of step duration computed with the exponential best-fit function (black line) (see Fig. 3, in Goslow et al. 1973).

Fig. 6.

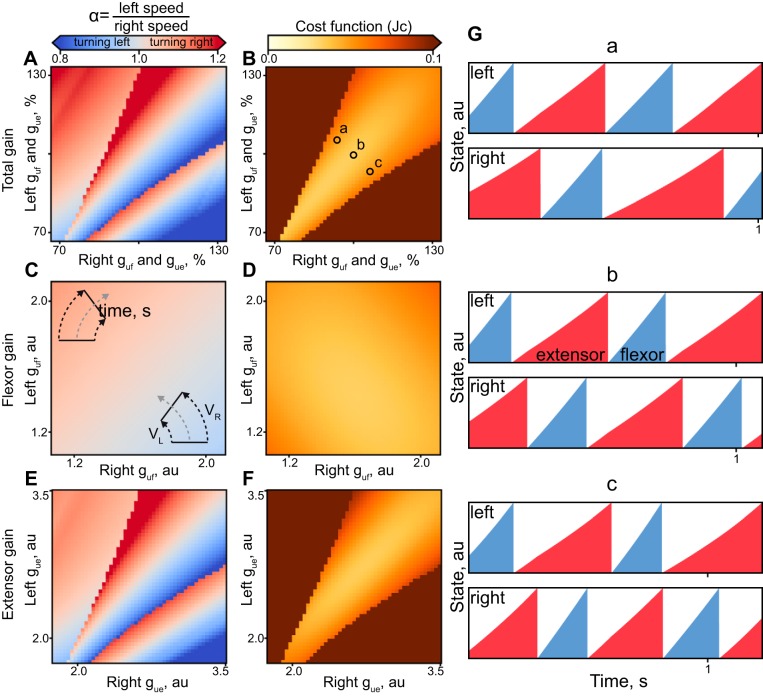
External inputs generate asymmetric gait in the model. The coupled and uncoupled input gain parameters (g_ue, g_uf) were related to the velocity asymmetry (left panels) with the corresponding cost function outputs (right panels). A and B: the input gains of flexors and extensors were varied together for each limb. C and D: only flexor input gains (left and right g_uf) were manipulated for each limb. E and F: only extensor input gains (left and right g_ue) were manipulated for each limb. Insets in C indicate the steering direction for two selected parameter sets. G: “raw” data showing the integration rates with simulation parameters (a, b, and c) selected in B.

Fig. 7.

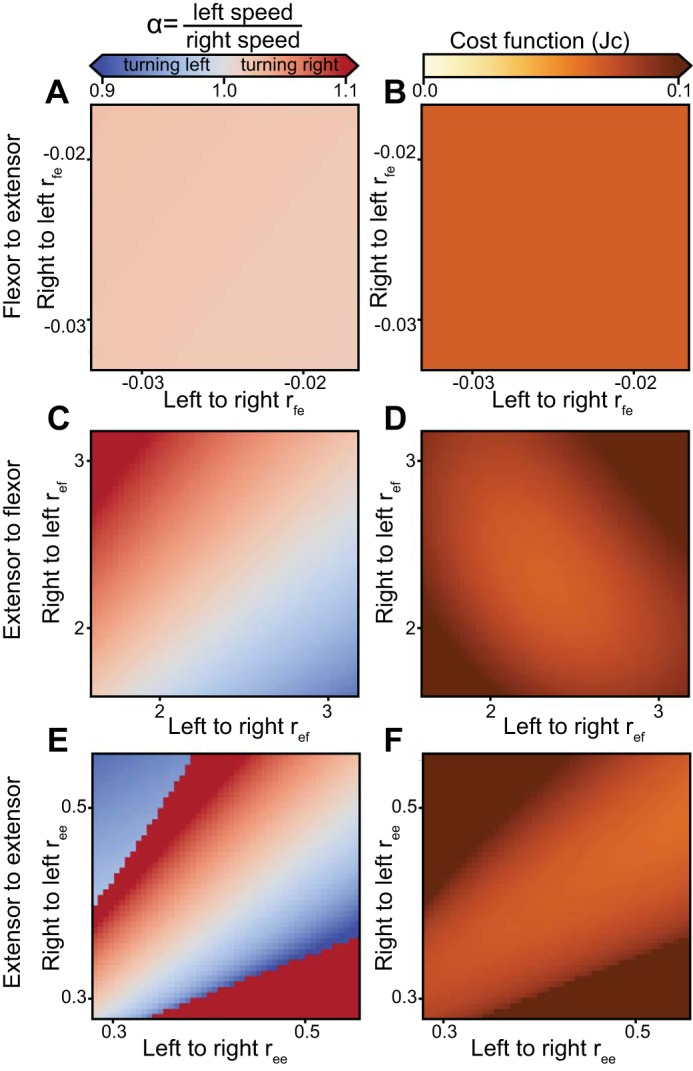
Intrinsic parameters generate asymmetric gait in the model. The uncoupled intrinsic parameters (r_fe, r_ef, r_ee) were related to the velocity asymmetry (left panels) with the corresponding cost function outputs (right panels). A and B: the flexor-to-extensor weights (r_fe). C and D: the extensor-to-flexor weights (r_ef). E and F: the extensor-to-extensor weights (r_ee).

Optimization and parameter perturbation.

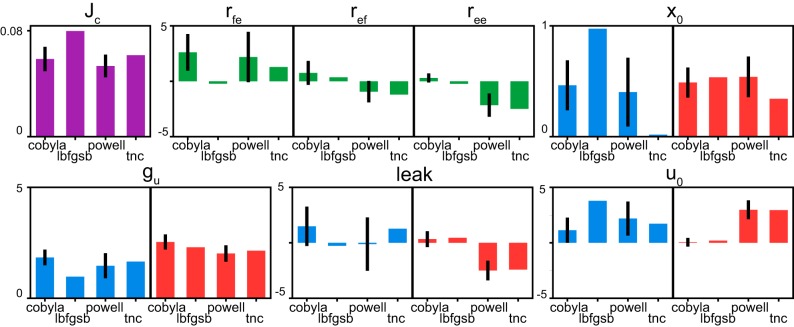
Globally optimal sets of parameters were found numerically using a combination of the basin-hopping algorithm (Wales and Doye 1997) in SciPy (Oliphant 2007) and several constrained local minimizers: the nonlinear optimization algorithm COBYLA (Powell 1964), the truncated Newton algorithm (Nocedal and Wright 2006), the L-BFGS-B algorithm (Byrd et al. 1995), and Powell’s method (Powell 1964). First, the global optimal parameter set (z*) was found. During optimization, the starting value for the basin-hopping algorithm was obtained from a brute-force search over the complete parameter space. Other algorithms were then used to optimize parameters sequentially to arrive at the optimal solution [z* = argmin(J_c)]. Second, we created a normal multivariate distribution to evaluate the nature of close-to-optimal solutions. For this, the distribution was defined by the mean at z* and the covariance matrix with the diagonal elements set to 0.01z* or the equivalent of the standard deviation set at 1% of the value of the optimal solution. The data set of 10⁵ points was then drawn from this distribution and used in the comparison between the analytical and numerical solutions in Fig. 3A. Third, the intermediate solutions of the first step corresponding to local minima were selected to determine the full functional range of parameters in the model, excluding sets with large cost values (J_c > 10). The adjusted for symmetricity range for each parameter is shown as the span of the y-axes in Fig. 4. Fourth, we used a uniform distribution across the symmetric full range of parameters to create another data set of 10⁵ values for the analysis of the expanded range comparison shown in Fig. 3, B and C. Fifth, we created the parameter data set perturbed by 10% from z*. Similar to step 2 above, we created the normal multivariate distribution with the mean at z* and the covariance diagonal elements set to 0.1z*. Sixth, we randomly drew 40 starting seeds and tasked the basin-hopping algorithm (set to 200 iterations for each seed) to repeat the optimization using one of the four local optimization algorithms. This final step in the analysis generated 160 optimal sets for all local algorithms in our analysis. The comparison of parametric distributions is shown for one-third of the best solutions in Fig. 4. The cut of solutions was necessary to reject expected minimization failures with nonconverging searches or those terminating with large J_c values.

Fig. 3.

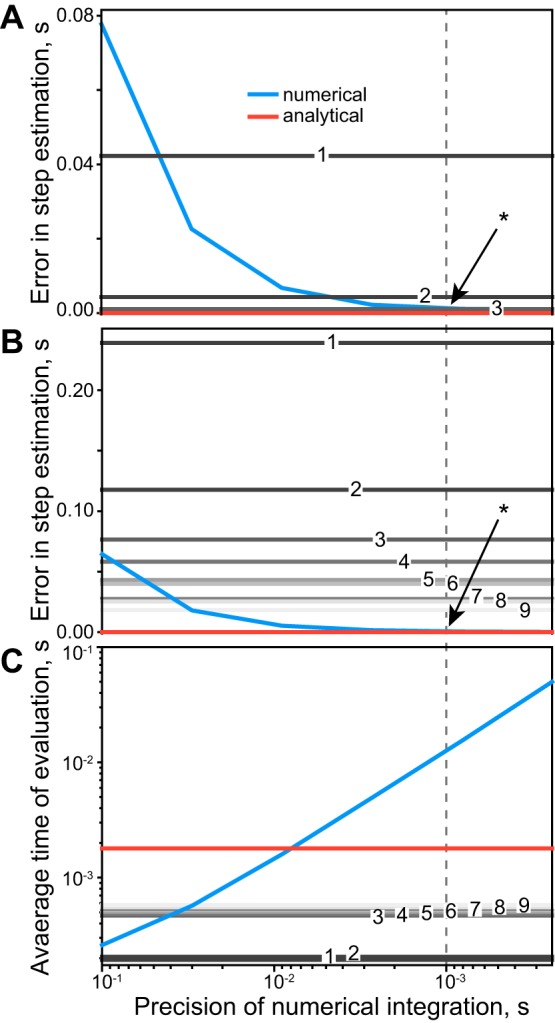
The comparison of analytical and numerical solutions. The measures of numerical (blue), analytical (red), and analytical approximations of different orders (shades of gray with order numbers) are plotted as functions of numerical precision, where the dashed line indicates the most relevant for real-time simulation precision of 1 ms. A: full cycle error in the estimation of phase transition times using the 1% neighborhood of the optimal solution. Because the higher orders of approximations provide the same high precision as the cubic approximations, powers τ⁴–τ⁹ are not displayed. B: similar to A; the errors are shown for the random distribution of parameters. C: average central processing unit time needed to calculate a full step period of 1.25 s (average from Halbertsma’s equations) in Python/NumPy implementation. The data presented in all subplots were averaged over 10⁵ trials.

Fig. 4.

Analysis of parameter sensitivity. The distributions of model parameters and cost function (J_c) are shown for the selection of best optimization sets. Each subplot shows a mean with standard deviation of the parameter values in blue (flexor), red (extensor), and green (mixed) for four types of minimization algorithms. The vertical axis range reflects the full feasible range of parameters as determined by the examination of intermediate solutions (see step 6 in section Optimization and parameter perturbation of methods), with the exception for the J_c values. cobyla, Nonlinear optimization algorithm COBYLA; lbfgsb, L-BFGS-B algorithm; powell, Powell’s algorithm; tnc, Truncated Newton’s.

Phenomenological models of locomotion.

We used several phenomenological models created to describe the relationships between different parameters of stepping during locomotion in our analysis. The relationships between stance and swing phases relative to cycle duration were taken from the study by Halbertsma (1983). The relationship between step cycle duration (T_c) and limb speed (V) was taken from the study by Goslow et al. (1973), where V = (1.84·T_c)^−1.68 (see Fig. 2, bottom). Here, we define the limb speed as the scalar rate of progression during one step cycle. The locomotor velocity is then a vector describing the change in the body’s position as a function of limb speeds. Both studies used best-fit functions to describe data from a small sample of cats, yet these relationships have been recently confirmed with a large subject pool (Frigon et al. 2015).

In the analysis of asymmetric locomotion, we introduced a simple geometrical relationship for walking on a curve. The turn radius of an asymmetric bipedal walk (Eq. 5) was expressed as a function of hip width (L) and an asymmetry parameter α = V_left/V_right:

$$R=\frac{L}{\left|\alpha -1\right|}$$ (5)

The corresponding heading direction change during a single step can be stated as:

$$\gamma =\text{arctan}\left(\frac{V_{\text{right}}-V_{\text{lef}\mathrm{t}}}{L}{T}_C\right)$$ (6)

where γ denotes the heading direction angle from forward direction; T_c is full step cycle period.

RESULTS

Comparison of analytical and numerical solutions.

In this study, the continuous dynamics between phase transitions was demonstrated with a CPG model expressed as a system of interacting oscillators and solved either numerically or analytically using an iterative algorithm (Eq. 3). Analytical solutions were validated in simulations producing experimentally observed periods of flexor and extensor activations in overground locomotion (for example, see Fig. 2). This model was further extended to analyze asymmetric gait and test the ability of this circuit to embed asymmetric gait control.

A high-precision numerical approach carries a processing cost that usually exceeds that of analytical methods. Figure 3 shows the comparison of the processing cost between the numerical and analytical solutions for this model (Eq. 1). The error of evaluating phase transitions with the numerical method (blue line) and the analytical solutions using the root-finding algorithm (red line) was the same at the precision for numerical integration set to 10⁻³ s (intersection marked with asterisk, Fig. 3, A and B). The analytical solutions to Eq. 3, found by expanding the hyperbolic terms, linear to the ninth power, are shown with shades of gray in Fig. 3. Here, the difference between the analytical and numerical estimations of the time of phase transitions was evaluated with the root-mean-square metric of simulation quality. Shown in Fig. 3A, the quadratic approximation (gray line marked with a 2) provided similar quality to the analytical solutions (red line), with sets of close-to-optimal parameters (in 1% vicinity of the optimal set; see step 2 in section Optimization and parameter perturbation in methods). When the model parameters were chosen randomly from the full range of feasible parameters (steps 3 and 4 in methods), quadratic solutions did not provide desirable precision and performed worse than the numerical method, with other powers only approaching a reasonable threshold of >10 ms error (Fig. 3B), which is the order of a motor unit action potential.

Figure 3 shows the comparison of the processing cost between analytical and numerical solutions for this model (Eq. 1). The analytical solution was the best choice for precise real-time applications of this model, outperforming the numerical method by close to an order of magnitude. However, if estimation errors of >10 ms are insignificant in a specific application, e.g., using electromyographic-driven simulations with aggressive low-pass filtering, then high orders of analytical approximations could provide appropriate solutions with even lower computational load than the full analytical solution. The approximations of powers 3–9 use the eigenvalue approach to find roots of polynomials, which is relatively costly but still more precise than some of the comparable numerical integrators. The quadratic approximation (gray line marked 2) provided the lowest computational cost and similar quality to the analytical solution (red line), but only with the close-to-optimal parameter sets (the lowest 10% cost J_c as defined by Eq. 4).

Parametric sensitivity.

A perturbation analysis was used to investigate the parametric sensitivity of suboptimal solutions that satisfy Eq. 4. This analysis compared optimal values found by several different local minimization methods after a 10% normal parametric perturbation (for details, see steps 5 and 6 in section Optimization and perturbation in methods). From 160 solutions, the 33% with the lowest J_c were as follows: 30 by COBYLA, 1 by L-BFGS-B, 22 by Powell’s algorithm, and 2 by Truncated Newton’s. COBYLA and Powell’s algorithms provided 95% of the best solutions in this problem. The distribution of parameters in Fig. 4 with similar cost (J_c) across all methods indicates that similar outputs could be produced with disparate circuit parameters. The parameters in the model were differently conserved across similar solutions: the input weights (G_u) had lower variability relative to other parameters, i.e., the static leak (x₀), static input (u₀), and interlimb connection weights (green, r_ij).

Behavioral implications of CPG morphology.

The velocity hypothesis states that descending signals to a CPG are the desired speeds of each leg. We wanted to test further if the analytical solution to the ODEs would produce the same or a different speed prediction for the modality of inputs. The direct relationship between the descending input and the temporal characteristics of stepping (step cycle, swing, and stance durations) was extracted from the second-order solution to Eq. 3. Although it has a complex nonlinear form (Eq. 7), its combination with the solution from Goslow et al. (1973) for the relationship between step cycle period and forward speed produced a linear result shown in Fig. 5 (r² = 0.999, P < 0.001 for left and right limbs).

$$V={\left(\frac{k_1+k_{2}u}{k_3-\sqrt{k_4+k_{5}u}}+k_6\right)}^{1.68}$$ (7)

where k_i are configuration-dependent constants, u is descending input, and V is the forward speed of locomotion.

Fig. 5.

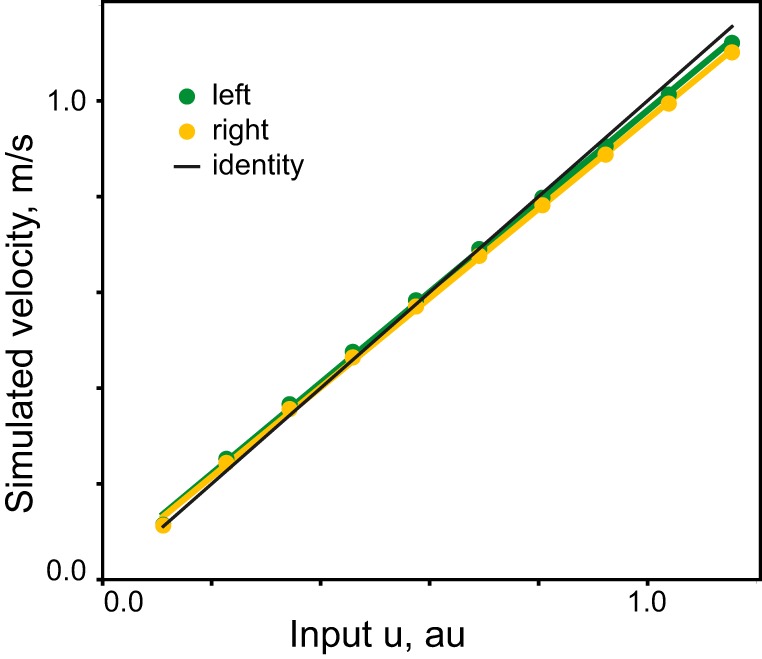
The relationship between the simulated CPG command signal to each limb and forward velocity. The analytical solution for the full step cycle was calculated over the set of 10 input values for each limb (u). Each value produced simulated step cycle duration values, which was then plotted as forward velocity calculated with the experimental relationship from Goslow et al. (1973) for each limb. The identity (y = x) is plotted in black. au, Arbitrary units.

We further explored the role of this descending command for velocity regulation in the generation of asymmetric gait. Asymmetric patterns were simulated by uncoupling the gains for the left and right inputs of both flexors and extensors (g_uf1, g_ue1, g_uf2, g_ue2) in Eq. 2 and varying them independently by 33% of the optimal parameter set (Table 1). The C and M components responsible for pattern symmetricity and simulated speed-related errors were removed from the J_c (Eq. 4) in this analysis. The simulated speed of walking for the left and right limbs was then calculated from the generated bilateral phases (Fig. 6). The parameter asymmetricity led to a steady gradient of the speed differences (α = V_left/V_right, see methods).

Table 1.

Optimal model parameters

x0f	x0e	guf	gue	glf	gle	u0f	u0e	rfe	ref	ree
0.244	0.376	1.59	2.62	−0.689	0.828	2.26	−0.174	−0.025	2.38	0.418

The parameter set (z*) for Eq. 2 that satisfies Eq. 4 is shown.

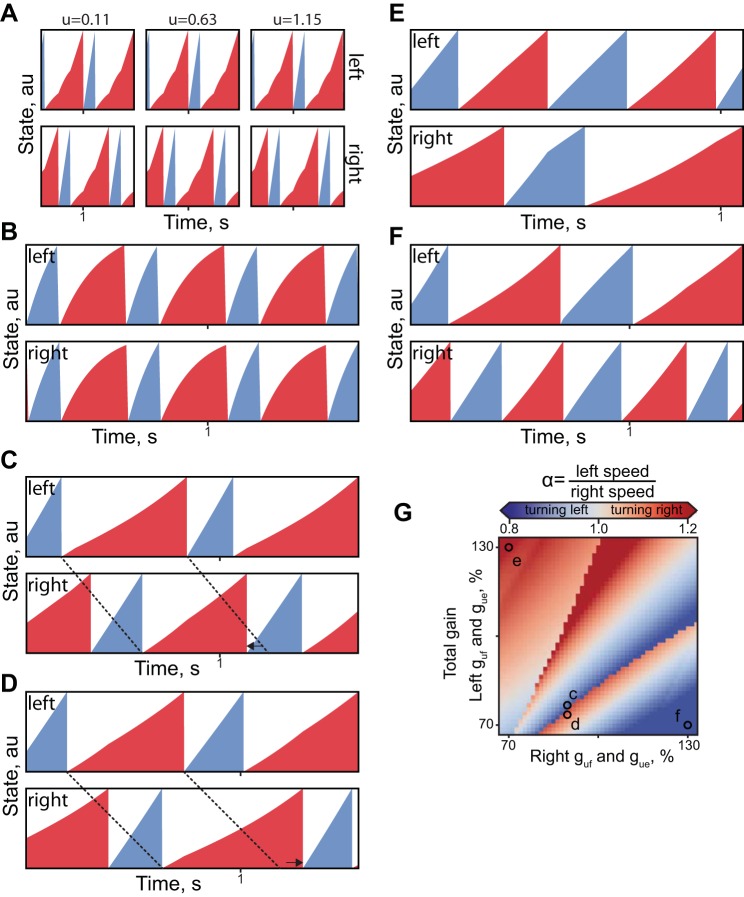
Figure 6, A and B, shows that variation of both inputs (g_uf, g_ue) together can produce asymmetric walking, α = 1.1, with the turn diameter as low as 10 m (calculated from Eq. 5, or heading direction γ = 10° change per step, see Eq. 6). Only the parameter combinations corresponding to the continuous gradient around the midline produced appropriately accurate simulations with low J_c (Fig. 6B). Uncoupled inputs to flexors and extensors can similarly generate asymmetric gaits, with α up to 1.2 (γ = 20°). The gradient of cost for extensors was orthogonal to that for flexors in Fig. 6, D and F; the increased possible range of asymmetric speeds was associated with increased cost, as indicated in Fig. 6B, with the cost trough extending along the diagonal unity.

Figure 7 shows that the intrinsic parameters in the model can also produce asymmetric gaits. Symmetric connections (e.g., in Eq. 2, r_fe = r₁₄ = r₄₁) were uncoupled (r₁₄ ≠ r₄₁) and varied independently. As in the analysis above, α and J_c were calculated for parameter variations of up to ±33% of the optimal value. The connections from flexor to contralateral extensor did not provide a suitable gradient of asymmetric walking speeds in the explored range of parameters (Fig. 7A). Possible reasons are a low magnitude of the optimal value for this parameter (r_ef, in Table 1) and the near constant relationship between swing duration and locomotor speed (Fig. 2). The variation of extensor-to-flexor and extensor-to-extensor parameters (r_ef, r_ee) produced asymmetric gaits (Fig. 7, C and E) with a turn diameter of 10 m (heading direction γ = 10° per step). These were comparable to the above result obtained from the analysis of external inputs. The profile of J_c was different for the gaits generated by variation of r_ee and r_ef parameters (Fig. 7, D and F). The extensor-to-flexor parameter r_ef increased steering angle with a smaller increase in cost (Fig. 7F) than that of the extensor-to-extensor parameter, r_ee (Fig. 7D). However, r_ee could regulate asymmetric gaits over a larger range of velocities than r_ef, as indicated by the diagonally extending trough in the J_c in Fig. 7F.

DISCUSSION

In this study, we developed a novel analytical description of a simple CPG model for locomotor phase timing and further expanded our previous model (Yakovenko et al. 2005) to include not only externally driven asymmetric rhythmogenesis, but also the opportunity to internalize this asymmetric transformation within the structure of a CPG. Our three central results are as follows: 1) the model can be solved analytically; 2) the analytical solution converges on the same conclusion that the input to the CPG is in the modality of limb forward speed; and 3) the minimalistic model of a CPG built with coupled oscillating leaky integrators offers multiple opportunities for embedding asymmetric control.

What is the goal of using analytical solutions of neurophysiological models?

Numerical solutions are usually the preferred option of solving complex models. For example, a biophysical CPG model can capture the neurological basis of activity in detail, often using hundreds of approximated parameters and their reconfiguration during failures in the motor execution (Rybak et al. 2006).

Complex models with multiple estimated transformations may produce ensemble behavior that reproduces the expected outcome; however, the role of elements and their network properties are hard to predict and analyze. The choice of a simple rate network with continuous variables in this model, ignoring spike rate adaptation, dendritic processes, membrane dynamics, synaptic conductances, and plasticity, has the advantage of focusing on the computation performed by the network connectivity (Abbott et al. 2016). Unlike models that are not analytically solvable, simple models are often insightful and capable of identifying specific targets that modify circuit behavior (Barnett and Cymbalyuk 2014b; Izhikevich 2004; Schaal and Sternad 1998; Tabak et al. 2000). For example, in the study of Barnett and Cymbalyuk (2014b), two saddle node bifurcations, one for equilibria and one for periodic orbits, allowed the independent manipulation of silent and spiking phase of bursting activity. The employed bifurcation control method relies on the manipulation of a controlling parameter near a transition between different regimes responsible for spiking and bursting properties. Spardy et al. (2011a) showed how the dynamic system analysis could identify the silent and bursting periods of the system’s oscillation, the effect of sensory inputs on the range of behavior, and the operation of the CPG model in response to simulated spinal cord injury. This description was based on the simplified model (Markin et al. 2010; Spardy et al. 2011b) that uses two types of neuron implementations consisting of one- or two-dimensional differential equations for a single limb flexor-extensor CPG. Similar to other much more complex implementations (Caplan et al. 2014; Morris and Lecar 1981; Rybak et al. 2006), even this simplified formulation produces a challenging system of equations for 10 neurons with 33 connections between them. The model did noticeably have problems resolving locomotor phases for fast cycle durations (<800 ms, see Fig. 3 in Spardy et al. 2011b). In contrast, our simple CPG model had only four parameters within a reciprocally connected system of two leaky integrators and simulated the same behavior without the aberrations at the extremes of experimental data (Yakovenko et al. 2005). This basic model that we extended in this study was used to describe, for the first time, the novel flexibility of extensor- and flexor-dominant phase regulation.

As in other models, we were concerned that expanding the model’s parametric space to describe two limbs could introduce an uncontrollable increase in errors associated with the corresponding parametric expansion. The bilateral half-centers for two limbs required a system of 4 differential equations and the set of either 7 coupled (see Eq. 2) or 16 uncoupled intrinsic and 4 extrinsic (input) parameters. The results for the expanded model in Fig. 2 showing phase modulation over the full range of walking velocities without limitations at the extremes was not a forgone conclusion. Overall, the increased parametric complexity in the model did not lead to an overfitting problem that could have appeared from estimating too many parameters from a low-dimensional set of behavioral data. Instead, the model consistently converged on similar solutions without the loss of validity indicated by the J_c.

Overfitting and underfitting are two major concerns in the selection of appropriate levels of abstraction for models (Lever et al. 2016). In the words of John von Neumann, “With four parameters I can fit an elephant and with five I can make him wiggle his trunk.” Here, our relatively simple model generates low-dimensional output in the form of the phase characteristic in normal and asymmetric locomotion. Models based on Hodgkin-Huxley formalism could generate the same phase-duration characteristic, albeit with the use of large-model parameter sets that extend into hundreds and thousands. Remarkably, the solutions from these two different representations are similar, supporting the experimental and computational observations that the same network activity could be generated by the underlying disparate mechanisms (Caplan et al. 2014; Goaillard et al. 2009; Grashow et al. 2009; Prinz et al. 2004). Still, the convergence of our parameter search on the physiological network solution is validated only by the constraining behavioral data and extent of simulated validation using parameter sensitivity analysis. Even in this minimalistic model, the exploration of a 20-dimensional parameter space was challenging and led us to implement the analysis of a coupled symmetric model first, where the parameters representing spinal neural elements mirrored across the midline were set to the same values. The perturbations in each parameter achieved with different minimization algorithms produced robust solutions, where small changes did not lead to large changes in outcome (Fig. 4). Thus the model may not be overfitting for these particular phenomena under study.

It is important to note that the model structure was not optimized in this study; instead, we have chosen the simplest mechanistic model of neural processing with structural elements identified by neurophysiology. Moreover, the quality of fit to the experimental data was very high (R² of ~0.999). The high R² values are often used to support model validity. The typical additional validation is the analysis of residuals. The low values of residuals have no particular meaning when experimental data reconstruction is this precise. Then, the only possible failure of this model is the assumption that it is overly complicated or overfitting the experimental data, which is contradicted by the minimalistic design. This model has already been refined to the simplest mechanistic form.

Embedding of asymmetric gait control in extrinsic and intrinsic parameters.

Even in our relatively simple model, there is a complicated relationship between intrinsic connections and extrinsic inputs. An indication of this fact is the capacity for representing the same behavior within parameters corresponding to different anatomical structures. Thus it was necessary to uncouple the parameters in Eq. 2 to further extend the sensitivity analysis with the goal of exploring the functionality “hidden” in the complexity to generate falsifiable hypotheses or model predictions.

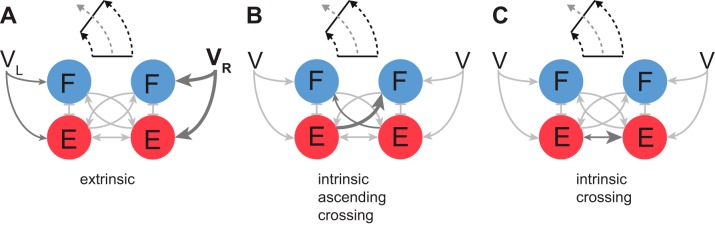
We chose asymmetric gait as the test task because it results from the normal control of steering or heading direction (Galbreath et al. 2014; Yakovenko 2011), and it may contain indicators of long-term adaptations to injury. First, we “forced” the model to internalize the control of asymmetric stepping by changing only extrinsic parameters. The mechanism using only input gains of flexor half-centers, and less so extensor half-centers, was a robust method of changing the interlimb speed differential. This was also expressed as a change in the heading direction in this model. In Fig. 6, the tuning of input gains to flexor half-centers led to asymmetric speed ratios of 0.9–1.1, which corresponds to an estimated heading direction change of ±10° over one step cycle (about a 10-m turn diameter). This suggests that a single external input representing a heading direction could generate a realistic range of asymmetric gaits in this model. Second, we can similarly constrain the solution to the locus of intrinsic parameters responsible for the influences among four half-centers in the model. It was intriguing to see the capability of this model to embed the asymmetric processing within these pathways. Moreover, the simulations suggested that not all parameters are equal targets in that respect. The extensor-to-flexor and extensor-to-extensor (r_ef and r_ee in Fig. 7) parameters embedded the ability to generate asymmetric gaits with a reasonable turn diameter of 10 m, which is consistent with a “step turning” strategy, characterized by a wide base of support throughout the turn. It is likely that steeper turning would require the transition to a different “spin turning” strategy (Hase and Stein 1999; Taylor et al. 2005). The alternative CPG configurations are illustrated in the schematic in Fig. 8. In studies of spinal segmental connectivity, these parameters would correspond to the “gains” of propriospinal pathways connecting rhythmogenic networks within the spinal enlargement (Kiehn 2011). Given the more rostral distribution of flexors than extensors within the lumbosacral enlargement (Ivanenko et al. 2008; Yakovenko et al. 2002), r_ef and r_ee pathways would have the network representations shown in Fig. 8, B and C. Overall, relatively complex behavior, like steering, could be controlled with both extrinsic and intrinsic mechanisms available in this simple model.

Fig. 8.

Schematic representation of multiple CPG configurations for steering. A: the configuration based on the external inputs to CPG. B and C: two possible configurations of intrinsic connections producing the same asymmetric patterns as in A. V, limb speed; V_L, left V; V_R, right V; F, flexor; E, extensor.

The analysis makes specific predictions about the propriospinal pathways that could be involved in long-term adaptations to asymmetricity. Human subjects could learn to compensate for the external perturbations applied to limbs while minimizing the overall limb impedance (Dingwell et al. 2002; Shadmehr and Mussa-Ivaldi 1994). Even gross cortical inputs, like those generated by transcortical magnetic stimulation, can be compensated by the adaptation of transmission gains contributing to the regulation of locomotion (Schubert et al. 1999). Our results suggest that this adaptation can take place not only within pathways projecting to a CPG, but also within the limited locus of interactions between model’s half-centers. While this model has no realistic learning dynamics, the examination was limited to the naive symmetric and adapted asymmetric states. This learning function could be implemented in future work with the use of simple learning mechanisms (Franklin et al. 2008; Wu et al. 2014) where intrinsic and whole system parameters (Ijspeert et al. 2013) could be updated under the reinforcement learning dynamics (Mahmoudi et al. 2013; Schultz 2013).

Overall, the model demonstrated that the general locomotor patterns for symmetric and asymmetric gaits may be achieved by the superposition of commands and intrinsic interactions within the minimalistic structure of a CPG. This novel flexibility of functional representation for asymmetric pattern generation has not been previously demonstrated in models, and it posits specific predictions for mal- or adaptations to asymmetry due to peripheral or central abnormalities.

The simple model of locomotor rhythm generation.

This model is not likely producing the overfitting of behavior as indicated by the sensitivity analysis. However, the excessive number of parameters relative to the number of observed values may hinder CPG models that do not address this methodological issue. Still, there is the alternative possibility that this model is instead underfitting the locomotor patterns associated with asymmetric gait. To discuss the appropriate level of abstraction that limits the possibility of underfitting for this task, we need to examine the concept of neuromechanical tuning (Prochazka and Yakovenko 2007; Ting et al. 2015). Specifically, locomotor control is a phenomenon produced by multiple elements that combine predictive and reactive functions. In analogy with Smith’s predictor (Smith 1957), the specific role of the CPG is to predict the mechanical interactions between the limb and ground. To this extent, our model can reproduce the transformation from input speeds to appropriate inter- and intralimb coordination of multiple muscle groups without the need for molecular level dynamics (Yakovenko 2011). The CPG function could then be specified as a dynamic transformation of simple, i.e., related to limb speed, high-level signals into complex granular functional subdivisions of temporal activations appropriate for locomotion. Both analytical and numerical solutions of our minimalistic CPG model support the hypothesis that the main function of a CPG is the transformation of high-level locomotor signals associated with whole limb function, i.e., the speed of locomotion, into low-level phasic activity patterns of limb muscles. This computational inference agrees with previous studies demonstrating that the one-dimensional input to the MLR in the form of stimulation magnitude or frequency can be transformed by a CPG into specific velocity-dependent phasic activity in vertebrates (Shik et al. 1966; Smetana et al. 2010). The underfitting for CPG models describing the phase-duration characteristic would be classified by the inability to use high-level signals related to the forward velocity as the control signal for asymmetric gait. We demonstrated that this model can readily transform limb velocity-related inputs into asymmetric phase characteristics. Moreover, the model can embed these high-level representations within its internal structure. As shown previously (Yakovenko et al. 2005), it can also generate both flexor-dominated and extensor-dominated phase regulation at different speeds.

The model supports the idea that the CPG inputs are limb speeds. The positive relationship between the excitatory input and the frequency of network output oscillations has been previously modeled in CPG models using Hodgkin-Huxley formalism (Danner et al. 2016; Shevtsova et al. 2015). In contrast, our model does not assume the shape and relationship of CPG input with limb speed; this linear relationship was demonstrated by solving inversely the calculation performed by the structure proposed by T. G. Brown with the assumption of leaky integration (Yakovenko 2011). This model was first introduced to describe the atypical flexor-dominated pattern in fictive locomotion induced by the stimulation of MLR and exhibiting the increased slope of phase vs. cycle duration for flexors rather than extensors (Yakovenko et al. 2005). The network state could be explained by the possible shift in the balance of descending drives that lack the extensor-biased limb load feedback and may have increased flexor biased inputs from MLR, e.g., see Fig. 5 in Frigon and Gossard (2009), where MLR stimulation increases the duration of flexor bursts.

The regulation of velocity-related control signals within supraspinal pathways remains to be poorly understood. The presence of spinocerebellar loops contributing to the modulation of vestibulospinal neurons (Arshavsky et al. 1978; Arshavsky and Orlovsky 1986) warrants a theoretical reexamination of these contributions in the context of limb speed control. Cerebellum output to the motor cortex updates limb and body state to modulate the state-dependent activity of its output, pyramidal tract neurons and also receives inputs from networks in posterior parietal cortex responsible for planning and converting visual information (Drew and Marigold 2015). The modulated discharge of neurons shows tuning to many velocity-related parameters during locomotion and reaching movements (Yakovenko and Drew 2015). Theoretically, the velocity command can be extracted by the integration of dynamic neural discharge, or it may be represented in the activity of subpopulations of neurons with static discharge profiles. This leads to a complete closed-loop view of the steering control achieved by multiple supraspinal networks contributing to the transformation from optical flow to the control of heading direction (Warren et al. 2001) with the use of limb speed inputs to CPG, described in this study.

To conclude, in this paper we report for the first time a model of bilateral CPG with analytical and numerical solutions capable of generating symmetric and asymmetric gaits appropriate for whole body steering. The steering behavior can be generated by either extrinsic limb velocity-related inputs to left and right half-center oscillators or embedded asymmetry within intrinsic propriospinal gains from extensor half-centers to the contralateral flexor or extensor half-centers. Moreover, these asymmetric changes may correspond to either a natural control of limb velocity adjustments regulating the heading direction or pathological changes to the inputs or structure of the locomotor CPG. The existence of multiple network states capable of generating the same empirical observations is a novel identified challenge for CPG models.

GRANTS

This study was supported by National Institute on Aging Grant AG052375-01A1 (A. Sobinov) and National Institute of General Medical Sciences Grants P20GM109098 and U54GM104942 (S. Yakovenko).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.S. and S.Y. conceived and designed research; A.S. performed experiments; A.S. and S.Y. analyzed data; A.S. and S.Y. interpreted results of experiments; A.S. and S.Y. prepared figures; A.S. and S.Y. drafted manuscript; A.S. and S.Y. edited and revised manuscript; A.S. and S.Y. approved final version of manuscript.

APPENDIX

Analytical Solution

The bilateral CPG model produces flexor (swing) and extensor (stance) phases for two limbs in relation to extrinsic input and intrinsic structure. To obtain these phases, Eq. 1 needs to be integrated in time between the state changes. Numerical integration was previously used (Yakovenko 2011) to generate swing and stance periods. The same transition points can be calculated analytically by transforming Eq. 1 into a matrix Cauchy problem:

$$\{\begin{array}{c}\dot{x}-Ax=B\\ x\left(t=0\right)=x_0\end{array}$$ (A1)

where A = G_l + G represents the intrinsic structure of the CPG, B = U₀ + G_uu represents the state-independent inputs, and x₀ is the initial condition. In the case of a nonsingular matrix A, this system has a vector form solution:

$$x=A^{-1}\left(e^{At}-I\right)B+e^{At}{x}_0$$ (A2)

where I is the identity matrix. This analytical expression of states x [with dimensionality (4 × 1) for a model of bilateral CPG] describes the progression of all locomotor phases in time between the state changes. The remaining task is then to calculate the transition times and corresponding phase durations for a full step cycle. Eq. A2 was evaluated for all three possible bilateral combinations of concurrent flexor-extensor activity during a full step cycle, namely: 1) left flexion and right extension (states x₁ and x₄); 2) left extension and right extension (states x₂ and x₄); and 3) left extension and right flexion (states x₂ and x₃). States may have repeated more than once within the step cycle, when CPG activity was highly asymmetric. The dimensionality of the problem can be reduced from 4 to 2 because only 2 integrators are active at any given time with the following parameters:

$$A=\left(\begin{array}{cc}{a}_{ii}& a_{ij}\\ a_{ji}& a_{jj}\end{array}\right),A^{-1}=\left(\begin{array}{cc}{\tilde{a}}_{ii}& {\tilde{a}}_{ij}\\ {\tilde{a}}_{ji}& {\tilde{a}}_{jj}\end{array}\right),B=\left(\begin{array}{c}{b}_i\\ b_j\end{array}\right),x_0=\left(\begin{array}{c}{x}_{0i}\\ x_{0j}\end{array}\right)$$ (A3)

where i ϵ {1,2} and j ϵ {3,4} are the indexes of the two active integrators. We can then find the time-of-phase transitions τ for a given integrator k by inserting the reduced parameter set (Eq. A3) into Eq. A2 and assuming x_i or x_j is equal to 1. Solving for τ yields the following transcendental equation:

$$z_1\cdot \cosh \left(q\tau \right)+z_2\cdot \frac{\sinh \left(q\tau \right)}{q}=z_3\cdot e^{-s\tau }$$ (A4)

where z₁, z₂, z₃, s, and q are parameters describing the model configuration, as follows:

$$s=\frac{a_{ii}+a_{jj}}{2}$$

$$q=\sqrt{{\left(s-a_{jj}\right)}^2+a_{ij}\cdot a_{ji}}$$

$$z_1=d_1+d_4$$

$$z_2=\left(s-a_{jj}\right)\cdot d_1+a_{ij}\cdot d_2+a_{ji}\cdot d_3-\left(s-a_{jj}\right)\cdot d_4$$

Four-element vector D = [d₁, d₂, d₃, d₄] and z₃ depend on whether the model is solved for i (left) limb: D = (ã_ii·b_i + x_0i; ã_ii·b_j + x_0j; ã_ij·b_i; ã_ij·b_j), z₃ = 1 + ã_ii·b_i + ã_ij·b_j, or j (right) limb: D = (ã_ji·b_i; ã_ji·b_j; ã_jj·b_i + x_0i; ã_jj·b_j + x_0j), z₃ = 1 + ã_ji·b_i + ã_jj·b_j.

The τ was then found numerically using Brent’s method and analytically by expanding the hyperbolic functions using a Maclaurin series. We used the NumPy “roots” function (Horn and Johnson 1999) to solve the polynomials of power over 2. Next, the periods of activity of flexors and extensors during a step cycle were obtained with the following iterative algorithm:

• Calculate the time τ_i when state x_i reaches 1.

• Calculate the time τ_j when state x_j reaches 1.

• Calculate the state of all integrators at time point τ = min(τ_i, τ_j).

• Reset the state from 1 to 0, deactivate it, and activate the reciprocal ipsilateral state. For example, switch from an active left flexor to an active left extensor.

• If a full step cycle is completed (all 4 states reached value 1 at least once), stop; otherwise, go to step 1.

The code implementing the algorithm and parameters in Python is available on https://bitbucket.org/nishbo/cpg.

Simulations with Nonoptimal Parameters

The model can generate a rich variety of patterns using parameters shaped by the J_c. The illustration of these insightful “outtakes” is shown in Fig. A1. The omission of the J_c components responsible for the cycle duration range (Fig. A1A) results in the trivial best-fit solution that fits the desired phase relationship, but it may not reflect the range of phases with the increased magnitude of inputs (G_u = 0). Similarly, removing the cost of unphysiological bilateral flexor coactivation may result in the simulations that resemble hopping behavior (Fig. A1B). The rapid switching in the heading direction can be simulated by forcing the system to cross the heading direction transition shown in Fig. A1, C and D, between points c and d in Fig. 6G. In this region, the asymmetric change in G_u for flexors and extensors flips the speed of left and right limbs as indicated by the difference of stance phase (dashed lines). The drop in the J_c of parameters in d was associated largely with the H component of Eq. 4 (Hc = 0.05, Hd = 0.2). Selecting the parameters at the extremes (see e and f in Fig. A1G) shows the examples of reduced coupling within the network. The patterns could drift relative to each other as in Fig. A1F. The double-stepping, a physiological behavior (see Fig. 5 in Yakovenko 2011) could also be generated by the large difference in the input to flexors and extensors.

Fig. A1.

Solutions with the varied manipulations of the optimization algorithm. A: examples of patterns optimized without the range cost (M, k₂ = 0 in Eq. 4). B: simulation without the cost of bilateral flexor activation (O, k₃ = 0 in Eq. 4). C and D: simulations with uncoupled asymmetric G_u parameters selected on the different sides of the heading direction transition (points c and d in G). E and F: simulations with uncoupled asymmetric G_u in points e and f of G. G repeats Fig. 6A with regions marked with letters corresponding to plots of this figure.