Light-induced dilation in nanosheets of charge-transfer complexes

Significance

Photostrictive compounds are promising device materials because of their fundamental photophysical properties and light-induced strain applications. Although molecular charge-transfer crystals exhibiting light–matter interactions have been successfully deployed in optoelectronics, an air-stable molecular material that couples photons and electrons, achieving photostriction through the coupling of light and mechanical degrees of freedom, has not yet been discovered. Herein, we report a substantial light-induced dilation in a molecular material at room temperature, which is accompanied by simultaneous photocurrent generation. This finding opens avenues for coupling optical, electronic, and mechanical functionalities for possible use in remote wireless photoswitchable devices.

Abstract

We report the observation of a sizable photostrictive effect of 5.7% with fast, submillisecond response times, arising from a light-induced lattice dilation of a molecular nanosheet, composed of the molecular charge-transfer compound dibenzotetrathiafulvalene (DBTTF) and C₆₀. An interfacial self-assembly approach is introduced for the thickness-controlled growth of the thin films. From photoabsorption measurements, molecular simulations, and electronic structure calculations, we suggest that photostriction within these films arises from a transformation in the molecular structure of constituent molecules upon photoinduced charge transfer, as well as the accommodation of free charge carriers within the material. Additionally, we find that the photostrictive properties of the nanosheets are thickness-dependent, a phenomenon that we suggest arises from surface-induced conformational disorder in the molecular components of the film. Moreover, because of the molecular structure in the films, which results largely from interactions between the constituent π-systems and the sulfur atoms of DBTTF, the optoelectronic properties are found to be anisotropic. This work enables the fabrication of 2D molecular charge-transfer nanosheets with tunable thicknesses and properties, suitable for a wide range of applications in flexible electronic technologies.

Light–matter interaction-induced photostriction is of significant interest due to its rich photophysics and broad applications in wireless photoactuators, adaptive optics, and artificial muscle technologies (1–3). Photostriction has been reported in electrically polar compounds, nonpolar semiconductors, ferroelectrics, and organic polymers. The mechanism of photostriction differs based on the nature of the material. Previous work has observed converse piezoresponse in light-modulated photovoltaic compounds, photoisomerization-induced volumetric changes in organic polymers, and an excess electron–hole pair-driven deformation in nonpolar semiconductors (4, 5). The photostriction process arising from molecular bond evolution has been studied extensively, but the mechanisms connecting light-induced size changes to deformation are still debated, particularly in new material platforms with fast response times and large photostrictive response.

Molecular charge-transfer (CT) crystals show promise as a novel class of photostrictive materials (6, 7). In contrast to inorganic materials with high covalent or ionic bonds, organic molecular solids have weak intermolecular interactions, such as hydrogen bonds, π-π stacking, van der Waals, and CT-induced electrostatic interactions (8), which result in distinct lattice deformations under photoexcitation due to the large intermolecular spacing. In addition, molecular CT crystals display long-range stacked electron donor and acceptor components. This stacking is driven by unique molecular arrangements and leads to dipole formation and additional spontaneous polarization. Furthermore, the superior optoelectronic properties of CT solids can lead to changes in the surface electric field and elastic strain due to the converse piezoelectric effect, which leads to deformation of the sample. These clues suggest the possibility of molecular CT systems with useful photostrictive properties. In this study, we consider dibenzotetrathiafulvalene (DBTTF) and the fullerene C₆₀ as the electron donor and acceptor, respectively, for the construction of ultrathin CT network nanosheets. As a tetrathiafulvalene derivative, the flat-shaped DBTTF molecule tends to form low-dimensional arrangements in which π-electrons provide conduction bands for charges. The fullerene C₆₀ is known to be an acceptor possessing a number of characteristic features, namely, high-level electronic structure, lower symmetry, and intrinsic polarizability (9). Due to the high intermolecular interactions between DBTTF and C₆₀ molecules, a long-range ordered packing arrangement of molecular CT nanosheets can be formed.

In comparison with 3D molecular CT salts, the corresponding 2D molecular nanosheets, with a nanoscale vertical dimension, have a large specific surface area (∼square centimeter), which enables the material to absorb light with an ultrathin thickness and consequently enhance light–matter interactions (10). In addition, the high specific surface area allows the surface phase to be as crucial as its bulk counterpart, providing an alternative way of modulating the surface phase for engineering the intrinsic physical properties of 2D nanomaterials, especially for surface sensitive systems (11). Therefore, 2D molecular nanosheets have the potential to open a new paradigm in photostriction. However, forming a well-defined freestanding molecular 2D nanosheet has remained a daunting task due to the relatively weak binding forces between the constituent molecules (12–14). As a result, developing a well-defined large-area production of 2D molecular CT nanosheets has become a substantial challenge.

Results and Discussion

Herein, we report an air–liquid interfacial self-assembly method for the controlled growth of 2D crystalline DBTTF-C₆₀ nanosheets with advantageous electronic, optoelectronic, and photostrictive properties. Many of these unique features of the nanosheets arise from the ability of DBTTF molecules to reside in two distinct conformations––the boat and chair structures. The chair is the lowest energy conformation when complexed with C₆₀, and the boat conformation becomes more prevalent in ultrathin films than in bulk. Thus, the proportion of DBTTF molecules adopting the chair conformation decreases with decreasing film thickness, and the accompanying changes in the optical and electronic properties can be rationalized by considering the relative fractions of chair and boat conformers. We further observe a substantial light-induced photostrictive effect with the thickness variation of ΔH/H reaching up to 5.7% in thin DBTTF-C₆₀ nanosheets, which is much larger than that seen in many inorganic materials. Based on experimental results and electronic structure calculations, both DBTTF conformations flatten under light excitation, which increases the size of the unit cell and contributes to photostriction in the nanosheet. We additionally suggest that excess charge carriers can also contribute to photostriction. This photostriction discovery opens up applications for these fascinating charge transfer materials, enabling device paradigms such as photodriven microsensing and microactuation.

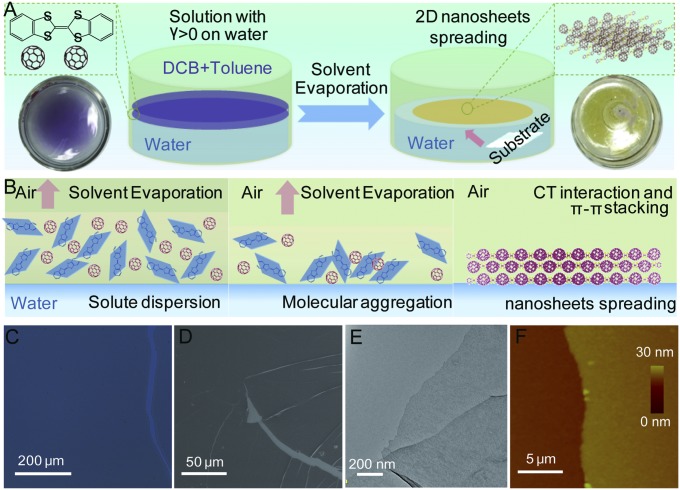
The self-assembled DBTTF-C₆₀ nanosheets are grown on a liquid–liquid interface due to the positive spreading coefficient, S = γ_bv − γ_tv − γ_tb, where the surface tension of the liquid substrate γ_bv is larger than the sum of the surface tension between the liquid substrate and the surrounding vapor γ_tv, and the interfacial tension between the spreading solution and the liquid substrate γ_tb (15–17). The ortho-dichlorobenzene/toluene mixed solvent with a suitable solvent formulation (20% of ortho-dichlorobenzene) shows both a positive spreading coefficient and a medium evaporation rate, which makes it suitable for the self-assembly of DBTTF-C₆₀ nanosheets at the interface (Fig. 1A). In this context, the DBTTF and C₆₀ molecules are dissolved in the mixed solvent and spread on the surface of water/dimethylformamide (DMF) mixed solvent substrate (50% of DMF) smoothly at room temperature and in an atmospheric environment. When the top solution is gradually evaporated, the DBTTF and C₆₀ begin to aggregate and nucleate through intermolecular and hydrophobic interactions, which are enhanced at the hydrophobic solvent–water interface (Fig. 1B) (18, 19). The DBTTF-C₆₀ nanosheets grow gradually along the horizontal direction by consuming the remaining DBTTF and C₆₀ molecules and finally spread uniformly on the top of the water surface after evaporation of the solvent. The as-prepared DBTTF-C₆₀ nanosheets could then be readily transferred onto any artificial substrates for further studies. We use optical microscopy, scanning electron microscopy (SEM), transmission electron microscopy (TEM), and atomic force microscopy (AFM) to characterize the morphology of the resulting films (Fig. 1 C–E). A continuous and flat morphology of DBTTF-C₆₀ nanosheets with a large lateral dimension (∼square centimeter) and subnanometer thickness are shown with partially folded sheets and wrinkles, indicating the flexibility of the film. The chemical composition of DBTTF-C₆₀ nanosheets is confirmed by elemental mapping images with a uniform element distribution of carbon and sulfur elements, implying chemical uniformity (Fig. S1). As shown in Fig. 1F, the typical AFM height image shows smooth and compact thin films with a small roughness of ∼0.5 nm and an average thickness of 20 nm.

Fig. 1.

Formation and morphology of DBTTF-C₆₀ nanosheets. (A) Schematic illustration of self-assembling DBTTF-C₆₀ nanosheets at the water–air interface. (B) Three sequential stages during the self-assembling procedure. (Left) Solvent with mixed solutes and positive spreading coefficient spreading on water. (Middle) Solvent evaporation induced aggregation and nucleation. (Right) Self-assembly and film growth on water. (C) Optical, (D) SEM, (E) TEM, and (F) AFM images of typical DBTTF-C₆₀ nanosheet.

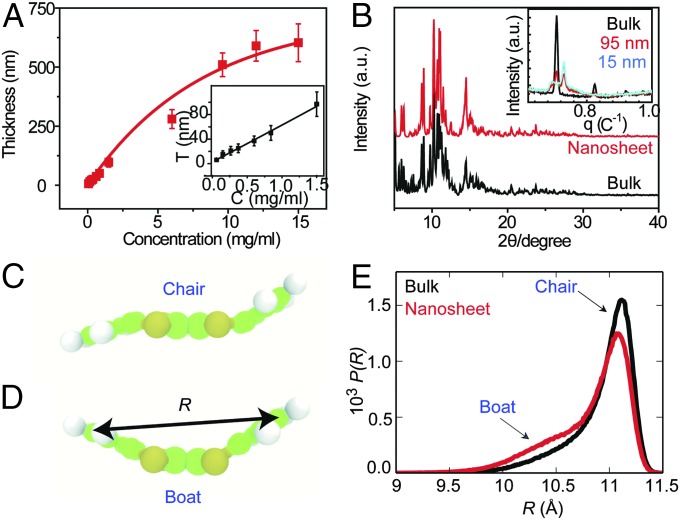
The thickness of the DBTTF-C₆₀ nanosheets can be well controlled by varying the concentration of the solution (Fig. 2A). All films exhibit good reproducibility and are continuous and flat, with large surface areas (∼square centimeter). The corresponding AFM images (Fig. S2) illustrate typical samples with an average thickness of nearly 10, 90, and 300 nm. All exhibit continuous, smooth, and compact thin-film morphologies. We performed synchrotron X-ray and small-angle X-ray scattering (SAXS) experiments to characterize the variation in the internal structure of the DBTTF-C₆₀ films with different thickness. When the DBTTF-C₆₀ film is sufficiently thick, it is equivalent to a bulk phase, and the structure is resolved with the triclinic centrosymmetry space group P-1. One DBTTF molecule in the chair conformation lies between two C₆₀ molecules with short intermolecular contacts at distances of S(DBTTF)•••C(C₆₀): 3.17–3.44 Å, C(DBTTF)•••C(C₆₀): 3.16–3.37 Å, which is less than the sum of the van der Waals radii of the contact atoms, suggesting the existence of significant intermolecular interactions. The contact distances between C₆₀ molecules are in the range of 3.22–3.39 Å. However, when the thickness of the film decreases to nanoscale sizes from bulk to 15 nm, a new diffraction peak signals the appearance of the boat conformation in the nanosheet, rather than the chair conformation of bulk DBTTF (Fig. 2B, Inset), while in the thin-film structure, one DBTTF molecule in the boat conformation lies between two C₆₀ molecules with short intermolecular contacts at distances of S(DBTTF)•••C(C₆₀): 3.27–3.83 Å and C(DBTTF)•••C(C₆₀): 3.38–3.61 Å.

Fig. 2.

Thickness control and structural information of DBTTF-C₆₀ nanosheets. (A) Effect of varying solute concentration. (B) Bulk DBTTF-C₆₀ crystal without disorder and DBTTF-C₆₀ nanosheets with disorder. (Inset) SAXS of DBTTF-C₆₀ nanosheets with decreasing film thickness. (C and D) Illustration of the DBTTF molecule in a (C) chair- and (D) boat conformation. (E) Probability distributions of the DBTTF end-to-end distance, R, obtained from MD simulations of the bulk solid and a thin film indicates increased conformational disorder in the nanosheet.

To further characterize the structure in the DBTTF-C₆₀ bulk and nanosheets, we perform classical molecular dynamics (MD) simulations and quantum-mechanical density-functional theory (DFT)-based electronic structure calculations (see Supporting Information for details). We first focus on the degree of conformational disorder in the material, as characterized by the amount of chair and boat conformers in the bulk and the thin film, where examples of the two conformations are shown in Fig. 2 C and D. Our DFT calculations predict the energy difference between the chair and boat conformations in the DBTTF/C₆₀ crystal to be roughly 4k_BT at 300 K, such that both conformers are expected under ambient conditions. Indeed, the MD simulations produce a range of conformations in the bulk and thin films, as quantified by the probability distribution of the end-to-end distance R of the DBTTF molecules, where an “end” is the midpoint of the C–C bond on the benzyl group that is furthest from the center of the molecule. The distributions consist of a main peak near the expected distance for the chair conformation and a shoulder near the value of R for the boat conformation, as shown in Fig. 2E. We observe an increase in the size of the shoulder in the roughly 29-nm-thick thin film, with a corresponding decrease of the main peak of P(R), indicating an increase in the fraction of the DBTTF boat conformation in the nanosheet. The boat conformation is the energetically stable form of DBTTF in vacuum, and the chair is stabilized in the crystal through interactions with C₆₀. Disruption of these DBTTF-C₆₀ interactions by surface-induced disorder destabilizes the chair conformation, enables DBTTF to relax to the boat conformation, and increases the population of boat conformations in the thin film.

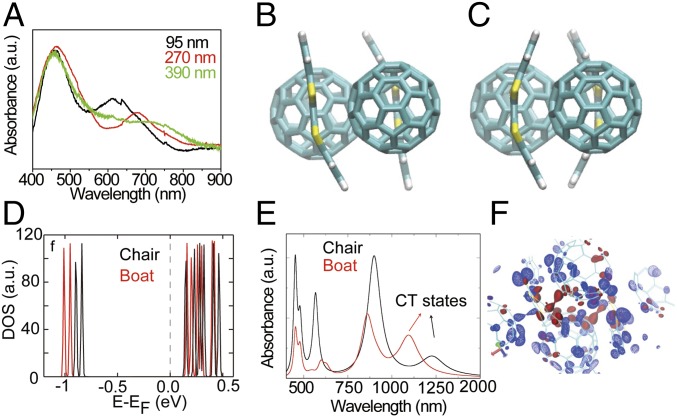
The above results suggest that the content of the boat conformation increases as the films become thinner. To further investigate this, we probed the optical properties of DBTTF-C₆₀ nanosheets. The photoabsorption spectra of DBTTF-C₆₀ nanosheets of varying thickness are shown in Fig. 3A. Compared with the absorption from the pure DBTTF and C₆₀, the 2D DBTTF-C₆₀ nanosheets exhibit a broad absorption spectrum that extends into the near-infrared region, indicating a robust CT interaction between the donor and acceptor molecules. In addition, as the thickness of DBTTF-C₆₀ nanosheets is increased, the CT band is gradually red-shifted. The conformation of the DBTTF molecules affects the degree of CT, the electronic properties of the materials, and consequently the observed absorption spectra. Such thickness-induced CT effects can be understood by considering the electronic structure of the chair and boat conformations, along with their prevalence in the bulk crystal and thin films.

Fig. 3.

Photoabsorption in DBTTF-C₆₀ nanosheets. (A) The photoabsorption spectra of DBTTF-C₆₀ nanosheets with various thicknesses. To facilitate comparison, the spectra are normalized by the area under the first peak (near 450 nm). (B) Chair- and (C) boat structures of the DBTTF-C60 complex. (D) The electronic DOS of DBTTF-C₆₀ in the boat and chair conformation as obtained from ground-state DFT calculations. (E) Calculated absorption spectra of DBTTF-C₆₀ complexes in with DBTTF in the boat and chair conformation, as obtained from time-dependent density functional perturbation theory. (F) Charge-density isosurface plots of the CT states (HOMO to LUMO) as shown in the absorption spectra for the chair (blue) and boat (red) complexes. Nuclear structures of the two complexes are overlaid.

We perform ground-state DFT calculations to understand the electronic structure of the CT states in the DBTTF-C₆₀ complex, and we compute optical absorption spectra using time-dependent density-functional perturbation theory. Crystal structures of the complex are studied with DBTTF in either the chair or boat conformation (Fig. 3 B and C). The electronic densities of states (DOS) (Fig. 3D) predict that the highest occupied molecular orbital (HOMO) of the chair is closer to the Fermi level, and closer to the lowest unoccupied molecular orbital (LUMO), than the HOMO of the boat. Thus, the HOMO–LUMO gap of the chair complex is smaller than that of the boat structure by ∼0.12 eV (Table S1), and the CT state of the chair is lower in energy. From the atomic partial DOS (PDOS), we find that the HOMO comprises the p states of S atoms in DBTTF molecules, while the p states of C atoms in C₆₀ molecules contribute to the LUMO for both complexes (Fig. S3). This suggests that CT is occurring between the n orbitals of the S atoms in DBTTF and the π*-orbitals of the C atoms in C₆₀, as found previously for similar complexes (20–22). The PDOS shows the significant density of C p states in the HOMO of DBTTF, supporting the possibility of π to π* transitions between DBTTF and C₆₀. CT in this manner is qualitatively similar in both the chair and boat complexes and results in spatial separation of charge in the CT state, with an accumulation of holes on the DBTTF molecules and electrons on the C₆₀ molecules. This is evidenced by the charge-density isosurfaces of the HOMO and LUMO states in Fig. S4. The calculated absorption spectra span from the visible to the near-infrared. The HOMO–LUMO excitation peaks at ∼1,100 nm (1.10 eV) and ∼1,250 nm (0.98 eV) correspond to CT states involving boat and chair conformations of DBTTF, respectively, Fig. 3E. The identification of these peaks as corresponding to CT states is supported by examination of the excited-state charge densities, shown in Fig. 3F.

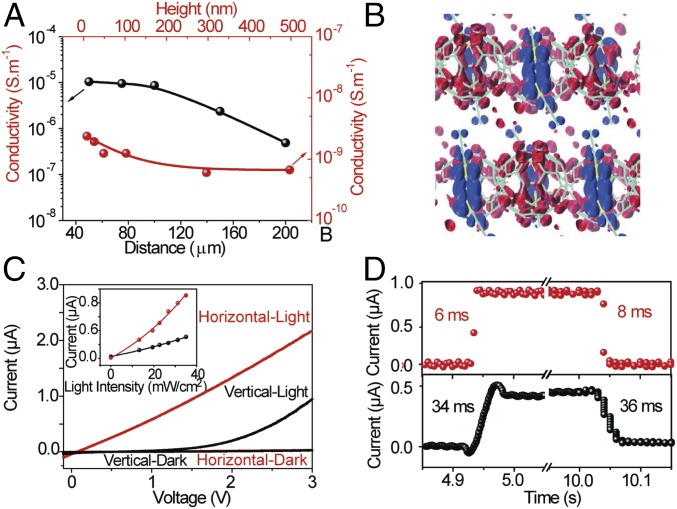
We additionally probe the carrier transport and optoelectric properties of the DBTTF-C₆₀ nanosheets. Fig. 4A shows the height and in-plane distance-dependent conductivities σ along the in-plane and out-of-plane directions. The conductivity, σ = (I × L)/(V × S), compares the electrical anisotropy between the horizontal and vertical directions, where I is the current, L is the distance between two electrodes, V is the applied bias, and S is the cross-sectional area of the 2D DBTTF-C₆₀ nanosheets. The conductivity along the in-plane direction is nearly an order of magnitude larger than that along the out-of-plane direction, resulting from the unique π-π stacking arrangement and substantial overlap of molecular orbitals, which leads to a larger charge-carrier density and mobility along the in-plane direction. In addition, the conductivity decreases nonlinearly with increasing vertical height or in-plane distance (horizontal width of the nanosheet), which results from the change in the proportion of boat and chair conformations of the DBTTF molecules. Our DFT calculations suggest that CT in the in-plane (xy) direction is higher than that along the out-of-plane direction (z) (Fig. 4B), because the orbitals undergoing CT are closer in the xy plane than in the z dimension. The calculated average minimum distance between the S atom of the DBTTF molecules (charge donor) and the C atom of C₆₀ molecules (charge acceptor) along the in-plane direction (∼3.5 Å) is smaller than that along the out-of-plane direction (∼4.5 Å) by ∼1 Å. The close proximity of the HOMO and LUMO orbitals in the xy plane suggests that CT is more facile in this direction than in the z plane and, consequently, that the conductivity is higher along the in-plane direction than along the out-of-plane direction. Fig. 4C shows the I–V curves of a representative nanosheet along the in-plane and out-of-plane directions with a photoexcitation of 34.5 mW/cm². The current density for both orientations increases, with a higher photocurrent along the in-plane orientation, which is further supported by the light-intensity–dependent current density (Fig. 4C, Inset). Fig. 4D shows the time-dependent current density in both directions under light excitation of 34.82 mW/cm². The current density in the in-plane direction drastically increases with a much faster photoresponse than that out of plane. The rise and decay time constants can be obtained by fitting the temporal response to I_rise = I₀ − A₁exp[(t − t₀)/τ₁] and I_decay(t) = I₀ + A₂exp[(t − t₂)/τ₂], where I₀ is the dark current, A is the constant, and τ₁ and τ₂ are the rise and decay time constants, respectively. The fitted photoresponse times, τ₁ and τ₂, in the out-of-plane direction are 34.1 ± 1.2 and 36.2 ± 1.3 ms, while the analogous response times in the in-plane direction are 6.4 ± 0.8 and 8.5 ± 0.8 ms, respectively. This anisotropy in the charge transport and photoelectric experiments arises from the unique π-π stacking arrangements in the nanosheet and the substantial overlap of molecular orbitals in the in-plane direction.

Fig. 4.

Electronic and optoelectric properties of DBTTF-C₆₀ nanosheets. (A) Measured conductivities along the parallel and vertical directions with various heights and in-plane distances (widths) of DBTTF-C₆₀ nanosheets. (B) Charge-density isosurfaces for the HOMO (blue) and LUMO (red) obtained from DFT calculations. (C) Current–voltage (I–V) curves of DBTTF-C₆₀ nanosheets along the parallel and vertical directions with and without external light excitation. (Inset) Photocurrent of DBTTF-C₆₀ nanosheets along the parallel and vertical directions with various external light excitation. (D) Photoresponse time of DBTTF-C₆₀ nanosheets along the parallel and vertical directions with external light excitation of 34.82 mW/cm².

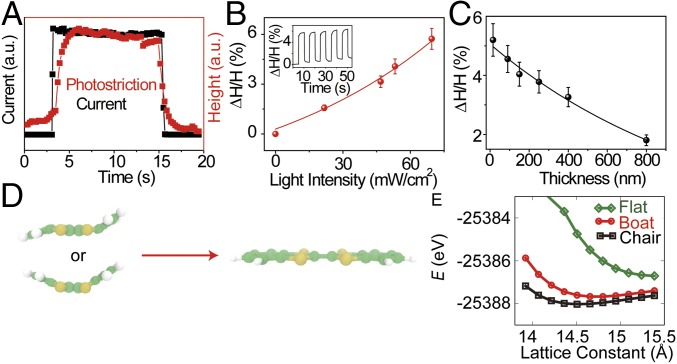
The DBTTF-C₆₀ complex exhibits structural transformations upon application of external stimuli. Our experiments demonstrate light-induced volume changes at room temperature, which are suggested to occur by structural transformations. When the light (69.28 mW/cm²) illuminates the DBTTF-C₆₀ nanosheet, a height change (ΔH/H) is observed and the profile closely follows the shift in photocurrent density (Fig. 5A). This photostrictive effect is directly related to the charge-carrier generation from the light excitation, which serves as the electronic origin of the photostriction in DBTTF-C₆₀ nanosheets. In addition, the photostrictive response is found to follow the external light intensity (Fig. 5B), which provides further evidence for the correlation between the photostriction and photogenerated carriers. As the light intensity increases to 69.28 mW/cm², the DBTTF-C₆₀ nanosheets with an average thickness of 20 nm show a sizable photostrictive effect with ΔH/H of ∼5.7%, which is much larger than that of most inorganic photostrictive materials. The atoms of inorganic crystals are closely packed with strong covalent or ionic bonds, which decrease the capability of lattice deformation. However, organic materials are held together by weak interactions, namely hydrogen bonds, and van der Waals or CT interactions, leading to distinct lattice deformations due to the large intermolecular spacings in these materials. In addition, a thickness-dependent photostrictive effect is observed in DBTTF-C₆₀ nanosheets. As the thickness of the film is increased, the photostrictive effect of ΔH/H decreases with a nearly exponential decay relationship (Fig. 5C).

Fig. 5.

Photostriction phenomenon in the DBTTF-C₆₀ nanosheets. (A) Height change of DBTTF-C₆₀ nanosheets with light excitation of 69.28 mW/cm², which closely follows the change in photocurrent density. (B) Photostrictive height change with increasing light intensity. (Inset) Height change with the light on and off. (C) The maximum height change of DBTTF-C₆₀ nanosheets with decreasing thickness at the light excitation of 69.28 mW/cm². (D) Schematic illustrating the flattening of the chair and boat conformation under light irradiation. (E) Total energy as a function of lattice constant in the z direction for a DBTTF-C₆₀ unit cell with DBTTF in the chair, boat, and flat (excited-state) conformations.

When light illuminates the nanosheets, CT from DBTTF to C₆₀ induce flattening of the DBTTF molecule, independent of whether it is in the boat or chair conformation; the cationic DBTTF⁺ excited state is flat (Fig. 5D). This conformational change upon excitation would increase the size of the unit cell, and is suggested to contribute significantly to the substantial height change observed here. To verify this conclusion, we performed DFT calculations of the DBTTF-C₆₀ system to determine the optimal lattice constants with DBTTF in the chair, boat, and flat cationic excited state, as shown in (Fig. 5 D and E); energy as a function of the x- and y-lattice constants are shown in Fig. S5. In all cases, the chair conformation is lowest in energy, and the excited-state conformation is highest in energy. The most significant change in the unit-cell size occurs along the z direction, with a 6.5 and 5.0% increase upon electronically exciting the chair and boat conformation, respectively, to the flat excited state, in good agreement with ∆H/H for ultrathin films.

The smaller relative height changes experimentally found in the thicker films could be due to three possibilities: (i) According to the Beer–Lambert law, the intensity of incident light decays exponentially from the surface to the inner region of materials, which decreases lattice dilatation within the inner portion of the materials. This will play a role in the thickness-dependent photostriction observed here. (ii) The lattice dilation is larger for the boat form than the chair form of DBTTF upon transformation to the flat conformation. This is consistent with boat conformations of DBTTF being more prevalent in thin nanosheets than in bulk or thick nanosheets. However, this disagrees with the above DFT calculations that show that the unit cell of the boat conformation increases by 1.5% less than the chair conformation upon flattening. (iii) An excess electron, physically resulting from photoexcitation, increases the volume of the system with respect to the pure solid upon interacting with the lattice and forming a polaron. This is supported by pseudopotential-based path integral MD simulations discussed in Supporting Information. Due to the Beer–Lambert law, discussed above, more polarons will be generated in thin films than in thick films, contributing to the thickness dependence of photostriction.

Conclusion

In summary, a liquid–liquid interfacial self-assembly technique has been developed for the fabrication of 2D thickness-controlled molecular DBTTF-C₆₀ nanosheets, which exhibit large surface areas, compact ordered structures, and smooth morphologies. Theoretical calculations, simulations, and experiments support the existence of both boat and chair conformations of the DBTTF molecules in the DBTTF-C₆₀ nanosheets, where the chair conformation dominates, but the boat conformation is induced by interfacial effects and more prevalent in thin films. Both conformations show strong CT interactions, with the CT states of the boat being red-shifted (higher in energy) with respect to those of the chair. In addition, significant anisotropy was found in charge transport and photoelectric experiments, which is suggested to result from the unique molecular arrangements in the film that lead to larger overlaps of molecular orbitals for the in-plane direction. Notably, we observe a large light-induced photostrictive effect with height change of ∼5.7% in organic DBTTF-C₆₀ CT nanosheets. The excited cationic state of DBTTF is found to be flat, and this flattening upon photoexcitation increases the length of the unit cell, contributing to the distinct photostriction phenomenon observed in the film. Additional contributions to photostriction are suggested to arise from the accommodation of charge carriers through polaron formation. Our findings yield a platform for 2D molecular CT nanosheets with potential applications in flexible 2D photodriven microsensors and actuators. The design and fabrication of molecular CT nanosheets demonstrated here enable the flexibility necessary for the selection of the next-generation 2D films for fundamental and practical engineering applications.

Materials and Methods

Materials.

DMF, DBTTF, isopropyl alcohol, ortho-dichlorobenzene, toluene, and acetone are purchased from Sigma-Aldrich. Fullerene (C60) powder is obtained from Alfa Aesar.

Self-Assembly of DBTTF-C₆₀ Nanosheets at Liquid–Liquid Interface.

The DBTTF-C₆₀ nanosheets are grown on a liquid–liquid interface due to the positive spreading coefficient, S = γ_bv − γ_tv − γ_tb, where the surface tension of the liquid substrate γ_bv is larger than the sum of the surface tension between the liquid substrate and the surrounding vapor γ_tv, and the interfacial tension between the spreading solution and the liquid substrate γ_tb. The Petri dish containers were ultrasonic treated with toluene/acetone, isopropanol, and deionized water for 20 min, respectively and then plasma treated for 20 min before using. After that, deionized water/DMF mixed solvent (50% of DMF) was filled in the Petri dish to half-height. When the solvent is stationary, the mixed solvent of 0.4 mL with various solute concentrations from 0.1 to 15 g/L was dropped on the water surface. The organic solvent was then spread throughout the water surface. Parafilm was used to cover the top of the Petri dish with several holes to control the evaporation rate and stability. Along with the slow evaporation of the solvent, the DBTTF-C₆₀ nanosheets grew gradually along the horizontal direction by consuming the remaining DBTTF and C₆₀ molecules and finally spread uniformly on the top of the water surface after evaporation of the solvent. After the growth was finished, the film could then be picked up by various templates for further use.

Characterization.

The optical images were recorded by an Olympus BX51 microscope and processed by a computer. SEM images were taken from FEI Quanta450FEG. The TEM images were taken with a JEOL JEM-1400. AFM images were recorded on a Bruker dimension icon AFM equipped with a Cr/Pt-coated Si probe (radius < 25 nm, resonant frequency 13 kHz). The diffraction images were collected at wavelength of 0.8 Å with a MAR300 CCD detector under SER-CAT 22-BM beamline at Advanced Photon Source, Argonne National Laboratory. Data were integrated, scaled, and merged by HKL-2000. The structure was solved by SHELXT and refined by SHELXL. The crystal structure was presented and analyzed with Mercury software. UV-vis spectra were recorded on an Agilent model HP8453 UV-vis spectrophotometer. Current-voltage (I–V) characteristics of the devices are measured in a nitrogen atmosphere glovebox with a CHI 422 Series Electrochemical Workstation with or without an illumination from OSL2 fiber illuminator calibrated by Newport Power Meter with model 1918-R.

In-Plane and Out-of-Plane Device Fabrication.

For the vertical device, 12 × 12 mm² of glass substrate with prepatterned indium tin oxide (ITO) electrodes were used. After the electrodes were ultrasonic cleaned by acetone, isopropanol, and deionized water for 10 min and then plasma treated, respectively. The films with various thicknesses were directly transferred onto the substrate. The coated device was annealed at 100 °C for 10 min in the glovebox, and then quickly cooled to room temperature. To generate an array of patterned electrodes, an 80-nm-thick Al layer was evaporated at a rate of 0.1 nm/s through a shadow mask. The final device area was defined by the overlap between the top and bottom electrodes, which was about 0.6 × 1.75 mm². For the lateral device, the prepatterned ITO electrodes were ultrasonic treated by acetone, isopropanol, and deionized water for 20 min, respectively, and then plasma treated for 20 min. The films were directly transferred onto the ITO electrodes. The coated device was annealed at 100 °C for 10 min in the glovebox, and then quickly cooled to room temperature. The distance of the two electrodes was from 50 to 200 μm and the electrode length was 0.5 cm.

Photostriction.

The photostriction response measurements were conducted on an AFM (Bruker Multimode 8) according to the previous literature (3). During the photostriction test, the light from the laser diode (MDL-III-405) was guided into the built-in optical microscope of the AFM, shined from top of the AFM tip. As the light propagated through and was focused by the optical lens, the light was no more collimated and could be shined beneath the AFM tip. The light intensity at the sample location was carefully calibrated using a commercial energy meter (Newport 843-R). The beam area was about 0.1 cm². Tests were carried out on ScanAsyst mode using aluminum reflective coating tips with a spring constant of 0.4 N/m.

Computational Details.

DFT calculations.

Our calculations are based on first-principles DFT, time-dependent density-functional perturbation theory as implemented in the Quantum ESPRESSO code (23, 24). We use a hybrid functional with the Heyd–Scuseria–Ernzerhof (HSE) (25) parameterization of the exchange-correlation energy functional with norm-conserving pseudopotentials (26). The HSE functional yields accurate bandgap predictions, which are in agreement with experimental measurements (27). An energy cutoff of 30 Ry was used for truncating the plane-wave basis set to represent wave functions. The parameters used in the work give excellent results for the similar complexes studied in our earlier work (20, 21). The structures were relaxed until the magnitude of the Hellman–Feynman force on each ion was smaller than 0.03 eVÅ⁻¹. Brillouin zone integrations were carried out with a uniform small mesh of k points. The Grimme parameterization (28) was used to include the van der Waals interactions. The boat structure for the DBTTF-C₆₀ complex was built using the Avogadro (29) software. The crystal coordinates of the DBTTF-C₆₀ in the chair structure were used from the Cambridge Crystallographic Data Centre (30). The complex structure (chair and boat) contains 172 atoms, out of which 120 belongs to the C₆₀ and the remaining 52 are associated with DBTTF, respectively.

MD simulations.

All MD simulations were performed in the canonical ensemble (constant number of particles, volume, and temperature) using the LAMMPS software package and the generalized AMBER force field (31). A constant temperature of 300 K was maintained using a Nosé–Hoover thermostat (32–34). Initial configurations were obtained from the crystal structure. Short-ranged interactions were truncated at a distance of 12 Å, and long-ranged electrostatic interactions were evaluated using the particle mesh Ewald method (35). The thin-film system was generated by extending a bulk system in the z direction, thereby creating an interface with a large vacuum region.

Path integral MD (PIMD) of a solvated electron in DBTTF-C₆₀ were performed using LAMMPS. The interactions between the electron and the lattice were described by the Mayer pseudopotential for C₆₀–electron interactions (36) and Shaw pseudopotentials for all other electron–atom interactions (37). Short-ranged cutoffs in the Shaw pseudopotentials were chosen to reproduce the ionization potential of the atoms. The electron was discretized into P = 1,024 beads, each with nearest-neighbor harmonic bonds, whose force constants are prescribed by the path integral isomorphism (38, 39). The DBTTF-C₆₀ lattice was treated classically (P = 1). A constant temperature of 300 K was maintained by using Nosé–Hoover thermostats (32–34), such that the electron beads were massively thermostatted to appropriately preserve the canonical distribution (40–42). Time integration of the equations of motion was performed using a larger, fictitious electron mass of 36.6 a.u., which yields the same structural and thermodynamic averages while enabling the use of a larger timestep of 0.01 fs, for efficient sampling.

Data and Materials Availability.

All data needed to evaluate the conclusions in the paper are present in the paper and/or Supporting Information.