Biophysical studies of protein solubility and amorphous aggregation by systematic mutational analysis and a helical polymerization model

Abstract

At concentrations above solubility, a protein aggregates, most often into amorphous aggregates, and loses its function. However, unlike amyloidogenic aggregates, which are β-sheeted fibrillar aggregates often related to neurodegenerative diseases, amorphous aggregates, where proteins aggregate/oligomerize without forming specific high-order structures, are rarely the focus of biophysical studies. Hence, protein solubility with respect to amorphous aggregation remains to be fully characterized from a biophysical viewpoint. Here, I briefly describe the structural nature of proteins in amorphous aggregates before discussing systematic mutational analyses that aim to rationalize the contribution of individual amino acids to the solubility of a protein. The discussion is expected to demonstrate that protein solubility, and, accordingly, amorphous aggregation, can be understood using thermodynamic and biophysical rationales similar to those used in the study of protein stability or, more recently, amyloidogenesis. Finally, I will argue that the mathematical formalism of the helical polymerization model (HPM) proposed by Oosawa, Kasai, and Asakura’s group can be readily adapted to provide a thermodynamic description of a system containing amorphous aggregates and soluble particles. The HPM and HPM-derived models imply the presence of nuclei or seeds for amorphous aggregates, similar to those hypothesized in crystallogenesis and amyloidogenesis.

Introduction

Protein solubility issues are encountered in diverse areas of protein chemistry. Practically, solubility problems can be overcome by optimizing the sample’s solution condition (Shiraki et al. 2002; Arakawa and Tsumoto 2003; Hamada and Shiraki 2007). Biophysical studies of protein solubility and, thus, amorphous aggregation performed using exhaustive mutational and thermodynamic analysis are still scarce (Iwura et al. 2014; Kamal et al. 2016). A potential reason for this limited interest may be that amorphous aggregates are rarely related to diseases. Another reason may be the absence of high-order structures in amorphous aggregates, which is in sharp contrast with the regularly structured β-sheeted fibrils observed in amyloid aggregates.

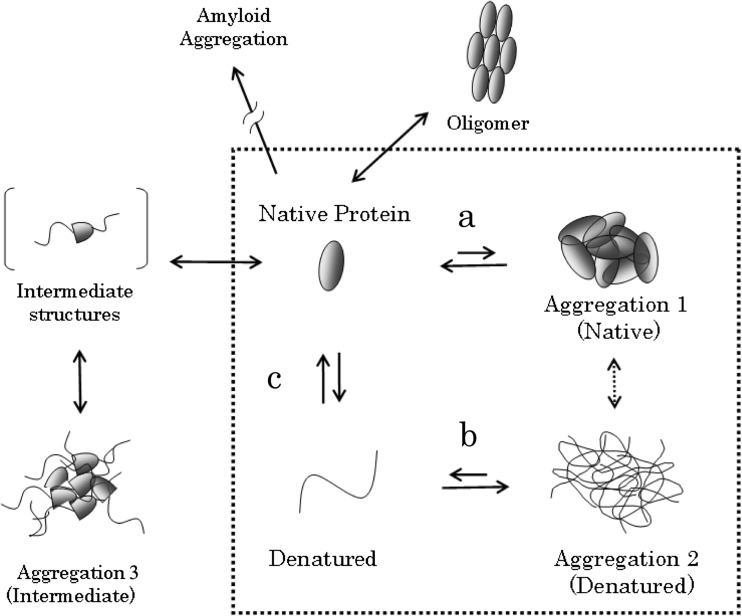
Despite the fact that thermodynamic analysis does not require structural information per se, the structural nature of both the aggregated state and the soluble state can impact on the energetics of protein association and, consequently, the thermodynamics of amorphous aggregation as well as solubility (Fig. 1). A well-known example is the unfolded protein having an aggregation tendency much higher than the same protein in the folded state, where the hydrophobic residues are buried into the protein interior (Baldwin 2012). Thus, protein stability, which is a protein’s internal property, strongly influences its solubility or aggregation propensity, which is a colloidal property.

Fig. 1.

Conceptual diagram of protein aggregation. In this paper, we simplify our discussion by restricting it to the four states depicted within the dotted frame. Arrows a and b describe, respectively, the aggregation of natively folded and denatured (or unfolded) proteins. c describes the structural stability of proteins. In this review, we consider aggregation 1, 2 and 3 as “amorphous” aggregates. Diagram adapted with permission from Kato A. et al. [Seibutsu Butsuri, 48, 185–9 (2008), in Japanese: edited by the Biophysical Society of Japan]

Several factors may mislead the thermodynamic analysis of amorphous aggregation or solubility. An important and obvious factor is the slow kinetics of aggregation, which may lead to erroneous interpretations if the measurements are not performed under equilibrium conditions. Additionally, amorphous aggregation can be reversible, but it is not always so, and one should obviously apply equilibrium thermodynamics only to systems that are reversible (Schön et al. 2017). Furthermore, as discussed above, we should keep in mind that the structural states of both the soluble and the aggregated state do strongly influence the thermodynamics of protein aggregation.

Here, I describe systematic mutational experiments that aim at providing a biophysical rationale for protein solubility with respect to amorphous aggregation. I show that, with careful consideration of key factors such as equilibrium or aggregation rates, one can use thermodynamic concepts to describe a protein’s solubility or aggregation tendency. Finally, I discuss how the helical polymerization model (HPM) (Oosawa and Kasai 1962), initially proposed by Oosawa et al. to analyze the transition of G-actin to F-actin, can be readily adapted to provide a thermodynamic description of protein solubility and amorphous aggregation at the molecular level.

Structure of proteins in amorphous aggregates

It is a popular belief that amorphous aggregation occurs upon the unfolding of proteins. Here, I describe two recent NMR experiments showing that the association of natively folded or near-natively folded proteins can, indeed, form amorphous aggregates.

The first example is γD-crystallin, whose aggregation is famous for provoking cataracts, a rare example of a disease caused by amorphous aggregates. It was believed that γD-crystallin aggregates because the protein denatures (unfolds) upon aging, UV radiation, or sidechain oxidization. However, solid-state NMR indicated that proteins aggregated under physiological conditions kept a well-ordered, native-like conformation, with no evidence of dynamic or static disorder (Boatz et al. 2017). To date, Boatz et al. mention that γD-crystallin formed different aggregates at acidic pH.

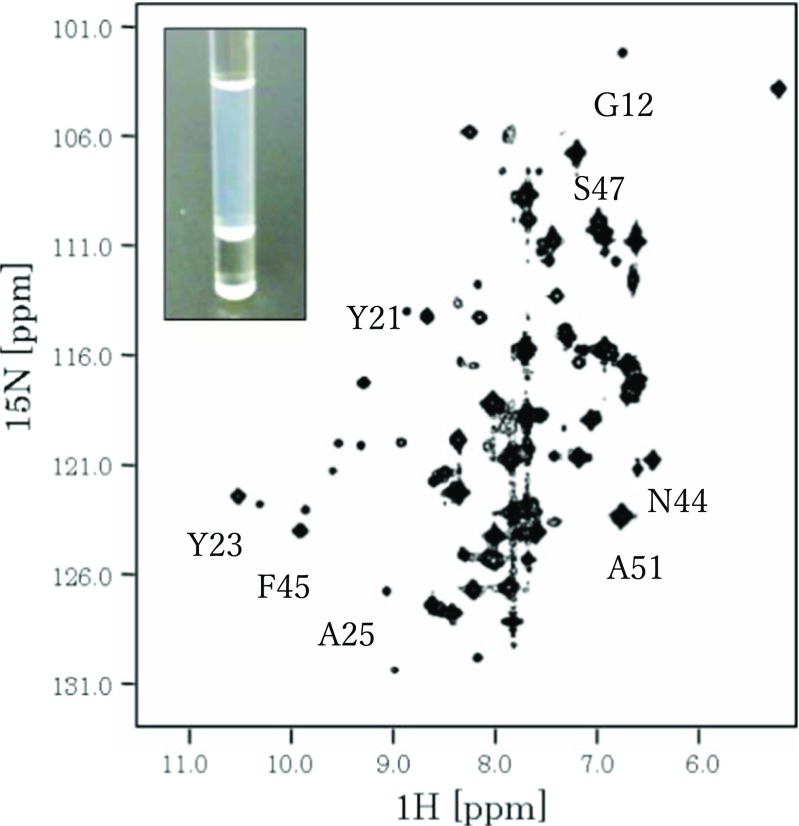
In the second example, 15N hetero single quantum correlation (HSQC) spectra showed that a low-solubility bovine pancreatic trypsin inhibitor (BPTI) variant, BPTI-22 (a BPTI variant containing 22 alanines), associated in a native-like structure (Kato et al. 2007). At a low concentration of 250 μM, BPTI-22 yielded a high-quality NMR spectrum (HSQC spectra) with sharp and well-dispersed peaks. On the other hand, at a concentration of 3.8 mM, the peaks broadened because of aggregation (Fig. 2) but appeared at the same chemical shift position as at 250 μM, strongly suggesting that the aggregated BPTI-22 retained a native-like structure.

Fig. 2.

NMR spectrum (HSQC) of a low-solubility BPTI variant (BPTI-22) measured at 3.8 mM. The cross-peak shapes in the HSQC spectrum of BPTI-22 (3.8 mM) are broad, indicative of aggregation. However, the positions of several cross-peaks are the same as in the native spectrum, strongly suggesting that the overall BPTI fold remains intact. The assignments of cross-peaks with typical chemical shift positions are transferred from Kato et al. (2007), where the measurement and data analysis parameters are also given. The inset shows a photograph of the NMR sample

These two examples show that amorphous aggregates do not result solely from the association of denatured proteins, as often imagined, but they can also result from the association of natively or near-natively folded proteins.

Hydrophobicity models and protein solubility

Hydrophobicity (and, thus, its counterpart, hydrophilicity) models are commonly used for rationalizing the solubility of proteins and other macromolecules (Kyte and Doolittle 1982). However, the original purpose of the hydrophobic/hydrophilic model was to describe an equilibrium between a molecule’s (often amino acid) solubility in a polar (aqueous) and a non-polar environment (Nozaki and Tanford 1971). This model provides a good rationale for the structural stabilization of globular proteins by approximating its interior as non-polar and its exterior as polar (Kauzmann 1959; Tanford 1997), and, thus, for unfolded proteins having a higher aggregation tendency than natively folded proteins. On the other hand, the model is poorer at describing changes in protein solubility or amorphous aggregation tendency upon a single or a few mutations. This is especially true when the natively or near-natively folded proteins aggregate by keeping their hydrophobic residues buried in the protein’s interior.

Amino acid’s solubility parameters

The solubility of individual amino acids have been measured, independently from hydrophobic scales, in the early 1970s and standard values for amino acid solubility have been compiled (Lide (ed) 2009). However, such solubility measurements are subject to artifacts because they were carried out at extremely high peptide (or amino acid) concentrations, which can cause jellification, poor phase separation, sticky fluids, pH shifts, etc. (Kramer et al. 2012).

Two recent studies have measured the contribution of amino acids to the relative solubility change of a model protein using a systematic mutational analysis. In one of them, the solubility of ribonuclease Sa was examined by systematically mutating Thr76, which is located on its molecular surface, to all of the 20 natural amino acids (Trevino et al. 2007). This mutational analysis is probably the first attempt to determine the contribution of amino acids to protein solubility in a systematic way.

In the second example, we determined the amino acid’s contribution to a protein’s solubility by measuring the solubility of a model protein, a simplified BPTI variant (Kuroda and Kim 2000), to which we fused 5-residue peptide tags composed of a single amino acid type (Kato et al. 2007; Islam et al. 2012). BPTI’s solubility was defined as the fraction of proteins remaining in the supernatant after a 20-min centrifugation at 5 °C and in the presence of 1.3 M ammonium chloride, and this was carried out for ten representative amino acids (acidic, basic, etc.). As anticipated, positively charged residues significantly increased the solubility of the protein (despite the presence of ammonium chloride), at both pH 4.7 and 8.7, whereas the hydrophobic 5-Ile tag markedly reduced the solubility of BPTI. 5-Asp and Glu tags barely affected BPTI’s solubility at pH 4.7, but increased solubility eight- to ten-fold at pH 8.7, attributable to the side chains ionization. Noteworthy, such pH dependence is not described in hydrophobicity scales. Overall, these two studies suggest that systematic mutational analysis measuring relative solubility changes could yield a solubility propensity scale, which might provide the basis for calculating the relative solubility of a polypeptide from its amino acid sequence alone.

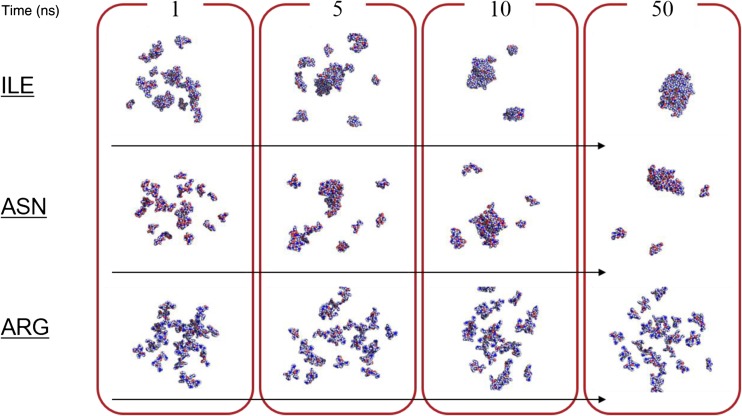
Let us describe a recent molecular dynamics (MD) study that we carried out in order to decipher the molecular mechanisms of peptide and protein’s solubility, and where we used multi-peptide systems containing 27 to 54 tetra-peptides and 3 × 10⁴ water molecules (Kuroda et al. 2016). The clustering of tetra-peptides made of a single amino acid type representing all natural amino acids, except Gly and Cys, was monitored during 100-ns simulations. The results (fractions of tetra-peptides forming clusters) were, overall, in line with experimental amino acid’s solubility as well as hydrophobicity scales (Table 1), and also demonstrated a concentration dependency for Ala₄ peptides. Additionally, the calculations indicated that the solubility of peptides containing charged amino acids originated from repulsive Coulomb energies, whereas “hydrophobic” amino acids, lacking repulsive electrostatic interaction, clustered predominantly through van der Waals interactions and accessorily through main-chain H-bonds. Finally, statistical analysis indicated that small clusters containing 2–4 peptides formed first and grew or merged into larger clusters, suggesting the existence of nuclei in amorphous aggregation (Fig. 3). Altogether, this benchmark type study was surprising in that the solubility of amino acids is fairly well reproduced using standard MD simulation methods, without a need to introduce artificial attractive or repulsive forces (Table 1).

Table 1.

Averaged mean cluster size, solubility, and hydrophobicity scales

Amino acid residues	Parameters
	MCS a	Individual amino acid solubilityb (g/kg)	Hydropathyc	Hydrophilicityd (kcal/mol)	Hydrophobicitye (kcal/mol)	Contribution to protein solubilityf (mg/mL)	Average number of monomersa
Ile	25.1	34.2	4.5	0.2	2.5	0.1	0.6
Leu	26.2	23.8	3.8	0.1	1.8	na	0.3
Val	22.6	88.0	4.2	0.4	1.5	na	1.2
Gln	24.4	42.0	− 3.5	11.8	− 0.3	4.7	1.2
Asn	19.0	25.1	− 3.5	12.1	− 0.2	15.4	3.9
Thr	12.0	90.6	− 0.7	7.3	0.4	na	5.4
Ser	6.2	250.0	− 0.8	7.5	− 0.3	4.6	9.0
Ala	3.4	166.9	1.8	0.5	0.5	na	13.7
Pro	2.6	1625	− 1.6	na	− 3.3	2.0	12.9
Asp	1.1	5.4	− 3.5	13.3	− 7.4	14.2	25.4
Glu	1.0	8.6	− 3.5	12.6	− 9.9	11.0	26.5
Arg	1.0	182.6	− 4.5	22.3	− 11.2	8.9	24.6
Lys	1.1	5.8	− 3.9	11.9	− 4.2	17.0	25.4
Phe	23.1	27.9	2.8	3.2	2.5	na	0.4
Tyr	21.8	0.5	− 1.3	8.5	2.3	na	1.4
Trp	24.8	13.2	− 0.9	8.3	3.4	na	0.7
His	25.1	43.5	− 3.2	12.6	0.5	0.9	0.5
Met	24.8	56.0	1.9	3.9	1.3	na	0.7

^aMCS values are the mean cluster sizes. MSCs and the number of monomers averaged over the last 10 ns of simulation are reported in Kuroda et al. (2016).

^bLide ed, (2009)

^cKyte and Doolittle (1982)

^dWolfenden et al. (1981)

^eNozaki and Tanford (1971)

^fIslam et al. (2012)

Fig. 3.

All atom molecular dynamics simulations of amino acid solubility. The calculations were performed for more than 18 systems, each containing 27 tetra-peptides and about 30,000 water molecules. The tetra-peptides were made of a single amino acid type for all natural peptides, except Gly and Cys. Snapshots at 1, 5, 10, and 50 ns for tetra-peptides made of Ile, Asn, and Arg are shown. The peptides are shown using van der Waals representation. Water molecules are not shown. Details are given in Kuroda et al. (2016)

Time dependence of solubility and aggregation rates

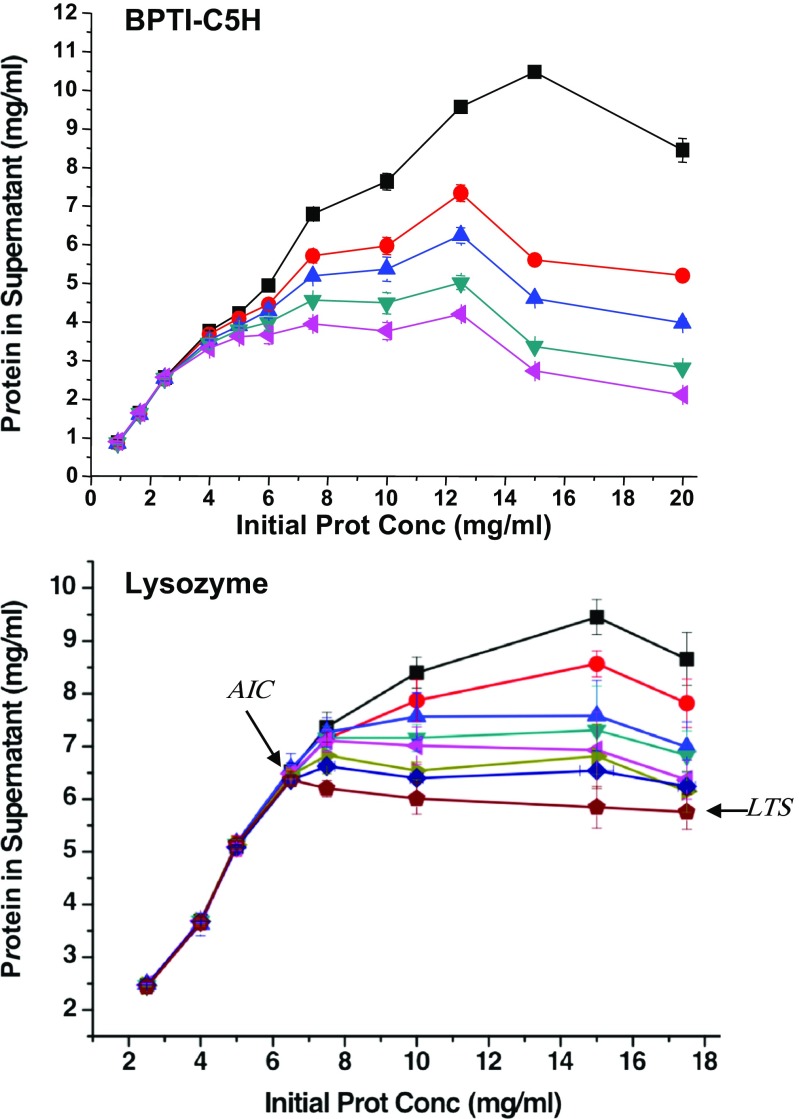
Aggregation rates are an essential, but often overlooked, factor in biochemical and biophysical studies of amorphous aggregation. Despite a few earlier reports (Nohara et al. 1999), a systematic approach for rationalizing protein’s amorphous aggregation kinetics has yet to be developed. We recently expanded our aforementioned work by Islam et al. (2012) in order to analyze the contribution of individual amino acids to the kinetics of protein aggregation (Khan et al. 2013). The major finding of the study was that, for each amino acid, in addition to a parameter describing its aggregation rate, at least two solubility parameters would be necessary for rationalizing the time dependence of protein solubility (Fig. 4). We coined these two parameters, the aggregation initiation concentration (AIC) and the long-term solubility (LTS).

Fig. 4.

Time dependence of the aggregation process. The concentrations of BPTI-C5H (a) and lysozyme (b) in the supernatant measured after centrifugation at 20,000 × g for 20 min are shown on the vertical axis. BPTI-C5H samples were incubated at 25 °C for 20 min, 60 min, 6 h, 12 h, 24 h, and 48 h before centrifugation (a). Lysozyme samples were incubated for 20 min, 6 h, 12 h, 1 day, 2 days, and 7 days before centrifugation (b). The other experimental details are given in Khan et al. (2013). The total protein concentration is indicated on the horizontal axis. The aggregation initiation concentration (AIC) and long-term solubility (LTS) for lysozyme are indicated by arrows

Early in our study, we noticed that, besides the type of amino acids fused, BPTI’s solubility depended on the equilibration time. For example, the amount of protein in the supernatant of the His-tagged variant, BPTI-C5H, reduced sharply from 10.5 mg/mL to 2.5 mg/mL with the extension of equilibration time from 20 min to 48 h, which was obviously indicative of a slow aggregation rate (Fig. 4a). In addition, we observed that the protein concentration in the supernatant or “apparent solubility” reduced faster for solutions with a high total protein concentration, which was highly unexpected. For example, BPTI-C5H aggregated faster at a total protein concentration of 20.0 mg/mL compared to that of 15.0 mg/mL (Fig. 4a).

Thus, protein concentration in the supernatant of a saturated sample, measured after 20 min, did not persist, and we termed this solubility “transient solubility (TS)”. TS is not a fundamental parameter in defining a protein’s solubility. Rather, it may be erroneously taken for a protein’s solubility if one measures the amount of protein in the supernatant before the system reaches equilibrium. TS decreased with time only when the total protein concentration was higher than the AIC, and reached the LTS after 48 h, at which time we assumed that equilibrium was reached. With respect to the nucleation-extension or helical polymerization model (see next section), the AIC would correspond to the minimum concentration at which an aggregation nucleus can form, whereas the LTS (or actually the final equilibrium solubility) is the minimum concentration at which growth of the nucleus to large aggregates occurs. In many ways, both the LTS and the AIC could be considered as the “solubility” of a protein, but we believe that the LTS is close to the final equilibrium solubility and is an important parameter. Similarly, the AIC is also an important parameter because the protein concentration in the supernatant remains constant over the long term if the total protein concentration is lower than the AIC, where no nucleus can form.

The AIC and LTS are also valid for describing the aggregation of natural proteins, as shown for lysozyme, though it took longer to reach equilibrium (Fig. 4b). For a solution with a total protein concentration of 15.0 mg/mL, the lysozyme concentration was 6.9 mg/mL after 48 h and, finally, 5.8 mg/mL after 7 days of equilibration in 1.7 M ammonium sulfate and pH 4.7, which can be considered to have reached equilibrium. On the other hand, samples prepared at 6.5 mg/mL, which was the AIC under this condition, did not aggregate.

Furthermore, the slow rate of aggregation could provide a rationale for a peculiar observation that lysozyme’s solubility was higher when the total concentration was higher (Trevino et al. 2008). We speculate that this bizarre observation might originate from the slow speed of precipitation and the fact that lysozyme’s “solubility” was measured before the system had reached equilibrium. A similar situation is visible in Fig. 4b, where lysozyme dissolved at 15 mg/mL has an “apparent solubility” (or TS) of 8.3 mg/mL, as measured after a 60-min incubation. However, the apparent solubility is only 7.3 mg/mL when the total protein concentration is 10.0 mg/mL. This effect eventually disappeared at longer incubation time as the system moved toward equilibrium.

The helical polymerization model applied to protein’s amorphous aggregation

The HPM was initially developed to describe the formation of F-actin (Oosawa and Kasai 1962). The HPM provides a theoretical framework for systems that undergo an abrupt transition from a monomeric state to an oligomeric or colloidal state (Oosawa and Kasai 1962). Besides actin (Arisaka et al. 1975), HPM-derived models have been applied to various systems, such as tobacco mosaic virus (Klug and Durham 1972) and tubulin (Sutherland and Sturtevant 1976).

To date, thermodynamic models do not require structural information as discussed above. Before describing how the HPM formalism applies to protein amorphous aggregation, let us first discuss the more popular linear model. In the linear model (Fig. 5a), the equilibrium constant (Sutherland and Sturtevant 1976) for adding a single monomer to the aggregate is k_a. According to the linear model, the concentration (M_i) of aggregates containing i molecules is written in terms of the free monomer concentration in the supernatant m as:

$$M_i={k_{\mathrm{a}}}^{\left(i-1\right)}{m}^i$$ 1

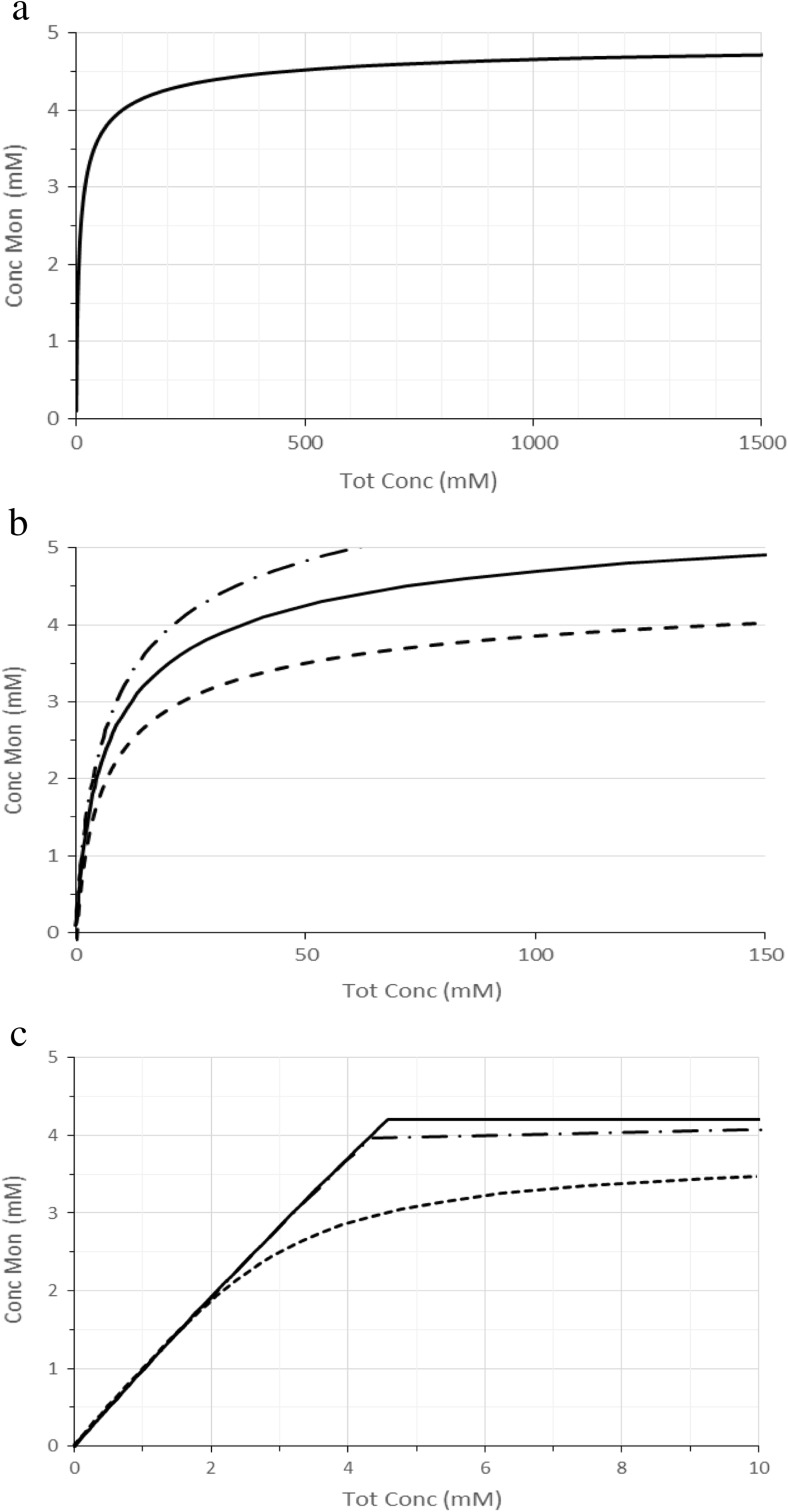
Fig. 5.

Protein solubility simulated using the Oosawa–Kasai polymerization model. The total amount of protein (m_Tot) is shown on the horizontal axis and the concentration of monomeric proteins (m) in the supernatant is shown on the vertical axis. The curves in a and b were calculated by using a linear polymerization model with an association constant (k_a) of 0.2 (1/5) mM⁻¹. In b, the curves calculated for k_a with 1/6 mM⁻¹ and 1/4 mM⁻¹ are shown with dashed-dotted and dashed lines, respectively. The curves in c were calculated by using a helical polymerization model (HPM) with an association k_b = 0.25 (1/4) mM⁻¹ and k₀ = 0.01 (1/100) mM⁻¹ and assuming that monomers remain in the supernatant. The value of k₀ had no visible influence on the curves within a range of 0.1 M⁻¹~0.01 M⁻¹. Similarly, j had a minor influence on the curve’s appearance, as shown here for j = 2 (dashed line), 10 (dashed-dotted line), and 25 (solid line). The curves essentially overlapped for j above 25

The amount of protein molecules (m_Tot) is then given by:

$$m_{\mathrm{Tot}}=\sum _{i=1}^{\infty }{\mathit{iM}}_i=\sum _{i=1}^{\infty }{{\mathit{ik}}_{\mathrm{a}}}^{\left(i-1\right)}{m}^i=\frac{m}{{\left(1-k_{\mathrm{a}}m\right)}^2}$$ 2

The major problem in applying Eq. 2 to experimental observations is that the number of monomers in the supernatant rises gradually as m_Tot, the total number of protein molecules, increases to a limit value at infinite total concentration (Fig. 5a). Equation 2 could provide an explanation for solubility increasing along with total protein concentration (Trevino et al. 2008), but such an observation is anecdotal and counter-intuitive, and it is reasonably assigned to slow aggregation rates as discussed above. Thus, Eq. 2 does not yield a sharp transition with a concentration above which newly added molecules associate, i.e., a solubility value, which contradicts experimental observation.

The HPM overcomes this conundrum by introducing two equilibrium constants. It considers that the first molecules associate with a low association constant k₀. Once the aggregate reaches a certain size (j), it assumes that each newly added molecule associates with a novel association constant k_b. For amorphous aggregation, it is reasonable to assume that k_b < k₀ because the interactions are non-specific, and the surface to which a molecule can bind is larger for an aggregate than for a monomeric molecule.

Thus, according to the HPM, the concentration M_i of aggregates containing i molecules is expressed in terms of the free monomer concentration (m) as:

$$M_i={\mathit{ik}}_0^{\left(i-1\right)}{m}^i\mathrm{\text{for}}i<j,\mathrm{\text{and}}{M}_i=i{k}_0^{\left(j-1\right)}{k}_b^{\left(i-j+1\right)}{m}^i\mathrm{\text{for}}i\ge j$$ 3

The total protein concentration m_Tot is:

$$\begin{array}{llll}{m}_{\mathrm{Tot}}={\sum }_{i=1}^{j-1}i& k_0^{i-1}{m}^i+{\sum }_{i=j}^{\infty }i& k_0^{j-1}& k_{\mathrm{b}}^{\left(i-j+1\right)}{m}^i\end{array}$$ 4

This value is valid at equilibrium and does not take into account aggregation rates. k₀ and k_b would roughly correspond, to the AIC and the LTS, respectively (Khan et al. 2013). Let us examine how Eq. 4 describes the free monomer concentration m as a function of total protein molecules m_Tot using the three parameters, k₀, k_b, and j (Fig. 5b). First, k_b is experimentally determined by measuring the critical concentration. k₀ is assumed to be smaller than k_b but it cannot be determined precisely as the curve is strongly dependent on k₀/k_b. However, by computing m as a function of m_Tot, for k₀/k_b = 0.1~10⁻⁴, one sees that k₀ has no experimentally detectable effect on the amount of monomers (data not shown). Similarly, j, which is the size of aggregates at which the association constant changes from k₀ to k_b, has little influence if it is larger than 10-mers (Fig. 5c). Thus, in equilibrium, protein amorphous aggregation is well described using the HPM with essentially one variable, k_b, the others having no or little experimentally detectable effect on the curve’s appearance.

A direct consequence of the HPM and HPM-derived models is the existence of a seed or a nucleus in the formation of amorphous aggregates (Xue 2015). Both our MD simulation and observation of an AIC are in line with the existence of a nucleus in amorphous aggregation. However, we note that the nucleus is a “thermodynamic state” which are unlikely to contain a specific structure. Moreover, the number of molecules in the seed can vary within the fitting error of j, which is large for amorphous aggregation (j > ~10).

Scope and limitation of the HPM for describing amorphous aggregation

The HPM provides a good description for amorphous aggregation. However, we note that, unlike previous systems described using the HPM, there are most probably no specific structures in amorphous aggregates (including in the seeds), and the parameters discussed in the previous section are obviously averaged values and their structural interpretation should be carried out judiciously.

Aggregation in the denatured state is readily incorporated in the HPM by considering:

$$\mathrm{\text{Native monomer}}\underset{k_{\mathrm{\text{denaturation}}}}{\to }\mathrm{\text{Denatured monomer}}\underset{k_0}{\to }\mathrm{\text{Denatured aggregate}}$$

This aggregation scheme yields $\widetilde{k_0}=k_0{k}_{\mathrm{\text{denaturation}}}$, where $\widetilde{k_{\mathrm{0}}}$ is the new association constant and k_denaturation is the equilibrium constant between the native and denatured state of the monomer. Similarly, one could presumably include the time dependence of protein aggregation using an HPM-derived formalism as previously shown by Oosawa and Asakura (1975) or more sophisticated models (Hall et al. 2015).

We also note that the present model holds at low protein concentration, and exactly only for infinitely dilute systems, which is somewhat contradictory in the case of amorphous aggregation, as it necessarily occurs at fairly high concentration. One calculates that, at 1 mM (about 6.5 mg/mL), a BPTI molecule is surrounded by a sphere of solvent molecules with a radius approximately equal to six times its own radius. The solution is, thus, dense and one can expect that molecular crowding may start to influence the thermodynamics at concentrations where solubility experiments are usually carried out (Zimmerman and Minton 1993; Hall and Minton 2002).

Conclusion

The main point of our discussion was to present thermodynamic and mutational analyses of protein solubility with respect to amorphous aggregation. It appears that a thermodynamic description of protein amorphous aggregation is indeed reasonable within the mathematical framework provided by the helical polymerization model (HPM). Both the HPM and molecular dynamics (MD) simulation suggest the existence of a nucleus or seed during the formation of aggregates, which is in line with the experimental observation of an aggregation initiation concentration (AIC) and a long-term solubility (LTS) in both bovine pancreatic trypsin inhibitor (BPTI) variants and lysozyme. Further biophysical investigation of protein solubility and amorphous aggregation are worthy of being carried out, as molecular crowding and aggregation kinetics remain to be taken fully into account.

Compliance with ethical standards

Conflict of interest

Yutaka Kuroda declares that he has no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by the author.