Structure from Dynamics: Vibrational Dynamics of Interfacial Water as a Probe of Aqueous Heterogeneity

Abstract

The structural heterogeneity of water at various interfaces can be revealed by time-resolved sum-frequency generation spectroscopy. The vibrational dynamics of the O–H stretch vibration of interfacial water can reflect structural variations. Specifically, the vibrational lifetime is typically found to increase with increasing frequency of the O–H stretch vibration, which can report on the hydrogen-bonding heterogeneity of water. We compare and contrast vibrational dynamics of water in contact with various surfaces, including vapor, biomolecules, and solid interfaces. The results reveal that variations in the vibrational lifetime with vibrational frequency are very typical, and can frequently be accounted for by the bulk-like heterogeneous response of interfacial water. Specific interfaces exist, however, for which the behavior is less straightforward. These insights into the heterogeneity of interfacial water thus obtained contribute to a better understanding of complex phenomena taking place at aqueous interfaces, such as photocatalytic reactions and protein folding.

1. Introduction

Understanding the dynamic properties of aqueous interfaces is important not only for a fundamental understanding of aqueous interfaces but also because the water interface constitutes the site for a variety of important chemical reactions. Examples for water interfaces as reactive environments are abundant: ions at the air/water interface are important oxidants at the marine boundary layer and provide a reaction site for heterogeneous chemical reactions.^1,2 Chemical reactions “on water” have been shown to exhibit drastic acceleration of reaction rates.³⁻⁵ The interface between water and surfactants impacts a variety of processes, varying from corrosion and wetting to drug delivery.⁶ Moreover, water is involved in biological processes, such as protein folding.⁷ Understanding the fundamental dynamics of the water interface, e.g., interfacial hydrogen-bond dynamics and energy relaxation pathways, is the gateway to understanding the impact of interfacial water on a broad range of biological, chemical, and physical processes.

The unique properties of interfacial water arise from the termination of the network of hydrogen bonds at the interface. Depending on the nature of the interface—specifically, whether it is able to accept and/or donate hydrogen bonds (i.e., hydrophilic) or not (i.e., hydrophobic)—the interfacial properties of water at the interface will be substantially different from water in bulk. In order to determine the structure of specifically interfacial water, a surface-selective technique is required. Sum frequency generation (SFG) is a surface-selective technique with the ability to investigate the structure of interfacial water.⁸⁻¹¹ While SFG spectroscopy is a powerful tool to study the structure of molecular systems, the spectral complexity of water is overwhelming. Time-resolved SFG and multidimensional SFG spectroscopies are capable of disentangling the structural anomalies of interfacial water, utilizing vibrational dynamics as a probe. Recent advances in SFG spectroscopy provide the means to experimentally determine the vibrational dynamics of interfacial water in real time using time-resolved SFG spectroscopy.

Decades of bulk studies have laid the foundation for the surface-selective experiments. In bulk, the third-order nonlinear optical techniques of pump–probe and 2D IR spectroscopies have been extensively used to probe the structure and both structural and vibrational dynamics of water.¹²⁻¹⁷ Many of these studies have focused on the O–H stretch vibration in the broad spectral region from 3100 to 3500 cm^–1. The large width of the O–H stretching band is due to variations in the hydrogen-bond strength for different O–H groups¹⁹ but has also been attributed to inter- and intramolecular coupling of O–H groups of water. Specifically, the two O–H groups in a single H₂O molecule generate the symmetric and antisymmetric O–H stretch modes. Furthermore, the O–H stretching mode exhibits a Fermi resonance resulting from a mixing of the O–H stretch mode with the H–O–H bending overtone mode. Since these occur in a single water molecule, this Fermi resonance can also be considered as intramolecular coupling.¹⁸ In addition, intermolecular coupling causes a delocalization of O–H stretch quanta over several O–H groups.^20,21 These intra/intermolecular couplings of the O–H stretch modes critically affect the vibrational dynamics of bulk water. The effects of this coupling on the vibrational dynamics have been elucidated by comparing results for pure H₂O and isotopically diluted water, in which coupling between different OH groups is reduced. For instance, in bulk water, following the excitation of OH groups oriented preferentially along the polarization direction of the exciting infrared field, the loss of the transient anisotropy induced by the excitation pulse can be followed using polarized probe pulses. The anisotropy decay depends strongly on the concentration of OH groups in water: in pure water, the anisotropy decays under 180 fs,^14,15,22 while it takes between 0.5 and 1.0 ps²³⁻²⁶ for isotopically dilute water. In pure water, near-resonant energy transfer between (slightly) differently oriented OH groups gives rise to fast anisotropy decay, while anisotropy decay in isotopically dilute water requires slower molecular reorientation.

Differences exist between bulk water and interfacial water. First, the surface contains a lower density of water molecules and therefore reduces the number of coupled modes, which is expected to change the rate and pathway of energy flow. In addition, the interface may consist of free O–H molecules that terminate the end of the hydrogen-bonding network. The free O–H stretching mode is at 3700 cm^–1, a higher frequency compared to the bonded O–H stretching mode due to the unhindered O–H vibrational motion. Thus, interfacial water deviates structurally from bulk water, potentially leading to different vibrational dynamics as well. Moreover, changing the type of interface—water in contact with a hydrophobic or hydrophilic medium—may change the interactions and thereby alter the dynamics of the interfacial water.

In this Feature Article, we highlight recent work aimed at obtaining structural details of water from time-resolved SFG spectroscopy. The time scales of the vibrational dynamics can be used to assess the nonuniformity of water; i.e., the frequency dependence of the vibrational dynamics of bulk and interfacial water can report on the structural differences or heterogeneity of water. While time-resolved SFG spectroscopy experiments on interfacial water can be used to determine the rate and mechanism of energy dissipation, intra- and intermolecular coupling of the O–H vibrational modes, and the rotational dynamics of the O–H vibrational modes in real time, the scope of this article is centered on using vibrational lifetimes as a probe for structural heterogeneity of water. A comprehensive review on time-resolved SFG can be found in the literature²⁷ as well as a review on 2D vibrational spectroscopies at surfaces.²⁸ Note that, additionally, there exists a wealth of literature reporting studies using bulk-sensitive techniques of the dynamics of confined, non-bulk-like water in reverse micelles (see, e.g., refs (29−32)).

2. Methods

2.1. Principles of Time-Resolved SFG

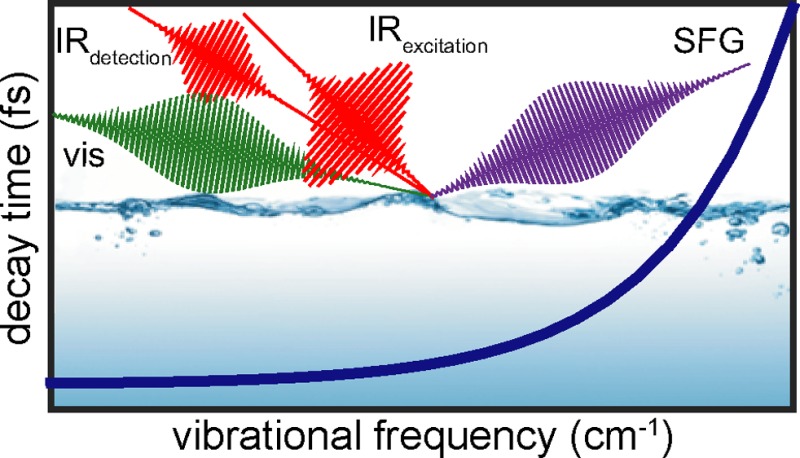
SFG spectroscopy is ideally suited to probe the structure of water at interfaces. As an even-, second-order (χ⁽²⁾) nonlinear spectroscopy, SFG has as a selection rule that, in the dipole approximation, the SFG signal cannot originate from the bulk of centrosymmetric media: symmetry must be broken in order for SFG to be generated, and symmetry breaking by definition occurs at an interface. In the SFG experiments, a broadband infrared (IR) pulse, typically 400–700 cm^–1, and a narrowband visible pulse, ranging from sub-1 cm^–1 to 20 cm^–1,³³ are overlapped spatially and temporally at the surface of the sample. If the IR pulse is resonant with vibrational modes of interfacial molecules, for example, the hydrogen-bonded O–H stretch region in the case of water, the generation of the sum frequency of the two incident fields (i.e., the SFG signal) will be resonantly enhanced. As such, the vibrational response of molecules specifically at the interface can be obtained. This vibrational response can then be used to understand the structure of the molecules at the interface.

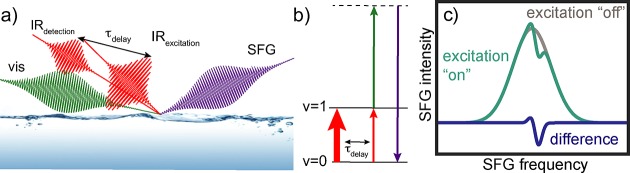
Time-resolved SFG (TR-SFG) spectroscopy is an extension of conventional SFG spectroscopy. Where SFG is a second-order (χ⁽²⁾) nonlinear spectroscopy, TR-SFG is also an even-order (fourth-order) spectroscopy, therefore equally surface specific. Conventional and heterodyne-detected SFG are both second-order spectroscopies, which provide the surface analogue of bulk infrared or Raman spectroscopy through the second-order nonlinear optical response. TR-SFG is a fourth-order spectroscopy, which allows disentangling the different contributions to the second-order nonlinear optical response, e.g., by the possibility to burn spectral holes in the second-order line width. This provides information that cannot be obtained from conventional SFG spectroscopy. The vibrational energy lifetime T₁, for instance, is a quantity that cannot be inferred from the static SFG spectrum. TR-SFG involves adding an additional IR pulse, known as the IR excitation pulse, to a SFG experiment (Figure 1a). The IR excitation pulse excites molecular vibrations (in a non-surface-specific manner) from the ground state to the first vibrational excited state (Figure 1b), thereby producing population in the first vibrational excited state. Subsequently, the SFG probe pair, an IR detection pulse and a visible pulse, are used to interrogate changes in the vibrational response of the surface molecules as a result of the IR excitation. Figure 1c illustrates the difference between the signal with and without the excitation pulse. Since the IR excitation pulse reduces the population in the ground state, less ground state oscillators are available for generating SFG, causing a decrease in the SFG signal. Simultaneously, SFG generated from the excited state becomes detectable and may appear red-shifted relative to the fundamental, due to the anharmonicity of the vibrational potential. The spectrum of interest in a TR-SFG experiment is the difference spectrum between the excitation pulse on and off or the ratio between the spectra with and without the excitation pulse. The resulting difference spectrum reflects the bleach of the fundamental vibrational transition and the excited state SFG signal (Figure 1c). The time evolution of the population can be followed by changing the time delay between the IR excitation pulse and the visible/IR SFG probe. Therefore, the IR pulses must be short in the time domain to provide sub-picosecond time resolution. A typical scheme for TR-SFG, as shown in Figure 1a, reflects different incident angles for each incoming beam in order to spatially separate the desired SFG signal.

Figure 1.

TR-SFG spectroscopy schematic: (a) the experimental geometry, (b) the energy level diagram of the pump–probe process, and (c) an example of the SFG signals with the excitation on, the excitation off, along with the difference spectrum.

2.2. Homodyne vs Heterodyne Detection

In analogy to conventional SFG spectroscopy, TR-SFG experiments can be performed in two manners: using homodyne detection, i.e., simply measuring the SFG intensity, or using phase-resolved, also known as heterodyne, detection. On the one hand, the homodyne detection TR-SFG experiments evaluate the change in intensity ΔI(t) of the SFG signal, i.e.,

1

where χ_exc⁽²⁾ = χ₀ + Δχ is the second-order nonlinear susceptibility with the excitation pulse and χ₀⁽²⁾ is the second-order nonlinear susceptibility without the excitation pulse. On the other hand, phase-resolved detection measures the imaginary part of χ⁽²⁾, Imχ⁽²⁾, which provides information on the absolute orientation of interfacial molecules. Phase-resolved detection, also known as heterodyne detection, utilizes a local oscillator, and the interference between the local oscillator and the SFG signal is detected, yielding the phase information on the molecular vibration.³⁴ The phase-resolved signal Imχ⁽²⁾ can be compared to the infrared and Raman bulk spectra. The (time-resolved) phase-resolved spectrum is obtained from the difference between the excitation off and excitation on spectra

2

It is important to note that the different detection techniques result in significantly different spectra. The intensity of the spectral features varies on the basis of the detection method. In order to understand the discrepancies in intensity, we begin the discussion with the relationship between the second-order nonlinear susceptibility and the number density by

3

If 10% of a population is excited from the ground state to the first excited vibrational state, a fraction of 0.9 (out of 1) remains in the ground state. The intensity is roughly equal for the bleach and the excited state peaks in the difference spectra for the phase-resolved detection regime. In contrast, for homodyne detection, the SFG intensity is given by the square of χ⁽²⁾. Thus, the 0–1 transition intensity is proportional to the square of the difference between the population in the ground and first excited states: (N₀ – N₁)² = (0.9 – 0.1)² = 0.64, while the 1–2 transition intensity is significantly lower, being proportional to the excited state population squared, corrected for the twice larger transition dipole moment of the excited state: (2N₁)² = (2 × 0.1)² = 0.04. As such, the peaks corresponding to the 0–1 transition dominate the homodyne spectrum. Beyond the intensity differences, one expects the vibrational dynamics inferred from homodyne and phase-resolved experiments to be very similar. Briefly, eq 1 can be expanded to

4

where (Δχ⁽²⁾(t))² is negligibly small compared with the other terms. The homodyne signal can be compared to the phase-resolved signal, where the χ⁽²⁾ is separated into real and imaginary components, as follows:

5

Since the real and imaginary components are related via the Kramer–Kronig relations, the time dependences of the real and imaginary components are not independent. Therefore, the extracted time components should roughly be the same between homodyne and heterodyne detections. Details of the theoretical treatment of both intensity and phase-resolved TR-SFG can be found in ref (35).

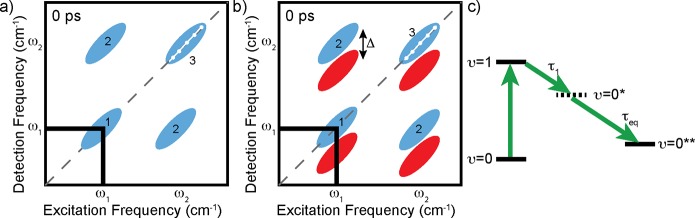
TR-SFG experiments can also be performed using multiple excitation frequencies, similar to 2D IR and 2D NMR experiments. Combining the spectra from the different excitation frequencies allows for the construction of a 2D SFG spectrum. A wealth of knowledge can be extracted from a 2D SFG spectrum; the additional dimension in the frequency axis can clarify ambiguities in linear spectra and provide further details on the structure and dynamics of the system. A brief overview of 2D SFG spectroscopy, illustrated in Figure 2a and b, is given below to facilitate the understanding of the data and to elucidate the differences in 2D SFG spectra reported in the literature. 2D SFG was first reported by Bredenbeck et al.,³⁶ and subsequently first applied to the study of aqueous surfaces by Zhang et al.^37,38 Further developments to TR-SFG, including pulse shaping technologies^39,40 and non-collinear setups,⁴¹ have demonstrated increasingly widespread applications and improvements in the signal-to-noise.

Figure 2.

Schematics of (a) an intensity, or homodyne-detected, 2D SFG spectrum and (b) a phase-resolved, or heterodyne-detected, 2D SFG spectrum. (c) Model of energy relaxation with a four-level system.

The 2D spectrum in Figure 2a is representative of a homodyne-detected 2D spectrum and has two types of peaks: peaks that lie along the diagonal (peaks 1 and 3) and peaks (2 and 2) that are not on the diagonal, known as cross-peaks, or off-diagonal peaks.^42,43 The peaks along the diagonal (1 and 3) originate from the response of the system at the same frequency where the excitation has occurred: exciting and probing with the same frequency. Cross-peaks (2) result from a response at frequencies different from the excitation frequency. Cross-peaks originate from coupled oscillators—exciting one affects the other—and can provide structural details on the system or provide insight into energy transfer and/or anharmonic coupling between different vibrational modes.

The 2D spectrum in Figure 2b, a cartoon of a heterodyne-detected 2D spectrum, appears different from the 2D spectrum in Figure 2a. The blue peaks correspond to a combination of a bleach of the fundamental vibrational state and stimulated emission, and the red peaks originate from an excited state absorption, i.e., 1–2 transition. As mentioned previously, while the intensity of the 1–2 transition peak is less intense for the homodyne detection compared to the heterodyne detection, it is approximately equal in intensity for the heterodyne signal. Therefore, the excited state peaks, i.e., the red peaks in Figure 2b, are visible and have the same intensity as the peaks for the 0–1 transition, while absent in Figure 2a. Due to anharmonicity, the 1–2 transition frequency differs by an amount Δ from the 0–1 transition frequency, resulting in peak pairs with one negative peak (blue) and one positive (red) peak.⁴² The excited-state response would be located at ω₁–Δ along the detection (SFG) frequency axis.

2.3. Vibrational Dynamics

2D SFG spectra recorded as a function of time between excitation and probe pulses give access to the vibrational dynamics of aqueous interfaces. Upon changing the time delay between the excitation IR and probe IR pulses, vibrational dynamics on sub-picosecond to hundreds of picosecond time scales can be investigated. The waiting time (or population time) is commonly displayed in 2D spectra, as illustrated in Figure 2a and b. Collecting spectra at multiple time delays is equivalent to TR-SFG experiments. The aim of the time-resolved experiments is to determine the dynamics of the system, such as energy transfer or energy dissipation as well as the structural heterogeneity of water.

The time-resolved measurements have several varieties; the simplest time-resolved experiment is a one-color pump–probe experiment. In this measurement, the pump and probe pulses are at the same frequency, which is equivalent to measuring the time evolution of peak 1 (Figure 2a and b). The process of energy relaxation from the excited state to the ground state is measured in such experiments, for which the signal, however, could also contain contributions from spectral diffusion (see below). Figure 2c is a typical model used to describe the energy relaxation of the O–H stretch vibration of hydrogen-bonded water, where the molecular vibration relaxes to an intermediate state, followed by relaxation from the intermediate state to a heated ground state. This heated ground state is characterized by the steady-state response of the system at slightly elevated temperatures (normally 3–5 K), as the result of dissipation of the excess vibrational energy.^15,44 Determining the vibrational modes that form the intermediate state for energy relaxation is complicated due to the strong coupling in water. Experimental and theoretical studies show that the dominant energy relaxation pathway is from the hydrogen-bonded O–H stretching modes to the O–H bending vibrations of the same molecule, i.e., intramolecular vibrational relaxation (IVR).⁴⁵⁻⁴⁷ The overtone of the bending vibrational mode is similar in energy to the O–H stretch vibration, which makes the Fermi resonance a viable relaxation pathway. From the bending mode overtone, the relaxation continues to a broad distribution of delocalized low-frequency modes.⁴⁸ Vibrational conical intersections are expected to play a role in the vibrational relaxation dynamics due to the coupling between the O–H stretch vibration and the low frequency hydrogen-bonding modes.⁴⁹ The one-color pump–probe experiment reports on the vibrational relaxation time(s) of the excited state. Differences in the T₁ lifetimes with respect to excitation frequency can report on the heterogeneity of the O–H groups in the bulk or at the surface.

However, not only could vibrational relaxation cause the disappearance of the bleach signal, but reorientation can also contribute. Thus, the bleach relaxation, with time scale τ, could have contributions from the vibrational relaxation, molecular reorientation dynamics, and spectral diffusion. The reorientation dynamics can in principle be obtained using polarization controlled pump–probe experiments.^50,51 The excitation pulse excites molecules aligned along the polarization axis of the excitation pulse, either s- or p-polarization. The molecules are subsequently probed with polarized light, either parallel or perpendicular to the excitation pulse. The polarized pump excitation produces an anisotropic distribution of excited molecules. For bulk water, the decay of this pump-induced anisotropy can be obtained from polarization-resolved pump–probe measurements.⁵² This experimental approach, as well as calculations of reorientation dynamics in the bulk, relies on the fact that the solutions are isotropic, where the molecules are oriented randomly. At the surface, the interfacial molecules are not in an isotropic environment. As a result, the orientation of interfacial water molecules is anisotropic under steady state already, and extracting the reorientational dynamics from the additional anisotropy induced by the excitation is substantially more complicated for the interface than the bulk.⁵³ The mechanism for reorientation in the bulk consists of three steps: a hydrogen bond is broken, the water molecule rotates, and a new hydrogen bond is formed.⁵⁴ The reorientation dynamics of HDO in bulk D₂O occurs on an effective time scale of ∼2.5 ps.^55,56 For interfacial water, reorientation dynamics of the free O–H stretch, which is the part of the water molecules that terminate the hydrogen-bond network, has been shown to reorient 3 times faster than the bulk.^50,57

It should be noted that most of the literature assigns the bleach relaxation directly to vibrational relaxation.⁵⁸⁻⁶⁰ This could be due to the fact that the reorientation dynamics are fast and the bleach relaxation is dominated by the vibrational relaxation. However, in order to remain consistent and clear in this Feature Article, we will refer to the bleach relaxation (τ), rather than vibrational relaxation (T₁), for all experiments where reorientation and/or spectral diffusion have not been taken into account.

Indeed, the bleach relaxation also contains contributions from spectral diffusion. Spectral diffusion is the time variance in the vibrational frequency of a molecular oscillator and can be used to quantify the time-dependent variations in the hydrogen-bond strength and near-resonant vibrational energy transfer in water. Energy can flow between differently hydrogen-bonded O–H stretch modes that constitute the broad O–H peak, as seen in bulk studies.⁶¹ The inhomogeneous broadening of the peaks in a 2D spectrum can be used to report on the heterogeneity of the O–H groups. The slope of a peak in a 2D spectrum, illustrated as the white line in peak 3 from Figure 2a, reveals the structural heterogeneity of the O–H modes. When the ensemble is homogeneous, i.e., when all of the O–H groups are indistinguishable, the oscillators respond similarly regardless of the excitation frequency, and as a result, the slope of the on-diagonal response in the 2-D spectrum is zero. For a completely inhomogeneous system, i.e., when all O–H groups have a slightly different vibrational frequency, the infrared absorption line is inhomogeneously broadened, and only those O–H groups that are resonant with the excitation pulse will respond to that excitation. In this case, the response of the O–H groups in the two-dimensional spectrum will lie along the diagonal; i.e., the slope equals 1. The effects of spectral diffusion can contribute to the bleach relaxation lifetimes in TR-SFG experiments, and often, it is difficult to separate the effects of spectral diffusion from intramolecular vibrational relaxation and reorientation dynamics, especially when the full spectral and time-domain response are not completely recorded.

However, even with complete spectrally and time-resolved measurements, it can remain challenging to unravel the details of the dynamics, as a result of the intermixing of the different relaxation pathways. One way to simplify the vibrational relaxation pathways is to study isotopically diluted water. Isotopic dilution of water can exclude the contribution of the energy splitting of the two identical O–H groups, the Fermi resonance, and the intermolecular coupling, differentiating the spectra of the O–H stretch modes at the water–air and isotopically diluted water–air interface.^8,62,63 This allows us to determine if the two peaks in the hydrogen-bonded water region are from two different types of water or two coupled vibrational modes.^11,64 Transitioning from H₂O to HDO can also be used to differentiate between relaxation pathways. An HDO molecule does not have the same intramolecular coupling inherent to a H₂O molecule due to a lack of degeneracy between the O–H and O–D stretching modes with the bending overtone. Thus, specific IVR pathways are eliminated from the relaxation scheme and the relaxation time of other processes, such as reorientation, can be measured.

It should be noted that differences in the vibrational dynamics of bulk H₂O and D₂O have been reported, beyond the anticipated longer vibrational lifetimes for heavy water. 2D IR spectroscopy results suggest the molecular vibrations in D₂O are more localized than those in H₂O.⁴⁷ A recent study discovered that nuclear quantum effects influence the reorientation and hydrogen-bond dynamics for H₂O but are negligible in D₂O.⁶⁵ The differences in the vibrational dynamics of D₂O and H₂O should be accounted for in the interpretation of time-resolved experiments.

A summary of the three main physical phenomena accessible using time-resolved SFG is listed in Table 1. While each experiment explores important observations and chemical dynamics, the focus of this Feature Article is on the structural heterogeneity of interfacial water. Thus, we concentrate on IVR and the change of vibrational relaxation lifetimes with respect to the excitation frequency. As mentioned previously, the T₁ lifetimes are convoluted with other relaxation dynamics, and thus, we discuss the bleach decay lifetime. The conversation begins by exploring the water–air interface (section 3.1). Subsequently, we explore inhomogeneous water structures at various interfaces, including biologically relevant surfaces (section 3.2) and solid surfaces (section 3.3).

Table 1. List of the TR-SFG Experiments Discussed Here, the Data Obtained, and the Overall Significance of the Observations.

phenomenon	experiment	observation	relevance
intramolecular vibrational relaxation (IVR)	one-color pump–probe	bleach lifetime τ, reflecting vibrational relaxation (lifetime T1)	rate and mechanism of energy dissipation
IVR and reorientation	polarization controlled pump–probe	polarization-dependent bleach signal, reflecting anisotropy decay	rotational dynamics
spectral diffusion	two-color pump–probe and 2D SFG	time-dependent 2-D response reflecting frequency–frequency correlation function	structure fluctuations/structural reorganization
			intra/intermolecular coupling
			Förster energy transfer

3. Discussion

3.1. Water/Air Interface

The static IR absorption spectrum of bulk water is composed of a broad band. Likewise, the static SFG spectrum at the water–air interface contains a comparably broad band in addition to a sharp peak at 3700 cm^–1.^66,67 For the Imχ⁽²⁾ spectra, the sign of the signal, negative or positive, provides details about the absolute orientation of the interfacial water molecules. A negative peak, centered at 3450 cm^–1, reveals that the hydrogen atoms of the H-bonded water O–H groups are pointing toward the bulk (down). Conversely, a positive peak, centered at 3700 cm^–1, corresponds to free O–H groups oriented with hydrogen atoms directed toward the surface (up). It should be noted that a positive peak at lower frequencies was revealed in many phase-resolved SFG spectra.^8,62,66,68 However, a recent study determined there is no positive peak at or below 3100 cm^–1 and an apparent resonance appeared due to phase inaccuracy in measurements.^67,69 This is also confirmed by ab initio MD simulations⁷⁰⁻⁷² as well as force field MD simulations.^73,74 Regardless, the static phase-resolved SFG spectra of the water/air interface already reveal different structures of interfacial water when comparing the 3450 and 3700 cm^–1 vibrational modes.

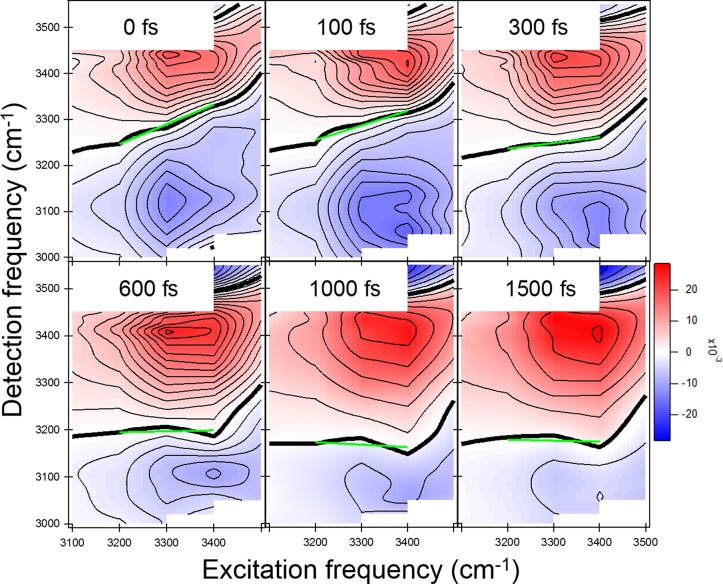
The heterodyne-detected 2D SFG (HD-2D-SFG) response of the surface of pure H₂O is depicted in Figure 3. With HD-2D-SFG, two peaks appear in the 2-D spectrum, one for the 0–1 transition and a red-shifted 1–2 transition, as illustrated in Figure 2b. The nodal line (thick black line in Figure 3) is the line between the 0–1 peak and the 1–2 peak. The temporal evolution of the tilt of the nodal line provides a measurement for spectral diffusion.⁴² On the basis of nodal line analysis, the HD-2D-SFG spectra indicated there are two different spectral diffusion rates for water molecules at the water/air interface: one below 3400 cm^–1 and one above 3400 cm^–1 in the spectral region from 3200 to 3500 cm^–1.⁷⁵ Thus, there are at least two subensembles of water molecules in the hydrogen-bonded region. This heterogeneity cannot be captured in the phase-resolved static SFG measurements.

Figure 3.

HD-2D-SFG experimental spectrum of the water/air interface. The thick black line represents the nodal line, and the green line represents a linear fit to the nodal line slope for excitation frequencies in the spectral range 3200–3400 cm^–1. Reprinted with permission from ref (75). Copyright 2014 John Wiley and Sons.

The next question that presents itself is how heterogeneous are the hydrogen bonds of interfacial water molecules. This question can be answered by extracting vibrational lifetimes from time-resolved experiments due to the correlation between vibrational lifetime and hydrogen-bond strength.⁷⁶ Discrepancies exist in the literature as to whether or not the lifetime of the O–H stretch is frequency-dependent. Some studies at the water/air interface revealed no frequency dependence to the IVR in the spectral region from 3100 to 3500 cm^–1.⁷⁷⁻⁷⁹ However, other studies illustrated the relaxation time of bulk water and interfacial water is dependent on frequency. The discrepancies have been attributed in part due to the effects from different excitation pulse powers.⁷⁹ Furthermore, the extent of the blue shift in the spectrum depended upon the excitation frequency.

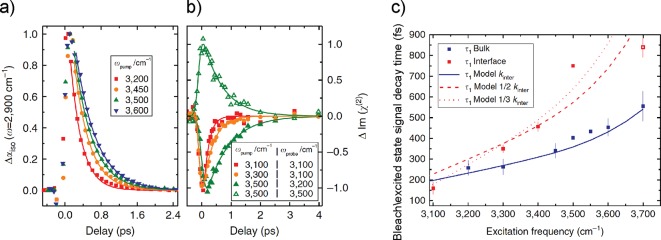
We have recently reported results of experiments to determine the vibrational lifetimes of bulk and interfacial water measured with ultrafast vibrational spectroscopic techniques. The data are reproduced in Figure 4a and b.⁶⁶ For the bulk experiments, the excitation pulses ranged from 3200 to 3700 cm^–1 and the frequency of the probe pulse was centered at the 1–2 transition at 2900 cm^–1. For the data shown in Figure 4a, the heat has been subtracted from the data and single exponential fits were applied to extract the τ₁ lifetimes. A similar approach was applied for the TR-SFG experiments. The pump and probe frequencies were specifically chosen to eliminate heat contributions, allowing only the bleach decay to be observed with no effect from a heated ground state. A four-level model was used to fit the data (see Figure 2c). The thermalization equilibrium time, τ_eq, was fixed at 550 fs.

Figure 4.

Time evolution plots of (a) infrared pump–probe experiment for bulk water with different excitation frequencies and detected at 2900 cm^–1 and (b) SFG for the air/water interface with different excitation and probe frequencies. (c) Experimental relaxation times of bulk (blue) and interfacial water (red) with model calculations accounting for spectral diffusion from energy transfer, summarized in Figure 5. The dashed and dotted lines are for, respectively, relaxation rates calculated with intermolecular energy transfer rates amounting to ¹/₂ and ¹/₃ of bulk rates, to account for the reduced water density at the interface. Reprinted with permission from ref (66). Copyright 2015 Nature Publishing Group.

The inferred bulk and interfacial water bleach decay time constants are shown in Figure 4c. The results illustrate a variation of vibrational decay time with the excitation frequency over the spectral range from 3100 to 3700 cm^–1 for both bulk and interfacial water. The bulk vibrational lifetimes increase from 250 to 550 fs with excitation frequencies increasing from 3300 to 3700 cm^–1. The change in vibrational lifetime with respect to excitation frequency is even more pronounced at the interface across the same 3300–3700 cm^–1 frequency range, varying from 350 to 750 fs for hydrogen-bonded O–H groups. Figure 4c shows a strong frequency dependence of the bleach relaxation and thus indicates water in both the bulk and at the interface is heterogeneous.

Figure 4c clearly illustrates a trend of increasing vibrational decay time with increasing frequency, but the question is why τ varies. The free O–H vibration differs from the hydrogen-bonded O–H groups, since the rate of energy dissipation is correlated to the number of coordinated water molecules.⁴⁶ Fewer water molecules in the inner hydration shell lead to slower energy relaxation. Thus, a free O–H vibration has slower energy relaxation than an O–H oscillator in the hydrogen-bond network. Within the broad hydrogen-bonded O–H region, faster vibrational decay at lower frequencies has been attributed to the increasing proximity, with decreasing frequency, to the transition frequency of the bend overtone. In H₂O, the bend overtone frequency is around 3240 cm^–1.⁸⁰ The O–H stretch vibrations transfer their excess energy to the bend mode, as illustrated in Figure 5. When the O–H modes overlap with the bend overtone, there is direct energy transfer. The other oscillators (Lorentzians in pink) transfer energy via Förster transfer or change in the hydrogen-bond strength. As such, the efficiency of the energy transfer from the O–H stretch mode to the HOH bending mode depends on the integral overlap, illustrated in the shaded pink regions. Therefore, oscillators with frequencies that overlap more with the bend overtone are expected to exhibit faster vibrational energy relaxation.

Figure 5.

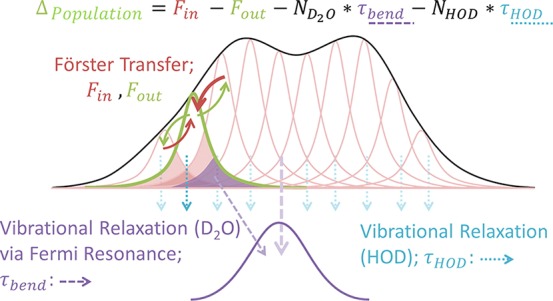
Schematic of vibrational energy relaxation. Near-resonant vibrational Förster energy transfer between different O–H (or in this case O–D) groups with slightly different frequencies gives rise to spectral diffusion within the inhomogeneously broadened absorption band. The rate of energy transfer is given by the spectral overlap (pink areas). The bend overtone spectrum is shown schematically in purple below. For OD groups that overlap spectrally with the bend overtone (purple areas), coupling to that bend overtone allows for vibrational relaxation to occur. Reprinted with permission from ref (81). Copyright 2016 American Chemical Society.

3.2. Water–Biosurface

One might imagine that the water structure at the interface could change if molecules are absorbed on water. Biomolecules add an additional level of complexity to the water–air interface; the measured interface is water in contact with lipids or surfactants at the air interface, as overviewed below. One reason for the increased complexity of these systems is the addition of charged molecules to the surface. The surface charge can induce an electric field, which not only aligns water but also gives rise to a contribution to the SFG intensity from a possible χ⁽³⁾ contribution.^82,83 The additional signal source can affect the effective probing depth.

Using phase-resolved SFG measurements, it can readily be shown that the water in contact with positively and negatively charged lipids/surfactants has opposite net orientation; i.e., the spectral features have opposite signs (Figure 6). The static phase-resolved spectra of positively charged lipids in aqueous solution reveal negative spectral features in the region from 3100 to 3500 cm^–1, indicating the O–H groups of the water molecules are on average aligned with their hydrogens pointing toward the bulk.^84,85 On the basis of the phase-resolved spectra, water in contact with positively charged lipids at the air interface aligns in a similar fashion as water at the water–air interface for the hydrogen-bonded O–H groups. The water at the negatively charged biomolecule surface is oriented with the hydrogens of the O–H modes pointing on average toward the air (up).⁸⁶

Figure 6.

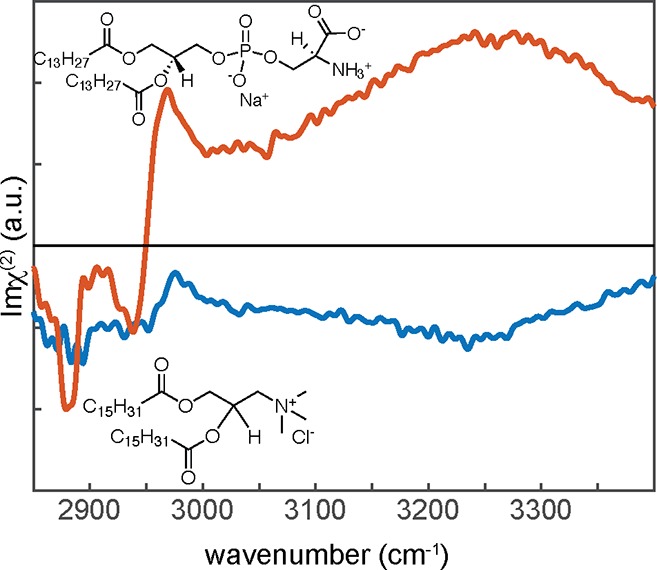
Phase-resolved SFG spectra in the O–H stretch region for positively charged DPTAP (blue) and negatively charged DMPS (red) lipids/surfactant interfaces. Adapted with permission from ref (84). Copyright 2011 American Chemical Society.

A fundamental question is whether such an ordered structure of water near positively and negatively charged surfaces affects the heterogeneity of the interfacial water. In order to investigate the structural heterogeneity of the water in contact with differently charged biosurfaces, we review the TR-SFG results.

3.2.1. Positively Charged Lipid/Surfactant Interface

Positively charged lipids/surfactant, such as DPTAP and CTAB, have been studied with homodyne- and heterodyne-detected TR-SFG spectroscopies.^{34,81,86−88} Homodyne-detected TR-SFG measurements for isotopically diluted water as well as the neat D₂O in contact with DPTAP were completed, and the τ₁ values were measured. These are plotted with respect to the infrared frequency for three DPTAP samples with different isotopic dilutions of HOD in H₂O, illustrated in Figure 7. The bleach recovery times for all samples vary with respect to frequency, which again demonstrates the heterogeneity of interfacial water in contact with a positively charged lipid.

Figure 7.

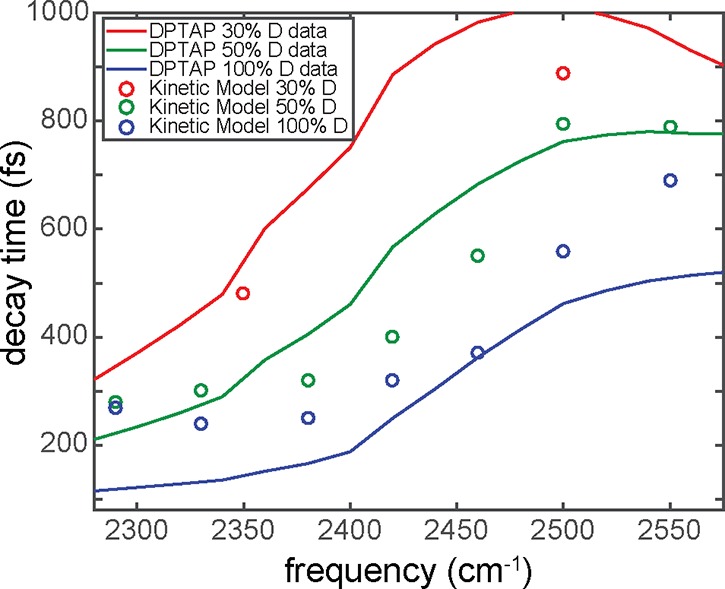
Plot of the τ₁ decay versus excitation frequency of DPTAP in different isotopic dilutions of water. The results were modeled (solid lines), with the model depicted in Figure 5, with energy transfer rates given by the concentration of O–D groups. Adapted with permission from ref (81). Copyright 2016 American Chemical Society.

This time-resolved data for water in contact with DPTAP could be described with a four-level system (Figure 2c) in a similar manner to the time-resolved data at the water/air interface.⁶⁶ Since D₂O was used in this study, the relaxation time scale from the intermediate state to the heated ground state, τ_eq, was set to 700 fs,⁸⁹ instead of 550 fs used for pure H₂O. The frequency-dependent lifetimes were modeled with a kinetic model. The model (depicted in Figure 5) incorporates Förster energy transfer and vibrational relaxation through the bend overtone.⁶⁶ The results of the kinetic model are represented by the solid lines in Figure 7 and also illustrate the frequency dependence of the bleach decay lifetimes. Isotopic dilution experiments were also performed to test the robustness of the model. Isotopically diluted water changes the static SFG spectra, since the overlap of the bending overtone and OH stretch mode is missing and the intra/intermolecular couplings are absent. This missing overlap of the bending overtone and OH stretch mode critically affects the τ₁ values, where the vibrational relaxation times are elongated for isotopic diluted systems.

In this study, a change in the vibrational relaxation decay with frequency, i.e., structural heterogeneity, was observed. Since the lifetime versus frequency can be modeled with the same model as the water–air interface, the results imply that water at a positively charged lipid monolayer/air interface behaves in a similar manner to bulk water.

3.2.2. Negatively Charged Lipid/Surfactant Interfaces

We have seen that positively charged biointerfaces behave in a manner similar to bulk water based on TR-SFG experiments, but what about negatively charged lipid/surfactants? The phase-resolved spectra for positive and negative biomolecules reveal different net orientations of the water molecules, yet the spectra do not provide information on the heterogeneity within each system. How does the heterogeneity of water in contact with a positive biomolecule differ from water in contact with a negative biomolecule?

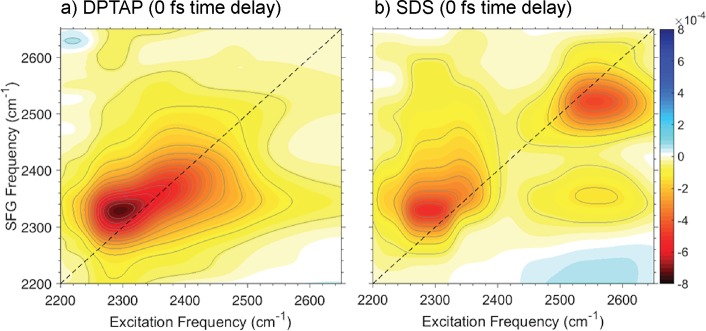
The answer can be obtained from 2D SFG spectra such as those shown in Figure 8. There is one elongated feature along the diagonal in the 2D SFG spectrum of water at the DPTAP/air interface (Figure 8a). For water at the SDS/air interface, there are two distinct peaks, indicating two subsets of O–H groups (Figure 8b). Additionally, cross-peaks are not observed for the positive lipids or the water/air interface yet clearly visible for the negative surfactant. The cross-peaks reveal that there are two coupled ensembles of water.

Figure 8.

2D SFG spectra in the O–D stretch spectral region of water underneath monolayers of (a) positively charged DPTAP and (b) negatively charged SDS in D₂O at 0 fs time delay. The 2D SFG spectrum of DPTAP reveals one elongated feature along the diagonal, whereas the 2D SFG spectrum of SFG has two separate peaks along the diagonal. Adapted with permission from refs (81) and (89), respectively. Copyright 2016 and 2015 American Chemical Society.

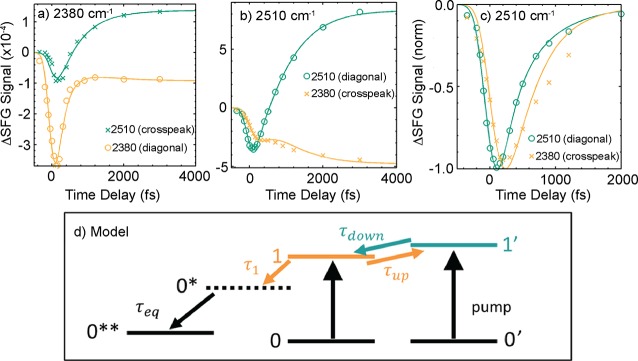
The two types of water at the SDS/water interface were probed with excitation pulses centered at 2380 and 2510 cm^–1, and the time evolution plots are shown in Figure 9. The traces cannot be fit with the four-level model described previously, since there are two types of water. A slightly more complex model, shown in Figure 9d, is used to incorporate two different ground states and two different vibrational excited states. Excess vibrational energy can be transferred between the two vibrational excited states, ν = 1 and ν = 1*. The authors concluded that energy transfer with time scales τ_down from the higher frequency O–D stretch mode to the lower frequency O–D stretch mode is a major relaxation pathway for the higher frequency mode. In contrast, energy transfer from the lower frequency O–D stretch mode to the higher frequency mode is less favorable, in accordance with Boltzmann’s law. Furthermore, converting the vibrational quanta delocalized over several chromophores to a localized mode can only occur at the cost of an entropic penalty.⁸⁹ The vibrationally excited O–D group relaxes through an intermediate state to a hot ground state, similar to the four-level model. On the basis of the fits, the time scales of the bleach relaxation were found to vary with excitation frequency. Again, the frequency-dependent variations in the vibrational relaxation dynamics expose the structural heterogeneity of water in contact with a negatively charged surfactant.

Figure 9.

SDS/water interface showing different vibrational relaxation dynamics when the excitation pulse is centered at (a) 2380 cm^–1 and (b) 2510 cm^–1. The spectra shown in part c are obtained from heat-correcting and normalizing the spectra from part b, with excitation pulses centered at 2510 cm^–1. The experiments were performed in 100% D₂O. Lines in panels a–c are the results of model calculations using the model shown in part d, which shows the energy levels used to describe the SDS/water interface. Reprinted with permission from ref (89). Copyright 2015 American Chemical Society.

In conclusion, the dynamics of interfacial water at a positive lipid/air interface resembles the dynamics of bulk-like water and water at the water/air interface, while there are two types of water in contact with negative surfactant molecules, as evident from the 2D SFG and TR-SFG results. The TR-SFG results showed both positively and negatively charged surfactant-covered interfaces exhibit structural heterogeneity of the water molecules on the basis of the frequency dependency of the bleach lifetimes.

Having established the molecular level insight into the interfacial dynamics near positively/negatively charged lipids and surfactants, current studies focus on more complex biointerfaces. One focus is on the water dynamics near the zwitterionic lipid/water interfaces; the structure and dynamics of water near a zwitterionic lipid⁹⁰⁻⁹³ can be similar to the structure and dynamics of water near a mixed positively/negatively charged lipid monolayer.⁴⁴ This can be accessed using 2D SFG and TR-SFG spectroscopy.^94,95 These results help shed light on the structure of water in contact with biosurfaces containing both cationic and anionic groups, a complex system that is a major component of biological membranes.

3.3. Water–Silica

The dynamics of water in contact with mineral surfaces plays a role in a broad range of processes, including chemical weathering and radioactive nuclear waste storage.⁹⁶ Thus, elucidating the dynamics of water in contact with mineral substrates, in particular, metal oxides, is essential and has also been probed with TR-SFG spectroscopy. The inhomogeneity of water and the effects of surface charge on the dynamics of interfacial water were studied with aqueous solutions in contact with solid substrates. In fact, McGuire and Shen⁶⁰ completed the very first femtosecond TR-SFG experiments on the water–silica interface. The system studied was silica in contact with H₂O at pH 5.7. The data was fit to a biexponential decay, with 300 fs for the bleach relaxation and 700 fs for the thermalization time constant. There was no frequency dependence observed for τ₁ when excited with 3200 and 3400 cm^–1 excitation pulses.

Further experiments, by the Borguet group, explored the vibrational dynamics of the silica/water interface at different pHs for pure water and isotopically diluted water.^58,59 For the pure water experiments,⁵⁸ the time evolution plots were fit to a four-level model, as described in Figure 2c. For the isotopically diluted experiments,⁵⁹ the time-resolved evolution plots were fit to single exponentials to extract the bleach lifetimes. Isotopically diluted water time-resolved experiments have shown that the temperature increase following vibrational relaxation is negligible and, thus, a three-level model suffices.^24,97 The lower pH solutions revealed slower dynamics than the higher pH samples, as illustrated in Figure 10. Moreover, the vibrational relaxation time scales drastically differ with excitation frequency for both negative (pH 12) and neutral (pH 2) silica surfaces. The dashed lines are from a theoretical model that correlates the intramolecular vibrational relaxation with the hydrogen-bond strength of O–H stretch vibration, i.e., the O–H stretch frequency.⁷⁶ This model was first introduced to describe frequency-dependent vibrational lifetimes obtained from SFG experiments on water underneath lipid monolayers.⁹⁸ The experimental and theoretical data are in good agreement and illustrate the inhomogeneity of water at the silica–water interface, seen for both pH 2 and pH 12. Similar to the water–air interface, the bleach relaxation lifetimes increase as a function of excitation frequency.

Figure 10.

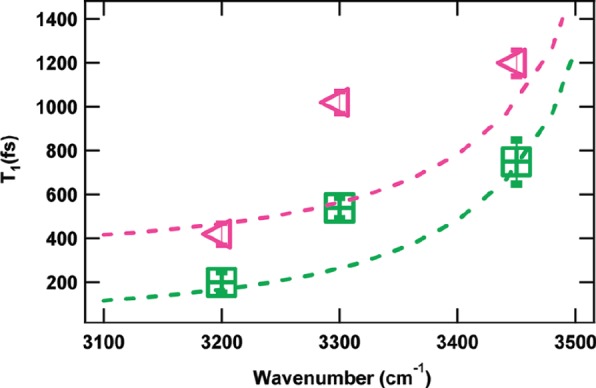
Vibrational dynamics of the O–H stretch mode at the HDO/silica interface at pH 12 (green squares) and pH 2 (pink triangles). The dashed lines represent the fit based on a theoretical model. The vibrational relaxation lifetimes in the plot do not take into account reorientation or spectral diffusion and, thus, are referred to as bleach relaxation lifetimes in this review. Reprinted with permission from ref (58). Copyright 2010 American Chemical Society.

4. Conclusion and Future Directions

TR-SFG spectroscopy provides a means to measure the vibrational dynamics of aqueous interfaces. As highlighted here, the obtained bleach relaxation lifetimes can serve as a probe for structural heterogeneity of interfacial water. The newly developed tools that have enabled these measurements have so far been applied to reveal the heterogeneity of water at relatively simple interfaces, yet there is no fundamental impediment to studying water at more complex interfaces that are relevant for important technologies. In many of these technologies, the same questions appear relevant: How is water arranged at extended surfaces? What is the role of surface charge on that arrangement? How, and to what extent, do counterions screen that charge? These are central questions in membrane biophysics, electrochemistry, and electrocatalysis, and are equally relevant for water at mineral surfaces in atmospheric systems as well as water at the surface of photocatalysts. While many continuum models exist to describe water at (charged) interfaces, in which water is represented as a dielectric continuum,⁹⁹ insights into the molecular-level details of the water arrangement are crucial to eventually predict reactivity (electrochemistry, electrocatalysis, atmospheric processes) and transport (biomembranes, lining fluids) at, and across, the interface, respectively. The potential of TR-SFG spectroscopy is nicely illustrated by a recent study of the partially hydrated electrons at the air/water and air/indole solution interface utilizing TR-SFG spectroscopy.¹⁰⁰ The samples were excited with UV-excitation and probed with TR-SFG spectroscopy to understand the structure of the surrounding water molecules and “follow” the dynamics of the partially hydrated electron. Further understanding of hydrated electrons can provide insight into electron-driven processes on water surfaces. In the same way that TR-infrared spectroscopy on bulk aqueous systems has led to breakthroughs in our understanding of those systems,^52,101,102 TR-SFG spectroscopy on aqueous surfaces is expected to lead to breakthroughs in our understanding of interfacial water.

Biographies

Jenée D. Cyran received her B.S. degree from Allegheny College in Pennsylvania, USA. She earned her Ph.D. in 2015 from Colorado State University in the group of Amber Krummel. She is currently an Alexander von Humboldt postdoctoral fellow in the Molecular Spectroscopy Department at the Max Planck Institute for Polymer Research (MPIP).

Ellen H. G. Backus is leading the “Water at Interfaces” group in the Molecular Spectroscopy Department at the Max Planck Institute for Polymer Research (MPIP) in Mainz, Germany. Her research focusses on the structure and dynamics of water at various interfaces and is supported by a Minerva Grant from the Max Planck Society and an ERC Starting Grant. She obtained her Ph.D. in 2005 from Leiden University in the group of Mischa Bonn and Aart Kleyn. After a postdoctoral stay at the University of Zurich with Peter Hamm and an independent postdoctoral position in the group of Huib Bakker at AMOLF in Amsterdam, she moved in 2012 to Mainz.

Yuki Nagata is a group leader at the Max Planck Institute for Polymer Research (MPIP), Mainz, Germany, and works on the molecular dynamics simulation of surface-specific vibrational spectroscopy at the aqueous interfaces. He received his Ph.D. from Kyoto University, Japan, under the supervision of Professor Yoshitaka Tanimura. After a research position at BASF Ludwigshafen, Germany, and a postdoctoral stay in Professor Shaul Mukamel’s group, University of California, Irvine, USA, he joined the MPIP. His main research interests are the interfacial water and theory of vibrational surface spectroscopy.

Mischa Bonn is a director at the Max Planck Institute for Polymer Research (MPIP), Mainz, Germany. He works on label-free (ultrafast) vibrational spectroscopy and microscopy of biomolecular systems and water in such systems. He received his Ph.D. in 1996 from the University of Eindhoven for research performed at AMOLF in Amsterdam. After postdoctoral research at the Fritz Haber Institute in Berlin and Columbia University in New York, he worked at Leiden University from 1999 as an assistant then associate professor. In 2004, he became a group leader at AMOLF. In 2011, he joined the MPIP. His research interests are the structure and dynamics of molecules at interfaces and electron transfer across interfaces.

The authors declare no competing financial interest.