Abstract
The spleen selectively removes cells with intracellular inclusions, for example, detached nuclear fragments in circulating erythrocytes, called Howell–Jolly Bodies (HJBs). With absent or deficient splenic function HJBs appear in the peripheral blood and can be used as a simple and non‐invasive risk‐indicator for fulminant potentially life‐threatening infection after spleenectomy. However, it is still under debate whether counting of the rare HJBs is a reliable measure of splenic function. Investigating HJBs in premature erythrocytes from patients during radioiodine therapy gives about 10 thousand times higher HJB counts than in blood smears. However, we show that there is still the risk of false‐positive results by unspecific nuclear remnants in the prepared samples that do not originate from HJBs, but from cell debris residing above or below the cell. Therefore, we present a method to improve accuracy of image‐based tests that can be performed even in non‐specialized medical institutions. We show how to selectively label HJB‐like clusters in human blood samples and how to only count those that are undoubtedly inside the cell. We found a “critical distance” d crit referring to a relative HJB‐Cell distance that true HJBs do not exceed. To rule out false‐positive counts we present a simple inside‐outside‐rule based on d crit—a robust threshold that can be easily assessed by combining conventional 2D imaging and straight‐forward image analysis. Besides data based on fluorescence imaging, simulations of randomly distributed HJB‐like objects on realistically modelled cell objects demonstrate the risk and impact of biased counting in conventional analysis. © 2017 The Authors. Cytometry Part A published by Wiley Periodicals, Inc. on behalf of ISAC.
Keywords: fluorescence imaging, splenic function, Jolly bodies, image analysis
Introduction
The spleen as the largest lymphoid organ in humans, filters bacteria, and damaged red blood cells from the blood stream, and is considered to play an important role in fighting infections 1, 2, 3, 4. Even minor infection can potentially develop into a life‐threatening infection for a patient who lost the spleen 2, 5 by injury, underlying medical conditions like thrombocytopenia, or cancer to name a few. Besides administering prophylactic antibiotics and vaccinations 6 asplenic and hyposplenic patients with no or diminished splenic function should be monitored on a regular base to avoid post‐splenectomy infections which can be fatal 2. Therefore, simple, robust, and reliable assays and methods are required to maximize such patients' life expectancy.
In the last century nuclear imaging modalities such as spleen scintigraphy were widely used to determine splenic function, however, with the disadvantage of being invasive and time‐consuming 7, 8. Other methods determine the immunological function of the spleen by correlating the splenic volume and spleen dependant functional B cell subsets 7.
Suitable indicators for an elevated infection risk after splenectomy are pitted erythrocytes 9, 10 or Howell Jolly Bodies (HJBs) 11. Both can be used for scoring splenic function in an imaging or spectroscopic approach 2, 8, the latter only for asplenia as its sensitivity has been disputed and most likely insufficient to quantify mild forms of hyposplenism 12, 13. Pits are characteristic depressions on erythrocyte membranes arising from a specific membrane defect, which impairs the formation of the vacuoles and finally leads to the appearance of pitted erythrocytes 9, 10. HJBs are named after the researchers William Howell 14 and Justin Jolly 15 who observed nuclear remnants in circulating red blood cells already in the late 19th and early 20th century and related these observations particularly to the impaired function of the spleen 10. Today, we know that these nuclear remnants accumulate in splenectomized humans where the spleen cannot clear the blood from micronucleated erythrocytes 16. Generally, a reliable detection or scoring based on these occurrences is often challenging. Counting pitted erythrocytes is the more sensitive method to rate even different degrees of splenic dysfunction, however it requires specialized microscopes equipped with Nomarski optics 17. An HJB‐based scoring is less sensitive for detecting different degrees 2 as the HJBs are rare so that the absence of HJB is not indicative of normal functioning splenic tissue 18, however, the presence of HJBs is indicative for a loss of splenic function and an elevated risk of infection 17, 18. Furthermore, HJB detection is possible by conventional wide‐field (fluorescence) microscopes, which makes the HJB or related micronuclei methods widely used. Besides imaging there are other techniques to detect HJB‐like micronuclei based on flow cytometry based scoring 18, 19, 20, 21, 22, 23. These techniques typically allow measurements of large cell numbers in short time intervals. This increases precision; however, not necessarily accuracy as careful validation is often difficult. Common challenges and pitfalls are insufficiently specific markers or the missing spatial information in flow cytometry and the usually neglected 3D cell geometry in imaging approaches. The pitfalls may lead to false positive or false‐negative scoring results, for example, by apoptotic cells 23 which are particularly crucial when detecting relatively rare events.
In the blood of healthy persons, HJBs are extraordinarily rare. Therefore, HJBs can only be explored if their frequency is increased by pathological events. Thus, this investigation was performed in transferrin positive reticulocytes (Tf‐Rets) from patients during radioiodine therapy. In these premature erythrocytes HJBs are 1–10 thousand times more frequent than in blood smears 21, 22, 24. Tf‐Rets arise in bone marrow when late erythroblasts extrude their nuclei and they appear in blood not before three days later. In peripheral blood not more 0.1–0.2% of all erythrocytes are still Tf‐Rets. In contrast to the biconcave mature erythrocytes Tf‐Rets are more globe‐shaped with a multilobular surface 25. About 3 days after a bone marrow exposure to about 500 mSv low dose rate in the course of a radioiodine therapy HJB‐frequency in Tf‐Rets increased from about 0.2% to up to 5% for some days.
Here, we present imaging and analysis method in such Tf‐Rets to access splenic function. As Tf‐Rets are the youngest erythrocytes in blood keeping the same stage for typically 2–5 h in healthy adults their number of spleen passages is much smaller and the frequency of HJBs in Tf‐Ret is much higher than in mature erythrocytes.
The final method is based on two‐dimensional wide‐field fluorescence imaging and a robust image analysis filter to eliminate unspecific nuclear remnants from the image analysis and prevent false‐positive results. The analysis filter accounts for the three‐dimensional shape of the sphered erythrocytes on the microscope slide, which makes the method remarkably reliable. The method is validated by three‐dimensional imaging and simulations, which allowed modeling HJBs distributions under the given experimental conditions and cell shape.
Materials and Methods
Chemicals and Other Reagents
CD71 magnetic microbeads (human, Cat. No. 130–046–201), LS columns (Cat. No 130–021–101) and MidiMax separator (Cat. 130–042–302) were purchased from Miltenyi Biotec GmbH (Bergisch‐Gladbach, Germany) and Retic‐CountTM reticulocytes whole blood control test (Cat. No. 340999) from BD Biosciences, Heidelberg, Germany. DNA stain Safe‐Green (Cat. No. G108‐P) was purchased from Applied Biological Materials, Richmond BC, Canada. DNA stain Hoechst 33258 (Cat. No. H3569) (Cat. No. D9542) as well as all chemicals not specifically mentioned here were obtained from Sigma‐Aldrich (Deisenhofen, Germany). Plasma membrane stain CellMaskTM Deep Red (Cat. No. C1004661) and mounting medium ProlongTM Gold antifade solution (Cat. No. P36930) were purchase from Thermo Fisher Scientific GmbH (Darmstadt, Germany) and polylysine slides (Cat. No. J2800AMNZ) from Gerhard Menzel B.V. & Co. KG, Braunschweig, Germany. The following buffers were used: Dulbecco's Phosphate buffered saline pH 7.4 (PBS), PBS with 0.5% bovine serum albumin (PBSA) and PBSA with 2 mM EDTA (EDTA‐PBSA).
Blood Samples
Blood samples were from radioiodine therapy patients of the Department of Nuclear Medicine, University Hospital Würzburg, Würzburg, Germany. Blood was taken by venipuncture with K3EDTA monovettes (Cat. No. 04.1917.100) from Sarstedt AG (Nümbrecht, Germany). For this study, 8 samples from 5 patients were analyzed. The study was approved by the ethical review committee of the Medical Faculty of the University of Würzburg, ref. No. 144/12. All subjects gave written informed consent prior to therapy.
Immunomagnetic Isolation of Transferrin Receptor‐Positive Reticulocytes (Tf‐Ret)
The isolation was mainly performed following the description of Sun and co‐workers 26. In brief, 0.5 mL EDTA blood was added to 14 mL 4–8°C cold EDTA‐PBSA, mixed and suspended cells were centrifuged at 300× g for 8 min. The cell pellet was re‐suspended in 0.9 mL EDTA‐PBSA, followed by addition of 10 µL anti‐CD71 magnetic beads diluted with 90 µL EDTA‐PBSA during vigorous vortexing. Cells were incubated for 20 min in an ice bath and mixed every 5 min. Cells were again washed by adding 13 mL EDTA‐PBSA. The sediment was filled up to 3 mL, 2.4 mL of which were loaded on a positive magnetic selection column LS placed in the magnetic field of a MidiMACS Separator. Shortly before, the column was prepared by washing with 6 mL EDTA‐PBSA. The transferrin receptor‐negative cells passed through the column while transferrin‐positive cells were retained. Magnetic separation was performed at room temperature. The column was twice rinsed with 3 mL EDTA‐PBSA. Then the column was removed from the separator and was rinsed with 3 mL PBSA to remove, the transferrin receptor‐positive cell fraction. Cells of the magnetic fraction were once washed with PBSA and were filled up to 200 µL.
The purity of the Tf‐Ret preparation was examined by flow cytometry (Navios, Beckman‐Coulter) with thiazol orange as reticulocyte stain (Retic‐CountTM reticulocyte kit). In the magnetic fraction 90–95% of all cells were reticulocytes the rest were erythrocytes and nucleated cells, respectively.
Fixation and Cytospin
Reticulocytes were sphered and fixed in principal as described by Abramsson‐Zetterberg et al. 24. In brief, 20 µL of cells suspended in PBS were added to 100 µL PBS containing 12 µg/mL sodium dodecyl sulfate (SDS) during careful mixing. Exactly 1 min later 0.5 mL fixative (2% paraformaldehyde in PBS with 6 µg/mL SDS) was added while vortexing. 10–20 min later fixed cell preparation was diluted with fixative up to a cell concentration of about 1 × 106 cells per mL. Cells were prepared by cytospin centrifugation (6 min, 1,200 rpm) for confocal and fluorescence microscopy (Cytospin 2, Shandon Southern Instruments, Sewickley, PA). About 0.3 × 106 cells were applied per slide
Staining
DNA was stained by Hoechst 33258 Safe‐Green and membranes by CellMaskTM Deep Red. The provided stock stain solutions (10 mg/mL for Hoechst or 5 mg/mL for CellMask) were diluted 1:1000 with PBS to prepare working solution. Staining solution (150 µL) was pipetted onto the cell spot and slides were kept in the dark for 10 min at room temperature. Then cells were rinsed three times with PBS and briefly air‐dried. Finally 10 µL mounting medium ProlongTM Gold antifade solution was given on the cells and a coverslip was placed on. Cells were imaged within 12 h.
Fluorescence Imaging
For 3D imaging, confocal imaging were performed by a Laser Scanning confocal microscope (Leica SP5, Leica Microsystems CMS GmbH, Mannheim, Germany) in two detection (color) channels (HJB‐Hoechst or HJB‐Safe‐Green and membrane‐CellMask Deep Red excitation: 405, 488, 633 nm; emission: 460–500 nm,500–550, and 670–720 nm) using an 40×/1.3 objective lens. For generation of a 3D image of erythrocytes typically 50 images (slices) per channel were acquired. The lateral (xy) stack dimensions were equal to 2,048 × 2,048 voxels with lateral (xy) and axial (z) voxel dimensions of 94.7 nm and 168 nm, respectively.
Image Deconvolution
The primary confocal data (Leica LIF‐File format) were imported to SVI Huygens deconvolution software (ver. 15.10, Scientific Volume Imaging B.V., Hilversum, The Netherlands) and deconvolved using the theoretical Point‐Spread Function (PSF) defined by objective lens, sample and acquisition parameters (Algorithm: Classic Maximum Likelihood Estimator, quality change threshold: 0.05; automatic background estimation radius: 0.7 µm, maximum number of iterations: 50 (typically converging around 10, automatic brick mode).
Image Segmentation
Deconvolved images were segmented and analyzed using Bitplane Imaris 8.1. Wherever applicable, depending on the image stack quality, all cells within a stack were segmented, total numbers and cell features were acquired. In all other cases, largest possible regions of interest were defined, and features only of cells within these boundaries were analyzed. In short, cells were segmented using a custom made pipeline involving iso‐surfaces creation, channel masking, and usage of the Imaris cell module in combination. Due to missing cell nucleus and a membrane‐only staining, cell segmentation was performed in a cascade of multiple steps for ensuring solid cell recognition and separation.
Step 1: Segmentation of the cell membranes as Iso‐surfaces (Background subtraction 0.4 µm; smoothing diameter 0.190 µm, minimum object volume set to 1,000 voxels)
Step 2: Generation of a “virtual” cell nucleus by creating a new channel that defines the central cell lumen compartments: For this, we used the iso‐surface objects of the cell membranes for duplicating and masking a new channel. The values inside the surfaces were set to 0 and values outside the surface to 250.
Step 3: Final cell segmentation with Bitplane Imaris 8.1. Cell Module to avoid over fragmentation with nucleus parameters set to the “virtual” nucleus channel (see Step 2), seed point diameter set to 2.5 µm with smoothing to 0.190 µm using an automatic intensity threshold. Minimum object volume was set to 1,000 voxels.
Step 4: Segmentation of Howell Jolly Body (HJBs) objects using the iso‐surface segmentation algorithm on the HJB‐staining channel. Smoothing was set to 0.190 µm, the threshold manually adjusted with a minimum object volume of 10 voxels.
Image Analysis
For further data analysis object position, number, size, volume, and so forth. were exported from Bitplane Imaris and analysis performed using Microsoft Excel 2013 (Microsoft Corporation, Redmond, CA), IBM SPSS Statistics 23 (IBM Corporation, Armonk, NY), Origin PRO 8.6 (OriginLab Corporation, Northampton, MA) and SigmaPlot 12 (Systat Software, San Jose, CA). Stacks of insufficient quality (saturation, fragmented membrane staining, bacteria contamination, etc.) were discarded.
For HJB distance and location determination two different methods based on either 3D or soley 2D information were compared. In 3D, we determined the largest and the second largest ellipsoid half axis of the cell with Imaris software. The mean of both values defines the average radius of the respective cell. The 2D method considered the maximum extent of the cell projected along the x‐ and y‐axis of the image stack divided by two. The mean of both half‐axis represents the average radius of the respective cell. Both methods were statistically compared during later analysis. To analyze whether a HJB was inside or outside the most proximal cell the overlap of the two objects (cell and HJB) was determined and thresholded as following: A binary channel was created by masking cell objects in Imaris (“0” outside, “1” inside the cell lumen). Within the HJB volume the mean intensity of this binary channel defined the fraction of HJB overlapping with the cell lumen, ranging from 0 (fully outside) to 1 (fully inside cell lumen).
The center‐to‐center distance between HJBs and their closest cells was determined by the centers of mass projected to the xy‐plane with normalization to the respective cell's mean radius. We calculated the projected HJB‐Cell distance (d'/r) by projecting the HJB‐Cell center‐to‐center distance (d) to the xy‐plane (d') and normalizing it to the closest cell's xy‐projected mean radius (r).
Despite deconvolution, the point spread function (PSF) may still add a bias to the HJB‐ and cell‐shape analysis. Therefore, instead of a 0/1 binary distribution HJB‐cell‐overlap values show a bimodal distribution with shifted peaks at 0.96 and 0.11 overlap when k‐means cluster analysis is performed. Finally, the resulting cluster border overlapcrit = 0.54 represents the lower HJB‐cell overlap threshold.
Distance versus overlap data distribution was fitted against a modified Gompertz model 27:
| (1) |
with coefficients: a = 0.9786, k = 10.5348, x c=0.8635.
The intersection of the data fit and the overlap border defined the threshold for maximum HJB distance and defined whether a HJB has to be considered inside or outside the most proximal cell.
Statistical Analysis
If not stated otherwise, data was depicted as mean value ± standard deviation (SD). Significance levels were set as follows: P ≥ 0.05 as not significant (n.s.); P < 0.05 as significant (*); P < 0.01 as very significant (**), and P < 0.001 as extremely significant (***).
Simulation of HJB Distributions
Cell‐ and HJB‐like objects were simulated reflecting the geometry of the imaging experiments as described above using MATLAB R2011b (The MathWorks, Natick, MA).
First, 300 non‐overlapping cells with a size of 3 µm radius were randomly placed in a planar manner (single layer, no cell‐cell overlaps) covering 200 × 200 µm. As a cell model, we used a spherical cap with same sphericity of 0.87 like analyzed cells. Sphericity ψ was calculated according to 28
| (2) |
for a known volume V P and surface A P.
For a spherical cap with radius r and height of cap h it reads:
| (3) |
Second, HJBs were simulated with a radius R of 0.32 ± 0.26 µm within same area at a height z between R (HJB situated on glass slide) and 3.46 µm + R µm (HJB situated on spherical cap) and assuming a random HJBs distribution. To address the resolution limit of the microscope a minimum radius R for HJB was assumed to be 0.2 µm.
Third, the 2D and 3D Euclidian distance d 2D were calculated as follows:
| (4) |
| (5) |
serving as key parameters with cell centers x c , y c , z c, and HJB centers x HJB , y HJB , z HJB.
All results for those key parameters are stored with 6,000 cumulative repeats for statistical relevance. Relative distance between cell and jolly body along x‐axis, y‐axis, z‐axis were calculated and normalized to the respective cell radius. Histogram plots were performed in Origin 8.6 (OriginLab Corporation, Northampton, MA). To allow for direct comparison to microscopy images, here, the center of mass determined the position of cell so that
| (6) |
with spherical cap radius R and height h derived from 29.
The cell‐HJB overlap is defined by their distance d as both overlapping spheres create two spherical caps with radius r c, height h c, radius r HJB, and height r HJB, respectively, so that
| (7) |
| (8) |
The relative overlap of a HJB with a cell is determined by V ovl /V max with
| (9) |
Results
First, the HJB distribution was assessed in 2D and 3D (see Fig. 1A). In contrast to the 2D projection, the 3D confocal measurements allow for the determination of the true volumetric cell‐overlap after reconstruction of the respective image stacks. Overall, we screened 32 image stacks and reconstructed 6,617 erythrocytes with 287.7 ± 154.45 cells per stack in average. The average cell radius was 3.02 ± 0.32 µm or 3.05 ± 0.31 µm for 3D or 2D imaging, respectively, with no significant differences (paired t test with P = 0.284). Mean cell sphericity was 0.87 ± 0.05.
Figure 1.
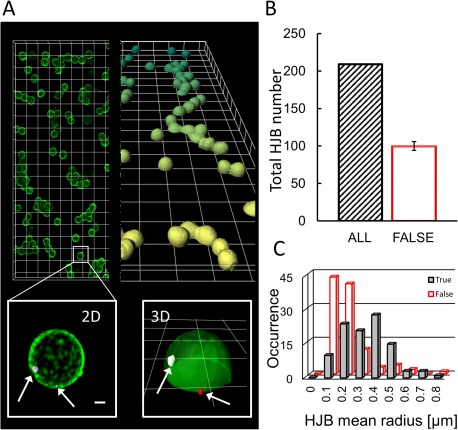
3D versus 2D image analysis reveals the number of “true” HJBs. (A) Typical overview of a of a blood smear sample containing sphered, fluorescently labeled erythrocytes ([light] green, CellMask TM Green) with magnified region of interest (lower panels) highlighting the detected DNA remnants (grey inside the cell and red outside the cell, Hoechst 33258) in a 2D Maximum intensity projection (xy) of a confocal image stack (left, scale bar = 1 µm), and a full 3D reconstruction of the same stack (right, overview grid = 10 µm, magnification grid = 5 µm); (B) The number of classified HJBs is different for 2D screening (black slashed column, n HJB=209) versus a full‐fledged 3D‐analysis (open red column) with half of the DNA stains were found (n HJB_out = 104) outside the cell representing just HJB‐like objects and thus false HJBs. (C) Size histogram plot of HJBs versus HJB‐like objects. True HJB and false HJBs show a largely overlapping size distribution.
For the 2D case (xy‐projection), we identified 209 cell‐associated HJBs (see Fig. 1B, grey bar, typical imaging example shown in Fig. 1A), 6.33 ± 4.47 HJBs per stack in average with the occurrence of 25 HJBs per 1,000 cells. The average HJB radius based on the xy‐projection was 0.32 ± 0.26 µm, the mean HJB‐cell distance (center‐to‐center) 2.22 ± 0.84 µm resulting in a relative mean distance of 0.74 ± 0.28 cell radii.
To determine the “true” HJBs defined as nuclear remnants found solely inside the cell we ran a full‐fledged 3D analysis on the identical sample and its 209 HJBs for comparison. Based on 3D confocal imaging with sufficient confocal image stacks we analyzed for each HJB its real volumetric overlap with its closest cell (voxel = 0 if HJB fully outside, voxel = 1 if fully inside). We performed k‐means cluster analysis (see “Image analysis” in the Materials and Methods Section) to quantify the bimodal data distribution with two centers at 0.91 and 0.11 overlap; a cluster border of 0.54 was set to be the lower threshold so that a HJB fulfilling or exceeding this value was considered to be inside the cell, and thus a “true” HJB. Interestingly, we found 105 true HJBs (see Fig. 1B, open red bar), the other 104 were situated outside of the cells. In other words, only half of the previously identified HJBs were true HJBs as revealed by 3D analysis.
Next, we tested whether the two HJB(‐like) populations (inside/outside) could be a priori distinguished by size, which would lead to a simple straight‐forward filter to exclude unspecific particles in a 2D‐imaging approach. The histogram plots in Figure 1C show the largely overlapping size distributions of the two populations: Even if the mean object radii is distinct (r HJB_in=0.39 ± 0.15; r HJB_out=0.25 ± 0.12; paired t test: P < 0.001), the large overlap prohibits a reliable scoring and would only give a vague tendency.
Next, we searched for spatial or “distance” cues linked to HJB‐cell overlap. Therefore, we assessed the HJB‐cell overlap subject to the normalized projected HJB‐Cell distance d'/r (see Fig. 2A) where r is the cell radius and d' the projected distance of the HJB from the cell center. Interestingly as described in Figure 2C, the overlap decreased with increasing HJB‐Cell distance d'/r (negative correlation, Spearman‐rho: r = −0.811, P < 0.01). The applied data fit (Gompertz: a = 0.98, k = 10.53, and x c=0.86) exhibited early on a plateau close to full overlap (0.98) followed by a steep drop before leveling at zero overlap. The data fit intersect the minimum HJB‐Cell overlap (y = 0.54) at x = d'/r = 0.81 = d crit. This value (d crit=0.81) represents the upper threshold for reliably scoring true HJBs when soley 2D image analysis is applied. In other words, objects located below this critical distance have to be considered true HJBs inside the cell, and HJB‐like objects located outside otherwise. With our a priori 3D knowledge of true HJBs, we tested this threshold using the xy‐projected 2D normalized distances of the very same data set. We found 103 true HJBs (located inside cells) including five false positive HJB‐like objects. The other 106 objects were found outside cells, including seven false negative objects (see Fig. 2C).
Figure 2.
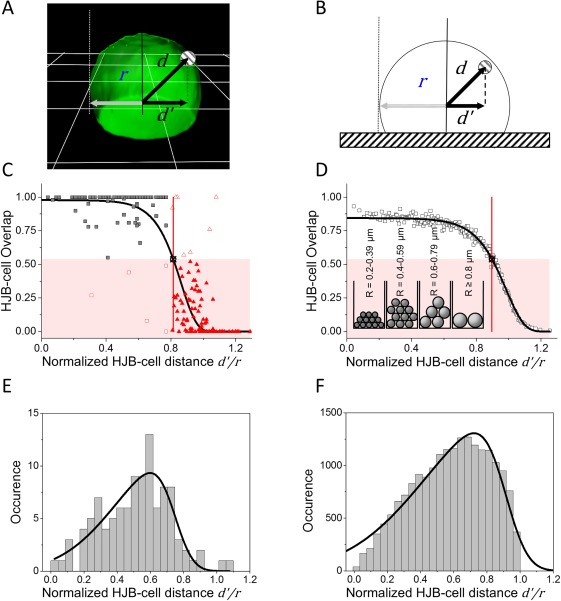
The probability to find a true HJB (inside cell) strictly depends on its projected distance to the nearest cell center (d'/r). (A) 3D‐reconstructed cell (green, grid = 5 µm). The projected HJB‐Cell center distance (d'/r) is determined by the xy projected centers of mass (d') normalized to the closest cell's ‐projected mean radius (r). (B) Scheme of computationally simulated cells. (C) Plot of the resulting normalized HJB‐cell‐overlap for the experimental data (square and triangle symbols, n total=209). Overall data distribution was fitted with a modified Gompertz model (black solid curve, parameters: a = 0.98, k = 10.53, and x c = 0.86). The highlighted area (red) indicates HJBs outside of the cell (overlap < 0.54). The intersection (black crossed circle) of the data fit with this threshold at d'/r = 0.81 = d crit defines the distance limit for true HBJs (black squares (n inside=98; n outside=111) including false positive (n = 5, open red squares) and false negative (n = 7, open red triangles) samples. (D) Overlap found for simulations of randomly distributed HJB(‐like) objects in or at cells corresponding to (C) (open black squares, n = 201; data set n total=30,065, reduced by 1:150 for plotting). Data fit against the Gompertz model in black (solid line, parameters: a = 0.84, k = 9.07, and x c=0.99). The intersection of the data fit with the threshold is located at d'/r = 0.9. Inset shows fraction (amount of spheres ×1,000) of size sorted HJB (E) Experimental and (F) simulated data distribution of HJB inside cells (overlapHJB‐cell>0.54) exhibiting a skewed normal distribution with σ = 0.34, α = −3.80, μ = 0.74, A = 4.63 for experimental data and σ = 0.47, α = −4.35, μ = 0.91, A = 873.6 for simulations.
In a following step, it was investigated whether the experimentally derived threshold could be already determined by the cell geometry when assuming a fully random distribution of HJB within cells. Thus, we simulated a virtual cell stack considering the densely packed sphered cells on the glass slide including their slightly asymmetric shape (see Fig. 2B). We also simulated randomly distributed HJBs (n HJB_total=30,065, 6,000 cumulative repeats). We plotted the HJB distribution for the simulated data (see Fig. 2D) the same way as before the experimental data (panel B). For the sake of clarity, we equally reduced plotted data points by 1:150. As expected, the experimental and simulated data distributions look similar, however the data fit intersected the HJB‐Cell overlap threshold (0.54) at d'/r = 0.90, and not at 0.81 as found for the imaging data. When further analyzing the true‐HJB data only (HJBs with ≥54% cell overlap), one notes skewed normal distributions for both simulated and experimental data when such true HJBs were plotted in a histogram in respect to normalized position within the cell. Quantitatively, however, the simulated data show a slight shift toward the cell periphery (fitpeak_exp=0.60 and fitpeak_sim=0.72, see Figs. 2E and 2F). These histograms were fitted as a normalized probability distribution function with a negative skewness according to Mathematica online documentation 30, 31:
| (10) |
with conjugated error function erfc, scale parameter σ, shape parameter α, location parameter μ, and an adaptive factor A as indicated in Figures 2E and 2F.
The reason for the difference between experimental and simulated data becomes apparent when cumulatively plotting normalized HJB 3D positions relative to the cell center of mass and indicating HJB‐cell overlap in false colors (see Fig. 3). Concerning a distribution‐overlap‐interlink within each and in between experimental and simulated data sets (see Fig. 3) we first looked at the xy‐plane. The 2D plots in Figure 3 elucidate that for both experimental and simulated data the HJB‐cell‐overlap divides into two zones: First, a central zone with the vast majority of HJBs (fully) located inside the cell; and second, an outer ring zone following the respective cell shape (d'/r ≥ 0.81 and d'/r sim ≥ 0.90) with most HJBs situated outside the cell (see Figs. 3A and 3B with histogram panels) as already indicated in Figure 2. Note, the higher density of the simulated data is due to the higher sample number that was chosen for maximal precision; the appearance of few red data points in the middle of the cell area are due to the projection plot, and refer to outside HBJ‐like objects above the cell.
Figure 3.
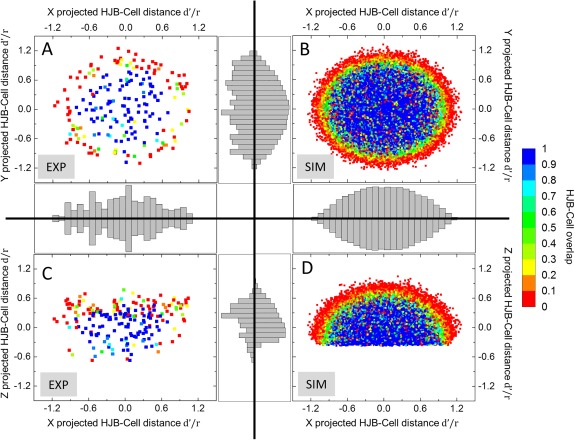
2D‐plot of HJB positions and cell‐overlap in experimental and simulated data. (A) xy‐projected HJB positions (n = 209) derived from imaging data. The HJB‐Cell‐overlap can be divided into two zones: The center area with mainly true HJBs (overlapHJB‐cell≥0.54) and the outer ring (d'/r ≥ 0.81) with mostly HJB‐like objects outside the cell (overlapHJB‐cell<0.54). (B) xy‐projection of simulated HJBs (n = 28,313) showing a similar pattern with center biased concentration of true HJBs, and an outer rim (d'/r ≥ 0.90) with predominantly false HJBs. (C) xz‐projection of imaged HJBs. False HJBs describe a clear shape‐independent bias toward the apical membrane of the cell, whereas the majority of true HJB are concentrated to the center and base of the cell. (D) xz‐projection of the simulated HJBs. In contrast to experimental data, HJBs show no bias in z with a similar distribution as observed in the xy‐projection in (B). Color‐code represents HJB‐Cell overlap from HJB fully outside to fully inside cell (0–1). Integrated histogram plots describe data distribution along respective projection axis: binning size = 0.1; experimental data occurrence scales: x = 0–22, y = 0–16, z = 0–40; simulation data occurrence scales: x = 0–2,100, y = 0–2,100, z = 0–1,500.
The situation is different when looking at the HJB‐distribution along the z‐axis (see Figs. 3C and 3D). While the simulated HJBs exhibited a comparable distribution as observed in the xy‐plane (see Fig. 3D), the experimental data show a distinct distribution with the outside HJBs exhibiting a clear shape‐independent bias toward the apical cell membrane (see Fig. 3C) with a ring‐like distribution on top of the apical membrane. Only few HJBs were situated adjacent to basal membrane of the cell close to the substrate. Note, this biased distribution could be unmasked only by 3D analysis. As a result, the experimentally determined threshold (derived from the graphs in Fig. 2C) is more accurate than the theoretically determined threshold as for the latter the bias was not obvious and thus could not been taken into account.
Discussion
Here, we show that HJB‐based scoring in sphered erythrocytes after temporary HJB increase in Tf‐Rets during radioiodine therapy is possible, however prone to false positive results, if nuclear remnants from cell debris residing outside the cells are not filtered out by image analysis. Those HJB‐like objects outside the cell represented half of all identified objects, and could not be distinguished a priori by size or shape in our study under typical experimental conditions. Typically, HJB‐screening studies are performed in 2D for simplicity and time efficiency, and therefore, lack the HJBs' in‐depth position information. To overcome this dilemma of simplicity versus accuracy, we found a reliable imaging analysis filter that operates in 2D and is related to the relative 3D position of HBJ‐like objects to the adjacent cell. We identify true HJBs with high accuracy and only minor share of false positive and false negative objects (2.39% and 3.35% respectively, derived from Fig. 2).
Generally, HJB‐based scoring has been discussed in literature as one of the most straight forward, however not the most sensitive technique, particularly for mild forms of hyposplenism. Even if sensitivity remains an issue, we show that it is possible to make the scoring significantly more reliable in monitoring asplenic patients when the relative HJB location to its adjacent cell is considered.
The method presented is simple and fast as it requires only two‐dimensional wide‐field fluorescence imaging and a robust image analysis filter to eliminate unspecific nucleotide from the image analysis and prevent false‐positive results. The presented data filter can be easily implemented in freeware software such as FIJI (see Supporting Information S1 for FIJI protocol), and should be also straight forward to be implemented in commercial automated imaging platforms 32 for micronucleus scoring. Thus, image processing and analysis can be managed with or without specialized commercial software depending on user demands. Note, the commercial software (Bitplane IMARIS 8.1) that has been used here for validating the novel method is not a requirement for the application of the method. For calibration one single 3D measurement of sphered erythrocytes is recommended, however not essential as long as the sample preparation protocol provided here is kept unchanged. Strictly spoken, no measurements would be required to determine the filter threshold when assuming fully randomized distribution of HJBs on/in cell of known shape: Such threshold could be pinpointed by solely simulations when considering cells' & HJB's realistic sizes, shapes and densities. Interestingly, when comparing experimental data with respective cell‐HJB simulations we found a different distance threshold (d crit=0.81 vs. d crit_SIM=0.90). The reason is an axial HJB distribution bias resulting in a HJB concentration gradient toward the apical cell membrane. The experimentally determined lateral HJB distribution fully matches the lateral simulation counterpart. This bias may not only be introduced by the shape of the sphered erythrocytes, but also influenced by the sample preparation and the fact that HJB(‐like) objects can easily sediment on or at the apical cell membrane. Such bias is the Achilles Heel of most 2D‐techniques that can only take assumptions from the projection of a 3D situation. Here, we show that we can easily unmask this bias and thus allow 2D images analysis to be as reliable as its 3D counterpart. The approach presented here is time efficient, and does not require complex microscopy platforms, which may be unavailable for routine work in most clinical research environments. In complex High‐Throughput‐Screening applications, the presented technique could help to increase the accuracy of the scoring without losing acquisition speed.
Supporting information
Supporting Information
Acknowledgments
Our special recognition is to the patients who generously donated blood specimens for this study. The authors thank the coworkers from our radionuclide therapy ward Dr. Malte Kircher, Dr. Constantine Lapa and Dr. Andreas Schirbel for help, as well as Prof. Dr. Andreas Buck and Dr. Udo Steigerwald for the permission to use their laboratory facilities.
Literature Cited
- 1. Bisharat N, Omari H, Lavi I, Raz R. Risk of infection and death among post‐splenectomy patients. J Infect 2001;43:182–186. [DOI] [PubMed] [Google Scholar]
- 2. de Porto AP, Lammers AJ, Bennink RJ, ten Berge IJ, Speelman P, Hoekstra JB. Assessment of splenic function. Eur J Clin Microbiol Infect Dis 2010;29:1465–1473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Singer DB. Postsplenectomy sepsis. Perspect Pediatr Pathol 1973;1:285–311. [PubMed] [Google Scholar]
- 4. Styrt B. Infection associated with asplenia: Risks, mechanisms, and prevention. Am J Med 1990;88:33N–42N. [PubMed] [Google Scholar]
- 5. Di Sabatino A, Carsetti R, Corazza GR. Post‐splenectomy and hyposplenic states. Lancet 2011;378:86–97. [DOI] [PubMed] [Google Scholar]
- 6. Davies JM, Lewis MP, Wimperis J, Rafi I, Ladhani S, Bolton‐Maggs PH. Review of guidelines for the prevention and treatment of infection in patients with an absent or dysfunctional spleen: Prepared on behalf of the British Committee for Standards in Haematology by a working party of the Haemato‐Oncology task force. Br J Haematol 2011;155:308–317. [DOI] [PubMed] [Google Scholar]
- 7. Armas R, Thukar ML, Gottschild A. A simple method for spleen imaging with 99mTc‐labeled erythrocytes. Radiology 1979;132:215–216. [DOI] [PubMed] [Google Scholar]
- 8. Gotthardt M, Bröker S, Schlieck A, Bauhofer A, Herbst B, Béhé B, Corstens FH, Behr M, Görg C. Scintigraphy with 99mTc‐labeled heat‐altered erythrocytes in diagnosing hyposplenia. Prospective comparison to 99mTc‐labeled colloids and colour‐coded duplex ultrasonography. Nuclearmedizine 2007;48:135–140. [PubMed] [Google Scholar]
- 9. Koyama S, Kihira H, Aoki S, Ohnishi H. Postsplenectomy vacuole. A new erythrocyte inclusion body. Mie Med J 1962;11:425–443. [Google Scholar]
- 10. Neilan BA, Perry JF. Persistence of vacuolated RBCs after splenectomy in adults. JAMA 1980;243:1741–1742. [PubMed] [Google Scholar]
- 11. Sears DA, Udden MM. Howell‐Jolly bodies: A brief historical review. Am J Med Sci 2012;343:407–409. [DOI] [PubMed] [Google Scholar]
- 12. Corazza GR, Ginaldi L, Zoli G, Frisoni M, Lalli G, Gasbarrini G, Quaglino D. Howell‐Jolly body counting as a measure of splenic function. A reassessment. Int J Lab Hematol 1990;12:269–275. [DOI] [PubMed] [Google Scholar]
- 13. Dhawan V, Spencer RP, Pearson HA, Sziklas JJ. Functional asplenia in the absence of circulating Howell‐Jolly bodies. Clin Nucl Med 1977;2:395–396. [Google Scholar]
- 14. Howell WH. The life‐history of the formed elements of the blood, especially the red blood corpuscles. J Morphol 1890;4:57–116. [Google Scholar]
- 15. Jolly MJ. Recherches sur la formation des globules rouges des mammiferes. Arch d'anatomie Microsc 1907;9:133–314. [Google Scholar]
- 16. Felka T, Lemke J, Lemke C, Michel S, Liehr T, Claussen U. DNA degradation during maturation of erythrocytes' molecular cytogenetic characterization of Howell‐Jolly bodies. Cytogenet Genome Res 2007;119:2–8. [DOI] [PubMed] [Google Scholar]
- 17. Kirkineska L, Perifanis V, Vasiliadis T. Functional hyposplenism. Hippokratia 2014;18:7–11. [PMC free article] [PubMed] [Google Scholar]
- 18. Lammers AJ, de Porto AP, Bennink RJ, van Leeuwen EM, Biemond BJ, Goslings JC, van Marle J, ten Berge IJ, Speelman P, Hoekstra JB. Hyposplenism: comparison of different methods for determining splenic function. Am J Hematol 2012;87:484–489. [DOI] [PubMed] [Google Scholar]
- 19. Harrod VL, Howard TA, Zimmerman SA, Dertinger SD, Ware RE. Quantitative analysis of Howell‐Jolly bodies in children with sickle cell disease. Exp Hematol 2007;35:179–183. [DOI] [PubMed] [Google Scholar]
- 20. Nüsse M, Kramer J. Flow cytometric analysis of micronuclei found in cells after irradiation. Cytometry Part A 1984;5A:20–25. [DOI] [PubMed] [Google Scholar]
- 21. Gravé J, Biko J, Lorenz R, Reiners C, Stopper H, Vershenya S, Vukicevic V, Hempel K. Evaluation of the reticulocyte micronucleus assay in patients treated with radioiodine for thyroid cancer. Mutat Res 2005; 583:12–25. [DOI] [PubMed] [Google Scholar]
- 22. Stopper H, Hempel K, Reiners C, Vershenya S, Lorenz R, Vukicevic V, Heidland A, Grawe J. Pilot study for comparison of reticulocyte‐micronuclei with lymphocyte‐micronuclei in human biomonitoring. Toxicol Lett 2005;156:351–360. [DOI] [PubMed] [Google Scholar]
- 23. Nüsse M, Marx K. Flow cytometric analysis of micronuclei in cell cultures and human lymphocytes: Advantages and disadvantages. Mutat Res/Genet Toxicol Environ Mutagen 1997;392:109–115. [DOI] [PubMed] [Google Scholar]
- 24. Abramsson‐Zetterberg L, Zetterberg G, Bergqvist M, Grawé J. Human cytogenetic biomonitoring using flow‐cytometric analysis of micronuclei in transferrin‐positive immature peripheral blood reticulocytes. Environ Mol Mutagen 2000;36:22–31. [DOI] [PubMed] [Google Scholar]
- 25. Malleret B, Xu F, Mohandas N, Suwanarusk R, Chu C, Leite JA, Low K, Turner C, Sriprawat K, Zhang R. Significant biochemical, biophysical and metabolic diversity in circulating human cord blood reticulocytes. PLoS One 2013;8:e76062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Sun PL, Li Zhi D, Liu ZM, Yang LJ, Liu JY, Cao J. Analysis of micronuclei in the transferrin‐receptor positive reticulocytes from peripheral blood of nasopharyngeal cancer patients undergoing radiotherapy by a single‐laser flow cytometer. J Radiat Res 2005;46:25–35. [DOI] [PubMed] [Google Scholar]
- 27. Gompertz B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos Trans R Soc London 1825;115:513–583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Wadell H. Volume, shape, and roundness of quartz particles. J Geol 1935;43:250–280. [Google Scholar]
- 29. Harris JW, Stocker H. Handbook of Mathematics and Computational Science. Springer Science & Business Media; 1998. [Google Scholar]
- 30. O'Hagan A, Leonard T. Bayes estimation subject to uncertainty about parameter constraints. Biometrika 1976;63:201–203. [Google Scholar]
- 31. Wolfram S. SkewNormalDistribution—Wolfram Language Documentation. 2016. Available at: https://reference.wolfram.com/language/ref/SkewNormalDistribution.html (accessed on December 9, 2016).
- 32. Rossnerova A, Spatova M, Schunck C, Sram RJ. Automated scoring of lymphocyte micronuclei by the MetaSystems Metafer image cytometry system and its application in studies of human mutagen sensitivity and biodosimetry of genotoxin exposure. Mutagenesis 2011;26:169–175. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information


