The actin filament twist changes abruptly at boundaries between bare and cofilin-decorated segments

Abstract

Cofilin/ADF proteins are actin-remodeling proteins, essential for actin disassembly in various cellular processes, including cell division, intracellular transport, and motility. Cofilins bind actin filaments cooperatively and sever them preferentially at boundaries between bare and cofilin-decorated (cofilactin) segments. The cooperative binding to actin has been proposed to originate from conformational changes that propagate allosterically from clusters of bound cofilin to bare actin segments. Estimates of the lengths over which these cooperative conformational changes propagate vary dramatically, ranging from 2 to >100 subunits. Here, we present a general, structure-based method for detecting from cryo-EM micrographs small variations in filament geometry (i.e. twist) with single-subunit precision. How these variations correlate with regulatory protein occupancy reveals how far allosteric, conformational changes propagate along filaments. We used this method to determine the effects of cofilin on the actin filament twist. Our results indicate that cofilin-induced changes in filament twist propagate only 1–2 subunits from the boundary into the bare actin segment, independently of the boundary polarity (i.e. irrespective of whether or not the bare actin segment flanks the pointed or barbed-end side of the boundary) and the pyrene fluorophore labeling of actin. These observations indicate that the filament twist changes abruptly at boundaries between bare and cofilin-decorated segments, thereby constraining mechanistic models of cooperative actin filament interactions and severing by cofilin. The methods presented here extend the capability of cryo-EM to analyze biologically relevant deviations from helical symmetry in actin as well as other classes of linear polymers.

Introduction

Members of the cofilin/ADF family of actin regulatory proteins (1, 2) bind actin filaments cooperatively (3–5) and promote severing preferentially at and near junctions between bare and cofilin-decorated (cofilactin) segments (3, 5–8), hereafter referred to as boundaries. Cofilin alters the average actin filament twist (9) and subunit tilt (10, 11). Bound cofilin molecules do not directly interact with one another (9), indicating that cooperative binding originates from allosteric conformational changes that propagate from bound cofilin(s) to vacant sites. Current models posit that this propagation occurs via allosteric alterations in filament twist (Ref. 8 and references therein), which is strongly linked to cofilin decoration.

Estimates of the length over which cofilin-induced conformational changes and cooperative binding interactions propagate along actin vary, ranging from N = 1–2 up to N > 100 subunits (3, 5, 12–20). Equilibrium (3, 6, 12, 21) and transient kinetic (12, 14) binding data are well described by models invoking positive cooperativity between nearest neighbors (N = 1–2). In contrast, differential scanning calorimetric (13) and spectroscopic lifetime (15) measurements estimate allosteric propagation of changes in structure, stability, and/or dynamics over N > 100 subunits. More recently, a single-molecule TIRF study measured positive cooperative binding interactions that propagated exponentially with a decay length of N ∼24 subunits (18), and atomic force microscopic imaging directly observed a change in the crossover distance of N ∼14 bare actin subunits toward the pointed-end side of the boundary but no propagation in the bare actin subunits toward the barbed-end side of the boundary (8).

Here, we present a procedure to analyze electron cryo-micrographs of actin filaments that capture the position, orientation, and cofactor (e.g. cofilin) binding occupancy of individual filament subunits. This procedure allowed us to establish with single subunit precision the allosteric propagation of filament twist induced by cofilin binding. Our analysis indicates that cofilin-linked changes in actin filament twist are local and propagate allosterically over a distance of only n = 1–3 subunits.

Results

Procedure for deriving filament geometry and cofilin occupancy from electron micrographs

We acquired a set of 500 micrographs of unlabeled actin filaments and 197 micrographs of pyrene-labeled actin filaments, both partially decorated with cofilin at a binding density (v) of ∼0.5 cofilin per actin subunit. Boundaries between bare and cofilin-decorated segments were manually identified from changes in the filament width and helical pitch (Fig. 1A). We limit our analysis here to boundaries defined by contiguous clusters of bound cofilin (majority N >10) flanked by bare regions (majority N >10) and were distinguishable by eye; smaller clusters are vulnerable to corruption from background noise levels inherent to cryo-EM. Because of the limited field of view at the magnification used here (0.5 × 0.5 μm), filaments and cofilin clusters often extended out of the field. We analyzed 97 boundaries with unlabeled actin: 85 with bare actin (i.e. no bound cofilin) flanking the barbed-end side of the cluster, and 12 with bare actin flanking the pointed-end side; and we analyzed 38 total boundaries with pyrene-labeled actin: 31 with bare actin flanking the barbed-end side of the cluster, and 7 with bare actin flanking the pointed-end side. All boundaries were validated objectively through single particle 3D classification analysis (discussed below).

Figure 1.

Identification of cofilin boundaries in cryo-EM micrographs of partially decorated actin. A, graphical representation of the procedure used in this work for analysis of actin filaments heterogeneously decorated by cofilin. An illustrative heterofilament model (left) is built from cofilactin (PDB code 3J0S (10)) and bare actin (PDB code 3J8I (28)) structures. Cofilin is colored blue; actin is colored in shades of green and orange. Adjacent to the model is a representative cryo-EM micrograph of a partially decorated filament with a single boundary between bare (top) and cofilin-decorated (bottom) regions and a close-up of the boundary region. Single-particle cryo-EM refinement and analysis yields the position and orientation of filament subunits within the micrograph, including axial rotations (φ) to be used for subsequent twist analysis. Subsequent masked 3D classification, without coordinate refinement, of individual subunit sites reveals two predominant structural classes, corresponding to bare and cofilin-decorated actin (right). B, flow chart of the procedure depicted in A. C, unsubtracted reconstructions of the bare (left) and cofilactin (right) classes for pyrene-labeled actin, corresponding to the assigned classes illustrated in A.

Imaged filaments were divided into overlapping square segments (repeating distance N = ∼1 filament subunit, dimensions N = ∼8–12 subunits) and processed using the IHRSR single-particle helical refinement method (22, 23), as implemented in the RELION software package (24, 25), to generate a 3D filament reconstruction (nominal resolution ≤8.3 Å). Bare and cofilin-decorated filament segments were included in the reconstruction, so the resulting “composite” map (Fig. 1A) exhibits features of both actin and cofilactin filaments. Accordingly, the density of bound cofilin is substantially weakened in this map (Fig. 1A). Moreover, because actin and cofilactin filament segments were present at approximately equal mole fractions, the helical twist of this map (−163.9°) is intermediate between the reported canonical (average) twist of cofilactin (−162.3° (10)) and bare actin (−166.6° (26)).

To measure the twist as a function of subunit axial position along the filament, we used alignment parameters from the preceding filament segment analysis to generate subunit-by-subunit coordinate models of each imaged filament, after filling in gaps (length ≤1–2 subunits) using an interpolation scheme (see under “Experimental procedures”). Our approach differs from the predominant method used for 3D structural determination of heterogeneous filaments by cryo-EM, in which boxed segments are compared with multiple reference volumes, sorted into corresponding conformational classes, and analyzed without explicitly considering the spatial relationships between the boxed segments (22). In contrast, performing a global alignment with a single common reference volume as done here allows us to determine the relative geometries of filament subunits in neighboring boxed segments, even when traversing boundaries between bare and decorated regions.

We note that the resolution of the resulting 3D composite map may be reduced due to the merging of different filament structural states. Despite the merging, the resolution is adequate to register the subunit position and orientation. Moreover, as demonstrated below, alignments produced by this analysis can be used to perform structural classification at the level of single subunits. Thus, highly detailed descriptions of individual filaments are obtained by combining the position/orientation and structural classification at the subunit level. We emphasize that distinct structural classes can subsequently be reconstructed in 3D by separating, reprocessing, and/or re-refining the corresponding image segments to potentially achieve higher resolution than the original composite map. Each of these properties of our method is illustrated below.

Structural classification of individual subunits

To distinguish cofilin-decorated from bare actin subunits, while ensuring that every filament subunit is included in the classification, we re-extracted a new set of filament segments from the micrographs using subunit-by-subunit coordinate models derived above. We then performed a focused 3D classification by subtracting all but the central subunit from image segments using a masked reference volume (see under “Experimental procedures”).

This procedure yielded bare and cofilin-decorated classes (Fig. 1A), with approximately half of the subunits assigned to each class. As a qualitative check of classification accuracy, we performed separate, unmasked reconstructions of each class (Fig. 1C). The bare actin class refined to ≤8.3 Å, whereas the cofilactin class refined to ≤7.9 Å. The resulting maps (Fig. 1C) exhibit density features and helical geometries indistinguishable from previously determined structures of actin (27, 28) and cofilactin (10) filaments, indicating that the classification assignments used here were accurate.

Method for detection of small variations in filament twist

The filament twist is defined by the difference in axial rotation angles between adjacent filament subunits (following the genetic one-start helix of actin filaments), where estimates of these axial rotation angles are taken from the Euler angles recorded during 3D structural refinement. Summing the twist values from our filament coordinate model yields the cumulative subunit rotation as a function of filament length. An important feature of this summation is that its uncertainty is independent of sample size (i.e. filament length), due to cancellation of all terms except those belonging to the first and last subunits; viz. if we let φ represent the measured axial orientation of a given subunit with uncertainty σ, then the cumulative subunit rotation for a filament of length N is estimated by (φ_N − φ_{N − 1}) + (φ_{N − 1} − φ_{N − 2}) + … + (φ₂ − φ₁). This sum reduces to (φ_N − φ₁) with uncertainty $\sqrt{{\phi }_N^2+{\phi }_1^2}$, according to error propagation, thus eliminating all other terms and their associated uncertainties. In other words, the uncertainty of a given sum depends only on the uncertainties associated with the first and the last subunits being considered. Moreover, because the sum scales linearly with filament length but its uncertainty does not, the relative uncertainty in the average cumulative subunit twist decreases linearly with filament segment length. Thus, cumulative subunit rotation is an exceptionally sensitive indicator of variations in twist along a filament.

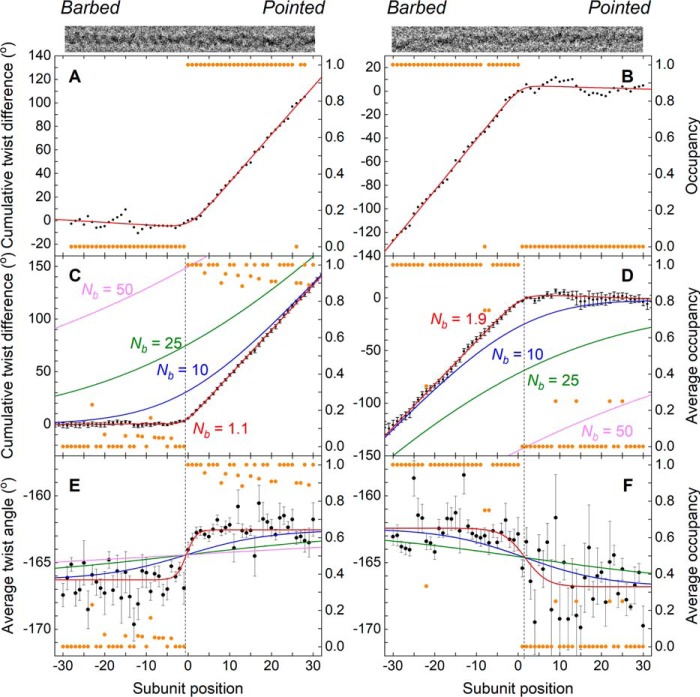
For purposes of presentation and to emphasize features of the transition region, we subtracted the average twist of bare actin (calculated from the linear fit of the bare actin region cumulative twist) from the cumulative subunit rotation to obtain a “cumulative twist difference” (Fig. 2, A–D). Given this definition (i.e. bare actin subtraction), bare actin segments exhibit no cumulative twist difference (e.g. Fig. 2, A, left-hand portion of graph, and B, right-hand portion of graph), whereas the twist of cofilactin segments gives rise to a net cumulative twist difference (e.g. Fig. 2, A, positive slope in the right-hand portion, and B, left-hand portion).

Figure 2.

Actin filament twist changes abruptly at boundaries between bare and cofilin-decorated segments. Results shown are for pyrene-labeled actin samples. Nearly identical behavior was observed with unlabeled actin, as described in the text. A, for an imaged filament with a boundary (top), the “net twist difference” (i.e. the excess twist with respect to a canonical bare actin filament, accumulated subunit-by-subunit starting from the left (barbed end)), is plotted together with the single-site cofilin occupancy. An abrupt, “hockey stick” transition from a measured excess twist value of ∼0° per subunit (corresponding to bare actin) to a value of ∼4° per subunit (corresponding a cofilin-decorated actin filament) coincides with the cofilin cluster boundary (n = 0). B, results similar to A for a filament where bare actin was found on the pointed-end side of a cluster and the accumulated “net twist difference” was calculated starting from the pointed end. C, quantities in A (cumulative net twist difference and cofilin occupancy) are averaged for 24 filaments where bare actin was found on the barbed-end side of a cofilin cluster. The error bar for the n^th estimate of the cumulative net twist difference is about the same as the error of n^th φ value, and the smooth red curve corresponds to the best fit of the data to an empirical function (integral of a sigmoid function; see “Experimental procedures”), which yields an estimate for the characteristic decay length of the twist transition, N_b, of 1.1 ± 0.1. Three other smooth curves (blue, green, and magenta) simulate conditions where N_b is constrained to (larger) values reported in the literature. D, results similar to C for four filaments where bare actin was found on the pointed-end side of a cluster. The fitted value for N_b was 1.9 ± 0.3. E, average axial rotation between subunits n and n − 1 for the population of 24 filaments in C. The smooth red curve represents the best fit of the data to an empirical sigmoid function (see “Experimental procedures”), yielding estimates for N_b (1.1 ± 0.3), the average twist for cofilactin (−162.6° ± 0.1) and the average twist for bare actin (−166.3° ± 0.2). This analysis reveals that the transition from the axial rotation corresponding to canonical actin to that of fully decorated cofilactin occurs within 1–2 subunits from the boundary. F, average axial rotation for the population of four filaments in D, and the corresponding fitted sigmoid function (yielding parameter estimates for N_b (2.6 ± 1.6), the average relative twist for cofilactin (−162.4° ± 0.4), and the average relative twist for actin (−166.8° ± 0.4). Magnitudes of the uncertainty bars are larger than in E due to smaller sample size; nevertheless, the transition in axial rotation value is localized to no more than 1–2 subunits. Smooth curves in E and F depict simulations where N_b is constrained to previously reported values, as in C and D. Note that in a minority of cases (33/97 for unlabeled actin and 10/38 for pyrene-labeled actin), the precise position of the boundary could not be unambiguously determined based on the classification results; such cases were therefore excluded from detailed twist analysis.

Changes in filament twist occur abruptly and bidirectionally at boundaries

The cumulative twist difference displays an abrupt transition at boundaries between bare and cofilin-decorated segments within an individual filament (Fig. 2, A and B). Averaging this quantity over many boundaries reduces the noise and reveals that this structural transition occurs abruptly. With unlabeled actin, this transition occurs over a length of 0.74 ± 0.05 subunits at the barbed-end side of cluster (n = 57) and 1.6 ± 0.5 subunits at the pointed-end side (n = 7), comparable with pyrene-labeled actin, which occurs over 1.1 ± 0.1 (n = 24) subunits at the barbed-end side of cluster (Fig. 2C) and 1.9 ± 0.3 (n = 4) subunits at the pointed-end side (Fig. 2D). This observation indicates that allosteric propagation of the cofilactin twist into the bare actin segment occurs bidirectionally, with minimal differences between the barbed and pointed-end sides of the cofilin clusters.

The twist change at a given boundary appears to also spread bidirectionally into the bare and cofilin-decorated segments, as determined from the best fit of the average twist angle (Fig. 2, E and F), i.e. the midpoint of the “twist transition” lies between the bare and cofilin-decorated filament segments, extending ∼1 subunit to each side of the boundary (Fig. 2, E and F).

Discussion

Method for directly correlating regulatory protein occupancy with filament geometry

Here, we present a structure-based method for classifying individual filament subunits with distinct structural states while maintaining their spatial relationships, including subunits positioned across topological boundaries. This method is general and readily applicable to other classes of linear, helical polymers. Previous cryo-EM methods have not resolved filament occupancy at the level of individual subunits because classification was performed on particles that included multiple subunits and binding sites. Such approaches obscure the precise location of the boundary.

Allosteric effects of cofilin on actin filament twist

Here, we show that actin filaments partially decorated with cofilin display an abrupt and marked change in twist at boundaries between bare and cofilactin segments (Fig. 2). A recent AFM⁵ study (8) reported that cofilactin-like twist propagates >10 subunits into bare actin segments from the pointed-end side of cofilin clusters. We observe no detectable long-range propagation of the cofilactin-like twist into the bare actin segment or vice versa (i.e. into the cofilin cluster), nor do we detect a significant bias toward the filament barbed or pointed ends (Fig. 2). A potential explanation for this discrepancy is filament tethering to a surface (e.g. membrane or glass, either directly or through a binding protein), which has been shown to affect filament structural dynamics and cofilin-severing activity (29), and differences in actin and/or cofilin isoforms (3, 4) in some cases.

Limitations in boundary zone characterization

The structural discontinuity at the boundary is likely sharper than estimated by our analysis. Particle parameters used to calculate net twist values were derived by aligning particles within masks that include up to nine subunits, so that the estimated position and orientation of a given subunit is influenced by neighbors up to four subunits away. In addition, the smoothing algorithm implemented here (local fitting using a seven-subunit window centered on the subunit of interest using the method of least-trimmed squares; see under “Experimental procedures”) introduces further correlations between the estimated position and orientation of a given subunit relative to that of its neighbors, although this effect may be partially mitigated due to our discarding (or “trimming”) two outliers from each fitting window. Both of these effects could smooth the structural transition at the boundary relative to its true geometry. Nonetheless, the geometric transitions reported here abruptly change at the boundary, indicating that cofilin-induced cooperative conformational changes in actin are local and limited to nearest-neighbor interactions. We reiterate that these conclusions are derived from analysis of cofilin cluster sizes N >10 in length. Accordingly, we cannot eliminate the possibility that conformational changes in the filament propagate farther from small clusters (N <10) than larger clusters.

Origins of cooperative binding interactions

Our results and analyses indicate that cofilin-linked changes in actin filament twist are local (i.e. not long-range). If one assumes that cooperative cofilin binding originates from allosteric changes in filament twist, as might be expected because cofilin changes the filament twist, this observation explains why a nearest neighbor cooperativity model accounts for both equilibrium (3, 6, 12, 21) and transient kinetic (12, 14) binding data. It is possible that long-range, sub-stoichiometric effects observed by calorimetry (13, 20), phosphorescence anisotropy (15), AFM (8), or super-resolution fluorescence microscopy (18) originate from factors other than changes in filament twist.

Implications for filament severing

Filament fragmentation occurs preferentially at boundaries between bare and cofilin-decorated segments (3, 5–8), but the structural origins of this behavior have not been established. Our results suggest that subunits directly adjacent to the boundary adopt conformations distinct from those within bare and cofilin-decorated segments. The lack of complementarity with neighboring subunits could potentially render these subunit interfaces more susceptible to fragmentation (e.g. phase boundary problem (5, 30, 31)), thereby accounting for the observed preferential severing at and near boundaries. Alternatively, or in addition (because multiple severing pathways may exist), severing could occur in the adjacent, bare segment that adopts a cofilactin-like twist but without the stabilizing cofilin–actin interactions (10). However, our data indicate that the region susceptible to severing via this pathway would be limited to the nearest neighbors immediately adjacent to the boundary.

Asymmetries in boundary polarity

Because of the polarity of actin, two types of cluster boundaries exist: those with bare actin positioned at the pointed-end side of the cluster, and those with the bare actin positioned at the cluster barbed end. Although quantifying the boundary types by cryo-EM has its limitations and assumptions, our sampling methods identified significantly more boundaries with bare actin positioned at the barbed-end side of the cluster. Several phenomena could give rise to our observation. For example, barbed-end boundaries may be more readily identified than pointed-end ones. Alternatively, this behavior could arise if severing occurred preferentially at the pointed-end side of the cluster, as reported (32, 33). A third possible explanation would be a mechanism in which cofilin clusters grew asymmetrically and more rapidly in the pointed-end direction (8), such that clusters extended to the filament pointed end.

Experimental procedures

Protein purification and modification

Rabbit skeletal muscle actin and recombinant human non-muscle cofilin-1 proteins were purified as described (19). Actin was labeled with pyrene (N-(1-pyrene)iodoacetamide, Thermo Fisher Scientific, catalog no. P29) as described previously (3). Immediately before polymerization, calcium-actin monomers were converted to magnesium-actin with addition of EGTA and MgCl₂ and equilibrated on ice for 5 min (34). Actin was polymerized by addition of 0.1 volume of 10× KMI6.6 buffer (500 mm KCl, 20 mm MgCl₂, 200 mm imidazole, 10 mm NaN₃), yielding final solution conditions of 0.2 mm ATP, 50 mm KCl, 2 mm MgCl₂, 2 mm DTT, 1 mm NaN₃, 20 mm imidazole (pH 6.6), and equilibrated at room temperature for 1 h. Cofilin binding to pyrene actin filaments was measured by fluorescence (3, 12, 19). Cofilin binding to unlabeled actin was measured by cosedimentation (19). Samples with a cofilin-binding density (v) of ∼0.5 cofilin per actin were used for cryo-EM sample preparation.

Sample freezing and cryo-EM data collection

Actin filaments decorated with cofilin at a binding density (v) of ∼0.5 were applied without dilution to holey carbon grids (C-flat^TM CF-1.2/1.3–4C; Protochips, Inc, Morrisville, NC, or Quantifoil R1.2/1.3; Micro Tools GmbH, Grosslöbichau, Germany). No glow discharge was applied to C-flat grids prior to sample application; Quantifoil grids were gently glow-discharged (20 s at 15 mA on a sputter coater device). Grids were subsequently blotted and plunge-frozen in liquid ethane using a home-built cryo-fixation device. Movie frames of samples with pyrene-labeled actin were collected on an F20 electron microscope at a nominal defocus of 3–4 μm using a K2 camera in electron-counting mode (∼1.3 electrons/pixels/s, nominal pixel size, 1.247 Å, ∼4000 × 4000 pixels); samples with unlabeled actin were collected on a Titan Krios microscope at a nominal defocus of 1.6–3.2 μm, using a K2 camera in super-resolution mode (∼1.3 electrons/physical pixels/s; nominal pixel size, 0.666 Å, ∼8000 × 8000 virtual pixels). Movie frames were aligned with Motioncor2 software (35), which was also used to bin the Krios frames by two (final pixel size, 1.333 Å, ∼4000 × 4000 pixels).

Helical reconstruction

Filaments partially decorated with cofilin were manually selected using the boxer program from the EMAN software package (36), and the resulting boxed segments (approximately one per 27-nm repeat) were processed further using RELION. Following an initial round of refinement with a partial (composite) dataset, a tight filament mask was generated using the relion_mask_create tool (corresponding to a length of 7–9 actin subunits), and 26 rounds of refinement were performed with the entire (composite) dataset, followed by three additional rounds of refinement with a truncated filament mask (length of approximately N = 3–5 subunits).

Obtaining continuous filament paths via smoothing and interpolation

Refined box segment x and y displacements were added to box segment coordinates to produce estimates of the subunit coordinates (x, y) with respect to the micrograph coordinate system. The distance (d) between consecutive subunit coordinate estimates was used to identify duplicates (i.e. cases where RELION refinements for two or more box segments were centered on the same subunit) or gaps (corresponding to subunits for which no centered box segment was identified); duplicate subunits were discarded, and the coordinates and Euler angles for “gap” subunits were estimated by interpolation from measured values from neighboring points. The resulting estimates of subunit coordinates (x, y) and orientations (Euler angles φ, θ, ψ, where φ represents the axial twist) were parameterized with respect to the subunit number (n), and this parameterization was used to perform a final smoothing step using the method of least trimmed squares (37). For smoothing, each of the coordinates (x(n), y(n), φ(n), θ(n), and ψ(n)) was re-estimated by performing least-squares linear fitting using a seven-subunit window centered on n. For each estimated value, trimming was performed by enumerating all ways to select five of the seven measured coordinate values (x, y, or φ) within the designated window (21 total possibilities) and choosing the combination that yielded the lowest residual. The corresponding fitting parameter values were used to re-estimate the given coordinate value located at subunit n.

Parametric fitting of the filament twist

The measured, subunit-dependent twist angle, Δφ_n = (φ_n − φ_{n − 1}) (Fig. 2, E and F), was fitted to a sigmoidal empirical function in Equation 1,

$$\Delta \phi \left(n\right)=\Delta {\phi }_f-\frac{\Delta {\phi }_f-\Delta {\phi }_i}{1+e^{\frac{n-n_0}{N_b}}}$$ (1)

where n is the subunit number; n₀ is the midpoint of the twist transition; N_b is characteristic decay length of the twist transition; Δφ_i is asymptotic value of the twist angle at n = −∞, and Δφ_f is the asymptotic value of the twist angle at n = +∞.

The cumulative twist (Equation 2)

$$\begin{array}{c}{\Phi }_n={\displaystyle \sum \Delta {\phi }_i}={\displaystyle {\sum }_{i=2}^n\left({\phi }_i-{\phi }_{i-1}\right)}\\ ={\phi }_n-{\phi }_1\end{array}$$ (2)

was transformed to the cumulative twist difference (φ_{n, diff}) by subtracting the cumulative twist of canonical, bare actin (Φ_{i, bare}) according to Equation 3,

$${\Phi }_{n,\text{diff}}={\displaystyle {\sum }_{i=2}^n\left(\Delta {\phi }_i-\Delta {\phi }_{i,\text{bare}}\right)}=\left({\phi }_n-{\phi }_{n,\text{bare}}\right)-\left({\phi }_1-{\phi }_{1,\text{bare}}\right)=\left({\phi }_n-{\phi }_{n,\text{bare}}\right)$$ (3)

where we have set the value of φ_{1, bare} (which is arbitrary) equal to φ₁. Experimentally determined values of Φ_{n, diff} (Fig. 2, A–D) were fitted to the function Φ_diff(n), obtained by subtracting the twist of canonical, bare actin Δφ_bare from Equation 1 and integrating with respect to n (Equation 4),

$${\Phi }_{\text{diff}}\left(n\right)=C_{1}n+C_2{N}_b\ln \left(1+e^{\frac{n-n_0}{N_b}}\right)+C_3$$ (4)

where C₁, C₂, and C₃ are parameters determined by the fit.

Determining occupancies of individual sites

We used a combined particle subtraction and 3D classification strategy (38) as adapted for helical assemblies (39) to determine the cofilin occupancy of the central actin subunit in each box segment. After reconstructing the composite map, PDB coordinates of actin (PDB code 3J8I (28)) and cofilactin (PDB code 3J0S (10)) filaments were fitted into the cryo-EM density of the central subunit using UCSF Chimera (40). A “central subunit mask” was generated from these atomic models by generating a density map using the pdb2mrc tool of EMAN2 (41), low-pass filtering the map to 30 Å, and generating a mask (10-Å soft edge) using the relion_mask_create tool from RELION. This central subunit mask was then subtracted from a mask of the full reconstructed filament using the relion_image_handler tool from RELION, and the resulting “reverse” mask was used in conjunction with the composite map to generate a new stack of box segments from which all but the central subunit had been subtracted. This “subtracted” particle stack was then separated into two classes with a subsequent round of masked 3D classification, using the central subunit mask and constraining the particle shift and Euler parameter values to those obtained from the prior refinement. Unsubtracted box segments corresponding to the two classes were then separately subjected to an additional refinement step (15 iterations for the actin class, 22 iterations for the cofilactin class), using a newly-generated tight subunit mask (length of ∼7–9 subunits).

Author contributions

A. H. data curation; A. H., W. C., X. L., and C. V. S. software; A. H., W. C., E. M. D. L. C., and C. V. S. formal analysis; A. H., W. C., E. M. D. L. C., and C. V. S. validation; A. H., W. C., W. A. E., E. M. D. L. C., and C. V. S. investigation; A. H., W. C., E. M. D. L. C., and C. V. S. visualization; A. H., X. L., E. M. D. L. C., and C. V. S. methodology; A. H., W. C., E. M. D. L. C., and C. V. S. writing-original draft; E. M. D. L. C., and C. V. S. writing-review and editing; W. A. E., E. M. D. L. C., and C. V. S. resources; E. M. D. L. C. and C. V. S. conceptualization; E. M. D. L. C. and C. V. S. supervision; E. M. D. L. C. and C. V. S. funding acquisition; E. M. D. L. C. project administration; C. V. S. author contributions. E. M. D. L. C. and C. V. S. conceived the project. A. H., W. C., and W. A. E. performed experiments. A. H., W. C., and X. L. analyzed experimental data. A. H., W. C., E. M. D. L. C., and C. V. S. wrote the article.