Matched Molecular Pair Analysis on Large Melting Point Datasets: A Big Data Perspective

Abstract

A matched molecular pair (MMP) analysis was used to examine the change in melting point (MP) between pairs of similar molecules in a set of ∼275k compounds. We found many cases in which the change in MP (ΔMP) of compounds correlates with changes in functional groups. In line with the results of a previous study, correlations between ΔMP and simple molecular descriptors, such as the number of hydrogen bond donors, were identified. In using a larger dataset, covering a wider chemical space and range of melting points, we observed that this method remains stable and scales well with larger datasets. This MMP‐based method could find use as a simple privacy‐preserving technique to analyze large proprietary databases and share findings between participating research groups.

Introduction

Quantitative structure–property relationship (QSPR) models for predicting the melting point of an arbitrary compound are useful tools in drug discovery, as the melting point of a compound strongly correlates with its solubility, and could therefore be used to guide the optimization of compound absorption, distribution, metabolism, and excretion (ADME) properties. One of the first equations relating aqueous solubility to the MP was developed by Yalkowsky et al. in 1980,1 and since then, further improvements have been made to the relationship.2, 3 The revised General Solubility Equation (GSE) is as follows [Eq. (1)]:

$${\displaystyle \log S_{\mathrm{a}\mathrm{q}.}=-0.01\left(MP-25\right)-\log P_{\mathrm{o}\mathrm{c}\mathrm{t}/\mathrm{w}\mathrm{a}\mathrm{t}}+0.5}$$ (1)

in which $\log S_{\mathrm{a}\mathrm{q}}$ is the aqueous solubility of the molecule ($S_{\mathrm{a}\mathrm{q}}$ in mol L⁻¹), $\mathrm{M}\mathrm{P}$ is the compound melting point (in °C), and $\log P_{\mathrm{o}\mathrm{c}\mathrm{t}/\mathrm{w}\mathrm{a}\mathrm{t}}$ is the octanol/water partition coefficient. The term $\mathrm{M}\mathrm{P}-25$ , which represents the crystallinity of the solute, is set at zero if the compound's melting point is less than 25 °C.

Various other methods have been developed for predicting aqueous solubility;4, 5, 6, 7, 8 however, most of these methods require the use of many parameters and a large training set to build the model. In contrast, the GSE requires only two physicochemical properties, and is based on deductive modelling.

There are numerous methods to predict compound melting points, roughly falling into two groups: physics‐based methods and statistical methods. Physics‐based methods can be further divided into two categories: direct methods, and free‐energy methods.9 Direct methods dynamically simulate the melting process and, whilst relatively straightforward, have generally poor accuracy. Free‐energy methods attempt to satisfy phase equilibrium conditions, are more accurate, and are computationally expensive to apply.10

However, in‐silico prediction of the melting point by these methods is nontrivial, as all of these methods require a crystal structure to be applied, negating their usefulness in the prediction of MPs of compounds that lack a crystal structure, such as virtual compounds. Zhang and Maginn attempted to circumvent this by using predicted crystal structures to predict the MP of two compounds and achieved predictions with an error of 15–25 °C, despite the predicted crystal structures differing from the experimental ones.11

Statistical methods have existed since as early as 1881, when Mills derived an accurate MP model for hydrocarbons using fitted constants and the number of methyl groups, but the model is only applicable to that particular chemical class.12 Many similar studies have been performed since,13 each devoted to a particular chemical series, often trained on tens to hundreds of compounds. However, larger datasets have been used as well, such as the study performed by Karthikeyan et al.14 who used neural networks on a set of 4173 diverse compounds to train various models, producing a final model with mean absolute errors in the range of 33–40 °C. The largest MP prediction model to date was published by Tetko et al.,15 who used ∼275 000 compounds and nonlinear methods to build models whose prediction error is close to the estimated experimental error of the source data, that is, 33 °C for compounds in the drug‐like range (50–250 °C).

In 2012 Schultes et al. published an analysis on the melting point of ∼5000 drug‐like compounds16 from both public and in‐house datasets based on simple physical chemical descriptors. They found correlation between several molecular descriptors, such as simple atom counts and property predictions, and the compound MPs by performing a matched molecular pair (MMP) analysis on the dataset. An MMP is a pair of molecules that differ by only a single minor structural change (Figure 1).17

Figure 1.

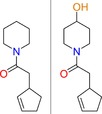
An example of a matched molecular pair: the structures differ by a hydroxy group (highlighted).

Our current study is aimed at validating Schultes’ analysis on a much larger dataset covering a more diverse chemical space with a wider range of melting points, corresponding to a greater statistical power. Based on this study, a large number of MP‐related structural changes are derived. Furthermore, solubility changes, predicted by applying ΔMP data and the GSE equation, were also derived with a good correlation to both the experimental solubility data and the prediction of another solubility model.

Results and Discussion

Descriptor analysis

We found that the descriptor with the greatest impact on MP change is the number of hydrogen bond donors (Table 1). Our validation study with the much larger dataset (PATENTS dataset) shows that the findings of Schultes et al. have the same general characteristics as our results, notably with their public dataset part. An exception is the halogens, where we found the same general trend but with overall average changes to be positive, and spread over a narrower range. It should be noted, however, that in halogen descriptor analysis, we specified that the scale of logP _calc change should be small (<0.5), whereas in the Schultes study this was unconstrained. The Schultes data has been adapted from their published table, with standard deviations converted into standard errors, and their reported mean ΔT _m values normalized according to the mean descriptor changes.

Table 1.

Descriptor results for all compounds.

Descriptor changed Dataset[a]	# of samples	Mean descriptor change	ΔT m/Δdescriptor [°C]	±SEM [°C]	p value[b]
Fluorine atoms PATENTS dataset Schultes In‐House Karthikeyan	17 297 24 41	1.29 1.3 1.8	1.2 −0.77 −3.9	±0.3 ±7.3 ±7.7	<0.0001 n.s. n.s.
Chlorine atoms PATENTS dataset Schultes In‐House Karthikeyan	9893 9 188	1.04 1.0 1.0	6.2 −10 7.0	±0.4 ±14 ±3.4	<0.0001 n.s. <0.05
Bromine atoms PATENTS dataset Schultes In‐House Karthikeyan	2804 16 128	1.02 1.0 1.2	14 47 20	±0.8 ±9.0 ±4.1	<0.0001 <0.001 <0.0001
Iodine atoms PATENTS dataset Schultes In‐House Karthikeyan	400 1 8	1.02 1.0 1.0	20 10 39	±2.2 NA ±3.2	<0.0001 n.s. <0.05
H‐bond donors PATENTS dataset Schultes In‐House Karthikeyan	12 889 36 46	1.02 1.1 1.1	23 44 25	±0.5 ±7.7 ±9.0	<0.0001 <0.0001 <0.05
H‐bond acceptors PATENTS dataset Schultes In‐House Karthikeyan	24 358 13 263	1.16 1.0 1.7	11 36 12	±0.3 ±13 ±3.1	<0.0001 <0.05 <0.0001
Rotatable bonds PATENTS dataset Schultes In‐House Karthikeyan	68 531 61 155	1.27 1.3 2.0	−7.3 −16 −6.0	±0.2 ±4.9 ±4.3	<0.0001 <0.0001 <0.001
logP calc PATENTS dataset Schultes In‐House Karthikeyan	24 818 103 390	0.92 0.5 0.7	4.6 −2.0 2.9	±0.4 ±3.7 ±2.2	<0.0001 n.s. n.s.

[a] The PATENTS dataset comprises the ∼275 000 compound dataset we used in the study; the Schultes In‐House and Karthikeyan datasets are those used in the Schultes study.16 [b] n.s.=non‐significant (p>0.05).

The increase in melting point with the respective increase of hydrogen bond donors and acceptors can be clearly justified by the increase in intermolecular interactions, which lead, mainly, to crystal lattice stabilization. Notably, the change in MP from hydrogen bond donors is almost twice that of hydrogen bond acceptors. This could be due to the following reasons:

1. Donors can interact with a wider variety of systems, for example donor to pi‐system interactions. Further, donors generally have more degrees of freedom from rigid scaffolds than acceptors, as they can be bound to rotationally unrestricted acceptors, meaning they can potentially cover a larger volume of space and are hence new donors are more likely to be able to be involved in interactions than new acceptors.

2. A substantial proportion of donors are amines, and amines can sometimes be protonated to form a positively charged group. This may create ionic interactions in the lattice, forming strong intermolecular interactions and hence increasing the lattice stabilization and thus MP.

The decrease in melting point from increasing numbers of rotatable bonds is likely due to the resultant higher flexibility of the molecule resulting in a higher melting entropy, and hence a more favorable molten state, as described by Dannenfelser and Yalkowsky,18 and in some molecules an increase in the number of rotatable bonds can lead to less efficient crystal packing, also lowering the MP. Further, the halogen trend we observed correlates well with the known intermolecular halogen bonding series, with MP increasing down the series. Interestingly, the MP change per chlorine atom in the Schultes dataset is not just contradictory to our results but also to the influence of bromine and iodine in their own datasets, likely due to the low sample number (derived from only nine samples). This example justifies the necessity of carrying out this kind of analysis with a larger dataset, providing greater statistical power for the observed MP changes.

CSP3 fraction analysis

We also analyzed the fraction of sp³ carbon (CSP3 fraction) as a descriptor. We initially performed an analysis with all other descriptors from Table 1 constrained, considering the CSP3 fraction to have changed if there was a difference of 2 % or more between the members of the pairs. This analysis (#1 in Table 2) showed a ΔT _m of −7.3 °C per 10 % change of CSP3 fraction, which could be considered to be the most correct evaluation of the atom composition change of the molecules (“pure” CSP3 contribution). If we removed some constraints, allowing other descriptors from Table 1 to change simultaneously with CSP3 fraction (see #2–#6 in Table 2) larger changes in ΔT _m were observed. The largest ΔT _m of −14 °C was calculated for MMPs in which the CSP3 fraction increased while the number of rotatable bonds were also allowed to change in any direction. Because the increase of CSP3 fraction is frequently accompanied by an increase of the number of rotatable bonds, both these changes synergistically contributed to large ΔT _m change. Similar synergistic effects were observed for the number of hydrogen bond donors and acceptors, which appear to contribute to the unconstrained CSP3 ΔMP indirectly. The logP _calc and Halogen descriptors contributed smaller changes in ΔT _m, which were not statistically significant relative to the “pure” CSP3 contribution. The largest decrease ΔT _m of −19 °C (for a 10 % increase in CSP3 fraction) was observed when we did not have any constraints on the change of other descriptors. This change was 2.6‐fold larger than the one calculated for the constrained value of ΔT _m=−7.3 °C, which corresponded to the change caused by this descriptor alone. Considering that CSP3 is gaining popularity in drug discovery studies, our result suggests that caution should be taken in interpreting the effect of this descriptor by analyzing its possible correlations with other descriptors, that is, the effects due to CSP3 can be driven by correlated changes in other related descriptors rather than by this descriptor alone.

Table 2.

CSP3 results for all compounds in the PATENTS database.^[a]

Experiment	Unconstrained descriptors	Descriptors unchanged	# of samples	Mean CSP3 change [%]	ΔT m [°C] for 10 % increase of CSP3	±SEM [°C]
1	CSP3	nRot Halogen Donors Acceptors logP calc	29 874	8	−7.3	5.6
2	CSP3 nRot	Halogen Donors Acceptors logP calc	80 284	8	−14	3.5
3	CSP3 Halogen	nRot Donors Acceptors logP calc	46 893	8	−8.6	4.3
4	CSP3 Donors	nRot Halogen Acceptors logP calc	38 154	8	−13	5.2
5	CSP3 Acceptors	nRot Halogen Donors logP calc	45 495	8	−12	4.7
6	CSP3 logP calc	nRot Halogen Donors Acceptors	49 267	9	−8.5	4.1
7	CSP3 nRot Halogen Donors Acceptors logP calc	n.a.	641 192	10	−19	1

[a] p values: <0.0001. The CSP3 fraction was considered to have changed when the difference was ≥2 % (0.02). logP _calc was considered to be constrained if the change was ≤0.5. n.a.: not available.

Aqueous solubility predictions

Further, we analyzed the change in solubility in matched pairs according to the general solubility equation, to test the accuracy of the proposed GSE technique. We modified the GSE [Eq. (1)] to calculate the difference of the values [Eq. (2)], and then compared the resulting GSE ΔlogS, and the predicted ΔlogS calculated using ALOGPS,19 to known solubility data. To do this, we used matched molecular pairs generated from the dataset used to create the ALOGPS solubility model, in order to investigate the efficacy of this GSE technique against both experimental data and an existing solubility model (Figure 2).

$${\displaystyle \Delta \log S_{\mathrm{G}\mathrm{S}\mathrm{E}}=-0.01\Delta MP-\Delta \log P_{\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{c}}}$$ (2)

Figure 2.

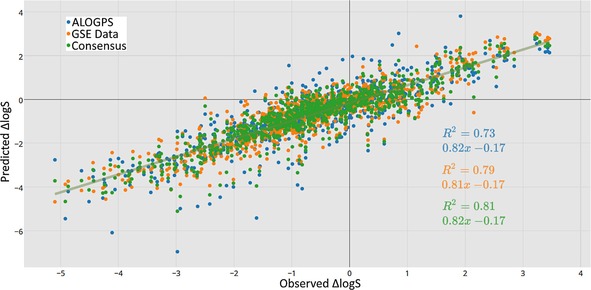
Correlation between predicted and observed ΔlogS, and the results of a consensus model of the two approaches.

The results revealed that both the GSE and ALOGPS methods provide accurate predictions of changes in the solubility of molecules in MMPs (RMSE of 0.71 and 0.61 log units, respectively). The structural features that frequently appeared in the highest‐deviated pairs for the GSE method (see Supporting Information) were long alkyl chains, and the loss/gain of nitrogen‐containing functional groups. The method had a tendency to overstate the hydrophobicity of increasing chain length, and tended to overestimate the hydrophilicity of amine functions, with an exaggerated logP _calc contribution. This is not unexpected, as the GSE was designed to be an approximation for rigid molecules,20 and is not accounting for the large rotational degrees of freedom of these molecules. The GSE method performed generally well for small molecules, and rigid fused‐ring system. There is no correlation in the errors (R ²=0.27) between the two predictive methods, implying a consensus of the two models should give improved results. Indeed, a simple averaging of the two predictions gives a model with greater accuracy (RMSE of 0.57).

Functional group analysis

The functional group analysis was carried out among all MMPs to identify important functional group transformations which affect MPs. A complete list of the functional group endpoints and conversions from this study are available in the Supporting Information and they are generally consistent with known trends. A few transformation examples are shown in Table 3 to highlight the resultant notable MP changes. For example, the conversion between an acid and its ester results in a decrease in melting point. This is due to a decrease in intermolecular bonding from the loss of hydrogen bond donors, and resultant destabilization of the crystal lattice—likewise with amides to esters, and with for example, tertiary to secondary amides. The conversion into heavier halides is consistent with the trend observed in intermolecular halogen bonding, with heavier halides being more easily polarized, resulting in a stronger crystal lattice.21

Table 3.

The most common and most influential results of the functional group analyses.

		# of samples	Mean ΔT m [°C]	±SEM [°C]	p value
Most influential functional group substitutions
From	To
sulfonamides	sulfonic acids	39	90	±17	<0.0001
phosphonic acid esters	phosphonic acids	37	85	±9	<0.0001
thiocarboxylic acid esters	thiocarboxylic acid amides	22	73	±7	<0.0001
dialkyl ethers	carboxylic acid secondary amides	20	72	±10	<0.0001
carboxylic acid esters	carboxylic acid primary amides	176	68	±4	<0.0001
Most common functional group substitutions
From	To
carboxylic acid esters	carboxylic acids	7056	65	±0.6	<0.0001
aryl fluorides	aryl chlorides	6039	7.0	±0.5	<0.0001
aryl chlorides	aryl bromides	3322	5.1	±0.6	<0.0001
aryl fluorides	aryl bromides	1883	13	±0.8	<0.0001
carboxylic acid tertiary amides	carboxylic acid secondary amides	1570	31	±1.4	<0.0001
Most influential functional group endpoints
Group
pyrazoles (HS)[a]		21	−70	±17	<0.0001
sulfenic acid derivatives		49	−55	±6	<0.0001
thiocarboxylic acids		25	52	±8	<0.0001
1,3‐diphenols		22	51	±8.5	<0.0001
alkyl iodides		21	48	±13	<0.0005
Most common functional group endpoints
Group
nitriles		4618	18	±0.8	<0.0001
arenes		4278	7.3	±0.7	<0.0001
nitro compounds		3842	22	±0.8	<0.0001
aryl chlorides		3499	6.2	±0.8	<0.0001
carboxylic acid esters		3486	−18	±0.9	<0.0001

[a] HS: shows high specificity, indicating that fusion with other rings is disallowed.

We exported the functional group conversions into a directed graph (Figure 3). Analysis of subgraphs showed that a large majority of the transformations are consistent within the network to within a reasonable degree of accuracy. Whilst only one of the subgraphs is additive to within predicted error, the pairs sets involved were acyclic, and so a small amount of bias can be expected; a couple of sources of error are considered later. We found that many of these functional group conversions can be justified in terms of simple descriptor changes previously reported, for example:

Figure 3.

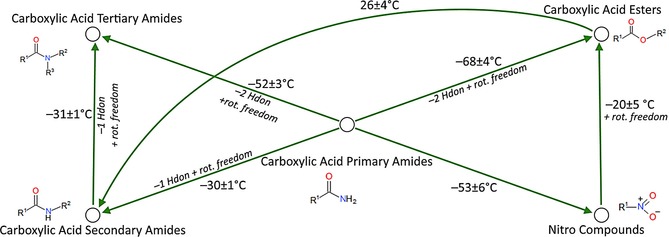
Examples of functional group transformations.

• The transformation between a primary amide and a secondary amide results in a ΔMP on average of −30 °C, equivalent to the loss of a hydrogen bond donor and addition of bond rotation (Table 1).

• The conversion from a primary amide to a tertiary amide (−52 °C) is approximately equivalent to the loss of two hydrogen bond donors and a gain in rotational freedom

• The conversion from a primary amide to a carboxylic acid ester (−68 °C) is approximately equivalent to the loss of two hydrogen bond donors, and the gain of some rotational freedom with the replacement of the rotationally restricted C−N amide bond and addition of the ester group.

Although these MMPs are derived from MP data, given the strong correlation between compound solubility and MP, they could be very useful for optimizing compound solubility either by modifying specific functional groups in the parent structure or indirectly predicting new compound's solubility via MP prediction through some additive or group based method.

However, when functional groups are to be considered in a networked manner, the analysis should be performed with caution and the results examined carefully. We consider two potential sources of error for such analyses:

1. If cyclic subgraphs are to be analyzed, then the limit on the maximum number of transformed atoms may come into effect. For example, consider two transformations, each adding groups comprising six atoms. The final pair would exceed the maximum number of transformed atoms and be excluded, introducing bias.

2. If the functional groups to be considered are chemically irrelevant or insignificant (e.g., start/endpoint considered to be loss of C−H hydrogen, instead of addition of replacement group), then the observed relationship would be inherent noise, especially if smaller datasets are used.

This suggests the need to be careful in the selection of functional groups to be analyzed in the case of a similar functional group‐type analysis.

Conclusions

We have investigated the influence of simple descriptors on the melting point of a large number of compounds. It was found that changes in selected simple 2D descriptors have a quantifiable and significant effect on the melting point of these compounds, and that solubility predictions using this method are comparable to existing techniques, indicating that this is a viable method for predicting the properties of derivative compounds. This is of useful consequence in the lead optimization phase of drug design, aiding in silico prediction or exclusion of alternative compounds, with respect to solubility optimization. In general our results are in line with previous findings, and further show that long lists of significant functional group optimizations can be mined from existing data, with potential practical application. Further to this, using this technique to discover relationships between descriptors and properties is a method that could be used to mine and disseminate information from proprietary chemical databases; as no underlying structures need be released, the only source of structural information in the results comes from the functional group analyses, which can be easily curated before publication were the dataset to contain IP‐sensitive information. Such analyses are known to work, with companies such as MedChemica performing MMP analysis22 on large pharmaceutical datasets to identify and distribute rule‐based structural changes for ADMET optimization.

Experimental Section

Datasets: For this study, we used a dataset published by Tetko et al.15 The dataset is publicly available on OCHEM23 (Online Chemical Database with Modelling Environment), and contains 275 133 compounds covering a wide range of melting points, primarily in the drug‐like range (50–250 °C). These data were taken from sources including patents,15 research papers published by Bradley24 and Bergström,25 Enamine26 and the existing OCHEM database.26 The Bradley, Bergström and Enamine datasets are all highly curated and of good quality, and the errors associated with the various sources involved in the patent dataset are discussed in the original publication referenced. After filtering incomplete records, and compounds with a molecular weight >1000 Da, the remaining molecules were standardized, neutralized, and salts were removed with ChemAxon, and the structures were cleaned. After filtering we ended up with a set of 275 008 molecules with melting points ranging from −199 °C to 517 °C (Figure 4).

Figure 4.

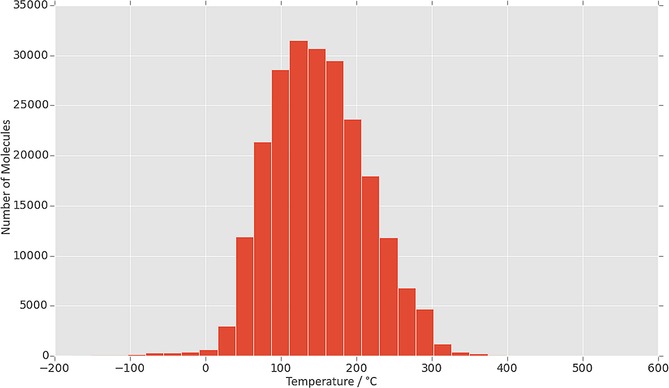
A histogram of the melting points of all compounds used in the study. The majority of compounds involved were in the drug‐like range of 50–250 °C.

Matched molecular pairs and descriptors: We used ALOGPS27 to calculate the octanol/water partition coefficient (logP _calc), CDK28 to calculate the number of hydrogen bond donors and acceptors, and OEstate29 to generate other molecular descriptors, which include 1) the number of each type of halogen atom in the molecule, and 2) the number of rotatable bonds, resulting in a total of eight analyzed descriptors. As one can see, a normalized variance‐covariance principal component analysis (PCA) plot using these descriptors (Figure 5) provides reasonable discrimination between compounds with low (blue) and high (red) melting points. The first two components cover >40 % of the variance of the whole dataset. The number of hydrogen bond donors and acceptors as well as the number of rotatable bonds contribute the highest loading for the first principal component (PCA 1), whilst the logP _calc dominates the second principal component (PCA 2). The outlying structures with the greatest PCA 1 are large molecules with many carbonyl and hydroxy groups.

Figure 5.

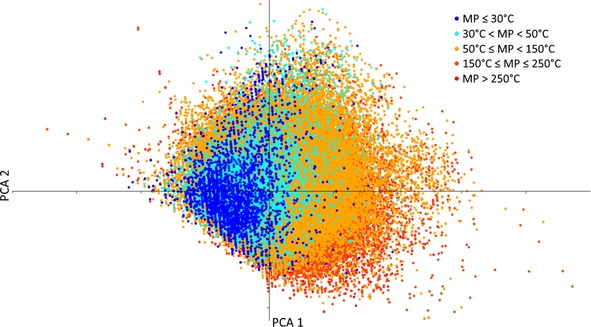
A PCA plot of the two first principal components of the eight descriptors used in the analysis. The change of color from blue to red indicates increasing compound melting point. The PCA plot was generated using the PAST35 software package.

The assembled dataset was used to calculate matched molecular pairs (MMPs). The matched molecular pair technique has been used in the analysis of many properties.30, 31, 32, 33 In the case of this study, the transformed part of the molecule has no more than 10 atoms, and fewer atoms than the main scaffold of the molecule.34 Initially over 2.5 million MMPs were generated. After removing some transformation schemas, which resulted in identical pairs, 917 831 unique pairs were ultimately collected. From this list of MMPs, we were interested in the pairs where only a single descriptor changed, and the other descriptors remain constant. By relating structural changes to ΔMP, we hope to identify matched pair rules suitable for ADME optimization, in which experimental lead compounds can be used as a starting point to predict the changes associated with virtual derivative compounds, with higher accuracy than is involved in predicting these properties from ordinary modelling methods.

Additionally, we performed a functional group analysis using ToxAlerts.36 ToxAlerts is an analytical feature of OCHEM intended for the identification of potentially toxic functional groups, however it also contains an extended functional group (EFG) category.37 This category allows the easy identification of the (binary) presence of over 500 different functional groups, of which 472 were present in the dataset. We examined both transformations that resulted in the substitution of functional groups across the pair, and transformations that had an endpoint of only a single additional functional group, with no fixed start point. Examples of functional group transformations can be found in the Supporting Information.

Data processing: Data resulting from the OCHEM‐based analysis were further processed using in‐house code written in VB.NET and Python: The analysis performed with OCHEM resulted in three files: molecule ID with descriptor information, Matched Molecular Pairs including molecule IDs with respective temperatures, and functional group presences with respective molecule IDs. Once the data were exported from OCHEM, the data processing was performed in‐house. First, we checked for redundant pairs (different transformation schemas that resulted in the same matched pairs), and then created a hash dictionary matching each molecule in each pair to its respective descriptors and ToxAlerts, to allow rapid iteration through the MMP list, and to allow easy identification of pairs for which incomplete information was available. The list of pairs was then iterated through, and differences were calculated—all valid pairs (where only a single descriptor, or 1–2 ToxAlerts changed) were grouped according to their respective descriptors and indexed for statistical analysis; p values were calculated using bootstrap hypothesis testing, due to the volume and unknown distribution of the resulting data as described elsewhere.38 Plots were created using a Python script, executed on conclusion of the statistical analyses.

Conflict of interest

I.V.T. is CEO of BIGCHEM GmbH, which develops the OCHEM platform (http://ochem.eu) used in this study. Other authors declare no conflicts of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

M. Withnall, H. Chen, I. V. Tetko, ChemMedChem 2018, 13, 599.