Abstract
A weakly focused laser beam can exert sufficient radiation pressure to manipulate microscopic particles over a large depth range. However, depth-resolved continuous measurement of radiation-pressure force profiles over an extended range about the focal plane has not been demonstrated despite decades of research on optical manipulation. Here, we present a method for continuous measurement of axial radiation-pressure forces from a weakly focused beam on polystyrene micro-beads suspended in viscous fluids over a depth range of 400 μm, based on real-time monitoring of particle dynamics using optical coherence tomography (OCT). Measurements of radiation-pressure forces as a function of beam power, wavelength, bead size, and refractive index are consistent with theoretical trends. However, our continuous measurements also reveal localized depth-dependent features in the radiation-pressure force profiles that deviate from theoretical predictions based on an aberration-free Gaussian beam. The combination of long-range radiation pressure and OCT offers a new mode of quantitative optical manipulation and detection with extended spatial coverage. This may find applications in the characterization of optical tractor beams, or volumetric optical manipulation and interrogation of beads in viscoelastic media.
OCIS codes: (110.4500) Optical coherence tomography, (350.4855) Optical tweezers or optical manipulation
1. Introduction
The ability of optical forces to manipulate microscopic particles was first demonstrated in 1970 by Ashkin [1]. Using a low numerical aperture (NA) beam to illuminate a suspension of latex beads in water, his seminal experiments revealed two phenomena: the acceleration of particles along the beam propagation direction by scattering-mediated axial radiation pressure, and the pulling of particles into the optical axis of the beam by gradient forces in the radial direction. The latter has formed the basis for the now ubiquitous single-beam high-NA gradient force optical traps, also widely known as “optical tweezers” (OTs) [2]. Since its conception in 1986, OTs have enabled numerous breakthroughs in the nanoscale sciences and the study of sub-cellular biological processes [3–5]. Advances in both theoretical and experimental approaches have established ways to quantify the femtonewton-to-piconewton forces exerted by an optical trap [5–9], and enabled quantitative optical manipulation at nanometer-to-micrometer length scales.
The applications of optical manipulation have predominantly been limited to manipulation of micro-particles in 2D plane(s), i.e., confined to a small depth range (a few micrometers) about the focal plane. This is because OTs utilize high-NA beams, which can only exert significant optical forces near the focal plane. In order to overcome this limitation, optical manipulation based on Bessel beams [10–13], other interferometric structured beams such as optical tractor beams [14–17], as well as holographic OTs [18–20], have been developed to enable parallel manipulation over a larger axial range. These experiments typically utilize wide-field imaging from the side [14] or digital holographic microscopy [15,17] to observe the axial motion of the particles. For the acceleration of particles along the beam axis, Ashkin’s original configuration of radiation pressure from a low-NA Gaussian beam could also exert transversely localized axial force over a greater depth range than is accessible with conventional OTs. Radiation pressure from a low-NA beam has been leveraged in relatively few applications, including optical stretching of cells [21–23], particle sorting [24–27], particle levitation [28,29], and parallelized optical pushing of biomolecules on a plane [30]. However, the supporting measurement of the radiation-pressure force profile over an extended depth range has not been demonstrated experimentally. Although extensive theoretical works have conducted estimates of the magnitude of radiation-pressure forces as a function of distance from the focal plane for both Gaussian [9,31–34] and other shaped beams [17,35–37], experimental measurements of radiation-pressure force have only been performed at a single depth or a limited set of selected depths [9,13,17,28,32,38–40]. In order to take full advantage of optical manipulation with larger axial coverage, it is important to be able to experimentally measure the depth-resolved radiation-pressure force profile over an extended depth range.
We present an experimental method based on real-time monitoring of particle dynamics with OCT to reconstruct depth-resolved axial radiation-pressure force profile of an optical manipulation beam. Although OCT has been combined with OTs for imaging of cells in a micro-flow environment [41], OCT imaging of particle dynamics induced by radiation pressure has not been demonstrated. Using a low-NA Gaussian beam for demonstration, we investigated the effects of beam power, wavelength, bead size, and refractive index on radiation pressure and provide comparisons with theoretical predictions. We show that radiation pressure from an actual (experimentally achieved) beam may yield a substantially different force profile over an extended depth range compared to the theoretical predictions based on an ideal Gaussian beam description. We also demonstrate that radiation pressure from a low-NA beam can induce detectable changes in the dynamics of microscopic particles over a depth range of several hundred micrometers about the focal plane.
2. Theoretical framework
2.1 Forces on a dielectric particle from a weakly-focused laser beam
In his seminal paper, Ashkin conceptually described the magnitude of radiation-pressure force exerted by a focused low-NA laser beam with power on a neutral particle in vacuum as , where is the speed of light in vacuum and is a proportionality constant [1]. This simplified expression was based on the transfer of photon momentum as a result of backscattering events. The factor describes the scattering of photons incident upon the bead, accounting for the effects of bead shape and size, beam characteristics, refractive index mismatch between the bead and the medium, and the location of the bead relative to the beam focus. For a bead of radius comparable to the wavelength of the beam, i.e. Mie particles, Ashkin had estimated to be on the order of 0.1. A more rigorous estimation of the factor can be obtained via Generalized Lorenz-Mie Theory (GLMT) [34]. GLMT provides a formulation that enables computation of the radiation pressure cross-section in the direction parallel to the optical axis of the beam (hereafter referred to as the axial direction), , which describes the fraction of incident photon energy density that gives rise to radiation pressure in the axial direction. accounts for the component of the change in linear momentum of all photons that have interacted with the bead. Then, the resultant axial radiation-pressure force on the bead is given by:
| (1) |
where denotes the radius of the bead, denotes the radius of the beam, and denotes the refractive index of the medium. denotes the variation of the radiation pressure cross-section as a function of for the specified beam parameters and properties of the bead and the medium. In Eq. (1), corresponds to the magnitude of axial radiation-pressure force per unit power density, while the factor in front describes the average power density of the Gaussian beam over the area projected along where the beam intersects the bead (for ). We note that under the GLMT formulation [34], optical force cannot strictly be separated into scattering and gradient forces [2]; however, in order to help convey some physical intuition, for the case of our low-NA forcing beam we shall refer to any radial component of the force as ‘gradient force’ [5,42].
2.2 Dynamics of a sphere in viscous fluid under an externally applied force
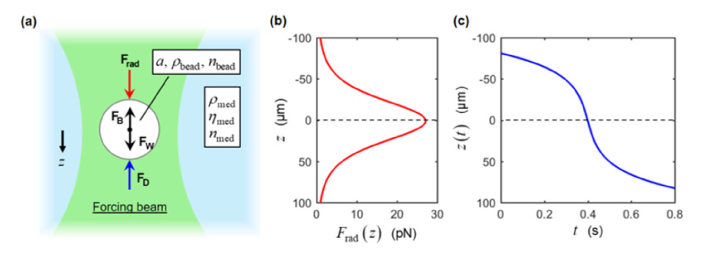
The dynamics of a spherical mass illuminated by a weakly focused beam in viscous fluid is governed by the radiation-pressure force from the beam, , the fluid drag force, , the buoyancy force, , and the weight of the sphere, , as shown in Fig. 1(a). For a spherical bead with radius and density in a fluid medium with viscosity and density , the equation of motion in the axial direction is given by:
| (2a) |
| (2b) |
where , , and denote the axial position, velocity, and acceleration of the bead, respectively. Throughout the rest of this paper, we shall define as the focal plane of the forcing beam, with the unit vector pointing in the propagation direction of the beam, i.e. is above the focal plane (the converging part of the beam) and is below the focal plane (the diverging part of the beam). In Eq. 2(b), the second term on the right-hand-side describes the effective weight of the bead, , and the last term corresponds to the Stokes’ drag force on a sphere in the laminar flow regime [43]. We note that is described as being time-varying to reflect the depth-dependent variation in as the bead is displaced along the axial direction. Figures 1(b) and 1(c) show simulations of the depth-dependent and the resulting trajectory of a sphere initially located 80 µm above the focal plane and moving at its terminal velocity in a viscous medium while illuminated by a low-NA Gaussian beam. The axial trajectory first exhibits acceleration, followed by deceleration after the bead passes through the focal plane of the forcing beam. Thermal forces that give rise to Brownian motion are neglected from the model in Eqs. 2(a) and 2(b) because the root mean-squared displacement due to Brownian motion (estimated from for = 1 s and = 298 K) of a micron-size bead in water is on the order of ≤1 µm, two orders of magnitude smaller than the axial displacement simulated in Fig. 1(c). Our method is based on using OCT to measure , and then solving the equation of motion in Eq. 2(b) at each instant in time for , from which the depth-dependent is obtained.
Fig. 1.
Factors affecting the dynamics of a spherical particle in viscous fluid illuminated by a low-NA beam. (a) Diagram showing the different types of forces exerted on a sphere in viscous fluid, illuminated by a weakly focused laser beam. (b) Theoretical depth-dependent profile of Frad exerted by a weakly focused Gaussian beam (w0: 3.2 µm; λ: 789 nm; P: 100 mW) on a dielectric bead (a: 1.5 µm; nbead: 1.5786; ρbead: 1.05 g/cm3) obtained from GLMT. (c) Axial bead trajectory as a result of Frad in (b) obtained from Eq. 2(b) (ρmed: 1 g/cm3; ηmed: 1 mPa∙s; nmed: 1.3294).
3. Methods
3.1 Experimental setup
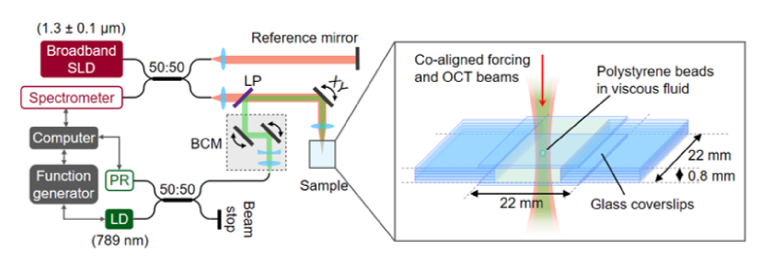
The optical setup, shown in Fig. 2, consisted of a spectral-domain (SD)-OCT system, with a broadband superluminescent diode (Thorlabs, LS2000B) with a center wavelength of 1300 nm and full-width-half-maximum bandwidth of 200 nm, for measuring bead trajectories, and a fiber-coupled laser diode at the wavelength of 789 nm (Frankfurt Laser Company, FLU0786M250, HI780 fiber output), to act as the forcing beam. In one experiment, we switched the forcing laser diode to one with a wavelength of 976 nm (Innovative Photonic Solutions, I0976SB0500PA). Unless stated otherwise, we used the 789-nm laser as the forcing beam. The OCT beam was focused with an NA of 0.14, and OCT transverse and axial resolutions were 4.5 μm and 3.7 μm in air, respectively.
Fig. 2.
Experimental setup and sample configuration. The optical setup consisted of an SD-OCT system and a forcing beam combined in free space with the OCT sample arm beam. The forcing beam and the OCT beam were co-aligned at the sample. SLD: superluminescent diode, LD: laser diode, PR: photoreceiver, LP: long-pass dichroic filter, BCM: beam control module, XY: two-axis galvanometer.
The forcing beam was combined with the OCT sample arm beam in free-space via a beam control module (BCM) and a long-pass dichroic filter. The BCM was adjusted so that the forcing beam was co-aligned with, and focused to, the same position in 3D space as the OCT beam after going through the same OCT sample arm objective lens. A photoreceiver (Newport, 2051-FS) was used to detect the reflected confocal response of the forcing beam. The co-alignment between the OCT beam and the forcing beam was verified before each experiment by imaging a USAF target and ensuring that (1) the depths at which the glass surface of the USAF target produced the largest OCT intensity and the largest reflected confocal response of the forcing beam were co-planar, and (2) the en face OCT image and the reflected confocal image of the USAF target were aligned. The waist radius, , and the confocal parameter, (where ), of the forcing beams were measured to be 3.37 µm and 121.44 µm for the 789-nm laser, and 3.20 µm and 112.48 µm for the 976-nm laser, respectively.
3.2 Preparation and characterization of samples
The samples consisted of non-absorbing polystyrene beads of different sizes (Sigma-Aldrich LB5 and LB30; Spherotech PP-10-10, PP-15-10, PP-20-10, PP-40-10, and PP-45-10) in fluid media of varying refractive index and physical properties. The polystyrene beads were assumed to have a density of 1.05 g/cm3 as reported by the manufacturers. The polystyrene beads were added at appropriate concentrations for each bead size to achieve mean particle separation of 15 µm. The fluid media were based on multiple concentrations of glycerol (Fisher, G33-500) in water solutions and dimethyl sulfoxide (DMSO) (Fisher, D128-500). Relevant physical properties of the samples are provided in Table 1. Dynamic viscosity was measured by a shear rheometer (TA Instruments, DHR-3) in a concentric cylinder geometry. Three repetitions of a shear rate sweep (1-100 s−1) flow test were performed for each sample. The viscosity was obtained by linear regression of the measured shear stress as a function of the applied shear rate. Mass density was measured by weighing 2-22 mL (in 2 mL increments) volumes of each fluid sample. The density was obtained from linear regression of the measured mass as a function of fluid volume.
Table 1. List of fluid samples and relevant properties.
| Fluid | Density (g/cm3) | Viscosity (mPa∙s) | Refractive index | |||
|---|---|---|---|---|---|---|
| Water | 1.00 ± 0.02 | 1.1 ± 0.1 | 1.3294b | |||
| 10% glycerola | 1.01 ± 0.02 | 1.3 ± 0.1 | 1.3469c | |||
| 20% glycerola | 1.03 ± 0.02 | 1.7 ± 0.1 | 1.3608c | |||
| 30% glycerola | 1.06 ± 0.02 | 3.7 ± 0.1 | 1.3748c | |||
| 40% glycerola | 1.09 ± 0.02 | 5.6 ± 0.1 | 1.3893c | |||
| DMSO | 1.10 ± 0.02 | 1.3 ± 0.1 | 1.4699d |
Percentage indicates volume percent of glycerol in distilled water.
Refractive index of water obtained from [44].
Refractive index is assumed to scale linearly with glycerol volume fraction [45] and calculated based on refractive index of glycerol [46] and water [44].
Refractive index of DMSO obtained from [47].
3.3 Data acquisition
One sample was made for each experimental condition. Three M-mode data sets were acquired in each sample, with the beams positioned at different transverse locations in the sample for each data set. The forcing beam was operated at a constant power (ranging from 50 to 180 mW) after the initial turn-on in each data set. The OCT beam had a power of 4 mW at the sample. At these power levels, we expected contributions from the OCT beam to be <0.7 pN under our experimental conditions (based on GLMT), and at least one order of magnitude smaller than that from the forcing beam. Each M-mode image recorded the time-varying depth of each bead that entered the imaging axis (which was aligned to the optical axis of the forcing beam) over a time period of 33 s at a line scan rate of 120 kHz (this temporal oversampling was to ensure that fast dynamics could be captured). In this configuration, the forcing beam would (1) pull the beads towards its optical axis via the gradient force, and (2) push the beads downward against the buoyancy and drag forces via . We note that because of the gradient force in the radial direction, there was no need to align each bead to the imaging axis manually, thereby allowing the trajectories of multiple beads to be measured in a single continuous M-mode acquisition.
All experiments were conducted at the laboratory temperature, controlled at 23 ± 0.5 °C. The changes in the temperature-dependent viscosity of the glycerol-water mixtures is expected to be on the order of –0.03 mPa·s/°C at this temperature [48,49], corresponding to the error in calculation due to viscosity fluctuation on the order of ± 0.18 pN, corresponding to 0.5-3% of the expected .
3.4 Reconstruction of depth-dependent radiation-pressure force
First, the spatial-domain M-mode OCT image was reconstructed by a standard SD-OCT reconstruction method (background subtraction, spectrum resampling, dispersion correction, and Fourier transformation). For each imaged bead, the depth of the bead in each A-scan was extracted by (1) manually locating at least 5 points along the trajectory of the bead from the OCT image, (2) interpolating between the located points via cubic spline interpolation, and (3) searching, via an automated algorithm, for the pixel with maximum OCT intensity in each A-scan in the vicinity of the interpolated curve. Then, the displacement of the bead from the focal plane of the forcing beam (determined from the OCT focal plane on the OCT image) was calculated from the optical path length; this provided position of each bead.
The velocity and acceleration of each bead were obtained by numerically differentiating the raw z(t) using a finite difference method with second order polynomial curve fitting over a sliding window [50]. Briefly, the raw over the window was fit to a second-order polynomial function via least-square curve-fitting, where is the A-scan index and is an integer. Then, the first and second derivatives at the ith A-scan are given by: and . The size of the sliding window was determined for each bead based on the time-averaged speed of the bead over its entire trajectory. The time-averaged speed is given by , where corresponded to the first time point at which the bead appears on the image and corresponded to either the time point at which the bead disappeared from the image (via diffusion away from the imaging axis), or the time point at which it is joined by one or more beads (we excluded trajectories produced by two or more conjoined beads), whichever occurred first. The window size was given by . Lastly, and were substituted into Eq. 2(b) to solve for , from which we obtained .
3.5 Measurement of depth-dependent forcing beam profiles, and theoretical prediction of radiation-pressure force
The depth-dependent intensity profile, , of the forcing beam was obtained by measuring the reflected confocal intensity from a glass slide surface, translated to different depths about the focal plane, using a photoreceiver. The focal plane was determined as the depth at which the reflected confocal intensity was at its maximum. The curve was normalized with respect to this maximum value, such that .
The 3D point spread function (PSF) of the forcing beam was obtained by taking the reflected confocal images of a single 2.29-μm polystyrene bead, resting on an AR-coated convex lens, translated to different depths about the focal plane. The depth-dependent beam radius, , was obtained from the radius of the en face bead intensity image at each depth by (1) locating maximum bead intensity, corresponding to the ‘center’ of the PSF, (2) taking a slice through the ‘center’ of the PSF and locating points and , corresponding to radial distances at which the bead intensity was of the maximum value on either side of the PSF ‘center’, and (3) calculating the beam radius as . Steps (2) and (3) were repeated 10 times with the slice in step (2) taken at varying angles, , where . The final curve was obtained from the average of all 10 realizations. From the measured , we extracted the beam waist radius, , and the confocal parameter, , by curve fitting the measured to:
| (3) |
Equation (3) has the functional form that is similar to the description of a Gaussian beam, but without enforcing the relationship , where is the Rayleigh range.
For the theoretical comparison with the measured , we implemented the GLMT formulation to calculate the of a Gaussian beam on a homogeneous spherical particle (using localized approximation of the first-order Davis beam, LA1, for the beam shape coefficient [33]) in MATLAB (R2016b) and obtained the theoretical prediction of from Eq. (1). Noting that we did not experimentally achieve an ideal Gaussian beam, our theoretical predictions utilize an equivalent Gaussian beam with the same confocal parameter, i.e., and , for each of the forcing beams.
4. Results
4.1 Axial motion of beads in viscous media
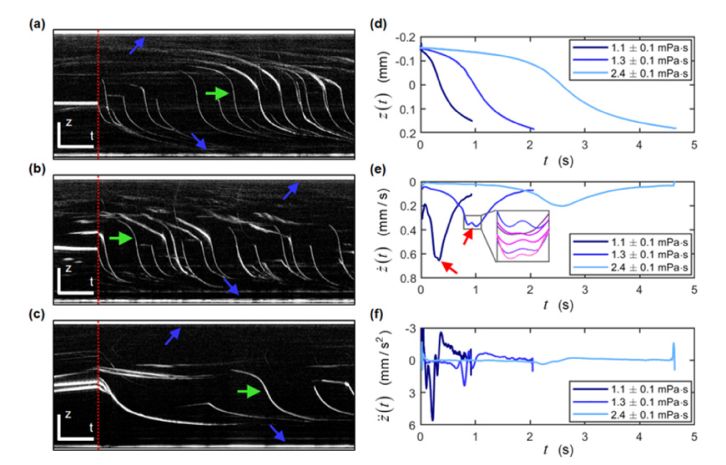
Figures 3(a)–3(f) shows the M-mode OCT images and representative bead motions in 3 concentrations of glycerol-water solutions. The beads were initially at their equilibrium velocity, governed by , , and . Figure 3(c) shows that the beads in 30% glycerol-water mixture were initially floating upward at equilibrium due to the higher density of the medium at this concentration (). Immediately after the forcing beam power (140 mW) was turned on (red dotted lines in Figs. 3(a)–(c)), the beads were accelerated downward by depth-dependent from the forcing beam, producing trajectories similar to that simulated in Fig. 1(c). Notably, multiple beads appear within the imaging axis after illumination by the forcing beam, thus, each M-mode data set contained the trajectories of multiple beads.
Fig. 3.
Dynamics of beads accelerated by radiation pressure in media with different viscosity. M-mode OCT images in (a) water (ηmed: 1.1 ± 0.1 mPa∙s), (b) 10% glycerol (ηmed: 1.3 ± 0.1 mPa∙s), and (c) 30% glycerol (ηmed: 2.4 ± 0.1 mPa∙s). Red dotted lines indicate the moment when the forcing beam was turned on. Blue arrows indicate glass surfaces. Green arrows indicate beads whose motions were plotted in (d)-(f). Scale bar: 200 µm (vertical) and 3 s (horizontal). (d) Axial position of a bead in each sample as a function of time. (e)-(f) Axial velocity and acceleration obtained by first and second derivatives of trajectories in (d). Red arrows in (e) point to the two local maxima in the velocity profiles, inset shows a zoomed-in view of the two local maxima from measurements of multiple beads (see Section 4.2 and 5.1 for further information).
A representative bead trajectory and corresponding velocity and acceleration profiles, obtained via numerical differentiation, in each sample are shown in Figs. 3(d)–3(f). In all three samples, the beads reached their maximum velocity and decelerated after passing through the focal plane. We observed two local maxima in the velocity profiles (red arrows and inset in Fig. 3(e)), corresponding approximately to the instances when the beads were passing through the focal plane. These features were consistently observed on multiple beads in media with different glycerol concentrations and power levels of the 789-nm forcing beam (data not shown) but were not present in the simulation in Fig. 1(c). The maximum velocity and acceleration decreased with increasing viscosity of the medium.
4.2 Depth-dependent radiation-pressure force
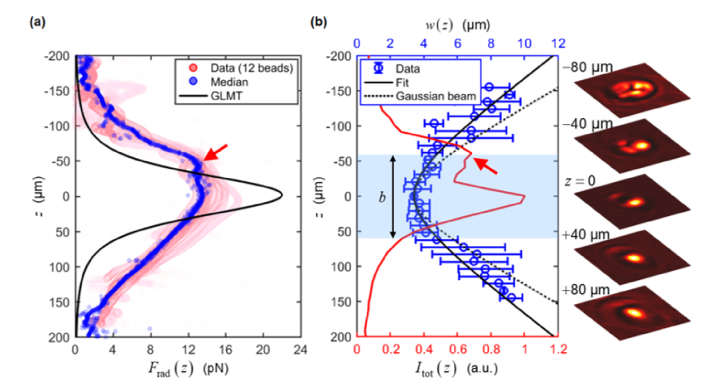
The depth-dependent radiation-pressure force was obtained for each bead from its trajectory. In order to compare for different experimental conditions (each contained data from 5 to 16 beads), we obtained the median values of from all beads at each depth. The comparison with theoretical prediction by GLMT in Fig. 4(a) shows that the measured was lower around the focal plane but the measured force had a larger depth coverage than the theoretical predictions. To investigate the discrepancy between experiments versus theoretical prediction based on a Gaussian beam, we compared the measured to the measured PSF of the forcing beam in Fig. 4(b). Both the total beam intensity, , and the beam radius, , profiles showed evidence of aberrations and deviations from the theoretical Gaussian beam profile. Particularly, the measured confocal parameter (obtained from fitting the measured to Eq. (3)) was b = 121.44 µm, whereas the expected confocal parameter of a Gaussian beam with the same waist radius would have been = 90.39 µm. Moreover, the curve exhibited a local maximum above the focal plane (≈ -50 µm), which also manifested in the measured (red arrows in Figs. 4(a) and 4(b)). The en face images of the PSF indicate the depth-dependent impact of optical aberrations. We note that the curve for the 976-nm beam (not shown) also exhibited a local maximum above the focal plane, although less prominently than the 789-nm beam.
Fig. 4.
Depth-dependent profiles of radiation-pressure force and the point spread function (PSF) of the 789-nm forcing beam. (a) Comparison of measured Frad(z) (a: 3 µm; medium: 10% glycerol) to the theoretical prediction by GLMT for a Gaussian beam with zR = b/2. (b) Depth-dependent profiles of reflected confocal intensity, Itot(z), and 1/e2 radius, w(z), of the forcing beam. From the fit curve of measured data, the forcing beam w0 = 3.37 µm and b = 121.44 µm. En face images of the PSF are provided at selected depths; each image was normalized by its maximum intensity and has a field-of-view of 30 µm × 30 µm. In (a-b), red arrows point to the local maxima above the focal plane that manifested in the measurements of both Itot(z) and Frad(z).
4.3 Effects of beam power, bead size, relative refractive index, and wavelength
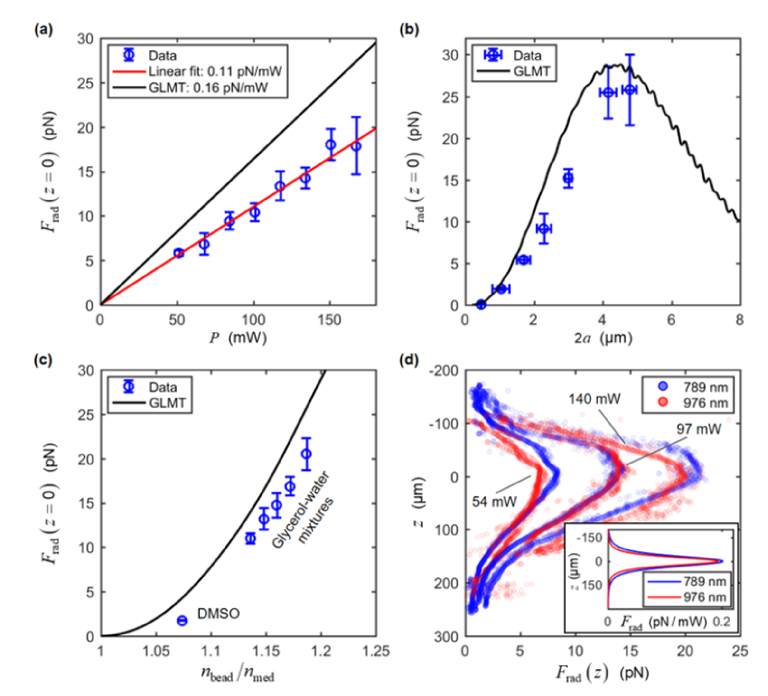
We compared the focal plane force, , measured with different forcing beam power, bead sizes, and relative refractive indices between the bead and the medium in Figs. 5(a)‒5(c). The results were also compared to the theoretical predictions by GLMT. We investigated the expected linear relationship between and the forcing beam powers by measuring on 3-µm diameter beads in 10% glycerol at different forcing beam powers. Figure 5(a) shows that the measured was indeed linearly proportional to the forcing beam power, but had lower magnitude per unit power than the theoretical prediction by GLMT (0.11 pN/mW measured versus 0.16 pN/mW predicted).
Fig. 5.
Effects of beam power, wavelength, bead size, and refractive index on radiation-pressure force. (a) Frad at the focal plane as function of forcing beam power (a: 1.5 µm; medium: 10% glycerol). (b) Frad at the focal plane as a function of bead diameter (P: 140 mW; medium: 10% glycerol). (c) Frad at the focal plane as a function of relative refractive index (a: 1.5 um; P: 140 mW). (d) Comparison of depth-dependent Frad from the forcing beam with wavelength of 789 nm versus 976 nm (a: 1.5 um; P: 54, 79, 140 mW; medium: water). Plotted data points represent median values of Frad(z) obtained from N = 16 beads for 789 nm and N = 15 beads for 976 nm. Inset shows GLMT predictions of Frad(z) per unit power for the two cases. In (a-c), vertical error bars represent ± 1 standard deviation of results obtained from N = 10-16 beads (except in (b), N = 5 for 2a = 0.46 µm and in (c), N = 7 for DMSO). In (b), horizontal error bars represent the bead size distribution reported by the manufacturers.
The effect of varying the bead size was investigated by measuring on beads of different diameters in 10% glycerol. Figure 5(b) shows that the measured increased monotonically with the diameter of the beads. This trend was consistent with the GLMT predictions, even though the absolute measured force magnitude at each bead size was approximately 20-30% lower. We also investigated the effect of varying the relative refractive index, , by measuring on 3-µm diameter beads in media of different refractive indices. Similar to the previous case, Fig. 5(c) shows that increases with increasing mismatch between and as predicted by GLMT, but the measured force magnitude was approximately 20-30% lower.
Lastly, we compared on 3-um diameter beads in water for forcing beam wavelengths of 789 nm and 976 nm; the latter wavelength has over an order of magnitude larger absorption by water [44]. These two wavelengths were chosen to investigate the contributions of any absorption-mediated forces [38,51,52], in order to determine whether our measured forces from the 789-nm beam could be predominantly attributed to scattering-mediated radiation pressure. Figure 5(d) shows that the measured was comparable between the two wavelengths, with the force being slightly lower with the 976-nm beam. The ratio of per unit power between the two wavelengths, i.e. , is 0.937 for the measurement, comparable to the theoretical prediction of 0.957.
5. Discussion
5.1 Comparisons with theory, and implications for theoretical prediction of radiation pressure forces in the presence of optical aberrations
The measured profile exhibited lower focal plane forces but had a larger depth coverage compared to the theoretical prediction. We attribute the discrepancy between experiment and theoretical prediction to the depth-dependent impact of optical aberrations in our forcing beam. Although we accounted for the actual beam divergence by calculating for input to the GLMT formulation from the measured confocal parameter, this approach could not account for the presence of aberrations in the forcing beam (Fig. 4(b)). Another factor that led to lower measured relative to the theoretical prediction could be the entry into the forcing beam path of one or more beads above another; typically, this occurred over 100 µm above each bead (Figs. 3(a)–3(c)). However, we believe that this effect was minimal because >99% of the total scattered intensity of our forcing beam off a Mie particle was in the forward direction (average cosine of phase function, g ~0.9) based on GLMT simulation. Furthermore, a commercial-grade simulator based on the finite-difference time-domain method by Lumerical Inc. [53] predicted <2.5% decrease in due to the presence of another bead located at –100 µm directly above it, corresponding to a drop in of <0.6 pN. Further work is needed to investigate the role of wavefront distortion on for more isotropic scattering cases and more highly scattering media.
Although the absolute magnitude of the measured was lower than the theoretical prediction, we validated that the trends of measured as a function of relevant parameters agree with theory. Firstly, the linear relationship between and the power of the forcing beam, which is expected regardless of the beam characteristics, is confirmed (Fig. 5(a)). Secondly, the expected increasing trends in as approaches w0 (i.e., a larger fraction of photons encounter the bead), and as the mismatch between and increases are also observed (Figs. 5(b) and 5(c)).
Lastly, the comparison to with a 976-nm forcing beam also agrees with theoretical predictions (Fig. 5(d)). This comparison establishes that the contribution of absorption-mediated forces [38,51,52] (if present) in our measurements at 789 nm is negligible because the two wavelengths produced relative that agrees with the theoretical predictions of at these two wavelengths, despite the 976-nm beam having over an order of magnitude larger absorption by water than the 789-nm beam [44]. We note that under different experimental conditions, where the bead displacements are significantly lower than those observed here, the contribution of absorption to the measured bead trajectories could be more significant.
Utilizing co-aligned beams and OCT line-scan imaging, axial trajectories of polystyrene beads under externally applied radiation-pressure force from the forcing beam were monitored in real-time. The measured bead trajectories exhibited unexpected cycles of rapid acceleration and deceleration that resulted in two local maxima in the velocity profiles (red arrows in Fig. 3(e)). These particle dynamics subsequently revealed the existence of two local maxima in the profiles, which coincided with the two maxima observed in the measured reflected confocal intensity profile of the forcing beam (red arrows in Figs. 4(a) and 4(b)). This behavior can be predominantly attributed to the optical aberrations in the forcing beam. In conventional high-NA optical manipulation, spherical aberrations due to beam propagation through interfaces with refractive index mismatch have been previously described [54] and incorporated into GLMT simulation (as opposed to an ideal Gaussian beam approximation used here) to more realistically model the experiment [55]. However, results from ray trace simulation suggest that this phenomenon is negligible for our low-NA forcing beam [56], and that aberrations of the beam are predominantly due to the aberrations of the BCM and OCT free-space optics. The effects of indeterminate wavefront distortions (e.g., those present in the en face views of the PSF in Fig. 4(b)) would be challenging to theoretically simulate without experimental measurement of the beam aberrations. An approach to determine the beam shape coefficient for GLMT formulation from an experimentally measured beam intensity profile has been developed [57], but the extension of this approach to predicting radiation pressure of an actual beam, with experimental comparisons, has not been done. Our results demonstrate the importance of being able to experimentally measure the depth-dependent force profile from an actual beam, which, in practice, inevitably contains some level of aberrations that are not completely characterized, and therefore deviates from a theoretical description of the beam [34,58]. Our method for depth-resolved axial radiation-pressure force measurement can provide an additional experimental approach to investigate the effects of beam non-ideality on radiation pressure and help improve theoretical predictions of radiation-pressure forces in the presence of optical aberrations.
5.2 Possible extensions of the presented experiments
Even with low-NA beams, the effects of both axial and radial components of the optical force on microscopic particles have previously been demonstrated [1,32]. Although the experiments presented here quantitatively measures acting in the axial direction only, the M-mode OCT images also qualitatively show the effects of the force in the radial direction on the beads. This is evident from the appearance of ‘new’ beads on the image every 1-3 s in the presence of the forcing beam (note the number of beads that appear on the OCT images after the red dotted lines in Figs. 3(a)–3(c)), as opposed to having only 1-2 beads on the image before the forcing beam was turned on. These ‘new’ beads were not originally within the PSF of the OCT beam, but were later pulled towards the optical axis of the forcing beam (co-aligned with the OCT beam) by the gradient force. The presented experimental setup can be modified to accommodate scanning of the OCT beam independent of the forcing beam (e.g., having the two beams in a counter-propagating configuration). Utilizing high-speed volumetric OCT imaging, 3D dynamics of the beads can be captured that allows for depth-resolved quantification of both axial and radial optical forces by solving the equations of motion in Eqs. 2(a) and 2(b) extended to 3D.
Our method for measurement is not only applicable for charactering a low-NA near-Gaussian beam, but can also be applied to characterize radiation-pressure forces from other types of beams. Of particular interest could be the measurement of axial force profiles on different types of particles along the propagation distance of optical conveyor or tractor beams, which have been rigorously derived from theory but have not been fully characterized experimentally [14–17,20,35–37]. In addition, our method may also be applied to characterize axial force profiles in trapping configurations (as opposed to transport of particles), such as conventional high-NA OTs, axial OTs [59,60], or Bessel beam optical traps [10–13]. In these cases, axial position detection with nanometer resolution is required to track particle displacement over hundreds of nanometers. Typical approaches employed in optical manipulation for nanometer-scale 3D particle tracking are back-focal plane interferometry with a quadrant photodiode (QPDs) or a position sensitive detector [5,59], and digital holographic microscopy with a high-speed camera [5,61]. Although not leveraged in the presented experiments, SD-OCT is also capable of axial position detection with sub-nanometer displacement sensitivity via the phase of the complex OCT signals (not to be confused with the micrometer-scale axial resolution of the OCT system) [62]. In SD-OCT, the axial displacement is directly obtained from the change in phase of the OCT signal, unlike in QPD-based back-focal plane interferometry, where the displacement is obtained from voltage-to-displacement conversion. Compared to the computationally intensive reconstruction of axial position from 2D holograms in digital holographic microscopy, the axial displacement can be obtained from the raw SD-OCT signal via 1D Fourier transformation and calculation of the phase angle of the OCT signal. Lastly, OCT operates in reflection mode, whereas back-focal plane interferometry and digital holographic microscopy in optical manipulation typically operate in transmission mode. Imaging in the reflective configuration can be advantageous when conducting measurements in thick or optically dense samples.
Although our presented experiments were designed to measure , our experimental approach is generally applicable to the measurement of forces in the axial direction that cannot be accounted for by known bead-medium interactions (e.g., buoyancy and drag forces). In our experiments, was the dominant external force that led to measurable changes in the dynamics of beads (note that our measurements with 976-nm beam in Fig. 5(d) rules out any significant contribution of absorption-mediated forces). However, if the experimental conditions were to change such that other types of external forces were present, the same experimental approach could be used to measure those forces. For instance, radiometric forces [51,52] can be measured by replacing the non-absorbing polystyrene beads with highly absorbing particles.
5.3 Potential for a new mode of optical manipulation with extended depth range
Our results demonstrate that the radiation pressure from a low-NA forcing beam could influence the dynamics of polystyrene beads over a depth range of several hundred micrometers (Figs. 3(a)–3(d)). This implies that parallel, but transversely localized, manipulation of multiple microscopic particles distributed over a large axial range can be achieved by a single low-NA beam. Combined with real-time detection of particle dynamics over an extended depth-of-field by OCT, radiation pressure from a low-NA beam, with a large confocal parameter, may open up new opportunities for quantitative optical manipulation and detection over spatial scales currently inaccessible to conventional single-beam gradient force optical traps. We note that the 400-µm depth range demonstrated here was limited by the axial coverage of the forcing beam, but in principle, OCT measurements of axial optical forces on a particle with millimeter-scale coverage is possible.
The ability to capture fast dynamics and quantify the magnitude of on multiple particles distributed across depths in parallel with a simple OCT setup and a low-NA beam may be beneficial for quantitative experiments in optical chromatography or particle sorting based on radiation pressure [24–27]. Real-time detection of particle motion over an extended axial range in optical manipulation is typically achieved with either a wide-field imaging system in a side-viewing configuration [14] or, more recently, digital holographic microscopy [15,17,61]. Here, we showed that OCT can offer another alternative mode of real-time particle displacement tracking for optical manipulation over an extended axial range. Compared to the existing suite of techniques, an OCT-based approach offers its own unique advantages. Firstly, OCT can facilitate measurements in a co-axial, epi-illumination configuration with the forcing beam and allow reconstruction of particle displacement via simple established algorithms. This can be beneficial when achieving side-view-wide-field or trans-illumination imaging is experimentally inconvenient or impractical. Secondly, OCT is suitable for imaging in scattering media, which may be particularly desirable in some biological applications, such as measurements in turbid cell suspensions. In a recent study, optical force has been proposed as a potential tool for diagnosis and sorting of blood cells with morphological diseases, such as red blood cells infected with the malaria parasite, into different stages of disease progression [63]. Combining the presented experimental configuration with a flow system used in particle sorting experiments, our method for quantification of may provide a new tool for quantitative optical sorting of cells in whole blood by stage of disease.
Our experimental approach is not restricted to the measurement of optical forces. Once the profile for the forcing beam has been characterized, measured dynamics of beads (together with refractive indices of the beads and the medium) can be used to quantify the mechanical properties of the medium. In the case of beads suspended in viscous fluid, as presented here, the viscosity can be measured. If the beads were to be embedded in viscoelastic materials (such as hydrogels of biological relevance), the viscoelastic moduli of these materials could be quantified. This concept has been exploited by OT-based active microrheology (OT-AMR) [64–66] to characterize the microscale mechanical properties below the surface of the viscoelastic biological media, i.e., beyond the reach of atomic force microscopy. Typical transverse forces employed in OT-AMR are on the order of 1-10 pN (for typical oscillation amplitudes of 50-100 nm) [64–66]. Our measurements confirm that forces in this range can also be achieved by a low-NA beam with a power of less than 100 mW. While OT-AMR excels at precise measurements on a selected number of beads over a limited depth below the surface (due to the use of a high-NA optical trap) [66], the use of a low-NA forcing beam is unique in its extended depth range over which transversely localized can be applied. By enabling parallel manipulation and measurements of multiple beads distributed over a depth range of several hundred micrometers, the combination of OCT imaging and optical manipulation based on low-NA radiation pressure has the potential to extend existing OT-based mechanical microscopy techniques to enable high-throughput volumetric measurements.
6. Conclusion
We have presented a new method for depth-resolved quantification of radiation-pressure forces based on the measurements of axial bead trajectories with OCT. After obtaining the axial velocity and acceleration of the beads by numerical differentiation of measured bead trajectories, radiation-pressure force acting in the axial direction as a function of depth on each bead was determined by solving the equation of motion that describes the dynamics of a moving sphere in a viscous fluid. Here, we used OCT for real-time monitoring of particle dynamics because it enables real-time axial position detection over a large depth range in a simple epi-illumination configuration. With appropriate modification to the experimental setup and sample configuration presented here, our measurements of axial radiation-pressure force may alternatively be achieved with traditional wide-field imaging from the side or digital holographic microscopy often employed for particle tracking in optical manipulation. Experimental measurements were compared to theoretical predictions of radiation-pressure force based on GLMT. We investigated the effects of beam power, wavelength, bead size, and relative refractive index, and found that our measurements exhibit general trends that are consistent with theory. However, due to the presence of aberrations and deviations from an ideal Gaussian beam profile, our measured depth-dependent radiation-pressure forces have lower magnitude around the focal plane, but a larger depth coverage than an ideal Gaussian beam. This highlights the importance of experimentally characterizing the radiation-pressure force profile from an actual (non-ideal) beam, as this can be challenging to accurately predict from theory. Lastly, our use of OCT to measure the dynamics of particles under manipulation by long-range axial optical forces may find applications in the study of optical manipulation methods with an extended depth coverage. Our method also provides a quantitative foundation for future applications that combine volumetric micromanipulation and OCT detection of bead dynamics in viscoelastic media.
Acknowledgments
The authors thank Dr. Michael Lamont for his useful suggestions on taking numerical derivatives of experimental data. The authors also thank Jeffrey A. Mulligan for insightful discussion and careful proof-reading of the paper. This work made use of the Cornell Center for Materials Research Shared Facilities which are supported through the NSF MRSEC program (DMR-1719875).
Funding
Funded in part by: National Institutes of Health (NIH) (NIBIB-R21EB022927, Adie); Cornell Discovery and Innovation Research Seed Award (Adie).
References and links
- 1.Ashkin A., “Acceleration and trapping of particles by radiation pressure,” Phys. Rev. Lett. 24(4), 156–159 (1970). 10.1103/PhysRevLett.24.156 [DOI] [Google Scholar]
- 2.Ashkin A., Dziedzic J. M., Bjorkholm J. E., Chu S., “Observation of a single-beam gradient force optical trap for dielectric particles,” Opt. Lett. 11(5), 288–290 (1986). 10.1364/OL.11.000288 [DOI] [PubMed] [Google Scholar]
- 3.Grier D. G., “A revolution in optical manipulation,” Nature 424(6950), 810–816 (2003). 10.1038/nature01935 [DOI] [PubMed] [Google Scholar]
- 4.Stevenson D. J., Gunn-Moore F., Dholakia K., “Light forces the pace: optical manipulation for biophotonics,” J. Biomed. Opt. 15(4), 041503 (2010). 10.1117/1.3475958 [DOI] [PubMed] [Google Scholar]
- 5.Bowman R. W., Padgett M. J., “Optical trapping and binding,” Rep. Prog. Phys. 76(2), 026401 (2013). 10.1088/0034-4885/76/2/026401 [DOI] [PubMed] [Google Scholar]
- 6.Ermilov S., Anvari B., “Dynamic Measurements of Transverse Optical Trapping Force in Biological Applications,” Ann. Biomed. Eng. 32(7), 1016–1026 (2004). 10.1023/B:ABME.0000032464.79116.07 [DOI] [PubMed] [Google Scholar]
- 7.Sarshar M., Wong W. T., Anvari B., “Comparative study of methods to calibrate the stiffness of a single-beam gradient-force optical tweezers over various laser trapping powers,” J. Biomed. Opt. 19(11), 115001 (2014). 10.1117/1.JBO.19.11.115001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wright W. H., Sonek G. J., Berns M. W., “Parametric study of the forces on microspheres held by optical tweezers,” Appl. Opt. 33(9), 1735–1748 (1994). 10.1364/AO.33.001735 [DOI] [PubMed] [Google Scholar]
- 9.Schut T. C. B., Hesselink G., de Grooth B. G., Greve J., “Experimental and Theoretical Investigations on the Validity of the Geometrical Optics Model for Calculating the Stability of Optical Traps,” Cytometry 12(6), 479–485 (1991). 10.1002/cyto.990120603 [DOI] [PubMed] [Google Scholar]
- 10.Arlt J., Garces-Chavez V., Sibbett W., Dholakia K., “Optical micromanipulation using a Bessel light beam,” Opt. Commun. 197(4-6), 239–245 (2001). 10.1016/S0030-4018(01)01479-1 [DOI] [Google Scholar]
- 11.Garcés-Chávez V., McGloin D., Melville H., Sibbett W., Dholakia K., “Simultaneous micromanipulation in multiple planes using a self-reconstructing light beam,” Nature 419(6903), 145–147 (2002). 10.1038/nature01007 [DOI] [PubMed] [Google Scholar]
- 12.Ayala Y. A., Arzola A. V., Volke-Sepúlveda K., “3D micromanipulation at low numerical aperture with a single light beam: the focused-Bessel trap,” Opt. Lett. 41(3), 614–617 (2016). 10.1364/OL.41.000614 [DOI] [PubMed] [Google Scholar]
- 13.Ayala Y. A., Arzola A. V., Volke-Sepulveda K., “Comparative study of optical levitation traps: focused Bessel beam versus Gaussian beams,” J. Opt. Soc. Am. B 33(6), 1060–1067 (2016). 10.1364/JOSAB.33.001060 [DOI] [Google Scholar]
- 14.Cizmar T., Garces-Chavez V., Dholakia K., Zemanek P., “Optical conveyor belt for delivery of submicron objects,” Appl. Phys. Lett. 86(17), 174101 (2005). 10.1063/1.1915543 [DOI] [Google Scholar]
- 15.Ruffner D. B., Grier D. G., “Optical Conveyors: A class of Active Tractor Beams,” Phys. Rev. Lett. 109(16), 163903 (2012). 10.1103/PhysRevLett.109.163903 [DOI] [PubMed] [Google Scholar]
- 16.Brzobohatý O., Karásek V., Šiler M., Chvátal L., Čižmár T., Zemánek P., “Experimental demonstration of optical transport, sorting and self-arrangement using a ‘tractor beam’,” Nat. Photonics 7(2), 123–127 (2013). 10.1038/nphoton.2012.332 [DOI] [Google Scholar]
- 17.Ruffner D. B., Grier D. G., “Universal, strong and long-ranged trapping by optical conveyors,” Opt. Express 22(22), 26834–26843 (2014). 10.1364/OE.22.026834 [DOI] [PubMed] [Google Scholar]
- 18.Liesener J., Reicherter M., Haist T., Tiziani H. J., “Multi-functional optical tweezers using computer-generated holograms,” Opt. Commun. 185(1-3), 77–82 (2000). 10.1016/S0030-4018(00)00990-1 [DOI] [Google Scholar]
- 19.Curtis J. E., Koss B. A., Grier D. G., “Dynamic holographic optical tweezers,” Opt. Commun. 207(1-6), 169–175 (2002). 10.1016/S0030-4018(02)01524-9 [DOI] [Google Scholar]
- 20.Cizmar T., Brzobohaty O., Dholakia K., Zemanek P., “The holographic optical micro-manipulation system based on counter-propagating beams,” Laser Phys. Lett. 8(1), 50–56 (2011). 10.1002/lapl.201010100 [DOI] [Google Scholar]
- 21.Guck J., Ananthakrishnan R., Mahmood H., Moon T. J., Cunningham C. C., Käs J., “The Optical Stretcher: A Novel Laser Tool to Micromanipulate Cells,” Biophys. J. 81(2), 767–784 (2001). 10.1016/S0006-3495(01)75740-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Guck J., Schinkinger S., Lincoln B., Wottawah F., Ebert S., Romeyke M., Lenz D., Erickson H. M., Ananthakrishnan R., Mitchell D., Käs J., Ulvick S., Bilby C., “Optical deformability as an inherent cell marker for testing malignant transformation and metastatic competence,” Biophys. J. 88(5), 3689–3698 (2005). 10.1529/biophysj.104.045476 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lautenschläger F., Paschke S., Schinkinger S., Bruel A., Beil M., Guck J., “The regulatory role of cell mechanics for migration of differentiating myeloid cells,” Proc. Natl. Acad. Sci. U.S.A. 106(37), 15696–15701 (2009). 10.1073/pnas.0811261106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Imasaka T., Kawabata Y., Kaneta T., Ishidzu Y., “Optical Chromatography,” Anal. Chem. 67(11), 1763–1765 (1995). 10.1021/ac00107a003 [DOI] [Google Scholar]
- 25.Kim S. B., Kim J. H., Kim S. S., “Theoretical development of in situ optical particle separator: cross-type optical chromatography,” Appl. Opt. 45(27), 6919–6924 (2006). 10.1364/AO.45.006919 [DOI] [PubMed] [Google Scholar]
- 26.Dholakia K., MacDonald M. P., Zemanek P., Cizmar T., “Cellular and Colloidal Separation Using Optical Forces,” in Methods Cell Biol. (2007), pp. 467–495. [DOI] [PubMed] [Google Scholar]
- 27.Zabetian M., Saidi M. S., Shafii M. B., Saidi M. H., “Separation of microparticles suspended in a minichannel using laser radiation pressure,” Appl. Opt. 52(20), 4950–4958 (2013). 10.1364/AO.52.004950 [DOI] [PubMed] [Google Scholar]
- 28.Benabid F., Knight J., Russell P., “Particle levitation and guidance in hollow-core photonic crystal fiber,” Opt. Express 10(21), 1195–1203 (2002). 10.1364/OE.10.001195 [DOI] [PubMed] [Google Scholar]
- 29.Chow T. H., Lee W. M., Tan K. M., Ng B. K., Sheppard C. J. R., “Resolving interparticle position and optical forces along the axial direction using optical coherence gating,” Appl. Phys. Lett. 97(23), 231113 (2010). 10.1063/1.3519976 [DOI] [Google Scholar]
- 30.Sitters G., Laurens N., de Rijk E. J., Kress H., Peterman E. J. G., Wuite G. J. L., “Optical Pushing: A Tool for Parallelized Biomolecule Manipulation,” Biophys. J. 110(1), 44–50 (2016). 10.1016/j.bpj.2015.11.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Liebert R. B., Prieve D. C., “Force Exerted by a Laser Beam on a Microscopic Sphere in Water: Designing for Maximum Axial Force,” Ind. Eng. Chem. Res. 34(10), 3542–3550 (1995). 10.1021/ie00037a043 [DOI] [Google Scholar]
- 32.Nemoto S., Togo H., “Axial force acting on a dielectric sphere in a focused laser beam,” Appl. Opt. 37(27), 6386–6394 (1998). 10.1364/AO.37.006386 [DOI] [PubMed] [Google Scholar]
- 33.Ren K. F., Gréhan G., Gouesbet G., “Prediction of reverse radiation pressure by generalized Lorenz-Mie theory,” Appl. Opt. 35(15), 2702–2710 (1996). 10.1364/AO.35.002702 [DOI] [PubMed] [Google Scholar]
- 34.Gouesbet G., Grehan G., Generalized Lorenz-Mie Theories, 2 ed. (Springer International Publishing, 2017), p. 331. [Google Scholar]
- 35.Ambrosio L. A., Zamboni-Rached M., “Optical forces experienced by arbitrary-sized spherical scatterers from superpositions of equal-frequency Bessel beams,” J. Opt. Soc. Am. B 32(5), B37–B46 (2015). 10.1364/JOSAB.32.000B37 [DOI] [Google Scholar]
- 36.Yang M., Wu Y., Ren K. F., Sheng X., “Computation of radiation pressure force exerted on arbitrary shaped homogeneous particles by high-order Bessel vortex beams using MLFMA,” Opt. Express 24(24), 27979–27992 (2016). 10.1364/OE.24.027979 [DOI] [PubMed] [Google Scholar]
- 37.Wu F. P., Zhang B., Liu Z. L., Tang Y., Zhang N., “Optical trapping forces of a focused azimuthally polarized Bessel-Gaussian beam on a double-layered sphere,” Opt. Commun. 405, 96–100 (2017). 10.1016/j.optcom.2017.07.066 [DOI] [Google Scholar]
- 38.Dimova R., Pouligny B., “Absorbing microspheres in water: laser radiation pressure and hydrodynamic forces,” in Scattering of Shaped Light Beams and Applications, Gouesbet G., Grehan G., eds. (2000), pp. 45–65. [Google Scholar]
- 39.Abbas M. M., Craven P. D., Spann J. F., Witherow W. K., West E. A., Gallagher D. L., Adrian M. L., Fishman G. J., Tankosic D., LeClair A., Sheldon R., Thomas E., Jr, “Radiation pressure measurements on micron-size individual dust grains,” J. Geophys. Res. 108(A6), 1229 (2003). 10.1029/2002JA009744 [DOI] [Google Scholar]
- 40.Mu W., Li Z., Luan L., Spalding G. C., Wang G., Ketterson J. B., “Force measurement on microspheres in an optical standing wave,” J. Opt. Soc. Am. B 25(5), 763–767 (2008). 10.1364/JOSAB.25.000763 [DOI] [Google Scholar]
- 41.Choi W. J., Park K. S., Eom T. J., Oh M. K., Lee B. H., “Tomographic imaging of a suspending single live cell using optical tweezer-combined full-field optical coherence tomography,” Opt. Lett. 37(14), 2784–2786 (2012). 10.1364/OL.37.002784 [DOI] [PubMed] [Google Scholar]
- 42.Neuman K. C., Block S. M., “Optical Trapping,” Rev. Sci. Instrum. 75(9), 2787–2809 (2004). 10.1063/1.1785844 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lamb H., Hydrodynamics, 6th ed. (C.U.P, 1932), p. 738. [Google Scholar]
- 44.Hale G. M., Querry M. R., “Optical Constants of Water in the 200-nm to 200-microm Wavelength Region,” Appl. Opt. 12(3), 555–563 (1973). 10.1364/AO.12.000555 [DOI] [PubMed] [Google Scholar]
- 45.Takamura K., Fischer H., Morrow N. R., “Physical properties of aqueous glycerol solutions,” J. Petrol. Sci. Eng. 98–99, 50–60 (2012). 10.1016/j.petrol.2012.09.003 [DOI] [Google Scholar]
- 46.Rheims J., Koser J., Wriedt T., “Refractive-index measurements in the near-IR using an Abbe refractometer,” Meas. Sci. Technol. 8(6), 601–605 (1997). 10.1088/0957-0233/8/6/003 [DOI] [Google Scholar]
- 47.Kozma I. Z., Krok P., Riedle E., “Direct measurement of the group-velocity mismatch and derivation of the refractive-index dispersion for a variety of solvents in the ultraviolet,” J. Opt. Soc. Am. B 22(7), 1479–1485 (2005). 10.1364/JOSAB.22.001479 [DOI] [Google Scholar]
- 48.Segur J. B., Oberstar H. E., “Viscosity of Glycerol and Its Aqueous Solutions,” Ind. Eng. Chem. 43(9), 2117–2120 (1951). 10.1021/ie50501a040 [DOI] [Google Scholar]
- 49.Gonzalez J. A. T., Longinotti M. P., Corti H. R., “The Viscosity of Glycerol-Water Mixture Including the Supercooled Region,” J. Chem. Eng. Data 56(4), 1397–1406 (2011). 10.1021/je101164q [DOI] [Google Scholar]
- 50.Ahnert K., Abel M., “Numerical differentiation of experimental data: local versus global methods,” Comput. Phys. Commun. 177(10), 764–774 (2007). 10.1016/j.cpc.2007.03.009 [DOI] [Google Scholar]
- 51.Huisken J., Stelzer E. H. K., “Optical levitation of absorbing particles with a nominally Gaussian laser beam,” Opt. Lett. 27(14), 1223–1225 (2002). 10.1364/OL.27.001223 [DOI] [PubMed] [Google Scholar]
- 52.Schermer R. T., Olson C. C., Coleman J. P., Bucholtz F., “Laser-induced thermophoresis of individual particles in a viscous liquid,” Opt. Express 19(11), 10571–10586 (2011). 10.1364/OE.19.010571 [DOI] [PubMed] [Google Scholar]
- 53.Lumerical Inc , Lumerical FDTD Solutions. https://www.lumerical.com/tcad-products/fdtd.
- 54.Neves A. A. R., Fontes A., Cesar C. L., Camposeo A., Cingolani R., Pisignano D., “Axial optical trapping efficiency through a dielectric interface,” Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 76(6), 061917 (2007). 10.1103/PhysRevE.76.061917 [DOI] [PubMed] [Google Scholar]
- 55.Arita Y., McKinley A. W., Mazilu M., Rubinsztein-Dunlop H., Dholakia K., “Picoliter Rheology of Gaseous Media Using a Rotating Optically Trapped Birefringent Microparticle,” Anal. Chem. 83(23), 8855–8858 (2011). 10.1021/ac2024365 [DOI] [PubMed] [Google Scholar]
- 56.Adie S. G., Graft B. W., Ahmad A., Dabarsyah B., Boppart S. A., Carney P. S., “The impact of aberrations on object reconstruction with interferometric synthetic aperture microscopy,” Proc. SPIE 7889, 78891O (2011). 10.1117/12.875592 [DOI] [Google Scholar]
- 57.Polaert H., Gouesbet G., Gréhan G., “Laboratory determination of beam-shape coefficients for use in generalized Lorenz-Mie theory,” Appl. Opt. 40(10), 1699–1706 (2001). 10.1364/AO.40.001699 [DOI] [PubMed] [Google Scholar]
- 58.Hodges J. T., Gréhan G., Gouesbet G., Presser C., “Forward scattering of a Gaussian beam by a nonabsorbing sphere,” Appl. Opt. 34(12), 2120–2132 (1995). 10.1364/AO.34.002120 [DOI] [PubMed] [Google Scholar]
- 59.Chen Y. F., Blab G. A., Meiners J. C., “Stretching Submicron Biomolecules with Constant-Force Axial Optical Tweezers,” Biophys. J. 96(11), 4701–4708 (2009). 10.1016/j.bpj.2009.03.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Yehoshua S., Pollari R., Milstein J. N., “Axial Optical Traps: A New Direction for Optical Tweezers,” Biophys. J. 108(12), 2759–2766 (2015). 10.1016/j.bpj.2015.05.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Lee S. H., Grier D. G., “Holographic microscopy of holographically trapped three-dimensional structures,” Opt. Express 15(4), 1505–1512 (2007). 10.1364/OE.15.001505 [DOI] [PubMed] [Google Scholar]
- 62.Chang E. W., Kobler J. B., Yun S. H., “Subnanometer optical coherence tomographic vibrography,” Opt. Lett. 37(17), 3678–3680 (2012). 10.1364/OL.37.003678 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Gongora J. S. T., Fratalocchi A., “Optical force on diseased blood cells: Towards the optical sorting of biological matter,” Opt. Lasers Eng. 76, 40–44 (2016). 10.1016/j.optlaseng.2015.04.019 [DOI] [Google Scholar]
- 64.Mizuno D., Head D. A., MacKintosh F. C., Schmidt C. F., “Active and Passive Microrheology in Equilibrium and Nonequilibrium Systems,” Macromolecules 41(19), 7194–7202 (2008). 10.1021/ma801218z [DOI] [Google Scholar]
- 65.Kotlarchyk M. A., Shreim S. G., Alvarez-Elizondo M. B., Estrada L. C., Singh R., Valdevit L., Kniazeva E., Gratton E., Putnam A. J., Botvinick E. L., “Concentration Independent Modulation of Local Micromechanics in a Fibrin Gel,” PLoS One 6(5), e20201 (2011). 10.1371/journal.pone.0020201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Keating M., Kurup A., Alvarez-Elizondo M., Levine A. J., Botvinick E., “Spatial distributions of pericellular stiffness in natural extracellular matrices are dependent on cell-mediated proteolysis and contractility,” Acta Biomater. 57, 304–312 (2017). 10.1016/j.actbio.2017.05.008 [DOI] [PMC free article] [PubMed] [Google Scholar]