Intraoperative evaluation of device placement in spine surgery using known-component 3D-2D image registration

Abstract

Purpose

Intraoperative x-ray radiography/fluoroscopy is commonly used to assess the placement of surgical devices in the operating room (e.g., spine pedicle screws), but qualitative interpretation can fail to reliably detect suboptimal delivery and/or breach of adjacent critical structures. We present a 3D-2D image registration method wherein intraoperative radiographs are leveraged in combination with prior knowledge of the patient and surgical components for quantitative assessment of device placement and more rigorous quality assurance (QA) of the surgical product.

Methods

The algorithm is based on known-component registration (KC-Reg) in which patient-specific preoperative CT and parametric component models are used. The registration performs optimization of gradient similarity, removes the need for offline geometric calibration of the C-arm, and simultaneously solves for multiple component bodies, thereby allowing QA in a single step (e.g., spinal construct with 4–20 screws). Performance was tested in a spine phantom, and first clinical results are reported for QA of transpedicle screws delivered in a patient undergoing thoracolumbar spine surgery.

Results

Simultaneous registration of 10 pedicle screws (5 contralateral pairs) demonstrated mean target registration error (TRE) of 1.1 ± 0.1 mm at the screw tip and 0.7 ± 0.4° in angulation when a prior geometric calibration was used. The calibration-free formulation, with the aid of component collision constraints, achieved TRE of 1.4 ± 0.6 mm. In all cases, a statistically significant improvement (p < 0.05) was observed for the simultaneous solutions in comparison to previously reported sequential solution of individual components. Initial application in clinical data in spine surgery demonstrated TRE of 2.7 ± 2.6 mm and 1.5 ± 0.8°.

Conclusions

The KC-Reg algorithm offers an independent check and quantitative QA of the surgical product using radiographic / fluoroscopic views acquired within standard OR workflow. Such intraoperative assessment could improve quality and safety, provide the opportunity to revise suboptimal constructs in the OR, and reduce the frequency of revision surgery.

A Introduction

Intraoperative x-ray radiography/fluoroscopy is widely used to guide and evaluate the delivery of surgical devices (e.g., guide wires, screws, plates, and rods), but the assessment of device placement is often limited to qualitative interpretation of radiographic views in relation to the 3D patient anatomy. One such example is in spine surgery procedures in which screws are placed through the spinal pedicle in close proximity to critical anatomical structures such as nerves (e.g., spinal cord) and major vessels (e.g., aorta). Screw malplacement in this context is defined as perforation (i.e., breach) of the vertebral cortex and is commonly classified by severity (types 1–3) based on position of the screws with respect to the cortical boundaries of the pedicle and vertebral body (Kast et al 2006) and/or neurological impact (Ranawat et al 1979). Clinical studies suggest overall maximum permissible errors of 1 mm and 5° (Rampersaud et al 2001). This tight margin of error is also evident in the high number of malplacements encountered in 28–40% of surgeries (Gertzbein and Robbins 1990, Laine et al 2000). While x-ray fluoroscopy is commonly used for both guidance and quality assurance (QA) following instrumentation, qualitative interpretation of projection images may challenge unambiguous targeting of vertebral levels, verification of individual screws due to overlap (e.g., bilateral screws in LAT projections), reliable assessment of medial or lateral pedicle breach (in AP views), and/or determining screw depth (in LAT views).

The current gold standard for verification of pedicle screw placement is postoperative CT, which can accurately detect breaches (Lehman et al 2007). Although metal implants present artifacts that degrade image quality (especially at the implant boundary), a greater shortfall of this approach is assessment outside the OR and after the procedure from which positive findings – if clinically significant – are an indication for secondary (revision) surgery. Approximately 1–2% of all screw placement cases (Gautschi et al 2011) necessitate such revision surgery, which can result in additional morbidity and cost. Introduction of intraoperative CT (Tormenti et al 2010) or C-arm cone-beam CT (CBCT) (Siewerdsen et al 2005, Tabaraee et al 2013) presents a means to obtain such verification in the OR, recognizing that factors of dose, cost, and additional workflow may limit broad utilization. However, the value of intraoperative 3D visualization and its effect on QA of the surgical product is evident in studies that show 18.4% of spine screws (Sembrano et al 2012) and 32.7% of ankle screws (Franke et al 2012) were revised intraoperatively following CT or CBCT imaging.

Alternatively, 3D-2D image registration offers a method for accurate 3D localization directly from intraoperative 2D images. In a broad spectrum of procedures, including spine surgery, these methods can extend the utility of intraoperative 2D imaging that is already present in standard workflow, thus circumventing specific challenges and limitations associated with 3D imaging and/or surgical tracking systems. Integrating such methods into natural workflow, however, requires these solutions to respect and adapt to the procedure (e.g., C-arm placement, radiographic protocols, etc.). The performance of 3D-2D registration relies on a multitude of factors including, but not limited to: the specific algorithm used, the number and perspective of 2D images acquired (Uneri et al 2014a), the dose and image quality (Uneri et al 2014b), complexity of the surgical scene, and uncertainty in prior information such as a prior calibrated perspective x-ray imaging geometry. Recent work on vertebral level localization from single radiographs handles complexities due to mismatches in 3D and 2D image content via a robust similarity metric (De Silva et al 2016). Geometric uncertainty has also been treated by (Mitrović et al 2015) via simultaneous registration and calibration of biplane C-arm views acquired during intracranial endovascular interventions and by (Ouadah et al 2016) via 3D-2D registration for “self-calibration” in C-arm CBCT imaging.

3D-2D registration methods have also been applied in contexts apart from imaging, such as statistical models of patient anatomy (Sadowsky et al 2007) and device implants (Jaramaz and Eckman 2006). In pedicle screw placement procedures, recent work showed the feasibility of using “known components” (KC) (Uneri et al 2015a) to identify an individual screw and compute its position with respect to a CT image of the patient. In a real clinical setting, however, the radiographic scene is often more complex, presenting a high density of instrumentation, including multiple screws that may overlap in the radiographic scene and lead to degeneracies in registration. A comparable problem was addressed by (Lin et al 2013), where the poses of individual vertebrae were solved while avoiding vertebral collisions by identifying them in 2D images. Similarly (Prins et al 2010) demonstrated improvements in registration accuracy by identifying and avoiding collisions between multiple rigid bodies involved in knee prostheses.

In this work, a 3D-2D registration method is presented wherein prior knowledge of the patient and surgical components is leveraged to match preoperative 3D data and intraoperative 2D radiographs for quantitative assessment of pedicle screw placement. Advances from previous work are derived and evaluated to address key challenges to clinical translation, including: avoiding the need for prior offline geometric calibration (offering greater flexibility in view acquisition on a broader range of imaging systems that may be ill suited to reliable calibration); performing registration of multiple components simultaneously in a single step (e.g., spinal construct with 4–20 screws), rather than sequential QA per component; and constraining the registration solution against component collisions. Performance was evaluated in a spine phantom with 10 pedicle screws, an example implementation of screw placement QA is illustrated, and first application of the method in clinical data is reported.

B Methods

B.1 Registration algorithm

The proposed algorithm combines two gradient-based, rigid 3D-2D registrations that work in tandem to solve for the 3D pose and shape of the components within the patient’s frame of reference. These distinct stages are depicted in Figure 1. In each stage, 2D intraoperative radiographic projections are registered to the respective source of 3D prior information (the patient CT image P, or the device component model C) by iterative maximization of gradient similarity between the radiographs (R_θ) and digitally reconstructed radiographs (DRRs) of the input 3D data (P or C). This work advances beyond the original algorithm reported in (Uneri et al 2015a) with key improvements essential to clinical translation, including: automatic radiographic pose estimation, thereby avoiding the need for offline geometric calibration of the C-arm; and the ability to solve for multiple component bodies simultaneously with enforced collision constraints. The former aspect extends applicability beyond well-calibrated, computer-controlled C-arms and allows increased degrees of freedom (DoF) in C-arm positioning (e.g., oblique views for which even high-end C-arms may lack calibration). Moreover, the method permits registration of multiple components (e.g., acquired in a single QA step performed near the end of the case), rather than step-wise sequential verification of each component throughout the procedure.

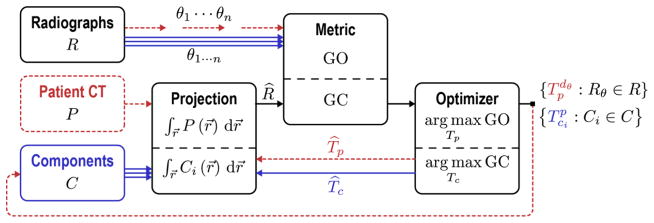
Figure 1.

Flowchart for the Known-Component Registration (KC-Reg) algorithm. Two stages operate in tandem: registration of 2D radiographs (P) acquired at perspective views (θ) to: (i) the 3D patient CT (P) shown by dotted paths; and (ii) the 3D models of surgical components (C) shown by solid paths. The “Projection” is a GPU-accelerated forward projection operation that generates DRRs. The similarity “Metric” is a gradient-based objective function (GO for patient registration and GC for component registration) that is then maximized by the “Optimizer” (CMA-ES). The registration yields transforms T that relate the 3D positions of surgical components within the reference frame of the patient CT, allowing quantitative assessment of the surgical construct.

B.2 Patient registration

The patient registration stage is based on the method in (Otake et al 2012), and computes the transformation relating one or more radiographs to the preoperative patient CT (P) acquired for surgical planning (or alternatively, a C-arm CBCT acquired during the procedure). The projection step computes the DRR (R̂) from P as follows:

$$\begin{gathered} \widehat{R}(u,v)={\int }_{x}P\left(\overrightarrow{r}(x)\right)\stackrel{.}{\overrightarrow{r}}(x)\mathrm{d}x \\ ={\int }_{\overrightarrow{r}}P(\overrightarrow{r})\mathrm{d}\overrightarrow{r} \end{gathered}$$ (1)

where each pixel (at location u, v) of R̂ is defined as a line integral along its corresponding ray r⃗, approximated by the sum of uniformly sampled and trilinearly interpolated samples in P. A ray is defined by the origin (x-ray source position, s) and a direction γ:

$$\overrightarrow{r}(x)=s+\gamma x$$ (2)

where s and γ may be obtained from the geometric calibration of the imaging system, represented as a projection matrix H, which defines the homography between 3D and 2D spaces as described in (Galigekere et al 2003). Substituting s and γ, (2) can be expressed in terms of H for a given pixel location u, v as:

$${\overrightarrow{r}}_H(x)=-H_{3\times 3}^{-1}{H}_4-H_{3\times 3}^{-1}{[\begin{array}{lll}u\hfill & v\hfill & 1\hfill \end{array}]}^{T}x$$ (3)

Assuming an offline (prior) calibration that provides H̃_θ for a given view, R̂ can be computed at a given patient pose $T_p^w$ (with respect to the calibrated world frame, w) using:

$$H={\stackrel{\sim }{H}}_{\theta }{T}_p^w$$ (4)

thus effectively transforming the calibrated geometry to be defined about the current patient pose. Modifying the projective geometry in this manner is an alternative to interpolation of the 3D image P that would otherwise increase computational cost and introduce additional artifacts.

The metric step compares the DRRs at candidate poses to the actual radiographs using gradient orientation (GO) as a similarity metric. The GO metric has been shown (De Silva et al 2016) to be robust against image content mismatch, such as that presented by surgical devices (e.g., screws, retractors, etc.) in the radiograph (but not the preoperative CT):

$$\begin{gathered} \text{GO}(f,m)=\frac{1}{N}\sum _{\nabla f>t_f,\nabla m>t_m,\alpha >t_{\alpha }}1-\frac{ln(\mid \alpha (\nabla f,\nabla m)\mid +1)}{2} \\ \text{where},\alpha (f,m)={\mathit{cos}}^{-1}\frac{f·m}{\Vert f\Vert \Vert m\Vert } \end{gathered}$$ (5)

where GO is defined between the fixed (f) R and moving (m) R̂ in terms of the angular alignment (α) of image gradients (∇). The thresholds t_f and t_m are selected as the median value of the ∇f and ∇m, respectively, while t_α = 45° ensures that only well-aligned gradients contribute to the similarity metric.

The optimizer step then maximizes the similarity metric through an iterative optimization process, where the objective function is expressed as:

$$\begin{gathered} {\widehat{T}}_p^w=\underset{T_p^w}{argmax}{\sum }_{\theta }\text{GO}\left(R_{\theta },{\int }_{\overrightarrow{r}}P({\overrightarrow{r}}_H)\mathrm{d}{\overrightarrow{r}}_H\right) \\ \text{where},H={\stackrel{\sim }{H}}_{\theta }{T}_p^w \end{gathered}$$ (6)

This objective is solved for the sole unknown parameter, patient pose $T_p^w$ (represented by 6 DoF) using the covariance matrix adaptation evolution strategy (CMA-ES) (Hansen and Ostermeier 2001). CMA-ES is a derivative-free, evolutionary algorithm with robust performance in optimizing such non-linear, non-convex functions. Its comparably slow convergence properties were mitigated by GPU-parallelized implementation of the projection (Eq. 1) and metric (Eq. 5) computations to achieve runtimes of ~0.1–1 s/iteration (contingent on factors such as component model complexity). A convergence criterion (rather than a specified number of maximum iterations) was used to terminate iterations when the change in transformation parameters was less than a threshold value of 0.1 mm or 0.1°.

The optimization problem described here and extended below uses a number parameters and variables that can affect registration performance. Previous work investigated many of these factors: for example, the number of projection views and their angular separation was evaluated in (Uneri et al 2014a) to reveal a minimum angular separation of 10–15° to achieve the same geometric accuracy as provided by 90° separation. The same work also identified a joint dependence on CT slice thickness and detector binning, as well as an optimal magnification level (object at C-arm isocenter), findings that guided the selection of parameters in the studies below. In (Uneri et al 2014b), the effect of radiographic dose was evaluated and demonstrated robust results with the dose reduced by a factor of 5 from typical fluoroscopic dose. Evaluation of capture range in the same study showed robustness of the algorithm for initialization error within a few vertebrae (3–4 cm), recognizing that other methods exist for vertebra localization that could be used in conjunction with KC-Reg (Otake et al 2012).

B.2.1 Calibration-free patient registration

For cases in which a prior geometric calibration of the imaging system is not available (e.g., mobile radiography or uncalibrated oblique views), the projective transform may be reformulated instead to solve for the view-specific patient pose, $T_p^d$, with respect to the detector coordinate frame. Noting that a projective transform H is composed of intrinsic (K) and extrinsic ( $T_w^s$) parameters:

$$H{T}_p^w=([K\mid 0]T_w^s)T_p^w$$ (7)

where $T_w^s$ describes the world (w) coordinate frame with respect to the x-ray source (s). Assuming a known fixed 3 DoF translation ( $T_d^s$) between the source and detector (d), the remaining 6 DoF detector pose $T_d^w$ can be refactored and combined with patient pose as follows:

$$\begin{gathered} H{T}_p^w=[K\mid 0]{(T_d^w{T}_s^d)}^{-1}{T}_p^w \\ =[K\mid 0]T_d^s{T}_w^d{T}_p^w \\ =[K\mid 0]T_d^s{T}_p^d \\ =H^{\prime }{T}_p^d \end{gathered}$$ (8)

to yield $T_p^d$, which describes the patient pose with respect to a given detector pose. The new calibration-free optimization can then be reformulated for each unique view θ as:

$$\begin{gathered} {\widehat{T}}_p^{d_{\theta }}=\underset{T}{argmax}\text{GO}\left(R_{\theta },{\int }_{\overrightarrow{r}}P({\overrightarrow{r}}_H)\mathrm{d}{\overrightarrow{r}}_H\right) \\ \text{where},H=H^{\prime }{T}_p^{d_{\theta }} \end{gathered}$$ (9)

the solution to which relates the imaging geometry and patient pose. That is to say, the patient pose is no longer be defined by a single 6 DoF transform with respect to the calibrated C-arm world (w), but is instead described by a set of transforms per radiographic view (θ).

B.3 Component registration

The component registration extends the original formulation in (Uneri et al 2015a) which uses the preceding patient registration results (calibrated or calibration-free approach described in Section B.2) and the same set of radiographs to resolve the pose and shape of the components (C_i) within the patient reference frame. For the current work, parametric shape models were used, which do not rely on exact 3D models of the instrument that may be proprietary to the manufacturer. The screw component model comprises a shaft (long, thin cylinder), a head (short, thick cylinder), and a tip (cone), as depicted in Figure 2b, and is governed by 5 DoF. The component pose – owing to the radial symmetry of the model – is also 5 DoF, unlike the 6 DoF patient pose.

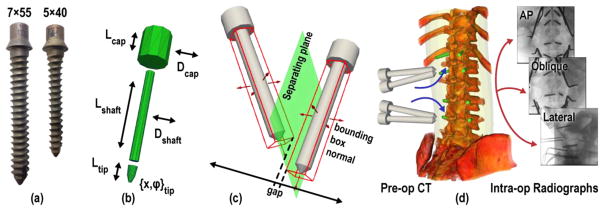
Figure 2.

Known-components. (a) Titanium pedicle screws of different sizes delivered in the phantom experiments. (b) Parametric model of a screw, showing the DoF governing its pose and the shapes of its multiple parts. (c) Collision constraint based on the separating axis of oriented bounding boxes for which a gap within the projection on to that axis implies that the components do not intersect. (d) Contralateral screws registered simultaneously to the patient CT by 3D-2D registration of AP, OBL, and LAT views.

DRRs of the components were computed as in (Eq. 1), differing only in that rays were integrated over convex triangular mesh representations of the component model as in (Uneri et al 2015b) instead of a volumetric voxel grid.

Contrary to the patient registration wherein the GO metric offers robustness against the strong gradients presented by metal devices, the component registration specifically exploits such gradients by instead maximizing the gradient correlation (GC) metric, defined in (Penney et al 1998):

$$\begin{gathered} \text{GC}(f,m)=\frac{1}{2}\{\text{NCC}({\nabla }_{x}f,{\nabla }_{x}m)+\text{NCC}({\nabla }_{y}f,{\nabla }_{y}m)\} \\ \text{where},\text{NCC}(f,m)=\frac{{\sum }_i(f_i-\overline{f})(m_i-\overline{m})}{\sqrt{{\sum }_i{(f_i-\overline{f})}^2}\sqrt{{\sum }_i{(m_i-\overline{m})}^2}} \end{gathered}$$ (10)

The objective function for optimization of a component pose in patient coordinates ( $T_c^p$, 5 DoF) and its shape parameters (S, 5 DoF) may then be expressed as:

$$\begin{gathered} {\widehat{T}}_c^p,\{{\widehat{S}}_j\}=\underset{T_c^p,S_c}{argmax}{\sum }_{\theta }\text{GC}\left(R_{\theta },{\sum }_j{\int }_{\overrightarrow{r}}{C}_j({\overrightarrow{r}}_H)\mathrm{d}{\overrightarrow{r}}_H\right) \\ \text{where},H=H^{\prime }{\widehat{T}}_p^{d_{\theta }}{T}_c^p{S}_j \end{gathered}$$ (11)

where the patient pose ${\widehat{T}}_p^{d_{\theta }}$ obtained in (Eq. 9) presents a common patient-centric reference frame that allows use of multiple views in identifying the 3D component pose by summing their respective contribution for all R_θ. The component parts (C_j) – corresponding to the screw shaft, head, and tip in the current context – are projected in an additive manner to obtain a composite DRR. Previous implementation in (Uneri et al 2015a) applied various shape parameters by creating modified copies of the input component mesh per tested sample. While this approach allows more complex parameterization, the simple models in the current work can be defined simply as scaling operations, for example:

$$S_{\text{shaft}}=\left[\begin{array}{ccc}\widehat{r}/r_0& 0& 0\\ 0& \widehat{r}/r_0& 0\\ 0& 0& \widehat{l}/l_0\end{array}\right]$$ (12)

where r̂ (radius) and l̂ (length) are the 2 DoF associated with the screw shaft, and the scaling is defined with respect to their initial values r₀ and l₀. Since scaling is a linear operation, S_j was included in H as in (Eq. 11) to scale the components during projection, thereby reducing the computational cost and memory usage.

B.3.1 Simultaneous component registrations

The formulation in (Eq. 11) handles a single component at a time, which may suffice in clinical scenarios in which each implant is sequentially placed and verified. For the (perhaps more broadly applicable) scenario in which the entire surgical construct (e.g., multiple screws placed across multiple vertebral levels) is to be evaluated, a simultaneous registration is desirable to provide QA of the full surgical construct. Taking further the example of spine surgery, a vertebra is commonly instrumented from contralateral sides, and while individually registering each screw is plausible, the confounding gradients from the contralateral screw may adversely affect registration, creating local optima or simply converging on the unintended screw. A simultaneous solution of multiple components has the advantage of more streamlined workflow, reduced radiation dose, and potentially broader utilization in procedures that do not use fluoroscopy throughout the case. To address this, (Eq. 11) was reformulated to simultaneously solve for multiple components present in the radiographic views as follows:

$$\begin{gathered} \{{\widehat{T}}_{c_i}^p\},\{{\widehat{S}}_{i,j}\}=\underset{T_c^p,S_c}{argmax}{\sum }_{\theta }\text{GC}\left(R_{\theta },{\sum }_i{\sum }_j{\int }_{\overrightarrow{r}}{C}_{i,j}({\overrightarrow{r}}_H)\mathrm{d}{\overrightarrow{r}}_H\right) \\ \text{where},H=H^{\prime }{\widehat{T}}_p^{d_{\theta }}{T}_{c_i}^p{S}_{i,j} \end{gathered}$$ (13)

where i, j denote the j^th part (e.g., shaft) of the i^th component.

B.3.2 Constraint on component collisions

While simultaneous registration of multiple components accounts for otherwise confounding gradients, degenerate solutions can still arise when two components match to the same gradients, for example when they partially overlap in some of the projection views. A collision constraint was therefore defined to address this challenge, based on the separating axis theorem (SAT). The SAT states that if two convex objects are not penetrating, there exists an axis for which the (orthogonal) projection of the objects will not overlap (Gottschalk et al 1996). The theorem readily extends to 3D, since the separating axis is always a line (i.e., normal to the separating plane).

Given two components A and B, bounding boxes can be computed from their corresponding triangular meshes (Figure 2c) with extents (e_i) along each dimension, oriented by a known translation (t) of its centroid and rotated by R. It follows from the SAT that an axis x separates A and B if and only if:

$$\mid t_A-t_B·x\mid >\sum _{\mathrm{i}=1}^3\frac{e_{A,i}}{2}|R_{A,i}·x|+\sum _{\mathrm{i}=1}^3\frac{e_{B,i}}{2}|R_{B,i}·x|$$ (14)

That is to say, when orthogonally projected onto the axis x, the centroids of the boxes should be separated by more than their combined radii. The use of oriented bounding boxes allows for both further simplification of this expression as shown in (Gottschalk et al 1996), and more importantly, in limiting the number of potential separating axes to 15, i.e. 3 surface normals per box (face-face collisions) and their 9 cross-products (face-edge and edge-edge collisions). The components are said to be non-colliding if any of the tested 15 axes satisfy (Eq. 14), in which case new samples are drawn from the population.

B.4 Joint patient and component registration

The fundamental premise underlying the presented optimization approach is that the objective function (similarity metric) is maximized at the true physical location of the patient and component. While the calibration-free patient registration allows more freedom in C-arm positioning, obtaining a 3D patient pose from a single radiographic view is challenging, and was shown in (Uneri et al 2014a) to have limited accuracy in 3D pose determination. The use of multiple projections in the component registration offers a degree of robustness to outliers in the former stage; however, large or systematic errors may introduce local maxima that confound the optimization or displace the location of the global maximum such that the fundamental premise no longer holds (i.e., the detected optimum no longer represents the correct physical location).

One approach to mitigate these effects involves joint optimization of the patient and component objectives as follows:

$$\begin{gathered} \left\{T_p^{d_{\theta }}\right\},\{{\widehat{T}}_{c_i}^p\},\{{\widehat{S}}_{c_i}\}=\underset{T_c^p,S_c}{argmax}{\sum }_{\theta }max\left\{\begin{array}{c}\text{GC}\left(R_{\theta },{\int }_{\overrightarrow{r}}P\left({\overrightarrow{r}}_{Hp}\right)\mathrm{d}{\overrightarrow{r}}_{Hp}\right),\\ \text{GC}\left(R_{\theta },{\sum }_i{\sum }_j{\int }_{\overrightarrow{r}}{C}_{i,j}({\overrightarrow{r}}_{H_c})\mathrm{d}{\overrightarrow{r}}_{H_c}\right)\end{array}\right\} \\ \text{where},H_p=H^{\prime }{T}_p^{d_{\theta }} \\ \text{and}{H}_c=H_p{T}_{c_i}^p{S}_{c_i} \end{gathered}$$ (15)

which essentially combines the solutions presented in (Eq. 9) and (Eq. 13). A major challenge of this formulation is the increased number of DoF, requiring 6 DoF per view for $T_p^{d_{\theta }}$, and 10 DoF per screw for ${\widehat{T}}_{c_i}^p$ and Ŝ_ci. For 3 radiographic views and 2 contralateral screws, this amounts to a total of 38 DoF, and while this is substantially larger than the preceding approaches described above, CMA-ES optimization has been shown to work robustly for problem dimensions of up to 320 (Hansen and Ostermeier 2001).

To further accommodate the increased DoF and improve convergence characteristics, the joint solution is applied by restarting a previously converged optimization (e.g., using one of the solutions in previous sections). In this manner, the “joint restart” approach fine-tunes the registration estimate using the component to regularize otherwise independent individual patient registrations, since the component similarity across all views is maximized only if the underlying patient registration is correct. Note that this assumes a rigid relationship between the patient and components across multiple radiographic views, which is a fair assumption for rigid implants in bony anatomy. The combined contribution from the patient anatomy and components therein is computed as the maximum similarity to ensure intensity invariance. While the max operation necessitates the use of same metric (GC), the primary benefit of GO in handling mismatch is not as critical in this case, since the mismatches are predominantly caused by the components that – by definition – are modeled in the joint formulation.

B.5 Estimation of screw shape

The parametric component models used in this application allow flexible definition of screws without exact (and often proprietary) knowledge of their shape. The component registration presented in previous sections was shown to solve for these shape parameters along with the poses. As pedicle screws are typically characterized by their diameter and length, this provides an opportunity to uniquely identify the delivered screws, such that they can be validated against an intended surgical plan. For the employed component model, the screw diameter is taken as the diameter of the shaft cylinder, while the screw length is estimated as the shaft length + the conical tip. The accuracy of such parameters from the KC-Reg solution was evaluated in comparison to the (true) screw, and previous work (Uneri et al 2015b) showed a classification approach to detect mismatch between the planned and delivered screw. In this way, the same KC-Reg algorithm used to QA screw placement can also be used to assess the size of each screw and confirm relative to those defined in the surgical plan.

B.6 Experiments and evaluation

B.6.1 Phantom experiments

The performance of the KC-Reg algorithm was first evaluated in experiments using an anthropomorphic spine phantom (Sawbones, Pacific Research Laboratories, Seattle WA USA) within a soft-tissue holder (Figure 3a). Preoperative (pre-op) and postoperative (post-op) CT scans were acquired prior to and following placement of instrumentation, respectively, using a standard spine imaging protocol (100 kVp, 100 mAs, and 0.5 mm slice thickness from C1 to sacrum; Toshiba Aquilion ONE). Sets of 3 intraoperative radiographs (nominally anterior-posterior [AP], oblique [OBL], and lateral [LAT]) were acquired in the course of device placement using a mobile C-arm (Cios Alpha mobile C-arm, Siemens Healthcare) with a flat-panel detector (PaxScan 3030X, Varian Imaging Products, Palo Alto CA USA) covering a 30×30 cm² field of view (at the detector plane, nominally 20×20 cm² at the patient) at 0.388×0.388 mm² pixel size. The radiographic technique was 70 kVp (+2 mm Cu to simulate ~15 cm water additional to the fairly thin spine holder) and 47 mA × 11.2 ms pulse width (0.5 mAs) for 3 frames. Measured entrance surface dose was 29.9 ± 0.2 μGy/frame, which is much lower than conventional radiographic ranges of 0.2–0.3 mGy (Uffmann and Schaefer-Prokop 2009) and is near the upper end of the nominal fluoroscopic range of 6–28 μGy/frame (Mahesh 2001).

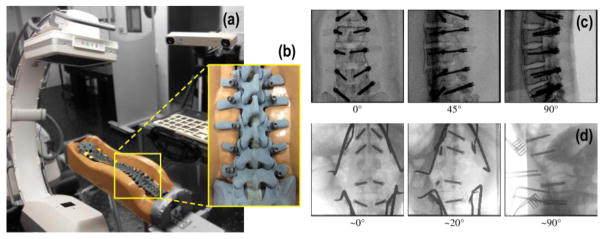
Figure 3.

Phantom and clinical studies. (a) The C-arm was used to acquire radiographs of a spine phantom at varying angular views. (b) Close-up of the instrumented spine phantom. (c) AP, OBL, and LAT views of the lumbar (L1–L5) section of the instrumented spine phantom. (d) Clinical studies in which intraoperative radiographs were obtained using the same C-arm. The projections show AP, OBL, and LAT views of a patient undergoing thoracolumbar spine surgery with screws delivered at T12–L4. Additional instruments (e.g., retractors) are also visible.

The experiment emulated a standard lumbar fixation procedure, wherein vertebrae L1–L5 were instrumented with transpedicle screws (Centaur system, Stryker, Kalamazoo MI USA). A variety of device trajectories were delivered, including well placed screws as well as trajectories purposely delivered with various grades of pedicle breach according to Kast’s criteria (Kast et al 2006). Planning data were generated for all datasets in the form of simple linear trajectories down the pedicle, and a clinically acceptable region was demarked by the bony anatomy such that the trajectory lies interior to the cortex of the spinal pedicle and anterior cortex of the vertebral body.

Experiments were performed with and without C-arm geometric calibration to test the calibration-free methodology. For the “calibrated” case, geometric calibration was obtained immediately prior to experiments using a spiral BB phantom (Navab 1996) and an iterative least squares method based on Levenberg-Marquardt optimization.

To focus the registration on the bony anatomy of the spine, simple soft-tissue thresholding was applied on the preoperative CT. A volumetric mask around the spine was automatically generated similar to the method described in (Ketcha et al 2016b) using the planned trajectories. The 2D images were downsampled to 1×1 mm² and 3D images to 0.5×0.5×0.5 mm³, based on an approximate magnification factor of 2, which helps suppress noise and improve computational performance. The surgical plan provided to the registration system included specification of the number of screw trajectories and their desired orientation with respect to preoperative CT. In the current study, registrations were performed individually for each vertebral level, simultaneously solving the pose estimation for contralateral (left and right) screw pairs for each case.

B.6.2 Clinical study

The method was also applied for the first time in clinical data for a patient (47-year-old male) undergoing thoracolumbar posterior fusion. The preoperative CT image was acquired at 120 kVp and 250 mAs with 1 mm slice thickness (SOMATOM Definition Flash, Siemens Healthcare, Forcheim Germany). The vertebrae T12, L1, L3 and L4 were instrumented, spinal rods were attached, and a cage was placed between L1–L3. The radiographs shown in Figure 3b were acquired prior to attachment of the spinal rods as part of the standard procedure for qualitative assessment of screw placement. Radiographic technique was 80 kVp, 10.8 mAs. The same C-arm used during the phantom experiments was employed to obtain AP (~0°), OBL (~20°), and LAT (~90°) views. The C-arm was repositioned outside its calibrated orbit according to surgical requirements (surgeon’s preferred views for this patient setup), making it infeasible to use a geometric calibration; therefore, 3D-2D registration in the clinical study exclusively used the calibration-free formulation.

B.6.3 Evaluation of geometric accuracy

The performance of the KC-Reg algorithm was evaluated over 10 pedicle screws delivered in the phantom experiments and in 8 pedicle screws delivered in the clinical study. The geometric accuracy was quantified separately for translational and rotational components of the screw using screw tip locations and screw principle axes, respectively, such that:

$$\begin{gathered} {\text{TRE}}_x={\Vert {\left[T_c^p\right]}_4-{\left[T_c^{\stackrel{\sim }{p}}{T}_{\stackrel{\sim }{p}}^p\right]}_4\Vert }_2 \\ {\text{TRE}}_{\varphi }={cos}^{-1}\left({\left[T_c^p\right]}_3·{\left[T_c^{\stackrel{\sim }{p}}{T}_{\stackrel{\sim }{p}}^p\right]}_3\right) \end{gathered}$$ (16)

where $T_c^{\stackrel{\sim }{p}}$ is the true component pose segmented from the postoperative image (p), and $T_{\stackrel{\sim }{p}}^p$ is the rigid registration of preoperative and postoperative images obtained using adaptive stochastic gradient descent optimization of mutual information. The 4^th column of the transformation is the translation component, and the 3^rd (z) orthonormal column of the rotation matrix is the principal axis of the screw. TRE values are reported as mean ± interquartile range (IQR) and are evaluated with respect to the statistical significance in observed differences using the Mann-Whitney-Wilcoxon rank-sum test (p < 0.05 considered statistically significant, otherwise marked as “p-value NS”). In addition to pose determination, the performance of component shape estimation was quantified through comparison against specified dimensions of the screws. Screw diameters are typically quantized to 1 mm steps, and screw lengths to 5 mm steps; therefore, estimation to within ±0.5 mm and ±2.5 mm, respectively, was considered to be a successful categorization of screw type.

Finally, the KC-Reg solutions were used to overlay component representations within the preoperative image (augmented also by the planned trajectory and the vertebral cortex) to demonstrate the utility of KC-Reg as a tool for operating room quality assurance (ORQA). In this form, the screw pose and shape can be analyzed quantitatively with respect to the plan and visualized in relation to surrounding anatomy to more conspicuously highlight suboptimal placement (viz., breach) and provide a basis for revision of the surgical product within the same case (i.e., avoiding potential post-operative morbidity and/or repeat surgery).

C Results

C.1 Calibration-free patient registration

Figure 4 summarizes the performance of the sequential component registration [as in (Eq. 11)], the benefits of a prior C-arm geometric calibration, and the extent to which a calibration-free registration can be achieved. The screws implanted in the spine phantom were sequentially registered with and without the use of a prior geometric calibration, placing each screw in turn (from L5 to L1 left side, then the same on the contralateral side) and acquiring an AP, OBL, and LAT projection at each step. The overall registration accuracy (TRE_x and TRE_ϕ) is shown in Figure 4a–b for both the calibrated and calibration-free formulations [(Eq. 6) and (Eq. 9), respectively]. The results show that a prior calibration helps to reduce outliers and improve overall accuracy, resulting in a fairly modest improvement from TRE_x = 5.5 ± 2.8 mm (mean ± IQR) to 4.4 ± 3.7 mm (p-value ~NS, with the improved mean related primarily to reduction in outliers from false local optima) and TRE_ϕ = 3.4 ± 4.9° to 2.2 ± 0.6° (p < 0.05). While each method demonstrates basic feasibility, the predominant limiting factor for both approaches was observed to be outliers arising from gradients presented by the contralateral screw, which are unaccounted for in the sequential (single component) formulation and lead to false optima in the objective space. For example, Figure 4c–d shows aggregate registration results overlaid on postoperative CT of the L1 vertebra. The potential for outliers is evident in the calibration-free result (including some that suggest false-positive anterior breach), and while the calibrated result tends to eliminate such outliers, the sequential single-body registration result overall falls short of clinically acceptable errors [e.g., <2–4 mm error associated with that of surgical tracking systems (Labadie et al 2005)]. The combined run-time for the patient and component registrations was ~1.5 min per screw.

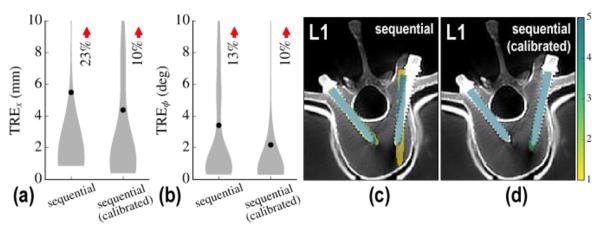
Figure 4.

Sequential component registration with and without geometric calibration of the C-arm. (a) Positional and (b) angular TRE with and without calibration. (c–d) Visualization of aggregate registration results superimposed on post-CT (c) without calibration and (d) with calibration. The colorscale overlay represents an aggregation of registration results over 5 repeat trials. The calibrated solution is seen to improve robustness, but the single-body approach still yields a fairly high registration error (upper bound of the IQR in TRE >4 mm).

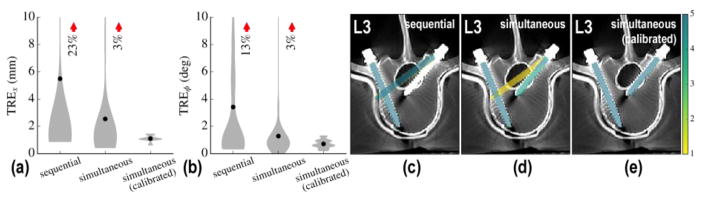
C.2 Simultaneous component registrations

Simultaneous registration of multiple components [as in (Eq. 13)] was tested for both calibrated and calibration-free patient registration. The results in Figure 5 show improvement over the sequential approach. For calibration-free registration, the simultaneous registration of multiple component bodies showed a reduction in mean TRE_x from 5.5 ± 2.8 mm for sequential to 2.5 ± 0.6 mm for simultaneous and mean TRE_ϕ from 3.4 ± 4.9° for sequential to 1.3 ± 0.8° for simultaneous. For registration with C-arm calibration, the TRE was further reduced to 1.1 ± 0.1 mm and 0.7 ± 0.4° (p < 0.01 and < 0.05, respectively). In the calibration-free formulation, a few degenerate solutions were still observed due to overlapping component gradients in radiographs as shown for the L3 vertebra in Figure 5.

Figure 5.

Simultaneous component registration. (a) Positional and (b) angular TRE for calibration-free sequential, simultaneous, and calibrated simultaneous solutions. (c–e) Aggregate registration results overlaid on post-op axial slices of the L3 vertebra. The sequential solution (c) is seen to converge at a false global optimum. The simultaneous solution (d) better avoids such degenerate a solution. The simultaneous approach using prior calibration (e) exhibits a high degree of accuracy with no outliers.

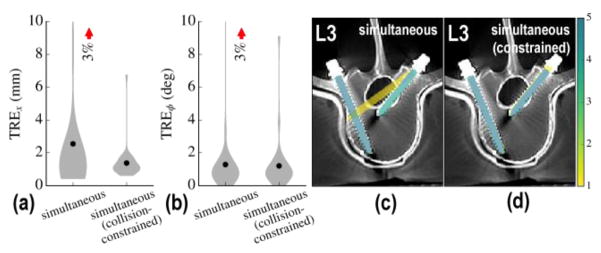
C.3 Constraint on component collisions

While the calibrated simultaneous solution was able to robustly converge at the solution, its calibration-free counterpart still exhibited outliers that are consistent with the overlap degeneracy observed in the sequential solutions. Using the method described in (Eq. 14) to identify and constrain component collisions, these local minima were effectively removed from the objective space. Figure 6 shows results for the calibration-free, simultaneous solution without and without collision constraint. The method is shown to avoid the outliers observed in the unconstrained case and yields a reduction in TRE to 1.4 ± 0.6 mm and 1.2 ± 0.7° approaching the performance of the calibrated solution (p-value ~NS compared against the calibrated solution).

Figure 6.

Constraint on component collisions. (a) Positional and (b) angular TRE with and without collision constraint for the simultaneous multi-body solution without C-arm geometric calibration. (c–d) Corresponding aggregate of registration results superimposed on post-op axial slices of the L3 vertebra for the (c) unconstrained and (d) constrained solution. The latter is found to avoid outliers arising from component overlap in radiographs.

Taken together (comparing Figure 6a with Figure 4a, for example), the simultaneous registration with collision constraint provided major improvement in accuracy and robustness in comparison to the previously reported sequential method for both the calibrated and calibration-free formulation (p < 0.05 in each case). While the overall run-time was increased to ~2.5 min (simultaneously solving for two screws within a vertebra), the computation time per screw (~1.25 min) was actually reduced (originally ~1.5 min).

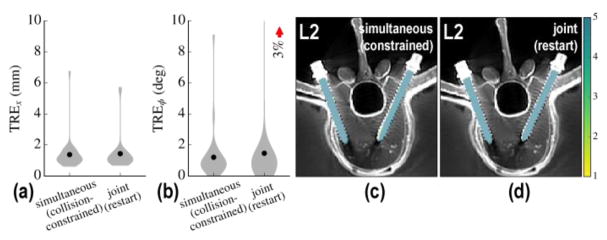
C.4 Joint patient and component registration

Extending the results summarized above to the joint solution described in (Eq. 15) greatly increases the number of DoF in the formulation. To promote faster convergence, therefore, the approach was initialized by the result of the calibration-free, collision-constrained, simultaneous formulation. As depicted in Figure 7, the joint restart did not improve registration accuracy in the phantom studies (no change in mean TRE). However, the intrinsic robustness of the joint approach against outliers in single-view patient registration warranted further investigation under more challenging scenarios, shown in the clinical studies, below. The run-time of the joint restart also increased the run-time to ~6 min, despite GPU parallelization.

Figure 7.

Restart using joint registration. (a) Positional and (b) angular TRE for the initial solution and after restarting with joint registration. (c–d) Corresponding post-op axial slices on L2 vertebra overlaid with aggregate registration solution. Restarting with joint registration did not show a statistically significant improvement in TRE in the phantom experiments (but is shown to add stability in the more complex clinical studies below).

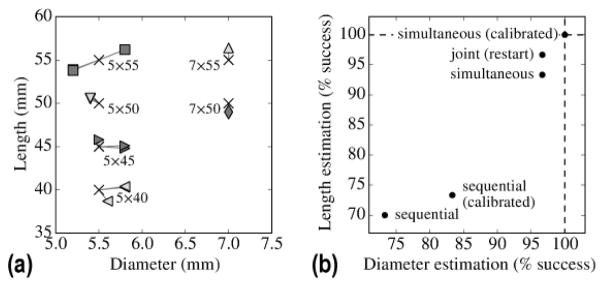
C.5 Estimation of screw shape

As described in Section B.5, the KC-Reg method also yields information relating to component shape (e.g., screw length and diameter) in a manner that could be valuable to QA / validation of the surgical construct. The estimated length and diameter for each of 10 screws in the phantom study are shown in Figure 8a based on KC-Reg results from the calibration-free, simultaneous registration, demonstrating reliable estimation of the component shapes. Figure 8b shows the rate of successful estimation of screw diameter and length for different registration methods, evaluated over 10 screws, repeated over 5 trials to account for the stochasticity of the CMA-ES optimization. Successful categorization of screw type taken as deviation <0.5 mm dimaeter and <2.5 mm length as described in Section B.6.3. The improvements demonstrated for component pose determination (as quantified by TRE, above) are similarly evident with respect to screw shape estimation, where the simultaneous registrations perform better than the sequential approaches, and calibrated simultaneous registration showed the best performance (accurate categorization of screw size in all cases).

Figure 8.

Estimation of screw size from the KC-Reg result. (a) Screw length and diameter as estimated by the calibration-free, simultaneous KC-Reg parameters at solution compared to the true values (marked by “X”). (b) Successful estimation of component shapes for the presented registration methods. Similar to the TRE results, the simultaneous solutions overall performed better than the sequential approaches and achieved 100% accuracy with the added benefit of C-arm geometric calibration.

C.6 Clinical study

The phantom studies summarized above provided a systematic evaluation of the KC-Reg algorithm performance under conditions of: (calibrated vs. calibration-free); (sequential vs. simultaneous); (with and without collision constraint); and (with and without joint restart). Those findings guided implementation of the KC-Reg approach for the first time to a clinical study, with initial findings summarized in Figure 9. The results show the KC-Reg solution for simultaneous component registration, with and without collision constraint, and with joint restart. In each case, the calibration-free registration was used – as both a more aggressive test of performance under challenging conditions and because in common practice, the C-arm may be positioned outside its calibrated orbit (e.g., craniocaudal oblique). The results are therefore conservative with respect to what might achieved with a geometric calibration of the C-arm.

Figure 9.

Application of KC-Reg in clinical data. (a) Positional and (b) angular TRE for 8 screws and 3 repeat registrations. (c) Corresponding post-op axial slices on all instrumented vertebrae. A monotonic improvement in accuracy and reduction in outliers was observed when using collision constraint and joint restart formulations. Main sources of error were in matching the tip of screws in L3 and a slight offset error in T12.

The results show a monotonic improvement in TRE_x from 3.9 ± 3.4 mm for the simultaneous approach to 3.2 ± 2.5 mm with the addition of the collision constraint. The corresponding improvement in TRE_ϕ was from 3.1 ± 1.8° to 2.5 ± 1.8°, respectively. Contrary to the phantom experiments, the benefit of the joint restart became clear in the clinical study, showing improved robustness to outliers associated with erroneous matching of a screw to strong anatomical gradients. The joint restart improved TRE_x to 2.7 ± 2.6 mm (p-value ~NS, with the improved mean related mostly to reduction in outliers) and 1.5 ± 0.8° (p < 0.01). These initial clinical results demonstrate the realistic challenges associated with registration in complex scenes of anatomy and instrumentation.

An additional challenge may arise from the quality of the preoperative CT image that forms the 3D input to the registration process. For example, consistent with (Uneri et al 2014a) CT slice thickness >1 mm was found to challenge accurate 3D-2D registration. However, the results also demonstrate the potential of the KC-Reg method in real clinical data, resulting in registration accuracy comparable to that of a surgical navigation system (Labadie et al 2005) but without additional workflow (i.e., operating on fluoroscopic images already acquired in the course of the intervention) and without additional equipment (beyond the mobile C-arm that is already integral to the procedure).

C.7 Operating room quality assurance (ORQA)

The results obtained from the patient and component registration stages may be combined with the input images and models to create a QA report at the conclusion of the case, allowing evaluation of the surgical product and opportunity to revise (before leaving the OR) if necessary. The system is not necessarily intended to replace postoperative CT (which may be valuable, for example, in detecting hemorrhage or other soft-tissue morbidity); rather, it provides a means to detect device malplacement in the OR that might otherwise go unnoticed until postoperative CT. It also yields a quantitative measurement of the surgical construct relative to patient anatomy and the surgical plan that could be of value in providing quantitative measures for each case in the interest of longer-term, larger-scale, population-based analysis of the correlation between device placement and variation in treatment outcome.

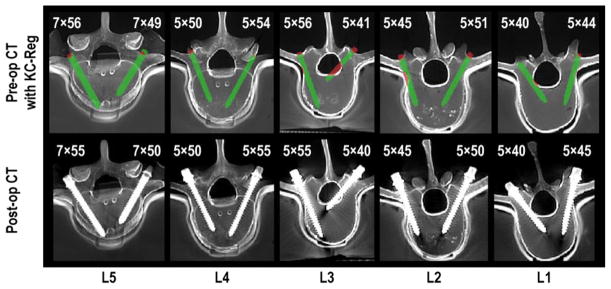
In Figure 10, one such ORQA example is shown in which the calibrated simultaneous KC-Reg was used to annotate preoperative CT images with 3D component registration obtained immediately following screw placement. In the top row of Figure 10, the bony cortex of the vertebra demarks a safe margin within the pedicle and vertebral body. The cortex boundary may be defined as part of preoperative planning – perhaps automatically as in (Goerres et al 2016). Portions of the screw that lie outside the acceptable regions are marked automatically (red) to delineate breaches – for example, a number of breaches purposely delivered in the spine phantom evident in Figure 10. The ORQA process furthermore provides a means by which to validate that the screw delivered to the patient (as measured in the length and diameter estimates from KC-Reg, per Figure 8) matches the intended screw (e.g., the screw defined in preoperative planning). For example in Figure 10, the top row shows the computed diameter × length estimates from KC-Reg, and the bottom row the actual screw dimensions; a mismatch could be used to flag a deviation from the plan and potentially suboptimal / unintended screw selection. The screws shown in Figure 10 all correctly match the surgical plan to within <0.5 mm in diameter and <2.5 mm in length.

Figure 10.

Quality assurance of pedicle screw placement using KC-Reg. The top row shows axial pre-op CT slices annotated with registered 3D screw parameters (obtained from 3 radiographic views) and estimated screw sizes. Preoperatively obtained vertebral cortex boundaries are used to conspicuously highlight the breaches in red, including the medial breach in L3 and the lateral breach in L2. The bottom row shows corresponding post-op axial slices, confirming the breaches predicted by KC-Reg in the top row and confirming the actual screw sizes.

D Discussion

The KC-Reg algorithm offers a registration-based solution for quantitative measurement and QA of the surgical product. For procedures that use fluoroscopic guidance, KC-Reg can operate within existing workflow and could aid surgeons by means of a near real-time, independent check on pedicle screw breaches, facilitating immediate revision if necessary and potentially avoiding postoperative morbidity and/or revision surgery. The approaches reported in this work extend the capability of the algorithm in handling complex radiographic scenes. The results conclusively demonstrate (i) accurate registration with or without geometric calibration of the imaging system, (ii) capability to solve for multiple surgical devices (components), while (iii) avoiding unrealistic pose estimates in which components would collide. Simultaneously solving for multiple components could allow QA of the surgical product from radiographic acquisitions at the conclusion of a case, potentially improving workflow and reducing radiation dose compared to using dedicated image acquisition for each screw. While prior geometric calibration of the C-arm was shown to improve robustness, the proposed alternative absolves this dependency and extends applicability beyond well calibrated, computer-controlled C-arms and allows increased DoF in C-arm positioning.

In phantom studies, the simultaneous component registrations outperformed the sequential solutions – irrespective of a prior C-arm calibration – demonstrating both the feasibility and necessity of solving for multiple component bodies to avoid degeneracies that may otherwise arise. The simultaneous solution with prior calibration provided the best results with TRE equal to 1.1 ± 0.1 mm and 0.7 ± 0.4°, which are comparable to or better than previously reported clinically permissible errors of ~1 mm and ~5° (Rampersaud et al 2001). This highlights the importance of resolving view geometry during the patient registration stage, from which errors may propagate to introduce local optima in the subsequent component registration. As most of these local minima were observed to arise from high intensity gradients of the screws themselves, additional constraints were helpful in mitigating them. Inclusion of a 3D collision constraint in the simultaneous solution specifically helped calibration-free formulations to approach the performance of the calibrated solution. The joint formulation, which was expected to provide robustness against outliers in single-view patient registration, showed no difference over other approaches. This is possibly due to the simplicity of the phantom, since an improvement was observed in the clinical dataset.

An expected feature/drawback of the proposed improvements is the resulting increase in DoF. The increased problem complexity was particularly apparent in the optimization, which lead to increased number of CMA-ES iterations. The run-times for the studies reported above was ~1.5 min per registration for the sequential and ~2.5 min for the simultaneous approaches (~1.25 min per screw), which increased to upwards of 6 min when joint restart was invoked, despite GPU parallelization. The general approach to keeping DoF to a minimum would be to make use all available information, whenever possible. For example, having exact knowledge of components as in (Uneri et al 2015a) would reduce the complexity of component models, which could improve the overall convergence characteristics. Further improvements in run-time (e.g., <1 min to be more consistent with OR workflow) are the subject of future work involving more optimal implementation and higher-speed, multi-GPU processing.

The work presented here includes the first application of KC-Reg in a clinical study, where the method yielded TRE of 2.7 ± 2.6 mm and 1.5 ± 0.8° without C-arm calibration, using the simultaneous solution followed by a joint restart. Extending this work to clinical studies with many patients, varying anatomy and components will likely need to address a number of experimental challenges. One such problem is high-intensity unmodeled components, such as retractors and rods, which may occlude the components of interest within the radiographic views. To minimize this problem, the images for the presented clinical data were acquired prior to rod placement. This also is sensible from a QA standpoint, since revisions to screw placement would be more easily performed before rods are attached. While patient deformation during surgery is also a likely source of error, applying the solution on the vertebra-scale would take advantage of the local rigidity of the bony anatomy. For handling gross deformations (e.g. due to patient positioning on the OR table), recent work by (Ketcha et al 2016a) offers a solution using a multi-stage process that iteratively converges on locally rigid regions. The preoperative image quality in clinical practice varies, both due to differences in CT scanner technology and the 3D reconstructions produced; for example, the CT slices were twice as thick for the clinical study than that of the phantom study. Strongly non-isotropic 3D data degrades the quality of the DRRs and would be especially challenging for the calibration-free formulation, since the single-view patient registration is more susceptible to errors.

Future work includes integration of KC-Reg with an in-house image guidance and navigation platform (Uneri et al 2012) to assess the workflow requirements in translation to clinical studies. Such integration would also allow use of the algorithm alongside other technologies, such as surgical trackers or robotic systems. Ongoing work includes development and assessment of the ORQA process in preclinical studies to identify what aspects of surgical product validation are most useful and least obtrusive to workflow as a precursor to prospective use in clinical studies.