Neuroanatomical Correlates of Performance in a State-Wide Test of Math Achievement

Abstract

The development of math skills is a critical component of early education and a strong indicator of later school and economic success. Recent research utilizing population-normed, standardized measures of math achievement suggest that structural and functional integrity of parietal regions, especially the intraparietal sulcus, are closely related to the development of math skills. However, it is unknown how these findings relate to in-school math learning. The present study is the first to address this issue by investigating the relationship between regional differences in grey matter volume (GMV) and performance in grade-level mathematics as measured by a state-wide, school-based test of math achievement (TCAP math)in children from 3^rd to 8^th grade. Results show that increased GMV in the bilateral hippocampal formation and the right inferior frontal gyrus, regions associated with learning and memory, is associated with higher TCAP math scores. Secondary analyses revealed GMV in the left angular gyrus had a stronger relationship to TCAP math in grades 3-4 than in grades 5-8 while the relationship between GMV in the left inferior frontal gyrus and TCAP math was stronger for grades 5-8. These results suggest that the neuroanatomical architecture related to in-school math achievement differs from that related to math achievement measured by standardized tests, and that the most related neural structures differ as a function of grade level. We suggest, therefore, that the use of school-relevant outcome measures is critical if neuroscience is to bridge the gap to education.

Introduction

Early math skills are a strong predictor of an individual’s academic achievement (Duncan et al., 2007), college entry (Bynner & Parsons, 1997), employment status (Ritchie & Bates, 2013), and physical and mental health (Bynner & Parsons, 2006). On a societal level, small increases in a nation’s numeracy rate are related to observable increases in GDP (OECD, 2010). With this in mind, many governments have dedicated resources and implemented new initiatives to enhance math education (British Council, 2010; The White House, Office of the Press Secretary, 2010). One broad trend in these efforts is the application of neuroscience to questions of education. There are now international conferences, professional societies, graduate education programs, and scientific journals dedicated to this burgeoning field of ‘educational neuroscience’. This field is defined by the belief that understanding the neurocognitive foundations of academic skills will contribute to improvements in the efficacy of educational interventions and pedagogical methods, and in turn, lead to better utilization of resources dedicated to education.

As a result of applying neuroscience methods to educationally relevant topics, several advances have been made in our understanding of the neurocognitive foundations of math-related abilities. Functional magnetic resonance imaging (fMRI) has provided detailed information about the neural correlates of basic numeracy skills (Bulthé, De Smedt, & Op de Beeck, 2014; Hubbard, Piazza, Pinel, & Dehaene, 2005; Price & Ansari, 2011), specific deficits in math learning disabilities (Price, Holloway, Räsänen, Vesterinen, & Ansari, 2007; Rosenberg-Lee et al., 2015), and individual variability in response to basic numeracy training (Kucian et al., 2011). Specifically, a significant body of research indicates that populations of neurons in the intraparietal sulcus (IPS) support the processing of numerical magnitude (Ansari & Dhital, 2006; Cantlon, Brannon, Carter, & Pelphrey, 2006; Cantlon & Brannon, 2006). Further, individual variability in the efficiency of this processing, measured behaviorally and with patterns of neural activation, is related to individual differences in math performance (Bugden & Ansari, 2011; Halberda, Mazzocco, & Feigenson, 2008; Mazzocco, Feigenson, & Halberda, 2011). Additionally, activation of the left angular gyrus (AG) has been associated with the processing of numerical symbols (Price & Ansari, 2011), fluent retrieval of arithmetic facts (Delazer et al., 2005), and individual differences in math competence (Grabner et al., 2007). Several anatomical studies have identified structural abnormalities such as reduced GM, abnormal sulcul geometry, and reduced white matter integrity in the bilateral IPS and surrounding white matter tracts in children with mathematical learning difficulties (Han et al., 2008; Isaacs, Edmonds, Lucas, & Gadian, 2001; Lubin et al., 2013; Rykhlevskaia, Uddin, Kondos, & Menon, 2009; Starke et al., 2013). More recently, increased grey matter volume of the left IPS has been shown to correlate with higher math scores in typically developing populations (Li, Hu, Wang, Weng, & Chen, 2013; Price, Wilkey, Yeo, & Cutting, 2016). Taken together, the extant literature suggests that the functional and structural integrity of domain specific numerical processing regions in the superior and inferior parietal lobes play a key role in the development of math competence.

However, questions still remain regarding the extent to which neuroscience research methods can ‘bridge the gap’ to educational relevance (Bruer, 1997, 2006). One source of concern in this respect is the relationship between measures of math performance employed in previous studies and content being learned in the classroom in differing educational contexts. The most frequently used measures of math performance, such as the Woodcock Johnson Test of Achievement (Bugden, Price, McLean, & Ansari, 2012) or the Test of Early Mathematics Ability (Emerson & Cantlon, 2012), index individual achievement levels on a wide range of math skills and may include only a small portion of content that was covered in a student’s classroom during a given year. These standardized measures of achievement provide important metrics of how a student’s math competency compares to their peers in absolute terms (i.e. what is an individual’s maximum level of math skill on a wide range of math-related content?), but they are designed to be administered to a wide age/ability range. By necessity, they are not tailored to be sensitive to a student’s educational setting. In contrast, one recent study investigated the functional and anatomical neural predictors of response to an 8-week arithmetic intervention (Supekar et al., 2013). They found that volume and intrinsic functional connectivity of the right hippocampus predicted gains in arithmetic competence much better than did volume or connectivity in the IPS or AG. In other words, when they tailored their outcome measure to be sensitive to fluency and strategic efficiency of the math skill being taught, a region typically associated with memory encoding and retrieval (Eichenbaum, 2000) predicted gains better than regions typically associated with number processing or arithmetic. In comparison to previous studies of the neuroanatomical correlates of math competence (Table 1), the results of Supekar et al. (2013) suggest that the neural correlates of math competence may vary depending on the proximity of the outcome measure to the educational experience. However, the outcome measure used in that study was experimenter defined, albeit closely tied to the learning experience, leaving open the question of whether school-based math measures engage the same neurocognitive mechanisms as standardized math measures. If the effort to apply neuroscience research findings to education is to achieve the goal of having a direct impact on curriculum and pedagogy, measures of math performance used in research must be closely tied to what is happening in school. If researchers only use measures of math achievement that are distally related to classroom environments, it will remain difficult for neuroscience to bridge the gap to educational application. The present study addresses this issue by assessing the relationship between regional grey matter (GM) volume and scores on the Tennessee Comprehensive Achievement Program (TCAP) math subtest in a cross-sectional sample of students in grades 3-8. To the best of our knowledge this is the first study to relate brain structure to math performance utilizing a school-based test of math achievement.

Table 1.

Studies of Neuroanatomical Differences Underlying Math Competence

Study	Age (sd)	Study Design	Anatomical Metric	Index of Math Competency	Type of Math Math Measure	Main Findings
Isaacs et al. 2001	15.83 (1.1)	LMA vs. HMA	GMV	WOND	Norm-based	LMA show lower GMV in left IPS.
Han et al. 2013	10.8 (0.4)	LMA vs. HMA	morphometric differences	WRAT (arithmetic)	Norm-base	Anatomical differences in the L occipital- temporal cortex, L orbital-frontal cortex, and R insular cortex relates to LMA vs. HMA.
Rotzer et al. 2008	9.3 (0.2)	LMA vs. HMA	GMV	ZAREKI-R (Num. Proc. & Calculation)	Norm-based	LMA showed reduced GMV in R IPS, anterior cingulum, L IFG, and bilateral middle frontal gyri.
Rykhlevskaia et al. 2009	8.8 (0.7)	LMA vs. HMA	GMV	WIAT (Num. Ops. & Math Reasoning)	Norm-based	LMA show reduced GMV in bilateral superior parietal lobe, IPS, fusiform gyrus, para-hippocampal gyrus, and R anterior temporal cortex.
Ranpura et al. 2013	8-14	LMA vs. HMA	CSA, CT , and GMV	WOND	Norm-based	LMA show reduced CSA in subcentral gyri, reduced CT in L temporal and R IFG, and less GMV in R parrahippocampal gyrus and R parietal lobe.
Cappelletti & Price 2014	22-74	LMA vs. HMA	GMV	Dyscalculia Screener Graded Difficulty Arithmetic	Norm-based Norm-based	LMA show reduced GMV in R IPS.
Lubin et al. 2013	10 (0.6)	High vs. Low Number Skills	GMV	Number Line Estimation Visual Numeracy Estimation	Experimental Experimental	LMA show reduced GMV in L IPS, bilateral Angular Gyrus. And occipito-temporal areas.
Starke et al. 2013	6.3-7.9	TA	GMV	TEDI-MATH Number Comparison Task	Norm-based Experimental	Positive relationship between GMV and numerical distance effect in multiple parietal regions and superior temporal gyrus.
Li et al. 2013	10.48 (0.4)	TA	GMV & FA	WISC (arithmetic)	Norm-based	Arithmetic scores positively correlated with GMV in R IPS.
Price et al. 2016	7.44 (0.3)	TA	GMV	WCJ-III (App. Problems & Calculation)	Norm-based	Composite math scores positively correlated with GMV in L IPS.
Supekar et al. 2013	8.7 (0.1)	TA	GMV	Arithmetic Verification Arithmetic Production	Linked to instruction outcomes	GMV in R hippocampus predicted math performance gains.

LMA = Low Math Ability; HMA = High Math Ability; TA = Typically Achieving, individual differences; GMV = Grey Matter Volume; CSA = Cortical Surface Area; CT = Cortical Thickness; WOND = Wechsler Objective Numeric Dimensions Test; WRAT = Wide Range Achievement Test; ZAREKI-R = Neuropsychological Test Battery for Number Processing and Calculation in Children, Revised; WIAT = Wechsler Individual Achievement Test; WCJ-III = Woodcock Johnson III

The TCAP is a measure of grade-level concept mastery closely related to classroom learning in the preceding school year. It is used as a metric of student achievement and is incorporated into the student’s year-end grade. As such, information gathered from the TCAP can influence students’ courses and educational opportunities in following years. Based on the previous functional and structural neuroimaging studies of the correlates of math achievement, two hypotheses are investigated. If performance on school-based measures of math competence is driven by domain-general cognitive abilities, such as executive functioning or memory formation, TCAP scores would be expected to correlate with volumetric differences in the in the prefrontal cortex, and the hippocampal formation. If, however, variability in structures associated with the processing of numerical magnitude and verbally represented numerical information are driving school math achievement, TCAP scores should correlate with differences in the bilateral IPS or AG. It is important to note that these hypotheses are not mutually exclusive, and a pattern of overlap and dissociation is possible, reflecting shared and distinct neurocognitive mechanisms underlying school-based measures of math competence.

Methods

Participants

The present data were collected as part of a larger scale, cross-sectional study investigating the development of reading comprehension (Aboud, Bailey, Petrill, & Cutting, in press). The current sample (n = 49) comprises participants for whom end-of-year state tests of math achievement were available for the grade completed prior to MRI scans. The following exclusion criteria were applied prior to recruitment. 1) previous diagnosis of intellectual disability; 2) known, uncorrectable visual impairment; 3) treatment of any psychiatric disorder (other than ADHD) with psychotropic medications; 4) history of known neurological disorder (e.g., epilepsy, spina bifida, cerebral palsy, traumatic brain injury; 5) documented hearing impairment greater than or equal to 25 dB loss in either ear; 6) medical contraindication to MRI procedures (e.g., metal devices); and 7) the history of or presence of a pervasive developmental disorder; and 8) if during testing, parental responses from the Diagnostic Interview for Children and Adolescents-IV (DICA-IV; Reich, Leacock, & Shanfeld, 1997) indicate the presence of any severe psychiatric diagnoses, including major depression, bipolar disorders, and conduct disorder. Individuals meeting criteria for ADHD, oppositional defiant disorder (ODD), adjustment disorder, and mild depression were not necessarily excluded from participation. The Institutional Review Board of Vanderbilt University approved all procedures. Written consent and assent was obtained from all children and participants.

Forty-one students were classified as right-handed, 6 as ambidextrous, and 2 as left-handed (Edinburgh Handedness Inventory, Oldfield, 1971). Two students had a confirmed diagnosis of ADHD and were regularly receiving medication at the time of the scan. No other behavioral disorders were confirmed. Scanning took place during the summer or school year after the completion of the grade that corresponds to the TCAP tests utilized for the analysis in this study. Descriptive and cognitive data and information regarding time between scan and TCAP are presented in Table 2. Although participants in the current sample demonstrated a large range in both TCAP math and TCAP reading scores, mean scores were at or above state averages for both measures. Raw scores on the TCAP math and TCAP reading were z-transformed using normative data obtained from the state of Tennessee Department of Education. Shapiro-Wilk tests show that neither measure violated normality (TCAP math p = 0.0.25, TCAP reading p = 0.49), suggesting that the present sample comprised a representative range of math performance.

Table 2.

Descriptive statistics of student sample

	Mean	SD	Range
Age at scan (years)	11.47	1.14	10.06 – 14.77
Grade	4.7	1.14	3 - 8
Average months from TCAP to scan	8.2	3.6	1.5 – 13.5
TCAP math (z-score)	0.52	0.86	-1.22 – 2.06
TCAP reading (z-score)	0.56	0.96	-2.03 – 2.51
Performance IQ (WASI)*	105.5	13.4	77 – 134
Verbal IQ (WASI)	111.9	14.6	70 - 138
Full Scale IQ (WASI)*	109.9	13.6	78-136

^*n = 48 for Performance IQ and Full Scale IQ

Note: SD, standard deviation; TCAP, Tennessee Comprehensive Assessment Program; WASI, Wechsler Abbreviated Scale of Intelligence

Standardized cognitive measures used for assessment

The Wechsler Abbreviated Scale of Intelligence (WASI), including the vocabulary, similarities, block design, and matrix reasoning subtests, was administered at the time of scan as a measure of global IQ (Weschler, 1999). The vocabulary and similarities subtests combine to form a measure of Verbal IQ. The block design and matrix reasoning subtests provide a measure of Performance IQ. Verbal IQ and Performance IQ are combined as a measure of Full Scale IQ (bivariate correlations Table 3).

Table 3.

Pearson r values for bivariate correlations between academic and cognitive measures

Measure (n = 49)	1	2	3	4
1. TCAP math
2. TCAP reading	.758**
3. Performance IQ*	.639**	.389**
4. Verbal IQ	.609**	.642**	.454**
5. Full Scale IQ*	.720**	.603**	.840**	.862**

^*n = 48 for Performance IQ and Full Scale

^**indicates p < .001

Grade-level achievement test

Student scores on the Tennessee Comprehensive Assessment Program (TCAP) were obtained from parents when they visited the lab and were administered at school during four school years from 2010 to 2013. It includes subtests in Reading/Language Arts (Reading), Mathematics, Science, and Social Studies. Only the Math and Reading subtests were used for this study. The TCAP is an end-of-year assessment, typically administered in April of each year during Tennessee’s August—June school year. The math subtest has a duration of 84-93 minutes depending on grade level and year of test administration. It contains items in the following categories: (1) mathematical processes, (2) number and operations, (3) algebra, (4) geometry and measurement, (5) data analysis, statistics, and probability. For example, in 3^rd grade, items considered for the number and operations category would include identifying the place value of numbers in the ones, tens, hundreds, thousands, and ten-thousands positions. Items in the same category in 8^th grade would include using scientific notation to compute products and quotients (see supplementary Table S1 for more detailed description of content at each grade level). The reading subtest has a duration of 123-150 minutes depending on grade level and year of test administration. It contains items in the following categories: (1) Language, (2) Vocabulary, (3) Writing and Research, (4) Communication and Media, (5) Logic, (6) Informational Text, (7) and Literature. Items on the test are directly aligned with the state curriculum content standards (https://www.tn.gov/education/article/academic-standards-archive). Both math and reading scores are z-scores derived from an individual’s score compared to means and standard deviations of students across all of Tennessee who took the same test, in the same year, at the same grade level as the individual represented in this sample.

Image acquisition

T1-weighted MRI was performed on a Philips Achieve 3T scanner with an 8-channel head coil in the year following TCAP achievement tests. Average time in months between TCAP and scan was M= 8.2 and ranged from 1.5 to 13.5. Magnetization Prepared Rapid Gradient Recalled Echo (MP-RAGE; (Mugler & Brookeman, 1990)) anatomical scans were acquired according to the following parameters: 256×256 scan resolution; 170 slices; 1mm slice thickness; 7.975s TR; 3.67s TE; Flip Angle=7°; voxel size 1mm³ isotropic; acquisition time 392s;oriented AC-PC.

Voxel-based morphometry

Images were analyzed using SPM8 (Wellcome Trust Centre for Neuroimaging, http://www.fil.ion.ucl.ac.uk), on a MATLAB platform (version 8.6, Mathworks, Natick, MA). Anatomical images for all analyses were processed according to the VBM protocol described by Ashburner (2010) with the following specifications. T1-weighted structural scans were first segmented to obtain separate GM, WM, and cerebral spinal fluid (CSF) images (Ashburner & Friston, 2005). GM, WM, & CSF values were summed to create a metric of global brain volume. Second, a population-specific template was created using diffeomorphic anatomical registration (DARTEL) (Ashburner, 2007). Third, each subject’s GM map was transformed to the customized template space based on the sample of 49 participants and then normalized into MNI space by corregistering with the Montreal Neurological Institute (MNI152) brain template. The warped images were modulated by the Jacobian determinants derived from DARTEL to obtain maps of GM volume maintaining an isotropic voxel resolution of 1.0 × 1.0 × 1.0 mm³. Two options exist in SPM8 for handling the effects of warping of GM that affect subsequent interpretation (Mechelli, Price, Friston, & Ashburner, 2005). One option is to leave voxel intensities “unmodulated” thereby preserving the concentration of GM in each voxel and changing the total amount of GM. Analyses on unmodulated images should be interpreted as findings related to GM concentration or density. The second option is to scale the intensity of GM by the Jacobian determinants derived from spatial normalization at each voxel, “modulated” normalization. This procedure results in preserved volumetric data. All subsequent analyses were performed on “modulated” data utilizing the second option of normalization and thus the present results are interpreted in terms of regional GM volume. In the final stage of preprocessing, the GM volume maps were smoothed with a full-width at half-maximum Gaussian kernel of 10mm to normalize the data.

Grade-level math achievement and whole brain grey matter volume

To investigate whether regional GM volume relates to individual differences in math achievement scores on the TCAP, we ran a linear regression model with TCAP math scores as the independent variable and VBM derived GM volume maps as the dependent variable. Age at time of scan, sex, and TCAP reading were included as covariates in the model to control for anatomical differences related to age, sex, overall brain volume, and reading ability. All independent variables were orthogonalized with respect to the previous variables in the regression model. The regression analysis was run on the whole brain with a GM mask and an absolute threshold mask of 0.01. A cluster level correction threshold of p< 0.05 was applied using the REST AlphaSim correction (uncorrected p< .001, minimum cluster threshold: 403 voxels) (Song et al., 2011, http://restfmri.net/forum/REST).

Grade-level median split contrast

Previous research suggests that the neural correlates of math competence vary throughout development (Ranpura et al., 2013; Rosenberg-Lee, Barth, & Menon, 2011; Venkatraman, Ansari, & Chee, 2005). Therefore, to investigate whether the above relationship differs as a function of grade, we split the sample into two groups with a median grade-level split and ran a contrast that compared the slope of relationship between GM volume and TCAP math scores of the lower grade levels to the slope of the higher grade levels. Only sex and TCAP reading were included as covariates of non-interest. The split resulted in one group of students in 3^rd and 4^th grade (n = 25) and one group of students in 5^th to 8^th grade (n = 24) (Table 4). These groups did not differ in performance IQ, verbal IQ, TCAP reading, TCAP math, or time between scan and TCAP (p> 0.48 for all t-tests)or in variance of the same variables (p> .25 for all Levene’s tests). Analysis was run using a GM mask and an absolute threshold mask of 0.01. A cluster level correction threshold of p <0.05 was applied (uncorrected p<.001, minimum cluster threshold: 403 voxels) as in the original analysis.

Table 4.

Descriptive statistics of grade-level split groups

	3rd & 4th Grade (n = 25)	5th to 8th Grade (n = 24)
Age at scan (years)	10.5 (0.52)	12.1 (1.16)
Grade	3.8 (0.41)	5.63 (0.88)
TCAP to scan (months)	8.2 (4.00)	8.2 (3.12)
TCAP math (z-score)	0.60 (0.94)	0.43 (0.78)
TCAP reading (z-score)	0.54 (0.99)	0.59 (0.95)
Performance IQ (WASI)*	106.1 (14.94)	105.0 (11.91)
Verbal IQ (WASI)	111.0 (14.36)	112.9 (15.10)
Full Scale IQ (WASI)*	109.8 (14.02)	110.0 (13.48)

^*n = 48 for Performance IQ and Full Scale IQ

Note: SD, standard deviation; TCAP, Tennessee Comprehensive Assessment Program; WASI, Wechsler Abbreviated Scale of Intelligence

3. Results

Grade-level math achievement and whole brain grey matter volume

This analysis revealed three clusters of voxels in which greater GM volume was related to higher TCAP math scores after controlling for age, sex, global brain volume, and TCAP reading scores. No clusters showing the inverse relationship were found. The three clusters were identified as the large portions of the left and right hippocampal formations including the hippocampus proper (CA1, CA3, Dentate Gyrus, Entorhinal Cortex, and Subiculum) and the right inferior frontal gyrus, pars orbitalis (right IFGorb) (Fig. 1 , Table 5). Cohen’s d effect sizes were calculated using the formula $d=\frac{2t}{\sqrt{\mathit{df}}}$ from peak t values from each cluster (df= 44). Anatomical descriptions of each cluster were identified from maximum probabilities derived from SPM 8 Anatomy Toolbox v2.15 (Eickhoff et al., 2005) (Table 5). Due to the relatively high variability in time between TCAP and scan (Table 2), the regression was repeated with the inclusion of time between TCAP and scan as a covariate. Results again revealed three clusters of voxels of the same anatomical description as the original analysis showing a positive relationship between GM volume and higher TCAP math. In other words, inclusion of time between TCAP and scan as a covariate did not alter the pattern of results. Because TCAP math and TCAP reading are highly correlated (r = .758), we calculated variance inflation factor (VIF’s) for each covariate in the regression model. All covariates had VIF’s of less than 2.5 (TCAP reading = 2.40), indicating low inflation due to collinearity (Menard, 1995). To investigate the relationship between grey matter and math independent of the influence of reading, we conducted an additional analysis in which reading was not included as a covariate, continuing to control for overall global brain volume, age, and sex. One large cluster in the right middle temporal gyrus showed a positive relationship between GMV and scores on TCAP math (p < .05 cluster corrected, p <.001 uncorrected, voxels = 833, see Supplementary Figure S1 for details). The relation between grey matter volume in left hippocampal formation, right hippocampal formation, and right IFGorb region and math competence remained significant only at an uncorrected threshold of p < .05, uncorrected.

Fig. 1.

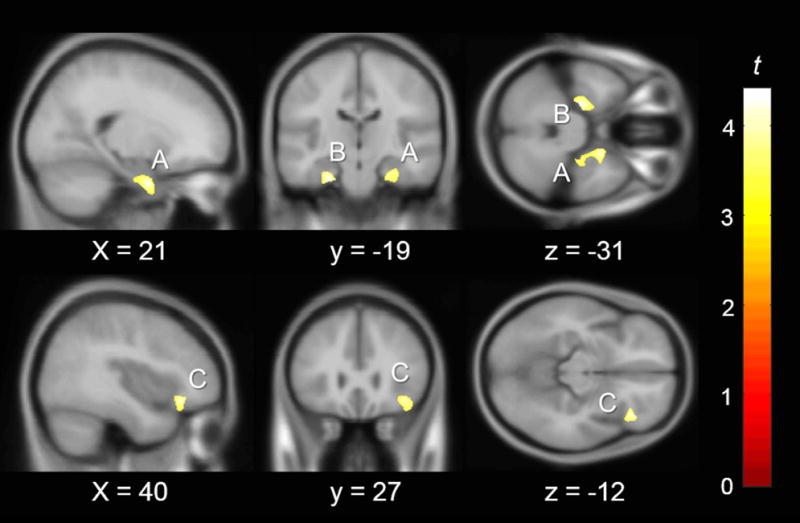
Significant clusters of GM related to TCAP math after controlling for GBV, age, sex, and TCAP reading (p< .05 cluster corrected, p< .001 uncorrected) overlaid on the MNI 152 template (n = 49). MNI slice coordinate listed. Cluster letters correspond to Table 5. (A) R Hippocampal Formation (B) L Hippocampal Formation (C) R inferior frontal gyrus, pars orbitalis.

Table 5.

VBM Cluster results for grey matter analysis

Cluster	Peak MNI (x y z)	Cluster Size	Peak t	Effect Size **	BA	Anatomical Description
A	(19 2 -34)	2866	4.39	1.32	27, 28, 34, 35	R Hippocampal Formation
B	(-22 -14 -34)	1481	4.25	1.30	27, 28, 34, 35	L Hippocampal Formation
C	(39 29 -12)	913	4.16	1.25	47	R Inferior Frontal Gyrus, pars orbitalis

^*All results cluster corrected at p<0.05, voxels = 403, uncorrected p<0.001.

^**All effect sizes reported as Cohen’s d.

Grade-level median split contrast

The contrast between the slopes of the 3^rd-4^th grade group and the 5^th-8^th grade group, revealed three significant clusters (Figure 2, Table 6). One negative cluster was identified in the left AG, PGp. This means that in the 3^rd-4^th grade group, GM volume in the left AG was more strongly related to TCAP math scores than it was for 5^th-8^th grade students. In order to ensure that the left AG was related to TCAP math for this group, independent of its difference from the 5^th-8^th grade group, we ran a whole brain regression analysis predicting GM from TCAP math, controlling for sex and TCAP reading, which included only the 3^rd-4^th grade group. The same left AG cluster was positively correlated with TCAP math at p<.005, uncorrected (voxels = 1043). Conversely, two positive clusters were identified, one in the left inferior frontal gyrus, pars orbitalis (left IFGorb) and one in the left cerebellum, lobules VIIa & VIIIb (Diedrichsen, Balsters, Flavell, Cussans, & Ramnani, 2009), where the relationship between GM volume and TCAP math scores was stronger for the 5^th-8^th grade students. In order to ensure that the left IFGorb and left cerebellum were related to TCAP math for this group, independent of its difference from the 3^rd-4^th grade group, we ran a whole brain regression analysis predicting GM from TCAP math, controlling for sex and TCAP reading, which included only the 5^th-8^th grade group. The left IFGorb was positively correlated with TCAP math at p < .005, uncorrected (voxels = 126), however, the left cerebellum cluster was not.

Fig. 2.

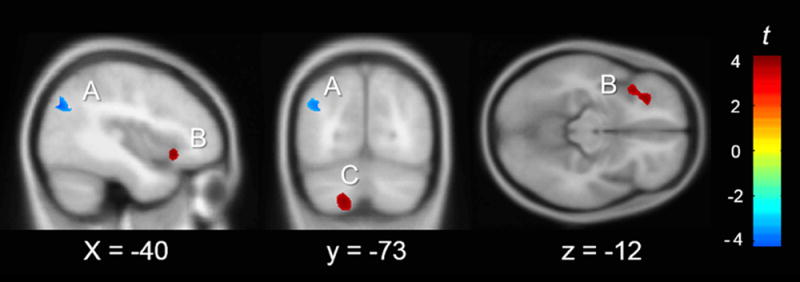
Significant clusters where slope of TCAP math predicting GMV is significantly different for grade-level split. Positive t-values indicate a greater slope for the higher grade levels (5^th to 8^th), negative t-values indicate a greater slope for the lower grade levels (3^rd and 4 ^th). Overlaid on the MNI 152 template (n = 49). MNI slice coordinate listed. Cluster letters correspond to Table 6. (A) L Angular Gyrus, PGp (B) L IFG, orb (C) L Cerebellum, lobules VIIa & VIIIb.

Table 6.

VBM Cluster results for Grade-Level Split

Cluster	Peak MNI (x y z)	Cluster Size	Peak t	Effect Size **	BA	Anatomical Description
A	(-40 -76 32)	741	4.17	1.29	39	L Angular Gyrus, PGp
B	(-29 32 -10)	893	4.16	1.28	47	L inferior frontal gyrus, pars orbitalis
C	(-17 -72 -50)	1016	3.86	1.19	-	L Cerebellum, lobules VIIa&VIIIb

^*All results cluster corrected at p<0.05, voxels = 403, uncorrected p<0.001.

^**All effect sizes reported as Cohen’s d.

Discussion

The current study is the first to investigate the relationship between regional differences in GM volume and performance in grade-level mathematics as measured by a state-wide, school-based test of math achievement. We observed three regions in which greater regional GM volume was related to better performance on the TCAP math subtest when controlling for global brain volume, age, sex, and TCAP reading. These regions include the right and left hippocampal formations (including the hippocampus proper, entorhinal cortex, and subiculum) and the right inferior frontal gyrus (IFGorb). Effect sizes were strongest in the hippocampal formations bilaterally and peaked in the entorhinal cortex of each cluster (right d = 1.32, left d = 1.30).

In contrast with to previous literature linking structural integrity and functional activation patterns of the IPS with math achievement, GM volume of the IPS was not related to TCAP math performance in the current study (Han et al., 2008; Isaacs et al., 2001; Lubin et al., 2013; Price et al., 2016; Ranpura et al., 2013; Rotzer, Kucian, Martin, Aster, et al., 2008). The three regions observed in the present study are associated with a wide range of domain-general cognitive abilities.The bilateral hippocampal formation has been consistently associated with generalized learning behaviors such as the encoding and retrieval of declarative memories (Eichenbaum, 2000) including but not limited to arithmetic fact knowledge (Cho et al., 2012; Qin et al., 2014). The IFGorb is involved in sensory integration, affective value reinforcers, decision-making, and visuo-spatial working memory (Kringelbach & Radcliffe, 2005; Metcalfe, Ashkenazi, Rosenberg-Lee, & Menon, 2013; Rotzer et al., 2009). In addition to their domain-general roles, the hippocampus and IFGorb have been previously associated with math development. Cho et al. (2012) demonstrated that children with higher arithmetic retrieval fluency have greater activation in the right hippocampus and parahippocampal gyrus during arithmetic problem solving, while Supekar et al (2013) showed increased GM volume in the hippocampus was related to gains in arithmetic ability in response to a tutoring intervention. Starke et al. (2013) reported an association between white matter in the right IFG and the numerical distance effect in 6-7-year-old children, and Rotzer et al. (2008) reported that children with Dyscalculia have decreased GM in the left IFG. Thus, in concert with previous findings, the present results suggest that the domain general functions supported by the hippocampus and IFG play a crucial role in the effective acquisition of school-relevant math skills.

While domain specific mechanisms such as numerical magnitude processing are undoubtedly important factors in the development of mathematical knowledge, the current findings suggest that school-based math competence is associated primarily with higher GM volume in regions known to have a domain-general role in learning (i.e. bilateral hippocampus and the right IFGorb). It should be noted that there were substantial differences between regression models with and without the inclusion of TCAP reading as a covariate. However, given that appropriate statistical procedures were undertaken to avoid multicollinearity and that the metrics for inflation due to multicollinearity are low, it is unlikely that the current findings are a spurious result of multi-collinearity. Instead, we suggest that the differences in results when controlling for versus not controlling for TCAP reading likely reflect meaningful differences between the isolating academic processes and associated neural correlates specific to math by controlling for another, broad measure of academic achievement, reading, versus not. An alternative explanation of differences between the two models is that individual differences between reading and math scores (i.e. discrepancy) within an individual are influencing the models, but it is difficult to conceptualize why a discrepancy between to measures would be associated with a specific neural correlate, and thus this explanation seems unparsimonious. Future research should confirm the nature of this relationship by exploring this relationship with the inclusion of other academic measures.

To investigate the potential influence of grade-level on our findings, we contrasted the relation between GM volume and TCAP math scores in grades 3-4 versus grades 5-8. Students in grades 3-4 showed a stronger positive relationship between GM and TCAP math in the left AG than students in the higher grades. The left AG has been associated with numerical symbol processing and individual differences in arithmetic fluency retrieval (Delazer et al., 2005; Grabner et al., 2007; Price & Ansari, 2011) and thus, the present results suggest these processes are more important for math performance in the lower grade levels. Although results at the whole-group level do not support our domain-specific hypothesis, results from the grade-level split may indicate the importance of this relationship earlier in development. Conversely, students in grades 5-8 showed a stronger positive relationship between GM volume and TCAP math in the left IFGorb and the cerebellum. Similar to the right IFGorb found in the whole-group analysis, the left IFGorb has been implicated in rule-learning, decision making, and visuospatial working memory, suggesting that math skills in the higher grade levels are drawing on a greater variety of domain general executive functions. Indeed, TCAP content in the lower grades tends to focus on basic computations of numerical quantities, while in the higher grades it requires the utilization of strategies, orders of operations, and rule-learning. The left cerebellum region was not present in the whole brain analysis or either of the independent analyses with the 3^rd-4^th or 5^th-8^th grade groups and thus further empirical investigation is required before we can draw conclusions on the mechanisms underlying this result. Further, applying a grade-level split was necessary due to unequal representation of grade-level in our sample, which results in a rather coarse comparison of the mean correlations between grey matter and math in each group. It would be interesting in future studies to ensure equal distributions of participants among grades in order to gain a more nuanced understanding of neuroanatomical changes across year of schooling.

It is possible that the observed grad-level differences could be due to neuroanatomical maturation as opposed to changes in content on the TCAP itself. However, given that the AG is associated with fluency of arithmetic fact retrieval and arithmetic proficiency in adults (Delazer et al., 2005; Grabner et al., 2007), it seems more likely that the current results are driven by content differences in the TCAP across grades. Nonetheless, further empirical investigation is required to confirm this speculation.

In conclusion, the current results suggest two significant implications for our understanding of the neural correlates of math competence and the future of educational neuroscience research respectively. First, the neuroanatomical mechanisms most related to math competence measured by in-school math tests differ from those related to performance on standardized math measures. The former are related to domain-general cognitive mechanisms associated with memory encoding and retrieval, while the latter are associated with domain-specific numerical processing regions (Li et al., 2013; Price et al., 2016). This suggests that when investigating math competence, standardized measures may not always be an appropriate proxy for the skills and abilities necessary for in-school math achievement. Furthermore, the neural correlates most related to math competence depend on the math content being assessed, and thus, considering the role of development and environment in the relation between neuroscience and education is of critical importance.

The second and related implication stemming from these results is that for neuroscience to bridge the gap to education, future research should utilize math measures closely related to the learning environment in addition to more traditional standardized measures of math achievement. Though the current results do not offer any direct suggestions for the improvement of educational approaches, they offer insights distinct from previous literature focused on standardized achievement measures. The two types of performance measures may provide unique and complimentary insights into the neural correlates of math learning that pave the way for more effective pedagogical approaches and improved educational outcomes.

Supplementary Material

1. Figure S1.

Significant clusters of GM related to TCAP math after controlling for GBV, age, sex. Not controlling for TCAP reading. (p < .05 cluster corrected, p < .001 uncorrected) overlaid on the MNI 152 template (n = 49). MNI slice coordinate listed.

2. Table S1.

Tennessee Comprehensive Assessment Program (TCAP), grades 3 – 8 mathematics framework.

Research Highlights.

• Investigates relationship between whole-brain grey matter (GM) volume and performance on the math section of a state-wide, school-based test of math achievement in grades 3-8.

• Greater GM volume in the bilateral hippocampus and right inferior frontal gyrus was associated with higher performance on grade-level tests of math achievement.

• For grades 3-4, the relationship between GM volume in the left angular gyrus and math was stronger; for grades 5-8, the left inferior frontal gyrus.

• GM in regions of the brain associated with generalized learning and memory are more closely related to in-school math achievement than areas of the brain associated with magnitude processing (i.e. intraparietal sulcus).