Abstract
Purpose
The purpose of this educational report is to provide an overview of the present state‐of‐the‐art PET auto‐segmentation (PET‐AS) algorithms and their respective validation, with an emphasis on providing the user with help in understanding the challenges and pitfalls associated with selecting and implementing a PET‐AS algorithm for a particular application.
Approach
A brief description of the different types of PET‐AS algorithms is provided using a classification based on method complexity and type. The advantages and the limitations of the current PET‐AS algorithms are highlighted based on current publications and existing comparison studies. A review of the available image datasets and contour evaluation metrics in terms of their applicability for establishing a standardized evaluation of PET‐AS algorithms is provided. The performance requirements for the algorithms and their dependence on the application, the radiotracer used and the evaluation criteria are described and discussed. Finally, a procedure for algorithm acceptance and implementation, as well as the complementary role of manual and auto‐segmentation are addressed.
Findings
A large number of PET‐AS algorithms have been developed within the last 20 years. Many of the proposed algorithms are based on either fixed or adaptively selected thresholds. More recently, numerous papers have proposed the use of more advanced image analysis paradigms to perform semi‐automated delineation of the PET images. However, the level of algorithm validation is variable and for most published algorithms is either insufficient or inconsistent which prevents recommending a single algorithm. This is compounded by the fact that realistic image configurations with low signal‐to‐noise ratios (SNR) and heterogeneous tracer distributions have rarely been used. Large variations in the evaluation methods used in the literature point to the need for a standardized evaluation protocol.
Conclusions
Available comparison studies suggest that PET‐AS algorithms relying on advanced image analysis paradigms provide generally more accurate segmentation than approaches based on PET activity thresholds, particularly for realistic configurations. However, this may not be the case for simple shape lesions in situations with a narrower range of parameters, where simpler methods may also perform well. Recent algorithms which employ some type of consensus or automatic selection between several PET‐AS methods have potential to overcome the limitations of the individual methods when appropriately trained. In either case, accuracy evaluation is required for each different PET scanner and scanning and image reconstruction protocol. For the simpler, less robust approaches, adaptation to scanning conditions, tumor type, and tumor location by optimization of parameters is necessary. The results from the method evaluation stage can be used to estimate the contouring uncertainty. All PET‐AS contours should be critically verified by a physician. A standard test, i.e., a benchmark dedicated to evaluating both existing and future PET‐AS algorithms needs to be designed, to aid clinicians in evaluating and selecting PET‐AS algorithms and to establish performance limits for their acceptance for clinical use. The initial steps toward designing and building such a standard are undertaken by the task group members.
Keywords: PET/CT, PET segmentation, treatment assessment, treatment planning
1. Introduction
Positron emission tomography (PET) has the potential to improve the outcome of cancer therapy because it allows the identification and characterization of tumors to be conducted based on their metabolic properties,1 which are inherently tied to cancer biology. PET is helpful in delineating the tumor target for radiation therapy, in quantitating tumor burden for therapy assessment, in determining patient prognosis and in detecting and quantitating recurrent or metastatic disease. This is especially true when the cancer lesion boundaries are not easily distinguished from surrounding normal tissue in anatomical images. Combined PET/CT (computed tomography) and PET/MRI (magnetic resonance imaging) provide both anatomical/morphological and functional information in one imaging session. In addition to segmentation, this allows for the division of the tumors into subregions based on metabolic activity, which could potentially be used to treat/evaluate these subregions differentially (e.g., by increasing the dose to the more aggressive and radioresistant sub‐volumes, an approach known as “dose painting”2). Accurate delineation of the metabolic tumor volume in PET is important for predicting and monitoring response to therapy. Aside from standardized uptake value (SUV) measurements,3, 4 other parameters (e.g., total lesion glycolysis (TLG) or textural and shape features, as well as tracer kinetic parameters) with complementary/additional predictive/prognostic value can be extracted from PET images.
For radiation therapy, leaving parts of the tumor untreated, because its extent is underestimated by anatomic imaging, or conversely irradiating healthy tissue because boundaries between the tumor and the adjacent normal tissue cannot be defined, can result in suboptimal response and/or (possibly severe) adverse side‐effects. It has been shown in several clinical studies that PET, using the [18F]2‐fluoro‐2‐deoxy‐D‐glucose (Fluorodeoxyglucose) radiotracer (18F‐FDG PET), has led to changes in clinical management for about 30% of patients.5, 6, 7 Other studies, involving nonsmall‐cell lung cancer (NSCLC)8, 9, 10 and head‐and‐neck (H&N) cancer11 have demonstrated that the incorporation of PET imaging in radiotherapy planning can result in significant changes (either increase or decrease) in treatment volumes.
In addition, the quantitative assessment of the metabolically active tumor volume, may provide independent prognostic or predictive information. This has been shown in several malignancies, including locally advanced esophageal cancer,12 non‐Hodgkin lymphoma,13 pleural mesothelioma,14 cervical and H&N cancers,15 and lung cancer.16
These promising data impose the need to establish and validate algorithms for the segmentation of PET metabolic volumes before and during treatment. The gross tumor volumes (GTV) defined by PET are intended to contain the macroscopic extend of the tumors. Currently, inaccuracies in defining PET‐based GTV arise from variations in the biological processes determining the radiotracer uptake, as well as from physical and image acquisition phenomena which affect the reconstructed PET images.4, 17, 18, 19, 20, 21, 22 Furthermore, uncertainty can be introduced by the segmentation process itself. It has been shown that volume differences of up to 200% can arise from using different GTV contouring algorithms.23
Regardless of these uncertainties, many radiation oncology departments have started using PET/CT for lesion delineation in radiation treatment planning (RTP)1, 7, 8, 9, 11, 24 Numerical auto‐segmentation techniques can be used for guidance in the PET delineation process, which have been shown to reduce intra‐ and inter‐observer variations25, 26 and some commercial vendors are now offering tools for semi‐automatic delineation of tumor volumes in PET images for radiotherapy planning or response assessment. While these approaches may work reasonably well when applied in conjunction with anatomical imaging and clinical expertise, their accuracy and limitations have not been fully assessed.
Due to the complexity of the problem of PET‐based tumor segmentation and due to the abundance of potentially applicable numerical approaches, a large variety of automatic, semi‐automatic and combined PET‐AS approaches have been proposed over the past 20 years.27, 28, 29, 30 Multiple semi‐automatic approaches derived from phantom data as well as fully automated algorithms differing in terms of the algorithmic basis, fundamental assumptions, clinical goals, workflow, and accuracy have been proposed. In addition, algorithms for segmenting combinations of images from PET and other imaging modalities have appeared in literature.31, 32, 33, 34 The majority of these approaches have been tested on either simplistic phantom studies or patient datasets, where the ground truth is largely unknown. Finally, only a few of these algorithms have been tested for their ability to segment lesions with irregular shapes or nonuniform activity distributions, which are essential for the implementation of accurate delineation protocols. In addition, most methods have been evaluated using different datasets and protocols, which makes comparing the results difficult, even impossible. As a result, in essence, there is currently no commonly adopted technique for reliable, routine, clinical PET image auto‐segmentation.
In this educational report, we provide a description with examples of the main classes of PET‐AS algorithms (section 2), highlight the advantages and the limitations of the current techniques (section 2.B.4) and discuss possible evaluation approaches (section 2.B.5). In that section, the types of available image datasets and the existing approaches for contour evaluation are discussed with the intention of laying out a basis for a standard for effective evaluation of PET auto‐segmentation algorithms. The clinician interested in the practical aspects of PET segmentation may find most useful section 4.C.4, which highlights the biological, physiological, and image acquisition factors affecting the performance of the PET‐AS methods, as well as preliminary guidelines for their acceptance and implementation.
2. Description and classification of the algorithms
The following is a glossary of the abbreviations, definitions, and notations used in this report:
Abbreviations
- ARG
Adaptive Region Growing
- ATS
Adaptive Threshold Segmentation
- BTV
Biological Target Volume
- CT
Computed Tomography
- CTV
Clinical Target Volume
- DSC
Dice Similarity Coefficient
- DWT
discrete wavelet transforms
- FTS
Fixed Threshold Segmentation
- EM
Expectation Maximization
- FCM
Fuzzy C‐Means
- FDG
[18F]2‐fluoro‐2‐deoxy‐D‐glucose (Fluorodeoxyglucose)
- FLT
18F‐3′‐fluoro‐3′‐deoxy‐ L‐thymidine
- FMISO
18F‐fluoromisonidazole
- FOM
Figure of Merit
- GTV
Gross Tumor Volume
- H&N
Head and Neck
- ML
Maximum Likelihood
- MRI
Magnetic Resonance Imaging
- MVLS
Multi Valued Level Sets
- NEMA
National Electrical Manufacturers Association
- NGTDM
neighborhood gray‐tone difference matrices
- NSCLC
Non‐Small Cell Lung Cancer
- PET
Positron Emission Tomography
- PET‐AS
PET Auto ‐ Segmentation
- PPV
Positive Predictive Value
- PSF
Point Spread Function
- PTV
Planning Target Volume
- PVE
Partial Volume Effect
- ROC
Receiver Operating Characteristic
- SNR
Signal to Noise Ratio
Definitions
ROI (Region of Interest): A 2D or 3D region drawn on an image for purposes of restricting and focusing analysis to its contents. It is closely related to and often used interchangeably with volume of interest (VOI).
SUV (Standardized Uptake Value): A measure of the intensity of radiotracer uptake in an object (lesion or body region) or region of interest; measured activity in that region is normalized to the injected activity and some measurement of patient size, most commonly weight (mass).
TLG (Total Lesion Glycolysis): The integral of the FDG‐SUV over the volume, or the product of the mean FDG‐SUV and the volume. The same paradigm can be applied to other radiotracers and is called for instance Total Proliferative Volume, or Total Hypoxic Volume in the case of FLT or FMISO, respectively.
VOI (Volume of Interest): A 3D region defined in a set of images for purposes of restricting and focusing analysis to its contents. It is closely related to and often used interchangeably with region of interest (ROI).
Notations
I : The image set.
I VOI : The VOI in image set I that the segmented region is taken from.
: The segmented region from image set I.
I i : The intensity of the i th element (image pixel) from image set I. This intensity is often normalized with respect to activity and weight to SUV.
ξ i : Normalized uptake for the th voxel (see Appendix II).
T : Threshold. Commonly used in threshold segmentation. It defines the value at which a voxel is segregated between one set and another.
T* : The estimated segmentation threshold.
: Volume as a function of threshold.
V known : The known volume of a segmented object.
x i : The position of the i th voxel.
: The cluster center of the k th cluster at the n th iteration.
: The membership probability of the th pixel in the k th cluster at the n th iteration.
N : The number of images sets/modalities.
: The internal/external mean intensities of the enclosed contour region at level set = 0 in the i th image set.
: User‐defined importance weights for inclusion/exclusion from a region defined by the enclosed contour at level set in the i th image set.
ϕ : A level set function.
Ω: The domain of the image.
2.A. Possible classifications
The first objective of this document was to provide introductory information about the different classes of PET auto‐segmentation (PET‐AS) algorithms. Classifications of PET‐AS algorithms can be based on several different aspects:
The segmentation/image processing algorithm employed and its assumptions and complexity;
The use of pre‐ and post‐processing steps;
The level of automation;
The first classification, relying on the type of image segmentation paradigm (e.g., simple or adaptive thresholding, active contours, statistical image segmentation, clustering, etc.), has been used in previous reviews.27, 29, 35, 36 In most cases, detailed descriptions of the numerical algorithms and their assumptions and limitations are given.
The second classification is based on the use of pre‐ and post‐processing steps. Most algorithms do not use pre‐processing steps, although some use either denoising or deconvolution image restoration techniques before the segmentation or as part of the algorithm itself.37, 38 Other algorithms require either an image‐based database39, 40 to build a classifier (i.e., learning algorithms), or phantom acquisitions for the optimization of parameters (i.e., adaptive threshold algorithms).
Regarding the third classification based on automation, Udupa, et al.41 divide image segmentation into two processes: recognition and delineation, and point to the “essential” need of “incorporation of high‐level expert knowledge into the computer algorithm, especially for the recognition step.” For this reason, most existing algorithms rely on the identification of the tumor first, by the user drawing a volume of interest (VOI) around the tumor to delineate (denoted from here onwards as “standard user interaction”, see Table 1), whereas other approaches require the identification of the tumor after the segmentation process in the resulting map (e.g., Belhassen, et al.28). Other examples of manual interaction are user‐definition of background regions (used by some of the adaptive threshold algorithms), manual selection of markers to initialize the algorithm,42 or the manual input of parameters in case of failure of the automatic initialization.43 Furthermore, the level of automation can be quite difficult to assess, as factors such as the requirement of building a classifier for each image region, the individual optimization for each combination of scanner system/reconstruction algorithm, the selection and validation of the parameters of the optimization approach, or finally, the detection of lesions to segment, are usually not included in these assessments. In practice, all algorithms require some level of user interaction.
Table 1.
Summary of the main characteristics of some representative advanced PET‐AS algorithms (not an exhaustive list) and their respective evaluation
| Reference(s) | Image segmentation paradigm(s) used | User interactiona | Pre‐ and post‐processing steps | Aimed applicationb | Validation data and ground truthc | Accuracy evaluation on realistic tumorsd | Robustness evaluatione | Repeatability evaluationf |
|---|---|---|---|---|---|---|---|---|
| Tylski, et al. 2006243 | Watershed | Std + multiple markers placement | None | Global | PA(1): Vol. and CiTu images | No | No | No |
| Werner‐Wasik, et al. 2012135 | Gradient‐based | Std + initialization using drawn diameters | Unknown | Global | PA(5): Diam. 31 MCST: Vol. | Yes | Yes | Yes |
| Geets, et al. 200737 | Gradient‐based | Std + initialization | Denoising and deconvolution steps | Global | PS(1) and PA(1): Vol. + Diam. 7 CiTuH: Complete | No | No | No |
| El Naqa, et al. 2008130 | AT + active contours | Std + several parameters to set | None | Global | PA(1): Vol. 1 CiTu – Ø | Yes | No | Yes |
| El Naqa, et al. 200731 | Multimodal (PET/CT) active contours | Std + initialization of the contour shape, selection of weights | Normalization and registering of PET and CT images, deconvolution of PET images. | GTV definition on PET/CT | PA(1): Vol. 2 CiTu: MC(1), FT | Yes | No | No |
| Dewalle‐Vignion, et al. 2011140 | Possibility theory applied to MIP projections | Std | None | Global | PA(1): Vol. 5 MCST: Vox. 7 CiTuH: Complete | Yes | No | No |
| Belhassen and Zaidi 201028 | Improved Fuzzy C‐Means (FCM) | A posteriori interpretation of resulting classes in the segmentation of entire image | Denoising, wavelet decompositions | Global | 3 AST: Vox. 21 CiTuH: Diam. 7 CiTuH: Complete | Yes | No | No |
| Aristophanous, et al. 200765 | Gaussian mixture modeling without spatial constraints | Std + initialization of the model and selection of the number of classes | None | Pulmonary tumors | 7 CiTu: Ø | No | No | Yes |
| Montgomery, et al. 200764 | Multi scale Markov field segmentation | A posteriori interpretation of resulting segmentation on the entire image | Wavelet decompositions | Global | PA(1) : Vol. 3 CiTu: Ø | No | No | No |
| Hatt, et al. 200769 | Fuzzy Hidden Markov Chains | Std | None | Global | PS(1) and PA(2): Vox. | No | No | No |
| Hatt, et al. 2009,68 2010,70 201143 | Fuzzy locally adaptive Bayesian (FLAB) | Std | None | Global | PS(1) and PA(4): Vox. 20 MCST: Vox. 18 CiTuH: Diam. | Yes | Yes | Yes |
| Day, et al. 200960 | Region growing based on mean and SD of the region | Std + optimization on each scanner | None | Rectal tumors | 18 CiTu: MC(1) | No | No | No |
| Yu, et al. 2009,40 Markel, et al. 201398 | Decision tree built based on learning of PET and CT textural features | A posteriori interpretation of resulting segmentation on the entire image | Learning for building the decision tree | GTV definition of H&N and lung tumors | 10 CiTu: MC(3) 31 CiTu: MC(3) | No | No | No |
| Sharif, et al. 2010273, 2012244 | Neural network | A posteriori interpretation of resulting segmentation on the entire image. | Learning for building the neural network | Global | PA(1): Vol. 3 AST: Vox. 1 CiTuH: Diam. | No | No | Yes |
| Sebastian, et al. 2006138 | Spherical Mean shift | Std | Resampling in a different spatial domain | Global | 280 AST: Vox. | No | No | No |
| Janssen, et al. 2009152 | Voxels classification based on time‐activity curve | Std + Initialization and choice of the number of classes | Only on dynamic imaging, denoising and deconvolution steps | Rectal tumors in dynamic imaging | PA(1): Vol. + Diam. 21 CiTu: MC(1) | No | No | No |
| De Bernardi, et al. 2010245 | Combined with PVE (image reconstruction) | Std + initialization | PSF model of the scanner and access to raw data required | Global | PA(1): Vol. | No | Yes | No |
| Bagci, et al. 201333 | Multimodal random walk | Std | Multimodal images registration | Global for PET/CT or PET/MR | 77 CiTu: MC(3) PA(1) | Yes | No | No |
| Onoma, et al. 2014246 | Improved random walk | Std | None | Global | PA(1), 4 AST: Vox, 14 CiTu: MC(2) | Yes | No | No |
| Song, et al. 201332 | Markov field + graph cut | Std | None | Global | 3 CiTu: MC(3) | Yes | No | No |
| Hofheinz, et al. 201361 | Locally adaptive thresholding | Std + one parameter to determine on phantom acquisitions | None | Global | 30 AST: Vox. | Yes | No | No |
| Abdoli, et al. 2013141 | Active contour | Std + several parameters to optimize | Filtering in the wavelet domain | Global | 1 AST: Vox. 9 CiTuH: Complete. 3 CiTuH: Complete 2 CiTuH: Complete | No | Yes | No |
| Mu, et al. 2015247 | Level set combined with PET/CT Fuzzy C‐Means | Std | None | Specific to cervix | 7 AST: Vox, 27 CiTu: MC(2) | Yes | No | No |
| Cui, et al. 2015134 | Graph cut improved with topology modeling | Std + one free parameter previously optimized | PET/CT registration | Specific to lung tumors and PET/CT | 20 PA(1), 40 CiTu(2) | Yes | No | No |
| Lapuyade‐Lahorgue, et al. 2015248 | Generalized fuzzy C‐means with automated norm estimation | Std | None | Global | PA(4): Vol. 34 MCST: Vox. 9 CiTu: MC(3). | Yes | Yes | Yes |
| Devic et al., 2016249 | Differential uptake volume histograms for identifying biological target sub‐volumes | Selection of three ROIs encompassing PET avid area; iterative decomposition of differential uptake histograms into multiple Gaussian functions | None | Isolation of glucose phenotype driven biological sub‐volumes specific to NSCLC, | None | No | No | No |
| Berthon et al., 201673 | Decision tree based learning using nine different segmentation approaches (region growing, thresholds, FCM, etc.) with the goal of selecting the most appropriate method given the image characteristics | Std | Learning on 100 simulated cases to train/build the decision tree | Global | 85 NSTuP: Vox. | Yes | No | No |
| Schaefer et al., 201699 | Consensus between contours from 3 segmentation methods (contrast‐oriented, possibility theory, adaptive thresholding) based on majority vote or STAPLE | Std | None | Global | 22 CiTuH; Complete 10 CiTu: MC(4) 10 CiTu: MC(1) | Yes | No | Yes |
std = « standard » interaction (i.e., the metabolic volume of interest is first manually isolated in a region of interest that is used as an input to the algorithm.)
global = not application specific.
PA(x) = Phantom (spheres) Acquisitions on x different scanners; PS(x) = Phantom (spheres) Simulations on x different scanners; AST = Analytically Simulated Tumors; MCST = Monte Carlo Simulated Tumors; NSTuP = Non spherical tumors simulated in phantoms (thin‐wall inserts, printed phantoms, etc.). CiTu = Clinical Tumors; CiTuH = Clinical Tumors with Histopathology; Vol. = only volume; Vox. = voxel‐by‐voxel; Diam = histopathology maximum diameter; Complete = 3D histopathology reconstruction; MC(x) = manual contouring by x experts; FT = fixed threshold, AT = adaptive threshold.
Highly heterogeneous, complex shapes, low contrasts, and rigorous ground truth.
Requires multiple acquisitions on different systems and a large number of parameters.
With respect to repeated automated runs or delineation by multiple users.
In the following section, we used the first classification scheme with emphasis on the algorithm complexity.
2.B. Classes of algorithms for PET auto‐segmentation
2.B.1. Fixed and adaptive threshold algorithms
Segmentation via a threshold is conceptually simple. It consists of defining a specific uptake (often expressed as a fixed fraction or percentage of SUV) between the background and imaged object's intensities (tracer uptake) and then using that intensity to partition the image and recover the true object's boundaries. All voxels with intensities at or above the threshold are assigned to one set while the remaining voxels are assigned the other (Appendix I). The details of how the threshold and the uptake values are normalized are discussed in Appendix II.
The decision to use threshold segmentation is generally based upon its simplicity and the ease of implementation. Threshold segmentation carries a number of implied assumptions that should be understood and accounted for. These are:
The true object has a well‐defined boundary and uniform uptake near its boundary, i.e., the image is bi‐modal.
The background intensity is uniform around the object.
The noise in the background and in the object is small compared to the intensity change at the tumor edge.
The resolution is constant near the edges of the object.
The model, used to define the threshold, is consistent with its application, e.g., a segmentation scheme designed for measuring tumor volume may not be appropriate for radiation therapy and vice versa (see section 5.B).
In practice, these assumptions rarely hold and some effort is required to determine their validity/acceptability in the context of the intended application.
Several points above are illustrated in a review of PET segmentation by Lee.29 In this review, the effect of the thickness of the phantom wall on estimating the segmentation threshold and the dependence of this effect on the Point Spread Function (PSF) of the PET scanner, were shown via mathematical analysis. This work also showed that to obtain the correct threshold on a phantom with cold walls (a certain thickness of material without any uptake, such as the plastic surrounding spheres in physical phantoms), a lower threshold is required than for the case without walls, and that due to the limited PET spatial resolution, small volumes require higher thresholds. This was further investigated recently, demonstrating the important impact of cold walls on the segmentation approaches, and the potential improvement brought by thin‐wall inserts.44, 45 A similar result was shown by Biehl, et al.,46 who concluded that for NSCLC the optimal threshold for their specific scanner and protocol was related to volume as shown in Appendix I. Finally, it is interesting to note that, given knowledge of the local PSF and the assumption of uniform uptake, the threshold for the lesion's boundary can be estimated analytically, with the result being independent from the tumor‐to‐background ratio, provided the background has been subtracted beforehand.47
Generally, threshold segmentation can be loosely categorized into two separate categories: fixed threshold segmentation (FTS) and adaptive threshold segmentation (ATS). In FTS, a general test/model of the problem is developed and a set of parameters is estimated by minimizing the error of the model to deduce an “optimal” threshold, . The threshold value may be dependent or not (e.g., 42% of peak lesion activity48 or SUV = 2.549) on the tumor‐to‐background ratios. Other tumor or image aspects are generally ignored. For ATS, an objective function is chosen that generates a threshold based upon the properties of each individual tumor/object and PET image. In this case, rather than depending on simple measures, such as tumor‐to‐background ratio, the threshold calculation depends upon an ensemble of lesion properties such as volume46, 48, 50, 51, 52 or SUV mean‐value,53 and thus makes the threshold segmentation process iterative.
Both FTS and ATS have been discussed in several recent literature reviews of general segmentation in PET27, 29, 36, 54 Each of these reviews provides a fairly complete literature survey of the state of various threshold segmentation algorithms. In addition, the review by Zaidi and El Naqa54 provides a brief description and summary of the rationale of many ATS algorithms. These are summarized in Table A1 of Appendix I.
2.B.2. Advanced algorithms
A list of some of the advanced PET‐AS algorithms published is given in Table 1, with a focus on the evaluation protocols that were followed. Below they are divided into three subcategories (advanced algorithms applied directly to PET images, approaches combined with image processing or reconstruction, and those dealing with multiple imaging modalities), which are discussed in separate subsections 2.B, Statistical, Learning and texture‐based segmentation algorithms.
Gradient‐based segmentation
The underlying assumption in threshold‐based delineation (2.B.1) is that the uptake within the target is significantly different from that in the background. With this idea in mind, the gradient naturally finds the transition contour that delineates a high‐uptake volume from the surrounding low uptake regions. The immediate advantage of this alternative method is that uptake inside and outside the target need not be uniform for successful segmentation, nor need it be constant along the contour.
In practice, the method consists of computing the gradient vector for each voxel and then using it to form a new image composed of the gradient magnitude values. Segmentation based on gradient information is an important part of what the human visual system does when looking at natural scenes. The difficulty lies in interpreting the gradient image to translate the relevant information into target contours. The general idea is to locate and follow the crests of the gradient magnitude. The points where the gradient is the largest in magnitude (where the second derivative, or Laplacian, is null) correspond to the target contours. There are several ways to locate the crests. For instance, adaptive contours or “snakes” with various smoothness constraints can be programmed in such a way that the contours are attracted toward the crest.55 Another very popular way to track the gradient crests is the watershed transform. It considers the gradient image as a landscape in which the gradient crests are mountain chains. Then it “floods” the landscape and keeps a record of the boundaries of all hydrographic basins that progressively merge as the water level rises. The hierarchy of all basins can be displayed as a tree in a dendrogram. Clustering tools can help in identifying the branch that gathers all basins corresponding to the target.
The quality of gradient‐based segmentation depends on the accuracy and precision of the gradient information, which can be biased by spatial resolution blur. For objects with a concave or convex surface, the uptake spill‐in and spill‐out caused by blur tends to slightly shift, smooth, and distort the real object boundary. This effect can be partially compensated for with deblurring methods, such as deconvolution algorithms and some tools for Partial Volume Effect (PVE) correction. The gradient computation is affected by the image noise. Therefore, denoising tools are needed as well, provided they do not decrease the image resolution.
The algorithm described by Geets, et al.37 relies on deblurring and denoising tools prior to segmentation. The deblurring parameters are adjusted according to the resolution of the PET system and are therefore PET‐camera dependent. The watershed transform is applied to the gradient magnitude image and a clustering technique creates a hierarchy of basins. The user can choose the tree branch associated with the high‐uptake region in the images expected to correspond to the target volume. In the case of a low tumor‐to‐background ratio (surrounding inflammation, other causes of tracer concentration, uptake reduction due to treatment), the hierarchy can get more complicated and the branch corresponding to the target volume might be difficult to isolate. This usually indicates that the images do not convey enough information for the target volume to be accurately delineated. This approach has been validated using phantom PET acquisitions as well as clinical datasets of both H&N37 and lung56 tumors with tridimensional (3D) histopathology reconstructions as ground truths.
Region growing and adaptive region growing
Region growing algorithms start from a seed region inside the object and progressively include the neighboring voxels to the region if they satisfy certain similarity criteria.57, 58, 59 Similarity is often calculated based on image intensity, but can be based on other features such as textures. Let I( x ) represent the image intensity at x . The similarity criteria can be a fixed interval: I( x ) ∈ [lower, upper], or a confidence interval: I( x ) ∈ [m − fσ, m + fσ], where m and σ are the mean intensity and standard deviation of the current region, and f is a factor defined by the user.59 Region growing with a fixed interval is essentially a connected threshold algorithm. Small f restricts the inclusion of voxels to only those having very similar intensities to the mean in the current region, and thus can result in under growth. Large f relaxes the similarity criteria, and thus may result in over growth into neighboring regions. It is often difficult, if not impossible to identify experimentally an optimal f for all objects. For example, four different f values were experimentally determined based on the maximum intensity and its location using phantoms by Day, et al.60 The authors noted that these f values are specific to their clinic.
To overcome this limitation, an adaptive region growing (ARG) algorithm that can automatically identify f for each specific object in PET was proposed by Li, et al.55 As illustrated in Fig. 1, in ARG f is varied from small to large values so that the grown volume changes from the small seed region to the entire image. A sharp volume increase occurs at a certain f*, where the region grows just beyond the object (e.g., high activity sphere or tumor) into the background (low activity water or normal tissue). As the background typically consists of large homogeneous regions, a great number of voxels are added to the current region at this transition point. The ARG algorithm automatically identifies f* for which the volume would be increased by more than 200% at the next iterative value of f. The resulting volume V* was proven to be quite an accurate representation of the homogeneous object. The quality of the segmentation performed by ARG depends mainly on the homogeneity of the background and the contrast between the tumor and background. The performance of ARG in segmenting tumors with various levels of heterogeneous uptake still needs to be studied. The ARG algorithm does not have any parameters that require experimental determination. It uses the intrinsic contrast between a tumor and its neighboring normal tissue in each image to determine the tumor boundary. Therefore, it can be directly applied to various imaging conditions such as different scanners or imaging protocols.
Figure 1.
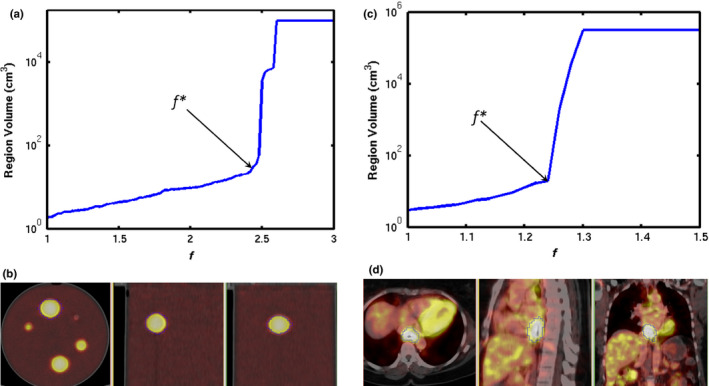
An illustration of applying the adaptive region growing (ARG) algorithm to PET: (a) plot of segmented volume growing as a function of f, the arrow indicates the location of the transition point f* for a spherical lesion in a PET/CT of a phantom; (b) the thin blue contour indicates the delineated volume V*; (c) – (d) selection of f* and the corresponding delineation for an esophageal tumor. [Color figure can be viewed at wileyonlinelibrary.com]
Another approach based on adaptive region growing has been proposed by Hofheinz, et al.,61 in which the approach was made able to deal with heterogeneous distributions. The method is based on an adaptive threshold, in which instead of a lesion‐specific threshold for the whole ROI, a voxel‐specific threshold is computed locally in the close vicinity of the voxel. The absolute threshold Tabs for the considered voxel is then obtained based on a parameter T previously determined with phantom measurements (T = 0.39): Tabs =T×(R‐Bg)+Bg, where R is a tumor reference value (e.g., ROI maximum) and Bg is the background. Region growing algorithms use statistical properties (mean and standard deviation) of the region to stop the iterative process.60 The algorithms, which exploit the statistical properties of a noisy function and a noisy argument and rely on probabilistic calculations, are described in the next subsection.
Statistical
Statistical image segmentation: Statistical image segmentation aims at classifying voxels and creating regions in an image or volume based on the statistical properties of these regions and voxels, by relying on probabilistic calculations and estimation for the decision process. Numerous approaches have been proposed; most are based on Bayesian inference. In essence, it is assumed that the observed image Y (usually taking its values in the set of real numbers) is a noisy and degraded version of a ground truth field X (usually taking its values in several classes C). Therefore, X has to be estimated from Y, assuming that X and Y can be modeled as realizations of random variables. These algorithms usually combine an iterative estimation procedure of the parameters of interest, since parameters defining the distributions of X and Y are not known in real situations. In addition, a decision step to classify voxels (i.e., assigning a label among the possible values of X to each voxel, based on its observation Y) and the estimated distributions of X and Y, are required. Hence, the voxel classification is carried out based on the previously estimated statistical properties and the resulting probabilities for each voxel to belong to a specific class or region.
Spatial and observation models: The parameters of interest are usually defined within both a spatial model of X (also called a priori model) and an observation model of Y (also called a noise model). Most spatial models are based on Markovian modeling of the voxels field, such as Markov chains, fields, or trees, although simpler spatial neighboring definitions (blind, adaptive or contextual) also exist.62 Noise models are used to model uncertainty in the decision to classify a given voxel, and are most often defined using Gaussian distributions, but more advanced noise models have also been proposed, allowing for the modeling of correlated, multidimensional and non‐Gaussian noise distributions.63 Parameters estimation is usually carried out using algorithms such as Expectation Maximization (EM), Stochastic EM (SEM), or Iterative Conditional Estimation (ICE), depending on the assumptions of the model. These methods have been demonstrated to provide robust segmentation results in several imaging applications, such as astronomical, satellite, or radar images, by selecting appropriate noise models.
Adaptation to PET image segmentation: Some of the algorithms above, have been applied to PET image segmentation. One example is the use of a multiresolution model applied to wavelet decomposition of the PET images within a Markov field framework.64 Another approach is a mixture of Gaussian distributions for classification without spatial modeling.65 Although these models are robust for noisy distributions of voxels (each voxel has an assigned label, but its observation is noisy), they do not explicitly take into account imprecision of the acquired data (a given voxel can contain a mixture of different classes). Therefore, they do not include the modeling of the fuzzy nature of PET images. As a result, to be applied efficiently to PET images, which are not only intrinsically noisy but also blurry due to PVE, more recent models can be used that allow the modeling of the imprecision within the statistical framework, using a combination of “hard” classes and a fuzzy measure. In such a model, the actual image, X does not take its values in a set number of classes, but in a continuous [0,1] interval: the fuzzy Lebesgue measure being associated with the open interval (0,1) and the Dirac measure being associated with {0} and {1}.66 Such a model has been proposed using Markov chains67 and fields62 and also using local neighborhoods without Markovian modeling. These models retain the flexibility and robustness of statistical and Bayesian algorithms versus noise, with the added ability to deal with more complex distributions, due to the presence of both hard and fuzzy classes in the images. The Fuzzy Locally Adaptive Bayesian (FLAB) method takes advantage of this model,68 which had previously been proposed within the context of Markov chains.69 In addition, FLAB modeling has been extended to take into account heterogeneous uptake distributions by considering three classes and their associated fuzzy transitions instead of only two classes and one fuzzy transition. The extended FLAB model has been validated on phantom acquisitions and simulated tumors, as well as clinical datasets.70
Learning and texture‐based segmentation algorithms
For PET image segmentation, the learning task consists of discriminating tracer uptake in lesion voxels (foreground) from surrounding normal tissue voxels (background) based on a set of extracted features from these images.28 Two common categories of statistical learning approaches have been proposed: supervised and unsupervised.71, 72 Supervised learning is used to estimate an unknown (input, output) mapping from known (labeled) samples called the training set (e.g., classification of lesions given a database of example images). In unsupervised learning, only input samples are given to the learning system without their labels (e.g., clustering or dimensionality reduction).
In machine learning and classification, there are two steps: training and testing. In the training step, the optimal parameters of the model are determined given the training data and its best in‐sample performance is assessed. This is usually followed by a validation step, aimed at optimal model selection. The testing step then specifically aims to estimate the expected (out‐of‐sample) performance of a model with respect to its chosen training parameters. A recent example of such a development is the ATLAAS method,73 which is an automatic decision tree that selects the most appropriate PET‐AS method based on several image characteristics, achieving significantly better accuracy than any of the PET‐AS methods considered alone. There are also numerous other types of machine learning techniques that could be applied to PET segmentation, such as random forest, support vector machines, or even deep learning techniques,74 which have been applied to the task of image segmentation in other modalities such as MRI or CT.75, 76 Although these approaches are promising for the future of PET image segmentation, the use of these techniques for PET is currently rather scarce in the literature.77 Today these techniques are exploited to classify patients in terms of outcome based on characteristics extracted from previously delineated tumors.78, 79
PET‐AS algorithms can be trained on pathological findings or physician contours. The advantage of training an algorithm using these contours is that additional information, not present in the PET image, is taken into account since the physician draws contours based on additional a priori information (anatomical imaging, clinical data, etc.). On the other hand, training algorithms using physician contours can be biased by the particular physician's background, goals, or misconceptions.
One of the most used approaches to extract image features that can be used for segmentation is texture analysis. Uptake heterogeneity in PET images can be characterized using regional descriptors such as textures. Unlike intensity or morphological features, textures represent more complex patterns composed of entities or sub‐patterns, that have unique characteristics of brightness, color, slope, size, etc.80 “Image texture” can refer to the relative distribution of gray levels within a given image neighborhood. It integrates intensity with spatial information resulting in higher order histograms when compared to common first‐order intensity histograms. Texture‐based algorithms heavily use image statistical properties; however, since human visual perception often relies on subtle visual properties, such as texture, to differentiate between image regions of similar gray level intensity, they are separated from the iterative, model‐based approaches described in the previous section.
Furthermore, the human visual system is limited in its ability to distinguish variations in gray tone and is subject to observer bias. Variation in image texture can reflect differences in underlying physiological processes such as vascularity or ordered/disordered growth patterns. The use of automated computer algorithms to differentiate tumor from normal tissue based on textural characteristics may offer an objective and potentially more sensitive algorithm of tumor segmentation than those based on simple image thresholds. Among the methods that have been suggested to calculate image texture features are those based on (a) Gabor filters, (b) discrete wavelet transforms (DWT), (c) the co‐occurrence matrix, (d) neighborhood gray‐tone difference matrices (NGTDM), and (e) run‐length matrices.
Gabor filters81 and DWT82 measure the response of images to sets of filters at varying frequencies, scales and orientations. The Gabor filter (a Gaussian phasor), using a bank of kernels for each direction, scale, and frequency, can produce a large number of nonorthogonal features, which makes processing and feature selection difficult. DWTs take a multiscale approach to texture description. Orthogonal wavelets are commonly used resulting in independent features. DWT, however, have had more difficulty discriminating fractal textures with nonstationary scales.83
The co‐occurrence matrices proposed by Haralick, et al.84 and spatial gray level dependence matrix (SGLDM) features, are based on statistical properties derived from counting the number of times pairs of gray values occur next to each other. These are referred to as “second‐order” features because they are based on the relationship of two voxels at a time. The size of a co‐occurrence matrix is dependent on the number of gray values within a region. Each row (i) and column (j) entry in the matrix is the number of times voxels of gray values i and j occur next to each other at a given distance and angle. Higher order features refer to techniques that take into account spatial context from more than two voxels at a time. Amadasun and King proposed several higher order features based on NGTDM.85 For every gray level i, the difference between this level, and the average neighborhood around it, is summed over every occurrence to produce the ith entry in the NGTDM.
Another category of higher order features makes use of “run‐length matrices”. In this case, analysis of the occurrence of consecutive voxels in a particular direction with the same gray level is used to extract textural descriptors such as energy, homogeneity, entropy, etc.86 However, run‐length matrices are a computationally intensive means of deriving texture descriptors.86
Although textural features have been used to characterize uptake heterogeneity within tumors after the segmentation step,15, 79 their use as a means of automatic segmentation can also provide additional information beyond simple voxel intensity that may improve the robustness of delineation criteria. This has been shown in multiple modalities including ultrasound (US)87 and MRI.88 PET and CT textures in the lung have been used in a series of applications including differentiating between malignant and benign nodes,89, 90 judging treatment response,15, 16 diagnosing diffuse parenchymal lung disease,91, 92, 93 determining tumor staging, detection and segmentation.94 With dual modality PET/CT systems (also PET/MRI in the near future95, 96), it is also possible to make use of image textures from PET and CT (MRI) in combination to improve image segmentation results. However, this leads to including anatomy for tumor volume characterization, instead of characterizing the functional part of the tumor only. In two separate studies, combinations of PET and CT texture features in images of patients with H&N cancer97 and those with lung cancer98 improved tumor segmentation with respect to the dual modality ground truth, versus using PET and CT separately. This is discussed in more detail in section 2.B.4 below.
Within the learning category would also fall the recent approaches to account for a set or contours generated via multiple automatic methods, through averaging/consensus methods,99 statistical methods such as the “inverse–ROC (receiver operating characteristic)” approach,100 STAPLE (simultaneous truth and performance level estimation)‐derived methods,101 majority voting,102 or decision tree73 to generate a surrogate of truth. Most of these methods would need some type of “training” or preliminary determination of parameters for the particular type of lesions and may therefore avoid the limitations of the individual methods used.
2.B.3. Combined with image processing and/or reconstruction
The limited and variable resolution of PET scanners, which results in anisotropic and spatially variant blur affecting PET images, leads to PVE, spill‐in and spill‐out of activity in nearby tissues17 and is therefore one of the main challenges for segmentation and for uptake quantification of oncologic lesions. In principle, all the segmentation strategies not explicitly intended for blurred images, but widely used for imaging modalities less affected by PVE than PET (e.g., thresholding, region growing, gradient‐based algorithms, etc.),103 can be applied to PET images after a PVE recovery step.104 PVE recovery can be performed after105, 106, 107, 108, 109 or during image reconstruction with algorithms taking into account a model of the scanner PSF.110, 111, 112 These images, however, should be handled with caution since PVE recovery techniques can introduce artifacts (e.g., variance increase related to the Gibbs phenomenon). The accuracy of PVE‐recovered images can be improved by introducing regularizations such as a priori models, constraints, or iteration stopping rules. An approach of this kind has been followed by Geets, et al.37 (described in section 2.B.2), where a gradient‐based segmentation algorithm was applied on deblurred and denoised images. To avoid the Gibbs phenomenon artifacts near the edges, deconvolution was refined with constraints on the deconvolved uptake.
An alternative approach to account for blur is to model it explicitly in the segmentation procedure. For example, FLAB,68 described in section 2.B.2, or FHMC (Fuzzy Hidden Markov Chains),69 parameterize a generic form of uncertainty to assign special intermediate classes for the blurry borders of the main classes. Such algorithms, if combined with a post‐segmentation PVE recovery technique for objects of known dimension/shape, like recovery coefficients, geometric transfer matrix17 or VOI‐based deconvolution,113 may also be able to provide an estimate of PVE‐recovered lesion uptake inside the delineated borders.114
Another means to account for PVE recovery in segmentation is to model it in an iterative process. The lesion border estimate can be iteratively refined using the result of the PVE recovery inside the lesion area and vice versa. Such an approach can potentially improve the estimation accuracy while providing a joint estimate of lesion borders and uptake. This approach was originally proposed by Chen, et al. for spherical objects.115 More recently, De Bernardi, et al. have further developed the idea by proposing a strategy that combines segmentation with a PVE recovery step obtained through a targeted maximum likelihood (ML) reconstruction algorithm with PSF modeling in the lesion area.38 A scheme of the approach is shown in Fig. 2.
Figure 2.
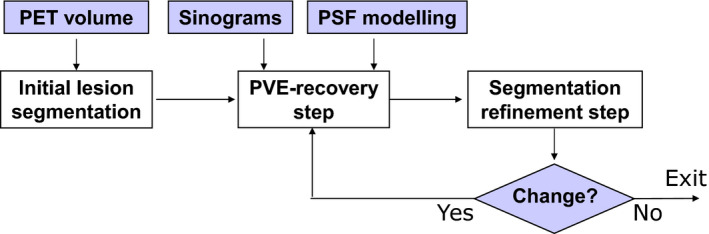
A schematic representation of the algorithm proposed by De Bernardi, et al.,38 which combines segmentation and PVE recovery within an iterative process. [Color figure can be viewed at wileyonlinelibrary.com]
To reduce blur in the latter approach, algorithms using transition regions between lesion and background are employed. These regions correspond to spill‐out due to PVE and are modeled by regional basis functions in the PVE recovery reconstruction step. The reconstruction adjusts the activity inside each region according to the ML convergence with respect to the sinogram data. The subsequent segmentation refinement step acts on the lesion borders in the improved image, until borders no longer change. A requirement of the algorithm is that a model of the scanner PSF and access to raw data are available. Conversely, the advantage is that a joint estimate of lesion borders and activity can be obtained.
In the work of De Bernardi, et al.,38 the segmentation was obtained using k‐means clustering and the refinement was achieved by smoothing the result with the local PSF and by re‐segmenting. The algorithm, suited for the simplest case of homogeneous lesions, was validated in a sphere phantom study. More recently, an improved strategy was proposed, in which the segmentation is performed with a Gaussian Mixture Model and PVE recovery is performed on a mixture of regional basis functions and voxel intensities. The algorithm was validated on a phantom in which lesions are simulated with zeolites (see section 4.C.1).116
2.B.4. Segmentation of multimodality images
Multimodality imaging is of increasing importance for cancer detection, staging, and monitoring of treatment response.117, 118, 119, 120, 121
In radiotherapy treatment planning, significant variability can occur when multiple observers contour the target volume.122 This inter‐observer variability has been shown to be reduced by combining information from multimodality imaging and performing single delineations on fused images, such as CT and PET, or MRI and PET.25, 123, 124, 125, 126, 127 However, traditional visual assessment of multimodality images is subjective and prone to variation. Alternatively, algorithms have been proposed for integrating complementary information into multimodality images by extending semi‐automated segmentation algorithms into an interactive multimodality segmentation framework to define the target volume.31, 32, 33, 34
Consequently, the accuracy of the overall segmentation results would be improved, although, as a word of caution, it should be emphasized that the goal may be different from mono‐modality delineation and its realization would depend on the application endpoint combined with the clinical association objective of the different image modalities. For instance, in radiotherapy planning, the main rationale behind the use of combining several images of different modalities to define the GTV is that they complement each other by combining different aspects of the underlying biology, physiology, and/or anatomy. However, in reality, this may not be the case for all patients and all pathologies, for example, the lesion may not be seen in the additional modality, or may exhibit an artifact. In addition, misregistration between the different modalities and respiratory motion may lead to a potentially erroneous GTV if the images were simply fused without careful consideration of geometric correspondence and the logic by which the different image data are combined (union, intersection, or other forms of fusion).
Exploitation of multimodal images for segmentation has been applied to define myocardial borders in cardiac CT, MRI, and ultrasound using a multimodal snake deformable model.128 Another example is the classification of coronary artery plaque composition from multiple contrast MRI images using a k‐means clustering algorithm.129 To define tumor target volumes using PET/CT/MRI images for radiotherapy treatment planning, a multivalued deformable level set approach was used as illustrated in Fig. 3.31 This approach was extended further later on using the Jensen Renyi divergence as the segmentation metric.34
Figure 3.
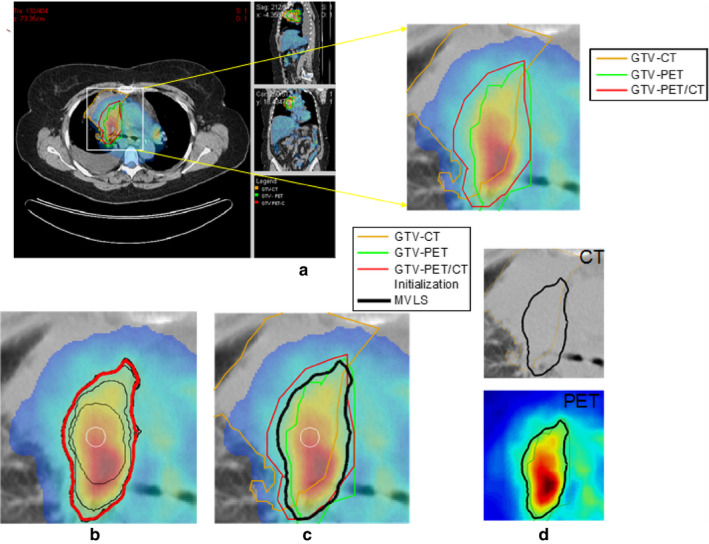
(a) PET/CT images of a patient with lung cancer in case of atelectasis (lung collapse), with manual segmentation for CT (orange), PET (green) and fused PET/CT (red). (b) The multivalued level sets (MVLS) algorithm initialized (white circle), evolved contours in steps of 10 iterations (black), and the final contour (red). (c) MVLS results shown along with manual contour on the fused PET/CT. (d) MVLS contour superimposed on CT (top) and PET (bottom). Reproduced with permission from El Naqa, et al.31 [Color figure can be viewed at wileyonlinelibrary.com]
Mathematically, approaches that aim at simultaneously exploiting several image modalities represent a mapping from the imaging space to the “perception” space as identified by experts such as radiation oncologists.130 Several segmentation algorithms are amenable to such generalization.131 Among these, algorithms are multiple thresholding, clustering such as k‐means and fuzzy c‐means (FCM) and active contours. In the case of multiple thresholding, CT volumes can be used to guide selection of PET thresholds46 or using thresholds on the CT intensities to constrain the PET segmentation.131 These conditions are typically developed empirically but could be optimized for a specific application. For clustering, the process is carried out by redefining the image intensities and clustering centers as vectors (with elements being the intensities of the different modalities) in contrast to the typical scalars used in single modality images.129 The formalism for FCM is given in Appendix I.B. However, both thresholding and clustering algorithms in their basic form suffer from loss of spatial connectivity, which is accounted for in active contour models using a continuous geometrical form such as the level sets. The level set provides a continuous implicit representation of geometric models, which easily allows for adaptation of topological changes and its generalization to different image modalities. Assuming there are N imaging modalities, then using the concept of multivalued level sets (MVLS)132, 133 the different imaging modalities are represented by a weighted level set functional objective of the different modalities and the target boundary is defined at the zero level set31 (Appendix I.B).
Finally, other approaches based on the Markov field combined with graph‐cut methods,32 as well as random walk segmentation33 or including topology,134 were developed and validated on clinical images for multimodal (PET, CT, MRI) images tumor segmentation with promising results.
2.B.5. Vendor implementation examples
Here, we provide a brief summary of several vendor implementations of PET‐AS methods at the time when this report was written. Therefore, it may not describe the PET‐AS methods provided by all vendors at the time of publication due to constant evolution of vendor software. Vendors also provide tools for manual segmentation that have been omitted for brevity. Since the algorithms implemented by vendors are not exactly known, the summary, and classification provided below do carry a significant degree of uncertainty.
Gradient‐based edge detection tool is avaible by MIM Software Inc. (Cleveland, OH, see Section 2.B.2) and Table 1,135, 136). VelocityAI (Varian Medical Systems|Velocity Medical Solutions, Atlanta, GA) also point that their tool uses “rates of spatial change” in the segmentation process. PET‐AS methods based on region growing tools (Section 2.B.2) are available by Mirada XD (Mirada Medical, Oxford, UK) and RayStation (RaySearch Laboratories AB, Stockholm, Sweden).
Adaptive thresholding approaches (Section 2.B.1) are available by VelocityAI (the method by Daisne, et al.137), GE Healthcare VCARTM system (V 1.10) (GE Healthcare Inc., Rahway, NJ, the method by Sebastian, et al.,138 see Table 1), and ROVER (ABX GmbH, Radeberg, Germany, an iterative approach following Hofheinz et al26, 61).
Finally, practically all vendor implementations use some type of fixed or adaptive threshold‐based method (Section 2.B.1). For example, Varian's Eclipse V.10 (Varian Medical Systems, Inc., Palo Alto, CA) as well as other vendor implementations including Philips Healthcare PinnacleTM (Philips Healthcare, Andover, MA) and Raystation allow users to perform PET segmentation using thresholding in different units (Bq/ml or different SUV definitions), and percent from peak SUV.
3. Comparison of the pet‐as algorithms based on current publications
A comparison of PET‐AS algorithms based on published reports is difficult and subject to controversy because each algorithm has been developed and validated (and often optimized) on different datasets, often using a single type of scanner and/or processing software. However, some limited conclusions can be drawn. For instance, it is possible to compare the algorithms based on their level of validation as well as those algorithms that have been applied to the same datasets. Table 2 contains a survey of various papers in which several algorithms were compared, providing the type of datasets and methods used, the conclusions of the study, as well as some comments.
Table 2.
A summary of segmentation method comparisons and reviews
| No. | Reference | Compared methods | Images or phantoms used | Results and/or recommendations reported by the authors | Limitations and comments by TG211 or others as cited |
|---|---|---|---|---|---|
| Comparison studies | |||||
| 1 | Nestle, et al. 200523 | Visual segmentation, 40% of SUVmax threshold, SUV>2.5 threshold, and an adaptive threshold | Patient scans | Large differences between volumes obtained with the four approaches | Only visual segmentation used as a surrogate of truth and only clinical data. |
| 2 | Schinagl, et al. 2007250 | Visual segmentation, 40% and 50% of SUVmax threshold, and adaptive thresholding | 78 Clinical PET/CT images of head and neck | The five methods led to very different volumes and shapes of the GTV. Fixed threshold at SUV of 2.5 led to the most disappointing results. | The GTV was defined manually on CT and used as a surrogate of truth for PET‐derived delineation and only clinical data was used. |
| 3 | Geets, et al. 2007,37 Wanet, et al. 201156 | Fixed and adaptive thresholding, gradient‐based segmentation | Phantom (spheres), simulated images, clinical images of lung and H&N cancers with histopathology 3D measurements | More accurate segmentation with gradient‐based approach compared to threshold | Issues associated with the 3D reconstruction of the surgical specimen used as gold standard. |
| 4 | Greco, et al. 2008251 | Manual segmentation, 50% SUVmax, SUV>2.5 threshold and iterative thresholding | 12 Head and neck cancer patients. | Thresholding PET‐AS algorithms are strongly threshold‐dependent and may reduce target volumes significantly when compared to visual and physician‐determined volumes. | Reference GTVs defined manually on CT and MRI. |
| 5 | Vees, et al. 2009252 | Manual segmentation, SUV>2.5 threshold, 40% and 50% of SUVmax threshold, adaptive thresholding, gradient‐based method and region growing. | 18 Patients with high grade glioma |
PET often detected tumors that are not visible on MRI and added substantial tumor extension outside the GTV defined by MRI in 33% of cases. The 2.5 SUV isocontour and “Gradient Find” “segmentation techniques performed poorly and should not be used for GTV delineation”. |
Ground truth derived from manual segmentation on MRI. |
| 6 | Belhassen, et al. 2009253 | Three different implementations of the fuzzy C‐means (FCM) clustering algorithm | Patient scans | Incorporating wavelet transform and spatial information through nonlinear anisotropic diffusion filter improved accuracy for heterogeneous cases | No comparison with other standard methods |
| 7 | Tylski, et al. 201042 | Four different threshold methods (% of max activity and three adaptive thresholding), and a model‐based thresholding | Spheres in an antropomorphic torso phantom as well as non spherical simulated tumors | Large differences between volumes obtained with different segmentation algorithms. Model‐based or background‐adjusted algorithms performed better than fixed thresholds. | No clinical data, limited to threshold‐based algorithms only, only volume error considered as a metric |
| 8 | Hatt, et al. 2010,70 201143, 143 | Fixed and adaptive thresholding, Fuzzy C‐means, FLAB | IEC phantom (spheres); simulated images, clinical images with maximum diameter measurements in histopathology | Advanced algorithms are more accurate compared to threshold‐based and are also more robust and repeatable. | For clinical images, only maximum diameters along one axis were available from histology. |
| 9 | Dewalle‐Vignion, et al. 2011,140 2012254 | Manual segmentation, 42% of SUVmax, two different adaptive thresholding, fuzzy c‐mean and an advanced method based on fuzzy set theory. | Phantom images, simulated images, clinical images with manual delineations | The advanced algorithm is more accurate and robust than threshold‐based and closer to manual delineations by clinicians |
Only manual delineation for surrogate of truth of clinical data. Comments: Interesting use of various metrics for assessment of image segmentation accuracy. |
| 10 | Werner‐Wasik, et al. 2012135 | Manual segmentation, fixed thresholds at 25% to 50% of SUVmax (by 5% increments) and gradient‐based segmentation | IEC phantom (spheres) in multiple scanners, simulated images of lung tumors | A gradient‐based algorithm is more “accurate and consistent” than manual and threshold segmentation. | Only volume error used as a metric of performance. Comment: The need for joint, manual and CT based verification by nuclear medicine physicians, radiologists, and radiation oncologists was highlighted in follow‐up communications.255 |
| 11 | Zaidi, et al. 2012139 | Five thresholding methods, Standard and improved fuzzy c‐means, level set technique, stochastic EM. | Patient scans with histopathology 3D measurements (same as #5 above) N/A |
The automated Fuzzy c‐means algorithm provided was shown to be more accurate than five thresholding algorithms, the level set technique, the stochastic EM approach and regular FCM. Adaptive threshold techniques need to be calibrated for each PET scanner and acquisition/processing protocol and should not be used without optimization. |
Issues associated with the 3D reconstruction of the surgical specimen used as gold standard. See Table 1 |
| 12 | Shepherd, et al. 2012100 | 30 methods from 13 different groups. | Tumor and lymph‐node metastases in H&N cancer and physical phantom (irregular shapes). Simulated, experimental and clinical studies | Highest accuracy is obtained from optimal balance between interactivity and automation. Improvements are seen from visual guidance by PET gradient as well as using CT. | A small number of objects (n = 7) were used for the evaluation. |
| 13 | Schaefer, et al. 2012148 | One adaptive thresholding technique | Phantoms, same threshold algorithm, different scanners | The calibration of an adaptive threshold PET‐AS algorithm is scanner and image analysis software‐ dependent. | Confirmation of previous findings about adaptive threshold segmentation. |
| 14 | Schinagl et al. 2013256 | Visual, SUV of 2.5, fixed threshold of 40% and 50%, and two adaptive threshold‐based methods using either the primary or the metastasis | Evaluation of the segmentation of metastatic lymph nodes against pathology in 12 head and neck cancer patients |
SUV of 2.5 was unsatisfactory in 35% of cases; for the last four methods: i) using the node as a reference gave results comparable to visual ii) using the primary as a reference gave poor results; |
Shows the limitations of threshold‐based methods. |
| 15 | Hofheinz, et al. 2013,61 | Voxel‐specific adaptive thresholding and standard lesion‐specific adaptive threshold | 30 simulated images based on real clinical datasets. | The voxel‐specific adaptive threshold method was more accurate than the lesion‐specific one in heterogeneous cases | Only simulated data were used. |
| 16 | Lapuyade‐Lahorgue, et al. 2015248 | Improved generalized fuzzy c‐means, fuzzy local information C‐means and FLAB61 (Table 1) | 34 simulated tumors and nine clinical images with consensus of manual delineations. Three acquisitions of phantoms for robustness of evaluation. | In both simulated and clinical images, the improved generalized FCM led to better results than another FCM implementation and FLAB, especially on complex and heterogeneous tumors, without any loss of robustness on data acquired in different scanners. | Only nine clinical images used. |
| Reviews | |||||
| 1 | Boudraa, et al. 200627 | N/A | Mostly clinical images | Extensive review of the fomalism of image segmentation algorithms used in nuclear medicine (not specific to PET and clinical oncology) | Only a few algorithms have been rigorously validated for accuracy, repeatability and robustness. |
| 2 | Lee, 201029 | N/A | Simulated and mostly clinical images | Discussed the main caveats of threshold‐ based techniques including the effect of phantom cold walls on threshold. A discussion of the available and desirable validation datasets and approaches is also included. | Extensive review of nuclear medicine image segmentation algorithms (not specific to PET and clinical oncology) |
| 3 | Zaidi and El Naqa, 201054 | N/A | Simulated, experimental and clinical studies | Despite being promising, advanced PET‐AS algorithms are not used in the clinic. | |
| 4 | Hatt, et al. 201143 | N/A | N/A | Only a few algorithms have been rigorously validated for accuracy, repeatability and robustness. | See the three last columns of Table 1 |
| 5 | Kirov and Fanchon, 2014,176 | N/A | Clinical images with pathology derived ground truth. | Articles comparing PET‐AS methods are summarized separately for lesions in five groups based on location in the body with a focus on the accuracy, usefulness and the role of the pathology‐validated PET image sets. | |
| 6 | Foster, et al. 201436 | N/A | N/A | “although there is no PET image segmentation method that is optimal for all applications or can compensate for all of the difficulties inherent to PET images, development of trending image segmentation techniques which combine anatomical information and metabolic activities in the same hybrid frameworks (PET‐CT, PET‐CT, and MRI‐PET‐CT) is encouraging and open to further investigations.” | Most exhaustive review of the state‐of‐the‐art in 2014. Uses a similar classification of methods as in the present report. |
Most of the algorithms have been optimized/validated on phantom acquisitions of spheres, as this is a common tool in PET imaging to evaluate the sensitivities, noise properties, and spatial resolution of PET scanners. On one hand, most algorithms usually give satisfactory results in these phantom acquisitions, even for varying levels of noise and contrast levels. However, homogeneous spheres on a homogeneous background are not realistic tumors. The number of algorithms that have been successfully applied to realistic simulated tumors or real clinical tumors with an acceptable surrogate of truth (e.g., histopathological measurements) is much smaller. Finally, algorithms that have been validated for robustness against several scanner models and their associated reconstruction algorithms are even less numerous since the datasets are not usually made publicly available.
It should also be emphasized that there are a few algorithms that have been applied to common (although not publically available) datasets. For instance, the gradient‐based algorithm by Geets, et al.,37 the improved fuzzy c‐means (FCM) by Belhassen and Zaidi,28, 139 the theory of possibility applied to Maximum intensity projections (MIP) by Dewalle‐Vignon, et al.140 and the contourlet‐based active contour model by Abdoli, et al.141 have all been applied to a dataset of seven patients with 3D reconstruction of the surgical specimen in histology (from a dataset of nine patients originally obtained in a study by Daisne, et al.142), with 19 ± 22%, 9 ± 28%, 17 ± 13% and 0.29 ± 0.6% volume mean errors, respectively. Similarly, the improved fuzzy c‐means by Belhassen, et al.,28 FLAB by Hatt, et al.70, 143 and the level sets and Jensen‐Rényi divergence algorithm by Markel, et al.34 were applied to the NSCLC tumors dataset with maximum diameters from MAASTRO (Maastricht Radiation Oncology)124 (with ± 6% error for FLAB, ± 15% for the improved FCM and ± 14.8% for the level sets approach, respectively). In addition, most of the advanced algorithms that have been proposed have been compared to some kind of fixed and/or adaptive thresholding using their respective test datasets and have, for the most part, demonstrated improvements in accuracy and robustness. In particular, it was observed that fixed and adaptive thresholding might lead to over 100% errors in cases of small and/or low‐contrast objects and significant underestimation (−20 to −100%) in cases of larger volumes with more heterogeneous uptake distributions, whereas advanced methods were able to provide more satisfactory error rates (around or below 10 to 20% errors).143, 144 However, it is possible that simpler, e.g., adaptive threshold PET‐AS‐methods optimized for a specific body site, may perform comparably well or even better than some of the more advanced techniques.145
In the largest comparison to date, Shepherd, et al.100 segmented 7 VOIs in PET using variants of threshold‐, gradient‐, hybrid image‐, region growing‐, and watershed‐based algorithms, as well as more complex pipeline algorithms. Along with manual delineations, a total of 30 distinct segmentations were performed per VOI and grouped according to type and dependence upon complementary information from the user and from simultaneous CT. According to a statistical accuracy measure that accounts for uncertainties in ground truth, the most promising algorithms within the wider field of computer vision were a deformable contour model using energy minimization techniques, a fuzzy c‐means (FCM) algorithm, and an algorithm that combines variants of region growing and the watershed transform. Another important finding was that user interaction proved in general to benefit segmentation accuracy, highlighting the need to incorporate expert human knowledge, and this in turn was made more effective by visualization of PET gradients or CT from PET‐CT hybrid imaging.
There is little information to date concerning the comparison of the performance of an algorithm using datasets from different scanners and/or with the implementation of that algorithm in different software packages. In one study,146 an adaptive threshold segmentation algorithm was applied in three centers using two similar types of scanners from the same manufacturer. The authors demonstrated that significant differences were observed in the optimal threshold values depending on the center and imaging protocols, despite that both the scanner and reconstruction method were the same. In addition, significant differences were also observed, depending on the reconstruction settings (Fig. 4). They concluded that synchronization of imaging protocols can facilitate contouring activities between cooperating sites. In another investigation, dependence of the segmentation threshold providing the correct sphere volume on the reconstruction algorithm was also observed for small spheres.147
Figure 4.
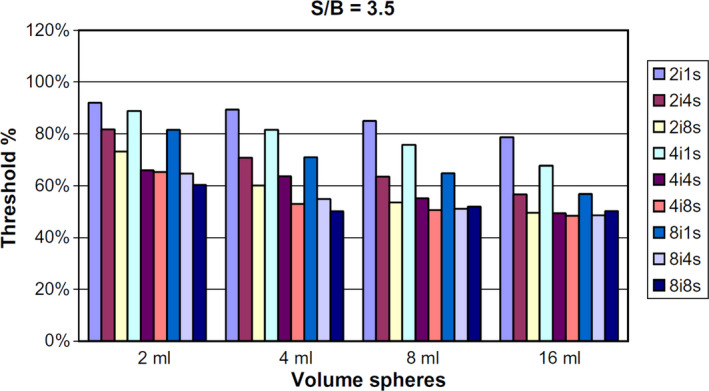
Variation in the optimal threshold value (y axis) obtained according to different settings of the PET reconstruction with varying number of iterations and subsets (from two iterations one subset to eight iterations eight subsets, colored bars), and for spheres of different volumes (x axis) and a sphere‐to‐background ratio of 3.5, for one single scanner model. Reproduced with permission from Ollers, et al.146 [Color figure can be viewed at wileyonlinelibrary.com]
In a German multicenter study,148 Schaefer, et al. evaluated the calibration of their adaptive threshold algorithm (contrast‐oriented algorithm) for FDG PET‐based delineation of tumor volumes in eleven centers, using three different scanner types from two vendors. They observed only minor differences in calibration parameters for scanners of the same type, provided that identical imaging protocols were used, whereas significant differences were found between scanner types and vendors. After calibrating the algorithm for all three scanners, the calculated SUV thresholds for auto‐contouring did not differ significantly.
On the other hand, the FLAB algorithm by Hatt, et al. showed robustness to scanner type and performed well without pre‐optimization, on four different scanners from three vendors (Philips GEMINI GXL and GEMINI TF, Siemens Biograph 16 and GE Discovery LS) using a large range of acquisition parameters such as voxel size, acquisition duration, and sphere‐to‐background contrast.43
While the natural incentive is to create algorithms which perform universally well across body sites and disease types, for at least one body site it was shown145 that simpler (e.g., adaptive threshold) methods may perform comparably well if specifically optimized for these conditions. At present, there is not a sufficient amount of published data to give specific recommendations for each clinical site. The emerging consensus99 and decision tree73 based methods, however, provide a potential to provide adequate solution for each site if appropriately adapted and trained.
Given the above results, the validation of PET‐AS algorithms, as described in current publications, does not provide sufficient information regarding which of the known approaches would be most accurate, applicable, or convenient for clinical use. In the following sections, we attempt to lay the basis for a framework that avoids the methodological weaknesses of the past and addresses the challenges inherent in segmentation in PET.
4. Components of an evaluation standard
A main conclusion of the work of this task group is that a common and standardized evaluation protocol or “benchmark” to assess the performance of PET–AS methods is needed. The design of such a protocol requires:
Selection of evaluation endpoint and definition of performance criteria;
Selection of a set of images;
Selection of contour evaluation tools;
4.A. Evaluation endpoints
For radiation therapy the PET image is most often used to segment the so‐called gross tumor volume (GTV) which contains the macroscopically observable (demonstrable) disease.149 Based on the GTV is later generated the clinical target volume (CTV), which is supposed to include additional volume with a high probability of microscopic tumor extensions.149 The planning target volume (PTV) encompasses the CTV and adds an additional margin for set‐up error and organ motion.149 The sub‐target volume (sub‐GTV) lies within the GTV and locates one or more metabolically distinct sub‐volumes such as tumor growth, burden, or hypoxia. Segmentation of the sub‐GTV assumes availability of additional functional information, which can come from PET or from other imaging modalities.2 Within this context, the smallest number of cells with uptake that is possible to image using PET has been assessed as 105 cells.150
The endpoint for evaluating PET‐AS algorithms can be selected at different levels of approximation of the tumor border. We consider the following three levels of approximation ordered from least to most accurate:
The PET avid tumor volume in the PET image as obtained through standard reconstruction, which typically leaves some of the physical artifacts (such as limited spatial resolution, motion), not routinely and/or fully corrected;
The PET avid tumor volume after optimal correction of more subtle artifacts such as resolution, motion and noise;
The spatial distribution of the biological quantity of clinical interest (e.g., the distribution of cells exhibiting a certain metabolic trait, e.g., proliferation).
The ideal endpoint for evaluating PET‐AS algorithms if they are to facilitate reaching the clinical goal is (c). However, variations in the biological environment of the lesion (e.g., perfusion and inflammation) and other biological and physical uncertainty in PET images decrease the accuracy of numerical algorithms in aiming at the clinical endpoint (e.g., the GTV). The less ambitious endpoint (b) of contouring the volume based on the real tracer distribution is feasible, provided that important factors, such as PVE, motion and noise are accurately taken into account or corrected with state‐of‐the‐art approaches (either within reconstruction or post‐reconstruction).
Finally, most algorithms have been and can be evaluated against the activity as seen in the standard PET image (a). This case concerns standard acquisitions with routine clinical systems for which some of the physical artefacts (attenuation, scattered and random events, etc.) are corrected, but no correction is applied for others (e.g., spatial resolution, motion, statistical noise, and post‐filtering). This method is currently widely used. Nevertheless, for future standardized evaluation protocols, our task group recommends considering the three endpoints listed above.151 Such future work should also consider segmenting radiotherapy targets using multispectral images from hybrid imaging studies31, 33, 34, 97 dynamic imaging152, 153 and/or multitracer PET images.154
4.B. Definition of performance criteria: accuracy, precision (reproducibility and repeatability) efficiency and robustness
In instrumental science any measurement tool can be characterized by its accuracy (degree of closeness to the true value) and precision (degree to which repeated measurements under unchanged conditions give the same results). Precision can be further stratified into repeatability and reproducibility. Reproducibility often implies that tools or operators are different, whereas repeatability relies on experimental conditions that are kept as identical as possible. For complex tools such as segmentation algorithms, stratification into reproducibility and repeatability is not necessary and precision suffices, provided all parameters are identified, including those for which the operator has control, e.g., the region of an image used to characterize the background tracer uptake.
For a given segmentation algorithm we define accuracy as the correctness of retrieving the true 3D object spatial extent, shape, and volume based on the reconstructed activity distribution in a PET image, irrespective of the correlation between this distribution and the underlying physiological process. This means that an image segmentation algorithm is not expected to differentiate specific from nonspecific tracer uptake (e.g., inflammation and tumor in the case of FDG) if they are of the same intensity.
Within the context of this report, repeatability1 is defined as the ability of a given algorithm to reach the same result when applied multiple times on a single image replicate (single acquisition), given potentially differing algorithmic initializations.43 In such a task, deterministic, fixed threshold approaches will always give the same result when applied to a given image. On the other hand, more advanced algorithms are susceptible to providing different results when applied with multiple runs on the same image because they could rely on more complex initializations or estimation processes, including random ones.
We define robustness as the ability of a given algorithm to generate consistent, segmented volumes under varying acquisition and image reconstruction conditions, including issues related to statistical counts and multiple replicates (multiple acquisition of the same object) due to noise.43 This robustness is determined as the variability in the segmentation results when a PET‐AS algorithm is applied on images of the same object acquired using various scanners, and for each scanner, under various contrast and noise conditions, using different reconstruction and associated correction algorithms.
Finally, an important parameter of the algorithms is their efficiency, which may determine their practical viability.41 Efficiency includes workflow and computational complexity required for completion of the segmentation task. Considering the computing power evolution and possibilities (parallel computing, graphical processing units, etc.), the main limiting factor is workflow and human interaction.
Below is laid out, the vision of the task group for a future standard for PET‐AS method evaluation. It has two main components: (a) Benchmark image set; (b) Performance evaluation criteria.
4.C. Benchmark image sets
This section is dedicated to the selection of the benchmark images, which should cover a realistic range of parameters so that it ensures that the tested PET‐AS algorithms can meet the challenges that may be encountered in various clinical cases. However, to allow for a practical and realistic evaluation and interpretation of the results, the number of images and datasets should be kept to a minimum. Therefore, the images that are likely to offer the most realistic, rigorous way to assess the performance of the various algorithms should be selected. A classification of the possible types of benchmark images is given in Table 3.
Table 3.
Advantages and disadvantages of the different methods used for generation of test images
| Experimental images | Simulated images | ||||
|---|---|---|---|---|---|
| Simple phantoms | Realistic phantoms | Clinical images | Forward projected images | Monte Carlo (MC) simulations | |
| Advantages: |
|
|
|
|
|
| Disadvantages: |
|
|
|
|
|
The advantages and disadvantages of the different classes of datasets and of particular published image sets are discussed in more detail below. The various phantoms considered for a common PET‐AS evaluation protocol are summarized in Appendix III.
4.C.1. Physical phantoms
The main advantage of physical phantoms is that their PET images contain the same degradations, namely resolution, noise, scatter, etc., as clinical PET scans, while also ensuring that the ground truth is both reproducible and known for repeated testing using prescribed conditions.
Most PET‐AS algorithms are initially developed and optimized against simple phantoms containing uniform activity spheres or cylinders. Therefore, these phantoms are essential in evaluating segmentation accuracy for well‐defined, simple‐shaped objects. However, spherical targets oversimplify the segmentation problem and can erroneously favor an algorithm that would break down in the presence of a complex topology or heterogeneous tracer uptake distribution seen in real tumors. Testing the PET‐AS algorithms against these images can nevertheless provide: (a) assurance that the algorithms compared are trustworthy for simple cases; (b) agreement limits for initial, basic evaluation; (c) opportunity for verifying algorithm operation over time (e.g., routine quality assurance), and (d) a convenient tool for testing the robustness of the algorithms under different experimental conditions using for instance the National Electrical Manufacturers Association (NEMA) image quality phantom (Fig. T.A2.1 in Appendix III),155 available in most PET centers. However, with few exceptions156, 157 these phantoms contain objects with cold walls in a homogeneous background.155 Furthermore, most of the algorithms have already been optimized and assessed on these simplistic, physical phantom acquisitions at the development stage.
More realistic phantoms are of interest for more demanding evaluations with respect to the activity distribution endpoint. The contribution by Zito, et al.158 regarding the use of phantoms containing zeolites (microporous, aluminosilicate minerals commonly used as commercial adsorbents, which can absorb aqueous solutions of (18)F‐FDG) is promising. This phantom allows tumor‐like objects to be generated with any desired shape, size, and contrast levels without cold walls. They also provide ground truth with sub‐voxel resolution that is available from the associated co‐registered CT images.
A limitation of these images (e.g. obtained from zeolite phantoms) is the lack of control and knowledge of the potential heterogeneity of the tracer uptake in the background and the “tumor.” Several alternatives allow experimental modeling of nonuniform activity inside the lesions and in the background. These phantoms include structures generated by stacking paper sheets containing PET images printed with radioactive ink159, 160 (see Fig.T.A2.6. in Appendix III), or 3D printers using radioactive ink.161 Another option for generating nonuniform uptake distributions is the use of thin sheets to displace activity (see Fig.T.A2.7 in Appendix III).162
4.C.2. Simulated images
Virtual or numerical phantoms associated with a PET image generation process represent an inexpensive, precise way to test PET software and clinical methodologies.163 One definition of a virtual or numerical PET simulation framework corresponds to any computer‐generated object that is processed to produce a PET‐like image. It should be clear that virtual phantoms are distinct from the resulting PET images and represent a reference source distribution from which the PET‐like image is produced. To be useful the resulting image needs to be representative of what is observed in the images produced by a real PET camera.
Generating PET‐like images for virtual phantoms can be done in several ways. Below we describe methods that range from simple to complex, as more realism is included in the simulation, and therefore, in the produced images.
Inserted tumor PET‐like images
The simplest method is to insert an object with added noise, representing a tumor, directly into an existing PET image.164 However, this method requires considerable effort to blend the noise and edge characteristics of the lesion into the image to avoid obvious edges from threshold or texture mismatches. This method is the least realistic of the various approaches for generating PET‐like images. Because of these weaknesses and the difficulties in accurately matching the noise/spatial resolution properties of real PET images, it is not further discussed.
4.C.2.2. Forward projected tumors
Alternatively, a more robust method is to consider a synthetic lesion that can be forward projected, have noise added and then inserted into the noiseless forward‐projection of an existing PET image that is scaled appropriately to match the desired noise level of the tumor. The projection data can then be reconstructed to preserve the basic characteristics of the original image. Care must be taken to ensure that the forward and backward projectors are matched, i.e., adjoint, that the original PET image is sufficiently oversampled and that the reconstruction process does not greatly alter the underlying PET image. Although this process is conceptually simple, its realism is limited by inaccuracies introduced in modeling the spatial variation in the PSF, the noise model and the effects of the reconstruction process.
Forward projected phantom images
Forward projected phantoms and tumors represent a middle ground between full Monte Carlo PET simulations of phantoms and directly inserting tumors into PET images. This has been implemented in an open source simulation tool165 and used in several PET studies, as it is a standard means for evaluating image reconstruction methods.166, 167
In this method, noiseless tumor and phantom images are forward projected and scaled to produce a similar number of total counts as would be seen in the equivalent projection data and then fused, which represents the reference images. Noise is then added to the resulting projection data via a Poisson distribution to create PET‐like projection data. These data are then reconstructed to produce the PET‐like images of the original virtual phantom. Additional realism can be included by blurring the images with a PSF (derived from physical parameters: positron range, annihilation photon noncollinearity, detector solid angle, block effects, etc.), adding attenuation, random, and scatter counts and altering the fidelity of the projection matrix or the type of reconstruction. This process is described in Fig. T.A2.8. in Appendix III. Motion can also be simulated by applying the appropriate motion‐blurring kernel to the image prior to forward projecting the image into sinogram space. This method can be extended to insert realistic tumors into existing PET images.165
Monte Carlo simulations
The most realistic data can be obtained by simulating the entire positron emission, annihilation, interaction, and detection processes with Monte Carlo (MC) simulations. The subsequent projection data can be reconstructed to produce very realistic images.
Using recent, state‐of‐the‐art anthropomorphic phantoms such as the XCAT (4D NURBS‐based Cardiac‐Torso)168 or Zubal phantoms168, 169 and MC simulators such as SORTEO (Simulation Of Realistic Tridimensional Emitting Objects),170 GATE (Geant4 Application for Tomography Emission)171, 172 or SimSET (Simulation System for Emission Tomography),173 combined with scanner system modeling (geometry, detectors, etc.),174 can provide highly realistic simulations, including respiratory motion144 with regular or irregular respiratory signals. Simulated tumors can be placed in various anatomical locations and generated with nonspherical shapes and complex uptake distributions, including realistic “activity gradients” (see Fig. T.A2.9 in Appendix III). PET data are then simulated by assigning an uptake to each organ/tumor of the anatomical phantom. Parameters such as tumor‐to‐background ratio or intra‐tumor heterogeneities can be varied within any desired range. Similarly, it is possible to generate various noise realizations, as well as various SNR ratios, by selecting different parts of the overall simulated list mode data (lines of response) before reconstruction. It is therefore also possible to select lines of response corresponding to true coincidences only, or including the random and scattered data. Different scanner designs and reconstruction algorithms and/or parameters (number of iterations, post‐filtering smoothing, voxel dimensions, etc.) can also be modeled if detailed information about the scanner is available; hence, this method allows the assessment of robustness and “universality” of the PET‐AS algorithms.
Simulated data can provide a high level of realism without the disadvantages and inconveniences of real phantom acquisitions. It is possible to increase the number of activity levels to realistic numbers approximating ground truth to the voxel level achievable by some experimental approaches.161, 162 This however can increase the complexity and time required for the design of the simulation.
4.C.3. Clinical images
In patients, the “ground truth” is defined by the actual underlying extent of disease; however, the true biological margins are usually unknown. This is in contrast to phantoms, where the ground truth is clearly defined by the phantom design and therefore well‐known. For clinical images the following surrogates of truth can be used: (a) a consensus of several physicians or expert‐drawn contours and/or (b) histopathological measurements of lesions resected within a reasonably short timeframe after the image acquisition and for which special precautions are taken as described below.
Consensus of several physician‐drawn contours
If the clinical endpoint is selected as the decision basis in the absence of histopathology information, consensus of several physician‐drawn contours is sometimes used as a surrogate of truth. When the segmentation contours can potentially be used in different clinical applications, images contoured by several experts or physicians from different specializations (e.g., the study by Bayne et al.175 in which two radiologists, two radiation oncologists and two nuclear medicine physicians contoured five NSCLC patients), might reduce bias due to personal and specialty‐based preferences at the price of a likely slightly higher inter‐observer variability due to differences in training and habits. On the other hand, when considering a specific clinical application, such an approach may be less accurate than using consensus of contours drawn by several specialists in this specific application. Indeed, contouring by physicians from only one specialty, e.g., radiation oncologists,25 may provide more reliable estimates for an endpoint corresponding to the goals of this specific sub‐specialty (target volume definition in this case).
The use of the consensus‐based methods discussed at the end of section 2.B.2, which can account for a set of manual contours, may be expected to reduce errors under certain assumptions about the operators, as differences in performance or training can be taken into account (e.g., within the STAPLE framework).
Histopathological validation of PET image segmentation
This type of PET‐AS validation can be carried out using PET images of tumor specimens for which histopathological characterization is also available. In this case, PET‐AS contours can be tested directly against the histopathology‐derived contours. At present, these data serve as the most clinically relevant ground truth of tumor extent. However, there are several sources of errors that limit the accuracy of this surrogate of truth for PET‐AS validation: (a) variable amount of deformation of the surgical specimen after excision, (b) time difference between the PET scan and the specimen excision, (c) uncertainty associated with manual delineation (usually by a single observer) of the tumor boundaries in digitized histopathology, and (d) imperfect co‐registration of histopathology slices and PET volumes. While these errors can potentially limit the validity of the comparison, histopathological validation is an important part of thorough PET‐AS evaluation. At present, there are several datasets in which effort was made to minimize these errors.176 Examples are: the lung tumor dataset from the MAASTRO (Maastricht Radiation Oncology) team with pathology‐validated maximum diameters,124 the tumor datasets used in the study from the Jefferson Medical College (max. diameter),177 the HNSCC (Head and Neck Squamous Cell Carcinoma),142 the NSCLC56 full 3D volumes reconstruction datasets from the Université Catholique de Louvain studies and the lobectomy‐based dataset from The Netherlands Cancer Institute (NKI).178 Despite the challenges with respect to the accuracy of the reference contours, these pathology‐validated images provide an important test for PET‐AS methods. This justifies the need for further improvement of the current experimental approaches, as well as development of new techniques to improve the accuracy of histopathological validation.176, 179, 180
It is important to note that because histopathological validation of PET image segmentation is carried out for a particular tissue and tracer pair, it cannot be implied that the results apply to alternative PET tracer/tissue combinations; hence, one should exercise care when using PET‐AS algorithms to segment tracer/tissue pair images different from those for which they were validated. It should be noted that evaluating PET segmentation against anatomic or surgical delineation could be potentially misleading since biodistribution of a particular PET radiotracer may not conform to these structures. This is especially true for non‐FDG tracers such as hypoxia probes where the entire tumor volume is not expected to display uptake.
4.C.4. Blind study and updates
To facilitate the training and validation of PET‐AS algorithms, it would be optimal to separate the images of the future standard into two groups: (a) With ground truth given to the PET‐AS developers for learning/training and (b) Blind study (without ground truth) for testing. The rationale behind (a) is that some algorithms, e.g., the learning algorithms may need to be trained, whereas (b) will ensure more objective evaluation and validation. Simple geometrically shaped phantoms naturally fall in the first category, whereas clinical images are a natural candidate for the second group. Simulated images, or complex shape experimental phantoms, can be distributed among the two.
Since both experimental and numerical phantoms are currently in rapid development, it is important to make provisions for updating and expanding the set of images. The benchmark's goal can be better reached if it can facilitate and encourage the sharing of new acquired datasets by contributing users. As new data and PET‐AS algorithms become available, the evaluation process can be organized so that the new, shared datasets become gradually included in the standard. For example, a rule may be considered according to which, a certain fraction of the images (e.g., ~60%) must have been used for evaluating at least ten algorithms.
4.D. Figures of merit
Choosing the best set of Figures of Merit (FOM) depends on the complexity of the segmentation problem as well as on the evaluated endpoint. For example, when using spheres in a standard compartmental phantom, shape modifications and volume translations are unlikely to be observed. In this case, simple volumetric differences may be enough. In more realistic images, inaccuracies in shape or location are more likely and need to be detected with a more complex FOM. A statistical approach can further distinguish between two types of errors with respect to assigning a voxel to a lesion or normal tissue: Type I — false positives and Type II — false negatives. The various FOMs are discussed in detail in Appendix IV. The FOMs listed in Table 4 are considered for use in a future standard.
Table 4.
A comparison of various volume/contour agreement measures and their sensitivities to the properties of the segmented lesions. The important properties are whether they account for volume differences, shape discrepancies, false positive vs. false negative. The computational complexity is graded between easy (+) and complicated (+++), although none of the metrics are particularly slow to compute using modern toolkits and computers (Barycenter distance is the distance between the centers of mass of two sets)
| Evaluation metrics | Location | Size | Shape | Type I/II | Complexity |
|---|---|---|---|---|---|
| Volume difference | no | yes | no | no | + |
| Barycenter distance | yes | no | no | no | ++ |
| Jaccard similarity coefficient | yes | yes | yes | no | ++ |
| Dice similarity coefficient (DSC) | yes | yes | yes | no | ++ |
| Hausdorff distance | yes | no | yes | no | +++ |
| Sensitivity + Positive Predictive Value (PPV) | yes | yes | yes | yes | ++ |
Most of these FOMs have advantages and drawbacks, some of which are listed in Table 4. For example, optimizing sensitivity alone would favor methods that encompass and therefore overestimate the true volume. Similarly, optimizing positive predictive value alone would instead favor methods that underestimate the true volume. Other criteria are not strict enough (e.g., volume difference), computationally expensive (e.g., Hausdorff distance181), or unable to distinguish between the two error types (false positive and false negative, e.g., Jaccard and DSC). Therefore, we caution against using a single performance metric for segmentation evaluation and rather suggest reporting several FOMs such as the combination of sensitivity and positive predictive value, to convey complementary information.
Notice that the Type I/II error distinction in sensitivity and PPV requires the knowledge of which of the two volumes is the actual ground truth, whereas other measures treat both volumes in the same way. In the absence of a ground truth volume (neither A nor B is preferred), then the Dice similarity coefficient can be used instead of Sensitivity + PPV.
As discussed in section 4.B, some image datasets, e.g., simulated and experimental images, may have more accurately defined ground truth than others, (e.g., clinical images accompanied by pathological results or manual contours). In the case of a less accurately defined ground truth, the inverse‐ROC approach, used by Shepherd, et al.,100 can give a reliable evaluation of the algorithms, provided a set of contours (e.g., manual delineations) that encompass the ground truth contour exist.
Due to the complexity of the PET segmentation problem, more appropriate evaluation metrics could be defined based on the clinical endpoint. In the case of radiotherapy treatment planning, an example would be the geometrical concordance of the delivered dose distributions to the PET segmentation contour and the treatment outcome. Tools which can account for such information have recently been proposed.182
5. Discussion of segmentation limitations, dependencies, and implementation
5.A. Biological limitations of the segmentation concept
It has long been realized that cancer is an abnormal growth caused by unregulated cell proliferation. Cancerous tissue morphology is highly irregular and characterized by chaotic vascularization, resulting in a unique pattern of blood flow for every tumor, which modifies PET tracer availability and uptake in a way unique for each patient. Also, different parts of the same tumor can have very different micro‐environmental status, including different levels of glucose metabolism. Other factors affecting intratumoral PET tracer distribution are the presence of necrosis and stromal tissue intertwined with cancer cells. As a result, the intratumoral pattern of FDG uptake is highly heterogeneous.
While it is possible to carry out in vitro studies to relate PET tracer binding/uptake to environmental parameters of the cells in culture, direct in vivo application of such data is highly speculative and lacks strong foundation due to the reasons listed above. The uniqueness and stochastic nature of the factors governing PET tracer uptake and its intratumoral distribution in each patient represents one of the biggest challenges for PET image segmentation. The complexity of the problem hampers the widespread adoption of auto‐segmentation tools for routine clinical use.
Other factors can also potentially affect PET‐based lesion segmentation. Tumors may lack a well‐defined boundary separating them from the surrounding normal tissues. Microscopic cancer extensions can produce additional blurring of this idealized, macroscopic boundary. Furthermore, in addition to heterogeneities of tracer uptake in the lesion, surrounding normal structures are likely to be characterized by different levels of tracer uptake. Inflammation, if present, can result in further complications by significantly increasing FDG uptake. Correspondingly, the biological meaning of the segmented volume should be interpreted in the context of all these biological factors governing image formation in PET. Therefore, both PET image segmentation as well as interpretation of the segmentation result are very nontrivial tasks and should be approached with caution. However, for situations where tumor delineation is needed, e.g., radiation therapy treatment planning, the right choice of properly validated PET‐AS methods used as a guidance tool by the physician can result in increased target definition accuracy and better treatment.
5.B. Dependence on segmentation task
There may be significant differences in terms of tumor segmentation algorithm parameterization and use, depending on the task. At the same time, it should be emphasized that most published methods have been proposed either as a general PET segmentation approach, which can be used in any application (although rarely tested or validated for all), or as a method developed and validated for a specific clinical application (e.g., radiotherapy planning, without being tested in another setting).
In treatment planning the PET information can be used in two ways:183
Target volume delineation: The PET‐based GTV should safely encompass the entire tumor volume without missing regions with low radiotracer accumulation. To avoid cancer under treatment, even equivocal voxels would usually be included. However, to avoid over irradiation of too large a volume of normal tissue, the GTV should not be larger than needed. To account for microscopic disease the radiation oncologist then draws the CTV by adding a margin to the GTV (section 4.A).
Uncertainties to the tumor contour for external radiotherapy may be generated based on the accuracy of the method as determined during the evaluation stage. The delineation uncertainty can be approximated as a shell or annular volume around the segmented volume. The thickness of the annular shell could, for example, be derived from the average thickness of the annular volume between the overlap and union volumes of the segmentation and reference surfaces determined during the evaluation stage. Other options are to use distance metrics between these surfaces, which can be based on the Hausdorff distance or similar methods.184
Target substructure determination: In contrast, PET‐based definition of tumor sub‐volumes for so‐called biologically conformal radiotherapy or dose painting2 requires a different approach. In dose painting, radiation is shaped according to the PET uptake, theoretically delivering higher dose to the radiation resistant and/or tumor‐rich parts of the tumor. To achieve this goal, one needs to rely on a detailed understanding of the underlying tumor biology and PET signal (e.g., PET tracer uptake and retention mechanisms), as well as how to determine the dose prescription function based on the PET signal. In that specific context, radiotracers different than FDG have been investigated, e.g., use of FMISO‐PET might indicate hypoxic regions and the use of FLT‐PET might indicate tumor proliferative regions, where increased dose is needed. In such cases, PET‐AS methods would need to be able to define both the entire tumor volume as well as sub‐volumes with different levels of activity. In some rare cases, multitracer datasets can be available and the images combined to define a biological target volume (BTV). Methods based on information fusion have been proposed to address this specific challenge.154, 185, 186, 187
For treatment response assessment:
Segmentation can be used for the estimation of various uptake measurements (mean SUV, total SUV, heterogeneity of uptake using, e.g., histogram‐derived first‐order features or more complex second and third order textural features), which may correlate better with the clinical outcome than less comprehensive metrics, such as maximum or peak SUV.
Automatic segmentation can be used for more consistent longitudinal tracking of treatment response to various cancer therapies. Repeatability and reproducibility of segmentation in this case could be more important than absolute accuracy, especially within the context of the known relatively high test–retest variability in PET scan imaging188, 189
The PET avid volume and/or on tumor‐to‐background ratio may change as a result of therapy. Therefore, for PET‐AS methods which are dependent on these parameters (e.g., some adaptive threshold methods23, 52) use of the same method for segmentation of PET images before and after therapy without proper adjustment of parameters may result in incorrect and inconsistent segmentation. This may then affect the accuracy of the metrics derived from the segmented volume. In general, using FDG for adaptive radiation therapy may be problematic due to change in the SNR as a result from reduction in the tumor uptake and/or inflammation. This means that, for example, a threshold set to 42% of peak activity may provide erroneous results if the tumor/background ratio changes substantially or if the PET avid volume decreases under a certain value.48 This volume was found to be about 1.5 mL for older PET scanners but will be partial volume and therefore scanner dependent. Similarly, if the PET avid volume has an irregular shape with both wide and thin parts, the threshold may have to be adapted to the effective size of these parts of the volume.
The time saved using automatic segmentation is also important; lack of time in daily practice is one of the major limitations preventing investigators from using ROI‐based methods for treatment response assessment in cases where volume (or volume‐derived) information is important. As a result, in current practice, SUVmax and SUVpeak, which are less dependent on accurate edge and volume definition, are more widely used for response assessment. Automatic segmentation provides consistency and time efficiency in longitudinal studies. However, consistency is harder to achieve for PET measures dependent on the segmented volume (e.g., SUVmean, SUVtotal), compared to measures that do not depend on it, but simply follow the voxel(s) with highest activity concentration anywhere within the GTV (e.g., SUVmax, SUVpeak).
In addition, even for a single clinical goal (e.g., radiation treatment planning), the PET‐AS methods may meet different requirements for different disease types and body sites. This may profoundly affect the method evaluation process. For example, this may result in favoring relatively simple, e.g., adaptive threshold methods, optimized for each lesion type versus more complex advanced methods, which may do equally well in different parts of the body. During the development of a future evaluation standard, this possibility may be investigated by sorting the performance results of the PET‐AS methods between body sites and tumor types.
5.C. Dependence on scanner, image acquisition, and reconstruction protocol
One major consideration in PET image analysis is the lack of standardization of clinical imaging protocols resulting from hardware and software variability, as well as the variation in procedures between clinical centers (injected dose, delay between injection, and acquisition, acquisition duration, etc.). Thus, every post‐acquisition, post‐reconstruction analysis, and extraction of relevant parameters from PET images depend on the actual qualitative and quantitative characteristics of the analyzed PET image (e.g., resolution and noise), which are strongly influenced by the acquisition protocol. For this reason, users are cautioned to always evaluate and validate published PET‐AS methods for their specific clinical application and scanning protocol before clinical use.
Recently, there have been several efforts to propose ways for the standardization of imaging procedures. These efforts have sought to minimize the impact of acquisition protocols on the resulting visual quality and quantitative accuracy and consistency of PET images4, 190, 191, 192 One of the main reasons is to help improve consistency in multicenter trials that combine images acquired from different clinical centers, scanners, and imaging protocols.
These efforts are to be encouraged. By reducing the existing variability in PET images encountered in clinical practice, they will contribute toward improved data consistency, which will facilitate the use of PET‐AS algorithms across different centers and thus allow the use of advanced quantitative tools for treatment assessment. This will also contribute to reducing the dependence of PET defined tumor volumes on the specific instrumentation and protocols in a given clinical center.
The quality of an image is defined by several parameters, which may have different importance for different tasks.193, 194, 195, 196 Segmentation differs from typical diagnostic tasks in that it seeks to identify the boundary locations and therefore uses a much larger parameter space. Based on this, there is an expectation that this problem is more ill‐posed and requires less noisy data to reduce errors.
This can be achieved by modifying the injected activity, uptake period, acquisition, and image reconstruction. Increasing the injected activity may improve the noise equivalent count rate. Typically, for radiation therapy simulation the injected activity is unaltered from that used for diagnostic imaging and it is possible that the risk from therapy is large enough that it outweighs the risks associated with injecting a larger amount of activity. For the case of FDG‐PET, a 1‐hour post‐injection delay is used; however, the contrast ratio of uptake to background continues to increase with time. This 1 h selection is due to tradeoffs between workflow, consistency, diagnostic efficacy, etc. Increased dwell times over the tumor regions and/or additional spot scans can also be used to improve the images.
Increasing the number of counts in the data using these approaches would allow achieving higher resolution image by increasing the number of iterations while preserving the noise level.197, 198 Beyond this, some penalized image reconstruction methods with edge preserving prior models have been developed.199, 200, 201, 202, 203 These may produce images with edges that are more easily segmented. These trade‐offs may be considered for future protocol optimizations together with the risks associated with higher doses related to therapy.
5.D. Dependence on tracer type and physical isotope
Current investigations are dominated by FDG and 18F‐based tracers. This is understandable because FDG remains the most widely used radiotracer in oncologic imaging. However, there is a growing interest in non‐FDG tracers, including radiolabeled amino acids such as L‐methyl‐11C‐methionine (MET) or O‐(2‐18F‐fluoroethyl)‐L‐tyrosine (FET) for brain tumor delineation, proliferation markers such as 18F‐3′‐fluoro‐3′‐deoxy‐L‐thymidine (FLT) or hypoxia tracers such as 18F‐fluoromisonidazole (FMISO). At least some of these agents show a lower intensity of uptake in tumor lesions than FDG (e.g., FLT and FMISO), and thus physicians may apply different criteria for what constitutes significant radiotracer uptake (for instance in comparison to background reference regions or blood activity). In fact, little attention has been given to the question of how the use of these alternate radiotracers can affect the accuracy of the various segmentation algorithms. Most of the segmentation approaches have been designed for FDG‐PET. Also most fixed and adaptive threshold‐based methods are optimized for a specific range of tumor‐to‐background ratios. However, some methods have been used successfully on different radiotracers204, 205 For some tracers, a lower target‐to‐background ratio may lead to significant problems in the use of threshold‐based algorithms. Tracers other than FDG may be of great interest for dose painting and contouring of tumor sub‐volumes. However, for isotopes other than 18F, differing physical parameters, such as positron range and emission of cascade gamma rays, may degrade image quality and must be taken into account. This emphasizes the need for more robust algorithms that can deal with varying contrast and noise levels in reconstructed images. Histological validation of such tracer accumulation is necessary to determine sensitivity, specificity, and detection limits before these agents can be considered for dose modulation.
It should be noted that multitracer datasets have been acquired in research protocols and clinical trials to investigate the complementary value of different tracers. Since the acquisition and investigation of multitracer data is currently in its dawn and their segmentation is a very specific and challenging task outside common clinical practice, we are limiting their discussion only to this paragraph. Several novel methods have been developed to segment such data, usually with the goal of deriving a single biological target volume (BTV) from multitracer images. The use of information fusion has been suggested to achieve this as early as 2011185, 186, 187 and some recent fusion‐based methods have been evaluated with promising results.154
New, more sophisticated pattern recognition/machine learning algorithms are also on the horizon; these may make use of more subtle image characteristics, including noise distribution, underlying PSF, and nominal biological distribution. Such algorithms will require training sets of expert identified and segmented data and will only be valid for the type of data they were trained to process (see section 2.B.2). Therefore, while at present most segmentation schemes are radiotracer/isotope agnostic, this may rapidly change, as more sophisticated image‐processing techniques become available.
5.E. Effect of motion
Motion can have an important impact on the apparent size, shape, and contrast of lesions in PET images, especially in the thoracic area, due to respiratory motion. There has been a significant advancement of respiratory motion correction algorithms based on breath hold, external or internal gating, deformation corrections and post‐frame summing, blur deconvolution and others.206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223 Of these, the data driven gating approaches of PET images promise to yield comparable results with less discomfort for the patients than hardware driven approaches.219, 220, 221 Recent works have highlighted their applicability in clinical settings.224, 225 The development of synergistic algorithms, which encompass entire workflows226, or account for motion simultaneously with segmentation, are also expected.227, 228, 229
In the context of stereotactic body radiotherapy (SBRT), it has been shown that it may be useful to derive respiratory correlated target volumes from gated (4D) PET/CT scans in addition to 4D‐CTs.228, 230, 231 However, the current common practice still is to segment the PET volume integrated over the scan time. If PET‐AS algorithms are evaluated on clinical images against the activity as seen in the uncorrected PET image, endpoint a) as described in section 4.A, the potential effect of breathing motion in these images is disregarded. If the CT images are also used in the segmentation process, the uncorrected PET images should not be used for cases potentially affected by motion due to possible misalignment between the CT and PET.
5.F. Guidelines for acceptance and implementation for PET auto‐segmentation algorithms
Vendors have adapted and further developed some of the PET‐AS methods when implementing them in commercial software. However, the number of published algorithms is much larger than the number of those implemented (see section 2.B). The algorithms implemented by vendors, while being adaptations of published algorithms, may have modifications and enhancements that have a “black box” quality if vendors are reluctant to disclose proprietary techniques. Therefore, the vendors may have specific recommendations on how to test their PET‐AS algorithms, which the user should address first.
An additional factor to consider is the variability in implementations in the various commercial software visualization and analysis platforms. As it has been recently demonstrated, even for very simple metrics such as SUVmax, considerable variability has been shown to exist across various vendors and software, likely due to implementation errors, as well as different interpretation of, or assumptions about the data.232 The developed digital reference object is a very useful tool that will allow verification and validation of the vendor's implementation. Similar observations were made regarding contours and volumes that were substantially modified when transferred from one station to another.233 It is, indeed, not uncommon to transfer segmentation results such as contours from one station to another (e.g., a nuclear medicine‐dedicated analysis station to a radiotherapy planning station) and the user should verify their consistency. In that respect, considerable standardization efforts are needed to ensure that adopted PET‐AS methods will be correctly implemented and the results are compatible across the various platforms of different vendors.
Following vendor suggested acceptance testing, this task group envisions a three phase procedure (Table 5) for the implementation of segmentation algorithms that reflect the different level of closeness to reality of the PET images (see section 2.B.5). The images to be used in the three stages would contain lesions represented by; (a) spherical/cylindrical objects, (b) irregularly shaped objects, and (c) human datasets. Since each of these image types may present a different evaluation endpoint (4.A) and specific challenges that depend on how it was generated, this will allow a more thorough evaluation of PET‐AS methods.
Table 5.
Stages of evaluation of PET auto‐segmentation (PET‐AS) methods. DSC (Dice Similarity Coefficient), PPV (Positive Predictive Values), HD (Hausdorff Distance)
| Step | 1. Vendor acceptance | 2. Basic evaluation | 3. Phase two evaluation: | 4. Phase three evaluation | 5. Impact evaluation |
|---|---|---|---|---|---|
| Objective | Proper functioning of software | Accuracy for clinic‐specific images; robustness to image properties | Accuracy, repeatability and robustness for realistic shapes and variable uptake; | Accuracy, repeatability and robustness for clinical images from the intended application | Evaluation of clinical impact |
| Datasets | Vendor recommendation | Simple objects in uniform background; repeated acquisitions | Irregular shape and/or nonuniform uptake lesions in experimental or digital phantoms without cold wall; multiple realizations | Clinical images | Clinical images, treatment plans and follow‐up records |
| Ground truth | Vendor recommendation | CT defined voxel level accuracy. | High resolution CT or digital ground truth defined at voxel level accuracy. | Digitized histopathology and/or consensus of several manual delineations | Treatment outcome data |
| Metrics | Vendor recommendation | Volume errors, DSC | DSC, Sensitivity, PPV, HD | DSC, Sensitivity, PPV, HD, Statistical evaluation of clinical endpoint (prognostic/predictive value) | Statistical multiparameter treatment outcome analysis |
Most current implementation tests typically stop with the first phase, incorrectly assuming that the PET‐AS algorithm would be sufficiently accurate for realistic clinical images. For the first phase, phantoms with spherical inserts (diameter: 1 cm–4 cm) imaged at varying object‐to‐background ratios (e.g., 2:1 to 10:1) can be used. In addition, iodinated contrast can be used to aid in segmenting the ground truth volumes and in excluding the wall of the objects in the CT images. Simple shape (e.g., spherical) objects in uniform background, preferably without cold wall,156, 157, 158 are also most convenient for robustness evaluation across scanners and reconstruction schemes.
For the second phase, a combination of physical phantoms capable of constructing irregularly shaped objects100, 158 and nonuniform activity distributions,162 as well as numerically simulated phantoms that contain irregular shaped objects and/or nonuniform uptake, can be selected among the family of phantoms discussed in 4.C.1 and 4.C.2. Finally, for the third phase for which we suggest using clinical images, the main limitation is insufficient knowledge of the ground truth. As discussed in 4.C.3, ground truth surrogates such as pathology findings of excised specimens and/or statistical consensus from several manually drawn contours (preferably by different experts) can be used. Since both ground truth surrogates have a fair degree of uncertainty, the benchmark dataset should ideally comprise both of these image types.
The evaluation metrics for assessment of the segmentation accuracy are described in 4.D. While several of these tools can be used, a combined metric, e.g., including sensitivity, positive predictive value and Hausdorff distance is expected to provide a more reliable method assessment. However, further investigations are needed to generate a combined evaluation metric that is not affected by biases of the metrics or correlations between them. We suggest that the results of the evaluation stage be used to estimate the contouring uncertainty as discussed in section 5.B.
A standard, which will provide access to the selected benchmark datasets and various performance metrics, is currently under construction by members of the task group.151, 234, 235 As pointed out in the last column of Table 5, the ultimate evaluation of segmentation will be analyzing the outcome of treatments using the respective segmentation approach.
Ideally, a segmentation algorithm would be portable across different scanners with their individual and sometimes proprietary reconstruction schemes and parameters. Since this may not always be realistic for many PET‐AS algorithms, the implementation should be appropriately tagged as being optimized for specific scanner types and protocols.
The minimum requirements for an algorithm depend on the intended application goal: diagnostic, therapy planning, or treatment/prognostic assessment. For diagnosis, the most important aspect of the PET‐AS method is its ability to identify the tumor (not necessarily exact extents/boundaries) for a large range of tumor sizes on either original or PVE corrected images, to provide the most accurate volume and the associated activity.
For radiotherapy planning, the minimum requirements include the PET‐AS's accuracy in the delineation of the gross tumor volume and the ability to identify sub‐volumes (for dose boosting/painting/redistribution applications), as is its ability to achieve a high sensitivity (to be sure to include the entire target) with minimal loss of specificity (to reduce irradiation of healthy tissues and organs at risk).
In the case of response assessment, the main requirement is that the portion of the tumor image that maximizes the predictive power of the particular parameter (biomarker) used, is correctly segmented. As a result, for this type of segmentation task, the link to the physical aspects of the tumor and imaging system are difficult to convincingly establish, and the need for the clinical impact evaluation step (Step 4, Table 5) is especially important.236
Also in most cases, for follow‐up and therapy assessment applications, the PET‐AS algorithm will have to be applied to serial scans independently, although developments dedicated to consider simultaneously sequential scans are also being developed.185, 186, 237, 238, 239, 240 Therefore, its robustness versus different contrast, heterogeneity and tumor size is extremely important to provide nonbiased results regarding the evolution of tumors during therapy. AAPM Task Group 174 (Utilization of 18F‐Fluorodeoxyglucose Positron Emission Tomography (FDG‐PET) in Radiation Therapy) is working toward standardizing the methodology used for sequential scanning (or even inter‐patient scanning for clinical trial patients), so as to allow segmentation techniques to be used for fair comparison between the pre‐ and intra/post‐treatment PET scans.
Type of disease and body site dependence of the performance of PET‐AS methods should also be expected. This means that the user should evaluate the chosen PET‐AS algorithm for the intended body site. Furthermore, within the context of multicentric studies, it is important that the chosen algorithm be validated for robustness against the varying noise and texture properties associated with different scanner models and reconstruction algorithms and their associated parameters (voxel sizes, etc.). Alternatively, the algorithm should be easy to adapt/optimize to the characteristics of each individual center/scanner. Scanning the same phantom at the involved institutions and comparing PET‐AS method performance is suggested. The limitations of the selected phantom need to be well‐understood as discussed in 4.C.
5.G. The complementary role of manual and auto‐segmentation for PET
To satisfy the requirements laid out in the previous sections, PET‐AS algorithms need to accurately account for the physical and technical sources of bias and uncertainty in the PET images. In addition, the ideal PET‐AS algorithm should be able to account for anatomical, physiological, and other clinical information not present in a PET image, which can alter the location of a contour. Although some of the algorithms listed in Table 1 promise to answer most of the physical requirements, accounting for clinical information not present in the PET image is beyond the capabilities of the available PET‐AS algorithms. As a result, there is a need for active physician involvement in the segmentation process. Therefore, at present and in the near future, automatically generated contours can be used only as a starting point for GTV delineation by the physician, who may decide to change them based on his/her knowledge. It is likely that human supervision will remain necessary, both before and after the process of automatic contouring, although this rule may change in the future.241 A recent work has presented a method for head‐and‐neck, in which user interaction is kept minimal but exploited nonetheless so that the user can provide simple cues to guide the segmentation algorithm in an efficient and intuitive manner.242
5.G.1.
Before auto‐contouring
Because automatic contouring algorithms cannot distinguish between malignant and benign tissue tracer uptake, the selection of the lesion, i.e., the diagnostic decision to regard a certain region of elevated tracer uptake as malignant, must be done by a knowledgeable physician. This step includes all forms of diagnostic decision making, considering clinical information not present in the image, topography, pattern, and anatomical location of the suspected uptake, as well as the probability for malignant spread.
After auto‐contouring
The review and editing of the final contour is required for consistency with known diagnostic information, including findings by other imaging modalities, endoscopy results and clinical knowledge. The contours drawn on the same lesion may differ if the goal is therapeutic (need to include all malignant tissue) compared to the case when the goal is diagnostic (need to mark structures containing tumor with a high probability).
To ensure a smooth workflow in daily practice, the contouring software should facilitate both automatic contouring and user interactions for lesion selection and contour editing or algorithm guidance (by providing better initialization, for example204). It is also necessary to enable co‐viewing or fusing of the PET scan with other imaging modalities to include all diagnostic information in the contouring process. In this context, beyond the application of well‐designed and thoroughly evaluated algorithms for automatic contouring, the use of multimodality imaging and collaboration between radiation oncologists and/or oncologists, and imaging specialists (e.g., diagnostic radiologist and/or nuclear medicine expert) are necessary to ensure better understanding of planning images.
6. Conclusions
Given the large number of published PET‐AS algorithms, their different level of validation and because most of these published algorithms are not yet implemented in commercially available software, recommending a single PET‐AS method is challenging and premature. Furthermore, even if such a recommendation could be made it may become obsolete considering the rapid development of the field. Instead, we have provided basis for understanding the logic and the limitations of the main classes of approaches and a framework for their rigorous evaluation and comparison, which we believe will be of greater value for future developments.
As reviewed in this report, there is accumulating evidence in the literature pointing to the higher accuracy and robustness of the approaches based on more advanced image segmentation and analysis paradigms, when supplemented with manual and visual verification, compared to simple threshold‐based approaches. These advantages, however, come at the expense of the ease of implementation and understanding of the simpler algorithms. At the same time, it is possible that simpler (e.g., adaptive threshold) methods may perform comparably well, if not better, for a certain body site/disease type if specifically optimized for these conditions. Recent algorithms which employ some type of consensus or automatic selection between several PET‐AS methods have a potential to overcome the limitations of the individual methods when appropriately trained. In either case, accuracy evaluation is required for each different PET scanner and scanning and image reconstruction protocol. For the simpler, less robust approaches, adaptation to scanning conditions, tumor type and tumor location by optimization of parameters is necessary. The results from the method evaluation stage can be used to estimate the contouring uncertainty. All PET‐AS contours should be critically verified by a physician.
Clearly, further research for solving the dilemma of PET image segmentation is needed, and one potential solution for going forward is the creation of a standardized protocol (i.e., a benchmark) for consistent evaluation and comparison of the PET‐AS methods. This task group suggests the following considerations for generating such a standard:
The evaluation endpoints need to be clearly separated based on algorithmic accuracy and clinical relevance. In order of increasing clinical relevance the reference choices are: (a) the unmodified PET images; (b) the tracer distribution corrected for image artifacts; (c) the underlying histopathology.
At present, the benchmark needs to consist of several image datasets of different types: experimental (phantoms), numerically simulated and clinical, to compensate for the deficiencies of each of them. Also, a complete set of images should include images from all body sites, since algorithm performance may depend on local tracer uptake specifics.
The performance of the methods needs to be evaluated using different metrics, which include volume overlap measures, classification evaluation tools as well as voxel‐to‐voxel distance metrics.
These considerations are the core of the guidelines for PET‐AS algorithm evaluation presented in more details in section 5.F.
A standard that conforms to these requirements will provide a more objective comparison of the algorithms by mitigating the large variability in image sets and metrics used for evaluation. At present, a benchmark following these recommendations is under development within the task group. Different PET‐AS methods are currently being tested within this framework to evaluate the benchmark design and components.151, 234, 235 A publicly available tool such as this should aid users in evaluating current algorithms to increase confidence in selecting the most adequate PET‐AS method to use for a particular application under physician supervision and to provide reference criteria to evaluate future methods.
Acknowledgments
We want to thank D. Nelson (MiM Software, Cleveland, OH), for his contribution as a consultant (industry observer) and the very helpful staff of the American Association of Physicists in Medicine for providing support to the task group. The work on this report was funded in part by the American Association of Physicists in Medicine and the contribution from few of us (CRS, HS and ASK) was funded in part through the NIH/NCI Cancer Center Support Grant P30 CA008748.
Appendix I. PET‐AS formalism examples
A) Fixed and adaptive threshold algorithms
Thresholding could be expressed as follows:
| (A1) |
where the indicator function for threshold T, the segmented subset of the voxels within a Volume of Interest (VOI) in image I, and . is the uptake value (generally normalized to SUV) at voxel i.
The optimal thresholds for performing segmentation are often found by minimizing the difference between known volumes, , (typically a phantom study) and the volumes defined by applying different thresholds, . This often is described as,
| (A2) |
which could be solved by a least‐squares estimation technique. In addition, it is possible to add some topological constraints to ensure its connectedness and/or that it is simply connected, to avoid islands or holes within the segmentation ROI. In case of NSCLC, the optimal threshold for a specific scanner and protocol46 was related to volume via,
| (A3) |
where . is the maximum uptake in the segmented subset and the segmented volume. The functional forms of various threshold segmentation schemes are given in Table A1.
Table A1.
Functional forms of various threshold segmentation schemes generalized for common representation and to reduce patient dependence
| Comments | Threshold Estimator | |
|---|---|---|
| Drever, et al.'s single‐parameter FTS fit257: It is most notable for its use of the histogram's mode for more stable estimation of the background. |
|
|
| Nestle, et al.'s single‐parameter FTS fit23: This fit uses the mean of voxels greater than 70% of the lesion's maximum. The use of the mean instead of the maximum uptake reduces the variability. |
|
|
| Daisne, et al.'s show a two‐parameter FTS fit model137: The scaling parameter, , can be recast as a mean‐value or volume‐based measure for an ATS algorithm.258 |
|
|
| Schaefer, et al.'s two‐parameter FTS fit30: This fit is extended from Nestle's scheme above.23 |
|
|
| Erdi, et al.'s two‐parameter FTS fit48. It was noted that a fixed threshold of 42% worked well for large lung tumors, however, the authors go on to say that its use should be limited to homogeneous uptake distributions. |
|
|
| Black, et al.'s two‐parameter ATS fit53: The use of the mean SUV to make the algorithm more stable to noise requires a threshold for its calculation. |
|
|
| Biehl, et al.'s two‐parameter ATS fit46: The volume is the GTV defined by CT. This algorithm was shown to work for a range of tumor volumes in NSCLC. |
|
|
| Jentzen, et al.'s three‐parameter ATS fit51: The parameters were fitted from phantom data. The volume parameter requires a threshold. |
|
|
| Nehmeh, et al.'s four‐parameter ATS fit52: The fit used Monte Carlo simulation results to avoid cold wall effects. |
|
|
| Burger, et al.'s Background Subtracted Lesion (BSL)259: Not meant as segmentation but rather a volume estimation scheme, an equivalent volume threshold can be found (Li et al.260) Note that this method tends to overestimate the volume by including spill‐out. | Procedure: T, such that the volume from this threshold matches the BSL volume derived from histogram analysis |
B) Segmentation of multimodality IMAGES
In the case of Fuzzy C‐Means (FCM) multimodality segmentation, a fuzzy membership function and the cluster center are updated according to
| (A4) |
where is the fuzzy membership probability that image pixel belongs to cluster at iteration, is the updated cluster center intensity and b is real number greater or equal to 1103, 139.
In the case of Multi Valued Level Sets (MVLS), the objective functional for N imaging modalities could be presented as:
| (A5) |
where is the intensity from imaging modality m at image location x, is the level set function. corresponds to the pixel intensity mean values inside (outside) of the contour C m . H is the Heaviside function and are user‐defined parameter pairs providing relative importance weights for each of the imaging modalities m. The target boundary is defined at the zero level and the integrals are over the space Ω of each image type.
Appendix II. Uptake normalization and threshold parameter estimation
Uptake normalization
Preprocessing the uptake data is important for inter‐patient comparisons and for defining a segmentation scheme. The most common uptake preprocessing is the conversion into SUV. The use of it or something similar is essential to making the selection of a threshold activity independent and applicable across patients and institutions.47 SUV itself comes in many flavors, with normalization being carried out with respect to total body mass, lean body mass, body surface area, etc. Beyond SUV, it has been advocated normalizing patient data to the aortic arch (RTOG 1106)261, 262 or to mean liver uptake. For inter‐patient comparisons these normalizations are likely sufficient, but for segmentation, the tumors themselves may need additional and individual normalization.
For segmentation, further normalizing the intensity within the images or VOI allows for greater consistency between different image sets. Although several segmentation algorithms based on contour detection or region determination through contrast measurements do not require nor benefit from any SUV conversion, such SUV normalization is often used for segmentation. Many algorithms23, 30, 53, 257, 258, 263 rely on subtracting the background activity from the images. In such cases, the segmentation effectively uses a function of this form:
| (A6) |
where is a reference voxel value and is the background value, often . As a further simplification, the image can be normalized solely to under the assumption that is small and does not vary much between images. The maximum contrast results in and all voxels for which within the VOI are included in the segmented volume. While alternatives to the equation above exist, the various values that compose it are often similar. As a result, some discussion regarding their choice is useful.
In choosing the values used to define the equation above, some care is necessary to ensure that they are relatively insensitive to the segmentation region and image noise.264 In the case of the background value, is often taken to be the mean intensity over a large region, where the mean is taken from voxels that are far enough from the edge of the object to avoid PVE. Alternatively, when using a histogram approach the mode (the most frequent value) of the voxels’ intensity distribution can be chosen instead of the mean, since it has the advantage of being less susceptible to PVE.263, 265. In either case, both the mean and the mode are typically well‐defined and relatively insensitive to image noise.
On the other hand, for the reference uptake value, , the choice of the maximum intensity voxel in the object tends to be sensitive to the image noise thus using is problematic.23, 30, 53, 258 Virtually all phantom‐based threshold models assume that the activity is uniform in the lesion. Yet the maximum intensity voxel of a region is sensitive to the size of the object; large objects may exhibit a larger variation in their maximum SUV than small ones. In patient data this is less clear due to tumor heterogeneity, but it has prompted the use of alternative definitions to maximum SUV for characterizing tumor uptake, such as peak SUV, a grouping of the 10 highest uptake voxels, or similar.266 One approach described in Nestle, et al.23 and later expanded on by Schaefer, et al.30 is to define the reference value as the mean of a region defined by a percent threshold of the maximum voxel (in both papers 70% max SUV). This approach helps reduce the noise associated with a single voxel and provides some stability to the measurement. Using mean uptake as an argument makes the threshold a function of the segmentation boundary and requires an iterative solution.
Appendix III. PET phantoms
III.1.
Table A2.
A summary of the existing phantoms that are considered as potential candidates to provide data for a future PET‐AS evaluation protocol
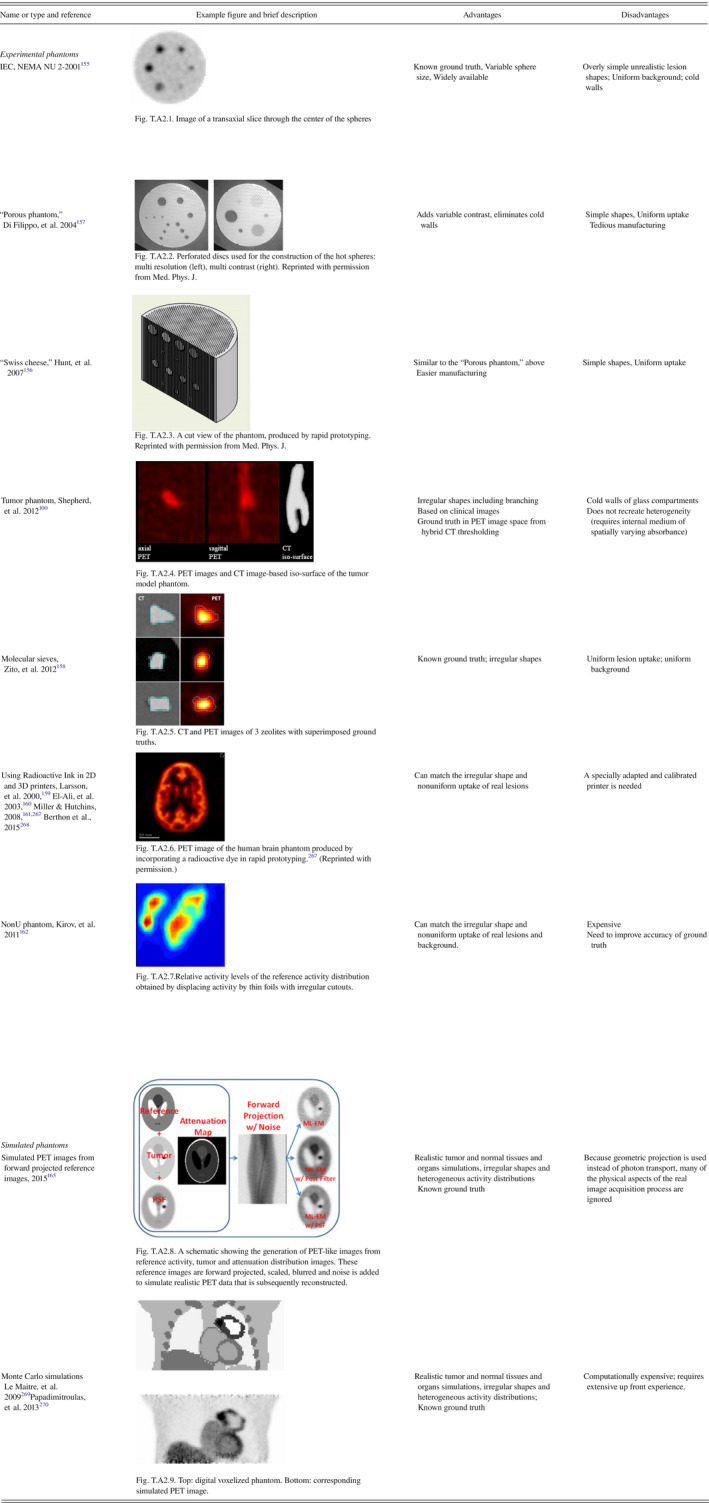
Appendix IV. Evaluation metrics for segmentation tools
Agreement between sets of voxels
Let A and B be two volumes lying in space S composed of voxels. This space can be the 3D image matrix or the field of view of a scanner. Volumes A and B are subsets of this space. A and B are therefore sets of voxels.
The measured volume of A is equal to v|A|, where v is the voxel size expressed in volume units and |A| denotes the cardinality of A. The voxel size does not need to be specified and the volume of A can be expressed by its cardinality without loss of generality.
The agreement between A and B basically depends on the cardinality of their intersection . The disagreement is reflected by the two set differences and , i.e., elements of A that are not elements of B and vice versa, respectively. There are therefore two types of errors. These are also absolute errors. The simplest normalization factor is . In this case, we have
| (A7) |
The first term is known as the Jaccard similarity coefficient, which varies between 0 and 1. For example, let us assume that A and B are different volumes but and . Given this then we have and the Jaccard coefficient is equal to 1/3, whereas the overlap actually represents 50% of A. This distortion of the intuitive perception of the overlap is addressed by the Dice Similarity Coefficient (DSC), which is defined as
| (A8) |
The normalization factor is the inverse of the average volume. In the same example as above, the DSC is equal to 1/2 and concurs with the intuition. It can easily be verified that the DSC varies between 0 and 1.
At this point, both A and B have been considered on the same footing. Let us now define A as representing some ground truth (i.e. a reference volume) and that B is defined as an observation of A with some inaccuracies. In this case, and are the numbers of false negatives (FN) and false positives (FP), respectively. This, and the above information, can be written in a confusion matrix as
| (A9) |
where is the number of true negatives (TN), which is obviously of little interest, as it depends primarily on the unimportant volume of space S, contrary to true positives (TP) in . The most natural normalization factor here is |A|. The ratio is closely related to the DSC, provided we have . We have here a single equality given by
| (A10) |
because
| (A11) |
can obviously be larger than 1 as soon as . This issue can be addressed using the specificity and sensitivity, defined by
| (A12) |
Because the number of true negatives depends on the space volume, the specificity makes little sense and only the sensitivity conveys useful information. The specificity can be replaced with the positive predictive value (PPV) (see Fig.A1 for visual illustration of sensitivity and PPV), defined as
| (A13) |
All quantities described above assume that set operations can be computed. If only the cardinalities and are known, then only the volume difference can be found. The normalization factor can be either or . The volume difference has two critical shortcomings. First, there is no possibility of distinguishing Type I and Type II errors, aside from the difference sign. Second, the volume difference is overly optimistic: it can be optimal with actually no overlap ( but ). The overlap can be approximated with the distance between the centroids (or barycenters) of A and B, for instance.
Hausdorff distance
If set A is rewritten as and set B as , then can denote the distance between voxels and . This distance can be the Euclidean distance from the center of to the center of . Starting from this voxel‐to‐voxel distance, the Hausdorff distance is defined as:271
| (A14) |
The first term calculates the maximum of the distances from each element of A to the closest element of B. The second term performs the symmetric computation, with respect to B instead of A. The maximum of these two quantities is the Hausdorff distance and they can be considered separately to extract information about errors of Types I and II.
Figure A1.
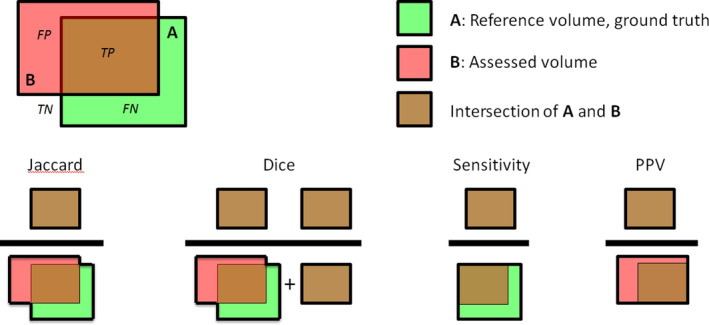
A graphical illustration of the Jaccard and the Dice similarity coefficients, and of the sensitivity and the positive predictive value (PPV).
The main shortcoming of the Hausdorff distance is its (relative) computational complexity. Notice also that the maximum and minimum operators involved in the definition are very sensitive to image noise. A straightforward variant of the Hausdorff distances addresses this issue by replacing the max operators with averages. This leads to a modified Hausdorff distance272:
| (A15) |
The Hausdorff distance is good at reflecting translations between A and B, as well as shape discrepancies. Its interpretation, in terms of volumetric changes, is less obvious. In that sense, it is complementary to the volume difference and to overlap indexes.
The Hausdorff distance can be computed on contours and surfaces as well, instead of sets of voxels. However, in this case the implementation is more specific and requires the user to make some specific choices and/or to adjust additional parameters.
It can be noted that all quantities described above depend on the image matrix or voxel grid. The finer the grid is, the closer the estimated quantities will be to their actual value.
Note
The term reproducibility or repeatability is also used to denote the variability assessed using double baseline PET scan acquisitions (repeated acquisitions at a few days interval without treatment). This “physiological” reproducibility is a different topic than the repeatability/reproducibility of the PET‐AS algorithm discussed here.
References
- 1. MacManus M, Nestle U, Rosenzweig KE, et al. Use of PET and PET/CT for radiation therapy planning: IAEA expert report 2006‐2007. Radiother Oncol. 2009;91:85–94. [DOI] [PubMed] [Google Scholar]
- 2. Ling CC, Humm J, Larson S, et al. Towards multidimensional radiotherapy (MD‐CRT): biological imaging and biological conformality. Int J Radiat Oncol Biol Phys. 2000;47:551–560. [DOI] [PubMed] [Google Scholar]
- 3. Huang SC. Anatomy of SUV. Standardized uptake value. Nucl Med Biol. 2000;27:643–646. [DOI] [PubMed] [Google Scholar]
- 4. Boellaard R. Standards for PET image acquisition and quantitative data analysis. J Nucl Med. 2009;50:11S–20S. [DOI] [PubMed] [Google Scholar]
- 5. Gambhir SS, Czernin J, Schwimmer J, Silverman DH, Coleman RE, Phelps ME. A tabulated summary of the FDG PET literature. J Nucl Med. 2001;42:1S–93S. [PubMed] [Google Scholar]
- 6. Heron DE, Andrade RS, Beriwal S, Smith RP. PET‐CT in radiation oncology: the impact on diagnosis, treatment planning, and assessment of treatment response. Am J Clin Oncol. 2008;31:352–362. [DOI] [PubMed] [Google Scholar]
- 7. Zaidi H, Vees H, Wissmeyer M. Molecular PET/CT imaging‐guided radiation therapy treatment planning. Acad Radiol. 2009;16:1108–1133. [DOI] [PubMed] [Google Scholar]
- 8. Nestle U, Weber W, Hentschel M, Grosu AL. Biological imaging in radiation therapy: role of positron emission tomography. Phys Med Biol. 2009;54:R1–R25. [DOI] [PubMed] [Google Scholar]
- 9. Mac Manus MP, Hicks RJ. The role of positron emission tomography/computed tomography in radiation therapy planning for patients with lung cancer. Semin Nucl Med. 2012;42:308–319. [DOI] [PubMed] [Google Scholar]
- 10. Mac Manus MP, Everitt S, Bayne M, et al. The use of fused PET/CT images for patient selection and radical radiotherapy target volume definition in patients with non‐small cell lung cancer: results of a prospective study with mature survival data. Radiother Oncol. 2013;106:292–298. [DOI] [PubMed] [Google Scholar]
- 11. Gregoire V, Haustermans K, Geets X, Roels S, Lonneux M. PET‐based treatment planning in radiotherapy: a new standard? J Nucl Med. 2007;48(Suppl 1):68S–77S. [PubMed] [Google Scholar]
- 12. Chua S, Dickson J, Groves AM. PET imaging for prediction of response to therapy and outcome in oesophageal carcinoma. Eur J Nucl Med Mol Imaging. 2011;38:1591–1594. [DOI] [PubMed] [Google Scholar]
- 13. Cazaentre T, Morschhauser F, Vermandel M, et al. Pre‐therapy 18F‐FDG PET quantitative parameters help in predicting the response to radioimmunotherapy in non‐Hodgkin lymphoma. Eur J Nucl Med Mol Imaging. 2010;37:494–504. [DOI] [PubMed] [Google Scholar]
- 14. Lee HY, Hyun SH, Lee KS, et al. Volume‐based parameter of 18)F‐FDG PET/CT in malignant pleural mesothelioma: prediction of therapeutic response and prognostic implications. Ann Surg Oncol. 2010;17:2787–2794. [DOI] [PubMed] [Google Scholar]
- 15. El Naqa I, Grigsby P, Apte A, et al. Exploring feature‐based approaches in PET images for predicting cancer treatment outcomes. Pattern Recognit. 2009;42:1162–1171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Vaidya M, Creach KM, Frye J, Dehdashti F, Bradley JD, El Naqa I. Combined PET/CT image characteristics for radiotherapy tumor response in lung cancer. Radiother Oncol. 2012;102:239–245. [DOI] [PubMed] [Google Scholar]
- 17. Soret M, Bacharach SL, Buvat I. Partial‐volume effect in PET tumor imaging. J Nucl Med. 2007;48:932–945. [DOI] [PubMed] [Google Scholar]
- 18. Alessio AM, Kinahan PE, Cheng PM, Vesselle H, Karp JS. PET/CT scanner instrumentation, challenges, and solutions. Radiol Clin North Am. 2004;42:1017–1032. [DOI] [PubMed] [Google Scholar]
- 19. Lartizien C, Kinahan PE, Swensson R, et al. Evaluating image reconstruction methods for tumor detection in 3‐dimensional whole‐body PET oncology imaging. J Nucl Med. 2003;44:276–290. [PubMed] [Google Scholar]
- 20. Visvikis D, Griffiths D, Costa DC, Bomanji J, Ell PJ. Clinical evaluation of 2D versus 3D whole‐body PET image quality using a dedicated BGO PET scanner. Eur J Nucl Med Mol Imaging. 2005;32:1050–1056. [DOI] [PubMed] [Google Scholar]
- 21. Mawlawi O, Pan T, Macapinlac HA. PET/CT imaging techniques, considerations, and artifacts. J Thorac Imaging. 2006;21:99–110. [DOI] [PubMed] [Google Scholar]
- 22. Kirov AS, Schmidtlein CR, Kang H, Lee N. Rationale, instrumental accuracy, and challenges of PET quantification for tumor segmentation in radiation treatment planning. In: Hsieh C‐H ed. Positron Emission Tomography‐Current Clinical and Research Aspects. InTech, 2012. [Google Scholar]
- 23. Nestle U, Kremp S, Schaefer‐Schuler A, et al. Comparison of different methods for delineation of 18F‐FDG PET‐positive tissue for target volume definition in radiotherapy of patients with non‐small cell lung cancer. J Nucl Med. 2005;46:1342–1348. [PubMed] [Google Scholar]
- 24. Terezakis SA, Hunt MA, Kowalski A, et al. [18F]FDG‐positron emission tomography coregistration with computed tomography scans for radiation treatment planning of lymphoma and hematologic malignancies. Int J Radiat Oncol Biol Phys. 2011;81:615–622. [DOI] [PubMed] [Google Scholar]
- 25. Steenbakkers RJ, Duppen JC, Fitton I, et al. Reduction of observer variation using matched CT‐PET for lung cancer delineation: a three‐dimensional analysis. Int J Radiat Oncol Biol Phys. 2006;64:435–448. [DOI] [PubMed] [Google Scholar]
- 26. Hofheinz F, Potzsch C, Oehme L, et al. Automatic volume delineation in oncological PET. Evaluation of a dedicated software tool and comparison with manual delineation in clinical data sets. Nuklearmedizin. 2012;51:9–16. [DOI] [PubMed] [Google Scholar]
- 27. Boudraa AO, Zaidi H. Image segmentation techniques in nuclear medicine imaging. In: Zaidi H, ed. Quantitative Analysis in Nuclear Medicine Imaging. New York: Springer; 2006:308–357. [Google Scholar]
- 28. Belhassen S, Zaidi H. A novel fuzzy C‐means algorithm for unsupervised heterogeneous tumor quantification in PET. Med Phys. 2010;37:1309–1324. [DOI] [PubMed] [Google Scholar]
- 29. Lee JA. Segmentation of positron emission tomography images: some recommendations for target delineation in radiation oncology. Radiother Oncol. 2010;96:302–307. [DOI] [PubMed] [Google Scholar]
- 30. Schaefer A, Kremp S, Hellwig D, Rube C, Kirsch CM, Nestle U. A contrast‐oriented algorithm for FDG‐PET‐based delineation of tumour volumes for the radiotherapy of lung cancer: derivation from phantom measurements and validation in patient data. Eur J Nucl Med Mol Imaging. 2008;35:1989–1999. [DOI] [PubMed] [Google Scholar]
- 31. El Naqa I, Yang D, Apte A, et al. Concurrent multimodality image segmentation by active contours for radiotherapy treatment planning. Med Phys. 2007;34:4738–4749. [DOI] [PubMed] [Google Scholar]
- 32. Song Q, Bai J, Han D, et al. Optimal co‐segmentation of tumor in PET‐CT images with context information. IEEE Trans Med Imaging. 2013;32:1685–1697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Bagci U, Udupa JK, Mendhiratta N, et al. Joint segmentation of anatomical and functional images: applications in quantification of lesions from PET, PET‐CT, MRI‐PET, and MRI‐PET‐CT images. Med Image Anal. 2013;17:929–945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Markel D, Zaidi H, El Naqa I. Novel multimodality segmentation using level sets and Jensen‐Rényi divergence. Med Phys. 2013;40:121908. [DOI] [PubMed] [Google Scholar]
- 35. Hatt M, Boussion N, Cheze‐Le Rest C, Visvikis D, Pradier O. Metabolically active volumes automatic delineation methodologies in PET imaging: review and perspectives. Cancer Radiother. 2012;16:70–81. [DOI] [PubMed] [Google Scholar]
- 36. Foster B, Bagci U, Mansoor A, Xu ZY, Mollura DJ. A review on segmentation of positron emission tomography images. Comput Biol Med. 2014;50:76–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Geets X, Lee JA, Bol A, Lonneux M, Gregoire V. A gradient‐based method for segmenting FDG‐PET images: methodology and validation. Eur J Nucl Med Mol Imaging. 2007;34:1427–1438. [DOI] [PubMed] [Google Scholar]
- 38. De Bernardi E, Faggiano E, Zito F, Gerundini P, Baselli G. Lesion quantification in oncological positron emission tomography: a maximum likelihood partial volume correction strategy. Med Phys. 2009;36:3040–3049. [DOI] [PubMed] [Google Scholar]
- 39. Iglesias JE, Sabuncu MR. Multi‐atlas segmentation of biomedical images: A survey. Med Image Anal. 2015;24:205–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Yu H, Caldwell C, Mah K, Mozeg D. Coregistered FDG PET/CT‐based textural characterization of head and neck cancer for radiation treatment planning. IEEE Trans Med Imaging. 2009;28:374–383. [DOI] [PubMed] [Google Scholar]
- 41. Udupa JK, Leblanc VR, Zhuge Y, et al. A framework for evaluating image segmentation algorithms. Comput Med Imaging Graph. 2006;30:75–87. [DOI] [PubMed] [Google Scholar]
- 42. Tylski P, Stute S, Grotus N, et al. Comparative assessment of methods for estimating tumor volume and standardized uptake value in (18)F‐FDG PET. J Nucl Med. 2010;51:268–276. [DOI] [PubMed] [Google Scholar]
- 43. Hatt M, Cheze Le Rest C, Albarghach N, Pradier O, Visvikis D. PET functional volume delineation: a robustness and repeatability study. Eur J Nucl Med Mol Imaging. 2011;38:663–672. [DOI] [PubMed] [Google Scholar]
- 44. Berthon B, Marshall C, Edwards A, Evans M, Spezi E. Influence of cold walls on PET image quantification and volume segmentation: a phantom study. Med Phys. 2013;40:082505. [DOI] [PubMed] [Google Scholar]
- 45. Berthon B, Marshall C, Evans M, Spezi E. Evaluation of advanced automatic PET segmentation methods using nonspherical thin‐wall inserts. Med Phys. 2014;41:022502. [DOI] [PubMed] [Google Scholar]
- 46. Biehl KJ, Kong FM, Dehdashti F, et al. 18F‐FDG PET definition of gross tumor volume for radiotherapy of non‐small cell lung cancer: is a single standardized uptake value threshold approach appropriate? J Nucl Med. 2006;47:1808–1812. [PubMed] [Google Scholar]
- 47. Van Dalen JA, Hoffmann AL, Dicken V, et al. A novel iterative method for lesion delineation and volumetric quantification with FDG PET. Nucl Med Commun. 2007;28:485–493. [DOI] [PubMed] [Google Scholar]
- 48. Erdi YE, Mawlawi O, Larson SM, et al. Segmentation of lung lesion volume by adaptive positron emission tomography image thresholding. Cancer. 1997;80:2505–2509. [DOI] [PubMed] [Google Scholar]
- 49. Paulino AC, Johnstone PA. FDG‐PET in radiotherapy treatment planning: pandora's box? Int J Radiat Oncol Biol Phys. 2004;59:4–5. [DOI] [PubMed] [Google Scholar]
- 50. Biehl KJ, Kong F, Dehdashti F, et al. FDG‐PET definition of gross tumor volume for radiotherapy of non‐small‐cell lung cancer: is a single SUV threshold approach appropriate? J Nucl Med. 2006;47:1808–1812. [PubMed] [Google Scholar]
- 51. Jentzen W, Freudenberg L, Eising EG, Heinze M, Brandau W, Bockisch A. Segmentation of PET volumes by iterative image thresholding. J Nucl Med. 2007;48:108–114. [PubMed] [Google Scholar]
- 52. Nehmeh SA, El‐Zeftawy H, Greco C, et al. An iterative technique to segment PET lesions using a Monte Carlo based mathematical model. Med Phys. 2009;36:4803–4809. [DOI] [PubMed] [Google Scholar]
- 53. Black QC, Grills IS, Kestin LL, et al. Defining a radiotherapy target with positron emission tomography. Int J Radiat Oncol Biol Phys. 2004;60:1272–1282. [DOI] [PubMed] [Google Scholar]
- 54. Zaidi H, El Naqa I. PET‐guided delineation of radiation therapy treatment volumes: a survey of image segmentation techniques. Eur J Nucl Med Mol Imaging. 2010;37:2165–2187. [DOI] [PubMed] [Google Scholar]
- 55. Li H, Thorstad WL, Biehl KJ, et al. A novel PET tumor delineation method based on adaptive region‐growing and dual‐front active contours. Med Phys. 2008;35:3711–3721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Wanet M, Lee JA, Weynand B, et al. Gradient‐based delineation of the primary GTV on FDG‐PET in non‐small cell lung cancer: a comparison with threshold‐based approaches, CT and surgical specimens. Radiother Oncol. 2011;98:117–125. [DOI] [PubMed] [Google Scholar]
- 57. Adams R, Bischof L. Seeded region growing. IEEE Trans Pattern Anal Mach Intell. 1994;16:641–647. [Google Scholar]
- 58. Pavlidis T, Liow YT. Integrating region growing and edge‐detection. IEEE Trans Pattern Anal Mach Intell. 1990;12:225–233. [Google Scholar]
- 59. Ibanez L, Schroeder W, Ng L, Cates J. The ITK Software Guide. Clifton Park, NY: Kitware Inc.; 2017. [Google Scholar]
- 60. Day E, Betler J, Parda D, et al. A region growing method for tumor volume segmentation on PET images for rectal and anal cancer patients. Med Phys. 2009;36:4349–4358. [DOI] [PubMed] [Google Scholar]
- 61. Hofheinz F, Langner J, Petr J, et al. An automatic method for accurate volume delineation of heterogeneous tumors in PET. Med Phys. 2013;40:082503. [DOI] [PubMed] [Google Scholar]
- 62. Pieczynski W. Modèles de Markov en traitement d'images. Trait Signal. 2003;20:255–278. [Google Scholar]
- 63. Delignon Y, Marzouki A, Pieczynski W. Estimation of generalized mixtures and its application in image segmentation. IEEE Trans Image Process. 1997;6:1364–1375. [DOI] [PubMed] [Google Scholar]
- 64. Montgomery DW, Amira A, Zaidi H. Fully automated segmentation of oncological PET volumes using a combined multiscale and statistical model. Med Phys. 2007;34:722–736. [DOI] [PubMed] [Google Scholar]
- 65. Aristophanous M, Penney BC, Martel MK, Pelizzari CA. A Gaussian mixture model for definition of lung tumor volumes in positron emission tomography. Med Phys. 2007;34:4223–4235. [DOI] [PubMed] [Google Scholar]
- 66. Caillol H, Pieczynski W, Hillion A. Estimation of fuzzy Gaussian mixture and unsupervised statistical image segmentation. IEEE Trans Image Process. 1997;6:425–440. [DOI] [PubMed] [Google Scholar]
- 67. Salzenstein F, Collet C, Lecam S, Hatt M. Non‐stationary fuzzy Markov chain. Pattern Recogn Lett. 2007;28:2201–2208. [Google Scholar]
- 68. Hatt M, Cheze le Rest C, Turzo A, Roux C, Visvikis D. A fuzzy locally adaptive Bayesian segmentation approach for volume determination in PET. IEEE Trans Med Imaging. 2009;28:881–893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Hatt M, Lamare F, Boussion N, et al. Fuzzy hidden Markov chains segmentation for volume determination and quantitation in PET. Phys Med Biol. 2007;52:3467–3491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Hatt M, Cheze le Rest C, Descourt P, et al. Accurate automatic delineation of heterogeneous functional volumes in positron emission tomography for oncology applications. Int J Radiat Oncol Biol Phys. 2010;77:301–308. [DOI] [PubMed] [Google Scholar]
- 71. Duda RO, Hart PE, Stork DG. Pattern Classification, 2nd edn. New York: Wiley; 2001. [Google Scholar]
- 72. Jain AK, Murty MN, Flynn PJ. Data clustering: a review. ACM Comput Surv. 1999;31:264–323. [Google Scholar]
- 73. Berthon B, Marshall C, Evans M, Spezi E. ATLAAS: an automatic decision tree‐based learning algorithm for advanced image segmentation in positron emission tomography. Phys Med Biol. 2016;61:4855–4869. [DOI] [PubMed] [Google Scholar]
- 74. LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521:436–444. [DOI] [PubMed] [Google Scholar]
- 75. Avendi MR, Kheradvar A, Jafarkhani H. A combined deep‐learning and deformable‐model approach to fully automatic segmentation of the left ventricle in cardiac MRI. Med Image Anal. 2016;30:108–119. [DOI] [PubMed] [Google Scholar]
- 76. Cha KH, Hadjiiski L, Samala RK, Chan HP, Caoili EM, Cohan RH. Urinary bladder segmentation in CT urography using deep‐learning convolutional neural network and level sets. Med Phys. 2016;43:1882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Kerhet A, Small C, Quon H, et al. Application of machine learning methodology for PET‐based definition of lung cancer. Curr Oncol. 2010;17:41–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Lian C, Ruan S, Denoeux T, Jardin F, Vera P. Selecting radiomic features from FDG‐PET images for cancer treatment outcome prediction. Med Image Anal. 2016;32:257–268. [DOI] [PubMed] [Google Scholar]
- 79. Hatt M, Tixier F, Pierce L, Kinahan PE, Le Rest CC, Visvikis D. Characterization of PET/CT images using texture analysis: the past, the present.. any future? Eur J Nucl Med Mol Imaging. 2017;44:151–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Materka A, Strzelecki M. Texture analysis methods – A review. In: COST B11. Brussels: Technical University of Lodz, Institute of Electronics. 1998. [Google Scholar]
- 81. Jain AK, Farrokhnia F. Unsupervised texture segmentation using Gabor filters. Pattern Recogn. 1991;24:1167–1186. [Google Scholar]
- 82. Arivazhagan S, Ganesan L. Texture classification using wavelet transform. Pattern Recogn Lett. 2003;24:1513–1521. [Google Scholar]
- 83. Stachowiak GP, Podsiadlo P, Stachowiak GW. A comparison of texture feature extraction methods for machine condition monitoring and failure analysis. Tribol Lett. 2005;20:133–147. [Google Scholar]
- 84. Haralick RM, Shanmugam K. Textural features for image classification. IEEE Trans Syst Man Cybern. 1973;3:610–621. [Google Scholar]
- 85. Amadasun M, King R. Textural features corresponding to textural properties. IEEE Trans Syst Man Cybern. 1989;19:1264–1274. [Google Scholar]
- 86. Galloway M. Texture analysis using grey level run lengths. Comput Vision Graph. 1975;4:172–179. [Google Scholar]
- 87. Mohamed S, Youssef A, El‐Saadany E, Salama MM. Artificial life feature selection techniques for prostrate cancer diagnosis using TRUS images. In: International Conference Image Analysis and Recognition. 2005:903–913. [Google Scholar]
- 88. Woods BJ, Clymer BD, Kurc T, et al. Malignant‐lesion segmentation using 4D co‐occurrence texture analysis applied to dynamic contrast‐enhanced magnetic resonance breast image data. J Magn Reson Imaging. 2007;25:495–501. [DOI] [PubMed] [Google Scholar]
- 89. McNitt‐Gray MF, Har EM, Wyckoff N, Sayre JW, Goldin JG, Aberle DR. A pattern classification approach to characterizing solitary pulmonary nodules imaged on high resolution CT: preliminary results. Med Phys. 1999;26:880–888. [DOI] [PubMed] [Google Scholar]
- 90. Silva AC, Paiva AC, Carvalho PCP, Gattass M. Semivariogram and SGLDM methods comparison for the diagnosis of solitary lung nodule. Pattern Recognition and Image Analysis. Pt 2, Proceedings 3523, 2005;479–486. [Google Scholar]
- 91. Uppaluri R, Hoffman EA, Sonka M, Hartley PG, Hunninghake GW, McLennan G. Computer recognition of regional lung disease patterns. Am J Resp Crit Care. 1999;160:648–654. [DOI] [PubMed] [Google Scholar]
- 92. Kauczor HU, Heitmann K, Heussel CP, Marwede D, Uthmann T, Thelen M. Automatic detection and quantification of ground‐glass opacities on high‐resolution CT using multiple neural networks: comparison with a density mask. Am J Roentgenol. 2000;175:1329–1334. [DOI] [PubMed] [Google Scholar]
- 93. Chabat F, Yang GZ, Hansell DM. Obstructive lung diseases: texture classification for differentiation at CT. Radiology. 2003;228:871–877. [DOI] [PubMed] [Google Scholar]
- 94. Ganeshan B, Abaleke S, Young RCD, Chatwin CR, Miles KA. Texture analysis of non‐small cell lung cancer on unenhanced computed tomography: initial evidence for a relationship with tumour glucose metabolism and stage. Cancer Imaging. 2010;10:137–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95. Pichler BJ, Kolb A, Nagele T, Schlemmer HP. PET/MRI: paving the way for the next generation of clinical multimodality imaging applications. J Nucl Med. 2010;51:333–336. [DOI] [PubMed] [Google Scholar]
- 96. Zaidi H, Del Guerra A. An outlook on future design of hybrid PET/MRI systems. Med Phys. 2011;38:5667–5689. [DOI] [PubMed] [Google Scholar]
- 97. Yu H, Caldwell C, Mah K, et al. Automated radiation targeting in head‐and‐neck cancer using region‐based texture analysis of PET and CT images. Int J Radiat Oncol Biol Phys. 2009;75:618–625. [DOI] [PubMed] [Google Scholar]
- 98. Markel D, Caldwell C, Alasti H, et al. Automatic segmentation of lung carcinoma using 3D texture features in 18‐FDG PET/CT. Int J Mol Imaging. 2013;2013:980769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99. Schaefer A, Vermandel M, Baillet C, et al. Impact of consensus contours from multiple PET segmentation methods on the accuracy of functional volume delineation. Eur J Nucl Med Mol Imaging. 2016;43:911–924. [DOI] [PubMed] [Google Scholar]
- 100. Shepherd T, Teras M, Beichel RR, et al. Comparative study with new accuracy metrics for target volume contouring in PET image guided radiation therapy. IEEE Trans Med Imaging. 2012;31:2006–2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101. Warfield SK, Zou KH, Wells WM. Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Trans Med Imaging. 2004;23:903–921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102. McGurk RJ, Bowsher J, Lee JA, Das SK. Combining multiple FDG‐PET radiotherapy target segmentation methods to reduce the effect of variable performance of individual segmentation methods. Med Phys. 2013;40:042501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103. Pham DL, Xu C, Prince JL. Current methods in medical image segmentation. Annu Rev Biomed Eng. 2000;2:315–337. [DOI] [PubMed] [Google Scholar]
- 104. Bettinardi V, Castiglioni I, De Bernardi E, Gilardi MC. PET quantification: strategies for partial volume correction. Clin Transl Imaging. 2014;2:199–218. [Google Scholar]
- 105. Lucy LB. An iterative technique for the rectification of observed distributions. Astron J. 1974;79:745. [Google Scholar]
- 106. Richardson WH. Bayesian‐based iterative method of image restoration. J Opt Soc Am. 1972;62:55. [Google Scholar]
- 107. Kirov AS, Piao JZ, Schmidtlein CR. Partial volume effect correction in PET using regularized iterative deconvolution with variance control based on local topology. Phys Med Biol. 2008;53:2577–2591. [DOI] [PubMed] [Google Scholar]
- 108. Boussion N, Cheze Le Rest C, Hatt M, Visvikis D. Incorporation of wavelet‐based denoising in iterative deconvolution for partial volume correction in whole‐body PET imaging. Eur J Nucl Med Mol Imaging. 2009;36:1064–1075. [DOI] [PubMed] [Google Scholar]
- 109. Barbee DL, Flynn RT, Holden JE, Nickles RJ, Jeraj R. A method for partial volume correction of PET‐imaged tumor heterogeneity using expectation maximization with a spatially varying point spread function. Phys Med Biol. 2010;55:221–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110. Alessio AM, Stearns CW, Tong S, et al. Application and evaluation of a measured spatially variant system model for PET image reconstruction. IEEE Trans Med Imaging. 2010;29:938–949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111. Jakoby BW, Bercier Y, Watson CC, Bendriem B, Townsend DW. Performance characteristics of a New LSO PET/CT scanner with extended axial field‐of‐view and PSF reconstruction. IEEE Trans Nucl Sci. 2009;56:633–639. [Google Scholar]
- 112. De Bernardi E, Mazzoli M, Zito F, Baselli G. Resolution recovery in PET during AWOSEM reconstruction: a performance evaluation study. IEEE Trans Nucl Sci. 2007;54:1626–1638. [Google Scholar]
- 113. Teo BK, Seo Y, Bacharach SL, et al. Partial‐volume correction in PET: validation of an iterative postreconstruction method with phantom and patient data. J Nucl Med. 2007;48:802–810. [DOI] [PubMed] [Google Scholar]
- 114. Boussion N, Hatt M, Visvikis D. Partial volume correction in PET based on functional volumes. J Nucl Med. 2008;49:388P. [DOI] [PubMed] [Google Scholar]
- 115. Chen CH, Muzic RF Jr, Nelson AD, Adler LP. Simultaneous recovery of size and radioactivity concentration of small spheroids with PET data. J Nucl Med. 1999;40:118–130. [PubMed] [Google Scholar]
- 116. De Bernardi E, Soffientini C, Zito F, Baselli G. Joint Segmentation and Quantification of Oncological Lesions in PET/CT: Preliminary Evaluation on a Zeolite Phantom. Anaheim, California: IEEE NSS MIC 2012, October 29 ‐ November 3, 2012, 2012;3306–3310. [Google Scholar]
- 117. King AD. Multimodality imaging of head and neck cancer. Cancer Imaging. Spec No A, 2007;7:S37–S46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118. Munley MT, Marks LB, Scarfone C, et al. Multimodality nuclear medicine imaging in three‐dimensional radiation treatment planning for lung cancer: challenges and prospects. Lung Cancer. 1999;23:105–114. [DOI] [PubMed] [Google Scholar]
- 119. Chen R, Parry JJ, Akers WJ, et al. Multimodality imaging of gene transfer with a receptor‐based reporter gene. J Nucl Med. 2010;51:1456–1463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120. DeFeo EM, Wu C‐L, McDougal WS, Cheng LL. A decade in prostate cancer: from NMR to metabolomics. Nat Rev Urol. 2011;8:301–311. [DOI] [PubMed] [Google Scholar]
- 121. Hsu AR, Cai W, Veeravagu A, et al. Multimodality molecular imaging of glioblastoma growth inhibition with vasculature‐targeting fusion toxin VEGF121/rGel. J Nucl Med. 2007;48:445–454. [PubMed] [Google Scholar]
- 122. Smith WL, Lewis C, Bauman G, et al. Prostate volume contouring: a 3D analysis of segmentation using 3DTRUS, CT, and MR. Int J Radiat Oncol Biol Phys. 2007;67:1238–1247. [DOI] [PubMed] [Google Scholar]
- 123. Buijsen J, Van den Bogaard J, Van der Weide H, et al. FDG‐PET‐CT reduces the interobserver variability in rectal tumor delineation. Radiother Oncol. 2012;102:371–376. [DOI] [PubMed] [Google Scholar]
- 124. Van Baardwijk A, Bosmans G, Boersma L, et al. PET‐CT‐based auto‐contouring in non‐small‐cell lung cancer correlates with pathology and reduces interobserver variability in the delineation of the primary tumor and involved nodal volumes. Int J Radiat Oncol Biol Phys. 2007;68:771–778. [DOI] [PubMed] [Google Scholar]
- 125. Metwally H, Courbon F, David I, et al. Coregistration of prechemotherapy PET‐CT for planning pediatric Hodgkin's disease radiotherapy significantly diminishes interobserver variability of clinical target volume definition. Int J Radiat Oncol Biol Phys. 2011;80:793–799. [DOI] [PubMed] [Google Scholar]
- 126. Anderson CM, Sun W, Buatti JM, et al. Interobserver and intermodality variability in GTV delineation on simulation CT, FDG‐PET, and MR images of head and neck cancer. Jacobs J Radiat Oncol. 2014;1:006. [PMC free article] [PubMed] [Google Scholar]
- 127. Zheng Y, Sun X, Wang J, Zhang L, Di X, Xu Y. FDG‐PET/CT imaging for tumor staging and definition of tumor volumes in radiation treatment planning in non‐small cell lung cancer. Oncology letters. 2014;7:1015–1020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128. Sebbahi A, Herment A, De Cesare A, Mousseaux E. Multimodality cardiovascular image segmentation using a deformable contour model. Comput Med Imag Grap. 1997;21:79–89. [DOI] [PubMed] [Google Scholar]
- 129. Zheng J, El Naqa I, Rowold FE, et al. Quantitative assessment of coronary artery plaque vulnerability by high‐resolution magnetic resonance imaging and computational biomechanics: a pilot study ex vivo. Magn Reson Med. 2005;54:1360–1368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130. El Naqa I. Radiotherapy informatics: targeted control. Enterp Imaging Ther Radiol Manag. 2008;18:39–42. [Google Scholar]
- 131. Yang D, Zheng J, Nofal A, Wu Y, Deasy J, El Naqa I. Techniques and software tool for 3D multimodality medical image segmentation. J Radiat Oncol Inform. 2009;1:1–21. [Google Scholar]
- 132. Chan TF, Sandberg BY, Vese LA. Active Contours without Edges for Vector‐Valued Images. J Vis Commun Image Represent. 2000;11:130–141. [Google Scholar]
- 133. Shah J. Curve evolution and segmentation functionals: application to color images. Int Conf Image Process Proc. 1996;1:461–464. [Google Scholar]
- 134. Cui H, Wang X, Zhou J, et al. Topology polymorphism graph for lung tumor segmentation in PET‐CT images. Phys Med Biol. 2015;60:4893–4914. [DOI] [PubMed] [Google Scholar]
- 135. Werner‐Wasik M, Nelson AD, Choi W, et al. What is the best way to contour lung tumors on PET scans? Multiobserver validation of a gradient‐based method using a NSCLC digital PET phantom. Int J Radiat Oncol Biol Phys. 2012;82:1164–1171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136. Fogh SE, Farach A, Intenzo C, et al. Pathologic correlation of PET‐CT based auto contouring for radiation planning in lung cancer. Int J Radiat Oncol Biol Phys. 2010;78:S202–S203. [Google Scholar]
- 137. Daisne JF, Sibomana M, Bol A, Doumont T, Lonneux M, Gregoire V. Tri‐dimensional automatic segmentation of PET volumes based on measured source‐to‐background ratios: influence of reconstruction algorithms. Radiother Oncol. 2003;69:247–250. [DOI] [PubMed] [Google Scholar]
- 138. Sebastian TB, Manjeshwar RM, Akhurst TJ, Miller JV. Objective PET lesion segmentation using a spherical mean shift algorithm. Lect Notes Comput Sc. 2006;4191:782–789. [DOI] [PubMed] [Google Scholar]
- 139. Zaidi H, Abdoli M, Fuentes CL, El Naqa IM. Comparative methods for PET image segmentation in pharyngolaryngeal squamous cell carcinoma. Eur J Nucl Med Mol Imaging. 2012;39:881–891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140. Dewalle‐Vignion AS, Betrouni N, Lopes R, Huglo D, Stute S, Vermandel M. A new method for volume segmentation of PET images, based on possibility theory. IEEE Trans Med Imaging. 2011;30:409–423. [DOI] [PubMed] [Google Scholar]
- 141. Abdoli M, Dierckx RA, Zaidi H. Contourlet‐based active contour model for PET image segmentation. Med Phys. 2013;40:082507. [DOI] [PubMed] [Google Scholar]
- 142. Daisne JF, Duprez T, Weynand B, et al. Tumor volume in pharyngolaryngeal squamous cell carcinoma: comparison at CT, MR imaging, and FDG PET and validation with surgical specimen. Radiology. 2004;233:93–100. [DOI] [PubMed] [Google Scholar]
- 143. Hatt M, Cheze‐le Rest C, Van Baardwijk A, Lambin P, Pradier O, Visvikis D. Impact of tumor size and tracer uptake heterogeneity in (18)F‐FDG PET and CT non‐small cell lung cancer tumor delineation. J Nucl Med. 2011;52:1690–1697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144. Hatt M, Maitre AL, Wallach D, Fayad H, Visvikis D. Comparison of different methods of incorporating respiratory motion for lung cancer tumor volume delineation on PET images: a simulation study. Phys Med Biol. 2012;57:7409–7430. [DOI] [PubMed] [Google Scholar]
- 145. Berthon B, Marshall C, Evans M, Spezi E. Implementation and optimization of automatic 18F‐FDG PET segmentation methods. Eur J Nucl Med Mol Imaging. 2013;39(Suppl 2):S385. [Google Scholar]
- 146. Ollers M, Bosmans G, Van Baardwijk A, et al. The integration of PET‐CT scans from different hospitals into radiotherapy treatment planning. Radiother Oncol. 2008;87:142–146. [DOI] [PubMed] [Google Scholar]
- 147. Knausl B, Hirtl A, Dobrozemsky G, et al. PET based volume segmentation with emphasis on the iterative TrueX algorithm. Z Med Phys. 2012;22:29–39. [DOI] [PubMed] [Google Scholar]
- 148. Schaefer A, Nestle U, Kremp S, et al. Multi‐centre calibration of an adaptive thresholding method for PET‐based delineation of tumour volumes in radiotherapy planning of lung cancer. Nuklearmed‐Nucl Med. 2012;51:101–110. [DOI] [PubMed] [Google Scholar]
- 149. Mackie TR, Gregoire V. International Commission on Radiation Units and Measurements (ICRU) Report 83. Prescribing, Recording, and Reporting Photon‐Beam Intensity‐Modulated Radiation Therapy (IMRT). Vol. 10(1) 2010.
- 150. Fischer BM, Olsen MWB, Ley CD, et al. How few cancer cells can be detected by positron emission tomography? A frequent question addressed by an in vitro study. Eur J Nucl Med Mol Imaging. 2006;33:697–702. [DOI] [PubMed] [Google Scholar]
- 151. Berthon B, Spezi E, Galavis P, et al. Towards a standard for the evaluation of PET Auto‐Segmentation methods: requirements and implementation. Med Phys. 2017, accepted for publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152. Janssen MH, Aerts HJ, Ollers MC, et al. Tumor delineation based on time‐activity curve differences assessed with dynamic fluorodeoxyglucose positron emission tomography‐computed tomography in rectal cancer patients. Int J Radiat Oncol Biol Phys. 2009;73:456–465. [DOI] [PubMed] [Google Scholar]
- 153. Shepherd T, Owenius R. Gaussian process models of dynamic PET for Functional Volume Definition In Radiation Oncology. IEEE Trans Med Imaging. 2012;31:1542–1556. [DOI] [PubMed] [Google Scholar]
- 154. Lelandais B, Ruan S, Denoeux T, Vera P, Gardin I. Fusion of multi‐tracer PET images for dose painting. Med Image Anal. 2014;18:1247–1259. [DOI] [PubMed] [Google Scholar]
- 155. NEMA NU 2‐2001 . Performance Measurements of Positron Emission Tomographs. Rosslyn, VA: National Electrical Manufacturers Association; 2001. [Google Scholar]
- 156. Hunt DC, Easton H, Caldwell CB. Design and construction of a quality control phantom for SPECT and PET imaging. Med Phys. 2009;36:5404–5411. [DOI] [PubMed] [Google Scholar]
- 157. DiFilippo FP, Price JP, Kelsch DN, Muzic RF Jr. Porous phantoms for PET and SPECT performance evaluation and quality assurance. Med Phys. 2004;31:1183–1194. [DOI] [PubMed] [Google Scholar]
- 158. Zito F, De Bernardi E, Soffientini C, et al. The use of zeolites to generate PET phantoms for the validation of quantification strategies in oncology. Med Phys. 2012;39:5353–5361. [DOI] [PubMed] [Google Scholar]
- 159. Larsson SA, Jonsson C, Pagani M, Johansson L, Jacobsson H. A novel phantom design for emission tomography enabling scatter‐ and attenuation‐”free” single‐photon emission tomography imaging. Eur J Nucl Med. 2000;27:131–139. [DOI] [PubMed] [Google Scholar]
- 160. El‐Ali H, Ljungberg M, Strand SE, Palmer J, Malmgren L, Nilsson J. Calibration of a radioactive ink‐based stack phantom and its applications in nuclear medicine. Cancer Biother Radiopharm. 2003;18:201–207. [DOI] [PubMed] [Google Scholar]
- 161. Miller M, Hutchins G. 3D Anatomically accurate phantoms for PET and SPECT imaging. J Nucl Med. 2008;49:65P. [Google Scholar]
- 162. Kirov AS, Sculley E, Schmidtlein CR, et al. A new phantom allowing realistic non‐uniform activity distributions for PET quantification, abstract presented at the 2011 joint AAPM/COMP meeting. Med Phys. 2011;38:3387. [Google Scholar]
- 163. Zaidi H, Xu XG. Computational anthropomorphic models of the human anatomy: The path to realistic Monte Carlo modeling in medical imaging. Annu Rev Biomed Eng. 2007;9:471–500. [DOI] [PubMed] [Google Scholar]
- 164. Wang W, Georgi JC, Nehmeh SA, et al. Evaluation of a compartmental model for estimating tumor hypoxia via FMISO dynamic PET imaging. Phys Med Biol. 2009;54:3083–3099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165. Berthon B, Häggström I, Apte A, et al. PETSTEP: generation of synthetic PET lesions for fast evaluation of segmentation methods. Med Phys. 2015;31:969–980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166. Shepp LA, Vardi Y. Maximum likelihood reconstruction for emission tomography. IEEE Trans Med Imaging. 1982;1:113–122. [DOI] [PubMed] [Google Scholar]
- 167. Asma E, Ahn S, Ross SG, Chen A, Manjeshwar RM. Accurate and consistent lesion quantitation with clinically acceptable penalized likelihood images. Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), 2012 IEEE, . 4062‐4066 2012.
- 168. Segars WP, Sturgeon G, Mendonca S, Grimes J, Tsui BM. 4D XCAT phantom for multimodality imaging research. Med Phys. 2010;37:4902–4915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169. Zubal IG, Harrell CR, Smith EO, Rattner Z, Gindi G, Hoffer PB. Computerized three‐dimensional segmented human anatomy. Med Phys. 1994;21:299–302. [DOI] [PubMed] [Google Scholar]
- 170. McLennan A, Reilhac A, Brady M. SORTEO: Monte Carlo‐based simulator with list‐mode capabilities. 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2009;3751–3754 [DOI] [PubMed]
- 171. Jan S, Benoit D, Becheva E, et al. GATE V6: a major enhancement of the GATE simulation platform enabling modelling of CT and radiotherapy. Phys Med Biol. 2011;56:881–901. [DOI] [PubMed] [Google Scholar]
- 172. Jan S, Santin G, Strul D, et al. GATE: a simulation toolkit for PET and SPECT. Phys Med Biol. 2004;49:4543–4561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173. Harrison R, Gillispie S, Schmitz R, Lewellen T. Modeling block detectors in SimSET. J Nucl Med. 2008;49;410. [PMC free article] [PubMed] [Google Scholar]
- 174. Lamare F, Turzo A, Bizais Y, Le Rest CC, Visvikis D. Validation of a Monte Carlo simulation of the philips allegro/GEMINI PET systems using GATE. Phys Med Biol. 2006;51:943–962. [DOI] [PubMed] [Google Scholar]
- 175. Bayne M, Hicks RJ, Everitt S, et al. Reproducibility of “intelligent” contouring of gross tumor volume in non‐small‐cell lung cancer on PET/CT images using a standardized visual method. Int J Radiat Oncol Biol Phys. 2010;77:1151–1157. [DOI] [PubMed] [Google Scholar]
- 176. Kirov AS, Fanchon L. Pathology‐validated PET image data sets and their role for PET segmentation. Clin Trans Imaging. 2014;2:253–267. [Google Scholar]
- 177. Fogh SE, Kannarkatt J, Farach A, et al. Pathologic correlation of PET‐CT based auto contouring for radiation treatment planning in lung cancer. J Thorac Oncol. 2009;4:S528–S529. [Google Scholar]
- 178. van Loon J, Siedschlag C, Stroom J, et al. Microscopic disease extension in three dimensions for non‐small‐cell lung cancer: development of a prediction model using pathology‐validated positron emission tomography and computed tomography features. Int J Radiat Oncol Biol Phys. 2012;82:448–456. [DOI] [PubMed] [Google Scholar]
- 179. Axente M, He J, Bass CP, et al. An alternative approach to histopathological validation of PET imaging for radiation therapy image‐guidance: a proof of concept. Radiother Oncol. 2014;110:309–316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 180. Fanchon LM, Dogan S, Moreira AL, et al. Feasibility of in situ, high‐resolution correlation of tracer uptake with histopathology by quantitative autoradiography of biopsy specimens obtained under 18F‐FDG PET/CT guidance. J Nucl Med. 2015;56:538–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 181. Dubuisson M‐P, Jain AK. A modified Hausdorff distance for object matching. Pattern Recognition, 1994. Vol. 1‐Conference A: Computer Vision #x0026; Image Processing., Proceedings of the 12th IAPR International Conference on, 1994;1:566–568. [Google Scholar]
- 182. Kim H, Monroe JI, Lo S, et al. Quantitative evaluation of image segmentation incorporating medical consideration functions. Med Phys. 2015;42:3013–3023. [DOI] [PubMed] [Google Scholar]
- 183. Gregoire V, Jeraj R, Lee JA, O'Sullivan B. Radiotherapy for head and neck tumours in 2012 and beyond: conformal, tailored, and adaptive? Lancet Oncol. 2012;13:e292–e300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 184. Skretting A, Evensen JF, Londalen AM, Bogsrud TV, Glomset OK, Eilertsen K. A gel tumour phantom for assessment of the accuracy of manual and automatic delineation of gross tumour volume from FDG‐PET/CT. Acta Oncol. 2013;52:636–644. [DOI] [PubMed] [Google Scholar]
- 185. David S, Visvikis D, Roux C, Hatt M. Multi‐observation PET image analysis for patient follow‐up quantitation and therapy assessment. Phys Med Biol. 2011;56:5771–5788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 186. David S, Visvikis D, Quellec G, et al. Image change detection using paradoxical theory for patient follow‐up quantitation and therapy assessment. IEEE Trans Med Imaging. 2012;31:1743–1753. [DOI] [PubMed] [Google Scholar]
- 187. Lelandais B, Gardin I, Mouchard L, Vera P, Ruan S. Segmentation of biological target volumes on multi‐tracer PET images based on information fusion for achieving dose painting in radiotherapy. Med Image Comput Comput Assist Interv ‐MICCAI. 2012;15:545–552. [DOI] [PubMed] [Google Scholar]
- 188. Frings V, De Langen AJ, Smit EF, et al. Repeatability of metabolically active volume measurements with 18F‐FDG and 18F‐FLT PET in non‐small cell lung cancer. J Nucl Med. 2010;51:1870–1877. [DOI] [PubMed] [Google Scholar]
- 189. Hatt M, Cheze‐Le Rest C, Aboagye EO, et al. Reproducibility of 18F‐FDG and 3′‐deoxy‐3′‐18F‐fluorothymidine PET tumor volume measurements. J Nucl Med. 2010;51:1368–1376. [DOI] [PubMed] [Google Scholar]
- 190. Boellaard R, Delgado‐Bolton R, Oyen WJ, et al. FDG PET/CT: EANM procedure guidelines for tumour imaging: version 2.0. Eur J Nucl Med Mol Imaging. 2015;42:328–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 191. Wahl RL, Jacene H, Kasamon Y, Lodge MA. From RECIST to PERCIST: evolving Considerations for PET response criteria in solid tumors. J Nucl Med. 2009;50:122s–150s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 192. MacFarlane CR, American College of Radiologists . ACR accreditation of nuclear medicine and PET imaging departments”. J Nucl Med Technol. 2006;34:18–24. [PubMed] [Google Scholar]
- 193. Barrett HH. Objective assessment of image quality: effects of quantum noise and object variability. J Opt Soc Am A. 1990;7:1266–1278. [DOI] [PubMed] [Google Scholar]
- 194. Barrett HH, Abbey CK, Clarkson E. Objective assessment of image quality. III. ROC metrics, ideal observers, and likelihood‐generating functions. J Opt Soc Am A. 1998;15:1520–1535. [DOI] [PubMed] [Google Scholar]
- 195. Barrett HH, Denny JL, Wagner RF, Myers KJ. Objective assessment of image quality. II. Fisher information, Fourier crosstalk, and figures of merit for task performance. J Opt Soc Am A. 1995;12:834–852. [DOI] [PubMed] [Google Scholar]
- 196. Barrett HH, Kupinski MA, Mueller S, Halpern HJ, Morris JC, Dwyer R. Objective assessment of image quality VI: imaging in radiation therapy. Phys Med Biol. 2013;58:8197–8213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 197. Fessler JA, Rogers WL. Spatial resolution properties of penalized‐likelihood image reconstruction: space‐invariant tomographs. IEEE T Image Process. 1996;5:1346–1358. [DOI] [PubMed] [Google Scholar]
- 198. Barrett HH, Wilson DW, Tsui BMW. Noise properties of the EM algorithm. 1. Theory. Phys Med Biol. 1994;39:833–846. [DOI] [PubMed] [Google Scholar]
- 199. Yu DF, Fessler JA. Edge‐preserving tomographic reconstruction with nonlocal regularization. IEEE Trans Med Imaging. 2002;21:159–173. [DOI] [PubMed] [Google Scholar]
- 200. Fessler JA, Ficaro EP, Clinthorne NH, Lange K. Grouped‐coordinate ascent algorithms for penalized‐likelihood transmission image reconstruction. IEEE Trans Med Imaging. 1997;16:166–175. [DOI] [PubMed] [Google Scholar]
- 201. Krol A, Li S, Shen L, Xu Y. Preconditioned alternating projection algorithms for maximum a posteriori ECT reconstruction. Inverse Prob. 2012;28:115005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 202. Rapisarda E, Presotto L, De Bernardi E, Gilardi MC, Bettinardi V. Optimized Bayes variational regularization prior for 3D PET images. Comput Med Imag Grap. 2014;38:445–457. [DOI] [PubMed] [Google Scholar]
- 203. Ahn S, Ross SG, Asma E, et al. Quantitative comparison of OSEM and penalized likelihood image reconstruction using relative difference penalties for clinical PET. Phys Med Biol. 2015;60:5733–5751. [DOI] [PubMed] [Google Scholar]
- 204. Arens AI, Troost EG, Hoeben BA, et al. Semiautomatic methods for segmentation of the proliferative tumour volume on sequential FLT PET/CT images in head and neck carcinomas and their relation to clinical outcome. Eur J Nucl Med Mol Imaging. 2014;41:915–924. [DOI] [PubMed] [Google Scholar]
- 205. Henriques de Figueiredo B, Zacharatou C, Galland‐Girodet S, et al. Hypoxia imaging with [18F]‐FMISO‐PET for guided dose escalation with intensity‐modulated radiotherapy in head‐and‐neck cancers. Strahlenther Onkol. 2015;191:217–224. [DOI] [PubMed] [Google Scholar]
- 206. Low DA, Nystrom M, Kalinin E, et al. A method for the reconstruction of four‐dimensional synchronized CT scans acquired during free breathing. Med Phys. 2003;30:1254–1263. [DOI] [PubMed] [Google Scholar]
- 207. Wink N, Panknin C, Solberg TD. Phase versus amplitude sorting of 4D‐CT data. J Appl Clin Med Phys. 2006;7:77–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 208. Olsen JR, Lu W, Hubenschmidt JP, et al. Effect of novel amplitude/phase binning algorithm on commercial four‐dimensional computed tomography quality. Int J Radiat Oncol Biol Phys. 2008;70:243–252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 209. Nehmeh SA, Erdi YE, Rosenzweig KE, et al. Reduction of respiratory motion artifacts in PET imaging of lung cancer by respiratory correlated dynamic PET: methodology and comparison with respiratory gated PET. J Nucl Med. 2003;44:1644–1648. [PubMed] [Google Scholar]
- 210. Qiao F, Pan T, Jr Clark JW, Mawlawi OR. A motion‐incorporated reconstruction method for gated PET studies. Phys Med Biol. 2006;51:3769. [DOI] [PubMed] [Google Scholar]
- 211. Pai‐Chun Melinda C, Osama M, Sadek AN, et al. Design of respiration averaged CT for attenuation correction of the PET data from PET/CT. Med Phys. 2007;34:2039–2047. [DOI] [PubMed] [Google Scholar]
- 212. Berlinger K, Sauer O, Vences L, Roth M. A simple method for labeling CT images with respiratory states. Med Phys. 2006;33:3144–3148. [DOI] [PubMed] [Google Scholar]
- 213. Qiao F, Pan T, Clark JJW, Mawlawi O. Joint model of motion and anatomy for PET image reconstruction. Med Phys. 2007;34:4626–4639. [DOI] [PubMed] [Google Scholar]
- 214. Dawood M, Buther F, Lang N, Schober O, Schafers KP. Respiratory gating in positron emission tomography: a quantitative comparison of different gating schemes. Med Phys. 2007;34:3067–3076. [DOI] [PubMed] [Google Scholar]
- 215. Bruyant PP, Rest CCL, Turzo A, Jarritt P, Carson K, Visvikis D. A method for synchronizing an external respiratory signal with a list‐mode PET acquisition. Med Phys. 2007;34:4472–4475. [DOI] [PubMed] [Google Scholar]
- 216. Nehmeh SA, Erdi YE, Meirelles GS, et al. Deep‐inspiration breath‐hold PET/CT of the thorax. J Nucl Med. 2007;48:22–26. [PubMed] [Google Scholar]
- 217. Sureshbabu W, Mawlawi O. PET/CT imaging artifacts. J Nucl Med Technol. 2005;33:156–161; quiz 163‐154. [PubMed] [Google Scholar]
- 218. Chang G, Chang T, Pan T, Clark JW Jr, Mawlawi OR. Implementation of an automated respiratory amplitude gating technique for PET/CT: clinical evaluation. J Nuc Med. 2010;51:16–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 219. Buther F, Ernst I, Dawood M, et al. Detection of respiratory tumour motion using intrinsic list mode‐driven gating in positron emission tomography. Eur J Nucl Med Mol Imaging. 2010;37:2315–2327. [DOI] [PubMed] [Google Scholar]
- 220. Schleyer PJ, O'Doherty MJ, Barrington SF, Marsden PK. Retrospective data‐driven respiratory gating for PET/CT. Phys Med Biol. 2009;54:1935–1950. [DOI] [PubMed] [Google Scholar]
- 221. Kesner AL, Kuntner C. A new fast and fully automated software based algorithm for extracting respiratory signal from raw PET data and its comparison to other methods. Med Phys. 2010;37:5550–5559. [DOI] [PubMed] [Google Scholar]
- 222. El Naqa I, Low DA, Bradley JD, Vicic M, Deasy JO. Deblurring of breathing motion artifacts in thoracic PET images by deconvolution methods. Med Phys. 2006;33:3587–3600. [DOI] [PubMed] [Google Scholar]
- 223. Yalavarthy PK, Low D, Noel C, et al. Current role of PET in oncology: Potentials and challenges in the management of non‐small cell lung cancer. 2008 42nd Asilomar Conference on Signals, Systems and Computers, 1067‐1071. 2008.
- 224. Buther F, Vehren T, Schafers KP, Schafers M. Impact of data‐driven respiratory gating in clinical PET. Radiology. 2016;281:229–238. [DOI] [PubMed] [Google Scholar]
- 225. Kesner AL, Chung JH, Lind KE, et al. Validation of software gating: a practical technology for respiratory motion correction in PET. Radiology. 2016;281:152105. [DOI] [PubMed] [Google Scholar]
- 226. Kesner AL, Schleyer PJ, Buther F, Walter MA, Schafers KP, Koo PJ. On transcending the impasse of respiratory motion correction applications in routine clinical imaging – a consideration of a fully automated data driven motion control framework. EJNMMI Physics. 2014;1:8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 227. Aristophanous M, Yap JT, Killoran JH, Chen AB, Berbeco RI. Four‐dimensional positron emission tomography: implications for dose painting of high‐uptake regions. Int J Radiat Oncol Biol Phys. 2011;80:900–908. [DOI] [PubMed] [Google Scholar]
- 228. Aristophanous M, Berbeco RI, Killoran JH, et al. Clinical utility of 4D FDG‐PET/CT scans in radiation treatment planning. Int J Radiat Oncol Biol Phys. 2012;82:e99–e105. [DOI] [PubMed] [Google Scholar]
- 229. Lamb JM, Robinson C, Bradley J, et al. Generating lung tumor internal target volumes from 4D‐PET maximum intensity projections. Med Phys. 2011;38:5732–5737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 230. Guerra L, Meregalli S, Zorz A, et al. Comparative evaluation of CT‐based and respiratory‐gated PET/CT‐based planning target volume (PTV) in the definition of radiation treatment planning in lung cancer: preliminary results. Eur J Nucl Med Mol Imaging. 2014;41:702–710. [DOI] [PubMed] [Google Scholar]
- 231. Chirindel A, Adebahr S, Schuster D, et al. Impact of 4D‐(18)FDG‐PET/CT imaging on target volume delineation in SBRT patients with central versus peripheral lung tumors. Multi‐reader comparative study. Radiother Oncol. 2015;115:335–341. [DOI] [PubMed] [Google Scholar]
- 232. Pierce LA, Elston BF, Clunie DA, Nelson D, Kinahan PE. A Digital Reference Object to Analyze Calculation Accuracy of PET Standardized Uptake Value. Radiology. 2015;277:538–545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 233. Withofs N, Bernard C, Van der Rest C, et al. FDG PET/CT for rectal carcinoma radiotherapy treatment planning: comparison of functional volume delineation algorithms and clinical challenges. J Appl Clin Med Phys. 2014;15:4696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 234. Shepherd T, Berthon B, Galavis P, et al. Design of a benchmark platform for evaluating PET‐based contouring accuracy in oncology applications. Eur J Nucl Med Mol Imaging. 2012;39:S264. [Google Scholar]
- 235. Berthon B, Spezi E, Schmidtlein CR, et al. Development of a software platform for evaluating automatic PET segmentation methods. Radiother Oncol. 2013;111:S166. [Google Scholar]
- 236. Mamede M, Abreu ELP, Oliva MR, Nose V, Mamon H, Gerbaudo VH. FDG‐PET/CT tumor segmentation‐derived indices of metabolic activity to assess response to neoadjuvant therapy and progression‐free survival in esophageal cancer: correlation with histopathology results. Am J Clin Oncol. 2007;30:377–388. [DOI] [PubMed] [Google Scholar]
- 237. Necib H, Garcia C, Wagner A, et al. Detection and characterization of tumor changes in 18F‐FDG PET patient monitoring using parametric imaging. J Nucl Med. 2011;52:354–361. [DOI] [PubMed] [Google Scholar]
- 238. Mi HM, Petitjean C, Vera P, Ruan S. Joint tumor growth prediction and tumor segmentation on therapeutic follow‐up PET images. Med Image Anal. 2015;23:84–91. [DOI] [PubMed] [Google Scholar]
- 239. Mi HM, Petitjean C, Dubray B, Vera P, Ruan S. Prediction of lung tumor evolution during radiotherapy in individual patients with PET. IEEE Trans Med Imaging. 2014;33:995–1003. [DOI] [PubMed] [Google Scholar]
- 240. Sampedro F, Escalera S, Domenech A, Carrio I. A computational framework for cancer response assessment based on oncological PET‐CT scans. Comput Biol Med. 2014;55:92–99. [DOI] [PubMed] [Google Scholar]
- 241. Obara P, Liu H, Wroblewski K, et al. Quantification of metabolic tumor activity and burden in patients with non‐small‐cell lung cancer: is manual adjustment of semiautomatic gradient‐based measurements necessary? Nucl Med Commun. 2015;36:782–789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 242. Beichel RR, Van Tol M, Ulrich EJ, et al. Semiautomated segmentation of head and neck cancers in 18F‐FDG PET scans: a just‐enough‐interaction approach. Med Phys. 2016;43:2948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 243. Tylski P, Bonniaud G, Decenciere E, et al. 18F‐FDG PET images segmentation using morphological watershed: a phantom study. In: 2006 IEEE Nuclear Science Symposium Conference: 2063–2067.
- 244. Sharif MS, Abbod M, Amira A, Zaidi H. Artificial neural network‐statistical approach for PET volume analysis and classification. Advances in Fuzzy Systems. ID 327861, 2012;10. [Google Scholar]
- 245. De Bernardi E, Fiorani Gallotta F, Gianoli C, Zito F, Gerundini P, Baselli G. ML segmentation strategies for object interference compensation in FDG‐PET lesion quantification. Methods Inf Med. 2010;49:537–541. [DOI] [PubMed] [Google Scholar]
- 246. Onoma DP, Ruan S, Thureau S, et al. Segmentation of heterogeneous or small FDG PET positive tissue based on a 3D‐locally adaptive random walk algorithm. Comput Med Imaging Graph. 2014;38:753–763. [DOI] [PubMed] [Google Scholar]
- 247. Mu W, Chen Z, Shen W, et al. A segmentation algorithm for quantitative analysis of heterogeneous tumors of the cervix with 18F‐FDG PET/CT. IEEE Trans Biomed Eng 2015;62:2465–2479. [DOI] [PubMed] [Google Scholar]
- 248. Lapuyade‐Lahorgue J, Visvikis D, Pradier O, Cheze Le Rest C, Hatt M. SPEQTACLE: an automated generalized fuzzy C‐means algorithm for tumor delineation in PET. Med Phys. 2015;42:5720–5734. [DOI] [PubMed] [Google Scholar]
- 249. Devic S, Mohammed H, Tomic N, et al. FDG‐PET‐based differential uptake volume histograms: a possible approach towards definition of biological target volumes. Br J Radiol. 2016;89:20150388. [DOI] [PubMed] [Google Scholar]
- 250. Schinagl DA, Vogel WV, Hoffmann AL, Van Dalen JA, Oyen WJ, Kaanders JH. Comparison of five segmentation tools for 18F‐fluoro‐deoxy‐glucose‐positron emission tomography‐based target volume definition in head and neck cancer. Int J Radiat Oncol Biol Phys. 2007;69:1282–1289. [DOI] [PubMed] [Google Scholar]
- 251. Greco C, Nehmeh SA, Schoder H, et al. Evaluation of different methods of 18F‐FDG‐PET target volume delineation in the radiotherapy of head and neck cancer. Am J Clin Oncol. 2008;31:439–445. [DOI] [PubMed] [Google Scholar]
- 252. Vees H, Senthamizhchelvan S, Miralbell R, Weber DC, Ratib O, Zaidi H. Assessment of various strategies for 18F‐FET PET‐guided delineation of target volumes in high‐grade glioma patients. Eur J Nucl Med Mol Imaging. 2009;36:182–193. [DOI] [PubMed] [Google Scholar]
- 253. Belhassen S, Llina Fuentes CS, Dekker A, De Ruysscher D, Ratib O, Zaidi H. Comparative methods for 18F‐FDG PET‐based delineation of target volumes in non‐small‐cell lung cancer. J Nucl Med 2009;50:27P. [Google Scholar]
- 254. Dewalle‐Vignion AS, Yeni N, Petyt G, et al. Evaluation of PET volume segmentation methods: comparisons with expert manual delineations. Nucl Med Commun. 2012;33:34–42. [DOI] [PubMed] [Google Scholar]
- 255. Lacout A, Marcy PY, Giron J, Thariat J. Gradient‐PET based delineation may be improved with combined post contrast high resolution CT scan: in regard to Werner‐Wasik M et al. (Int J Radiat Oncol Biol Phys 2011 Apr 28). Int J Radiat Oncol Biol Phys. 2012;82:496; author reply 496‐497. [DOI] [PubMed] [Google Scholar]
- 256. Schinagl DA, Span PN, Van den Hoogen FJ, et al. Pathology‐based validation of FDG PET segmentation tools for volume assessment of lymph node metastases from head and neck cancer. Eur J Nucl Med Mol Imaging. 2013;40:1828–1835. [DOI] [PubMed] [Google Scholar]
- 257. Drever L, Robinson DM, McEwan A, Roa W. A local contrast based approach to threshold segmentation for PET target volume delineation. Med Phys. 2006;33:1583–1594. [DOI] [PubMed] [Google Scholar]
- 258. Vauclin S, Doyeux K, Hapdey S, Edet‐Sanson A, Vera P, Gardin I. Development of a generic thresholding algorithm for the delineation of 18FDG‐PET‐positive tissue: application to the comparison of three thresholding models. Phys Med Biol. 2009;54:6901–6916. [DOI] [PubMed] [Google Scholar]
- 259. Burger IA, Vargas HA, Apte A, et al. PET quantification with a histogram derived total activity metric: superior quantitative consistency compared to total lesion glycolysis with absolute or relative SUV thresholds in phantoms and lung cancer patients. Nucl Med Biol. 2014;41:410–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 260. Li G, Schmidtlein CR, Burger IA, Ridge CA, Solomon SB, Humm JL. Assessing and accounting for the impact of respiratory motion on FDG uptake and viable volume for liver lesions in free‐breathing PET using respiration‐suspended PET images as reference. Med Phys. 2014;41:091905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 261. Kong F, Machtay M, Bradley J, Ten Haken R, Xiao Y, Matuszak M. RTOG 1106/ACRIN 6697: Randomized phase II trial of individualized adaptive radiotherapy using during‐treatment FDG‐PET/CT and modern technology in locally advanced non‐small cell lung cancer (NSCLC). 2012.
- 262. Kong FM, Frey KA, Quint LE, et al. A pilot study of [18F]fluorodeoxyglucose positron emission tomography scans during and after radiation‐based therapy in patients with non small‐cell lung cancer. J Clin Oncol. 2007;25:3116–3123. [DOI] [PubMed] [Google Scholar]
- 263. Drever L, Roa W, McEwan A, Robinson D. Iterative threshold segmentation for PET target volume delineation. Med Phys. 2007;34:1253–1265. [DOI] [PubMed] [Google Scholar]
- 264. Krak NC, Boellaard R, Hoekstra OS, Twisk JW, Hoekstra CJ, Lammertsma AA. Effects of ROI definition and reconstruction method on quantitative outcome and applicability in a response monitoring trial. Eur J Nucl Med Mol Imaging. 2005;32:294–301. [DOI] [PubMed] [Google Scholar]
- 265. Burger IA, Vargas HA, Beattie BJ, et al. How to assess background activity: introducing a histogram‐based analysis as a first step for accurate one‐step PET quantification. Nucl Med Commun. 2014;35:316–324. [DOI] [PubMed] [Google Scholar]
- 266. Vanderhoek M, Perlman SB, Jeraj R. Impact of the definition of peak standardized uptake value on quantification of treatment response. J Nucl Med. 2012;53:4–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 267. Miller M, Hutchins G. 3D Anatomically accurate phantoms for PET and SPECT imaging. IEEE Nuclear Science Symposium and Medical Imaging Conference Record, Proceedings paper, M26‐8, 2007;49:4252–4256. [Google Scholar]
- 268. Berthon B, Marshall C, Holmes R, Spezi E. A novel phantom technique for evaluating the performance of PET auto‐segmentation methods in delineating heterogeneous and irregular lesions. EJNMMI Physics. 2015;2:13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 269. Le Maitre A, Segars WP, Marache S, et al. Incorporating patient‐specific variability in the simulation of realisticwhole‐body 18F‐FDG distributions for oncology applications. Proc IEEE. 2009;97:2026–2038. [Google Scholar]
- 270. Papadimitroulas P, Loudos G, Le Maitre A, et al. Investigation of realistic PET simulations incorporating tumor patient's specificity using anthropomorphic models: creation of an oncology database. Med Phys. 2013;40:112506. [DOI] [PubMed] [Google Scholar]
- 271. Munkres JR. Topology. (2nd ed.). Prentice Hall; 2000. [Google Scholar]
- 272. Aspert N, Santa‐Cruz D, Ebrahimi T. Mesh: measuring errors between surfaces using the Hausdorff distance. IEEE Int Conf Multimed Expo (ICME). 2002;1:705–708. [Google Scholar]
- 273. Sharif MS, Abbod M, Amira A, Zaidi H. Artificial neural network‐based system for PET volume segmentation. Int J Biomed Imaging. ID 105610, 2010;11. [DOI] [PMC free article] [PubMed] [Google Scholar]


