Tissue oxidative metabolism can increase the difference between local temperature and arterial blood temperature by up to 1.3^oC: Implications for brain, brown adipose tissue, and muscle physiology

ABSTRACT

Tissue temperature increases, when oxidative metabolism is boosted. The source of nutrients and oxygen for this metabolism is the blood. The blood also cools down the tissue, and this is the only cooling mechanism, when direct dissipation of heat from the tissue to the environment is insignificant, e.g., in the brain. While this concept is relatively simple, it has not been described quantitatively. The purpose of the present work was to answer two questions: 1) to what extent can oxidative metabolism make the organ tissue warmer than the body core, and, 2) how quickly are changes in the local metabolism reflected in the temperature of the tissue? Our theoretical analysis demonstrates that, at equilibrium, given that heat exchange with the organ is provided by the blood, the temperature difference between the organ tissue and the arterial blood is proportional to the arteriovenous difference in oxygen content, does not depend on the blood flow, and cannot exceed 1.3^oC. Unlike the equilibrium temperature difference, the rate of change of the local temperature, with respect to time, does depend on the blood flow. In organs with high perfusion rates, such as the brain and muscles, temperature changes occur on a time scale of a few minutes. In organs with low perfusion rates, such changes may have characteristic time constants of tens or hundreds of minutes. Our analysis explains, why arterial blood temperature is the main determinant of the temperature of tissues with limited heat exchange, such as the brain.

Abbreviations

BAT

Brown Adipose Tissue

Aim

We used a simple mathematical model of heat production and transfer to answer two questions: 1) how much warmer than the body core can a tissue with active metabolism be, and 2) how quickly do changes in local metabolism manifest themselves in the tissue temperature?

Organ temperature changes due to local metabolism

Here, we consider an organ that intrinsically generates heat due to ongoing oxidative metabolism (Box 1, Fig. 1). Importantly, oxygen, which is necessary for this process, is delivered by the bloodstream, which is also responsible for the removal of heat from the organ. In this section, we describe how much warmer the organ is, as compared with the incoming arterial blood. Let $\Delta T_{org}$ be the difference between the organ temperature $\left(T_{org}\right)$ and core body temperature ($T_c)$:

$$\mathrm{ }\Delta T_{org}=T_{org}-T_c.$$

Box 1. Mathematical model describing changes of local temperature in presence of oxidative metabolism.

In the model depicted at the Figure 1, the rate of heat generation is proportional to the product of the arteriovenous difference in oxygen content (${AV}_{O2}$, in ml O₂/ml blood), the heat produced from the utilization of one unit of oxygen ($\alpha$, in J/ml O₂), and the blood flow per unit of organ mass (BF, in ml/min/g). The amount of heat removed by the circulation is proportional to the blood flow, the heat capacity of the blood (C_b, in J/ml), and the temperature difference between the blood leaving the tissue and the blood entering the tissue (in °C). The temperature of incoming blood is equal to the core body temperature (T_c), while the outgoing blood temperature, according to Pennes’ proposition [1], is equal to the organ temperature (T_org), assuming complete equilibration during its passage [2,3]. The organ can also have direct (non-circulatory) heat exchange with its environment. The heat dissipation rate ($\gamma$) is a coefficient of the linear relationship between heat flow and the temperature difference between the organ and its environment. We denote the temperature of the environment (ambient temperature) by $T_a$ and assume that $T_a$, $T_c$ and BF are constant. Finally, we denote the heat capacity of the organ by $C_{org}$ (in J/g).

Combining all of the above, the organ temperature obeys the following differential equation, whose right-hand side includes three terms, viz., metabolic heat production, heat transfer to the body core, and heat dissipation to the environment, respectively:

$$C_{org} \frac{{dT}_{org}}{dt}=\alpha \cdot {AV}_{O2}\cdot BF+C_b\cdot BF\cdot \left(T_c-T_{org}\right)+\gamma \left(T_a-T_{org}\right).$$ (1)

At equilibrium, the temperatures do not change, so the rate of change of the organ temperature is equal to zero. By equating the right-hand side of Equation (1) to zero

$\alpha \cdot {AV}_{O2}\cdot BF+C_b\cdot BF\cdot \left(T_c-T_{org}\right)+\gamma \left(T_a{- T}_c){ +\gamma (T}_c-T_{org}\right)=0$

and rearranging the terms,

$(\gamma +C_b\cdot BF) \left(T_c-T_{org}\right)=- \alpha \cdot {AV}_{O2}\cdot BF-\gamma \left(T_a{- T}_c\right)$

one can find that the difference between the organ temperature $\left(T_{org}\right)$ and core body temperature ($T_c)$:

$$\Delta \mathrm{ }{T}_{org}=T_{org}-T_c=\frac{\alpha \bullet {AV}_{O2}}{C_b+\frac{\gamma }{BF}}-\frac{T_c-T_a}{C_b\bullet \frac{BF}{\gamma }+1}.$$ (2)

The second term of the right-hand side of Equation (2), the one with the negative sign, defines the temperature difference between the organ and the core due to heat dissipation to the environment in the absence of oxidative metabolism. When the environment is colder or warmer than the body core, the relative weight of this term increases with the heat dissipation rate $\gamma .$ In contrast, increasing blood flow protects the temperature of the organ from the effects of environment (both cold and hot). This exchange with the environment is not dependent on local metabolism per se, and is outside of scope of this analysis.

Therefore, we concentrate on the first term of the right-hand side of Equation (2) which is associated with oxidative metabolism. Importantly, as the dissipation coefficient $\gamma$ increases, the denominator increases, which results in a smaller metabolic contribution to the temperature difference. Therefore, the maximum possible effect of oxidative metabolism on equilibrium temperature difference ($\Delta T_{org}^{max}$) is observed when no heat dissipation to the environment occurs $(\gamma =0)$, i.e.,

$${\Delta T}_{org}^{max}=\frac{\alpha \bullet {AV}_{O2}}{C_b} .$$ (3)

Figure 1.

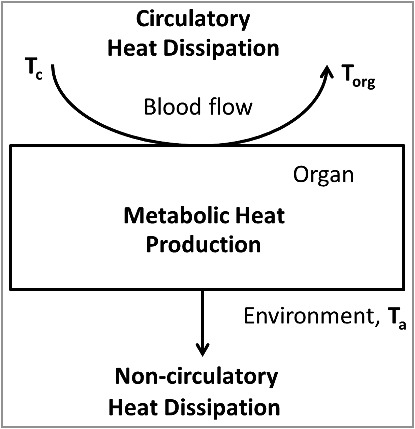
Simplified model of organ temperature control by oxidative metabolism, the circulation and non-circulatory heat dissipation. The heat production in the organ is proportional to the arteriovenous difference in oxygen content. The amount of heat removed by the circulation is proportional to the blood flow and the temperature difference between the blood leaving the tissue (equal to the organ temperature, T_org) and the blood entering the tissue (core body temperature, T_c). The amount of heat dissipating to the environment is proportional to the difference between organ temperature and ambient temperature.

According to the mathematical analysis presented in Box 1, the effect of oxidative metabolism on local temperature is proportional to the arteriovenous difference in oxygen content (${AV}_{O2}$), and the maximal difference between the temperatures of the organ and the body core in absence of non-circulatory heat exchange with the environment is:

$$\Delta T_{org}^{max}=\frac{\alpha }{C_b} {AV}_{O2}.$$

This equation demonstrates that, given that the heat from one unit of oxygen ($\alpha$) and the heat capacity of the blood (C_b) are constant, the maximum temperature difference is achieved when all oxygen is cleared from fully saturated arterial blood. The oxygen capacity of hemoglobin is 1.34–1.36 ml O₂/g [4,5]. In most healthy mammals, the amount of hemoglobin in the blood does not exceed 15 g/100 ml [5], and hemoglobin is almost completely saturated with oxygen in the arterial blood in physiological conditions. Therefore, the total amount of oxygen in blood is usually < 0.2 ml O₂/ml blood [5].

The heat that can be generated from one unit of oxygen $\left(\alpha \right)$ depends on the substrate. When the substrate is carbohydrates, the energy generated from 1 ml of oxygen is 21.13 J, and is 19.69 J when the substrate is fat [6]. For the upper estimate, we use the greater value (carbohydrate). The heat capacity of blood (C_b) can be estimated to be 3,600 J/kg/°C, or 3.4 J/ml/°C [7]. Therefore, if the blood is completely cleared of oxygen after passing through the organ (venous oxygen content is zero), then the maximum possible temperature difference is:

$$\Delta T_{org}^{max}=\frac{21.13\bullet 0.2}{3.4}\approx 1.24(°\mathrm{C})<1.3(°\mathrm{C}).$$

For example, if at rest the muscle temperature is the same as core body temperature and is 37.0°C, in no condition can it rise above 38.3°C solely due to the metabolic consequences of an intense workout, assuming other variables and parameters (e.g., core temperature and blood flow) remain unchanged. If local temperature is significantly lower than the core temperature, as is often the case in studies of interscapular adipose tissue in rodents [8], there is significant non-circulatory dissipation to the environment. As explained in Box 1, in the presence of non-circulatory heat dissipation from the organ to the environment ($\gamma >0$), the greatest possible temperature increase solely mediated by the oxidative metabolism (the first term in Equation (2)) will be smaller than 1.3°C. For example, if core temperature is 37°C, local temperature with inactive metabolism is 34°C, and ambient temperature is 22°C, we can use Equation (2) from Box 1 with ${AV}_{O2}=0$ to estimate that $BF\cdot C_b/\gamma =4$. Considering this, we can further conclude that the maximal increase of local temperature after the local metabolism is switched on will be limited by

$$T_{org}^{on}-T_{org}^{off}=\frac{\alpha \cdot {AV}_{O2}}{C_b+\frac{\gamma }{BF}}=\frac{1.24}{1+1/4} \approx 1(°\mathrm{C}).$$

In this example, local temperature cannot exceed 35°C, if only oxidative metabolism does change.

Some additional limitations should also be noted. First, most certified thermometers have an absolute precision of 0.1°C, which results in 0.2°C precision for the difference between two measured temperatures. Many devices used by physiologists have even lower precision. Furthermore, in this paper, we assume that the core (or, to be more precise, the extra-brain compartment of the core) is isothermal and has the exact same temperature as the “arterial blood.” In real life, however, blood in different arteries and different core locations has slightly different temperatures (see, e.g., ref. [9]), and some sites (e.g., the rectum) can be attributed to the core or the shell, depending on the conditions [10]. These facts should be considered while interpreting temperature differences between the tissue of interest and arterial blood (or body core), as reported in various studies.

Variations of tissue temperature in the absence of circulation

What happens to the tissue temperature if the blood flow is completely stopped? On one hand, the blood can no longer remove excessive heat from the tissue in circulatory arrest, which might lead to dramatic overheating. On the other hand, there is no oxygen supply to support additional metabolism under these conditions. Therefore, to estimate the magnitude of the possible temperature change after an abrupt circulation blockade, we need to consider how much oxygen is stored in the tissue itself.

There are two major sources of stored oxygen: intracellular proteins (myoglobin) and intra-organ reserves of oxygenated blood. While myoglobin is believed to help maintain oxygen in the contracting muscle, the amount of myoglobin is very limited. Even if all the oxygen from the completely saturated myoglobin of a muscle is utilized to produce heat, the temperature of the tissue would rise by less than 0.1°C: 500 nmol myoglobin/g of muscle [11] × 22.4 ml O₂/ mmol myoglobin (one molecule of oxygen per each molecule of myoglobin) × 21.13 J/ml O₂ (heat from a unit of oxygen) / 3.42 J/°C/g (heat capacity of muscle) [12] ≈ 0.06°C. Therefore, under normal conditions, the myoglobin-bound oxygen cannot provide a noticeable amount of heat.

Another source of oxygen during circulatory arrest is the intra-organ reserve of oxygenated blood. However, this second source also appears insufficient to cause biologically significant hyperthermia in most cases. For example, the brain contains approximately 3 ml of blood per 100 g of tissue [13], which has 0.45 g of hemoglobin (15 g Hb / 100 ml blood), carrying ≤ 0.6 ml of oxygen (1.34 ml O₂/g Hb). If all this oxygen would be used at once, it would increase the tissue temperature by approximately 0.03°C (21.13 J/ml O₂, with a brain tissue heat capacity of 3.6 J/°C/g) [12]. Two other organs that have significant amounts of intra-organ blood are the liver (30 ml blood/100 g tissue [14], which, if used completely, can translate into a 0.3°C increase in local temperature) and the spleen (up to 80 ml blood/100 g tissue [15]). For example, Barcroft and Stephens [16] report that, in dogs, cats, horses, and sheep, the spleen can release a substantial amount of blood (up to 20% of the circulating volume) into the systemic circulation following hemorrhage, hypoxia, exercise, and other conditions. Furthermore, according to Barcroft and Poole [17], the hemoglobin concentration, as well as the hematocrit, are 50% higher in the splenic blood than in the systemic circulation, which can increase the maximum possible oxygen storage per volume of blood. However, in both the spleen and the liver, the blood is stored in capacitive vessels and, most likely, is not saturated with oxygen.

Dynamics of metabolism-induced changes in organ temperature

How fast does the local temperature converge to a new equilibrium if the oxygen consumption in the organ is changed in a step-wise manner? For a rough estimate, we assume that all other parameters in the differential equation (1) remain constant, and non-circulatory heat dissipation to the environment does not occur. According to Equation 6 in Box 2, the half-life for reaching the new equilibrium in these conditions can be calculated as:

Box 2. Dynamics of local temperature after step-wise activation of oxidative metabolism

In the absence of heat dissipation $(\gamma = 0)$, if the core temperature is constant, Equation (1) from Box 1 can be rewritten as

$$C_{org} \frac{{d(T_{org}-T}_c)}{dt}=\alpha \cdot {AV}_{O2}\cdot BF-C_b\cdot BF\cdot \left(T_{org}-T_c\right)$$ (4)

After denoting $\Delta \mathrm{ }{T}_{org}=T_{org}-T_c$, we have

$$\frac{C_{org}}{C_b\bullet BF}\cdot \frac{d\Delta T_{org}}{dt}=\frac{\alpha }{C_b} \cdot {AV}_{O2}-\Delta T_{org}$$ (5)

If initial ${AV}_{O2}=0$, then $T_{org}=T_c$, and, therefore, $\Delta T_{org}=0$.

For a linear differential equation in the form of $\tau \cdot \frac{dy}{dx}=y_{eq}-y$, with the initial condition of $y \left(0\right)=0$, the solution is $y\left(t\right)=y_{eq} \left(1-e^{-\frac{t}{\tau }}\right)$, where $y_{eq}$ is new equilibrium, and $\tau$ is time constant. To characterize the convergence process to a new equilibrium, the time to reduce the deviation from equilibrium by half (a.k.a. the half-life, or $t_{1/2}$) is often used. It relates to the time constant $\tau$ as $t_{1/2}=\tau \mathrm{l}\mathrm{n}2\approx 0.7\tau .$

From the above, if ${AV}_{O2}$ changes abruptly, the convergence to new equilibrium is characterized by half-life

$$t_{1/2}=0.7\frac{C_{org}}{C_b\bullet BF}.$$ (6)

$$t_{1/2}=0.7\frac{C_{org}}{C_b\cdot \text{BF}}.$$

For muscles, the heat capacity is $C_{org}=3.59 J/g/$°C [18], whereas the blood flow during intense contractions reaches $BF=0.5$ ml/g/min. Therefore,

$$t_{1/2}=0.7\cdot \frac{3.59}{3.4}\cdot \frac{1}{0.5}\approx 1.5 \left(\mathrm{m}\mathrm{i}\mathrm{n}\right).$$

Similar values of blood flow and heat capacity were reported for the brain [19], so the half-life in the brain will be in a similar range, i.e., 1–2 min. Accordingly, the equilibrium of the temperature difference between arterial blood and the brain during challenges is reached within a few minutes. For example, Fonseca et al. demonstrated that the maximum brain-blood temperature difference was reached at 6 min after the beginning of constant intensity exercise [20]. Temperature changes in the brain do, in fact, occur faster than in other organs [21], but the reason for this is not higher metabolism, but higher blood flow.

The same formulas describe situations when the body temperature changes abruptly, and local tissue temperatures follow the body core temperature. Metabolically active organs (which also have high local circulation), such as the brain, have characteristic convergence times in the range of a few minutes. In the experiments of Hayward and Baker [22,23], animals were injected with cold saline or given cold food or drinks. The resulting temperature decrease was delayed in the brain, as compared to the arterial blood. The temperature of gray matter was stabilized within 4–6 min [22,23]. The temperature responses of white matter and of subcutaneous tissues of the scalp, which have lower perfusion, had a longer delay, for up to 10 min (Fig. 2). Hypercapnia, which increases blood flow, “accelerated clearance of a bolus injection of cold saline,” [23] thus confirming that the time required for local temperature convergence to the equilibrium depends on the blood flow.

Figure 2.

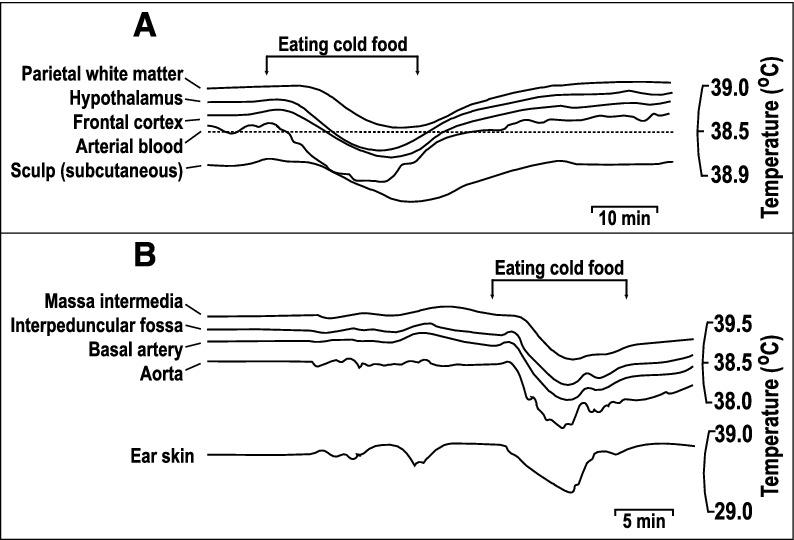
Comparison of brain and arterial blood temperature dynamics during body cooling induced by the consumption of cold food. A. A monkey fills cheek pouches with bananas chilled to 10°C and eats them (arrows). Note that the rapid cooling of arterial blood was followed by cooling of the frontal cortex and hypothalamus with a short delay. In contrast, the parietal subcortical white matter and subcutaneous tissue of the scalp demonstrated significant thermal inertia, as evident from the long delays in the response onset and nadir at each of these locations. B. A rabbit eats cold, chopped apples (arrows). The temperature dynamics in the aorta, basilar artery, and interpeduncular fossa were nearly identical (for clarity, the authors lowered the traces from the aorta and basilar artery), whereas those in the massa intermedia and ear skin were delayed. Replotted from the data reported in ref. [22].

Understanding the organ temperature dynamics could help reconstruct the time course of the metabolism that drives thermal changes. Usually, the difference between the brain and other core sites reaches a maximum within a few minutes. Kiyatkin et al. [21] studied the dynamics of temperature in various brain structures using different experimental paradigms (tail pinch, exposure of a rat to a mouse or to another rat, etc.) and compared them with the changes in the temperature of arterial blood. Figure 3 represents a summary of responses to a tail pinch. The maximum increase in temperature of each structure was reached between 10 and 20 min (Fig. 3A, B), however, the brain-blood temperature difference reached its maximum at 3–4 min post-stimulus (Fig. 3C). The brain temperature started rising virtually immediately (Fig. 3D), and was nearly linear until the temperature difference reached its maximum after 3–4 min. After that, the brain temperature started gradually converging back to the blood temperature. Does this pattern correspond to variations in local brain metabolism? The calculations above (see Equation (5)) show that, at this timescale, the level of oxidative metabolism defines the rate of change of temperature, i.e., the slope of the temperature curves in Fig. 3D, rather than the temperature itself. Therefore, the observed temperature transient is probably due to an abrupt increase of the brain metabolism right after the pinch, followed by a quick reduction of brain metabolic activity. In summary, abrupt changes in metabolism result in a gradual response of the local temperature on a timescale of minutes.

Figure 3.

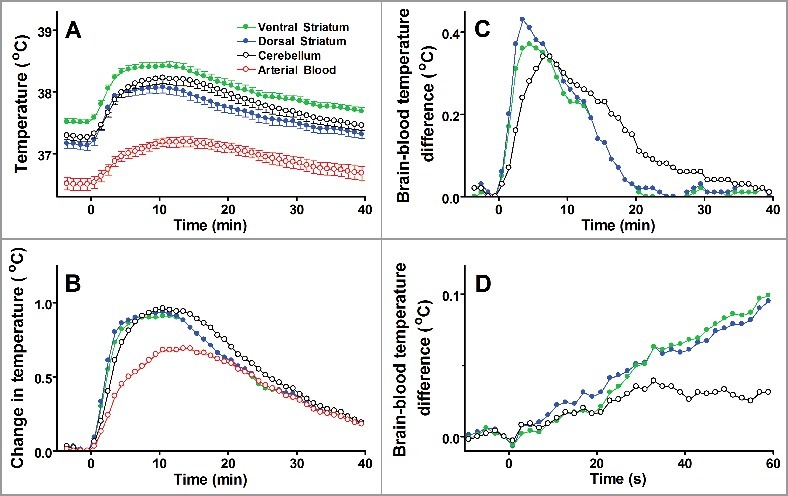
Tail pinch induces an immediate increase of heat production in the brain, which is much shorter than systemic hyperthermia. A. Absolute temperatures reached their maximums in 10–15 min. B. The amplitude of temperature change (from prestimulation baseline) was higher in the brain than in the blood. C. Temperature differences between the blood and each brain structure are shown. The dynamics in the striatum is faster than in the cerebellum. D. The onsets of temperature responses to a tail pinch (first minute of responses shown in panel C). The data (mean ± SE) are replotted from ref. [21].

Brain temperature

As it was shown in many studies, local temperatures depend on the temperature of the arterial blood. For example, the brain is highly metabolically active; it is responsible for 20–25% of the total oxygen consumption [24]. Without producing any physical work, all cerebral metabolic activity is eventually converted into heat. Yet, as it was discovered half a century ago, brain temperature follows arterial blood temperature [22,23]. This experimental finding agrees with basic physics. As shown above, at equilibrium, if there is no heat exchange between the organ and its environment (other than through the circulation), the organ temperature cannot be more than 1.3°C higher than the arterial blood temperature. Furthermore, the core temperature in rats fluctuates between ∼37 and 38°C, with a potential to decrease to ∼36°C during sleep [25,26] and to increase to ∼39°C during intense exercise [27–32] or pharmacological stimulation [33–35]. As such, the physiological range of the core temperature is almost three times wider than the maximum effect of local metabolism. Obviously, in extreme situations, deep core body temperature may be even lower than 36°C or higher than 39°C, but the brain-blood temperature gradient is still bounded by 1.3°C. This does not diminish the importance of local metabolism; in many situations, having a brain temperature 1.3°C lower or higher is equivalent to living or dying (see, e.g., ref. [35]).

The above estimates assume that all consumed oxygen originates from the blood. But what is the actual range of the difference in arteriovenous oxygen content, and into what actual brain-core temperature difference does this oxygen consumption translate? With 3.0-3.5 ml/100 g/min of oxygen consumption in the human brain [19], 55–60 ml/100 g/min of blood flow [24,36], and 0.2 ml O₂/ml blood, the percentage of oxygen extracted by the brain from the blood is 25–30%, assuming that the arterial blood is fully saturated with oxygen in healthy subjects. This oxygen extraction figure is supported by direct measurements of oxygen content in the jugular vein [37]. This range of arteriovenous oxygen difference translates into a 0.3-0.4^oC contribution of oxidative metabolism to the brain temperature, which is consistent with the numbers obtained by Hayward and Baker in deep brain structures in monkeys (Fig. 4) [23]. Conversely, the difference between the brain temperature and the temperature of incoming arterial blood can be recalculated into the oxygen extraction. For example, if at the maximum oxygen extraction, the blood-tissue temperature difference is close to 1.3°C, then the difference of 0.4°C translates into ∼1/3 of the oxygen consumed during arteriovenous transfer.

Figure 4.

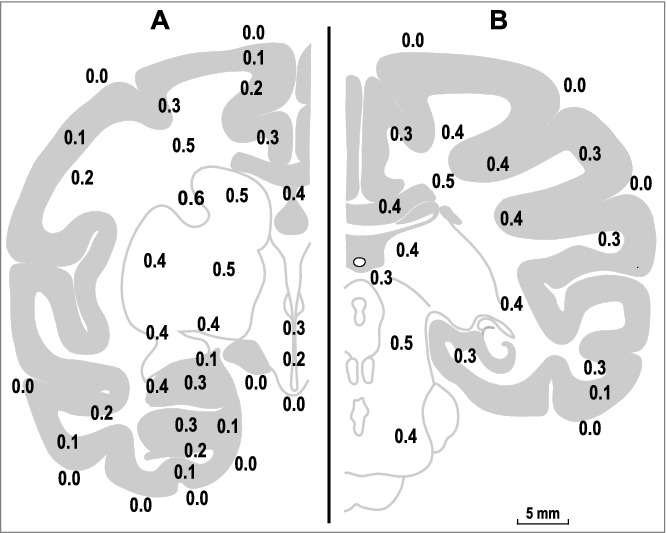
Temperature differences between the arterial blood and various brain and subarachnoid sites in the monkey. The data are shown on two representative coronal sections, A (frontal coordinate of 14.3 mm) and B (frontal coordinate of 0.3 mm), adapted from Olszewski, 1952 [38]. Note that, for the deep structures, the brain-blood temperature differences are in the range of 0.2-0.6°C. It is possible that non-circulatory dissipation to the environment is more significant in cortical structures and decreases the brain-blood temperature difference. The map of the brain-blood temperature differences is replotted from data reported in ref. [23].

It is important to reemphasize that the temperature difference is linked to the percentage of oxygen extraction, not absolute oxygen consumption. To correlate changes in local temperature with the oxygen consumption, the local blood flow needs to be known. Counterintuitively, an increase in the oxygen consumption (per 1 g of tissue) does not necessarily result in an increase in local temperature. If oxygen consumption is increased in parallel with a proportional increase in tissue perfusion (so that the arteriovenous oxygen extraction is not changed), the local temperature will not change either. Moreover, if the tissue perfusion “overshoots” the oxygen consumption, the local temperature can decrease. Hence, an increase in the local temperature can be accompanied by either an increase or a decrease in local metabolism, depending on the tissue perfusion and oxygen extraction in the organ.

Another important aspect that is underappreciated in the literature is how fast the brain temperature adapts to variations in metabolism. Unlike the equilibrium temperature itself, the rate of temperature change depends on the blood flow. In highly perfused organs, like the brain, the half-life of the organ temperature is in the range of a few minutes. If the local metabolism changes, the local temperature reaches a new equilibrium within 3–4 min. And, vice versa, if there is an abrupt change in the arterial temperature (e.g., as described in refs. [22,23]), the brain temperature will follow the arterial blood temperature with a lag of a few minutes. Noteworthy, the time constant of this process (half-life) can be used as a measure of local brain perfusion.

Importance of the blood flow for controlling the brain temperature is well known and easy to understand. When physiologists want to deliver (or remove) heat to (or from) a tissue at a certain rate in experiments with heating (or cooling) perfusion devices, they often have only one tool at their disposal: to adjust the perfusion flow based on the inflow-outflow perfusate temperature difference [39]. By analogy, it is often assumed that increasing the blood flow will predictably cool the brain, and decreasing the flow will warm it. However, the connection is more complex (as shown above), and the result of changing the flow also depends on the arteriovenous deoxygenation. The amount of oxygen taken from the blood depends on how long the blood releases oxygen to the tissue. For example, arterial vasodilation increases blood flow (in ml blood/g tissue) due to an increase in the arteriole diameter, i.e., due to a decrease in the resistance. The time during which the blood releases oxygen to the tissue is inversely proportional to the average blood speed, which, in turn, is proportional to the square of the vessel's diameter, according to Hagen-Poiseuille's Law. The amount of cleared oxygen is proportional to the vessel's surface, which grows linearly with its diameter. As a result, vasodilation in the resistance section of the circulatory path (i.e., arterial vasodilation) is likely to reduce oxygen extraction in the organ. In contrast, vasodilation in the capacitive section of the circulatory path (i.e., venous vasodilation) does not increase the perfusion volume, but may increase the passage time, resulting in an increased extraction of oxygen, and consequently, an increased local temperature. This could be one of the mechanisms for a simultaneous increase in both the blood flow and the oxygen extraction. However, a blood flow increase is most likely associated with a decreased oxygen extraction ratio. This is different from a traditional, simplistic interpretation of brain cooling due to increased blood flow, which does not account for the oxygen extraction.

Increasing the blood flow to modify the brain temperature was one of the main approaches in the studies of Hayward and Baker [22,23]. For example, they induced hypercapnia in monkeys using 8–10% CO₂ in inhaled air. It is known to produce cerebral vasodilatation [24] and to narrow the brain-body temperature gradients. Similarly, hypocapnia, induced with hyperventilation, widens the brain-blood temperature gradients [23]. In this context, “widening of brain-blood temperature gradient” means increasing the difference between brain and blood (core body) temperatures, while “narrowing” means decreasing it. A general idea behind this statement is that, when vasodilation occurs, the amount of blood (which removes heat) increases, and the brain cools down. However, this idea does not account for the fact that the increased blood supply also results in more oxygen being delivered. As we have shown, if the same fraction of oxygen is utilized (the same arteriovenous difference in the oxygen content, or the same venous oxygen concentration, as we assume that the arterial concentration is close to saturation), the brain temperature will not change.

Another interesting point related to the Hayward and Baker study [23] concerns the effect of circulatory arrest on the brain. In their study, a high dose of barbiturate was used to stop the heart, while the brain temperature was recorded. After the circulation had stopped, the temperature of deep brain structures rose by 0.25°C. According to our estimates, the oxidative processes in that case could not be responsible for more than 0.03°C, i.e., one eighth of the total change. Besides oxidation, other reactions occur in the tissue, including glycolysis (which does not require oxygen), dissipation of the membrane potentials, etc. In any scenario, the danger of stopped brain circulation is not associated with overheating.

Brown adipose tissue (BAT) temperature

Measuring BAT temperature is a well-accepted approach to estimate non-shivering thermogenesis in rodents [40]. BAT activation can be visualized in uninstrumented rodents [41] (Fig. 5), and techniques are now being developed to assess BAT activity in humans based on the temperature of BAT skin projections [42]. Activation of thermogenesis in the interscapular BAT of rats and mice has been extensively documented during cold exposure and at the onset of hyperthermic responses to various stimuli, as reviewed by Meyer et al. [40]. The same review mentions examples of how physiologists differ in their approaches to collecting and interpreting BAT temperature data and, especially, on how they relate temperature data to BAT thermogenesis. This issue has become extremely important after it was found that BAT is active in adult humans [43], and that it may play a role in the development of obesity [44].

Figure 5.

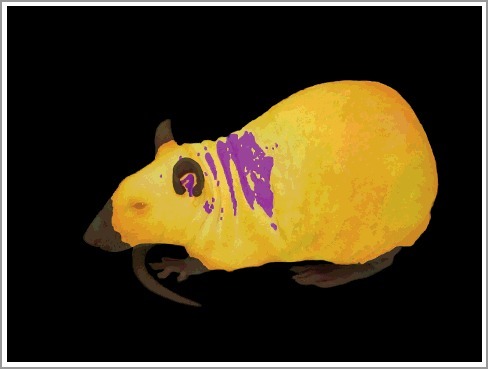
A genetically hairless rat (Crl:CD-Hrhr) exposed to cold. Two images of the animal are overlaid. The bottom layer is a regular (visible spectrum) photograph. The top layer is a semi-transparent, color-coded infrared thermogram. In the thermogram, temperatures from 31.0 to 37.0°C are coded with shades of yellow (from dark to light, respectively), temperatures below 31.0°C are coded with black, and temperatures above 37.0°C are coded with purple. As a result, the vasoconstricted hairless skin over the heat-exchange organs appears black, whereas the haired skin over the rest of the body is yellow. The external acoustic meatus and the skin over the interscapular brown adipose tissue have higher temperatures and show as purple. Reused from ref. [41].

There is a consensus that an increase in BAT temperature should exceed the concurrent core temperature increase in order for the latter to be attributed to BAT thermogenesis. In other words, the BAT-core temperature difference should increase when BAT is stimulated. At thermoneutrality, by definition [45,46], BAT is not activated, so its oxygen extraction is minimal. Indeed, the BAT temperature in unanesthetized, fully conscious rats adapted to the experimental conditions and exposed to a thermally neutral environment is very close to the deep (e.g., colonic) temperature, usually slightly (by 0.1–0.2°C) lower [47–50]. Following any activation of BAT, the BAT temperature increases faster than the core temperature, and the former becomes higher than the latter, with the difference between the two rapidly increasing (Fig. 6; also see refs. [44–50]). However, sympathetic activation increases not only the absolute intensity of metabolism in BAT, but also the blood flow through this tissue. Therefore, the BAT-core temperature difference due to additional metabolic activity in BAT is offset by increased blood flow as it increases heat dissipation. As a result, the BAT-core temperature difference reflects arteriovenous difference in oxygen content, rather than absolute increase in BAT metabolism.. Please note that in some cited studies conducted in rats (e.g., ref. [50]), instead of measuring BAT temperature, the authors aimed to place the tip of the BAT thermocouple in the proximity of Sulzer's vein [51], which, in essence, collects the heat generated by interscapular BAT and sends it (through the inner vertebral plexus and the azygos and superior cava veins) [52] to the heart for further distribution throughout the body.

Figure 6.

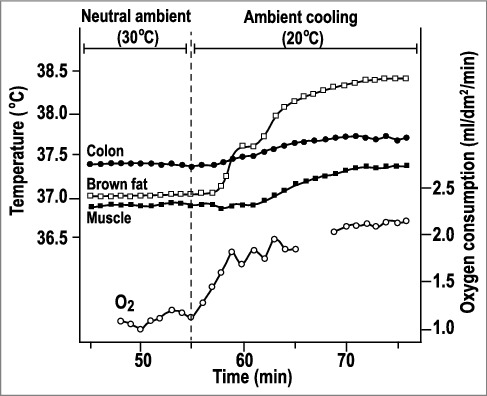
Temperature responses of a rat to ambient cooling. Exposure to 20°C induced cold thermogenesis (increased oxygen consumption), which resulted in increased colonic and muscle temperatures, despite the increased heat dissipation. Initially, the BAT temperature was slightly below the colonic temperature, but increased to 0.8°C above the colonic temperature during cold exposure. Replotted from data reported in ref. [53].

Interestingly, the BAT-core temperature difference was found empirically to be a good index of BAT thermogenesis in the early 1970s [49]. More recently, it was formally proposed to be used as a BAT “thermogenesis index” [50]. The present work lays a theoretical foundation for such a use. It also suggests that, for infrared studies in humans, a good measure of the thermogenic activity of a BAT depot should be based on a temperature difference between a skin projection of this depot and the body core — not on the skin projection temperature per se. In practice, the BAT-colonic temperature difference shows a strong linear correlation with the whole body oxygen consumption in a wide range of colonic temperatures, as it was found during endotoxin-induced fever in rats (Fig. 7; also see ref. [49]), and often approaches 1.0°C [25,47,48,50,54,55].

Figure 7.

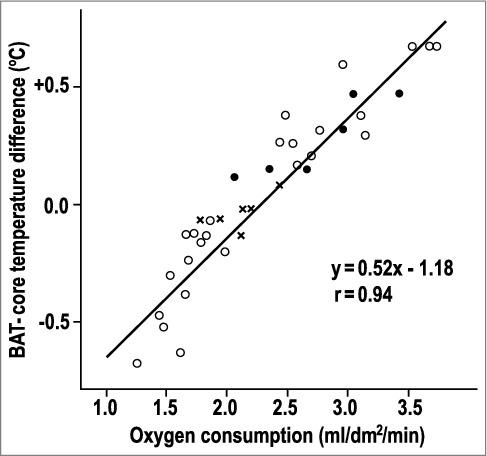
The BAT-blood temperature difference correlates with total body oxygen consumption. The graph combines experiments in unanesthetized rats exposed to 20°C (closed circles), with those exposed to one of 25 other ambient temperatures (open circles), with those exposed to 30°C and injected with an endotoxin that causes fever (crosses). Replotted from data reported in ref. [49].

It is often emphasized that BAT temperature is supposed to increase faster than the core temperature when BAT thermogenesis is activated. This means that the BAT-core temperature difference should increase over time, which is only possible during the transition from baseline equilibrium at rest (with a low arteriovenous oxygen difference) to a high metabolic state (with a high arteriovenous oxygen difference). This is exactly what is observed during BAT activation in experiments (see above). Considering the massive blood supply to the activated BAT, we estimate the half-life for this process to be in the minute range.

It is noteworthy that some depots of BAT, both in rodents (e.g., interscapular) and in humans (e.g., supraclavicular) are located relatively superficially under the skin and, hence, are subjected to non-circulatory heat dissipation to the environment (via subcutaneous tissues and the skin). Indeed, when these depots are activated, their projections on the skin in infrared images are seen as “hot spots,” both in rodents (reviewed in ref. [40]), especially hairless rodents [41], and humans (reviewed in ref. [42]). One can speculate that the high blood flow in the activated BAT makes the effect of heat dissipation to the environment negligible, thus resulting in BAT-blood temperature differences close to the theoretical maximum, which is often the case (Figs. 6,8). It is striking, however, that increases in BAT temperature (from pre-activation levels) of a substantially higher magnitude (2–3°C) are often reported as well (see, e.g., Figure 8). Absolute increases in BAT temperature of this magnitude can be easily explained in those cases when the core and BAT temperatures rise simultaneously. In those cases, the BAT-core temperature difference (limited to 1.3°C) is superimposed on the increase in core body temperature (which can comprise several degrees).

Figure 8.

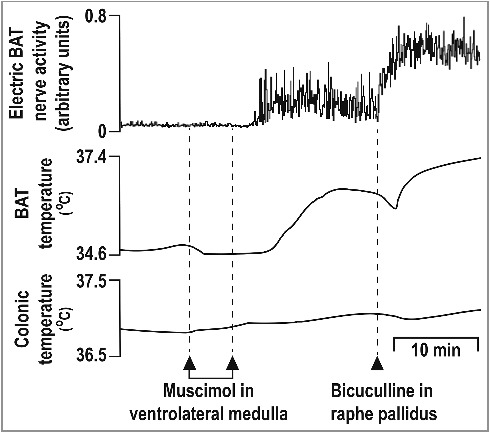
Experimental manipulations can increase BAT temperature in an anesthetized, cooled rat preparation by more than 2°C. Replotted from data reported in ref. [8].

This explanation, however, is not universal. For example, in the experiment shown in Fig. 8, a very large increase in BAT temperature (several degrees) is accompanied by only a small increase in colonic temperature (several tenths of a degree). In cases like this, the baseline blood flow is usually low enough to allow for a substantially negative BAT-core temperature difference at baseline, due to non-circulatory heat dissipation from the inactive tissue with minimal blood flow to the environment ($C_b\cdot BF/\gamma \lesssim 1$ in the denominator of the second term in the right-hand side of Equation (2)). During BAT stimulation, the increased blood flow makes this term negligible ($C_b\cdot BF/\gamma \gg 1$). Figure 8 agrees with this interpretation: the temperature of BAT in an anesthetized, cooled rat preparation before intrabrain injections of muscimol and bicuculine is substantially lower than that of the core (34.6 vs. 36.9°C). After the injections, BAT temperature rapidly rises by several degrees to eliminate this difference, and only then increases above the colonic temperature (and never exceeds it by more than 1.3°C). Unfortunately, unlike the experiment shown in Figure 8, many papers do not report the core temperature dynamic, thus, complicating interpretation of the results.

Temperature in muscles

During exercise, body temperature increases due to the activation of another heat-producing thermoeffector: contracting muscles. According to our calculations, the effect of local metabolism on the equilibrium temperature difference between muscles and the body core is defined by the ratio of extracted oxygen only, and does not depend on the rate of blood flow. Unlike the brain with its relatively high basal metabolism, muscles do not produce much heat at rest. Therefore, at rest, muscles have temperatures close to that of the core or slightly lower, due to heat dissipation to the environment. Our calculations show that, regardless of exercise intensity, the difference between muscle and core temperatures cannot exceed 1.3°C. Consistent with this, the muscle-core temperature difference at the highest workload was found to be ∼1.0°C [31,56]. In the study by Cotter et al. [57], core temperature (as an average between esophageal and rectal temperatures) and muscle temperature (in the m. vastus lateralis) were measured simultaneously in healthy adult volunteers during exercise. While the individual muscle-core temperature differences were not reported, the difference between the group's mean muscle temperature and the group's mean core temperature (calculated by us based on the figures) was negative before the exercise, then increased, and peaked at ∼1.3°C.

Summary

• At equilibrium, the temperature difference between an organ tissue and the arterial blood supplied to this organ is directly proportional to the arteriovenous difference in oxygen content and does not depend on the blood flow.

• Tissue-arterial blood temperature differences cannot exceed a maximum theoretical limit of 1.3°C, which corresponds to the situation where all oxygen is extracted from 100% saturated blood and metabolized in a single passage through the tissue. Non-circulatory heat dissipation from the organ to the environment makes the actual differences smaller than the theoretical limit.

• Time constants of local temperature dynamics depend on blood flow. In organs with high perfusion, such as the brain and contracting muscles, temperature stabilizes within a few minutes after a perturbation. In organs with low perfusion, temperature converges to a new equilibrium within a few tens to a few hundreds of minutes.

• Our analysis supports that and explains why the arterial blood temperature is the main determinant of the temperature of tissues, including brain and brown adipose tissues.

Recommendations for physiologists

• Any assessment of tissue thermogenesis should not be based on a measure of this tissue temperature alone, but rather on a tissue-core temperature difference. For example, an index of BAT activation, as assessed by infrared imaging, can be proposed as the temperature difference between a skin projection of the depot of interest and the body core.

• Changes in either an organ's blood flow alone or metabolism alone are not sufficient to predict the change in the organ's temperature, as the organ's thermal balance depends on both the production and removal of heat. Conversely, an increase in tissue temperature does not necessarily imply an increased metabolism.

• Considering the significant inertia of thermal responses, it may take minutes to hours to reach new temperature equilibrium after a perturbation, depending on the level of tissue perfusion.

• The proposed basic model can be instrumental for data interpretation and experimental design in various areas of physiology dealing with temperature, metabolism, blood flow, and their interactions.

Disclosure of potential conflicts of interest

The authors have no conflicts of interest to disclose.

Acknowledgements

The authors thank Dr. Eugene Kiyatkin for providing original data for Figure 2. The authors also would like to express sincere gratitude to anonymous reviewers for providing invaluable feedback for the revision of the manuscript.