Abstract
Disordered protein chains and segments are fast becoming a major pathway for our understanding of biological function, especially in more evolved species. However, the standard definition of disordered residues: the inability to constrain them in X-ray derived structures, is not easily applied to NMR derived structures. We carry out a statistical comparison between proteins whose structure was resolved using NMR and using X-ray protocols. We start by establishing a connection between these two protocols for obtaining protein structure. We find a close statistical correspondence between NMR and X-ray structures if fluctuations inherent to the NMR protocol are taken into account. Intuitively this tends to lend support to the validity of both NMR and X-ray protocols in deriving biomolecular models that correspond to in-vivo conditions. We then establish Lindemann-like parameters for NMR derived structures and examine what order/disorder cutoffs for these parameters are most consistent with X-ray data and how consistent are they. Finally, we find critical value of L = 4 for the best correspondence between X-ray and NMR derived order/disorder assignment, judged by maximizing the Matthews correlation, and a critical value L = 1.5 if a balance between false positive and false negative prediction is sought. We examine a few non-conforming cases, and examine the origin of the structure derived in X-ray. This study could help in assigning meaningful disorder from NMR experiments. Running Title: NMR X-ray comparison
Keywords: Lindemann Parameter, NMR, X-ray, Proteins in-vivo
I. INTRODUCTION
The understanding that disordered proteins and protein fragments are major factors in biology Dunker et al. (1998); Uversky (2013); Oldfield and Dunker (2014); Dolan et al. (2015); Mittag et al. (2015); Berlow, Dyson, and Wright (2015); Lazar et al. (2016), and especially in more evolved organisms Iakoucheva et al. (2002); Ward et al. (2004); Haynes et al. (2006); Romero et al. (2006), has lent great importance to their identification and characterization. Historically, due to most protein structures being derived from X-ray experiments on the protein in its crystal form, and the ability of this technique to see only stationary atoms, disordered residues were defined as those residues for which coordinates could not be deciphered from the X-ray data Zhang et al. (2012). Indeed such residues have a special comment in a standard PDB file Berman et al. (2000), numbered ‘465’. In essence however these residues can be more aptly labeled as disordered despite crystallization. As we shall show below, some residues loose their disorder due to the crystallization of the protein.
What is the relationship between protein structures obtained from X-ray experiments and those obtained from NMR experiments? Protein structure mediates the interactions that govern all known living systems. In the realm of nano-scale fabrication, protein-design present a good opportunity for building fine scale complex nano-structures, while in chemistry they can greatly expand our understanding and manipulation of complex reactions, for example as catalysts Vetsch et al. (2004); Varpness et al. (2005); Meyer (2008). In principle, due to proteins containing many interacting subsystems, proteins can also be used to test the most fundamental properties of complex systems in the classical and quantum realm. For living systems of course proteins are crucial and their manipulation holds the promise to revolutionize the medical and biotechnology fields. To fully utilize all of these exciting advancements one should try to understand as best as possible the relationship between the protein sequence, its structure (in a dynamical sense), and its function.
A protein is a directed chain of the 20 or so naturally occurring amino-acids Martí-Renom et al. (2000); Wright and Dyson (1999); Chiti and Dobson (2006). The sequence of the protein is determined by the genetics, and the dynamic structure of the protein is responsible for the function. In its static form the sequence-structure assumption states that under certain conditions and given a sequence, a protein will be in a well defined structure. A more dynamic form would state that given a sequence a protein will be in a structural state, allowing for states where a given protein attains a well defined structure only upon binding or some other interaction, and states which don’t go into a stable protein structure at all. It is immediately clear that even this more general form is lacking. A more precise statement would be that given a sequence and environmental conditions a protein would attain some statistically stable static or dynamic structure. What are the limits of this ansatz? Of course it depends on what we mean by statistically stable. In this case we mean that if we repeat an experiment on the same protein, under the same conditions then statistical averages will concur with one another. This depends on the time scale for which statistical averages are taken and it is assumed that they are longer enough to reasonably sample the accessible phase space. Life itself is a manifestation of the validity of this ansatz. But of course life has its limits, per current knowledge it can survive at a narrow band of possible circumstances in the universe. As circumstances change, so does the relationship between sequence, environmental conditions, and structure. What are these relationships as circumstances change between X-ray crystallography (X-ray) and nuclear magnetic resonance (NMR) experiments? We will compare protein structures obtained from NMR and X-ray.
As more models of proteins become available the question of the correspondence of these laboratory produced results to functional proteins needs careful examination. We get protein structures mostly by X-ray. Currently, as of 2016, the PDB Berman et al. (2000) is about 90% X-ray and 10% NMR. In both cases a significant perturbation is applied to the studied systems. Another perturbation, which we shall not address here, is that in most cases and especially for human proteins, they are manufactured for lab analysis in model organisms, typically bacteria. Hence, some issues can arise, for example with the epigenetic control of the protein structure/function. Here we shall focus on post protein isolation issues. Post isolation we get protein structures by either X-ray or NMR. In X-ray, the system is forced to crystallize and the sample is bombarded with strong radiation. In NMR we use chemical manipulation and strong magnetic fields. Do these results differ or agree in the structures they give? If they agree it is an indication that the produced structures are valid representation of functioning proteins for post protein isolation.
Assigning disorder is typically achieved using X-ray resolved protein structure and assigning as disordered any residue that cannot be resolved. However, NMR offers an advantage over X-ray in that protein structure is obtained for samples in solution, without the need to crystallize the protein. This enables capturing more of the dynamics of protein structure and may enable in the future dynamic observation of the structures associated with protein function. It would be beneficial to be able to assign disorder to a protein chain based on NMR resolved structures.
II. MATERIALS AND METHODS
A. NMR/X-ray Datasets
The most exact comparison one can make, between NMR and X-ray structures, is to have a set of identical proteins that have both NMR and X-ray structures. Some special cases like that exist Billeter et al. (1989); Braun et al. (1992); Wagner, Hyberts, and Havel (1992); Blake et al. (1992); Engh et al. (1993); Gallagher et al. (1994); Muchmore et al. (1996); Gajhede et al. (1996); Massiah et al. (1996); Fraenkel and Pabo (1998); Haliloglu and Bahar (1999); Philippopoulos and Lim (1999); Delaglio, Kontaxis, and Bax (2000); Lindorff-Larsen et al. (2005); Garbuzynskiy et al. (2005); Yang et al. (2007); Andrec et al. (2007), and we will use these later to establish a definition of disorder based on NMR structures. However, the current small number of such specific comparisons makes drawing general conclusions regarding general proteins difficult. To get a dataset that is not prohibitively small for drawing conclusions we shall start by resorting to statistical analysis.
We would like to estimate the correspondence between X-ray and NMR derived structures. To this end we built the following datasets. We started out by collecting all protein chains with coordinates obtained from NMR and deposited into the PDB Berman et al. (2000). This led to a set of over 5000 protein chains. Out of this set we searched for matching sequences of X-ray derived structures. We use a PSI-BLAST search S. F. Altschul and T. L. Madden and A. A. Schäffer and J. Zhang and Z. Zhang and W. Miller and D. J. Lipman (1997) with one iteration against a custom non-redundant database of all X-ray pdb structures. A match here and in what follows will be considered if the e-value is bellow 10−15. This set of matching sequences contained 1940 protein pairs. In some cases the sequential match does not correspond to a structural overlap since different parts of the sequence have been solved by NMR or X-ray. For 1594 matching chain pairs, we can calculate structural similarity. We use the publicly available TMscore program Zhang and Skolnick (2004); Xu and Zhang (2010) to achieve this. However, as we shall see later, much of the discussion will be more clearly understood using the RMSD (Root Mean Square Deviation) measure of similarity since it does not involve an arbitrary cutoff for proximal residue pairs as do the TMscore, MaxSub Siew et al. (2000), or GDT Zemla et al. (1999) approaches.
Initial baseline observations are obtained by applying the same technique for the matching X-RAY structures found before. For each one of the X-ray structure that are a match to an NMR structure, we search for a distinct matching X-ray structures with e-value less than 10−15. Distinct refers to the PDB ID and we again restrict ourselves to cases where a TM Score can be calculated. In total we have 969 NMR structures for which there is a matching X-ray structure, which in turn also has a distinct matching X-ray structure. For brevity we shall refer to NMR/X-ray pairs as belonging to dataset DSN and to X-ray/X-ray pairs as belonging to dataset DSX.
B. Cumulative Probability Distributions
One characteristic of either NMR or X-ray derived structural representations of a protein, is the distribution of (e.g.) the RMSD for the sets of matching sequences described above. If NMR and X-ray protocols produce statistically identical structures for a given protein sequence, then the distributions of RMSD values over the datasets DSN and DSX should also be statistically similar.
To calculate the cumulative probability distribution (CPD) we take the following steps. The steps for the TMScore, MaxSUB, or GDTScore are similar. The RMSD values between pairs are sorted and printed along with their line numbers. Line numbers are normalized as fractions of the dataset. In this representation the natural interpretation of the line-number-density is of the probability of obtaining an RMSD value smaller than the corresponding RMSD value in the dataset. One should note that these probability distributions are not probability densities. Their derivatives, if they exist, are.
C. Lindemann-like Parameters
Lindemann parameters were introduced to capture the transition betwee solids and liquids on the molecular scale Lindemann (1910); Shapiro (1970); Zahn, Lenke, and Maret (1999); Zhou, Vitkup, and Karplus (1999); Chakravarty, Debenedetti, and Stillinger (2007). Their definition being the ratio between the mean fluctuations of an molecule and some baseline distance obtained from the crystalline phase. A Lindemann parameter above approximately 0.2 indicates the liquid phase. Here we wish to carry these ideas to proteins, specifically for characterizing residues as either ordered or disordered.
Proteins can be thought of as directed, curved, one-dimensional objects. However, they lack the organized structure of a lattice. If we consider residues to be the basic unit cell and estimate the Cα distances between consecutive residues we obtain a distribution peaked around 3.5Å. However, these are bounded residues that are not expected to come apart. Following Zhou et al. Zhou, Vitkup, and Karplus (1999), we can give an estimate of nearest-neighbor non-bounded heavy-atom distance at 4.5Å.
We chose a slightly different approach. NMR determination of protein structure produces multiple structure models. These correspond to approximate solutions of the constraints on the protein structure obtained from the NMR experiment. Hence, they model structural states the protein visits during its evolution. We can use these multiple models to estimate the fluctuations in the motion of individual residues and compare it to a baseline fluctuation, d, representative of the fluctuations of the structured parts of the protein. We made this choice of baseline since it can be calculated for any form of the parameter. Here we define a Lindemann-like Parameter, L, as:
| (1) |
with σ the standard deviation, x, y, z the coordinates of the spatial vector ri which is the position of the Cα atom of residue i, and d is the mean spatial fluctuations of the Cα atoms of structured protein fragments.
As a test we also introduce an additional parameter using the geometric mean of the standard deviation of the individual components, as,
| (2) |
In this case the comparison is to a baseline value for the geometrical mean for fluctuations of the Cα atoms of structured protein fragments, dg. We note that Lg is only coordinate system independent from a statistical point of view. However, as we shall see later it is useful. A more complete discussion of additional parameters to measure NMR disorder will be presented in future work. We also note that our choice of normalizing the fluctuations by a baseline fluctuation value deviates from the standard definition of Lindemann parameters, and this is the reason we call them Lindemann-like here. We chose an alternate normalization route to enable future work on other Lindemann like parameters.
To carry out a detailed comparison between NMR and X-ray disorder assignments, we use the Northeast Structural Genomics Consortium’s database of NMR/X-ray matched pairs Everett et al. (2016). In this dataset we have 41 protein chains for which structure was resolved by both NMR and X-ray methods. The average sequence length for this set is 109 residues with a standard deviation of 32 residues.
III. RESULTS
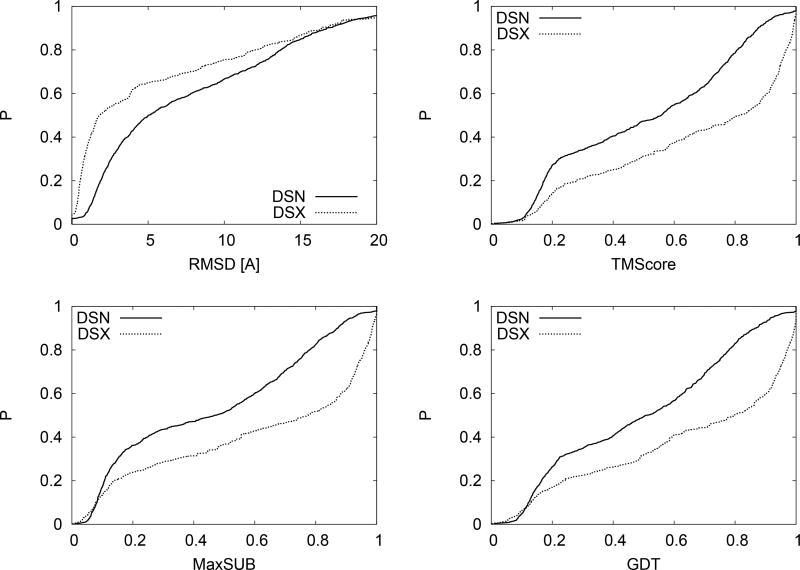
In Fig. 1 we give the probability distribution plots for four types of structure similarity measures over the datasets DSN and DSX. The four types of structure similarity measures are: RMSD, TMScore, MaxSUB, and GDTScore. We used the TMScore Zhang and Skolnick (2004); Xu and Zhang (2010) program of 1/1/2012 to calculate them. These scores are calculated for structurally aligned pairs. The RMSD is a local measure of the average spatial deviations between individual residues in two structures (PDB coordinate files). TM, Max-SUB, and GDT scores give the fractions of residues that are within a given cutoff distance. The three methods use varying cutoffs and methods of defining distances. From Fig. 1 it is obvious that NMR and X-ray have significantly different distribution functions. For example, while over 55% of DSX pairs have RMSD less than 3Å, this occurs for only about 35% of DSN pairs. Similar trends are observed for the three other parameters. The overall trend is that the most significant difference occurs for comparisons between similar structures (RMSD< 5Å) with approximately 10% difference in the probability distributions for 5Å <RMSD< 10Å. That is, the NMR/X-ray dataset contains significantly fewer instances of more structurally similar pairs than X-ray/X-ray pairs.
FIG. 1.
Comparison between cumulative probability distributions (CPDs) of structural similarity parameters for a dataset of NMR/X-ray pairs (DSN) and X-ray/X-ray pairs (DSX). The most significant difference occurs for comparisons between similar structures (RMSD< 5Å) with approximately 10% difference for intermediate ranges.
A. Investigating the Baseline
The baseline set, DSX, may have inherent biases that are not due to any fundamental difference between NMR and X-ray derived structures. For example candidate X-ray structures were taken from those that are a close sequential match to NMR derived structures. This restriction may impose too much of a burden on the calculation. To control for this we also constructed another baseline set. We randomly selected X-ray chains and stopped when we had 969 chains for which matching distinct (in the sense of PDB ID) X-ray derived chains were found. We designate this set as DSXR.
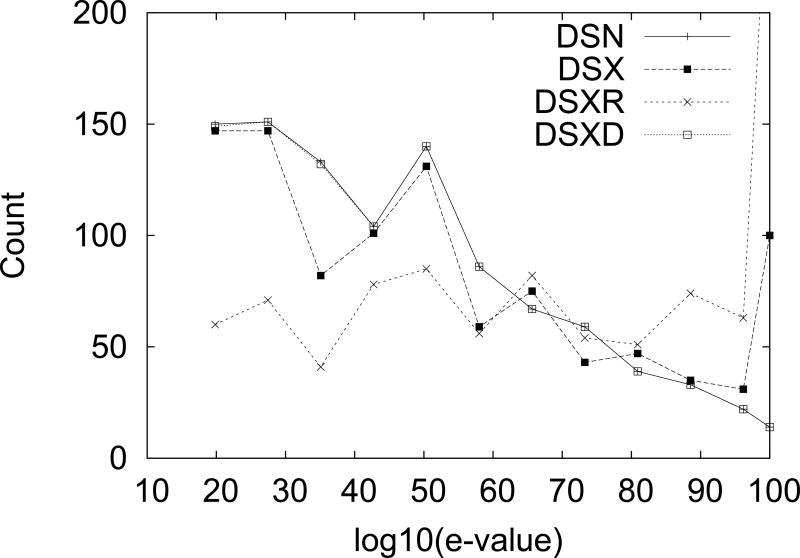
Furthermore, comparison of the distributions of e-value scores in datasets DSN and DSX reveled significant differences. Differences were also found between them and DSXR. To control for these a dataset of matching X-ray pairs with an e-value distribution similar to the one of DSN was constructed. This set will be designated as DSXD. In Fig. 2 we give the distribution of the logarithm of the inverse of the e-values for the different datasets. We truncate any e-value lower than 1−100 to 1−100. We use the inverse of the e-value for clarity, higher values on the X-axis mean higher sequential match. In general we see that DSX has more low e-value pairs (closer matches) and less high e-value pairs than DSN. DSXR has an even higher proportion of low e-value pairs than DSX. DSXD and DSN have matching e-value distributions by construction.
FIG. 2.
Comparison between e-values distribution for the different dataset considered in the text. Note that DSXD is designed to match the distribution of DSN.
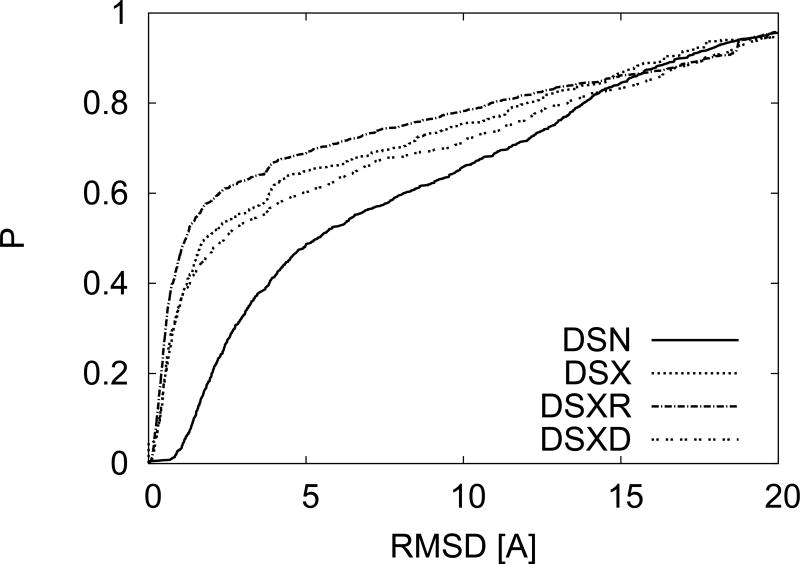
In Fig. 3 we add to Fig. 1 the RMSD distribution obtained for these two additional baseline sets. We see that the intuitively understandable trend of higher e-value correlating with lower RMSD is maintained. However we still see considerable differences between the RMSD distributions of DSN and DSXD, which were designed to have identical e-value distributions. Hence the differences observed so far between NMR and X-ray derived structures are not entirely due to considerations of the e-value distribution or a particular choice of X-ray structures.
FIG. 3.
Comparison between CPDs resulting from the different constraints on the e-value distributions as described in Fig. 2. Even matching the e-value distribution does produce the same CPD.
B. NMR Fluctuations
While X-ray derived structures are set in the crystal formed by the proteins, NMR structures are derived from proteins in solution that are more free to change their coordinates. Hence, these fluctuations are an inherent difference between the NMR and X-ray protocols and should not influence our conclusion of the fit between structures derived by these protocols and in-vivo proteins. In a previous study the fluctuations associated with NMR derived models were studied from the vantage point of predicting them Zhang, Faraggi, and Zhou (2010). Here, we can calculate the fluctuations of NMR directly from the structures using the different models given with each PDB entry.
The question of how to combine these fluctuations in the probability distributions discussed above is more subtle. For one thing we need to realize that RMSD is a measure of distance and hence it is intuitive that its values should be added. The other three structure characteristics we use (TMscore, MaxSUB, GDTscores) are all fractions of residue pairs within a cutoff distance. Therefore, they should be interpreted to be probabilities and combining them together should be carried out by multiplication.
Though we know of no formal stipulation, it seems that model structures from NMR experiments would be ranked according to some fitness parameter/s. Therefore we calculated the mean NMR fluctuations with respect to the first model. That is, structure similarity scores were calculated for all models relative to the first and the means and standard deviations were calculated.
How to combine the deviations associated with sequential matching and fluctuations in solution? More specifically, which instances to combine? We use the construct of DSN and DSX as a way to address this point. That is, in constructing the dataset DSN, for each of the 969 matching X-ray derived structures, corresponding distinct X-ray matching structures were found in DSX. Each of the structure similarity scores between sequential matches in DSX can be combined with the NMR fluctuations associated with the corresponding NMR derived structure in DSN.
Now that we have a way to associate between fluctuations due to sequential matching and solute, our final step is to combine the structure similarity scores for the set DSX into an estimated value that would be expected if sequential matching was done between NMR and X-ray derived structures (as in DSN). We approach this using the following rational. The details of which part of the protein is affected by which fluctuation is critical for this estimation.
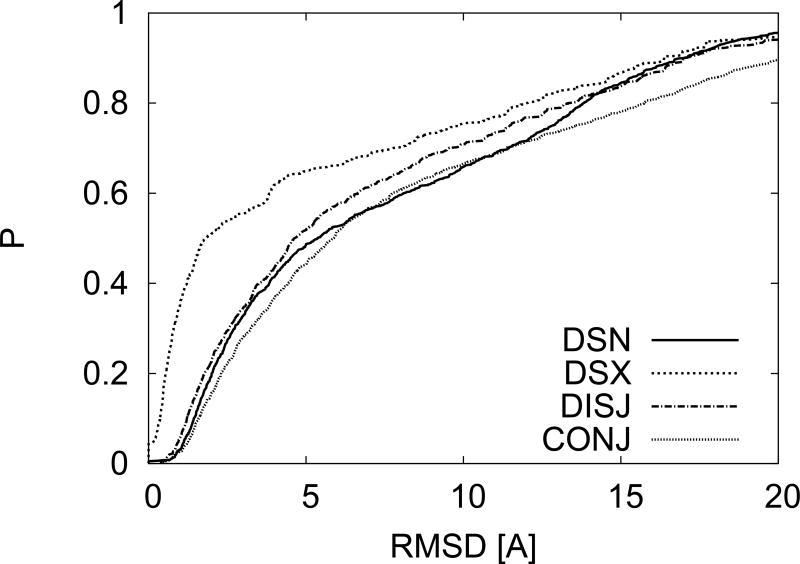
We start by considering how to combine the RMSD values between matching pairs and RMSF (Root Mean square fluctuations). If we assume that the RMSD and RMSF occur at similar locations along the protein and that they are uniformly distributed then the RMSD of the hypothetical fluctuating X-ray system would be equal to the sum of the RMSD and RMSF from the two types of fluctuations. On the other hand if we assume that these fluctuations occur at disjoint areas of the protein then the fluctuations of the hypothetical fluctuating X-ray system would be equal to the square-root of the sum of the square RMSD plus the square RMSF. In Fig. 4 we give the results of the probability distributions using either of these assumptions. The label DISJ refers to fluctuations occurring in disjointed regions and the label CONJ refers to fluctuations occurring in similar regions. For reference we also give the probability distributions for DSN and DSX. We see that if we add NMR fluctuations to the fluctuations associated with sequential match for X-ray structures the resulting probability distribution largely agrees with the one for sequential matching for NMR.
FIG. 4.
CPDs for RMSD that result from adding NMR fluctuations to X-ray structures. The two types of approaches to adding the NMR fluctuations are described in the text and produce curves that are similar to DSN.
Due to the use of a cut-off based measure, combination of the separate effects into an effective score for TM, MaxSUB, and GDT is significantly more complicated. For each protein the details of fluctuations due to sequential mismatch and NMR will determine the effective score. We give several examples. In one case, if the fluctuations affect different regions of the protein (disjointed), the resulting score would be the sum of the fractions of residues outside the cutoff distance. On the other hand if the fluctuations are more evenly spread their combination can turn two high scores (> 0.8) into a low score (< 0.4) since entire regions that are inside the cutoff distance for both fluctuations separately can become outside the cutoff distance upon combination. Such considerations are outside the scope of this paper.
C. NMR Disorder
We start by investigating the value of d, and dg, for the three secondary structure states: helix (H), sheet (E), and coil (C). We use the DSSP program Kabsch and Sander (1983) to assign secondary structure based on the restrictive 8 to 3 map as discussed in Faraggi et al. (2012). In Table I we give the average fluctuations using a Euclidean distance (AF) and using a geometrical mean (AFG), with standard deviations (SD) for residue fluctuations (of Cα atom) for residues of the three types of secondary structure states. We see that for the two structured states, H and E, a value of d = 1Å is consistent when using Euclidean distance. For a geometric mean we find a value of dg = 0.5 Å.
TABLE I. Average Residue Fluctuations.
Average residue fluctuations using the standard Euclidean approach (AF) and using a geometrical mean (AFG). Standard deviations (SD) over all residues of a given secondary structure type are given following their corresponding parameter. Based on these values we select d = 1 Å and dg = 0.5 Å.
| Secondary Structure | AF (Å) | SD (Å) | AFG (Å) | SD (Å) |
|---|---|---|---|---|
| Sheet | 0.60 | 0.39 | 0.33 | 0.21 |
| Helix | 0.81 | 0.85 | 0.44 | 0.46 |
| Coil | 3.43 | 5.25 | 1.87 | 2.92 |
Average residue fluctuations using the standard Euclidean approach (AF) and using a geometrical mean (AFG). Standard deviations (SD) over all residues of a given secondary structure type are given following their corresponding parameter. Based on these values we select d = 1 Å and dg = 0.5 Å. We note that the sheet structure seems most rigid. Note also that these averages were taken on the NMR solutions of these structure. Residues denoted as ‘Coils’ in Table I include residues missing coordinates in their X-ray structure model.
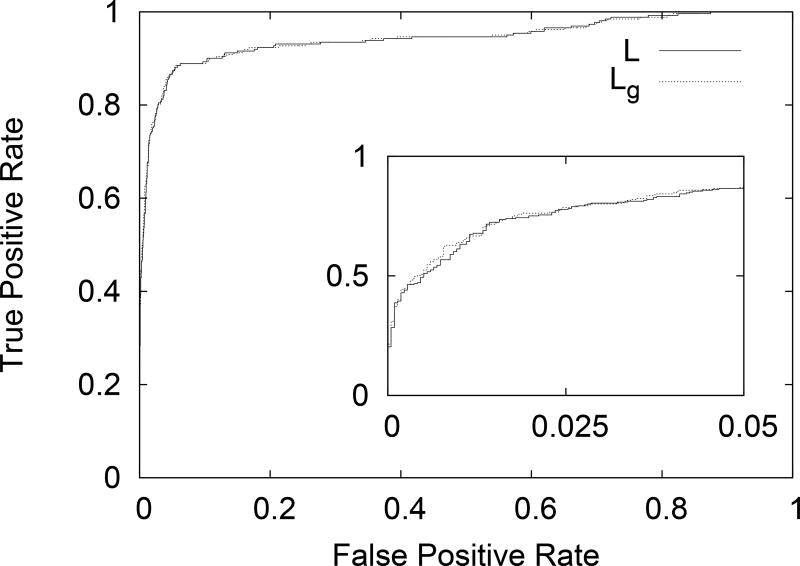
We continued by calculating the Lindemann-like parameters L, and Lg, for the residues in the NMR structure models. We then align these results with order/disorder assignments based on the existence/absence of coordinates in the corresponding X-ray structure model. Receiver Operating Characteristic (ROC) curves are then calculated for distinguishing the order/disorder state of a residue based on L or Lg values, with the obvious trend of increasing Lindemann-like parameter indicating disorder. We plot these results in Fig. 5. The inset shows the same plot restricted to low False Positive Rate and shows the slight advantage of Lg over L. Area Under the Curve (AUC) was calculated from these ROC curves. We find that the parameter L produces an AUC of 0.943, while use of Lg to distinguish between ordered and disordered residues yields an AUC of 0.944. Again, a slight advantage for using Lg. The reason for this, we suspect, is that the geometric mean is better able to distinguish between isotropic and periodic motion. This will be investigated in future studies.
FIG. 5.
ROC curve for distinguishing the order/disorder state of a residue based on L or Lg values, with the obvious trend of increasing Lindemann-like parameter indicating disorder. The inset shows the same plot restricted to low False Positive Rate and shows the slight advantage of Lg over L.
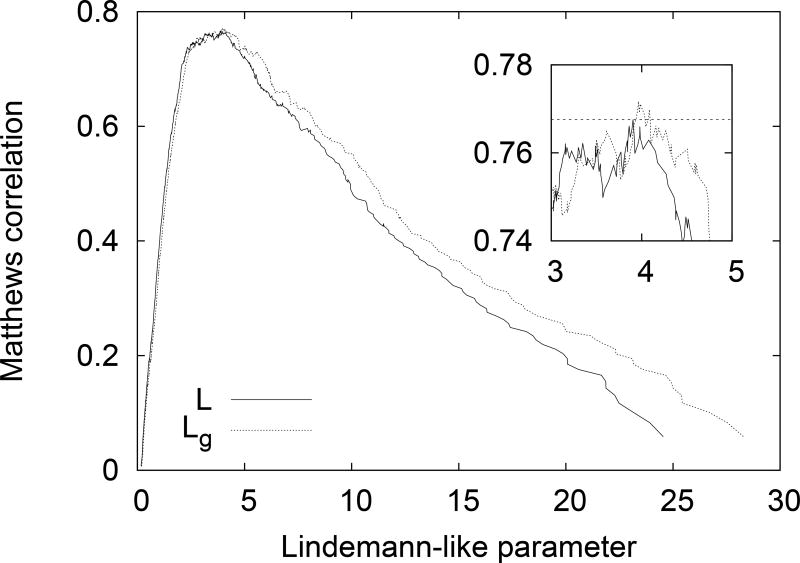
We also calculated the Matthews correlation, M, for all possible threshold values for both L and Lg. Plots for both cases are given in Fig. 6. The inset shows the range of thresholds for which maximum Matthews correlation is obtained. We find a maximum value of M = 0.771 using the threshold Lg = 3.96. For the more standard Lindemann-like parameter we find a maximum value of M = 0.768 for the threshold value L = 3.90. Note that we can infer a distance scale from L but not from Lg. In both cases we find similar results, with the maximum correlation obtained for Lindemann-like parameters threshold approximately four times the value for structured cases. We note that the Matthews correlation surpass 0.7 for thresholds above 2.0 approximately. This value can be useful for cases when avoiding false negatives may be more important. It is worth while to note that disorder appears to be associated with stronger fluctuations than the 0.2 Lindemann threshold for liquids. This is consistent with previous results of Zhou et al. Zhou, Vitkup, and Karplus (1999) indicating the structured surfaces of structured proteins having Lindemann parameters of the order of that of liquid. If we use the standard definition of the Lindemann parameter, with the same normalization as Zhou et al. we arrive at an approximate relationship Ld = Lc/4, with Ld the Lindemann parameter and Lc defined earlier. Based on our results here this would correspond to a Lindemann parameter for the transition to disorder in the range [0.5, 1]. To achieve disorder one needs more fluctuations than at the surface of structured proteins.
FIG. 6.
Matthews correlation calculated for distinguishing the order/disorder state of a residue based on L or Lg values, with the obvious trend of increasing Lindemann-like parameter indicating disorder. The inset shows the same plot restricted to the area of maximum correlation, the dotted line at 0.768 shows the maximum value for L and that Lg is slightly better.
D. Case Studies
During the course of this work we came across seemingly peculiar cases where the RMSF and (e.g.) TM score would point in different directions with respect to the degree of structural match between the different NMR models. Either the RMSF would be relatively high indicating structural instability but the TMscore would also be high indicating structural stability. Or, the RMSF would be relatively low and so would the TMscore be. Besides being anomalies deserving attention, these cases also suggested the presence of disorder. Here we analyze several such examples.
We start off with the case of the major urinary protein Timm et al. (2001); Phelan et al. (2010). This protein’s NMR structure (PDB ID: 2L9C) came up with a sequential match to an X-ray structure (PDB ID: 1I06). In both cases these are single chain proteins however the NMR model is for a single chain in solution while the X-ray structure was achieved for the crystallized protein complexed with synthetic pheromones 2-sec-butyl-4,5-dihydrothiazole and 6-hydroxy-6-methyl-3-heptanone. The RMSF found for the NMR models was 11.9Å while the TMscore was 0.87. Further examination of the structures revealed that indeed the NMR structure seems to have some core structure however the terminals seem to obtained a well defined structure only upon binding to the pheromones. A similar example is the immunodeficiency virus. Where NMR structure (PDB ID: 2K4E) has a relatively structured core and flapping terminals which become structured upon binding in a crystallized triplet structure (PDB ID: 1ED1). In this case the RMSF was 11.5Å and the TMscore was 0.87. Both disorder prediction with SPINE-D Zhang et al. (2012) and missing coordinates from the X-ray structure indicate the existence of long disordered terminals for these proteins.
Another interesting case is that of the DNA binding protein GAL4. In this case the RMSF for the NMR structures (PDB ID: 1HBW) was relatively low at 5.7Å while the TMscore was 0.42. Inspection of the structures reveled that this protein in solution is composed of a set of independent helices, each stable and flopping about. For this protein the X-ray solved sequential match we found was crystallized while bound to DNA (PDB ID: 3COQ). In this state interactions with the DNA support the localization of the different helices relative to each other. About 30% of this protein was found to be disordered.
This work can also help identify disordered regions of proteins that are mistakenly labeled as ordered by X-ray studies due to experimental constraints (e.g., crystal contacts). We will call these cases of disagreement between NMR and X-ray results Type I disagreements. Additionally, a region will be ordered or disordered depending on the boundary conditions it is experiencing (e.g., binding). Comparing disorder assignments from NMR and X-ray experiments can help identify MORF regions Yan et al. (2016), regions that change their structure as a functional of the boundary conditions they are experiencing. We will call these cases of disagreement between NMR and X-ray result Type II disagreements. It is interesting to investigate several cases that exhibit these types of behavior.
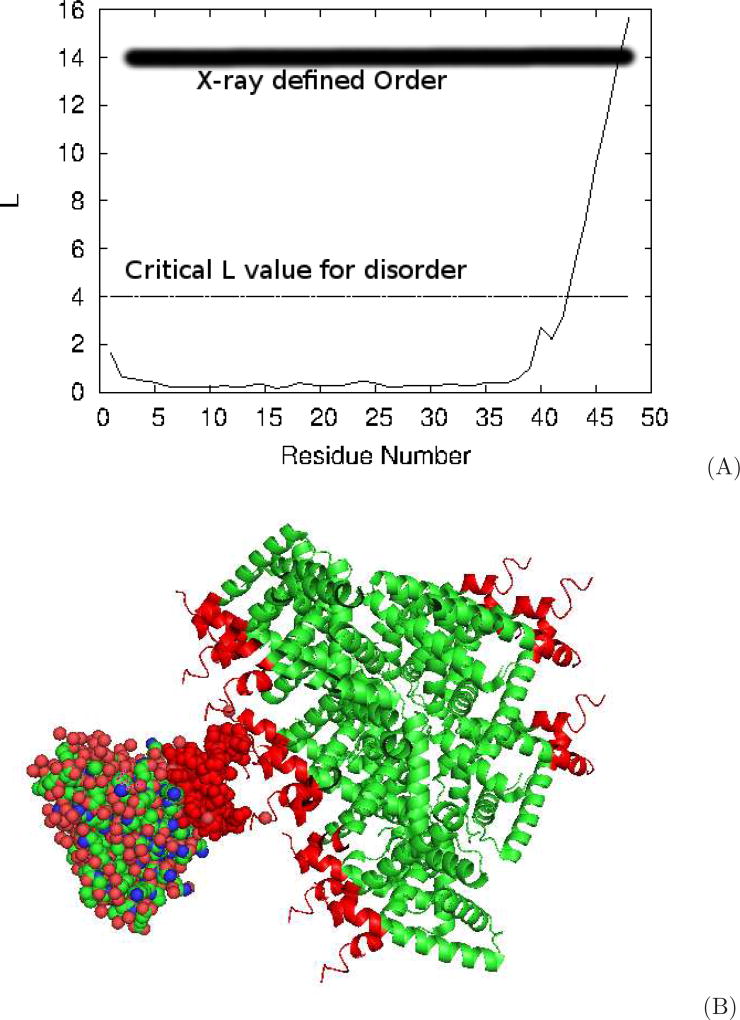
We start with the end region of the folded n-terminal fragment of UPF0291 protein YnzC from Bacillus subtitles. The PDB IDs for the NMR and X-ray solved structures are 2JVD and 3BHP respectively Berman et al. (2000); Aramini et al. (2008); Kuzin et al. (2008). That region was labeled ordered by X-ray, while according to NMR the last residue has the largest fluctuations in the set of (X-ray labeled) ordered residues. In Fig. 7A we give the value of L as a function of the residue number for 2JVD. If we use a order/disorder cutoff of Lc = 4, indicated by the line in the plot, residues 43–48 are determined disordered by NMR. Indeed, observation of the PyMol Schrödinger, LLC (2015) movie of successive NMR solved structures shows the fragment flopping around. In Fig. 7B we give the cartoon image of the protein packed in the crystal structure as reported in the PDB and constructed using the PyMol ‘symexp’ command. The fragment in question is labeled red in all copies of the protein and we include one space fill copy to better visualize distances. It is clear that in this case we have both Type I and Type II disagreements. We have Type I in contacts appearing between the end regions of opposing chains in the crystal, with a minimum distance between Cα on opposing chains close to 4 Å. Probably more important in this case, the protein was crystallized in trimer form. In this form the three end fragments provide binding opportunistic to each other and stabilize their structure. It is not surprising then that with the lack of these two restraints, NMR solutions show the end fragment disordered.
FIG. 7.
Conflicting results between crystal and NMR structures resulting from crystal packing. A) Lindemann-like parameter L versus the residue number along the chain showing the highly fluctuating C-terminus tail of this structure. B) Crystal packing cartoon of the protein showing the tail-to-tail orientation and proximity of opposing tails.
As another case, we chose randomly from the set of X-ray labeled ordered residues with L > 4 and obtained residue 158 an uncharacterized protein from Chlorobium tepidum. It is part of the C-terminus tail of the protein. In the solution NMR structure (PDB ID: 2KCU) this tail is formed from residues 156–166 with L > 4. For residue 158, L = 6.7. The corresponding crystal structure (PDB ID: 3E0H) of this protein show only residues 156–158 of the tail with all three residues having coordinates (i.e., ordered). The rest of the tail, residues 159–166, were cleaved to allow for crystallization. Inspection of the crystal packing revels binding of residue 158 to residues 78 and 79 of the nearest crystal duplicate. This interaction, plus the fact that much of the disordered part was removed allow for stabilization of this fragment in the crystal structure. We can categorize this case as a Type I disagreement.
This protein also allows us to investigate cases of disagreement that are not restricted to the terminal regions. Residues 139–146 are labeled ordered by X-ray, however this fragment exhibits L > 3.5 in NMR. Examination of the crystal packing shows that this fragment is flanked on three sides by fragments from other crystal contacts. Most significantly there is binding between residue 141 in this fragment and residue 157 in the nearest crystal duplicate, with a minimum distance between Cαs below 4Å. This interaction acts to stabilize this fragment enough to allow for it to be visualized in the X-ray diffraction patterns. We can categorize this case as a Type I disagreement as well.
We also have opposite cases where structure was not observed in X-ray yet NMR shows a stable fixed structure. Residues in Q8ZP25 from Salmonella Typhimurium Parish et al. (2008) demonstrate such a case. Residues 26 to 33 in the X-ray solved structure (PDB ID: 2ES7) are identified as disordered, however this same region shows up as a stable helix with L < 0.5 in the NMR solution (PDB ID: 2JZT). There is agreement between the solutions for the disordered tails of this protein, as well as a strongly disordered loop centered around residue 49. We speculate that in this and similar cases the strongly fluctuating dynamics of these disordered regions of the protein obscure the diffraction patterns for parts of the proteins.
IV. CONCLUSIONS
We have presented a comparison between the distributions of structural alignment scores, for sequentially aligned pairs of protein chains. We have done this separately for a large set where one member of each pair is an NMR derived structure and the other structure derived from X-ray crystallography, and for another set where both structures are derived from X-ray experiments. We find that at face value these two approaches for obtaining protein structure yield significantly differing results for both RMSD and more sophisticated structure similarity scores.
The difference between the structural similarity scores was analyzed and it was shown that it cannot be attributed to the difference between the sequential alignment distributions. It was shown that the difference can be attributed, at least from the statistical point of view, to the fluctuations inherent to the NMR protocol. That is, if for a set of X-ray structures we pair them each with its near (e-value< 10−15) sequential match and combine with the difference in their structure the mean fluctuations across NMR derived structures of this close sequential match; then the distribution of their structural correspondence resembles that of a set of NMR structures. This lends support to the validity of both NMR and X-ray protocols in deriving biomolecular models that correspond to in-vivo conditions.
We have also investigated and compared the transition to disorder in both NMR and X-ray studies. We introduced a Lindemann-like parameter for fluctuations in NMR models and described how disorder assignment can be made for NMR structures. Since we hope this work will spur further progress in the area of NMR disorder assignment, a note about the choice of cutoff Lc. We have set Lc = 4 arbitrarily in this exploratory study due to this value producing the maximum Matthews correlation value. However, an examination of the data revels this choice of Lc produces 96/261 false negatives, i.e., residues marked disordered by X-ray but with L < 4 by NMR, and 31/2140 false positives, i.e., residues marked ordered by X-ray but with L > 4. This imbalance is due to size imbalance between the different groups, with many more ordered residues than disordered ones. We can correct this misalliance, achieving about 10% false positive and false negative classification by taking Lc = 1.5. It is the opinion of the authors of this work that further studies should determine the most effective cutoff values and uses for NMR disorder assignment.
Acknowledgments
This work was supported in part by The Research Institute at Nationwide Children’s Hospital, by the Lilly Endowment, Inc., through its support for the Indiana University Pervasive Technology Institute, by the Indiana METACyt Initiative, and by the National Science Foundation under Grants No. CNS-0521433, and CNS-0723054. We also gratefully acknowledge the financial support provided by the National Institutes of Health (NIH) through Grants R01GM072014 and R01GM073095.
References
- Andrec M, Snyder DA, Zhou Z, Young J, Montelione GT, Levy RM. A large data set comparison of protein structures determined by crystallography and nmr: statistical test for structural differences and the effect of crystal packing. Proteins: Structure, Function, and Bioinformatics. 2007;69:449–465. doi: 10.1002/prot.21507. [DOI] [PubMed] [Google Scholar]
- Aramini JM, Sharma S, Huang YJ, Swapna G, Ho CK, Shetty K, Cunningham K, Ma L-C, Zhao L, Owens LA, et al. Solution nmr structure of the sos response protein ynzc from bacillus subtilis. Proteins: Structure, Function, and Bioinformatics. 2008;72:526–530. doi: 10.1002/prot.22064. [DOI] [PubMed] [Google Scholar]
- Berlow RB, Dyson HJ, Wright PE. Functional advantages of dynamic protein disorder. FEBS letters. 2015;589:2433–2440. doi: 10.1016/j.febslet.2015.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat T, Weissig H, Shindyalov IN, Bourne PE. The protein data bank. Nucleic Acids Research. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Billeter M, Kline AD, Braun W, Huber R, Wüthrich K. Comparison of the high-resolution structures of the α-amylase inhibitor tendamistat determined by nuclear magnetic resonance in solution and by x-ray diffraction in single crystals. Journal of molecular biology. 1989;206:677–687. doi: 10.1016/0022-2836(89)90575-5. [DOI] [PubMed] [Google Scholar]
- Blake PR, Day MW, Hsu BT, Joshua-Tor L, Park J-B, Hare DR, Adams MW, Rees DC, Summers MF. Comparison of the x-ray structure of native rubredoxin from pyrococcus furiosus with the nmr structure of the zinc-substituted protein. Protein Science. 1992;1:1522–1525. doi: 10.1002/pro.5560011113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braun W, Vasak M, Robbins A, Stout C, Wagner G, Kägi J, Wüthrich K. Comparison of the nmr solution structure and the x-ray crystal structure of rat metallothionein-2. Proceedings of the National Academy of Sciences. 1992;89:10124–10128. doi: 10.1073/pnas.89.21.10124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakravarty C, Debenedetti PG, Stillinger FH. Lindemann measures for the solid-liquid phase transition. The Journal of chemical physics. 2007;126:204508. doi: 10.1063/1.2737054. [DOI] [PubMed] [Google Scholar]
- Chiti F, Dobson CM. Protein misfolding, functional amyloid, and human disease. Annu. Rev. Biochem. 2006;75:333–366. doi: 10.1146/annurev.biochem.75.101304.123901. [DOI] [PubMed] [Google Scholar]
- Delaglio F, Kontaxis G, Bax A. Protein structure determination using molecular fragment replacement and nmr dipolar couplings. Journal of the American Chemical Society. 2000;122:2142–2143. [Google Scholar]
- Dolan PT, Roth AP, Xue B, Sun R, Dunker AK, Uversky VN, LaCount DJ. Intrinsic disorder mediates hepatitis c virus core–host cell protein interactions. Protein Science. 2015;24:221–235. doi: 10.1002/pro.2608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunker AK, Garner E, Guilliot S, Romero P, Albrecht K, Hart J, Obradovic Z, Kissinger C, Villafranca JE. Protein disorder and the evolution of molecular recognition: theory, predictions and observations. Pac Symp Biocomput. 1998;3:473–484. [PubMed] [Google Scholar]
- Engh RA, Dieckmann T, Bode W, Auerswald EA, Turk V, Huber R, Oschkinat H. Conformational variability of chicken cystatin: comparison of structures determined by x-ray diffraction and nmr spectroscopy. Journal of molecular biology. 1993;234:1060–1069. doi: 10.1006/jmbi.1993.1659. [DOI] [PubMed] [Google Scholar]
- Everett JK, Tejero R, Murthy SB, Acton TB, Aramini JM, Baran MC, Benach J, Cort JR, Eletsky A, Forouhar F, et al. A community resource of experimental data for nmr/x-ray crystal structure pairs. Protein Science. 2016;25:30–45. doi: 10.1002/pro.2774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faraggi E, Zhang T, Yang Y, Kurgan L, Zhou Y. Spine x: improving protein secondary structure prediction by multistep learning coupled with prediction of solvent accessible surface area and backbone torsion angles. Journal of computational chemistry. 2012;33:259–267. doi: 10.1002/jcc.21968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraenkel E, Pabo CO. Comparison of x-ray and nmr structures for the antennapedia homeodomain–dna complex. Nature Structural & Molecular Biology. 1998;5:692–697. doi: 10.1038/1382. [DOI] [PubMed] [Google Scholar]
- Gajhede M, Osmark P, Poulsen FM, Ipsen H, Larsen JN, van Neerven RJ, Schou C, Løwenstein H, Spangfort MD. X-ray and nmr structure of bet v 1, the origin of birch pollen allergy. Nature Structural & Molecular Biology. 1996;3:1040–1045. doi: 10.1038/nsb1296-1040. [DOI] [PubMed] [Google Scholar]
- Gallagher T, Alexander P, Bryan P, Gilliland GL. Two crystal structures of the b1 immunoglobulin-binding domain of streptococcal protein g and comparison with nmr. Biochemistry. 1994;33:4721–4729. [PubMed] [Google Scholar]
- Garbuzynskiy SO, Melnik BS, Lobanov MY, Finkelstein AV, Galzitskaya OV. Comparison of x-ray and nmr structures: Is there a systematic difference in residue contacts between x-ray-and nmr-resolved protein structures? Proteins: Structure, Function, and Bioinformatics. 2005;60:139–147. doi: 10.1002/prot.20491. [DOI] [PubMed] [Google Scholar]
- Haliloglu T, Bahar I. Structure-based analysis of protein dynamics: Comparison of theoretical results for hen lysozyme with x-ray diffraction and nmr relaxation data. Proteins: Structure, Function, and Bioinformatics. 1999;37:654–667. doi: 10.1002/(sici)1097-0134(19991201)37:4<654::aid-prot15>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
- Haynes C, Oldfield CJ, Ji F, Klitgord N, Cusick ME, Radivojac P, Uversky VN, Vidal M, Iakoucheva LM. Intrinsic disorder is a common feature of hub proteins from four eukaryotic interactomes. PLoS Comput Biol. 2006;2:e100. doi: 10.1371/journal.pcbi.0020100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iakoucheva LM, Brown CJ, Lawson JD, Obradović Z, Dunker AK. Intrinsic disorder in cell-signaling and cancer-associated proteins. Journal of molecular biology. 2002;323:573–584. doi: 10.1016/s0022-2836(02)00969-5. [DOI] [PubMed] [Google Scholar]
- Kabsch W, Sander C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
- Kuzin A, Su M, Seetharaman J, Janjua H, Cunningham K, Maglaqui M, Owens L, Zhao L, Xiao R, Baran M, et al. Crystal structure of upf0291 protein ynzc from bacillus subtilis at resolution 2.0 a. Northeast Structural Genomics Consortium target SR384. 2008;10 [Google Scholar]
- Lazar T, Schad E, Szabo B, Horvath T, Meszaros A, Tompa P, Tantos A. Intrinsic protein disorder in histone lysine methylation. Biology Direct. 2016;11:30. doi: 10.1186/s13062-016-0129-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindemann F. Molecular frequencies phys. Z. 1910;11:609–612. [Google Scholar]
- Lindorff-Larsen K, Best RB, DePristo MA, Dobson CM, Vendruscolo M. Simultaneous determination of protein structure and dynamics. Nature. 2005;433:128–132. doi: 10.1038/nature03199. [DOI] [PubMed] [Google Scholar]
- Martí-Renom MA, Stuart AC, Fiser A, Sánchez R, Melo F, Šali A. Comparative protein structure modeling of genes and genomes. Annual review of biophysics and biomolecular structure. 2000;29:291–325. doi: 10.1146/annurev.biophys.29.1.291. [DOI] [PubMed] [Google Scholar]
- Massiah MA, Worthylake D, Christensen AM, Sundquist WI, Hill CP, Summers MF. Comparison of the nmr and x-ray structures of the hiv-1 matrix protein: Evidence for conformational changes during viral assembly. Protein science. 1996;5:2391–2398. doi: 10.1002/pro.5560051202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer TJ. Catalysis: The art of splitting water. Nature. 2008;451:778–779. doi: 10.1038/451778a. [DOI] [PubMed] [Google Scholar]
- Mittag T, Marzahn M, Lee J, Palud A, Marada S, Nourse A, Taylor J, Ogden S. The role of protein disorder and self-association in the formation of cellular bodies. The FASEB Journal. 2015;29:109–2. [Google Scholar]
- Muchmore SW, Sattler M, Liang H, Meadows RP, Harlan JE, Yoon HS, Nettesheim D, Chang BS, Thompson CB, Wong S-L, et al. X-ray and nmr structure of human bcl-xl, an inhibitor of programmed cell death. Nature. 1996;381:335–341. doi: 10.1038/381335a0. [DOI] [PubMed] [Google Scholar]
- Oldfield CJ, Dunker AK. Intrinsically disordered proteins and intrinsically disordered protein regions. Annual review of biochemistry. 2014;83:553–584. doi: 10.1146/annurev-biochem-072711-164947. [DOI] [PubMed] [Google Scholar]
- Parish D, Benach J, Liu G, Singarapu KK, Xiao R, Acton T, Su M, Bansal S, Prestegard JH, Hunt J, et al. Protein chaperones q8zp25_salty from salmonella typhimurium and hyae_ecoli from escherichia coli exhibit thioredoxin-like structures despite lack of canonical thioredoxin active site sequence motif. Journal of structural and functional genomics. 2008;9:41. doi: 10.1007/s10969-008-9050-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phelan MM, McLean L, Simpson DM, Hurst JL, Beynon RJ, Lian L-Y. 1h, 15n and 13c resonance assignment of darcin, a mouse major urinary protein. Biomolecular NMR assignments. 2010;4:239–241. doi: 10.1007/s12104-010-9253-6. [DOI] [PubMed] [Google Scholar]
- Philippopoulos M, Lim C. Exploring the dynamic information content of a protein nmr structure: Comparison of a molecular dynamics simulation with the nmr and x-ray structures of escherichia coli ribonuclease hi. Proteins: Structure, Function, and Bioinformatics. 1999;36:87–110. doi: 10.1002/(sici)1097-0134(19990701)36:1<87::aid-prot8>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- Romero PR, Zaidi S, Fang YY, Uversky VN, Radivojac P, Oldfield CJ, Cortese MS, Sickmeier M, LeGall T, Obradovic Z, et al. Alternative splicing in concert with protein intrinsic disorder enables increased functional diversity in multicellular organisms. Proceedings of the National Academy of Sciences. 2006;103:8390–8395. doi: 10.1073/pnas.0507916103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschul SF, Madden TL, Schäffer AA, Zhang J, Zhang Z, Miller W, Lipman DJ. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucl. Aci. Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrödinger, LLC. The PyMOL molecular graphics system, version 1.8. 2015 [Google Scholar]
- Shapiro JN. Lindemann law and lattice dynamics. Physical Review B. 1970;1:3982. [Google Scholar]
- Siew N, Elofsson A, Rychlewski L, Fischer D. Maxsub: an automated measure for the assessment of protein structure prediction quality. Bioinformatics. 2000;16:776–785. doi: 10.1093/bioinformatics/16.9.776. [DOI] [PubMed] [Google Scholar]
- Timm DE, Baker L, Mueller H, Zidek L, Novotny MV. Structural basis of pheromone binding to mouse major urinary protein (mup-i) Protein Science. 2001;10:997–1004. doi: 10.1110/ps.52201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uversky VN. A decade and a half of protein intrinsic disorder: biology still waits for physics. Protein Science. 2013;22:693–724. doi: 10.1002/pro.2261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varpness Z, Peters J, Young M, Douglas T. Biomimetic synthesis of a h2 catalyst using a protein cage architecture. Nano letters. 2005;5:2306–2309. doi: 10.1021/nl0517619. [DOI] [PubMed] [Google Scholar]
- Vetsch M, Puorger C, Spirig T, Grauschopf U, Weber-Ban EU, Glockshuber R. Pilus chaperones represent a new type of protein-folding catalyst. Nature. 2004;431:329–333. doi: 10.1038/nature02891. [DOI] [PubMed] [Google Scholar]
- Wagner G, Hyberts SG, Havel TF. Nmr structure determination in solution: a critique and comparison with x-ray crystallography. Annual review of biophysics and biomolecular structure. 1992;21:167–198. doi: 10.1146/annurev.bb.21.060192.001123. [DOI] [PubMed] [Google Scholar]
- Ward JJ, Sodhi JS, McGuffin LJ, Buxton BF, Jones DT. Prediction and functional analysis of native disorder in proteins from the three kingdoms of life. Journal of molecular biology. 2004;337:635–645. doi: 10.1016/j.jmb.2004.02.002. [DOI] [PubMed] [Google Scholar]
- Wright PE, Dyson HJ. Intrinsically unstructured proteins: re-assessing the protein structure-function paradigm. Journal of molecular biology. 1999;293:321–331. doi: 10.1006/jmbi.1999.3110. [DOI] [PubMed] [Google Scholar]
- Xu J, Zhang Y. How significant is a protein structure similarity with tm-score=0.5? Bioinformatics. 2010;26:889–895. doi: 10.1093/bioinformatics/btq066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan J, Dunker AK, Uversky VN, Kurgan L. Molecular recognition features (morfs) in three domains of life. Molecular BioSystems. 2016;12:697–710. doi: 10.1039/c5mb00640f. [DOI] [PubMed] [Google Scholar]
- Yang L-W, Eyal E, Chennubhotla C, Jee J, Gronenborn AM, Bahar I. Insights into equilibrium dynamics of proteins from comparison of nmr and x-ray data with computational predictions. Structure. 2007;15:741–749. doi: 10.1016/j.str.2007.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zahn K, Lenke R, Maret G. Two-stage melting of paramagnetic colloidal crystals in two dimensions. Physical review letters. 1999;82:2721. [Google Scholar]
- Zemla A, Venclovas Č, Moult J, Fidelis K. Processing and analysis of casp3 protein structure predictions. Proteins: Structure, Function, and Bioinformatics. 1999;37:22–29. doi: 10.1002/(sici)1097-0134(1999)37:3+<22::aid-prot5>3.3.co;2-n. [DOI] [PubMed] [Google Scholar]
- Zhang T, Faraggi E, Xue B, Dunker AK, Uversky VN, Zhou Y. Spine-d: accurate prediction of short and long disordered regions by a single neural-network based method. Journal of Biomolecular Structure and Dynamics. 2012;29:799–813. doi: 10.1080/073911012010525022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang T, Faraggi E, Zhou Y. Fluctuations of backbone torsion angles obtained from nmr-determined structures and their prediction. Proteins: Structure, Function, and Bioinformatics. 2010;78:3353–3362. doi: 10.1002/prot.22842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Skolnick J. Scoring function for automated assessment of protein structure template quality. Proteins: Structure, Function, and Bioinformatics. 2004;57:702–710. doi: 10.1002/prot.20264. [DOI] [PubMed] [Google Scholar]
- Zhou Y, Vitkup D, Karplus M. Native proteins are surface-molten solids: application of the lindemann criterion for the solid versus liquid state. Journal of molecular biology. 1999;285:1371–1375. doi: 10.1006/jmbi.1998.2374. [DOI] [PubMed] [Google Scholar]