Transfer Function Analysis of Dynamic Blood Flow Control in the Rat Kidney

Abstract

Renal blood flow is regulated by the myogenic response (MR) and tubuloglomerular feedback (TGF). Both mechanisms function to buffer not only steady pressure perturbations but also transient ones. In this study, we develop two models of renal autoregulation—a comprehensive model and a simplified model—and use them to analyze the individual contributions of MR and TGF in buffering transient pressure perturbations. Both models represent a single nephron of a rat kidney together with the associated vasculature. The comprehensive model includes detailed representation of the vascular properties and cellular processes. In contrast, the simplified model represents a minimal set of key processes. To assess the degree to which fluctuations in renal perfusion pressure at different frequencies are attenuated, we derive a transfer function for each model. The transfer functions of both models predict resonance at 45 and 180 mHz, which are associated with TGF and MR, respectively, effective autoregulation below ~100 mHz, and amplification of pressure perturbations above ~200 mHz. The predictions are in good agreement with experimental findings.

1 Introduction

The kidneys not only filter metabolic wastes and toxins from the body, they also regulate the body’s water balance, salt balance, acid-base balance, and blood pressure. One requirement for maintaining normal kidney function is that renal blood flow be kept within a narrow range. When renal blood flow falls outside of that range, so does the fluid flow through the nephrons, which are the main functional units of the kidney. As a result, the ability of the kidney to maintain water, salt, and acid-base balance may be compromised. Nephron fluid flow depends, in large part, on glomerular filtration rate (GFR), which is controlled by several systemic and renal mechanisms (Cupples and Braam 2007; Just 2007; Holstein-Rathlou and Marsh 1994b).

One of the autoregulatory mechanisms is the myogenic response (MR), in which the afferent arteriolar muscles respond to perturbations in intraluminal pressure or stretch with active force development, thereby enabling the arterioles to constrict, reducing renal blood flow and GFR (Cupples and Braam 2007; Just 2007; Holstein-Rathlou and Marsh 1994b). Another contributing mechanism is the tubuloglomerular feedback (TGF), where the nephrons control renal blood flow and GFR by responding to variations in the ionic composition of the loop of Henle outflow (Cupples and Braam 2007; Just 2007; Holstein-Rathlou and Marsh 1994b).

Autoregulatory responses can be classified as steady state or dynamic (Griffin et al. 2004; Bidani et al. 2003). Steady state renal autoregulation, which is the kidney’s ability to buffer time-independent blood pressure perturbations, has been well characterized experimentally (Hayashi et al. 1992; Shipley and Study 1951; Dokkum et al. 1999; Arendshorst 1979; Rothe et al. 1971; Kirchheim et al. 1987) and theoretically (Kleinstreuer et al. 2008; Loutzenhiser et al. 2002; Marsh et al. 2005; Oien and Aukland 1983; Sgouralis and Layton 2012, 2013, 2014, 2015, 2016). For example, our group has recently developed autoregulation models that simulate the actions of MR and TGF on renal blood flow (Sgouralis and Layton 2014, 2016). These models represent detailed ionic transport and muscle mechanics of the afferent arteriole, glomerular filtration, and tubular transport. The models predict that over a wide range of steady perfusion pressures (~80–180 mmHg), the combined actions of MR and TGF yield stable renal blood flow and GFR. That prediction is consistent with experimental findings (Holstein-Rathlou and Marsh 1994b; Cupples and Braam 2007).

Dynamic renal autoregulation is the ability of the kidney to buffer transient pressure perturbations. Dynamic autoregulation is important, because renal perfusion pressure is continuously perturbed by heart beat, breathing, movement, excitement, hormonal, and other systemic factors. Nonetheless, despite substantial experimental efforts, for example Holstein-Rathlou and Marsh (1994b), Just et al. (1998), Just (2007), Just and Arendshorst (2003), Chon et al. (2008), Cupples and Braam (2007), Flemming et al. (2001), Griffin et al. (2004), Wang et al. (2007), Sakai et al. (1986), and He and Marsh (1993), dynamic autoregulation has remained relatively less investigated theoretically.

In vivo experimental studies of dynamic autoregulation typically record renal perfusion pressure and renal blood flow over the same time period. The recorded time series are then transformed to the frequency domain, and the resulting spectra are analyzed using a transfer function (Cupples and Braam 2007; Holstein-Rathlou and Marsh 1994b). One can use the transfer function to compare the power contents of the fluctuations in perfusion pressure and renal blood flow and to determine the extent to which perturbations in perfusion pressure of different frequencies are attenuated. To date, the assessment of the transfer function has been the focus of only three theoretical studies (Loutzenhiser et al. 2002; Holstein-Rathlou et al. 1991; Holstein-Rathlou and Marsh 1994a), all of which evaluate the transfer function numerically rather than analytically.

The goal of this study is to investigate the kidney’s full autoregulatory response to dynamic pressure perturbations using a transfer function. In particular, we aim to: (i) quantify the individual contributions of MR and TGF in stabilizing renal blood flow under transient perturbations, (ii) identify bottleneck processes that limit the autoregulatory efficiency, (iii) assess the impact of an array of physiologic factors on renal autoregulation, such as vascular compliance and spontaneous vasomotion, and (iv) provide an explicit form of the transfer function that could be used in future studies. Additionally, we aim to assess the feasibility of constructing a control system with the characteristics of renal autoregulation, i.e., having a feedback system such as TGF and a feedforward system such as MR coupled to an autonomous oscillator, that yields transfer function responses similar to those obtained on the rat kidney.

To achieve these goals, we conduct simulations using two mathematical models of renal autoregulation. Both models represent a single superficial nephron of a rat kidney together with its associated vasculature, but with different levels of complexity: One is a comprehensive model adopted from our recent study of renal autoregulation (Sgouralis and Layton 2014), and the other is a simplified model that allows an asymptotic evaluation of the transfer function. By comparing the predictions of the two models, we also determine the extent to which the simplified model can reproduce the characteristics of dynamic autoregulation predicted by the comprehensive model.

2 Mathematical Model

We have developed two models of renal hemodynamics to study the kidney’s autoregulatory response. Both models are formulated for a single superficial nephron and predict blood flow through the associated afferent arteriole.

The first model, which we refer to as the full model, is based on a comprehensive model recently developed by Sgouralis and Layton (2014). The full model includes a detailed representation of the autoregulatory processes and captures essential nephron functions in a rat kidney (see below). Solutions to model equations are obtained numerically.

The second model, which we refer to as the simplified model, includes a minimal set of autoregulatory elements necessary to reproduce key experimental observations in the rat kidney. The simplified model is essentially a linearized form of the full model. Solutions to the simplified model are obtained asymptotically, and explicit formulas are provided to leading-order approximations.

We analyze the autoregulatory response of both models to transient pressure perturbations by means of a transfer function. A transfer function H(f) of a system is given by the ratio between an input signal ϕ(t) and an output signal ψ(t) in the frequency domain:

$$H\left(f\right)=\frac{\mathcal{F}\psi \left(t\right)}{\mathcal{F}\varphi \left(t\right)},$$ (1)

In Eq. (1), $\mathcal{F}$ denotes the Fourier transform. For renal hemodynamics, the input signal ϕ(t) and the output signal ψ(t) are typically chosen to be renal perfusion pressure and renal blood flow, respectively (Cupples and Braam 2007; Holstein-Rathlou and Marsh 1994b). Attenuation is measured by the admittance gain which is given by |H(f)| (Holstein-Rathlou and Marsh 1994b).

2.1 Full Model

The full model represents a superficial nephrovascular unit which includes an afferent arteriole, a glomerulus, a proximal tubule, and a short loop of Henle. A schematic diagram is shown in Fig. 1. The representation of the model components is based on our previous work (Sgouralis and Layton 2012, 2013, 2014).

Fig. 1.

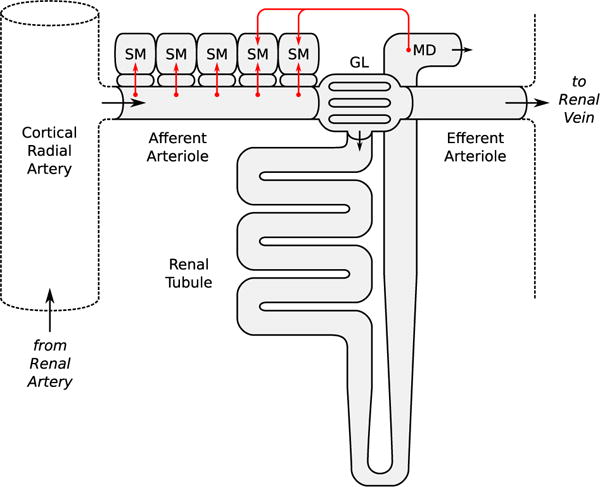
Schematic diagram of the nephrovascular unit represented in the full model. Arrows indicate fluid flow direction and sensor/effector sites of the autoregulatory mechanisms. SM smooth muscle layer, GL glomerulus, MD macula densa (Color figure online)

The model afferent arteriole consists of a series of smooth muscle cell models (Sgouralis and Layton 2012, 2013, 2014), electrically coupled via gap junctions and via an endothelial layer. The ionic transport dynamics of each smooth muscle cell, influenced by the autoregulatory mechanisms, determine the local vascular tone. The resulting vascular resistance is the main determinant of blood flow and single-nephron glomerular filtration rate (SNGFR).

Each smooth muscle model incorporates cell membrane potential, transmembrane ionic transport, cytosolic Ca²⁺ regulation, and muscle contraction. The interactions between the Ca²⁺ and K⁺ fluxes, which are mediated by voltage-gated and voltage-calcium-gated channels, respectively, give rise to the development of spontaneous oscillations in membrane potential. This in turn results in oscillations in cytoplasmic [Ca²⁺] and muscle tone.

2.1.1 Membrane Potential

The afferent arteriole extends from the cortical radial artery (z = 0) to the glomerulus (z = L_AA). The afferent arteriolar wall is composed of an endothelial layer, which is surrounded by a layer of smooth muscle cells, as shown in Fig. 1. The rates of change of the membrane potentials of the smooth muscle and endothelial compartments, denoted v_m(t, z) and v_e(t, z), respectively, are given by:

$$C_{\mathrm{m}}\frac{\mathrm{d}}{\mathrm{d}t}{v}_{\mathrm{m}}\left(t,z\right)=-I_{\mathrm{L}}\left(t,z\right)-I_{\mathrm{K}}\left(t,z\right)-I_{\text{Ca}}\left(t,z\right)+I_{\text{mm}}\left(t,z\right)+I_{\text{me}}\left(t,z\right)+I_{\text{MR}}\left(t,z\right)+I_{\text{TGF}}\left(t,z\right),$$ (2)

$$C_{\mathrm{e}}\frac{\mathrm{d}}{\mathrm{d}t}{v}_{\mathrm{e}}\left(t,z\right)=-I_{\text{me}}\left(t,z\right)+I_{\text{ee}}\left(t,z\right),$$ (3)

where C_m and C_e denote cellular capacitances; I_L(t, z), I_K(t, z), and I_Ca(t, z) denote transmembrane leak current, potassium current, and calcium current, respectively; I_mm(t, z), I_me(t, z), and I_ee(t, z) are gap-junctional currents; and I_MR(t, z) and I_TGF(t, z) are MR- and TGF-induced currents (see below). The transmembrane currents are given by:

$$I_{\mathrm{L}}\left(t,z\right)=g_{\mathrm{L}}\left(v_{\mathrm{m}}\left(t,z\right)-v_{\mathrm{L}}\right),$$ (4)

$$I_{\mathrm{K}}\left(t,z\right)=g_{\mathrm{K}}n\left(t,z\right)\left(v_{\mathrm{m}}\left(t,z\right)-v_{\mathrm{K}}\right),$$ (5)

$$I_{\text{Ca}}\left(t,z\right)=g_{\text{Ca}}m\left(t,z\right)\left(v_{\mathrm{m}}\left(t,z\right)-v_{\text{Ca}}\right),$$ (6)

where n(t, z) and m(t, z) denote the fraction of open K⁺ and Ca²⁺ channels, respectively. The model assumes that n(t, z) depends on v_m(t, z) and cytosolic [Ca²⁺], whereas m(t, z) depends only on v_m(t, z). For details see Chen et al. (2011) and Sgouralis and Layton (2014).

Neighboring cells communicate via gap junctions (Brink 1998). We consider gap-junctional currents passing between smooth muscles, denoted I_mm(t, z), between smooth muscles and the endothelium, denoted I_me(t, z), and between endothelial cells, denoted I_ee(t, z). The gap-junctional currents in Eqs. (2) and (3) are given by:

$$I_{\text{me}}\left(t,z\right)=g_{\text{me}}\left(v_{\mathrm{e}}\left(t,z\right)-v_{\mathrm{m}}\left(t,z\right)\right),$$ (7)

$$I_{\text{mm}}\left(t,z\right)=g_{\text{mm}}\frac{{\partial }^2{v}_{\mathrm{m}}\left(t,z\right)}{\partial z^2},$$ (8)

$$I_{\text{ee}}\left(t,z\right)=g_{\text{ee}}\frac{{\partial }^2{v}_{\mathrm{e}}\left(t,z\right)}{\partial z^2}.$$ (9)

where g_mm, g_me, g_ee denote the corresponding conductances. Details can be found in Sgouralis and Layton (2012, 2013, 2014).

Myogenic response

We assume that the activity of non-selective cation channels of the smooth muscle membrane responds to changes in intravascular pressure, such that elevations in local intravascular pressure depolarize the surrounding smooth muscles. To induce pressure-dependent changes in membrane potential, we apply a current I_MR(t, z) in Eq. (2), which is described by:

$$\frac{\mathrm{d}}{\mathrm{d}t}{I}_{\text{MR}}\left(t,z\right)=k_{\text{MR}}\left(I_{\text{MR}}^{\ast }\left(P\left(t,z\right),z\right)-I_{\text{MR}}\left(t,z\right)\right),$$ (10)

where P(t, z) denotes local intravascular pressure and k_MR is a rate constant. To represent a depolarizing current at elevated blood pressure, we assume that the target current $I_{\text{MR}}^{\ast }\left(P,z\right)$ is an increasing function of luminal pressure having the saturable form:

$$I_{\text{MR}}^{\ast }\left(P,z\right)=I_{\text{MR}}^{min}+\frac{I_{\text{MR}}^{max}-I_{\text{MR}}^{min}}{1-\left(\frac{I_{\text{MR}}^{max}}{I_{\text{MR}}^{min}}\right)\exp \left(-s_{\text{MR}}\left(P-P\ast \left(z\right)\right)\right)}.$$ (11)

The parameters $I_{\text{MR}}^{max}$, $I_{\text{MR}}^{min}$, and s_MR determine the dynamic range and sensitivity of MR (Sgouralis and Layton 2014). The reference pressure profile P*(z) is chosen such that at baseline perfusion pressure $I_{\text{MR}}^{\ast }\left(P\left(z\right),z\right)$ is zero.

Tubuloglomerular feedback

The TGF current is similarly given by:

$$\frac{\mathrm{d}}{\mathrm{d}t}{I}_{\text{TGF}}\left(t,z\right)=k_{\text{TGF}}\left(I_{\text{TGF}}^{\ast }\left(C_{\text{MD}}\left(t\right),z\right)-I_{\text{TGF}}\left(t,z\right)\right).$$ (12)

where k_TGF is a rate constant. The target current $I_{\text{TGF}}^{\ast }\left(C_{\text{MD}},z\right)$, which is applied to the smooth muscles spanning only the distal L_TGF of the afferent arteriole, exhibits a sigmoidal dependence on intratubular macula densa [Cl⁻] (denoted C_MD(t)),

$$I_{\text{TGF}}^{\ast }\left(C_{\text{MD}},z\right)=\{\begin{array}{ll}0,\hfill & 0\le z<L_{AA}-L_{\text{TGF}},\hfill \\ I_{\text{TGF}}^{min}+\frac{I_{\text{TGF}}^{max}-I_{\text{TGF}}^{min}}{1-\left(\frac{I_{\text{TGF}}^{max}}{I_{\text{TGF}}^{min}}\right)\exp \left(-s_{\text{TGF}}\left(C_{\text{MD}}^{\ast }-C_{\text{MD}}\right)\right)},\hfill & L_{\text{AA}}-L_{\text{TGF}}\le z\le L_{\text{AA}}\hfill \end{array},$$ (13)

where $C_{\text{MD}}^{\ast }$ denotes the operating macula densa [Cl⁻], set to 32 mM (Layton et al. 1991). The parameters $I_{\text{TGF}}^{max}$, $I_{\text{TGF}}^{min}$, and s_TGF determine the dynamic range and open-loop gain of TGF; for details see Sgouralis and Layton (2014).

2.1.2 Smooth Muscle Contractile Mechanism

Cytosolic [Ca²⁺], denoted c(t, z), is assumed in equilibrium with the buffer B_T and is related to influx though the membrane channels I_Ca(t, z) by:

$$\frac{\mathrm{d}}{\mathrm{d}t}c\left(t,z\right)=\frac{{\left(K_d+c\left(t,z\right)\right)}^2}{{\left(K_d+c\left(t,z\right)\right)}^2+K_d{B}_{\mathrm{T}}}\left(-{\alpha }_{\text{Ca}}{I}_{\text{Ca}}\left(t,z\right)-k_{\text{Ca}}c\left(t,z\right)\right),$$ (14)

where the constant α_Ca relates Ca²⁺ influx to changes in cytosolic [Ca²⁺], and k_Ca characterizes calcium extrusion from the cytosol (Chen et al. 2011). Cytosolic [Ca²⁺] determines the phosphorylation level ψ(t, z) according to:

$$\psi \left(t,z\right)=\frac{{\left(c\left(t,z\right)\right)}^3}{c_{\mathrm{M}}^3+{\left(c\left(t,z\right)\right)}^3},$$ (15)

which in turn determines the fraction of formed crossbridges, denoted ω(t, z), according to:

$$\frac{\mathrm{d}}{\mathrm{d}t}\omega \left(t,z\right)=k_{\psi }\left(\frac{\psi \left(t,z\right)}{\psi \left(t,z\right)+{\psi }_{\mathrm{M}}}-\omega \left(t,z\right)\right).$$ (16)

Vasomotion is driven by the balance between Laplace tension T_P(t, z), which is influenced by local blood pressure, and local vascular tone T_wall(t, z), which is influenced by the smooth muscles. The Laplace tension is given by:

$$T_{\mathrm{P}}\left(t,z\right)=\left(P\left(t,z\right)-P_{\text{ext}}\right)R_{\text{AA}}\left(t,z\right),$$ (17)

where P_ext denotes the extravascular pressure. The vascular tone consists of a passive T_pass(t, z) and an active component T_act(t, z). The active component generates the stress:

$$T_{\text{act}}\left(t,z\right)=\omega \left(t,z\right)T_{\text{act}}^{max}\left(t,z\right),$$ (18)

where $T_{\text{act}}^{max}\left(t,z\right)$ is the maximum active tension that can be generated at a given vessel circumference (see below) and the muscle activation level is taken equal to the fraction of formed crossbridges ω(t, z).

For a given luminal radius R_AA(t, z), the following wall tensions are developed:

$$T_{\text{pass}}\left(t,z\right)=C_{\text{pass}}^0\exp \left(C_{\text{pass}}^1\left(\frac{R_{\text{AA}}\left(t,z\right)}{R_{\text{AA}}^c}-1\right)\right)+C_{\text{pass}}^2,$$ (19)

$$T_{\text{act}}^{max}\left(t,z\right)=C_{\text{act}}^0\exp \left(-{\left(\frac{R_{\text{AA}}\left(t,z\right)/R_{\text{AA}}^c-C_{\text{act}}^1}{C_{\text{act}}^2}\right)}^2\right).$$ (20)

The difference between T_P(t, z) and T_wall(t, z) drives the changes in vascular radius R_AA(t, z) according to:

$$\frac{\mathrm{d}}{\mathrm{d}t}{R}_{\text{AA}}\left(t,z\right)=\frac{1}{{\tau }_c}\left(T_{\mathrm{P}}\left(t,z\right)-\xi \left(z\right)T_{\text{wall}}\left(t,z\right)\right).$$ (21)

Because the pressure P(t, z) decreases along the vessel, baseline T_P(t, z) also decreases axially. To achieve an approximately uniform baseline radius, a factor ξ(z), which decreases linearly along the vessel, is included in Eq. (21) to scale the wall tension accordingly.

2.1.3 Vascular Blood Flow

We assume that the blood pressure at the entrance of the cortical radial artery (Fig. 1), which is referred to as the renal perfusion pressure P_RA(t), is known a priori. The cortical radial artery is modeled as a fixed resistor Ω_RA. Thus, the pressure at the afferent arteriole’s inlet is given by:

$$P\left(t,0\right)=P_{\text{RA}}\left(t\right)-Q\left(t\right){\Omega }_{\text{RA}},$$ (22)

where Q(t) denotes the blood flow. The value of Ω_RA is chosen such that at baseline it accounts for a pressure drop of 5 mmHg (Sgouralis and Layton 2014).

Arteriolar blood flow is approximated by Poiseuille flow. Thus, the pressure gradient along the afferent arteriole lumen is given by:

$$\frac{\partial P\left(t,z\right)}{\partial z}=-\frac{8\mu }{\pi {\left(R_{\text{AA}}\left(t,z\right)\right)}^4}Q\left(t\right),0<z<L_{\text{AA}},$$ (23)

where μ denotes the apparent blood viscosity. This implies that arteriolar blood flow Q(t) can be computed, given the pressure drop along the vessel and the vascular resistance Ω_AA(t), by:

$$Q\left(t\right)=\frac{P\left(t,0\right)-P\left(t,L_{\text{AA}}\right)}{{\Omega }_{\text{AA}}\left(t\right)}.$$ (24)

The overall arteriolar resistance is computed from the radius profile:

$${\Omega }_{\text{AA}}\left(t\right)=\frac{8\mu }{\pi }{\displaystyle {\int }_0^{L_{\text{AA}}}\frac{dz}{R_{\text{AA}}{\left(t,z\right)}^4}.}$$ (25)

We assume that the model afferent arteriole is connected in series to a post-glomerular resistor Ω_EA(t), with outlet pressure similar to the pressure in the renal vein P_v. Post-glomerular blood flow is given by the difference between arteriolar flow Q(t) and SNGFR (denoted Q_F(t)) and is related to pressure drop and vascular resistance according to the Poisuille law:

$$Q\left(t\right)-Q_{\mathrm{F}}\left(t\right)=\frac{P_{\text{GL}}\left(t,L_{\text{GL}}\right)-P_v}{{\Omega }_{\text{EA}}\left(t\right)}.$$ (26)

In Eq. (26), P_GL(t, L_GL) is the blood pressure at the end of the glomerular capillary network (see below). Efferent arteriole resistance Ω_EA(t) changes passively with blood pressure; for details see Sgouralis and Layton (2014).

2.1.4 Glomerular Filtration

SNGFR is determined by considering the filtration process through the model glomerulus, which is represented as a single capillary of equivalent surface area that extends from y = 0 to y = L_GL. The two end points correspond to the connections with the afferent and efferent arterioles, respectively. Let Q_GL(t, y) and C_GL(t, y) denote the plasma flow and plasma protein concentration, respectively. Conservation of plasma mass is given by:

$$\frac{\partial Q_{\text{GL}}\left(t,y\right)}{\partial y}=-K_f\left(P_{\text{GL}}\left(t,y\right)-P_{\mathrm{F}}\left(t\right)-\pi \left(t,y\right)\right),$$ (27)

where K_f is the ultrafiltration coefficient. Blood pressure P_GL(t, y) is assumed to decrease linearly along the capillary, i.e.,

$$P_{\text{GL}}\left(t,y\right)=P\left(t,L_{\text{AA}}\right)-y\frac{\mathrm{\Delta }{P}_{\text{GL}}}{L_{\text{GL}}},$$ (28)

where ΔP_GL is a constant. P_F(t) denotes the pressure in the Bowman space which is assumed equal to the proximal tubule inflow pressure; for details see Sgouralis and Layton (2014). The colloid osmotic pressure π(t, y) depends on local protein concentration C_GL(t, y) according to the empirical relation:

$$\pi \left(t,y\right)={\alpha }_{\text{GL}1}{C}_{\text{GL}}\left(t,y\right)+{\alpha }_{\text{GL}2}{C}_{\text{GL}}^2\left(t,y\right).$$ (29)

The glomerular capillaries are impermeable to protein, so C_GL(t, y)Q_GL(t, y) = C_GL(t, 0)Q_GL(t, 0), which together with Eq. (27) results in:

$$\frac{\partial C_{\text{GL}}\left(t,y\right)}{\partial y}=\frac{K_f}{Q_{\text{GL}}\left(t,0\right)}\frac{C_{\text{GL}}^2\left(t,0\right)}{C_{\text{GL}}\left(t,0\right)}\left(P_{\text{GL}}\left(t,y\right)-P_{\mathrm{F}}\left(t\right)-\pi \left(t,y\right)\right).$$ (30)

Plasma protein concentration entering the glomerulus C_GL(t, 0) is assumed fixed at 5.5 g/dl. Plasma enters at a rate determined by hematocrit Ht and arteriolar blood flow:

$$Q_{\text{GL}}\left(t,0\right)=\left(1-Ht\right)Q\left(t\right).$$ (31)

By integrating Eq. (30) over the model glomerulus, one obtains C_GL(t, L_GL), which is used to compute Q_GL(t, L_GL) from the conservation of plasma mass. SNGFR is given by:

$$Q_{\mathrm{F}}\left(t\right)=Q_{\text{GL}}\left(t,0\right)-Q_{\text{GL}}\left(t,L_{\text{GL}}\right).$$ (32)

2.1.5 Tubular Transport

The model renal tubule represents a proximal tubule connected to a short loop of Henle; see Fig. 1. Model equations, which describe intratubular pressure, water flow, and intratubular [Cl⁻], can be found in Sgouralis and Layton (2014).

2.1.6 Transfer Function

The transfer function for the full model uses the following input and output signals:

$$\varphi \left(t\right)=\frac{P_{\text{RA}}\left(t\right)-P_{\text{RA}}^{\text{ref}}}{P_{\text{RA}}^{\text{ref}}},$$ (33)

$$\psi \left(t\right)=\frac{Q\left(t\right)-Q^{\text{ref}}}{Q^{\text{ref}}}$$ (34)

where $P_{\text{RA}}^{\text{ref}}$ and Q^ref denote the time averages of renal perfusion pressure and blood flow, respectively.

The model equations are discretized over a 1-h time interval using a step of Δt = 0.01 s. Renal perfusion pressure P_RA(t_n) at the discrete time levels:

$$t_n=n\mathrm{\Delta }t,n=0,\dots ,36\times {10}^4$$ (35)

is obtained as follows. Initially, Gaussian white noise of unit variance θ_n is generated in the time domain. Subsequently, by an application of the fast Fourier transform, θ_n is transformed to the frequency domain Θ_n. The power contained in Θ_n is distributed equally among all frequencies, indicating that θ_n contains fluctuations of significant amplitude even at arbitrarily high frequencies. To avoid large errors arising from the numerical scheme that is used for the time stepping of the model equations, we remove from Θ_n the power above 1 Hz. This results in significant smoothing in the time domain without affecting the power content at the frequencies of interest in this study (i.e., below 1 Hz). Finally, the resulting spectrum ${\stackrel{\sim }{\Theta }}_n$ is transformed back to the time domain ${\stackrel{\sim }{\theta }}_n$. A realization of the signals θ_n and ${\stackrel{\sim }{\theta }}_n$, in the time and frequency domains, is shown in Fig. 2a1, a2.

Fig. 2.

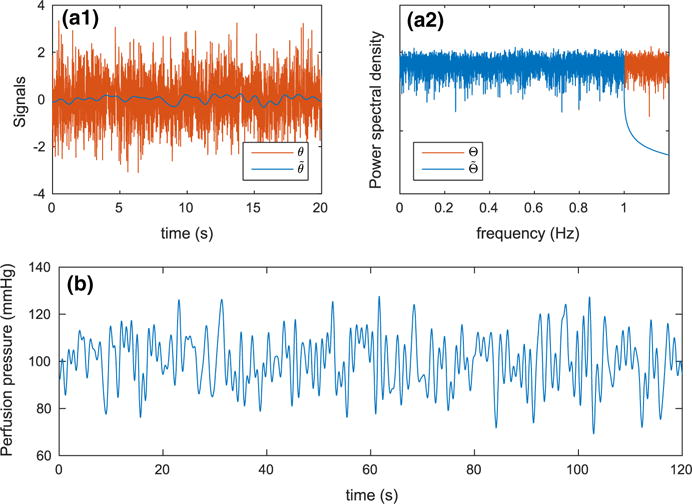
A realization of the signals used in the evaluation of renal perfusion pressure P_RA(t_n). a1 White noise before the removal of high-frequency fluctuations θ_n and after ${\stackrel{\sim }{\theta }}_n$. a2 Power spectral densities of θ_n and ${\stackrel{\sim }{\theta }}_n$. b Corresponding renal perfusion pressure. Note that the removal of power above 1 Hz (a2) results in substantial smoothing in the time domain (a1) (Color figure online)

At time level t_n, renal perfusion pressure is given by:

$$P_{\text{RA}}\left(t_n\right)=P_{\text{RA}}^{\text{ref}}+P_{\mathrm{p}}\frac{{\stackrel{\sim }{\theta }}_n}{\stackrel{\sim }{\sigma }},$$ (36)

where $P_{\text{RA}}^{\text{ref}}=100$ mmHg, P_p = 10 mmHg, and $\stackrel{\sim }{\sigma }$ is the standard deviation of ${\stackrel{\sim }{\theta }}_n$. A typical time course of renal perfusion pressure is shown in Fig. 2b.

For a given realization of the initial signal θ_n, a transfer function H_θ(f_n) is calculated by the ratio:

$$H_{\theta }\left(f_n\right)=\frac{S_{\varphi \psi }\left(f_n\right)}{S_{\varphi \varphi }\left(f_n\right)},$$ (37)

where S_ϕϕ(f_n) is the autospectrum of ϕ(t_n) and S_ϕψ(f_n) is the cross-spectrum of ϕ(t_n) and ψ(t_n). The transfer function H_θ(f_n) is estimated using Welch’s method (Welch 1967), in which the time series of ϕ(t_n) and ψ(t_n) are subdivided into 6-min segments with 50% overlap. This results in ten segments of data to which the Hanning window is applied. Fast Fourier transforms are implemented on the windowed segments and averaged to calculate the auto- and cross-spectra. This procedure is repeated for 32 realizations of θ_n, and an overall transfer function H(f_n) is taken by the average of the H_θ(f_n)’s.

2.2 Simplified Model

The simplified model consists of two components: (i) a hemodynamic component that describes arteriolar blood flow and glomerular filtration and (ii) a vascular resistance component that describes the contractile mechanism of the vascular wall and the activation of the autoregulatory mechanisms. This model is essentially a linear approximation of the full model described in the previous section. The approximation is valid in the limit of infinitesimal perturbations in renal perfusion pressure and vascular resistance. A schematic diagram is shown in Fig. 3.

Fig. 3.

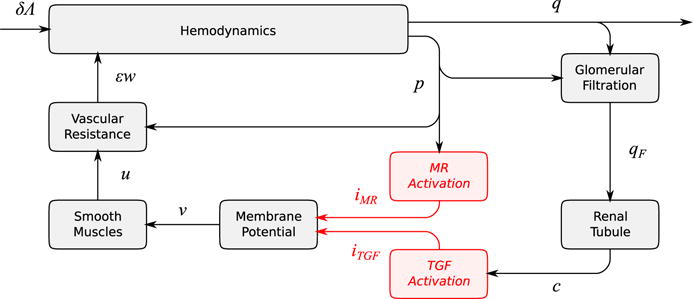
Schematic diagram of the nephrovascular unit represented in the simplified model. Perturbations from the reference state: δΛ, perfusion pressure; q, blood flow; p, blood pressure; q_F, SNGFR; c, macula densa [Cl⁻]; v, smooth muscle membrane potential; u, smooth muscle activation; εw, vascular resistance. Currents mediating the myogenic response and tubuloglomerular feedback are denoted by i_MR and i_TGF, respectively (Color figure online)

2.2.1 Hemodynamics

Model perfusion pressure, denoted by P_RA(t), consists of a time-independent component $P_{\text{RA}}^{\text{ref}}$ and a time-varying perturbation:

$$P_{\text{RA}}\left(t\right)=P_{\text{RA}}^{\text{ref}}+\delta \Lambda \left(t\right),$$ (38)

where δ is a non-dimensional parameter and Λ(t) has dimensions of pressure. It is assumed that δ ≪ 1 and Λ(t) = O(1).

Let P(t, z), Q(t), and r(t, z) denote blood pressure, blood flow, and vascular resistance per length along the afferent arteriole. As in the full model, we describe blood flow by Poisuille’s equation using the following boundary value problem:

$$\frac{\partial P\left(t,z\right)}{\partial z}=-Q\left(t\right)r\left(t,z\right),0<z<L_{\text{AA}},$$ (39)

$$P\left(t,0\right)=P_{\text{RA}}\left(t\right),P\left(t,L_{\text{AA}}\right)=P_D\left(t\right),$$ (40)

where L_AA is the length of the afferent arteriole and P_D(t) is glomerular capillary pressure. We assume that the pressure drop is negligible along the cortical radial artery and along the glomerular capillaries. Thus, P_D(t) is equal to both the afferent arteriole outlet and the efferent arteriole inlet pressures. If one assumes Poisuille flow along the efferent arteriole, then:

$$P_D\left(t\right)=P_v+\left(Q\left(t\right)-Q_F\left(t\right)\right)R_{\text{EA}}\left(t\right),$$ (41)

where P_v is the venous pressure which is assumed constant and Q_F (t) denotes SNGFR. Efferent arteriolar resistance, denoted R_EA(t), changes passively with blood pressure, according to:

$$R_{\text{EA}}\left(t\right)=R_{\text{EA}}^{\text{ref}}-s_{\text{EA}}\left(P_D\left(t\right)-P_D^{\text{ref}}\right),$$ (42)

where s_EA > 0 is a constant that characterizes the compliance of efferent arteriole, and $P_D^{\text{ref}}$ and $R_{\text{EA}}^{\text{ref}}$ denote reference values for P_D(t) and R_EA(t), respectively. SNGFR depends on glomerular capillary pressure and blood flow, i.e.,

$$Q_F\left(t\right)=g\left(P_D\left(t\right),Q\left(t\right)\right),$$ (43)

for some function g(P, Q) that approximates plasma conservation in the glomerular capillaries [e.g., Eqs. (27) and (32) of the full model].

Given r(t, z), Eqs. (39)–(43) form a closed system that allows the evaluation of P(t, z) and Q(t). Assuming sufficiently small deviations from the baseline resistance, r(t, z) can be written as:

$$r\left(t,z\right)=r^{\text{ref}}\left(z\right)+\epsilon w\left(t,z\right),$$ (44)

where ε ≪ 1 and w(t, z) = O(1). The evaluation of ε w(t, z) is described in the next section.

The reference state is chosen to be the unperturbed system, which corresponds to δ = 0 and ε = 0 (Eqs. 38, 44). Let q(t), p(t, z), and q_F(t) denote the deviations of blood flow Q(t), pressure P(t, z), and SNGFR Q_F (t) from their respective baseline values. Linearizing the system of Eqs. (39)–(44) around the reference state, and solving the resulting leading-order system, we obtain the following approximations:

$$q\left(t\right)=B_1\delta \Lambda \left(t\right)-B_1{Q}^{\text{ref}}{\displaystyle {\int }_0^{L_{\text{AA}}}\epsilon w\left(t,x\right)\mathrm{d}x}+O\left({\delta }^2\right)+O\left(\delta \epsilon \right)+O\left({\epsilon }^2\right),$$ (45)

$$p\left(t,z\right)=\left(1-B_1{\displaystyle {\int }_0^z{r}^{\text{ref}}}\left(x\right)\mathrm{d}x\right)\delta \Lambda \left(t\right)-Q^{\text{ref}}{\displaystyle {\int }_0^z\epsilon w\left(t,x\right)\mathrm{d}}x+B_1{Q}^{\text{ref}}{\displaystyle {\int }_0^z{r}^{\text{ref}}\left(x\right)}\mathrm{d}x{\displaystyle {\int }_0^{L_{\text{AA}}}\epsilon w\left(t,x\right)\mathrm{d}x+O\left({\delta }^2\right)}+O\left(\delta \epsilon \right)+O\left({\epsilon }^2\right),$$ (46)

$$q_F\left(t\right)=B_2\delta \Lambda \left(t\right)-B_2{Q}^{\text{ref}}{\displaystyle {\int }_0^{L_{\text{AA}}}\epsilon w\left(t,x\right)}\mathrm{d}x+O\left({\delta }^2\right)+O\left(\epsilon \delta \right)+O\left({\epsilon }^2\right).$$ (47)

These approximations are valid up to leading orders with respect to δ and ε perturbations. Detailed derivation and the definitions of B₁ and B₂ can be found in the SUPPLEMENT.

2.2.2 Vascular Resistance

The afferent arteriole resistance perturbation ε w(t, z) consists of an active component and a passive component. The active component is a linear function of smooth muscle activation perturbation u(t, z). The passive component is assumed to be a linear function of pressure perturbations p(t, z). Thus,

$$\epsilon w\left(t,z\right)=s_{\mathrm{M}}u\left(t,z\right)-s_{AA}p\left(t,z\right),$$ (48)

where s_M > 0 characterizes the sensitivity of vascular resistance to muscle activation and s_AA > 0 characterizes the compliance of the afferent arteriole. Muscle activation perturbation u(t, z) is described by the first-order kinetics:

$$\frac{\partial u\left(t,z\right)}{\partial t}=k_{\mathrm{m}}\left(s_{m}v\left(t,z\right)-u\left(t,z\right)\right),$$ (49)

where the target activation s_mv(t, z) is a linear function of membrane potential perturbation v(t, z). The constant s_m > 0 characterizes the sensitivity of muscle activation to membrane potential.

Afferent arteriole smooth muscle membrane potential is known to oscillate spontaneously (Cupples and Braam 2007; Holstein-Rathlou and Marsh 1994b). To model the spontaneous oscillations, we describe the kinetics of v(t, z) by a driven linear oscillator:

$$\frac{{\partial }^{2}v\left(t,z\right)}{\partial t^2}+{\eta }_{\mathrm{s}}\frac{\partial v\left(t,z\right)}{\partial t}=k_{\mathrm{s}}\left(\lambda \frac{{\partial }^{2}v\left(t,z\right)}{\partial z^2}+i_{\text{MR}}\left(t,z\right)+i_{\text{TGF}}\left(t,z\right)-v\left(t,z\right)\right).$$ (50)

The driving force is given by gap-junctional coupling characterized by conductance λ and the currents i_MR(t, z) and i_TGF(t, z), which are mediated by the autoregulatory mechanisms (see below). We assume zero fluxes across the end points of the model vessel; thus, the boundary conditions for Eq. (50) are:

$$\frac{\partial v\left(t,0\right)}{\partial z}=0,\frac{\partial v\left(t,L_{\text{AA}}\right)}{\partial z}=0.$$ (51)

Myogenic response activation

Pressure perturbation p(t, z) induces a transmembrane current i_MR(t, z) that follows the first-order kinetics:

$$\frac{\partial i_{\text{MR}}\left(t,z\right)}{\partial t}=k_{\text{MR}}\left(i_{\text{MR}}^{\ast }\left(t,z\right)-i_{\text{MR}}\left(t,z\right)\right),$$ (52)

with the target current given by:

$$i_{\text{MR}}^{\ast }\left(t,z\right)=s_{\text{MR}}p\left(t,z\right),$$ (53)

where s_MR > 0 characterizes the sensitivity of membrane potential to pressure perturbations. Pressure elevations induce a depolarizing current that, taken in isolation, raises membrane potential v(t, z) (Eq. 50) and muscle tone u(t, z) (Eq. 49) and consequently increases arteriolar resistance ε w (t, z) (Eq. 48). Pressure drops induce polarization and reduce arteriolar resistance.

Tubuloglomerular feedback activation

Let c(t) denote the perturbation of macula densa [Cl⁻] from its reference value. Tubuloglomerular feedback is mediated by the current i_TGF(t, z), which follows the first-order kinetics:

$$\frac{\partial i_{\text{TGF}}\left(t,z\right)}{\partial t}=s_{\text{TGF}}\left(i_{\text{TGF}}^{\ast }\left(t,z\right)-i_{\text{TGF}}\left(t,z\right)\right),$$ (54)

with the target current given by:

$$i_{\text{TGF}}^{\ast }\left(t,z\right)=\{\begin{array}{ll}0,\hfill & 0\le z<L_{\text{AA}}-L_{\text{TGF}}\hfill \\ s_{\text{TGF}}c\left(t\right),\hfill & L_{\text{AA}}-L_{\text{TGF}}\le z\le L_{\text{AA}},\hfill \end{array}$$ (55)

where s_TGF > 0 characterizes the sensitivity of the afferent arteriole’s distal segment to c(t). Elevations in macula densa [Cl⁻] lead to depolarization of the afferent arteriole, thereby increasing vascular resistance. Drops in macula densa [Cl⁻] induce polarization and reduce arteriolar resistance.

Note that even though the TGF current is applied only to the distal segment of the afferent arteriole, the TGF signal is expected to spread along the arteriole due to the coupling term λv_zz in Eq. (50).

2.2.3 Transfer Function

Equations (48)–(55) describe the model resistance in the time domain. To facilitate the evaluation of the transfer function, we reformulate those equations in the frequency domain. We begin by considering the frequency responses corresponding to Eqs. (49), (50), (52), and (54):

$$h_{\mathrm{m}}\left(f\right)=\frac{k_{\mathrm{m}}}{2\pi if+k_{\mathrm{m}}},$$ (56)

$$h_{\mathrm{s}}\left(f\right)=\frac{k_{\mathrm{s}}}{-4{\pi }^2{f}^2+2\pi if{\eta }_{\mathrm{s}}+k_{\mathrm{s}}},$$ (57)

$$h_{\text{MR}}\left(f\right)=\frac{k_{\text{MR}}}{2\pi if+k_{\text{MR}}},$$ (58)

$$h_{\text{TGF}}\left(f\right)=\frac{k_{\text{TGF}}}{2\pi if+k_{\text{TGF}}},$$ (59)

where f denotes frequency and $i=\sqrt{-1}$. The time-to-frequency transformation that yields the above frequency responses can be found in the supplement.

To close the TGF loop, one must link the SNGFR perturbations q_F(t) with the macula densa [Cl⁻] perturbations c(t). To accomplish that, we assume the following relationship in the frequency domain:

$$\mathcal{F}c\left(t\right)=s_{\text{TB}}{h}_{\text{TB}}\left(f\right){\mathcal{F}}_{q_F}\left(t\right),$$ (60)

where s_TB > 0 is a constant characterizing the dependence of macula densa [Cl⁻] to SNGFR and h_TB(f) is the frequency response of the tubular segment. We assume:

$$h_{\text{TB}}\left(f\right)=e^{-55i\left(f+f^2\right)}\left(1+0.90\left(e^{-2\left(f+275f^2\right)}-1\right)\right),$$ (61)

where f is in Hz. Equation (61) approximates the frequency response of the tubular component of the full model. For the identification of the frequency response of the tubular component of the full model, we use Welch’s method (Welch 1967) over time series of SNGFR (prescribed) and macula densa [Cl⁻] (predicted), as described in Sect. 2.1.6.

Figure 4 shows the frequency response h_TB(f) used in the simplified model, i.e., Eq. (61), and the frequency response of the tubular segment of the full model. It is well established that the renal tubule acts as a low-pass filter between SNGFR and macula densa [Cl⁻] perturbations with a cutoff frequency above 100 mHz (Cupples and Braam 2007; Holstein-Rathlou and Marsh 1994b; Young and Marsh 1981; Sakai et al. 1986; Layton et al. 1997), a characteristic that Eq. (61) reproduces sufficiently well.

Fig. 4.

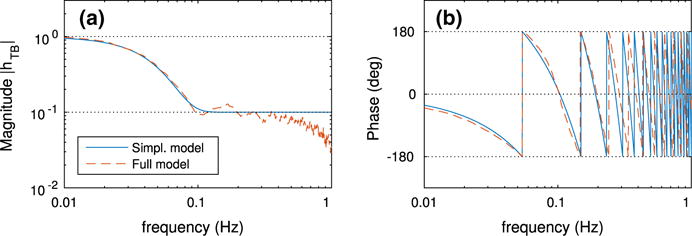
Frequency response of the renal tubule h_TB(f) for the simplified and full models (Color figure online)

To evaluate the transfer function, we use the following input and output signals:

$$\varphi \left(t\right)=\frac{P_{\text{RA}}\left(t\right)-P_{\text{RA}}^{\text{ref}}}{P_{\text{RA}}^{\text{ref}}},$$ (62)

$$\psi \left(t\right)=\frac{Q\left(t\right)-Q^{\text{ref}}}{Q^{\text{ref}}},$$ (63)

which are analogous to those of the full model (e.g., Eqs. 33, 34). Using the expansions (45)–(47), one obtains the following approximation of the transfer function (details given in the SUPPLEMENT):

$$\begin{gathered} H\left(f\right)=\frac{P_0^{\text{ref}}{B}_1}{Q^{\text{ref}}}\frac{1-Q^{\text{ref}}\frac{L_{\text{AA}}}{2}{K}_{\text{MR}}\left(f\right)}{1-Q^{\text{ref}}\left(\mathcal{l}-\frac{1}{2}{L}_{\text{AA}}\right)K_{\text{MR}}\left(f\right)+Q^{\text{ref}}{L}_{\text{TGF}}{K}_{\text{TGF}}\left(f\right)} \\ +O\left(\delta \right)+O\left({\epsilon }^2/\delta \right)+O\left(\epsilon \right), \end{gathered}$$ (64)

which is valid up to leading orders of δ and ε. The terms K_MR(f) and K_TGF(f) are given by:

$$K_{\text{MR}}\left(f\right)=s_{\mathrm{M}}{s}_m{s}_{\text{MR}}{h}_{\mathrm{m}}\left(f\right)h_{\mathrm{s}}\left(f\right)h_{\text{MR}}\left(f\right)-s_{\text{AA}},$$ (65)

$$K_{\text{TGF}}\left(f\right)=B_2{s}_{\mathrm{M}}{s}_m{s}_{\text{TGF}}{s}_{\text{TB}}{h}_{\mathrm{m}}\left(f\right)h_{\text{TGF}}\left(f\right)h_{\text{TB}}\left(f\right),$$ (66)

Equation (64) contains an O(ε²/δ) term, which becomes unbounded if δ decreases faster than ε². In this study, we restrict our attention to scenarios where the afferent arteriole sufficiently absorbs the pressure perturbations. In such scenarios, pressure and resistance perturbations are of the same order, i.e., ε = O(δ). So, it follows that the right-hand side of Eq. (64) remains bounded.

2.3 Parameters

2.3.1 Full Model

Values of selected parameter for the full model are given in Table 1. For a complete list see Sgouralis and Layton (2014) and the references therein.

Table 1.

Parameter values for the full model

Parameter	Value	Units
$P_{\text{RA}}^{\text{ref}}$	100	mmHg
Qref	280	mmHg
LAA	303	μm
LTGF	60	μm
kCa	190	Hz
αCa	645	nM/mV
kψ	2	Hz
ψM	0.1	Dimensionless
kMR	0.5	Hz
$I_{\text{MR}}^{min}$	−21.35	mV/s
$I_{\text{MR}}^{max}$	1.29	mV/s
sMR	0.76	1/mmHg
kTGF	0.5	Hz
$I_{\text{TGF}}^{min}$	−27	mV/s
$I_{\text{TGF}}^{max}$	32	mV/s
sTGF	1.75	1/mM
$R_{\text{AA}}^c$	12	μm
$C_{\text{pass}}^0$	0.16	mmHgcm
$C_{\text{pass}}^1$	6	Dimensionless
$C_{\text{pass}}^2$	−0.23	mmHgcm
$C_{\text{act}}^0$	1.5	mmHgcm
$C_{\text{act}}^1$	1	Dimensionless
$C_{\text{act}}^2$	0.47	Dimensionless

2.3.2 Simplified Model

A list of the parameter values used in the simplified model is given in Table 2. Afferent arteriole reference resistance is assumed uniform throughout the vessel:

$$r^{\text{ref}}\left(z\right)=\frac{P_{\text{RA}}^{\text{ref}}-P_D^{\text{ref}}}{Q^{\text{ref}}{L}_{\text{AA}}}.$$ (67)

Efferent arteriole compliance and reference resistance are set by:

$$s_{\text{EA}}=s_{\text{AA}}{L}_{\text{AA}},$$ (68)

$$R_{\text{EA}}^{\text{ref}}=\frac{P_D^{\text{ref}}-P_v}{Q^{\text{ref}}-Q_{\mathrm{F}}^{\text{ref}}}.$$ (69)

Table 2.

Parameter values for the simplified model

Parameter	Value	Units
$P_{\text{RA}}^{\text{ref}}$	100	mmHg
Qref	280	nl/min
$Q_{\mathrm{F}}^{\text{ref}}$	30	nl/min
$P_D^{\text{ref}}$	50	mmHg
Pv	3.75	mmHg
LAA	300	μm
LTGF	60	μm
γ	3	Dimensionless
km	2	Hz
kMR	0.5	Hz
kTGF	0.5	Hz
ks	1.28	Hz2
ηs	0.25	Dimensionless
sTB	5	mMmin/nl
sAA	0.01	min/nl/cm
β	0.65	Dimensionless

The transfer function in Eq. (64) depends on the products s_Ms_ms_MR and s_Ms_ms_TGF for which no a priori choices can be made. As reference values, we have chosen the expressions:

$${\left(s_{\mathrm{M}}{s}_m{s}_{\text{MR}}\right)}^{\ast }=s_{\text{AA}}+\frac{2}{Q^{\text{ref}}{L}_{\text{AA}}}$$ (70)

$${\left(s_{\mathrm{M}}{s}_m{s}_{\text{TGF}}\right)}^{\ast }=\frac{2\gamma }{B_2{Q}^{\text{ref}}{L}_{\text{TGF}}{s}_{\text{TB}}}\left(1-\frac{\mathcal{l}}{L_{\text{AA}}}\right)$$ (71)

Analytic derivation of these expressions and the definition of ℓ are given in the SUPPLEMENT. With the above choices, the simplified model predicts perfect steady state autoregulation and an open-loop gain for the TGF system of γ > 0 that are valid up to leading orders of ε and δ perturbations. Given that we have neglected higher order terms, for example in Eqs. (45)–(47), such (s_Ms_ms_MR)* and (s_Ms_ms_TGF)* are poor approximations of the actual values. Thus, we use instead

$$s_{\mathrm{M}}{s}_m{s}_{\text{MR}}=\beta {\left(s_{\mathrm{M}}{s}_m{s}_{\text{MR}}\right)}^{\ast }$$ (72)

$$s_{\mathrm{M}}{s}_m{s}_{\text{TGF}}=\beta {\left(s_{\mathrm{M}}{s}_m{s}_{\text{TGF}}\right)}^{\ast }$$ (73)

where β is a dimensionless scaling factor, chosen such that the transfer functions of the simplified and full models are of similar magnitude at frequencies below 10 mHz.

3 Results

3.1 Baseline Time Courses: Full Model

We applied a steady arterial pressure of P_RA(t) = 100 mmHg to the full model and computed the baseline solution. Figure 5 shows the time courses of afferent arteriole resistance (panel a1) and blood flow (panel a2). Even in the absence of perturbations in perfusion pressure, the model exhibits spontaneous oscillations with two fundamental frequencies (panel b). The slow oscillation at 45 mHz with large amplitude is mediated by TGF; the faster oscillation at 180 mHz with a small amplitude is generated by the spontaneous ionic fluxes in the afferent arteriole smooth muscles. The other frequency peaks either are harmonics of the fundamental peaks (e.g., 90 and 360 mHz) or arise from nonlinear interactions (heterodyning) of the two fundamental peaks.

Fig. 5.

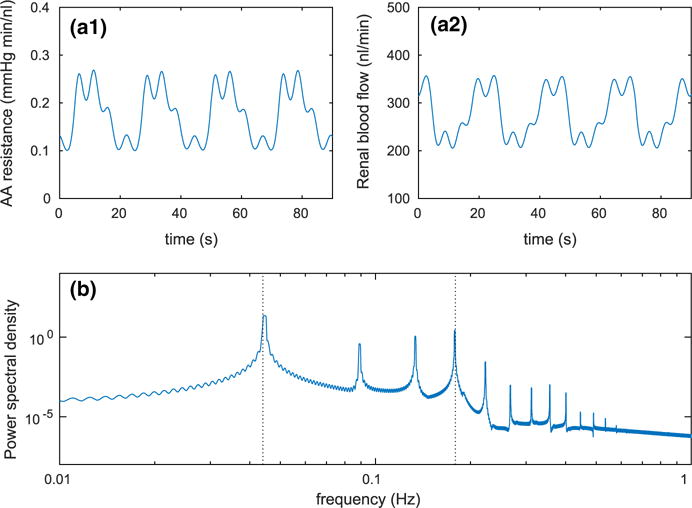
Baseline dynamics of the full model. a1 Time course of afferent arteriole resistance Ω_AA(t). a2 Time course of blood flow Q(t). b Power spectral density of blood flow Q(t); dotted lines indicate the fundamental frequencies of tubuloglomerular feedback 45 mHz and spontaneous vasomotion 180 mHz (Color figure online)

The oscillations at 45 and 180 mHz are initiated by periodic changes in afferent arteriole smooth muscle membrane potential, which translate into fluctuations of smooth muscle cytosolic [Ca²⁺] and vascular tone. The resulting vasomotion alters the vascular resistance and blood delivery to the glomerulus, which then transmits the fluctuations to SNGFR and downstream tubular transport (time courses not shown).

3.2 Response to Sinusoidal Perturbations: Full Model

We studied the full model response to sinusoidal, single-frequency pressure perturbations. Figure 6 shows the time courses of perfusion pressure, key autoregulatory currents, and the resulting blood flow for three characteristic frequencies: 10, 100, and 1000 mHz.

Fig. 6.

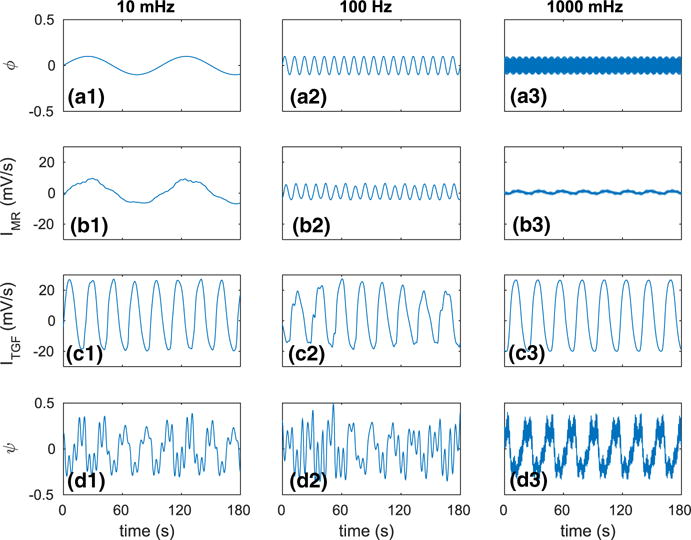
Autoregulatory responses to single-frequency pressure perturbations of the full model. a1–a3 Oscillatory renal perfusion pressure input signal ϕ(t). b1–b3 Corresponding MR current obtained at afferent arteriole’s entrance. c1–c3 Corresponding current mediating TGF. d1–d3 Resulting blood flow output signal ψ(t) (Color figure online)

For the slow pressure perturbation at 10 mHz (panel a1), a strong MR is activated (panel b1), which sufficiently adjusts the vascular tone and absorbs most of the perturbation. The signature of the slow perturbation can be seen in the amplitude modulation of the blood flow oscillations (panel d1). The dominant frequency in the blood flow oscillations arises from TGF (panel c1).

For the intermediate perturbation at 100 mHz (panel a2), MR is only partially activated (panel b2). As a result, a significant fraction of the pressure perturbation reaches the tubular system. However, owing to the damping effect of the renal tubule, much of that perturbation does not reach the macula densa and thus does not allow the TGF system to provide further compensation (panel c2). The combined effect is a significant imprint of the pressure perturbation on renal blood flow (panel d2).

For the fast perturbation at 1000 mHz (panel a3), MR is only minimally activated (panel b3), allowing nearly all of the imposed perturbation to pass on to the tubular system. Again, due to damping in the tubular system, that perturbation does not reach macula densa and elicits no TGF compensation (panel c3). As a result, the effect of the pressure perturbation is clearly visible in the blood flow oscillations (panel d3).

3.3 Response to Pressure Fluctuations: Full and Simplified Models

Processes that perturb renal perfusion pressure induce fluctuations over a wide range of frequencies (Holstein-Rathlou and Marsh 1994b; Cupples and Braam 2007; Holstein-Rathlou et al. 1995), and thus single-frequency forcing (e.g., Sect. 3.2) is not representative of in vivo conditions. To study the ability of the model afferent arteriole to buffer broadband perturbations, we computed the transfer functions for the full and simplified models. For the full model, the transfer function is evaluated numerically as described in Sect. 2.1.6. For the simplified model, we use the leading-order asymptotic approximation given by Eq. (64).

It follows from the definition of the transfer function (Eq. 1) that fluctuations at frequencies with |H(f)| = 1 are neither attenuated nor amplified by the system (in this case the model afferent arteriole), which implies that for these frequencies the model afferent arteriole behaves like a rigid tube (Cupples and Braam 2007; Just 2007). Fluctuations at frequencies with |H(f)| > 1 are amplified by the system, whereas fluctuations at frequencies with |H(f)| < 1 are attenuated. For the frequencies at which attenuation occurs, |H(f)| provides a measure of the autoregulatory effectiveness (Just and Arendshorst 2003), with lower values indicating more effective autoregulation (i.e., larger damping of the imposed perturbations).

Figure 7 shows the transfer functions of the two models. For frequencies higher than ~200 mHz, both models predict a slight amplification of the pressure perturbations, indicating that the autoregulatory mechanisms are unable to buffer such fast fluctuations. The amplification seen in this frequency range is due to passive distention of the arteriolar walls.

Fig. 7.

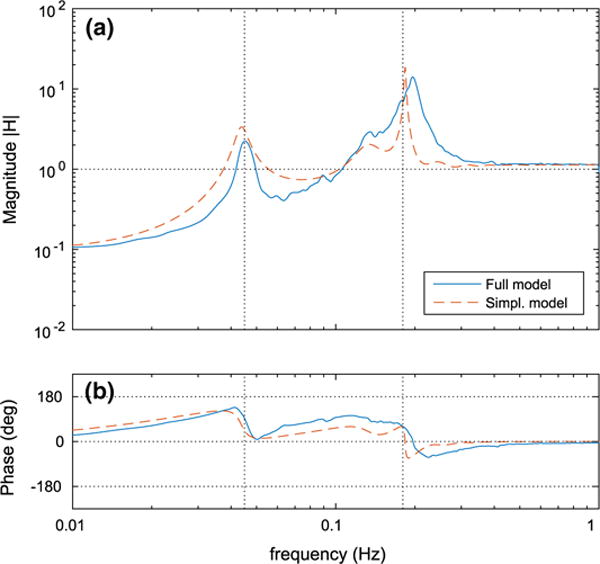
Transfer function H(f) evaluated using the full and the simplified models. a Transfer function magnitude |H(f)|. b Transfer function phase angle $\widehat{H}\left(f\right)$. Vertical dotted lines indicate the baseline fundamental frequencies of spontaneous vasomotion (180 mHz) and TGF (45 mHz) (Color figure online)

On the other side, both models predict significant attenuation at the lowest frequencies, indicating effective autoregulation. Autoregulatory effectiveness increases with decreasing frequency. That is, the slower the pressure perturbations are, the better the afferent arteriole is at buffering them. Fluctuations of intermediate frequencies, with the exception of the frequency bands around 45 and 180 mHz, are generally less well autoregulated.

The amplification of the fluctuations at the frequency bands around 45 mHz and 180 mHz is due to the spontaneous oscillations introduced by TGF and the smooth muscle transmembrane ionic fluxes, respectively. For the unperturbed case, these oscillations are shown in Fig. 5. The peaks seen in the transfer function magnitude (Fig. 7a) indicate resonance of the associated oscillators with the pressure perturbations. Due to the nonlinearity of the smooth muscle oscillator of the full model, Eq. (2), the peak at 180 mHz appears wider than in the simplified model.

Notably, both models predict a secondary peak near 135 mHz. This peak is associated with the second harmonic of TGF oscillation and is sufficiently close to the natural frequency of the smooth muscle oscillator to get amplified.

Both models predict similar phase spectra with sharp transitions at the resonance frequencies of the oscillations (Fig. 7b). Near the TGF operating frequency, both models predict phases that jumps from approximately 0° to 130°. Near the MR operating frequency, both models predict jumps from approximately −60° to 60° (simplified model) or 90° (full model). In the intermediate frequency range, the simplified model predicts lower phase than the full model. As noted above, such differences likely stem from the different representations of the smooth muscle oscillators in the two models: The full model uses a third-order nonlinear oscillator, Eq. (2), whereas the simplified model uses a second-order linear oscillator, Eq. (50).

At the high frequency range, the predicted phase of both models is 0^◦, indicating that renal blood flow oscillates in phase with perfusion pressure. This is yet another demonstration of the inefficiency of the autoregulatory mechanisms in the high frequency range.

3.4 Responses of Individual Autoregulatory Processes: Simplified Model

The transfer function is a result of a number of individual processes, including MR, TGF, tubular transport, arteriolar passive distention, and membrane potential spontaneous spiking. Such processes cannot be isolated and studied individually in the experimental setting. To better characterize the behaviors of these individual processes, we show their frequency responses (Eqs. 56–59, 61) in Fig. 8. These frequency responses are computed using the simplified model; it would be difficult, if not impossible, to derive response functions for the individual processes in the full model. For these response functions, a large value implies that the fluctuations at that frequency are easily transmitted to the vascular resistor such that an autoregulatory response can be induced. For values significantly below 1, the model is unable to respond to and buffer fluctuations at the corresponding frequencies. In other words, responses substantially lower than 1 indicate bottleneck processes.

Fig. 8.

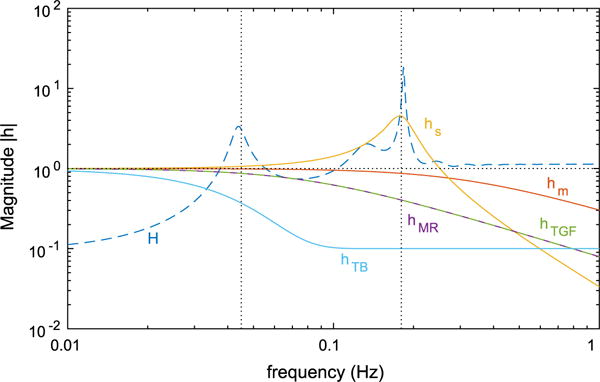
Frequency responses of the components of the simplified model: h_s(f) membrane potential oscillator, h_m(f) muscle activation, h_TB(f) renal tubule, h_MR(f) myogenic response activation, h_TGF(f) TGF activation, H(f) resulting transfer function. Vertical dotted lines indicate the baseline fundamental frequencies of spontaneous vasomotion (180 mHz) and TGF (45 mHz) (Color figure online)

Figure 8 shows that the frequency responses of MR h_MR(f), TGF h_TGF(f), muscle kinetics h_m(f), and tubular transport h_TB(f) are qualitatively similar. Their response curves are monotonically decreasing with increasing frequency, meaning that those processes act as low-pass filters to pressure perturbations and permit mostly low-frequency fluctuations to affect the smooth muscle potential and thus elicit an autoregulatory response. The response of muscle oscillator h_s(f) is rather distinct: It amplifies the autoregulatory currents near 180 mHz, as evidenced by the prominent resonance peak, and it also exhibits much sharper cutoff at high frequencies, which further limits the ability of the autoregulatory mechanisms to buffer fast fluctuations.

As seen in Eq. (64), the transfer function H(f) of the simplified model can be computed from the individual frequency responses. As noted, owing to the low-pass behavior of h_TB(f), h_MR(f), h_TGF(f), h_s(f), and h_m(f), low-frequency perturbations can more effectively reach the active component of the vascular resistance and induce an autoregulatory response. In contrast, fast pressure oscillations are less effectively transmitted and thus less effective in eliciting a compensatory response of the vascular resistor. Indeed, the primary response to the high-frequency fluctuations is a passive one that leads to amplification of flow perturbations.

In summary, three main bottlenecks can be identified. With increasing “severity,” these are: activation of the autoregulatory mechanisms h_MR(f) and h_TGF(f), smooth muscle oscillator h_s(f), and tubular transport h_TB(f), which limit the transmission of signals above ~800, ~600, and ~100 mHz, respectively.

3.5 Transfer Function Sensitivity on Selected Parameters: Simplified Model

In the next set of simulations, we investigate the effect of variations in tubular damping, properties of the smooth muscle oscillator, and vascular compliance on the overall autoregulatory response. Such effects are difficult to assess experimentally. Figure 9a exhibits the effect of tubular damping. We simulated a less compliant tubule by modifying the tubular frequency response (Eq. 61) as follows (the difference is in the second exponential):

$$h_{\text{TB}}\left(f\right)=e^{-55i\left(f+f^2\right)}\left(1+0.90\left(e^{-0.2\left(f+275f^2\right)}-1\right)\right).$$ (74)

With the modified response function, the model tubule allows the transmission of perturbations from SNGFR to macula densa [Cl⁻] for frequencies up to ~130 mHz (baseline and modified frequency responses of the tubule are shown on Fig. 10a). Consequently, the contribution of TGF in the intermediate frequency band ~45–180 mHz increases, which leads to increased autoregulatory effectiveness within this band. Interestingly, in this case the model predicts two prominent peaks near the MR operating frequency. The faster of the two corresponds to the oscillation shown in Fig. 5. The slower peak is an amplification of the second harmonic of TGF. Despite the double resonance near 180 mHz, the model predicts improved autoregulation near 45 mHz, where the fundamental peak associated with TGF is considerably attenuated.

Fig. 9.

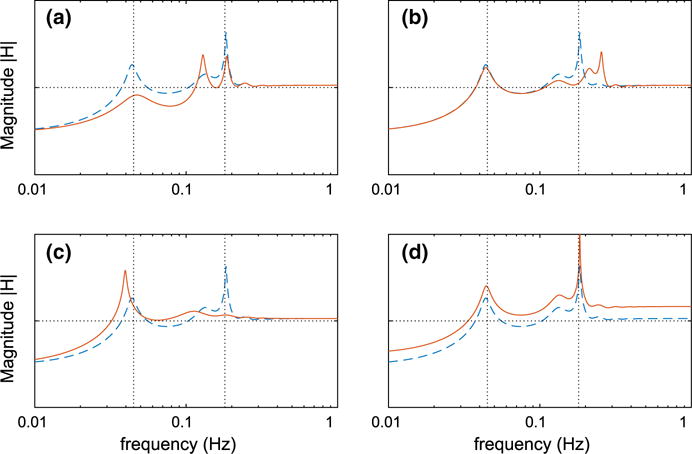
Effect of modifying selected components on transfer function magnitude. All panels show the transfer function of the simplified model with altered parameters (solid line) and baseline (dashed line). a Reduced tubular damping (cut off is at ~130 mHz while baseline is at ~100 mHz). b Natural frequency of spontaneous vasomotion (set to 250 mHz while baseline is 180 mHz). c Overdamping of smooth muscle oscillator (η_s = 2.5 while baseline η_s = 0.25). d Increased vascular compliance (10 times baseline). Vertical dotted lines indicate the baseline fundamental frequencies of spontaneous vasomotion (180 mHz) and TGF (45 mHz) (Color figure online)

Fig. 10.

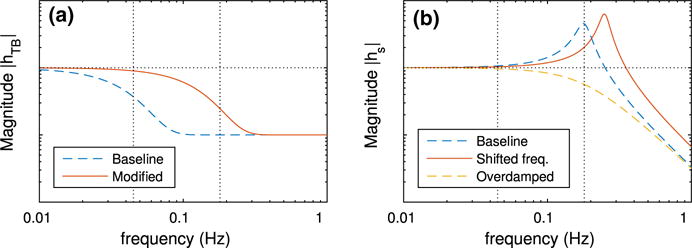
Effect of modifying selected parameters on frequency responses. a Tubular frequency responses h_TB(f) corresponding to Fig. 9a. b Arteriolar oscillator frequency responses h_s(f) corresponding to Fig. 9b, c. Vertical dotted lines indicate the baseline fundamental frequencies of spontaneous vasomotion (180 mHz) and TGF (45 mHz) (Color figure online)

Panel b exhibits the effect of varying the natural frequency of the smooth muscle oscillator (Eq. 50). For this case, smooth muscles are set to oscillate at 250 mHz (compare with baseline natural frequency at 180 mHz, Fig. 10b). This results in a shift in the associated resonance peak without a significant change in the autoregulatory response in the low or high frequency range.

Panel c exhibits the effect of overdamping the smooth muscle oscillator. The damping coefficient η_s (Eq. 50) is set to 2.5 (compare with baseline at η_s = 0.25, Fig. 10b). At sufficiently high damping, the resonance peak at 180 mHz is lost. Further, the reduced responsiveness of the smooth muscles leads to a reduction of the autoregulatory effectiveness at the low frequency range.

Panel d exhibits the effect of vascular compliance. We increase afferent and efferent arteriolar compliances (s_AA in Eq. 48 and s_EA in Eq. 42) by a factor of 10 relative to baseline. Model simulations suggest that the more compliant vessels yield more pronounced passive responses and are thus less effective in attenuating slow oscillations and more prone to amplifying fast perturbations. The vascular compliance has a uniform effect throughout the entire frequency domain in reducing the attenuation.

3.6 Inhibition of Autoregulatory Mechanisms: Full and Simplified Models

To assess the individual contributions of MR and TGF to dynamic renal autoregulation, we evaluate the transfer function using the full model and the simplified model, with the two mechanisms selectively inhibited. To simulate inhibition of a mechanism in the full model, we set the associated target current in Eq. (10) or (12) to zero. In the simplified model, we set the associated sensitivity in Eq. (53) or (55) to zero. The resulting transfer functions are shown in Fig. 11.

Fig. 11.

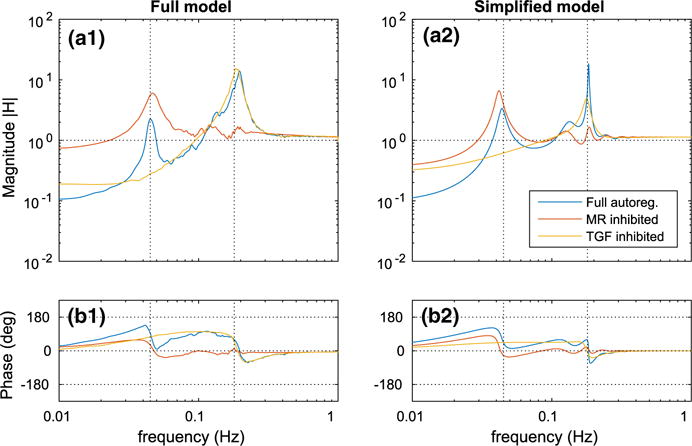
Transfer function H(f) evaluated with the autoregulatory mechanisms selectively inhibited. a1–b1 Full model. a2–b2 Simplified model. Vertical dotted lines indicate the baseline fundamental frequencies of spontaneous vasomotion (180 mHz) and TGF (45 mHz) (Color figure online)

With MR inhibited, the smooth muscle oscillator is excited only by the TGF forcing, which, due to the damping along the renal tubule (see Fig. 4a), contains little or no power near the muscle oscillator’s natural frequency. Consequently, both models predict a significant reduction of the resonance peak at 180 mHz. With TGF inhibited, the system is unable to generate feedback oscillations; therefore, as predicted by both models, the peaks at 45 mHz are eliminated.

As expected, inhibition of either mechanism impedes autoregulatory effectiveness at the low frequency range for both models. In the full model, the reduction following the inhibition of MR is more prominent than TGF, indicating that MR is the dominant mechanism in buffering pressure perturbations. Nevertheless, simultaneous operation of MR and TGF results in stronger autoregulation at the low frequency range as the predicted attenuation at 10 mHz is stronger than the sum of the individual attenuations.

Analogous to the case of full autoregulation (e.g., Fig. 7), both models predict similar transfer functions in terms of magnitude and phase; however, the nearly perfect correspondence is lost. The biggest discrepancy appears in the transfer function magnitude following the inhibition of MR. In this case, the simplified model predicts a lower reduction in attenuation at 10 mHz than the full model (compare Fig. 11A1, A2). Such discrepancies arise due to the nonlinearities of the involved processes.

It is noteworthy that the nearly perfect correspondence of the two models, for example Fig. 7, can be recovered even in this case (results not shown) by properly adjusting the scaling factor β in Eqs. (72) and (73).

3.7 Modulation of Autoregulatory Mechanisms: Simplified Model

Nitric oxide (NO) and angiotensin II (Ang II) are two key modulators of renal autoregulation (Cupples and Braam 2007; Just 2007). Neither NO nor Ang II is believed to significantly alter steady state autoregulation (Just 2007). Instead, they modulate MR and TGF sensitivities to triggering signals and affect the dynamics of the autoregulatory responses. Motivated by this observation, we varied the sensitivity of the individual autoregulatory mechanisms in the simplified model and assessed the effects on the resulting transfer function. We consider three scenarios: (i) modulated TGF, for which we varied s_TGF (Fig. 12a), (ii) modulated MR, for which we varied s_MR (Fig. 12b), (iii) modulated TGF and MR, for which we varied s_MR and s_TGF simultaneously (Fig. 12c). Each transfer function is computed with the associated sensitivities increased/reduced fivefold relative to their baseline values.

Fig. 12.

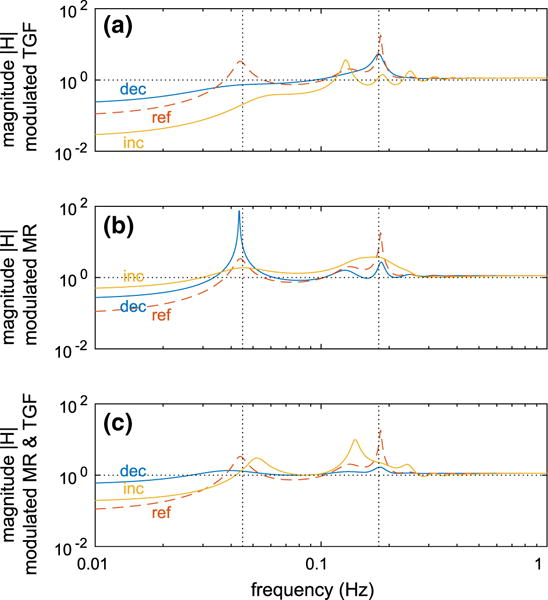
Transfer function H(f) evaluated using the simplified model with modulated autoregulation. a Modulated TGF, b modulated MR; c modulated TGF and MR. In all panels, “ref ” indicates baseline sensitivity s_MR or s_TGF, “inc” fivefold increased baseline sensitivity, “red” fivefold reduced baseline sensitivity. Vertical dotted lines indicate the baseline fundamental frequencies of spontaneous vasomotion (180 mHz) and TGF (45 mHz) (Color figure online)

Modulation of TGF leads to either improved or reduced autoregulatory effectiveness at the lower frequencies (panel a), depending on whether s_TGF increases or reduces. This trend is expected given that s_TGF is directly proportional to the open-loop gain of the feedback system.

Modulation of MR leads to significant reduction of the autoregulatory effectiveness at the lower frequencies (panel b), even when s_MR is increased. A smaller s_MR reduces the capability of MR to compensate for pressure perturbations, thereby reducing the effectiveness of the overall autoregulation. In contrast, a larger s_MR causes MR to overcompensate, which also results in reduced autoregulatory effectiveness. This counterintuitive prediction stems from the feedforward nature of MR (see transfer function in Eq. 64).

As expected, simultaneous modulation of both mechanisms leads to reduced autoregulatory effectiveness (panel c); but the reduction is not much different from the case of modulated MR (panel b), which indicates that the effect of MR dominates that of TGF. This result is in agreement with Sect. 3.6.

4 Discussion

The principal objective of this study is to investigate the dynamic autoregulatory response of the rat kidney. That response is particularly crucial to kidney function, because in vivo renal perfusion pressure is continuously perturbed by various physiological processes (Marsh et al. 1990; Cupples et al. 1996; Brown et al. 2006; Wagner and Persson 1994). Uncontrolled renal perfusion pressure destabilizes the operation of the nephrons leading to absence of body homeostasis and glomerular barotrauma with severe consequences (Cupples et al. 1996; Loutzenhiser et al. 2006). A popular and reliable means for analyzing such time-dependent control systems is the transfer function (Holstein-Rathlou and Marsh 1994b).

While the transfer function has been utilized in many experimental studies of renal blood flow, for example Bidani et al. (2003), Griffin et al. (2004), Holstein-Rathlou and Marsh (1994b), Just et al. (1998), Just and Arendshorst (2003), Knudsen et al. (2004), Sakai et al. (1986) and He and Marsh (1993)), its theoretical analysis remains lacking. Thus, a contribution of this study is to conduct a theoretical analysis of renal autoregulation using the transfer function. To accomplish that, we derived transfer functions for two models of renal autoregulation: a comprehensive model that is based on our previous work (Sgouralis and Layton 2014), and a newly developed simplified model, Sect. 2.2. It is noteworthy that the transfer function of the simplified model is the first such function of which the evaluation is done asymptotically rather than numerically. Thus, a transfer function which explicitly demonstrates the relation between the various autoregulatory elements is obtained, Eq. (64).

Another goal of this study is to develop a simple model of renal hemodynamic control that yields sufficiently accurate dynamic responses, but (i) that requires a substantially lower computational cost than the full model and (ii) that has explicit solutions. The simplified model presented in this study meets these requirements. A comparison between the full model and the simplified model, as shown in Fig. 7, indicates general agreement in both the magnitude and phase of the predicted transfer function. The most notable discrepancies are: (i) in the phase spectra, especially in the intermediate frequency range, 45–180 mHz, Fig. 7b; (ii) when one of the autoregulatory components, for example MR, is inhibited, the full model predicts a considerably smaller attenuation at the lower frequencies compared with the simplified model, as shown in Fig. 11. In general, such discrepancies can be attributed to the nonlinear nature of the the full model’s representation of the underlying phenomena.

The key difference between the two models of this study is:

• The smooth muscles in the full model represent the intracellular processes in details, Sects. 2.1.1 and 2.1.2, whereas in the simplified model the intracellular process are lumped together in two equations, Eqs. (49) and (50).

• The representation of the smooth muscle membrane potential used in the full model utilizes a third-order nonlinear oscillator, Eq. (2), whereas the simplified model utilizes a second-order linear oscillator, Eq. (50). In principle, one could use third-order oscillators in both models; however, the straightforward interpretation of “natural frequency” and “damping” would then be lost.

• The full model contains a detailed representation of the renal tubule that accounts for water and solute transport, Sect. 2.1.5, whereas the simplified model contains only an approximation of the tubular fluid [Cl⁻] at the macula densa, Eq. (61).

• The evaluation of SNGFR in the full model is achieved through a detailed representation of the glomerulus that takes into account spatial differences along the capillaries, Sect. 2.1.4, whereas in the simplified model it is done by means of an approximation that is space independent, Eq. (43).

• The simplified model is only valid in the limit of infinitesimal perturbations of renal perfusion pressure.

4.1 Model Predictions

The response curves of the transfer functions, as shown in Fig. 7, predict that both models: (i) can effectively buffer fluctuations at frequencies up to ~100 mHz; (ii) exhibit resonance at ~45 and ~180 mHz, corresponding to the TGF and spontaneous vasomotion, respectively; (iii) exhibit sharp transitions in the phase spectra at the resonance frequencies; and (iv) predict slight amplification of perturbations and zero phases above ~200 mHz. These predictions are consistent with experimentally obtained transfer functions (for an in-depth comparison with the experimental findings see Sect. 4.2 below).

Using the simplified model, as shown in Fig. 8, we verify that the absence of autoregulation at the high frequency range is caused by three limiting process: activation of the autoregulatory mechanisms, smooth muscle oscillators, and tubular transport. Further, Fig. 9d verifies that the amplification of the pressure perturbations at high frequencies, which is typically observed in measurements of dynamic autoregulation, is caused by the passive dilation of the renal vasculature.

Both of the models allow perfect isolation of the autoregulatory mechanisms on the same preparation, something that has not been achieved in experimental models yet. Based on the transfer functions of Fig. 11, we conclude that TGF, when acts alone, has a minor contribution to dynamic autoregulation compared with MR. However, simultaneous operation of TGF and MR results in synergistic interaction, and the resulting transfer functions predict stronger attenuation at the lower frequency range than the sum of the individual contributions.

4.2 Comparison with Experimental Data

The transfer function of renal autoregulation has been assessed in a number of experimental studies. Table 3 summarizes key characteristics of dynamic autoregulation that are predicted by the models in the present study and that were estimated experimentally.¹ In particular, Table 3 indicates: (i) whether peaks in the transfer function are found in the TGF and MR frequency bands (assumed to span 10–100 and 100–300 mHz, respectively); (ii) gain values at selected low and high frequencies (set to 10 mHz and 1 Hz, respectively); (iii) the location of the TGF and MR peaks (evaluated from the gain maxima); and (iv) the phase jumps occurring across the TGF and MR peaks. For (ii), the low and high frequencies have been chosen to lie in the frequency ranges where dynamic autoregulation is expected to be fully and minimally developed, respectively (Cupples and Braam 2007). Due to the presence of significant dumping in the experimental preparations, the resulting transfer functions do not contain sharp phase transitions, which makes the interpretation of the phase spectra difficult. For this reason, the jumps shown in Table 3 are computed as follows:

• –
  MR phase jump is the maximum difference Δp_MR of the phase over the range 0.1 Hz to f_MR from the phase at 1 Hz, where f_MR denotes the frequency of the MR peak, i.e.,

  $$\mathrm{\Delta }{p}_{\text{MR}}=\underset{f\in \left[0.1,f_{\text{MR}}\right]}{max}\left(\widehat{H}\left(f\right)-\widehat{H}\left(1\right)\right)$$ (75)
• –
  TGF phase jump is the maximum difference Δp_TGF of the phase over the range 0.01 Hz to f_TGF from the phase at 1 Hz, where f_TGF denotes the frequency of the TGF peak, i.e.,

  $$\mathrm{\Delta }{p}_{\text{TGF}}=\underset{f\in \left[0.01,f_{\text{TGF}}\right]}{max}\left(\widehat{H}\left(f\right)-\widehat{H}\left(1\right)\right)$$ (76)

Table 3.

Comparison of the autoregulatory responses predicted by the models of this study and the experimental observations

	TGF Peak	MR Peak	LF Comp. (%)	HF Magn. (%)	TGF Freq. (mHz)	MR Freq. (mHz)	TGF Phase (°)	MR Phase (°)
Full model (full autoregulation)	✓	✓	90	15	45	190	130	90
Full model (TFG inhibited)	–	✓	80	15	–	183	–	80
Full model (MR inhibited)	✓	✓	30	15	45	186	135	12
Simplified model (full autoregulation)	✓	✓	90	15	44	183	124	61
Simplified model (TGF inhibited)	–	✓	70	15	–	177	–	49
Simplified model (MR inhibited)	✓	✓	60	15	43	185	180	29
Ref. Sakai et al. (1986) (normotensive, atrial fibrillation)	✓	✓	n/a	10	30–100*	100–250	n/a	15
Ref. Daniels et al. (1990) (control)	✓	✓	70	20*	40–60*	150*	45*	60*
Ref. Daniels et al. (1990) (obstruction)	–	✓	60	20*	–	150*	–	45*
Ref. Holstein-Rathlou et al. (1991)	✓	✓	60	20	30–40	150	57	57*
Ref. Holstein-Rathlou et al. (1991) (tubular pressure)	✓	✓	n/a	n/a	30–40	150	90*	30*
Ref. He and Marsh (1993) (control)	✓	✓	70*	n/a	54	100–200	n/a	n/a
Ref. Chen and Holstein-Rathlou (1993) (Wistar-Kyoto)	–	✓	70*	100*	–	100–140	-	70*
Ref. Janssen et al. (1995)	n/a	✓	n/a	20*	n/a	200*	n/a	57*
Ref. Cupples et al. (1996) (halothane)	✓	✓	60*	30*	30–50	100–150	n/a	n/a
Ref. Cupples et al. (1996) (isoflurance)	✓	✓	60*	30*	30–50	150–200	n/a	n/a
Ref. Ajikobi et al. (1996) (SD, isoflurane, control)	✓	✓	45	50*	50*	200*	52	46
Ref. Ajikobi et al. (1996) (SD, isoflurane, furosemide)	–	✓	31	20*	–	n/a	–	23
Ref. Ajikobi et al. (1996) (SD, halothane, control)	✓	✓	49	50*	50	120*	114	63
Ref. Ajikobi et al. (1996) (SD, halothane, furosemide)	–	✓	49	20*	–	120*	–	63
Ref. Karlsen et al. (1997)(S-L)	✓	✓	n/a	n/a	40	200	n/a	n/a
Ref. Karlsen et al. (1997)(R-L)	✓	✓	n/a	n/a	30–40*	200–250*	n/a	n/a
Ref. Karlsen et al. (1997) (SPD-N)	✓	✓	n/a	n/a	50	200	n/a	n/a
Ref. Just et al. (1998) (control)	✓	✓	52	n/a	27	130	45	45
Ref. Just et al. (1998) (Furo-II)	–	✓	35	n/a	–	130*	–	n/a
Ref. Abu-Amarah et al. (1998) (Wistar, denervated)	✓	✓	80*	0*	40–60*	210	30*	45*
Ref. Abu-Amarah et al. (1998) (Wistar, innervated)	✓	✓	80*	50*	40–60*	210*	n/a	45*
Ref. Just et al. (1999) (control)	✓	✓	60*	n/a	30	150*	n/a	n/a
Ref. Lessard et al. (1999) (Wistar)	✓	✓	70	n/a	50*	260	90*	90*
Ref. Wang et al. (1999) (control)	✓	✓	70*	30*	30–50*	250	45*	60*
Ref. Wang et al. (2000) (Brown Norway, control)	✓	✓	80*	30*	40	200*	n/a	n/a
Ref. Wang et al. (2000) (Wistar, control)	✓	✓	85*	30*	20*	200*	n/a	n/a
Ref. Wang and Cupples (2001) (Wistar, control)	✓	✓	80*	80*	30–40*	250*	45*	45*
Ref. Wang and Cupples (2001) (Brown Norway, control)	✓	✓	60*	30*	40*	200*	45*	45*
Ref. Pires et al. (2001) (intact)	✓	✓	80*	80*	50	250	45*	45*
Ref. Loutzenhiser et al. (2002)	✓	✓	70*	10*	40–60*	250	57*	90*
Ref. Sandgaard et al. (2002)	✓	✓	60*	120*	30	200	n/a	n/a
Ref. Just et al. (2002) (control)	✓	✓	50*	100*	30	100	n/a	n/a
Ref. Cupples et al. (2002) (forced, control)	✓	✓	70*	100*	30–40*	250	45*	45*
Ref. Just and Arendshorst (2003)	✓	✓	n/a	n/a	30–40	100–200	n/a	n/a
Ref. Griffin et al. (2004) (control)	✓	✓	50*	60*	30–60*	250*	45*	90*
Ref. Knudsen et al. (2004)(Dahl R)	✓	✓	n/a	n/a	40	200	n/a	n/a
Ref. Shi et al. (2006) (control prior furosemide)	✓	✓	70*	100*	40*	200*	86*	45*
Ref. Shi et al. (2006) (furosemide)	–	✓	40*	100*	–	200*	–	30*
Ref. Bell et al. (2006) (control C)	✓	✓	50*	100*	50*	200*	n/a	n/a
Ref. Wang et al. (2007) (100 mmHg)	–	✓	40*	50*	–	160	–	23*
Ref. Scully et al. (2013) (control)	–	✓	70*	100*	–	180*	–	68*
Ref. Moss et al. (2016) (control prior UO)	✓	✓	60*	20*	20–40*	200*	n/a	n/a

Compensation and magnification are given by 1 −|H(f)| and |H(f)| − 1, respectively

“LF comp.” compensation at 1 Hz; “HF magn.” magnification at 1 Hz. n/a indicates values that are not reported or cannot be inferred from the provided data or figures

^*Values obtained from visual inspection of the provided figures

We note that the phase jumps computed by Eqs. (75) and (76) are expected to underestimate the true jumps.

The experimental transfer functions exhibit a peak in the range 100–250 mHz, which is attributed to the operation of MR or spontaneous vasomotion. That same peak is predicted by both models. It is noteworthy that the models predict an MR peak even with inhibited MR. This result is in agreement with the experimental transfer functions estimated in rats of the Brown Norway strain which show substantially impaired MR and thus should be compared with models lacking an active MR (Wang et al. 2000). A second peak, located in 30–60 mHz, is also present in most of the experimental transfer functions. This peak is attributed to the operation of TGF and is missing from preparation in which TGF is inhibited by either ureteral obstruction (e.g., Daniels et al. 1990; Moss et al. 2016), administration of furosemide (e.g., Shi et al. 2006; Just et al. 1998; Ajikobi et al. 1996), or induced hydronephrosis (e.g., Cupples and Loutzenhiser 1998). Similarly, such peak is present in every model that includes an active TGF and is missing from all models in which TGF is inhibited.

The models that represent an active TGF predict a prominent TGF peak with gain values significantly above 1, see Figs. 7 and 11. This differs from the experimental transfer functions which typically show a peak gain lower than 1. That discrepancy likely arises from the fact that the experimental transfer functions utilize whole kidney blood flow measurements and thus contain autoregulatory contributions of many nephrons with differing lengths and transport properties. In contrast, the models represent only one superficial nephron. In vivo measurements and in silico simulations indicate that different types of nephrons oscillate with different frequencies (Holstein-Rathlou 1987; Leyssac 1986; Layton et al. 1991). Hence, whole kidney blood flow measurements tend to average out the oscillations, resulting in a lower apparent peak gain. Holstein-Rathlou and coworkers have noted a similar reduction in the peak gain of the TGF oscillations associated with whole kidney transfer functions, relative to single-nephron transfer functions (Holstein-Rathlou et al. 1991). Indeed, transfer functions computed utilizing proximal tubule pressure (a single-nephron variable) and utilizing whole kidney blood flow indicated TGF peaks of peak gain above 1 and below 1, respectively (Holstein-Rathlou et al. 1991).

Compared with the experimental data, the models appear to predict stronger autoregulatory responses at low-frequency perturbations. When both TGF and MR are active, the models predict 90% compensation of the perturbations at 10 mHz. The same values estimated experimentally range from 80–85% in Wistar rats to 40–50% in Sprague–Dawley rats. The stronger compensation predicted by the models may be attributed to many factors, predominantly the sensitivity of MR to pressure perturbations and the sensitivity of TGF to macula densa [Cl⁻] perturbations. In the full model, these are characterized by the parameters s_MR and s_TGF, see Eqs. (11) and (13). Similar to our previous work (Sgouralis and Layton 2014), we assigned values to these parameters assuming (i) the resulting model predicts perfect steady autoregulation and (ii) the open-loop gain of the TGF system is equal to 3. In vivo those assumptions might not be satisfied. Characteristically, if s_MR and s_TGF are adjusted to reflect an ~2% error in steady autoregulation or an open-loop gain of ~2.9, the model predicts an attenuation of ~75% of a 10 mHz perturbation (results not shown).

At high frequencies, both the models and experimental observations indicate an absence of autoregulation. In particular, at 1 Hz the models predict 15% magnification of the pressure perturbation. This value is within the range 10–20% of the experimental estimates (e.g., Holstein-Rathlou et al. 1991; Sakai et al. 1986).

Substantial variability is found in the experimental data concerning the phase spectrum. Jumps as low as 15° and as high as 65° have been reported across the MR peak (e.g., Sakai et al. 1986; Ajikobi et al. 1996), and jumps as low as 45^◦ and as high as 115^◦ have been reported across the TGF peak (e.g., Just et al. 1998; Ajikobi et al. 1996). Model predictions are qualitatively similar, although the precise values differ. For example, the full model predicts phase jumps across the MR and TGF peaks of 90° and 130°, respectively.

4.3 Perspectives and Future Work

Interesting blood flow dynamics such as transient synchronization of large clusters of nephrons have been reported (Holstein-Rathlou et al. 2011; Scully et al. 2013, 2014). In a future work, we plan to study these phenomena by extending the single-nephron model to a network model that simulates dynamic autoregulation at the cortical radial artery or whole kidney level. A typical cortical radial artery feeds into 30–40 nephrons, whereas a rat kidney contains ~30,000–40,000 nephrons (Casellas et al. 1994; Nordsletten et al. 2006). Given its substantially lower computational cost, the simplified model developed in the present study can be a useful component in such large scale networks.

Further, the explicit formulas derived in this study may provide the basis for a detailed analysis of the impact of internephron coupling on dynamic autoregulation. Such an analysis could distinguish the contributions between hydrodynamic and electrotonic coupling at different frequency ranges (Sgouralis and Layton 2016).