Implications of intercorrelation between hepatic CYP3A4‐CYP2C8 enzymes for the evaluation of drug–drug interactions: a case study with repaglinide

Abstract

Aims

Statistically significant positive correlations are reported for the abundance of hepatic drug‐metabolizing enzymes. We investigate, as an example, the impact of CYP3A4–CYP2C8 intercorrelation on the predicted interindividual variabilities of clearance and drug–drug interactions (DDIs) for repaglinide using physiologically based pharmacokinetic (PBPK) modelling.

Methods

PBPK modelling and simulation were employed using Simcyp Simulator (v15.1). Virtual populations were generated assuming intercorrelations between hepatic CYP3A4–CYP2C8 abundances derived from observed values in 24 human livers. A repaglinide PBPK model was used to predict PK parameters in the presence and absence of gemfibrozil in virtual populations, and the results were compared with a clinical DDI study.

Results

Coefficient of variation (CV) of oral clearance was 52.5% in the absence of intercorrelation between CYP3A4–CYP2C8 abundances, which increased to 54.2% when incorporating intercorrelation. In contrast, CV for predicted DDI (as measured by AUC ratio before and after inhibition) was reduced from 46.0% in the absence of intercorrelation between enzymes to 43.8% when incorporating intercorrelation: these CVs were associated with 5th/95th percentiles (2.48–11.29 vs. 2.49–9.69). The range of predicted DDI was larger in the absence of intercorrelation (1.55–77.06) than when incorporating intercorrelation (1.79–25.15), which was closer to clinical observations (2.6–12).

Conclusions

The present study demonstrates via a systematic investigation that population‐based PBPK modelling incorporating intercorrelation led to more consistent estimation of extreme values than those observed in interindividual variabilities of clearance and DDI. As the intercorrelations more realistically reflect enzyme abundances, virtual population studies involving PBPK and DDI should avoid using Monte Carlo assignment of enzyme abundance.

What is Already Known about this Subject

• Current population‐based physiologically‐based pharmacokinetic (PBPK) models do not consider intercorrelations between the abundances of different enzymes when using Monte Carlo simulations to generate virtual individuals.

• Statistically significant positive correlations are reported for enzyme abundance between certain drug‐metabolizing enzymes.

What this Study Adds

• The study for the first time incorporates intercorrelation of enzymes into population‐based PBPK model.

• The impact of intercorrelation was assessed for clearance and DDI variability of the model compound repaglinide.

• Here we present a practical approach to assessing enzyme intercorrelations and their potential impact on drug clearance and DDIs.

Introduction

Pharmacokinetic drug–drug interactions (DDIs) can alter systemic exposure to drugs, and result in reduced treatment efficacy or increased risk of adverse drug reactions (ADRs). Quantitative DDI assessments are important in anticipating the clinical risks associated with DDIs prior to market approval and during post‐marketing surveillance. Physiologically based pharmacokinetic (PBPK) approaches may be used to estimate the risk of DDIs, and validated PBPK models allow the quantitative prediction of the magnitude of DDIs in various clinical situations, including in special populations 1, 2, 3. DDI predictions using validated PBPK models have influenced the labelling recommendations for several drugs, such as ibrutinib and eliglustat 4, 5. The approaches described above have focused mainly on the prediction of a single ‘average’ outcome for change in systemic exposure. However, in individual subjects, severe ADRs may be induced by the unexpected magnitude of DDIs based on a large interindividual variability in metabolic clearance 6. It is therefore important to consider not only the average DDI effect but also the population distribution in DDI outcomes and the theoretically conceivable extremes in outcome in individual subjects 6.

Interindividual variability in hepatic drug clearance can be anticipated by incorporating sources of variability such as demographic factors (e.g., age and sex) and physiological factors (e.g., hepatic blood flow, enzyme/transporter levels and activity) 7. Data from clinical pharmacokinetic studies are not amenable to separation of the role of variable intrinsic clearances by various metabolic pathways and their intercorrelations. In contrast, in silico approaches, such as PBPK models, can provide such information about the contribution of single covariate factors, or about the interaction between them. One of the key physiological factors determining interindividual variability in hepatic drug clearance is enzyme abundance, which is affected by age, sex, body and liver weight, and dietary habits, as well as genetic polymorphisms. However, without considering the intercorrelation between physiological parameters (e.g., liver volume and hepatic blood flow, and liver volume and kidney volume), physiologically implausible parameter combinations will be generated when sampling from a population distribution that may lead to overestimation in the interindividual variability of pharmacokinetic parameters, such as clearance 8. To account for this, state‐of‐the‐art PBPK models consider the intercorrelation between organ/tissue volumes and blood flows 7, 9.

Until recently, it has been challenging to consider the intercorrelation between the expression levels of drug‐metabolizing enzymes and transporters due to the lack of reliable quantitative data. Historically, measuring enzyme and transporter expression levels relied on assessment of gene expression (mRNA) or immuno‐quantification assays, which tended to generate semi‐quantitative analyses, not amenable to multiplexing, even when robust quality controls were applied, and therefore these methods were generally unable to uncover expression correlations 10. However, novel methods in quantitative proteomics driven by recent advances in LC–MS technology made it possible to reliably measure multiple enzymes and transporters in individual tissue samples in the same experiment, therefore allowing robust consideration of intercorrelations of these proteins 11. Although drug‐metabolizing enzyme intercorrelations have recently been reported 12, the quantitative impact of such relationships on pharmacokinetic outcomes has not been extensively explored. A PBPK model incorporating a CYP3A4–CYP3A5 intercorrelation produced a reasonable oral clearance estimate of tacrolimus, a substrate of both CYP3A4 and CYP3A5, in individuals displaying high or low basal concentration of CYP3A4 13. Given a credible range of predicted drug clearance in PBPK models incorporating the reported intercorrelation between two enzymes, the PBPK models could predict the theoretically conceivable extreme risk of DDIs.

This report describes a proof‐of‐principle study for the prediction of interindividual variability in drug clearance and DDIs by incorporating intercorrelation between two drug‐metabolizing enzymes into a PBPK model. To achieve the aim of this study, we investigate, as an example, the impact of CYP3A4–CYP2C8 intercorrelation on the prediction of interindividual variability in drug clearance and DDIs of repaglinide, a probe substrate for CYP2C8 inhibition studies 14. Repaglinide, a short acting anti‐diabetic drug, is mainly metabolized by CYP2C8 and CYP3A4, and is also a substrate of the hepatic uptake transporter, organic anion transporting polypeptide (OATP) 1B1 15, 16, 17. Systemic exposure of repaglinide is increased by inhibitors of CYP2C8, CYP3A4 and OATP1B1 18, 19. In the present study, we generated virtual populations assuming a CYP3A4–CYP2C8 intercorrelation, and assessed the effect of the intercorrelation on the prediction of interindividual variability in clearance and magnitude of DDI of repaglinide using PBPK modelling. Furthermore, theoretically conceivable extreme values of clearance and DDI generated under various assumptions regarding the intercorrelations were investigated and compared with clinical observations.

Methods

Assessing intercorrelation between hepatic CYP3A4 and CYP2C8 abundances

Hepatic CYP3A4 and CYP2C8 abundance data usable for correlation analysis were obtained from the literature (Figure 1A) 20. The protein expression was measured simultaneously in a set of 24 individual human liver microsomes (HLM) using a multiplexed QconCAT‐based proteomic method, designed to allow robust assessment of expression intercorrelation. Individual values for each HLM sample were obtained directly from authors of the original research article. A linear regression model was developed (using IBM SPSS Statistics 24, IBM, New York, USA) to assess the correlation between hepatic CYP3A4 and CYP2C8 protein expression as previously reported 13. The model was as follows:

$$\mathrm{CYP}2\text{C8}\left(\text{pmol}/\mathrm{mg}\text{microsomal protein}\right)={\mathrm{C}}_0+{\mathrm{C}}_1·\mathrm{CYP}3\text{A4}\left(\text{pmol}{\mathrm{mg}}^{–1}\right)$$

where C₀ is the baseline level of CYP2C8 protein expression, and C₁ is the slope. A coefficient of variation (CV) describing residual variability in CYP2C8 protein expression was determined from the sum of squares of the least squares linear regression analysis and the mean relative CYP2C8 abundance of the dataset. It should be noted that assigning CYP2C8 as the dependent variable was arbitrary and does not infer any causality (an alternative of defining CYP3A4 could equally be applied). The correlation was only the manifestation of potential common regulatory pathways (e.g., known regulatory factors such as FXR, PXR, CAR, AhR, etc.).

Figure 1.

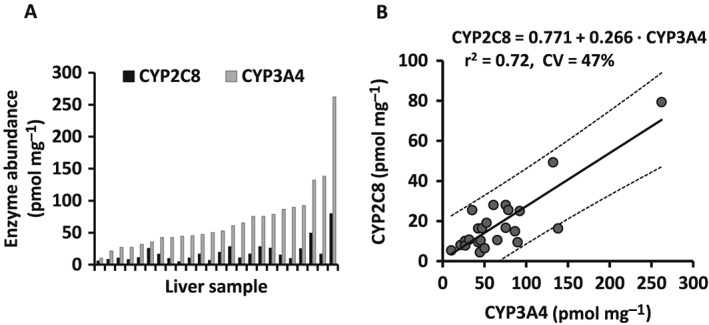
Reported enzyme abundance (A) and correlation plot (B) for CYP2C8 and CYP3A4 protein contents in 24 individual liver samples 20. Solid and dashed lines represent the regression line and the 95% prediction intervals, respectively. Standard errors for slope and baseline were 0.035 and 2.997, respectively. CV, coefficient of variation

Development of a PBPK model using intercorrelation between CYP3A4 and CYP2C8

PBPK modelling and simulation were employed using the Simcyp^® Simulator (v15.1; Certara, Sheffield, UK). Virtual populations, assuming different magnitudes of intercorrelation between CYP3A4 and CYP2C8, were generated by altering physiological parameters in the ‘healthy volunteers’ population template within the Simcyp Simulator population library (Table 1). Hepatic CYP3A4 and CYP2C8 abundances for default healthy volunteers were generated independently using mean population values of CYP3A4 and CYP2C8 of 137 and 24 pmol mg^–1 and associated CVs of 41% and 81% for CYP3A4 and CYP2C8, respectively. Input parameters for CYP3A5 were substituted by the corresponding values of CYP2C8 in the population template when assessing intercorrelation between CYP3A4 and CYP2C8. The current version of the Simcyp Simulator allows enzyme intercorrelation where hepatic CYP3A5 abundance is predicted from CYP3A4 abundance based on a linear model. Default parameter values for baseline, slope and CV of the enzyme intercorrelation module were substituted by parameter values derived from intercorrelation between hepatic CYP3A4 and CYP2C8. Default values of CYP3A5 abundance in the gastrointestinal tract and frequency of CYP3A5 extensive metabolizers (EM) were also substituted by values for CYP2C8. This value was set to 1.00 because complete loss‐of‐function of CYP2C8 variants is very rare 14.

Table 1.

Summary of input population parameters

	Simcyp default	CYP3A4–CYP2C8 correlation	Comments
Demographic
CYP phenotype
CYP3A5 EM frequency	0.17	1.00	CYP2C8 EM frequency
Liver
CYP enzyme abundance
CYP2C8 mean (pmol mg –1 )	24	24
CYP2C8 CV (%)	81	81
CYP3A4 mean (pmol mg –1 )	137	137
CYP3A4 CV (%)	41	41
CYP3A5 mean (pmol mg –1 )	Predicted	Predicted	Substituted by CYP2C8
CYP3A5 CV (%)	Predicted	Predicted	Substituted by CYP2C8
Enzyme correlation
Baseline	62.775	0.771	Substituted by CYP3A4‐CYP2C8 correlation
Slope	0.3934	0.266
CV (%)	24	47
Gastrointestinal tract
CYP enzyme abundance
CYP3A4 mean (pmol mg –1 )	66.2	66.2
CYP3A4 CV (%)	60	60
CYP3A5 mean (pmol mg –1 )	24.6	0	Substituted by CYP2C8
CYP3A5 CV (%)	60	0	Substituted by CYP2C8

CV, coefficient of variation

The pre‐validated repaglinide compound file in the Simcyp compound library was adapted to use the enzyme intercorrelation module based on an intercorrelation between hepatic CYP3A4 and CYP2C8 (Table 2). Physicochemical parameters (molecular weight, log P _o:w, acid/base status and pKa), fraction unbound in plasma and blood/plasma ratio were obtained from data in the literature and public databases 21, 22. A full PBPK distribution model for repaglinide was developed using the Rodgers and Rowland method assigning perfusion‐limited distribution to all tissues except liver 23. Permeability‐limited distribution of repaglinide into the liver was adopted to account for transporter‐mediated intrinsic clearance (CL_int,T) for the sinusoidal uptake transporter OATP1B1. Default values of V_max and K_m for repaglinide metabolism in HLM were 300.8 pmol min^–1 mg^–1 and 2.3 μM for CYP2C8, and 958.2 pmol min^–1 mg^–1 and 13.2 μM for CYP3A4, respectively 15. The enzyme kinetic values in HLM were converted into values in microsomes from a recombinant system with transformation of V_max values using default mean abundance data of CYP2C8 and CYP3A4. In the modified repaglinide model for CYP3A4–CYP2C8 correlation, the converted enzyme kinetic values for recombinant CYP2C8 and CYP3A4 were used as parameter values for recombinant CYP3A5 and CYP3A4, respectively. The other parameters were not changed from the pre‐validated values.

Table 2.

Summary of input parameters used for repaglinide simulations

	Simcyp default	CYP3A4–CYP2C8 correlation	Comments
Molecular weight (g mol −1 )	452.6	452.6
log P	3.98	3.98
Compound type	Ampholyte	Ampholyte
pK a	4.2, 6.0	4.2, 6.0
Blood/plasma ratio	0.62	0.62
Fraction unbound in plasma	0.023	0.023
Absorption
Model	First‐order	First‐order
Fraction absorbed	0.98	0.98
Absorption rate constant (l h −1 )	1.6	1.6
Fraction of drug unbound in enterocyte	1	1
Caco‐2 permeability (×10 −6 cm s −1 )	24.1	24.1
Predicted P eff,man (×10 −4 cm s −1 )	3.89	3.89
Distribution
Model	Full PBPK	Full PBPK
V ss (l kg −1 )	0.24	0.24
K p scalar	3.3	3.3
Elimination
HLM, CYP2C8 K m (μM)	2.3		Transferred to parameter for recombinant
HLM, CYP2C8 V max (pmol min −1 mg −1 )	300.8		Transferred to parameter for recombinant
HLM, CYP3A4 K m (μM)	13.2		Transferred to parameter for recombinant
HLM, CYP3A4 V max (pmol min −1 mg −1 )	958.2		Transferred to parameter for recombinant
Recombinant, CYP3A4 K m (μM)		13.2	CYP3A4 Km in HLM
Recombinant, CYP3A4 V max (pmol min −1 mg −1 )		6.99	Calculated from CYP3A4 Vmax in HLM
Recombinant, CYP3A5 K m (μM)		2.3	CYP2C8 Km in HLM
Recombinant, CYP3A5 V max (pmol min −1 mg −1 )		12.53	Calculated from CYP2C8 Vmax in HLM
CL R (l h −1 )	0.013	0.013
Hepatic transport
OATP1B1 CL int,T (μL min −1 million cells −1 )	246	246
CL PD (ml min −1 million hepatocytes −1 )	0.089	0.089

CL_{int, T}, transporter‐mediated intrinsic clearance; CL_PD, passive diffusion clearance; CL_R, renal clearance; Full PBPK model, full physiologically‐based pharmacokinetic model; HLM, human liver microsomes; K_m, Michaelis–Menten constant; K_p, tissue to plasma partition coefficient; P_eff,man, human jejunum permeability; V_max, maximum rate of metabolism; V_ss, volume of distribution at steady state

Gemfibrozil, a clinically relevant CYP2C8 inhibitor, was used for the virtual DDI study. It is mainly metabolized to gemfibrozil 1‐O‐β glucuronide (Gem‐Glu) which is a mechanism‐based inhibitor of CYP2C8 24. In addition, both parent gemfibrozil and the glucuronide metabolite inhibit OATP1B1 in vitro 25 and in vivo 26. The pre‐validated compound files of gemfibrozil and Gem‐Glu supplied in the Simcyp compound library were developed with modifications, where inhibitory parameter values of CYP2C8 were used as those of CYP3A5 (Table 3).

Table 3.

Summary of input parameters used for model of gemfibrozil and its metabolite, gemfibrozil 1‐O‐β glucuronide

	Gemfibrozil			Gemfibrozil 1‐O‐β glucuronide
	Simcyp default	CYP3A4–CYP2C8 correlation	Comments	Simcyp default	CYP3A4–CYP2C8 correlation	Comments
Molecular weight (g mol −1 )	250.3	250.3		426.5	426.5
log P	4.29	4.29		2.40	2.40
Compound type	Monoprotic acid	Monoprotic acid		Monoprotic acid	Monoprotic acid
pK a	4.7	4.7		3.1	3.1
Blood/plasma ratio	0.75	0.75		0.75	0.75
Fraction unbound in plasma	0.008	0.008		0.028	0.028
Absorption
Model	First‐order	First‐order
Fraction absorbed	1	1
Absorption rate constant (l h −1 )	0.81	0.81
Lag time (h)	0.25	0.25
Distribution
Model	Full PBPK	Full PBPK		Minimal PBPK	Minimal PBPK
V ss (l kg −1 )	0.083	0.083		0.081	0.081
Elimination
HLM, CYP2C9 CL int (μl min −1 mg −1 )	41.2	41.2
Recombinant, UGT2B7 K m (μM)	2.1	2.1
Recombinant, UGT2B7 V max (pmol min −1 mg −1 )	353	353
rUGT Scalar – Liver	1.33	1.33
rUGT Scalar – Intestine	0.13	0.13
rUGT Scalar – Kidney	1.27	1.27
CL iv (l h −1 )				5.54	5.54
CL R (l h −1 )	0.035	0.035		2.55	2.55
Interactions
CYP1A2 K i (μM)	79.5	79.5
CYP2C8 K i (μM)	9.0		Transferred to CYP3A5	0.8		Transferred to CYP3A5
CYP2C8 MBI K app (μM)				19.0		Transferred to CYP3A5
CYP2C8 MBI K inact (μM)				13.0		Transferred to CYP3A5
CYP2C9 K i (μM)	5.8	5.8
CYP2C19 K i (μM)	23.3	23.3
CYP3A4 K i (μM)	210.2	210.2
CYP3A5 K i (μM)		9.0	Substituted by CYP2C8		0.8	Substituted by CYP2C8
CYP3A5 MBI K app (μM)					19.0	Substituted by CYP2C8
CYP3A5 MBI K inact (μM)					13.0	Substituted by CYP2C8
UGT1A1 K i (μM)	276.2	276.2		276.2	276.2
OATP1B1 K i (μM)	0.01	0.01		0.01	0.01

CL_int, intrinsic clearance; CL_iv, in vivo intravenous clearance; CL_R, renal clearance; PBPK, physiologically‐based pharmacokinetic model; HLM, human liver microsomes; K_app, concentration of mechanism‐based inhibitor associated with half maximal inactivation rate; K_i, concentration of inhibitor that supports half maximal inhibition; K_inact, inactivation rate of the enzyme; K_m, Michaelis–Menten constant; V_max, maximum rate of metabolism; V_ss, volume of distribution at steady state

Design of virtual studies

Virtual studies for clinical pharmacokinetics and DDIs of repaglinide were simulated using the default number of trials (10) and modified virtual populations (up to 100 trials). The simulation results were compared to pharmacokinetic data from a published clinical trial in which repaglinide was administered either alone or with pretreatment with gemfibrozil 19. Observed data for plasma repaglinide concentration profiles were obtained directly from authors of the original research article. The trial design (number of subjects, age range and proportion of females) was replicated as closely as possible to ensure that the characteristics of virtual subjects were matched to those of the clinical trial 19. An age range of 19–29 years was obtained directly from the authors of the original research article. Replicate virtual trials simulated in 10 subjects each (nine males and one female) receiving a single oral dose of repaglinide 0.25 mg were performed in the absence and presence of pretreatment with 600 mg gemfibrozil twice daily. The influence of the number of trials on simulation outcome was assessed by incremental increase of trials from 10 to 100. DDI effects were characterized by ratios between before and after inhibition for maximum concentration (C _max) of repaglinide and the area under the concentration–time curve (AUC) from administration to 9 h.

Statistical analyses

Distributions of predicted oral clearance and DDI effects were compared between virtual individuals assuming no correlation and intercorrelation using the Kolmogorov–Smirnov test. CV values for each trial were extracted and the median CV from the sets of virtual trials were used for comparison of the effect of considering or omitting intercorrelations between the enzymes.

Results

Assessing intercorrelation between hepatic CYP3A4 and CYP2C8 abundances

The correlation between CYP3A4 and CYP2C8 protein expression in 24 individual HLMs obtained from Achour et al. 20 is shown in Figure 1B. Linear regression analysis indicated a strong correlation between the two enzymes (R = 0.85; P < 0.0001). The linear model was described as follows:

$$\mathrm{CYP}2\text{C8}\left(\text{pmol}{\mathrm{mg}}^{–1}\right)=0.771+0.266·\mathrm{CYP}3\text{A4}\left(\text{pmol}{\mathrm{mg}}^{–1}\right)$$

The residual variability in CYP2C8 abundance was estimated to be 47% based on the residual sum of squares (1715) and mean CYP2C8 abundance of 18.9 pmol mg^–1 derived from the experimental dataset.

Hepatic CYP2C8 and CYP3A4 abundances in virtual individuals

Hepatic CYP2C8 and CYP3A4 protein contents in a population of 100 virtual individuals were generated assuming either no correlation or correlation between the two enzymes with CV of 0%, 47% and 100% (Figure 2). Default virtual individuals assuming no correlation between two enzymes showed higher CYP2C8/CYP3A4 ratio in virtual individuals with low CYP3A4 protein content (Figure 2A). Incorporation of correlation between CYP2C8 and CYP3A4 resulted in a consistent pattern in CYP2C8/CYP3A4 ratio according to the assigned residual variability (Figure 2B–D). Hepatic CYP2C8 and CYP3A4 abundances in virtual individuals assuming correlation between the two enzymes with residual variability of 47% (Figure 2C) showed a similar pattern to an actual correlation between HLM CYP3A4 and CYP2C8 protein expression (Figure 1B).

Figure 2.

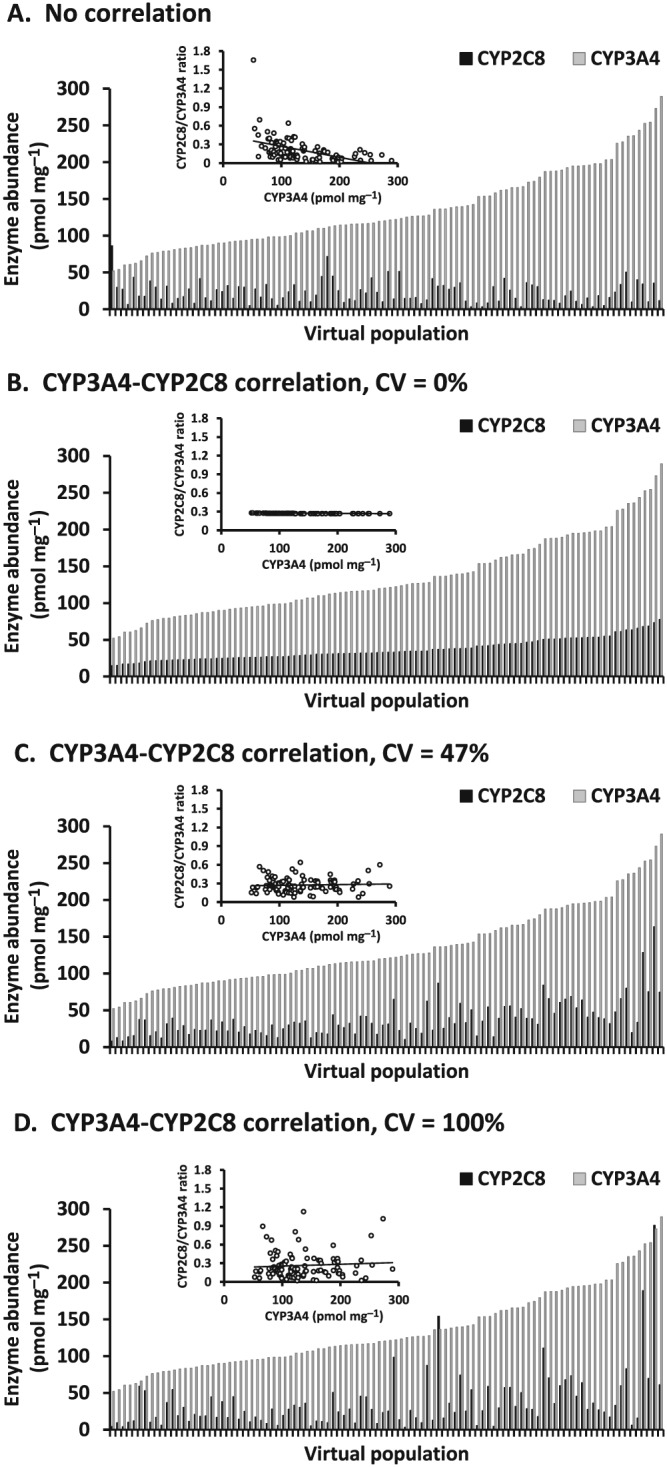
Hepatic CYP2C8 and CYP3A4 protein contents in a population of 100 virtual individuals generated assuming no correlation (A) and correlation between the two enzymes with coefficient of variation (CV) of 0% (B), 47% (C) and 100% (D). Correlation plots for CYP3A4 abundance and CYP2C8/CYP3A4 ratio are shown in the insets

Prediction of pharmacokinetic parameters of repaglinide

Predicted pharmacokinetic parameters, systemic clearance, oral clearance of repaglinide and the fraction of repaglinide escaping metabolism by the gut (F_G) and by the liver (F_H), were predicted in 1000 virtual individuals generated assuming no correlation and correlation between the CYP3A4 and CYP2C8 with residual variability of 47% (Figure 3). Systemic and oral clearance, and F_H were affected by the incorporation of correlation between the CYP3A4 and CYP2C8 within the virtual population, but F_G was not. The influence of CYP3A4–CYP2C8 intercorrelation on oral clearance was different among three groups classified by hepatic CYP3A4 abundance in microsomal protein: 5% lower estimate in low expression (<100 pmol mg^–1), 36% higher estimate in medium expression (100–199 pmol mg^–1), 107% higher estimate in high expression (≥200 pmol mg^–1). CV of the predicted oral clearance for individuals with low CYP3A4 expression was greater in the absence of intercorrelation than that assuming intercorrelation (74% vs. 48%), but that for individuals with medium and high expression showed little or no difference between the two populations (medium expression, 62% vs. 56%; high expression, 54% vs. 54%).

Figure 3.

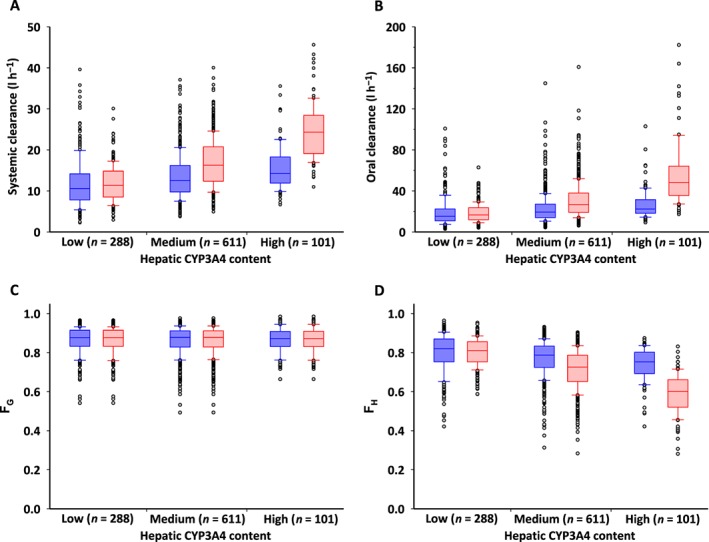
Influence of correlation between hepatic CYP3A4 and CYP2C8 on the prediction of systemic clearance (A), oral clearance (B) of repaglinide, and the fraction of repaglinide escaping metabolism by the gut (F_G) (C) and by the liver (F_H) (D). Low, medium and high hepatic CYP3A4 expression relate to abundances of <100, 100–199 and ≥200 pmol mg^–1 in microsomal protein, respectively. Blue and red boxes represent simulation of individuals assuming no correlation and correlation between CYP3A4 and CYP2C8, respectively. Closed circles indicate outliers that are beyond the quartiles by one‐and‐a‐half interquartile range

Prediction of repaglinide DDI

Simulated plasma repaglinide concentration profiles, after a single oral dose of 0.25 mg repaglinide without or with pretreatment with 600 mg gemfibrozil twice daily in 1000 virtual individuals generated assuming no correlation and correlation between CYP3A4 and CYP2C8, were comparable to observed data from the published clinical trial 19 (Figure 4). Mean values of the predicted AUC and C _max without and with gemfibrozil were within 1.5‐fold of the observed values (AUC: no correlation, 7.1 vs. 35.0 ng h⁻¹ ml⁻¹; intercorrelation, 6.0 vs. 27.7 ng h⁻¹ ml⁻¹; observed, 4.8 vs. 29.3 ng h⁻¹ ml⁻¹, and C _max: no correlation, 3.4 vs. 7.3 ng ml⁻¹; intercorrelation, 3.0 vs. 6.5 ng ml⁻¹; observed, 3.7 vs. 8.1 ng ml⁻¹) 19. Median CVs of the predicted AUC and C _max without and with gemfibrozil were similar between no correlation and intercorrelation scenarios (without gemfibrozil: AUC, 53.3% and 50.7%; C _max, 35.7% and 36.9%, and with gemfibrozil: AUC, 31.1% and 35.8%; C _max, 21.0% and 22.7%), but were lower than the observed values (without gemfibrozil: AUC, 89.8%; C _max, 71.3%, and with gemfibrozil: AUC, 26.3%; C _max, 39.7%) 19. Figure 5 shows the predicted AUC and C _max ratios (DDI/control) of repaglinide for 100 trials in 10 virtual individuals generated assuming no correlation and in the presence of correlation between hepatic CYP3A4 and CYP2C8, compared with reported clinical data (observed AUC ratio: mean, 6.1; range, 2.6–12, and C _max ratio: mean, 2.2; range, 1.4–2.9) 19. Median values of predicted AUC ratio were similar between virtual populations assuming no correlation and in the presence of intercorrelation (4.72 vs. 4.42), but the 5th and 95th percentiles were different between the two virtual populations (2.48–11.29 vs. 2.49–9.69). The range of predicted AUC ratio from minimum to maximum was larger for virtual populations assuming no correlation than that for those assuming intercorrelation (1.55–77.06 vs. 1.79–25.15). Predicted AUC ratios at higher than the maximum observed in clinical data (12‐fold) 19 were observed in 39 and 21 virtual individuals from simulations without and with the intercorrelation, respectively. Median values and 5th and 95th percentiles of predicted C _max ratio were almost the same between virtual populations assuming no correlation and those with the intercorrelation (median, 2.05 vs. 2.02; 5th and 95th percentiles, 1.46–3.72 vs. 1.45–3.69). However, the range of predicted C _max ratio from minimum to maximum was larger for virtual populations assuming no correlation than for populations with the intercorrelation (1.18–15.15 vs. 1.26–6.98). Predicted C _max ratios of more than the maximum observed in clinical data (2.9‐fold) 19 were generated in 145 and 137 virtual individuals without and with the intercorrelation, respectively.

Figure 4.

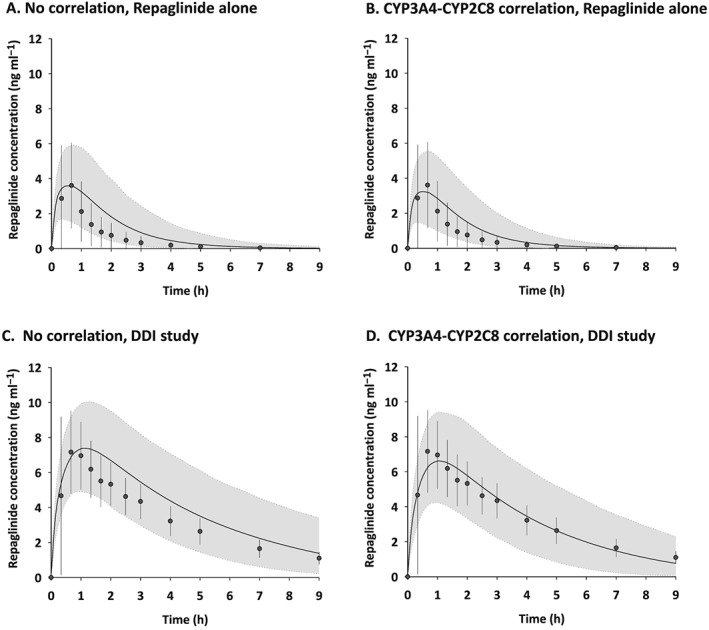
Simulated and observed plasma repaglinide concentration profiles after a single oral dose of 0.25 mg repaglinide without (A and B) and with pretreatment (C and D) of 600 mg gemfibrozil twice daily in virtual individuals generated assuming no correlation and correlation between CYP3A4 and CYP2C8. Simulations are presented as mean of all 10 trials (black solid lines) and 5th and 95th percentiles (grey areas). Observed data extracted from the literature 19 are presented as mean (closed circles) and standard deviation (error bars)

Figure 5.

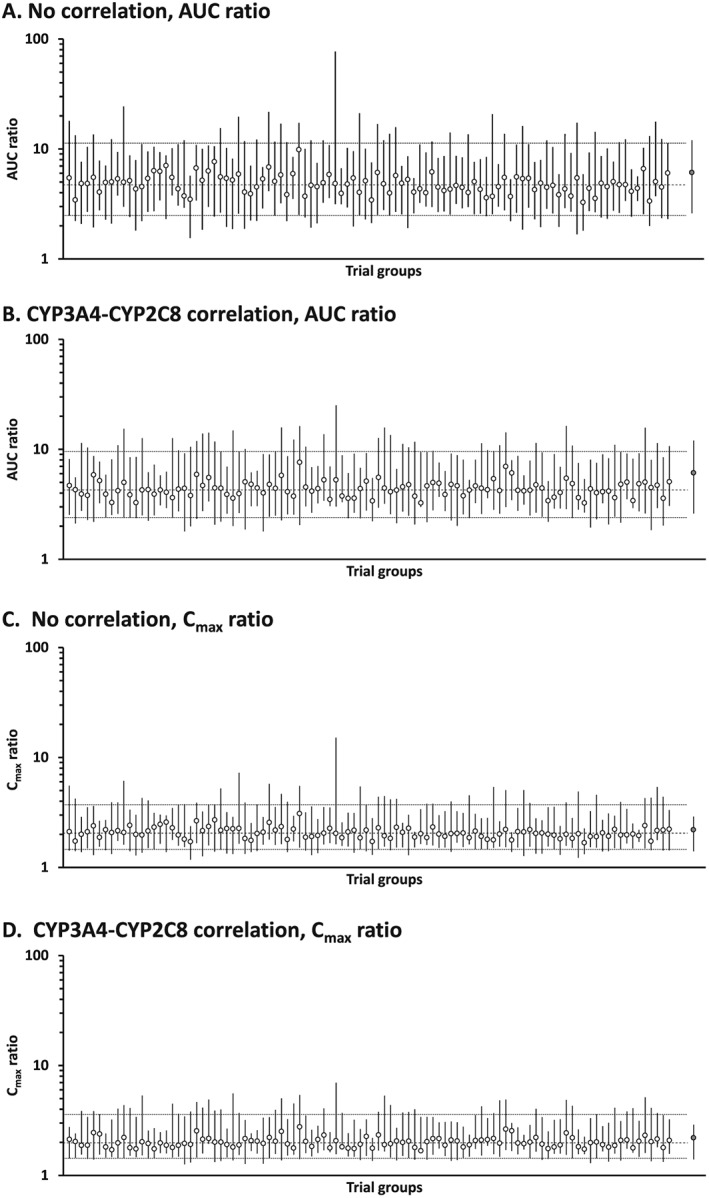
Predicted AUC ratio and C _max ratio (DDI/control) of repaglinide for 100 trials in 10 virtual individuals generated assuming no correlation (A and C) and correlation between hepatic CYP3A4 and CYP2C8 (B and D). Open and closed circles indicate simulated median (range) in each trial, and observed mean (range) extracted from the literature 19, respectively. Dashed and dotted lines represent median and 5th/95th percentiles of total simulated population, respectively

Cumulative distribution plots for predicted oral clearance, AUC ratio, and C _max ratio are shown for 1000 virtual individuals generated assuming no correlation and correlation between hepatic CYP3A4 and CYP2C8 (Figure 6). Individual values for CYP3A4–CYP2C8 correlation were normalized by the corresponding mean values for no correlation. Distributions for predicted AUC ratio were unequal between virtual individuals generated assuming no correlation and intercorrelation (P = 0.026), but those for oral clearance and C _max were not significantly different (P = 0.40 and P = 0.18, respectively). The frequency distributions were wider for predicted oral clearance and tighter for AUC ratio and C _max ratio in the virtual population assuming CYP3A4–CYP2C8 correlation than in the absence of intercorrelation. Extreme values were seen in both ends (1–5% and 95–99%) of the cumulative distribution for the predicted AUC ratio in the absence of intercorrelation (Figures 6E and 6H).

Figure 6.

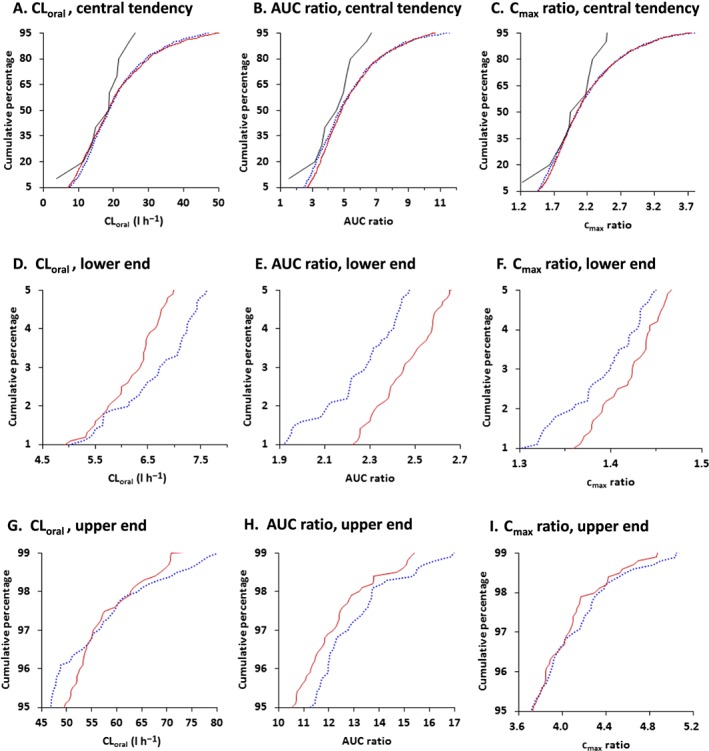
Cumulative distribution plots for predicted oral clearance (CL_oral), AUC ratio and C _max ratio (DDI/control) of repaglinide for 1000 virtual individuals generated assuming no correlation (dotted blue lines) and correlation (solid red lines) between hepatic CYP3A4 and CYP2C8. Predicted values for CYP3A4–CYP2C8 correlation were normalized by the corresponding mean values for no correlation. Cumulative distributions are shown as central tendency (5–95%; A, B, C), lower end (1–5%; D, E, F), and upper end (95–99%; G, H, I) in frequency distribution. Solid black lines represent cumulative distribution for observed oral clearance, AUC ratio and C _max ratio which were normalized by the corresponding median values for no correlation 19

Interindividual variability in clearance and DDI of repaglinide

CVs of oral clearance and predicted DDI (AUC ratio and C _max ratio) in 10 to 100 trials were compared between virtual populations generated assuming no correlation and correlation between CYP3A4 and CYP2C8 (Figure 7). Median CV of oral clearance in the 10 trials was 43.2% in the absence of intercorrelation between enzymes and 49.3% when CYP3A4–CYP2C8 abundances were considered to be intercorrelated. This difference in the median CV of oral clearance became smaller in the 100 trials (52.5% vs. 54.2%). In contrast, median CV of AUC ratio in the 100 trials was reduced from 46.0% in the absence of intercorrelation between the two enzymes to 43.8% when the intercorrelation was incorporated into the virtual population, with the exception of opposite results seen in the minimum number of trials (the 10 trials). Median CV of predicted C _max ratio was almost the same between virtual populations assuming no correlation and intercorrelation regardless of numbers of trials.

Figure 7.

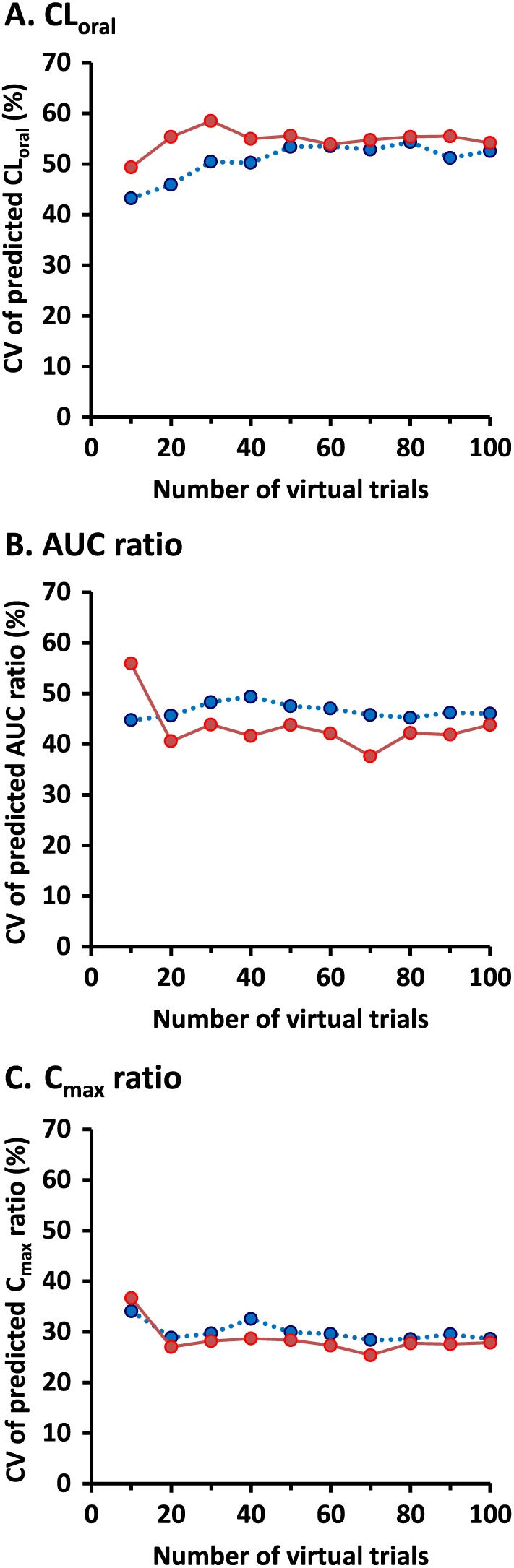
Coefficients of variation (CVs) in predicted oral clearance (CL_oral), AUC ratio and C _max ratio (DDI/control) of repaglinide for 10 to 100 trials in 10 virtual individuals generated assuming no correlation (dotted blue line and circles) and correlation between hepatic CYP3A4 and CYP2C8 (solid red line and circles)

Discussion

This report constitutes a proof‐of‐principle study to highlight the importance of intercorrelation between the hepatic amounts of two drug‐metabolizing enzymes in the prediction of interindividual variabilities in drug clearance and DDIs. The present study demonstrates, for the first time, that population‐based PBPK modelling incorporating such intercorrelation led to more consistent estimation of extreme values than those observed in interindividual variability of drug clearance and DDI. It should be the norm, rather than the exception, to consider this information when using population‐based PBPK models. Otherwise, a PBPK model that does not accurately consider the intercorrelation runs the risk of generating implausible combinations of physiological parameters. Furthermore, a more realistic prediction of interindividual variability of drug clearance may help to more accurately estimate the theoretically conceivable extreme risks of DDIs. This has clear implications for drug development and clinical drug use. A large interindividual variability in DDIs usually warrants additional caution in recommendation of dose adjustment, even if the average effect of DDI is tolerable based on the safety margin of the substrate drug. Therefore, incorporation of such correlation into a PBPK model should be considered in investigating the DDI risk and is likely to be particularly important for prediction of the clinical consequences of the DDI in individual patients.

A virtual population assuming intercorrelation between CYP3A4 and CYP2C8 was developed based on actual data on HLM enzyme abundance. The abundances of hepatic CYP2C8 and CYP3A4 were compared between virtual individuals generated assuming no correlation and correlation between two enzymes (Figure 2). Simcyp generates individual values of CYP2C8 abundance independently based on population mean and CV by default. Therefore, default virtual individuals with high and low CYP3A4 protein content can be accompanied by underestimated and overestimated values of CYP2C8 abundance, respectively. Although the interindividual variability of CYP2C8 and CYP3A4 protein expression in liver is high, the protein expression is correlated between the two enzymes 12, 20. Virtual individuals assuming correlation between the two enzymes with residual variability of 47%, which was estimated from linear regression analysis using hepatic CYP3A4 and CYP2C8 abundance data, were more reflective of an actual correlation between HLM CYP3A4 and CYP2C8 protein expression than those with residual variability of 0% and 100% (Figure 2B–C). These findings indicate that incorporation of an appropriate CV describing residual variability in CYP2C8 protein expression is important to generate virtual individuals assuming intercorrelation between two enzymes. The HLM sample of the individual with the highest CYP2C8 and CYP3A4 abundance (Figure 1A) may be derived from a CYP2C8 extensive metabolizer, such as individuals with CYP2C8*1/*3 genotype, who show a high metabolic clearance of repaglinide 27. However, CYP2C8 genotypes were unknown for the HLM samples used in this analysis.

The PBPK model assuming CYP3A4–CYP2C8 intercorrelation predicted the pharmacokinetic parameters of repaglinide, which is metabolized by CYP2C8 and CYP3A4. As expected, the individuals at the extreme ends of CYP3A4 abundance showed similar trends in the assigned CYP2C8 abundances reported for the population in the simulation outcome (Figure 2C). The CYP2C8‐mediated pathway displays high clearance under the assumption of intercorrelation when the CYP3A4‐mediated pathway shows high clearance, and consequently the overall clearance becomes a higher value. The incorporation of the intercorrelation into a PBPK model produced a greater median CV of oral clearance in the 10 trials of 10 virtual individuals than that in the default virtual individuals (Figure 7A). However, the difference in the median CV of oral clearance became small when the number of trials was increased. This does not mean that the increased number of trials in the default virtual population provided interindividual variability of oral clearance similar to the virtual population assuming intercorrelation. These findings suggested that the increased number of trials led to increase in the risk of physiologically implausible assignment of higher CYP2C8 abundance in the default virtual individuals with low hepatic CYP3A4 expression, resulting in implausible contribution of CYP2C8‐mediatated metabolism to oral clearance. Oral clearance was slightly higher in virtual individuals assuming intercorrelation than in the default individuals (Figure 3B). This may be associated with the improvement in simulated plasma concentration profiles of repaglinide when considering the intercorrelation (Figure 4B and 4D). These findings imply that a PBPK model ignoring a significant positive correlation between two enzymes underestimates the interindividual variability of oral clearance. These results are consistent with a previous report showing that a PBPK incorporating CYP3A4–CYP3A5 intercorrelation predicted more physiologically realistic estimates of population drug clearance and aided in the identification of extreme individuals 13.

Previous studies have demonstrated that a repaglinide PBPK model was useful to quantitatively predict several repaglinide DDIs, including the complex interaction with gemfibrozil 28, 29, 30. However, these PBPK approaches focused on the prediction of average DDI effects. Here, we examined the difference in the outcome of DDI prediction using a repaglinide PBPK model between virtual populations assuming and ignoring CYP3A4–CYP2C8 intercorrelation. Even though the average DDI effect was comparable between the two virtual populations, the interindividual variability of DDI effect could be more reflective of realistic CYP2C8 abundance in a virtual population assuming the intercorrelation (Figure 5). The DDI simulation in a virtual population assuming intercorrelation also provided a smaller maximum DDI effect than that in a virtual population ignoring the correlation. Ignoring a CYP3A4–CYP2C8 intercorrelation produced higher CYP2C8/CYP3A4 ratios in virtual individuals with low CYP3A4 protein (Figure 2A). High CYP2C8/CYP3A4 ratios correspond to a larger contribution of CYP2C8‐mediated pathway to repaglinide metabolism, resulting in high sensitivity to inhibition of CYP2C8. These findings suggest that the default model ignoring intercorrelation may overestimate the maximum DDI effect. PBPK simulation assuming intercorrelation between drug‐metabolizing enzymes may be an important approach to predict the theoretically conceivable extreme effects of DDI. These simulations based on DDI with gemfibrozil do not account for the impact of CYP3A4 inhibition on the intercorrelation because gemfibrozil is only an inhibitor of CYP2C8 and OATP1B1. This effect can be explored using other dual CYP3A4/CYP2C8 substrates, such as montelukast, pioglitazone and paclitaxel.

Theoretically conceivable interindividual variability in DDI effect under various assumptions regarding the intercorrelations was investigated and compared with clinical observations 19. CV of predicted DDI (as measured by AUC ratio) was reduced from 46.0% in the absence of intercorrelation between enzymes to 43.8% when the intercorrelation was incorporated into the virtual population (Figure 7). These CVs were associated with 5th and 95th percentiles of predicted DDI (2.48–11.29 vs. 2.49–9.69) (Figure 5). Distributions of the predicted AUC ratio were statistically different in populations of 1000 virtual individuals generated assuming no correlation and intercorrelation. The range of predicted DDI was larger in the absence of intercorrelation (1.55–77.06) than when incorporating intercorrelation (1.79–25.15), which was closer to clinical observations (2.6–12). Predicted DDI at more than 12‐fold in AUC ratio, which is the maximum observed in the clinical study 19, was more frequent in the absence of intercorrelation. Some of the extreme values might be an artefact of the model leading to virtual individuals who do not exist in real populations, though this finding cannot be confirmed unless a larger study is performed. This may be supported by other clinical observations that the maximum of AUC_0–∞ ratio after pretreatment with 600 mg of gemfibrozil twice daily is 15‐fold even when including other clinical trial designs 18, 19, 31. Prediction of DDIs using PBPK models is usually simulated in 10 (or 20) virtual trials which are used as an indication of consistency between the model and observed data rather than what the model can offer. The lower CVs for predicted DDI considering the intercorrelation were not changed by the increased number of trials except for the opposite results in the minimum number of trials (the 10 trials) (Figure 7B). This result suggests that accurate prediction of interindividual variability in DDIs is achieved by the incorporation of the intercorrelation into a PBPK model rather than the increase in the number of virtual trials.

PBPK modelling started out along the line of naïve pooled average predictions, mainly because of computational limitations 32. Precise prediction aiming to individualize dosing is becoming more important 1, and crucially requires the ability to accurately describe interindividual variability within PBPK modelling. Considering interindividual variability, a standard deviation is more informative than just an average, and a probability distribution is even more informative 33. Accurate prediction of interindividual variability is an important challenge that PBPK modelling needs to address to expand into new areas of application, such as precision dosing and virtual bioequivalence 1, 33, but it requires proteomic data of sufficient quality 11. Data used in the present analysis of intercorrelation and variability of hepatic CYP3A4 and CYP2C8 abundances were comparable to published meta‐analysis data (n = 134) 12 (Spearman correlation, 0.62 vs. 0.68; CV for CYP3A4, 77% vs. 81%; CV for CYP2C8, 87% vs. 68%) 12, 20. The influence of the regression parameter estimates for intercorrelation on the predicted clearance and DDI of repaglinide was confirmed using a regression model produced by excluding the data point with the highest value for CYP3A4. Although the regression parameter under exclusion of the single extreme values for high abundance of enzymes resulted in slightly different values of predicted oral clearance, they had a modest effect on predicted interindividual variabilities in oral clearance, AUC ratio and C _max ratio. The present study does not rule out other unidentified factors for accurate prediction of interindividual variability in drug clearance and DDIs, though it demonstrates the importance of hepatic enzymes intercorrelations.

Many drugs are metabolized by more than one drug‐metabolizing enzyme, such as CYP and uridine 5′‐diphospho‐glucuronosyltransferase (UGT) enzymes. Uptake and efflux transporters also mediate drug disposition through controlling membrane transport, such as absorption in the small intestine, uptake into hepatocytes and renal secretion. Therefore, knowledge of the protein expression of drug‐metabolizing enzymes and drug transporters is important in predicting drug clearance and DDIs in more realistic virtual populations. Statistically significant positive correlations can be found in enzyme abundance between not only CYP enzymes, but also between UGT enzymes and across CYP and UGT families 20. However, there is insufficient data in the literature about intercorrelation between drug‐metabolizing enzymes and drug transporters and their effects. Therefore, it is unknown whether drug‐metabolizing enzymes correlate with OATP1B1, which is known to contribute to the disposition of repaglinide. Construction of comprehensive network information for intercorrelation between pharmacokinetics‐related proteins is expected to generate more realistic virtual populations. The current version of the Simcyp Simulator provides an enzyme intercorrelation module based on a simple regression analysis. Regression analysis using centring may be adopted in future studies because it would be useful to infer biological interpretations for the intercept of the regression equation in relation to mean abundance.

In conclusion, incorporation of intercorrelation between the hepatic amounts of two drug‐metabolizing enzymes into a PBPK model could more accurately predict interindividual variabilities of drug clearance and DDI, corresponding to protein abundance generated assuming a significant positive correlation between two enzymes in the liver. It is suggested that DDI studies using virtual populations assuming intercorrelation can help to estimate theoretically conceivable extreme risk of DDIs. PBPK modelling and simulation should be focused on improvement in prediction of not only average values but also interindividual variability of DDI effect. A middle‐out approach to PBPK modelling is used extensively with parameter estimation in order to provide a reasonable characterization of clinical pharmacokinetic data 34. Without accurately considering intercorrelation, the estimated parameter variability would not be reflective of ‘true’ variability. This produces an increased risk of inaccurate prediction in other scenarios (e.g. DDIs) when perturbing the model, except when simply fitting PBPK models to observed clinical data. As the intercorrelations more realistically reflect enzyme abundances, virtual population studies involving PBPK and DDI should avoid using Monte Carlo assignment of enzyme abundance independently, when robust information on correlation exists. In the absence of information on intercorrelation of the enzyme abundance, implications of potential correlation for predicted variability should be borne in mind, where the potential impact can be evaluated as per the approach described herein.

Competing Interests

There are no competing interests to declare.

The authors would like to acknowledge the fruitful comments and discussion made by Dr Sibylle Neuhoff of Simcyp Limited (a Certara Company) and by the members at the Centre for Applied Pharmacokinetic Research (CAPKR), the University of Manchester.

Contributors

K.D., A.S.D. and A.R.H. participated in research design. K.D. and A.S.D developed the PBPK models. K.D., A.S.D. and B.A. performed data analysis. A.T. and J.T.B provided observed data from the reported clinical study. K.D., A.S.D., B.A. and A.R.H. interpreted the data. K.D. drafted the manuscript. All authors provided critical revisions to the manuscript and provided their approval for submission.

Doki, K. , Darwich, A. S. , Achour, B. , Tornio, A. , Backman, J. T. , and Rostami‐Hodjegan, A. (2018) Implications of intercorrelation between hepatic CYP3A4‐CYP2C8 enzymes for the evaluation of drug–drug interactions: a case study with repaglinide. Br J Clin Pharmacol, 84: 972–986. doi: 10.1111/bcp.13533.