Three-Material Decomposition in Multi-energy CT: Impact of Prior Information on Noise and Bias

Abstract

In order to perform material decomposition for a three-material mixture, dual-energy CT (DECT) has to incorporate an additional condition, typically the prior information related to certain physical constraints such as volume or mass conservation. With the introduction of photon-counting CT and other multi-energy CT (MECT) platform, more than 2 energy bins can be simultaneously acquired, which in principle can solve a three-material problem without the need of additional prior information. The purpose of this work was to investigate the impact of prior information on noise and bias properties of three-material decomposition in both DECT and MECT, and to evaluate if the prior information is still needed in MECT. Computer simulation studies were performed to compare basis image noise and quantification accuracy among DECT with prior information, and MECT with/without prior information. For given spectral configurations, the simulation results showed that significant noise reductions can be achieved in all the basis material images when prior information was included in the material decomposition process. Compared to DECT with prior information, MECT (N=3) with prior information had slightly better noise performance due to additional beam measurement and well preserved spectral separation. In addition, when wrong prior information ([−2.0%, 2.0%]) was intentionally introduced, the quantification accuracy evaluated by root-mean-square-error (RMSR) using MECT with prior information was less than 1.5mg/cc for gadolinium quantification and 1.2mg/cc for iodine quantification.

1. Introduction

Dual-energy CT (DECT) can quantify up to three materials in a mixture when prior information (e.g., volume/mass conservation) is applied as an additional physical constraint in addition to two spectral measurements [1, 2]. With the introduction of energy resolved photon-counting CT (PCCT) and other multi-energy CT (MECT) platform [3–7], more than 2 energy bins can be simultaneously acquired, which in principle can provide a stable solution to the three-material problem without the need of additional prior information, given that at least one of the materials has a distinctive K-edge. It remains unclear, however, if the prior information can still be beneficial in three- or multi-material decomposition in MECT.

The purpose of this study was to investigate the impact of prior information on noise and bias properties of three-material decomposition in both DECT and MECT. Both theoretical analysis and computer simulation were conducted for an imaging task involving three materials, iodine (I), gadolinium (Gd), and water, mimicking the application of multi-phase liver imaging in a single DECT/MECT scan. The prior information applied in this work is specifically the volume conservation. The impact of wrong prior information up to ±2.0% caused by violation of volume conservation was also analyzed.

2. Methods

2.1 Computer Simulation of DECT/MECT

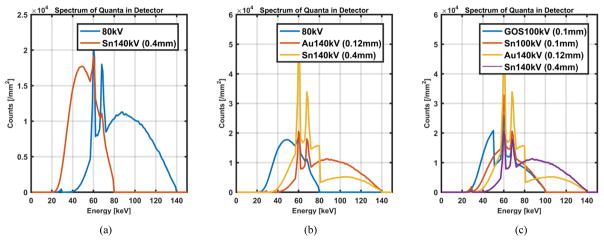
All the studies were performed using a simulation tool (DRASIM, Siemens Healthcare). A cylindrical water phantom in a diameter of 20 cm containing 8 inserts, including 3 I solutions (4, 6, 8 mg/cc), 3 Gd solutions (4, 6, 8 mg/cc), and 2 I/Gd mixtures (6/6, 4/4 mg/cc), was used in the simulation. The mass density in each solution was determined assuming volume conservation. Without loss of generality, the X-ray beam and spectra in DECT were based on a dual-energy scan configuration: 80kV/Sn140kV (Sn: 0.4mm) on a dual-source CT scanner (Flash, Siemens Healthcare) (Figure 1a), and the spectra in MECT were represented by the three/four energy beams similar to those in Ref [5]. In the MECT with triple-beam configuration (Figure 1b), one of the energy spectra was identical to the 80 kV beam in the DECT configuration whereas the other two were generated based on a “Twin Beam” design through adding a split filter (0.4mm Sn and 0.12mm Au) on the 140kV beam. In the MECT with quadruple-beam configuration (Figure 1c), two low energy spectra were generated from the 100 kV beam with one split filter (0.1mm GOS and 0.1mm Sn), whereas the other two were from the 140 kV beam with another split filter (0.4mm Sn and 0.12mm Au) which is identical to the high energy beams as in the triple-beam configuration. The selection of MECT spectra, especially with triple-beam configuration, was demonstrated to have similar or better spectral separation and noise performance as in a PCCT. The tube current-time products (mAs) were determined to match the total radiation dose output in DECT and MECT (CTDIvol: 16.4mGy).

Figure 1.

X-ray beams and spectra used in simulation of DECT and MECT.

2.2 Material Decomposition Method

To analyze the noise performance with and without prior information, a generic image-based material decomposition method without any noise reduction was used. A filtered-backprojection (FBP) method was employed to reconstruct images, based on which material decomposition was performed through solving linear equations for each pixel using Eq. (1), where n = 2 for DECT, n ≥ 3 for MECT, μ(E) was the linear attenuation coefficient (LAC) at energy E from measurements, and $\left(\frac{\mu }{{\rho }_{m0}}\right)(E)$ was the mass attenuation coefficient (MAC) at energy E for material m. Volume conservation was referred as $1={\sum }_{m=1}^3\frac{{\rho }_m}{{\rho }_{m0}}$ where ρ_m and ρ_m0 represented mass density in mixture and in its pure form for material m. In MECT, the equation system was overdetermined and solved using a least square optimization method. The coefficient matrix μ_m(E) was determined beforehand by a calibration procedure.

$$\begin{gathered} \{\begin{array}{c}\mu (E_1)={\sum }_{m=1}^3\left(\frac{\mu }{{\rho }_{m0}}\right)(E_1)·{\rho }_m\\ \mu (E_2)={\sum }_{m=1}^3\left(\frac{\mu }{{\rho }_{m0}}\right)(E_2)·{\rho }_m\\ ⋮\\ \mu (E_n)={\sum }_{m=1}^3\left(\frac{\mu }{{\rho }_{m0}}\right)(E_n)·{\rho }_m\\ 1={\sum }_{m=1}^3\frac{{\rho }_m}{{\rho }_{m0}}\end{array} \\ {\mu }_{\mathit{DECT}\_p}=\left[\begin{array}{ccc}\left(\frac{\mu }{{\rho }_{10}}\right)(E_1)& \left(\frac{\mu }{{\rho }_{20}}\right)(E_1)& \left(\frac{\mu }{{\rho }_{30}}\right)(E_1)\\ \left(\frac{\mu }{{\rho }_{10}}\right)(E_2)& \left(\frac{\mu }{{\rho }_{20}}\right)(E_2)& \left(\frac{\mu }{{\rho }_{30}}\right)(E_2)\\ 1/{\rho }_{10}& 1/{\rho }_{20}& 1/{\rho }_{30}\end{array}\right]{\mu }_{\mathit{MECT}}=\left[\begin{array}{ccc}\left(\frac{\mu }{{\rho }_{10}}\right)(E_1)& \left(\frac{\mu }{{\rho }_{20}}\right)(E_1)& \left(\frac{\mu }{{\rho }_{30}}\right)(E_1)\\ \left(\frac{\mu }{{\rho }_{10}}\right)(E_2)& \left(\frac{\mu }{{\rho }_{20}}\right)(E_2)& \left(\frac{\mu }{{\rho }_{30}}\right)(E_2)\\ & ⋮& \\ \left(\frac{\mu }{{\rho }_{10}}\right)(E_n)& \left(\frac{\mu }{{\rho }_{20}}\right)(E_n)& \left(\frac{\mu }{{\rho }_{30}}\right)(E_n)\end{array}\right]{\mu }_{\mathit{MECT}\_p}=\left[\begin{array}{ccc}\left(\frac{\mu }{{\rho }_{10}}\right)(E_1)& \left(\frac{\mu }{{\rho }_{20}}\right)(E_1)& \left(\frac{\mu }{{\rho }_{30}}\right)(E_1)\\ \left(\frac{\mu }{{\rho }_{10}}\right)(E_2)& \left(\frac{\mu }{{\rho }_{20}}\right)(E_2)& \left(\frac{\mu }{{\rho }_{30}}\right)(E_2)\\ & ⋮& \\ \left(\frac{\mu }{{\rho }_{10}}\right)(E_n)& \left(\frac{\mu }{{\rho }_{20}}\right)(E_n)& \left(\frac{\mu }{{\rho }_{30}}\right)(E_n)\\ 1/{\rho }_{10}& 1/{\rho }_{20}& 1/{\rho }_{30}\end{array}\right] \end{gathered}$$ (1)

2.3 Noise Magnification Analysis

The overall noise magnification effect was analyzed through determining the condition number of the coefficient matrix in Eq. (1). Specifically, the coefficient matrices for DECT with prior, and MECT without/with prior were listed after Eq. (1). The condition numbers were directly calculated using the definition for square coefficient matrix such as $\mathit{cond}\left({\mu }_{{\mathit{DECT}}_p}\right)=\Vert {\mu }_{{\mathit{DECT}}_p}\Vert \Vert {\mu }_{\mathit{DECT}\_p}^{-1}\Vert$ and $\mathit{cond}\left({\mu }_{\mathit{MECT},N=3}\right)=\Vert {\mu }_{\mathit{MECT},N=3}\Vert \Vert {\mu }_{\mathit{MECT},N=3}^{-1}\Vert$. For non-square coefficient matrix such as μ_{MECT,N = 4}, the condition numbers were calculated as $\mathit{cond}\left({\mu }_{\mathit{MECT},N=4}\right)=\Vert {\mu }_{\mathit{MECT},N=4}\Vert \Vert {\mu }_{\mathit{MECT},N=4}^{†}\Vert$, where ${\mu }_{\mathit{MECT},N=4}^{†}$ is called the Moore-Penrose pseudoinverse of μ_{MECT,N = 4}. Quantification accuracy and noise performance of each basis material was also analyzed and compared.

3. Results

3.1 Noise Magnification Analysis

The condition numbers of coefficient matrices for DECT with prior, and MECT (N=3, 4) with/without prior were calculated in Table 1. With prior information, both MECT with triple- and quadruple- configuration yielded smaller condition numbers, and therefore less noise magnifications were expected.

Table 1.

Condition number calculation of coefficient matrices for different scan configurations

Scan configuration	DECT w/Prior	MECT (N=3) w/o Prior	MECT (N=3) w/Prior	MECT (N=4) w/o Prior	MECT (N=4) w/Prior
Condition number	17.86	490.52	15.89	301.12	22.06

3.2 Material Decomposition Images

Figure 2 showed I (top row), Gd (middle row), and water (bottom row) maps acquired using DECT with prior (a–c), MECT (N=3) without prior (d–f), MECT (N=3) with prior (g–i), MECT (N=4) without prior (j–l), and MECT (N=4) with prior (m–o). Visually, one can see that lower noises can be achieved with the prior information. The observations in Figure 2 were consistent well with the aforementioned noise magnification analysis.

Figure 2.

Material decomposition results determined by DECT with prior, and MECT without/with prior.

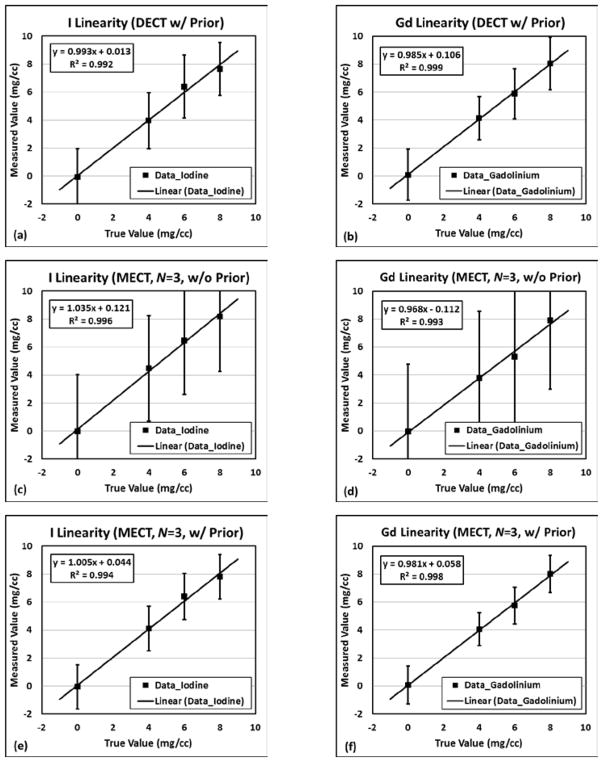
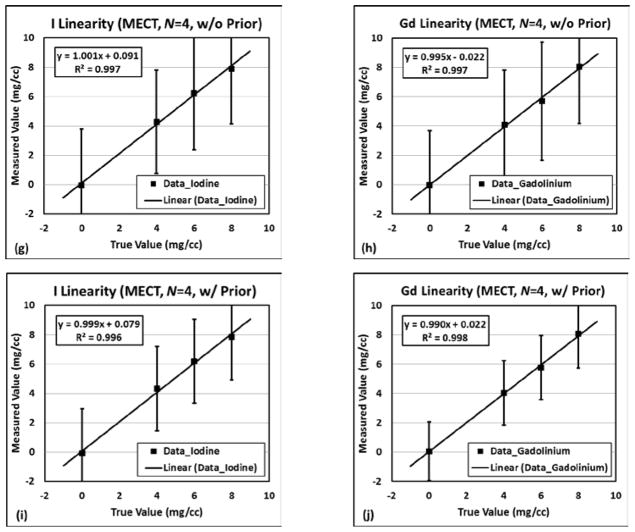
In terms of quantification accuracy, all the measurements in DECT and MECT with/without prior information performed linearly with nominal I/Gd concentrations, with R²>0.99, slopes ranged in between 0.968 and 1.035, and intercepts falling between −0.122 and 0.121, as demonstrated in Figure 3. The error bars also indicated better noise performances when prior information was incorporated into the material decomposition.

Figure 3.

Quantification accuracy results for I and Gd: (a)–(b) DECT with prior; (c)–(d) MECT (N=3) without prior; (e)–(f) MECT (N=3) with prior; (g)–(h) MECT (N=4) without prior; (i)–(j) MECT (N=4) with prior

3.3 Impact of wrong prior information

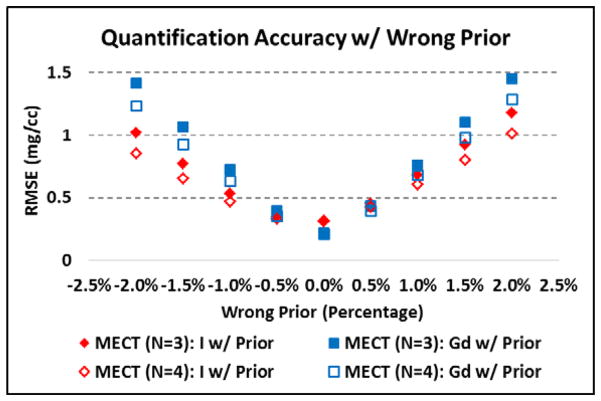
Since volume conservation is not always true, we investigated the impact of violation of volume conservation up to ±2.0%. As demonstrated in Figure 4, as the percentage of the wrong prior information increases, the quantification accuracy represented by root-mean-square-error (RMSE) was degraded in both of the triple- and quadruple-beam configurations in MECT, with the maximum value less than 1.5mg/cc for Gd quantification and 1.2mg/cc for I quantification.

Figure 4.

Material quantification accuracy with wrong prior information.

4. Conclusions

We investigated the impact of prior information on a three-material decomposition task for a mixture of I, Gd, and water in DECT and MECT. With given spectral configurations, both theoretical analysis and simulation results showed significant noise reductions when prior information was included in the material decomposition process. Meanwhile, similar or even better quantification accuracies can be achieved. When wrong prior information up to ±2.0% was intentionally introduced, quantification biases were observed but within reasonable ranges with RMSEs less than 1.5mg/cc for Gd quantification and 1.2mg/cc for I quantification.