The Effect of Biomechanical Variables on Force Sensitive Resistor Error: Implications for Calibration and Improved Accuracy

Abstract

Force Sensitive Resistors (FSRs) are commercially available thin film polymer sensors commonly employed in a multitude of biomechanical measurement environments. Reasons for such wide spread usage lie in the versatility, small profile, and low cost of these sensors. Yet FSRs have limitations. It is commonly accepted that temperature, curvature and biological tissue compliance may impact sensor conductance and resulting force readings. The effect of these variables and degree to which they interact has yet to be comprehensively investigated and quantified. This work systematically assesses varying levels of temperature, sensor curvature and surface compliance using a full factorial design-of-experiments approach. Three models of Interlink FSRs were evaluated. Calibration equations under 12 unique combinations of temperature, curvature and compliance were determined for each sensor. Root mean squared error, mean absolute error, and maximum error were quantified as measures of the impact these thermo/mechanical factors have on sensor performance. It was found that all three variables have the potential to affect FSR calibration curves. The FSR model and corresponding sensor geometry are sensitive to these three mechanical factors at varying levels. Experimental results suggest that reducing sensor error requires calibration of each sensor in an environment as close to its intended use as possible and if multiple FSRs are used in a system, they must be calibrated independently.

Introduction

Quantifying biomechanical forces between medical devices and human soft tissue has important implications for comfort, reducing tissue injury and improving device design (Dabling et al., 2012; Lebosse et al., 2011; Mak et al., 2010). Typical measurement of these interactions requires a sensor positioned at the interface between the tissue and medical device. Many biomechanical sensors are described in literature including those based on capacitance, fluid pressure, or optics (Dabling et al., 2012), with one of the more prevalent sensors being Force Sensitive Resistors (FSRs). FSRs are constructed of thin polymer films and change resistance with the application of pressure. With sensor thicknesses as little as 0.2 mm (Dabling et al., 2012), FSRs can be positioned between two contacting surfaces with little mechanical impact on the substrates. FSRs require minimal signal conditioning, and are easily integrated with hobbyist micro-controllers through advanced data acquisition systems. FSRs are inexpensive compared to similar technologies (Dabling et al., 2012; Lebosse et al., 2011), making them an attractive option for research and clinical applications.

FSRs have been employed in numerous biomechanical applications from prosthetic control and pressure measurements (Hebert et al., 2014; Junaid et al., 2014; Silver-Thorn et al., 1996) through gait studies (Moon et al., 2011; Rueterbories et al., 2010) and telerobotics (Yun et al., 1997) among many other biomechanical applications quantifying interface mechanics (Cascioli et al., 2011; Di Fazio et al., 2011).

However, FSRs have limitations; sensor drift and hysteresis have been shown to impact repeatability and accuracy in existing systems (Dabling et al., 2012, Herbert-Copley et al., 2013). Additionally, changes in accuracy and increases in drift error when curvature is applied to the sensors have been shown in prosthetic applications (Polliack et al., 2000), but can be minimized by calibration in the same curved configuration (Buis and Convery, 1997).

FSR manufacturers often recommend calibration and operating conditions to include flat, rigid surfaces at room temperature (Interlink Electronics, 2015; TekScan, 2015). Yet the human body hosts unavoidable curvatures, soft tissue compliances, and temperature differentials. The error imparted by these variables has yet to be comprehensively investigated, preventing researchers and clinicians from understanding the implications of their biological testing environment on sensor accuracy.

Objectives

This work investigates the effects of common biomechanical variables on FSR error with the intent of examining calibration practises and providing recommendations to improve accuracy in a clinical-research environment.

Methods

Variable Testing

Experimental Variables

A full factorial design-of-experiments approach was used (Montgomery D.C., 2012). Twelve unique combinations of temperature, curvature and compliance were introduced to each FSR in a semi-randomized order (Table 1). Temperature was evaluated at room (21°C) and body (37°C) temperature; curvature at the diameter of a 95^th percentile male thigh (215 mm), diameter of a 5^th percentile female wrist (44 mm) (NASA, 2008) and a flat surface; and material compliance of a human soft tissue analog (SynDaver Labs, Tampa, USA) and a rigid surface.

Table 1.

Combinations of Biomechanical Variables Tested

Combination	Temperature (°C)	Curvature (Diameter mm)	Compliance
1	21°C	215 mm	Rigid
2	21°C	44 mm	Rigid
3	21°C	Flat	Rigid
4	21°C	215 mm	Soft
5	21°C	44 mm	Soft
6	21°C	Flat	Soft
7	37°C	215 mm	Rigid
8	37°C	44 mm	Rigid
9	37°C	Flat	Rigid
10	37°C	215 mm	Soft
11	37°C	44 mm	Soft
12	37°C	Flat	Soft

Setup and Procedure

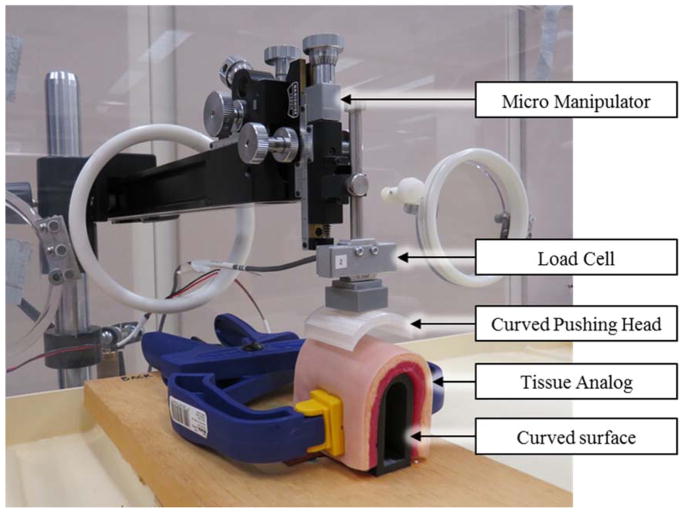
Interlink FSRs were selected for testing due to their widespread usage (Hebert et al., 2014; Jang et al., 2010; More and Lka, 2014; Rogers et al., 2010; Wang et al., 2010; Yun et al., 1997). Two small round (5 mm diameter), two medium round (13 mm diameter) and two 38 mm square (Models 400, 402 and 406 respectively, Interlink Electronics, Camarillo, USA) FSRs were tested. Once calibrated, manufacturer specifications state force accuracy in a range of ±6% to ±50% (Interlink Electronics, 2015). FSRs were wired to a data acquisition system (PCI 6259, National Instruments, Austin, TX, USA) connected to a 10 kΩ resistor in a voltage divider configuration (Interlink Electronics, 2015). FSRs were placed in-line with a load cell calibrated to an accuracy of ±0.02 N (LCM703, Omegadyne, Sunbury, USA) affixed to a micromanipulator (MM-3, Narishige Group, Tokyo JA) (Figure 1). Custom PLA-thermoplastic pushing heads were 3D printed to match the sensing surface dimensions of each FSR and introduce curvature as required (Figure 1). During testing, FSRs were pressed between the pushing head and the test surface. The testing assembly was located inside an incubator (Air-Shields C100, Soma Technology Inc., Bloomfield USA) allowing for precise temperature control.

Figure 1. Experimental Setup.

Experimental setup for testing of the 12 combinations of variables. Setup shown in the body temperature, 44 mm diameter, and soft compliance configuration.

Although the FSRs selected have a working range between 0 to 20 N of force (Interlink Electronics, 2015), a testing range of 0 to 10 N was used (Hollinger and Wanderley, 2006). The upper bound was limited to 10 N, as further force can cause discomfort if applied to human soft tissue over a small surface area (Antfolk et al., 2010; Armiger et al., 2013). Data collection was conducted according to ANSI/ISA 51.1 Standards (ANSI, 1995). Accordingly, FSRs were preconditioned and data logging was initiated mid-way through the force range. The FSRs were loaded to the maximum and minimum values three times at a consistent loading rate (Interlink Electronics, 2015) of 30 seconds/cycle. This loading rate was chosen to reflect a low frequency or static application and to avoid any time dependent dynamic effects (Interlink Electronics, 2015; Lebosse et al., 2011). FSR voltage and load cell forces were sampled at 100 Hz, low-pass filtered at 20 Hz and 10 Hz respectively, and logged at 10 Hz.

Data treatment

For each FSR, calibration equations mapping FSR voltage to applied load (load cell reading) were determined through fitting an inverse logarithmic equation (Eq. 1) as recommended (Interlink Electronics, 2015).

Equation 1.

Where F represent the force predicted from the calibration equation, V measured voltage from the FSR and a, b, and c are constants to be solved for each sensor and combination of variables.

$$F=a{e}^{bV}+c$$

Twelve equations per FSR were determined corresponding to the twelve combinations of temperature, curvature and compliance introduced. The fitted-root-mean-squared-error (RMSE-F), mean absolute error (MAE), and maximum error were calculated and recorded for each combination (Supplementary Table 1).

Data for each combination of biomechanical conditions was evaluated under three calibration strategies: self-fit calibration, each sensor calibrated 12 times, once for each combination of variables; baseline-fit, often recommended by manufacturers (Tekscan, 2015), each sensor is calibrated once under optimal conditions (flat, rigid, and room temperature); and cross-fit, one baseline calibration equation applied to all sensors of the same model. Mean differences in RMSE-F, MAE, and maximum error, corresponding to calibration fit strategy, were determined and statistically compared using paired t-tests, with p < 0.05 indicating significance.

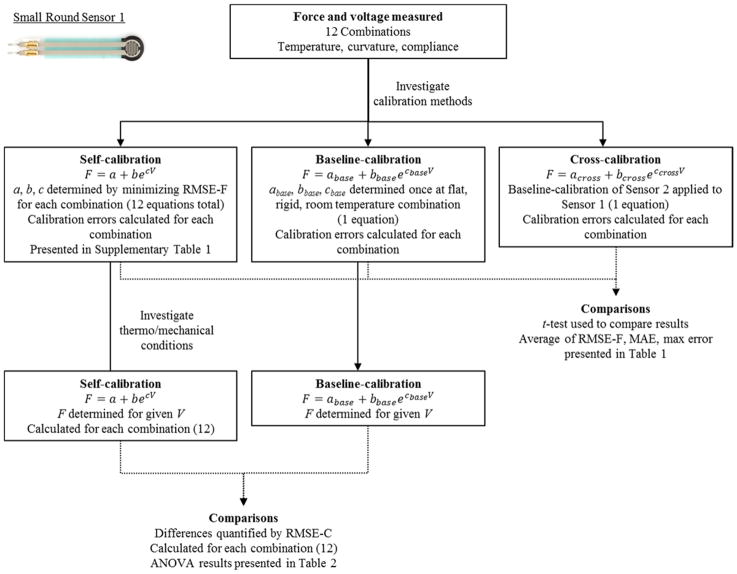
The Baseline calibration equation for each sensor was defined as the flat, rigid, room temperature condition. At each of the remaining 11 combinations, calibration equations were compared to the baseline using root means squared error (RMSE-C). This procedure was performed for each sensor independently, yielding twelve RMSE-C values for each of the six sensors. A graphical example is illustrated in Figure 2.

Figure 2.

Example of the data treatment process for small round sensor 1

Three analyses of variance (ANOVAs) were performed, one for each sensor model. Since two sensors of each model were used, this data was treated as replicate measures in the statistical analysis. Temperature, curvature and compliance were held as input variables with RMSE-C evaluated as the output measure, and blocking performed by sensor number. Initially, all main effects, 2-way and 3-way interactions were evaluated with p < 0.05 indicating significance. Non-significant variables were then removed from the model. Significant main effects, significant 2-way interactions, and the main effects corresponding to any significant interactions were reported.

Participant Testing

Two healthy participants were recruited. Ethics approval was obtained through our institute’s review board and participants gave written informed consent.

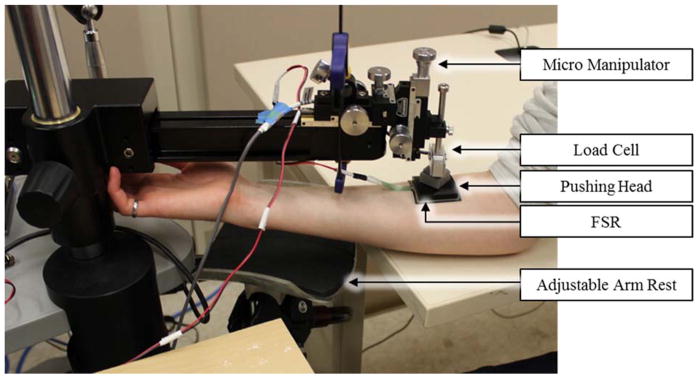
Participant testing closely paralleled the variable testing procedure described previously and was intended to simulate the implications of FSR usage in a biomechanical system. Participants’ arms were secured using an adjustable arm rest. Each FSR was adhered directly to the participants’ skin and given minimally 15 minutes to reach a stable temperature (approximately 32.5 – 34°C). Using the previously described preconditioning and loading procedures, the micromanipulator, load cell, and FSR pushing heads were then pressed tangentially onto each participant’s forearm directly over the sensor (Figure 3). FSR and load cell data was captured over a 0 to 10 N range for each FSR (small round FSRs limited to 0 – 8 N to reduce discomfort).

Figure 3.

Experimental Setup for Participant Trials

From this data, calibration equations were derived for each FSR using the same inverse logarithmic equation described previously. Comparing participant data against each sensor’s previously derived baseline equation; differences in mean RSME-C, MAE and Maximum error were evaluated using a paired t-test, with p < 0.05 indicating significance. Additionally, for each FSR, the participant calibration equations were plotted against their previously-derived baseline equations.

Results

Variable Testing

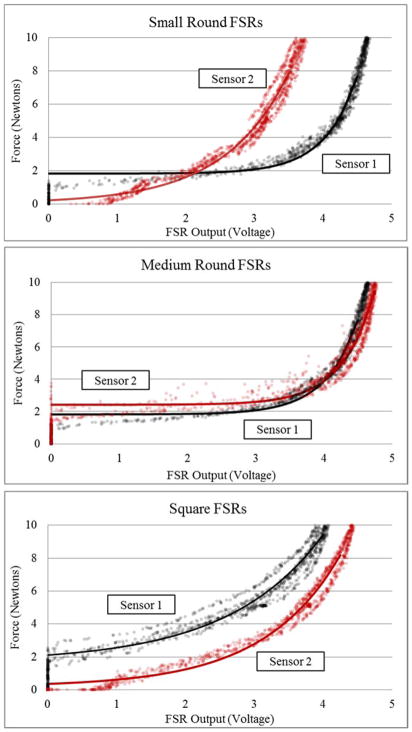
Baseline calibration curves for each of the six sensors are shown in Figure 4 and graphically highlight differences across sensors of the same model.

Figure 4. Baseline Calibration Curves.

Calibration curves for each of the 6 sensors’ force-voltage response in the room temperature, flat, rigid configuration (baseline). Calibration curves are transposed over the raw force-voltage data.

Mean RMSE-F, MAE and maximum error values categorized by sensor model are shown in Table 2. Over the tested 0 – 10 N range, all three error measures in all three sensor models were significantly lower when the self-fit calibration strategy was employed relative to the baseline and cross-fitting strategies.

Table 2.

Mean error based on calibration curve used to fit data

	Small			Medium			Square
	Self	Baseline*	Cross*	Self	Baseline*	Cross*	Self	Baseline*	Cross*
RMSE-F	0.8±0.4	3.0±1.4	3.6±2.3	0.4±0.1	2.2±0.9	2.2±0.8	0.6±0.3	2.5±1.7	2.9±1.6
MAE (N)	0.6±0.3	2.5±1.2	3.0±2.1	0.3±0.1	1.9±0.7	1.8±0.7	0.5±0.3	2.2±1.6	2.6±1.6
Max (N)	2.3±1.2	6.1±2.5	6.7±3.1	1.3±0.3	4.5±1.3	4.4±1.7	1.6±0.8	4.2±2.2	4.8±2.2

^*Indicates significantly different from self-calibration (p < 0.05), Where RMSE-F denotes the root mean squared error for the calibration curve fit to experimental data, MAE and Max denote the mean absolute error and maximum error in force units of Newtons (N)

Calibration equations were investigated to determine mechanical conditions responsible for differences from the baseline calibration equations (RMSE-C). The results of the ANOVA analyses (Table 3) and the means plots highlighting the effects of individual experimental variables with all others held constant are shown in Figure 5.

Table 3.

ANOVA Table and Effects Estimates for RMSE-C

	Variables	RMSE-C
		Effect Estimate	−95%	95%	p-value
Small FSR	Mean	1.92	1.62	2.22	-
	Sensor (blocked)	−0.84	−1.43	−0.24	<0.01*
	Temp	0.46	−0.14	1.05	0.12
	Curve	−0.40	−1.13	0.34	0.27
	Comp	−0.30	−0.90	0.30	0.31
	Temp-Comp	0.74	0.14	1.33	0.02*
R2 = 0.45	Curve-Comp	−1.03	−1.76	−0.30	<0.01*
Medium FSR	Mean	1.38	1.22	1.54	-
	Sensor (blocked)	−0.28	−0.60	0.03	0.07
	Curve	−0.17	−0.56	0.22	0.38
	Comp	−0.68	−1.00	−0.37	<0.01*
R2 = 0.33	Curve-Comp	−0.75	−1.14	−0.36	<0.01*
Square FSR	Mean	2.27	1.81	2.74	-
	Sensor (blocked)	0.44	−0.49	1.37	0.33
	Curve	−1.52	−2.66	−0.38	0.01*
	Curve(Q)	1.69	0.70	2.68	<0.01*
	Comp	0.43	−0.50	1.36	0.34
R2 = 0.76	Curve(Q)-Comp	1.57	0.58	2.56	<0.01*

^*Indicates statistical significance (p<0.05). Abbreviations Temp, Curve, and Comp denote temperature, curvature and compliance respectively. As curvature was tested at 3 levels, Curve(Q) signifies quadratic (non-linear) effects, whereas the absence of (Q) signifies linear effects. Hyphenated variables (ex. Temp-Curve) denote two way interaction effects.

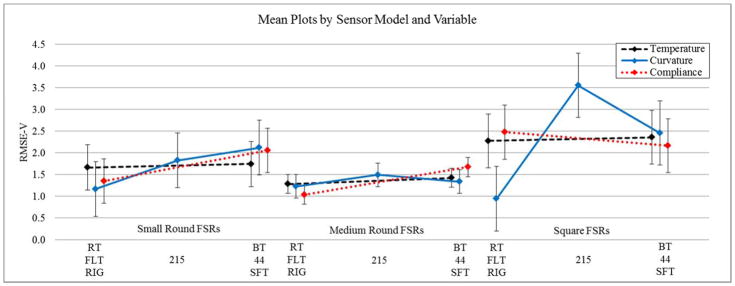
Figure 5. RMSE-C Mean Plots for each Experimental Variable according to Sensor Model.

Plots highlight the effects of individual experimental variables with all others held constant. Where RMSE-V denotes the root mean squared error relative to the baseline equations. RT and BT signify room temperature and body temperature respectively. 44, 215 and flat represent sensor curvature in millimetres and SFT and RIG denote soft tissue and rigid compliance respectively. Error bars represent the ±95^th confidence interval.

For the small round FSRs, ANOVA results suggested the presence of a significant linear effect of interactions between temperature and curvature as well as curvature and compliance. Blocking by sensor demonstrated a significant effect, with statistical differences in calibration equations across sensors of the same model. Medium round FSRs displayed a significant effect from tissue compliance, as well as an interaction effect between curvature and compliance. As curvature was tested at three values, both linear and quadratic main effects were evaluated. For the square FSRs, curvature was found to have both a linear and quadratic effect. Quadratic interaction effects were found between curvature and compliance.

Participant Testing

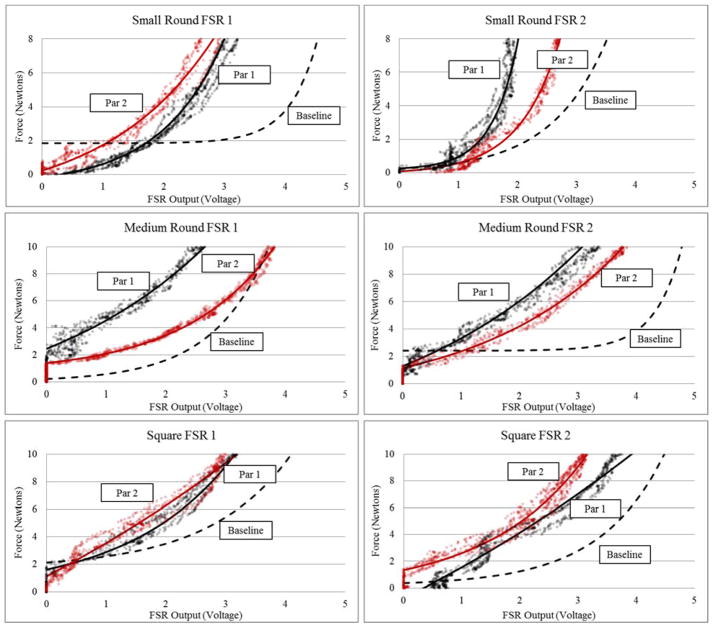
Participant data is plotted in Figure 6, highlighting differences in each FSRs force-voltage response at baseline conditions and on soft tissue. There were notable differences across sensors of the same model and between participants.

Figure 6. Participant Testing Data for Individual FSR Sensors.

Calibration curves plotted for each sensor and participant against the previously determined baseline calibration curve (under room temperature, flat, rigid conditions), where Par 1 and Par 2 abbreviates participant 1 and participant 2 respectively. Participant calibration curves are transposed over the raw force-voltage data.

Discussion

FSRs are attractive sensors for biomechanical applications due to their versatility, small profile and low cost. Yet FSRs have limitations such as sensor drift and hysteresis (Buis and Convery, 1997; Dabling et al., 2012; Herbert-Copley et al., 2013; Polliack et al., 2000b). To achieve optimal performance it is recommended that these sensors be used on flat, rigid surfaces at approximately room temperature (Interlink Electronics, 2015; TekScan, 2015). Yet in many biomechanical environments temperature differentials, curvatures and compliant tissues are unavoidable. Therefore, investigation of the effect of these variables is necessary to understand how calibration and implementation of FSRs may impact sensor accuracy.

The data supports the use of a self-fit calibration scheme to reduce calibration error and yield more accurate readings. The raw force and voltage data, and calibration curves demonstrated varying force-voltage responses from sensors of the same model even under optimal operating conditions (room temperature, flat, rigid). These curves (Figure 4) paired with the significantly higher cross-fit error data (Table 2) suggest that in a system using multiple FSRs of the same model, independent calibration equations for each sensor are necessary to minimize calibration error and improve the accuracy of the sensor readings.

The individual impact of manipulating temperature, curvature and compliance on calibration equations (in terms of RMSE-C) were investigated. No single variable impacted calibration equations for all three sensor models. Rather, each sensor model illustrated a unique combination of significant main effects and interaction effects that influenced RMSE-C values (Table 3). These main effects and interactions, if not held constant at the baseline values, will significantly impact the individual sensor’s calibration equation and force accuracy. Additionally, given that the self-fit calibration strategy yields significantly lower mean error values, error induced from biomechanical conditions of a sensor’s environment should be minimized by calibrating the FSR in an environment as close to its intended use as possible.

Participant testing highlighted that two participants tested in the same location of the body yielded different calibration curves and that these calibration curves strayed from the baseline curves for each sensor. Additionally, Figure 6 highlights changes in the dead band of each FSR (the small force application required to initially register a voltage change). By introducing the varying curvatures of a human forearm, the sensor is forced into physical configurations known to impact FSR performance such as mechanical deformation and shearing effects (Hall et al., 2008). These mechanical conditions can lower the dead band or induce an artificial preload into the sensor. In all, the biomechanical environment of a human forearm introduces inherent changes in temperature, curvature and tissue compliance relative to baseline conditions; these changes are clearly reflected in the calibration curves. These findings further illustrate the need to calibrate FSR sensors as close to their intended use as possible. In doing so, the resulting self-fit calibration equation will be specific to the participant and the individual set of mechanical variables they introduce to the sensing environment.

The results of this study highlight inherent advantages and disadvantages for each of the three calibration techniques evaluated: The self-fit strategy is a rigorous and more time consuming approach that significantly minimizes calibration error; The baseline-fit strategy is a time saving approach at the cost of increased error; The cross-fit strategy is the least time consuming approach yielding the highest calibration error.

Taken together, temperature, curvature and tissue compliance all have the potential to impact FSR calibration curves. The FSR models are sensitive to these three factors at varying levels, supporting two key recommendations:

1. Each FSR in a system should be calibrated independently. This may help reduce calibration error as multiple sensors of the same model demonstrated notable differences in force-voltage response.

2. FSRs must be calibrated in the environment of their intended use or as close as possible. This will ensure the corresponding calibration curve will account for the physical and mechanical variables affecting its force-voltage response. If the application of the FSR prohibits such a calibration strategy, the researcher or clinician must be aware of the implications on sensor accuracy.

Limitations and Future Considerations

The intent of this study was to identify biomechanical variables impacting FSR calibration and evaluate strategies to minimize calibration error. Expanding on this work and increasing the number of FSRs tested, would lend further confidence to the results discussed and provide the ability to develop a statistical model for the prediction of FSR error based on the biomechanical environment. Additional limitations of this work may lie in the choice of loading rate (30sec/ cycle). FSRs are sensitive to dynamic load rates. Further multivariate testing including load rate effects may be warranted. Finally, this work calibrates FSRs to a known force, as recommended by the manufacturer (Interlink Electronics, 2015) and standard practice in literature (Buis and Convery, 1997; Lebosse et al, 2011). Yet each sensor model has different sensing surface geometries. Calibration practices mapping FSR voltage to applied pressure may be more appropriate in future work as this would account for sensing surface geometry.