Abstract
Understanding hydrologic connectivity between wetlands and perennial streams is critical to understanding the reliance of stream flow on inputs from wetlands. We used the isotopic evaporation signal in water and remote sensing to examine wetland-stream hydrologic connectivity within the Pipestem Creek watershed, North Dakota, a watershed dominated by prairie-pothole wetlands. Pipestem Creek exhibited an evaporated-water signal that had approximately half the isotopic-enrichment signal found in most evaporatively enriched prairie-pothole wetlands. Groundwater adjacent to Pipestem Creek had isotopic values that indicated recharge from winter precipitation and had no significant evaporative enrichment, indicating that enriched surface water did not contribute significantly to groundwater discharging into Pipestem Creek. The estimated surface-water area necessary to generate the evaporation signal within Pipestem Creek was highly dynamic, varied primarily with the amount of discharge, and was typically greater than the immediate Pipestem Creek surface-water area, indicating that surficial flow from wetlands contributed to stream flow throughout the summer. We propose a dynamic range of spilling thresholds for prairie-pothole wetlands across the watershed allowing for wetland inputs even during low flow periods. Combining Landsat estimates with the isotopic approach allowed determination of potential (Landsat) and actual (isotope) contributing areas in wetland-dominated systems. This combined approach can give insights into the changes in location and magnitude of surface water and groundwater pathways over time. This approach can be used in other areas where evaporation from wetlands results in a sufficient evaporative isotopic signal.
1 Introduction
In the past decade, much has been learned about how wetlands interact with each other and with other aquatic systems through hydrological, chemical, and biological connectivity [Cohen et al., 2016; Rains et al., 2016; U.S. Environmental Protection Agency, 2015]. Interest in this subject has resulted from an increased appreciation of the importance of connectivity affecting function within wetland [Bornette et al., 1998; Dou et al., 2016; Leibowitz et al., 2016; Reid et al., 2015] and watersheds [Golden et al., 2016; Huang et al., 2011; Quinton et al., 2003]. In addition, this subject is of interest because of its relevance to the U.S. Clean Water Act [CWA; Alexander, 2015]. Specifically, the U.S. Supreme Court’s 2006 Rapanos decision suggested that certain aquatic systems, including wetlands not immediately adjacent to traditional navigable waters, should require a “significant nexus” to navigable waters in order to be protected by the CWA [Downing et al., 2007]. Justice Anthony Kennedy indicated that a water body has a significant nexus when it, either alone or in combination with similarly situated water bodies in the region, significantly affects the chemical, physical, or biological integrity of traditional navigable waters.
Leibowitz [2003] observed that wetlands occur along a hydrologic connectivity continuum. However, even wetlands towards the isolated end of this surface-water connectivity continuum can be connected to other aquatic systems through subsurface flows, intermittent surface-water connections, and movement of organisms and propagules [Mushet et al., 2013; Vanderhoof et al., 2016a; Winter and Rosenberry, 1995], while even streams considered perennial can vary temporally in surface-water connectivity [Godsey and Kirchner, 2014]. Several studies have addressed connectivity of wetlands with limited surface-water flows [Amado et al., 2016; Brannen et al., 2015; Leibowitz and Vining, 2003; Wright, 2010]. Additionally, in wetlands lacking more permanent surface-water connections with other aquatic systems, intermittent connections can occur during wet conditions through fill-and-spill or fill-and-merge mechanisms [Leibowitz et al., 2016; Spence and Woo, 2003]. In the former case, water from one wetland spills into another, causing a unidirectional hydrologic connection; while in the latter case, two wetlands merge through rising water levels, resulting in bidirectional exchanges. Wetlands can also be hydrologically connected through both groundwater [Winter and Rosenberry, 1995; Winter and LaBaugh, 2003] and surface water [LaBaugh et al., 2016; Leibowitz et al., 2016]. For example, groundwater can enter the up-gradient side of a wetland through discharge, and then exit the same wetland on the down-gradient side through recharge; recharge exiting one wetland can serve as the discharge entering a down-gradient wetland [Winter and LaBaugh, 2003]. This illustrates that hydrologic connectivity, which varies both spatially and temporally, is critical to wetland function at local-to-landscape scales.
More recently, research has focused on connectivity of wetlands with limited surface flows to downstream waters [Ameli and Creed, 2017; Evenson et al., 2015; McDonough et al., 2015; McLaughlin et al., 2014; Vanderhoof et al., 2016a; Vanderhoof et al., 2016b]. Researchers are now beginning to examine the effects of wetlands on watershed processes, in part because of their relevance to CWA jurisdiction. Cohen et al. [2016] argued that landscape function – processing and transport of matter, energy, and organisms – depends on the entire continuum of connectivity, from the more isolated end of the connectivity continuum to the perennial stream. Rains et al. [2016] described wetlands, including those with limited surface-water connections, as nodes in hydrologic networks that could affect flow regeneration, evapotranspiration, deep recharge, storage, and exchange due to source, sink, and lag functions. Marton et al. [2015] found that surficial-isolated wetlands function as biogeochemical reactors driving processes such as denitrification, which improves water quality at the landscape scale. This occurs in part because of longer residence times associated with reduced connectivity. Regardless of this importance, actual measures of the degree of connectivity between wetlands and streams at the watershed-scale are difficult to make, but critical for quantifying these functions, and for policy and decision making [Golden et al., 2017].
Golden et al. [2017] argue that integrating modeling and direct measurements of wetland connectivity are needed to support decision making and understanding of wetland services. A number of techniques have been used in wetland connectivity studies, but those involving field techniques are usually limited in their spatial or temporal extent. Shaw et al. [2012] and Wilcox et al. [2011] used stage or discharge measurements to study hydrologic connectivity of wetlands, but these were limited to interactions between a few wetlands rather than full watersheds. McDonough et al. [2015] used binary float switches that measured the presence or absence of water to examine hydrologic connectivity between wetlands and streams, but again because of the intensive nature of data collection, the spatial scale was limited. Remotely sensed imagery has greatly improved the spatial scale at which wetland connectivity can be studied, and include data sources such as Landsat Thematic Mapper [Vanderhoof et al., 2016b], IKONOS [Quinton et al., 2003], and LiDAR-based digital elevation models [DEMs; Lang et al., 2012]. Graph theory approaches conceptualize wetlands as nodes and movement of materials or organisms as edges and have been used to model biological connectivity between wetlands, including analyses of playas, prairie potholes, and Rainwater Basin wetlands [Ameli and Creed, 2017; McIntyre et al., 2014; Ruiz et al., 2014; Uden et al., 2014]. Liu et al. [2016] combined a graph theoretic approach with the HydroGeoSphere model to study hydrologic connectivity in synthetic wetland landscapes. Chu [2015] used a 10 m DEM to model wetland storage dynamics and resulting hydrologic connectivity patterns. However, these imagery-based studies are rarely linked with field hydrology studies.
Recent studies using models have also focused on wetland-dominated landscapes. In a prairie-pothole dominated watershed, Evenson et al. [2016] found that a modified Soil and Water Assessment Tool (SWAT) hydrologic model that included fill-and-spill flows from wetlands performed better than a conventional lumped SWAT model that lacked this capability. Model simulations demonstrated how fill-and-spill events in the watershed quickly declined following spring snowmelt. In the same pothole-dominated watershed, Wu and Lane [2016] used 1-m LiDAR data to map wetland depressions, and estimated their water-storage volume. These modeling and remote sensing studies provide important tools for understanding how prairie-pothole wetlands contribute to downstream waters. Such studies have collectively contributed to a broad understanding of the hydrologic behavior of wetlands. However, we have limited direct measurements and understanding of the collective influence of these wetlands at the catchment scale to guide model refinement. For example, we do not know the full extent to which wetlands are connected to the streams in watersheds in which they are situated, nor the predominant pathways through which wetland water flows to the stream. Different and combined approaches are also needed that can independently estimate contributing area and the importance of wetlands to perennial streamflow in watersheds [Golden et al., 2017].
Water stable isotopes can assist in understanding how and when wetlands are contributing to streamflow because wetlands can have unique isotopic signatures resulting from the evaporative-enrichment processes. As water evaporates, the heavy isotope preferentially remains behind, leaving an isotopic signature indicating the degree of evaporation that has occurred since that water fell as precipitation [Clark and Fritz, 1997; Gat, 2010]. Transpiration does not leave an evaporatively enriched signal in surface water because the evaporatively enriched pool of water within plants does not mix back with water flowing to the open stream [Jasechko et al., 2013]. Similarly, evaporatively enriched water from unsaturated soil appears to have little influence on the isotopic signal of stream water [Brooks et al., 2010; Brooks, 2015; Evaristo et al., 2015]. Thus, only evaporation from hydrologically connected surface water and saturated soils will create an evaporatively enriched isotopic signal in downstream waters. The proportion of surface water that leaves through evaporation is typically high in small, shallow, lentic systems [Brooks et al., 2014] such as prairie-pothole wetlands, and can potentially be used as an indicator of wetland contributions to streamflow if other potential sources, such as groundwater, are not evaporatively enriched. While direct evaporation from streams must also be considered, the proportion of water evaporating from lotic systems is far lower than that in lentic systems [Gibson et al., 2005]. The advantages of using water stable isotopes is that water collected at a stream outlet spatially integrates the isotopic signal from across the watershed. In addition, if groundwater inputs are not evaporatively enriched, isotopic approaches could provide insights on surface and subsurface flowpaths. This isotopic technique can then be compared with other larger-scale measures of wetland connectivity such as those from remote sensing to constrain and refine our understanding of connectivity at the watershed scale.
Our objective was to combine and compare isotopic and remote sensing approaches to quantify hydrologic wetland connectivity to downstream waters. We selected the Pipestem Creek watershed, a tributary to the James River in east-central North Dakota to quantify the extent of prairie-pothole wetlands that contribute to streamflow because this watershed has been a focus of research on prairie-pothole wetlands [Evenson et al., 2016; Leibowitz et al., 2016; Rosenberry et al., 2004; Winter, 1999; 2003]. Our approach was to use the evaporative signal in water stable isotopes to estimate the contribution of prairie-pothole wetlands to streamflow, and determine the areal extent of ponded surface water in wetlands necessary to generate the evaporative signal. First, we characterized the isotopic evaporation signal within prairie-pothole wetlands and the nearby stream from water samples collected during a 2-yr study period (2014–2015). Second, we estimated the surface-water area necessary to generate the evaporation signal observed in the stream over that time. We then compared these isotopically derived estimates of surface-water contributing area with aerial estimates of surficially connected wetlands (i.e., wetlands with permanent or seasonal surface water connections to the stream network) derived from Landsat images during our study period.
2 Materials and Methods
2.1 Study Site Description
The research was conducted in the Pipestem Creek watershed, which is located northwest of Jamestown, ND and has one active USGS gage (06469400) near Pingree, ND (Figure 1). The drainage area to the USGS gage was approximately 1672 km2 based on delineation using a 10 m digital elevation map; however, the actual contributing area is unknown and likely much smaller. Agricultural land use dominates the landscape, while prairie-pothole wetlands are distributed throughout the watershed [Evenson et al., 2016; Wu and Lane, 2016]. Pipestem watershed spans two different geologic regions within the Prairie Pothole Region: the Drift Plain to the east characterized by flatter topography, greater agricultural land-use, and a smaller area of wetlands (0.12 wetlands ha−1, 893.6 m2 wetland ha−1), and the Missouri Coteau to the west characterized by a more hummocky topography and a larger area of wetlands (0.11 wetlands ha−1, 1369.7 m2 wetlands ha−1) [Vanderhoof et al., 2016b]. The Missouri Escarpment connects the higher elevation Coteau to the lower elevation Drift Plain and contains a high density of small drainages (Figure 1).
Figure 1.
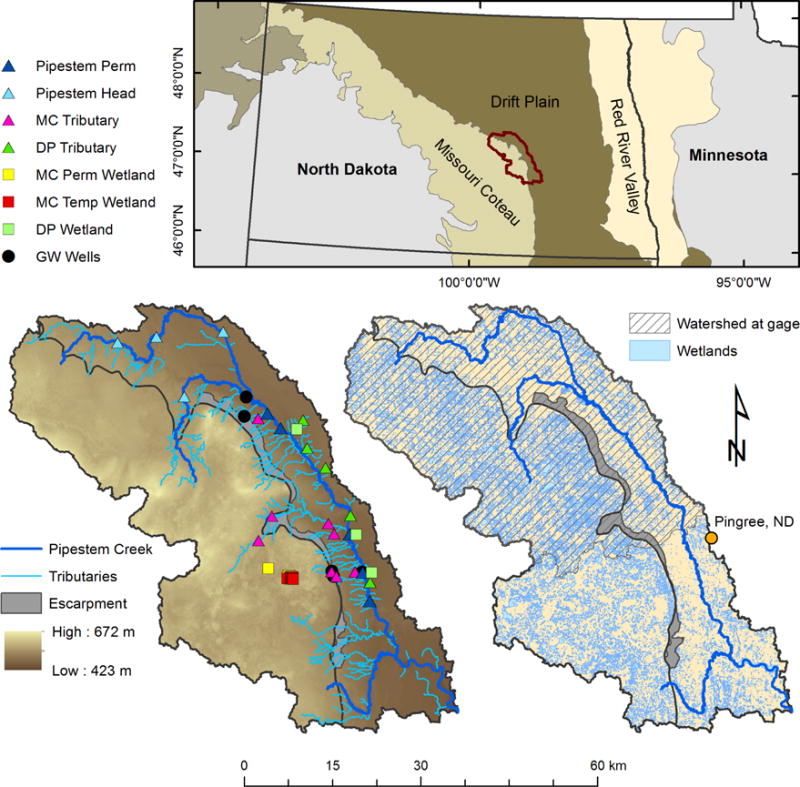
The study area location within North Dakota (Top panel) with the Pipestem watershed outlined in red. The watershed spans two geologic regions: The Missouri Coteau (light zone, western portion) and the Drift Plain (brown zone, eastern portion). Sample locations (lower left panel) and National Wetlands Inventory (NWI) wetland area (lower right panel) within Pipestem Creek Watershed (~2,740 km2 full area, 1672 km2 gaged watershed with hatch marks). The black line through the watershed center represents the geologic regional divide with the Missouri Escarpment, a distinct slope leading down to the Drift Plain from the Coteau, filled in grey. Sample wetlands within the Coteau are represented by yellow squares (permanent wetlands, MC Perm Wetland), and red squares (temporary wetlands, MC Temp Wetland) at Cottonwood Lake Research Area (note that many red and yellow symbols are overlapping in the CLRA). Sample wetlands in the Drift Plain are represented by green squares (DP Wetland). Sampling sites for tributaries draining from the Coteau are represented by pink triangles (MC Tributary), while sampling sites for tributaries draining from the Drift Plain are represented by green triangles (DP Tributary). Samples within Pipestem Creek are represented by dark blue triangles (Pipestem Perm) in the main stem and light blue in the headwaters (Pipestem Head). Black circles represent groundwater wells. These symbols and colors are consistent throughout the manuscript.
The Pipestem Creek watershed is home to the Cottonwood Lake Study Area (CLSA), one of the most studied wetland complexes in the United States and a long-term research site that is a part of the U.S. Geological Survey (USGS) Missouri Coteau Wetland Ecosystem Observatory (https://www.sciencebase.gov/catalog/item/52f0ffd9e4b0f941aa181fc6). CLSA is a 92-ha complex of 17 prairie-pothole wetlands near the town of Woodworth, North Dakota that has been studied since the mid-1960s [Swanson, 1987]. Research has described the geohydrological setting of the area [Winter, 2003], provided a detailed, long-term view of hydrological and geochemical dynamics within these wetlands [Goldhaber et al., 2014; LaBaugh and Swanson, 1992; LaBaugh et al., 1998; Winter and Rosenberry, 1995], and articulated how these dynamics respond to drought and flood conditions [LaBaugh et al., 1996; Rover et al., 2011; Winter and Rosenberry, 1998]. Historically, wetlands at the CLSA have been grouped into permanent wetlands denoted with a “P” and an identifying number, and temporary wetlands denoted with a “T” and identifying number. Temporary wetlands include class II and class III (temporarily and seasonally ponded, respectively) wetlands and permanent wetlands include class IV and class V (semi-permanent and permanently ponded, respectively) wetlands under the Stewart and Kantrud [1971] classification system. In this study, we use this terminology as a matter of convenience.
The area has a mean annual temperature of 3.5 °C and mean annual precipitation of 479 mm (1980-2016, Jamestown Municipal Airport ND, https://www.ncdc.noaa.gov). Winters are cold and dry with approximately 20% of the precipitation falling between November and April. The region is characterized by decadal long wet and dry periods [Winter and Rosenberry, 1998]: mean annual precipitation during the dry period from 1980 to 1992 was 410 mm while during the wetter period since 1993, it was 517 mm. Annual precipitation during the study period was 637 mm in water year (WY) 2014, which was a wet year, and 544 mm in WY 2015. Most of the difference in precipitation between the two years occurred during the winter: in WY 2014, 199 mm of precipitation fell from October 2013 through April 2014, whereas in WY 2015, only 56 mm fell from October 2014-April 2015, making the winter of 2015 one of the driest on record. This difference in winter precipitation had profound impacts on runoff and flow in Pipestem Creek: the average discharge in WY 2015 was one-third the rate in WY 2014 (0.42 vs 1.18 m3s−1), and both were below the average (1.6 m3s−1 WY 1980-2015). This difference between annual precipitation and discharge highlights the importance of seasonality on the rainfall-runoff relationship.
2.2 Sampling Design
In 2014, our objective was to characterize the extent of isotopic enrichment from evaporation for a permanent wetland, a temporary wetland and Pipestem Creek. Water samples were collected approximately twice a month from June to October at two wetlands in the CLSA: P1 was selected for the permanent wetland and T8 for the temporary wetland. Pipestem Creek was sampled at the three most downstream locations (denoted in dark blue triangles in Figure 1), including the USGS gaging station near Pingree, ND.
In 2015, our objectives were to quantify the spatial variation of water isotopes within the stream network, and to sample additional wetlands from the Drift Plain. We added four sites in the headwaters of Pipestem Creek, and two more upper watershed sites along the mainstem of Pipestem Creek (Figure 1). In addition, we added sampling sites in 8 smaller tributaries draining the Coteau and 5 tributaries draining the Drift Plain. We also added three Drift Plain wetlands and included all wetlands within the CLSA that have been monitored for over 30 years (permanent, N=7 and temporary, N=8). We sampled all sites at approximately monthly intervals during the summer (May–Sept) of 2015. We did not include further spatial sampling of Coteau wetlands because wetlands at the CLSA spanned a complete hydrologic gradient from groundwater recharge to groundwater discharge and are representative of other wetlands on the Coteau [Euliss et al., 2004; Euliss et al., 2014].
During the summer of 2015, we installed 6 groundwater-monitoring wells (Figure 1) along two transects to determine the isotopic signature of groundwater near Pipestem Creek. One transect was located in the upper Pipestem Creek near the junction of two main tributaries (Little Pipestem and Headwaters Pipestem Creek), and a second transect was located south of the USGS gage at the lower boundary of our water-sampling network (Figure 1). For each transect, we installed a water-table well within 80 m of Pipestem Creek, a staff gage to relate stream stage to the elevation of the nearby well, and a water-table well and deeper piezometer near the break in the Missouri Coteau slope. Water-table wells ranged in depth from 1.6 to 4.2 m, while piezometer depths ranged from 7.5 to 8.1 m. Wells were sampled in September during our final isotope sampling campaign.
To characterize the isotopic composition of precipitation for the study area, we used two approaches: we obtained precipitation isotope estimates, and sampled some precipitation events. We obtained monthly and annual estimates of water isotopes for local precipitation at the CLRA (elevation 560 m) from Waterisotopes.org, which uses global precipitation oxygen and hydrogen isotope data and empirically calculates the long-term average monthly and annual isotopic composition of precipitation at any location based on algorithms developed by Bowen and Wilkinson [2002] and refined by Bowen and Revenaugh [2003] and Bowen et al. [2005]. In addition, samples were collected from a precipitation collector (funnel with narrow tubing connected to a sealed sample bottle with a small air vent) during the summer at the Northern Prairie Wildlife Research Center, Jamestown, ND, located 41 km from the Pipestem Creek gage (elevation 424 m). Samples were collected within a day of the event to minimize evaporation.
2.3 Measurements
2.3.1 Stable Isotopes
Samples were collected in 20-ml glass vials with polyseal conical inserts within the cap to prevent evaporation. Vials were filled to avoid headspace, and samples were stored capside down until analysis. All samples were analyzed for water isotopes (δ2H, δ18O) on a Laser Absorption Water-Vapor Isotope Spectrometer (Model 908-0004, Los Gatos Research, Mountain View, CA) located at the Integrated Stable Isotope Research Facility at the Western Ecology Division of the U.S. Environmental Protection Agency, Corvallis, Oregon. All δ2H and δ18O values were expressed relative to Vienna-Standard Mean Ocean Water (V-SMOW) using δ notation:
| (1) |
where R is the ratio of 2H to 1H atoms or 18O to 16O atoms of the sample and the standard V-SMOW, and values were reported in parts per thousand (‰) by multiplying by 1000. Measurement precision (1 standard deviation) for the Laser Spectrometer was determined on duplicates of study samples spanning the range of sample values and was 0.2 and 0.1 ‰ for δ2H and δ18O, respectively. Accuracy based on quality control standards for each sample run averaged less than 0.1 ‰ for each isotope over the duration of the study with standard deviations of 0.2 and 0.1 ‰ for δ2H and δ18O, respectively.
2.3.2 Climate and streamflow data
Monthly climate data (precipitation, dewpoint, mean, maximum, and minimum temperature) for 2014–2015 were obtained using the Parameter-elevation Regressions on Independent Slopes Model (PRISM) algorithm [Daly et al., 2008]. Monthly mean potential evapotranspiration (PET) was estimated from temperature data using the Hamon equation including uncertainty of ±0.5 mm/day as found in Rosenberry et al., [2004]. Daily relative humidity (RH) and temperature data were obtained from USGS climate stations at the CLSA. Daily precipitation and temperature data from 1980 through 2015 were also obtained from the Jamestown Municipal Airport Station [USNOAA, 2016] located 35 km from the Pipestem gage. Streamflow data were obtained from the USGS 06469400 gage for Pipestem Creek [USGS, 2015].
2.4 Isotopic Modeling
2.4.1 Evaporation Index
Water enriched through evaporation can be isotopically distinguished from variation of incoming precipitation by using both δ2H and δ18O values. A measure of evaporation (d-excess) is calculated as d-excess= δ2H−8×δ18O [Clark and Fritz, 1997]. Isotopic values of water that plot on the Global Meteoric Water Line (GMWL, δ2H=8×δ18O+10; [Dansgaard, 1964]) have d-excess values of 10 (the intercept of the GMWL), while lower values indicate effects of evaporation.
In addition to d-excess, we developed an evaporation index specifically for water in Pipestem Creek to determine how important evaporatively enriched sources of water were to flow in Pipestem Creek. For this index, we first developed local evaporation lines (LEL) for each sampling period, which describe the linear relationship between δ18O and δ2H values collected from the wetland and stream water samples. Then for each sampling date, we employed a simple two end-member mixing model to describe the influence of evaporation on water within Pipestem. The no evaporation endpoint is defined as the isotopic value where the LEL crosses the GMWL. The maximum evaporatively enriched endpoint was represented by the water bodies consistently furthest out on the LEL, which were always the permanent wetlands. The index generates a value between zero and one, where zero is the isotopic value on the GMWL, and one has an enrichment signal similar to the permanent wetlands. We estimated uncertainty in these index values using isoerror [Phillips and Gregg, 2001], which calculates uncertainty in isotopic mixing models incorporating the uncertainty of the sources as well as the mixture. The isotopic variation in the permanent wetlands was used as uncertainty for the evaporatively enriched endpoint, while the regression uncertainty around the intercept of the LEL and GMWL was used for the non-evaporated endpoint.
2.4.2 Evaporative Open-water Surface-area Estimates
We estimated the area of open surface water necessary to generate the evaporative enrichment signal in Pipestem Creek by applying the following steady-state mass-balance equations [Gat, 2010; Gibson and Edwards, 2002]:
| (2) |
| (3) |
where I is inflow to the connected surface water system (possible combined sources: groundwater, overland flow and direct precipitation), Q is the streamflow at the Pipestem Creek USGS gage, and E is evaporation from upstream open surface waters contributing to streamflow. δI, δS, and δE are the isotopic values of inflow, streamflow, and evaporation fluxes, respectively. Substituting Q with I – E, and rearranging equation 3, we derive the following equation for evaporation:inflow [Gibson and Edwards, 2002; Gibson and Reid, 2010]:
| (4) |
E/I was estimated using both δ18O and δ2H values, and averaged. We estimated the error as the standard deviation between the two isotopic estimates. Using Pipestem Creek flow data (Q) and assuming E/I +Q/I =1, we estimated E = E/I*Q/(1−E/I), where E is a volume of water in the same units as Q. We estimated the open surface-water area (SWA) necessary to generate the volume of E by dividing by PET averaged over 30 days prior to sample collection. This estimate of connected surface-water area is a minimum estimate because we assumed that transpiration from flowing surface water is negligible. We used a first-order Taylor series expansion to attribute the variance of the three calculation variables (E/I, Q and PET) to the variance in SWA [Ver Hoef, 2012].
δS was measured from stream samples collected at the gaging station. We estimated δI by calculating the dual isotope (δ18O and δ2H) slopes of the local evaporation line (SLEL) using the stream and wetland data collected at each sampling time, and extrapolating back from the stream isotopic value to the GMWL (δ2H = 8×δ18O + 10) using the following equations:
| (5) |
| (6) |
| (7) |
where S is the slope of the GMWL and the LEL, BGMWL is the intercept of the GMWL, and Bx is the observation specific intercept for each stream observation (δS). This method allows δI to vary with deviations of δS around the LEL determined for each sampling time, and implies that within a sampling date, all LEL deviations are caused by changes in source water rather than LEL slope variation. This is a reasonable assumption because variations in LEL slope are caused by local climate conditions [Gat, 2010] and the wetlands and stream experience the same climate. In addition, our regression-based SLEL values were consistent with those estimated using the climate-based fractionation factors determined below [Equation 7 in Gat, 1996].
The isotopic value of evaporating water, δE, was estimated using the Craig-Gordon Model for open-water evaporation [Craig and Gordon, 1965]:
| (8) |
where h is atmospheric relative humidity, δA is the isotopic composition of atmospheric vapor, α* is the equilibrium fractionation between liquid and vapor (α*=1+ ε*), and ε* and εK are the equilibrium and kinetic enrichment factors, respectively. We estimated ε* using temperature data and the equations from Horita and Wesolowski [1994]. εK is influenced by relative humidity and boundary layer conditions and can be estimated by εK =CK(1-h) where CK was set to 14.2‰ for oxygen and 12.5‰ for hydrogen [Gibson and Edwards, 2002]. We assumed that δA was in isotopic equilibrium with evaporation flux-weighted precipitation (monthly precipitation isotopes weighted by monthly PET for three months prior to sample collection).
2.5 Surface-Water Mapping with Landsat Image Analysis
Surface-water extent was mapped using Landsat imagery (path 31, row 27). All Landsat Thematic Mapper images for 2014 and 2015 that were snow-free and contained <10% cloud cover were analyzed; we also included a May 26, 2014 image, which contained approximately 12% cloud cover. Four images from 2014 and 2015 (8 images total) spanning the growing season from spring (April/May) to fall (September) were analyzed. The images were atmospherically corrected and converted to surface reflectance values using the Landsat Ecosystem Disturbance Adaptive Processing System [Masek et al., 2006]. A minimum noise fraction transformation was applied to reduce within-image noise [Green et al., 1988]. The per-pixel water fraction was estimated using the Matched Filtering algorithm, a partial unmixing method in the ENVI software package (Exelis Visual Information Solutions, Inc, Herndon, Va) [Turin, 1960; Vanderhoof et al., 2016a]. The fraction-water output was linearly stretched to enhance our ability to distinguish between inundated and non-inundated pixels. CFmask, the quality-control layer provided with Landsat imagery, was used to mask out clouds and cloud shadows, while the National Land Cover Database (NLCD) 2011 was used to mask out impervious surfaces, defined as low, medium and high density development [Homer et al., 2015], which is often spectrally confused with surface water. Surface-water extent was defined conservatively as the sum of pixels containing >0.53 fraction water and represented inundated surfaces within an area of interest. This threshold was selected to best balance errors of omission and commission [for details see Vanderhoof et al., 2016a]. The classified surface-water images were clipped to the Pipestem Creek watershed extent, defined as upstream from the Pipestem Creek near Pingree, North Dakota USGS stream gage (USGS Gage #06469400). In Vanderhoof et al. [2016a], a Landsat time series for this path/row was validated using random points visually classified from 1-m resolution National Agricultural Imagery Program (NAIP) imagery (1500 total points, 298 inundated, 1202, non-inundated). Overall accuracy was 95.3%, with a 22.1% error of omission for water and a 1.7% error of commission for water [Vanderhoof et al., 2016a].
The stream network was defined by the High Resolution National Hydrography Dataset [USGS, 2013] and included (1) connectors and intermittent stream lines (width assumed to be 1 m), (2) perennial stream lines (width assumed to be 3 m) and (3) stream/river NHDArea. These three categories were added together to estimate total stream surface area above the USGS gage which was 221 ha. NAIP imagery collected in 2012 and 2014 was used to manually eliminate intermittent stream lines in ArcGIS 10.3 that did not show visual evidence of connecting to Pipestem Creek. Connected surface water was defined as surface-water polygons derived from the Landsat imagery that intersected the revised NHD stream network (Figure 2). The stream surface was removed from the estimates of surface-water area.
Figure 2.
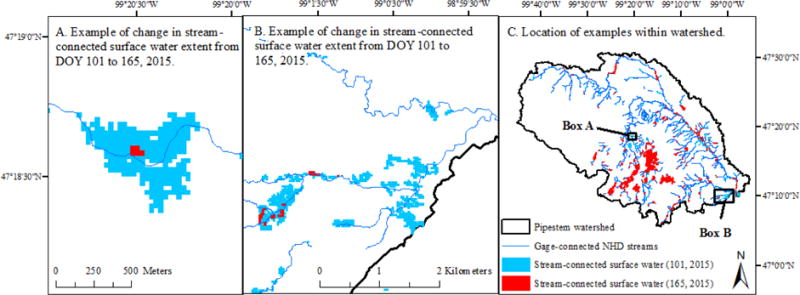
Examples of how connected wetland area was determined using Landsat data from images collected on April 11, 2015 (Day of year: DOY 101) and June 14, 2015 (DOY 165). The watershed depicted in C is the gaged watershed that is the crosshatched area in Figure 1.
3 Results
3.1 Isotopic composition of water within the Pipestem Watershed
Flow in Pipestem Creek varied between 0.01 and 2 m3 s−1 for the dates when water samples were collected (Table 1, Figure 3), which represented the range of summer (June-Sept) flow conditions, but did not capture some of the earlier peak flows. Peak flow of 11 m3 s−1 for the 2014 water year occurred during spring snowmelt in mid-April. In contrast, 2015 had a drier winter with no distinct snowmelt event: average flow in April 2015 was 0.5 m3 s−1 declining over the month from 0.9 to 0.3 m3 s−1. Peak flow in 2015 was 6.5 m3 s−1 and occurred in May after a heavy rainfall event (Figure 3). Most of the summer period is characterized by low flows: median flow rates from May to October were 0.65 and 0.28 m3 s−1 for 2014 and 2015 respectively.
Table 1.
Estimation of connected surface-water area (SWA) necessary to generate the evaporation/inflow signal (E/I, see methods for details). Q is the daily average flow from Pipestem Creek USGS gage on the sampling date. PET is the average PET for 30 days prior to sample collection. Error estimates are the standard deviation of the estimates from the two isotope values and the uncertainty around PET estimates.
| Date | E/I | Q (m3V−1) | Q/I | I (m3s−1) | E (m3s−1) | E (m3d−1) | PET (mm d−1) | SWA (ha) |
|---|---|---|---|---|---|---|---|---|
| 6/12/2014 | 0.22±0.02 | 0.91 | 0.78±0.02 | 1.16±0.03 | 0.26±0.03 | 22285±2530 | 2.94±0.5 | 758±128 |
| 6/26/2014 | 0.30±0.04 | 2.01 | 0.70±0.04 | 2.88±0.17 | 0.86±0.17 | 74720±14550 | 3.14±0.5 | 2380±447 |
| 7/13/2014 | 0.27±0.02 | 0.48 | 0.73±0.02 | 0.66±0.02 | 0.18±0.02 | 15191±1500 | 3.31±0.5 | 459±68 |
| 7/26/2014 | 0.35±0.02 | 0.28 | 0.65±0.02 | 0.43±0.01 | 0.15±0.01 | 12944±1070 | 3.46±0.5 | 374±52 |
| 8/14/2014 | 0.39±0.00 | 0.28 | 0.61±0.00 | 0.46±0.00 | 0.18±0.00 | 15658±37 | 3.30±0.5 | 475±64 |
| 8/29/2014 | 0.33±0.01 | 0.28 | 0.67±0.01 | 0.42±0.00 | 0.14±0.00 | 11863±290 | 3.21±0.5 | 369±52 |
| 9/15/2014 | 0.25±0.00 | 0.21 | 0.75±0.00 | 0.28±0.00 | 0.07±0.00 | 5906±130 | 2.26±0.5 | 261±53 |
| 10/3/2014 | 0.27±0.01 | 0.14 | 0.73±0.01 | 0.20±0.00 | 0.05±0.00 | 4717±300 | 1.72±0.5 | 274±77 |
| 5/15/2015 | 0.07±0.01 | 1.42 | 0.93±0.01 | 1.52±0.02 | 0.10±0.02 | 8825±1970 | 1.69±0.5 | 521±168 |
| 6/19/2015 | 0.23±0.04 | 0.65 | 0.77±0.04 | 0.85±0.04 | 0.20±0.04 | 17147±3860 | 3.07±0.5 | 558±113 |
| 7/30/2015 | 0.29±0.00 | 0.25 | 0.71±0.00 | 0.35±0.00 | 0.10±0.00 | 8927±147 | 3.78±0.5 | 236±28 |
| 9/10/2015 | 0.45±0.05 | 0.01 | 0.55±0.05 | 0.03±0.00 | 0.01±0.00 | 1050±193 | 2.97±0.5 | 35±7 |
Figure 3.
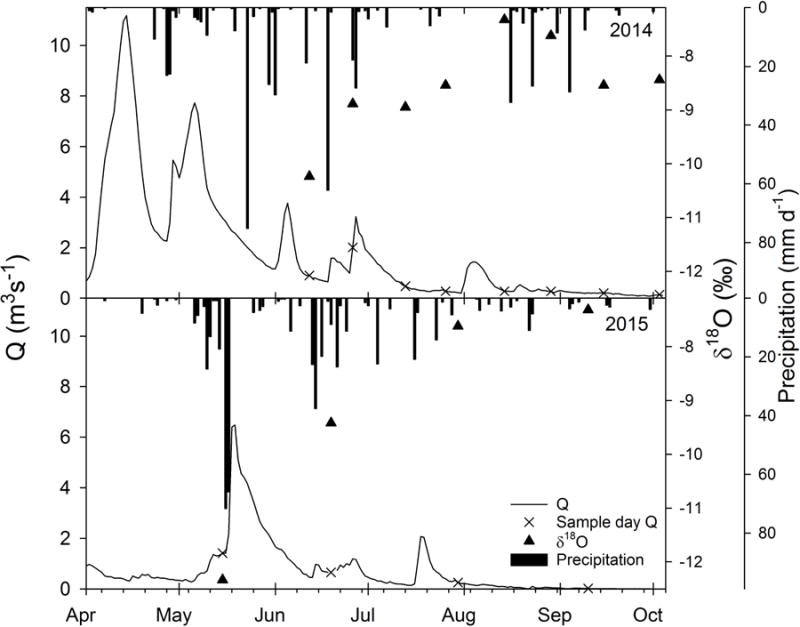
Daily precipitation (vertical bars, Jamestown Municipal Airport, ND station: GHCND:USW00014919), δ18O values of streamflow (triangles) and discharge (line with X indicating sampling days) from Pipestem Creek USGS gage at Pingree, ND (USGS 06469400) for the two study periods. Months begin at the large tick over the month name.
The δ18O values of samples collected at the USGS gage ranged from −12.3 to −7.3 ‰ (Figure 3). This variation of 5 ‰ occurred largely along a LEL, indicating that isotopic evaporative enrichment was largely responsible for isotopic shifts in the water within Pipestem Creek (Figures 4 and 5) rather than isotopic shifts due to precipitation inputs. During 2014, the isotopic composition of water within Pipestem Creek and the sampled wetlands plotted along one LEL that explained 97.6% of the variance (Figure 4, dashed line), while isotopic values of precipitation that fell during the sampling period plotted along the GMWL (diamonds in Figure 4). Rain events appeared to have a minimal influence on the isotopic composition of wetland and stream water. The LEL and GMWL intersect at −15.0 and −110.4 ‰ for δ18O and δ2H, respectively, which indicates the likely isotopic value of source water prior to any evaporative enrichment. This point resembled the average groundwater isotopic composition in 2015, and was more depleted than average precipitation for the region (white circle in Figure 4). Water within the permanent and temporary wetlands (squares) also varied in isotopic signatures along the LEL, with the permanent wetland having greater evaporative enrichment than the temporary wetland for a given sampling date. Both wetland and stream water became more evaporatively enriched through the summer.
Figure 4.
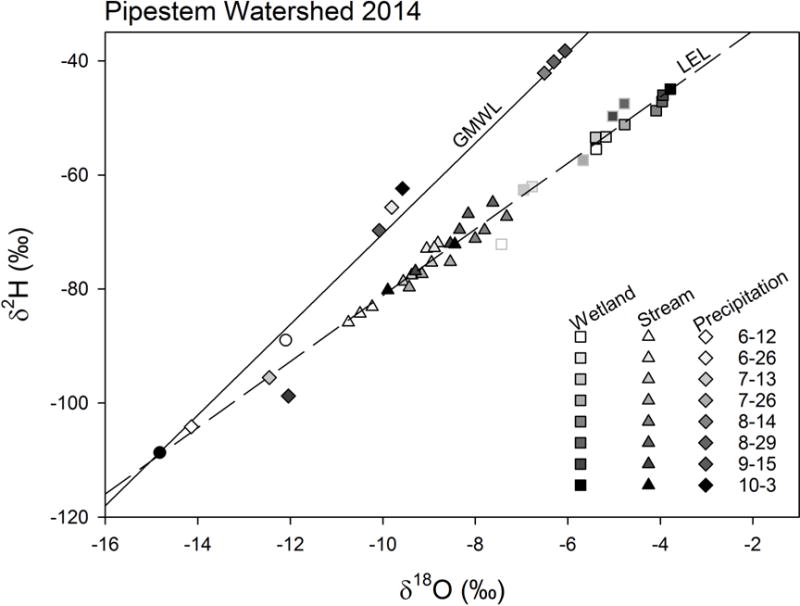
Dual isotope plot of 2014 stream and wetland data from Pipestem Creek watershed. Squares represent two wetlands measured over time: a permanent wetland (P1, in black outline) and a temporary wetland (T8, grey outline). Triangles represent samples from the three lower locations along Pipestem Creek (Figure 1). Symbols increase in darkness with time over the summer with white being June 12, 2014 and black being October 3, 2014. The solid line represents the Global Meteoric Water Line (GMWL: δ2H=8×δ18O+10) and the dashed line is the local evaporation line (LEL) estimated from all 2014 stream and wetland samples (δ2H=5.8× δ18O−23.1, R2adj =0.976). The white circle is the estimated isotope value for annual precipitation at this location from Waterisotope.org. The black circle is the average measured groundwater isotope value from 2015 (value not used to determine LEL). The diamonds are precipitation samples collected over the sampling period also shaded to indicate time.
Figure 5.
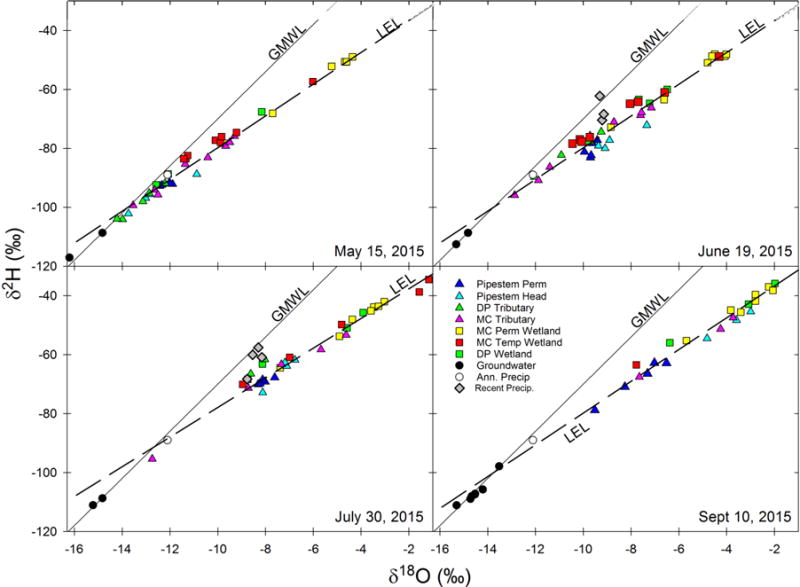
Dual isotope plot for the 4 sampling dates in 2015. Symbols for wetlands (squares) and streams (triangles) are the same as depicted in Figure 1. White circles represent estimated annual precipitation from Waterisotopes.org, and grey diamonds are recent precipitation events. The solid line is the GMWL, and the dashed line is the LEL (δ2H = 5.4× δ18O−25.9, R2adj =0.984). The July LEL was significantly different from other dates in 2015 (δ2H = 5.0× δ18O−27.6, R2adj =0.973). Black circles in May, June and July represent a groundwater seep, and the average of groundwater wells in September.
In 2015, we expanded the number of sampling points (Figure 1) and began sampling earlier in the season (Table 1), prior to the spring peak flow (Figure 3). On May 15, 2015, water isotope values within Pipestem Creek were clustered close to the GMWL (Figure 5), thus showing only slight evaporative enrichment. Water within the tributaries draining into Pipestem had low evaporative enrichment. Water in Drift Plain tributaries (green triangles) was more isotopically depleted than Pipestem Creek water, while water within tributaries draining from the Missouri Coteau (pink triangles) plotted along the LEL both above and below Pipestem Creek water, with some sites showing considerable evaporative enrichment similar to the temporary wetlands (red squares).
Water within permanent wetlands (yellow squares) had the most evaporatively enriched signal on most sampling dates (Figure 5), and this enrichment signal changed minimally over the course of the summer, which was similar to the pattern observed in 2014 (Figure 4). Five of the seven permanent wetlands clustered furthest out along the LEL throughout the summer, increasing on average by 6 and 1 ‰ for δ2H and δ18O, respectively. We used the average isotopic signal in those five permanent wetlands to represent the high end of the evaporation index for this site (see below). The isotopic composition of water in temporary wetlands was highly variable. Temporary wetlands tended to plot above the LEL, potentially indicating the influence of recent precipitation, particularly in May and June. In July, two temporary wetlands showed extreme evaporative enrichment, and two others were completely dry. By September, only one temporary wetland still had sufficient water for sampling.
Groundwater samples showed no signs of evaporative enrichment, plotting on or close to the GMWL (black circles, Figure 5). We monitored groundwater throughout the summer at a groundwater seep, until we installed the groundwater wells (see methods). Water from the groundwater seep was isotopically more depleted than water from groundwater wells, ranging from −117.1 to −111.1 ‰ for δ2H and from −16.2 to −15.2 ‰ for δ18O, and was the most depleted sample in May. Water from groundwater wells in September exhibited very little variation except for one value, and ranged from −109.0 to −97.9 ‰ for δ2H and from −14.7 to −13.5 ‰ for δ18O. The one groundwater sample that was more isotopically enriched than the rest (−97.9, −13.5) was from the deeper well located at the northern Coteau slope break. All other groundwater wells were similar in isotopic composition (−107.5 ± 1 ‰ SD, −14. 5 ± 0.2 ‰ SD) regardless of being located next to Pipestem Creek, at the Coteau slope break, or in the northern or southern part of the sampling area. As in 2014, the LEL for May, June and Sept 2015 intersect the GMWL near the groundwater isotopic values. The LEL in July had a significantly less steep slope (p<0.01) than the other three sampling periods and intersected the GMWL near the estimated isotopic value of annual precipitation.
The evaporative signal in tributary water originating from the Coteau was highly variable for each sampling date, with some tributaries showing little enrichment, and others showing evaporative enrichment similar to temporary wetlands. Tributary water originating from the Drift Plain was more similar to that within the Pipestem Creek mainstem. Tributaries to Pipestem Creek started drying up in July when only five of the eight sampled Coteau tributaries were flowing, along with two of the five Drift Plain tributaries. By September, only three Coteau tributaries were flowing, and none of the Drift Plain tributaries. Interestingly, one of the tributaries that ceased to flow was one that had little evaporative enrichment, while Coteau tributaries with high evaporative enrichment continued to flow into September.
Water within Pipestem Creek became more evaporatively enriched as the 2015 summer progressed, with water in the headwater sampling locations (light blue triangles) being slightly more evaporatively enriched than water in the mainstem (dark blue triangles, Figure 5). Isotopic values from Pipestem Creek (mainstem) water tended to be tightly clustered in the dual isotope plot except in September, when the evaporative enrichment signal decreased in the downstream direction, the opposite of what would be expected if most evaporation was occurring within the stream.
3.2 Isotopic estimates of source water contributions, and surface-water contributing area
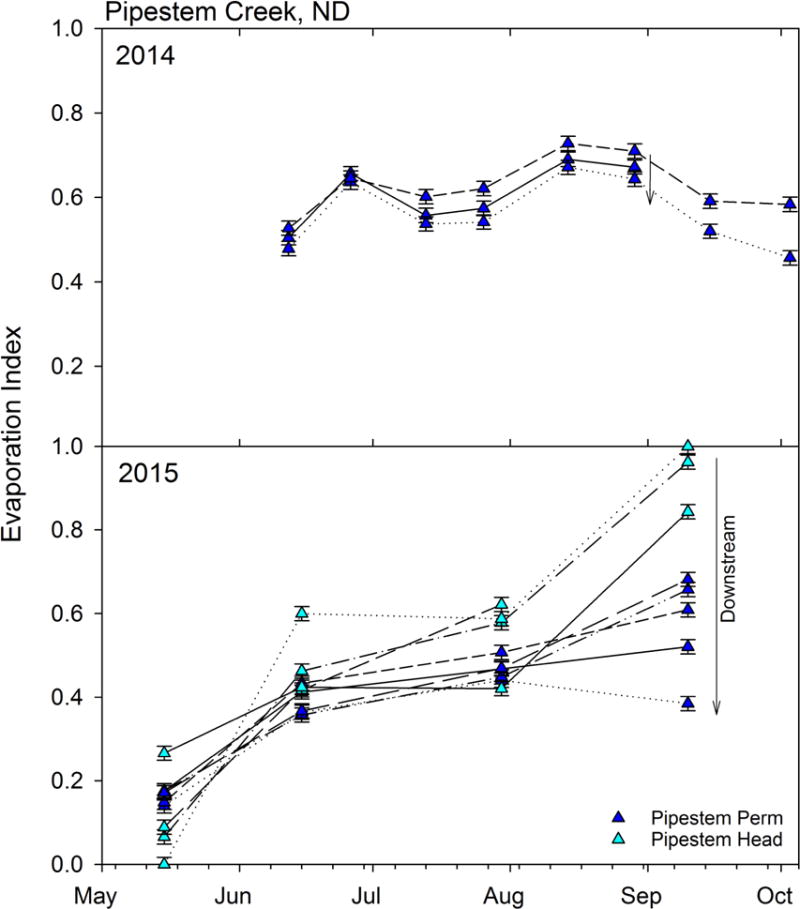
Using a simple two end-member mixing model, we calculated an evaporation index which indicates how similar in evaporative enrichment water within Pipestem Creek was to water in the highly evaporatively enriched permanent wetlands. In 2014, Pipestem Creek water had an average evaporation index value of 0.6, and this varied only slightly over the course of the summer (Figure 6). In addition, the evaporative signal decreased slightly in the downstream direction. In 2015, the evaporation index increased through the season. May values were generally low (0.14 ±0.08). In June and July, the evaporative index increased to 0.43±0.07 and 0.50±0.07, respectively. The evaporation index values were highest and varied most in September (0.71±0.21): the evaporative index decreased from 1 in the upper headwater to 0.38 at the lowest sampling point in the mainstem. The high evaporative index values illustrate the importance of surface water stored on the landscape to sustain flow throughout the summer, in addition to groundwater inputs.
Figure 6.
Changes in the evaporation index within Pipestem Creek over the two sample years. The evaporation index was calculated using a simple two end-member mixing model with the intersection of the GMWL and LEL being the unevaporated endmember (0) and the average of the Coteau permanent wetlands being the most evaporated endmember (1). Triangles in dark blue are in the main stem, and the light blue are the headwater locations. The arrows indicate the downstream direction of the sampling locations.
Evaporation can isotopically enrich any surface water, not just in wetlands. Therefore, we used discharge data and isotopic theory to estimate the amount of surface-water area (SWA) necessary to generate the observed signal within Pipestem Creek (see section 2.4.2). We estimated that on average 28.5 ± 0.1 % of the water that entered the surficially-connected water system left as evaporation, while the remaining water flowed past the USGS gage (E/I, Table 1). While the E/I proportions were relatively consistent over time, the flux of water flowing through the system was not (Figure 7), which caused our estimate of evaporative flux to vary from 1,050 to 74,720 m3 day−1. Using PET, we estimated the SWA necessary to generate the evaporative flux, which averaged 558±50 ha, and ranged from 35±7 to 2380±447 ha with a median value of 417 ha (Table 1).
Figure 7.
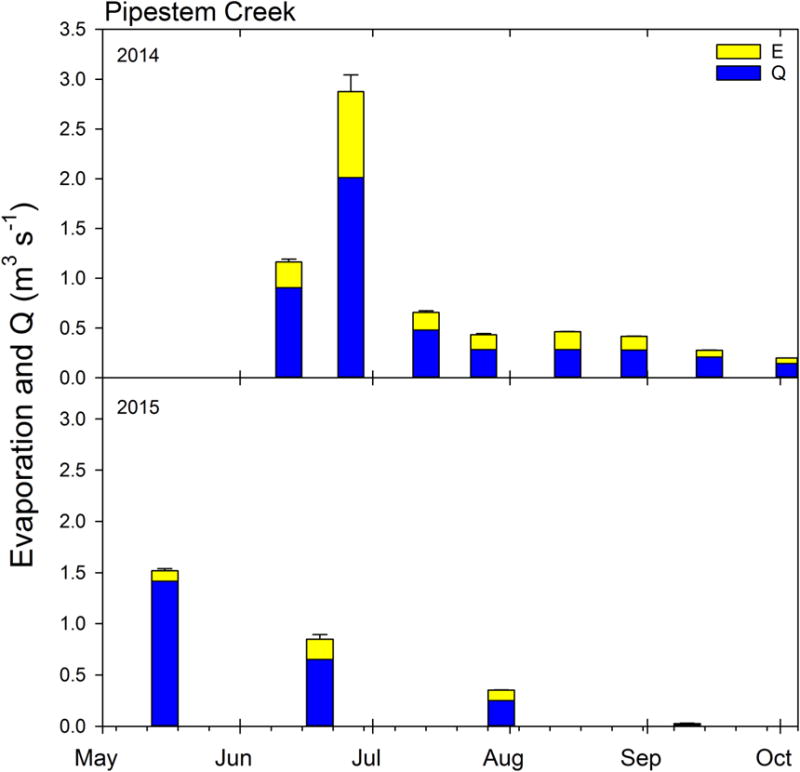
Evaporation from connected surface water (estimated from stable isotopes, see methods) and streamflow (Q) measured at Pipestem Creek USGS gage at Pingree, ND (USGS 06469400). Error bars are the standard deviation between the evaporation estimates from the two isotopes (see Table 1).
Our estimates of the SWA necessary to generate the observed evaporative enrichment signals primarily varied with flow in Pipestem Creek (Figure 8). The variance in Q accounted for 95.1% of variance in SWA, while PET and E/I account for 1.3 and 3.6 %, respectively. Basically, Q varied much more than the other two variables during the sampling periods. All but one of the SWA estimates were greater than the surface area of the Pipestem Creek stream network (221 ha), indicating pothole wetlands must be contributing evaporatively enriched water to Pipestem flow.
Figure 8.
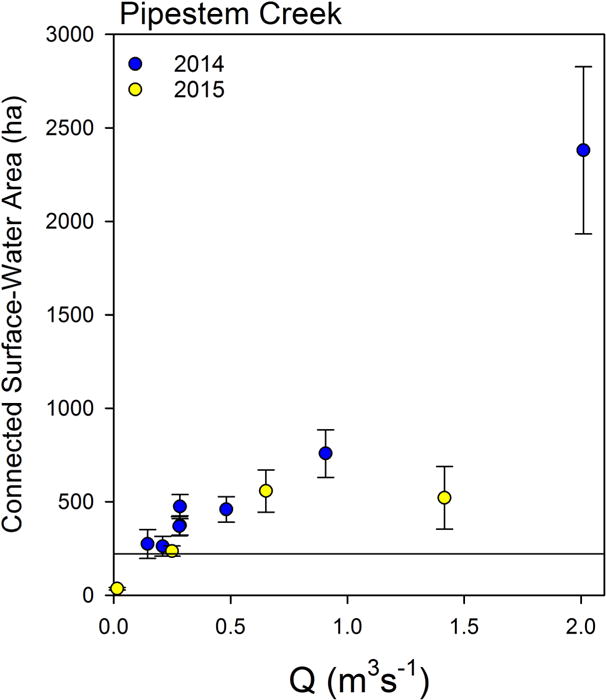
The relationship between connected surface-water area (SWA) and flow at Pipestem Creek USGS gage at Pingree, ND. The line at 221 ha indicates the SWA of the Pipestem Creek stream network. Error bars represent the standard deviation between estimates made from the two isotopes and ±0.5 mm/day for PET with each isotope.
For two dates with relatively high flows, the SWA estimates differed markedly because of differences in antecedent conditions (Table 1, Figure 8). The low SWA value associated with relatively high flow occurred on May 15, 2015, just before the annual peak flow (Figure 3). At that time, temporary wetlands and Pipestem Creek did not show clear evaporative enrichment, but the permanent wetlands did (Figure 5). Prior to sampling, a series of small rain events occurred, totaling 73 mm (Figure 3), whereas the earlier spring period was relatively dry. Only 7% of the water that entered the connected-water system had left through evaporation at that time (E/I =0.07), which was the lowest value we observed during the study (Table 1). In contrast, the high flow associated with high SWA in Figure 8 occurred after a more typical spring snowmelt on June, 26, 2014. This sampling occurred during a rising limb on the hydrograph of a 46-mm rain event, with 18 mm falling on the sampling day, and the remainder the following day (Figure 3). Isotopic composition of water within Pipestem Creek during this June event were more enriched than 2 weeks earlier, while the proportion of water that left through evaporation increased from 24% to 32%, and flow in Pipestem had nearly doubled from the previous sampling period (Table 1). On both May 15, 2015 and June 26, 2014, the permanent wetland monitored in 2014 (P1) contained water with similar evaporative enrichment signals (d-excess: −11.9‰ and −13.7‰ in June 2014 and May 2015, respectively), but the temporary wetland (T8) was less enriched on May 15, 2015 compared to June 26, 2014 (d-excess: −7.9‰ and −0.9‰ in June 2014 and May 2015, respectively). Given the similarity of evaporative enrichment of the permanent wetlands between the two dates, many more wetlands must have contributed to flow in Pipestem Creek in June 2014 than during the high flow event in May 2015 because of antecedent wetland storage differences. At high flow rates, antecedent conditions seem to be very important in determining wetland connectivity to Pipestem Creek.
3.3 Landsat estimates of wetland connectivity to streams
The average value of the Landsat-derived estimate of connected-surface water was similar to the highest value estimated using stable isotopes (2380 ha), and was an order of magnitude higher than the stream-network surface area (221 ha, determined from NHD). Using the Landsat method, stream-connected open-water area ranged from 1546 to 3036 ha and averaged 2432 ha for Landsat images collected during our study (Table 2), whereas the total area of surface water varied between 5546 and 9620 ha within the Pipestem watershed above the gage. On average, 33% of open-water surface area was classified as connected using the Landsat method. The Missouri Coteau contained nearly 95% of the total open-water surface area and the majority of the connected surface water (Table 2, Figure 9), even though most of the stream network is located within the Drift Plain ecoregion (Figure 1). While Drift Plain wetland surface-water areas are in closer proximity to Pipestem Creek, the percentage of surface-water area that was connected to the stream network was lower than in the Missouri Coteau (19.0% vs 33.6%, respectively), likely a result of the flatter topography.
Table 2.
Area (ha) of surface water within the Pipestem Creek watershed above the gauging station (USGS 06469400) near Pingree ND. Areal extent was determined from Landsat images available during the study period. The stream surface area was removed from the estimates of surface-water area. Stream surface area was defined using the high resolution National Hydrography Dataset (NHD) and included (1) connectors and intermittent stream lines (width assumed to be 1 m), (2) perennial stream lines (width assumed to be 3 m) and (3) stream/river NHDArea. For comparison, dates during drought and deluge periods (June 13, 1991 and July 5, 2011, respectively) are also included.
| Date | Drift Plain | Missouri Escarpment | Missouri Coteau | Connected Surface area (ha) | Total surface water (ha) | % Connected | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
||||||||||
| Connected (ha) | Total (ha) | % Connected | Connected (ha) | Total (ha) | % Connected | Connected (ha) | Total (ha) | % Connected | ||||
| 26-May-14* | 112.5 | 516.4 | 21.8 | 0.6 | 34.8 | 1.8 | 2922.7 | 7546.4 | 38.7 | 3035.8 | 8097.6 | 37.5 |
| 13-Jul-14 | 26.8 | 255.0 | 10.5 | 3.3 | 16.9 | 19.7 | 2018.5 | 6042.5 | 33.4 | 2048.6 | 6314.5 | 32.4 |
| 30-Aug-14 | 35.0 | 286.5 | 12.2 | 0.1 | 7.3 | 1.2 | 2016.4 | 5656.5 | 35.6 | 2051.4 | 5950.3 | 34.5 |
| 15-Sep-14 | 76.9 | 438.2 | 17.5 | 3.0 | 21.7 | 13.8 | 2623.3 | 7428.1 | 35.3 | 2703.3 | 7887.9 | 34.3 |
| 11-Apr-15 | 89.7 | 512.9 | 17.5 | 10.1 | 60.4 | 16.7 | 2666.0 | 9046.3 | 29.5 | 2765.8 | 9619.6 | 28.8 |
| 14-Jun-15 | 68.1 | 358.7 | 19.0 | 0.2 | 25.4 | 0.7 | 2447.1 | 6836.9 | 35.8 | 2515.4 | 7221.0 | 34.8 |
| 1-Aug-15 | 129.3 | 427.7 | 30.2 | 46.2 | 103.7 | 44.6 | 2615.2 | 8203.2 | 31.9 | 2790.7 | 8734.6 | 31.9 |
| 2-Sep-15 | 65.1 | 282.3 | 23.1 | 0.0 | 6.5 | 0.0 | 1481.0 | 5257.1 | 28.2 | 1545.9 | 5545.9 | 27.9 |
|
| ||||||||||||
| 13-Jun-91 | 141.4 | 249.2 | 56.7 | 0.9 | 10.9 | 8.3 | 650.2 | 1663.1 | 39.1 | 792.5 | 1923.2 | 41.2 |
| 5-Jul-11 | 307.2 | 1465.7 | 21.0 | 30.4 | 129.3 | 23.5 | 3254.4 | 12066.7 | 27.0 | 3592.1 | 13661.6 | 26.3 |
May 26, 2014 Landsat scene contained approximately 12% cloud cover.
Figure 9.
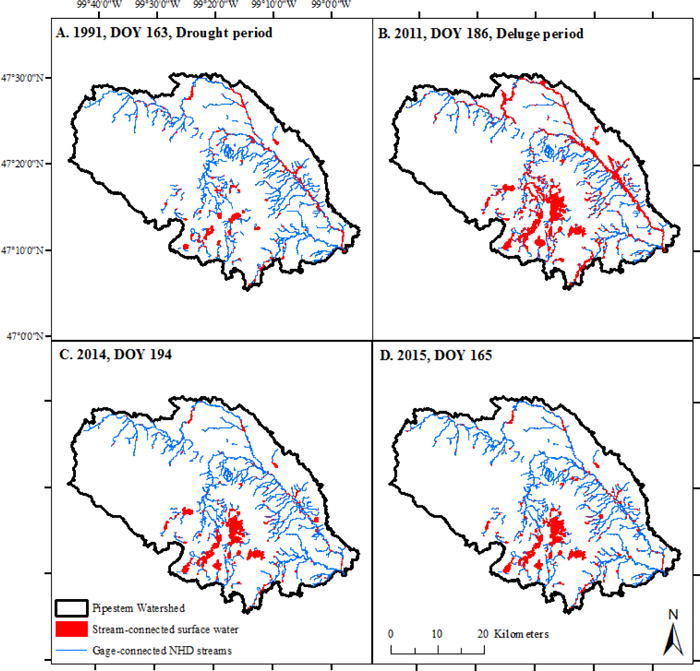
Surface waters connected to the NHD stream network within Pipestem Creek watershed above the USGS gage (crosshatched area in Figure 1). Connected waters are shown in red and the NHD network is shown in blue. Connectivity was determined using Landsat images (see methods). The collection dates for the panel images were (A) June 13, 1991, (B) July 5, 2011, (C) July 13, 2014, and (D) June 14, 2015.
For historical comparisons, we also analyzed the wettest and driest Landsat image available for the watershed (Figure 9, Table 2). The driest date for which imagery was available was June 13, 1991 (DOY 163) and total open-water surface area was estimated at 1923 ha with only 793 ha intersecting the NHD stream network. The wettest Landsat image was taken on July 5, 2011 (DOY 186), and total surface-water area was an order of magnitude higher (13,662 ha) with 3592 ha classified as stream-connected. Interestingly, the driest date had a higher percentage of surface-water area connected to the stream network (41 % as compared to 26 % on the wettest date) because wetlands near streams maintain water levels as compared to more distal wetlands which tend to reduce in area in dry periods.
4 Discussion
Our isotopic results provide inferred measures of wetland connectivity at the watershed scale that are vital to helping managers assess the importance of wetlands to downstream water [Golden et al., 2017]. Prairie-pothole wetlands contributed significant amounts of water to Pipestem Creek when streamflow exceeded 0.1 m3s−1 (Figure 8). The dynamic nature of isotopically-determined contributing area and the correlation between streamflow and contributing area are consistent with the fill-spill, fill-merge models in which potholes along the stream network act as reserve water sources that enter the stream during precipitation events [Evenson et al., 2016; Leibowitz and Vining, 2003; McDonnell, 2013; Shaw et al., 2012; Spence and Woo, 2003]. However, we also found that evaporatively enriched water contributed approximately half of the flow during rising and receding limbs of the hydrograph as well as under baseflow conditions (Figure 6). This suggests fill-and-spill was not just activated during precipitation events, but that a more complex process was responsible for sustaining streamflow during drier periods. Interestingly, we also found that these pothole wetlands did not contribute significantly to subsurface groundwater flows entering the perennial stream. Groundwater next to Pipestem Creek showed no sign of evaporative enrichment. This result was somewhat surprising given the density of wetlands within the watershed (Figure 1). Instead, this groundwater seems to have been recharged from unevaporated winter-dominated precipitation. At all levels of flow, the wetland contribution to streamflow can be accounted for by wetlands with a direct surface-water connection with the stream network as defined by NHD [Vanderhoof et al., 2016a]. The isotopic estimates of surface-water contributing area in this study were much smaller than the contributing area of wetlands characterized by Landsat images [Vanderhoof et al., 2016a] except at the highest discharge rates. Thus, the Landsat estimates represent the potential extent of contributing wetlands, whereas the actual extent of contributing wetlands may be much smaller, likely resulting from disconnections within the stream network itself [Godsey and Kirchner, 2014; Shaw et al., 2012]. In the Landsat analysis, we defined “connected surface water” as the intersection of a surface-water body with the NHD stream dataset, assuming that the NHD was continuous throughout its extent. Landsat imagery could not account for disconnections within the NHD stream network, but was very useful for identifying which areas were likely contributors. These analyses indicated that prairie-pothole wetlands located within the Missouri Coteau that were connected to NHD were the dominant source of evaporatively enriched water entering the perennial stream, and wetland water did not flow along subsurface groundwater flowpaths to the stream [Neff and Rosenberry, 2017]. In addition, wetland-stream connectivity was highly dynamic, expanding and contracting by orders of magnitude in wet–dry– wet cycles [Godsey and Kirchner, 2014], which greatly influences the actual connectivity of wetlands to downstream receiving waters.
4.1 Isotopic approaches for estimating wetland-stream connectivity
The isotopic signal generated by evaporation proved to be an excellent tracer for determining the contribution of water from prairie-pothole wetlands into Pipestem Creek and provided direct measures of wetland-stream connectivity at the watershed scale, although the measured temporal dynamics were limited by sampling frequency. Golden et al. [2017] argue that direct measures of connectivity are crucial to management and policy decisions regarding wetland protection.
The dual isotope (δ18O and δ2H) framework for detecting evaporative sources has been used successfully to separate sources of flow for other freshwater systems with extensive lakes and wetlands [Brock et al., 2007; Gibson and Edwards, 2002; Gibson et al., 2005; Gibson and Reid, 2010; Smith et al., 2015; Sprenger et al., 2017; Turner et al., 2014]; however, our study is the first to extend this technique to quantifying wetland surface water area contributing to flow. Brock et al. [2007] used the dual isotope approach to classify lakes based on the timing and extent of their connectivity to surrounding water sources. St. Amour et al. [2005] partitioned streamflow into three sources: wetlands, snowmelt and groundwater. They used the evaporation signal to represent surface-water contributions in fen- and bog-dominated systems compared to the non-evaporated sources of groundwater and snowmelt, and illustrated that in years with high surface water storage on the landscape, evaporatively enriched surface-water contributions to streamflow increased. Similarly, Turner et al. [2014] used temporal variation in d-excess as a way to apportion the flow contribution from lakes and wetlands to the Old Crow River in the Yukon Territory over a series of year. In a study more similar to ours, Gibson and Reid [2010] deduced variation in effective drainage area based on the variation between levels of evaporative enrichment in a stream and the lakes within the watershed. The Pipestem system was less complicated than some of these previous studies largely because the primary non-evaporated water source (groundwater) was spatially and temporally stable. This relative simplicity in the Pipestem watershed resulted in all sampled water from wetlands and streams plotting along a single LEL for each sampling period. This tight relationship indicated that evaporative enrichment caused most of the variation in water isotopes within the system on a particular date, rather than variation in non-enriched water sources with differing isotopic values (i.e., sources spread along the GMWL). While precipitation falling during the sampling period was isotopically variable, it had minimal impact on water isotopic composition in the permanent wetlands and Pipestem Creek (Figures 4 & 5). The exception was water within temporary wetlands where the isotopic composition tended to deviate from the LEL and plotted slightly above the LEL towards the GMWL, indicating the influence of recent precipitation.
This simplicity of one dominant source of water that is then evaporatively enriched while residing in surface water across the landscape allowed us to estimate wetland contribution using discharge data in combination with isotopic evaporation theory [Gibson and Edwards, 2002; Gibson and Reid, 2010]. Our isotopic estimates of connected surface-water area were greater than the surface area of the stream network, indicating that wetlands were contributing significant volumes of water to Pipestem Creek streamflow, except at the lowest flows (Figure 8). However, the isotopic method did not indicate which wetlands were contributing. Including a remote sensing component to map inundation helped identify which stream-connected surface- water areas were more likely to be connected (Figure 9) and indicated that most stream-connected potholes reside in the Missouri Coteau geologic region rather than in the Drift Plain ecoregion. While Landsat determination of connected surface water area (Table 2) seems to represent the upper bounds of pothole wetland-to-stream connectivity, the combination of these two approaches helps address both location and extent of connected wetlands in this dynamically connected system over the study period. This isotopic approach using the evaporative enrichment signal to estimate connected surface-water area could be used in other locations provided that there is one dominant non-evaporated water source that does not vary spatially across the watershed, and a tight LEL can be developed.
4.2 Groundwater and surface water flowpaths
Our data indicate that evaporatively enriched water followed direct surface-water connections with the stream network and did not flow via groundwater to the stream. Despite the high density of wetlands within the Pipestem watershed (Figure 1), groundwater samples collected from the wells had no detectable evaporative signal (Figure 5), indicating that water stored in pothole wetlands generally did not recharge the groundwater flowing to Pipestem Creek, which agrees with groundwater modeling results for the area [Neff and Rosenberry, 2017]. Although we only sampled groundwater at one location throughout the 2015 summer, and 7 locations in September 2015, the isotopic signatures were both temporally and spatially stable, and matched the intersection of the LEL and GMWL indicating that these isotopic values were representative of groundwater entering Pipestem Creek. Additional groundwater sampling since 2015 has also found similar unevaporated and depleted isotopic values (Brooks, unpublished data). This finding corroborates the importance of fill-and-spill mechanisms for hydrologic connectivity between wetlands and downstream water within pothole wetlands [Evenson et al., 2016; Shaw et al., 2012; Spence and Woo, 2003]. We could hypothesize that if in this wetland-dominated landscape, wetlands do not contribute to regional subsurface flowpaths, wetlands may also have a minimal role in subsurface flowpaths to streams in similar landscapes. More research is needed, but the isotopic approach highlighted here could be very useful for better understand wetland contributions to groundwater.
Our results also indicate that groundwater near Pipestem Creek was recharged by winter-dominated precipitation (e.g., snowmelt). In most years, snowmelt is abundant at a time with little or no transpiration. In years when the frozen soils are relatively dry, water is able to infiltrate and recharge groundwater [Shanley and Chalmers, 1999]. Later in the spring and summer, evapotranspiration is high and may prevent recharge of summer precipitation to groundwater. This scenario would explain the absence of a summertime-precipitation isotopic signal in our groundwater samples. Taken together, we infer that groundwater flowing toward Pipestem Creek is recharged from upland areas during spring snowmelt, but not to a measurable degree from wetlands within those upland areas.
Direct inputs of snowmelt-recharged groundwater was the other important source of water for Pipestem Creek flow, composing over 40% of the water in Pipestem throughout the two summers (Figure 6). We defined the unevaporated source of water feeding Pipestem Creek as the intersection of the LEL and the GMWL, and those intersections were at isotopic values similar to groundwater (Figure 4 and 5), which was more depleted than the estimated isotopic composition of annual precipitation or rainfall events during the study. The similarity of this intersection point over two years also indicates a large source with a stable isotopic signature such as groundwater, whereas precipitation isotopic signatures vary significantly over time. In addition, the evaporative signal in Pipestem Creek tended to decrease in the downstream direction (Figure 6), indicative of an increasing contribution of groundwater, particularly in the late summer low-flow periods.
4.3 Spatial and temporal dynamics of pothole wetland connectivity to downstream water
The difference between our Landsat and isotopic values of connected SWA highlight the dynamic nature of actual connectivity in this wetland-dominated system, and that the Landsat approach can account for all potential contributing wetlands. Using Landsat images, we estimated that approximately 33±3% of total surface-water area was connected to the NHD stream network during the two observation periods (Table 2), while the isotopic data suggested that the actual SWA contributing to flow at the Pipestem gage was much lower ranging from 30% to less than 1%, with an average of 7.6±7%. The two estimates converged when antecedent water storage in wetlands was high, and a precipitation event was sufficient to cause a fill-and-spill reaction in nearly all wetlands connected to the NHD network and presuming that the entire NHD stream network was connected (June, 2014). At other times, many wetlands connected to NHD and possibly portions of the NHD itself were not actively contributing to streamflow, but enriched wetland water was still contributing to Pipestem flow at all stages of the hydrograph (Figure 6). This highlights the fact that landscape storage of water is not just important for generating runoff in response to events [Spence, 2007], but also to sustaining flow between events. While each pothole wetland may have a threshold for spilling [Shaw et al., 2012], these thresholds varied sufficiently spatially that spilling can contribute to streamflow long after the peak of the spill event.
Pipestem Creek watershed straddles the boundary between two very different ecoregions with a significant slope between the two (Figure 1) and most of the contributing wetlands appear to be from the Missouri Coteau (Figure 9). The Missouri Coteau contains the majority of wetlands within the Pipestem Creek watershed, while the stream network is mostly contained in the Drift Plain ecoregion (Table 2, Figure 1). Tributaries draining from the Coteau were often both more evaporatively enriched and more persistent than tributaries draining the Drift Plain, which supports the concept of Coteau-connected wetlands sustaining Pipestem Creek flows. The slope of the Missouri Escarpment provides the driving force for the connection, setting up a cascading series of fill-and-spill wetlands near and along the Coteau slope, an effect that should most likely occur in areas of high topographic relief and an extended slope [Leibowitz et al., 2016], and contributes to the variation in wetland spilling thresholds in the Pipestem. The importance of these wetlands near the Missouri Escarpment to flow in Pipestem Creek supports the idea that geographical boundaries can control significant hydrological processes including connectivity [McDonnell, 2013; Winter, 1999].
This study took place in a wetter than normal decade with wetlands being fuller than during dry decades [Leibowitz et al., 2016; Zhang et al., 2009]. Regardless, the precipitation-runoff relationship between the two years reflects the complex interplay of precipitation timing, wetland storage, and flow [Spence, 2007]. While the two study years had greater than average precipitation, discharge was average for 2014 and below normal for 2015. In 2014, discharge in Pipestem Creek was typical of long-term seasonal patterns of discharge, with a large snowmelt pulse in April, and declining flows throughout the summer. In contrast, Pipestem Creek discharge in 2015 was more characteristic of flows during drier conditions without the snowmelt peak and with lower summer flows. Interestingly, the extent of total and connected wetlands determined using the Landsat data (Table 2) was similar between the two years, so the drier conditions in 2015 did not significantly reduce wetland area, as was seen on June 13, 1991, during an extreme dry period. However, the water depth of CLSA wetlands was on average 0.15 m lower in 2015 compared to 2014 [Mushet, 2016]. In regions with hummocky topography such as the Prairie Pothole Region, water levels and wetland area are often controlled by multi-year events rather than seasonal events [Aragon et al., 2011; Kuppel et al., 2015], particularly for larger wetlands [Zhang et al., 2009].
Regardless of the flow differences between years, the relationship between connected open-water surface area and flow (Figure 8) was similar, except during the highest-flow periods we sampled. During high flow, antecedent conditions and wetland storage were important in determining the volume of evaporatively enriched water in Pipestem Creek. On June 26, 2014, pothole wetlands were full from the spring snowmelt in April and May. We estimated that 30 % (2380 ha) of the total surface-water area contributed to flow on this date. In contrast, the winter of 2015 was one of the driest on record and flows were very low in April and May (Figure 3). Pothole wetland storage was low during a precipitation event just prior to our May 15, 2015 sampling. For a similar level of flow in Pipestem Creek, only 7 % (521 ha) of the total surface-water area contributed evaporatively enriched water to Pipestem flow, which is 1/3 of the contributing open-water area in June 2014 for an equivalent flow volume (normalized for flow differences). Indeed, water levels in 16 measured potholes at CLSA were on average 0.16 ± 0.12 (SD) m higher on June 17, 2014 than on May 4, 2015 [Mushet, 2016]. This difference between these two sampling events might reflect differences we could expect to see in wet and dry decades. In wet decades, storage in potholes on the landscape would be a much larger contributor to event-based discharge into Pipestem Creek as compared to drier decades when event discharge water may be composed of recent events or groundwater storage rather than open-water storage [Spence and Phillips, 2015]. This variability in connected open-water surface area at high streamflow highlights the importance of antecedent conditions for not only the timing of flow but the source of water as well [McDonnell, 2013; Shaw et al., 2012; Spence and Woo, 2003; Spence, 2007; Spence and Phillips, 2015]. Nevertheless, most of the flow dynamics within Pipestem Creek were matched by equivalent dynamics in the connected surface water contributing evaporatively enriched water (Figure 8), highlighting the importance of stored water on the landscape to flow within Pipestem Creek. It remains to be seen whether our findings would be similar during periods with lower antecedent conditions as would occur during periods of drought, or during higher flow conditions during spring snowmelt that we did not sample (Figure 3).
5 Conclusions
The evaporation signal in water isotopes was useful to assess connectivity between prairie-pothole wetlands and streamflow in Pipestem Creek, a low-gradient perennial headwater stream. Water stored within wetland ponds was characterized by evaporative enrichment that was used as a tracer indicating the relative importance of surface-water storage flowing within Pipestem Creek. The isotopic composition of water within wetland ponds and the stream network plotted along one local evaporation line, which varied only slightly over the two-year study period, indicating a common source of water dominated by winter recharge that we speculated was groundwater. Groundwater sampled in wells along Pipestem Creek was not evaporatively enriched, and its isotopic composition was consistent with snowmelt recharge. Our results indicate that prairie-pothole wetlands in the Pipestem Creek Watershed contributed significant amounts of water to streamflow through surface-water connections, and not through direct subsurface connections.
The degree of hydrologic connectivity between wetlands and the stream was highly dynamic, fluctuating with precipitation-event driven streamflow. We found that the ponded-water surface necessary to generate the evaporative signal in streamflow varied between 35 and 2380 ha over the two years with a median value of 417 ha. The surface-water area estimated for the stream network was 221 ha, thus wetland water contributed to stream flow for all but one sampling event. Landsat estimates of connected wetland surface-water area gave the upper bounds of the isotopic estimates because our remote sensing technique assumes that all NHD stream segments are flowing. We viewed the difference between isotopic and Landsat estimates as actual and potential estimates of contributing wetland surface-water area to flow in Pipestem Creek. The Landsat estimates had the added benefit of indicating which wetland areas were contributing. We found that Missouri Coteau wetlands with connections to NHD streams were the most likely sources of evaporatively enriched water to Pipestem Creek throughout both summers, and helped sustain flow during the summer low-flow period. Evaporatively enriched water from pothole wetlands contributed significant amounts of water during all stages of the hydrograph including base-flow. Combining the isotopic and Landsat approaches to estimating contributing area appears to be a promising technique for determining potential and actual contributing areas in these flat wetland-dominated systems. This combined isotope and Landsat technique could be invaluable to watershed managers for determining the source and location of wetlands contributing to downstream waters.
Key Points.
The evaporation signal in water isotopes was used to assess connectivity between prairie-pothole wetlands and streamflow.
Prairie-pothole wetlands contributed water to streamflow through surface-water connections, but not through groundwater connections.
Hydrologic connectivity between prairie-pothole wetlands and the stream was dynamic, fluctuating with streamflow.
Acknowledgments
Data
We thank Don Phillips and E. Henry Lee for statistical help. Jim Markwiese, Yi Yi, Brent Wolfe, and three anonymous reviewers provided comments on earlier versions. This manuscript has been subjected to EPA and USGS review and has been approved for publication. The views expressed in this paper are those of the authors and the USGS, and do not necessarily reflect the views or policies of the U.S. Environmental Protection Agency. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government. EPA generated data from this project will be available on the United States Environmental Protection Agency’s Environmental Dataset Gateway (https://edg.epa.gov/metadata/catalog/main/home.page). Water isotope data will also be available at Waterisotopes.org. USGS data from the Cottonwood Lake Study Area is available at: https://www.sciencebase.gov/catalog/item/52f0ffd9e4b0f941aa181fc6.
References
- Alexander LC. Science at the boundaries: scientific support for the Clean Water Rule. Freshwater Science. 2015 doi: 10.1086/684076. [DOI] [Google Scholar]
- Amado AA, et al. Investigating Hydrologic Connectivity of a Drained Prairie Pothole Region Wetland Complex using a Fully Integrated, Physically-Based Model. Wetlands. 2016:1–13. doi: 10.1007/s13157-016-0800-5. [DOI] [Google Scholar]
- Ameli AA, Creed IF. Quantifying hydrologic connectivity of wetlands to surface water systems. Hydrology and Earth System Sciences. 2017;21:1791–1808. doi: 10.5194/hess-2016-404. [DOI] [Google Scholar]
- Aragon R, et al. Surface and groundwater dynamics in the sedimentary plains of the Western Pampas (Argentina) Ecohydrology. 2011;4(3):433–447. doi: 10.1002/eco.149. [DOI] [Google Scholar]
- Bornette G, et al. Aquatic plant diversity in riverine wetlands: The role of connectivity. Freshwater Biology. 1998;39(2):267–283. doi: 10.1046/j.1365-2427.1998.00273.x. [DOI] [Google Scholar]
- Bowen GJ, Wilkinson BH. Spatial distribution of δ18O in meteoric precipitation. Geology. 2002;30:315–318. doi: 10.1130/0091-7613(002)030<0315:SDOOIM>2.0.CO;2. [DOI] [Google Scholar]
- Bowen GJ, Revenaugh J. Interpolating the isotopic composition of modern meteoric precipitation. Water Resour Res. 2003;39(10):1299. doi: 10.1029/2003WR002086. [DOI] [Google Scholar]
- Bowen GJ, et al. Global application of stable hydrogen and oxygen isotopes to wildlife forensics. Oecologia. 2005;143:337–348. doi: 10.1007/s00442-004-1813-y. [DOI] [PubMed] [Google Scholar]
- Brannen R, et al. Influence of shallow groundwater–surface water interactions on the hydrological connectivity and water budget of a wetland complex. Hydrol Process. 2015;29(18):3862–3877. doi: 10.1002/hyp.10563. [DOI] [Google Scholar]
- Brock BE, et al. Characterizing the Hydrology of Shallow Floodplain Lakes in the Slave River Delta, NWT, Canada, Using Water Isotope Tracers. Artic, Antarctic, and Alpine Research. 2007;39(3):388–401. doi: 10.1657/1523-0430(06-026)[BROCK]2.0.CO;2. [DOI] [Google Scholar]
- Brooks JR, et al. Ecohydrologic separation of water between trees and streams in a Mediterranean climate. Nature Geoscience. 2010;3:100–104. doi: 10.1038/NGEO722. [DOI] [Google Scholar]
- Brooks JR, et al. Stable Isotope estimates of lake water evaporation:inflow and residence time for lakes across the United States as a tool for national lake water quality assessments. Limnology and Oceanography. 2014;59(6):2150–2165. doi: 10.4319/lo.2014.59.6.2150. [DOI] [Google Scholar]
- Brooks JR. Water, bound and mobile: Isotopic data help to resolve global hydrologic fluxes. Science. 2015;349(6244):138–139. doi: 10.1126/SCICOM.aac4742. [DOI] [PubMed] [Google Scholar]
- Chu X. Delineation of pothole-dominated wetlands and modeling of their threshold behaviors. Journal of Hydrologic Engineering. 2015 doi: 10.1061/(ASCE)HE.1943-5584.0001224. [DOI] [Google Scholar]
- Clark ID, Fritz P. Environmental isotopes in hydrogeology. Lewis Publishers; New York, New York, USA: 1997. p. 328. [Google Scholar]
- Cohen MJ, et al. Do geographically isolated wetlands influence landscape functions? Prc Natl Acad Sci. 2016;113:1978–1986. doi: 10.1073/pnas.1512650113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craig H, Gordon LI. Deuterium and oxygen-18 variation in the ocean and the marine atmosphere. In: Tongiorgi E, editor. Proceedings of a conference on stable isotopes in oceanographic studies and paleotemperatures. Lab. di Geologia Nucleare.; Spoleto, Italy: 1965. pp. 9–130. [Google Scholar]
- Daly C, et al. Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States. International Journal of Climatology. 2008;28:2031–2064. doi: 10.1002/joc.1688. [DOI] [Google Scholar]
- Dansgaard W. Stable isotopes in precipitation. Tellus. 1964;16(4):436–468. doi: 10.1111/j.2153-3490.1964.tb00181.x. [DOI] [Google Scholar]
- Dou P, et al. Macrobenthos diversity response to hydrological connectivity gradient. Wetlands. 2016;36(Suppl 1):S45–S55. doi: 10.1007/s13157-014-0580-8. [DOI] [Google Scholar]
- Downing D, et al. Technical and scientific challenges in implementing Rapanos’ “Water of the United States”. Natural Resources and Environment. 2007;22(1):42–45. 62–63. doi. [Google Scholar]
- Euliss NH, et al. The wetland continuum: A conceptual framework for interpreting biological studies. Wetlands. 2004;24(2):448–458. doi: 10.1672/0277-5212(2004)024[0448:TWCACF]2.0.CO;2. [DOI] [Google Scholar]
- Euliss NH, et al. Placing prairie pothole wetlands along spatial and temporal continua to improve integration of wetland function in ecological investigations. J Hydrol. 2014;513:490–503. doi: 10.1016/j.jhydrol.2014.04.006. [DOI] [Google Scholar]
- Evaristo J, et al. Global separation of plant transpiration from groundwater and streamflow. Nature. 2015;525:91–94. doi: 10.1038/nature14983. [DOI] [PubMed] [Google Scholar]
- Evenson GR, et al. Geographically isolated wetlands and watershed hydrology: A modified model analysis. J Hydrol. 2015;529(Part 1):240–256. doi: 10.1016/j.jhydrol.2015.07.039. [DOI] [Google Scholar]
- Evenson GR, et al. An improved representation of geographically isolated wetlands in a watershed-scale hydrologic model. Hydrol Process. 2016 doi: 10.1002/hyp.10930. [DOI] [Google Scholar]
- Gat J. Oxygen and hydrogen isotopes in the hydrologic cycle. Annu Rev Earth Planet Sci. 1996;24:225–262. doi: 10.1146/annurev.earth.24.1.225. [DOI] [Google Scholar]
- Gat J. Isotope hydrology: A study of the water cycle. Imperial College Press; London, England: 2010. p. 189. [Google Scholar]
- Gibson JJ, Edwards TWD. Regional water balance trends and evaporation-transpiration partitioning from a stable isotope survey of lakes in northern Canada. Global Biogeochem Cycles. 2002;16(2):1026. doi: 10.1029/2001GB001839. [DOI] [Google Scholar]
- Gibson JJ, et al. Progress in isotope tracer hydrology in Canada. Hydrol Process. 2005;19:303–327. doi. [Google Scholar]
- Gibson JJ, Reid R. Stable isotope fingerprint of open-water evaporation losses and effective drainage area fluctuations in a subarctic shield watershed. J Hydrol. 2010;381:142–150. doi: 10.1016/j.jhydrol.2009.11.036. [DOI] [Google Scholar]
- Godsey SE, Kirchner JW. Dynamic, discontinuous stream networks: hydrologically driven variations in active drainage density, flowing channels and stream order. Hydrol Process. 2014;28:5791–5803. doi: 10.1002/hyp.10310. [DOI] [Google Scholar]
- Golden HE, et al. Relative effects of geographically isolated wetlands on streamflow: a watershed-scale analysis. Ecohydrology. 2016;9:21–38. doi: 10.1002/eco.1608. [DOI] [Google Scholar]
- Golden HE, et al. Integrating geographically isolated wetlands into land management decisions. Frontiers in Ecology and the Environment. 2017 doi: 10.1002/fee.1504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldhaber MB, et al. Hydrogeochemistry of prairie pothole region wetlands: role of long-term critical zone processes. Chem Geol. 2014;387:170–183. doi: 10.1016/j.chemgeo.2014.08.023. [DOI] [Google Scholar]
- Green AA, et al. A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Transactions on Geoscience and Remote Sensing. 1988;26(1):65–74. doi: 10.1109/36.3001. [DOI] [Google Scholar]
- Homer C, et al. Completion of the 2011 National Land Cover Database for the conterminous United States – representing a decade of land cover change information. Photogrammetric Engineering and Remote Sensing. 2015;81:345–354. doi. [Google Scholar]
- Horita J, Wesolowski D. Liquid-vapour fractionation of oxygen and hydrogen isotopes of water from the freezing to the critical temperature. Geochimi Cosmochim Acta. 1994;58:3425–3437. doi: 10.1016/0016-7037(94)90096-5. [DOI] [Google Scholar]
- Huang S, et al. Demonstration of a conceptual model for using LiDAR to improve the estimation of floodwater mitigation potential of Prairie Pothole Region wetlands. J Hydrol. 2011;405(3–4):417–426. doi: 10.1016/j.jhydrol.2011.05.040. [DOI] [Google Scholar]
- Jasechko S, et al. Terrestrial water fluxes dominated by transpiration. Nature. 2013;496:347–350. doi: 10.1038/nature11983. [DOI] [PubMed] [Google Scholar]
- Kuppel S, et al. What does it take to flood the Pampas?: Lessons from a decade of strong hydrological fluctuations. Water Resour Res. 2015;51:2937–2950. doi: 10.1002/2015WR016966. [DOI] [Google Scholar]
- LaBaugh JW, Swanson G. Aquatic Ecosystems in Semi-Arid Regions: Implications for Resource Management, edited by R D Robarts and M L Bothwell, pp. Environment Canada; Saskatoon: 1992. Changes in chemical characteristics of water in selected wetlands in the Cottonwood Lake area, North Dakota, U.S.A., 1967-1989; pp. 149–162. [Google Scholar]
- LaBaugh JW, et al. Changes in atmospheric circulation patterns affect midcontinent wetlands sensitive to climate. Limnology and Oceanography. 1996;41(5):864–870. doi: 10.4319/lo.1996.41.5.0864. [DOI] [Google Scholar]
- LaBaugh JW, et al. Hydrologic functions of prairie wetlands. Great Plains Research. 1998;8(1):17–37. doi. [Google Scholar]
- LaBaugh JW, et al. Changes in Pond Water Levels and Surface Extent Due to Climate Variability Alter Solute Sources to Closed-Basin Prairie-Pothole Wetland Ponds, 1979 to 2012. Wetlands. 2016:1–13. doi: 10.1007/s13157-016-0808-x. [DOI] [Google Scholar]
- Lang M, et al. Enhanced detection of wetland-stream connectivity using LiDAR. Wetlands. 2012;32(3):461–473. doi: 10.1007/s13157-012-0279-7. [DOI] [Google Scholar]
- Leibowitz SG. Isolated wetlands and their functions: An ecological perspective. Wetlands. 2003;23(3):517–531. doi: 10.1672/0277-5212(2003)023[0517:IWATFA]2.0.CO;2. [DOI] [Google Scholar]
- Leibowitz SG, Vining KC. Temporal connectivity in a Prairie Pothole complex. Wetlands. 2003;23(1):13–25. doi: 10.1672/0277-5212(2003)023[0013:TCIAPP]2.0.CO;2. [DOI] [Google Scholar]
- Leibowitz SG, et al. Intermittent Surface Water Connectivity: Fill and Spill Vs. Fill and Merge Dynamics. Wetlands. 2016 doi: 10.1007/s13157-016-0830-z. [DOI] [Google Scholar]
- Liu G, et al. Characterizing the Climate-Driven Collapses and Expansions of Wetland Habitats with a Fully Integrated Surface–Subsurface Hydrologic Model. Wetlands. 2016:1–11. doi: 10.1007/s13157-016-0817-9. [DOI] [Google Scholar]
- Marton JM, et al. Geographically isolated wetlands are important biogeochemical reactors on the landscape. BioSci. 2015;65:408–418. doi: 10.1093/biosci/biv009. [DOI] [Google Scholar]
- Masek J, et al. A Landsat surface reflectance data set for North America, 1990–2000. Geoscience and Remote Sensing Letters. 2006;3:68–72. doi: 10.1109/LGRS.2005.857030. [DOI] [Google Scholar]
- McDonnell JJ. Are all runoff processes the same? Hydrol Process. 2013;27:4103–4111. doi: 10.1002/hyp.10076. [DOI] [Google Scholar]
- McDonough OT, et al. Surface hydrologic connectivity between Delmarva bay wetlands and nearby streams along a gradient of agricultural alteration. Wetlands. 2015;35(1):41–53. doi: 10.1007/s13157-014-0591-5. [DOI] [Google Scholar]
- McIntyre NE, et al. Climate forcing of wetland landscape connectivity in the Great Plains. Frontiers in Ecology and the Environment. 2014;12(1):59–64. doi: 10.1890/120369. [DOI] [Google Scholar]
- McLaughlin DL, et al. A significant nexus: Geographically isolated wetlands influence landscape hydrology. Water Resour Res. 2014;50:7153–7166. doi: 10.1002/2013WR015002. [DOI] [Google Scholar]
- Mushet DM, et al. Complex spatial dynamics maintain Northern Leopard Frog (Lithobates pipiens) genetic diversity in a temporally varying landscape. Herpetological Conservation and Biology. 2013;8(1):163–175. doi. [Google Scholar]
- Mushet DM. Cottonwood Lake Study Area - Water Surface Elevations. U.S. Geological Survey; 2016. [Google Scholar]
- Neff B, Rosenberry DO. Groundwater Connectivity of Upland-Embedded Wetlands in the Prairie Pothole Region. Wetlands. 2017 doi: 10.1007/s13157-017-0956-7. in press. [DOI] [Google Scholar]
- Phillips DL, Gregg JW. Uncertainty in source partitioning using stable isotopes. Oecologia. 2001;127:171–179. doi: 10.1007/s004420000578. [DOI] [PubMed] [Google Scholar]
- Quinton WL, et al. Connectivity and storage functions of channel fens and flat bogs in northern basins. Hydrol Process. 2003;17(18):3665–3684. doi: 10.1002/hyp.1369. [DOI] [Google Scholar]
- Rains MC, et al. Geographically isolated wetlands are part of the hydrological landscape. Hydrol Process. 2016;30:153–160. doi: 10.1002/hyp.10610. [DOI] [Google Scholar]
- Reid MA, et al. Ecological significance of hydrological connectivity for wetland plant communities on a dryland floodplain river, MacIntyre River, Australia. Aquatic Sciences. 2015;78(1):139–158. doi: 10.1007/s00027-015-0414-7. [DOI] [Google Scholar]
- Rosenberry DO, et al. Comparison of 13 equations for determining evapotranspiration from a prairie wetland, Cottenwood Lake Area, North Dakota, USA. Wetlands. 2004;24(3):483–497. doi: 10.1672/0277-5212(2004)024[0483:COEFDE]2.0.CO;2. [DOI] [Google Scholar]
- Rover J, et al. Classifying the hydrologic function of prairie potholes with remote sensing and GIS. Wetlands. 2011;31(2):319–327. doi: 10.1007/s13157-011-0146-y. [DOI] [Google Scholar]
- Ruiz L, et al. Dynamic connectivity of temporary wetlands in the southern Great Plains. Landscape Ecology. 2014;29(3):507–516. doi: 10.1007/s10980-013-9980-z. [DOI] [Google Scholar]
- Shanley JB, Chalmers A. The effect of frozen soil on snowmelt runoff at Sleepers River, Vermont. Hydrol Process. 1999;13:1843–1857. doi: 10.1002/(SICI)1099-1085(199909)13:12/13<1843::AID-HYP879>3.0.CO;2-G. [DOI] [Google Scholar]
- Shaw DA, et al. The fill–spill hydrology of prairie wetland complexes during drought and deluge. Hydrol Process. 2012;26:3147–3156. doi: 10.1002/hyp.8390. [DOI] [Google Scholar]
- Smith A, et al. Identification of geographical influences and flow regime characteristics using regional water isotope surveys in the lower Nelson River, Canada. Canadian Water Resources Journal. 2015;40(1):23–35. doi: 10.1080/07011784.2014.985512. [DOI] [Google Scholar]
- Spence C, Woo M. Hydrology of subarctic Canadian shield: soil-filled valleys. J Hydrol. 2003;279:151–166. doi: 10.1016/S0022-1694(03)00175-6. [DOI] [Google Scholar]
- Spence C. On the relation between dynamic storage and runoff: A discussion on thresholds, efficiency, and function. Water Resour Res. 2007;43:W12416. doi: 10.1029/2006WR005645. [DOI] [Google Scholar]
- Spence C, Phillips RW. Refining understanding of hydrological connectivity in a boreal catchment. Hydrol Process. 2015;29(16):3491–3503. doi: 10.1002/hyp.10270. [DOI] [Google Scholar]
- Sprenger M, et al. Evaporation fractionation in a peatland drainage network affects stream water isotope composition. Water Resour Res. 2017;53:851–866. doi: 10.1002/2016WR019258. [DOI] [Google Scholar]
- St Amour NA, et al. Isotopic time-series partitioning of streamflow components in wetland-dominated catchments, lower Liard River basin, Northwest Territories, Canada. Hydrol Process. 2005;19(17):3357–3381. doi: 10.1002/hyp.5975. [DOI] [Google Scholar]
- Stewart RE, Kantrud HA. Classification of natural ponds and lakes in the glaciated prairie region. Bureau of Sport Fisheries and Wildlife, U.S. Fish and Wildlife Service; Washington DC: 1971. p. 57. [Google Scholar]
- Swanson GA. An introduction to the Cottonwood Lake area. Proceedings of the North Dakota Academy of Science. 1987;41:25. doi. [Google Scholar]
- Turin G. An introduction to matched filters. IRE Transactions on Information Theory. 1960;6:311–329. doi. [Google Scholar]
- Turner KW, et al. Characterising runoff generation processes in a lake-rich thermokarst landscape (Old Crow Flats, Yukon, Canada) using δ18O, δ2H and d-excess measurements. Permafrost and Periglacial Processes. 2014;25:53–59. doi: 10.1002/ppp.1802. [DOI] [Google Scholar]
- U.S. Environmental Protection Agency. Connectivity of streams and wetlands to downstream waters: A review and synthesis of the scientific evidence. Washington, DC: 2015. EPA/600/R-14/475F. [Google Scholar]
- Uden DR, et al. The role of reserves and anthropogenic habitats for functional connectivity and resilience of ephemeral wetlands. Ecol Apps. 2014;24(7):1569–1582. doi: 10.1890/13-1755.1. [DOI] [PubMed] [Google Scholar]
- USGS. High Resolution National Hydrography Dataset (NHD) 2013 ftp://nhdftp.usgs.gov/DataSets/Staged/States/FileGDB/HighResolution/
- USGS. Discharge data from Pipestem Creek, ND. 2015 http://waterdata.usgs.gov/nd/nwis/dv/?site_no=06469400&agency_cd=USGS&referred_module=sw.
- USNOAA. Daily Summaries Climate Data. 2016 https://www.ncdc.noaa.gov/cdo-web/datatools/findstation.
- Vanderhoof MK, et al. Temporal and spatial patterns of wetland extent influence variability of surface water connectivity in the Prairie Pothole Region, United States. Landscape Ecology. 2016a;31:805–824. doi: 10.1007/s10980-015-0290-5. [DOI] [Google Scholar]
- Vanderhoof MK, et al. Patterns and drivers for wetland connections in the Prairie Pothole Region, United States. Wetlands Ecology and Management. 2016b doi: 10.1007/s11273-016-9516-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ver Hoef JM. Who Invented the Delta Method? The American Statistician. 2012;66(2):124–127. doi: 10.1080/00031305.2012.687494. [DOI] [Google Scholar]
- Wilcox BP, et al. Evidence of surface connectivity for Texas Gulf Coast depressional wetlands. Wetlands. 2011;31(3):451–458. doi: 10.1007/s13157-011-0163-x. [DOI] [Google Scholar]
- Winter TC, Rosenberry DO. The interaction of ground water with prairie pothole wetlands in the Cottonwood Lake area, east-central North Dakota, 1979–1990. Wetlands. 1995;15(3):193–211. doi: 10.1007/bf03160700. [DOI] [Google Scholar]
- Winter TC, Rosenberry DO. Hydrology of prairie pothole wetlands during drought and deluge: A 17-year study of the cottonwood lake wetland complex in North Dakota in the perspective of longer term measured and proxy hydrological records. Climatic Change. 1998;40(2):189–209. doi: 10.1023/a:1005448416571. [DOI] [Google Scholar]
- Winter TC. Relation of streams, lakes, and wetlands to groundwater flow systems. Hydrogeology Journal. 1999;7:28–45. doi: 10.1007/s100400050178. [DOI] [Google Scholar]
- Winter TC. Hydrological, chemical, and biological characteristics of a prairie pothole wetland complex under highly variable climate conditions: the Cottonwood Lake Area, east-central North Dakota, edited by T C Winter. Denver, CO: 2003. Geohydrologic setting of the Cottonwood Lake area; pp. 1–24. (U.S. Geological Survey Professional Paper 1675). [Google Scholar]
- Winter TC, LaBaugh JW. Hydrologic considerations in defining isolated wetlands. Wetlands. 2003;23(3):532–540. doi: 10.1672/0277-5212(2003)023[0532:HCIDIW]2.0.CO;2. [DOI] [Google Scholar]
- Wright CK. Spatiotemporal dynamics of prairie wetland networks: power-law scaling and implications for conservation planning. Ecology. 2010;91(7):1924–1930. doi: 10.1890/09-0865.1. [DOI] [PubMed] [Google Scholar]
- Wu QS, Lane CR. Delineation and Quantification of Wetland Depressions in the Prairie Pothole Region of North Dakota. Wetlands. 2016;36(2):215–227. doi: 10.1007/s13157-015-0731-6. [DOI] [Google Scholar]
- Zhang B, et al. Systematics in the size structure of prairie pothole lakes through drought and deluge. Water Resour Res. 2009;45:W04421. doi: 10.1029/2008WR006878. [DOI] [Google Scholar]


