Integrated beam orientation and scanning‐spot optimization in intensity‐modulated proton therapy for brain and unilateral head and neck tumors

Abstract

Purpose

Intensity‐Modulated Proton Therapy (IMPT) is the state‐of‐the‐art method of delivering proton radiotherapy. Previous research has been mainly focused on optimization of scanning spots with manually selected beam angles. Due to the computational complexity, the potential benefit of simultaneously optimizing beam orientations and spot pattern could not be realized. In this study, we developed a novel integrated beam orientation optimization (BOO) and scanning‐spot optimization algorithm for intensity‐modulated proton therapy (IMPT).

Methods

A brain chordoma and three unilateral head‐and‐neck patients with a maximal target size of 112.49 cm³ were included in this study. A total number of 1162 noncoplanar candidate beams evenly distributed across 4$\pi$ steradians were included in the optimization. For each candidate beam, the pencil‐beam doses of all scanning spots covering the PTV and a margin were calculated. The beam angle selection and spot intensity optimization problem was formulated to include three terms: a dose fidelity term to penalize the deviation of PTV and OAR doses from ideal dose distribution; an L1‐norm sparsity term to reduce the number of active spots and improve delivery efficiency; a group sparsity term to control the number of active beams between 2 and 4. For the group sparsity term, convex L2,1‐norm and nonconvex L2,1/2‐norm were tested. For the dose fidelity term, both quadratic function and linearized equivalent uniform dose (LEUD) cost function were implemented. The optimization problem was solved using the Fast Iterative Shrinkage‐Thresholding Algorithm (FISTA). The IMPT BOO method was tested on three head‐and‐neck patients and one skull base chordoma patient. The results were compared with IMPT plans created using column generation selected beams or manually selected beams.

Results

The L2,1‐norm plan selected spatially aggregated beams, indicating potential degeneracy using this norm. L2,1/2‐norm was able to select spatially separated beams and achieve smaller deviation from the ideal dose. In the L2,1/2‐norm plans, the [mean dose, maximum dose] of OAR were reduced by an average of [2.38%, 4.24%] and[2.32%, 3.76%] of the prescription dose for the quadratic and LEUD cost function, respectively, compared with the IMPT plan using manual beam selection while maintaining the same PTV coverage. The L2,1/2 group sparsity plans were dosimetrically superior to the column generation plans as well. Besides beam orientation selection, spot sparsification was observed. Generally, with the quadratic cost function, 30%~60% spots in the selected beams remained active. With the LEUD cost function, the percentages of active spots were in the range of 35%~85%.The BOO‐IMPT run time was approximately 20 min.

Conclusion

This work shows the first IMPT approach integrating noncoplanar BOO and scanning‐spot optimization in a single mathematical framework. This method is computationally efficient, dosimetrically superior and produces delivery‐friendly IMPT plans.

1. Introduction

Intensity‐Modulated Proton Therapy (IMPT) is an advanced planning technique that fully takes advantage of the freedom of placing the characteristic proton Bragg peaks,¹ which are referred to as spots in IMPT planning, in the 3D space. With spot scanning technique,² the energy and intensity of the Bragg peaks of well‐defined narrow pencil beams can be modulated to generate a sophisticated dose distribution for tumor coverage and normal tissue sparing.^{3, 4} There are several variations of IMPT, including 2D modulation, distal edge tracking, 2.5D modulation, and 3D modulation.³ Among them, multifield optimization (MFO)‐IMPT³ utilizing all available degrees of freedom has the greatest versatility for normal organ sparing. This study focuses on MFO‐IMPT, which will be simply termed IMPT in the rest of paper.

A typical treatment planning process of IMPT involves three steps: first, a number of proton beams are manually selected by the dosimetrist. For complicated cases, multiple trials are needed to decide the number and orientations of beams; second, proton pencil‐beam dose calculation is performed for these beams; finally, inverse planning is carried out to obtain the intensity map and final dose distribution.⁴ Because of the unique proton beam physics, the need to further reduce body dose, the limited beam time, and to relieve the patient‐specific QA efforts, 2~4 proton fields are typically utilized in an IMPT session,^{4, 5} in contrast to the larger number of beams and arcs used in Intensity‐Modulated Photon Therapy (referred to as IMXT). Because of the small beam number, each beam of the IMPT plan heavily influences the final quality. The importance of beam orientation was highlighted in several studies.^{6, 7, 8} However, due to the vast search space, it is essentially impossible for a human operator to test all combinations and find the optimal set of beams. Therefore, there arises a need for beam orientation optimization (BOO) for IMPT.

For IMXT, BOO is viewed as a combinatorial problem, which by its nature is mathematically intractable for realistic BOO problems. The challenge is greater with the additional depth dimension in IMPT optimization. While methods for IMXT BOO have been developed using heuristic and stochastic algorithms to overcome the mathematical challenge,^{9, 10, 11, 12, 13, 14, 15} the BOO problem is rarely touched in IMPT. To our knowledge, the only work that attempts to explicitly attack the IMPT BOO problem was by Cao et al.,¹⁶ in which the coplanar BOO problem was treated as a combinatorial problem. To reduce the problem size, starting from a set of initial beams, a local search was performed to identify beams that improve dosimetric quality and robustness. This method is clearly limited in its ability of performing a global search in a large solution space. Noncoplanar space is commonly used in proton therapy because of the modern robotic patient positioning device typically installed in a proton treatment room.

In this paper, we present a novel framework to efficiently integrate BOO and scanning‐spot optimization that allows a global search in all feasible beams. The problem is formulated to include a dose fidelity term and hierarchical sparsity penalty terms, which reduce the number of active spots using an L1‐norm sparsity term, and control the number of active beams using a group sparsity term. Group sparsity, also known as structured sparsity, was originally used in optimizing x‐ray beam orientations and showed the potential of reducing the number of beams yet maintaining dense beamlets.¹⁷

In this work, different regularization and dose fidelity terms are introduced as well as a solver that is capable of handling a larger problem than the original IMXT BOO problem owing to the additional depth dimension.

2. Materials and methods

The group sparsity‐based integrated BOO and scanning‐spot optimization problem is formulated under two different dose fidelity terms, with either convex or nonconvex group sparsity term. The details are described as follows.

2.A. Problem formulation

The simultaneous beam orientation and scanning‐spot intensity optimization problem is formulated under the following general framework:

$$\begin{array}{cc}\hfill \underset{x}{\text{minimize}}& \mathrm{\Gamma }(Ax)+{\eta \Vert x\Vert }_1+\sum _{b\in B}{\alpha }_b{\Vert x_b\Vert }_2^p,\hfill \\ & \text{subject to}x\ge 0\hfill \end{array}$$ (1)

where the optimization variable $x$ is a vector of the intensities of all scanning spots. $A$ is the dose‐calculation matrix that transforms the spot intensities $x$ to dose. A single column of matrix $A$ contains the vectorized doses delivered to the voxels in the patient from one unit intensity spot; and $A$ includes columns of all the candidate spots from all candidate beams. $B$ is the set including all candidate beams, $x_b$ is a vector of spot intensities for the candidate beam $b$ (so $x$ is the concatenation of the vectors $x_b$), and ${\alpha }_b$ is the regularization parameter for beam $b$. $\mathrm{\Gamma }\left(\mathit{Ax}\right)$ is a dose fidelity term, to penalize dose deviation from prescriptions, ${\Vert x\Vert }_1$ provides sparsity regularization on the scanning spots, to reduce the number of active spots and improve delivery efficiency, and $\eta$ is the weighting parameter for spot sparsity. ${\sum }_{b\in B}{\alpha }_b{\Vert x_b\Vert }_2^p$ is the group sparsity term to control the number of active beams to between 2 and 4. The L2,$p$‐norm (0$<p\le 1$) encourages most candidate beams to be zero, resulting in a small number of beams being selected. A common choice for the exponent for the group sparsity term is $p=1$, which makes the objective function convex. However, in the BOO problem, the adjacent block columns of the dose‐calculation matrix (corresponding to adjacent candidate beams) can be correlated in homogeneous areas. Subsequently, the group restricted isometry property may not be well satisfied and the L2,1‐norm may lead to a degenerate solution, i.e., aggregated beams. To avoid degeneracy, the nonconvex group sparsity with $p=1/2$ is also explored in this study.

We choose the weighting parameter ${\alpha }_b$ on the individual beam $b$ to be:

$${\alpha }_b=c{\left(\frac{\Vert A_{\text{PTV}}^b\overrightarrow{1}{\Vert }_2}{n_b}\right)}^{p/2},$$ (2)

where $A_{\mathrm{PTV}}^b$ is the dose‐calculation matrix of planning target volume (PTV) for beam $b$, $n_b$ is the number of candidate spots in beam $b$, and $c$ is a regularization parameter. The term $\Vert A_{\mathrm{PTV}}^b\overrightarrow{1}{\Vert }_2$ in the numerator is used to ensure that beams penetrating different depths in the patient are unbiasedly weighted. Without this term, the group sparsity has a tendency toward only selecting beams passing through less tissue. The denominator $n_b$ prevents the group sparsity penalty from having a bias against the beams with more spots. By this weighting method, we are able to tune a single parameter $c$ to control the number of active beams in the solution to problem (1).

In this work, PTV is designated to be the target volume for dose optimization. Although the concept of PTV originally from x‐ray therapy is not exactly applicable in IMPT to maintain tumor coverage,^{18, 19} without losing generality, the term PTV here is used to indicate the target volume without additional implication of plan robustness.

2.B. Dose fidelity

The function $\mathrm{\Gamma }$ can take different forms based on the dosimetric goals and whether a compatible solver exists. Two different choices of $\mathrm{\Gamma }$ are implemented and compared in this work.

The first is the quadratic loss function, which is a common choice for dose fidelity. The overall cost is written as:

$$\mathrm{\Gamma }\left(\mathit{Ax}\right)=\sum _{s\in \mathrm{PTVs}}{w}_s\Vert A_{s}x-l_s{{\Vert }_2^2+\sum _{r\in \mathrm{OARs}}{w}_r\Vert {\left(A_{r}x-m_r\right)}_{+}\Vert }_2^2$$ (3)

where $l_s$ is the prescription dose to $s$th PTV and $m_r$ is the prescribed maximal allowed dose to $r$th OAR. The OAR penalty terms utilize the one‐sided quadratic function$\Vert z_{+}{\Vert }_2^2$, where $z_{+}=max\left(z,0\right)$. This component‐wise maximum allows us to consider only the voxels with doses larger than $m_r$ in the $r$th OAR. $m_r$ can also be set to 0 to penalize any nonzero dose in an OAR. The weights $w_s$ and $w_r$ are the structure‐specific weighting parameters to emphasize the different importance of different structures.

The quadratic penalty is mathematically desirable for being convex and differentiable. It heavily penalizes the dose volumes that exceed the constraint. However, in radiation therapy, more controls on the dose volume behavior are often desirable. For serial organs, such as the spinal cord, hot spots need to be avoided. However, for parallel structures, such as the parotid glands, the mean dose can be more important than the maximum dose. Therefore, the second type of function $\mathrm{\Gamma }$ we use is a linear combination of structure mean dose and maximum dose penalty, which is referred as the linearized equivalent uniform dose (LEUD)²⁰ cost function in this work. The LEUD penalty function is formulated as:

$$\begin{array}{cc}\hfill \mathrm{\Gamma }\left(Ax\right)=& \sum _{s\in \mathrm{PTVs}}\frac{w_s}{\sqrt{N_s}}{\Vert A_{s}x-l_s\Vert }_2\hfill \\ & +\sum _{r\in \text{OARs}}{w}_r\left({\gamma }_r\text{mean}\left(A_{r}x\right)+\left(1-{\gamma }_r\right)\text{max}\left(A_{r}x\right)\right)\hfill \\ & +I_{\le q}\left(Ax\right)\hfill \end{array}$$ (4)

where $N_s$ is the number of voxels in $s$th PTV, and the weighting factor ${\gamma }_r\in \left[0,1\right]$ balances the mean dose and maximum dose for different organs. The penalty on PTV is a voxel‐normalized L2‐norm. The L2‐norm is chosen because it has better PTV coverage than the L1‐norm (which is $\mathrm{mean}\left(\left|A_{s}x-l_s\right|\right)$), and is consistent with the OAR cost with regard to the order (quadratic term is in the order of 2, while mean dose is linear). Because the L1‐norm on OARs (mean dose) is not as sensitive to outliers, it allows for hot spots in parallel OARs. Therefore, in order to eliminate any dose higher than the upper bound dose $q$, an upper bound constraint $I_{\le q}\left(\mathit{Ax}\right)$ is added to the objective function. $I_{\le q}\left(z\right)$ is defined as:

$$I_{\le q}(z)=\left\{\begin{array}{cc}0& \text{if}z\le q\\ \infty & \text{otherwise}\end{array}\right.$$ (5)

2.C. Accelerated proximal gradient method

Equation (1) is difficult to solve using conventional gradient‐based methods because of the nondifferentiable group sparsity term. Other methods such as the interior point method are not able to handle the problem due to the large $A$ matrix size. The alternating direction method of multipliers (ADMM) method used in the previous study¹⁷ required longer computation time when solving a much smaller problem (72 candidate beams with two‐dimensional beamlets). In this study, an accelerated proximal gradient method known as Fast Iterative Shrinkage‐Thresholding Algorithm (FISTA)²¹ is adopted to minimize the proposed objective function. FISTA is a fast algorithm that has an optimal convergence rate of $O\left(1/k^2\right)$ among first‐order optimization methods.²¹ To solve an optimization problem using FISTA, the problem needs to be formulated in the form:

$$\underset{x}{\text{minimize}}f(x)+g(x)$$ (6)

where $f$ is a smooth convex function, which is continuously differentiable with Lipschitz continuous gradient ($\mathrm{\nabla }f$); $g$ is a function which is possibly nonsmooth, but has a proximal operator that can be evaluated efficiently. The proximal operator with step size t > 0 for function $g$ is defined by:

$${\text{prox}}_{\mathit{tg}}(x)=\underset{y}{\text{argmin}}g(y)+\frac{1}{2t}{\Vert y-x\Vert }_2^2$$ (7)

Once the optimization problem is formulated as in Eq. (6) and the conditions for $f\left(x\right)$ and $g\left(x\right)$ are satisfied, FISTA is relatively straightforward to implement as it only involves elementary matrix‐vector arithmetic operations and inexpensive proximal operator evaluations. FISTA with line search is used in this work, which follows the steps shown in Table 1.

Table 1.

Pseudo code for FISTA with line search

FISTA with line search
Initialize $x_0:=0$, $v_0:=x_0$, $t_0>0$ , 0$<r<1$ for $k=1,2,\dots$ do $t:=t_{k-1}/r$ Repeat $\theta :=\left\{\begin{array}{cc}1& \text{if}k=1\\ \text{positive root of}{t}_{k-1}{\theta }^2=t{\theta }_{k-1}^2\left(1-\theta \right)& \text{if}k>1\end{array}\right.$ $y:=\left(1-\theta \right)x_{k-1}+\theta v_{k-1}$ $x:=pro{x}_{\mathit{tg}}\left(y-t\mathrm{\nabla }f\left(y\right)\right)$ break if $f\left(x\right)\le f\left(y\right)+<\mathrm{\nabla }f\left(y\right),x-y>+\frac{1}{2t}{\Vert x-y\Vert }_2^2$ $t:=rt$ $t_k:=t$ ${\theta }_k:=\theta$ $x_k:=x$ $v_k:=x_k+\frac{1}{{\theta }_k}(x-x_k)$
End
Return $x$

2.D. Solving the BOO problem with FISTA

In the group sparsity‐based BOO problem, the objective function can be rewritten in the following format:

$$\begin{array}{cc}& f(x)=\mathrm{\Gamma }\left(Ax\right)\hfill \\ & g(x)=\eta \Vert {x\Vert }_1+\sum _{b\in B}{\alpha }_b{\Vert x_b\Vert }_2^p+I_{\ge 0}(x)\hfill \end{array}$$ (8)

where $I_{\ge 0}\left(x\right)$ is an indicator function, defined as:

$$I_{\ge 0}(x)=\left\{\begin{array}{cc}0& \text{if}x\ge 0\\ \infty & \text{otherwise}\end{array}\right.$$ (9)

For the quadratic fidelity formulation, the gradient of $f$ is given by:

$$\mathrm{\nabla }f(x)=A^{\mathrm{T}}\mathrm{\nabla }\mathrm{\Gamma }\left(Ax\right)=\sum _{s\in \mathrm{PTVs}}{w}_s{A}_s^{\mathrm{T}}\left(A_{s}x-l_s\right)+\sum _{r\in \text{OARs}}{w}_r{A}_r^{\mathrm{T}}{\left(A_{r}x-m_r\right)}_{+}$$ (10)

For the LEUD fidelity formulation, the L2‐norm on PTV, max dose of OAR and upper bound indicator function are not differentiable. In order to solve this problem, Moreau‐Yosida regularization is used to smooth the nondifferentiable function. Moreau‐Yosida regularization for function $f$ with parameter $\mu >0$ is given by:

$$f^{(\mu )}(x)=\underset{y}{inf}f(y)+\frac{1}{2\mu }{\Vert x-y\Vert }_2^2$$ (11)

$f^{(\mu )}\left(x\right)$ is a convex and differentiable approximation to $f\left(x\right)$, and its gradient can be calculated as:

$$\mathrm{\nabla }{f}^{(\mu )}(x)=\frac{1}{\mu }\left(x-\text{pro}{\mathrm{x}}_{\mu f}(x)\right)$$ (12)

Therefore, the problem of calculating the gradient of the function $f^{(\mu )}$ is transformed into calculating the proximal operator of function $f$. The gradient of the LEUD penalty after Moreau‐Yosida smoothing is:

$$\begin{array}{cc}\hfill \mathrm{\nabla }f(x)=& \sum _{s\in \text{PTVs}}\frac{w_s}{\sqrt{N_s}}{A}_s^{\mathrm{T}}\left(A_{s}x-l_s\right)min\left(\frac{\frac{w_s}{\sqrt{N_s}}}{\Vert A_{s}x-l_s{\Vert }_2},\frac{1}{{\mu }_1}\right)\hfill \\ & +\sum _{r\in \text{OARs}}\left(\frac{w_r{\gamma }_r}{N_r}{A}_r^{\mathrm{T}}\overrightarrow{1}+w_r\left(1-{\gamma }_r\right)A_r^{\mathrm{T}}{P}_{w_r\left(1-{\gamma }_r\right)B}\left(\frac{A_{r}x}{{\mu }_2}\right)\right)\hfill \\ & +A^{\mathrm{T}}\text{max}\left(Ax-q,0\right)/{\mu }_3\hfill \end{array}$$ (13)

where ${\mu }_1$, ${\mu }_2$ and ${\mu }_3$ are positive Moreau‐Yosida regularization parameters for the L2‐norm, L$\infty$ ‐norm, and indicator function, respectively. $N_r$ is the number of voxels in $r$th OAR. $B$ is the L1 unit ball and $P$ is the projection operator. See Appendix A for a detailed derivation. Note that applying Moreau‐Yosida smoothing to the group sparsity term would be unacceptable because in order to turn off beams, the beam intensities need to be exactly zero.

After obtaining the gradient of the function $f$, the next step is to derive a formula for the proximal operator of the function $g$. In the BOO problem, $g\left(x\right)$ is a separable sum: $g\left(x\right)={\sum }_{b=1}^B{g}_b\left(x_b\right)$, where

$$g_b\left(x_b\right)=\eta \Vert x_b{\Vert }_1+\sum _{b\in B}{\alpha }_b{\Vert x_b\Vert }_2^p+I_{\ge 0}\left(x_b\right)$$ (14)

It follows from the separable sum rule for proximal operators that the problem evaluating the proximal operator of $g\left(x\right)$ reduces to independently evaluating the proximal operators of the functions $g_b\left(x_b\right)$. To simplify notation, we derive an expression for the proximal operator of the function $h\left(x\right)=\eta \Vert {x\Vert }_1+\alpha {\Vert x\Vert }_2^p+I_{\ge 0}\left(x\right)$. Evaluating the proximal operator of $h$ requires solving the optimization problem:

$$\begin{array}{cc}\hfill \underset{x}{\text{minimize}}\eta & \Vert {x\Vert }_1+{\alpha \Vert x\Vert }_2^p+\frac{1}{2t}{\Vert \widehat{x}-x\Vert }_2^2\hfill \\ & \text{subject}\text{to}x\ge 0\hfill \end{array}$$ (15)

Due to the non‐negativity constraint, we have that $\Vert {x\Vert }_1=⟨x,\overrightarrow{1}⟩$, which implies that:

$$\begin{array}{cc}\hfill \eta ⟨x,\overrightarrow{1}⟩+\frac{1}{2t}& \Vert \widehat{x}{-x\Vert }_2^2=⟨x,\overrightarrow{1}⟩+\frac{1}{2t}{\Vert \widehat{x}-x\Vert }_2^2\hfill \\ & =\frac{1}{2t}{\Vert x-\left(\widehat{x}-\eta t\overrightarrow{1}\right)\Vert }_2^2+\frac{1}{2t}\left(\Vert \widehat{x}{\Vert }_2^2-{\Vert \widehat{x}-\eta t\overrightarrow{1}\Vert }_2^2\right)\hfill \end{array}$$ (16)

Since the second term does not depend on $x$, the problem (15) is reduced to

$$\begin{array}{cc}\hfill \underset{x}{\text{minimize}}& {\Vert x\Vert }_2^p+\frac{1}{2t\alpha }{\Vert x-\left(\widehat{x}-\eta t\overrightarrow{1}\right)\Vert }_2^2\hfill \\ & \text{subject}\text{to}x\ge 0\hfill \end{array}$$ (17)

which is equivalent to evaluating the proximal operator of the function ${\Vert x\Vert }_2^p+I_{\ge 0}\left(x\right)$ at the point $\left(x-\eta t\overrightarrow{1}\right)$, with a step size $t\alpha$. Accordingly, the proximal operator of function $h$ is:

$${\text{prox}}_{\mathit{th}}(x)={\text{prox}}_{{\alpha t\Vert ·\Vert }_2^p}\left(\text{max}\left(x-\eta t\overrightarrow{1},0\right)\right)$$ (18)

There is a known form of proximal operator for both L2,1‐norm and L2,1/2‐norm²²:

$$\begin{array}{cc}& {\text{prox}}_{{t\Vert ·\Vert }_2}(x)=x-x·min\left(\frac{t}{{\Vert x\Vert }_2},1\right)\hfill \\ & {\text{prox}}_{{t\Vert ·\Vert }_2^{\frac{1}{2}}}(x)=\left\{\begin{array}{cc}0,& {\text{if}t\Vert x\Vert }_2^{-1.5}>\frac{2\sqrt{6}}{9}\\ x\sqrt{\frac{2}{\sqrt{3}}\text{sin}\left(\frac{1}{3}\left(\text{arccos}\left(\frac{3\sqrt{3}}{4}t{\Vert x\Vert }_2^{-1.5}\right)+\frac{\pi }{2}\right)\right)},& \text{otherwise}\end{array}\right.\hfill \end{array}$$ (19)

By deriving the gradient of function $f$ and proximal operator of function $g$, the BOO problem is then readily solved using FISTA.

2.E. Evaluations

Four cases, which included three unilateral head‐and‐neck (H&N) patients and one skull base chordoma (CHDM) patient with simultaneous‐integrated boost (SIB), were evaluated in this study. We chose these cases with relatively smaller tumors to reduce the size of dose matrix that can be fit into a personal computer with 64 GB memory. The candidate beams included 1162 noncoplanar beams that were evenly distributed across the 4π steradians with 6° separation. For each candidate beam, the doses of all scanning spots covering the PTV and a 2.5 mm margin were calculated using matRad,^{23, 24} a MATLAB‐based 3D treatment planning toolkit. The dose‐calculation resolution was 2.5 mm with a cut‐off of 5 × 10⁻⁵ of the maximal dose. The prescriptions, PTVs, and number of scanning spots are shown in Table 2. The magnitude of the optimization problem can be estimated based on the product of the spot number per beam and the total number of candidate beams (1162). The average number of beamlets per beam needed in IMXT for the same patient is also given in Table 2 as a comparison of the BOO problem size in IMPT and in IMXT. The IMXT multileaf collimator resolution is 5 mm.

Table 2.

Prescription doses, PTV volumes, and average spots number per beam

Case		Prescription dose (GyRBE)	PTV volume (cc)	Average spots number per beam	Average IMXT beamlets number per beam
H&N #1		40	23.76	906	85
H&N #2		40	32.29	1109	103
H&N #3		66	33.64	1589	111
CHDM	PTV6300	63	86.07	3166	241
	PTV7400	74	26.42

A greedy BOO approach, column generation,^{25, 26} was also applied for each patient, as a comparison for our group sparsity method. The detail of column generation algorithm is provided in Appendix B. The dose fidelity term used in column generation method is LEUD cost.

The BOO plans were evaluated against plans with manually selected beams. The manual beam orientations were selected to avoid OARs as much as possible. In total, seven plans were generated for each patient: three plans with quadratic dose fidelity: manual plan (Quad‐MAN), L2,1/2‐group sparsity (Quad‐L2,1/2‐GS) and L2,1‐group sparsity(Quad‐L2,1‐GS); and four plans with LEUD dose fidelity: manual plan (LEUD‐MAN), L2,1/2‐group sparsity(LEUD‐L2,1/2‐GS), and L2,1‐group sparsity (LEUD‐L2,1‐GS), and column generation (LEUD‐CG). All H&N plans were normalized, so that 100% of the prescription dose covers 95% of the PTV volume. The CHDM plan with a simultaneous boost volume was normalized to have 100% of the 63 Gy prescription dose covering 95% of the PTV6300 volume.

For evaluation, PTV homogeneity, D95, D98, D99, maximum dose, and mean dose were evaluated. PTV homogeneity is defined as D95/D5. The maximum dose is defined as the dose to 2% of the structure volume, D2, following the recommendation by IRCU‐83.²⁷ The mean and maximum doses for OARs were also evaluated.

As an example to preliminarily illustrate the effect of beam orientation on the robustness, a robustness analysis was performed to the CHDM plans to compare the robustness between MAN plans and L2,1/2‐GS plans. Nine scenarios were incorporated to evaluate the plan robustness, including one nominal scenario (no uncertainties) and eight worst‐case scenarios, which consisted of (a) setup uncertainties, by shifting the isocenter of the CT image of ±3 mm along anteroposterior, superoinferior, and lateral directions; (b) range uncertainties, by scaling the CT number by ±3%.

3. Results

The matRad‐based dose calculation for all 1162 candidate beams using an i7 6‐core CPU and Matlab parallel computing toolbox took 30 min to 1 hr depending on the size of the tumor. The dose matrix size ranged from 20 to 70 MB per beam based on target size. The group sparsity‐based BOO process took 2–7 min and 3–20 min for the quadratic and LEUD cost to complete, respectively.

Three beams for each H&N case and four beams for the CHDM case were selected. Table 3 shows the beam arrangement for each patient and each plan. The couch and gantry angles follow IEC 61217 coordinate conventions. Figure 1 shows the beam arrangement of each plan for the CHDM patient. The beams selected by using the L2,1/2‐GS term were spatially well separated. In comparison, the L2,1‐GS term resulted in aggregated beams with both quadratic and LEUD cost terms, indicating a potential degeneracy issue with this group sparsity term. And the CG method tended to choose beams with short pathlengths to target. Interestingly, the beam orientations optimized by L2,1/2‐GS were similar to the actual angles selected by an experienced dosimetrist in this CHDM case.

Table 3.

Beam angles (gantry and couch angle) selected in each plan

Case	MAN	Quad		LEUD
		L2,1/2	L2,1	L2,1/2	L2,1	CG
H&N#1	(40, 0) (180, 0) (300, 0)	(38, 20) (159, 35) (282, 0)	(102, 272) (39, 290) (316, 18)	(78, 304) (300, 0) (315, 26)	(110, 328) (130, 16) (315, 26)	(89, 282) (132, 8) (73, 19)
H&N#2	(180, 0) (45, 45) (315, 315)	(145, 350) (60, 28) (315, 315)	(110, 282) (225, 71) (338, 35)	(134, 293) (96, 6) (320, 322)	(316, 46) (148, 23) (315, 315)	(296, 74) (159, 35) (37, 57)
H&N#3	(270, 0) (90, 275) (90, 0)	(36, 0) (300, 346) (114, 13)	(171, 315) (342, 270) (315, 314)	(36, 0) (294, 354) (113, 13)	(125, 345) (54, 30) (315, 314)	(57, 298) (329, 53) (21, 325)
CHDM	(60, 275) (270, 0) (90, 0) (180, 0)	(100, 280) (130, 16) (265, 350) (330, 290)	(105, 335) (275, 12) (240, 140) (142, 20)	(60, 290) (90, 354) (270, 348) (207, 332)	(84, 312) (81, 317) (210, 12) (62, 20)	(54, 270) (56, 323) (338, 57) (281, 341)

Figure 1.

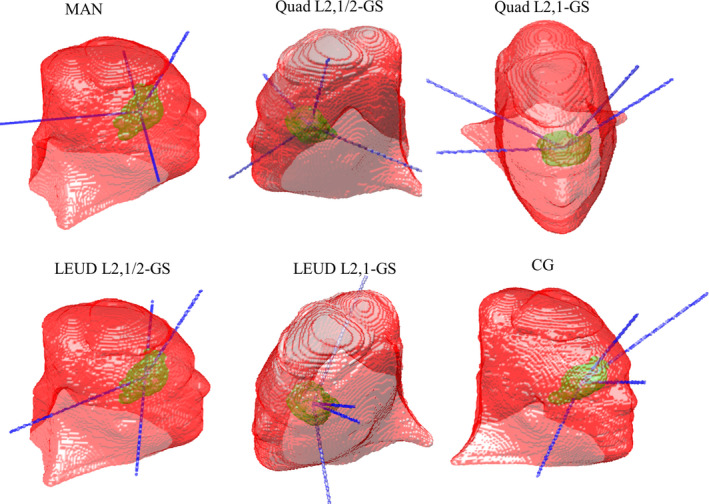
The beam arrangement of each plan for the CHDM patient.

Besides beam orientation selection, spot sparsification was achieved. Table 4 shows the percentage of active scanning spots. Generally, with the quadratic cost function, 30%~60% spots in the selected beams remained active. With the LEUD cost function, the percentages of active spots were within 35%~85%.

Table 4.

The ratio of number of active spots (number before “/”) over the number of total candidate spots (number after “/”) in the selected beams

Cost	Plan	H&N #1	H&N #2	H&N #3	CHDM
Quad	L2,1/2	967/2756 = 35.1%	912/3377 = 27.0%	2521/4759 = 53.0%	6532/12582 = 51.9%
	L2,1	1282/2646 = 48.5%	926/3238 = 28.6%	2532/4574 = 55.4%	6130/12618 = 48.58%
	MAN	1222/2725 = 44.8%	1028/3366 = 30.5%	2777/4835 = 57.4%	7072/12603 = 56.1%
LEUD	L2,1/2	1401/2741 = 51.1%	1212/3396 = 35.7%	3295/4760 = 69.2%	10596/12648 = 83.8%
	L2,1	1920/2773 = 69.2%	1315/2989 = 44.0%	2734/4582 = 60.0%	10689/12568 = 85.1%
	MAN	1545/2725 = 56.7%	1469/3366 = 43.6%	4116/4835 = 85.1%	10634/12603 = 84.3%

Figure 2 shows the DVHs comparison between GS plans and MAN plan for each patient. Tables 5 and 6 show the PTV and OAR statistics for each patient with quadratic cost function, respectively. Tables 7 and 8 show the PTV and OAR statistics for each patient with LEUD cost function, respectively. On average, the L2,1/2‐GS plans reduced the OAR [mean dose, maximum dose] from MAN plans by [2.38%, 4.24%] and[2.32%, 3.76%] of the prescription dose for Quad and LEUD cost, respectively, while achieving comparable target coverage.

Figure 2.

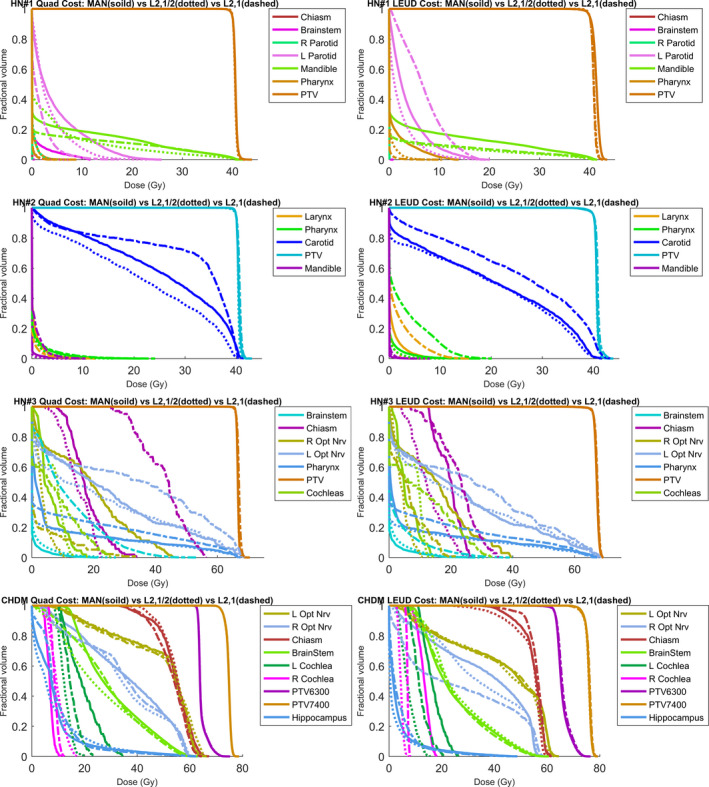
DVH comparison of the MAN plan (solid line), L2,1/2‐GS plan (dotted line) and L2,1‐GS plan (dashed line) for each patient. The plans with quadratic cost are listed on the left column and the plans with LEUD cost are on the right column.

Table 5.

PTV statistics for all patients under Quad cost

Case		Homogeneity			D95	D98	D99	Dmax	D95	D98	D99	Dmax
		MAN	L2,1/2	L2,1	L2,1/2 – MAN (GyRBE)				L2,1 – MAN (GyRBE)
H&N#1		0.972	0.979	0.969	−0.003	−0.245	−0.542	−0.298	+0.017	−0.074	−0.180	+0.214
H&N#2		0.972	0.974	0.970	+0.018	+0.159	+0.313	−0.246	+0.017	+0.077	+0.149	+0.053
H&N#3		0.981	0.981	0.972	−0.006	−0.061	−0.173	+0.069	+0.013	−0.207	−0.368	+0.723
CHDM	PTV6300	0.918	0.916	0.917	−0.003	−0.030	−0.060	+0.126	−0.012	−0.012	−0.050	−0.055
	PTV7400	0.953	0.953	0.953	−0.012	−0.012	−0.050	−0.055	−0.028	−0.058	−0.042	−0.054

Table 6.

OAR statistics for all patients under Quad cost

Case	L2,1/2 ‐ MAN (GyRBE)				L2,1 ‐ MAN (GyRBE)
	Dmean		Dmax		Dmean		Dmax
	Largest value	Average value	Largest value	Average value	Largest value	Average value	Largest value	Average value
H&N#1	−1.24 L Parotid	−0.52	−8.05 Brainstem	−2.78	−3.08 L Parotid	−0.53	−10.38 L Parotid	−2.55
H&N#2	−3.75 Carotid	−1.03	−2.13 Pharynx	−1.04	−0.23 Larynx	+0.78	−1.45 Larynx	+0.88
H&N#3	−20.14 TMJ	−2.96	−34.60 R Opt Nrv	−3.86	−26.25 TMJ	+1.75	−35.11 TMJ	+3.72
CHDM	−6.99 L Cochlea	−0.72	−16.40 L Cochlea	−0.99	−4.49 L Cochlea	+0.36	−11.20 L Cochlea	−1.16

Table 7.

PTV statistics for all patients under LEUD cost

Case		Homogeneity			D95	D98	D99	Dmax	D95	D98	D99	Dmax
		MAN	L2,1/2	L2,1	L2,1/2 – MAN (GyRBE)				L2,1 – MAN (GyRBE)
H&N#1		0.945	0.961	0.964	−0.010	+0.190	+0.291	−0.714	−0.021	+0.006	−0.227	−0.827
H&N#2		0.966	0.972	0.958	+0.009	−0.200	−0.276	−0.207	+0.013	−0.237	−0.526	+0.731
H&N#3		0.967	0.967	0.965	−0.002	−0.181	+0.069	+0.057	+0.007	−0.333	−0.288	+0.200
CHDM	PTV6300	0.885	0.886	0.881	+0.002	−0.037	+0.022	−0.058	+0.002	−0.198	−0.304	+0.242
	PTV7400	0.951	0.947	0.945	−0.352	−0.748	−0.957	−0.005	−0.264	−0.680	−1.044	+0.232

Table 8.

OAR statistics for all patients under LEUD cost

Cases	L2,1/2 – MAN (GyRBE)				L2,1 – MAN (GyRBE)
	Dmean		Dmax		Dmean		Dmax
	Largest value	Average value	Largest value	Average value	Largest value	Average value	Largest value	Average value
H&N#1	−1.49 L Parotid	−1.00	−6.75 Pharynx	−2.87	−0.98 Pharynx	−0.03	−8.96 Pharynx	−1.93
H&N#2	−0.76 Carotid	−0.270	−3.75 Larynx	−1.11	0.04 Mandible	+2.22	0.97 Mandible	+4.08
H&N#3	−16.15 TMJ	−2.51	−28.83 R Opt Nrv	−2.29	−19.52 TMJ	+0.76	−21.0 R Opt Nrv	+1.03
CHDM	−8.78 R Cochlea	−1.44	−10.99 R Cochlea	−1.01	−8.89 R Opt Nrv	−1.27	−9.59 R cochlea	−1.27

The L2,1‐GS method produced competitive plan for H&N#1 and CHDM case, but led to worse and OAR dose over MAN plan for H&N#2 and H&N#3 case with similar PTV coverage. The average decrease in OAR [mean dose, maximum dose] from MAN plans are [−0.96%, 0.09%] and [−1.15%, 1.23%] of the prescription dose for Quad and LEUD cost, respectively.

The limitation of using L2,1‐norm can be observed from the final value of dose fidelity cost. Figure 3 compares the convergence between L2,1/2‐norm and L2,1‐norm group sparsity for the H&N#3 case. For the quadratic and LEUD cost functions, the L2,1/2‐norm group sparsity method converged after about 800 iterations and 1800 iterations, respectively. In contrast, with an L2,1‐norm group sparsity term, the problem quickly converged within 30 iterations and 80 iterations under the quadratic and LEUD cost functions, respectively. However, the converged dose fidelity function values using the L2,1‐norm are substantially greater than the corresponding values of using the L2,1/2‐norm (~ ${10}^5$ for L2,1 vs. ~${10}^2$ for L2,1/2), showing a larger deviation from the prescription dose using L2,1‐norm in this case.

Figure 3.

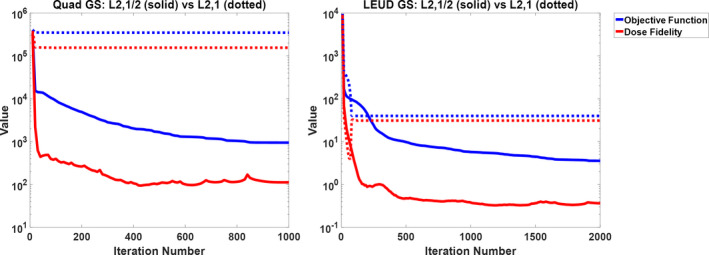
The convergence comparison between L2,1/2‐norm (solid) and L2,1‐norm (dotted) group sparsity for case H&N#3. Left is Quad‐GS and right is LEUD‐GS. The blue curve shows the value of entire cost function and the red curve shows the value of dose fidelity term.

The DVHs comparison between L2,1/2‐GS plans and CG plans is shown in Fig. 4. In all H&N cases, the CG method produced plans with similar PTV coverage as L2,1/2‐GS method, but the OAR dosimetry was inferior to the group sparsity algorithm. In the CHDM case, the CG plan performed comparably with the L2,1/2‐GS plan with regard to PTV and OAR dose. The CG methods reduced the mean dose to brainstem by 9.8 Gy over L2,1/2‐GS plan by forcing all beams entering from the anterior direction, increasing the risk of exposing the eyes to high dose with slight positioning error.

Figure 4.

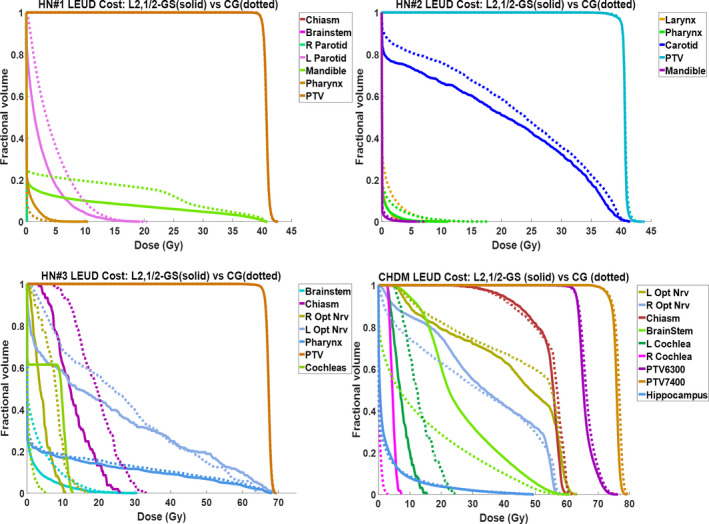
DVH comparison between L2,1/2‐GS plan (solid) and the CG plan (dotted) for each patient.

A robustness analysis for CHDM patient is shown in Fig. 5.The solid lines in each plot are the DVHs for the nominal case, and the bands bound the worst‐case distributions. The narrower the bands are, the less sensitive the plan is to uncertainties.¹⁹ The spread of the target DVHs at 95% coverage under given uncertainties is also measured. Under Quad cost, the range of spread for [PTV6300, PTV 7400] is [91.4% ~101.7%, 90.0%~99.9%] and [91.9% ~101.6%, 90.8%~100.0%] of the prescription dose for MAN and L2,1/2‐GS plan, respectively. Under LEUD cost, the range of spread for [PTV6300, PTV 7400] is [92.4% ~103.3%, 92.7%~100.6%] and [92.7% ~102.2%, 92.3%~101.6%] of the prescription dose for MAN and L2,1/2‐GS plan, respectively. The target sensitivity to uncertainties between MAN plans and BOO plans is comparable, and the MAN plans have greater uncertainties in left optic nerve, while Quad L2,1/2‐GS plan introduces larger uncertainties to left cochlea.

Figure 5.

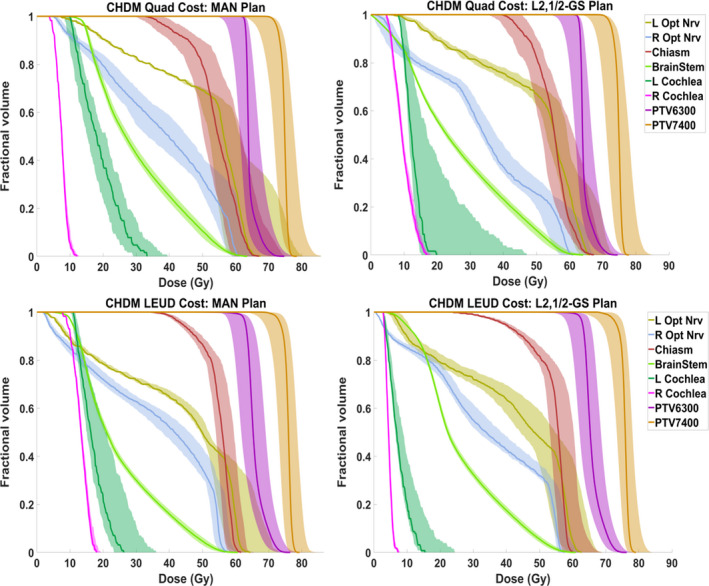
DVH bands of CHDM patient including all setup and range uncertainty distributions. The top rows are in Quad cost and bottom row in LEUD cost; the left columns are MAN plans and right column are L2,1/2‐GS plans.

4. Discussion

This work introduces a group sparsity‐based IMPT optimization method that simultaneously selects beams and optimizes the scanning‐spot intensity. In addition to the superior dosimetry compared with plans using manually selected beams, the planning method using optimized beams reduces the dependence on the individual operators who select beams based on experience and intuition.

Compared to the earlier coplanar x‐ray optimization study using group sparsity,¹⁷ the current work expands its scope in several ways. This is a new application to the IMPT problem, which is intrinsically a higher dimensional optimization problem than IMXT due to the additional modulation in the depth direction. The number of candidate beams in this study is an order of magnitude larger than in the original IMXT BOO study that used only 72 candidate beams. The optimization solver used in the original study was based on ADMM and is not well suited to the current much larger IMPT BOO problem, because the linear systems that ADMM requires to be solved at each iteration would be intractably large. Therefore, we developed an approach based on FISTA, which requires only matrix‐vector multiplications involving the dose‐calculation matrix. To enable the use of FISTA, we derived several key proximal operators. FISTA has been shown to have an optimal convergence rate of $O\left(1/k^2\right)$ among first‐order methods,²¹ and the numerical results demonstrate that FISTA is able to solve the large‐scale optimization problem in a clinically acceptable time. Although standard convergence results for FISTA assume that both $f$ and $g$ are convex,²¹ we have found that FISTA converged to a good solution even in the case of using the nonconvex L2,1/2‐norm group sparsity penalty.

In this study, two different group sparsity terms, L2,1 and L2,1/2 norms, were compared for the IMPT BOO problem. Although the L2,1‐norm is convex and offers certain computational advantages, it leads to suboptimal dosimetry and tends to converge to a worse fidelity value when compared against the nonconvex L2,1/2‐norm group sparsity term. Therefore, in this case, the ability to avoid degeneracy and select spatially separate beams appears to be dosimetrically advantageous. This finding shows that while the group sparsity method is well suited to solve the BOO problem, the selection of the sparsity function is a subtle point that can make a critical difference.

The group sparsity beam orientation optimization method was tested on two different dose fidelity functions: quadratic and LEUD terms. Compared to the quadratic dose fidelity term, the LEUD cost function with a combination of mean and maximum dose constraints is easier to tune to achieve desired DVHs. This is reflected in the process of creating plans for the four cases in this study: the quadratic L2,1/2‐GS method took on average 9–10 rounds of parameter tuning and the LEUD method took 4–5 rounds. The advantage of quadratic dose fidelity function is that while the structure parameters need to be tuned, the group sparsity regularization weighting parameter remains constant for a specific number of beams. In comparison, with LEUD dose fidelity, the group sparsity regularization weight is sensitive to the structure weighting parameter changes, requiring additional adjustment to maintain the desired number of beams. Quadratic dose fidelity also resulted in on average more sparse scanning spots.

The group sparsity BOO method was also compared against the greedy column generation BOO algorithm. The results show the GS method produces comparable or superior plans over CG. Specifically, the CG method tends to select aggregated beams with short pathlengths to the target such as the anterior beams in the CHDM case. The result indicates degeneracy that did not present in the IMXT BOO solution possibly due to the substantial difference in dose distribution between the first proton beam and photon beam. Additional heuristics such as minimal separating between selected beams may be enforced to ameliorate the problem.

The results show that nonconvex L2,1/2‐GS method creates more dosimetrically desirable plans. However, robustness is another important consideration in proton planning. In this manuscript, we provide a general and mathematically tractable framework for beam orientation optimization without explicitly considering robustness. The framework will allow us to more quantitatively describe the robustness by adding a regularization term. In a straightforward fashion, the uncertainties can be included as the stopping power (or density for further simplification) variation. Penalizing this term will push the beams toward more homogeneous paths. More sophisticated regularization terms can be constructed as dosimetric endpoints for a given shift or range uncertainty. That being said, the robustness and new regularization terms deserve a separate study. Without complicating the current manuscript too much, we performed a simple robustness analysis on one of the tested patients by simulating shifts and range uncertainties and the results showed no substantial difference between BOO plans and plans using manually selected beams.

The dose matrix size is determined by the target, which is limited to be approximately 110 cm³ to fit the calculation into a desktop with 64GB memory. For more general IMPT cases with larger tumor targets, either workstations with substantially larger memory, or methods to intelligently reduce the dose matrix size without impacting plan quality are needed. These methods include (a) nonuniform sampling resolution with a higher resolution in the target and nearby organs, and lower resolution in the volumes that are considered less critical and faraway from the target, (b) clustering of the proton pencil‐beam dose matrices, and (c) using heuristics to reduce the number of candidate beams. We will investigate these directions for more general integrated BOO and scanning‐spot optimization problems.

5. Conclusions

This work shows the first IMPT planning approach that integrates noncoplanar beam orientation and scanning‐spot optimization in a single mathematical framework, which was further formulated to have a computationally efficient solution despite its large problem size. This method resulted in dosimetrically competitive plans compared with the manual planning method for a brain and three unilateral head‐and‐neck cases and is less operator‐dependent.

Acknowledgment

This research is supported by DOE Grants No. DE‐SC0017057 and DE‐SC0017687, NIH Grants Nos. R44CA183390, R01CA188300, and R43CA183390.

Appendix A.

Calculate the Gradient of LEUD Cost

Equation (4) can also be written as the following format:

$$\mathrm{\Gamma }\left(\mathit{Ax}\right)=\sum _{s\in \text{PTVs}}\frac{w_s}{\sqrt{N_s}}{\Vert A_{s}x-l_s\Vert }_2+\sum _{r\in \text{OARs}}\left(\frac{w_r{\gamma }_r}{N_r}{\overrightarrow{1}}^{\mathrm{T}}\left(A_{r}x\right)+w_r\left(1-{\gamma }_r\right)\Vert A_r{x\Vert }_{\infty }\right)+I_{\le q}\left(\mathit{Ax}\right)$$ (A1)

where $N_r$ is the number of voxels in $r$th OAR.

Therefore, function $\mathrm{\Gamma }\left(z\right)$ can be formed as the summation of four subfunctions:

$$\begin{array}{cc}\hfill \mathrm{\Gamma }\left(z\right)=& \sum _{s\in \text{PTVs}}{f}_1\left(z_s\right)+\sum _{r\in \text{OARs}}\left(f_2\left(z_r\right)+f_3\left(z_r\right)\right)+f_4\left(z\right)\hfill \\ & f_1\left(z\right)=\frac{w}{\sqrt{N}}\Vert z-{l\Vert }_2\hfill \\ & f_2\left(z\right)=\frac{w\gamma }{N}{\overrightarrow{1}}^{\mathrm{T}}z\hfill \\ & f_3\left(z\right)=w\left(1-\gamma \right){\Vert z\Vert }_{\infty }\hfill \\ & f_4\left(z\right)=I_{\le q}\left(z\right)\hfill \end{array}$$ (A2)

$f_2\left(z\right)$ is differentiable and the gradient is:

$$\mathrm{\nabla }{f}_2\left(z\right)=\frac{w\gamma }{N}\overrightarrow{1}$$ (A3)

Moreau‐Yosida regularization is applied to $f_1$, $f_3$ and $f_4$. The proximal operators for these functions are:

$$\begin{array}{c}\hfill \mathrm{pro}{\mathrm{x}}_{\mu f_1}\left(z\right)=z-\left(z-l\right)·min\left(\frac{\mu w/\sqrt{N}}{\Vert z-{p\Vert }_2},1\right)\\ \hfill \mathrm{pro}{\mathrm{x}}_{\mu f_3}\left(z\right)=z-P_{w\left(1-\gamma \right)\mu B}\left(z\right)\\ \hfill \mathrm{pro}{\mathrm{x}}_{\mu f_4}\left(z\right)=\min \left(z,q\right)\end{array}$$ (A4)

where $B$ is the L1 unit ball, $P$ is the projection operator.

Then based on Eq. (12), the gradients of $f_1$, $f_3$ and $f_4$ after Moreau‐Yosida smoothing are:

$$\begin{array}{c}\hfill \mathrm{\nabla }{f}_1^{(\mu )}\left(x\right)=\left(z-l\right)min\left(\frac{\mu w/\sqrt{N}}{\Vert z-{l\Vert }_2},1\right)/\mu \\ \hfill \mathrm{\nabla }{f}_3^{(\mu )}\left(x\right)=P_{w\left(1-\gamma \right)B}\left(\frac{z}{\mu }\right)\\ \hfill \mathrm{\nabla }{f}_4^{(\mu )}\left(x\right)=\max \left(z-q,0\right)/\mu \end{array}$$ (A5)

Hence, the gradient of LEUD cost after approximation is written as:

$$\begin{array}{cc}\hfill \mathrm{\nabla }{f}^{(\mu )}\left(x\right)& =A^{\mathrm{T}}\mathrm{\nabla }\mathrm{\Gamma }\left(\mathit{Ax}\right)\hfill \\ & =\sum _{s\in \text{PTVs}}\frac{w_s}{\sqrt{N_s}}{A_s}^{\mathrm{T}}\left(A_{s}x-l_s\right)min\left(\frac{\frac{w_s}{\sqrt{N}}}{\Vert A_{s}x-l_s{\Vert }_2},\frac{1}{{\mu }_1}\right)\hfill \\ & +\sum _{r\in \text{OARs}}\left(\frac{w_r{\gamma }_r}{N_r}{A_r}^{\mathrm{T}}\overrightarrow{1}+{A_r}^{\mathrm{T}}{w}_r\left(1-{\gamma }_r\right)P_{w_r\left(1-{\gamma }_r\right)}\left(\frac{A_{r}x}{{\mu }_2}\right)\right)\hfill \\ & +A^{\mathrm{T}}\text{max}\left(Ax-q,0\right)/{\mu }_3\hfill \end{array}$$ (A6)

where ${\mu }_1$, ${\mu }_2$, and ${\mu }_3$ are positive Moreau‐Yosida regularization parameters for L2‐norm, L$\infty$ ‐norm, and indicator function, respectively.

Appendix B.

Column Generation‐based BOO

First, we define the master problem, which includes the whole candidate beam set $B$, as:

$$\begin{array}{c}\hfill \underset{d,x}{\mathrm{minimize}}\mathrm{G}\left(d\right)\\ & \mathrm{subject}\mathrm{to}d=\sum _{b\in B}{A}_b{x}_b\hfill \\ & x_b\ge 0,\mathrm{for}b\in B\hfill \end{array}$$

where

$$\mathrm{G}(d)=\sum _{s\in \mathrm{PTVs}}\frac{w_s}{\sqrt{N_s}}{\Vert d_s-l_s\Vert }_2+\sum _{r\in \mathrm{OARs}}{w}_r\left({\gamma }_r\mathrm{mean}\left(d_r\right)+\left(1-{\gamma }_r\right)\max \left(d_r\right)\right)+I_{\le q}\left(d\right)$$ (B1)

The variables have the same meaning as 2.1. In addition, here $A_b$ is the dose‐calculation matrix for beam $b$. It is obvious that the objective function is equivalent to the LEUB dose fidelity term in Eq. (4).

The master problem is designed to optimize the intensities of the scanning spots from all beams. The goal for BAO is to select a small number of beams. The beam not selected should have zero spot intensity. Then, the subproblem with selected beam set $B_{\mathrm{select}}$ is defined as:

$$\begin{array}{cc}& \underset{d,x}{\mathrm{minimize}}\mathrm{G}\left(d\right)\hfill \\ & \mathrm{subject}\mathrm{to}d=\sum _{b\in B_{\mathrm{select}}}{A}_b{x}_b\hfill \\ & x_b\ge 0,\mathrm{for}b\in B_{\mathrm{select}}\hfill \end{array}$$ (B2)

The Lagrange function for the master problem is:

$$L(x,d,u,v)=\mathrm{G}\left(d\right)+u(d-\sum _{b\in B}{A}_b{x}_b)-\sum _{b\in B}{v}_b{x}_b$$ (B3)

where $u$, $v$ are Lagrange multipliers associated with the constrains in the master problem.

The Karush‐Kuhn‐Tucker (KKT) conditions²⁸ are evaluated:

$$\begin{array}{cc}& d=Ax,d\le q,x_b\ge 0,\mathrm{for}b\in B\hfill \\ & v_b\ge 0\hfill \\ & u=\partial G(d)\hfill \\ & v_b=A_b^{\mathrm{T}}u,\mathrm{for}b\in B\hfill \end{array}$$ (B4)

Using the same smoothing approach as Section 2.D and FISTA, the subproblem can be solved to obtain optimal primal variable $x_b^{\ast },b\in B_{\mathit{select}}$, and optimal dual variables $u^{\ast }$, and $v_b^{\ast },b\in B_{\mathit{select}}$. Then, all $v_b,b\in B\backslash B_{\mathit{select}}$ are calculated by $v_b=A_b^{\mathrm{T}}u$. The $v_b^{\ast }$ in the selected set meets the non‐negative condition, but the $w_b$ in the rest set may be negative. In $B\backslash B_{\mathit{select}}$, the negative elements in vector $w_b$ are summed to produce a single value to evaluate this beam $b$. The beam with the most negative sum is supposed to help to optimize the master problem most, so this beam is added to $B_{\mathit{select}}$ and a new subproblem is formed and solved again. By this method, we can start from an empty selected set, add one beam per iteration, reach the desired number of beam, and then exit the iteration.