Guided by curvature: shaping cells by coupling curved membrane proteins and cytoskeletal forces

Abstract

Eukaryote cells have flexible membranes that allow them to have a variety of dynamical shapes. The shapes of the cells serve important biological functions, both for cells within an intact tissue, and during embryogenesis and cellular motility. How cells control their shapes and the structures that they form on their surface has been a subject of intensive biological research, exposing the building blocks that cells use to deform their membranes. These processes have also drawn the interest of theoretical physicists, aiming to develop models based on physics, chemistry and nonlinear dynamics. Such models explore quantitatively different possible mechanisms that the cells can employ to initiate the spontaneous formation of shapes and patterns on their membranes. We review here theoretical work where one such class of mechanisms was investigated: the coupling between curved membrane proteins, and the cytoskeletal forces that they recruit. Theory indicates that this coupling gives rise to a rich variety of membrane shapes and dynamics, while experiments indicate that this mechanism appears to drive many cellular shape changes.

This article is part of the theme issue ‘Self-organization in cell biology’.

1. Introduction

Eukaryote cells perform a large variety of different functions in the body. These functions involve requirements for the cells to assume different shapes, and dynamically reshape their membranes [1]. In order to shape (bend) the membrane the cells rely on a variety of physical forces [2–4], which involve controlling the local membrane lipid composition, composition of membrane-bound proteins [5], activity of membrane channels and pumps [6–8] and the recruitment of the cell's cytoskeleton. Over the past several decades the molecular components of all these processes have been slowly revealed, and it is often found that cells rely on a combination of mechanisms to achieve a robust shape change [9]. For example, endocytosis, which is the process of internalizing vesicles from the cell membrane, has several parallel pathways: sometimes it relies on a curved membrane-bound scaffold (composed of clathrin [10]), in conjunction with a locally distinct lipid composition, and other times it is totally dependent on the recruitment of actin polymerization [11–13]. How these different membrane components are localized and synchronized in space and time to produce the final desired dynamics is still not fully understood [14].

The above example highlights the complexity of mechanisms that control the cell shape, and the way they are usually entangled in the living cell. It is difficult to study and understand the effects of each of these mechanisms on its own, or in combination, in vivo. In vitro studies with controlled concentrations of purified components have been used to unravel the dynamics of membrane shapes, with increasing levels of sophistication. So far, most of these experiments do not include the forces that are produced by the cytoskeleton, and therefore, shed light on the passive processes that shape the membrane: variations in lipid composition and the presence of curved membrane proteins [15]. There have been several extensive reviews on the molecular components, such as lipids and curved proteins (such as the BAR (Bin–Amphiphysin–Rvs) domain proteins [16,17]) that can locally curve the membrane [18]. We term these components as ‘passive’ to distinguish them from the active cytoskeletal forces that arise from consumption of chemical energy.

While it has been so far very difficult to study by in vitro experiments the processes of membrane shape changes that involve the recruitment of the cytoskeleton [19], these processes have been studied theoretically. In this review, we concentrate on theoretical studies of the coupling between curved membrane components (CMC), such as lipid domains or membrane-bound proteins [20], and the active forces exerted by the cytoskeleton, which is recruited by the CMC. These forces can arise due to localized polymerization of cytoskeleton biopolymers (mostly cortical actin in eukaryotes [21]), and due to contractile forces applied to membrane-bound filaments by molecular motors.

We first present below a brief description of the general theoretical framework that was used for the analysis of the coupled membrane–CMC–cytoskeleton system. This is not meant to be detailed, but just to give a flavour of the type of physics and mathematics involved. Afterwards, each section is devoted to a different class of membrane shapes and dynamics that this coupling can produce. At the end of each section, following the theoretical part, we give experimental examples where this coupling was identified or is likely to exist.

2. Continuum model for coupled membrane-curved membrane component-cytoskeleton system

The theoretical analysis of the coupled system was carried out in terms of a continuum field model, where the dynamics of both the membrane and the local density of CMC are derived. We start by writing the continuum free energy, based on the elastic curvature energy of the Helfrich Hamiltonian [22], including the interactions between the membrane-adsorbed proteins and entropy [23]. For a flat membrane and isotropic spontaneous curvature this can generally be written as

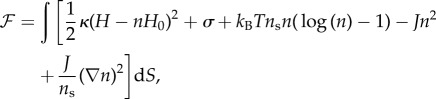2.1

where κ is the bending modulus of the membrane, H is the local mean curvature, n is the local density of CMC and H₀ is the spontaneous curvature of the CMC. In this form, the spontaneous curvature is assumed to be isotropic, and to couple only to the mean curvature. Other forms of curvature can take into account anisotropic shapes of the CMC, such as the BAR-domain proteins [24], where the orientation and position of the CMCs couple to both principal curvatures of the membrane [25–28]. The reorientations of the anisotropic CMC are driven by thermal rotations in the plane of the membrane [26,29]. Anisotropic CMC, considered as one-dimensional curved proteins [30], are not always aligned with one principal membrane curvature, even when the thermal rotation of the molecules is neglected [31]. In addition, one could also consider a coupling between the CMC and the Gaussian curvature [25]. Note that the bending energy (first term on the right-hand side of equation (2.1)) assumes that the CMC locally bends the membrane to conform to its shape. In the coarse-grained description, this amounts to the membrane having an effective spontaneous curvature that depends on the coverage fraction n of the membrane by the CMC. For a CMC that is not infinitely rigid and has a finite bending modulus [32], the form should become [33]

2.2

where κ′ is the bending modulus of the CMC.

The second term in equation (2.1) gives the effective membrane tension, which is usually positive such that it resists extensions in the membrane area. The third term gives the approximate entropy of the gas of CMC, which diffuses in the plane of the (fluid) membrane. The last two terms give the direct interaction between the CMC, which is taken to be attractive J > 0. The parameter n_s gives the saturation density of the CMC on the membrane, and is of order of the inverse area of a single CMC.

From this free energy the equations of motion for the membrane shape, and density of CMC, can be derived. For small deformations of a flat membrane, the membrane shape can be parametrized by the Monge gauge, using a single height field h(r) (figure 1a). The equation of motion for h(r) can be written as [34]

2.3

where ξ is some friction coefficient. The long-range hydrodynamic interactions are not described here, both for simplicity, and due to the fact that inside cells the dense cytoskeleton network greatly reduces long-range cytoplasmic flows. The first term on the right-hand side of equation (2.3) gives the forces that act to deform the membrane due to passive mechanisms, such as due to the spontaneous curvature of the CMC, which are therefore extracted from a variation of the free energy (equation (2.1)) with respect to the membrane shape deformation [34]. The elastic forces that act to restore the membrane to its flat shape arise from the membrane's resistance to bending (finite bending modulus κ) and resistance to stretching (positive membrane tension σ).

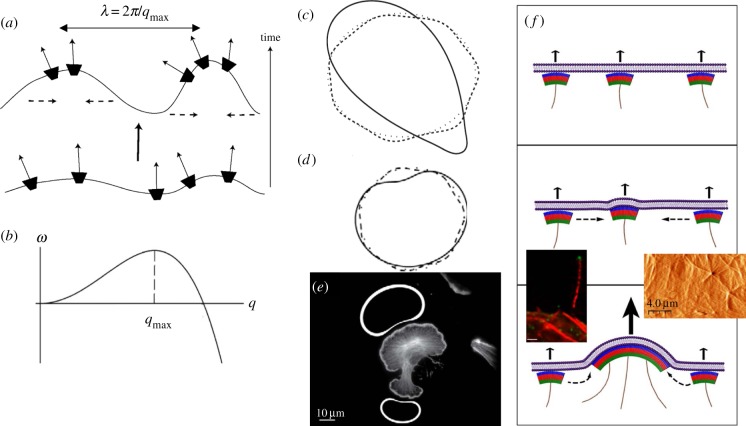
Figure 1.

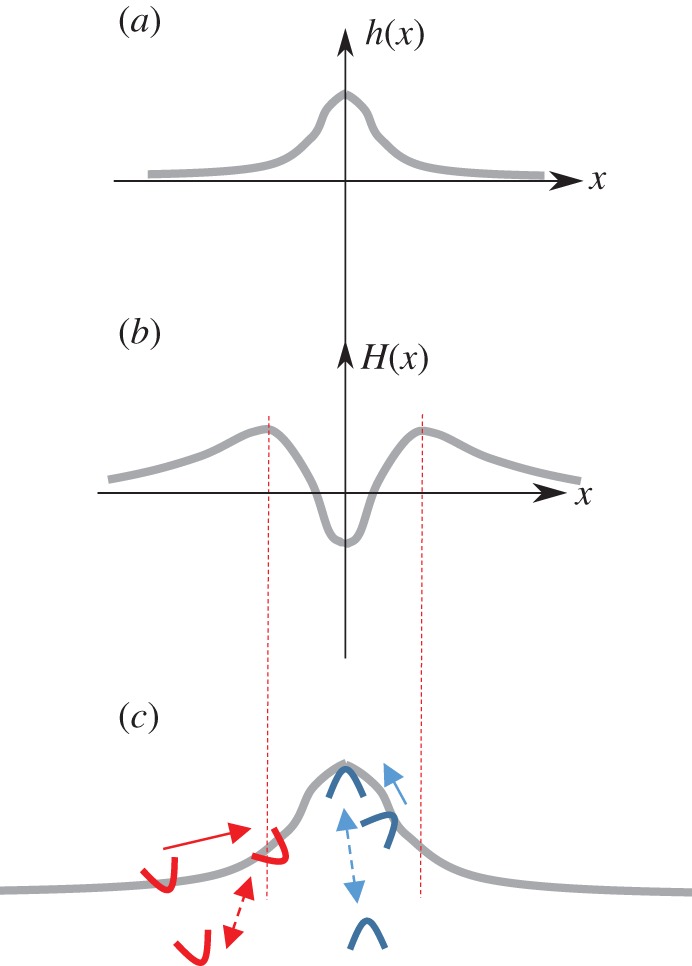
Schematic of a flexible membrane, with mobile curved membrane complexes (CMC). The membrane (grey solid line) can deform, (a) for example, in the form of a protrusion extending outwards from the cell. For small deformations the membrane shape can be characterized by a continuum field h(x), whose dynamics obey the equation of motion (2.3). (b) The corresponding mean curvature along the membrane is H(x). (c) The CMC will flow within the membrane, or adsorb directly from the cytoplasm, such that they tend to aggregate where their spontaneous curvature H₀ best fits the sign and magnitude of the membrane curvature: convex CMC (blue, outwards pointing arcs) flow to the protrusion tip where the curvature is negative, and concave CMC (red, inward pointing arcs) flow towards the most concave parts where the curvature is largest and positive (indicated by the vertical dashed red lines). For CMC that flow in the membrane, the aggregation current J_curv (equation (2.8)) is indicated by solid arrows. Adsorption of curved CMC from the cytoplasm to the membrane is also curvature-dependent, indicated by the dashed arrows.

In equation (2.3), the last term describes an additional, active force that is acting to deform the membrane, wherever the local concentration of CMC is different from its mean value 〈n〉. First, in order to keep the problem as simple as possible, it can be assumed that the local coverage fraction of CMC n(r) can be used as a measure of the local density of cytoskeleton network recruited to the membrane. Second, since the forces produced by the cytoskeleton arise from energy consuming processes, they cannot be derived from the free energy, and are therefore added to the equation of motion for the membrane shape. The direction of the active force depends on the sign of the parameter A: a positive value indicates that the cytoskeleton is pushing outwards, and there is a protrusive force acting on the membrane whenever n(r) > 〈n〉. A negative A indicates a dominant contractile force, pointing into the cell. It is assumed here that the average forces of the cytoskeleton, given by A〈n〉, are balanced by the finite compressibility/stretching of the cell, and are therefore removed from the force balance, leaving only local deviations in the active forces.

Next, the equation of motion for the dynamics of the density of CMC is given by the following conservation equation [7]

2.4

where Λ is the mobility of the CMC in the membrane and J is the total current of CMC on the membrane. Note that we assume here that the CMC are not directly propelled on the membrane by the active cytoskeleton-driven forces that they recruit, since these forces are mostly directed normal to the membrane. In our coarse-grained treatment, the normal direction of the local cytoskeletal forces on the membrane arises by averaging the forces of individual actin filaments, for example, which are oriented at various angles with respect to the membrane plane.

It is helpful to list the main currents that arise from this equation of motion [35]: the currents acting to disperse the CMC and prevent their aggregation arise from thermal diffusion (J_diff) and the resistance of the membrane to the deformation caused by the CMC aggregation (J_disp):

2.5

and

2.6

where the diffusion coefficient D = Λk_BT. Both of these currents are negative for a positive slope in the density, which means that the current is away from the high density region, and acts to disperse any aggregation. The current J_disp (equation (2.6)) arises from the resistance of the membrane to the deformation imposed by the CMC. It is, therefore, independent of the sign of the spontaneous curvature of the CMC (H₀) and is proportional to the bending modulus of the membrane.

The currents that act to aggregate the CMC arise from the direct attractive interaction J (J_agg), as well as due to the spontaneous curvature (J_curv):

2.7

and

2.8

The first of these currents, J_agg, depends on the strength of the direct attractive interaction J between the CMC. The response of curved CMC to the membrane shape, described by the current J_curv, is schematically shown in figure 1c: depending on the sign of the spontaneous curvature H₀, the current flows towards either maximal or minimal values of the curvature H (figure 1b,c).

To judge the strength of the opposing effects of the different currents, we can compare the dispersion due to thermal diffusion to the aggregating current due to spontaneous curvature (equations (2.5) and (2.8)). Equating these currents, we find a steady-state solution of the form

2.9

From this expression, we see that even if the spontaneous radius of curvature of the CMC is of molecular size, 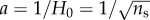, which is much smaller than the radius of membrane curvature, R = 1/H, the distribution of CMC on the membrane can be affected since the bending modulus is large: κ/k_BT ∼ 1 − 100, while a/R ∼ 0.1 − 10⁻³. This analysis demonstrates that curved proteins and lipid domains do respond to the shape of the membrane by aggregating where their spontaneous curvature best fits with the local membrane curvature, and the elastic bending energy is minimized (equations (2.1) and (2.2)). Such effects have been observed in bacteria, where curved membrane proteins aggregate near the poles [36–38] or at concave regions (such as nascent septa) [39,40].

Note that a similar accumulation of curved CMC to matching regions on the membrane arises due to the curvature-dependence of the adsorption of curved molecules (such as membrane proteins) from the cytoplasm to the membrane [41] (figure 1c). This tendency of curved proteins to accumulate in response to the imposed membrane curvature was observed in vitro [42–45] and in living cells [46]. Quantitative comparisons to the in vitro experiments support the use of the continuum theory described above, even on length-scales down to approximately 10 nm, close to the molecular size.

While the CMC respond to imposed membrane deformations, it is not as simple for these curved entities to initiate spontaneous aggregation and shape deformation. The conditions for initiation of phase separation, aggregation of CMC and the consequent formation of curved membrane shapes can be found by performing linear stability analysis of the coupled system (equations (2.1)–(2.4)). From such analysis of passive systems, it was found that the entropic cost prevents the aggregation of CMC in the limit of a flat membrane with small height deformations, unless direct attraction (J) is present [23]. Such attraction between the CMC results in the formation of dense aggregated scaffolds that bend the membrane [47,48]. The curvature effects can aid the aggregation by raising the critical temperature for the initiation of phase separation [23]. Since the aggregate of CMC necessarily involves a curved deformation of the membrane, it is suppressed by membrane tension, which acts to flatten the membrane [49]. All these passive effects have been extensively studied theoretically [50–53], and have also been exposed in experiments. For example, the role of membrane curvature near the phase separation transition was observed in [54,55]. Note that curvature alone was shown to maintain a stable aggregate when large-scale deformations, beyond the regime of small fluctuations, are considered [56].

In the presence of active forces, the deformations are greatly enhanced (equation (2.3)), which cause larger aggregation currents due to the spontaneous curvature of the CMC (equation (2.8)). A recent static calculation has shown the effect of the additional cytoskeletal force in maintaining the aggregation of curved proteins and associated membrane deformation [57]. In the sections below, the coupled systems were investigated for different geometries and combinations of curvatures and forces in the presence of active forces. Linear stability analysis was used to expose the regimes of spontaneous initiation of spatial and dynamic patterns. Nonlinear terms were included to allow us to follow the dynamics beyond the linear regime in some cases, mostly using numerical simulations.

3. Convex proteins coupled to protrusive forces: cellular protrusions

We start with the case of convex CMC, which means the curvature of the membrane at the tips of cellular protrusions (figures 1c,2a), which recruit protrusive forces of the cytoskeleton [34]. Protrusive forces, which push the membrane outwards, are mostly produced at the cell cortex by the polymerization of actin, but can also arise from polymerization of microtubules. Convex CMC (H₀ < 0), together with the protrusive force (A > 0, in equation (2.3)), act as a positive feedback (figure 2a): a small membrane shape fluctuation induces a local flow of CMC towards the most protrusive parts of the undulation. This flow causes an increase in n at the protrusive tip, which in turn causes the force of the cytoskeleton to increase there, further pushing that part of the membrane outwards with respect to the surrounding membrane. As the membrane protrudes, more convex CMC flow to the tip, giving rise to a positive feedback. Similarly, a random fluctuation in the density n can initiate this process.

Figure 2.

(a) Positive feedback for convex CMC that recruit protrusive forces of the cytoskeleton (thin solid arrows) [34]. The convex CMC flow in the membrane to the tips of the protrusions (dashed arrows). From Gov & Gopinathan [34]. In the regime of instability, the most unstable wavelength grows the fastest, as shown in (b): rate of growth ω as function of the wavevector q = 2π/λ (λ is the wavelength). (c) In a numerical simulations [35], an initially round membrane contour (dotted line) spontaneously develops small protrusions (and associated accumulations of convex CMC) at the wavelength of the most unstable mode (dashed line), as predicted by the linear stability analysis (b). At longer times, nonlinear effects cause coarsening, whereby protrusions merge to form fewer and larger structures (solid line). (d) Evolution of a membrane when driven by the recruited forces of actin polymerization (line scheme as in (c)). The final steady-state shape at long times is in the form of a fan-shaped membrane [35], with the convex CMC (and actin polymerization) spread along the convex parts, and absent (or greatly depleted) from the concave part. (e) The fan-shape steady-state solution of (d) agrees with the observed distribution of actin polymerization in lamellipodia of cells [35], where the actin is fluorescently labelled, and the calculated accumulation of CMC on the membrane is indicated by the thickness of the white line for the two fan-shaped steady-state contours (above and below the cell image). (c)–(e) From Kabaso et al. [35]. (f) Illustration of the process of aggregation of HIV viral coat complexes on an infected cell membrane [58]. The arrows indicate the protrusive force due to the actin polymerization (solid purple lines), which is recruited by the viral coat protein complexes (green–red–blue arcs). The bottom left panel shows a fluorescent image of a long cellular protrusion containing actin (red) and viral coat proteins at the tip (green). The bottom right panel shows an image of the height of the membrane (using atomic force microscopy (AFM)) during viral budding, where actin cables can be seen emerging from the budding sites. From Gladnikoff et al. [58].

When is this positive feedback strong enough to spontaneously destabilize the uniform density and flat membrane state, and initiate the formation of outwards pointing membrane protrusions? The condition for instability is satisfied above a critical strength of the recruited protrusive force of the cytoskeleton (A, equation (2.3)) and below a critical value of the membrane tension (σ) [23,58]. In the regime of instability, the protrusions will grow fastest at the wavelength for which the system is most unstable. In figure 2b, we plot a typical calculation of the rate of growth of fluctuations at different wavelengths (ω(q)), from the linear stability analysis [34]. At short wavelengths (large q), the bending energy cost is prohibitive while the amount of CMC accumulation at each tip is limited, and the fluctuations quickly disperse and the membrane flattens. This stable regime is indicated by the negative values of the growth rate ω < 0. However, above a certain critical wavelength, the process can become self-sustaining and an initial perturbation grows (ω > 0). A numerical simulation shown in figure 2c shows that periodically spaced protrusions are initiated by this positive feedback process at the wavelength of the most unstable mode predicted by the linear stability analysis (figure 2b).

At longer times, the protrusions, and their associated tip aggregates of convex CMC, may undergo a process of coalescence, as shown using a numerical simulation [35] in figure 2c. This process, where protrusions merge or grow larger at the expense of neighbouring protrusions, is called ‘coarsening’ and is driven by nonlinear terms in equations (2.3) and (2.4). An important feature is that the time-scale of the coarsening process increases dramatically when the positive feedback is weaker and occurs faster when it is stronger. This means that in cells where this mechanism is weak, for example, due to weak actin polymerization, the protrusions are likely to be found at the regular spacing at which they initiate, given by the most unstable mode. In cells that have a strong positive feedback, the protrusions undergo fast coarsening and the cell exhibits a smaller number of larger protrusions. Note that the adhesion of the cell membrane to an external substrate, through membrane-bound adhesion complexes, can also exert a protrusive force that stretches the membrane outwards, similar to the effect of actin polymerization [23,35]. When the adhesion complexes are convex shaped, we can have a positive feedback that is dominated by adhesion-induced protrusive forces, as shown in figure 2c.

The simulations shown in figure 2c,d describe a one-dimensional contour that marks the edge of a flat, two-dimensional cell. For adhering cells this cell edge has a high curvature in the direction that is normal to the plane of the calculation, i.e. where the membrane curves back to form a closed volume. Owing to this high convex curvature, it is natural to assume that the convex CMC are confined along this edge [34], as was done in these simulations (figure 2c,d [35]). When the convex CMC at the rim of the cell recruit the protrusive force of actin polymerization, the result is a ‘fan-shaped’ cell that resembles closely the shapes of lamellipodia structures in cells [35] (figure 2d,e). Recent experiments have found that the leading edge of the lamellipodia indeed involves the presence of curved proteins that recruit actin polymerization [59]. When the curved proteins are convex, and recruit actin polymerization, they drive lamellipodia extension (I. Begemann et al. 2017, private communication). This coupling was also shown to help maintain the highly curved leading edge of the lamellipodia using detailed simulations [60]. When the curved proteins are concave and lead to suppression of actin polymerization, the positive feedback has both the sign of the spontaneous curvature and of the active force reversed (H₀ > 0, A < 0), so works to destabilize the leading edge and results in membrane retraction [46].

When this mechanism for initiating cellular protrusions was first investigated theoretically [34], there were no known candidates for convex proteins that also recruit the protrusive forces of the cytoskeleton. However, such components were discovered shortly afterwards. A prime example is the IRSp53, an inverse-BAR (I-BAR) domain protein [61]. While it was already known to be part of a complex that recruits and promotes actin polymerization near the membrane [62,63], its convex shape was identified later [64]. This protein therefore has all the properties required to drive the positive feedback described above, and is indeed implicated in driving the initiation of cellular protrusions [65–68]. Another recently discovered example of convex CMC that recruits actin polymerization and induces cellular protrusions is the Formin FMNL2-Cdc42 complex [69].

Another example where convex CMC couple with the protrusive forces of the cytoskeleton to drive aggregation and protrusion is during the process of HIV budding [58]. The coat proteins of the HIV virus have the convex spontaneous curvature needed to form a closed shell (figure 2f). As they adsorb to the infected cell membrane, they aggregate to form a bud and eventually detach (figure 2f). Under normal conditions it was found that these complexes can recruit actin polymerization, and this enables the aggregation into buds to occur at much lower membrane density of viral proteins compared to the case when the actin recruitment is impaired [58]. Viral budding that is enhanced by hijacking the actin cytoskeleton can therefore occur faster, making the virus more potent. Similar processes seem to occur during the budding process of other retroviruses [70,71].

Whole-cell simulations that describe the shapes of cells, notably during motility, have been developed over recent years using the ‘phase-field’ [72–74] or ‘Cellular Potts Model’ [75–77] techniques. Such works allow to describe the dynamic shape deformations of cells that are driven by the internal forces of actin polymerization and contractility due to molecular motors. However, we are not aware of such simulations that have explicitly included the feedback from the membrane curvature, although one work includes implicitly a positive feedback between the protrusive motion and local curvature [77].

4. Curved proteins on cylindrical membranes: rings, constrictions and fission

Cellular membranes are often in the form of cylinders and tubes. Examples include the tubular shape of bacteria, where the inner fluid membrane is typically cylindrical with hemispherical ends. Inside eukaryote cells, cylindrical tubes are observed as parts of internal organelles, from the golgi to the endoplasmic reticulum (ER), as well as during the process of endocytosis. Such tubes are formed when the membrane, for example, conforms to the shape of the rigid cell wall of the bacteria, or when an adsorbed protein scaffold stabilizes this shape [3,78], or when the membrane is pulled by active forces, such as by molecular motors [79–81].

Tubular invaginations (extending into the cell) can be initiated by the reverse of the mechanism we described in the previous section for the initiation of cellular protrusions (figure 2a), using concave CMC (e.g. of the BAR-domain family), and where the recruited cytoskeleton ends up producing forces directed into the cell [82–85]. It simply amounts to reversing both the sign of the spontaneous curvature of the CMC, H₀ > 0, and the force of the cytoskeleton A < 0, in equations (2.3) and (2.4) (or turning figure 2a upside down). Such inwards-directed forces can arise, for example, when the actin polymerization is overwhelmed by contractile forces of myosin-II motors, resulting in a net retraction of the membrane into the cell [86]. Other possibilities include the sideways entrainment of the curved proteins to the treadmilling motion of the actin filaments, flowing backwards from the membrane. This mechanism may play an important role during endocytosis [13,14].

On such cylindrical membrane tubes there can be processes where the CMC undergo an instability and aggregation due to a positive feedback between their spontaneous curvature, the membrane shape and the recruited forces of the cytoskeleton (figure 3a–c). We consider convex (concave) arc-like CMC that adsorb to the inner (outer) side of the membrane tube. The CMC are taken to have cylindrical symmetry, i.e. their density is uniform around the cylinder's circumference. It is found that they can become unstable even in the absence of any direct attraction (J = 0 in equation (2.1)) [88]: if the membrane tube radius, determined by the balance of curvature and tension forces [88], is larger than the spontaneous radius of curvature of the CMC (1/H₀), the CMC act to constrict the tube. Such a constriction draws more CMC, which increase the local constriction, and drives a positive feedback. This is in contrast to the case of a flat membrane [23]. Note that such ring-like CMC, oriented along the circumference of the cylinder, are naturally anisotropic [89], and therefore couple more strongly (or even exclusively) to one of the principal curvatures of the cylinder, rather than to the mean curvature [87]: CMC that are convex and adsorbed to the inner side of the tube orient along the cylinder's circumference and couple to the cylinder's radius (figure 3a), while concave CMC (adsorbed to the inner side of the tube) align along the cylinder's axis and couple to axial deformations (figure 3b). In the later case, the positive feedback draws the CMC to the tip of the constriction, similar to the dynamics shown in figure 2a for flat membranes.

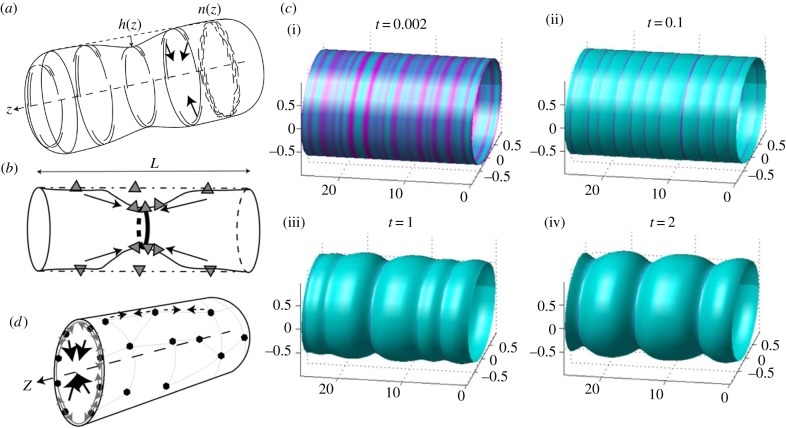
Figure 3.

(a) Positive feedback between convex (concave) CMC (short and long arcs) that adsorb to the inner (outer) side of a membrane tube and recruit forces of the cytoskeleton towards the tube axis (arrows) [34], either due to contraction or protrusive forces from the outside [87]. The rings show that the CMC are taken to be uniformly distributed around the circumference (axial symmetry). Arc-like CMC that are aligned along the circumference of the tube (as shown) sense mainly the radius of curvature of the tube. (b) Concave (convex) CMC (triangles) that adsorb on the inside (outside) of the membrane tube and are mostly aligned along the axis, and are therefore sensitive also to the curvature in the axial direction [87]. In this case, the positive feedback is due to the high curvature at the tip of the constriction, similar to the process shown in figure 2a for flat membranes. (c) Numerical simulations [88] of cylindrically symmetric distribution of convex CMC in the unstable regime, where small initial fluctuations (i) spontaneously grow to become condensed rings at the separation of the most unstable wavelength (ii). At longer times, nonlinear effects drive the coarsening of the rings into fewer and thicker rings (iii,iv). From Shlomovitz & Gov [88]. (d) A cortical actin–myosin network (thin polygons with filled circle nodes) that is adsorbed to the membrane can give rise to contractile forces (dashed lines with small arrows) that squeeze the tube towards its axis (large arrows pointing at the tube axis) [87]. (a)–(d) From Shlomovitz & Gov [87].

The instability involves formation of condensed rings at equal separations along the length of the cylindrical membrane [88] (figure 3c(i),(ii)), corresponding to the most unstable wavelength of the linear stability analysis (figure 2f). As for the case of protrusions, nonlinear effects drive the coarsening of the rings into fewer and thicker rings (figure 3c(iii),(iv)). Since the condensed rings contain more of the CMC, the membrane there bends, either inwards or outwards depending on the relation between the cylinder's natural radius and the spontaneous radius of the CMC. For inwards bending, the condensed rings initiate constrictions of the cylinder, which become more pronounced as the rings grow larger through the coarsening process (figure 3c(iii),(iv)). Numerical simulations have shown this process also on spherical vesicles [90].

In the presence of active forces, the spontaneous initiation of rings can occur more readily, due to the following positive feedbacks [87]: for CMC with a radius of curvature that induces constrictions, the recruitment of contractile forces, for example due to acto-myosin complexes (figure 3d) [91,92], gives such a positive feedback. The combination of curvature and contractile forces produces a robust mechanism for initiation of contractile rings [87]. A similar behaviour will occur if the CMC have the opposite curvatures, adsorb to the outer side of the cylindrical membrane and recruit contractile forces or protrusive forces that are directed inwards (towards the tube axis) [93]. This mechanism seems to play a role during actin-driven fission of cylindrical membrane invaginations [94], for example during endocytosis [95,96].

On a long tube, the instability described above initiates rings at the most unstable wavelength [97]. This phenomenon is indeed observed in in vitro experiments [44,98]. These rings serve to initiate fission of the membrane tubes, at the boundary between the dense CMC ring and the unconstricted membrane [97,99], as was observed in experiments [100]. Note that the instability leading to the formation of constricting rings can then serve to recruit further proteins and cytoskeletal elements that drive the final membrane fission [101]. In bacteria, the condensation of constricting rings (usually of FtsZ proteins) can mark the locations for the recruitment of the cell-wall building machinery [102], which forms the septum that divides the cell or organelle. The FtsZ filaments possess spontaneous curvature [103,104], may induce constrictive forces [105], and therefore both bend the membrane and are affected by its curvature [106]. In mitochondria, such rings serve to recruit the cytoskeleton of the cell, to complete the fission process [107]. In eukaryotes, the initiation of the contractile ring through the process we described may serve as the initial step for the formation of the ring that divides the cell during mitosis and gives rise to the condensation of the contractile forces at the site of the ring formation [108,109].

One interesting feature of this instability is that as the tube grows in length, it first reaches the conditions of instability when an unstable mode has a wavelength that is twice the tube length [87]. This means that the first instability should occur at the mid point along the tube length, making this instability a useful mechanism for dividing membrane tubes, or tubular cells, into two symmetric pieces. This mechanism may have allowed primitive cells to initiate symmetric division above a threshold cell length, which later became supplemented by further mechanisms that ensure the spatial and temporal accuracy of this process.

Note that the formation of a dense scaffold of curved proteins, and also the formation of an actin coat, can act to stabilize membrane tubules by providing a supporting structure that is rather static and rigid. It is, therefore, found that during the initial formation of tubes from the cell membrane the cortical actin network needs to be weakened [110]. Such rigid scaffolds act to inhibit the instability described above, preventing the break-up of the tubes into vesicles. On the other hand, a uniform polymerizing actin coat can exert an inwards pressure on the tube [111] that can drive a pearling instability [93].

5. Positive and negative feedbacks: oscillations and membrane waves

The recruitment of cytoskeletal forces by the curved CMC can give rise to positive feedback and instability, as we saw above, but can also produce a negative feedback. Consider a concave CMC on a flat membrane, that recruits the protrusive force of actin. An accumulation of the CMC will produce a small protrusion, which will drive the concave CMC to the sides where the curvature is more concave (figure 1c). As the CMC flow to the sides, so does the protrusive actin force that it recruits. This process gives rise to a decaying sideways motion (damped waves), which restores the membrane to its flat shape and the CMC to their uniform distribution [34]. While this negative feedback by itself does not spontaneously produce any membrane pattern, it may be a useful mechanism for cells in order to maintain uniformity and prevent aggregation. Such a mechanism is used by bacteria to maintain their straight cylindrical shape, where the equivalent of the protrusive force of the cytoskeleton is the cell-wall building process [40].

More interesting dynamics follow from the coupling between positive and negative feedback mechanisms. The convex CMC that recruit protrusive cytoskeletal forces provide a positive feedback that produces stationary protrusions, as we described above. We call these protrusions ‘stationary’ in the sense that they do not tend to propagate sideways in the plane of the membrane, at least in the linear regime (coarsening due to nonlinear terms can lead to sideways sliding [35]). When coupled to a negative feedback process, the system has a phase diagram with parameter regimes of damped oscillations and regimes of ‘wave instability’. In the wave instability regime, propagating or oscillatory perturbations grow in amplitude (due to the instability) and correspond to waves and oscillations that may be triggered spontaneously. The rate of growth of perturbations is now complex, ω(q) = ω′(q) + iω′′(q), with the imaginary part giving the oscillatory phase and the real part describing the rate of growth (or decay) of the amplitude. We describe examples for three such mechanisms below. Within the cell there are many overlapping feedbacks, so the simple and tractable models we give here serve as examples when few such feedbacks dominate. Other models have been proposed to couple the membrane shape with the actin cytoskeleton into a feedback network that produces waves [112], while there are also models for these waves that include the active forces of the cytoskeleton but do not involve the curvature of the membrane [113,114]. Recent experiments find propagating cellular waves involving all the ingredients of the theoretical model: membrane deformations and actin polymerization that is recruited by curved membrane proteins [115]. Note that other curved membrane proteins and lipids, which are not directly related to the mechanism driving the membrane waves, are affected by the propagating membrane undulations that can ‘sweep’ them due to their intrinsic curvature [33].

(a). Waves driven by myosin contractility

When the convex CMC recruit polymerization of cortical actin, the actin filaments provide a substrate for a host of actin-binding proteins. One such protein is myosin-II, which acts to pull anti-parallel actin filaments and transmit a force that pulls the membrane into the cell [86]. It is assumed that the myosin contractility acts, on average, to pull the membrane perpendicularly into the cell, since the cortical actin network is assumed to be locally uniform on the membrane. The active term in equation (2.3) becomes [116]

5.1

where A* is the strength of myosin-II contractility, and m is the local concentration of myosin at the cell cortex. The dynamics of the myosin field are described by the following additional equation of motion [116]

5.2

describing the adsorption/desorption kinetics of the myosin motors on the actin network (which is given by the local CMC concentration n).

When the contractile force overwhelms the protrusive force of the actin polymerization, the instability can change from production of stationary protrusions to propagating waves [116]. The dynamical process is as follows: convex CMC recruit protrusive actin forces and this results in their aggregation at the protrusive tip (figure 4a). Myosin-II builds up on the actin and reverses the motion of the membrane, such that it retracts and forms a local dip. The convex CMC flow and accumulate at the shoulders of the dip, where the process repeats itself (figure 4b).

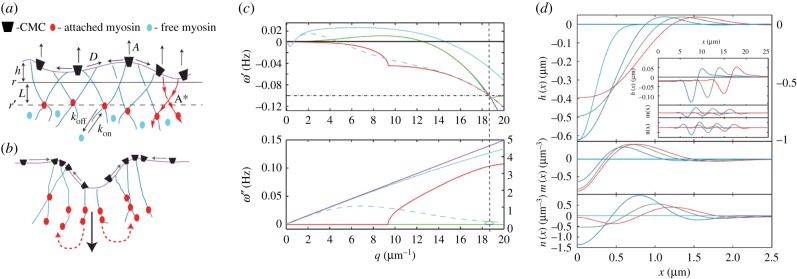
Figure 4.

(a) Schematic description of the model [116] with convex CMC that recruit actin polymerization (A), which in turn adsorbs myosin motors from the cytoplasm (equation (5.2)) that give rise to inwards contraction (A*, equation (5.1)). (b) Strong contraction (large downward black arrow) leads to CMC aggregation on the two sides (small arrows on the membrane), followed by the motors (dashed red arrows), leading to wave propagation sideways. (c) The evolution of the dispersion relation ω(q) as function of the myosin contractile strength A*. The case of A* = 0 is in dark blue, while the green, red and light blue show increasing values of A*. For the largest value the calculated analytical linear dispersion approximation is plotted in purple. The vertical dashed line denotes the wavevector at which waves first appear (q_ω). The horizontal dash-dotted line indicates the rate of myosin detachment k_off (see (a), equation (5.2)). The dashed light blue lines give the dispersion using a non-local myosin force kernel (for details see [116]). (d) One-dimensional simulation using our linearized model (without thermal noise), showing the formation of moving waves due to sudden perturbation in the membrane shape. We plot here the membrane height h(x), myosin m(x) and actin n(x) density fluctuations as a function of position and time; t = 0, 1, 2, 3 s (light blue, blue, green and red). Note that for the height profile at t = 0 use the right-hand scale. In the inset, we show the waves propagating at longer times; t = 60, 90, 120 s (blue, green and red). (All the panels from [116]).

This process gives rise to propagating waves with an almost linear dispersion relation: ω′′(q)∝qc (figure 4c), which correspond to waves with a well-defined propagation speed c, which is roughly independent of wavelength for large wavelengths (acoustic-like). The speed of propagation turns out to be largely independent of the rate of actin polymerization, while it strongly depends on the strength of myosin-II contractility A* [116,117], approximately as: 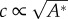. Within the wave, the actin concentration is at the leading front of the wave, while the myosin concentration is trailing, and they are oscillating out-of-phase with respect to each other (figure 4d).

This model can describe the spatio-temporal correlations of observed cellular membrane waves [118]. Direct experimental evidence for the role of myosin-II in membrane waves was reported in [119]. However, the role of curved membrane proteins was not reported in these studies. Within the model the waves are predicted to be excitable using mechanical perturbations of the membrane (figure 4d) and the actin cortex [117], which can serve to probe the frequency spectrum of the waves through the frequency-dependence of the amplitude of the excited waves. These predictions await future experiments [120].

(b). Waves driven by combining convex and concave curvatures

When the cell membrane has CMC of both curvature signs, and both recruit protrusive forces of the cytoskeleton (figure 5a,b), there can be a regime where wave instability occurs [41]. The key property to ensure the appearance of the wave instability is found to be that the convex CMC, which give the positive feedback, are recruited faster than the concave CMC, which give the negative feedback. The faster recruitment, through larger diffusion coefficient or higher adsorption rate from the cytoplasm, ensures that the positive feedback is maintained and not damped by the negative feedback. This is similar to the model with the myosin contractility described above, where the myosin (negative feedback) appears after the actin polymerization (positive feedback). An example of a feedback scheme for this model is shown in figure 5c [41].

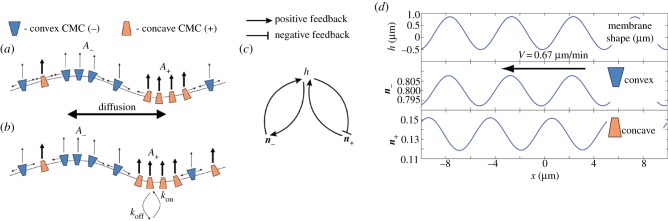
Figure 5.

Schematic description of the model combining CMC of both curvatures [41]. (a) The CMC diffuse in the membrane. (b) The CMC adsorbs to the membrane from a cytoplasmic reservoir. (c) Feedback diagram describing the main interactions in the model, where positive and negative feedback loops combine to produce oscillations (the densities of the two curved CMC are denoted by n_±). (d) Results of simulating a system where the convex CMC (−) are diffusing, while the concave CMC (+) are mainly adsorbing from the cytoplasm. A steady-state wave is shown, with the arrow showing the direction of propagation. The convex CMC are in-phase with the membrane while the concave CMC are in anti-phase. All panels from Peleg et al. [41].

The waves are found to exist above a minimal value of the actin polymerization force, and above this threshold value the waves' velocity increases with increasing actin polymerization force. Within the waves, the concave and convex CMC are displaced with respect to each other, as each follows the different curved region of the membrane undulation (figure 5d).

This model was proposed to explain the phenomenon of circular dorsal ruffles (CDR) [121], where some ingredients of this model exist: proteins of both curvature signs are localized in the waves [41,122], together with actin polymerization. In addition, myosin-II contractility was shown not to play a crucial role for this type of membrane waves [41]. This model offers an explanation for the observed displacement between the location of the concave proteins and the actin within the propagating CDR [122], as arising from the curved proteins following the undulations of the wave (figure 5d). Increasing membrane tension is predicted to diminish the amplitude of the waves, while leaving the wave velocity largely unaffected [41], in agreement with recent observations of membrane waves [119].

(c). Oscillations driven by a mechano-chemical negative feedback

Finally, another possible negative feedback that can be coupled to the positive feedback of the convex CMC and cytoskeleton protrusive forces (or concave CMC with inwards-directed cytoskeletal forces), is a biochemical negative feedback [123]. The negative feedback can arise due to a large variety of biochemical interactions within the cell. One such biochemical feedback is the influx of calcium ions into the cell through the membrane (figure 6). This influx, as well as the rate of outflux, can depend on the local concentration of membrane proteins, which affect the functioning of calcium channels and pumps [125,126]. The calcium influx can also depend on the shape deformation of the membrane, through stretch-activated channels [124]. Therefore, both the aggregation of the CMC and the protrusive force due to actin polymerization can induce higher overall influx of calcium. Higher cellular concentration of calcium ions in turn triggers an inhibition of the protrusive force of actin polymerization, either by activating actin-severing and capping proteins, or by activating myosin-II contractility.

Figure 6.

The overall feedbacks and coupling of a mechano-chemical negative feedback model [123], and the simpler subcases (i)–(iii) that give rise to wave instability. The cellular concentration of calcium ions C can directly inhibit the rate of actin polymerization, thereby acting to retract the membrane height (h), or inhibit the activity of the CMC (n). The height deformation is associated with local curvature that in turn can induce an increase in the net influx of calcium, through the opening of stretch-activated channels [124]. The aggregation of CMC can also result in increased influx of calcium due to reduction in the outward pumping of the ions [125], or due to the opening of calcium channels [126]. From Veksler & Gov [123].

The overall feedback scheme for this model is shown in figure 6, where the calcium is shown to inhibit the activity of the CMC or the actin polymerization force that pushes the membrane. The result of analysing this model is a phase diagram, where the oscillatory phase appears only below a threshold of actin polymerization activity. Oscillations and waves appear above a threshold of the calcium-driven negative feedback, i.e. strong calcium inhibition of the protrusive actin force, and a strong effect of the CMC and the actin on the calcium influx. Within the oscillatory regime, a higher actin protrusive force lowers the oscillation frequency, while a higher calcium-driven feedback increases it.

The predicted oscillations arising from this model may explain the shape fluctuations (i.e. twitching) of dendritic spines and filopodia [127,128]. When the activity of actin polymerization was decreased in this system through the addition of cytochalasin-D, the observed frequency of spontaneous fluctuations increased [129], which is in qualitative agreement with the model predictions. Another example for oscillations that may follow this model occurs in migrating cells [130], where calcium oscillations were found to be triggered at the leading edge, where the actin activity is localized and dependent on the functioning of calcium channels. Furthermore, the frequency of oscillations is observed to decrease with a decrease in the calcium concentration, as our model predicts (decrease in the calcium-driven feedback). Finally, recent experiments have linked membrane shape oscillations with actin polymerization, curved membrane proteins and calcium [131], therefore identifying all the key ingredients contained in the theoretical model.

6. Discussion

How cells determine their shapes, whether making stable (relatively static) or dynamic structures, remains an open puzzle. It has become clear over recent decades that a large number of proteins are responsible for shaping the cell membrane, interacting to form dynamic supra-molecular complexes. This complexity makes it difficult to unravel, and to extract the basic mechanisms. Nevertheless, the cell has to exert forces on the membrane in order to deform it, and needs to have ways to control these forces spatially and temporally. Through evolution, cells make use of every possible feedback mechanism in order to achieve this control. What we have shown here is that a most useful class of such feedbacks involves coupling curved membrane complexes, such as curved membrane proteins, with the active forces of the cytoskeleton. The curved component of this coupled system is a natural ingredient that allows it to guide components according to the shape of the membrane, which is the desired product. By coupling to the strong active forces produced by the cytoskeleton, the dynamics of the membrane proteins and the associated deformation of the membrane occur in highly non-equilibrium conditions. This means that structures can form in conditions where they would not form in thermodynamic equilibrium. This allows the cell to have control of when and where these structures appear. Indeed, the coupling between curved proteins, which bend and sense curvature, and the cytoskeleton, has been found to occur in a growing number of cellular processes.

Future challenges for this field include the ability to explore these complex feedbacks using well controlled in vitro experiments, where both the membrane and the cytoskeleton are reconstituted [132]. On the theory side, there remain the open challenges of exploring such coupled systems with more complex and realistic components, as well as beyond the linear regime, where large membrane deformations occur. These systems provide examples of non-equilibrium phase transitions and pattern formation, which are processes for which our current physics understanding is lacking. Studying them therefore enriches both our understanding of biology, and also expands the scope of physics.

Data accessibility

This article has no additional data.

Competing interests

I declare I have no competing interests.

Funding

No funding has been received for this article.