Abstract
Social networks can be adaptive for members and a recent model (Ilany and Akçay 2016 Nat. Comm. 7, 12084 (doi:10.1038/ncomms12084)) has demonstrated that network structure can be maintained by a simple process of social inheritance. Here, we ask how juvenile vervet monkeys integrate into their adult grooming networks, using the model to test whether observed grooming patterns replicate network structure. Female juveniles, who are philopatric, increased their grooming effort towards adults more than males, although this was not reciprocated by the adults themselves. While more consistent maternal grooming networks, together with maternal network strength, predicted increasing similarity in the patterning of mother–daughter grooming allocations, daughters' grooming networks generally did not match closely those of their mothers. However, maternal networks themselves were not very consistent across time, thus presenting youngsters with a moving target that may be difficult to match. Observed patterns of juvenile female grooming did not replicate the adult network, for which increased association with adults not groomed by their mothers would be necessary. These results suggest that network flexibility, not stability, characterizes our groups and that juveniles are exposed to, and must learn to cope with, temporal shifts in network structure. We hypothesize that this may lead to individual variation in behavioural flexibility, which in turn may help explain why and how variation in sociability influences fitness.
Keywords: social integration, social development, grooming, vervet monkeys, behavioural flexibility
1. Introduction
Social network position carries fitness consequences for individuals across a wide range of taxa [1–4]. The existence of mechanisms that serve to maintain network integrity following perturbations [5,6], further suggests that overall network structure, as well as individual network position, may confer benefits on individuals [7,8]. The stability of a network structure over time is vulnerable to changes in group membership however; a problem faced by all permanent, multigenerational groups. Understanding how animal social networks are formed and maintained is, therefore, an important but as yet, largely unanswered question.
Some recent progress on this front has been made in an important paper by Ilany & Akçay [7]. They demonstrate that a simple demographic and social process, whereby newborns ‘inherit’ their mothers’ social connections with a probability (pn) that exceeds that of forming unconnected, random associations (pr), could replicate network structure across a range of social species. Specifically, their model was able to reproduce the degree distribution, modularity and clustering coefficient distribution of observed networks. This last measure is especially significant because clustering is a feature that distinguishes social from other kinds of network. The model's success in reproducing clustering suggests that social inheritance mechanisms may be key to producing clusters in social networks and to preserving individual network position across generations: an outcome that can have demonstrable adaptive consequences [9].
While sustaining the overall social network through time is beneficial, it also seems possible that, under some circumstances, this is best achieved by varying aspects of network structure, rather than replicating it. Schradin [10], for example, has drawn a distinction between social flexibility and flexibility in social behaviour, where social flexibility refers to reversible changes in social and mating tactics at a group and population level, whereas flexibility in social behaviour refers to individual variability in response to changing circumstances. Some animal societies, most notably rodents, show the former kind of flexibility, whereas other species, including most of the primates, adjust individual behaviour patterns to preserve a particular group-level organization [10]. In the latter case, we might expect social networks to resist disruption and dissolution via adaptive variation in network characteristics. Some evidence to suggest this is the case that comes from wild baboons, where the death of the dominant female, and a subsequent period of rank instability, was accompanied by an increase in clustering in the proximity network, compensating for the disruption to the aggression network ([5]; see also [6] for captive macaques). Thus, in addition to a mechanism that enables individuals to integrate into, and thus sustain, the social network over time—and the mechanism provided by Ilany and Akçay's model seems entirely plausible and, indeed, empirically supported—unpredictable variation in group size and structure may select for animals that are able to respond flexibly to circumstance, and adjust network position accordingly. With respect to social inheritance, if a mother's social network shifts over time this may make it difficult for younger animals to match their mothers' social connections; that is, juveniles may face a moving target. Here, one would expect some degree of social inheritance, but not necessarily network replication.
This links directly to the question of the unusually long juvenile periods of anthropoid primates [11]. These are generally considered to be driven by the energetic demands of growing a large brain (i.e. constraint-based hypotheses) [12], combined with the need to learn the ecological and social skills that promote adult survival (i.e. functional hypotheses) [13,14]. Despite the importance of this extended juvenile period for adult performance [15], detailed studies of the juvenile period are still comparatively rare. Although variation in developmental trajectories is usually interpreted in terms of its potential influence on variation in adult social engagement and later fitness-related benefits [15], the actual processes, by which integration is achieved, are often left unspecified. That is, it is not clear how changes in patterns of grooming, if any, alter the structure and composition of juveniles’ social networks, and whether this results in concomitant shifts in the overall network structure of the group. There is, perhaps, the implicit assumption that, during the juvenile period, young animals learn the rules of social life, which they only apply once they reach adulthood. It is also possible that the juvenile period represents a period of gradual induction into the adult social network, and that youngsters are ‘social apprentices’, learning their skills on the job. A better sense of the dynamics of early social engagement, and how juvenile networks come to resemble those of adults, will permit a deeper understanding of whether the juvenile period represents a ‘rehearsal’ for adulthood, or whether it is used from the start to build relations and establish useful positions in the adult network. In this regard, where species show strong sex-based philopatry, it is reasonable to expect that juveniles of the philopatric sex will be more likely to work towards integration in their natal groups.
Our aim here is to assess the process by which juvenile vervet monkeys (Chlorocebus pygerythrus) become integrated into the adult grooming network, and the extent to which they do so. Vervets are small, territorial primates that inhabit riparian zones, and are widely distributed across Africa. They live in multi-male multi-female groups, which range from as few as six to more than 70 members [16]. Females are philopatric, while males migrate multiple times throughout their lives, leaving their natal groups at sexual maturity [17]. Vervets display linear dominance hierarchies, and females are co-dominant to males, such that both sexes can be ranked in a single group hierarchy [4]. Grooming is the predominant social behaviour in vervet groups (approx. 90% of all social time), and one that spans both juvenile and adult periods. In our study population, grooming and dominance rank are unrelated to each other, although such a relationship has been seen in other populations [18].
As female vervets are the philopatric sex, we (i) first confirm that female juveniles are more socially active than males with respect to integration (measured via the amount of time devoted to grooming adults), as indicated in previous studies of captive animals [19]. We go on to determine (ii) whether adult grooming targets juvenile females preferentially, given that global network structure reflects grooming received as well as given, and given that all group members should benefit from adaptive social structures. We then establish the degree of similarity between mother and female offspring grooming allocations—assessing grooming given and grooming received separately—at the end of the juvenile period to identify (iii) the extent to which juvenile females inherit their mother's grooming network, (iv) the factors that predict similarity, and (v) whether juvenile females are actively contributing to this process. Finally, we use Ilany and Akçay's model framework to test (vi) whether the inheritance of social ties by offspring from their mothers can replicate global network structure.
2. Methods
(a). Study population and subjects
Data were collected at the Samara Private Game Reserve in the semi-arid Karoo biome, Eastern Cape, South Africa [16], from three troops of vervet monkeys occupying adjacent and overlapping home ranges. These three groups (PT: N ≈ 24; RBM: N ≈ 37; RST: N ≈ 45) were fully habituated, and all group members were individually identifiable from natural markings. Vervets give birth to single offspring. The study subjects comprised the cohort of 28 infants born in the 2013 birth season (October–December) and their mothers. The number of juveniles and the representation of each sex at the beginning of the study were similar for each troop (PT: NFemale = 4, NMale = 3; RBM: NFemale = 5, NMale = 4; RST: NFemale = 6, NMale = 6). Sample size was reduced across the study period by the deaths of five mothers and one juvenile.
(b). Data collection
Data collection for this study began when all the infants in the cohort were nutritionally independent of their mothers and classified as juveniles (July 2014), and ended with the first confirmed pregnancy of a female cohort member (September 2016), taken conservatively to indicate an end to the juvenile period. Each troop was followed on foot by one or more researchers on each 10 h study day (PT: 434 days; RBM and RST: 465 days) and data were recorded onto electronic data loggers using proprietary software (Pendragon Forms). We obtained activity (foraging, moving, resting) and directional grooming data for our subjects (grooming given and received) and the identities of their adult grooming partners from instantaneous scan samples [20] collected every 30 min from all individuals that could be located within a 10 min time window [4]. This yielded 20 515 grooming episodes (PT: 6216; RBM: 6564 RST: 7735) across the 28 month study. We did not control for observations per animal, as we sample from well-habituated troops, where identities of all individuals are known. Given the coverage of the group made possible by the number of observers, the absence of an individual is less likely due to sampling lacunae, and more to do with the individual being less socially integrated in the troop. An individual's absence from a scan provides important information that is lost if we standardize by observation frequency (e.g. an individual observed in the group five times and 100 times would be made comparable). In addition, previous analyses revealed no qualitative differences between our scan samples and focal-animal sampling [18]. To examine temporal patterns in grooming exchanges, we divided the study period into seven consecutive four-month blocks, as this offered the best trade-off between adequate sample size and our ability to register any change in effort and network structure. To account for differences in their ages, we determined, for each juvenile, its age in days at the midpoint of each of the seven time blocks. Observational data collection protocols were approved by the University of Lethbridge Animal Welfare Committee (protocol 1505).
(c). Comparison of juvenile and mothers' grooming contributions and networks
To assess whether the extent to which juveniles gave grooming to, or received it from, adults were associated with juvenile age and sex, we entered the frequency with which juveniles groomed or were groomed as the response variables in two generalized linear mixed models (GLMMs), with standardized age and sex as predictors and total activity budget as the offset variable. As both response variables were best fitted by the negative binomial distribution (p ≈ 0.3), we specified a negative binomial error distribution. Juvenile identity (ID) was entered as a random effect. To allow the models to converge, we did not nest ID in troop.
We used cosine similarity values as our estimate of the similarity of a juvenile female's grooming network to that of her mother. Cosine similarity assesses the extent to which the patterning of values in two vectors (a, b) is similar, making it appropriate for differing sample sizes [21]. This metric is a measurement of orientation/style, not one of magnitude like Euclidean distance, and is expressed as the cosine of the angle between two vectors:
More details on calculating cosine values are given in the electronic supplementary material. In our case, these are the similarity of a juvenile's grooming allocations to those of its mother in any single time block. The outcome is bounded between 0 and 1, where zero indicates non-similarity, and 1 indicates identical allocation. We used grooming frequencies to derive three separate cosine similarity values: grooming received (in), grooming given (out) and combined (undirected) grooming (total), using the ‘lsa’ package [22] in R 3.3.1. [23]. To address the possibility that juveniles face a ‘moving target’ when forming grooming ties (i.e. whether variability in the mother's grooming network affected the similarity of a juvenile's grooming networks to that of its mother), we estimated the self-similarity of each adult female's grooming network by comparing her grooming distribution in each time block to that in the preceding one. For the first time block, we extracted maternal grooming data for the four-month block preceding the start of the study. To determine whether the similarity of daughter and mother grooming networks was associated with juvenile age, as well as the extent of the daughter's integration in the adult grooming network, we entered cosine in- and out-similarity as response variables in two linear mixed models (LMMs), with age, maternal grooming degree and strength as predictors. We also entered maternal self-similarity to account for the extent to which a mother's grooming network was consistent from one time block to the next. Juvenile ID, nested in troop, was entered as a random effect.
We cannot assume that in- and out-cosine similarity in grooming will necessarily correlate with each other, and hence that they will make an equal contribution to any measure of total cosine similarity. This is because we cannot assume that all grooming relations are mutual, i.e. if one animal chooses to groom another, this does not necessarily imply the other animal will groom them in return (whether in the same bout or on different occasions). We, therefore, tested whether in- and out-similarity were correlated, and assessed their respective contribution to total cosine similarity using an LMM controlling for juvenile age and with ID nested in troop as a random effect. We then evaluated the relative contributions of in- and out-similarity to the overall similarity of mother–daughter grooming networks by entering total cosine similarity as the response variable and cosine in-and out-similarity and daughter age as predictors in an LMM, specifying juvenile ID, nested in troop, as a random effect.
(d). Grooming network position
To ascertain whether the extent to which a juvenile's grooming network mirrored that of its mother was a function of the extent to which the mother was integrated into the adult grooming network, we constructed seven time-aggregated, weighted and directed association matrices for each troop. Following their relevance in earlier analyses [24,25], we used the package igraph [26] to derive estimates of grooming degree and grooming strength for each mother in each time block. Degree is the sum of each node's connections and indicates the extent of its connectedness to other nodes [27]. Strength is the sum of each node's connections weighted by the total frequency with which it interacts with other nodes. An individual with high strength is, therefore, either associated with many other group members and/or is strongly associated with a few group members [27].
(e). Global grooming network stability
Our expectation was that mother–daughter grooming network similarity underpins the extent to which the global network remained resilient to the introduction of new groomers [7]. To assess this, we first used the igraph package in R [25] to extract four global network measures that are potentially relevant to an interrogation of the structural stability of weighted grooming networks: clustering coefficient, modularity, eigenvector and betweenness centrality. The clustering coefficient (or transitivity) measures the propensity to form grooming ties with shared partners, here we use an undirected and weighted transitivity measure [28]. Modularity is the extent to which groomers form subgroups, and betweenness centrality describes the extent to which individuals act as bridges between other individuals. For modularity, we first used the walk-trap algorithm to identify clustering in the weighted and undirected network, and measured how well this clustering divides the network [29]. Betweenness centrality was first calculated at the individual level (i.e. how many times a node acted as a bridge between two other nodes was calculated) based on the weighted and undirected network, and the mean of these values was used to describe the group-level betweenness score [30]. We then ran permutation tests on the grooming networks of each of the three troops to determine which of these measures would be unlikely if observed grooming was randomly allocated between dyads (i.e. edge permutations). We obtained observed values for each of the four measures from the global grooming network in time block 7 and then generated 1000 random networks with the same number of nodes, where edges were randomly assigned using the weights present in the observed networks. We then compared the observed values for each measure to those measured on the randomly generated networks. We considered observed measures falling outside the 95% confidence intervals (CI) of the distribution of the measures in random networks to be associated with non-random grooming structure. In all three troops, two of the four measures—clustering and betweenness centrality—were consistent structural components of non-random grooming networks (electronic supplementary material, figure S1), while eigenvector centrality and modularity did not differ from randomly allocated grooming.
(f). Network replication
To examine the consequences of the estimated similarities in grooming between mothers and daughters on the stability of the social network, we used Ilany and Akçay's social inheritance model [7] as our mechanistic descriptor of the emergence of grooming networks. We first reproduced the unweighted social inheritance model in R [31], and then extended it to incorporate weighted edges. We did this, not only because Ilany and Akçay flag weighted networks as a natural extension of their model, but also because it reflects the weightings inherent in the use of cosine similarity. We then used grooming patterns observed in time block 7 to generate empirical values of pn, pr, en and er for use as parameters in models that assessed future replicability in the observed networks. We compared the observed and optimized grooming behaviours, as well as the resulting networks generated by observed and optimized behaviours against the actual network in time block 7 (see the electronic supplementary material for procedure).
(g). Statistical analysis
We conducted analyses in R and used the ‘lme4’ package [32] and ‘glmmADMB’ package [33] to run the LMMs and GLMMs, respectively. We used the ‘MuMIn’ package [34] to obtain marginal and conditional R2 values for the LMMs [35]. Continuous variables were mean centred and standardized, and analyses were run at the level of subject/time block. We checked the residuals for heteroscedasticity and autocorrelation as well as normality in the case of the LMMs. Variance inflation factors were all below 2.1. Problems with convergence meant that we did not specify random slopes in any of the models. The models we present are those that best met the necessary assumptions. We follow Colquhoun [36] in describing outcomes as indicating weak (p ∼ 0.05), moderate (p ∼ 0.01) or strong (p ∼ 0.001) evidence for effects.
3. Results
(a). Grooming contributions to time budgets
There was a high prevalence of zeros in the estimates of grooming given by juvenile males that are evident neither in the estimates of the grooming male juveniles receive, nor in the grooming activity of juvenile females (figure 1). As this makes it unlikely that we are dealing with a sampling issue, we flagged zero-inflation in the GLMMs. We found little evidence that adults increased their grooming effort as juveniles aged (table 1a; figure 1a). We found strong evidence for increased effort in the grooming given by juveniles over time, with females doing so at higher rates than males (table 1b, figure 1b).
Figure 1.
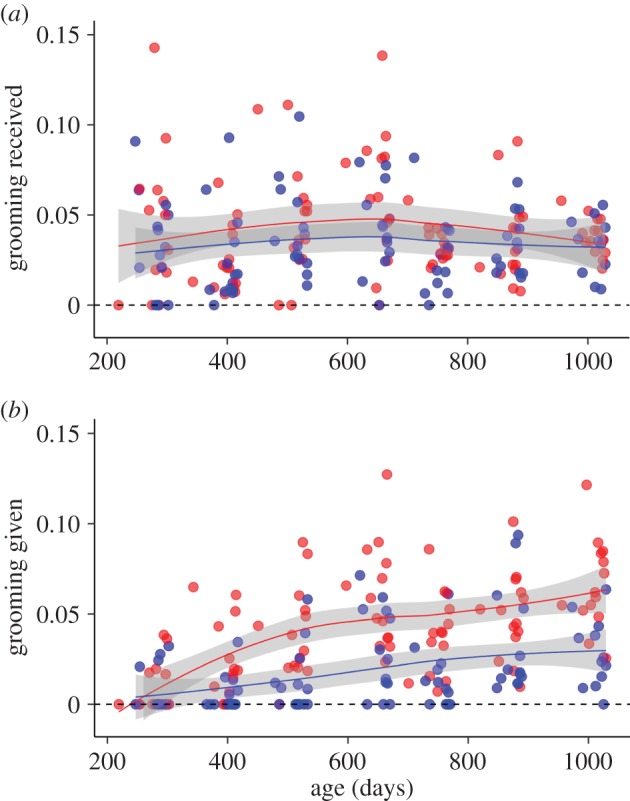
The relationship between juvenile age and the proportion of the activity budget in which (a) juveniles were groomed by adults and (b) juveniles groomed adults. Red circles: females; blue circles: males. The lines are loess fits (±95% CI) to the uncorrected data. (Online version in colour.)
Table 1.
Model outcomes for the frequency with which (a) juveniles received grooming from adults and (b) gave grooming to adults, in each time block. (s.e., standard error; CI, confidence intervals.)
| β | s.e. | Z | p-value | 95% CI | ||
|---|---|---|---|---|---|---|
| (a) grooming received | ||||||
| juvenile age | −0.006 | 0.044 | −0.134 | 0.893 | 0.316 | 0.517 |
| sex (ref: female) | −0.209 | 0.131 | −1.599 | 0.110 | −1.360 | −0.573 |
| intercept | −3.253 | 0.091 | −35.717 | <0.0001 | −3.431 | −3.065 |
full model: log likelihood = −429.21; N = 191. Full versus null model: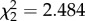 ; p = 0.289 ; p = 0.289 | ||||||
| (b) grooming given | ||||||
| juvenile age | 0.416 | 0.051 | 8.137 | <0.0001 | 0.316 | 0.517 |
| sex (ref: female) | −0.966 | 0.201 | −4.809 | <0.0001 | −1.360 | −0.572 |
| intercept | −3.329 | 0.135 | −24.723 | <0.0001 | −3.593 | −3.065 |
full model: log likelihood = −386.64; N = 191. Full versus null model: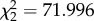 ; p = <0.0001 ; p = <0.0001 | ||||||
(b). Grooming network similarity
The extent to which the grooming networks of juvenile females matched those of their mothers, and those of mothers matched their own earlier networks, across the study is indicated in figure 2. The figure draws attention to individual variation both within and across time blocks and the absence of any strong general fidelity in grooming networks over time.
Figure 2.
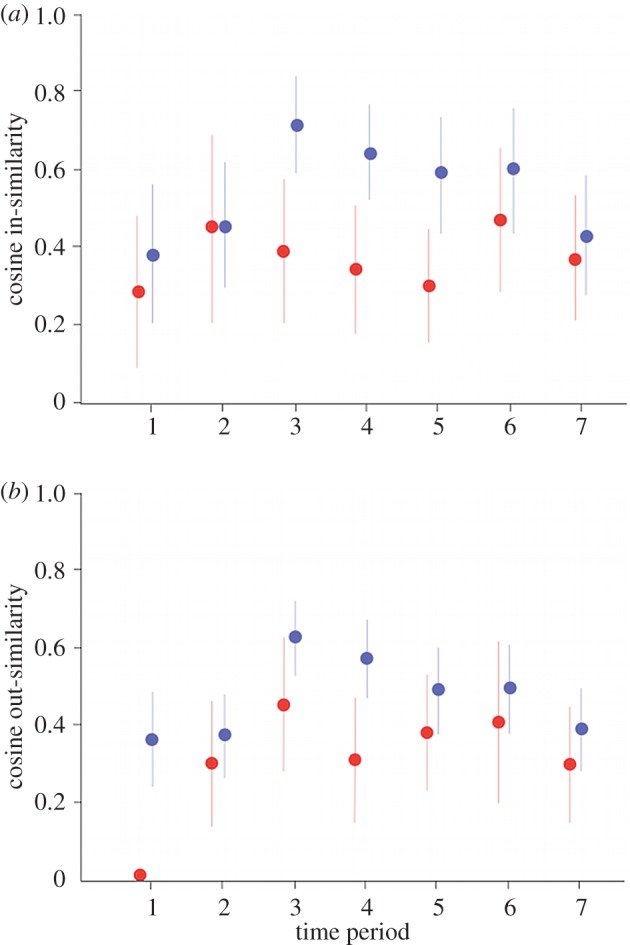
Mean cosine similarity values across the seven time blocks of the study: (a) similarity in grooming received from adults; (b) similarity in grooming given to adults. Values for female juveniles (red circles) are those that indicate the extent to which their grooming profiles matched those of their mothers. Values for mothers (blue circles) indicate the extent to which their grooming profiles in one time block matched their grooming in the previous one. Bars are 95% CI. (Online version in colour.)
We found weak to moderate evidence for the positive effect of maternal self-similarity on both cosine in- and out-similarity in the grooming networks of mothers and daughters (i.e. the more consistent the mother's network across time blocks, the greater the similarity between mother–daughter networks) and good evidence for a positive effect for maternal network strength on out-similarity (table 2). Although the overall model describing out-similarity differed from the intercept-only null model, with the fixed effects explaining a reasonable amount of variance, the model for in-similarity did not. We found, too, that mothers with more stable networks fostered juveniles who were also more stable, although the effect size was small and there was no time period effect (electronic supplementary material, table S1).
Table 2.
Model outcomes for the extent to which (a) cosine in-similarity and (b) cosine out-similarity are predicted by juvenile age, maternal grooming network consistency and maternal social integration. (s.e., standard error; d.f., degrees of freedom; CI, confidence intervals.)
| β | s.e. | d.f. | t | p-value | 95% CI | ||
|---|---|---|---|---|---|---|---|
| (a) in-similarity | |||||||
| juvenile age | −0.001 | 0.034 | 62.495 | −0.023 | 0.982 | −0.065 | 0.067 |
| mother self-similarity | 0.077 | 0.037 | 61.594 | 2.087 | 0.041 | 0.009 | 0.159 |
| mother in-strength | −0.027 | 0.042 | 62.314 | −0.643 | 0.523 | −0.104 | 0.062 |
| mother in-degree | 0.032 | 0.045 | 63.284 | 0.703 | 0.485 | −0.064 | 0.116 |
| intercept | 0.329 | 0.059 | 1.385 | 5.554 | 0.065 | 0.465 | 0.465 |
full model: log-restricted likelihood = −9.056; N = 73; 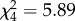 ; p = 0.207. ; p = 0.207.  ; ; 
| |||||||
| (b) out-similarity | |||||||
| juvenile age | 0.031 | 0.030 | 65.070 | 1.046 | 0.300 | −0.027 | 0.089 |
| mother self-similarity | 0.079 | 0.035 | 65.068 | 2.276 | 0.026 | 0.013 | 0.145 |
| mother out-strength | 0.126 | 0.041 | 38.612 | 3.050 | 0.004 | 0.047 | 0.206 |
| mother out-degree | −0.017 | 0.045 | 46.744 | −0.379 | 0.707 | −0.103 | 0.068 |
| intercept | 0.300 | 0.035 | 10.299 | 8.658 | <0.0001 | 0.230 | 0.367 |
full model: log-restricted likelihood = −4.875; N = 73; 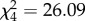 ; p < 0.0001. ; p < 0.0001. 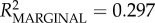 ; ; 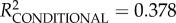
| |||||||
(c). Contributions to total cosine similarity
Out-similarity was a poor predictor of in-similarity (LMM controlling for juvenile age and with ID nested in troop as a random effect: β = 0.2 ± 0.118, 61.138 d.f., t = 1.69, p = 0.096; 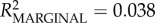 ), suggesting that the decision of who mothers and juveniles groom reflects a different process to the one influencing who mothers and juveniles are groomed by. In- and out-cosine similarity make equivalent contributions to total cosine similarity (table 3), which suggests these different processes were of equal importance in determining total cosine similarity.
), suggesting that the decision of who mothers and juveniles groom reflects a different process to the one influencing who mothers and juveniles are groomed by. In- and out-cosine similarity make equivalent contributions to total cosine similarity (table 3), which suggests these different processes were of equal importance in determining total cosine similarity.
Table 3.
The relative contributions of cosine in- and out-similarity to the estimate of total similarity. (s.e., standard error; d.f., degrees of freedom; CI, confidence intervals.)
| β | s.e. | d.f. | t | p-value | 95% CI | ||
|---|---|---|---|---|---|---|---|
| in-similarity | 0.127 | 0.014 | 58.812 | 9.247 | <0.0001 | 0.100 | 0.153 |
| out-similarity | 0.114 | 0.014 | 60.369 | 8.461 | <0.0001 | 0.086 | 0.140 |
| juvenile age | 0.014 | 0.016 | 60.871 | 0.914 | 0.364 | −0.011 | 0.048 |
| intercept | 0.441 | 0.020 | 1.982 | 22.392 | 0.002 | 0.398 | 0.485 |
full model: log-restricted likelihood = 42.462; N = 65;  p < 0.0001.
p < 0.0001. 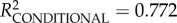
| |||||||
(d). Social inheritance and network stability
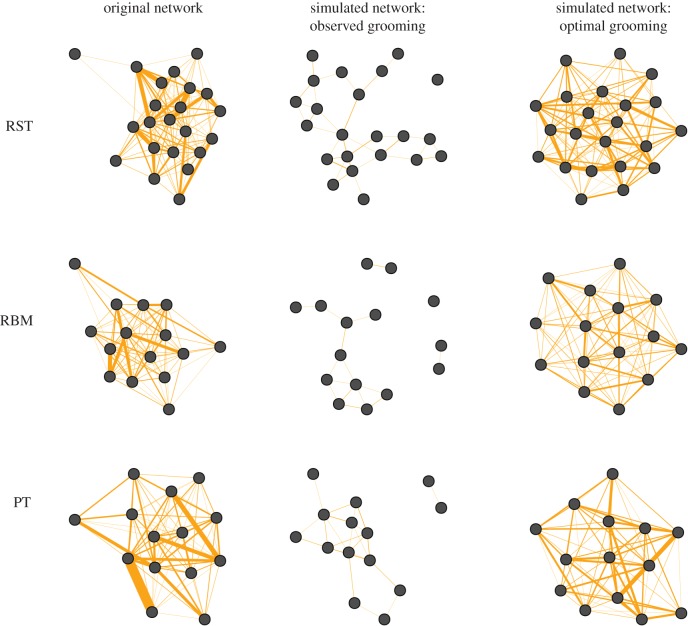
Here, we asked the question: if we assume that the juvenile patterns of grooming in time block 7 will be representative of their grooming throughout adulthood, will these grooming patterns replicate the observed total network structure? To answer this, we ran Ilany and Ackay's model by seeding it with the network structure at time block 7, and using our observed inherited pn versus ‘random’ pr ties to simulate change. As shown in the electronic supplementary material, figure S2, this process did not reproduce our observed networks. Specifically, network structures displayed lower degree, clustering and strength than seen in reality. This indicates that the stability of the current observed network would not be sustained over time as new members were added. This was despite our observed formation of grooming ties (pn, pr) being remarkably close to the optimal outcomes estimated for other social systems [7], i.e. with a greater probability of ties between juveniles and maternal contacts than between juveniles and non-maternal contacts.
Consequently, we then asked: what values would be needed to reproduce observed network structure? We, therefore, performed an optimization analysis to determine the mix of inherited pn versus ‘random’ pr ties needed for replication (‘simulated optimal’ in table 4, figure 3). As table 4 shows, these simulated values differed markedly from the distribution of grooming ties that were actually observed in each troop. Overall then, we found that replicating the network required a different mixture of ties from those we observed but, at the same time, our observed pattern of ties showed the same bias towards maternal contacts that was found to reproduce observed network structure for the four species in Ilany and Akçay's study.
Table 4.
Observed and optimal grooming allocation in the social induction model. (pn and pr represent the probability of grooming a mother's partner and non-partner, respectively. en and er represent the effort in grooming events directed towards mother's partner and non-partner.)
| group | behaviour | estimate | 95% CI: lower | 95% CI: upper | simulated optimal |
|---|---|---|---|---|---|
| grooming tie formation | |||||
| RST | pn | 0.39 | 0.27 | 0.53 | 0.58 |
| pr | 0.09 | 0.05 | 0.13 | 0.55 | |
| RBM | pn | 0.39 | 0.17 | 0.63 | 0.77 |
| pr | 0.05 | 0.00 | 0.12 | 0.89 | |
| PT | pn | 0.36 | 0.22 | 0.50 | 0.86 |
| pr | 0.08 | 0.02 | 0.15 | 0.73 | |
| grooming tie effort | |||||
| RST | en | 1.49 | 1.19 | 1.87 | 3.85 |
| er | 1.09 | 1.04 | 1.22 | 70.75 | |
| RBM | en | 1.29 | 1.07 | 1.64 | 3.51 |
| er | 1.25 | 1.25 | 1.75 | 68.51 | |
| PT | en | 1.42 | 1.11 | 1.84 | 5.36 |
| er | 1.60 | 1.20 | 2.40 | 120.76 |
Figure 3.
Visual comparison of the observed weighted networks of the three troops (time block 7) alongside the networks predicted after 500 removals and replacements, using either the grooming allocations derived from observations or those derived from optimizing grooming allocations to stabilize the network. (Online version in colour.)
4. Discussion
Our wild study groups confirmed findings from captive vervets [19] that juvenile females, as the philopatric sex, put more effort into grooming adults than do male juveniles, and that such effort increased across the juvenile period. The differences between males and females were clear but not particularly pronounced; in future work, it would be interesting to investigate whether there are differences with respect to the particular kinds of adults with which the two sexes interact. As far as network integration is concerned, however, the most pertinent finding is that female juvenile grooming effort was not reciprocated by adult group members, who neither groomed juveniles more frequently, nor increased their investment as juveniles approached adulthood (table 1a). In line with this, there was no overall similarity between mothers' and daughters’ grooming networks. Consequently, we have no evidence for convergence in the grooming networks of juveniles and adults, although in concert, they might still promote overall network stability.
In this regard, we did find that grooming by and of juvenile females tracked the self-similarity of maternal grooming allocations, and there was good evidence that mother–daughter out-similarity was predicted by maternal grooming network strength. We also found that total cosine similarity was predicted by both in- and out-cosine similarity to the same extent. Thus, mother–daughter grooming similarity was dependent on both the choice of partners by mothers and daughters and the likelihood of mothers/daughters being the recipient of grooming from particular others. Taken together, this suggests that mother–daughter association may influence the grooming choices of a mother's associates—especially those that are consistent over time—as well as daughters being influenced by their mothers. While this clearly confirms the operation of a process of social inheritance when mother's networks were consistent (see also [37]), the absence of an effect of juvenile age indicates that there was no cumulative consequence of repeated exposure to maternal associates. That is, we are not seeing a merging of mother–daughter affiliation patterns over time.
In line with this, our application of Ilany and Akçay's social inheritance model revealed that juveniles' observed values for maternal and non-maternal grooming associates could not reproduce the adult social network. Our simulations demonstrated that a network-replicating outcome was, in fact, possible, but that this would require a greatly increased probability of ties between juveniles and non-maternal contacts. Similarly, although the observed estimates of grooming effort (en, er) indicated that grooming frequency was broadly matched across maternal and non-maternal contacts, network-reproducing outcomes would require juveniles to place greater effort into non-maternal associations. In the case of PT, optimal behaviour predicted an increase in effort across both maternal and non-maternal partners. Qualitatively, therefore, it seems that non-maternal partners are likely to play an important role in replicating network structure in our study population. One obvious reason why this should be is that juvenile primates, especially in seasonal breeders like vervets, are highly likely to form relationships with the other members of their birth cohort, in addition to forming associations with adult group members. Such relationships may be maintained into adulthood, while retaining links to their mothers and any older siblings. At a functional level, forming relationships with age-mates is likely to be beneficial as the effort invested will (on average) yield higher returns: investing in age-mates in addition to adults increases the chances of sustaining a social network throughout their lives (i.e. adult social partners are likely to die before their juvenile associates). In addition to any other drivers, this suggests that there may be a steady turnover in network structure as younger cohorts reach maturity, with the result that clustering is likely to be structured by age-cohort as well as kinship. Thus, although juveniles may well inherit their mothers’ rank [19], they will not necessarily inherit her patterns of social engagement.
The networks generated from our actual data, in the absence of optimization, were sparser than those observed, with less robust structures. Given this, another possibility to consider is that, in our population, ongoing social dynamics may promote only short-term stability, and can be expected to shift over time in ways that, ultimately, are beneficial. This is more in keeping with what we know of temporal structure in primate networks [38,39], where adjustments in global network architecture reflect current socio-ecological demand [38] and may very well be adaptive [40]. If this is the case, then juveniles who track maternal grooming patterns that are only moderately consistent over time will necessarily be exposed to—and act in the context of—a changing social milieu, something that might be considered a helpful precondition for their future social flexibility, and ability to cope with varying circumstances. It will, therefore, be interesting to discover whether, as we continue to track our cohort members, those juveniles whose mothers displayed high social variability prove better able to cope socially with the ecological and demographic variation they encounter across adulthood. This, in turn, may help explain how and why variation in sociability across females arises, and how this gives rise to variation in the fitness-related benefits of sociality.
Supplementary Material
Acknowledgements
We thank Mark and Sarah Tompkins for the permission to work at Samara, and Kitty and Richard Viljoen for their continued logistic support. We are grateful to the many research assistants who contributed to the database. Dr Amiyaal Ilany, Professor Barbara Taborsky and two anonymous referees provided input that improved the manuscript.
Ethics
All procedures were approved by the University of Lethbridge Animal Welfare Committee (protocol no. 1505).
Data accessibility
Data and R code available through the Figshare Digital Repository (https://figshare.com/s/65b33994b3d62e6a594a).
Authors' contributions
L.B. and J.D.J. conceived the study and identified the research questions addressed here. J.D.J. and C.Y. collected the data. T.R.B., J.D.J. and S.P.H. undertook the analyses. J.D.J., T.R.B., L.B. and S.P.H. wrote the paper. J.D.J. and T.R.B. share first authorship. All authors gave final approval for publication.
Competing interests
We have no competing interests.
Funding
Funding for fieldwork was provided by NRF (South Africa) awards to S.P.H. and NSERC (Canada) grants to S.P.H. and L.B. L.B. is also supported by NSERC's Canada Research Chairs Program (Tier 1). T.B. is supported by a FQRNT Postdoctoral Fellowship and the Canada Research Chairs program (L.B.).
References
- 1.McDonald DB. 2007. Predicting fate from early connectivity in a social network. Proc. Natl Acad. Sci. USA 104, 10 910–10 914. ( 10.1073/pnas.0701159104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gómez JM, Perfectti F. 2012. Fitness consequences of centrality in mutualistic individual-based networks. Proc. R. Soc. B 279, 1754–1760. ( 10.1098/rspb.2011.2244) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.MacIntosh AJ, Jacobs A, Garcia C, Shimizu K, Mouri K, Huffman MA, Hernandez AD. 2012. Monkeys in the middle: parasite transmission through the social network of a wild primate. PLoS ONE 7, e51144 ( 10.1371/journal.pone.0051144) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Young C, McFarland R, Barrett L, Henzi SP. 2017. Formidable females and the power trajectories of socially integrated male vervet monkeys. Anim. Behav. 125, 61–67. ( 10.1016/j.anbehav.2017.01.006) [DOI] [Google Scholar]
- 5.Flack JC, Girvan M, de Waal FBM, Krakauer DC. 2006. Policing stabilizes construction of social niches in primates. Nature 439, 426–429. ( 10.1038/nature04326) [DOI] [PubMed] [Google Scholar]
- 6.Barrett L, Henzi SP, Lusseau D. 2012. Taking sociality seriously: the structure of multi-dimensional social networks as a source of information for individuals. Phil. Trans. R. Soc. B 367, 2108–2118. ( 10.1098/rstb.2012.0113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ilany A, Akçay E. 2016. Social inheritance can explain the structure of animal social networks. Nat. Comm. 7, 12084 ( 10.1038/ncomms12084) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Royle NJ, Pike TW, Heeb P, Richner H, Kolliker M. 2012. Offspring social network structure predicts fitness in families. Proc. R. Soc. B 279, 4914–4922. ( 10.1098/rspb.2012.1701) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Goldenberg SZ, Douglas-Hamilton I, Wittemyer G. 2016. Vertical transmission of social roles drives resilience to poaching in elephant networks. Curr. Biol. 26, 75–79. ( 10.1016/j.cub.2015.11.005) [DOI] [PubMed] [Google Scholar]
- 10.Schradin C. 2013. Intraspecific variation in social organization by genetic variation, developmental plasticity, social flexibility or entirely extrinsic factors. Phil. Trans. R. Soc. B 368, 20120346 ( 10.1098/rstb.2012.0346) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pereira ME, Fairbanks LA. 1993. Juvenile primates: life history, development and behavior. Chicago, Il: University of Chicago Press. [Google Scholar]
- 12.Leigh SR. 2004. Brain growth, life history, and cognition in primate and human evolution. Am. J. Primatol. 62, 139–164. ( 10.1002/ajp.20012) [DOI] [PubMed] [Google Scholar]
- 13.Joffe TH. 1997. Social pressures have selected for an extended juvenile period in primates. J. Hum. Evol. 32, 593–605. ( 10.1006/jhev.1997.0140) [DOI] [PubMed] [Google Scholar]
- 14.Johnson SE, Bock J. 2004. Trade-offs in skill acquisition and time allocation among juvenile chacma baboons. Hum. Nat. 15, 45–62. ( 10.1007/s12110-004-1003-y) [DOI] [PubMed] [Google Scholar]
- 15.Barrickman NL, Bastian ML, Isler K, van Schaik CP. 2008. Life history costs and benefits of encephalization: a comparative test using data from long-term studies of primates in the wild. J. Hum. Evol. 54, 568–590. ( 10.1016/j.jhevol.2007.08.012) [DOI] [PubMed] [Google Scholar]
- 16.Pasternak GM, Brown LR, Kienzle S, Fuller A, Barrett L, Henzi SP. 2013. Population ecology of vervet monkeys in a high latitude, semi-arid riparian woodland. Koedoe 55, 1078 ( 10.4102/koedoe.v55i1.1078) [DOI] [Google Scholar]
- 17.Henzi SP, Lucas JW. 1980. Observations on the inter-troop movement of adult vervet monkeys (Cercopithecus aethiops). Folia Primatol. 33, 220–235. ( 10.1159/000155936) [DOI] [PubMed] [Google Scholar]
- 18.Henzi SP, Forshaw N, Boner R, Barrett L, Lusseau D. 2013. Scalar social dynamics in female vervet monkey cohorts. Phil. Trans. R. Soc. B 368, 20120351 ( 10.1098/rstb.2012.0351) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fairbanks LA, McGuire MT. 1985. Relationships of vervet mothers with sons and daughters from one through three years of age. Anim. Behav. 33, 40–50. ( 10.1016/S0003-3472(85)80118-4) [DOI] [Google Scholar]
- 20.Altmann J. 1974. Observational sampling of behavior: sampling methods. Behaviour 49, 227–266. ( 10.1163/156853974X00534) [DOI] [PubMed] [Google Scholar]
- 21.Newman MEJ. 2010. Networks: an introduction. Oxford, UK: Oxford University Press. [Google Scholar]
- 22.Wild F. 2015. An open source LSA package for R. R package version 0.73 1. See https://cran.r-project.org/web/packages/lsa/index.html.
- 23.Core Team R. 2015. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- 24.McFarland R, Fuller A, Hetem RS, Mitchell D, Maloney SK, Henzi SP, Barrett L. 2015. Social integration confers thermal benefits in a gregarious primate. J. Anim. Ecol. 84, 871–878. ( 10.1111/1365-2656.12329) [DOI] [PubMed] [Google Scholar]
- 25.Josephs N, Bonnell T, Dostie M, Barrett L, Henzi SP. 2016. Working the crowd: sociable vervets benefit by reducing exposure to risk. Behav. Ecol. 27, 988–994. ( 10.1093/beheco/arw003) [DOI] [Google Scholar]
- 26.Csardi G, Nepusz T. 2006. The igraph software package for complex network research. InterJ. Complex Sys. 1695, 1–9. [Google Scholar]
- 27.Farine DR, Whitehead H. 2015. Constructing, conducting and interpreting animal social network analysis. J. Anim. Ecol. 84, 1144–1163. ( 10.1111/1365-2656.12418) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Barrat A, Barthelemy M, Pastor-Satorras R, Vespignani A. 2004. The architecture of complex weighted networks. Proc. Natl Acad. Sci. USA 101, 3747–3752. ( 10.1073/pnas.0400087101) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Clauset A, Newman MEJ, Moore C. 2004. Finding community structure in very large networks. Phys. Rev. E 70, 066111 ( 10.1103/PhysRevE.70.066111) [DOI] [PubMed] [Google Scholar]
- 30.Brandes U. 2001. A faster algorithm for betweenness centrality. J. Math. Sociol. 25, 163–177. ( 10.1080/0022250X.2001.9990249) [DOI] [Google Scholar]
- 31.Bonnell TR, Jarrett JD, Henzi SP, Barrett L.2017. SocialIntegrationNet: an R package for simulating induction in social networks. See github.com/tbonne/socialIntegrationNet .
- 32.Bates D, Mächler M, Bolker B, Walker S. 2014. Fitting linear mixed-effects models using lme4. arXiv preprint arXiv:1406.5823.
- 33.Skaug H, Fournier D, Nielsen A, Magnusson A, Bolker B.2013. Generalized linear mixed models using AD model builder. R package version 0.7 7. See http://glmmadmb.r-forge.r-project.org/ .
- 34.Barton K, Barton MK.2015. Package ‘MuMIn’. See ftp://155.232.191.229/cran/web/packages/MuMIn/ .
- 35.Nakagawa S, Schielzeth H. 2012. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods Ecol. Evol. 4, 133–142. ( 10.1111/j.2041-210x.2012.00261.x) [DOI] [Google Scholar]
- 36.Colquhoun D. 2014. An investigation of the false discovery rate and the misinterpretation of p-values. R. Soc. open sci. 1, 140216 ( 10.1098/rsos.140216) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.de Waal F. 1996. Macaque social culture: development and perpetuation of affiliative networks. J. Comp. Psychol. 110, 147–154. ( 10.1037/0735-7036.110.2.147) [DOI] [PubMed] [Google Scholar]
- 38.Henzi SP, Lusseau D, Weingrill T, Schaik CP, Barrett L. 2009. Cyclicity in the structure of female baboon social networks. Behav. Ecol. Sociobiol. 63, 1015–1021. ( 10.1007/s00265-009-0720-y) [DOI] [Google Scholar]
- 39.Rushmore J, Caillaud D, Matamba L, Stumpf RM, Borgatti SP, Altizer S. 2013. Social network analysis of wild chimpanzees provides insights for predicting infectious disease risk. J. Anim. Ecol. 82, 976–986. ( 10.1111/1365-2656.12088). [DOI] [PubMed] [Google Scholar]
- 40.Chapman CA, et al. 2016. Social behaviours and networks of vervet monkeys are influenced by gastrointestinal parasites. PLoS ONE 11, e0161113 ( 10.1371/journal.pone.0161113) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data and R code available through the Figshare Digital Repository (https://figshare.com/s/65b33994b3d62e6a594a).