Heritable spouse effects increase evolutionary potential of human reproductive timing

Abstract

Sexual reproduction is inherently interactive, especially in animal species such as humans that exhibit extended pair bonding. Yet we have little knowledge of the role of male characteristics and their evolutionary impact on reproductive behavioural phenotypes, to the extent that biologists typically consider component traits (e.g. reproductive timing) as female-specific. Based on extensive genealogical data detailing the life histories of 6435 human mothers born across four centuries of modern history, we use an animal modelling approach to estimate the indirect genetic effect of men on the reproductive phenotype of their partners. These analyses show that a woman's reproductive timing (age at first birth) is influenced by her partner's genotype. This indirect genetic effect is positively correlated with the direct genetic effect expressed in women, such that total heritable variance in this trait is doubled when heritable partner effects are considered. Our study thus suggests that much of the heritable variation in women's reproductive timing is mediated via partner effects, and that the evolutionary potential of this trait is far greater than previously appreciated.

1. Introduction

A trait's additive genetic variance is a direct determinant of its evolutionary response to selection [1] and is thus a key population parameter for evolutionary biologists to accurately quantify. Quantitative genetics provides a statistical framework for inferring additive genetic variances of complex (i.e. quantitative) traits in a population of phenotyped individuals of known relatedness [2–5]. Classical quantitative genetics models partition phenotypic variance into environmental and additive (i.e. heritable) genetic components from the perspective of the individual expressing the phenotype, such that any social interactions that impact phenotypic expression should be accommodated within the environmental variance. However, the behaviour of other individuals mediating these social interactions may itself be heritable, giving rise to indirect genetic effects (IGEs) [6–8]—also referred to as associate/associative genetic effects [7,9] or social genetic effects [10] in the literature.

Empirical research of IGEs has been largely limited to the quantification of maternal genetic effects [8,11]. Recently, however, studies of agricultural populations have demonstrated that IGEs can arise in a variety of scenarios involving interacting individuals [12,13]. Sexual reproduction is one such situation, particularly for animal species where social contact between mates extends beyond fertilization. For example, IGEs have been found for reproductive traits in avian species in which both parents continue to invest in their offspring after mating [14–16], although this is not a universal finding [17,18].

IGEs are particularly important for accurate evolutionary inference because covariances between direct and indirect genetic effects can dramatically alter the total additive genetic variance for a trait, and hence its evolutionary potential, either increasing (positive genetic covariance) or decreasing (negative genetic covariance) it [9,19]. With respect to heritable partner effects, a recent study of song sparrows (Melospiza melodia) reported a positive genetic covariance between female and male effects on laying date [16]. Conversely, Brommer & Rattiste [14] reported a negative genetic covariance between female and male effects on laying date in common gulls (Larus canus), meaning that genotypes associated with early laying in females are associated with a delaying effect when they occur in males. This negative genetic correlation in the female and male effects on reproductive timing limits the population response to individual-level selection [7] and reduces the total additive genetic variance below what would be quantified if the genetic covariance is ignored [19].

Unfortunately, generalizing the impact of heritable partner effects on reproductive timing is rendered impossible at present, because comparable studies are missing. This includes humans, for which the possibility of IGEs via partners appears to be unexplored. This paucity of knowledge regarding heritable partner effects in human populations is surprising, given (i) humans typically form durable pair bonds, with cohabiting pairs effectively creating a shared environment; and (ii) the availability of suitable datasets for quantifying such effects. Multi-generational genealogical databases contain the individual-level details necessary for quantitative genetics analyses of behavioural traits: in detailing the birth, marriage(s) and death of each individual, they allow reconstruction of both individual life histories and of the population pedigree (e.g. [20,21]). Such work has shown that reproductive timing in humans (which unlike, e.g. laying date in birds, is measured on a lifetime—rather than annual—scale) is heritable [20,22]. Indeed, a study of a recently established island population in Canada reported adaptive evolution of age at first birth over a 140-year period (an approximately five-generation time span) in response to negative selection on female age at first birth [20].

In the present study, we use an extensive genealogical dataset describing individual life histories for residents of two Swiss villages born across four centuries (1578–1977) to assess whether men have an indirect genetic effect on the reproductive timing of their partners. Using data indicating couples' socioeconomic status, we then assess the extent to which environmental confounding via culturally inherited status effects can account for observed partner effects. In so doing, our study expands the quantitative genetics approach to understanding the inheritance of human behaviours and explores the importance of the heritable social environment in determining expression of a reproductive behavioural trait intimately linked to individual fitness.

2. Methods

The data are taken from a genealogical archive [23] that details the parentage and major life events (birth, marriage(s), death) for residents of the eastern Swiss canton of Glarus, dating as far back as the sixteenth century. The analyses in the present study describe those individuals born or wedded in two village parishes: Linthal (46°55′ N 9°00′ E) and Elm (46°55′ N 9°10′ E). We expect these communities to be representative of central European society in general and the population is not expected to be unusually homogeneous (e.g. both Protestant and Roman Catholic parishioners are included (cf. [20])). Importantly, unmarried adults, individuals who died in early childhood and illegitimate children (i.e. those born out of wedlock) are recorded [23], giving realistic measures of individuals' reproductive performances.

Following the established approach to quantifying axes of reproductive behavioural variation in humans [24,25], reproductive timing was measured as the age at first birth (AFB), estimated as the time interval between the birth dates of the focal woman and her first child. Although measured in years, AFB estimates were not constrained to integer values. Of the 18 821 females in our overall dataset, 6435 were recorded as mothers. Although a small minority of mothers gave birth to their first child before the age of 18 (n = 72; 1.1%), they are—by definition—reproductively mature and for simplicity we thus refer to all individuals in our sample as women.

We adopted an animal modelling approach [2,26] to quantify the contributions of environmental and additive genetic effects to phenotypic variation in female AFB. The animal model is a particular form of linear mixed model, in which a population pedigree is used to define an inverse relatedness matrix, from which the additive genetic contribution to phenotypic variance (conditioned on any fixed effects: [27]) is inferred. Extra-pair paternities (EPPs) will generate errors in this social pedigree, but estimates of EPP rates for historical Western populations are so low (approx. 1%: [28,29]) that their quantitative impact is expected to be negligible [30]. In the absence of definitive information, all twins are assumed to be dizygotic (i.e. sharing a genetic relatedness of 50%, as per full siblings). Again, the quantitative impact of this will be minimal because the frequency of monozygotic twins is low (about 1 in 160 babies is a monozygotic twin: [31]).

To explore the quantitative genetics of female reproductive timing in our population, we ran a series of three animal models, all assuming a Gaussian error structure; although our focal trait exhibits positive skew (figure 1), initial animal models of log-transformed data gave quantitatively similar results but are less intuitively interpreted (results not shown). The first of these three models adopted a ‘classical’ animal model structure that ignored the potential for indirect genetic effects (IGEs) via the spouse. Birth year was included as a continuous variable to control for any long-term, secular trend in reproductive timing, with both linear and quadratic functions modelled. To control for additional spatio-temporal variation, we fitted parish-specific decadal birth cohort (parish cohort) as a random effect. A natal environmental effect was included to model the environmental effects common to sisters (this information was available for 4366 (68%) of the 6435 sampled women).

Figure 1.

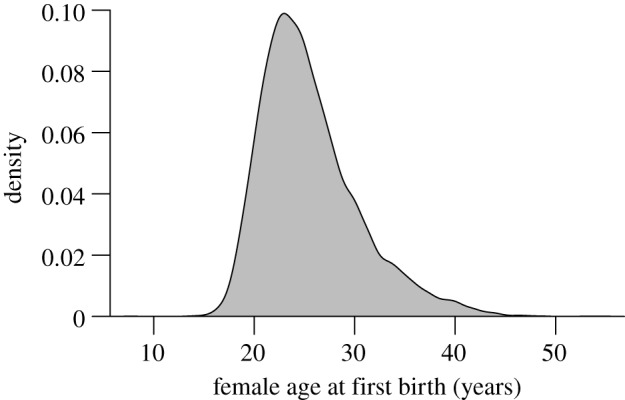
Density plot for female age at first birth for the 6435 phenotyped women (i.e. recorded mothers) in our dataset.

After this initial animal model, we constructed an ‘extended’ animal model in which the father of each woman's first child (hereafter: husband) was also included as a random effect linked to the pedigree, such that both direct and indirect additive genetic effects were estimated. This model also estimated the covariance between the direct (i.e. female) and indirect (i.e. male) additive genetic effects (i.e. σ_{A (direct, indirect)}), allowing us to estimate the total additive genetic variance in female reproductive timing, 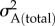, as [13,19]

where 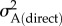and are the direct and indirect additive genetic variances, respectively. Total narrow-sense heritability was estimated as the magnitude of the total additive genetic variance relative to the (conditional [27]) phenotypic variance. To limit the potential for the shared environmental effects of siblings to bias additive genetic (co)variance estimates, we included the natal family identities of both the focal individual and her husband as random effects, and fitted the covariance between these (i.e. the natal environmental covariance).

We used the ASReml-R package (VSN International, Hemel Hempstead, UK) within the R framework (v.3.2.4: [32]) to conduct our analyses, which were based on restricted maximum-likelihood estimation (R scripts are archived online, along with the anonymized phenotypic and pedigree datasets: [33]). Fixed effects were tested using the z-statistic reported by ASReml-R. Random effects were tested by comparing the full model to a model in which the focal effect was excluded. The test statistic for each random effect was defined as twice the difference in log-likelihood between the two models. For the covariances, this was assumed to follow a χ² distribution with one degree of freedom. When testing individual variances, we assumed a mixture of χ² distributions with zero and one degree of freedom, respectively [34]. Owing to the simultaneous loss of the covariance term, when testing each of the natal environment and additive genetic variances, we extended this approach by assuming a mixture of χ² distributions with one and two degrees of freedom, and again used the mean p-value. The pruned pedigree (i.e. after removing non-informative individuals: [35]) contained 9530 individuals, with 5652 maternities, 5523 paternities and 5187 full sibships, with mean maternal and paternal sibship sizes of 2.00 and 2.12, respectively, a maximum pedigree depth of 14 generations, and 3829 founders.

As for direct genetic effects, biases in estimation of IGEs can arise through confounding of additive genetic and environmental effects. In studies of the quantitative genetics of human reproductive traits, a candidate source of such environmental confounding is socioeconomic status, as this often exhibits a pattern of vertical inheritance (transmitted intergenerationally by cultural means: [36]). To assess whether individual heterogeneity of husbands with respect to socio-economic status was responsible for upwardly biasing the IGE estimate, we incorporated a quantitative estimate of each couple's socio-economic merit, based on the husband's documented trade: for 3819 of the 6435 women included in our main sample (i.e. 59%), the archive details the occupation(s) of their partner (i.e. the husband siring their first child). Each occupation was classified following the HISCO system [37], and subsequently assigned a numerical score based on the HISCAM index [38]. The latter is a numerical stratification scale of historical occupations that was developed for application to Western populations (though specifically designed to span the period 1800–1938). If a husband was listed as having multiple occupations, he was assigned the highest scoring occupation. In our analysis, a husband lends his HISCAM score to his wife (i.e. spouses share a socio-economic status). We also included an interaction with the linear and quadratic birth year effects to model curvilinear temporality of this status effect on women's reproductive timing. Both birth year and HISCAM were mean-centred (mean birth year = 1855; mean HISCAM = 58.2). Individuals without a HISCAM score were excluded from this analysis. Owing to the smaller sample size, the informative pedigree was reduced in size (7819 individuals, with 4542 maternities, 4444 paternities and 3900 full sibships, with mean maternal and paternal sibship sizes of 1.93 and 2.03, respectively, a maximum pedigree depth of 14 generations, and 2610 founders).

3. Results

A ‘classical’ animal model of women's reproductive timing, which ignores the potential for partner effects, returns a heritability of 13 ± 3% [estimate ± s.e.] (table 1). Incorporating explicit consideration of indirect genetic effects via the husband indicates that both sexes contribute to the heritable variance in women's age at first birth (AFB), with direct and indirect heritability estimates of 10 ± 3% and 5 ± 2%, respectively (table 2). The genetic covariance between the female (direct) and male (indirect) genetic effects was large and positive, such that the total additive genetic variance in female reproductive timing was far greater than when estimated following a ‘classical’ quantitative genetic analysis in which the contribution of social partners is ignored. Indeed, when incorporating the positive covariance between the direct and indirect genetic effects, the total heritability for female reproductive timing was estimated to be 25 ± 5%, approximately double the estimate provided by the initial model. There were also moderate natal environmental effects that positively covaried, indicating that the childhood family environment had a consistent influence on males and females.

Table 1.

Results for a ‘classic’ animal model of female age at first birth (AFB) in Swiss women (n = 6435), in which the potential for indirect genetic effects via the spouse is ignored. Birth year is included as a fixed covariate to control for a secular change in phenotypic expression over the study period and is mean-centred. Parish cohort is defined as the parish-specific decade in which the individual was born. Wife's family represents the natal family of the focal individual. The effect estimates are the point estimates ± standard error. Fixed and random effects were tested via z scores or χ² scores, respectively.

	effect estimate	estimate relative to VP	z/χ2	p
fixed effects
birth year	−8.2 × 10−3 ± 1.8 × 10−3	—	−4.64	<0.001
(birth year)2	1.8 × 10−6 ± 1.3 × 10−5	—	0.14	0.886
random effects
wife's parish cohort	1.3 ± 0.3	0.052 ± 0.010	115	<0.001
wife's family	1.5 ± 0.5	0.063 ± 0.021	9.42	0.001
additive genetic (wife)	3.1 ± 0.7	0.130 ± 0.030	25.8	<0.001
residual	18.3 ± 0.8	0.755 ± 0.033	—	—

Table 2.

Results for an ‘extended’ animal model of female age at first birth (AFB) in Swiss women (n = 6435), in which genetic effects via the husband are estimated. This model differs from animal model 1 (table 1) only in introducing the genetic effect of the spouse (and the genetic covariance with the direct genetic effect). Birth year is mean-centred. Parish cohort is defined as the parish-specific decade in which the individual was born. Family terms represent the natal nuclear families of the focal individual or her husband. Total additive genetic variance is calculated following Bijma [19]. The effect estimates are the point estimates ± standard error. Fixed and random effects were tested via z scores or χ² scores, respectively.

	effect estimate	estimate relative to VP	z/χ2	p
fixed effects
birth year	−9.2 × 10−3 ± 1.8 × 10−3	—	−5.13	<0.001
(birth year)2	−4.3 × 10−6 ± 1.3 × 10−5	—	−0.33	0.740
random effects
wife's parish cohort	1.1 ± 0.2	0.045 ± 0.009	90.6	<0.001
wife's family	1.5 ± 0.5	0.064 ± 0.021	25.1	<0.001
husband's family	1.1 ± 0.4	0.045 ± 0.018	15.3	<0.001
additive genetic (wife)	2.4 ± 0.7	0.102 ± 0.029	51.9	<0.001
additive genetic (husband)	1.3 ± 0.4	0.052 ± 0.017	57.7	<0.001
residual	16.7 ± 0.8	0.693 ± 0.035	—	—
natal environmental covariance / correlation	1.2 ± 0.4 / 0.91 ± 0.39		13.6	<0.001
additive genetic covariance / correlation	1.2 ± 0.4 / 0.68 ± 0.30		31.6	<0.001
total additive genetic variance	6.1 ± 1.1	0.253 ± 0.046	59.7	<0.001

Our third model, incorporating explicit consideration of the influence of socio-economic heterogeneity within our sample population, reveals that socio-economic status predicts the age at first birth of a woman in a time-dependent manner (table 3). While the natal environmental correlation changed little in comparison to the previous model, the natal environmental variance terms for both women and their husbands were reduced in magnitude, suggesting that interfamilial heterogeneity with respect to socio-economic status may be a driver of the natal environmental effects reported in table 2. Nevertheless, inclusion of socio-economic status had a negligible impact on the variance attributable to indirect genetic (i.e. heritable husband) effects, suggesting that cultural inheritance of socio-economic status can be discounted as a driver of husbands' IGE on the reproductive timing of their partners.

Table 3.

Results for an ‘extended’ animal model of female age at first birth (AFB) in Swiss women (n = 3819), including socio-economic status of couples and its interaction with birth year as fixed covariates. The sample size for this model is lower than the preceding model (tables 1 and 2) due to incomplete records of husbands' occupation. Fixed effects are mean-centred. Parish cohort is defined as the parish-specific decade in which the individual was born. Family terms represent the natal nuclear families of the focal individual or her husband. Total additive genetic variance is calculated following Bijma [19], though note that the additive genetic covariance estimate was non-significant. The effect estimates are the point estimates ± standard error. Fixed and random effects were tested via z scores or χ² scores, respectively.

	effect estimate	estimate relative to VP	z/χ2	p
fixed effects
birth year	−3.0 × 10−3 ± 2.4 × 10−3	—	−1.21	0.226
HISCAM	3.8 × 10−3 ± 6.9 × 10−3		−1.21	0.580
(birth year)2	3.6 × 10−5 ± 2.0 × 10−5	—	1.84	0.065
HISCAM × birth year	4.9 × 10−5 ± 1.0 × 10−4	—	4.67	<0.001
HISCAM × (birth year)2	1.8 × 10−6 ± 8.1 × 10−7	—	2.24	0.025
random effects
wife's parish cohort	1.5 ± 0.3	0.066 ± 0.015	86.4	<0.001
wife's family	0.5 ± 0.7	0.024 ± 0.030	3.33	0.128
husband's family	0.6 ± 0.6	0.026 ± 0.026	3.95	0.093
additive genetic (wife)	4.5 ± 1.2	0.198 ± 0.051	19.4	<0.001
additive genetic (husband)	1.2 ± 0.6	0.053 ± 0.026	10.1	0.004
residual	14.3 ± 1.2	0.634 ± 0.058	—	—
natal environmental covariance / correlation	0.5 ± 0.6 / 0.87 ± 1.29		3.33	0.068
additive genetic covariance / correlation	1.2 ± 0.6 / 0.54 ± 0.35		3.67	0.055
total additive genetic variance	8.1 ± 1.7	0.360 ± 0.073	25.5	<0.001

4. Discussion

As previous quantitative genetics assessments have reported for human populations [20,22], we find women's reproductive timing exhibits moderate heritability in a historical Swiss population with records of individual life histories spanning much of modern history. However, by applying an ‘extended’ animal model that explicitly quantifies heritable partner effects, we show that a man's genotype has a considerable heritable influence on the reproductive timing of his partner. This indirect genetic effect is not explained by socio-economic heterogeneity, because controlling for a couple's socio-economic status has a negligible impact on the proportion of phenotypic variance in female reproductive timing that is attributable to heritable variance in partner effects. The positive covariance between the direct and indirect genetic effects means that total genetic variance in women's reproductive timing is far higher than is apparent when these heritable partner effects are ignored, which would facilitate rapid adaptive evolution in response to the negative selection that is widely reported to be acting on this trait [39].

As with direct genetic effects, indirect genetic effect estimates may be upwardly biased if environmentally derived similarity of relatives is not sufficiently considered. Our ‘extended’ animal models included a natal environmental effect for husbands that describes phenotypic resemblance of brothers that can be attributed to their shared childhood environment. Indeed, we find that this natal environmental effect for brothers is non-zero and covaries positively with the natal environmental effect for their sisters. In our third model, we went further in exploring potential environmental biasing of our estimate of the variance attributable to indirect genetic effects by incorporating an estimate of socio-economic status, because resources (e.g. pecuniary assets) could be culturally inherited via a patrilineal route that would partially mimic genetic inheritance. This third model indicated that a husband's socio-economic status does impact a woman's reproductive timing, although this effect is time sensitive and, indeed, reverses direction during the study period (which spans much of modern history), such that, in the latter part, women of higher socio-economic status enter motherhood later in life than their contemporaries. Clearly, in imposing a parabolic temporal dependence of the socio-economic status effect, our model is unlikely to describe the temporal dynamics of this process as realistically as alternative modelling approaches. Nonetheless, because there is no indication from our models that additive genetic (co)variance estimates are confounded with socio-economic status, further exploration of this sociological change is beyond the scope of the current paper and we conclude that the indirect genetic effect we report is unlikely to be driven by environmental confounding.

That women's reproductive timing features a large amount of ‘hidden’ genetic variation [14] may account for observations of significant adaptive response over a very few generations [20,40], when contemporary evolution of quantitative traits in response to selection has generally proved very difficult to demonstrate [41–43]. In particular, the positive additive genetic covariance between the female and male effects greatly increases the total additive genetic variance in women's reproductive timing, and thus the trait's total heritability. Unfortunately, a scarcity of similar studies—either on other human reproductive behavioural phenotypes, or on reproductive timing in other species with extended pair bonding—limits our ability to discern how common a phenomenon this may be. Similarly, an intraspecific comparison might reveal heterogeneity across human societies as to the importance of indirect genetic effects on sex-specific human reproductive behaviours. However, this requires the potential of genealogical records for informing quantitative genetics analyses of human behavioural phenotypes to be more widely realized. For example, such work offers anthropologists an opportunity to assess how variation in social structure impacts the evolutionary dynamics of traits closely related to biological fitness. Our study demonstrates that genealogical databases hold enormous potential, not only to enable perspectives of the evolutionary dynamics regulating human populations (i.e. human evolutionary demography) but also to offer insights into biological processes that are not amenable to study in other animal species [44,45].

From the perspective of the husband, the reproductive timing of his wife represents an extended phenotype [46]. Whether the indirect genetic effect is genetically correlated with a direct genetic effect on men's own reproductive timing is unknown but would be a worthwhile avenue for future research, because it would illuminate the evolutionary dynamics of human reproductive timing by adding details of the within- and between-sex genetic architecture [47].

Our results suggest that accurately forecasting evolutionary change in human reproductive timing will require explicit consideration of indirect sources of heritable variation. Griffing [9] illustrated how indirect genetic effects can drastically alter a population's response to individual-level selection, to the extent that positive selection can yield a negative evolutionary response if direct and indirect genetic effects are negatively correlated. Conversely, a positive genetic correlation between direct and indirect genetic effects, as we describe here for female reproductive timing in a modern human population, is expected to drive an accelerated response to selection. Thus, besides highlighting a social component to genetic variation in human reproductive behaviours that has hitherto been overlooked, our study suggests that female reproductive timing may respond particularly rapidly to the negative selection that has been described in multiple human populations [39].

Ethics

Access to the data has been approved by the relevant authorities and its use conforms to all legal regulations as well as institutional ethical guidelines.

Data accessibility

The anonymized data and code required to replicate our analyses are available from the Dryad Digital Repository (http://dx.doi.org/10.5061/dryad.72p93h1) [33].

Authors' contributions

S.R.E. conceived of the study, conducted the analyses and drafted the manuscript, and E.P. provided input at all stages. D.W. created the database that contains the transcribed archival data and, together with N.V., transcribed handwritten data. All the authors have read and approved the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This project was funded by the Swiss National Science Foundation (31003A_159462)