Meta-analytic principal component analysis in integrative omics application

Abstract

Motivation

With the prevalent usage of microarray and massively parallel sequencing, numerous high-throughput omics datasets have become available in the public domain. Integrating abundant information among omics datasets is critical to elucidate biological mechanisms. Due to the high-dimensional nature of the data, methods such as principal component analysis (PCA) have been widely applied, aiming at effective dimension reduction and exploratory visualization.

Results

In this article, we combine multiple omics datasets of identical or similar biological hypothesis and introduce two variations of meta-analytic framework of PCA, namely MetaPCA. Regularization is further incorporated to facilitate sparse feature selection in MetaPCA. We apply MetaPCA and sparse MetaPCA to simulations, three transcriptomic meta-analysis studies in yeast cell cycle, prostate cancer, mouse metabolism and a TCGA pan-cancer methylation study. The result shows improved accuracy, robustness and exploratory visualization of the proposed framework.

Availability and implementation

An R package MetaPCA is available online. (http://tsenglab.biostat.pitt.edu/software.htm).

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

High-throughput experimental techniques such as microarray and next-generation sequencing have been widely applied in biomedical research to monitor genome-wide DNA, RNA and epigenetic molecular activities and to detect disease-associated events or biomarkers (Bhattacharya and Mariani, 2009). As the experimental costs have dropped over the years, tremendous amounts of data have been generated and accumulated in public data depositories in the past two decades (e.g. Gene Expression Omnibus (GEO) and Sequence Read Archive (SRA) from NCBI, and ArrayExpress from EBI). Due to high experimental cost, and/or limitation of clinical tissue access, individual labs usually generate omics datasets with small to moderate sample sizes (e.g. n = 40–100). Statistical power and reproducibility of such small-n-large-p studies has long been a concern in the field. For example, prognostic tests in breast cancer that are generated based on genomic analyses have generally underperformed and only a few have proven reliable in clinical utility (Domany, 2014). An increasingly popular solution is to search the literature, seek similar datasets (of similar design and biological hypothesis) and perform data integration. In this context, the analytical questions and methods are analogous to traditional meta-analysis (Li and Tseng, 2011; Tseng et al., 2012). Since the microarray boom of the late 90 s, a convention has developed which displays genes on the rows and samples on the columns, which is in contrary to conventional practices in statistics. Under this data layout convention, multi-cohort data integration is often called ‘horizontal omics meta-analysis’ since datasets are laid out horizontally (Tseng et al., 2012). In contrast to horizontal meta-analysis, several large consortia (e.g. the Cancer Genome Atlas, TCGA) have generated multiple types of -omics data using samples in a single cohort. The datasets are aligned vertically and such data integration brings many new statistical challenges. These two types of omics data integration are illustrated in Supplementary Figure S1. Interested readers can refer to Richardson et al. (2016) for detailed reviews. In this article, we focus on horizontal meta-analysis, a relevant and practical issue for many individual labs which generate data of moderate sample size and need to combine with data from other labs. To date, methods for omics meta-analysis mostly focus on identifying differentially expressed (DE) genes or pathways. Methodologies for other types of statistical analysis, such as clustering (Huo et al., 2016), classification (Kim et al., 2016), dimension reduction, network analysis and pattern recognition are less addressed in the field. In this article, we propose a meta-analytic PCA framework (MetaPCA) for effective dimension reduction by combining multiple transcriptomic (or epigenetic) studies.

Dimension reduction for high-dimensional data plays a crucial role for down-stream pattern recognition, classification and clustering. Despite the development of many powerful dimension reduction techniques such as factor analysis, independent component analysis, projection pursuit, multidimensional scaling, nonnegative matrix factorization and partial least squares, principal component analysis (PCA) is probably the most classical and widely used dimension reduction method in daily data mining. It is an optimal linear projection technique in Euclidean space in the mean-squared error sense, and the resulting eigenvectors are weighted linear vectors of all features. Since it is well acknowledged that only a small subset of features are dominantly related to the genomic transcriptomic studies, including all features possibly undermines robustness and interpretability in the high-dimensional data. As a result, many variations of sparse PCA methods have been proposed in the literature (Hoyle and Rattray, 2004; Journée et al., 2010; Witten et al., 2009; Zou et al., 2006) for sparse selection of effective features. In particular, Zou et al. (2006) developed a sparse PCA approach using elastic net (eNet) penalty and Witten et al. (2009) proposed an alternative approach via penalized matrix decomposition (PMD); we will extend these two methods to formulate sparse MetaPCA in this article.

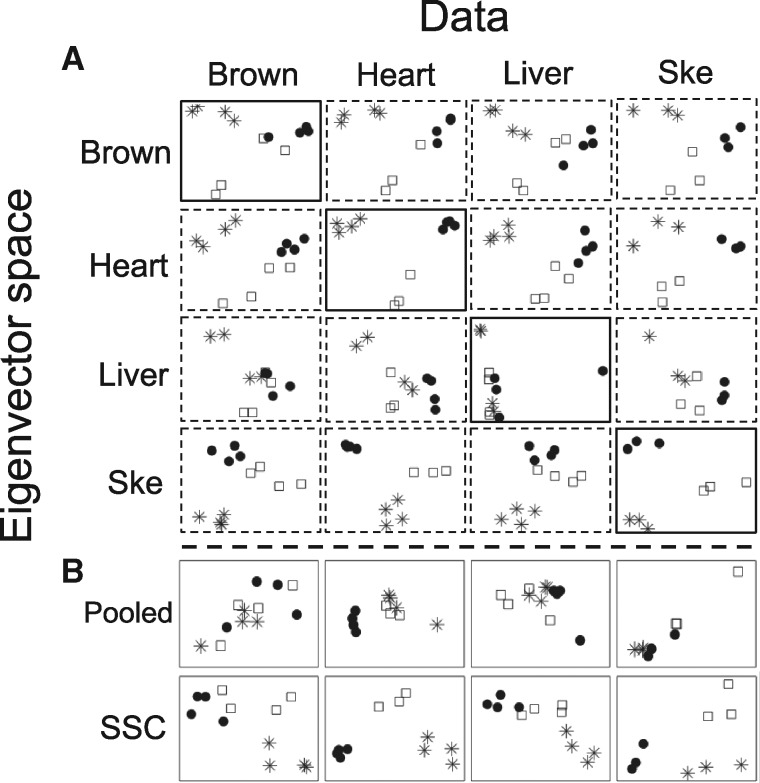
We use the following real example of mouse metabolism transcriptomic data (details shown later in Section 3.2.3) to demonstrate the motivation of MetaPCA. The deficiency of two enzymes ‘very long chain acyl-CoA dehydrogenase (VLCAD)’ and ‘long chain acyl-CoA dehydrogenas (LCAD)’ are known to cause metabolic diseases in children. Wild-type (WT), LCAD-deficient and VLCAD-deficient mice samples were sacrificed and four different types of tissues [brown fat (Brown), heart (Heart), liver (Liver) and skeleton (Ske)] were harvested for microarray transcriptomic experiments (see Supplementary Table S1). Figure 1A shows projections of each dataset (on the columns) to two-dimensional eigen-space that were obtained from each dataset (on the rows). When a study was projected onto its own eigen-space (diagonal plots in solid rectangles of Fig. 1A), heart and skeleton tissues appeared to have clear separation between the three genotyping groups (circle for WT, star for VLCAD and square for LCAD), while liver tissue had the worst separation. Particularly noted is that each study generated different eigen-spaces that are difficult for further biological investigation. It naturally raises three meta-analysis questions: (i) Can we develop a MetaPCA algorithm to combine information from all four transcriptomic studies and generate a meaningful common eigen-space? (i.e. directly merging studies is not appropriate due to a potential study design discrepancy and batch effect issue). (ii) To improve model interpretation, can regularization help variable selection in the MetaPCA dimension reduction? (iii) Does the common eigen-space from MetaPCA provide more effective dimension reduction (e.g. in terms of accuracy and robustness of classification and pattern recognition)? For example, Figure 1B shows a MetaPCA result [under the sum of squared cosines (SSC) criterion to be introduced later] that projects all four studies onto a common eigen-space. Samples of three genotypes are generally separated with more distinguishable patterns in all four tissues. (See Mouse Metabolism Data for more details later).

Fig. 1.

Dimension reduction via (A) individual study PCA and (B) MetaPCA (SSC), over the four mouse metabolism transcriptomic studies. The x-axis and y-axis refer to the first and second principal component projection. Solid circle, star and square symbols indicate wild-type (WT), very longchain acyl-coenzyme A dehydrogenase (VLCAD), and longchain acyl-coenzyme A dehydrogenase (LCAD) mutations, respectively. Brown represents brown fat tissue and Ske represents skeleton tissue

In the following, we will develop two MetaPCA frameworks by decomposing sum of variance (SV) or maximizing sum of squared cosines (SSC). The eNet and PMD regularization methods are applied to facilitate sparse MetaPCA. We will perform simulations to compare accuracy and robustness of MetaPCA with those of single study PCA and an existing method JIVE (Lock et al., 2013). We will show applications of MetaPCA to three transcriptomic examples from yeast cell cycle, prostate cancer, mouse metabolism and methylation data from TCGA pan-cancer studies. Finally, conclusion and discussion will be presented.

2 Materials and methods

2.1 MetaPCA via sum of variance decomposition

Let $X^{\left(m\right)}$ be an observed $p\times n^{\left(m\right)}$ data matrix of sample size $n^{\left(m\right)}$ and p features for study m ($1\le m\le M$). Denote by $S^{\left(m\right)}$ the maximum likelihood (ML) estimate of the p × p covariance matrix ${\Omega }^{\left(m\right)}$ of $X^{\left(m\right)}$. To test whether ${\Omega }^{\left(m\right)}$ ($1\le m\le M$) share a common eigenvector space, Flury (1984) considered a null hypothesis, H₀: $L^T{\Omega }^{\left(m\right)}L={\Lambda }^{\left(m\right)}$ ($1\le m\le M$), where L is the p × p common eigenvector matrix, and ${\Lambda }^{\left(m\right)}$ is the (study specific) diagonal eigenvalue matrix of study m. Flury and Gautschi (1986) developed an algorithm (known as FG algorithm) to compute the maximum likelihood estimate of the common eigenvectors to circumvent high computational cost of the ML estimate and to perform likelihood ratio test. To further alleviate the computation, Krzanowski (1984) proposed a simple alternative to estimate L by $L^T\left({\sum }_{m=1}^M{S}^{\left(m\right)}\right)L=\Lambda$, where L and Λ are the eigenvector and eigenvalue matrix of $T={\sum }_{m=1}^M{S}^{\left(m\right)}$. In the application of omics data, expression values of different studies are often generated from different experimental platforms and are of different measurement scale. As a result, the scales of $S^{\left(m\right)}$ are incomparable and we propose a weighted sum of covariance matrices: $T^{SV}={\sum }_{m=1}^M{w}^{\left(m\right)}{S}^{\left(m\right)}$, where $w^{\left(m\right)}$ is the reciprocal of the largest eigenvalue of $S^{\left(m\right)}$. The common principal components L are calculated from the eigen-decomposition of $T^{SV}:L^T\left(T^{SV}\right)L=\Lambda$ and K top common PCs should be retained for down-stream analysis. Selection of the optimal K will be described later in Section 2.4.

2.2 MetaPCA via sum of squared cosine maximization

Suppose we take the top $j^{\left(m\right)}$ eigenvectors of study m ($1\le m\le M$) and denote by $V^{\left(m\right)}$ = $(v_1^{\left(m\right)},\dots ,v_{j^{\left(m\right)}}^{\left(m\right)})\in {ℝ}^{p\times j^{\left(m\right)}}$ the resulting eigenvector matrix. Let $\mathbf{b}\in {ℝ}^p$ be an arbitrary unit vector in the p-dimensional space and ${\delta }^{\left(m\right)}$ be the angle between b and the vector most nearly parallel to it in the eigen-space spanned by $V^{\left(m\right)}$. MetaPCA via sum of squared cosine (SSC) seeks the optimal vector b such that the sum of angles ($\sum _m{\delta }^{\left(m\right)}$) is minimized. The following theorem formally states the objective and the algorithm.

Theorem 1.

Let $\mathbf{b}\in {ℝ}^p$ be an arbitrary unit vector in the p-dimensional space and ${\delta }^{\left(m\right)}$ be the angle between b and the vector most nearly parallel to it in the eigen-space spanned by $V^{\left(m\right)}$. The optimal vector b maximizing $\text{SSC}={\sum }_{m=1}^{M}co{s}^2{\delta }^{\left(m\right)}$ is given by the eigenvector ${\mathbf{b}}_1$ corresponding to the largest eigenvalue λ₁ of $T^{\text{SSC}}={\sum }_{m=1}^M{V}^{\left(m\right)}{V}^{\left(m\right)T}$ (Krzanowski, 1979).

The proof for this theorem is given in Supplementary notes. Geometrical illustration of maximizing the sum of squared cosines (SSC) for a common principal component space is given in Figure 2. In Figure 2A, we show a simple example with p = 3 dimensions and M = 2 studies combined. In each study, the first eigenvector (g₁ and g₂) was chosen to form one-dimensional eigen-space ($j^{\left(1\right)}=j^{\left(2\right)}=1$). For an arbitrary vector b (represented by the solid black vector), the dashed grey lines are obtained by parallel shifting b such that it intersects with g₁ and g₂. The angels between b and g₁ and between b and g₂ are δ₁ and δ₂. It can be easily shown that the optimal b in SSC sense is chosen as $(g_1+g_2)/\left|\right|g_1+g_2\left|\right|$. Figure 2B demonstrates a more complicated example with p = 3, M = 3 and $j^{\left(1\right)}=j^{\left(2\right)}=j^{\left(3\right)}=2$. The three 2D planes represent the eigen-spaces from M = 3 studies. For a arbitrary vector b, ${\delta }^{\left(1\right)},\hspace{0.17em}{\delta }^{\left(2\right)}$, and ${\delta }^{\left(3\right)}$ represent the angles of b to each eigen-space. Theorem 1 provides an algorithm to identify the optimal b that best conforms with the three eigen-spaces in the SSC sense. In an extreme and ideal situation that the eigen-spaces have overlap, b will be chosen from the overlap and optimal $\text{SSC}=M\hspace{0.17em}(=3)$. To achieve an effective dimension reduction in the meta-analytic framework, we expect to find an effective b such that the angles (${\delta }^{\left(1\right)},\dots ,{\delta }^{\left(M\right)}$) are small and SSC is large in real applications.

Fig. 2.

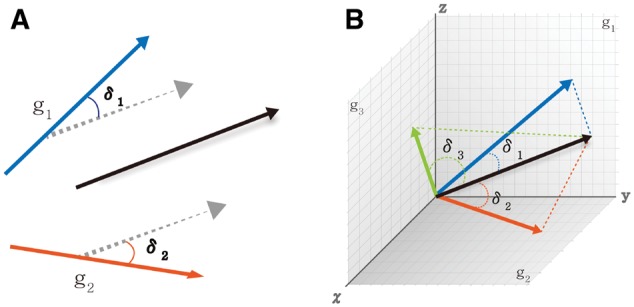
Geometrical illustrations for finding common principal component space using SSC criterion

Theorem 2 in Supplementary notes, extends Theorem 1 to detect subsequent eigen-vectors orthogonal to the previously identified optimal vector. For example, the eigenvector ${\mathbf{b}}_2$ corresponding to the second largest eigenvalue of $T^{\text{SSC}}$ will give the direction orthogonal to ${\mathbf{b}}_1$ and ${\sum }_{m=1}^M\hspace{0.17em}{\text{cos}}^2{\delta }^{\left(m\right)}$ is maximized. As a result, taking the top K eigenvectors of $T^{\text{SSC}}$ gives the K-dimensional common eigen-space of the M studies.

In summary, the second MetaPCA framework motivated by SSC criterion proceeds as below. The top $j^{\left(m\right)}$ eigenvectors are calculated from study m to form eigenvector matrix $V^{\left(m\right)}$. We then perform eigen-decomposition on $T^{\text{SSC}}={\sum }_{m=1}^M{V}^{\left(m\right)}{V}^{{\left(m\right)}^T}$ and select the top K eigenvectors to form the meta-analytic common eigen-space: $\left({\sum }_{m=1}^M{V}^{\left(m\right)}{V}^{{\left(m\right)}^T}\right)B^{SSC}={\Lambda }^{*}{B}^{SSC}$, where $V^{\left(m\right)}$ is a matrix consisting of $j^{\left(m\right)}$ leading eigenvectors, ${\Lambda }^{*}$ is a diagonal eigenvalue matrix and $B^{\text{SSC}}=({\beta }_1^{\text{SSC}},\dots ,{\beta }_K^{\text{SSC}})$ contains the top K eigenvectors. To select $j^{\left(m\right)}$ for study m ($1\le m\le M$), we suggest (from our experience) the choice of minimal $j^{\left(m\right)}$ such that PC projection explains >80% of total variance for study m. Strategy to determine the optimal K will be discussed in Section 2.4.

2.3 Variable selection of MetaPCAs (sparse MetaPCA)

Classical PCA produces loadings on all features. In many high-dimensional applications, a vast amount of noise features are present in the data. Failure to enforce sparsity (i.e. enforce zero estimates to noise features) by feature selection can undermine effective dimension reduction and hamper model interpretability. In this subsection, we introduce regularized MetaPCA frameworks (called sparse MetaPCA) for variable selection, for which we consider two popular sparse PCA methods: (i) regression-type sparse PCA together with the elastic net penalty (eNet) (Zou et al., 2006). (ii) sparse PCA based on penalized matrix decomposition (PMD) (Witten et al., 2009). Supplementary Table S4 shows four sparse MetaPCA methods by considering two MetaPCA objective formulation (SV and SSC) and two regularization methods (eNet and PMD). We will compare the four methods by simulation to recommend the best choice for practice.

2.4 Parameter selection

To determine the optimal dimension K, scree plot (Cattell, 1966) and an additional benchmark are used. In scree plot, eigenvalues are sorted in decreasing order on the y-axis. Selection of the optimal K is determined by an elbow point, at which the decreasing trend is declared as flat when $d(i,i+1)<\Delta$, where $d(i,i+1)=\frac{e\left(i\right)-e(i+1)}{e\left(i\right)},\hspace{0.17em}\Delta =0.1$ and e(i) refers to the eigenvalue of the ith leading principal component. In high-dimensional data, a majority of eigenvalues are small and similar in the tail (Sill et al., 2015). This criterion is usually effective to find the top K eigenvectors that are distinguishable from the noisy eigenvalues in the tail. Supplementary Figure S2 shows an example of scree plot. We will select K = 5 in the simulation scenario (See the caption of Supplementary Fig. S2).

The penalization constant λ or λ_j is a parameter that controls the number of effective features in the dimension reduction. To select the parameter, we propose a two-stage sequential searching strategy. We first determine the optimal K from (non-sparse) MetaPCA via scree plot, and given fixed K, we select the best λ via the scree plot based on G(a, b), a proportion of increased explained variance as a benchmark, where $G(a,b)=\frac{f\left(b\right)-f\left(a\right)}{f\left(b\right)}$ and f(z) is explained variance of PC when the z number of non-zero features of eigenvector matrix are applied. Here, note that the number of non-zero features corresponds to size of λ. Two arbitrary λ values are taken to produce a and b non-zero features of eigenvector matrix such that $G(a,b)<\Delta$, where $\Delta =0.1,\hspace{0.17em}0\le a,b\le P^{*}$, a < b and P* the number of entire non-zero features. We randomly generated datasets using the same scenario in Section 3.1.1. Supplementary Figure S3A–D shows that the stopping rule automatically chooses 20 nonzero features of true eigenvector matrix, suggesting that the selected penalization constant λ correctly leaves the true 20 non-zero features (See Supplementary Fig. S3).

2.5 An existing method (JIVE) for comparison

In an effort for vertical integration of multiple omics datasets (e.g. mRNA, miRNA expression, methylation and etc. See Panel B of Supplementary Fig. S1), Lock et al. (2013) proposed a Joint and Individual Variation Explained (JIVE) method by applying a generalized variation decomposition. JIVE decomposes the combined multi-omics dataset into a sum of three terms: (i) a low-rank approximation that accounts for common variation across multiple data, (ii) low rank approximations for structured variation unique to each data type and (iii) residual noise. Essentially, JIVE pursues simultaneous decomposition for common variation structure across all omics datasets as well as individual variation structure specific to a single omics dataset. In theory, JIVE can be seen as an extension of Principal Component Analysis (PCA) and was found to be superior to popular two-block methods such as Canonical Correlation Analysis and Partial Least Squares. Although JIVE was initially developed for vertical integration of multi-level omics datasets, the formulation can be directly applied to horizontal integration by simple matrix transposing. We will compare MetaPCA methods with JIVE by simulations and real applications.

2.6 Evaluation criteria

We first define a quantity ω to assess the similarity between two eigen-spaces. Consider two eigen-spaces spanned by eigenvector matrixes $V^{\left(1\right)}$ and $V^{\left(2\right)}$, where $V^{\left(1\right)}=(v_1^{\left(1\right)},\dots ,v_{j_1}^{\left(1\right)})\in {ℝ}^{p\times j_1}$ and $V^{\left(2\right)}=(v_1^{\left(2\right)},\dots ,v_{j_2}^{\left(2\right)})\in {ℝ}^{p\times j_2}$. The evaluation measure ω is given by: $\omega (V^{\left(1\right)},V^{\left(2\right)})={\sum }_{i=1}^{j_1}{\lambda }_i=\text{tr}(V^{{\left(1\right)}^T}{V}^{\left(2\right)}{V}^{{\left(2\right)}^T}{V}^{\left(1\right)})$, where λ_i is the ith largest eigenvalue of $V^{{\left(1\right)}^T}{V}^{\left(2\right)}{V}^{{\left(2\right)}^T}{V}^{\left(1\right)}$. Krzanowski (1979) proved that ${\sum }_{i=1}^{j_1}{\lambda }_i$ is equivalent to the angles between the two eigen-spaces spanned by $V^{\left(1\right)}$ and $V^{\left(2\right)}$, and hence $\omega (V^{\left(1\right)},V^{\left(2\right)})$ gauges the geometrical similarity between two matrices $V^{\left(1\right)}$ and $V^{\left(2\right)}$. We will use ω to benchmark whether MetaPCA effectively estimates the underlying true eigen-space in simulation. In addition, in order to quantify class separation, the classical Fisher discriminant scores [defined as the ratio of between class scatterness and within class scatterness, abbreviated as FDS (Friedman et al., 2001)] are used for evaluating the four real examples. A dimension reduction with large between class separation and small within class scatterness produces a large FDS and is considered biologically more meaningful.

3 Results

3.1 Simulation study

3.1.1 Accuracy of MetaPCA

In this section, we evaluate the two proposed MetaPCA frameworks (SV and SSC) compared with the standard single study PCA and JIVE. Details of the MetaPCA methods are left to Method Section. Below we outline our simulation setting:

Step 1 (True eigen-space): We considered a two-dimensional underlying true eigen-space spanned by $E=(e_1^T,e_2^T)$ and $\lambda =({\lambda }_1,{\lambda }_2)$ be the corresponding true eigenvalues, where $e_1=(\underset{10}{\underbrace{1,1,\dots ,1}},0,\dots ,0)/\sqrt{10}\in {\mathrm{R}}^{1\times p}$ and $e_2=(\underset{10}{\underbrace{0,0,\dots ,0}},\underset{10}{\underbrace{1,1,\dots ,1}}0,\dots ,0)/\sqrt{10}\in {ℝ}^{1\times p}$, p = 200, ${\lambda }_1=1000$ and ${\lambda }_2=800$.

Step 2 (Simulate datasets): By multiplying the true eigenvectors and eigenvalues, we created the underlying true common covariance matrix Σ, where $\Sigma =e_1^T{\lambda }_1{e}_1+e_2^T{\lambda }_2{e}_2+{\Theta }_{\rho },\hspace{0.17em}{\Theta }_{\rho }=\left\{{\theta }_{ij}\right\}$ and ${\theta }_{ij}=\rho \hspace{0.17em}(=1)$ if $1\le i,j\le 50$ or $51\le i,j\le 100$, otherwise ${\theta }_{ij}=0$. This configuration serves to impose gene correlation structures to Σ. We simulated covariance matrix ${\Sigma }^{\left(m\right)}$ for the mth study ($1\le m\le M$), where ${\Sigma }^{\left(m\right)}=\Sigma +E^{*\left(m\right)},E^{*\left(m\right)}=E^{{\left(m\right)}^T}·E^{\left(m\right)},E^{\left(m\right)}=({\mathrm{ϵ}}_1^{\left(m\right)},\dots ,{\mathrm{ϵ}}_{200}^{\left(m\right)}),{\mathrm{ϵ}}_i^{\left(m\right)}\sim MV{N}_p(0,W)$, $W=I·\left(\frac{1}{C}\right)$, $C\in \{1,2,10\}$ and C functions as the noise level and $I_{p\times p}$ is an identity matrix. We generated M simulated datasets of 20 samples and 200 features, $X^{\left(m\right)}=(x_1^{\left(m\right)},\dots ,x_{200}^{\left(m\right)})\sim MV{N}_{200}(0,{\Sigma }^{\left(m\right)})$ for $1\le m\le M$ and $1\le M\le 10$.

From single study PCA, we obtained the first two eigen-vectors $V^{\left(m\right)}=(v_1^{\left(m\right)},v_2^{\left(m\right)})$ from the mth simulated data $X^{\left(m\right)}$ ($1\le m\le M$). By applying MetaPCA frameworks to combine the M studies $(\mathrm{i}.\mathrm{e}.,\hspace{0.17em}{X}^{\left(1\right)},X^{\left(2\right)},\dots ,X^{\left(M\right)})$, we obtained the common eigenvector matrixes $B^{SV}=({\beta }_1^{SV},{\beta }_2^{SV})\in {ℝ}^{200\times 2}$ and $B^{SSC}=({\beta }_1^{SSC},{\beta }_2^{SSC})\in {ℝ}^{200\times 2}$ for SV and SSC criterion, respectively. Similarly, we applied JIVE to generate B^JIVE. To benchmark the performance, we calculated the angles between the derived eigenvector matrixes $V^{\left(1\right)},\dots ,V^{\left(M\right)},B^{SV},B^{SSC}$ and B^JIVE and the underlying true eigen-space E by $\omega (E,V^{\left(1\right)}),\hspace{0.17em}\cdots ,\hspace{0.17em}\omega (E,V^{\left(M\right)}),\hspace{0.17em}\omega (E,B^{SV}),\omega (E,B^{SSC})$ and $\omega (E,V^{JIVE})$, where ω is an evaluation measure (See Section 2 for details). By definition ω ranges from 0 to 2 in this application and ω = 2 represents perfect accuracy of eigen-space detection. The simulations were repeated for 50 times and averaged ω value was presented.

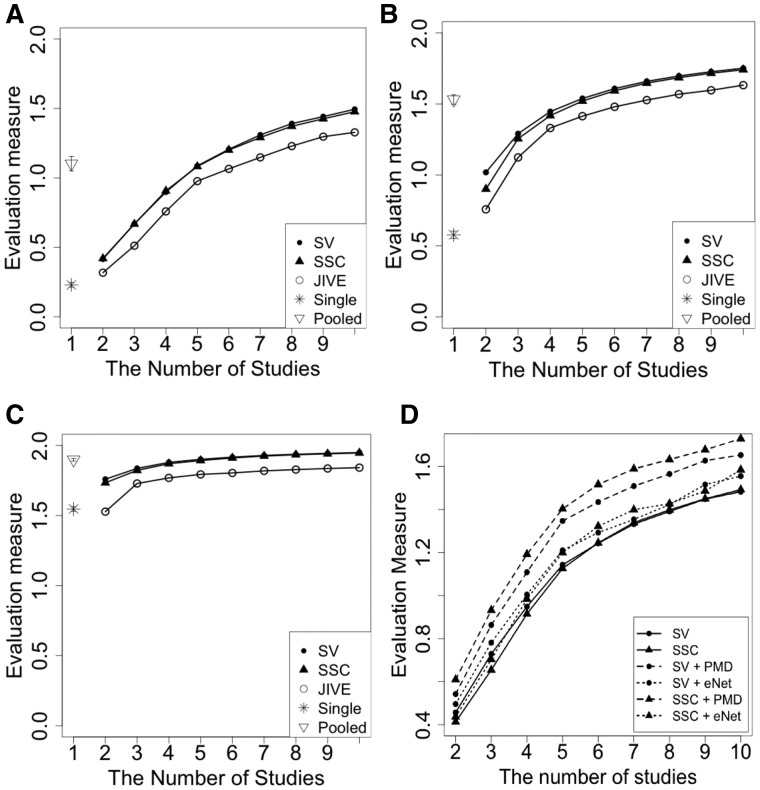
Figure 3A–C show the results comparing single study PCA, MetaPCA (SV), MetaPCA (SSC), JIVE and pooled analysis (with quantile normalization) for $C=0.1,0.5$ and 1. The result clearly demonstrates better performance (larger ω) for SSC and SV. This better performance is also shown in other simulations where we vary dependence structure, sample sizes and strength of dependent structure (See Supplementary Section 2 for additional simulation details and results in Supplementary Table S7).

Fig. 3.

Performance comparisons (MetaPCAs, PCA and JIVE) of the effects on the number of studies for estimating true eigenvector. ‘SV’, ‘SSC’ refer to MetaPCA (SV) and MetaPCA (SSC). ‘Single’ and ‘Pooled’ represents standard PCA of each individual study and standard PCA of pooled studies (combining all datasets by features), respectively (A: C = 0.1, B: C = 0.5, C and D: C = 1, where C is the noise level)

JIVE improves over single study PCA but is much worse than the two MetaPCA frameworks. When more studies are combined, the accuracy of eigen-space estimation is improved. For more noisy simulated data (larger C), the performance decreases as expected. SV appears to perform slightly better than SSC in this simulation but the difference is not noticeable.

Figure 3D compares the four sparse MetaPCA methods (SV + PMD, SV + eNet, SSC + PMD and SSC + eNet) and two MetaPCA methods (SV and SSC). We notice that all four sparse MetaPCA methods outperform the two MetaPCA approaches in estimating the common eigen-space. This shows the benefit of sparse feature selection to exclude many noisy features in dimension reduction. In addition, we also find that SSC + PMD consistently performs the best among the four sparse MetaPCA methods. We therefore recommend SSC + PMD for sparse MetaPCA in all subsequent applications.

3.1.2 Robustness of MetaPCA

In this subsection, we perform sensitivity analysis to evaluate the effect of noise features and outlier samples on dimension reduction performance. To mimic real data, we adopted the simulation scenario introduced by Qiu and Joe (2006) that generates simulated datasets with an adjustment of cluster separation levels, noise features and outlier samples.

We generated 100 samples which fell into three clusters separated by 100 signal features. In addition, noise features (20, 60 and 100) and outlier samples (5%, 10% and 20%) were also added. We then randomly split the dataset into four subsets, each containing equal size samples (i.e. 25 non-outlier samples from each cluster). Finally we added equal size outlier samples to each subset. Denote by $X^{\left(m\right)}$ ($1\le m\le 4$) four datasets. To generate data, we utilized ‘clusterGeneration’ package by Qiu and Joe (2006) in R (http://www.r-project.org/).

We applied two MetaPCA (SV, SSC), JIVE as well as single study PCA to perform dimension reduction (K = 2) in these four subsets. To benchmark each method, we exploited the Fisher discriminant scores (FDS; For details, see Method Section) on the dimension reduced data, which measures the ratio of between group variation and within group variation. The simulations were repeated 100 times and average values were presented.

Supplementary Figure S6 shows the resulting FDS values for different level of outliers, noise features and degree of cluster separation. When 20 noise features were added (first row panel), SV and SSC always performed better than JIVE and single study PCA. As outliers increased from 5% to 20%, performance of JIVE and single study PCA greatly decreased, while SV and SSC still performed similarly well. As the number of noise features increased to 100 (the third row panel), the performance of SV fell to a similar level with that of JIVE. For small degree of separation, SV performed nearly as bad as single study PCA. SSC became the only best performer that is robust to noise features. Putting these together, we recommend to apply SSC criterion for MetaPCA.

3.2 Applications to four real omics datasets

In this section, we applied MetaPCA (SSC) and sparse MetaPCA (SSC + PMD) to four high-throughput experimental applications. We obtained mRNA expression and methylation expression data of various diseases from GEO (http://www.ncbi.nlm.nih.gov/geo/) and TCGA Portal (https://tcga-data.nci.nih.gov/tcga/). We examined whether the proposed MetaPCA (SSC) and sparse MetaPCA (SSC + PMD) provided better cell cycle patterns or disease subtype separation in the joint dimension reduction.

3.2.1 Spellman’s cell cycle data

The famous Spellman’s yeast cell cycle data (Spellman et al., 1998) includes time-dependent gene expression profiles to monitor transcriptomic variation during yeast cell cycles. Yeast cells were arrested to the same cell cycle stage using four different synchronizing methods: α arrest (alpha), arrest of cdc15 or cdc28 temperature-sensitive mutant and elutriation (elu). A total of 18, 24, 17 and 14 time points were measured for each synchronization. Since the diverse synchronization methods can potentially lead to heterogeneity, we divided the samples into integrative analysis of four studies (alpha, cdc15, cdc28 and elu). Due to the regulatory nature of cell cycle, the expression profiles are expected to present cyclic patterns (Spellman et al., 1998). We matched gene symbols across all four studies and filtered out features using standard deviation (i.e. SD $\le$ 0.45, non-informative features with smaller variation) that left 1, 025 features. We imputed missing values via R package ‘impute’ (www.bioconductor.org/). We applied MetaPCA (SSC) and sparse MetaPCA (SSC + PMD) to assess whether features effectively revealed cyclic patterns of gene expression profiles compared with JIVE and single study PCA.

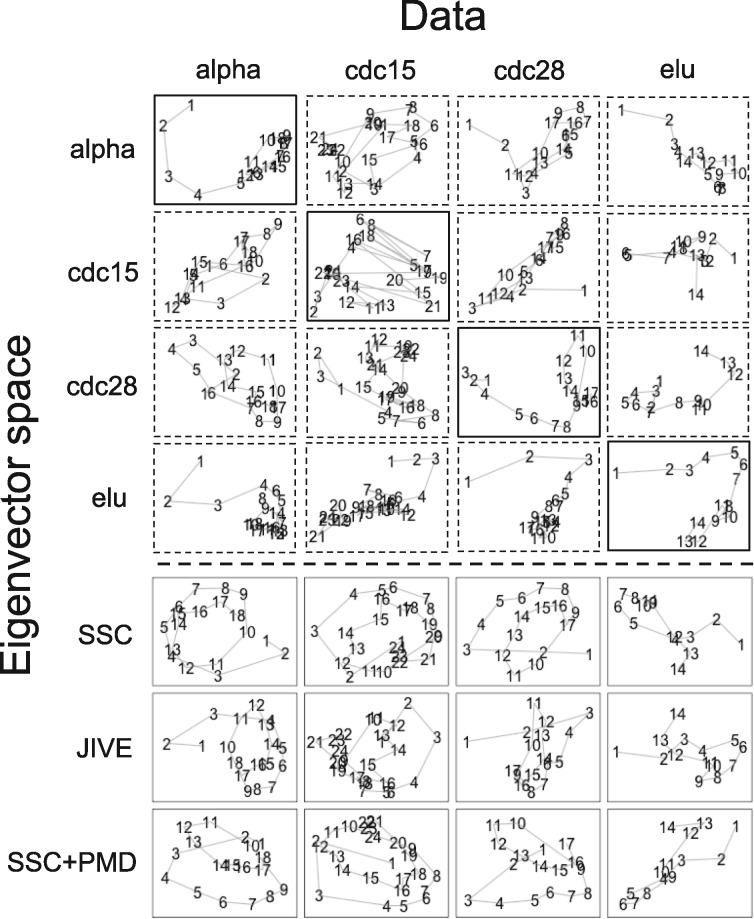
In Figure 4, each row refers to training study to estimate the leading top two eigenvectors. The first four rows use single study PCA to obtain the top two eigenvectors, while the last three rows combine four studies using SSC, JIVE and SSC + PMD to derive the joint eigen-space. Each column refers to a testing study that produces PC projections onto the trained eigenvector space. As a result, the diagonal plots of the first four rows (solid border lines) represent single study PCA results. In this example, the sample numbers indicate time points for roughly two cell cycles for alpha, cdc15 and cdc28, and one cell cycle for elu. In the single study PCA results of Figure 4, alpha, cdc28 and elu all showed somewhat clear cyclic pattern, while cdc15 produced oscillating artifacts. The non-cyclic oscillating artifact in cdc15 has been previously reported in Li et al. (2002). On the other hand, MetaPCA (SSC) consistently captured much better cyclic patterns in PC projections of all four studies. Particularly, MetaPCA (SSC) projection of cdc15 remarkably recovered its cyclic pattern. The result demonstrates MetaPCA’s ability to integrate information across all four studies and identify an improved common eigen-space. We also implemented the meta-analysis using JIVE and sparse MetaPCA (SSC + PMD). MetaPCA and sparse MetaPCA appeared to identify more noticeable cyclic patterns than those identified by JIVE (e.g. JIVE had weaker cyclic pattern in cdc28).

Fig. 4.

Two dimensional PC projections of PCA, MetaPCAs (SV, SSC), JIVE using four mRNA expression datasets of Spellman’s yeast cellcycle experiment. The numbers on the lines indicate time point during the two cell cycles. The first and second PC projections are on the x-axis and y-axis of each panel, respectively

3.2.2 Prostate cancer data

In the second application, we analyzed four prostate cancer microarray studies (Lapointe et al. 2004; Tomlins et al. 2007; Varambally et al. 2005; Yu et al. 2004), each with three types of samples (normal, primary tumor and metastasis; see Supplementary Table S1). We matched up features across the four studies and filtered non-informative features by the rank sum of feature mean and standard deviation (mean < 0.1, SD < 0.1; Wang et al. 2012), and imputed missing values. The preprocessing procedure produced 3, 056 features for further analysis.

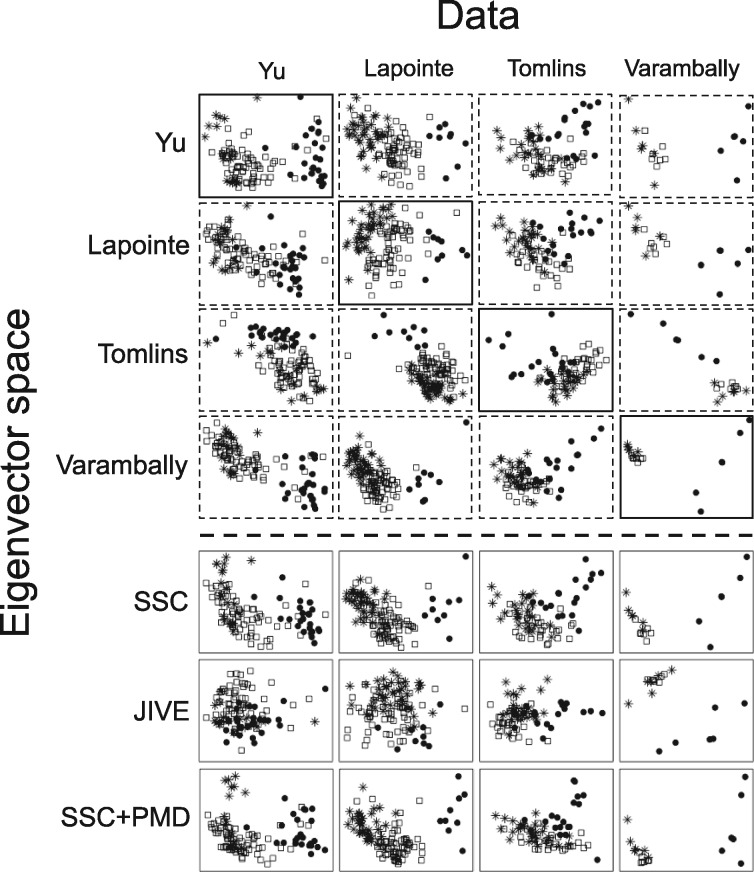
Figure 5 shows the single study PCA and meta-analytic PCA results. Although the dimension reduction did not utilize class label information, we plotted samples by class labels (star for normal, square for primary tumor and black dot for metastasis) to indicate whether the identified eigen-space is biologically meaningful to separate samples by class labels. In single study PCA when eigen-space identified by one study was applied to another study, the class separation often greatly decreased. For example, the FDS values were only 9 and 10.41 when study Yu and Varambally were projected to the eigen-space derived from Lapointe, much lower than those obtained from SSC (14.71 and 13.69) and SSC + PMC (15.34 and 21.17) in Table 1A. The MetaPCA and sparse MetaPCA methods provided a disciplined approach to identify a common eigen-space that better separates three biological classes. JIVE appeared to perform much worse than all other methods and the average FDS value of sparse MetaPCA (SSC + PMD) performed the best (average FDS = 18.93 compared to SSC’s 16.56 and JIVE’s 10.36). Although some single study PCA can produce high averaged FDS values (e.g. 16.5 for Yu and 18.81 for Varambally), the class labels may not be available in most applications and it is impossible to determine which single study eigen-space to choose for best dimension reduction. In Figure 5, Meta-PC projections (SSC and SSC + PMD) reveal the transitional pattern from normal (star) to primary tumor (square) and to metastasis tissues (circle). Note that the first leading Meta-PC (x-axis) projection accounts for larger separation across the class labels than the second leading Meta-PC (y-axis).

Fig. 5.

Two dimensional PC projections using four prostate cancer mRNA expression datasets; star (normal), square (primary tumor) and circle (metastasis tissues). The first and second PC projections are on the x-axis and y-axis, respectively

Table 1.

Fisher discriminant scores of PC projections (A: prostate cancer data, B: mouse metabolism data and C: TCGA cancer data)

A. Prostate cancer data
	Yu	Lapointe	Tomlins	Varambally		Average
Yu	15.37	24.01	10.58	16.04		16.50
Lapointe	9	21.20	11.14	10.41		12.94
Tomlins	9.82	19.86	10.67	8.04		12.10
Varambally	11.96	26.41	10.69	26.17		18.81
Pooled	6.39	12.41	6.74	6.93		8.12
SSC	14.71	26.45	11.37	13.69		16.56
JIVE	5.72	11.01	9.07	15.65		10.36
SSC+PMD	15.34	29.80	9.40	21.17		18.93
B. Mouse metabolism data
	Brown	Heart	Liver	Ske		Average
Brown	8.64	12.60	7.75	8.15		9.28
Heart	16.65	24.43	15.28	10.91		16.82
Liver	3.83	5.48	2.19	5.23		4.18
Ske	15.51	16.91	12.93	20.93		16.57
Pooled	5.15	11.66	6.59	7.30		7.68
SSC	8.28	15.05	8.40	8.93		10.17
JIVE	3.59	5.83	3.75	3.35		4.13
SSC+PMD	19.11	29.17	22.90	22.68		23.47
C. TCGA cancer data
	BRCA	COAD	KIRC	LUAD	READ	STAD	Average
BRCA	18.16	22.22	20.73	12.17	15.04	8.17	16.08
COAD	20.50	25.50	28.23	13.87	17.50	10.70	19.38
KIRC	22.59	29.13	32.70	16.25	20.33	13.78	22.46
LUAD	21.81	25.30	27.64	14.47	17.03	11.09	19.55
READ	20.27	21.29	18.43	11.06	15.35	7.02	15.57
STAD	21.84	26.17	29.34	14.89	17.40	11.98	20.27
Pooled	28.28	30.11	36.10	13.98	23.02	15.13	24.44
SSC	24.93	21.02	16.88	12.52	13.12	7.94	16.07
JIVE	19.69	20.15	18.50	10.68	12.77	8.90	15.11
SSC+PMD	16.96	29.66	27.12	14.72	20.34	13.98	20.46

3.2.3 Mouse metabolism data

It is known that an energy metabolism disorder in children is relevant to very long-chain acyl-coA dehydrogenase (VLCAD) deficiencies. On the other hand, long-chain acyl-CoA dehydrogenase (LCAD) deficient mice have impaired fatty acid oxidation, and suffer from disorders of mitochondrial fatty acid oxidation. We considered microarray experiments of mouse metabolism which were introduced and analyzed in (Li and Tseng, 2011). The datasets include mice profiles of three genotypes: wild-type (WT), LCAD knock-out (LCAD) and VLCAD knock-out (VLCAD). Four types of tissues [brown fat (Brown), skeletal (Ske), liver (Liver) and heart (Heart)] were analyzed and each tissue was considered as one study. We filtered out low-expressed and low-variable features (mean < 0.7, SD < 0.7), and matched up features across the four studies, which left 1304 gene features for further analysis. (See Supplementary Table S2).

Supplementary Figure S4 and Table 1B showed dimension reduction result of each PCA method and plotted samples by class labels (square for WT, dot for LCAD and star for VLCAD). Consistent with the prostate cancer result, sparse MetaPCA performed much better than the other methods (average FDS = 23.47 compared to SSC’s 10.17 and JIVE’s 4.13).

3.2.4 TCGA cancer data

In this section, we apply MetaPCA (SSC) to TCGA cancers datasets (Level 3 DNA methylation of beta values targeting on methylated and the unmethylated probes; https://tcga-data.nci.nih.gov/tcga/). We retrieved six cancer types [Breast carcinoma (BRCA), Colon carcinoma (COAD), Kidney renal clear cell carcinoma (KIRC), Lung adenocarcinoma (LUAD), rectum adenocarcinoma (READ), and Stomach Adenocarcinoma (STAD)] for an unsupervised analysis to explore common PC projection patterns. Pan-cancer analysis reveals common genetic or epigenetic alterations across multiple cancer types and offers the prospect of repurposing targeted therapies directed by fundamental molecular pathology of all tumors (Weinstein et al., 2013). We matched methylation probe features across all studies and filtered out probes by the rank sum of feature mean and standard deviation (mean < 0.7, SD < 0.7; Wang et al. 2012), and thereby we selected 910 probes for further analysis. Detailed information of TCGA methylation dataset is available in Supplementary Table S3.

Dimension reduction to each eigen-space is demonstrated in Supplementary Figure S5. The first eigenvector of sparse MetaPCA mostly separates tumor from adjacent normal. The second eigenvector is dominated by male/female difference. To quantify meaningful biological performance, we labeled samples with two clinical variables: tumor (square) versus adjacent normal (solid dot) and male (black) versus female (grey). The FDS values were calculated by treating four classes (male tumor, female tumor, male normal and female normal) and are shown in Table 1C. The sparse MetaPCA (SSC + PMD) method again performs better than majority of other approaches (average FDS = 20.46 compared to SSC’s 16.07 and JIVE’s 15.11). For pooled analysis, it happens to perform well in the TCGA pan-cancer analysis but performs poorly in the prostate cancer and mouse metabolism applications.

4 Conclusion and discussion

In this article, we proposed new MetaPCA and sparse MetaPCA frameworks, aiming to combine multiple transcriptomic or epigenomic datasets to identify a common eigen-space for dimension reduction. We proposed two meta-analytic criterions (sum of variance and sum of squared cosine, abbreviated as SV and SSC) and applied two sparse PCA methods (eNet and PMD). Simulation studies have shown that MetaPCA can accurately identify the common eigen-space and is robust to outliers and noise features, compared to JIVE and single study PCA. Sparse MetaPCA by eNet or PMD approaches provided not only better feature selection but also improved dimension reduction performance. The SSC criterion performed slightly better than SV and PMD was slightly better than eNet. As a result, we applied SSC criterion and PMD in all later applications. In applications, the first yeast cell cycle example showed improved cyclic pattern recognition by MetaPCA and sparse MetaPCA. In the next three examples of prostate cancer, mouse metabolism and TCGA pan-cancer methylation, the sparse MetaPCA consistently performed the best by using known class labels and Fisher discriminant scores as the benchmark. In Supplementary Table S8, a decent amount of differential expressed (DE) genes of mouse metabolism data implies the fact that PCA adequately separates three class labels. Yet it is also worth to note that samples under different conditions may not always separate well in PC dimensions especially due to shortage of DE genes.

In our simulation and applications, JIVE constantly performed the worst among the three integrative methods. This is reasonable since JIVE aims to estimate both the homogeneous and study-specific eigenvectors but our MetaPCA framework mostly focus on homogeneous structure alone. We also notice that JIVE typically requires higher computational cost since the estimation requires repeated iteration and permutation. As the author acknowledged, JIVE is not robust to outliers since it aims to estimate joint and individual variations simultaneously and the signal and noise are less distinguishable. In general, we expect MetaPCA to perform better in most genomic meta-analysis applications since data we meta-analyze are mostly homogeneous with only a reasonable amount of heterogeneity. In simulations, experiment designs are determined with dependence structure, sample sizes, strength of dependent structure and varying measurement scales. Importantly, MetaPCA (SV and SSC) is still superior as the methods effectively adapted for the diverse scenarios. In particular, when the number of data is relatively small and sample size is large, MetaPCAs work notably better than JIVE. Nonetheless such performance gaps remain the same even if the number of data increases.

One can calculate the likelihood ratio statistics in Flury (1984) where the null hypothesis is the existence of common covariance structures (i.e. simultaneous diagonalizable). In Supplementary Section 3, we have evaluated the likelihood ratio test in simulations and real applications. The result shows inadequacy of its application to small-n-large-p problems and all real applications rejected the null hypothesis ($P<{10}^{-20}$). When combining studies with large heterogeneity, it is possible that JIVE may perform better. To avoid including a contaminated or outlying study that may reduce performance of MetaPCA, quality control benchmarks proposed by Kang et al. (2012) (i.e. MetaQC) may be applied to determine study inclusion and exclusion criteria. An R package ‘MetaPCA’ and all programming code and datasets used in this article are available at http://tsenglab.biostat.pitt.edu/software.htm.

Funding

This research has been supported by NIH R01CA190766 and the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2017R1C1B5017528).

Conflict of Interest: none declared.