The Evolutionary History of Nebraska Deer Mice: Local Adaptation in the Face of Strong Gene Flow

Abstract

The interplay of gene flow, genetic drift, and local selective pressure is a dynamic process that has been well studied from a theoretical perspective over the last century. Wright and Haldane laid the foundation for expectations under an island-continent model, demonstrating that an island-specific beneficial allele may be maintained locally if the selection coefficient is larger than the rate of migration of the ancestral allele from the continent. Subsequent extensions of this model have provided considerably more insight. Yet, connecting theoretical results with empirical data has proven challenging, owing to a lack of information on the relationship between genotype, phenotype, and fitness. Here, we examine the demographic and selective history of deer mice in and around the Nebraska Sand Hills, a system in which variation at the Agouti locus affects cryptic coloration that in turn affects the survival of mice in their local habitat. We first genotyped 250 individuals from 11 sites along a transect spanning the Sand Hills at 660,000 single nucleotide polymorphisms across the genome. Using these genomic data, we found that deer mice first colonized the Sand Hills following the last glacial period. Subsequent high rates of gene flow have served to homogenize the majority of the genome between populations on and off the Sand Hills, with the exception of the Agouti pigmentation locus. Furthermore, mutations at this locus are strongly associated with the pigment traits that are strongly correlated with local soil coloration and thus responsible for cryptic coloration.

Introduction

Characterizing the conditions under which a population may adapt to a new environment, despite ongoing gene flow with its ancestral population, remains a question of central importance in population and ecological genetics. Hence, many studies have attempted to characterize selection–migration dynamics. Early studies focused on the distributions of phenotypes using ecological data to estimate migration rates (e.g., Clarke and Murray 1962; Endler 1977; Cook and Mani 1980); whereas later studies, focused primarily on Mendelian traits, documented patterns of genetic variation at a causal locus and contrasted that with putatively neutral loci to estimate selection and migration strengths (e.g., Ross and Keller 1995; Hoekstra et al. 2004; Stinchcombe et al. 2004, and see review of Linnen and Hoekstra 2009). Only recently have such studies expanded to examine whole-genome responses (see Jones et al. 2012; Feulner et al. 2015).

These selection–migration dynamics are well grounded in theory. Haldane (1930) first noted that migration may disrupt the adaptive process if selection is not sufficiently strong to maintain a locally beneficial allele. Bulmer (1972) went on to describe a two-allele two-deme model in which such a loss is expected to occur if m/s > a/(1 − a), where m is the rate of migration, s is the selection coefficient in population 1, and a is the ratio of selection coefficients between populations. More recent related work suggests that in order for a beneficial allele to reach fixation, s must be much larger than m (e.g., Lenormand 2002; Yeaman and Otto 2011, and see review of Tigano and Friesen 2016).

In addition to fixation probabilities, the migration load induced by the influx of locally deleterious mutations entering the population has also been well studied. Haldane (1957) found that the number of selective deaths necessary to maintain differences between populations is proportional to the number of locally maladapted alleles migrating into the population. Thus, the fewer loci necessary for the diverging locally adaptive phenotype, the lower the resulting migration load. More recently, Yeaman and Whitlock (2011) argued that with gene flow, the genetic architecture underlying an adaptive phenotype is expected to have fewer and larger-effect alleles compared with neutral expectations under models without migration (i.e., an exponential distribution of effect sizes [and see Rafajlović et al. 2017]). As recombination between these locally beneficial alleles may result in maladapted intermediate phenotypes, this model further predicts a genomic clustering of the underlying mutations (Maynard Smith 1977; Lenormand and Otto 2000). The relative advantage of this linkage will increase as the population approaches the migration threshold, at which local adaptation becomes impossible (Kirkpatrick and Barton 2006). Taken together, these studies make a number of testable predictions relating migration rate with the expected number of sites underlying the locally beneficial phenotype at the locus in question, the average effect size of the alleles, the clustering of beneficial mutations, and the conditions under which a locally beneficial allele may be lost, maintained, or fixed in a population.

These theoretical expectations, however, have proven difficult to evaluate in natural populations owing to a dearth of systems with concrete links between genotype, phenotype, and fitness. In one well-studied system, deer mice (Peromyscus maniculatus) inhabiting the light-colored Sand Hills of Nebraska (formed within the last 8,000 years following the end of the Wisconsin glacial period [Loope and Swinehart 2000]) have evolved lighter coloration than conspecifics on the surrounding dark soil (Dice 1941, 1947). Using a combination of laboratory crosses and hitchhiking-mapping, the Agouti gene, which encodes a signaling protein known to play a key role in mammalian pigment-type switching and color patterning (Jackson 1994; Mills and Patterson 1994; Barsh 1996, and see review of Manceau et al. 2010), has been implicated in adaptive color variation (Linnen et al. 2009). Moreover, using association mapping, specific candidate mutations have been linked to variation in specific pigment traits, which in turn contribute to differential survival from visually hunting avian predators (Linnen et al. 2013).

While previous research in this system has established links between genotype, phenotype, and fitness, this work has focused on a single ecotonal population located near the northern edge of the Sand Hills. Thus, the dynamic interplay of migration, selection, and genetic drift, as well as the extent of genotypic and phenotypic structuring among populations, remains unknown. To address these questions, we have sampled hundreds of individuals across a transect spanning the Sand Hills and neighboring populations to the north and south. Combining extensive per-locale soil color measurements, per-individual phenotyping, and 660,000 single nucleotide polymorphisms (SNPs) genome-wide, this data set provides a unique opportunity to evaluate theoretical predictions of local adaptation with gene flow on a genomic scale.

Results and Discussion

Environmental and Phenotypic Variation in and around the Nebraska Sand Hills

We collected P. maniculatus luteus individuals (N = 266) as well as soil samples (N = 271) from 11 locations spanning a 330-km transect across the Sand Hills of Nebraska (fig. 1; supplementary table 1, Supplementary Material online). As expected, we found that soil color differed significantly between “on” Sand Hills and “off” Sand Hills locations (F₁ = 307.4, P < 1 × 10⁻¹⁵; fig. 2). Similarly, five of the six mouse color traits also differed significantly between the two habitats (fig. 2). In contrast, mice trapped on versus off of the Sand Hills did not differ in other nonpigmentation traits including total body length, tail length, hind foot length, or ear length (see Supplementary Material online). Together, these results are consistent with strong divergent selection between habitat types on multiple color traits, but not other morphological traits.

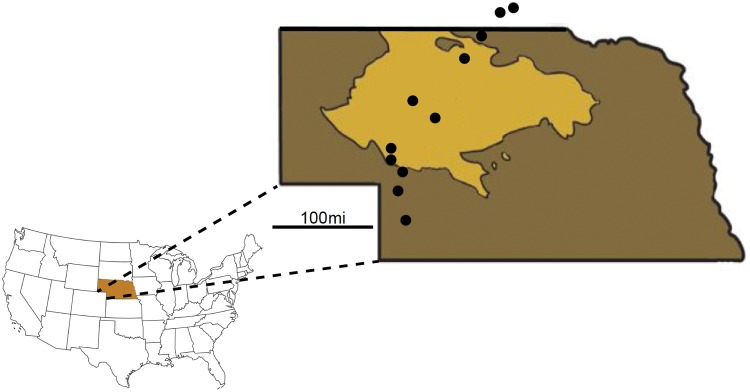
Fig. 1.

Sampling locations on (light brown) and off (dark brown, and out of state) of the Nebraska Sand Hills. Sampling spanned a 330-km transect beginning ∼120 km south of the Sand Hills and ending ∼120 km north of the Sand Hills.

Fig. 2.

Soil color and mouse color traits are lighter on the Nebraska Sand Hills. Box plots for each sampling site were produced using scaled (range: 0–1), normal-quantile transformed values for: soil brightness (B2), dorsal brightness (PC1), dorsal hue (PC2), ventral brightness (PC3), dorsal–ventral (D-V) boundary, and tail stripe. Soil is shown on the separated top panel, and the five pigment traits are given below. In all plots, higher values correspond to lighter/brighter color (y-axis). Gray shading indicates off the Sand Hills sites. Soil and five mouse color traits were significantly lighter on the Sand Hills (dorsal brightness: F₁ = 218.6, P < 1 × 10⁻¹⁵; dorsal hue: F₁ = 18.4, P = 2.4 × 10⁻⁵; ventral brightness: F₁ = 61.0, P = 1.5 × 10⁻¹³; dorsal–ventral boundary: F₁ = 104.6, P < 1 × 10⁻¹⁵; tail stripe: F₁ = 170.2, P < 1 × ${10}_{}^{\text{−}15}$, with the corresponding P-values given to the right of each panel. A sixth color trait (ventral hue [PC4]; [F₁ = 1.1, P = 0.30]) and four noncolor traits (total body length [F₁ = 0.11, P = 0.74], tail length [F₁ = 0.18, P = 0.67], hind foot length [F₁ = 3.0, P = 0.084], and ear length [F₁ = 0.48, P = 0.49]) did not differ significantly between habitats (see supplementary fig. 10 and table 11, Supplementary Material online).

We also examined habitat heterogeneity and phenotypic differences among sampling sites within habitat types. Both soil brightness and mouse color differed significantly among sites within habitats (soil: F₉ = 8.0, P = 1.9 × 10⁻¹⁰; dorsal brightness: F₉ = 10.5, P = 8.1 × 10⁻¹⁴; dorsal hue: F₉ =3.4, P = 6.7 × 10⁻⁴; ventral brightness: F₉ = 10.3, P = 1.4 × 10⁻¹³; dorsal–ventral boundary: F₉ = 6.6, P = 1.5 × 10⁻⁸; tail stripe: F₉ = 6.9, P = 7.5 × 10⁻⁹). Additionally, site-specific means for three of the color traits were significantly correlated with local soil brightness, including: dorsal brightness (t = 4.4, P = 0.0017), dorsal–ventral boundary (t = 3.9, P = 0.0034), and tail stripe (t = 3.1, P = 0.013). In contrast, site-specific means for dorsal hue and ventral brightness did not correlate with local soil color (dorsal hue: t = 2.385, P = 0.097; ventral brightness: t = 0.32; P = 0.77). These results suggest that the agents of selection shaping correlations between local soil color and mouse color vary among the traits.

The Genetic Architecture of Light Color in Sand Hills Mice

Genetic architecture parameter estimates derived from our association mapping analyses suggest that variants in the Agouti locus explain a considerable amount of the observed color variation in on versus off Sand Hills populations (table 1). Indeed, Agouti SNPs explain 69% of the total phenotypic variance in dorsal brightness and tail stripe. This analysis also provides estimates of the potential number of causal SNPs as well as the proportion of genetic variance that is attributable to major-effect SNPs. These estimates suggest that dozens of Agouti variants may be contributing to variation in color traits, but the credible intervals for SNP number are wide (table 1). One explanation for such wide intervals is that it is difficult to disentangle the effects of closely linked SNPs. Nevertheless, because the lower bound of the credible intervals for all but one color trait exceeds 1, our data indicate that there are multiple Agouti mutations with nonnegligible effects on color phenotypes. Estimates of PGE (percent of genetic variance attributable to major effect mutations) indicate that, whatever their number, these major effect mutations explain a considerable percentage of total genetic variance (e.g., 83% for dorsal brightness and 87% for dorsal–ventral boundary).

Table 1.

Hyperparameters Describing the Genetic Architecture of Five Color Traits.

Trait	h	PVE	rho	PGE	n_gamma
Dorsal brightness	0.50 (0.29, 0.7)	0.69 (0.57, 0.81)	0.62 (0.31, 0.92)	0.83 (0.64, 0.97)	117.2 (7, 286)
Dorsal hue	0.28 (0.07, 0.58)	0.26 (0.08, 0.45)	0.32 (0.02, 0.87)	0.30 (0, 0.86)	55.4 (0, 264)
Ventral brightness	0.33 (0.16, 0.51)	0.39 (0.23, 0.56)	0.43 (0.13, 0.82)	0.54 (0.22, 0.88)	80.6 (3, 271)
D-V boundary	0.44 (0.25, 0.64)	0.61 (0.46, 0.73)	0.75 (0.45, 0.98)	0.87 (0.7, 0.99)	70.5 (9, 256)
Tail stripe	0.51 (0.32, 0.69)	0.69 (0.56, 0.8)	0.64 (0.38, 0.89)	0.79 (0.61, 0.95)	123.9 (16, 284)

Note.—All parameters were estimated using a BSLMM model in GEMMA, 2,148 Agouti SNPs, and a relatedness matrix estimated from genome-wide SNPs. Parameter means and 95% credible intervals (lower bound, upper bound) were calculated from ten independent runs per trait. Interpretation of hyperparameters is as follows: PVE, the total proportion of phenotypic variance that is explained by genotype; PGE, the proportion of genetic variance explained by sparse (i.e., major) effects; h, an approximation used for prior specification of the expected value of PVE; rho, an approximation used for prior specification of the expected value of PGE; n_gamma, the expected number of sparse (major) effect SNPs.

Although our genetic architecture parameter estimates indicate that large-effect Agouti variants contribute to variation in each of the five color traits, the number and location of these SNPs vary considerably (fig. 3). To interpret these results, some background on the structure and function of Agouti is needed. Work in Mus musculus has identified two different Agouti isoforms that are under the control of different promoters. The ventral isoform, containing noncoding exons 1 A/1A’, is expressed in the ventral dermis during embryogenesis and is required for determining the boundary between the dark dorsum and light ventrum (Bultman et al. 1994; Vrieling et al. 1994). The hair-cycle isoform, containing noncoding exons 1B/1C, is expressed in both the dorsal and ventral dermis during hair growth, and is required for forming light, pheomelanin bands on individual hairs (Bultman et al. 1994; Vrieling et al. 1994). In Peromyscus, these same isoforms are present as well as additional, novel isoforms (Mallarino et al. 2017). Isoform-specific changes in Agouti expression are associated with changes in the dorsal–ventral boundary (ventral isoform; Manceau et al. 2011) and the width of light bands on individual hairs (hair-cycle isoform; Linnen et al. 2009). Both isoforms share the same three coding exons (exons 2–4); thus, protein-coding changes could simultaneously alter pigmentation patterning and hair banding (Linnen et al. 2013).

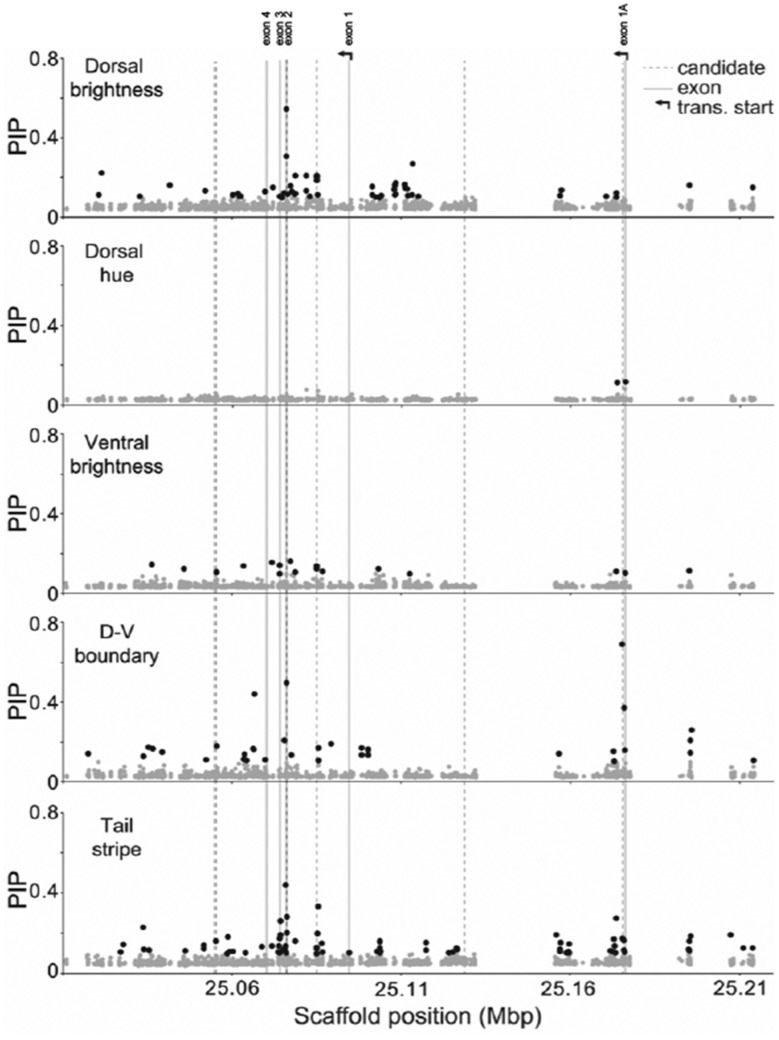
Fig. 3.

Association mapping results for Agouti SNPs and five color traits. Each point represents one of 2,148 Agouti SNPs included in the association mapping analysis, with position (on scaffold 16, see Materials and Methods) indicated on the x-axis and PIP estimated using a BSLMM in GEMMA on the y-axis. PIP values, which approximate the strength of the association between genotype and phenotype, were averaged across ten independent GEMMA runs. Black dots indicate SNPs with PIP > 0.1, dashed lines give the location of six candidate SNPs identified in a previous association mapping analysis of a single population (associated with tail stripe, D-V boundary, as well as dorsal brightness and hue; Linnen et al. 2013), gray lines give the location of Agouti exons, and arrows indicate two alternative transcription start sites.

Across the Agouti locus, we detected 160 SNPs that were strongly associated (posterior inclusion probability [PIP] in the polygenic BSLMM > 0.1) with at least one color trait (see Materials and Methods). By trait, the number of SNPs exceeding our PIP threshold was: 53 (dorsal brightness), 2 (dorsal hue), 16 (ventral brightness), 34 (dorsal–ventral boundary), and 81 (tail stripe). Additionally, patterns of genotype–phenotype association were distinct for each trait but consistent with Agouti isoform function (fig. 3). For example, we observed the strongest associations for dorsal brightness around the three coding exons (exons 2, 3, and 4, located between positions 25.06 and 25.11 Mb on the scaffold containing the Agouti locus) and upstream of the transcription start site for the Agouti hair-cycle isoform (fig. 3). In contrast, for dorsal–ventral boundary, the SNP with the highest PIP was located very near the transcription start site for the Agouti ventral isoform (fig. 3). Notably, a previously identified serine deletion in exon 2 (Linnen et al. 2009, 2013) exceeds our threshold for three of the color traits (dorsal brightness, dorsal–ventral boundary, and tail stripe) and was elevated above background association levels for the remaining two traits (dorsal hue and ventral brightness); and multiple candidates from those analyses are also recovered here (supplementary table 2, Supplementary Material online). Overall, our association mapping results thus reveal that there are many sites in Agouti that are associated with pigment variation.

We also estimated genetic architecture parameters and identified candidate pigmentation SNPs in the full data set (Agouti SNPs plus all SNPs outside of Agouti that had no missing data). For all five traits, including SNPs outside of Agouti led to a modest increase in PVE, PGE, and SNP-number estimates, but credible intervals overlapped with those of the Agouti-only data set for all parameter estimates (table 1 vs. supplementary table 3, Supplementary Material online). Additionally, although the highest-PIP SNPs were found in Agouti, we identified several non-Agouti candidate SNPs as well (supplementary table 4, Supplementary Material online). Together, these results suggest that while Agouti explains a considerable amount of color variation in mice living on and around the Nebraska Sand Hills, a complete accounting of non-Agouti regions associated with color will require a whole-genome resequencing approach.

The Demographic History of the Sand Hills Population

Inferring the demographic history of this region is of interest in and of itself, but also is a requisite step for downstream selection inference. Based on their genetic diversity, individuals from different sampling locations grouped according to their location and habitat, with a clear separation between individuals from on and off of the Sand Hills (fig. 4). The observed pattern of isolation by distance (IBD) was further supported by a significant correlation between pairwise genetic differentiation (F_ST/[1 − F_ST]) and pairwise geographic distance among sampling sites (P = 9.9 × 10⁻⁴). The pairwise F_ST values between sampling locations were low, ranging from 0.008 to 0.065, indicating limited genetic differentiation. Consistent with both patterns of IBD and reduced differentiation among populations, individual ancestry proportions (as inferred by sNMF and TESS) were best explained by three population clusters. Additionally, the ancestry proportions obtained with three clusters (fig. 4) returned low cross-entropy values (supplementary fig. 1, Supplementary Material online) particularly when accounting for geographic sampling location, again suggesting three distinct groups: 1) North of the Sand Hills, 2) on the Sand Hills, and 3) south of the Sand Hills. The population tree inferred with TreeMix also indicated low levels of genetic drift among populations, as well as primary differentiation between north and south populations, with the Sand Hills population occupying an intermediate position. This pattern is consistent with increased differentiation moving along the transect (fig. 4), which is likely owing both to simple IBD as well as the more complex settlement history inferred below.

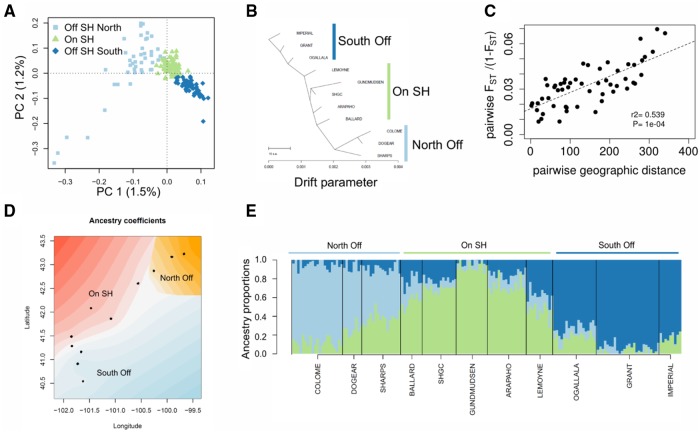
Fig. 4.

Genetic structure of populations on and off the Sand Hills. (A) PCA shows that individuals cluster according to their geographic sampling location, with a clear separation of individuals sampled on the Sand Hills (SH; green) from off the Sand Hills (blue). (B) TreeMix results for the tree that best fit the covariance in allele frequencies across samples. (C) An isolation-by-distance model is supported by a significant correlation between pairwise genetic differentiation (F_ST/[1 − F_ST]) and pairwise geographic distance among sampling sites. Significance of the Mantel test was assessed through 10,000 permutations. (D) Spatial interpolation of the ancestry proportion inferred, accounting for geographic sampling location, using TESS3 for K = 3 groups. Individuals are represented as dots, and the ancestry of the three groups is represented by a gradient of three colors. (E) Individual admixture proportions (inferred using TESS3) are consistent with IBD and reduced differentiation among populations. The number of clusters (K) best explaining the data was assessed as the K value reaching the lowest minimal cross-entropy at K = 3. All analyses were based on a subset of 161 individuals showing a mean depth of coverage larger than 8×, with all genotypes possessing a minimum coverage of 4×, sampling one SNP for each 1.5-kb block, resulting in a data set with 5,412 SNPs (supplementary table 8, Supplementary Material online).

Given the observed population structure, we next investigated models of colonization history based on three populations: Those inhabiting the Sand Hills and those inhabiting the neighboring regions to the north and to the south. This resulted in two different three-population demographic models, corresponding to different population tree topologies, which explicitly allow for bottlenecks associated with potential founder events, and for gene flow among populations (supplementary fig. 2, Supplementary Material online). Both models appeared equally likely (supplementary table 5, Supplementary Material online), and parameter estimates were similar and consistent across models, pointing to a recent divergence time among populations, evidence of a bottleneck associated with the colonization of the Sand Hills, and high rates of migration among all populations (supplementary table 6, Supplementary Material online). Note that the tested models did not specifically impose a bottleneck for the colonization of the Sand Hills, as population sizes could have remained high at the onset of the colonization of the Sand Hills.

To better distinguish between the models, we compared the likelihoods of the two models for bootstrap data sets containing a single SNP per 1.5-kb block, counting the number of bootstrap replicates with a relative likelihood (based on Akaike’s information criterion values) larger than 0.95 for each model. Using this approach, we identified a model with a topology in which the population on the Sand Hills shares a more recent common ancestor with the population off the Sand Hills to the south (supported in 81/100 bootstrap replicates, supplementary fig. 3, Supplementary Material online). This topology and the parameter estimates (supplementary table 6, Supplementary Material online) are consistent with a recent colonization of the Sand Hills from the south, namely: 1) A recent split within the last ∼4,000 years (95% CI: 3,400–7,900), 2) a stronger bottleneck associated with the colonization of the Sand Hills compared with the older split between northern and southern populations, and 3) higher levels of gene flow from south to north, including higher migration rates from the southern population into the Sand Hills (2Nm 95% CI: 12.5–24.0). Furthermore, this model fits well the marginal site frequency spectrum (SFS) for each sample as well as the 2D marginal SFS for each pair of populations (supplementary fig. 4, Supplementary Material online). Thus, this neutral demographic model nicely explains observed patterns of variation outside of the Agouti region, and suggests that, at least the most recent colonization represented by the currently sampled individuals, occurred considerably after the Sand Hills began to initially form (i.e., roughly 8,000 years ago).

The Selective History of the Sand Hills Population

Despite the high levels of gene flow inferred in our model, which results in low levels of differentiation among populations genome-wide (supplementary fig. 5a, Supplementary Material online), we observed high levels of differentiation among populations at the Agouti locus—variation that is further correlated with several phenotypic traits (fig. 5; supplementary figs. 5 and 6, Supplementary Material online). We observed the highest level of differentiation between mice sampled on either side of the northern limit of the Sand Hills, with a 100-kb region within Agouti exhibiting a continuous run of elevated genetic differentiation (supplementary fig. 6, Supplementary Material online). This pattern is consistent with the expectations of positive selection under a local adaptation regime. Within this 100-kb region, a subregion of 30 kb, located in intron 1 (i.e., between exon 1A and exon 1), displayed maximal differentiation (supplementary fig. 6, Supplementary Material online), making it difficult to precisely identify the target of selection. In contrast to the wide-range differentiation observed at Agouti on the northern side of the cline, a single narrow F_ST-peak of roughly 5 kb located in intron 1 was observed on the southern limit of the Sand Hills (fig. 5; supplementary fig. 6a, Supplementary Material online). Genome-wide comparison confirmed the overall genetic similarity between light-colored Sand Hills mice and the dark-colored population to the south, with the exception of a small number of variants putatively driving adaptive phenotypic divergence at Agouti (fig. 5; supplementary fig. 6a, Supplementary Material online).

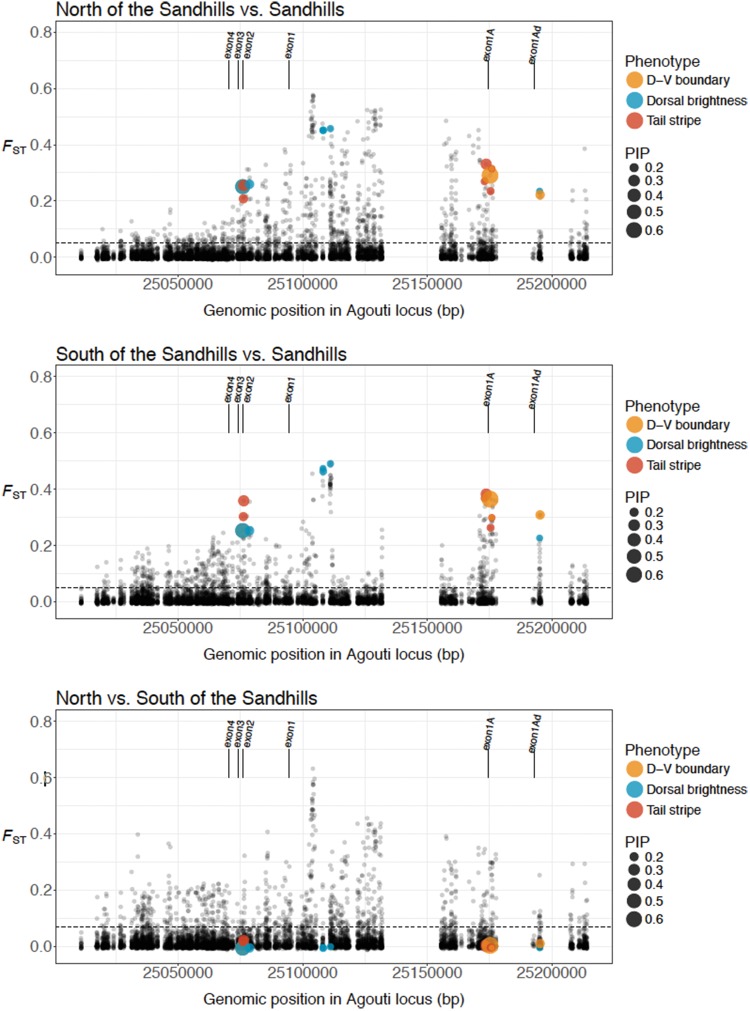
Fig. 5.

Genetic differentiation across the Agouti locus. Genetic differentiation observed between populations on the Sand Hills and populations north of the Sand Hills (top panel), populations on the Sand Hills and populations south of the Sand Hills (middle panel), and populations north and south of the Sand Hills. Dotted lines indicate the genome-wide average F_ST between these comparisons. As shown, differentiation is generally greatly elevated across the region, with a number of highly differentiated SNPs particularly when comparing on versus off Sand Hills populations, which correspond to SNPs associated with different aspects of the cryptic phenotype (PIP scores are indicated by the size of the dots as shown in the legend, and significant SNPs are labeled with respect to the associated phenotype). Populations to the north and south of the Sand Hills are also highly differentiated in this region, likely owing to differing levels of gene flow with the Sand Hills populations, yet the SNPs underlying the cryptic phenotype are not differentiated between these dark populations.

To test whether this pattern of differentiation could be the result of nonselective forces (see Crisci et al. 2012; Jensen et al. 2016), we calculated the HapFLK statistic, providing a single measure of genetic differentiation for the three geographic localities while controlling for neutral differentiation. Before calculating genetic differentiation at the target locus (i.e., Agouti), the HapFLK method computes a neutral distance matrix from the background data (i.e., the background regions randomly distributed across the genome) that summarizes the genetic similarity between populations with regard to the extent of genetic drift since divergence from their common ancestral population (supplementary fig. 7, Supplementary Material online). Consistent with the inferred demographic history of the populations, genome-wide background levels of variation suggest that individuals captured south of the Sand Hills are more similar to those inhabiting the Sand Hills, when compared with populations to the north. The HapFLK profile confirmed the significant genetic differentiation at the Agouti locus compared with neutral expectations (fig. 6). Interestingly, southern populations share a significant amount of the haplotypic structure observed in populations on the Sand Hills, with the exception of the candidate region itself. This is in keeping with high rates of on-going gene flow occurring between on and off Sand Hills populations, whereas selection maintains the ancestral Agouti alleles in the populations off the Sand Hills, and the derived alleles conferring crypsis on the Sand Hills.

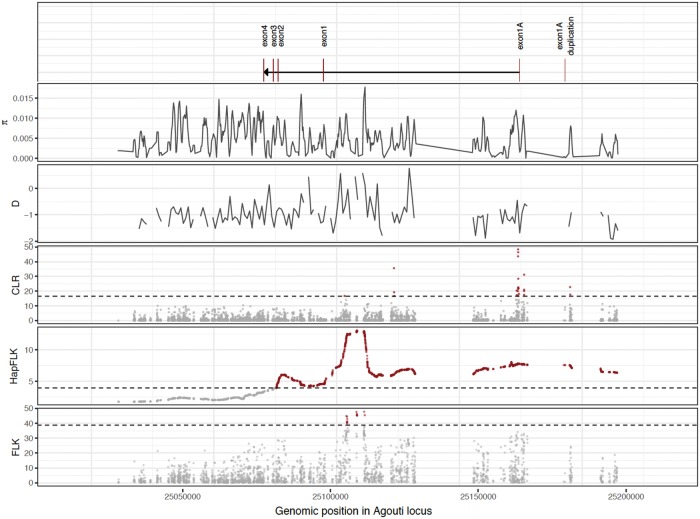
Fig. 6.

Comparison of tests of neutrality and selection across the Agouti locus. From the top: The exon structure, pairwise differences, Tajima’s D, CLR test, HapFLK, and FLK. The dashed lines indicate the significance threshold using parametric bootstrapping of the best-fitting demographic model.

Owing to low levels of linkage disequilibrium characterizing the Agouti region, adaptive variants could be mapped on a fine genetic scale. Specifically, there are three regions of increased differentiation (fig. 6): 1) A narrow 3-kb peak in the HapFLK profile (located in intron 1; supplementary table 7, Supplementary Material online) colocalizes with a region of high linkage disequilibrium (supplementary fig. 8, Supplementary Material online), suggesting a recent selective event; 2) a second highest peak of differentiation, located between exon 1A and the duplicated reversed copy, exon1A’, is the only significant region detected by the CLR test (supplementary fig. 9, Supplementary Material online) and contains strong haplotype structure (fig. 6), again suggesting the recent action of positive selection; and 3) a third highest peak of differentiation surrounds the putatively beneficial serine deletion in exon 2 previously described by Linnen et al. (2009), showing strong differentiation between on and off Sand Hills populations in our data set. Although several lines of evidence support the role of the serine deletion in adaptation to the Sand Hills, the linkage disequilibrium around this variant is low, suggesting that the age of the corresponding selective event is likely the oldest among the three candidate regions, with subsequent mutation and recombination events reducing the selective sweep pattern. Hence, as one may anticipate, this greatly expanded clinal data set served to identify younger and more geographically localized candidate regions from across the Sand Hills compared with previous studies, while still generally supporting the model proposed by Linnen et al. (2013) of multiple independently selected mutations underlying different aspects of the cryptic phenotype.

Predicted Migration Thresholds and the Conditions of Allele Maintenance

Although a number of strong assumptions must be made, it is possible to estimate the migration threshold below which a locally beneficial mutation may be maintained in a population. Given our high rates of inferred gene flow, it is important to consider whether observations are consistent with theoretical expectations necessary for the maintenance of alleles. Following Yeaman and Whitlock (2011) and Yeaman and Otto (2011), this migration threshold is defined in terms of both rates of gene flow as well as fitness effects of locally beneficial alleles in the matching and in the alternate environment. Given the parameter values inferred here, along with estimated population sizes, the threshold above which the most strongly beneficial mutations may be maintained in the population is estimated at m = 0.8—a large value indeed, given the inferred strength of selection (see Materials and Methods for details). For the more weakly beneficial mutations identified, this value is estimated at m = 0.07, again well above empirically estimated rates. Thus, our empirical observations are fully consistent with expectation in that gene flow is strong enough to prevent locally beneficial alleles from fixing on the Sand Hills, but not so strong so as to swamp out the derived allele despite the high input of ancestral variation. As such, parameter estimates fall in a range consistent with the long-term maintenance of polymorphic alleles.

Conclusions

The cryptically colored mice of the Nebraska Sand Hills represent one of the few mammalian systems in which aspects of genotype, phenotype, and fitness have been measured and connected. Yet, the population genetics of the Sand Hills region has remained poorly understood. By sequencing hundreds of individuals across a cline spanning over 300 km, fundamental aspects of the evolutionary history of this population could be addressed for the first time. Utilizing genome-wide putatively neutral regions, the inferred demographic history suggests a relatively recent colonization of the Sand Hills from the south well after the last glacial period. Further, high rates of gene flow are inferred between light and dark populations—resulting in genome-wide low levels of genetic differentiation as well as low levels of phenotypic differentiation of four traits unrelated to coloration across the cline. However, the Agouti region differs markedly in this regard, with high levels of differentiation observed between on and off Sand Hills populations, strong haplotype structure, and high levels of linkage disequilibrium spanning putatively beneficial mutations among cryptically colored individuals. In addition, we found these putatively beneficial mutations to be strongly associated with the phenotypic traits underlying crypsis, and these phenotypic traits were found to be in strong association with variance in soil color across the cline.

Together, these results suggest a model in which selection is acting to maintain the alleles underlying the locally adaptive phenotype on light/dark soil, despite substantial gene flow, which not only prevents the populations from strongly differentiating from one another but also prevents the cryptic genotypes from reaching local fixation. Furthermore, returning to the theoretical predictions outlined in the Introduction, the mutations underlying the cryptic phenotype are found to be few in number, of large effect size, and in close genomic proximity. As described by Yeaman and Whitlock (2011) in models of local adaptation with high migration, the establishment of a large effect beneficial allele may indeed facilitate the accumulation of other locally beneficial alleles in the same genomic region owing to the local reduction in effective migration rate (and see Aeschbacher and Burger 2014). Though speculative, such a model may indeed explain the accumulating observations of selection for crypsis generally targeting either the Agouti locus or the Mc1r locus in a given population, rather than both (i.e., a single region is targeted by selection, rather than two unlinked regions).

Our results are in keeping with this model, with the exon 2 serine deletion explaining a large proportion of variance in multiple traits underlying the cryptic phenotype, and with population-genetic patterns suggesting comparatively old selection acting on this variant. In addition, owing to the large-scale geographic sampling, multiple newly identified, genomically clustered and smaller effect alleles modulating individual traits are also identified, which are characterized by strong patterns of selective sweeps, indicative of more recent selection. This system thus provides an in-depth picture of the dynamic interplay of these population-level processes underlying this adaptive phenotype, and highlights a history characterized by remarkably strong local selective pressures as well as continuous high rates of gene flow with the ancestral founding populations.

Materials and Methods

Population Sampling

Collection

We collected P. maniculatus luteus individuals (N = 266) and corresponding soil samples (N = 271) from 11 sites spanning a 330-km transect starting ∼120 km north of the Sand Hills and ending ∼120 km south of the Sand Hills (fig. 1; supplementary table 1, Supplementary Material online). In total, five sampling locations were on the Sand Hills and six were located off of the Sand Hills (three in the north and three in the south). We collected mice using Sherman live traps and prepared flat skins according to standard museum protocols; these specimens are accessioned in the Harvard University Museum of Comparative Zoology’s Mammal Department. From each sample, we preserved liver tissue in 100% EtOH for subsequent DNA extraction. Collections were made under the South Dakota Department of Game, Fish, and Parks scientific collector’s permit 54 (2008) and the Nebraska Game and Parks Commission Scientific and Educational Permit (2008) 579, subpermit 697-700. This work was approved by Harvard University’s Institutional Animal Care and Use Committee.

Mouse color measurements

For each mouse, we measured standard morphological traits, including: total length, tail length, hind foot length, and ear length. We also characterized color and color pattern using methods modified from Linnen et al. (2013). In brief, to quantify color, we used a USB2000 spectrophotometer (Ocean Optics) to take reflectance measurements at three sites across the body (three replicated measurements in the dorsal stripe, flank, and ventrum). We processed these raw reflectance data using the CLR: Colour Analysis Programs v.1.05 (Montgomerie 2008). Specifically, we trimmed and binned the data to 300–700 nm and 1 nm bins and computed five color summary statistics: B2 (mean brightness), B3 (intensity), S3 (chroma), S6 (contrast amplitude), and H3 (hue). We then averaged the three measurements for each body region, producing a total of 15 color values (i.e., five summary statistics from each of the three body regions). To ensure values were normally distributed, we performed a normal-quantile transformation on each of the 15 color variables. Using these transformed values, we performed a principal component analysis (PCA) in STATA v.13.0 (StataCorp, College Station, TX). On the basis of the eigenvalues and examination of the scree plot, we selected the first four principal components, which together accounted for 84% of the variation in color. To increase interpretability of the loadings, we performed a VARIMAX rotation on the first four PCs (Tabachnick and Fidell 2001; Montgomerie 2006). After rotation, PC1 corresponded to the brightness/contrast (B2, B3, S6) of the dorsum; PC2 to the chroma/hue (S3, H3) of the dorsum; PC3 to the brightness/contrast (B2, B3, S6) of the ventrum; and PC4 to the chroma/hue (S3, H3) of the ventrum. Therefore, we refer to PC1 as “dorsal brightness”, PC2 as “dorsal hue”, PC3 as “ventral brightness”, and PC4 as “ventral hue” throughout.

To quantify color pattern, we took digital images of each mouse flat skin with a Canon EOS Rebel XTI with a 50-mm Canon lens (Canon U.S.A., Lake Success, NY). We used the quick selection tool in Adobe Photoshop CS5 (Adobe Systems, San Jose, CA) to select light and dark areas on each mouse. Specifically, we outlined the dorsum (brown portion of the dorsum with legs and tails excluded), body (outlined entire mouse with brown and white areas, legs and tails excluded), tail stripe (outlined dark stripe on tail only), and tail (outlined entire tail). We calculated “dorsal–ventral boundary” as (body—dorsum)/body and “tail stripe” as (tail—tail stripe)/tail. Thus, each measure represents the proportion of a particular region (tail or body) that appeared unpigmented; higher values therefore represent lighter phenotypes.

To determine whether color phenotypes (dorsal brightness, dorsal hue, ventral brightness, ventral hue, dorsal–ventral boundary, and tail stripe) differ between on Sand Hills and off Sand Hills populations, we performed a nested analysis of variance (ANOVA) on each trait, with sampling site nested within habitat. For comparison, we also performed nested ANOVAs on each of the four noncolor traits (total length, tail length, hind foot length, and ear length). All analyses were performed on normal-quantile-transformed data. Unless otherwise noted, we performed all transformations and statistical tests in R v3.3.2.

Soil color measurements

To characterize soil color, we collected soil samples in the immediate vicinity of each successful Peromyscus capture. To measure brightness, we poured each soil sample into a small petri dish and recorded ten measurements using the USB2000 spectrophotometer. As above, we used CLR to trim and bin the data to 300–700 nm and 1 nm bins as well as to compute mean brightness (B2). We then averaged these ten values to produce a single mean brightness value for each soil sample, and transformed the soil-brightness values using a normal-quantile transformation prior to analysis. To evaluate whether soil color differs consistently between on and off of the Sand Hills sites, we performed an ANOVA, with sampling site nested within habitat. Finally, to test for a correlation between color traits (see above) and local soil color, we regressed the mean brightness value for each color trait on the mean soil brightness for each sampling site—ultimately for comparison with downstream population genetic inference (see Joost et al. 2013).

Library Preparation and Sequencing

Library Preparation

To prepare sequencing libraries, we used DNeasy kits (Qiagen, Germantown, MD) to extract DNA from liver samples. We then prepared libraries following the SureSelect Target Enrichment Protocol v.1.0, with some modifications. In brief, 10–20 μg of each DNA sample was sheared to an average size of 200 bp using a Covaris ultrasonicator (Covaris Inc., Woburn, MA). Sheared DNA samples were purified with Agencourt AMPure XP beads (Beckman Coulter, Indianapolis, IN) and quantified using a Quant-iT dsDNA Assay Kit (ThermoFisher Scientific, Waltham, MA). We then performed end repair and adenylation, using 50 μl ligations with Quick Ligase (New England Biolabs, Ipswich, MA) and paired-end adapter oligonucleotides manufactured by Integrated DNA Technologies (Coralville, IA). Each sample was assigned one of 48 five-base pair barcodes. We pooled samples into equimolar sets of 9–12 and performed size selection of a 280-bp band (±50 bp) on a Pippin Prep with a 2% agarose gel cassette. We performed 12 cycles of PCR with Phusion High-Fidelity DNA Polymerase (NEB), according to manufacturer guidelines. To permit additional multiplexing beyond that permitted by the 48 barcodes, this PCR step also added one of 12 six-base pair indices to each pool of 12 barcoded samples. Following amplification and AMPure purification, we assessed the quality and quantity of each pool (23 total) with an Agilent 2200 TapeStation (Agilent Technologies, Santa Clara, CA) and a Qubit-BR dsDNA Assay Kit (Thermo Fisher Scientific).

Enrichment and Sequencing

To enrich sample libraries for both the Agouti locus as well as more than 1,000 randomly distributed genomic regions, and following Linnen et al. (2013), we used a MYcroarray MYbaits capture array (MYcroarray, Ann Arbor, MI). This probe set includes the 185-kb region containing all known Agouti coding exons and regulatory elements (based on a P. maniculatus rufinus Agouti BAC clone from Kingsley et al. 2009) and >1,000 nonrepetitive regions averaging 1.5 kb in length at random locations across the P. maniculatus genome.

After generating 23 indexed pools of barcoded libraries from 249 individual Sand Hills mice and one lab-derived nonAgouti control, we enriched for regions of interest following the standard MYbaits v.2 protocol for hybridization, capture, and recovery. We then performed 14 cycles of PCR with Phusion High-Fidelity Polymerase and a final AMPure purification. Final quantity and quality was then assessed using a Qubit-HS dsDNA Assay Kit and Agilent 2200 TapeStation. After enriching our libraries for regions of interest, we combined them into four pools and sequenced across eight lanes of 125-bp paired-end reads using an Illumina HiSeq2500 platform (Illumina, San Diego, CA). Of the read pairs, 94% could be confidently assigned to individual barcodes (i.e., we excluded read data where the ID tags were not identical between the two reads of a pair [4%] as well as reads where ID tags had low base qualities [2%]). Read pair counts per individual ranged from 367,759 to 42,096,507 (median 4,861,819).

Reference Assembly

We used the P. maniculatus bairdii Pman_1.0 reference assembly publicly available from NCBI (RefSeq assembly accession GCF_000500345.1), which consists of 30,921 scaffolds (scaffold N50: 3,760,915) containing 2,630,541,020 bp ranging from 201 to 18,898,765 bp in length (median scaffold length: 2,048 bp; mean scaffold length: 85,073 bp) to identify variation in the background regions (i.e., outside of Agouti). Unfortunately, the Agouti locus is split over two overlapping scaffolds (i.e., exon 1 A/A’ is located on scaffold NW_006502894.1 and exons 2–4 are located on scaffold NW_006501396.1) in this assembly, causing issues in the read mapping at this locus. Therefore, reads mapped on either of these two scaffolds were realigned to a novel in-house Peromyscus reference assembly in order to more reliably identify variation at the Agouti locus. The in-house reference assembly consists of 9,080 scaffolds (scaffold N50: 13,859,838) containing 2,512,380,343 bp ranging from 1,000 bp to 60,475,073 bp in length (median scaffold length: 3,275 bp; mean scaffold length: 276,694 bp). In the two reference assemblies, we annotated and masked seven different classes of repeats (i.e., SINE, LINE, LTR elements, DNA elements, satellites, simple repeats, and low complexity regions) using RepeatMasker v.Open-4.0.5 (Smit et al. 2013).

Sequence Alignment

We removed contamination from the raw read pairs and trimmed low quality read ends using cutadapt v.1.8 (Martin 2011) and TrimGalore! v.0.3.7 (http://www.bioinformatics.babraham.ac.uk/projects/trim_galore). We aligned the preprocessed, paired-end reads to the reference assembly using Stampy v.1.0.22 (Lunter and Goodson 2011). PCR duplicates as well as reads that were not properly paired were then removed using SAMtools v.0.1.19 (Li et al. 2009). After cleaning, read pair counts per individual ranged from 220,960 to 20,178,669 (median: 3,062,998). We then conducted a multiple sequence alignment using the Genome Analysis Toolkit (GATK) IndelRealigner v.3.3 (McKenna et al. 2010; DePristo et al. 2011; Van der Auwera et al. 2013) to improve variant calls in low-complexity genomic regions, adjusting Base Alignment Qualities at the same time in order to down weight base qualities in regions with high ambiguity (Li 2011). Next, we merged sample-specific reads across different lanes, thereby removing optical duplicates using SAMtools v.0.1.19. Following GATK’s Best Practice, we performed a second multiple sequence alignment to produce consistent mappings across all lanes of a sample. The resulting data set contained aligned read data for 249 individuals from 11 different sampling locations.

Variant Calling and Filtering

We performed an initial variant call using GATK’s HaplotypeCaller v.3.3 (McKenna et al. 2010; DePristo et al. 2011; Van der Auwera et al. 2013), and then we genotyped all samples jointly using GATK’s GenotypeGVCFs v.3.3 tool. Postgenotyping, we filtered initial variants using GATK’s VariantFiltration v.3.3, removing SNPs using the following set of criteria (with acronyms as defined by the GATK package): 1) The variant exhibited a low read mapping quality (MQ < 40), 2) the variant confidence was low (QD < 2.0), 3) the mapping qualities of the reads supporting the reference allele and those supporting the alternate allele were qualitatively different (MQRankSum<−12.5), 4) there was evidence of a bias in the position of alleles within the reads that support them between the reference and alternate alleles (ReadPosRankSum<−8.0), or 5) there was evidence of a strand bias as estimated by Fisher’s exact test (FS > 60.0) or the Symmetric Odds Ratio test (SOR > 4.0). We removed indels using the following set of criteria: 1) The variant confidence was low (QD < 2.0), 2) there was evidence of a strand bias as estimated by Fisher’s exact test (FS > 200.0), or 3) there was evidence of bias in the position of alleles within the reads that support them between the reference and alternate alleles (ReadPosRankSum<−20.0). For an in-depth discussion of these issues, see the recent review of Pfeifer (2017).

To minimize genotyping errors, we excluded all variants with a mean genotype quality of less than 20 (corresponding to P[error] = 0.01). We limited SNPs to biallelic sites using VCFtools v.0.1.12 b (Danecek et al. 2011), with the exception of one previously identified putatively beneficial triallelic variant (Linnen et al. 2013). We excluded variants within repetitive regions of the reference assembly from further analyses as potential misalignment of reads to these regions might lead to an increased frequency of heterozygous genotype calls. Additionally, we filtered variants on the basis of the Hardy–Weinberg equilibrium by computing a P-value for Hardy–Weinberg equilibrium for each variant using VCFtools v.0.1.12 b and excluding variants with an excess of heterozygotes (P < 0.01), unless otherwise noted. Finally, we removed sites for which all individuals were fixed for the nonreference allele as well as sites with more than 25% missing genotype information.

The resulting call set contained 8,265 variants on scaffold 16 (containing Agouti) and 649,300 variants within the random background regions. We polarized variants within Agouti using the P. maniculatus rufinus Agouti sequence (Kingsley et al. 2009) as the outgroup. Genotypes were phased using BEAGLE v.4 (Browning and Browning 2007). The Agouti data are available at: https://figshare.com/s/7ece137411ae5cf8ba56 and the random, genome-wide (i.e., non-Agouti) data are available at: https://figshare.com/s/b312029e47f34268a8ce.

Accessible Genome

To minimize the number of false positives in our data set, we subjected variants to several stringent filter criteria. The application of these filters led to an exclusion of a substantial fraction of genomic regions, and thus we generated mask files (using the GATK pipeline described above, but excluding variant-specific filter criteria, i.e., QD, FS, SOR, MQRankSum, and ReadPosRankSum) to identify all nucleotides accessible to variant discovery. After filtering, only a small fraction of the genome (i.e., 63,083 bp within Agouti and 6,224,355 bp of the random background regions) remained accessible. These mask files enabled us to obtain an exact number of the monomorphic sites in the reference assembly, which we then used to both estimate the demographic history of focal populations as well as a control to avoid biases when calculating summary statistics.

Association Mapping

To identify SNPs within Agouti that contribute to variation in mouse coat color, we used the Bayesian sparse linear mixed model (BSLMM) implemented in the software package GEMMA v 0.94.1 (Zhou et al. 2013). In contrast to single-SNP association mapping approaches (e.g., Purcell et al. 2007), the BSLMM is a polygenic model that simultaneously assesses the contribution of multiple SNPs to phenotypic variation. Additionally, compared with other polygenic models (e.g., linear mixed models and Bayesian variable selection regression), the BSLMM performs well for a wide range of trait genetic architectures, from a highly polygenic architecture with normally distributed effect sizes to a “sparse” model in which there are a small number of large-effect mutations (Zhou et al. 2013). Indeed, one benefit of the BSLMM (and other polygenic models) is that hyperparameters describing trait genetic architecture (e.g., number of SNPs, relative contribution of large- and small-effect variants) can be estimated from the data. Importantly, the BSLMM also accounts for population structure via inclusion of a kinship matrix as a covariate in the mixed model.

For each of the five color traits that differed significantly between on Sand Hills and off Sand Hills habitats (i.e., dorsal brightness, dorsal hue, ventral brightness, dorsal–ventral boundary, and tail stripe, see “Results and Discussion”), we performed ten independent GEMMA runs, each consisting of 25 million generations, with the first five million generations discarded as burn-in. Because we were specifically interested in the contribution of Agouti variants to color variation, we restricted our GEMMA analysis to 2,148 Agouti SNPs that had no missing data and a minor allele frequency (MAF) > 0.05. However, to construct a relatedness matrix, we used the genome-wide SNP data set. We aimed to maximize the number of individuals kept in the analyses, and hence we used less stringent filtering criteria than for the demographic analyses. Prior to construction of this matrix, we removed all individuals with a mean depth (DP) of coverage lower than 2×. Following the removal of low-coverage individuals, we treated genotypes with less than 2× coverage or twice the individual mean DP as missing data and removed SNPs with more than 10% missing data across individuals or with a MAF < 0.01. To remove tightly linked SNPs, we sampled one SNP per 1-kb block, choosing whichever SNP had the lowest amount of missing data, resulting in a data set with 12,920 SNPs (supplementary table 8, Supplementary Material online). We then computed the relatedness matrix using the R/Bioconductor (release 3.4) package SNPrelate v1.8.0 (Zheng et al. 2012). For all traits, we used normal quantile transformed values to ensure normality, and option “-bslmm 1” to fit a standard linear BSLMM to our data.

After runs were complete, we assessed convergence on the desired posterior distribution via examination of trace plots for each parameter and comparison of results across independent runs. We then summarized PIPs for each SNP for each trait by averaging across the ten independent runs. Following (Chaves et al. 2016), we used a strict cut-off of PIP > 0.1 to identify candidate SNPs for each color trait (cf. Gompert et al. 2013; Comeault et al. 2014). To summarize genetic architecture parameter estimates for each trait, we calculated the mean and upper and lower bounds of the 95% credible interval for each parameter from the combined posterior distributions derived from the ten runs.

To identify additional candidate regions contributing to color variation and to compare genetic architecture parameter estimates from Agouti to those obtained using the full data set (Agouti SNPs and non-Agouti SNPs), we repeated the GEMMA analyses as described above, but with a data set consisting of 8,616 SNPs that had no missing data and MAF > 0.05.

Population Structure

We investigated the structure of populations along the Nebraska Sand Hills transect with several complementary approaches. First, we used methods to cluster individuals based on their genetic similarity, including PCA and inference of individual ancestry proportions. Second, on the basis of SNP allele frequencies, we computed pairwise F_ST between sampled sites to infer their relationships. In addition, we inferred the population tree best fitting the covariance of allele frequencies across sites using TreeMix v1.13 (Pickrell and Pritchard 2012). Finally, we tested for IBD by comparing the matrix of geographic distances between sites to that of pairwise genetic differentiation (F_ST/[1 − F_ST]; Rousset 1997) using Mantel tests (Sokal 1979; Smouse et al. 1986) as well as methods to infer ancestry proportions accounting for geographic location.

For demographic analyses, we based all analyses on the background regions randomly distributed across the genome (i.e., excluding Agouti) and applied additional filters to maximize the quality of the data. First, we discarded individuals with a mean depth of coverage (DP) across sites lower than 8×. Second, given that the DP was heterogeneous across individuals, we treated all genotypes with DP < 4 or with more than twice the individual mean DP as missing data to avoid genotype call errors due to low coverage or mapping errors. Third, we partitioned each scaffold into contiguous blocks of 1.5 kb size, recording the number of SNPs and accessible sites for each block. To minimize regions with spurious SNPs (e.g., due to mis-alignment or repetitive regions), we only kept blocks with more than 150 bp of accessible sites and with a median distance among consecutive SNPs larger than 3 bp. This resulted in a data set consisting of 190 individuals with ∼2.8 Mb distributed across 11,770 blocks, with 284,287 SNPs and a total of 2,814,532 callable sites (corresponding to 2,530,245 monomorphic sites; supplementary table 9, Supplementary Material online). Fourth, to minimize missing data, we only kept SNPs with at least 90% of called genotypes, and individuals with at least 75% of data across sites in the data set. Finally, since many of the applied methods rely on the assumption of independence among SNPs, we generated a data set by sampling one SNP per block, selecting the SNP with the lowest amount of missing data.

The PCA and the pairwise F_ST (estimated following Weir and Cockerham 1984) analyses were performed in R using the method implemented in the Bioconductor (release 3.4) package SNPrelate v1.8.0 (Zheng et al. 2012). We inferred the ancestry proportions of all individuals based on K potential components using sNMF (Frichot et al. 2014) implemented in the R/Bioconductor release 3.4 package LEA v1.6.0 (Frichot et al. 2015) with default settings. We examined K values from 1 to 12, and selected the K that minimized the cross entropy as suggested by Frichot et al. (2014). We performed the PCA, F_ST and sNMF analyses by applying an extra MAF filter > (1/2n), where n is the number of individuals, such that singletons were discarded. To test for IBD, we compared the estimated F_ST values to the pairwise geographic distances (measured as a straight line from the most northern sample, i.e., Colome) between sample sites using a Mantel test, with significance assessed by 10,000 permutations of the genetic distance matrix. In addition, fine scale population structure was accounted for using the TESS3 R package (Caye et al. 2016). Given the similar cross-entropy values in sNMF for K = 1 to 3, 100 independent runs for each K value were performed with a tolerance of 10⁻⁶ and 200 iterations per run.

Demographic Analyses

To uncover the colonization history of the Nebraska Sand Hills, we inferred the demographic history of populations based on the joint SFS obtained from the random anonymous genomic regions, using the composite likelihood method implemented in fastsimcoal2 v3.05 (Excoffier et al. 2013). In particular, we were interested in testing whether the Sand Hills populations were founded widely from across the ancestral range, or whether there was a single colonization event. We also aimed to quantify the current and past levels of gene flow among populations. We considered models with three populations corresponding to samples on the Sand Hills (i.e., Ballard, Gudmundsen, SHGC, Arapaho, and Lemoyne) as well as off of the Sand Hills in the north (i.e., Colome, Dogear, and Sharps) and in the south (i.e., Ogallala, Grant, and Imperial). Specifically, we considered two alternative three-population demographic models, as those are best supported by the data, to test whether the colonization of the Sand Hills most likely occurred from the north or from the south, in a single event or serial events, thereby simultaneously quantifying the levels of gene flow between populations on and off of the Sand Hills (supplementary fig. 2, Supplementary Material online). In these models, we assumed that colonization dynamics were associated with founder events (i.e., bottlenecks), and the number and place of which along the population trees were allowed to vary among models. However, parameter values corresponding to a no size change model (i.e., no bottleneck) were included for evaluation. Mutation rates and generation times were taken following Linnen et al. (2009, 2013).

We constructed a 3D SFS by pooling individuals from the three sampling regions (i.e., on the Sand Hills as well as off of the Sand Hills in the north and south). For each of the 11,770 blocks of 1.5 kb size, 30 individuals (i.e., ten individuals from each of the three geographic regions) were selected such that all SNPs within a given block exhibited complete genotype information. Specifically, we selected the 30 individuals with the least missing data for each block, only including SNPs with complete genotype information across the chosen individuals, a procedure that maximized the number of SNPs without missing data while keeping the local pattern of linkage disequilibrium within each block. Note that we sampled genotypes of the same individuals within each block, but that at different blocks the sampled individuals might differ. For each block, we computed the number of accessible sites and discarded blocks without any SNPs.

The resulting 3D-SFS contained a total of 140,358 SNPs and 2,674,174 accessible sites (supplementary table 8, Supplementary Material online). The number of monomorphic sites was based on the number of accessible sites, assuming that the proportion of SNPs lost with the extra DP filtering steps, not included in the mask file, was identical for polymorphic and monomorphic sites. Given that there was no closely related outgroup sequence available to determine the ancestral allele for SNPs within the random background regions, we analyzed the multidimensional folded SFS, generated using Arlequin v.3.5.2.2 (Excoffier and Lischer 2010). For each model, we estimated the parameters that maximized its likelihood by performing 50 optimization cycles (-L 50), approximating the expected SFS based on 350,000 coalescent simulations (-N 350,000), and using as a search range for each parameter the values reported in the supplementary table 10, Supplementary Material online.

The model best fitting the data was selected using Akaike’s information criterion (Akaike 1974). Because our data set likely contains linked sites, the confidence for a given model is likely to be inflated. Thus, to compare models, we generated bootstrap replicates with one SNP sampled from each 1.5-kb block, which we assumed to be independent. We estimated the likelihood of each bootstrap replicate based on the expected SFS obtained for each model with the full set of SNPs (following Bagley et al. 2017). Furthermore, we obtained confidence intervals for the parameter estimates by a nonparametric block-bootstrap approach. To account for linkage disequilibrium, we generated 100 bootstrap data sets by sampling the 11,770 blocks for each bootstrap data set with replacement in order to match the original data set size. For each data set, we performed two independent runs using the parameters that maximized the likelihood as starting values. We then computed the 95 percentile confidence intervals of the parameters using the R-package boot v.1.3-18.

Selection Analyses

We used VCFtools v.0.1.12 b (Danecek et al. 2011) to calculate Weir and Cockerham’s F_ST (Weir and Cockerham 1984) in the Agouti region. We pooled the 11 sampling locations into three populations (i.e., one population on the Sand Hills and two populations off of the Sand Hills: One in the north and one in the south, see Demographic Analyses) and calculated F_ST in a sliding window (window size 1 kb, step size 100 bp) as well as on a per-SNP basis within Agouti to identify highly differentiated candidate regions for local adaptation.

To control for potential hierarchical population structure as well as past fluctuations in population size, we also measured genetic differentiation using the HapFLK method (Fariello et al. 2013). HapFLK calculates a global measure of differentiation for each SNP (FLK) or inferred haplotype (HapFLK) after having rescaled allele/haplotype frequencies using a population kinship matrix. We calculated the kinship matrix using the complete data set, excluding the scaffolds containing Agouti. We launched the HapFLK software using 40 independent runs (–nfit 40) and –K 40, only keeping alleles with a MAF > 0.05. We obtained the neutral distribution of the HapFLK statistic by running the software on 1,000 neutral simulated data sets under our best demographic model.

To map potential complete selective sweeps in the Agouti region, we utilized the CLR method (Nielsen et al. 2005) as implemented in the software Sweepfinder2 (DeGiorgio et al. 2016). For the analysis, we used the P. maniculatus rufinus Agouti sequence to identify ancestral and derived allelic states (see Variant Calling and Filtering). We ran Sweepfinder2 with the “–su” option, defining grid-points at every variant and using a precomputed background SFS. We calculated the cutoff value for the CLR statistic using a parametric bootstrap approach (as proposed by Nielsen et al. 2005). For this purpose, we reran the CLR analysis on 10,000 data sets simulated under our inferred neutral demographic model for the Sand Hills populations in order to reduce false-positive rates (see Crisci et al. 2013; Poh et al. 2014).

Calculating Conditions of Allele Maintenance

Following Yeaman and Whitlock (2011), the threshold for allele maintenance is defined as the migration rate that satisfies $\delta$=1/(4 N), which represents the criteria at which allele frequency changes owing to genetic drift are on the same order as frequency changes owing to the interplay between selection and migration. Further, in order to extend this migration threshold to the consideration of a phenotypic trait, they define the fitness (W) of phenotype (Z) as:

$$W=1–\Phi (\theta -Z/\left(2\theta \right){)}^{\gamma },$$

where $\Phi$ is the strength of stabilizing selection, $\theta$ is the locally adaptive phenotype which takes a positive value in the derived population and a negative value in the ancestral population, and $\gamma$ specifies a curvature for the function. Further, the effect size of the underlying mutation is given as $\alpha$. Following Yeaman and Otto (2011), $\delta$ may then be defined as:

$$\delta =\frac{\psi }{2}+\frac{1}{2}\sqrt{{\psi }^2-4\left(1-2m\right)\frac{W_{1,Aa}}{W_{1,AA}}\frac{W_{2,Aa}}{W_{2,AA}}-1},$$

where $\psi =\left(1-m\right)(\frac{W_{1,Aa}}{W_{1,AA}}+\frac{W_{2,Aa}}{W_{2,AA}})$, W_ij is the fitness of allele j in environment i, a is the allele beneficial in the ancestral environment and deleterious in the derived environment, and A is the allele that is beneficial in the derived environment. Finally, Yeaman and Whitlock (2011) define the migration threshold for a particular value of $\alpha$as:

$$m_{\text{threshold}}=\frac{1}{\frac{W_{1,Aa}}{W_{1,Aa}-W_{1,AA}\left(1+\frac{1}{4N}\right)}-\frac{W_{2,Aa}}{W_{2,AA}\left(1+\frac{1}{4N}\right)-W_{2,Aa}}}.$$

To compare with our empirical observations and inferred values, we take for the sake of example the identified serine deletion in exon 2, compared between the Sand Hills and the northern population. First, we set $\theta =\pm 1$ (i.e., positive on the Sand Hills, negative off of the Sand Hills), and $\gamma$ = 2 (i.e., a convex shape [Yeaman and Whitlock 2011]). Inference pertaining to the strength of selection acting on the cryptic phenotype has been made, most notably from previous predation experiments in which conspicuously colored phenotypes were attacked significantly more often than those that were cryptically colored, with a calculated selection index = 0.545 (Linnen et al. 2013). Furthermore, previous crossing experiments have suggested that the serine deletion is a dominant allele (Linnen et al. 2009). Finally, the most strongly associated trait has here been calculated near 0.5 (i.e., dorsal brightness). For the corresponding value of $\alpha$, this suggests a migration threshold of m = 0.8. Thus, for the serine deletion, it is readily apparent that our inferred migration rates are well below this expected threshold allowing maintenance (where the 95% CI is contained in m < 0.0004).

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.