New algorithms to represent complex pseudoknotted RNA structures in dot-bracket notation

Abstract

Motivation

Understanding the formation, architecture and roles of pseudoknots in RNA structures are one of the most difficult challenges in RNA computational biology and structural bioinformatics. Methods predicting pseudoknots typically perform this with poor accuracy, often despite experimental data incorporation. Existing bioinformatic approaches differ in terms of pseudoknots’ recognition and revealing their nature. A few ways of pseudoknot classification exist, most common ones refer to a genus or order. Following the latter one, we propose new algorithms that identify pseudoknots in RNA structure provided in BPSEQ format, determine their order and encode in dot-bracket-letter notation. The proposed encoding aims to illustrate the hierarchy of RNA folding.

Results

New algorithms are based on dynamic programming and hybrid (combining exhaustive search and random walk) approaches. They evolved from elementary algorithm implemented within the workflow of RNA FRABASE 1.0, our database of RNA structure fragments. They use different scoring functions to rank dissimilar dot-bracket representations of RNA structure. Computational experiments show an advantage of new methods over the others, especially for large RNA structures.

Availability and implementation

Presented algorithms have been implemented as new functionality of RNApdbee webserver and are ready to use at http://rnapdbee.cs.put.poznan.pl.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Understanding the RNA structure is crucial for learning the principles of RNA folding, its regulatory impact on transcription and translation, catalytic properties, specificity of RNA-protein interactions and viral infectivity (Mortimer et al., 2014). The RNA folding process has been shown to follow a hierarchical pathway in which domains are assembled sequentially (Batey et al., 1999; Brion and Westhof, 1997; Mustoe et al., 2014; Fig. 1). At first, upon folding of RNA strand, its selected nucleotide residues interact through base-pairing to form diverse secondary structure motifs like hairpin apical loops, bulges, internal and n-way junction loops, separated by stems that consist of stacked Watson-Crick and GU wobble base pairs mostly. By that means, the secondary structure is established at the molten globule state (Brion and Westhof, 1997). Subsequently, intramolecular tertiary interactions position the secondary structure elements with respect to each other, often bringing nucleotide residues from distant molecule parts to a close contact and initiating formation of structure motifs called pseudoknots. This generates the conformational space of RNA three-dimensional (3D) structures, to be related to their biological functions (Guo and Cech, 2002; Woodson, 2002).

Fig. 1.

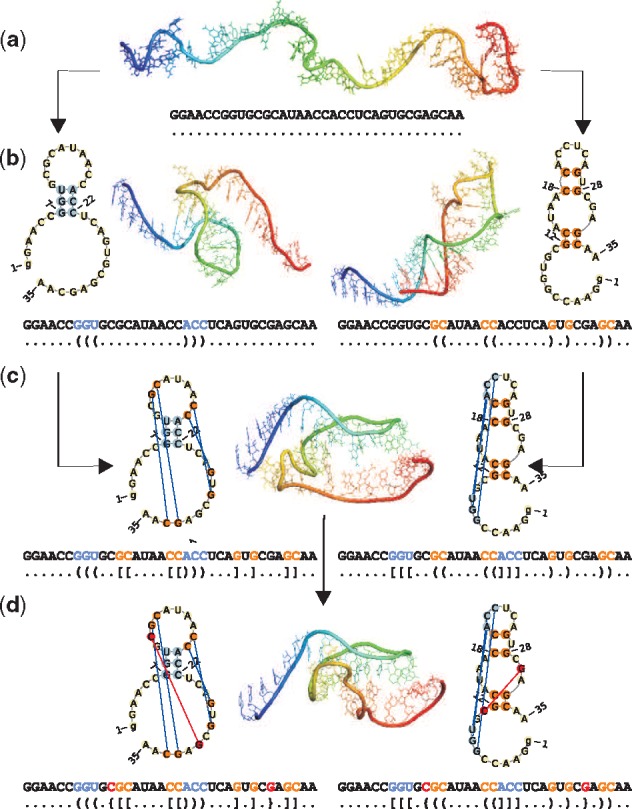
Subsequent tiers of cyanocobalamin aptamer (1DDY, chain A) folding pathway from (a) single-stranded form, through creation of (b) a hairpin and (c) first order pseudoknot of H-type, to (d) the final structure with second order pseudoknot of L-type

Large RNAs often contain pseudoknots, classified both on secondary and tertiary structure level. They occur when loop- or bulge-involved nucleotides pair with a single-stranded region outside to form a double helical segment. In general, four basic types of pseudoknots have been distinguished: H-type (loop—single-stranded region outside of the loop), K-type (loop—loop interaction), L-type and M-type (being more complex pseudoknots) (Kucharík et al., 2015). As the name suggest, pseudoknots are not real knots. Although pulling 5’ and 3’ ends of the RNA strand, pseudoknot yields a fully stretched chain, whereas physical knot tightens. Formation of pseudoknots makes RNA structures more compact and is often linked to biological function(s) attributed to that particular motif (Cho et al., 2009).

As the first observation of pseudoknot in turnip yellow mosaic virus structure (Rietveld et al., 1982), this motif and its biological functions were intensively studied (Staple and Butcher, 2005). It was shown (Antczak et al., 2014; Chiu and Chen, 2012) that over 53% of RNA structures in Protein Data Bank (Berman et al., 2000) contain pseudoknots. Among them 20% has simple H-type pseudoknots formed by two conflicting regions only, the remaining RNAs include more complex pseudoknots. Structure complexity in this sense corresponds to the tiers in RNA folding hierarchy (Mustoe et al., 2014). Simple pseudoknots appear first, followed by formation of more complicated ones when folding process advances. Such hierarchy is exemplified in Figure 1 which illustrates consecutive steps of cyanocobalamin aptamer folding along two alternative pathways. At first, the basic secondary structure including hairpin apical loop (left pathway) or hairpin and internal loops (right pathway) is established from a single-stranded form (Fig. 1b). Next, simple H-type pseudoknot is formed (Fig. 1c). In the final step, more complex L-type pseudoknot is created (Fig. 1d). The secondary structure on each level of Figure 1 has been encoded in dot-bracket notation and visualized by PseudoViewer (Byun and Han, 2009). The 3D structures in Figure 1(a–c) have been generated by RNAComposer (Popenda et al., 2012), while Figure 1d displays the X-ray structure of cyanocobalamin aptamer (Sussman et al., 2000). The tertiary structures have been visualized in PyMOL (DeLano, 2002) using the rainbow scale to label consecutive residues from 5’- (blue) to 3’-end (red).

Despite the considerable accumulation of experimental data and bioinformatics studies addressing pseudoknot problems, there are still some unresolved issues. For example, difficulties and ambiguity in pseudoknot encoding resulted in the fact that many computational methods cannot reliably handle them. Therefore, several algorithms have been developed to extract the core structure including nested base pairs only, by removing pseudoknots (Chiu and Chen, 2015; Smit et al., 2008). However, identifying which of two conflicted helical regions is responsible for a pseudoknot formation, and, thus, should be removed, is not an obvious procedure. For example, extraction of a nested structure for RNA shown in Figure 1d may end up in obtaining one of two structures displayed in Figure 1b which vary significantly. It has been agreed that an important decisive factor––although not always the only one––is the region’s length (number of base pairs in the region). That is, if we consider two conflicted double-stranded regions, the shorter one is regarded to have initiated pseudoknot formation, while the longer region is within the basic structure. Such simple rule has been followed i.a. in (Antczak et al., 2014; Ponty, 2006; Popenda et al., 2008; Rybarczyk et al., 2015; Smit et al., 2008), mostly applying fast greedy procedures sufficient to solve optimally not complicated structures (with H- and K-type pseudoknots). The problem becomes harder if conflicted regions have the same length and when pseudoknot involves more than two regions, like it is observed in L- and M-type pseudoknots. For such cases, greedy algorithms do not guarantee the optimal solution. Highly conflicted sub-structures have a significant impact on structure-based analysis, especially if this is made by automated, computational approaches. For many years, also text representation of their topology has been ambiguous. Conventional parentheses notation allowed to encode nothing more besides a nested RNA structure topology, and the first version of extended dot-bracket notation allowed to handle simple pseudoknots only (Byun and Han, 2009; Hofacker et al., 1994).

This situation resulted in slower than expected progress in the field of secondary-structure-based 3D structure prediction of pseudoknotted RNAs as well as in their annotation from 3D data (Miao et al., 2017; Purzycka et al., 2015). To advance studies in these directions, it is necessary to have an access to a reliable representation of RNA secondary structure with complex pseudoknots. Here, we propose new algorithms that can handle such RNAs and process them on the secondary structure level. Our methods are based on exhaustive search approach and provide exact (optimum) solution. They operate on BPSEQ-formatted data, handling all base pairs listed in the input file regardless of their types. They identify, count and classify pseudoknots and encode them in dot-bracket notation which reflects the RNA structure topology and hierarchy of the folding process. These new algorithms have been implemented within RNApdbee web server (http://rnapdbee.cs.put.poznan.pl), where they support the route from RNA 3D structure to secondary structure. They can be also run separately to allow the user for conversion of BPSEQ data to dot-bracket notation and graphical view of the secondary structure.

2 Materials and methods

The basic way of describing the RNA secondary structure is to list base pairs (e.g. in BPSEQ format), which are formed during the molecule folding to stabilize the structure. Usually, such base pairs are formed surrounded by other pairs, thus, creating longer double-stranded regions. Occasionally, single isolated base pairs occur in RNA structures.

A double-stranded (paired) region contains only nested base pairs. Two base pairs (i, i’) and (j, j’) are nested if i < j<j’<i’. However, sometimes we can find base pairs––we will call them crossed or conflicted––which form pseudoknot(s). A pseudoknot occurs if for any pair (i, i’) there exists another one, (j, j’), such that and i < j<i’<j’ (Studnicka et al., 1978). It is believed that in the process of RNA hierarchical folding nested base pairs are formed at first, while pseudoknotted ones bind in the next steps.

For many years, complete, unambiguous representation of pseudoknots in text and graphical form has been a non-trivial problem, especially in the case of highly conflicted structures. In (Popenda et al., 2008), we have introduced our first method for encoding pseudoknotted RNA structure in dot-bracket notation extended to dot-bracket-letter (DBL) (Table 1). DBL allowed to encode various pseudoknots, e.g. H-type: $(\hspace{0.17em}[\hspace{0.17em})\hspace{0.17em}]$, K-type: $(\hspace{0.17em}[\hspace{0.17em})\hspace{0.17em}(\hspace{0.17em}]\hspace{0.17em})$, L-type: $(\hspace{0.17em}[\hspace{0.17em}\{\hspace{0.17em})\hspace{0.17em}]\hspace{0.17em}\}$ and M-type pseudoknot: $(\hspace{0.17em}[\hspace{0.17em}\{\hspace{0.17em})\hspace{0.17em}(\hspace{0.17em}]\hspace{0.17em}\}\hspace{0.17em})$. The new method aimed to generate and clearly present DBL representation of the secondary structure topology based on the input BPSEQ data. All canonical and non-canonical base pairs listed in the input BPSEQ file were handled similarly. This First-Come-First-Served (FCFS) algorithm (Algorithm 1) was applied within the workflow of RNA FRABASE 1.0 (Popenda et al., 2008). Each double-stranded region was handled in the order determined by its first residue number, due to the residue arrangement in RNA sequence from 5’ to 3’-end. Every region was assigned an order (regorder) that translated into characters used to represent all of its base pairs in DBL notation (Table 1). Starting from the first in line region, which was assigned regorder = 0, the succeeding regions were pushed onto order-labelled stack(s) in order of their appearance in RNA sequence. If the newly pushed region was conflicting with anything already on current stack, a global order value was increased by 1, order-labelled stack (if non-existent) was created and current region pushed onto it with regorder = global order assigned. Once the closing of a region was found, the region was popped from its stack.

Table 1.

Base pair encoding in DBL notation

Region order (regorder):	0	1	2	3	4	5	6	7	8
Base pair representation:	()	[]	{}	< >	A a	B b	C c	D d	E e

Algorithm 1 FCFS algorithm from RNA FRABASE 1.0

Input:ssin – RNA secondary structure in BPSEQ format

Output:ssout – RNA secondary structure in DBL notation

1: function FCFS(ssin)

2:  regs ← findAllPairedRegions(ssin)

3:  n ← |regs|           ▹ count paired regions

4:  sortRegionsByStartPoint(regs)

5:  setRegionOrders(regs, n)   ▹ assign orders to regions

6:  ssout ← encodeBasePairs(regs)  ▹ encode solution in DBL

7:  returnssout

8: end function

9:

10: procedure setRegionOrders(regs, n)

11:  $regs[1].ord$ ← 0

12:  for$i\leftarrow 2 \text{to} n$do

13:   order ← 0

14:   for$j\leftarrow 1 \text{to} i-1$do

15:    if$regs[j].ord=order$ AND

16:     $conflicted(regs[j],regs[i])$then

17:     order ← order + 1

18:    end if

19:   end for

20   $regs[i].ord$ ← order

21:  end for

22: end procedure

In (Antczak et al., 2014), we have introduced a concept of a pseudoknot order and we have applied it in RNApdbee tool to compute orders of pseudoknot-forming regions. Following the approach presented in (Smit et al., 2008), we have defined the pseudoknot order as a minimum number of base pair set decompositions resulting in a nested structure. Thus, for example, if there is a pseudoknot structure involving three conflicted double-stranded regions, A, B, C and a decomposition of one region (preferably one including the least number of base pairs)––e.g. B––leads to a structure without conflicts, then the pseudoknot has an order equal to 1 (psorder = 1). Based on that, we can assign region orders in the following way. Region B selected for decomposition has regorder = 1 (the same as pseudoknot order), and the remaining regions, A and C, have regorder = 0 (since after decomposition they are not crossed). In general, a pseudoknot with psorder = k consists of regions with regorder = 0…k. The maximum order among regions involved in a pseudoknot is a pseudoknot order. Thus, H- and K-type pseudoknots are topologically simple with psorder = 1, while more complex L- and M-type pseudoknots have psorder = 2.

To compute pseudoknot orders and region orders (for the purpose of their further encoding and visualization), a modified version of Elimination Gain (EG) heuristics introduced in (Smit et al., 2008) was incorporated into RNApdbee. EG application results in obtaining RNA secondary structure topology which maximizes the length of double-stranded regions with small order value. However, since EG is based on a greedy approach, it does not guarantee finding an optimal solution. Thus, we have developed a Dynamic Programming (DP) algorithm applying the same criterion and we have compared its performance with EG heuristics.

Further study of RNApdbee-annotated secondary structures has led us to consider alternative criterion of optimality, which is a minimum pseudoknot order throughout the whole structure. Hence, we have proposed a new criterion function and we designed new algorithms to encode pseudoknotted RNA structures in DBL notation. The detailed description of our new algorithms is provided in the next section.

3 Algorithms

The presented algorithms apply different approaches to solve the problem of pseudoknot identification and classification, and pseudoknotted RNA secondary structure encoding. The Hybrid algorithm (HYB) combines heuristic and exact procedures. DP finds the solution by treating succeeding sub-problems. Each method optimizes solution with reference to own criterion function. The function used in DP (Section 3.1) aims to maximize the number of non-conflicted base pairs at each computational step. Function in HYB (Section 3.2) combines maximization of nested base pair number with minimization of the highest pseudoknot order for the entire structure.

3.1 Criterion function I

All existing heuristics for pseudoknot identification and removal [EG, Elimination Conflict (EC), etc.] that we have tested follow the same criterion to evaluate representation R(S) of RNA secondary structure S. It is defined by function fscoreI:

$$\begin{array}{l}fscoreI\left(R\right)={\sum }_{1\le i\le n,order\left(re{g}_i\right)=0}length\left(re{g}_i\right)\hfill \end{array}$$ (1)

where length(reg_i) denotes a length (number of base pairs) of the i-th region, order(reg_i) stands for the i-th region order and n is a number of paired regions in structure S.

The function (Formula 1) sums up lengths of all non-conflicted double-stranded regions in S. The representation R(S) with a maximum value of fscoreI wins. When the above-mentioned methods are used to determine pseudoknot orders, we run them iteratively. In every j-th iteration (j = 0, 1, 2,…), fscoreI is applied to select the maximum nested sub-structure. All non-conflicted regions in the best solution are assigned regorder = j and removed from structure S. Next iteration is processed with the reduced representation of S to identify regions with regorder = j + 1, etc.

fscoreI has been also applied to optimally evaluate partial solutions in newly developed DP algorithm (Section 3.3).

3.2 Criterion function II

An analysis of the results obtained by methods applying fscoreI for complex RNA structures made us propose a modified version of the criterion function. It is defined as two-element vector function fscoreII, where each element is a weighted sum of lengths of particular double-stranded regions in S:

$$\begin{array}{ll}fscoreII\left(R\right)=\hfill & \left[\begin{array}{l}\sum _{i=1}^n(1-x_i)·length\left(re{g}_i\right)\\ -1·\sum _{i=1}^{n}order\left(re{g}_i\right)·length\left(re{g}_i\right)\end{array}\right]\hfill \\ \hfill & \text{where} x_i=\{\begin{array}{ll}0,\hfill & \text{if} order\left(re{g}_i\right)=0\hfill \\ 1,\hfill & \text{otherwise}\hfill \end{array}\hfill \end{array}$$ (2)

The components of fscoreII are defined as follows: n denotes a number of paired regions in structure S; length(reg_i) stands for a length of the i-th region; order(reg_i) is the i-th region order (represented by appropriate character in DBL); x_i is an auxiliary variable.

In practice, the first element of the vector is the same as criterion function defined by Formula 1, i.e. fscoreII[1] = fscoreI. It sums up the lengths of all non-conflicted regions (with regorder = 0). The second element, fscoreII[2], is to sum up the lengths of conflicting regions multiplied by their orders. As, we aim to penalize R(S) for high order regions, the sum in fscoreII[2] is taken with a negative value.

Looking for a representation of structure S, we maximize values of both vector elements. Having two representations, R1(S) and R2(S), we define the following domination rule to decide which one is better:

$$\begin{array}{ll} \text{if} \hfill & fscoreII[1](R1)>fscoreII[1](R2)\hfill \\ \hfill & \text{or} (fscoreII[1](R1)=fscoreII[1](R2)\hfill \\ \hfill & \hspace{1em}\hspace{1em} \text{and} fscoreII[2](R1)>fscoreII[2](R2))\hfill \\ \hfill & \text{then} R1(S) \text{dominates} \text{over} R2(S)\hfill \end{array}$$ (3)

Two example representations of the secondary structure of cyanocobalamin (vitamin B12) aptamer (1DDY, chain A), R1 provided by HYB and R2 output by FCFS, are shown in Figure 2. As it can be seen from fscoreII values, R1 is better than R2, since it dominates on both vector elements (although, according to Formula 3, a domination on fscoreII[1] is sufficient for R1 to be the winner). The difference between R1 and R2 is already in location of zero-order regions. If these results were considered by the procedure aimed to obtain the nested structure by pseudoknot removal, we would observe significant differences at the level of both the secondary and the 3D structure. Figure 1b shows nested structure of cyanocobalamin aptamer that can be obtained by removal of pseudoknots identified by FCFS (left) and HYB (right).

Fig. 2.

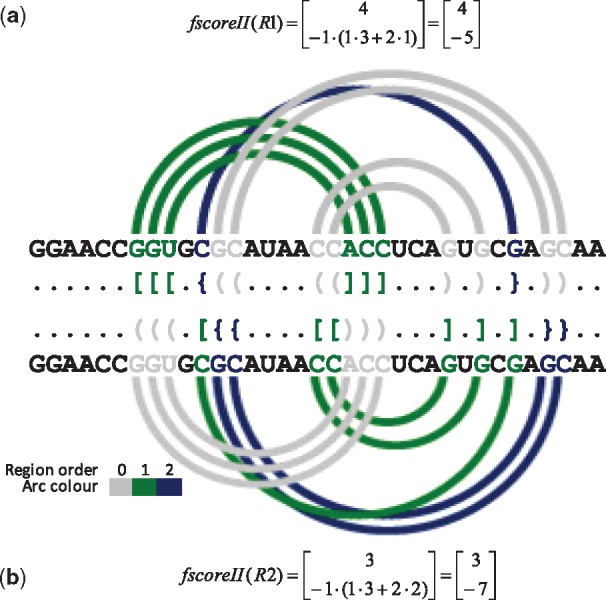
DBL representations of cyanocobalamin aptamer (1DDY, chain A) secondary structure encoded by (a) HYB and (b) FCFS, the corresponding arc diagrams and fscoreII values

3.3 DP algorithm

DP method (Algorithm 2) follows the optimality principle formulated by Richard Bellman (Bellman, 1952). The problem is broken into time separable sub-problems and the solution is accomplished by recursively solving Bellman’s equations. In our case, the sub-problem lies in the classification of a single base pair.

Algorithm 2 DP algorithm

Input:ssin – RNA secondary structure in BPSEQ format

Output:ssout – RNA secondary structure in DBL notation

1: function DynamicProgramming(ssin)

2:  solution ←$\varnothing$

3:  order ← 0

4:  do

5:   bps ← findNestedBasePairs(ssin)

6:   setBasePairOrders(bps, order)

7:   solution ←$solution\cup bps$

8:   order ← order + 1

9:   ssin ←$s\hspace{0.17em}\text{sin}\hspace{0.17em}\mathrm{\setminus }bps$

10:  while$bps\ne \varnothing$

11:  ssout ← encodeBasePairs(solution)

12:  returnssout

13: end function

14:

15: function findNestedBasePairs(ssin)

16:  rawBps ← getAllBasePairs(ssin)

17:  n ←$\left|rawBps\right|$

18:  bpSet ← treatBasePairSet (raw Bps)

19:  scoreMtx ← $createMatrix(n+2,0)$

20:  indexMtx ←$createMatrix(n+2,NN)$

21:  for each$base\hspace{0.17em}pair\hspace{0.17em}(i,i\prime )\in bpSet$do

22:   for$j\leftarrow i+2 \text{to} i\prime -1$do

23:    $j\prime$← getPairedBase(j, bpSet)

24:    if$(j\prime <i$ OR $j\prime >i\prime$ OR $j\prime >j)$then

25:     $updateMtx(i,j,scoreMtx,indexMtx)$   ▹ O1

26:    else if$(j\prime <j)$then

27:     nsc ←$scoreMtx[i+1][j\prime -1]+scoreMtx[j\prime ][j]$

28:     if$(scoreMtx[i+1][j-1]<nsc$ AND

29:      $scoreMtx[i+1][j]<nsc)$then

30:      $scoreMtx[i+1][j]$ ← nsc       ▹ O2

31:      $indexMtx[i+1][j]$ ← j

32:     else

33:      $updateMtx(i,j,scoreMtx,indexMtx)$  ▹ O1

34:     end if

35:    end if

36:   end for

37:   $scoreMtx[i][i\prime ]\leftarrow 1+scoreMtx[i+1][i\prime -1]$  ▹ O3

38:   $indexMtx[i][i\prime ]\leftarrow i\prime$

39:  end for

40:  nestedBps ←$\varnothing$

41:  $addNested(1,n,indexMtx,rawBps,nestedBps)$

42:  returnnestedBps

43: end function

44:

45: procedure updateMtx($i,j,scoreMtx,indexMtx$)

46:  if$(scoreMtx[i+1][j]<scoreMtx[i+1][j-1])$then

47:   $scoreMtx[i+1][j]\leftarrow scoreMtx[i+1][j-1]$

48:   $indexMtx[i+1][j]\leftarrow indexMtx[i+1][j-1]$

49:  end if

50: end procedure

51:

52: procedure addNested($i,i\prime ,indexMtx,rawBps,nestedBps$)

53:  if$(i<i\prime$ AND $indexMtx[i][i\prime ]\ne NN)$then

54:   $j\prime$ ← $indexMtx[i][i\prime ]$

55:   j ←$getPairedBase(j\prime ,rawBps)$

56:   nestedBps ←$nestedBps\cup (j,j\prime )$

57:   $addNested(j+1,j\prime -1,indexMtx,rawBps,nestedBps)$

58:   $addNested(i,j-1,indexMtx,rawBps,nestedBps)$

59:  end if

60: end procedure

The main DP procedure iteratively runs four operations: (i) find a set of nested base pairs in the input set, (ii) associate found base pairs with current order (initially set to 0) and add them to the solution, (iii) increase current order and (iv) remove obtained base pairs from the input set. In each iteration, an optimum subset of nested base pairs is found according to criterion function fscoreI (Formula 1). The algorithm stops when all base pairs are moved from the input set to the solution.

The first step is a key part of the algorithm. It starts from reading current input set (ssin) in BPSEQ format and preparing the data (treatBasePairSet). The latter includes: (i) base pair renumeration, (ii) addition of virtual edge pair and (iii) sorting base pairs with respect to the distance between indexes of paired residues (firstly) and first residue index (secondly) (Supplementary Fig. S1). Next, two DP matrices are allocated and filled recursively with numerical weights. We use scoreMtx matrix to store the ratings of consecutive optimum solutions (nested sets). A cell in indexMtx matrix keeps an index of the closing residue of outermost base pair in currently analyzed nested set. A change in scoreMtx initiates the corresponding modification in indexMtx.

There are three operations followed in filling the cells of scoreMtx:

• O1:$scoreMtx[i$+1$\left]\right[j]$=max$\left\{scoreMtx\right[i$+1$\left]\right[j],scoreMtx[i$+1$\left]\right[j$-1$\left]\right\}$

• O2:$scoreMtx[i$+1$\left]\right[j]$=max$\left\{scoreMtx\right[i$+1$\left]\right[j],scoreMtx[i$+1$\left]\right[j\prime$-1$]+scoreMtx[j\prime \left]\right[j\left]\right\}$

• O3:$scoreMtx\left[i\right][i\prime ]$=1+$scoreMtx[i$+1$\left]\right[i\prime$-1$]$

Their application depends on mutual position of considered base pairs, i.e. for every two base pairs $(i,i\prime ),\hspace{0.17em}(j,j\prime )\in s\hspace{0.17em}\text{sin},\hspace{0.17em}i+1<j<i\prime -1$:

• if $(j,j\prime )$ is nested and $i<j<j\prime <i\prime$ (Supplementary Fig. S2a), or $(i,i\prime ),\hspace{0.17em}(j,j\prime )$ are in conflict (Supplementary Fig. S2b) we perform operation O1,

• if $(j,j\prime )$ is nested, $j\prime <j$ (Supplementary Fig. S2c), and $scoreMtx[i$+1$\left]\right[j\prime$–1$]$+$scoreMtx[j\prime ]\left[j\right]$>$\left(scoreMtx\right[i$+1$\left]\right[j$–1$]$ and $scoreMtx[i$+1$\left]\right[j]$) we apply operation O2,

• if $(j,j\prime )$ is nested, $j\prime <j$ (Supplementary Fig. S2c), and $scoreMtx[i$+1$\left]\right[j\prime$–1$]$+$scoreMtx[j\prime ]\left[j\right]$ < = ($scoreMtx[i$+1$\left]\right[j$–1$]$ or $scoreMtx[i$+1$\left]\right[j]$) we apply operation O1.

Finally, for every $(i,i\prime )$ the algorithm performs operation O3. After filling the matrices, optimum solution (nested set) is back-tracked from indexMtx. Starting from i = 1, $i\prime$=n, if $indexMtx\left[i\right][i\prime ]$=$k\prime$ and $k\prime \ne NN$, then $k\prime$ is the closing residue number of base pair $(k,k\prime )$ in the solution. The opening residue, k, is gained from rawBps. Next, the procedure continues recursively into $indexMtx[k$+1$\left]\right[k\prime$–1$]$ and $indexMtx\left[i\right][k$–1$]$, until stepping into not set cell (NN) (Supplementary Fig. S1).

3.4 Hybrid algorithm

HYB that we introduced (Algorithm 3), combines two procedures, exhaustive search (exSearch) and random walk (randWalk), run depending on the number of conflicting regions in the pseudoknot structure. In the pre-processing stage, it identifies all regions which are not pseudoknot-involved. They obtain a zero order and are disregarded in further steps. Next, the algorithm finds disjoint pseudoknots. Two pseudoknots, P1 and P2, are disjoint if no region involved in the formation of P1 is in conflict with any region in P2. Disjoint pseudoknots are processed separately. All conflicting regions which form one pseudoknot are stored in single container. In detail, one container is a vector of region identifiers and corresponds to a chain of regions’ decompositions leading to a nested structure. A single container is processed iteratively to find the best decomposition chain. In every iteration, the vector is permuted by either exSearch or randWalk. Next, setRegionOrders (Algorithm 1) assigns orders to regions, and the solution is scored using fscoreII (Formula 2). The best permutation for the container is selected due to the domination rule (Formula 3). Thus, for each container one permutation is obtained. They are merged to create final solution for the input structure.

Algorithm 3 Hybrid algorithm

Input:ssin – RNA secondary structure in BPSEQ format

Output:ssout – RNA secondary structure in DBL notation

1: function Hybrid(ssin)

2:  regs ← findAllPairedRegions(ssin)

3:  ncfregs ← findNonConflictedRegions(regs)

4:  $setRegionOrders(ncfregs,|ncfregs|)$

5:  cfregs ←$regs\mathrm{\setminus }ncfregs$

6:  containerSet ← splitRegionsToContainers(cfregs)

7:  for each$container\in containerSet$do

8:   $container.bestSolution$ ← $\varnothing$

9:   $container.bestScore$ ← {0, 0}

10:   m ←$\left|container\right|$

11:   if$(m\le 8)$then

12:    exSearch(container, m)

13:   else

14:    randWalk(container, m)

15:   end if

16:  end for

17:  solution ← mergeBestSolutions(containerSet)

18:  ssout ← encodeBasePairs(solution)

19:  returnssout

20: end function

21:

22: procedure exSearch(container, m)

23:  for$k\leftarrow 1 \text{to} m!$do

24:   currSol ← generateNextSolution(container)

25:   setRegionOrders(currSol, m)

26:   updateBest(container, currSol)

27:  end for

28: end procedure

29:

30: procedure randWalk(container, m)

31:  for$k\leftarrow 1 \text{to} MAX\_ITERATIONS$do

32:   currSol ← shuffleRegions(container)

33:   setRegionOrders(currSol, m)

34:   updateBest(container, currSol)

35:  end for

36: end procedure

37:

38: procedure updateBest(container, currSol)

39:  currScore ← fScore(currSol)

40:  if$(currScore[1]>container.bestScore[1]$ OR

41:    $(currScore[1]=container.bestScore[1]$ AND

42:    $currScore[2]>container.bestScore[2]))$then

43:   $container.bestScore$ ← currScore

44:   $container.bestSolution$ ← currSol

45:  end if

46: end procedure

If the container includes up to eight conflicted regions, the exSearch procedure is used to produce succeeding solutions and to find the exact one, being the global optimum. That is, all permutations of regions within container are generated, order-assigned and scored. Then, the best one is selected as an optimum solution. At most, if the container stores eight regions, exSearch has to handle 40 320 solutions. Otherwise, randWalk is launched. This method generates and scores MAX_ITERATIONS = 10 000 random permutations, and provides the user with sub-optimal solution (Supplementary Fig. S3).

4 Results and discussion

In computational experiments, we have analyzed the performance of five algorithms: First-Come-First-Serve (FCFS) method (Popenda et al., 2008), EG and EC heuristics (Smit et al., 2008) and the new ones, Hybrid (HYB) and DP algorithms. All of them were implemented in Java (including EG and EC, originally developed in Python) and are available through RNApdbee web server (Antczak et al., 2014).

Quantitative experiments aimed to compare algorithms’ efficiency in solving (annotating and representing) secondary structures of complex pseudoknotted RNAs. The test set was built based on representative, non-redundant RNA 3D structure repository (Leontis and Zirbel, 2012). Initial set consisted of 1272 entries. In the preparation step, all of them were processed using 3DNA/DSSR running in two modes, without (mode I) and with helices’ analysis (mode II) (Lu and Olson, 2008). This resulted in obtaining base pair list for every RNA 3D structure. Next, RNAs without pseudoknots were removed to obtain two datasets, DS1 containing 209 structures (mode I) and DS2 with 283 structures (mode II). We processed every structure in DS1 and DS2 to find how many disjoint pseudoknots it included. It appeared that the majority, i.e. 154 structures in DS1 and 221 in DS2, had only one pseudoknot, but single structures contained up to 13 pseudoknots per structure (Table 2). All together, there were 466 pseudoknots identified in DS1 and 547 in DS2.

Table 2.

A number of instances in DS1 and DS2 which include k = 1…13 disjoint pseudoknots per one structure

# Pseudoknots per str.	1	2	3	4	5	6	7	8	9	10	11	12	13
# Structures in DS1	154	18	8	1	0	5	6	1	4	4	5	2	1
# Structures in DS2	221	25	8	1	0	5	6	1	4	4	5	2	1

Data in both sets were managed by all considered algorithms. Many structures included only first-order pseudoknots. In these, and a few other cases, all algorithms returned the same results, as expected. Solutions were different for 80 structures in DS1, and 172 structures in DS2. Our further analysis covered these cases only, i.e. subsets $DS1\prime$ (80 structures) and $DS2\prime$ (172 structures), respectively. $DS1\prime$ included structures with pseudoknots of up to the fifth order, $DS2\prime$––up to the eighth. Subsets processed equally by all algorithms, i.e. $DS1″$=$DS1\mathrm{\setminus }DS1\prime$ and $DS2″$=$DS2\mathrm{\setminus }DS2\prime$, included structures with pseudoknots of up to the second and the third order, respectively. A distribution of structures with the i-th highest pseudoknot order is summarized in Table 3. For example, [FCFS, 3] = 7 in the table’s part (a) means that in subset $DS1\prime$, FCFS algorithm found seven structures with pseudoknots of order $\le$3.

Table 3.

A number of structures with pseudoknot order psorder = 1…8, found in particular datasets

	(a)$DS1\prime$dataset					(b)$DS2\prime$dataset
Pseudoknot order	1	2	3	4	5	1	2	3	4	5	6	7	8
FCFS	162	36	7	3	1	138	52	59	16	9	3	5	1
EG	160	32	12	4	1	133	61	57	15	6	5	5	1
EC	160	35	9	4	1	132	63	55	15	6	7	4	1
DP	159	33	11	5	1	132	62	56	16	6	6	5	0
HYB	161	33	9	5	1	137	58	58	14	8	5	3	0
	(c) $DS1″$ dataset					(d) $DS2″$ dataset
All algorithms	123	6	0	0	0	87	17	7	0	0	0	0	0

In the first experiment, solutions provided by particular algorithms were evaluated using multi-criterion function fscoreII (Formula 2). For each input RNA structure S, provided in BPSEQ format, we obtained five structure representations $R1\left(S\right)$–$R5\left(S\right)$ encoded in DBL notation and we made their all-against-all comparison. For every pair of representations, we picked the winner applying Formula 3. This way, we counted how many times each algorithm won/lost a duel with every other one (draws were not considered). We also identified cases, in which one method dominated over all the others (won the battle) or lost with all the remaining algorithms (lost the battle; Tables 4 and 5).

Table 4.

All-against-all algorithm comparison for $DS1\prime$ dataset upon fscoreII

	FCFS	EG	EC	DP	HYB	# Duels won	# Battles won
FCFS	–	0	1	0	0	1	0
EG	75	–	22	1	2	100	1
EC	75	6	–	0	2	83	0
DP	79	6	22	–	1	108	0
HYB	78	12	23	7	–	120	7
# Duels lost	307	24	68	8	5	–	–
# Battles lost	71	0	1	0	0	–	–

Table 5.

All-against-all algorithm comparison for $DS2\prime$ dataset upon fscoreII

	FCFS	EG	EC	DP	HYB	# Duels won	# Battles won
FCFS	–	0	15	0	0	15	0
EG	169	–	94	1	5	269	0
EC	108	6	–	0	5	119	0
DP	170	18	95	–	5	288	1
HYB	167	28	98	25	–	318	25
# Duels lost	614	52	302	26	15	–	–
# Battles lost	107	0	15	0	0	–	–

It can be easily noticed that one method stands out among all. HYB algorithm is the one to have dominated in overwhelming part of duels. It has won 15% of battles for $DS2\prime$, and 9% of battles for $DS1\prime$ (compared to other methods winning 0 or 1 battle only), which means that for that percentage of instances it has generated the best solution and outperformed all other algorithms. The second place belongs to DP, and the third one is occupied by EG heuristics. The same relationship between the algorithms emerges from the analysis of lost duels and battles. HYB did not lose a single battle. The FCFS method, historically the first and the simplest of all, proved to be the least successful. In consequence, we decided to update RNA FRABASE by exchanging FCFS to HYB within its workflow.

The experiment with multi-objective fscoreII function was followed by a study of Pareto frontier. We have applied Pareto-based multi-objective algorithm to identify the front of non-dominated solutions. This experiment was run separately for each RNA structure from dataset DS1 (mode I, 209 instances) and from DS2 (mode II, 283 instances). For every instance, we obtained five solutions and we analyzed which ones were Pareto optimal. In two cases, two incomparable solutions were found for the instance: 4GMA–Z$\in DS1$ (Pareto front: [49,–10]; [48,–9]) and 4WCE–X$\in DS2$ (Pareto front: [951,–143]; [950,–142]). For every other RNA, single non-dominated solution was identified. For every algorithm, we have investigated for what fraction of DS1 or DS2 dataset it found Pareto optimal solution (i.e. included in the Pareto frontier). These results are provided in Table 6. For some instances (i.e. 8 instances from DS1, 25 instances from DS2) only one solution, obtained by exactly one method, has constituted Pareto frontier. In all but one of these cases, the Pareto optimal solution was found by HYB only.

Table 6.

Percentage of instances from dataset DS1 and DS2 for which Pareto optimal solution was found by the algorithm

Dataset	FCFS	EG	EC	DP	HYB
DS1	62.68%	94.25%	88.52%	96.17%	99.04%
DS2	39.58%	89.75%	63.60%	91.17%	98.59%

Next experiment was performed to examine algorithms’ performance with respect to the first criterion function, i.e. fscoreI (Formula 1). The experiment followed the same pattern as in the previous case, i.e. each RNA structure S was processed by five algorithms that provided various structure representations, $R1\left(S\right)$–$R5\left(S\right)$. They were compared against one another upon their evaluation with fscoreI. The results (Supplementary Table S1 and S2) show the advantage of DP algorithm over others. DP is the only method that has not lost any duel. It has also won most duels with other algorithms. The second place in fscoreI-based ranking belongs to HYB, and the third one to EG heuristic. Similarly as in the experiment based on fscoreII-ranking, FCFS method is the least successful of all.

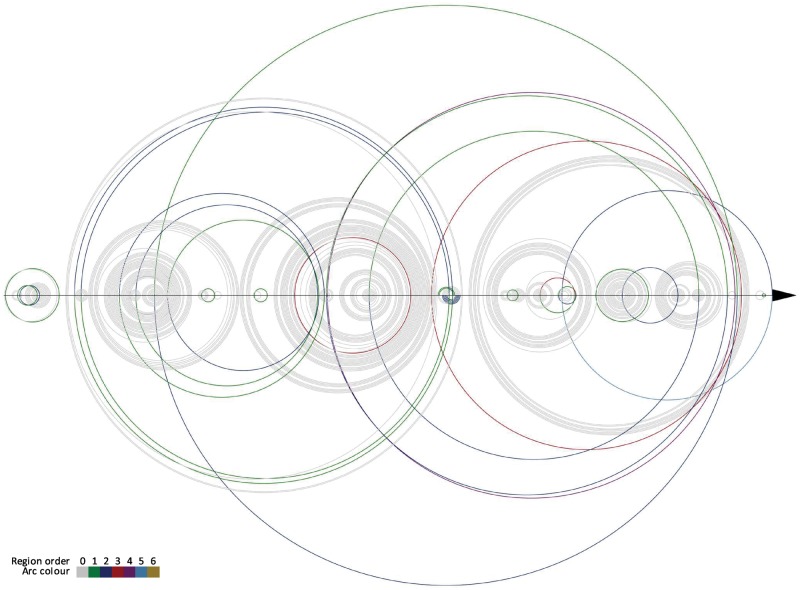
Finally, we have analyzed a single case experiment performed with all algorithms that were applied to process example RNA molecule. For this experiment, we have selected RNA from ribosomal subunit from human mitochondria, 3J7Y, chain A, (Brown et al., 2014), being one of the largest and most complex structures in our dataset. This RNA is composed of 1473 residues and includes 7 disjoint pseudoknots. In our experiment, base pair list for 3J7Y_A was obtained by 3DNA/DSSR in mode II (Lu and Olson, 2008). Next, different methods were used to annotate pseudoknots and determine their orders. One hundred double-stranded regions were found to form pseudoknots. The minimum highest pseudoknot order determined by HYB algorithm was 4, FCFS–5 and the remaining methods (EG, EG and DP)–6. From Table 7, we can read how many regions of the i-th order (i = 0…6) have been annotated by particular algorithms in this 100, in 3J7Y_A structure. Every method found 24 regions with non-zero order (Fig. 3). Fourteen regions were encoded differently by various algorithms. These differences can be spotted in DBL encoding provided in Figure 3. They are observed mainly in single base pair regions (i.e. isolated base pairs forming pseudoknots). To complete the view of 3J7Y_A pseudoknots we provide Figure 4 prepared using R-CHIE (Lai et al., 2012). It displays two arc diagrams, HYB- and FCFS-based, with all pseudoknot-involved base pairs, included in 100 mentioned regions. Diagrams resulting from other algorithms are shown in Supplementary Material (Supplementary Figs. S4 and S5). Each of these figures enables pairwise comparison of two representations returned by different methods.

Table 7.

A number of the i-th order regions identified in pseudoknots of RNA from ribosomal subunit from human mitochondria (3J7Y, chain A)

Region order (i)	0	1	2	3	4	5	6
# FCFS-identified i-th order regions	76	12	8	2	1	1	0
# EG/EC/DP-identified i-th order regions	76	13	6	2	1	1	1
# HYB-identified i-th order regions	76	13	7	3	1	0	0

Fig. 3.

A distribution of regions with non-zero order in the structure of RNA from ribosomal subunit from human mitochondria (3J7Y, chain A) and their encoding by considered algorithms

Fig. 4.

Arc diagrams of pseudoknot-involved regions in RNA from ribosomal subunit from human mitochondria (3J7Y, chain A) corresponding to HYB (top) and FCFS (bottom) results

5 Conclusion

RNA pseudoknots draw wide interest of researchers studying the RNA structure. But still, due to topological complexity, their classification and machine representation remain a challenge. In our work, we have addressed the problem of determination and assignment of pseudoknot order and encoding the pseudoknotted RNA structures in DBL notation. We have introduced new algorithms, Hybrid and DP, to handle this problem and we have compared them with already existing approaches, FCFS (Popenda et al., 2008), EG and ECs (Smit et al., 2008). We have proposed the new scoring function to better evaluate the solutions. The methods were tested using the representative set of 1272 non-redundant RNA 3D structures (Leontis and Zirbel, 2012). The computational experiment has identified HYB as the best one in the ranking made according to fscoreII. It finds machine representation of the secondary structure maximizing the number of non-conflicting base pairs and minimizing the highest pseudoknot order. If the first criterion (fscoreI) is considered, DP beats the other methods and HYB is just behind.

All considered algorithms have been made available within RNApdbee web server (http://rnapdbee.cs.put.poznan.pl) and are ready to be used and investigated in further experiments. We hope they will open new opportunity in modelling more accurate 3D structures of pseudoknotted RNAs (Miao et al., 2017), in particular in the case of secondary structure-based prediction (Antczak et al., 2016; Martinez et al., 2008; Parisien and Major, 2008; Popenda et al., 2012). They should facilitate an access to a proper secondary structure for those who annotate it from the tertiary data. They also allow to apply the preferable optimization criterion, based on fscoreI or fscoreII, depending on the user expectations.

We believe that an admittance to properly represented RNA secondary structure can contribute to explain the folding process and explore the RNA fragmentation pattern (Rybarczyk et al., 2016). The algorithms can be also useful in comparison and evaluation of predicted 3D models via their back-translation to the secondary structure level (Lukasiak et al., 2015; Wiedemann et al., 2017; Zok et al., 2014). Finally, they can cast a new light on the study of relationships between the sequence, secondary and tertiary structure of RNAs (Wiedemann and Milostan, 2016), as well as an investigation of structure-function relationship.