An exemplar-based approach to individualized parcellation reveals the need for sex specific functional networks

Abstract

Recent work with functional connectivity data has led to significant progress in understanding the functional organization of the brain. While the majority of the literature has focused on group-level parcellation approaches, there is ample evidence that the brain varies in both structure and function across individuals. In this work, we introduce a parcellation technique that incorporates delineation of functional networks both at the individual- and group-level. The proposed technique deploys the notion of “submodularity” to jointly parcellate the cerebral cortex while establishing an inclusive correspondence between the individualized functional networks. Using this parcellation technique, we successfully established a cross-validated predictive model that predicts individuals’ sex, solely based on the parcellation schemes (i.e. the node-to-network assignment vectors). The sex prediction finding illustrates that individualized parcellation of functional networks can reveal subgroups in a population and suggests that the use of a global network parcellation may overlook fundamental differences in network organization. This is a particularly important point to consider in studies comparing patients versus controls or even patient subgroups. Network organization may differ between individuals and global configurations should not be assumed. This approach to the individualized study of functional organization in the brain has many implications for both neuroscience and clinical applications.

1. Introduction

The human brain is functionally segregated into multiple spatially-distributed networks, and how best to divide or parcellate the brain into these networks is a fundamental question for neuroscience (Power et al., 2011; Yeo et al., 2011; Yang et al., 2016). Resting-state functional magnetic resonance imaging (fMRI) studies have consistently identified a number of brain networks that replicate across different datasets (Power et al., 2011; Yeo et al., 2011) and overlap with task activation patterns (Smith et al., 2009). The spatial organization of these networks is thought to support a wide range of cognitive functions (Dosenbach et al., 2007; Laird et al., 2011), and such networks have been shown to be altered in clinical disorders (Bush, 2011; Stern et al., 2012; Zhu et al., 2012).

The majority of previous work on parcellating the brain into networks has been focused on group-level analyses (Power et al., 2011; Yeo et al., 2011; Shen et al., 2013; Gordon et al., 2014) with the aim of defining a set of networks that generalizes over all individuals. Group-level analysis is typically accomplished by collapsing data from individuals, either by averaging the subject’s connectivity matrices (Power et al., 2011; Yeo et al., 2011) or by concatenating time courses from each subject, as in the case of Independent Component Analysis (ICA) (Beckmann et al., 2005; Smith et al., 2009). As a result, these approaches do not preserve information regarding inter-individual variability.

Nevertheless, emerging studies have highlighted the importance of inter-individual variability in functional connectivity in contributing to individual differences in behavior and cognition (Van Horn, Grafton et al., 2008; Baldassarre et al., 2012; Mueller et al., 2013; Zilles and Amunts, 2013; Calluso et al., 2015; Finn et al., 2015; Smith et al., 2015; Finn and Constable, 2016, Rosenberg et al., 2016). Such inter-individual variability in functional connectivity is likely to be expressed at the network level and thus should be revealed by functional parcellation schemes.

Accordingly, individual-level parcellation of the brain into networks has recently received increased attention. To enable functional network parcellation at the individual-level, one plausible approach is to apply a back-projection from the group-level parcellation. This approach has been prevalent in ICA studies; and techniques such as principal component analysis (PCA) back-projections (Calhoun et al., 2001) and GLM dual regression approaches (Beckmann et al., 2009) have been developed. However, studies have reported notable limitations for ICA approaches at the individual-level (Zuo et al., 2010), including shortcomings to address inter-subject variation, limitations in scaling to higher dimensions (i.e. finer grained parcellations), and high sensitivity to artifacts such as motion, scanner noise, and physiological noise (McKeown et al., 2003; Cole et al., 2010). To reduce the impact of ICA limitations in addressing inter-subject variability, extensions of this method such as independent vector analysis (IVA) have been proposed (Lee et al., 2008; Michael et al., 2014). While promising, IVA is highly sensitive to each individual data and suffers from excessive computational burden and memory requirements (Michael et al., 2014). More recently, studies have used functional connectivity, as derived from BOLD fMRI, to establish individualized networks (Eickhoff et al., 2015), using techniques such as k-means (Flandin et al., 2002; Kahnt et al., 2012), hierarchical clustering (Meunier et al., 2010; Moreno-Dominguez et al., 2014; Arslan and Rueckert, 2015), spectral clustering (Thirion et al., 2006; Van Den Heuvel et al., 2008, Craddock et al., 2012; Chen et al., 2013; Shen et al., 2013), and boundary mapping (Cohen et al., 2008; Gordon et al., 2014). Although many of these approaches are promising, none of them provide a unified framework that incorporates joint individual- and group-level functional network parcellations with a comprehensive correspondence across the identified networks.

Wang et al. parcellated resting-state fMRI data into a number of coherent networks using an iterative parcellation approach that requires an initial group-level parcellation as a reference (Wang et al., 2015). Their approach requires this initiation step and thus cannot be used when there is no representative group-level parcellation. Similarly, Shen et al. provided a joint individual- and group-level parcellation approach through optimization of a rotation function derived from individualized functional connectivity (Shen et al., 2013). This approach, however, requires the same dataset for the group- and individual- level parcellations and thus does not provide a generalizable parcellation scheme that can be used across datasets.

Here we develop a comprehensive parcellation framework that overcomes the above concerns through a three-step flexible pipeline. The proposed method exploits “exemplar-based clustering” that seeks to summarize the massive amount of data using a relatively small number of representative exemplars (Dueck and Frey, 2007; Badanidiyuru et al., 2014; Mirzasoleiman et al., 2016a, b). Using “exemplars” provides a flexible one-to-one mapping of the functional networks across subjects, easing localization of inter-individual variability over the cortex. Moreover, an intuitive notion of diminishing returns, known as “submodularity”, is utilized to provide an efficient optimization algorithm with provable bounds (Nemhauser et al., 1978). Unlike many other individual-level parcellations that are initiated from a group-level parcellation scheme to derive the corresponding functional networks for individuals (Zuo et al., 2010; Gordon et al., 2017b; Wang et al., 2015; Gordon et al., 2017a), our method moves a step forward by initiating from the individual data. We show that this approach has a higher sensitivity to individual variations and thus provides the basis for more powerful inferences. We evaluate our parcellation approach using clustering validation measures of stability and reproducibility. Finally, we compare our method with the two individual-level parcellations mentioned above – Shen et al. (Shen et al., 2013) and Wang et al. (Wang et al., 2015) – in two different aspects: (1) internal clustering evaluation, and (2) sensitivity to interindividual variations (i.e. predictive power). Of note, although there exists potentially interesting individual variability in functional organization both at the node- and network-levels, the focus of this initial work is to delineate the network-level organization. It should be noted, however, that the approach described here can be applied to voxel-level data in order to define a node-level functional atlas.

2. Theory

2.1. Overview

Exemplar-based clustering algorithms summarize massive datasets through the selection of a relatively small set of representative exemplars. Our proposed algorithm seeks to select K exemplar regions (representing our networks) across the cerebral cortex. The clustering algorithm then assigns each of the nodes to one of the exemplars, i.e., one of the networks.

Most techniques for identifying exemplars define an objective function that measures the “representativeness” of each set of exemplars with regard to the full dataset. Often, these objective functions satisfy an intuitive notion of diminishing returns called submodularity (Nemhauser et al., 1978): for instance, if given two sets of exemplars S₁ and S₂ with S₁ ⊆ S₂, adding a new element to S₁ is more beneficial than adding it to the superset, S₂, as the new element can potentially add more information to S₁ rather than S₂.When using this concept of submodularity, the problem of finding K exemplars can be reduced to maximizing a non-negative monotone submodular set function subject to a cardinality constraint (i.e., a bound on the number K of elements that can be selected) (Krause and Golovin, 2012; Mirzasoleiman et al., 2016a,b). Simple greedy algorithms can efficiently maximize these objective functions (Nemhauser et al., 1978). See Mirzasoleiman, et al. (Mirzasoleiman, et al., 2016a,b) for recent developments of submodular maximization methods.

In the following, we formally define submodular functions following the work of Krause et al. (Krause and Golovin, 2012), and define the greedy algorithm, and exemplar-based clustering. We subsequently present our algorithm and the details of our implementation.

2.2. Submodular functions

Submodularity is a property of set functions, i.e., functions f: 2^V → IR that assign each subset S ⊆ V a value f(S). Here, V is a finite set, commonly called the ground set, and S is a finite subset of V. The definition of submodularity relies on a notion of discrete derivative, also called the marginal gain. An important subclass of submodular functions (used in the proposed algorithm) includes those which are monotone.

Definition 1.1. (Discrete derivative)

For a set function f: 2^V → IR, S ⊆ V, and e ∈ V, let Δf(e|S) : = f(S ⊂ {e}) − f(S) be the discrete derivative of f at S with respect to e.

Definition 1.2. (Submodularity)

A function f: 2^V → IR is submodular if for every A ⊆ B ⊆ V and e ∈ V\B it holds that Δ(e|A) ≥ Δ(e|B). Meaning that adding an element e to a set A increases the utility at more than (or at least equal to) adding it to A’s superset, B, suggesting a natural diminishing returns.

Definition 1.3. (Monotonicity)

A function f: 2^V → R is monotone if for every A ⊆ B ⊆ V, f(A) ≤ f(B). Equivalently, function f is monotone if and only if all its discrete derivatives are nonnegative, i.e., for every A ⊆ V and e ∈ V it holds that Δ(e|A) ≥ 0.

2.3. The greedy algorithm for optimization of the submodular function

In general, maximizing a non-negative monotone submodular function subject to a cardinality constraint, i.e.,

$$\underset{S\subseteq V}{max}f(S)s.t.\mid S\mid \le K,$$ (1)

is NP-hard (Feige, 1998). However, a seminal result of Nemhauser et al. (Nemhauser et al., 1978) proves that a simple greedy algorithm provides the best approximation (≈63%) to the optimal solution. In practice, this approximation is significantly closer to the optimal solution (see Supplementary Materials and Figure S5 for an empirical evaluation). The greedy algorithm starts with an empty set S₀ = Ø, and at each iteration i, it selects and adds the element $\{e_i^{\ast }\}\in V$ such that the marginal gain is maximized, i.e.,

$$e_i^{\ast }=arg\underset{e\in V}{max}\mathrm{\Delta }f\left(e\mid S_{i-1}\right):=arg\underset{e\in V}{max}f\left(S_{i-1}\cup \{e\}\right)-f\left(S_{i-1}\right),$$ (2)

$$S_i=S_{i-1}\cup \{e_i^{\ast }\}.$$ (3)

The algorithm continues until the cardinality constraint is reached, i.e., until |S| =K.

2.4. Exemplar-based clustering

Exemplar-based clustering provides an approach to summarize the data by introducing a set of K exemplars that best represents the full dataset. A classic way of identifying such exemplars is solving the k-medoids problem, by minimizing the sum of pairwise distances between the elements of the dataset and the exemplars (see Friedman et al. (Friedman et al., 2001) for more details on k-medoids problems). Specifically, assume we are given a dissimilarity function d: V×V → R, where d encodes the dissimilarities between the elements of the ground set V. The k-medoids problem minimizes the following loss function:

$$L(S)=\frac{1}{\mid V\mid }\sum _{v\in V}\underset{e\in S}{min}d(v,e).$$ (4)

L(S) measures how much information we lose if we represent all the data points in each cluster, with its corresponding exemplar.

By introducing an appropriate auxiliary element v₀, we can turn L into a monotone submodular function, so that the minimization of (4) is equivalent to the maximization of the following monotone submodular function (5), and can be efficiently solved by the greedy algorithm:

$$f(S)=L(v_0)-L(S\cup v_0).$$ (5)

Technically, any vector v₀ satisfying the following condition can be used as an auxiliary exemplar:

$$\underset{v^{\prime }\in V}{max}d(v,v^{\prime })\le d(v,v_0),\forall v\in V\backslash S.$$ (6)

This condition implies that the distance between the auxiliary element and all of the data points must be greater than the pairwise distances between the data points.

Note that in contrast to the classical clustering algorithms (such as k-means), the exemplar-based clustering is very general in that it does not require the distance function d to be symmetric nor to obey triangle inequality. All it requires for d is nonnegativity. Here we used the squared Euclidean distance as the dissimilarity function:

$$d(x,x^{\prime })={\Vert x-x^{\prime }\Vert }^2.$$ (7)

Herein, we utilize the submodularity of our utility function further to implement an accelerated version of the greedy algorithm, called lazy greedy (Minoux, 1978).

2.5. Cortical parcellation algorithm

In this section, we deploy the aforementioned algorithm to parcellate the cerebral cortex into K functional networks. For each individual j ∈ {1,…, J}, we have a matrix $V_{N\times T}^j$, where N denotes the number of regions in the brain and T represents the number of time points. Each region n ∈ {1,…,N} of the brain, forms a vector in a T-dimensional space, denoted as $v_n^j$. We aim to find K exemplar labels S= {e₁, e₂, …, e_K} whose corresponding exemplar set for each individual j, i.e., $S^j=\{v_{e_1}^j,v_{e_2}^j,\dots ,v_{e_K}^j\}\subseteq V^j$, maximizes a desired utility function. In order to jointly consider the information of each individual and the group, we define a natural objective utility function as follows:

$$F(S)=\sum _{j=1}^J{f}^j\left(S^j\right),$$ (8)

where S is the exemplar label set and S^j is the set including the corresponding exemplar vectors in individual j. In addition, f^j(S^j) is the utility function of individual j defined according to equations (2)–(5), and J is the total number of subjects. Note that submodularity is preserved under non-negative linear combination and thus F(S) remains a non-negative monotone submodular function that can similarly be optimized by the greedy algorithm. Also note that f^j is a function that is locally defined for each individual j, meaning that it takes the label set S= {e_i} ∈ {1,…,N} of regions and considers the corresponding vectors in each individual. The algorithm finally selects the K exemplar labels for which the corresponding exemplar vectors in each individual minimize the sum of loss functions over all individuals. After K exemplars are obtained for each individual, the algorithm assigns each region n in individual j (i.e. vector $v_n^j$) to the closest exemplar, i.e.,

$$\text{Exemplar}\left(v_n^j\right)=arg\underset{e_i\in S}{min}\left(v_n^j,v_{e_i}^j\right).$$ (9)

Thus, the brain is parcellated into K networks each represented by an exemplar. In order to obtain the group-level parcellation, we employ a majority vote algorithm over all subjects. In other words, region n is assigned to network k if the majority of individuals vote for this assignment.

Overall, the proposed algorithm operates in three steps. First, the exemplar-search step finds the global exemplars over all subjects. Second, the individual-clustering step parcellates each individual’s brain by greedily maximizing a utility function, defined according to the group data. Third, the group-clustering step takes the majority vote of all individual clusters. The pseudocode in Fig. 1 shows each step in more detail.

Fig. 1. Pseudocode explaining the three steps of exemplar-based parcellation.

In the first step (exemplar-search), K = 2, …, 25 exemplars are derived for each individual with a group constraint, i.e. by greedily optimizing a nonnegative monotone submodular function defined as the summation of the utility function over individuals. In the second step (individual-clustering), for each single individual, every node in the cortical area is assigned to its closest exemplar, where closeness is defined using a squared Euclidean distance function. Finally, in the third step (group-clustering), the group-level parcellation is derived by majority voting over all individual-level parcellations (i.e. the node-to-network assignment vectors).

One significant advantage of this algorithm is that there is a straightforward mapping between the parcellation of each individual to every other individual, and to the group, as each network is represented by a global exemplar. Thus, we do not require another algorithm to retrieve the correspondences. This facilitates direct comparison between individuals and the group.

3. Material and methods

3.1. Participants and processing

Data were obtained from the 900 subject release dataset in Human Connectome Project (HCP) (Van Essen et al., 2013). Analysis was limited to 825 subjects for which the complete scan data were available for each of the two resting states: REST1 and REST2. For details of scan parameters, see Uğurbil et al. (Uğurbil et al., 2013) and Smith et al. (Smith et al., 2013). Starting with the minimally preprocessed HCP data (Glasser et al., 2013), further preprocessing steps were performed using BioImage Suite (Joshi et al., 2011) and included regressing 12 motion parameters (Movement_Regressors_dt.txt), regressing the mean time courses of the white matter and cerebrospinal fluid as well as the global signal, removing the linear trend, and low-pass filtering (as previously described in (Finn et al., 2015)). We employed a functional brain atlas (Shen et al., 2013) consisting of 188 nodes covering the cortex of the brain. This atlas was defined on a separate population of healthy subjects (Finn et al., 2015).

3.2. Functional distance matrix

Time courses from the two resting-state conditions (REST1 and REST2) and the two functional runs with opposing phase-encoding directions (left-right, “LR”, and right-left, “RL”) were concatenated and further used to generate a ground set consisting of N vectors in T-dimensional space. All the data points were normalized into a unit norm sphere centered at the origin, and a point with the norm greater than two was used as the auxiliary exemplar (Eq. (6) in the Theory Section 2.4). For each individual, the pairwise squared Euclidean distances between the data points were calculated, and a matrix of size 188 × 188 was obtained. Next, the greedy algorithm was employed to find the best K = {2, 3,…, 25} exemplars according to the algorithm described above.

3.3. Stability and convergence

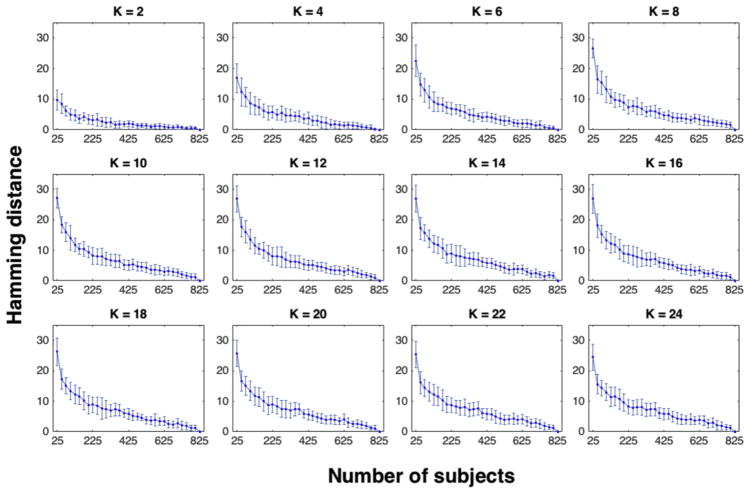
We examined the stability and convergence behavior of our group-level parcellation. Stability was defined as the robustness of the output to slight perturbations to the input (Von Luxburg, 2010), which was examined here in terms of the variations both in the group size and the selection of subsets of individuals from the larger group. Convergence was examined through the rate at which the output parcellation converged to the final result as the input merged to span the entire dataset. We started with twenty-five subjects and incremented the number of subjects used in the network parcellation in steps of twenty-five. At each step t, we employed the exemplar-search algorithm (part 1 in Algorithm) over the set of 25 × t subjects, which we refer to as the training set herein. Using the exemplars derived from the training set, we applied the individual-clustering algorithm (part 2 in Algorithm) over both the training set (i.e. 25 × t subjects) and the entire dataset (i.e. 825 subjects), obtaining two sets of individual-level parcellations. Next, we employed majority voting (part 3 in Algorithm) over both the training set and the entire dataset, and then calculated the Hamming distances (Hamming, 1950) between the group-level parcellation derived from the training set (which here is called the perturbed parcellation) and the full parcellation derived from the entire dataset (Fig. 3).

Fig. 3. Stability and convergence of the group-level parcellation algorithm as a function of group size and individual selection.

For each number of networks taking even values in the range K = 2, …, 25, the Hamming distance between the two parcellation schemes is displayed: 1) the group-level parcellation derived from the training set (that is a portion of the full dataset) and 2) the group-level parcellation derived by considering the entire dataset (with 825 subjects). On the x-axis, the number of subjects in the training set is displayed. On the y-axis, the Hamming distance (i.e. the number of network differences in the node-to-network assignment vectors) is displayed. Error bars correspond to the variations resulting from 100 permutations for the selection of subjects for the training set. The model is stable to the variation in the group size as the average difference between the perturbed parcellation using a subset of the subjects and the final parcellation using all the subjects is bounded and less than 30 (16% of the full vector with 188 nodes). The model converges to the final solution with a general decaying rate both in the average distance between the perturbed and the final parcellations and in the error bar lengths. Error bars are a proxy of the distances between perturbed parcellations using the same number of subjects selected from the entire dataset over 100 permutations.

3.4. Reproducibility of group-level parcellation

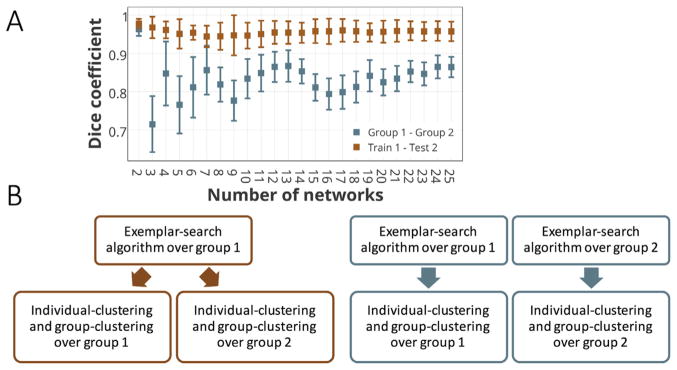
We investigated whether our proposed method was generalizable across different sets of subjects using two different pipelines (Fig. 4B). In the first pipeline, the dataset consisting of 800 subjects was split into two equal size subsamples, and the three-step parcellation algorithm – including exemplar-search, individual-clustering, and group-clustering – was applied on each half independently (Fig. 4B, Right). Finally, the overlap between the two group-level parcellation schemes was calculated using the Dice coefficient (Dice, 1945). The process was repeated 100 times for different permutations of subjects (Fig. 4A, blue error bars). In the second pipeline, the data set was similarly split into two equal size subsets, but this time, a training-testing strategy was utilized. We employed the first part of the algorithm (i.e. exemplar-search) over group 1 (referred to as the training set). Next, using the exemplars derived from the training set, we ran the rest of the algorithm (i.e. individual-clustering and group-clustering) over the individuals in group 2 (referred to as the testing set) as well as group 1 (the training set), obtaining two group-level parcellation schemes (Fig. 4B, Left). The overlaps between the two parcellations were computed using the Dice coefficient. The same process was repeated 100 times for different permutations of subjects (Fig. 4A, orange error bars). Note that in the second pipeline, there is a direct one-to-one mapping between the two parcellation schemes, through their common exemplars. In other words, all the regions with the same exemplar labels, are assigned to the same clusters (networks). This straightforward mapping across functional networks at individual-level and group-level is a unique advantage of the exemplar-based clustering. It also provides a cross-validation approach to the parcellation schemes through training-testing settings.

Fig. 4. Reproducibility of the group-level parcellation measured by the Dice coefficient.

A) Dice coefficients between the group-level parcellation of two equal-size sets (with 400 subjects). The reproducibility is examined by two different pipelines shown in part B. The colors match between the error bars (part A) and the diagrams (part B). The blue error bars represent the Dice coefficient between the parcellations derived by running the entire three-step algorithm over each subset (group 1 and group 2) separately, as displayed by the right (blue) diagram in part B. The orange error bars show the Dice coefficient between the two group-level parcellations with the same exemplars (derived from group 1). Due to having a setting similar to training-testing validation, group 1 is called train 1 here and group 2 is called test 2. It corresponds to the left (orange) diagram in part B. B) The two pipelines for addressing the reproducibility of the group-level parcellation algorithm. The Dice coefficient between the parcellation outcomes of the left diagram is depicted in orange, and the corresponding measure for the parcellation of the right diagram is depicted in blue in part A.

3.5. Reproducibility of individual-level parcellations across rest sessions

To investigate the reproducibility of parcellations at the individual- level, we repeated the parcellation analyses, this time taking into account the data from REST1 and REST2 scan sessions separately. As with the group-level reproducibility analysis, we employed two separate pipelines: First, we computed the individualized parcellations for each rest session, using the previously computed exemplars that were derived from the joint consideration of the two sessions. The advantage of this approach is that it preserves the correspondences between the resulting networks for each individual across the two sessions (referred to as the global exemplars). In the second pipeline, we recalculated the exemplars for the two rest sessions independently and used them to parcellate the individuals within each session. We refer to these as the local exemplars. For each pipeline, we calculated the Dice coefficients between the parcellation results of every individual in the two rest sessions: REST1 and REST2 (Figure S2).

3.6. Mapping highly variable regions

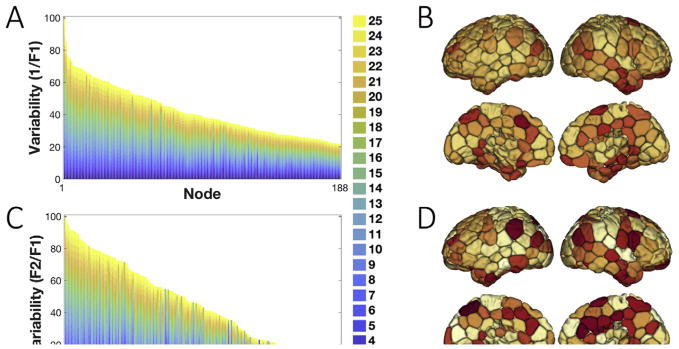
For each node in the cortex, we investigated the number of individuals that voted for the appointed network in the group-level parcellation; a measure labeled as F1 (or the frequency of the 1st mode). This measure captures the consistency of the node-to-network assignments across individuals, and thus, the inverse of F1 (1/F1) could be an indicator of the inter-individual variability. Another metric of interest in the literature is the frequency of the 2nd mode (known as F2), i.e., the number of occurrences for the second most frequent network assignment. To further address the confidence of the node-to-network-assignments across all individuals, the ratio between F1 and F2 (i.e. F1:F2 ratio) was calculated. Similarly, to underscore the variability of regions, the inverse ratio (i.e. F2:F1 ratio or F2/F1) was considered. A high value for the inverse F1 and the F2:F1 ratio reflects greater variability in the network assignment. For each node, the two inter-individual variability measures (1/F1, F2/F1) were calculated and summed up over the number of networks ranging from K = 2 to K = 25, then the resulting numbers were scaled to the range (0, 100) (Fig. 5).

Fig. 5. Inter-individual variability measured by the first and second votes in the majority voting.

A) The inverse F1 is displayed for all the cortical nodes in the brain, sorted from high to low. For all numbers of networks (K = 2, …, 25), inverse F1 measures are collapsed, scaled, and depicted in a barplot. As F1 measures the number of individuals who voted for the group-vote node-to-network assignment, the inverse F1 is a measure of variability between individuals and the group, with a higher measure indicating higher variability and lower confidence. B) The inverse F1 depicted on the brain after summing over all numbers of networks. C) The ratio between the second (F2) and the first (F1) vote for the node-to-network assignments is displayed for all cortical nodes in the brain, sorted from high to low. Similarly, the F2:F1 ratio is a measure of variability across individuals, as a high F1 and a low F2 corresponds to a confident network assignment reproduced across individuals. The barplot displays the corresponding measure for all numbers of networks (K = 2, …, 25) stacked on top of each other and scaled to the range (0,100). D) F2:F1 ratio depicted on the brain after summing over all numbers of networks. The higher-order association areas in the frontal, parietal and temporal lobes display higher inverse F1 and F2:F1 ratio values compared to primary-sensory areas.

3.7. Sex-prediction

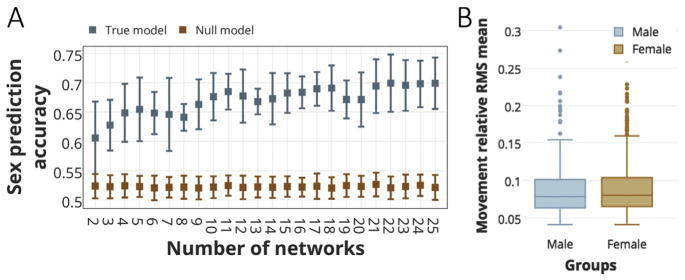
To illustrate that this individualized parcellation approach provides meaningful information, we next demonstrated a data-driven predictive model based on parcellation (i.e. node-to-network assignments) to predict the sex for each individual. We used a gradient boosting machine (GBM) with 100 estimators (also known as decision trees) and 0.05 learning rate (see the code for more details on parameters) in a ten-fold cross-validated setting (Friedman et al., 2001). Each time, we fed the predictive model with node-to-network-assignment vectors for the individuals in the training set as features, and their corresponding sex as output. We predicted sex for the unseen fold of data across a varying number of networks from K = 2 to K = 25. The reported accuracies are the mean and standard deviations across all ten folds (Fig. 6A, blue error bars). To confirm that our prediction results were highly significant, we applied a nonparametric permutation testing by generating a null distribution via randomly shuffling the outputs (i.e. sex) 100 times and running the generated vectors through our predictive model (Fig. 6A, orange error bars).

Fig. 6. Sex prediction accuracies using parcellation schemes as features, for the numbers of networks from K = 2 to K = 25.

A) The sex prediction accuracies for a 10- fold cross-validation using gradient boosting machine (GBM) as the classifier. The classifier is fed with the node-to-network assignment vectors (with 188 elements) as features and a binary output (male vs. female) is predicted for an unseen fold of subjects. The mean and standard deviation across all folds are depicted in blue error bars. To determine the significance of our predictive model, the accuracies derived from the null distributions are also depicted in orange error bars. B) 2-tailed t-test comparison of the head motion between the two sex groups. There are no significant differences in head motion between female (N = 458, mean = 8.9e-02, s.d. = 3.41e-02) and male (N = 367, mean = 8.8e-02, s.d. = 3.55e-02) subjects (two-tailed t-test: t(825) = 0.47, p = 0.64).

Of note, since we initially defined the network parcellations across all individuals and then used the same individuals for the sex prediction, these were not two independent samples. It is unlikely that this dependency has confounded the results, for two main reasons: first, the parcellation step was employed agnostic to the individuals’ sex. That is, the same parcellation algorithm was employed on both male and female subjects, with no prior knowledge on their sex. Second, the employed predictive model (GBM) is a non-parametric model with no sensitivity to the dependency of samples. Nevertheless, we tested for the potential biases by employing the parcellation and the prediction steps on two independent subsets. In one analysis, we split the entire population into two equal-size sets (each with 400 subjects) and employed the training-testing framework described earlier (see the second pipeline in Method Section 3.4 and Fig. 4B [Left]), i.e. defined the exemplars on the training set and used those exemplars to parcellate individuals in both training and testing sets. We next conducted our predictive analysis by training on one set and testing on the other. The accuracies remained significant (Figure S3) despite the smaller size of the training set. In another analysis, we employed both the parcellation and predictions in a 10-fold cross-validated setting. That is, we divided the entire population into 10 folds. At every step, the exemplars were calculated from the 9 training folds and used to parcellate the entire population. A GBM model was trained on the 9 training folds and tested to predict the sex for the one left-out testing fold. The entire procedure was repeated until each fold was left out once. The prediction accuracies remained significantly higher than chance (Figure S4).

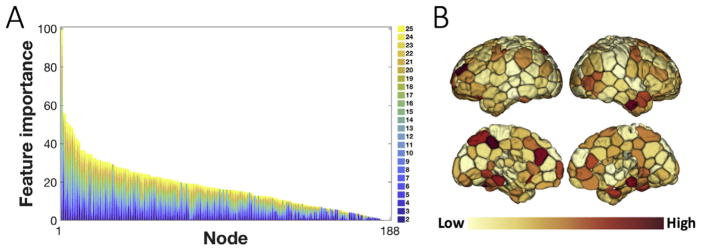
A benefit of using gradient boosting machines is that after the decision trees are constructed, it is relatively straightforward to retrieve the importance of each feature. Importance is explicitly calculated as the number of times that each feature was used to make key decisions in the single decision tree, i.e. decisions that improve the performance measure. The feature importance is weighted by the number of observations within each decision tree and then averaged across all of the trees within the model. As our GBM model was fit with 188 features indicating the network assignment of each node, we simply derived the importance of each node in sex identification by assessing the corresponding importance attribute. We further scaled the importance scores to the range (0, 100) as shown in Fig. 7.

Fig. 7. Node importance in the sex-discrimination predictive model.

A) The sorted distribution of node importance values in discriminating sex based on the parcellation schemes. The importance is derived from the “feature importance” attribute of the GBM sex classifier and scaled to the range (0,100). B) The feature importance measures depicted on the brain after summing up over all numbers of networks. Regions in the anterior and posterior cingulate cortex, precuneus, superior parietal lobule, superior frontal gyrus, parahippocampal gyrus and inferior temporal gyrus have relatively high importance scores.

3.8. Comparison with other approaches

We compared our proposed exemplar-based parcellation algorithm with two well-established individual-level parcellation methods: (1) our earlier rotation-based individual-level parcellation (Shen’s parcellation; Shen et al., 2013) and (2) Wang’s iterative scaling individual-level parcellation (Wang et al., 2015). Shen’s method had two free parameters, α which tunes the smoothing kernel’s standard deviation, and λ, which adjusts the level of similarity between individuals and the group. We set α = 0.2 and let λ take values in the range (0.1–0.6), with smaller numbers representing lower similarity. For the sake of clarity, we only report the results for the two ends of the interval (λ = 0.1 and λ = 0.6); similar results were found for other values of λ. For some specific number of networks (e.g. K = 17, 18) Shen’s algorithm terminated at some lower K values, and these were then used instead of the input K. Similarly, we derived the individualized parcellations for Wang’s method starting with their K = 7 and K = 17 group-level parcellation schemes (Yeo et al., 2011). For their averaging step, we deployed different weighting schemes, but the results were highly similar across different weighting schemes for the clustering evaluation measures and for sex-prediction analysis. Thus, we present results that used standard averaging.

To quantify the results of the comparison, we used two independent frameworks. In the first step, two clustering validation techniques were applied and in the second step, the sensitivity of these methods to inter-individual variability was examined through comparisons of the predictive power in a sex discrimination analysis.

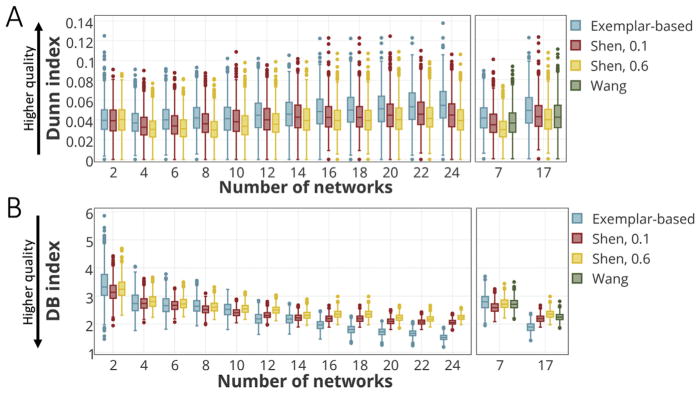
We utilized two internal clustering validation measures – the Dunn Index (Dunn, 1973) and the Davies-Bouldin Index (Davies and Bouldin, 1979) – that are commonly reported in the literature (Halkidi et al., 2001; Ghosh et al., 2007; Saitta et al., 2007; Ziegler et al., 2010; Fichtinger et al., 2011). Similar to all other internal clustering validations, the Dunn and the DB indices utilize the clustered data itself to measure compactness and cluster separation. The Dunn index identifies to what extent the clustering scheme is successful in maximizing the inter-cluster distance while minimizing the intra-cluster distance. For K clusters, the Dunn index is defined as the ratio between the minimal inter-cluster distance to the maximal intra-cluster distance, according to Eq. (10):

$${\mathit{Dunn}}_K=\underset{1<i,j<K}{min}\{\frac{{min}_{x\in C_i,y\in C_j}d(x,y)}{{max}_{1<k<K}{max}_{x,y\in C_k}d(x,y)}\},$$ (10)

where d(x, y) is the Euclidean distance between the two vectors x and y. Therefore, for a given assignment of clusters, a higher Dunn index indicates better clustering. We computed the Dunn index for each individual-level parcellation derived from the three different methods, for the number of clusters (networks) varying from K = 2 to K = 25. The Davies-Bouldin index (DB) measures the average similarity between each cluster and its most similar one, and is defined according to Eq. (11):

$${DB}_k=\frac{1}{K}\sum _{i=1}^K\underset{1<j<K,j\ne i}{max}\{\frac{{\left(\frac{1}{n_i}{\sum }_{x\in C_i}d{(x,c_i)}^2\right)}^{\frac{1}{2}}+{\left(\frac{1}{n_j}{\sum }_{x\in C_j}d{\left(x,c_j\right)}^2\right)}^{\frac{1}{2}}}{d\left(c_i,c_j\right)}\},$$ (11)

with n_i the number of points and c_i the centroid of cluster C_i. Since the objective is to obtain clusters with minimum intra-cluster and maximum inter-cluster distances, small values for DB are desired. Similarly, the DB indices were calculated using the three individual level parcellations (described above) for the number of clusters (networks) ranging from K = 2 to K = 25.

Finally, we assessed the predictive power of our proposed model in comparison with the two other approaches. We employed a sex-prediction analysis described previously, this time using the individual-level parcellations resulting from Shen’s and Wang’s algorithm. We calculated the accuracies for the number of networks varying in the range K = 2 to K = 25.

We note here that there is a subtle change in the accuracy results each time the algorithm is executed. This is due to the randomness of ten-fold-cross-validation and also the initial state of the GBM. In the comparison of different methods, we fixed all these parameters and thus the result is for the same initial state and the same assignments of data points to the folds.

3.9. Implementation

The parcellation code was written in Matlab. Clustering was performed on a workstation with 64 GB of RAM and a 3.4 GHz Intel Xeon processor with 24 cores. Run time for our proposed method with K = 25 was 442.15 s for the exemplar-search, 1.95 s for the individual-clustering, and 0.22 s for the group-clustering. Predictive analysis code was written in Python using scikit-learn library (Pedregosa et al., 2011).

4. Results

4.1. Visualization of parcellations as a function of the number of networks

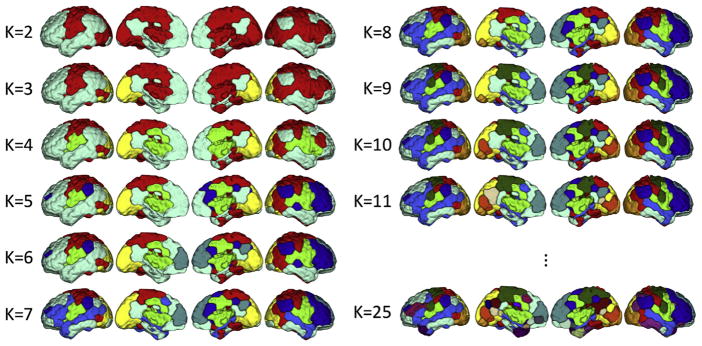
One advantage of using the greedy algorithm to solve the optimization of our submodular function is that it provides a hierarchy of nested clusters (through defining the new exemplars while maintaining the older ones) and hence enables an illustrative visualization for different granularities/resolutions as the number of networks is gradually incremented from K = 2 to K = 25. At K = 2, the brain is divided into two subnetworks that are associated with default mode network (DMN) – which is known as the task-negative network – and the rest of the brain, which attributes to the task-positive network. At K = 11, many canonical networks (including the DMN, frontoparietal network (FPN), and sensorimotor network (SMN)) are observable (Fig. 2). For K > 11 the changes are subtle and more difficult to observe (Figure S1).

Fig. 2. The group-level parcellation schemes for the number of networks ranging from K = 2 to K = 25.

At K = 2, the brain is roughly divided into the default mode network (DMN) and task-positive network. As K is increased, the greedy algorithm discovers new exemplars while preserving the former ones, and hence parcellates the brain in a hierarchical setting. For example, at K = 3, the visual network is separated from the DMN and task-positive network. When K is increased to K = 11, many canonical networks (including the DMN, frontoparietal network (FPN), and sensorimotor network (SMN)) are observable. K = 25 was the finest resolution parcellation derived here. For K > 11 the changes are subtle and more difficult to observe (Fig. S1).

4.2. Stability and convergence of group-level parcellation as a function of group size

For all numbers of networks, increasing the number of subjects in the training set (on average) decreases the distance between the perturbed parcellation, created with a subsample of subjects, and the final parcellation, created with all subjects (Fig. 3). The decrease in the error bars indicates that the distance between the perturbed parcellations resulting from random selection (of the same number) of subjects is also decaying. These findings suggest the algorithm converges to the final solution as the input expands to the entire set. Furthermore, for any number of networks, the average distance between the perturbed and the final parcellation is relatively small: when only using 25 subjects, the perturbed parcellation exhibited an average of 16% difference (i.e. 84% overlap) with the final parcellation. These findings suggest the stability of the algorithm to perturbations to the size of the input and to the selection of the subjects. That the exemplars derived from a relatively small portion of dataset produce parcellations highly similar to the final parcellation scheme (with 84% overlap on average) is a promising result with non-trivial implications for cross-dataset validations.

4.3. Reproducibility of group-level parcellations

Using two non-overlapping subsets, the Dice coefficients between the parcellation results of group 1 and group 2 are depicted in Fig. 4A (blue error bars). For all number of networks, there is on average more than 70% overlap between the two parcellations with the overlap generally greater than 80%. Using a training-testing replication method, the Dice coefficients between the training and testing group’s parcellation schemes are depicted in Fig. 4A (orange error bars). On average, the two parcellations have approximately 96% overlapping occurrences. As anticipated, the Dice coefficients for the second pipeline are significantly higher than the first, in part due to having common exemplars.

4.4. Reproducibility of individual-level parcellations across rest sessions

The Dice coefficients between each individual’s parcellations across the two rest sessions are depicted in Figure S2. The orange bars correspond to the analysis with global exemplars (across the two sessions). The blue bars display the comparison result using local session-specific exemplars. There is on average 72% overlap between the parcellation results across the two sessions, using the global exemplars. This number decreases to 63% when employing the local exemplars. We note that reliability of individual parcellations across different sessions is subject to various factors including system noise, physiological noise, and intrinsic cognitive processes (Krüger and Glover, 2001; Bennett and Miller, 2010). Thus, the reliability of the parcellation results could be confounded by factors other than the specific parcellation algorithm employed, and hence warrants further investigation.

4.5. Inter-individual variability of individual-level parcellations

Fig. 5 displays the sorted distribution of inter-individual variability (in node-to-network assignments) across nodes, using two measures of variability: 1/F1 (Fig. 5A) and F2/F1 (Fig. 5C). It suggests that there are regions with relatively high values for both measures summed across all numbers of networks. These regions, that follow relatively similar patterns for 1/F1 and F2/F1 across all numbers of networks, display high variation, and lower consensus, in their network assignments between the individual- and the group-level parcellation. These regions are predominantly localized in higher-order association cortices in the frontal, parietal and temporal lobes (Fig. 5B, D). In particular, the frontoparietal network, default mode network, and anterior cingulate cortex display high 1/F1 and F2/F1 scores. On the contrary, primary-sensory regions, including the visual network, sensorimotor network, and medial temporal lobe display relatively lower 1/F1 and F2/F1 values. These latter regions demonstrate a higher consistency between the individualized and the group-level parcellation.

4.6. Sex-predictions

Fig. 6A displays the sex prediction accuracies for a range of network numbers (K = 2, …,25), using gradient boosting machine (GBM) as the classifier. The accuracies are reported as the mean and standard deviation across all folds (blue bars). The accuracies for the null model are also depicted (orange bars).We observe that the model predicts sex for an unseen individual with the average accuracies ranging from 61% (for K = 2) to 70% (for K = 22), with the maximum of 75% (for K = 22). These reported accuracies are significantly higher than random accuracies (permutation test; p-value<1e-10), for all numbers of networks even as low as K = 2, suggesting meaningful information is stored in the individualized parcellations.

We also tested for differences in head motion between the two sex groups (Fig. 6B), as motion could be a confound for our predictive analysis. We calculated the average frame-to-frame displacement from the Movement_RelativeRMS.txt for each run and averaged over the 4 runs (REST1_LR, REST1_RL, REST2_LR, and REST2_RL). Using two-tailed t-tests, there were no significant differences in head motion between female (N = 458, mean = 8.9e-02, s.d. = 3.41e-02) and male (N = 367, mean = 8.8e-02, s.d. = 3.55e-02) subjects (two-tailed t-test: t(825) = 0.47, p = 0.64) (Fig. 6B).

To illustrate which regions were the most different between females and males, we utilized the “feature importance” attribute from gradient boosting machine classifier. Fig. 7A illustrates the sorted distribution of the importance scores for all the features used for classification, that is a vector of 188 cortical regions. We observe that regions in the anterior and posterior cingulate cortex, precuneus, superior parietal lobule, superior frontal gyrus, parahippocampal gyrus and inferior temporal gyrus (including anterior temporal pole) show relatively high importance scores (Fig. 7B). These regions, predominantly located in the default mode network (DMN) and the frontoparietal network (FPN), have been consistently associated with sex differences in the literature (Biswal et al., 2010; Scheinost et al., 2015).

4.7. Comparison with other methods

Fig. 8 displays the clustering evaluation results from three methods for varying number of networks, from K = 2 to K = 25 (Dunn Index: Fig. 8A; DB index: Fig. 8B). Fig. 8A (Left) reports the Dunn index for the exemplar-based and Shen parcellation for even Ks. Fig. 8A (Right) compares the same measure among all three parcellation approaches (exemplar-based, Shen, and Wang) for K = 7, 17. Higher values of Dunn index indicate a better clustering algorithm, with larger intra-cluster and smaller inter-cluster similarities. Fig. 8B (Left) depicts the DB index for the exemplar-based and Shen’s approach for even Ks. Fig. 8B (Right) displays the DB index for all three methods for K = 7 and K = 17. By definition, lower values for the DB index indicate a better clustering algorithm. These results suggest that our proposed exemplar-based algorithm is able to cohesively parcellate the brain for each individual, specifically for larger values of K.

Fig. 8. Comparison of clustering evaluation measures (the Dunn and the Davies-Bouldin (DB) indices) across the three methods.

A) The comparison of Dunn index between the exemplar-based method and Shen’s approach for even values of K = 2, …, 24 (Left), and the comparison of all three methods for K = 7 and K = 17 (Right). A higher Dunn index represents higher clustering quality with more compactness within clusters and more separation between clusters. B) The comparison of DB index between the exemplar-based method and Shen’s approach for even values of K = 2, …, 24 (Left) and the comparison of all three methods for K = 7 and K = 17 (Right). A lower DB index indicates a higher clustering quality.

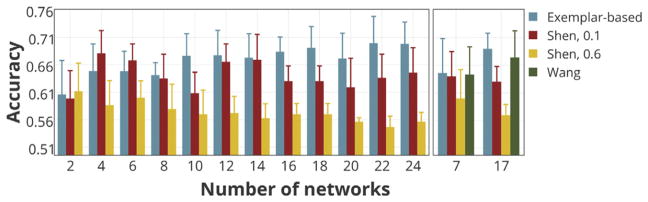
In the second step of comparison, we seek to address the model’s predictive power in a sex discrimination analysis, using a GBM classifier. Fig. 9 (Left) displays the classification accuracies (the mean and standard deviation across all folds) for exemplar-based parcellation and Shen’s method, with the number of networks ranging from K = 2 to K = 24, only taking even values. Fig. 9 (Right) compares the three methods for K = 7 and K = 17.

Fig. 9. Comparison of the models’ ability to preserve the inter-individual variability as measured by sex-prediction accuracies.

The individual-level parcellation schemes derived from each model are separately fed to the GBM classifier. The classification accuracies (the mean and standard deviation across all folds) for exemplar-based parcellation and Shen’s method are displayed with the numbers of networks ranging from K = 2 to K = 24, taking even values (Left). The classification accuracies for all three methods are displayed for K = 7 and K = 17 (Right).

5. Discussion

A novel algorithm has been introduced here that utilizes submodular optimization to parcellate the cerebral cortex into functional networks at both the group- and the individual-levels. At the group-level, the proposed algorithm has favorable stability, convergence, and replicability properties. At the individual-level, regions of high variability in parcellations overlap with known regions of high inter-individual variability in functional connectivity and parcellation. We showed that our algorithm performs well on internal clustering validation measures and more importantly it eliminates the cross-subject correspondence problem for a group when parcellating individuals. Finally, using only the individual differences in network parcellation vectors, we built a predictive model using a ten-fold cross-validated framework that predicts sex for the left out subjects with greater than 70% accuracy. This finding that network definitions are sex specific suggests that network studies need to take sex into account and that the same network should not be applied to the population as a whole. These prediction results show the benefit of individual-level parcellation for extracting additional information that would otherwise be missed by simply using a full group-level parcellation.

5.1. Exemplar-based clustering for individual network-level parcellation

Exemplar-based clustering algorithms have been successfully applied in a wide variety of data-mining applications. Exemplar-based approaches are conceptually similar to clustering methods such as k-means where we aim to find a set of representative points that best fit the data as a whole. Although k-means algorithms yield satisfactory results for problems with a small number of clusters, they generally suffer from sensitivity to the initialization (also called seeding). As the k-means cost function is highly non-convex, the commonly used iterative algorithms converge to local optima depending on the initialization. One key difference between the exemplar- based methods and k-means is that the former restricts the selection of the representative points to the actual observed data points. By doing so, instead of minimizing a continuous loss function, we maximize a discrete submodular function for which the classical greedy algorithm provides the best approximation to the optimal solution. Note that in general there are exponentially many possibilities. However, submodularity allows us to find a near-optimal solution in linear time (Mirzasoleiman et al., 2015). In fact, exemplar-based clustering is empirically more robust to noise and outliers than k-means methods or its close variants such as Wang’s iterative brain parcellation (Wang et al., 2015). There are other variations of k-means that include soft assignment of nodes to clusters, such as fuzzy c-means (FCM) (Bezdek, 2013). Similarly, the proposed exemplar-based approach could be extended to incorporate probabilistic assignment of nodes to networks, where the probability of assigning a node to a network is proportional to the inverse distance of the node to the corresponding exemplar. Finally, the greedy algorithm smoothly splits the old networks, similar to hierarchical clustering methods. This is in contrast to our earlier work (Shen et al., 2013) where for each value of K, a different network is proposed without preserving correspondences.

5.2. Comparison of algorithms for individual-level networks

We compared our exemplar-based parcellation with two other algorithms for delineating individual-level networks: Shen’s rotation based algorithm (Shen et al., 2013) and Wang’s iterative scaling algorithm (Wang et al., 2015). These two methods take contrasting approaches from each other to define individual-level networks, leading to different strengths and limitations. Shen’s method assumes that the entire dataset is accessible to jointly create new group- and individual-level networks. This method is well-suited for studies where the network structure of the current population is not applicable for preexisting parcellations and a new parcellation must be created. However, this method may give different group-level networks for each study, and thus lacks a one-to-one correspondence between studies. Alternatively, Wang’s method assumes a group-level parcellation can be modified to fit an individual’s networks with limited changes to the gross topology of the group-level networks. This algorithm is well-suited for many studies where a preexisting group-level parcellation is a reasonable assumption. However, if an individual’s networks differ from the group-level parcellation such as in the case of brain tumors or other pathology (Ghumman et al., 2016), it is not clear how well this algorithm will perform. Given these limitations, neither approach can generalize to multiple applications. In contrast, our exemplar-based parcellation algorithm can be used to accomplish either of these purposes. We show our algorithm’s ability to find exemplars and parcellate individual-level networks in the main analysis (Figs. 2 and 4) and to find individual-level networks given a set of exemplars in the split-half analysis (Figs. 3 and 4). In this sense, our algorithm generalizes these contrasting approaches.

5.3. The need for individualized networks

Our finding that individual-level parcellations can predict sex demonstrates a problem of group-level parcellations. As the sex prediction relies only on network organization (not the connectivity based on these networks, as reported in Satterthwaite et al. (Satterthwaite et al., 2015)), these results show that important information can be missed with group-level parcellations. If a basic characteristic such as sex in a cohort of healthy controls of a similar age results in different individualized networks, it is reasonable to assume that other characteristics linked to connectivity such as age (Hampson et al., 2012), cognition (Finn et al., 2015; Smith et al., 2015; Rosenberg et al., 2016), and neuropsychiatric diagnosis (Fornito and Harrison, 2012) could also show distinct individual-level networks. Overall, this finding suggests the need for individual-level parcellation algorithms, like our approach, to address individual differences, while maintaining a one-to-one correspondence of networks across subjects.

5.4. Localizing inter-individual variability

Our findings suggest that the greatest inter-individual variability in network organization is located in limbic, parietal, and prefrontal regions (Fig. 5). These findings are consistent with the previous studies that have examined inter-individual variability in connectivity (Mueller et al., 2013; Miranda-Dominguez et al., 2014; Finn et al., 2015; Mejia et al., 2016), and parcellations (Gordon et al., 2017b; Laumann et al., 2015; Wang et al., 2015). Accumulating evidence suggests that the neural systems subserving higher-order association cortices display more inter-individual variability in their connectivity profiles than those in sensorimotor regions (Frost and Goebel, 2012; Mueller et al., 2013). These regions further match with maps of evolutionary cortical expansion (Zilles et al., 1988) and long-range integration and regional segregation (Sepulcre et al., 2010), whose reflection on parcellation is expected.

5.5. Sex differences

Recent neuroimaging studies have reported sex differences in functional connectivity (Kilpatrick et al., 2006; Biswal et al., 2010; Scheinost et al., 2015; Zhang et al., 2016). We observed that regions in the anterior and posterior cingulate cortex, precuneus, superior parietal lobule, superior frontal gyrus, parahippocampal gyrus and inferior temporal gyrus exhibited relatively high importance scores in the sex prediction analysis. These regions, predominantly located in DMN and FPN, have been reported to display sex differences (Biswal et al., 2010; Scheinost et al., 2015). These regions have also been consistently identified as functional hubs in the brain (Zuo et al., 2012; van den Heuvel and Sporns, 2013), showing a high density of connections. When taken together, these observations suggest that functional hubs exhibit different network organization in males and females, consistent with previous studies (Tomasi and Volkow, 2012).

Note, however, that the main focus of the presented analysis was not to demonstrate sex differences in the functional organization of the brain. This could have been achieved using more informative features, such as functional connectivity matrices with information regarding all edges. Nor was it to distinguish between the two sex groups. Instead, the sex prediction was used to demonstrate that group effects can lead to different network definitions and thus patient versus control or patient group comparisons should not assume that the use of global network definitions is appropriate. As an aside, it is also interesting to note that given the minimal information stored in the functional node-to-network assignment vectors, composed of all integer values (1, 2, … K), it is impressive that such group effects can be detected.

5.6. Strengths and limitations

This study has several strengths. Unlike many other parcellation algorithms (Beckmann et al., 2005; Power et al., 2011; Yeo et al., 2011; Wang et al., 2015; Gordon et al., 2017a), our proposed approach does not depend on thresholds, or the selection of hyperparameters. Our method provides a one-to-one mapping across subjects and no additional algorithms are needed to map network correspondences. However, there are several limitations that should be noted. Individual-level networks could be influenced by individual differences in physiological noise (Rogers et al., 2007) and head motion (Van Dijk et al., 2012). As males and females did not show differences in motion, our network differences as a function of sex are unlikely due to the motion. In this work, the starting point was a 188-node functional atlas. It would be quite reasonable to begin, instead, at the voxel-level as individual node definitions may differ between the sexes, whereas our starting point assumes they are the same. Starting at the node level reduces the computational burden because the process of defining nodes already provides a large dimensionality reduction step. Moreover, as the atlas was derived from an independent dataset, this can reduce the chance of overfitting to the data of interest. On the other hand, it may cause propagation of registration noise and misalignment of the preexisting atlas. The approach described above, however, is applicable at the voxel-level and this can therefore be used to define nodes at the individual-level while maintaining cross-subject correspondences. Even though we started from a node-level atlas, the number of features used by the predictive model (d = 188) was relatively high comparing to the number of samples (n = 825). This may lead to a larger variance in the model and thus make it harder to generalize over novel subjects. We deliberately did not reduce the number of features in order to achieve higher accuracies, as we sought to employ a fully transparent and data-driven analysis of the feature space with all the nodes included as features. In this regard, we also did not force any prior knowledge on the importance of nodes. Nevertheless, the achieved accuracies are comparable (or higher for some Ks) to the previous models that have used full functional connectivity data (Satterthwaite et al., 2015).

5.7. Conclusion

In conclusion, we present a novel algorithm to parcellate individual- level networks using exemplar-based clustering with submodularity optimization. The algorithm compares favorably with existing algorithms when parcellating nodes into individual-level networks while maintaining cross-subject correspondences. Using networks defined at the individual-level, we demonstrated that brain network organization differs between the sexes as indicated by our ability to predict sex with greater than 70% accuracy. The sex prediction finding illustrates that individual parcellation of functional networks can reveal subgroups in a population and suggests that the use of a global network parcellation may overlook fundamental differences in network organization in subgroups. This is a particularly important point to consider in studies comparing patients versus controls or even patient subgroups. Network organization may differ between individuals and global configurations should not be assumed.

Appendix A. Supplementary data

Supplementary data related to this article can be found at https://doi.org/10.1016/j.neuroimage.2017.08.068.