Ultrahigh resolution retinal imaging by visible light OCT with longitudinal achromatization

Abstract

Chromatic aberrations are an important design consideration in high resolution, high bandwidth, refractive imaging systems that use visible light. Here, we present a fiber-based spectral/Fourier domain, visible light OCT ophthalmoscope corrected for the average longitudinal chromatic aberration (LCA) of the human eye. Analysis of complex speckles from in vivo retinal images showed that achromatization resulted in a speckle autocorrelation function that was ~20% narrower in the axial direction, but unchanged in the transverse direction. In images from the improved, achromatized system, the separation between Bruch’s membrane (BM), the retinal pigment epithelium (RPE), and the outer segment tips clearly emerged across the entire 6.5 mm field-of-view, enabling segmentation and morphometry of BM and the RPE in a human subject. Finally, cross-sectional images depicted distinct inner retinal layers with high resolution. Thus, with chromatic aberration compensation, visible light OCT can achieve volume resolutions and retinal image quality that matches or exceeds ultrahigh resolution near-infrared OCT systems with no monochromatic aberration compensation.

1. Introduction

Optical coherence tomography (OCT) has advanced the detection, diagnosis and monitoring of retinal diseases by enabling high-resolution volumetric and cross-sectional structural imaging of the retina [1], and more recently, by revealing vascular perfusion [2, 3]. Retinal OCT is usually performed with near-infrared light, and visualization of retinal layers with ultrahigh axial resolutions approaching two microns can be achieved with large near-infrared bandwidths [4–9]. Recent pilot studies have shown the capability of visible light spectral / Fourier domain (spectrometer-based) OCT to perform structural and functional imaging of the human retina [10–12] with improved axial resolution [13, 14] compared to near-infrared OCT. Visible light OCT also enables imaging of chromophores such as hemoglobin based on spectroscopic absorbance contrast [15–17].

The chromatic aberration of the eye however, limits the achievable resolution of visible light OCT. Chromatic aberration is substantially larger for visible wavelengths than for near infrared wavelengths [18]. In particular, both optical glass used in lenses and ocular media in the human eye exhibit large changes in refractive index with wavelength across the visible spectrum. The resulting chromatic aberrations are especially consequential in ultrahigh axial resolution and spectroscopic visible light OCT, where broad bandwidths are needed. Hence, we must consider the impact of chromatic aberrations in both the OCT sample arm (taken to include all elements in the optical path, including the human eye) and the spectrometer.

The first refraction at the corneal interface causes the most chromatic focal shift (~2/3 of that of the entire eye). However, all refractive elements induce some longitudinal chromatic aberration (LCA). LCA of the human eye is greater at visible wavelengths [19] than at near-infrared wavelengths [20] and LCA generates a ~2 diopter focal shift (defocus) across the visible spectrum [18]. While moderate dispersion can be compensated numerically in spectral / Fourier domain OCT without significant penalty [21], computational defocus correction incurs a penalty in signal-to-noise ratio and is hindered by excessive eye motion [22, 23]. If uncompensated, defocus degrades the image resolution. Though there are inter-subject differences, LCA differences are negligible across subjects and ages for numerical apertures less than 0.1 [24], which are typical for OCT ophthalmoscopy. Thus, achromatization of the eye based on population-averaged LCA can yield significant benefits [6, 25].

In spectral / Fourier domain OCT, high efficiency, high spectral resolution, and broad bandwidth spectrometers are required to achieve high sensitivity, large axial imaging range, and high axial resolution, respectively [21]. To achieve high spectral resolution, all wavelengths must be in focus at the spectrometer detector. Otherwise, performance suffers when the wavelengths in the spectrum do not focus to a line on the camera. Therefore, assuming linear dispersion of wavelengths, a chromatic focal shift that is nonlinear in wavelength can be detrimental in two ways. First, if out-of-focus light is not detected (misses the sensor), then the maximal system sensitivity is reduced, and if this effect is wavelength-dependent, the axial resolution is degraded. Second, out-of-focus light can degrade the spectral resolution of the spectrometer, by causing each wavelength to spread along the camera. This effect exacerbates the sensitivity roll-off in spectral / Fourier domain OCT [26], and is typically more severe at the edges of the spectrum, resulting in worse axial resolution for increased imaging depth. Though stationary samples can be positioned near zero delay where sensitivity and axial resolution are optimized, this is challenging in the human retina due to involuntary eye motion. Thus, in practice, chromatic aberrations in the spectrometer result in worse sensitivity and axial resolution for in vivo retinal imaging.

Here we present an achromatized visible light OCT system, with a reflective collimator and zero-power triplet achromatizing lens (AL) [25], placed in collimated space in the sample arm, to minimize LCA; and a reflective collimator in the spectrometer, with a focusing lens chosen for a linear chromatic focal shift, to minimize the sensitivity rolloff. After verifying ~20% improvement of the axial speckle size in vivo with achromatization, we imaged the normal human retina. Image resolution was sufficient to clearly visualize the retinal pigment epithelium (RPE) and Bruch’s membrane (BM) across a 6.5 mm field-of-view (FOV) for the first time, enabling morphometry that yielded thicknesses consistent with textbook histology. Finally, imaging over a smaller FOV with higher spatial sampling revealed distinct layers of the inner retina. These results show that with longitudinal achromatization, visible light OCT can achieve retinal image quality that matches or exceeds non-adaptive optics ultrahigh resolution near-infrared OCT systems.

2. Methods

2.1 System design

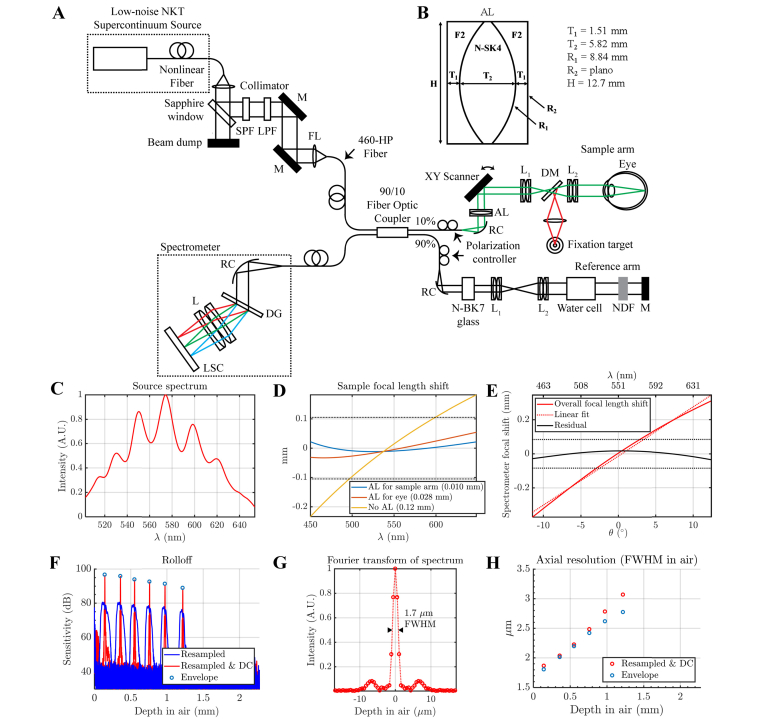
A fiber-based, LCA-corrected spectral/Fourier domain visible OCT system (Fig. 1(A)) for human retinal imaging was built, with a 156 MHz repetition rate supercontinuum light source (EXU3, NKT Photonics A/S, Birkerød, Denmark). The collimated beam was attenuated by a sapphire window, spectrally filtered to a range of 475 - 650 nm, and coupled to the input port of a broadband, 90/10, fused single-mode 460-HP fiber coupler (TW560R2A2, Thorlabs Inc.) designed for visible wavelengths [11]. The 10% arm of the fiber coupler was connected to the sample arm, which was integrated into an ophthalmoscope platform. A 7 mm focal length protected silver reflective collimator (90° off-axis parabolic mirror, RC02APC-P01, Thorlabs Inc.) was used to collimate without introducing chromatic aberrations. A custom zero-power triplet achromatizing lens (AL), shown in Fig. 1(B), was incorporated after the collimator, in collimated space, to correct for LCA in the eye. The beam was then scanned by a 2D galvanometric scanner (CTI 6210H, Cambridge Technology). The scan and ocular lenses were achromatic doublet pairs with 37.5 and 50 mm effective focal length, respectively. Together, these lenses formed a quasi-telecentric lens-based telescope, with a magnification of 1.33. A red LED was also imaged onto the subject's retina through a dichroic mirror for fixation.

Fig. 1.

(A) Fiber-based visible light spectral / Fourier domain OCT system for imaging the human retina (M: mirror, SPF: short pass filter, LPF: long pass filter, AL: achromatizing lens, RC: reflective collimator, L: lens, FL: focusing lens, DG: diffraction grating, LSC: line-scan camera, NDF: neutral density filter, DM: dichroic mirror). (B) Zero-power triplet achromatizing lens (AL) used in the sample arm. (C) Source spectrum measured by the spectrometer. (D) Zemax simulation of the focal shift at the retina for a model eye [27] over a broad design bandwidth (450-650 nm). With the AL designed to achromatize the entire sample arm, including the eye (blue line), the focal shift is much smaller than the diffraction limited range (dotted horizontal lines). The root-mean-squared defocuses are provided in the legend. (E) Zemax simulation of the spectrometer chromatic focal shift over the same bandwidth (450-650 nm). The overall focal shift (solid red line) versus angle (θ) is fit by a line approximating the line scan camera (dotted red line). The residual defocus (solid black line) is much smaller than the diffraction limited range (dotted horizontal lines). (F) The sensitivity rolloff of the system with depth (in air), both with and without dispersion compensation (DC) is shown. Note that the measured rolloff approaches the rolloff set by the interference envelope (circles). (G) The Fourier transform of the spectrum represents the point spread function achieved at or near zero delay. (H) Similar to the rolloff, the measured axial resolution approaches that set by the interference envelope, indicating correct resampling and dispersion compensation.

Zemax OpticStudio (Zemax, LLC, Washington, USA) simulations of LCA for three alternative approaches are further compared in Fig. 1(C): first, without achromatization; second, with achromatization of the eye; and third, with achromatization of the whole sample arm (all refractive surfaces including eye and lenses). The AL for the last approach is shown in Fig. 1(B). A human eye model provided by Zemax was employed in the simulations [27]. The source spectrum, as measured by the spectrometer, is shown in Fig. 1(C). The design bandwidth was chosen to be 450 nm – 650 nm. Only the strategy of achromatizing the entire sample arm, including the eye, resulted in a chromatic focal shift over the entire design bandwidth significantly lower than the diffraction limited range (dotted lines in Fig. 1(D)). Transverse chromatic aberrations (TCA) were not considered, and are discussed further in Section 4.3.

We used N-BK7 glass in the reference arm to approximately match chromatic dispersion caused by the AL in the sample arm. All other sample arm lenses were matched by identical lenses in the reference arm. The eye dispersion was coarsely balanced by a 20 mm water cell in the reference arm. Residual second- and third-order dispersion mismatches were numerically corrected in post-processing to optimize the axial image resolution. The second-order coefficient for dispersion correction was allowed to vary proportionate to the absolute lateral distance from the center of the field-of-view.

Chromatic aberrations were also considered in the spectrometer design. We used a reflective 50 mm focal length protected silver collimator (90° off-axis parabolic mirror, RC12APC-P01, Thorlabs Inc.) in the spectrometer to achieve achromatic collimation. An 1800 line per millimeter volume phase holographic grating (Wasatch Photonics) diffracted the light. Based on the grating equation, the diffraction angle θ is a function of wavelength λ. Assuming that the scan lens relationship holds (d = f × θ, where d is lateral displacement in the focal plane, and f is the focal length), the lateral displacement at the focal plane should be approximately proportional to θ(λ). Therefore, a lens with a chromatic focal shift that is linear in θ(λ) can focus all diffracted wavelengths onto a suitably tilted line. We chose an achromatic doublet pair with effective focal length of 125 mm, whose chromatic focal shift was reasonably linear over the spectral range of interest (root-mean-squared deviation of 15 µm from linear fit in Fig. 1(E)) to focus the diffracted spectrum onto a complementary metal-oxide semiconductor (CMOS) line scan camera (Basler SPL 4096-140km). We tilted the camera to match the quasi-linear focal shift, and minimize the residual error, as in our simulations (Fig. 1(E)). The sensitivity rolloff of the system was measured to be ~5 dB over 1 mm in air (Fig. 1F). The axial resolution approaches the FWHM of the Fourier transform of the spectrum (Fig. 1(G)) near zero delay and degrades with depth (Fig. 1(H)).

Light safety is crucial for ophthalmic instruments that use visible light. In addition to thermal considerations and the photochemical blue light hazard, exposures in the visible wavelength range are also limited by a new potential damage mechanism identified by Hunter et al. [28]. Accordingly, section 8.3.3 of ANSI Z136.1 – 2014 American National Standard for Safe Use of Lasers published by Laser Institute of America states that we must limit retinal radiant exposures to <5 J/cm² divided by V(λ), the photopic luminous efficiency function evaluated at wavelength λ, defined by International Commission on Illumination (CIE), as tabulated in Appendix I [29]. V(λ) has a maximum of 1.0 at 555 nm. We implemented a safeguard, based on the field-of-view imaged and spectrum multiplied by V(λ), to stop imaging when this limit is reached. The limit for cumulative retinal exposure over a period of 48 hours was calculated as 44 seconds, 8.2 minutes, and 294 minutes for fields-of-view of 0.09 mm²_, 1 mm², and 36 mm²_, respectively, with 0.15 mW incident power.

To minimize OCT illumination light exposure, we used an incident power of 0.03 mW at the cornea to optimize the alignment in real-time, and acquired images with an incident power of 0.15 mW, which enabled a sensitivity of 96 dB at 10 kHz axial scan rate [11]. Based on the newest ANSI standards [29], the illumination power for OCT acquisition is consistent with the maximum permissible exposure (MPE) for a 0.5 second, stationary point source, which represents an overly conservative assumption due to continuous beam scanning and shuttering in our system [11]. Two scan protocols were investigated. The first acquired a series of high-definition frames with 4096 axial scans with a 6.5 mm FOV along the fast (x) axis, with a separation of 5 µm between frames along the slow (y) axis, for outer retinal visualization and morphometry. The second rapidly acquired a series of frames consisting of 168 axial scans with a 0.16 mm FOV along the fast (x) axis, with a separation of 1.3 µm between frames along the slow (y) axis, for imaging of inner retinal layers by compounding of 9 frames. The human subjects protocol was approved by the UC Davis Institutional Review Board. The study was conducted in accordance with the tenets of the Declaration of Helsinki, and complied with the Health Insurance Portability and Accountability Act.

2.2 LCA and speckle size

In this section, we theoretically describe the spatial (axial and transverse) autocorrelation of the complex OCT signal, accounting for the presence of LCA. The spatial autocorrelation of a random speckle field is determined by the point spread function (PSF). Conversely, the autocorrelation can provide useful information about the ideal PSF, achievable in the absence of monochromatic aberrations and dispersion. To understand the principles behind this idea, we first individually consider each wavelength in the source spectrum, λ, corresponding to medium wavenumber k = 2πn/λ, where n is the medium refractive index. We start with the λ-dependent (k-dependent) point spread function (H) that describes the response to a point scatterer located at position (x,y,z₀) with respect to the center of the Gaussian beam focus,

$$\mathrm{H}\left(\stackrel{\rightharpoonup }{\mathrm{r}},{\mathrm{z}}_0,\mathrm{k}\right)=\sqrt{\frac{2}{\text{π}}}\frac{{\mathrm{E}}_{\text{R,0}}^{*}\text{(k)}{\mathrm{E}}_{\mathrm{S},0}\text{(k)}{\mathrm{\omega }}_{0,\mathrm{r}}}{{\text{ω}}_{\mathrm{r}}{\left({\mathrm{z}}_0\text{,k}\right)}^2}{{\displaystyle \mathrm{e}}}^{-\frac{{\text{2r}}^2}{{\text{ω}}_{\mathrm{r}}{\left({\mathrm{z}}_0\text{,k}\right)}^2}}{{\displaystyle \mathrm{e}}}^{\mathrm{-i}\left[{\text{2kz}}_0+\frac{{\text{2kr}}^2}{{\text{2R}}_{\mathrm{r}}\left({\mathrm{z}}_0,\mathrm{k}\right)}\text{-2ψ}\left({\mathrm{z}}_0,\mathrm{k}\right)\right]}.$$ (1)

H represents the Fourier transform (from z to k) of the standard OCT PSF (h). Note that r² = x² + y² is the transverse radial spatial coordinate, while E_S,0(k) and E_R,0(k) are the k-dependent complex electric field amplitudes for the sample and reference, respectively. Gaussian beam parameters are given by

$${\text{ω}}_{\mathrm{r}}\left({\mathrm{z}}_0,\mathrm{k}\right){\text{=ω}}_{0,\mathrm{r}}\sqrt{1+{\left[\frac{{\mathrm{z}}_0}{{\mathrm{z}}_{\mathrm{R}}\text{(k)}}\right]}^2}, {\mathrm{R}}_{\mathrm{r}}\left({\mathrm{z}}_0,\mathrm{k}\right){\text{=z}}_0\left\{1+{\left[\frac{{\mathrm{z}}_{\mathrm{R}}\text{(k)}}{{\mathrm{z}}_0}\right]}^2\right\}, \text{and} \mathrm{\psi }\left({\mathrm{z}}_0,\mathrm{k}\right)\text{=atan}\left[\frac{{\mathrm{z}}_0}{{\mathrm{z}}_{\mathrm{R}}\text{(k)}}\right].$$ (2)

In addition, the wavelength-dependent Rayleigh range is given by z_R(k) = kω_0,r²/2. For simplicity, we assume here that the beam waist ω_0,r does not depend on k or λ. It is a relatively straightforward modification to let ω_0,r→ ω_0,r(k). Importantly, ω_r(z₀,k) = ω_0,r (transverse beam waist) at the focus (z₀ = 0), and increases away from the focus (z₀≠0). The sample power (integral of the field modulus squared) in the Gaussian beam, with wavenumber k, is P_S(k) = |E_S,0(k)|²πω_0,r²/2.

The wavelength-dependent (k-dependent) autocorrelation (R) is then given by the autocorrelation of Eq. (1) in the transverse direction,

$$\mathrm{R}\left(\stackrel{\rightharpoonup }{\mathrm{r}}{,\mathrm{z}}_0,\mathrm{k}\right)=\frac{{\left|{\mathrm{E}}_{\mathrm{R},0}\text{(k)}\right|}^2}{\mathrm{1+}{\left[\frac{{\mathrm{z}}_0}{{\mathrm{z}}_{\mathrm{R}}\text{(k)}}\right]}^2}\frac{{\left|{\mathrm{E}}_{\mathrm{S},0}\text{(k)}\right|}^2}{2}{{\displaystyle \mathrm{e}}}^{-\frac{{\mathrm{r}}^2}{{\text{ω}}_{0,\mathrm{r}}^2}}=\frac{{\left|{\mathrm{E}}_{\mathrm{R},0}\text{(k)}\right|}^2{\mathrm{P}}_{\mathrm{S}}\text{(k)}}{{\mathrm{\pi \omega }}_{\mathrm{r}}{\left({\mathrm{z}}_0\mathrm{,k}\right)}^2}{{\displaystyle \mathrm{e}}}^{-\frac{{\mathrm{r}}^2}{{\text{ω}}_{\mathrm{0,r}}^2}}.$$ (3)

Here we reproduce the somewhat surprising result that the transverse width of the complex autocorrelation does not depend on defocus [30, 31], i.e. the decay with r is independent of z₀. This is because as the beam width (ω_r) increases away from the focus, the wavefront curvature (z₀/R_r) also increases, leaving the transverse autocorrelation width unchanged. Critically, the term 1/ω_r(z₀,k)² accounts for reduced coupling away from the focal plane, having a maximum of 1/ω_r(0,k)² = 1/ω_0,r² at the focus (z₀ = 0).

Next, we allow the focus to vary with k, i.e. z₀→z₀ + Δz₀(k) in Eq. (3), which simulates LCA. The transverse (r) autocorrelation function is obtained by integrating Eq. (3) over k.

$${\mathrm{R}}_{\text{trans}}\left(\stackrel{\rightharpoonup }{\mathrm{r}}{\mathrm{,z}}_0\right)=\frac{1}{\text{2π}}{\displaystyle \int \mathrm{R}\left[\stackrel{\rightharpoonup }{\mathrm{r}}{\text{,z}}_0{\text{+Δz}}_0\left(\mathrm{k}\right)\text{,k}\right]\text{dk}}=\left\{\frac{1}{\text{2π}}{\displaystyle \int \frac{{\left|{\mathrm{E}}_{\mathrm{R},0}\text{(k)}\right|}^2{\mathrm{P}}_{\mathrm{S}}\text{(k)}}{{\text{πω}}_{\mathrm{r}}{\left[{\mathrm{z}}_0{\text{+Δz}}_0\left(\mathrm{k}\right)\text{,k}\right]}^2}\text{dk}}\right\}{{\displaystyle \mathrm{e}}}^{-\frac{{\mathrm{r}}^2}{{\text{ω}}_{\text{0,r}}^2}}.$$ (4)

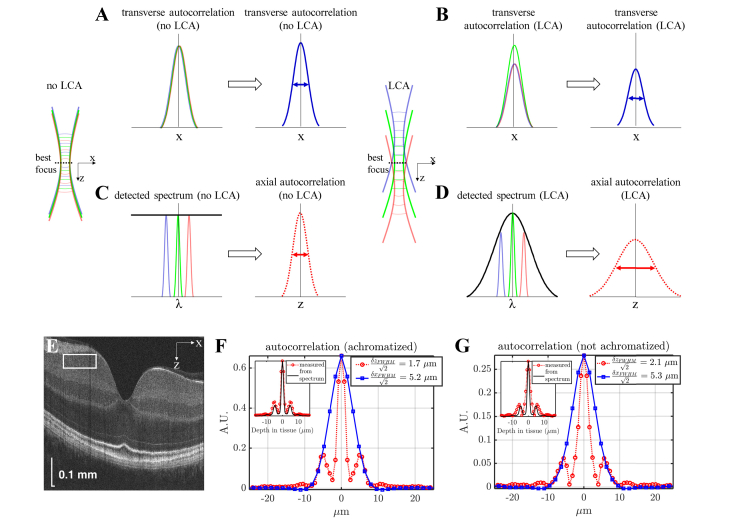
While the transverse width of the autocorrelation does not depend on z₀, the magnitude of the autocorrelation (related to the OCT signal level) does decrease if k values in the spectrum are out of focus [z₀ + Δz₀(k)≠0] due to the term in curly braces. A comparison of Eq. (4) and Eq. (1), the latter evaluated at z₀ = 0, shows that the transverse width of the PSF (H) is less than the transverse width of the autocorrelation (R_trans) by a factor of 1.41. The effects that are described mathematically in Eq. (4) are shown pictorially in Fig. 2(A)-2(B).

Fig. 2.

Assessing longitudinal chromatic aberration (LCA) in vivo from OCT speckle patterns. (A-B) A simple physical picture for the transverse autocorrelation based on Eq. (4). The transverse autocorrelation width is independent of defocus, and is the same with no LCA (A) and with LCA (B). However, with LCA (B), out-of-focus wavelengths are more weakly coupled, reducing the overall autocorrelation height and OCT signal level (B). (C-D) A simple physical picture for the axial autocorrelation based on Eq. (5). With no LCA, all wavelengths focus at the same axial plane, leading to uniform coupling across the spectrum (C), which maintains optimal axial autocorrelation width. However, with LCA, out-of-focus wavelengths are more weakly coupled, leading to unwanted shaping of the detected spectrum (D), which increases the axial autocorrelation width. (E) Ultrahigh resolution visible light OCT imaging of the macula (log scale) with a region-of-interest near the best focus to assess the complex speckle autocorrelation (F-G) Axial (dotted red) and transverse (solid blue) autocorrelations are shown. The best achievable axial (z) resolution, estimated from the spatial autocorrelation, was 1.7 µm full-width-at-half-maximum (FWHM) with achromatization (F) and 2.1 µm FWHM without achromatization (G). Sidelobes in the axial autocorrelation arise from ripples in the spectrum (insets in F-G show the Fourier transform of the spectrum squared). This represents a 20% improvement in the axial speckle size, achieved by achromatization. The transverse (x) resolution estimates based on the spatial autocorrelation were similar with and without achromatization (5.2 µm FWHM and 5.3 µm FWHM, respectively).

Similarly, the axial (z) autocorrelation function can be obtained from inverse Fourier transformation of Eq. (3), evaluated at r = 0.

$${\mathrm{R}}_{\text{axial}}\left({\text{z,z}}_0\right)=\frac{1}{\text{2π}}{\displaystyle \int \mathrm{R}\left[{\text{0,z}}_0\text{+Δz}\left(\mathrm{k}\right)\text{,k}\right]{{\displaystyle \mathrm{e}}}^{\text{i2kz}}\text{dk}}=\left[\frac{1}{\text{2π}}{\displaystyle \int \frac{{\left|{\mathrm{E}}_{\mathrm{R},0}\text{(k)}\right|}^2{\mathrm{P}}_{\mathrm{S}}\text{(k)}}{{\text{πω}}_{\mathrm{r}}{\left[{\mathrm{z}}_0{\text{+Δz}}_0\left(\mathrm{k}\right),\mathrm{k}\right]}^2}{{\displaystyle \mathrm{e}}}^{\text{i2kz}}\text{dk}}\right].$$ (5)

If all wavelengths are in focus without LCA, z₀ + Δz₀(k) = 0, and ω_r(0,k) = ω_0,r for all k in the source spectrum. If so, then the axial autocorrelation function width is determined by the inverse Fourier transform (from k to z) of the squared interference spectrum |E_R,0(k)E_S,0(k)|² ~P_S(k)². For a Gaussian spectrum, the axial width of the PSF [related to the inverse Fourier transform of the interference spectrum |E_R,0(k)E_S,0(k)| ~P_S(k)] is less than the axial width of the autocorrelation (R_axial) by a factor of 1.41. With LCA, some wavelengths are out-of-focus, i.e. z₀ + Δz₀(k)≠0 and ω_r[z₀ + Δz₀(k),k]>ω_0,r. This leads to unwanted shaping of the detected spectrum. For instance, assuming a monotonic longitudinal chromatic aberration with only the central wavelength (λ = λ₀ or k = k₀) in focus, we have that z₀ = 0, Δz₀(k₀) = 0, ω_r(0,k₀) = ω_0,r and ω_r[Δz₀(k),k]>ω_0,r for k≠k₀. The function 1/ω_r[z₀ + Δz₀(k),k]² that appears in the inverse Fourier transformation in Eq. (5), thus has a maximum at k = k₀ and serves to reduce the detected spectral bandwidth relative to the source spectral bandwidth. This increases the axial width of both the PSF and the autocorrelation function R_axial. The effects that are described mathematically in Eq. (5) are shown pictorially in Fig. 2(C)-2(D). It is important to remember that the axial and transverse resolutions estimated from autocorrelations are best case estimates, achieved only if the system is dispersion corrected and diffraction limited, respectively. In particular, the transverse autocorrelation width is not expected to be sensitive to LCA or TCA, while the axial autocorrelation width is not expected to be sensitive to TCA.

3. Results

3.1 Validating speckle size in vivo

The measured beam diameter (1/e² intensity) incident at the cornea was 1.55 mm. With this beam diameter, Gaussian propagation with a standard eye focal length of 16.7 mm and center wavelength (λ₀) of 575 nm yielded a diffraction-limited intensity distribution (and estimated OCT transverse resolution in the focal plane) of 4.6 μm full-width-at-half maximum (FWHM). A 1.4 μm axial resolution in tissue was estimated from a mirror reflection without the achromatizing lens in place [11], assuming a tissue refractive index of 1.4. However, these estimations represent nominal resolutions, not accounting for LCA of the human eye or achromatization. Thus, we also examined the autocorrelation of the complex speckle pattern in OCT images of the human retina, acquired by the system in Fig. 1, to determine the effect of achromatization in vivo. The left eye of a 36 year old male with no history of eye disease (eye length of 25.9 mm measured by the Zeiss IOLMaster) was dilated, cyclopleged, and imaged with and without achromatization. The focus was placed near the inner limiting membrane (ILM).

For a 1 diopter chromatic focal shift across the spectrum (Fig. 1(C)), assuming the center wavelength is in focus, theory [Eq. (4)-(5)] predicts that achromatization should achieve no change in transverse autocorrelation width, 19% reduction in axial autocorrelation width, and 25% increase in signal intensity (autocorrelation height) in the standard eye.

First, axial phase correction was performed on adjacent axial scans. Then, a rectangular region-of-interest (ROI) with dimensions of 50 μm (axial) × 900 μm (transverse) was chosen near the best focus (Fig. 2(E), white box). Next, the spatial autocorrelation was estimated by averaging over both the axial and transverse directions.

$$\hat{\mathrm{R}}\left(\text{mΔx,pΔz}\right)=\frac{1}{\text{(M-m)(P-p)}}{\displaystyle \sum _{\text{j=1}}^{\text{M-m}}{\displaystyle \sum _{\text{q=1}}^{\text{P-p}}\text{S[(j+m)Δx,(q+p)Δz]}{\mathrm{S}}^{*}\text{[jΔx,qΔz]}}}-\overline{{\left|\mathrm{S}\right|}_{\text{noise}}^2}\text{δ[m,p]}$$ (6)

In Eq. (6), S is the phase-corrected complex OCT signal, where * denotes complex conjugation, j and m are transverse indices, Δx is the transverse sampling interval, q and p are axial indices, Δz is the axial sampling interval, and the ROI size is M (transverse) × P (axial). The last term represents correction of the noise bias. The Kronecker delta function, δ[m,p], ensures that this correction is only applied at zero lag. The PSF transverse FWHM was estimated from the transverse width (δx_FWHM) of the real part of the autocorrelation estimate (after axial phase correction). With achromatization, within the ROI shown in Fig. 2(E), we estimated that δx_FWHM/1.41 = 5.2 μm (Fig. 2(F)), in approximate agreement with the theoretical estimate of 4.6 μm based on the beam diameter at the cornea. Speckle size results were similar in the ganglion cell layer (GCL) and inner plexiform layer (IPL). The diffraction limited transverse resolutions estimated using the autocorrelation in different sub-bands varied between ~5-6 μm, and increased from the shortest to the longest wavelength sub-band. This behavior is expected from the increase in the fundamental mode field diameter with wavelength in standard single mode 460-HP fiber. The axial width (δz_FWHM) of the absolute value of the autocorrelation estimate yielded a FWHM axial resolution estimate of δz_FWHM/1.41 = 1.7 μm at about 1/3 of the axial imaging range (Fig. 2(F)). Without achromatization [11], by similarly choosing a region-of-interest near the best focus, the complex OCT image speckle yielded estimates of δx_FWHM/1.41 = 5.3 μm and δz_FWHM/1.41 = 2.1 μm at about 1/3 of the axial imaging range (Fig. 2(G)).

The measured 2% reduction in transverse speckle size and 20% reduction in axial speckle size with achromatization agrees with predictions from theory [Eq. (4)-(5)]. While the improvement in signal intensity with achromatization is difficult to assess in a controlled fashion, we generally observed brighter images after achromatization. These results suggest that achromatization is needed to fully appreciate the benefits of broad visible light OCT bandwidths and optimize axial resolution.

Our observation that achromatization does not improve the transverse speckle size seems surprising at first. However, this observation is easily explained by the fact that the transverse width of the spatial autocorrelation function is not sensitive to defocus [Eq. (3) and Eq. (4)]. Similar observations have been made in the literature [30, 31] in the context of dynamic light scattering. Importantly, although achromatization does not reduce the transverse speckle size, it may improve the signal level [as per Eq. (4) and (5)], as well as the transverse resolution.

3.2 Comparison with near-infrared light OCT and visible light OCT without achromatization

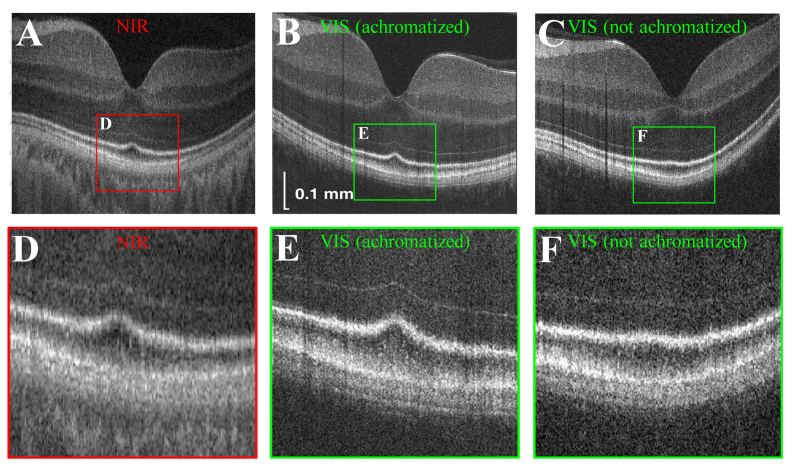
In Fig. 3, we compare near-infrared light OCT images to visible light OCT images of the same eye, both with and without achromatization. Near-infrared light OCT had an axial resolution of ~4 μm and a transverse resolution of ~15 μm. Visible light OCT without achromatization had a transverse resolution of ~10 μm, as described in our previous work [11]. In agreement with the theoretical and experimental speckle analysis described above, visible light OCT with achromatization most clearly delineated the outer retinal bands.

Fig. 3.

Comparison of near-infrared (NIR) light OCT (A,D) and visible (VIS) light OCT, with (B,E) and without (C,F) achromatization in the same eye. Near-infrared (A,D) and visible light OCT images without achromatization (C,F) consist of 2048 axial scans with transverse resolutions of 15 μm and 10 μm respectively. Visible light OCT images with achromatization (B,E) consist of 4096 axial scans with a transverse resolution of 5.2 μm. All images are on a logarithmic scale.

3.3 Outer retinal imaging and morphometry

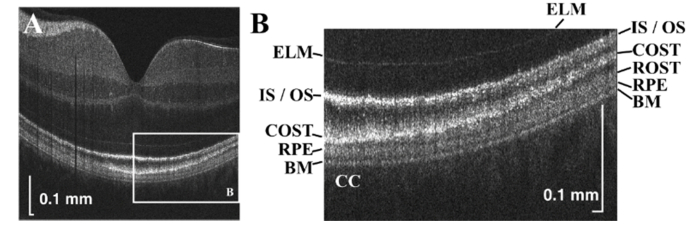
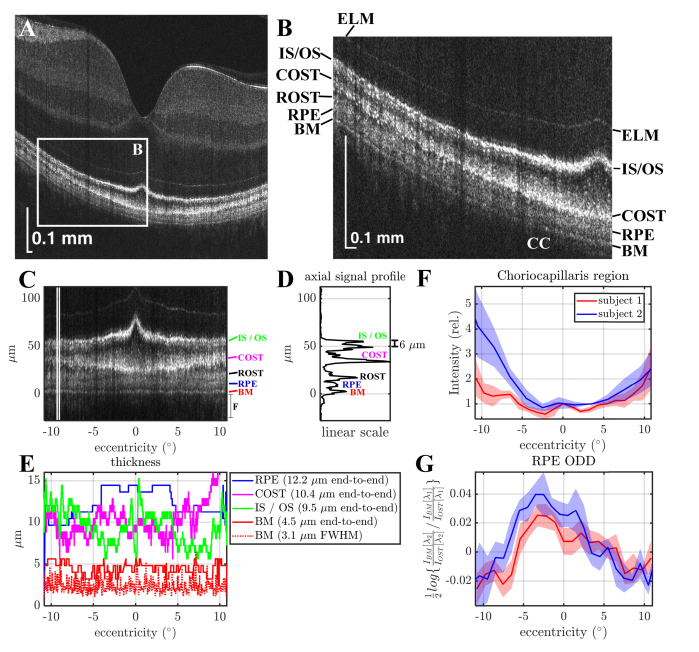
Ultrahigh resolution in vivo human retinal images (single B-scans) are shown in Fig. 4(A)-4(B). Bruch’s membrane (BM) is especially well-separated from the retinal pigment epithelium (RPE) across the entire 6.5 mm field-of-view. In agreement with previous work [32], the cone outer segment tips (COST) band touches the RPE in the fovea, but rises away from the RPE in the parafovea and perifovea, where the rod outer segment tips (ROST) band appears. These images further illustrate that the RPE band appears thicker in the fovea than in the parafovea and perifovea. At the same time, the IS / OS band appears thinner in the parafovea than in the peripheral macula, where it appears to split into two.

Fig. 4.

Visualization of outer retinal bands in a single B-scan. (A) Ultrahigh resolution visible light OCT imaging of the macula (square root scale). (B) Zoom of white box in panel A, showing six outer retinal bands, including the external limiting membrane (ELM), photoreceptor inner segment / outer segment junction (IS / OS), cone outer segment tip (COST), rod outer segment tip (ROST), retinal pigment epithelium (RPE), as well as Bruch’s membrane (BM). Posterior to BM is the choriocapillaris (CC). Sidelobes of the point spread function may result in “ghost” signals proximal to the IS / OS band.

To more quantitatively assess these trends, morphometry was performed by adapting an algorithm developed previously for outer retinal segmentation [32] on an additional B-scan through the foveal center (Fig. 5(A)-5(B)). The axial pixel size was 0.8 μm in tissue for layer segmentation. In Fig. 5(C), the flattened outer retina is shown, with the axial signal intensity profile averaged between the vertical white lines (Fig. 5(D)). The BM, RPE, and IS / OS band end-to-end thicknesses are shown as a function of retinal eccentricity (Fig. 5(E)), assuming a constant refractive index of 1.4. The boundaries for end-to-end thicknesses were determined by the segmentation algorithm. BM thickness was the distance between the BM inner and outer boundaries. RPE thickness was the distance between the RPE inner boundary and the BM inner boundary. The IS / OS junction and COST thicknesses were the distances between the IS / OS junction inner and outer boundaries and COST inner and outer boundaries, respectively. The segmentation algorithm initially placed boundaries at edges where the second derivative of the image intensity in the axial direction crossed zero and then corrected discontinuities as previously described [32]. The FWHM thickness of the BM band is also shown in the Fig. 5(E) legend. Determination of the FWHM thickness was not performed for the IS / OS band (two peaks in periphery), the COST band (irregular reflectance profile), and the RPE band (low contrast). The relative choriocapillaris region signal over an axial range of 24 μm distal to BM was quantified as a function of eccentricity in two subjects (Fig. 5(F)). The choriocapillaris signal increased with eccentricity. At the same time, the Optical Density Difference (ODD) of the RPE (Fig. 5(G)), defined as the natural logarithm of the ratio of the BM to distal OST signal in the 610 nm sub-band divided by the same ratio in the 560 nm sub-band, showed a peak in the fovea. This suggests that RPE attenuation due to melanin absorption and melanosome scattering may play a role in the appearance of distal layers. Other relevant factors include attenuation by photopigments, blood, and macular pigments.

Fig. 5.

Human outer retinal morphometry with visible light OCT. (A-B) A single B-scan with a zoom of the outer retina shows a transition from the fovea to periphery. (C) Zoom of the outer retina after flattening. (D) Average axial signal intensity profile between the white lines in A. (IS / OS: Inner Segment / Outer Segment Junction, COST: Cone Outer Segment Tips, ROST: Rod Outer Segment Tips, RPE: Retinal Pigment Epithelium, BM: Bruch’s Membrane). In addition to delineation of the layers on a linear scale, two peaks are evident in the IS / OS band at 9° eccentricity. (E) Thickness measurements of the BM, IS / OS junction, COST, and RPE bands (assuming a refractive index of 1.4). (F) The signal from the choriocapillaris (CC) is lowest in the fovea (0° eccentricity), and increases with eccentricity. (G) The optical density difference (ODD) of the RPE (defined as the natural logarithm of the ratio of the BM to distal OST signal in the λ₂ = 610 nm sub-band divided by the same ratio in the λ₁ = 560 nm sub-band) shows a peak near the fovea (shaded areas show standard deviations across 5 scans) in agreement with expected RPE melanin distribution [33]. Subjects 1 and 2 are males of age 36 and 26 respectively.

3.4 Inner retinal imaging

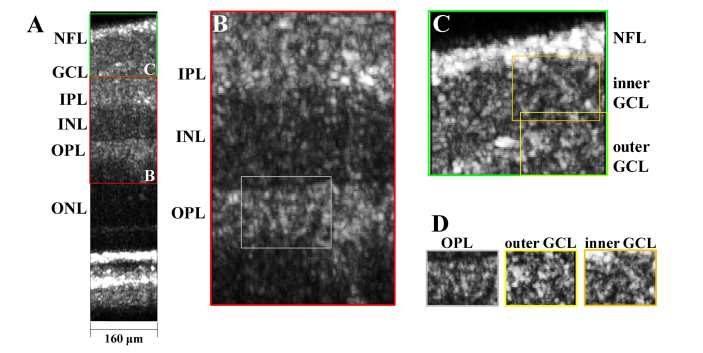
Imaging of the inner retina was investigated by performing motion correction of 9 consecutive frames in the raster scan protocol, convolving each frame with a rectangular kernel of 3 μm in the z direction by 3 μm in the x direction to reduce speckle, performing a maximum intensity projection along the slow (y) axis, and displaying the result on a linear scale (Fig. 6(A)). Distinct speckle patterns were noted in different retinal layers (Fig. 6(B)-6(D)).

Fig. 6.

(A) Inner retinal imaging with visible light OCT at ~2° nasal to the fovea over a small field-of-view (NFL: nerve fiber layer, GCL: ganglion cell layer, IPL: inner plexiform layer, INL: inner nuclear layer, OPL: outer plexiform layer, and ONL: outer nuclear layer). (B-C) Zooms of inner retinal layers. (D) Contrasting speckle patterns are observed in a synaptic layer (OPL), a cell soma layer (outer GCL), and an axonal layer (inner GCL).

4. Discussion

This study introduced an ultrahigh axial resolution achromatized visible light OCT system. Somewhat counter-intuitively, the transverse speckle size was not improved by achromatization. Rather, the axial speckle size was improved due to more uniform coupling of wavelengths across the spectrum (Fig. 2). Based on speckle autocorrelation measurements (Fig. 2), we conclude that a transverse resolution of 5.2 μm can be achieved with achromatization in young eyes with minimal monochromatic aberration [34]. The volume resolution of our system greatly exceeds that of commercial OCT systems, but not that of adaptive optics OCT [35]. Obviously, transverse resolution can be improved in the future with a larger beam diameter at the cornea and monochromatic aberration correction [6]. Below, we discuss several advances and limitations of this technology.

4.1 Outer retinal morphometry

The ophthalmic imaging community has continued to debate the interpretation of the outer retinal reflective bands seen in OCT (Fig. 4), ranging from the external limiting membrane (ELM) to the choriocapillaris (CC) [32, 36–40]. Corresponding in vivo imaging and histology are challenging to obtain in the human eye. However, a comparison of in vivo imaging and morphometry with known retinal morphology can help evaluate different OCT image interpretations.

Here, the ultrahigh axial resolution provided by visible light OCT improved delineation of the outer bands across a clinically relevant field-of-view (Fig. 4). In particular, a thickening and apparent splitting of the photoreceptor inner segment / outer segment (IS / OS) junction band was observed towards the peripheral macula, coinciding with the transition from a cone-dominated to a more rod-dominated retina (Fig. 5(C)). Around 10° eccentricity, the axial distance between the two IS / OS peaks was measured to be ~6 μm (Fig. 5(D)). At the same time, a thickening of the RPE band was observed in the fovea (Fig. 5(C)). Our study measured an in vivo RPE thickness of 14.0 µm in the fovea and 11.2 µm at an eccentricity of 7.5°, corresponding to ½ the eccentricity of the optic disk. A prior histological study [41] measured RPE cell height in 19 white subjects to be 10.3 ± 2.8 µm in the fovea and 8.8 ± 2.1 µm (mean ± std. dev.) in the parafovea at ½ the eccentricity of the optic disk. Our in vivo values are within the ranges of this prior ex vivo study. A recent in vivo adaptive optics OCT study reported an axial displacement of 8.9 ± 1.0 µm between the ROST and RPE bands in six subjects [42]. This previous measurement is smaller than our exact measurement of RPE thickness, based on the BM inner boundary and the RPE inner boundary. Segmentation of the RPE in polarization sensitive OCT, based on its polarization scrambling property, has also been reported [43]; however, thickness measurements were not reported because of the large analysis window.

Our measurements of RPE thickness (Fig. 5(C)) are estimated from the optical path length between the BM inner boundary and the RPE inner boundary, and are subject to several confounds. First, a constant refractive index of 1.4 was assumed, but the average refractive index of the melanin- and lipofuscin-rich RPE may be significantly higher. If so, our estimate of RPE thickness would be too large. Second, a thickness measurement based on optical path length cannot distinguish between an increase in physical size and an increase in refractive index caused by changes in cellular composition. The prominent increase in the RPE ODD near the fovea suggests an increase in RPE melanin concentration in the fovea (Fig. 5(G)), which has also been confirmed by histological measurements [41]. Last, BM inner boundary substituted for the RPE outer boundary in our RPE thickness measurements, potentially contributing further to overestimation of the RPE thickness. Clearly, more measurements are needed in a greater number of subjects for more detailed comparisons with literature.

Finally, an isolated backscattering band was observed posterior to the RPE but anterior to the choriocapillaris (CC). In accordance with prior studies [32, 42], we attribute this band to Bruch’s membrane (BM), whose thickness mostly comprises elastic and collagenous layers, which are expected to be highly scattering. The measured BM thickness (intensity FWHM) across the entire 6.5 mm FOV is 3.1 µm. Assuming that during the measurement, a Gaussian layer axial intensity profile is convolved with a Gaussian intensity PSF (FWHM = 1.7/√2 µm), a corrected BM thickness of 2.9 µm is derived. This is consistent with its accepted anatomical thickness of 2-4 µm [44]. This preliminary outer retinal morphometry lends support to our labelling of the outer retinal scattering bands (Fig. 4(B)). Our results suggest that ultrahigh resolution visible light OCT will enable more detailed layer measurements for correlation with textbook anatomy, providing a stronger foundation for interpreting images from commercial OCT instruments.

4.2 Inner retinal imaging

Typically, in adaptive optics OCT, cellular structures are visualized as en face images [42]. Here, due to the relatively slow imaging speed, we opted to demonstrate imaging of inner retinal layers in cross-section (Fig. 6). Cross-sectional views correspond with the standard histological slice preparation, and for our visible light OCT system, cross-sectional views enable better in-plane resolution than en face views due to the ultrahigh axial resolution. The maximum intensity projection of several consecutive frames reduced speckle and highlighted distinct speckle patterns in inner retinal layers (Fig. 6(B)-6(D)). Further work is required to assess the capability to visualize cellular structures [45, 46] with visible light OCT.

4.3 Transverse chromatic aberration (TCA)

Transverse chromatic aberration (TCA) leads to a lateral displacement of different wavelengths in the spectrum that varies across the field-of-view. For the human eye, TCA strongly depends the position of the beam relative to the pupil center. Assuming ~2 arcminutes of TCA (estimated for a 150 nm spectral span across a 20° visual field with perfect centration on the pupil [47]), we obtain a retinal displacement of ~10 μm between the longest and shortest wavelengths in our spectrum (~5 μm across the FWHM of the spectrum), which appears to be significant. However, it should be noted that this estimate does not account for either system TCA or the possibility of reducing TCA by moving the beam pivot out of the pupil center, closer to the nodal point. Though our results illustrate the benefits of correcting LCA, the effects of TCA are likely still present. Strategies to better characterize and manage TCA in visible light OCT are the subject of ongoing studies.

5. Conclusion

We addressed longitudinal chromatic aberrations (LCA) in our fiber-based spectral / Fourier domain visible light OCT system by replacing refractive with reflective optics where possible, and compensating the remaining LCA via achromatization. We estimated a volume resolution of 5.2 µm (transverse) × 5.2 µm (transverse) × 1.7 µm (axial), and visualized the outer retinal layers of the normal human retina across a 6.5 mm field-of-view, with sufficient clarity for segmentation and morphometry of the retinal pigment epithelium and Bruch’s membrane in a normal subject. Imaging over a smaller field-of-view revealed distinct inner retinal layer speckle patterns. In summary, chromatic aberrations are an important consideration in visible light OCT, and addressing them will further enable improvements in ultrahigh resolution imaging and broad bandwidth spectroscopy.

Funding

Glaucoma Research Foundation Catalyst for a Cure; National Institutes of Health (R01NS094681, R03EB023591, R21NS105043, R01EY028287, R01EY025231, and U01EY025477).

Disclosures

VJS: Optovue Inc. (P).