Abstract
Single molecule localisation (SML) microscopy is a fundamental tool for biological discoveries; it provides sub-diffraction spatial resolution images by detecting and localizing “all” the fluorescent molecules labeling the structure of interest. For this reason, the effective resolution of SML microscopy strictly depends on the algorithm used to detect and localize the single molecules from the series of microscopy frames. To adapt to the different imaging conditions that can occur in a SML experiment, all current localisation algorithms request, from the microscopy users, the choice of different parameters. This choice is not always easy and their wrong selection can lead to poor performance. Here we overcome this weakness with the use of machine learning. We propose a parameter-free pipeline for SML learning based on support vector machine (SVM). This strategy requires a short supervised training that consists in selecting by the user few fluorescent molecules (∼ 10–20) from the frames under analysis. The algorithm has been extensively tested on both synthetic and real acquisitions. Results are qualitatively and quantitatively consistent with the state of the art in SML microscopy and demonstrate that the introduction of machine learning can lead to a new class of algorithms competitive and conceived from the user point of view.
OCIS codes: (180.2520) Fluorescence microscopy, (100.0100) Image processing, (100.5010) Pattern recognition
1. Introduction
Single molecule localisation (SML) microscopy is an invaluable tool for biological discoveries [1,2], however its success in obtaining a super-resolved (or nanoscopy) image depends on the optimization of several parameters, both from the experimental and image processing sides [3,4]. With SML microscopy (e.g. PALM [5] and STORM [6]) fluorescent molecules are not active all together, they are activated at random space and time, with the aim to gather a stack of low resolution images made of few separated molecules each. A processing pipeline is then fundamental in order to obtain a super-resolved final image, circumventing the Abbe diffraction limit [7]. Generally, a SML algorithm achieved super-resolution in two main steps: a first phase of detection, or segmentation, where fluorescent molecules are localised at a pixel level, and a subsequent position refinement through fitting algorithms or faster and less accurate techniques, like centroids. These two phases are typically preceded by low-pass or band-pass filters in order to lower spurious signals contribution.
Despite such consolidated pipeline, the detection step is often made of heuristics e.g. the user is asked to select a threshold to discriminate active molecules based on image intensity, signal-to-noise ratio or the number of collected photons. The two extrema of a bad threshold selection are: an under-sampling of the biological structure, that cannot thus be recovered, or the presence of artefacts. The first effect has been experimentally demonstrated by [8] and it is in agreement with the Nyquist sampling theorem [9]; the second is due to background mistaken for active molecule, whenever the threshold is locally too low.
From a machine learning perspective, we can set the detection as a binary classification problem that can be addressed with a plethora of algorithms not yet exploited in SML microscopy. Among those we choose support vector machine (SVM) [10] because is able to obtain a spatial filter directly modelled on part of the acquired data, thus ideally being more robust to the acquisition variability that naturally characterize these images. Moreover, to finally localise the molecules with the required accuracy, we suggest the use of a linear and recursive formulation of non-linear Least Squares fitting, similarly to what originally proposed in [11].
This work is based on the learning framework investigated in [12]. Here, the proof of concept is extended and the pipeline of [12] is embedded within a GUI in order to be usable for the community. The efficacy of the approach is proved on real datasets and performance are compared with ThunderSTORM [13], the best proposal on SML low density images according to [14]. Though ThunderSTORM requires the user to select some parameters, it has also a default setting for non-experts.
There are other works aiming at the automation of the parameters selection, they rely mainly on Bayesian framework (like [15], [16], [17]), or statistical significance, as in SimpleSTORM, [18]. The proposed approach is more intuitive and it is not based on any assumption on noise statistics: our hypothesis is that each frame can be divided in smaller pieces, each one having or not an active molecule inside. We claim, and experimentally verify, that these two groups, or classes, are linearly separable and the separation line can be computed directly on the first frames of each acquisition.
The paper is organized as follows: Section 2 presents the methodological tools we used and their implementation details, Section 3 shows results on synthetic and real datasets comparing them with ThunderSTORM, conclusions are drawn in Section 4.
2. Methods
2.1. Support vector machines for detection of candidate regions
Support vector machine (SVM) [10] belongs to the max-margin supervised machine learning family and has demonstrated good performance in several applications. The idea behind our SVM-based algorithm is that activations and background are linearly separable and the separation among them is the hyerplane below:
| (1) |
where x is each vectorized image patch lying on the hyperplane represented by the parameters w and b. The way to find w and b values is to formulate an optimization problem like in:
| (2) |
where the first part of the objective function is a margin defined as the minimum distance among the closest examples of the two classes, the support vectors, and the hyperplane that separate them, while the second part is a regularization term, here ψ is the hinge loss function. The optimization is performed over a training dataset made of representatives of both classes. Each data object xi has an associated label yi ∈ {−1, +1} that is used to minimize the miss-classification error.
From Eq. (2) we can see how the optimization problem is convex thus algorithms to solve it are particularly efficient [19]. In any case, the learning is performed off-line at the beginning of the acquisition session, with a very limited computational burden. For the SVM implementation, we used liblinear [20], which implements the SVM with linear kernel and the value of the constant C (see Eq. (2)) is chosen with a k-fold cross-validation step, k = 5, before the training. As detailed in [12], the best patches dimension is 7 × 7 and its representation in Eq. (2), xi, is obtained with a simple vectorisation, which means that patch intensities are used as features.
By producing a spatial filter, the SVM algorithm both encloses pre-processing and detection. At inference, when a new image is given, a linear transformation is applied on each frame. Such transformation, formalised by a convolution of the image with a filter (the so-called SVM model), has the peculiarity of being learned from the dataset that has to be analysed. Thus, the framework provides a custom filter with the property of being discriminative given the possible sensor noise and aberrations of the instrument. Specifically, the filter is a patch of 7 × 7 made of the hyperplane coefficients of Eq. (1), normalised to have ‖w‖ = 1.
The normalisation is fundamental because the obtained model is not affected by the absolute intensity of the frames used for training and this is crucial in order to be consistent with a dropping in background intensity over time which affects real experiments.
The SVM model computed over a given dataset is thus an ad hoc spatial filter that is used in the pipeline to detect the activated molecules. Its output is a binary value for the assigned class, 1 if a patch has a molecule and −1 otherwise. We consider as candidates for a subsequent localisation refinement only patches labelled with 1.
2.2. Localisation at subpixel scale
Each emitting molecule is typically represented as a bivariate Gaussian function. This function is considered to be a good approximation of the point spread function of a microscope, thus localising an emitting molecule has the meaning of estimating the Gaussian peak. Two are the approaches generally proposed: Maximum Likelihood Estimation or Least Square fitting. We suggest [3] for an extensive comparison of the two methods. Based on [3], [14] and [4], we opted for a Least Squares fitting that does not need any camera noise model. However, the SVD-based detection approach proposed above is valid with any fitting methods. We do not detach from the literature for the subpixel estimation but, rather than applying a non-linear Least Squares fitting of a Gaussian, a parametrized Gaussian is linearised as proposed by [11].
In particular, each molecule is represented by:
| (3) |
where σx, σy, µx, and µy are the x, y variances and mean values of the Gaussian, respectively, while k is proportional to the number of photons.
Taking the logarithm of Eq. (3) is a convenient step because the solution of the Least Squares can be obtained from the inversion of a linear system in {A, B, C, D, E}, defined as in Eq. (4) and (5):
| (4) |
| (5) |
The quadratic function under consideration represents a bi-dimensional Gaussian if and only if the following constraints are met:
| (6) |
The implemented algorithm verifies that these conditions hold, if not the patches are discarded. Each single patch is composed by the tuples (xi, yi, Ii) with xi, yi representing the position and Ii the grey scale intensity of the i pixel. All the elements in the tuple are positive integers, Ii because a negative value has no physical meaning, xi and yi because they are indexes. For a patch with N pixels, our goal is to minimize:
| (7) |
where is the logarithm of Ii, so that the sum of squared differences between the model and the data is minimum.
Computing the derivative of the residual sum of squares with respect to each parameter and setting it to zero, we obtain the linear system:
| (8) |
where
| (9) |
A good strategy is to weigh the data, since in logarithmic scale a larger error is associated with small values of Ii. Our goal (at each iteration) is now to minimize the following expression:
| (10) |
where the weight wi is the squared predicted value of the model obtained in the previous iteration. This leads to the following linear system:
| (11) |
where:
| (12) |
and
| (13) |
with k being the current iteration number; G0(xi, yi) is an initial guess, a Gaussian centered in the origin of the detected patch under analysis. The outcome of this step is a list of points for which the iterative procedure has converged. The number of iterations that states the convergence is N = 20, regardless the dataset. A check on the convergence allows the algorithm to discard points for which this condition is not reached.
2.3. 2D localisation pipeline and GUI
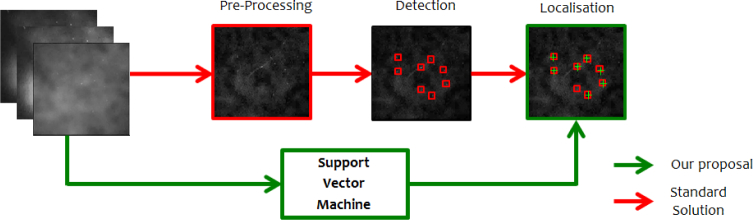
Our proposal is sketched in Fig. 1 where it is compared with the schematic of the most common pipelines in the literature. The first green block, called Support Vector Machine aims at substituting the red blocks of Pre-Processing and Detection. Localisation, instead, is a common operation even if the suggested approach has some novelties with respect to what is proposed in the literature of SML microscopy [4] and [21].
Fig. 1.
Pipeline for SML. The standard solution is presented on top (red arrows) while our proposal is at the bottom, underlined with green arrows. The Support Vector Machine block aims at substituting the red blocks of Pre-Processing and Detection, localisation is a common step instead.
The pipeline is embedded within a GUI that, together with the main functions like loading datasets or exporting results, guides the user in the training of the algorithm. The user is asked to select some active molecules while examples from the background are selected automatically. Few selections are enough to have good performance, as detailed in Section 3.
2.4. Datasets
In order to evaluate the performance of our proposal, both synthetic and real datasets are used. While synthetic datasets ease a quantitative evaluation of the algorithm, real datasets are fundamental to check the behaviour in case of real acquisition scenario.
Synthetic datasets are taken from the 2013 SML microscopy challenge described in [22]. They have various levels of difficulty, depending on the amount and kind of simulated noise while the biological structure to be imaged is mainly a bundle of Tubulin protein. Each dataset provides a collection of frames in uncompressed 16-bits TIFF format; Table 1 shows more details about them with Tubulin II being the dataset with the highest auto-fluorescent noise.
Table 1.
Properties of the synthetic datasets in use, for detailed informations on the acquisition settings refer to [22].
| DATASET | # of molecules | # of frames | Resolution (nm/pixel) | Dimension |
|---|---|---|---|---|
| Bundled | 81049 | 12000 | 100 | 64 × 64 |
| TubulinI | 100000 | 2401 | 150 | 256 × 256 |
| TubulinII | 100000 | 2401 | 150 | 256 × 256 |
The proposed pipeline is then tested also on real datasets, not just to be sure that the algorithm is able to face real acquisitions, but also to test if the SVM, though a supervised algorithm, is applicable to real conditions in which the training dataset has to be created without ground truth.
The 2013 Challenge website provides access also to four experimental datasets, courtesy of the Laboratory of Experimental Biophysics in EPFL, Switzerland. We have used the acquisitions named TubulinsLS and TubulinAF647. The first one is taken imaging Tubulin filaments, the other one is a fixed cell, stained with mouse anti-alpha-tubulin primary antibody and Alexa647 secondary antibody, Tab. 2 summarizes the images acquisition conditions.
Table 2.
Properties of the real datasets in use, for other information (frame rate, laser wavelength, etc.) refer to [22].
| DATASET | NA | # of frames | Resolution (nm/pixel) | Dimension |
|---|---|---|---|---|
| TubulinsLS | 1.3 | 15000 | 100 | 64 × 64 |
| TubulinAF647 | 1.46 | 9990 | 100 | 128 × 128 |
2.5. Evaluation metrics
In the SML evaluation protocol, having a true positive (TP) means that a localisation is matched with a point of the Ground Truth (GT) and this implies that it must be spatially close enough to it. Following [14], we select a radius equal to the full-width half-maximum (FWHM) of the PSF, in our case around 250 nm. The remaining localised molecules farthest from the radius, unpaired, are categorized as false positives (FP). Finally, GT molecules that are not associated are called false negatives (FN).
Detection rate and localisation accuracy are the performance indexes commonly used in SML community, together with Fourier Ring Correlation [23,24] which is useful in the case of real datasets when ground truth is not available. The Jaccard index (JAC) is used for monitoring the detection, while the root mean square error (RMSE) is used for the accuracy. Only the detections matched with the GT contribute to the equation 14 as:
| (14) |
where N = TP and a =accuracy.
For the sake of completeness we present the results also in terms of Precision and Recall indexes, with formulas as follow: Jaccard J = TP/(FN + FP + TP), Precision p = TP/(TP +FP) and Recall r = TP/(TP + FN).
3. Results
3.1. Synthetic data analysis
Preliminary results of the proposed method was presented in [12]. The evaluation was purely quantitative and it was performed on the synthetic datasets of 2013 SML microscopy Challenge [22]. The obtained results were compared with the best performing software of the Challenge, namely ThunderSTORM [13], revealing a good detection ability of our pipeline. Results was close or at the level of ThunderSTORM and the proposal stands out with better performance in two of the three datasets.
However, in order to obtain the spatial filter (SVM model) for the detection task, the classifier needs to be trained. To this end, in [12] each dataset was divided exactly in two non-overlapping stacks of frames; from the first, samples of positive and negative classes are extracted based on GT information while the other frames were used as test set, to evaluate the performance of the pipeline and reconstruct the super-resolved image.
Such way of building the training set is typical in classification problems but it is not realistic for SML microscopy acquisition, questioning the usability of the approach. Here we demonstrate that there is no need for a big amount of data by explicitly characterize the behavior of the pipeline as the cardinality of the training set changes. We embed the algorithm proposed in [12] in a wider framework made of a GUI and a simpler yet effective way to create a training set. Besides being easier to use, this system allows a quick selection of few positive samples and the generation of the training dataset from them.
A drawback in not having the GT information is the need to assume the highest local maxima within a patch as the pixel location of an activation, which is not always the case due to the presence of shot noise. This workaround has an impact on the detection ability if we compare the results shown in [12] with the column named SVM-half of Table 3. In particular, such a training set composition lead to a more selective identification of activations, as the Jaccard index reflects.
Table 3.
Performance comparison among ThunderSTORM (TS), our SVM-based approach with half of the acquired stack used for the training (SVM-half) and the same SVM approach using for training only 20 activations (SVM-few).
| Dataset | Jacc (%) | Acc (nm) | Prec (%) | Rec (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||
| TS | SVM half | SVM few | TS | SVM half | SVM few | TS | SVM half | SVM few | TS | SVM half | SVM few | |
| Bundled | 93 | 81.7 | 87.2 | 14.5 | 14 | 14.3 | 99.8 | 100 | 99.9 | 93.2 | 81.7 | 87.2 |
| TubulinI | 74.4 | 47.3 | 64.5 | 22.2 | 17.2 | 18 | 96.2 | 100 | 99.9 | 76.7 | 47.3 | 64.5 |
| TubulinII | 67.3 | 42.3 | 48.8 | 27.7 | 22.2 | 23.8 | 98.4 | 100 | 79.9 | 68.1 | 42.3 | 55.6 |
Table 3 shows the performance of ThunderSTORM and the SVM-based approach with two different sizes of the training set. Namely, SVM-half means that half of the images are used to build the SVM while SVM-few referred to a manual selection, through the GUI, of 20 activations. Comparing the two kinds of training, we can say that all the performance that we can obtain with few activations are in line with what we have using half of the dataset, looking at indexes like Accuracy and Precision, and are much better in terms of Jaccard and Recall. A possible explanation is that with too much data the algorithm tends to be driven by the activation patches that are more common. Instead, the reason of the drop in Precision we have on TubulinII dataset is that the dataset has more variability, being the noisiest, and the use of only 20 points penalizes the performance.
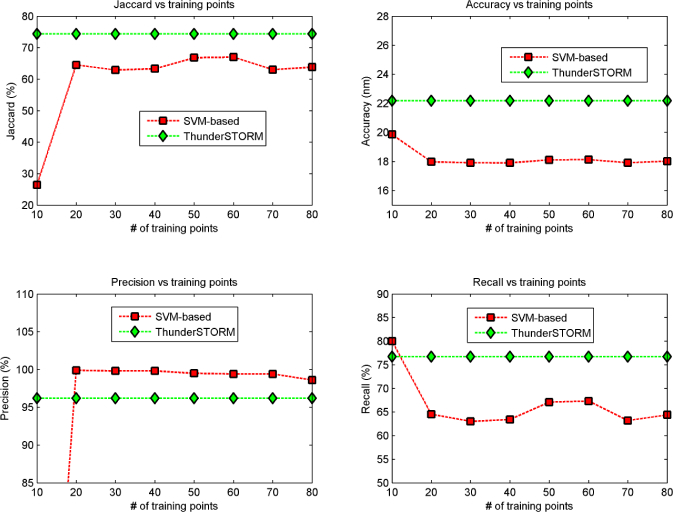
We remark that the manual selection does not need to be precise because the algorithm automatically shift the selection on the closest pixel with a local maxima intensity. Looking at this selection from a different perspective, the user is only asked to select few areas within one or more frames where to find positive activations, its selection will be refined by the algorithm prior to be used. For each new selected pixel, also the number of background samples increases, so that the training set is equally divided into activations and background (i.e. it is balanced). Whenever the manual selection is completed, the SVM is trained and the processing can start on the remaining frames. Regarding the number of activations needed, Fig. 2 represents the performance of the whole pipeline when the SVM of the detection step is trained increasing the number of positive samples from 10 to 80, with a step of 10. We can see how on TubulinI with the selection of few points, the Jaccard measurement is not as favourable as in ThunderSTORM and the reason is a poor recall, while there is an improvement of Precision and Accuracy with respect to the competitor; these results are in agreement with what we observe in all the analysed datasets.
Fig. 2.
Quantitative results over the synthetic dataset Tubulin I. The measurements taken into account are, clock wise starting from top-left: Jaccard, Accuracy, Precision and Recall.
We can conclude that there is no need for the user to select a large amount of activations: decreasing their number, the performance remains stable until a value between 10–20 selections, for which there is a drop. The user can select a reasonable yet arbitrary amount of activations without impairing the processing outcome. In this context, it is important to highlight that for a not-expert user the selection of few activations is more intuitive than to chose arbitrary thresholds.
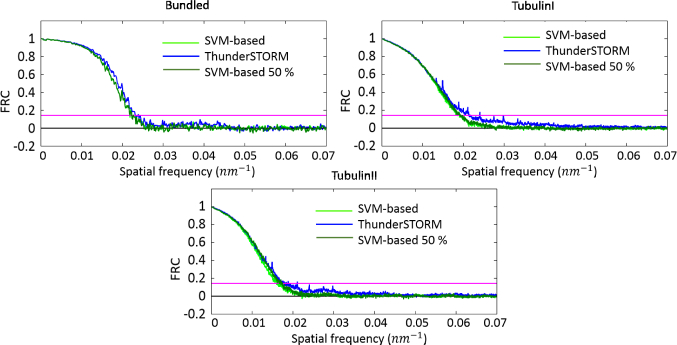
Fig. 3 shows the super-resolved images obtained by our algorithm, second and third column, and the ones reconstructed by ThunderSTORM. Images underline the strength and limit of our pipeline: the reconstruction is less noisy with respect to ThunderSTORM outputs, however not all the TPs are detected, resulting in a structure made of fewer molecules in some regions. This prudential approach is quantitative measurable and it clearly emerges observing the behaviour of Precision and Recall measurements, see Fig. 2 as example on Tubulin I dataset. However, comparison of the proposed method and ThunderSTORM via the FRC analysis does not show significant differences, as it is possible to see from Fig. 4.
Fig. 3.
Results over the synthetic datasets Bundled Of Tubulin (top), Tubulin I (centre) and Tubulin II (bottom). Our software is run neglecting the ground truth. Column wise, detail of super-resolved images obtained by ThunderSTORM, by the SVM with half of the available images for the training and by the SVM with 20 selections. The scale bar values are 0.3 µm for Bundled Of Tubulin (top), and 1.2 µm for Tubulin I and Tubulin II.
Fig. 4.
Quantitative comparison of our algorithm with ThunderSTORM. The FRC is computed for the synthetic datasets, clock-wise starting from top-left: Bundled Of Tubulin, Tubulin I and Tubulin II.
3.2. Real data analysis
In the previous Section we have seen how it is possible to achieve performance in line with a state of the art algorithm, such as ThunderSTORM, without the need of a time-consuming training and without the definition of arbitrary thresholds – now replaced by an intuitive labelling procedure for the user.
We are proposing a pipeline without mentioning any hypothesis on noise or background statistical behaviour. In fact, the detection task is based on the only assumption that the two classes, activation and background, are linearly separable. In order to verify the benefits of the approach with real acquisitions, thus real background, we run the algorithm on several Tubulin datasets.
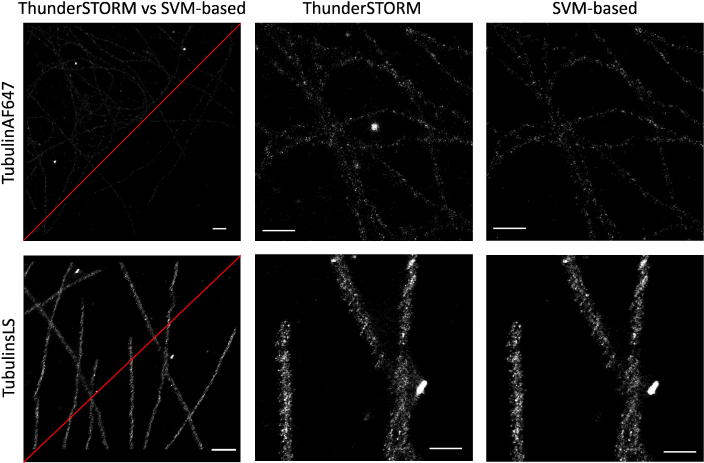
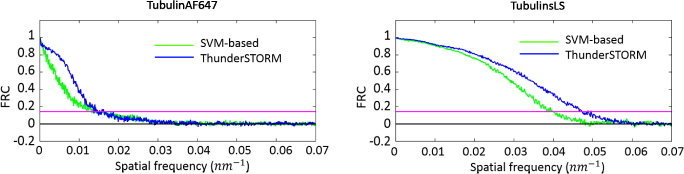
Figure 5 presents the qualitative evaluation of our approach on TubulinAF647 and TubulinsLS datasets [22], comparing it with ThunderSTORM. While on ThunderSTORM we use the default set-up, on our pipeline we manually select 20 activations within the first frames. As it is evident from the FRC, Fig. 6, the performance are exactly the same on TubulinAF647 while there is a loss of few nm on TubulinLS. However, the final super-resolved images present sensibly less artefacts with respect to ThunderSTORM reconstructions. This observation is valid on both datasets as shown in Fig. 5, where a magnification underlines how ThunderSTORM detected spurious activations and some big spots that our algorithm is more robust to discard. This later difference, explain also the drop in correlation at low spatial frequencies in TubulinAF647 in the FRC curve for our method with respect to ThunderSTORM.
Fig. 5.
Results over the real datasets TubulinAF647 (top) and TubulinsLS (bottom). Column wise, from left to righ: super-resolved images obtained by ThunderSTORM, upper left corner, and our SVM-based algorithm, scale bar 1 µm (top) and 0.7 µm (bottom); a detail of ThunderSTORM reconstruction and a detail of our SVM-based algorithm, scale bar 0.6 µm (top) and 0.3 µm (bottom).
Fig. 6.
Quantitative results (FRC) over the real datasets TubulinAF647 and TubulinsLS.
4. Conclusions
Within SML microscopy, processing after image acquisition is fundamental to obtain a super-resolved image. Unfortunately, state of the art algorithms rely on thresholds heuristically chosen by the user to accomplish molecules detection.
We experimentally demonstrate that it is possible to formulate the detection step as a classification problem, resulting in the building of a custom filter for each dataset to analyse. Such training step is not always necessary, filters are saved and can be reused but we advice the retraining in case the acquisition conditions differs too much. In particular, the same filters can be used to analyses a long series of experiments where microscope and sample conditions does not change, which is a typical scenario in SML microscopy.
The SVM filter has performances in line with the state of the art but it is conceived to be threshold free, learning directly from the dataset the division between molecules and background. The supply of few molecules to the algorithm prevents also the use of a pre-processing step, reducing the introduction of artefacts and the computational load of the algorithm; this is further reduced adopting the linearisation of a LS fitting, which eventually is a very accurate tool.
As future work, we plan to test our algorithm on a broader range of samples (with different signal-to-noise/background ratios) and to extend our method to 3D by accounting for PSF with distortions related to their position in depth. The detector has to be extended to encode such distortions, for instance by designing appropriate kernels. Moreover, our fitting algorithm can be possibly extended without strong modifications the algorithmic structure, especially if the PSF model is still an exponential function. Another significant challenge in the context of SML microscopy, which is not currently addressed by our SVM approach, is the ability to work under high-density molecular conditions, i.e., low sparsity. Solution to this problem can still be searched in the field of machine learning, but within other approaches, such as neural networks. The complete MATLAB source code for our SVM-based localisation approach is available from Code 1 [25]
Acknowledgments
The authors are grateful to Dr. Francesca Cella Zanacchi and Dr. Francesca Pennacchietti (Istituto Italiano di Tecnologia) for fruitful discussions.
A typographical correction was made to the body text.
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References and links
- 1.Hell S. W., Sahl S. J., Bates M., Zhuang X., Heintzmann R., Booth M. J., Bewersdorf J., Shtengel G., Hess H., Tinnefeld P., Honigmann A., Jakobs S., Testa I., Cognet L., Lounis B., Ewers H., Davis S. J., Eggeling C., Klenerman D., Willig K. I., Vicidomini G., Castello M., Diaspro A., Cordes T., “The 2015 super-resolution microscopy roadmap,” J. Phys. D: Appl. Phys 48, 443001 (2015). 10.1088/0022-3727/48/44/443001 [DOI] [Google Scholar]
- 2.Sahl S. J., Hell S. W., Jakobs S., “Fluorescence nanoscopy in cell biology,” Nat. Rev. Mol. Cell Biol. 18, 685–701 (2017). 10.1038/nrm.2017.71 [DOI] [PubMed] [Google Scholar]
- 3.Small A., Stahlheber S., “Fluorophore localization algorithms for super-resolution microscopy,” Nat. Methods 11, 267–279 (2014). 10.1038/nmeth.2844 [DOI] [PubMed] [Google Scholar]
- 4.Deschout H., Zanacchi F. C., Mlodzianoski M., Diaspro A., Bewersdorf J., Hess S. T., Braeckmans K., “Precisely and accurately localizing single emitters in fluorescence microscopy,” Nat. Methods 11, 253–266 (2014). 10.1038/nmeth.2843 [DOI] [PubMed] [Google Scholar]
- 5.Betzig E., Patterson G. H., Sougrat R., Lindwasser O. W., Olenych S., Bonifacino J. S., Davidson M. W., Lippincott-Schwartz J., Hess H. F., “Imaging intracellular fluorescent proteins at nanometer resolution,” Science 313, 1642–1645 (2006). 10.1126/science.1127344 [DOI] [PubMed] [Google Scholar]
- 6.Rust M. J., Bates M., Zhuang X., “Stochastic optical reconstruction microscopy (storm) provides sub-diffraction-limit image resolution,” Nat. Methods 3, 793 (2006). 10.1038/nmeth929 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Abbe E., “Beiträge zur theorie des mikroskops und der mikroskopischen wahrnehmung,” Archiv für mikroskopische Anatomie 9, 413–418 (1873). 10.1007/BF02956173 [DOI] [Google Scholar]
- 8.Shroff H., Galbraith C. G., Galbraith J. A., Betzig E., “Live-cell photoactivated localization microscopy of nanoscale adhesion dynamics,” Nat. Methods 5, 417–423 (2008). 10.1038/nmeth.1202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nyquist H., “Certain topics in telegraph transmission theory,” Transactions of the American Institute of Electrical Engineers 47, 617–644 (1928). 10.1109/T-AIEE.1928.5055024 [DOI] [Google Scholar]
- 10.Cortes C., Vapnik V., “Support-vector networks,” Machine learning 20, 273–297 (1995). 10.1007/BF00994018 [DOI] [Google Scholar]
- 11.Guo H., “A simple algorithm for fitting a gaussian function,” IEEE Signal Process. Mag. 28, 134–137 (2011). 10.1109/MSP.2011.941846 [DOI] [Google Scholar]
- 12.Colabrese S., Castello M., Vicidomini G., Del Bue A., “Learning-based approach to boost detection rate and localisation accuracy in single molecule localisation microscopy,” in “Image Processing (ICIP), 2016 IEEE International Conference on,” (IEEE, 2016), pp. 3184–3188. [Google Scholar]
- 13.Ovesnỳ M., Křížek P., Borkovec J., Švindrych Z., Hagen G. M., “Thunderstorm: a comprehensive imagej plug-in for palm and storm data analysis and super-resolution imaging,” Bioinformatics 30, 2389–2390 (2014). 10.1093/bioinformatics/btu202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sage D., Kirshner H., Pengo T., Stuurman N., Min J., Manley S., Unser M., “Quantitative evaluation of software packages for single-molecule localization microscopy,” Nat. Methods 12, 717–724 (2015). 10.1038/nmeth.3442 [DOI] [PubMed] [Google Scholar]
- 15.Cox S., Rosten E., Monypenny J., Jovanovic-Talisman T., Burnette D. T., Lippincott-Schwartz J., Jones G. E., Heintzmann R., “Bayesian localization microscopy reveals nanoscale podosome dynamics,” Nat. Methods 9, 195–200 (2012). 10.1038/nmeth.1812 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hu Y. S., Nan X., Sengupta P., Lippincott-Schwartz J., Cang H., “Accelerating 3b single-molecule super-resolution microscopy with cloud computing,” Nat. Methods 10, 96–97 (2013). 10.1038/nmeth.2335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tang Y., Hendriks J., Gensch T., Dai L., Li J., “Automatic bayesian single molecule identification for localization microscopy,” Scientific Reports 6, 33521 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Köthe U., Herrmannsdörfer F., Kats I., Hamprecht F. A., “SimpleSTORM: A fast, self-calibrating reconstruction algorithm for localization microscopy,” Histochem. Cell Biol. 141, 613–627 (2014). 10.1007/s00418-014-1211-4 [DOI] [PubMed] [Google Scholar]
- 19.Boyd S., Vandenberghe L., Convex optimization (Cambridge university press, 2004). 10.1017/CBO9780511804441 [DOI] [Google Scholar]
- 20.Fan R.-E., Chang K.-W., Hsieh C.-J., Wang X.-R., Lin C.-J., “Liblinear: A library for large linear classification,” J. Mach. Learn. Res. 9, 1871–1874 (2008). [Google Scholar]
- 21.Smith C. S., Joseph N., Rieger B., Lidke K. A., “Fast, single-molecule localization that achieves theoretically minimum uncertainty,” Nat. Methods 7, 373–375 (2010). 10.1038/nmeth.1449 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.“2013 isbi grand challenge localization microscopy,” http://bigwww.epfl.ch/smlm/challenge2013/index.html. Accessed: 12-12-2016.
- 23.Banterle N., Bui K. H., Lemke E. A., Beck M., “Fourier ring correlation as a resolution criterion for super-resolution microscopy,” J. Struct. Biol. 183, 363–367 (2013). 10.1016/j.jsb.2013.05.004 [DOI] [PubMed] [Google Scholar]
- 24.Nieuwenhuizen R., Lidke K., Bates M., Puig D., Grünwald D., Stallinga S., Rieger B., “Measuring image resolution in optical nanoscopy,” Nat. Methods 10, 557–562 (2013). 10.1038/nmeth.2448 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Colabrese S., “SVM for Single Molecule Localisation Microscopy,” https://doi.org/10.6084/m9.figshare.5977453. Accessed: 14-3-2018. [DOI] [PMC free article] [PubMed]