First-principles calculations of Raman vibrational modes in the fingerprint region for connective tissue

Abstract

Vibrational spectroscopy has been widely employed to unravel the physical-chemical properties of biological systems. Due to its high sensitivity to monitoring real time "in situ" changes, Raman spectroscopy has been successfully employed, e.g., in biomedicine, metabolomics, and biomedical engineering. The interpretation of Raman spectra in these cases is based on the isolated macromolecules constituent vibrational assignment. Due to this, probing the anharmonic or the mutual interactions among specific moieties/side chains is a challenge. We present a complete vibrational modes calculation for connective tissue in the fingerprint region (800 – 1800 cm⁻¹) using first-principles density functional theory. Our calculations accounted for the inherent complexity of the spectral features of this region and useful spectral markers for biological processes were unambiguously identified. Our results indicated that important spectral features correlated to molecular characteristics have been ignored in the current tissue spectral bands assignments. In particular, we found that the presence of confined water is mainly responsible for the observed spectral complexity.

The rapid, noninvasive and high spatial resolution capabilities of Raman spectroscopy technique have been employed to obtain biochemical and structural pieces of information of biological samples. Biomedicine [1], metabolomics [2], biomedical engineering [3,4] are examples of fields where this tool have been successfully used to acquire high-quality data. In particular, several optical-biopsy studies have shown that molecular interaction features in cells and tissues which cannot be accessed by conventional histopathology can be probed by this technique [5]. Raman is of special interest due to their high capability to detect "in vivo" biochemical and molecular variations in tissues [5].

To a first approximation, spectrum of biological tissue is a convolution of isolated biological macromolecules (e.g., carbohydrates, proteins, lipids, deoxyribonucleic acid, ribonucleic acid) spectra. Hence, the tissue vibrational bands assignment is usually made based on isolated macromolecules assignment. There are several literature compilations (see, e.g., refs. [6–9]) listing the vibrational bands of biological tissues constituents. These compilations eventually are used to perform a qualitative interpretation of the spectra. However, a large amount of relevant pieces of information is absent from one using this qualitative vibrational assignment. Anharmonic interactions which couple harmonic vibrational modes are an example [10, 11]. Moreover, mutual interactions among specific moieties could be analyzed only in comparative basis. The usage of computational simulations of small specific parts and short time intervals of the macromolecule is another method to understand this interactions. These approaches usually obscure relevant physical-chemical data from the environment. At scale of real biology they are in fact only a small part of the overall picture [12].

Computer simulations are a suitable tool to interpret experimental data aiming to understand biochemical changes translating structural changes that lead to macroscopic biological processes. Vibrational spectroscopy of macromolecules and tissues is an important class of experimental data addressing this issue. The atomistic models based on quantum mechanical calculations have better prediction capabilities of the materials properties. However, due to its inherent complexity, atomistic modeling of biological systems are still in the early stages. In a previous work [13], we presented a computational model for skin (STmod). This model consisted of a collagen peptide cutout including confined water submitted to periodic boundary conditions. The model was able to successfully explain important experimental structural and general biochemical trends of normal and inflammatory tissues.

In the present work a detailed vibrational modes assignment of a connective tissue based on the STmod is presented. To the best of our knowledge this is the first report on literature concerning complete vibrational assignment for a tissue. The vibrational calculations were performed on C_n (n – 8), C_1s, D₀, and D₁ unit cells of STmod. The numeric subscript indicates the number of water molecules inside the unit cell. The "s" subscript related to the presence of external water solvating the C₁ model. Starting from a hydrated collagen peptide each unit cel was obtained and calculations performed on periodic boundary conditions. More details concerning the obtainment of these structures and previous characterizations as well could be found in ref. [13]. Figure 1 shows the unit cell for C₀, C_1s, C₂, and D₀ structures.

Fig. 1.

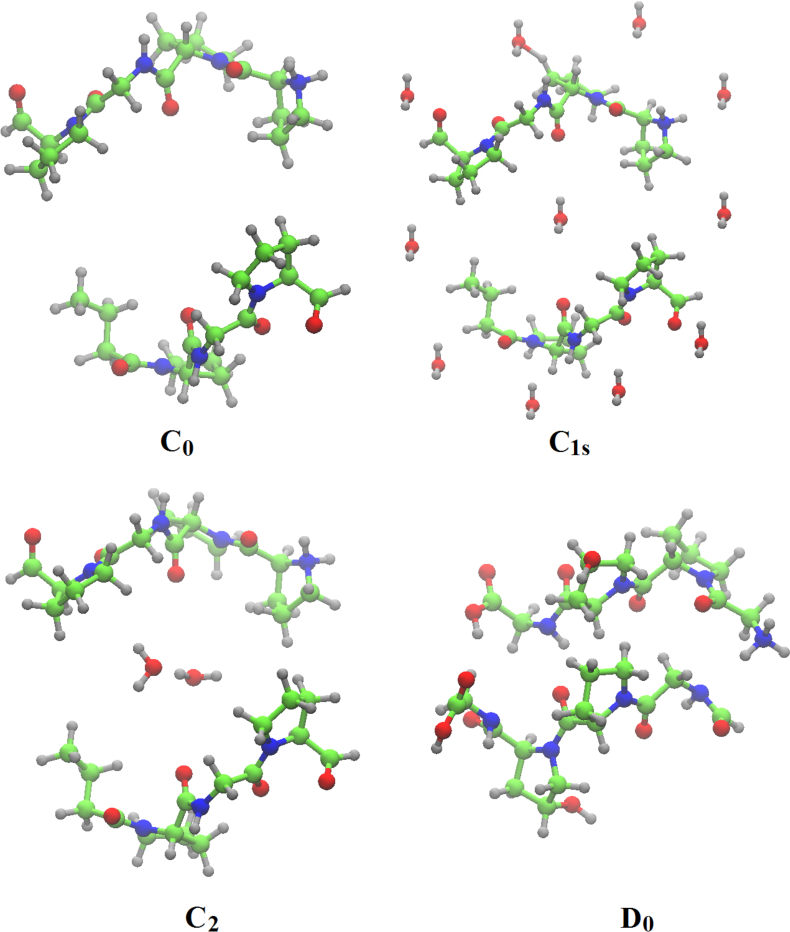
Unit cells for C₀, C_1s,C₂, and D₀ unit cells. Structural pieces of information are found on Table I of ref. [13].

Density Functional Theory (DFT) [14,15] was used in order to obtain the equilibrium geometries and harmonic frequencies. The simulations were implemented in the CPMD program [16] using the BLYP functional [17] augmented with dispersion corrections for the proper description of van der Waals interactions [18, 19]. The cutoff energy was considered up to 100 Ry. The wavefunctions were optimized and then the vibrational modes were obtained using the Hessian matrix. Finally the linear response from the values of polarization and polar tensors of each atom in the system was calculated to evaluate the eigenvectors of each vibrational mode. The Raman-active modes were obtained from the atomic polar tensors for each atom in the system and the corresponding eigenvectors of Hessian [20]. Harmonic frequencies were compared to experimental Raman data of normal (NM) oral mucosa tissue (see ref. [3] for experimental details). The spectra were simulated as a convolution of Gaussian lineshape peaks centered on the calculated frequencies using the Fityk [21] program. The linewidth was chosen to be 20 cm⁻¹. Figure 2(a) presents the results from the fingerprint region. The experimental Fourier-Transform (FT) Raman spectrum of NM is also shown.

Fig. 2.

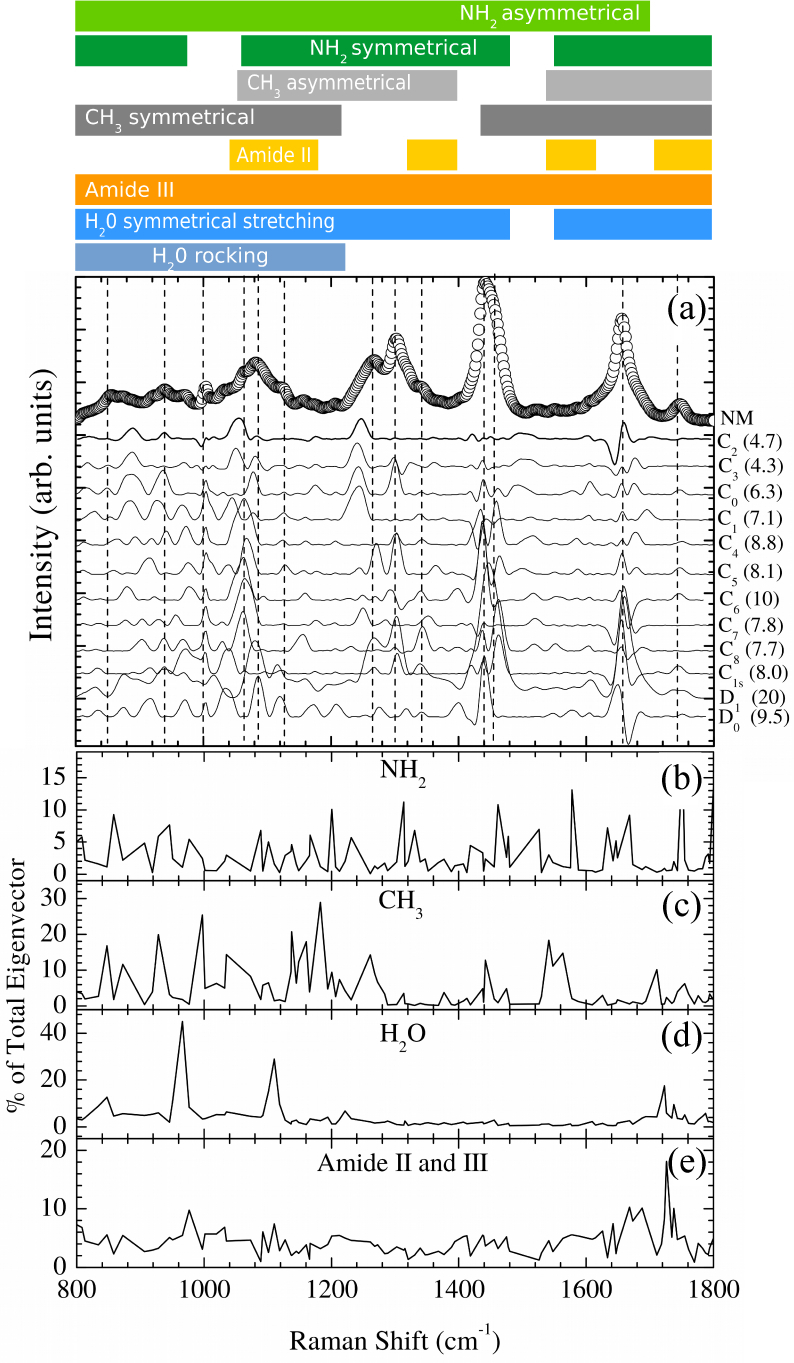
(a) Experimental FT-Raman spectra for normal oral mucosa tissue (circles, NM) compared to C_n(n = 0 – 8), C_1s, D₀, and D₁ STmod models in the fingerprint region. Solid lines are the residuals of the experimental data fitted to each model. The fitting standard deviation (in 10⁻⁴ arb. units) in each case is shown in the right of each model symbol. The vertical dashed lines indicate the position of the thirteen more intense bands (≳ 10% of band of maximum intensity at ∼ 1440 cm⁻¹). C₂ and C₃ lines represent those models with large set of experimentally represented bands. The wavenumber-axis projection of amine (b), methyl (c), water (d), and Amide II and III (e) partial eigenvectors contributions are also shown. The top scheme represents the qualitative additional bands assignment based on Table 1. Summary of experimental data acquisition details: Six pieces of biopsied NM tissues were investigated. The tissue samples were stored in liquid nitrogen (77K) in cryogenic vials prior to FT-Raman spectra recording. The Raman spectra were measured (300 scans) on 5 different points totalizing 30 spectra. A Bruker RFS 100/S FT-Raman spectrometer was used with a Nd:YAG laser operating at 1.064 nm as excitation light source. The laser power at the sample was kept at 230 mW and the spectrometer resolution was set to 4 cm⁻¹. The samples were brought to room temperature and kept moistened in 0.9% physiological solution to preserve their structural characteristics, and placed in a windowless aluminum holder for the Raman spectra collection.

From direct inspection, we found that C₂ and C₃ models presented the large set of experimentally represented bands (thirteen). The vertical dashed lines indicates the position of the thirteen more intense bands (≳ 10% of band of maximum intensity at ~ 1440 cm⁻¹). The residuals of the experimental data fitted to each model are also shown (solid lines in Fig. 2(a)). We notice that C₂ and C₃ presented the smallest residuals. The fitting standard deviation (σ) is shown in the right side of the Fig. 2(a) for each case. C₂ and C₃ models also presented smallest σ (4.7 × 10⁻⁴ and 4.3 × 10⁻⁴, respectively). Thus C₂ and C₃ represent the best models to NM data. It is important to notice that the C₃ model presented a set of negative high frequency (≳ 940 cm⁻¹) modes indicating some degree of mechanical instability. Thus, we concluded that C₂ is the suitable model to represent the connective tissue from the vibrational modes point of view.

The connective tissue vibrational modes assign based on C₂ model is shown in Table 1. The comparison between the present work and literature bands assignment are also shown. We notice that our results presented extra pieces of information. The most striking feature is the activation of methyl, methylene, and amine side chains vibrations along the fingerprint spectral window. Figure 2b)-2e) shows the percentage contribution to the total eigenvectors projected on the wavelength axis for some of these vibrations. Amine vibrations (Fig. 2(b)) are present in almost the entire region weighting around 10% of contribution. It is possible to observe that methyl groups contributions (Fig. 2(c)) are ≳ 10% below 1300 cm⁻¹ and around 1450, 1550, and 1700 cm⁻¹. The side chains are key factors determining the properties and reactivity of molecules. Thus, one expect that molecular transformations under, e.g., pathological processes, will display overall changes in the fingerprint vibrational region. Our calculations indicated that the side chains vibrational activation occurs only under the presence of confined water. The anhydrous C₀ model presented these bands only in the high wavenumber region (3000 – 4000 cm⁻¹). The water dimer itself presents spectral features around 900 and 1600 − 1750 cm⁻¹ (Fig. 2(d)) usually undescribed. Amide II and III vibrations are also present on the overall spectra weighting around 5% (Fig. 2(e)).

Table 1.

Connective tissue Raman bands assignment based on C₂ model. Additional vibrations compared to usual assignment (based on refs. [6–9]) in the fingerprint region are shown in $\text{blue}$. It is important to notice that torsion and stretching modes of at least one of the rings, C-C, CH, CN, NH, C=O, CH₃, OH stretching, CH₂ symmetrical and asymmetrical stretching, Amide III, and H₂O scissoring vibrations appeared in all bands in some degree.

Experimental (cm−1)	Assignment
800 – 880	${\text{CH}}_3\text{symmetrical}\text{stretching}$; C-C stretching; and C-C-H deformation usually of proline, hydroxyproline, and collagen backbone
880 – 980	${\text{CH}}_3{\text{ and confined H}}_2\text{O symmetrical stretching};\text{C}=\text{O wagging};{\text{CH}}_2\text{twisting};{\text{CH}}_2,{\text{CH}}_3{\text{ and confined H}}_2\text{O rocking}$; C-C stretching; and C-C wagging usually of proline, hydroxyproline, and collagen backbone
980 – 1, 050	${\text{CH}}_3{\text{ symmetrical and asymmetrical stretching; CH and CH}}_2{\text{twisting; CH}}_2{\text{and CH}}_3\text{ rocking};{\text{CH}}_3\text{ scissoring}$, C-C aromatic ring stretching usually of proline and collagen
1, 050 – 1, 150	${\text{CH}}_3{\text{NH}}_2{\text{ symmetrical and asymmetrical stretching; CH and CH}}_2{\text{ twisting; CH}}_2{\text{ and CH}}_3\text{ rocking}$, C-C stretching; C-O stretching; C-N stretching vibration; usually of collagen, several bands of moderate intensity, belonging to Amide III and other groups (proteins)
1, 150 – 1, 230	${\text{CH}}_3{\text{ and NH}}_2{\text{ symmetrical and asymmetrical stretching; CH wagging; CH}}_2{\text{ twisting; CH}}_2{\text{, CH}}_3\text{ rocking}$; C-C aromatic; CH2 wagging vibrations from proline side chains; C-C/C-N stretching (proteins); several bands of moderate intensity, belonging to Amide III and other groups (proteins), differences in collagen content, hydroxyproline, proteins, including collagen I
1, 230 – 1, 280	${\text{CH}}_3{\text{ asymmetrical stretching; CH wagging; CH}}_2\text{ twisting}$; CH2 wagging; C-N stretching; C-N in plane stretching; CHα′ rocking; second Amide; several bands of moderate intensity, belonging to Amide III and other groups (proteins), differences in collagen content, protein band
1, 280 – 1, 320	${\text{CH}}_3{\text{ asymmetrical stretching; CH wagging; CH}}_2{\text{ and CH}}_3\text{ rocking}$, CH2; CH3 twisting; CH2 bending; CH2 wagging; CH2 deformation; several bands of moderate intensity, belonging to Amide III and other groups (proteins); differences in collagen content, bending mode of collagen
1, 320 – 1, 400	${\text{NH}}_2{\text{ symmetrical and asymmetrical stretching; NH}}_2\text{ rocking}$, CH and CH2 deformation; CH2 bending; CH3; CH2 twisting; CH rocking; C=O symmetric stretch; CH2 wagging in collagen; CH3 and CH2 deforming modes of collagen, several bands of moderate intensity, belonging to Amide III and other groups (proteins)
1, 400 – 1, 480	${\text{CH}}_3{\text{ symmetrical stretching; NH}}_2{\text{ symmetrical and asymmetrical stretching; CH}}_2{\text{ twisting; CH}}_2{\text{, CH}}_3{\text{ and NH}}_2\text{ rocking}$; CH2 stretching/CH3 asymmetric deformation; CH2 wagging; CH, CH2, CH3 deformation; CH2 scissoring; C-H and CH2 bending mode of proteins, collagen
1, 480 – 1, 540	${\text{NH}}_2{\text{ asymmetrical stretching; NH}}_2\text{ rocking}$; C-N stretching vibration C=C stretching in benzenoid ring, Amide II, collagen
1, 540 – 1, 620	${\text{CH}}_3{\text{ and confined H}}_2{\text{O symmetrical stretching; CH}}_3{\text{ and NH}}_2{\text{ asymmetrical stretching; CH, CH}}_2{\text{ and OH wagging; CH}}_2{\text{ and NH}}_2{\text{ twisting; CH}}_2{\text{ and NH}}_2\text{ rocking}$; C-C stretching; Amide I; Amide II
1, 620 – 1, 700	${\text{CH}}_3{\text{, NH}}_2{\text{ and H}}_2{\text{O symmetrical stretching; CH}}_3{\text{ and NH}}_2{\text{ asymmetrical stretching; CH and CH}}_2{\text{ wagging; CH}}_2{\text{ and NH}}_2{\text{ twisting; CH}}_2{\text{ and CH}}_3{\text{ rocking; CH and CH}}_2\text{ scissoring}$; C=C stretching band; C=O stretching of collagen, Amide I, differences in collagen content, intermolecular bending mode of water, proteins, including collagen I
1, 700 – 1, 800	${\text{CH}}_3{\text{, NH}}_2{\text{ and H}}_2{\text{O symmetrical stretching; CH}}_3{\text{ asymmetrical stretching; Amide II; CH}}_2{\text{ and OH wagging; CH}}_2{\text{ and NH}}_2{\text{ twisting; CH}}_2{\text{, CH}}_3{\text{ and NH}}_2{\text{ rocking; CH}}_2\text{ scissoring}$; Amide I; C=O stretching vibrations

In fact, experimentally observed spectral changes in fingerprint region for tissues have been qualitatively reported to correlate to water content (see, e.g., refs. [22–25]). Elderly and diabetis [22, 23], oral cancer [24], cervical cancer [25] to name but a few, are examples of physiological situations where spectral complexity emerges beyond the isolated molecule vibrational bands assignment. Protein-water interactions are known to play a critical role in the function of several biological systems and macromolecules including collagen in tissues [26]. Small changes in structure and dynamical behavior of water molecules at the peptide-water interface can effectively change both the structure and dynamics of the protein function [27]. Our model indicates the complexity emerges due to the presence of confined water enabling distant and isolated side chains coupling. A large set of wagging, scissoring, twisting and rocking vibrations of side chains usually assigned to high-wavenumber region (≳ 2000 cm⁻¹) appeared in the fingerprint region damped to usually assigned vibrations (see Table 1). Coexistence of symmetrical and asymmetrical stretchings are also present in a more complicated fashion that go beyond the protein, collagen, proline and hydroxyproline usual bands assignment. Interestingly, the region 880 − 940 cm⁻¹ appeared to retain information about the confined water content (Fig. 2 (a) and (d)). vibrations. In fact, the main components of the eigenvectors in this region are confined water (30%) and CH₃,CH,C-C,C-C-H (70%) modes.

We notice that the qualitative and quantitative pieces of information generated by our analysis enable state useful spectral markers which could be correlated to biological process of interest. We will comment two examples.

Confined Water

Since the 800 – 880 cm⁻¹ region is dominated by C,H vibrations (Table 1) the difference between the integrated areas of these two regions will be a suitable qualitative quantifier for the confined water content,

$${[H_{2}O]}^{\mathit{\text{confined}}}\propto I_{880-940}-I_{800-880}$$ (1)

a key parameter for describing important processes, as just commented in the previous discussion. For example, we estimated the [H₂O]^confined in NM and inflammatory fibrous hyperplasia (IFH) tissues using our published data (ref. [3]). We found that confined water is ~ 2 times more abundant in the inflammatory tissue than in the normal one in agreement with the hydropic degeneration process experienced in IFH [3].

Methylation

The 800 – 880 cm⁻¹ region could also be used to probe the protein methylation process. Protein methylation is the process through which methyl groups are added to proteins under the action of specific enzymes, the methyltransferases. Usually it occurs on nitrogen atoms in N-terminals and cannot be reversed creating new amino acid residues. [28]. The above-cited spectral region does not present amine nor hydroxyl contributions being exclusive of methyl and protein backbone vibrations. Thus computing their ratio to N-H stretching appearing in the high-wavenumber region [3],

$$C{H}_3^{\mathit{\text{protein}}}\propto \frac{I_{800-880}}{I_{N-H}}$$ (2)

will give a useful protein methyl quantifier. Usually the methyl band ~ 2940 cm⁻¹ in the high-wavenumber region is considered to evaluate the methylation. However, it includes contributions of lipids and proteins [3]. Protein methylation modulates cellular and biological processes including transcription, RNA processing, protein interactions and protein dynamics [29]. Methyl-binding protein domains and improved antibodies with broad specificity for methylated proteins are being used to characterize the so-called protein methylome. They also have the potential to be used in high-throughput assays for inhibitor screens and drug development [30]. We made a rough estimate of the $C{H}_3^{\mathit{\text{protein}}}$ of NM and IFH tissues using our published data (ref. [3]). We found that methylated protein amount is ~ 3.6 times in IFH. This large increase is coherent with the established knowledge concerning chronic inflammatory processes as IFH.

In summary, our vibrational modes calculation for connective tissue in the fingerprint region indicated that important spectral features correlated to molecular characteristics have been ignored within the usual tissue spectral bands assignments. Our results showed that confined water is mainly responsible for the observed spectral complexity. The inherent complexity of the spectral features of this region was rationalized by our calculations and useful spectral markers for biological processes identified.

Funding

Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq - 311146/2015-5); Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP - 2011/19924-2).

Disclosures

The authors declare that there are no conflicts of interest related to this article.