Distinguishing between whole cells and cell debris using surface plasmon coupled emission

Abstract

Distinguishing between whole cells and cell debris is important in microscopy, e.g., in screening of pulmonary patients for infectious tuberculosis. We propose and theoretically demonstrate that whole cells and cell debris can be distinguished from the far-field pattern of surface plasmon coupled emission (SPCE) of a fluorescently-labeled sample placed on a thin metal layer. If fluorescently-labeled whole cells are placed on the metal film, SPCE takes place simultaneously at two or more different angles and creates two or more distinct rings in the far field. By contrast, if fluorescently-labeled cell debris are placed on the metal film, SPCE takes place at only one angle and creates one ring in the far-field. We find that the angular separation of the far-field rings is sufficiently distinct to use the presence of one or more rings to distinguish between whole cells and cell debris. The proposed technique has the potential for detection without the use of a microscope.

1. Introduction

Accurate detection and enumeration of biological cells is important for diagnosis and prognosis of many diseases, and hence for human health. The presence of a particular cell in a sample or the density of a particular cell greater than or smaller than a critical value can be a signal that a patient’s health is deteriorating and require immediate medical attention. However, cell counts are often inaccurate due to background noise, especially cell debris [1,2]. Cell debris is organic waste left over after a cell dies, which is an inevitable consequence of a cell life-cycle. Healthy cells can deteriorate into cell debris due to damage by adverse physical, chemical, infectious, biological, nutritional or immunological factors [3]. Cell debris also occurs when cells are damaged during processing for detection and enumeration [4]. When occurring within a sample, cell debris may interfere with the goal that necessitated the sample. Most often, cell debris is counted as whole cells, generating false positives. The counting of cell debris as whole cells becomes more serious in cases when identification of more than one type of cells is needed and when the density of target cells is low so that the cell identification must be performed in a high-throughput environment.

Distinguishing between intact cells and cell debris is an important but difficult task. A prime example is the enumeration of mycobacterium tuberculosis cells using acid-fast staining with auramine O [5]. While the technique preferentially labels the cell wall of the mycobacterium, it suffers from false positives because the stain will label whole cells as well as cell debris, resulting in higher counts [6]. Another important example is the enumeration of circulating tumor cells (CTCs) that are shed from primary tumor cells. Identification of CTCs is important for early detection, prediction of treatment response, and prognosis of cancer. In an early stage, the density of CTCs is small, and usually, if the total number of tumor cells found is 5 or more per 7.5 ml blood, a blood sample is positive [7]. However, often CTCs are damaged and fragmented in vivo and in vitro during the cell preparation processes, which causes inaccurate detection and misinterpretation [4]. Additionally, the cell cycle analysis of different stem cells is difficult in some cases because of cell debris [2, 8]. In general, similar problems can arise when using fluorescently-labeled antibodies for detection, as the cell debris still contain the same receptors as the whole cells. Therefore, standard methods for counting that rely on labeling with subsequent cell visualization using microscopy can lead to false positives, and ultimately to inaccurate results.

Cell debris is often eliminated from the cell count using histogram analysis [9, 10]. Using computer algorithms, cell debris can be removed from the cell count with high reliability. However, the greater the number of cell debris, the more difficult it is to accurately remove cell debris from the count. Also, different models show variable results for the same analysis [9, 10]. Besides, a technique based on histogram analysis requires a large data set, and it is impractical to apply when the expected cell count is only few per ml of sample, as is expected in the enumeration of mycobacterium tuberculosis, circulating tumor cells, and certain stem cells. False positives due to the cell debris can also be largely eliminated using automated microscopy combined with image analysis [11]. However, the cost of such systems can be prohibitively high, so that such systems are not suitable for screening at point-of-care and/or in low resource settings. There is a real need for methods with a decreased number of false positives that can be deployed in the field without significantly increasing the cost of the screening.

Surface plasmon coupled emission (SPCE) from a thin metal layer on a glass substrate has been used to detect biological samples [12–14, 22–26]. In this technique, a biological sample such as a protein is placed on the metal layer and labeled with a fluorescent molecule. When the fluorescent molecule is excited by a laser, the light that is emitted has a color that is different from the color of the light that excites the molecule. The emitted light from the fluorescent molecule is coupled into a glass prism within a sharp and clearly defined angle [15, 16]. The angle of emission depends on the index of the sample layer, i.e., the protein. The emission cone can be detected by a camera, and the protein can be readily detected. Importantly, the divergent but highly directional emission cone can be observed without the use of a microscope. The detection volume of SPCE is low compared to other surface-based methods, such as total internal reflection based microscopy [17–19], due to the distance-dependent coupling of fluorescence in SPCE [20–22]. The thin metal film also couples differently to horizontal and vertical dipoles. This technique requires minimal hardware. The system is light, fast, and sensitive. The SPCE-based bio-molecule detection system is also inexpensive—our group has published methods how to produce very low-cost SPCE substrates [23]. Recently, SPCE has also been used for sensing of bulk targets by using plasmon waveguide resonances [14,24]. SPCE has important applications to microscopy and sensing of proteins, and has attracted a large amount of interest [12–14].

In this work, we show that the distance-dependent coupling of fluorophore light to SPCE can be used to distinguish a whole cell from cell debris. A key physical distinction between a whole cell and cell debris that we will exploit is that the former is a volume of cytoplasm that is bound by a cell wall while the latter is only a piece of a cell wall. Therefore, a whole cell is necessarily a three-layer structure, with two wall layers separated by cytoplasm, while debris is only a one-layer structure. We also exploit the fact that the fluorescence from the bottom layer of the cell couples to the plasmonic modes via near-field interaction, while the fluorescence from the top side of the cell couples via hybrid plasmonic-cavity modes [21, 27]. We show that the SPCE from fluorescently-labeled whole cells placed on a thin metal layer deposited on a glass prism is qualitatively different from the SPCE when cell debris is placed on a thin metal layer. We find that once the fluorescent labels are excited by a laser in a reverse Kretschmann configuration, the fluorescently-labeled whole cells create at least two distinct intensity rings in the far-field, in contrast to fluorescently-labeled cell debris, which only creates one intensity ring. The distinct far-field patterns can be captured by camera and used to distinguish between whole cells and cell debris.

The rest of the paper is organized as follows: In Sec. 2, we describe the setup to be used to distinguish between whole cells and cell debris. In Sec. 3, we discuss the theory of SPCE for a fluorescently-labeled cell and the simulation approach to solve for SPCE. In Sec. 4, we show the SPCE dynamics, i.e., the near- and far-field profiles of fluorescently-labeled whole cells and cell debris. In Sec. 5, we draw conclusions.

2. Setup

The equipment necessary for the proposed technique is the same as that used in other SPCE-based systems [14, 20, 26]. In Fig. 1, we show a schematic illustration of the setup that we simulated. A 50-nm-thin silver layer is deposited on a bulk glass prism. In practice, the thin silver layer can also be deposited on a glass slide that is index-matched to the prism and then glued to the prism. The epi-layer of the silver is coated with a 10-nm glass (SiO₂) layer, which protects the silver from the reactive species in the cell environment. The thin SiO₂ layer also acts as a spacer between the metal layer and fluorophore labels attached to the cell, so that the energy of nearby fluorophores is not quenched due to enhanced non-radiative relaxation in the metal [28, 29].

Fig. 1.

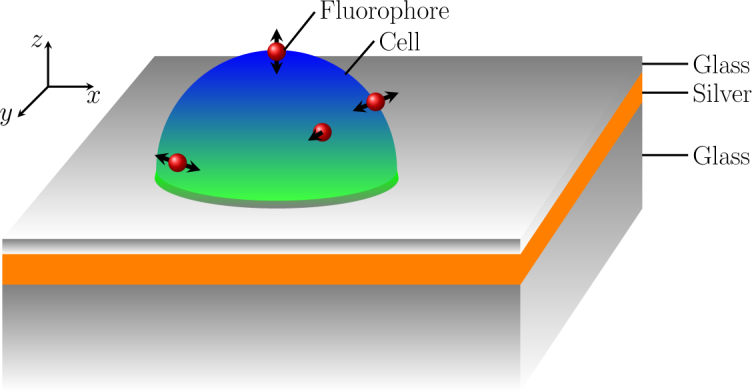
Schematic illustration of a cell on an SPCE slide.

The fluorescently-labeled samples such as whole cells and cell debris are placed on the spacer layer. The whole cells and cell debris are labeled using fluorescent dye molecules in suspension before being placed on the spacer layer. A host of different fluorophores such as rhodamine B, auramine O, fluorescein, and diI are used to label cell samples for fluorescent imaging and microscopy [14,30–32]. In this work, we assume that the sample is labeled either by rhodamine B or auramine O. While rhodamine B absorbs light at 550 nm and emits at 570 nm [33], auramine O absorbs light at 430 nm and emits at 450 nm [30]. We found similar SPCE dynamics when rhodamine B and auramine O are used to label the samples, and therefore, present results only when the samples are labeled using rhodamine B. The fluorophore labels attached to the walls of whole cells and cell debris are excited by unpolarized laser light in a reverse Kretschmann configuration so that the laser source is on the same side as whole cells and cell debris with respect to the SPCE slide [34]. The incident light excites fluorophore labels with equal intensity throughout the sample region. The excited fluorophore labels radiate light with polarization parallel to the plane of their dipole moments. The radiation from fluorophores excites surface plasmons at the metal surface and couples to SPCE in the prism side. The emission patterns are captured in the far field in the prism side using a charge coupled device camera, which is connected to a computer to process the captured images. The images can also be directly captured by a mobile phone using an appropriate optical arrangement and subsequently processed using an installed application software [35].

Usually, the intact and whole cells have a spherical or ovoid shape [36, 37]. However, when they are placed on the slide, the lower surface of the whole cells deforms and sits flat on the surface, so that whole cells can be treated as hemispheres or half-ovoids as shown in Fig. 1. In practice, there may be a spatially varying nanoscale gap of ∼10 nm between the cell wall and the spacer [38]. The contact between the cell wall and the spacer can be improved by using different adhesion techniques including heating up the sample for few minutes as is often done for tuberculosis samples or using capture antibodies as is often done for CTC or stem cells. As a consequence, whole cells and cell debris will firmly attach to the surface of SiO₂ spacer layer during the detection. Even when there is a nanoscale gap of ∼10 nm in the contact between the cell wall and the spacer, the SPCE dynamics will not change noticeably as the wavelength of the light is much greater than 10 nm. We note that SPCE-based techniques have been exploited for detection of cells [14] including microscopy of live cells [26]. In an SPCE-based technique, cells and debris can be deposited on the top of the slide following techniques used in total internal reflection fluorescence microscopy [32].

In a whole cell, the intra-cellular components are protected by the cell wall. Therefore, a cell placed on the slide can be treated as a three-layer structure as shown in Fig. 1. On the other hand, the cell wall of the debris lies flat on the spacer and only has the thickness of the cell wall. The whole cells, when in suspension, can be assumed to be spherical with a radius of 1–2 µm, which is surrounded by a cell wall ∼15–20 nm thick [39, 40]. In this work, we assume that a whole cell, when placed on the slide, has a radius of 1 µm in the x-y-plane at the position where it touches the spacer, a height of 300 nm, and a wall-thickness of 15 nm. We have also varied the dimensions of the cell to understand the change of SPCE dynamics with the change of the size of the cell as well as the suitability of the proposed technique. The physical model that we use is simple, but sufficiently complex to accurately simulate fluorescence interactions with actual cellular structures. Similar models have been used in other contexts, e.g., in total internal reflection fluorescence microscopy, and have been found to match well with experimental findings [17, 41, 42].

3. Simulation approach

To determine the electrodynamics when fluorophore labels on the cell wall are excited, we solve Maxwell’s equations using Lumerical, a commercial software package, to carry out three-dimensional full-field finite difference time domain (FDTD) simulations. We assume that the whole cells and the cell debris are labeled using fluorophore rhodamine B, which emits like a dipole at 570 nm. We consider fluorophores that are oriented in the x-, y-, and z-directions, although the fluorophores that are oriented in the x-y plane do not couple much energy to SPCE compared to that of the fluorophores oriented in the z-direction [21]. If the dipoles are randomly oriented, their contribution to SPCE can be calculated by taking the components of the dipole moments in the x-, y-, and z-directions. While the near-field profile due to the interaction of the incidence of radiation from the fluorophores on the metal surface is obtained directly by solving Maxwell’s equations using an FDTD technique, the far-field profile is obtained by projecting the angular spectrum representation of the near-field profiles onto the far field. The far-field intensity profile is calculated using

$$I={\displaystyle \sum _n\left({|E_{x,n}|}^2+{|E_{y,n}|}^2+{|E_{z,n}|}^2\right)},$$ (1)

where E_x,n, E_y,n, and E_z,n are the electric field components in the x-, y-, and z-directions in the far field due to the n-th dipole. Usually, several fluorophores will be attached to the cell wall distributed over the surface area, although mostly within a diffraction-limited area due to the relative size of the cell and the wavelength of the excitation or emission light. However, the near-field and far-field patterns will depend on the mechanism by which the fluorophore light couples to SPCE. In the first mechanism, fluorophore light couples to SPCE by direct energy transfer to the plasmons of the metal layer. In the second mechanism, the radiating fluorophore light couples to the cell; a part of the coupled light may excite surface plasmons on the metal surface, and thus may couple to SPCE. Irrespective of the position of the fluorophore on the cell wall, the near-field and far-field patterns will be qualitatively the same. Therefore, in essence, the far-field pattern will depend on the fluorophores that are attached to the whole cells and the cell debris at the bottom and at the top surfaces. Thus, the far-field intensity becomes

$$I={|E_{x,b}|}^2+{|E_{x,t}|}^2+{|E_{y,b}|}^2+{|E_{y,t}|}^2+{|E_{z,b}|}^2+{|E_{z,t}|}^2,$$ (2)

where E_x,b and E_x,t are the x-directed electric field components at the far field due to fluorophores that are located at the bottom and top of the cell, respectively, and E_y,b, E_y,t, E_z,b, and E_z,t are analogously defined.

In this work, we assume that the intra-cellular components and the cell wall are represented by an effective index of 1.38 [36,37]. In practice, the intra-cellular components and the cell wall may have slightly different indices from the effective index. However, the intra-cellular components and the cell wall have dimensions much smaller than the wavelength of the light and the overall size of the cell. Therefore, the assumption of an effective index for the cell will not change the result noticeably [43, 44]. The indices of refraction of different layers of the SPCE structure are taken from Palik [45]. While the refractive index of silver is dispersive and will change with the fluorophore emission wavelengths, the refractive indices of other materials, including that of cells remain nearly constant as the emission wavelength changes. We assume a background index of 1. If the cells are submerged in a buffer medium that provides a different background index, the SPCE dynamics will be qualitatively the same, except for a quantitative change in the coupled energy to SPCE. To calculate the near-field dynamics, we chose a grid size of only 5 nm in the z-direction and 10 nm in the x-y plane so that the smallest features are properly resolved. We considered a computational volume of 6 µm × 6 µm × 6 µm with the cell at its center. We applied perfectly matched layer boundary conditions at the simulation boundaries in all directions. We ran FDTD simulations until the energy confined within the simulation region decayed to 10⁻⁶ of its value at the beginning.

4. SPCE dynamics

In this section, we present and discuss the near-field and far-field profiles for both cell debris and whole cells. In our discussion of the near field profile, we present and discuss the radiation patterns for the x-, y-, and z-oriented fluorophores located at the bottom and top of cell debris and whole cells. In our discussion of the far-field profile, we present and discuss the electric field intensities for different cell heights and for different angular regions. While an analysis of the near-field profile provides insight into the physics that is due to the interaction of fluorescent labels with an SPCE structure, an analysis of the far-field profile shows the usefulness of this technique to distinguish between whole cells and cell debris.

4.1. Cell debris

4.1.1. Near-field profile

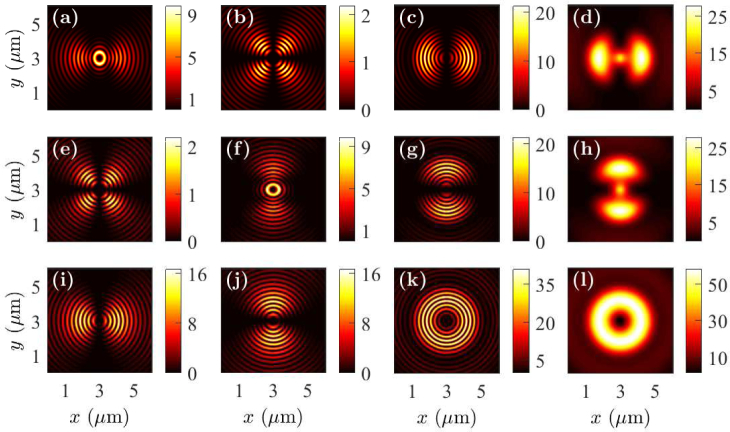
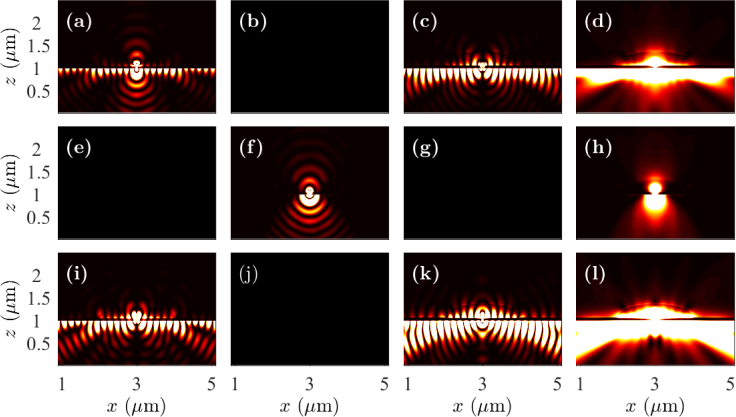
In Fig. 2, we show the near-field intensity profiles for cell debris when the fluorophores are oriented in the x-, y-, and z-directions. The fluorophores are located on the top of the cell debris and at the center of the sample in the x-y plane. The near-field profiles are recorded in the x-y plane at z = 500 nm within a glass prism away from the metal-glass interface. The near-field intensity profiles vary significantly when the orientations of the fluorophore dipole moments change. When the fluorophore dipoles are oriented in the x- and y- directions, a small amount of fluorophore radiation couples to the prism-side in the near field below the fluorophore position by direct transmission. However, a more intense radiation pattern is limited to specific angular regions away from the center when the fluorophore is oriented in the x- and y-directions. We note that the light coupled away from the center region is p-polarized as the electric field components are zero at x = 0 for the x-oriented dipole and at y = 0 for the y-oriented dipole. Therefore, the light coupled away from the center region is due to SPCE. The near-field radiation pattern is circular, intense, and uniform in all directions, when the dipole is oriented in the z-direction. Therefore, the total energy coupled to SPCE for the fluorophores that are oriented in the x- and y-directions is much smaller than that for the fluorophores oriented in the z-direction.

Fig. 2.

Near-field profiles in the x-y plane when the fluorophore is on the top of cell debris with the dipole oriented in the (a)–(d) x-direction, (e)–(h) y-direction, and (i)–(l) z-direction. Electric field components |E_x|² are drawn in (a), (e), and (i); |E_y|² are drawn in (b), (f), and (j); |E_z|² are drawn in (c), (g), and (k); and |E_x|² + |E_y|² + |E_z|² are drawn in (d), (h), and (l).

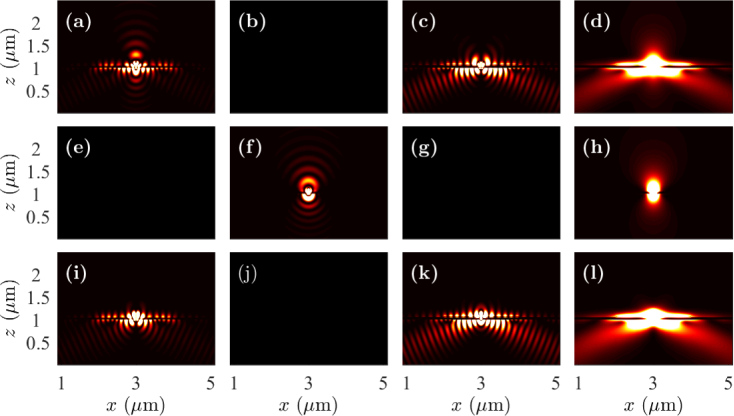
In Fig. 3, we show the near-field intensity profiles in the x-z plane drawn through the center of the cell debris when the fluorophores are oriented in the x-, y-, and z-directions. The fluorophores are located on the top of the cell debris and at the center of the sample in the x-y plane. We will note that the field intensities are not drawn to scale in this figure, and the intensities at the prism side have been amplified for improved visualization. However, the intensity profiles have been scaled equally in all cases so that the relative change in the dynamics due to the change in dipole orientation can be understood. We note that the electric field is coupled to surface plasmons along the silver-glass interface in the x-direction when the fluorophores are oriented in the x- and z-directions, as is expected from Fig. 2. The excitation of surface plasmons, and hence, the coupling of fluorophore radiation to SPCE is stronger when the dipole is oriented in the z-direction than when oriented in the x-direction. We observe directional SPCE in the near-field in the prism side. However, we do not observe excitation of surface plasmons, and hence, SPCE for the fluorophore oriented in the y-direction. The field components |E_y|² for the dipole oriented in the x-direction, |E_x|² and |E_z|² for the dipole oriented in the y-direction, and |E_y|² for the dipole oriented in the z-direction are zero in the x-z plane. We observe similar intensity profiles in the y-z plane drawn through the center of the cell debris, except that the intensity profiles for x- and y-oriented fluorophores are interchanged. Therefore, we do not show the near-field intensity profiles in the y-z plane.

Fig. 3.

Near-field profiles in the x-z plane when the fluorophore is on the top of cell debris with the dipole oriented in the (a)–(d) x-direction, (e)–(h) y-direction, and (i)–(l) z-direction. Electric field components |E_x|² are drawn in (a), (e), and (i); |E_y|² are drawn in (b), (f), and (j); |E_z|² are drawn in (c), (g), and (k); and |E_x |² + |E_y|² + |E_z|² are drawn in (d), (h), and (l).

The near-field profiles remain same qualitatively when the fluorophores are at the bottom of the cell debris. Therefore, we do not show the near-field profiles of cell debris when the fluorophores are at the bottom.

4.1.2. Far-field profile

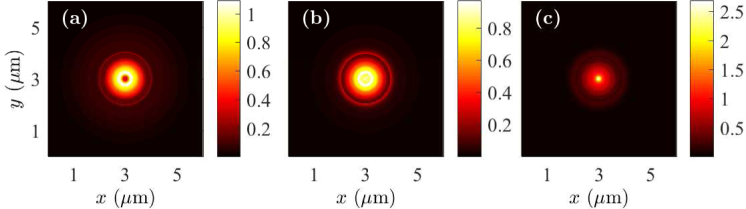
We project the near-field profiles obtained in the x-y plane for the cell debris to the far field to calculate the far-field intensity profiles. We also calculate the angle-resolved emission profiles. In Figs. 4(a) and 4(b), we show the far-field intensity profiles |E_x|² + |E_y|² + |E_z|² when the fluorophores are on the top and bottom of cell debris, respectively. In each case, the field intensity forms a distinct ring in the far field. The obtained far-field intensity profile is a clearly defined ring, which is due to the coupling of fluorophore radiation to SPCE. In Figs. 4(c) and 4(d), we show the far-field intensity vs. the angle θ, which is the inclination angle of the emission from the normal direction. The two peaks in Figs. 4(c) and 4(d) correspond to the angles at which the peak SPCE occurs. We find that the peak emission angle is ∼50 degrees in both cases. However, we note that the peak intensity decreases when the fluorophore is at the bottom of the cell debris.

Fig. 4.

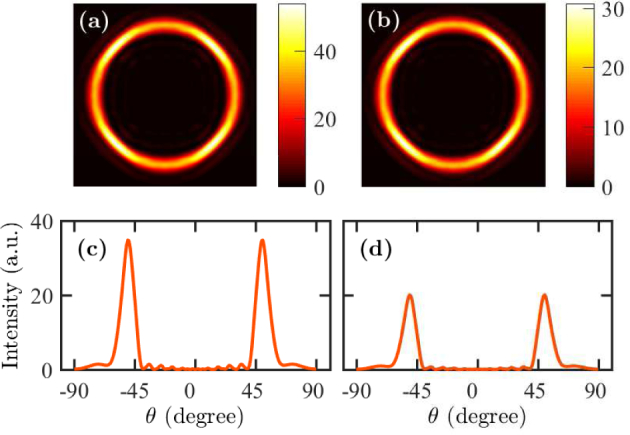
Far-field patterns for fluorescently-labeled cell debris when the fluorophore is (a) on the top and (b) at the bottom. Angle-resolved emission profiles for fluorescently-labeled cell debris when the fluorophore is (c) on the top and (d) at the bottom.

Since the cell debris is only 15 nm thick, the interaction of the fluorophore radiation with the SPCE structure in the near field, and hence, the projected far field do not qualitatively change when the fluorophore is located at the bottom of the cell debris from that when the fluorophore is on the top. Since the fluorophores are closer to the metal layer when they are at the bottom of the cell debris, they experience increased quenching by non-radiative relaxation to the metal layer. Therefore, the coupled energy to SPCE decreases when the fluorophores are at the bottom of the cell debris.

4.2. Whole cells

4.2.1. Near-field profile

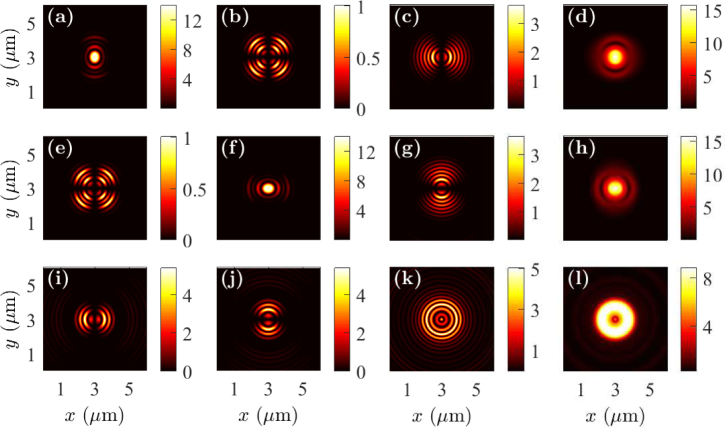
In Fig. 5, we show the near-field intensity profiles for whole cells when the fluorophores are oriented in the x-, y-, and z-directions. The fluorophores are located on the top of the whole cell and at the center of the sample in the x-y plane. The near-field profiles are recorded in the x-y plane at z = 500 nm within a glass prism away from the metal-glass interface. The near-field patterns vary significantly when the orientations of the fluorophore dipole moments change. As in the case of cell debris, the near-field radiation patterns are limited to specific angular regions when the fluorophores are oriented in the x- and y-directions. By contrast, the near-field radiation pattern is circular, intense, and uniform in all directions when the fluorophore is oriented in the z-direction. The coupled light away from the center region is due to SPCE as the electric field components are zero at x = 0 for x-oriented dipole and at y = 0 for y-oriented dipole. The energy coupled to SPCE for fluorophores that are oriented in the x- and y-directions is smaller than that of fluorophores that are oriented in the z-direction. We note that the coupled light intensity to the prism side is smaller when the fluorophore is on the top of a whole cell than that when the fluorophore is on the top of cell debris, which is due to the height of a whole cell. We also note that the coupled light to the prism side concentrates closer to the center in the near field of a whole cell than that of cell debris, which signifies that the emission angle can be smaller for a whole cell than that for cell debris.

Fig. 5.

Near-field profiles in the x-y plane when the fluorophore is on the top of a whole cell with the dipole oriented in the (a)–(d) x-direction, (e)–(h) y-direction, and (i)–(l) z-direction. Electric field components |E_x|² are drawn in (a), (e), and (i); |E_y|² are drawn in (b), (f), and (j); |E_z|² are drawn in (c), (g), and (k); and |E_x|² + |E_y|² + |E_z|² are drawn in (d), (h), and (l).

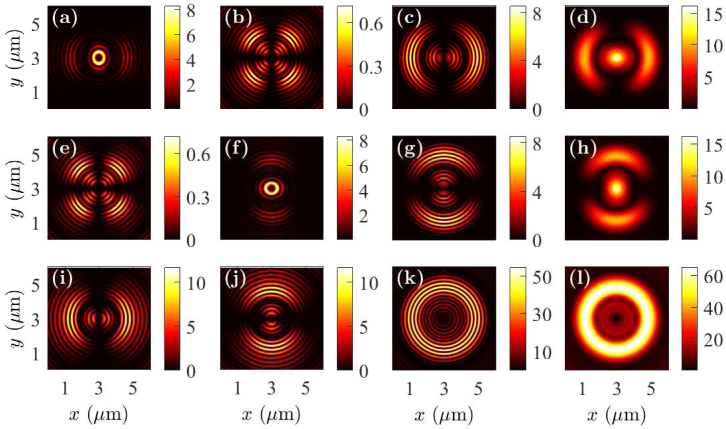
In Fig. 6, we show the near-field intensity profiles when the fluorophores are at the bottom of a whole cell and at the center of the sample in the x-y plane. Since the whole cell has a height of 300 nm, we find that the near field profiles are different when the fluorophores are on the top from when the fluorophores are at the bottom of the cell. Since the fluorophore is much closer to the metal layer when at the bottom of the cell, the direct coupling of fluorophore radiation to SPCE is more efficient than when the fluorophore is on the top of the cell. Therefore, the radiation coupled to the outer ring in the near field is more intense than to the inner ring.

Fig. 6.

Near-field profiles in the x-y plane when the fluorophore is on the bottom of a whole cell with the dipole oriented in the (a)–(d) x-direction, (e)–(h) y-direction, and (i)–(l) z-direction. Electric field components |E_x|² are drawn in (a), (e), and (i); |E_y|² are drawn in (b), (f), and (j); |E_z|² are drawn in (c), (g), and (k); and |E_x|² + |E_y|² + |E_z|² are drawn in (d), (h), and (l).

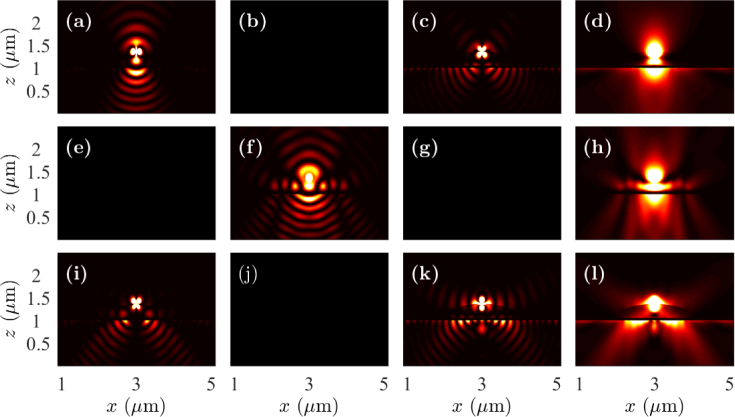
In Figs. 7 and 8, we show the near-field intensity profiles in the x-z plane drawn through the center of the whole cell when the fluorophores are oriented in the x-, y-, and z-directions. The fluorophores are located on the top and and at the bottom of a whole cell in Figs. 7 and 8, respectively. In each case, the fluorophores are at the center of the sample in the x-y plane. We note that the intensity profiles are not drawn to scale and the intensity coupled to the prism-side has been amplified for improved visualization. However, the intensity profiles have been scaled equally in each case so that the change in the dynamics due to the change in the position of the fluorophore can be understood. The metal-prism interface is at z = 1 µm and the prism is at z < 1 µm. We observe transmission of a small amount of light directly through the metal layer in both cases. In Fig. 7, we observe light coupling to surface plasmons at silver-glass interface and directional emission pattern, especially in Figs. 7(i) and 7(k), when the fluorophore is oriented in the z-direction. The coupling of the fluorophore light to the prism side in Fig. 7(i) occurs at a smaller angle than that in Fig. 7(k). Figure 7(i) is an example of fluorophore light being coupled to cavity modes first, and then being available in the prism side. By contrast, Fig. 7(k) is an example of excitation of plasmon modes by direct incidence of the fluorophore light. In Fig. 8, we observe stronger light coupling to surface plasmons when the fluorophore is located at the bottom than that when on the top of a whole cell. By contrast, we observe weaker light coupling to hybrid-plasmonic mode when the fluorophore is located at the bottom than that when on the top of a whole cell. In both Figs. 7 and 8, the field components |E_y|² for the dipole oriented in the x-direction, |E_x|² and |E_z|² for the dipole oriented in the y-direction, and |E_y|² for the dipole oriented in the z-direction are zero in the x-z plane. We observe similar near-field intensity profiles in the y-z plane except that the intensity profiles for x- and y-oriented dipoles are interchanged.

Fig. 7.

Near-field profiles in the x-z plane when the fluorophore is on the top of a whole cell with the dipole oriented in the (a)–(d) x-direction, (e)–(h) y-direction, and (i)–(l) z-direction. Electric field components |E_x|² are drawn in (a), (e), and (i); |E_y|² are drawn in (b), (f), and (j); |E_z|² are drawn in (c), (g), and (k); and |E_x|² + |E_y|² + |E_z|² are drawn in (d), (h), and (l).

Fig. 8.

Near-field profiles in the x-z plane when the fluorophore is at the bottom of a whole cell with the dipole oriented in the (a)–(d) x-direction, (e)–(h) y-direction, and (i)–(l) z-direction. Electric field components |E_x|² are drawn in (a), (e), and (i); |E_y|² are drawn in (b), (f), and (j); |E_z|² are drawn in (c), (g), and (k); and |E_x|² + |E_y|² + |E_z ² are drawn in (d), (h), and (l).

In Fig. 9, we draw near-field intensity profiles in the x-y plane through different cross-sections of the cell to study the excited modes in the cell cavity. The fluorophore is located at the top of the cell and oriented in the z-direction. We note that light is strongly coupled to the cell cavity. The light confined in cavity modes couples to SPCE and appears at the prism-side in a different angular region than the region that couples directly to SPCE.

Fig. 9.

Near-field profiles of |E_x|² + |E_y|² + |E_z|² on different cross-sections of a whole cell in the x-y planes when the fluorophore is on the top of the cell. The cross-sections are taken at (a) 50 nm, (b) 100 nm, and (d) 150 nm height within the cell.

4.2.2. Far-field profile

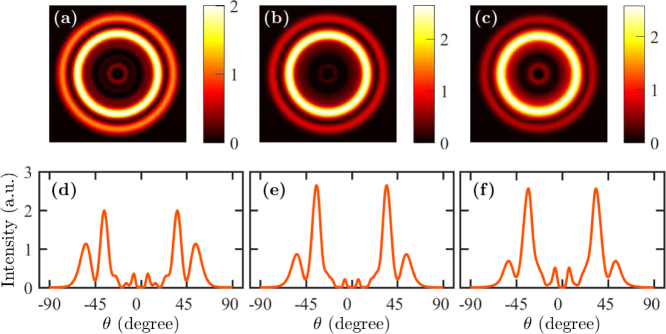
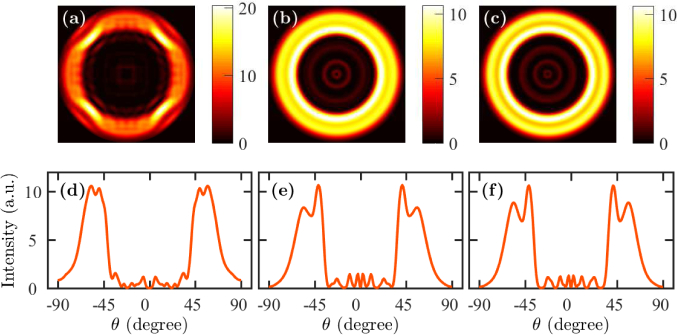
In Figs. 10(a)–(c), we show far-field profiles for a fluorescently-labeled whole cell when the fluorophore is located at the top and at the center of the cell in the x-y plane. The fluorophore is oriented in the z-direction. We vary the height of the cell from 300 nm to 500 nm while keeping other dimensions and parameters constant. In each case, we note that the field intensity forms at least two distinct rings in the far field. We note that the peak intensities of the rings change with the height of the cell, however, the angles that correspond to the peak intensities do not change much. The outer ring is due to the direct coupling of radiation from the fluorophore to SPCE, which is similar to that happens with cell debris. However, the emission angle changes from that of cell debris due to the change in the cell height. The inner rings are due to the coupling of light from the excited modes in the cell cavity. Cavity modes are formed due to the contrast in refractive indices of the cell and the surrounding medium—the metal layer at one end and the reflection due to the large index contrast between the cell wall and the surrounding medium. We observe more than one ring as several cavity modes can be excited within the cavity. However, only one cavity mode contributes significantly to the emission through the metal layer.

Fig. 10.

Far-field patterns when the fluorophore is on the top of a whole cell with a height of (a) 300 nm, (b) 400 nm, and (c) 500 nm. Angle-resolved emission profile when the fluorophore is on the top of a whole cell with a height of (a) 300 nm, (b) 400 nm, and (c) 500 nm.

In Figs. 10(d)–(f), we show the far-field intensity vs. the angle θ. We find that there are two strong peaks in the emission profile at angles ∼36 and ∼54 degrees. The emission profiles are narrow and the peaks are clearly separated. With the change in the height of the whole cell, the peak intensity of the outer ring decreases, but that of the inner ring increases. The peak emission angle does not change much when the height of the cell varies. However, we can deduce that the angular separation of the two rings that appear with whole cells is significant—the primary emission maximum is at ∼54 degrees, while the secondary emission maximum is at ∼36 degrees—so that it is possible to use the presence or absence of a second ring to distinguish between whole cells and cell debris.

In Figs. 11(a)–(c), we show far-field profiles for a fluorescently-labeled whole cell when when the fluorophore is located at the bottom and at the center of the cell in the x-y plane. The fluorophore is oriented in the z-direction. Again, we vary the height of the cell from 300 nm to 500 nm while keeping other dimensions and parameters constant. We note that the light intensity that directly couples to SPCE is stronger with the fluorophore at the bottom than that with the fluorophore on the top of the cell. The far-field profile is split into more than one ring.

Fig. 11.

Far-field patterns when the fluorophore is at the bottom of a whole cell with a height of (a) 300 nm, (b) 400 nm, and (c) 500 nm. Angle-resolved emission profile when the fluorophore is on the top of a whole cell with a height of (a) 300 nm, (b) 400 nm, and (c) 500 nm.

In Figs. 11(d)–(f), we show the far-field intensity vs. the angle θ. We find that two peaks emerge in the angular region of the primary emission when the cell height increases. The outer ring is due to the direct coupling of the fluorophore radiation to SPCE and the inner rings are due to the emission caused by the excitation of hybrid cavity-surface plasmon modes. The peak emission angles for the distinct rings do not change much when the fluorophore is at the bottom of cell debris from that when the fluorophore is on the top of cell debris.

The emission profiles of the whole cells and cell debris are quite distinct in terms of number of rings. While the far-field intensity profile of cell debris exhibits a single ring, the far-field intensity profile of whole cells exhibits at least two distinct rings. The angular separation of the rings that appear with whole cells in addition to the primary emission is significant enough to use the presence or absence of secondary rings to distinguish between whole cells and cell debris. The far-field rings can be observed easily by using only a camera. Standard classifier approaches can be used in order to assign the respective patterns to the class of whole cells or cell debris. Image processing techniques, such as the Hough transform [46, 47], can be utilized to speed up the classification. We note that we investigated the technique with auramine O fluorophores in addition to rhodamine B fluorophores. We also investigated the technique when the radius of the cell varies. We have found similar results irrespective of the fluorophore labels and the cell size.

5. Conclusion

In conclusion, we have shown that SPCE of a fluorescently-labeled cell can be used to distinguish between the whole cells and cell debris. A fluorescently-labeled whole cell produces a distinctly different SPCE far-field pattern from that of cell debris. The distinct far-field patterns can be captured by camera and used for identification of the sample. The proposed technique can be utilized to design low-cost and light-weight equipment that is suitable for point-of-care testing.

Disclosures

The authors declare that there are no conflicts of interest related to this article.