Freshening by glacial meltwater enhances melting of ice shelves and reduces formation of Antarctic Bottom Water

Glacial meltwater stops bottom-water formation, allowing warm ocean waters to reach Antarctic ice shelves and drive rapid melting.

Abstract

Strong heat loss and brine release during sea ice formation in coastal polynyas act to cool and salinify waters on the Antarctic continental shelf. Polynya activity thus both limits the ocean heat flux to the Antarctic Ice Sheet and promotes formation of Dense Shelf Water (DSW), the precursor to Antarctic Bottom Water. However, despite the presence of strong polynyas, DSW is not formed on the Sabrina Coast in East Antarctica and in the Amundsen Sea in West Antarctica. Using a simple ocean model driven by observed forcing, we show that freshwater input from basal melt of ice shelves partially offsets the salt flux by sea ice formation in polynyas found in both regions, preventing full-depth convection and formation of DSW. In the absence of deep convection, warm water that reaches the continental shelf in the bottom layer does not lose much heat to the atmosphere and is thus available to drive the rapid basal melt observed at the Totten Ice Shelf on the Sabrina Coast and at the Dotson and Getz ice shelves in the Amundsen Sea. Our results suggest that increased glacial meltwater input in a warming climate will both reduce Antarctic Bottom Water formation and trigger increased mass loss from the Antarctic Ice Sheet, with consequences for the global overturning circulation and sea level rise.

INTRODUCTION

The Antarctic Ice Sheet is losing mass at an increasing rate (1, 2), with the largest loss observed in glaciers that flow into the Amundsen Sea in West Antarctica (3). In East Antarctica, ice loss has been reported on the Sabrina Coast (2, 4), where the Totten Glacier is thinning and its grounding line is retreating (5). On both the Amundsen Sea and Sabrina Coast continental shelves, warm (>0°C) and saline (salinity > 34.7 g kg⁻¹) Modified Circumpolar Deep Water (MCDW) spreads poleward in the bottom layer in deep troughs (6–8). Where MCDW reaches ice shelf cavities, it drives rapid basal melt, as observed at the Totten and Moscow University ice shelves on the Sabrina Coast (7, 9) and Pine Island, Thwaites, Dotson, and Getz ice shelves in the Amundsen Sea (10–13). Rapid basal melt of these ice shelves is believed to be a major driver of the mass loss of the glaciers that they buttress (4, 14–16).

Most of the continental shelf around Antarctica is characterized by cold waters formed in coastal polynyas and, consequently, by low rates of ice shelf basal melt. Coastal polynyas are regions of enhanced sea ice formation, where water masses are modified by atmospheric cooling, wind stress, and salt flux associated with brine rejection. Strong buoyancy loss in the most active polynyas is sufficient to overturn the entire water column to produce cold (approximately at the surface freezing point) and saline (>34.6 g kg⁻¹) Dense Shelf Water (DSW; also referred to as High-Salinity Shelf Water). Examples of strong polynyas are found in the Ross Sea (17), Weddell Sea (18), Adélie Coast (19), and Cape Darnley/Prydz Bay region (20, 21). DSW formed in these regions is exported to the continental slope, where it mixes with ambient water to form Antarctic Bottom Water, a key component of the global overturning circulation and abyssal ventilation (22, 23).

However, not all polynyas produce DSW. The Dalton Polynya on the Sabrina Coast and the Amundsen Polynya in the Amundsen Sea (see location in Fig. 1A) are among the most active of Antarctic polynyas in terms of the volume of sea ice formed each year [~50 and 120 km³, respectively (24)]. However, the convection driven by winter buoyancy loss does not reach the bottom, and no DSW is formed. The water column remains stratified year-round, with relatively fresh (<34.55 g kg⁻¹) Winter Water (WW) overlying the saltier MCDW (7, 25). The absence of full-depth convection and DSW formation allows warm MCDW to spread across the continental shelf to the ice shelf cavities, where it drives the rapid basal melt observed on the Sabrina Coast and Amundsen Sea. Given that ice shelves in these regions buttress a volume of marine-based ice equivalent to more than 4 m of global sea level rise (26, 27), it is essential to understand the processes that regulate their basal melt.

Fig. 1. Water properties on the Sabrina Coast.

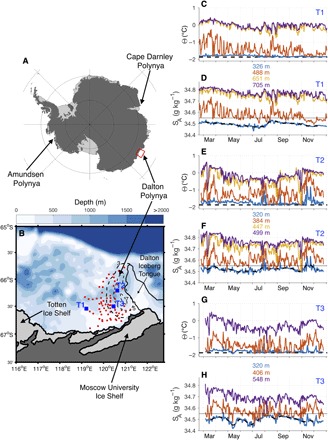
Map (B) of the Sabrina Coast [red rectangle in (A)] with bathymetry and coastline overlaid (81). Oceanographic stations where conductivity-temperature-depth (CTD) and oxygen isotope measurements have been collected are shown in red, whereas moorings T1, T2, and T3 are shown in blue. Black dashed lines are contours of the 2014 annual sea ice production (in meters) in the Dalton Polynya (24). Time series of conservative temperature Θ and absolute salinity S_A, low-pass filtered using a fourth-order 40-hour Butterworth filter, are shown for T1 (C and D), T2 (E and F), and T3 (G and H) with indicated depths. A 30-day low-pass filter is shown in black dashed lines for salinity time series at the shallowest instrument of each mooring, whereas the thin black lines represent S_A = 34.55 g kg⁻¹ (that is, upper salinity limit for WW). The black dashed lines in (C), (E), and (G) are the surface freezing temperatures for a salinity of 34.4 g kg⁻¹.

Earlier studies have shown that local and remote atmospheric forcing can drive variability in basal melt of ice shelves on the Sabrina Coast and in the Amundsen Sea by influencing the MCDW properties and depth of the WW-MCDW interface on the continental shelf (14, 28–31). However, it is not yet understood why active polynyas in these regions do not form DSW. Here, we use observations and a simple model to investigate the links between sea ice formation in coastal polynyas, DSW formation, and basal melt of ice shelves. We find that increased stratification induced by input of glacial meltwater inhibits formation of DSW and allows warm MCDW to reach ice shelf cavities where it drives basal melt.

RESULTS

Seasonal changes in continental shelf waters on the Sabrina Coast

Three moorings deployed on the continental shelf measured the evolution of water mass properties and stratification on the Sabrina Coast from February to December 2014 (see Fig. 1 and Materials and Methods). Two moorings (T2 and T3) were located in the Dalton Polynya, and a third mooring (T1) was located to the west of the polynya, closer to the Totten Ice Shelf. The water column remains stratified year-round at all three locations, and no DSW is present. MCDW is found in the bottom layer throughout the year at each mooring location, with absolute salinity ranging between ~34.65 and ~34.8 g kg⁻¹ and conservative temperature ranging between ~−0.5° and ~0.5°C (Fig. 1, C to H). Because MCDW does not interact with the atmosphere, temporal variability in this water mass is associated with offshore variability and cross-shelf exchange (31).

Cold (approximately at the surface freezing point), fresh (~34.5 g kg⁻¹) WW overlies the MCDW layer. At T1, the shallowest instrument at 326-m depth remains in the WW layer and provides a record of the seasonal evolution of WW properties. The salinity of the WW increases in July and August, reflecting the salinification and deepening of the winter mixed layer driven by brine released during sea ice formation. More surprising, however, is the steady freshening of the WW layer between February and July and between August and December. An increase in WW salinity in winter and freshening in other seasons is also discernible at the shallowest instruments at moorings T2 and T3. However, at these locations, the shallowest instrument does not remain regularly in the WW layer, and vertical displacements of the sharp WW-MCDW interface, presumably driven by winds, result in substantial variability at the two shallowest instruments.

It is not immediately clear why the deep WW layer freshens throughout most of the year. In Lützow-Holm Bay in East Antarctica, WW freshening in autumn has been explained by Ekman convergence of surface waters, causing accumulation and downwelling of fresh sea ice melt in summer (32). However, WW freshening on the Sabrina Coast occurs also in other seasons, including in September and October when sea ice is forming, and is observed below 300-m depth, too deep to be affected by Ekman downwelling of surface waters (32). A hypothesis we now test is that glacial meltwater exiting nearby ice shelf cavities can explain the depth, timing, and magnitude of the freshening signal.

WW freshened by glacial meltwater on the Sabrina Coast

We use summer observations of oxygen isotope and salinity to quantify the sources of freshwater to shelf waters on the Sabrina Coast (see Materials and Methods). We assume that saline MCDW, high in the oxygen isotope δ¹⁸O (Fig. 2A), represents pure ocean water, whereas fresh WW and surface layers, low in δ¹⁸O, are a mixture of MCDW, sea ice melting/freezing, and meteoric water. Meteoric water is supplied by direct precipitation into the ocean or from snow accumulated on the Antarctic Ice Sheet, which enters the ocean as glacial meltwater. Under these assumptions, we can use δ¹⁸O and salinity data to estimate the fraction of meteoric water and sea ice melt in the water column (33), where negative fractions of sea ice melt indicate freezing.

Fig. 2. Freshwater input on the Sabrina Coast.

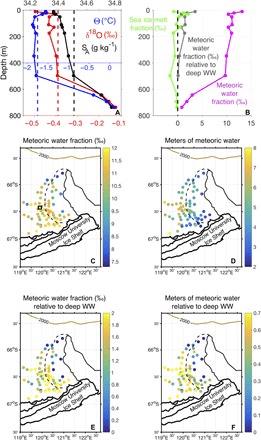
(A) Vertical profiles of conservative temperature Θ, oxygen isotope δ¹⁸O, and absolute salinity S_A from station 21 [black square in (C)]. The vertical black (red) dashed line represents S_A (δ¹⁸O) used to estimate the meteoric water fraction relative to deep WW (see Materials and Methods). The dashed blue line is Θ = −1.75°C, the upper temperature limit for WW. (B) Vertical profiles at station 21 of the fractions of meteoric water (magenta), sea ice melt (green), and meteoric water relative to deep WW (gray) (see Material and Methods). (C) Vertically averaged meteoric water fraction above the MCDW layer. The black dashed line delimits the Dalton Polynya, defined as the area where the annual sea ice production is larger than 3 m. (D) Meters of meteoric water. (E) Same as (C) but relative to deep WW. (F) Meters of meteoric water accumulated above the MCDW layer since the commencement of mixed-layer retreat.

Example vertical profiles show that the meteoric water fraction is ~0‰ in the MCDW layer and increases upward to values between 10 and 13‰ in the WW and surface layers (Fig. 2B). The sea ice melt fraction is zero in the MCDW layer, negative in the WW layer because of sea ice growth during the previous winter, and positive near the surface because of summer sea ice melt. Figure 2C shows the meteoric water fraction averaged between the base of the WW layer and the surface. Relatively high concentrations of meteoric water (~10‰) are observed in the domain, with higher values (~12‰) near the coast and lower values in the northern polynya (~8 to 9‰). By vertically integrating the fractions, we find that typically 4 to 5 m of meteoric water accumulate in the water column, with higher values west of the polynya and lower values near the coast (Fig. 2D). The lower inventory near the coast reflects the shallower bathymetry and thinner WW layer there [about 250 to 300 m thick; (7)].

We now estimate the rate of meteoric water input to determine whether it is sufficient to explain the freshening seen in the mooring observations. The same method is applied, except that as pure ocean water, we use a water type representative of the mixed layer at the end of winter (see Materials and Methods). We can thus quantify the meteoric water accumulated above the MCDW layer between the commencement of the mixed-layer retreat (that is, restratification) and the time of the summer survey (34). For this analysis, we use WW found below 400-m depth as pure ocean water (see Fig. 2A for the properties of this “deep” WW). This water preserves the properties of the winter mixed layer without being largely affected by glacial meltwater released by nearby ice shelves since the end of winter convection, which accumulates in the top 300 to 400 m of the water column (7).

The vertical profile shown in gray in Fig. 2B highlights the addition of meteoric water to the water column above 400-m depth since the commencement of mixed-layer retreat. The spatial pattern of meteoric water fraction relative to deep WW (Fig. 2E) is similar to that of total meteoric water (Fig. 2C), indicating stronger input in the southern polynya, close to the Moscow University Ice Shelf. This is expected because fractions calculated relative to deep WW represent a subset of the total values (34). The inventories and concentrations relative to deep WW (Fig. 2, E and F) are smaller than the total values (Fig. 2, C and D), the latter reflecting accumulation of meteoric water over time scales longer than a few months.

Considering all stations, the linear average of the meteoric water accumulated since the end of winter convection is 0.5 m, with a standard error of 0.04 m. Mooring observations show that the mixed layer starts to shoal around September, about 3 months before the summer survey. The rate of meteoric water input into the water column during these 3 months is then estimated to be ~0.17 m month⁻¹. Assuming that the WW freshening rate (~0.01 g kg⁻¹ month⁻¹) detected by the mooring observations after September is representative of the domain of the summer survey and vertically homogeneous between 400-m depth and the surface, a rate of ~0.12 m of freshwater input per month is obtained, in good order-of-magnitude agreement with our estimate of the rate of meteoric water input. In addition, the rate of decrease in WW salinity between March and July is similar to that observed after September, further confirming that the observed WW freshening is caused by sustained input of meteoric water at depths shallower than 300 to 400 m. Processes such as eddy-induced restratification (35) can also contribute to the freshening, but the consistency between the observed salinities and the estimated meteoric water input indicates that meteoric water is the primary source of the observed freshening.

The tracers used here to quantify the meteoric water content cannot differentiate between the contributions from glacial meltwater and precipitation into the ocean. The 2014 average rate of precipitation minus evaporation in the domain of our survey from ERA-Interim reanalysis (36) is ~0.03 m month⁻¹. Although the rate at which precipitation is mixed into the ocean is uncertain, the precipitation rate is less than 20% of the rate estimated for the meteoric water input, suggesting that glacial meltwater is the dominant source of meteoric water. A previous study of Silvano et al. (7) shows that most of the glacial meltwater found in the area of our survey comes from basal melt of the Moscow University Ice Shelf, which, after exiting the ice shelf cavity, is advected westward by the coastal current toward the Dalton Polynya. The authors found higher concentrations of glacial meltwater in the southern polynya, in agreement with our results of higher meteoric water fractions in the same area. We conclude that glacial meltwater released by the Moscow University Ice Shelf explains the WW freshening revealed by mooring observations.

Influence of glacial meltwater input on stratification of shelf waters

We now seek to understand how meteoric water input influences the mixed-layer evolution during winter in the Dalton Polynya. We use a bulk mixed-layer model (see Materials and Methods) to investigate the processes involved in producing wintertime water masses and stratification. The model is run from March (beginning of the winter season) to September, after which the mixed layer shoaled at all mooring locations. Initial conditions are based on in situ observations collected by a profiling float around the time of the mooring deployment (see Materials and Methods and fig. S1). The model is forced by salt flux at the ocean surface based on satellite-derived sea ice production [see Materials and Methods and fig. S1B; (24)]. The input rate of meteoric water is set to 0.15 m month⁻¹, an intermediate value between the freshening rate inferred from mooring observations and that calculated from δ¹⁸O and salinity data. The input of 0.15 m of freshwater per month is sufficient to compensate ~35% of the salt flux by sea ice production (see Materials and Methods). In our model runs, we reduce the surface salt flux by 35% to simulate the freshening impact of the meteoric water injected into the ocean.

The experiment with meteoric water input included shows good agreement with mooring observations (Fig. 3, A and B). The water column is destratified to ~350-m depth by the end of September, and the mixed-layer salinity reaches ~34.5 g kg⁻¹, as observed. If the contribution from meteoric water is not taken into account, convection extends to the seafloor and the mixed-layer salinity (~34.6 g kg⁻¹) is higher than observed. The largest uncertainty in the model is associated with sea ice production, whereas other factors such as changes in initial conditions have less effect (see Materials and Methods). Even considering the ±25% (37) uncertainty in sea ice production, the experiment without the meteoric water contribution cannot reproduce the observations (see shaded red area in Fig. 3, A and B). Our results show that meteoric water, mostly in the form of glacial meltwater released by the Moscow University Ice Shelf, acts to reduce deepening and salinification of the mixed layer in the Dalton Polynya. Therefore, DSW is not formed, and warm MCDW intruding onto the shelf at the longitude of the Dalton Polynya and further west floods the bottom layer (8), ultimately delivering enough heat to the base of the Totten Ice Shelf to drive rates of basal melt that are among the highest in Antarctica (38).

Fig. 3. Mixed-layer evolution in Antarctic polynyas.

Modeled temporal evolution of mixed-layer depth (A) and absolute salinity S_A (B) in the Dalton Polynya. In red, we show the case with no meteoric water included. In black, meteoric water is included by reducing the surface salt flux by 35%. Shaded areas represent uncertainty in the model output related to uncertainty in sea ice production [±25% (37)], whereas blue bars indicate the range of observed WW properties. (C and D) Same as (A) and (B) for the Amundsen Polynya. Surface salt flux is reduced by 75% in the black line case. Blue bars are based on WW variability in different years (6, 12, 25). (E and F) Same as (A) and (B) for the Cape Darnley Polynya but only showing the no–meteoric water case because it reproduces observations of DSW formation (20). Note that the y axis stops at the full depth of the ocean, different in (A), (C), and (E) (figs. S1 to S3).

The Amundsen Polynya is one of the most productive polynyas in Antarctica, forming more than twice as much sea ice as the Dalton Polynya (24). We next examine whether input of glacial meltwater can also explain the lack of DSW formation in the Amundsen Sea. Initial conditions in the Amundsen Polynya are based on data collected in late summer 2007, and the model is integrated between March and October 2007, when strong sea ice production is observed (see Materials and Methods and fig. S2). Multiyear observations from this area show that the WW salinity is of the order of 34.3 g kg⁻¹ and that the maximum mixed layer depth is about 400 m (6, 12, 25). In the absence of freshwater input, the mixed layer in the model reaches the bottom and is much saltier (~34.6 g kg⁻¹) than observed (Fig. 3, C and D). To reproduce observed values, the net surface salt flux needs to be reduced by ~75% (Fig. 3, C and D).

To compensate 75% of the salt flux provided by sea ice formation, about 0.4 m of freshwater must be added to the ocean each month. Freshwater input from melting of sea ice is small in this location (25). The 2007 precipitation minus evaporation rate in the region is ~0.06 m month⁻¹ in the ERA-Interim reanalysis. Melting of icebergs can also contribute to meteoric water input to the Amundsen Polynya, but recent modeling studies indicate that the iceberg contribution is smaller than that of precipitation (39, 40). Most of the meteoric water input must therefore come from glacial meltwater released by melting ice shelves. By integrating over the area of the Amundsen Polynya, we find that ~8.5 km³ month⁻¹ of freshwater is required to offset 75% of the surface salt flux supplied by sea ice formation. The primary source of glacial meltwater to the Amundsen Polynya is likely basal melt of upstream ice shelves (for example, Crosson, Pine Island, and Thwaites). The combined basal mass loss of these ice shelves is about 20 km³ month⁻¹ over the 2003–2008 period (41, 42). Most of the glacial meltwater released by these ice shelves is transported westward in the coastal current to the Amundsen Polynya in the top 300 to 400 m of the water column (11). [Meltwater exits the cavity beneath the Dotson Ice Shelf south of the polynya (fig. S2A), but the core of this outflow is located on the western edge of the polynya (12) and therefore likely has less impact on convection in the Amundsen Polynya.) Basal melt of upstream ice shelves therefore provides sufficient freshwater input to compensate a large fraction of the salt flux released during sea ice formation in the Amundsen Polynya. As a result, winter convection does not extend to the seafloor, no DSW is formed, and warm MCDW flowing through the Dotson Trough (fig. S2A) can reach the Dotson (12) and Getz ice shelves (13) and drive rapid basal melt.

We have shown that DSW formation is inhibited in polynyas downstream of the outflow from “warm-cavity” ice shelves characterized by rapid rates of basal melt. In contrast, observations in the Ross Sea (17), Weddell Sea (18), Adélie Coast (43), and Prydz Bay (21) show that, although glacial meltwater released by nearby cold-cavity ice shelves can reduce the DSW salinity, it is not sufficient to prevent the top-to-bottom convection necessary for DSW formation. Next, we apply the model to the Cape Darnley Polynya where similar rates of sea ice formation to the Amundsen Polynya (24) drive formation of DSW (20). We use data from a CTD-instrumented elephant seal collected in late summer 2011 as initial conditions and surface salt fluxes from March to October 2011 (see Materials and Methods and fig. S3). The model run without meteoric water input produces a mixed layer that reaches the bottom with salinity values around 35 g kg⁻¹ (Fig. 3, E and F), in good agreement with the properties of the DSW formed in 2011 (20). This result confirms that mixed-layer deepening is not greatly affected by glacial meltwater reaching the Cape Darnley Polynya. The primary source of glacial meltwater here is basal melt of the upstream Amery Ice Shelf (44), where basal melt rates are relatively low, being mostly driven by cold DSW formed in Prydz Bay polynyas (45).

DISCUSSION

On the Sabrina Coast and in the Amundsen Sea, input of glacial meltwater is sufficient to partially compensate brine supplied during sea ice formation, reducing the depth and salinity of the winter mixed layer. This mechanism helps explain why polynyas in these regions do not produce DSW, despite strong buoyancy loss. In cold regions such as Prydz Bay (21), glacial meltwater can reduce the salinity of the DSW escaping the continental shelf, thus freshening the resulting Antarctic Bottom Water. However, in Prydz Bay, the low rates of ice shelf basal melt are insufficient to prevent the formation of cold DSW, and the water column is completely destratified during winter convection (45). In contrast, on the Sabrina Coast and in the Amundsen Sea, the absence of deep convection and DSW formation allows warm MCDW to persist at depth throughout the year within the polynya and further downstream, where it can reach ice shelf cavities. In these regions, glacial meltwater thus both prevents DSW formation and supports rapid basal melt by inflow of warm MCDW to ice shelf cavities (Fig. 4A).

Fig. 4. Impact of glacial meltwater on dense water formation and shelf stratification.

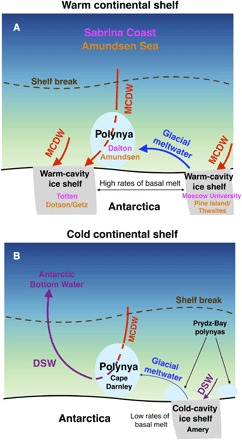
On warm continental shelves, as those on the Sabrina Coast and in the Amundsen Sea (A), MCDW drives rapid ice shelf basal melt. The large volume of glacial meltwater prevents DSW formation in polynyas downstream of the meltwater outflow. MCDW remains in the bottom layer throughout the year in the polynya and further downstream, where it can access the ice shelf cavities. On cold continental shelves, the ice shelf cavities are filled by cold shelf waters, and basal melt rates are low. Glacial meltwater input is not sufficient to suppress winter convection in polynyas downstream of the meltwater outflow, as seen at Cape Darnley Polynya (B), allowing formation of DSW, the precursor to Antarctic Bottom Water.

The model used here is very simple, but the fact that the observed properties of the winter mixed layer can be reproduced in very different polynya systems suggests that the model captures key elements of the interplay between polynya activity, stratification, dense water formation, and ice shelf basal melt. Studies of these regions using more comprehensive models have produced different and sometimes conflicting results. For example, some regional models show formation of DSW in the Dalton Polynya (30, 46), possibly because the impact of glacial meltwater from the Moscow University Ice Shelf is not well reproduced. Other models reproduce the observed stratification on the Sabrina Coast and in the Amundsen Sea, but the modeled rates of sea ice formation in the polynyas tend to be underestimated (47, 48) or the rates of ice shelf basal melt tend to be overestimated (14). A common feature found in many regional modeling studies is that interannual variability in waters formed in coastal polynyas affects the basal melt of nearby ice shelves (14, 29, 30), confirming the primary role of coastal polynyas in regulating the delivery of ocean heat to the margin of the Antarctic Ice Sheet. However, regional models of coastal polynyas face a number of challenges, including the complex and time-evolving icescape (49), the poorly known bathymetry (9, 50), the small spatial scale of ocean processes happening near ice shelves (51) and at the shelf break (52), and uncertainties in air-sea forcing, including the impact of fine-scale atmospheric phenomena such as katabatic winds (53). Climate models have also been used to study the impact of glacial meltwater input to the Southern Ocean (54, 55). They show that glacial meltwater drives a freshening of shelf waters and Antarctic Bottom Water. However, processes happening in coastal polynyas and beneath the ice shelves cannot be accurately represented in these coarse resolution models. Our study highlights that the coupled interplay between coastal polynyas, water mass formation, and ocean-ice shelf interaction must be properly represented in models that aim to simulate the present and future behavior of the Antarctic Ice Sheet and Southern Ocean overturning circulation.

Currently, Antarctic shelf waters are mostly cold, and basal melt rates are low at many ice shelves, indicating that glacial meltwater input is insufficient to prevent DSW formation, as found at Cape Darnley Polynya (Fig. 4B). In regions such as the Weddell Sea (56), Ross Sea (57), and Prydz Bay (58), DSW floods the bottom layer, and MCDW can only access the ice shelf cavities sporadically at mid-depth, with limited impact on basal melt rates. A decrease of DSW formation in a warmer climate might lead to a reduced circulation in cold-cavity ice shelves and a slight decrease in basal melt (59). However, projections simulating the impact of sustained emissions of anthropogenic greenhouse gases show that melting of Antarctic ice shelves and glaciers will increase in the coming decades and centuries in response to warming of the ocean and atmosphere (60) and redirection of warm coastal currents (61). There is already evidence of freshening of bottom waters in the Weddell and Ross seas associated with recent increase of glacial mass loss in the upstream Antarctic Peninsula (62) and Amundsen Sea (63), respectively. We show that present rates of glacial meltwater input are sufficient to prevent DSW formation in some locations, despite strong air-sea forcing and buoyancy loss. This mechanism can help explain past and projected future behavior of the Antarctic Ice Sheet and Southern Ocean (64–66). Our results suggest that a further increase in the supply of glacial meltwater to Antarctic shelf waters may trigger a transition from a cold regime (characterized by full-depth convection, low rates of ice shelf basal melt, and active bottom water formation) to a warm regime (characterized by year-round stratification, high rates of ice shelf basal melt, and reduced bottom water formation). A slowdown of DSW formation in response to increased glacial meltwater input would have consequences for the deep overturning circulation and abyssal ventilation. At the same time, meltwater-induced changes in stratification would facilitate the spreading of warm waters across the continental shelf to ice shelf cavities, driving increased ice shelf basal melt, reduced buttressing of the Antarctic Ice Sheet, and additional rise in sea level.

MATERIALS AND METHODS

Oceanographic observations

An oceanographic survey was conducted on the continental shelf of the Sabrina Coast (115° to 125°E) onboard the Aurora Australis (cruise AU1402) between 24 December 2014 and 7 January 2015 (7). Oceanographic profiles were collected using a Seabird 911plus CTD with dual temperature and conductivity sensors and calibrated against bottle samples. Here, we included the analysis of 68 CTD stations (see location in Fig. 1B) collected during this expedition along with measurements of the ratio of stable oxygen isotopes in seawater (δ¹⁸O, the standardized ratio of ${\mathrm{H}}_2^{18}\mathrm{O}$ to ${\mathrm{H}}_2^{16}\mathrm{O}$). δ¹⁸O data were extracted from water samples at various depths using a Finnigan DELTAplus mass spectrometer at the Institute of Low Temperature Science, Hokkaido University, Japan. Measurements for each sample were duplicated, and the precision of the replicates was estimated to be 0.02‰.

Three moorings (T1, T2, and T3) were deployed on the continental shelf of the Sabrina Coast (see location in Fig. 1B) in February 2014 during the NBP1402 expedition on the US R/V Nathaniel B. Palmer and recovered in January 2015 during the AU1402 voyage. Measurements, including temperature, salinity, and pressure, were collected at four different depths between about 300 m and the bottom at each location. Salinity measurements at the second deepest instrument of mooring T3 showed some drift, and therefore data from this instrument were excluded from our analysis. For more details about records and specific instruments, the reader is referred to table S1.

In addition, we used salinity and temperature data acquired between the beginning of February and the first week of March 2015 by a profiling float deployed during the AU1402 voyage (see location of profiles in fig. S1A). We also included in our analysis shipboard measurements of surface salinity and temperature collected in the Dalton Polynya during the Nathaniel B. Palmer survey between the last week of February and the first week of March 2014 [see location in fig. S1A; (67)]. Finally, CTD data from the Amundsen and Cape Darnley polynyas were used. Data from the Amundsen Polynya were collected on 27 February 2007 onboard the R/V Nathaniel B. Palmer [fig. S2; (13)]. Data from Cape Darnley Polynya were acquired on 22 February 2011 by a CTD-instrumented elephant seal [seal deployment ft07, seal number 346, seal tag number Cy27, and platform number 00022332; fig. S3; (20, 68, 69)]. All temperature and salinity data in this study have been converted to absolute salinity S_A (in grams per kilogram, g kg⁻¹) and conservative temperature Θ (in degrees Celsius, °C) (70).

Quantification of freshwater sources

S_A and δ¹⁸O can be used as conservative tracers to estimate fractions (f) of meteoric water and sea ice melt in the water column (33). The fraction of sea ice melt can be negative in the case of net sea ice growth. We assumed that the observed values (“obs”) of S_A and δ¹⁸O represent a mixture of sea ice melt (“sim”), meteoric water (“met”), and oceanic water (MCDW). The mass balance is then given by

$$\{\begin{array}{c}{\mathit{f}}^{\text{sim}}+{\mathit{f}}^{\text{met}}+{\mathit{f}}^{\text{MCDW}}=1\\ {\mathit{f}}^{\text{sim}}{\mathit{S}}_{\mathrm{A}}^{\text{sim}}+{\mathit{f}}^{\text{met}}{\mathit{S}}_{\mathrm{A}}^{\text{met}}+{\mathit{f}}^{\text{MCDW}}{\mathit{S}}_{\mathrm{A}}^{\text{MCDW}}={\mathit{S}}_{\mathrm{A}}^{\text{obs}}\\ {\mathit{f}}^{\text{sim}}{\mathrm{\delta }}^{18}{\mathrm{O}}^{\text{sim}}+{\mathit{f}}^{\text{met}}{\mathrm{\delta }}^{18}{\mathrm{O}}^{\text{met}}+{\mathit{f}}^{\text{MCDW}}{\mathrm{\delta }}^{18}{\mathrm{O}}^{\text{MCDW}}={\mathrm{\delta }}^{18}{\mathrm{O}}^{\text{obs}}\end{array}$$ (1)

S_A and δ¹⁸O values for MCDW were chosen to be 34.8 g kg⁻¹ and −0.1‰, respectively, based on our observations on the Sabrina Coast. Values relative to sea ice (${\mathit{S}}_{\mathrm{A}}^{\text{sim}}$ = 6.2 g kg⁻¹ and δ¹⁸O^sim = 1.2‰) were obtained from sea ice core measurements collected on the Sabrina Coast continental shelf in 2007 during Sea Ice Physics and Ecosystems eXperiment [SIPEX (71)]. Salinity of the meteoric water was set to zero. δ¹⁸O^met is the most uncertain parameter because of the large difference in δ¹⁸O values for precipitation in the region [~−20‰ (72)] and the value relative to the glacial ice that feeds the ice shelves on the Sabrina Coast [~−40‰ (72)]. We chose an intermediate value for δ¹⁸O^met equal to −30‰. Given the range in the δ¹⁸O^met end-member, the uncertainty in the calculated meteoric water and sea ice melt fractions is less than 1%, diminishing when averages of numerous samples are calculated. Uncertainties associated with other end-members or errors in the measurements had a marginal impact on this calculation compared to the uncertainty in δ¹⁸O^met.

We followed the method described by Meredith et al. (34) to estimate the meteoric water accumulated between the commencement of the mixed-layer retreat and the time of the AU1402 survey. A modified version of the balance shown in Eq. 1 was used, considering deep (below 300- to 400-m depth in the case of the Sabrina Coast) Winter Water (dWW) as the ambient water to calculate the fractions of meteoric water and sea ice melt above the MCDW layer

$$\{\begin{array}{c}{\mathit{f}}^{\text{sim}}+{\mathit{f}}^{\text{met}}+{\mathit{f}}^{\text{dWW}}=1\\ {\mathit{f}}^{\text{sim}}{\mathit{S}}_{\mathrm{A}}^{\text{sim}}+{\mathit{f}}^{\text{met}}{\mathit{S}}_{\mathrm{A}}^{\text{met}}+{\mathit{f}}^{\text{dWW}}{\mathit{S}}_{\mathrm{A}}^{\text{dWW}}={\mathit{S}}_{\mathrm{A}}^{\text{obs}}\\ {\mathit{f}}^{\text{sim}}{\mathrm{\delta }}^{18}{\mathrm{O}}^{\text{sim}}+{\mathit{f}}^{\text{met}}{\mathrm{\delta }}^{18}{\mathrm{O}}^{\text{met}}+{\mathit{f}}^{\text{dWW}}{\mathrm{\delta }}^{18}{\mathrm{O}}^{\text{dWW}}={\mathrm{\delta }}^{18}{\mathrm{O}}^{\text{obs}}\end{array}$$ (2)

S_A and δ¹⁸O of deep WW were set to 34.51 g kg⁻¹ and −0.39‰, respectively, based on observations of WW below 400-m depth (Fig. 2A). By vertically integrating f^met, we obtained the meters of meteoric water accumulated above the MCDW layer since the commencement of the mixed-layer retreat.

Mixed-layer model

We used a bulk model to simulate the mixed layer during winter months, based on the works of Kraus and Turner (73) and Niiler and Kraus (74). More recent studies (47, 48) have used the same model to assess the role of atmospheric forcing on ocean stratification around Antarctica. In the latter studies, the authors couple the ocean model with a sea ice model forced by atmospheric reanalysis data. They succeed in reproducing the bulk ocean stratification on the Antarctic continental shelf, confirming the validity of the model for this region. However, the estimated rates of sea ice growth are much lower than those based on satellite observations in some coastal polynyas, including the Amundsen and Dalton polynyas. This might be due to the absence in their model of fast ice and glacier tongues, which allow the formation of polynyas in their lee, as it occurs in the regions considered in this study (49).

The model assumes a balance in the mixed layer between sources and sinks of turbulent kinetic energy. We further assumed that wind stirring acts to keep the mixed layer “well-mixed,” without influencing the energy budget (75). The main sources/sinks of energy to the mixed layer are those associated with entrainment of deep water and surface buoyancy fluxes. The power required to entrain deep water into the mixed layer was obtained as

$${\mathit{P}}_{\mathrm{E}}=\mathit{w}({\mathit{d}}_{\text{mix}}\mathrm{\Delta }\mathit{b}+{\mathit{c}}_{\mathit{m}}^2)$$ (3)

where w is the mixed-layer entrainment rate (in meters per second, m s⁻¹), d_mix is the mixed-layer depth (in meters, m), and c_m is a parameter describing the unsteadiness in the budget of turbulent kinetic energy and equals 0.03 m s⁻¹ (76). Δb is the difference in the buoyancy across the mixed-layer base, here expressed as

$$\mathrm{\Delta }\mathit{b}=\mathit{g}\mathrm{\alpha }({\mathit{T}}_{\text{mix}}-{\mathit{T}}_{\mathit{b}})-\mathit{g}\mathrm{\beta }({\mathit{S}}_{\text{mix}}-{\mathit{S}}_{\mathit{b}})$$ (4)

where T_mix (T_b) and S_mix (S_b) are the temperature and salinity, respectively, in (directly below) the mixed layer, g is the gravitational acceleration (9.81 m s⁻²), α is the thermal expansion coefficient (4 × 10⁻⁵ K⁻¹), and β is the saline contraction coefficient (8 × 10⁻⁴ kg g⁻¹).

We assumed that salt flux dominates the surface buoyancy flux. This is based on the fact that the mixed-layer temperature during winter is approximately constant at the surface freezing point (75), and therefore, the influence of surface heat loss (used to form sea ice) on the buoyancy budget is minimal. The power input per unit density (in cubic meters per cubic second, m³ s⁻³) to the mixed layer from buoyancy flux was calculated as

$${\mathit{P}}_{\mathrm{S}}={\mathit{c}}_1{\mathit{d}}_{\text{mix}}\mathit{g}\mathrm{\beta }{\mathit{F}}_{\mathrm{S}}$$ (5)

where c₁ is a coefficient describing the frictional energy dissipation of convective mixing and equals 0.83 when the mixed layer is deepening (77), and F_S is the salt flux (in grams per kilogram meters per second, g kg⁻¹ m s⁻¹) into the mixed layer. For reasons mentioned above, F_S was estimated using satellite-derived sea ice production from ERA-Interim data (24), whose uncertainty is ~25% (37). Estimates of sea ice production in Antarctic polynyas using this technique have been found to be consistent within 20 to 25% of estimates derived from in situ oceanographic observations (24). Following Cavalieri and Martin (78), the flux of salt ${\mathit{F}}_{\mathrm{S}}^{\prime }$ in units of kilograms per square meter per second (kg m⁻² s⁻¹)is given by ${\mathit{F}}_{\mathrm{S}}^{\prime }=0.69\times {10}^{-3}{\mathrm{\rho }}_{\mathrm{i}}\mathit{V}{\mathit{S}}_{\mathrm{O}}$, where V is the rate of sea ice growth (in meters per second, m s⁻¹), ρ_i is the density of sea ice (920 kg m⁻³), and S_O is the salinity at the ocean surface assumed to be 34 g kg⁻¹. This formula indicates that 69% of salt is rejected back into the ocean during sea ice growth and implies a sea ice salinity of ~10.5 g kg⁻¹. This value represents the early stages of sea ice growth in coastal polynyas (79), as compared to the lower salinity (6.2 g kg⁻¹) used to calculate sea ice melt in Eq. 1, representative of older sea ice. The flux F_S into the mixed layer was then computed as ${\mathit{F}}_{\mathrm{S}}=\frac{1}{{\mathrm{\rho }}_{\mathit{w}}}(1000-{\mathit{S}}_{\text{mix}}){\mathit{F}}_{\mathrm{S}}^{\prime }$, where ρ_w is the density of seawater (1027 kg m⁻³) and 1000 g kg⁻¹ is the salinity of pure salt (48). Monthly mean salt fluxes averaged over the polynya were used as forcing to the model. The polynya was defined as the area where the annual sea ice production is higher than 3 m.

From the above relationship between salt flux and rate of sea ice growth, we found that sea ice has to grow by ~1.7 m to bring the salinity of the meteoric water that accumulates in the Dalton Polynya between March and September (1.05 m) from zero to WW values (~34.5 g kg⁻¹). The area-averaged cumulative sea ice production in the Dalton Polynya during the same period is 4.8 m, implying that ~35% of sea ice production is required to offset the injection of meteoric water into the water column. We included in the model of the Dalton Polynya the effect of meteoric water input by reducing the satellite-derived surface salt flux by 35%, implicitly assuming that the input was entirely distributed over the modeled mixed layer.

Using Eqs. 3 to 5, we obtained from energy and salt conservation that the temporal evolution of mixed-layer depth and salinity are given by

$$\{\begin{array}{c}\frac{\mathit{d}}{\mathit{d}\mathit{t}}{\mathit{d}}_{\text{mix}}=\frac{{\mathit{P}}_{\mathrm{S}}}{({\mathit{d}}_{\text{mix}}\mathrm{\Delta }\mathit{b}+{\mathit{c}}_{\mathit{m}}^2)}\\ \frac{\mathit{d}}{\mathit{d}\mathit{t}}{\mathit{S}}_{\text{mix}}=\frac{{\mathit{F}}_{\mathrm{S}}}{{\mathit{d}}_{\text{mix}}}+\frac{\mathit{w}}{{\mathit{d}}_{\text{mix}}}({\mathit{S}}_{\mathit{b}}-{\mathit{S}}_{\text{mix}})\end{array}$$ (6)

where $\mathit{w}=\frac{\mathit{d}({\mathit{d}}_{\text{mix}})}{\mathit{d}\mathit{t}}$. As discussed above, we assumed the mixed-layer temperature during months of sea ice formation to be constant at the surface freezing point (with reference salinities for the mixed layer of 34.4, 34.2, and 34.7 g kg⁻¹ for the Dalton, Amundsen, and Cape Darnley polynyas, respectively). Variability of the freezing point with changes in S_mix did not influence the output of the model, as confirmed by Martinson (75) by showing that the freezing point dependence on salinity affects the mixed-layer depth in the Southern Ocean by ~1%. (Note that we used a constant value of 34 g kg⁻¹ for the salinity at the ocean surface when we estimated the surface salt flux ${\mathit{F}}_{\mathrm{S}}^{\prime }$ (see above). Varying the ocean surface salinity by ±0.7 g kg⁻¹ in the estimate of the surface salt flux resulted in minimal changes of the modeling results (<10 m and <0.01 g kg⁻¹ of d_mix and S_mix, respectively, at the end of the model runs).

Equation 6 was integrated using a finite-difference second-order Runge-Kutta scheme, with a time step of 15 min and a vertical resolution of the ocean profile of 0.5 m. The model is not sensitive to time and vertical resolutions because using a time step of 1 day or a vertical resolution of 2 m results in negligible changes of the output. During mixed-layer deepening, salinity and temperature values were set to S_mix and to the surface freezing point above d_mix and kept constant below. Initial conditions were based on in situ observations at the end of the summer before the simulated winter in the Amundsen and Cape Darnley polynyas (figs. S2 and S3). In the Dalton Polynya, CTD profiles at the end of the summer before the simulated winter (that is, 2014) are not available. For this polynya, we used data collected by a profiling float between February and early March 2015 (fig. S1, C and D). We note that (i) the surface salinity in the float profiles is similar to that observed at the end of summer 2014 during the Nathaniel B. Palmer survey and that (ii) the properties of the WW and MCDW along with the depth of their interface in the float profiles are similar to those observed by the moorings in early March 2014 (fig. S1, C and D), implying that ocean conditions in 2014 and 2015 were similar. Furthermore, as shown below, the sensitivity of the model to small changes in properties of the initial ocean profiles is small compared to the uncertainty in estimates of sea ice production. This indicates that possible small changes of the initial conditions between 2014 and 2015 did not influence the output of the model.

Analysis of the wind curl over the Dalton Polynya using the ERA-Interim reanalysis (36) indicates that vertical velocities associated with Ekman dynamics are more than one order of magnitude smaller than velocities associated with buoyancy forcing. This is consistent with the fact that convective processes dominate in terms of mixed-layer deepening near the coast in Antarctica (47, 48). Therefore, we did not include Ekman vertical velocities in our model.

We ran several sensitivity tests in the Dalton Polynya varying one of the parameters in the initial conditions in each simulation. We varied the surface salinity between 33.15 and 33.3 g kg⁻¹ (based on the range of values measured during the Nathaniel B. Palmer survey in 2014; see fig. S1D), the bottom salinity/temperature between 34.65 and 34.8 g kg⁻¹/−0.5° and +0.5°C (based on the variability observed at the mooring locations), and the salinity at the base of the seasonal pycnocline between 34.3 and 34.4 g kg⁻¹ (to consider possible changes of the seasonal pycnocline between 2014 and 2015). We also varied the depth of the WW-MCDW interface between 300 and 400 m based on the variability observed at the mooring locations and the maximum depth of the profiles between 350 and 600 m to account for variability of the seafloor depth in the Dalton Polynya (7). All of the above tests were run for both simulations including and excluding meteoric water input. In all cases, the change in mixed-layer depth is less than 30 m, and the change in salinity is less than 0.03 g kg⁻¹ at the end of the model run. These changes are smaller than those associated with the uncertainty in the surface salt flux (see Fig. 3, A and B).

The model did not include diapycnal mixing because observations on the Antarctic continental shelf show that vertical fluxes in the pycnocline associated with diapycnal mixing are one (or more) order of magnitude smaller than winter surface fluxes (80). Petty et al. (47) include the effect of advection by restoring the ocean properties beneath the mixed layer to some reference values during spring and summer, when the mixed layer is retreating. Because we were not simulating the retreating period, we did not include any restoration of the ocean properties. We do note, however, that reducing the net surface salt flux due to input of meteoric water is a way of including the advection of freshwater. Our sensitivity tests in the Dalton Polynya indicate that MCDW variability does not substantially affect the mixed-layer evolution, suggesting that MCDW advection is not of primary importance. This is consistent with the fact that the mixed layer never reaches the core of the MCDW layer in the Dalton (and Amundsen) Polynya. At Cape Darnley Polynya, our simulation is also in good agreement with the observations, suggesting that wintertime MCDW advection has a small impact on DSW formation there.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/4/eaap9467/DC1

fig. S1. Dalton Polynya.

fig. S2. Amundsen Polynya.

fig. S3. Cape Darnley Polynya.

table S1. Moorings on the Sabrina Coast.

Reference (82)