Heritable stress response dynamics revealed by single-cell genealogy

Single yeast cells preserve a memory of their mothers’ dynamic response to stressful conditions.

Abstract

Cells often respond to environmental stimuli by activating specific transcription factors. Upon exposure to glucose limitation stress, it is known that yeast Saccharomyces cerevisiae cells dephosphorylate the general stress response factor Msn2, leading to its nuclear localization, which in turn activates the expression of many genes. However, the precise dynamics of Msn2 nucleocytoplasmic translocations and whether they are inherited over multiple generations in a stress-dependent manner are not well understood. Tracking Msn2 localization events in yeast lineages grown on a microfluidic chip, here we report how cells modulate the amplitude, duration, frequency, and dynamic pattern of the localization events in response to glucose limitation stress. Single yeast cells were found to modulate the amplitude and frequency of Msn2 nuclear localization, but not its duration. Moreover, the Msn2 localization frequency was epigenetically inherited in descendants of mother cells, leading to a decrease in cell-to-cell variation in localization frequency. An analysis of the time dynamic patterns of nuclear localizations between genealogically related cell pairs using an information theory approach found that the magnitude of pattern similarity increased with stress intensity and was strongly inherited by the descendant cells at the highest stress level. By dissecting how general stress response dynamics is contributed by different modulation schemes over long time scales, our work provides insight into which scheme evolution might have acted on to optimize fitness in stressful environments.

INTRODUCTION

In nature, cells are continuously exposed to unpredictable environmental changes, which can perturb their intracellular conditions required for maintaining optimal growth. In yeast Saccharomyces cerevisiae, stressful conditions can initiate a gene expression program, called the environmental stress response (ESR), that alters the expression of nearly 900 genes (1). Information about a wide variety of stress stimuli, including nutrient depletion, changes in osmolyte concentration and temperature, and oxidative agents, is transmitted through dedicated sensing pathways. Among such pathways are the cyclic adenosine monophosphate protein kinase A (cAMP-PKA), AMP-activated kinase (Snf1), target of rapamycin complex 1 (TORC1), and high-osmolarity mitogen-activated protein kinase A (HOG1 MAPK) pathways. These pathways ultimately converge in the activation of general stress response transcription factor Msn2 (2, 3). In the absence of stress, Msn2 is phosphorylated by upstream PKA and localizes to the cytoplasm of yeast cells. On application of stress stimulus, Msn2 is dephosphorylated and localizes to the nucleus (4, 5) where it binds to stress response elements (STREs) on the DNA and activates the expression of hundreds of genes (6, 7).

Lately, a growing number of experimental studies have revealed that the magnitude of stress stimulus can be encoded in the temporal dynamics of transcription factor localization. When subjected to calcium stress, the transcription factor Crz1 localizes to the yeast nucleus in persistent and irregular bursts. Calcium concentration was found to modulate the frequency of the Crz1 localization (8). It was proposed that in situations where downstream genes differ in their transcription factor binding affinities, controlling the fraction of time that Crz1 is active in the nucleus leads to proportional expression of those genes for all concentrations of calcium. Further, the type of stress has also been shown to be encoded in the localization dynamics of transcription factors (9). Glucose stress was found to cause duration modulation of the transient initial pulse of Msn2 and frequency modulation of subsequent sporadic bursts. In contrast, oxidative stress induced a sustained nuclear entry of Msn2, with its amplitude being modulated by stress intensity, while osmotic stress caused duration modulation of the initial Msn2 localization pulse. It was demonstrated that different dynamics of Msn2 could give rise to distinct downstream gene expression responses depending on the corresponding promoter architectures. Studies on other stress response pathways in bacteria (10–12) and mammalian cells (13–20) have shown that the activity of their respective transcription factors could be dynamically regulated by stress, suggesting that this mode of information transmission is a ubiquitous phenomenon in influencing gene expression.

Despite these studies, for a process as general as stress response, it is not well understood how clonal populations differ in their stress response dynamics and how single cells respond to stressful conditions over multiple generations. Isogenic cells are known to display variations in gene expression and in network activity levels (21, 22). Specifically, in the context of stress response, cells exhibit significant heterogeneity in localization dynamics of Msn2. This heterogeneity is believed to predominately arise from noise in upstream signaling networks, which is further amplified by the small number (~100) of Msn2 molecules per cell (23). Moreover, such phenotypic differences can be propagated to the descendants of an ancestor cell, a phenomenon referred to as epigenetic inheritance (24–27). Little is known about the fidelity of this process.

Using a custom-designed microfluidic platform coupled to a fluorescence microscope, we tracked families of single S. cerevisiae cells over multiple cell generations to investigate the role of glucose starvation stress on the dynamics of Msn2 nuclear localization. We found that glucose stress modulated the amplitude and frequency of the Msn2 localization bursts. Moreover, the frequency and pattern of the bursts were found to be inherited in the lineages of the ancestor cells, the strength and time scale of which were modulated by the intensity of the stress. Our results suggest that cells tune the degree of variability in the Msn2 burst frequency through epigenetic inheritance to potentially improve the fidelity of the responses in their lineages. Our approach for the investigation of the single-cell stress response dynamics is general and hence is applicable to other tractable organisms for studying any noisy network activity in them.

RESULTS

Measuring long-term Msn2 nuclear localization dynamics under glucose limitation stress

To gain quantitative insights on how the dynamics of Msn2 nuclear localization is influenced by glucose limitation stress over a long time scale, we monitored nuclear localization of Msn2 in single yeast cells using a strain (MC01) having Msn2 tagged to yellow fluorescent protein (YFP). This strain also had a synthetic promoter carrying six tandem STREs driving the cyan fluorescent protein (P_STRE-CFP). CFP expression from this promoter served as a reporter of the general Msn2-mediated gene expression (Fig. 1A). We grew cells in three different glucose concentrations (2, 0.25, and 0.1%) and used time-lapse microscopy to measure CFP expression levels. A concentration of 2% glucose represents the stress-free condition, while 0.1% glucose was expected to correspond to a high magnitude of stress. Indeed, the analysis of the single-cell CFP levels confirmed these expectations (Fig. 1B), leading to the determination of the three environments used in this study. To maintain healthy cell growth, we did not choose glucose concentrations lower than 0.1%.

Fig. 1. Strain background, choice of glucose limitation stress, experimental setup, and single-cell Msn2 localization trajectories.

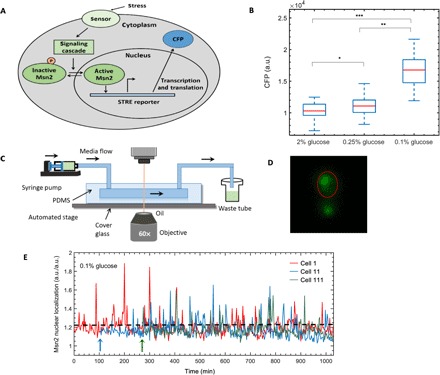
(A) Pictorial representation of Msn2 translocation and activation of a synthetic promoter driving CFP in response to stress. (B) Glucose stress concentrations to be applied in lineage experiments. CFP expression of cells from three different glucose concentrations was collected from microscopy experiments, and the boxplots show distribution of CFP from single cells for each glucose concentration. For each boxplot, red line denotes median or 50th percentile; bottom of the blue box denotes the lower quartile or 25th percentile; top of the blue box denotes the upper quartile or 75th percentile of the distribution. *, significant difference (P = 0.03) in CFP expression between 2% glucose and 0.25% glucose; **, significant difference (P = 1.6 × 10⁻¹⁴) in CFP expression between 0.25% glucose and 0.1% glucose; ***, significant difference (P = 9.3 × 10⁻¹⁷) in CFP expression between 2% glucose and 0.1% glucose. Numbers of cells used for analysis in 2, 0.25, and 0.1% glucose concentrations are 36, 28, and 30, respectively. (C) Schematic showing a typical experimental setup of a time-lapse movie. (D) Snapshot from a time-lapse movie of cells showing Msn2 nuclear localization in 0.1% glucose. Nuclear localization of Msn2 has been quantified by an image analysis algorithm, without using a nuclear marker (Supplementary Materials). (E) Msn2 nuclear localization trajectories of three representative cells in 0.1% glucose. Msn2 nuclear localization is a ratio of two quantities (mean Msn2 nuclear localization in nucleus and mean Msn2 localization in whole cell), each having arbitrary unit (a.u.). Hence, the single-cell Msn2 nuclear localization values in our study are unitless. Cell 11 and cell 111 are the daughter and granddaughter cells, respectively, of cell 1. Arrows denote the time of birth of a new cell. Dashed horizontal lines denote the threshold used to quantify nuclear localization burst of Msn2.

We tracked nuclear translocation dynamics of Msn2-YFP in ancestor yeast cells and their progenies for multiple generations using a microfluidic platform, which facilitated continuous long-term growth of cells under uniform media conditions. Each experiment started with a single ancestor cell trapped in a monolayer facilitated by an optimal height of the microfluidic chamber (fig. S1). With glucose media flowing into and out of the chamber at a constant rate, fluorescence and bright-field images of single cells were acquired every 2.5 min and analyzed in a genealogical manner as the cells grew and divided. In a typical movie lasting 15 to 18 hours, the starting mother cell underwent up to five to six cell divisions, leading to a monolayer colony of cells at the end of the movie (Fig. 1C and fig. S1). Due to glucose limitation stress, Msn2 localized to the nucleus (Fig. 1D) and shuttled between the cytoplasm and the nucleus, resulting in specific localization dynamics (9).

To quantify the Msn2 nuclear localization intensities in a cell, we developed an algorithm to estimate localization levels of Msn2 indirectly from the YFP pixel intensities in the whole cell without directly using a nuclear marker. This approach allowed us to minimize phototoxicity on cells and ensured that cells grew in a healthy fashion over the long time scales needed for lineage tracking (figs. S2 to S4 and tables S1 and S2). The algorithm we developed integrated information from both location and intensity of the brighter YFP pixels in the whole cell (figs. S5 to S8). For every cell with a measured cellular area (C in units of pixels), the corresponding nuclear area (N in units of pixels) was estimated based on our experimentally characterizing the relationship between nuclear-to-cellular area ratio as a function of the cellular area (fig. S6 and table S3). For each of the N pixels in the cell, 14 nearest-neighbor pixels were chosen, leading to the formation of N groups of 15 pixels. Next, the group with the highest mean YFP intensity and the lowest mean inter-pixel distances was selected. Nucleus was considered as a circular area, with its center located at the centroid of that particular group and with its diameter determined from the value of N. Finally, Msn2 localization of a single cell was defined as the ratio of the average YFP pixel intensity in the estimated nucleus and the average YFP pixel intensity in the whole cell. The algorithm performed well based on our validation using a nuclear marker (figs. S7 and S8). Moreover, its performance was much better than previous methods (8, 28) that estimated nuclear localization indirectly from the whole cell without using a nuclear marker (fig. S7, A and B), even in the presence of weak nuclear localization signals (fig. S7C).

Isogenic yeast cells exhibited markedly different Msn2 nuclear localization behavior over different periods of time, including cytoplasmic localization, nucleocytoplasmic oscillation, or continuous nuclear enrichment (Fig. 1E and fig. S9). To determine when a nuclear localization event occurred in a cell at a given time, single-cell trajectories of Msn2 nuclear localization intensities were thresholded at 1 SD above the mean of the localization traces obtained from cells grown in the 2% glucose environment. Our results were robust to the choice of the threshold level used for identifying the localization events (figs. S10 to S12 and table S4).

Measuring Msn2 nuclear localization in single yeast cells and their progenies

For each experiment performed in one of the three glucose concentrations, we quantified Msn2-YFP levels in a lineage-dependent manner until the end of the fourth generation (Fig. 2, A to C). The duration of each experiment was determined by the time taken by one ancestor cell to complete four generations. Cells were tracked from birth to the end of the experiment. The boundary of each cell was traced, and each cell is assigned a unique label corresponding to its genealogical position in the lineage tree. Since cells take more time to complete their cell cycle when stressed (fig. S3), the duration of a time-lapse movie varied between 15 and 18 hours, depending on the intensity of the stress applied to cells in that experiment. For each concentration of glucose, five independent experiments were performed, generating time series Msn2-YFP localization data for 239 individual cells in different positions of the lineage trees and 224 mother-daughter pairs.

Fig. 2. Msn2 localization in single cells collected in a lineage-dependent manner in different glucose concentrations.

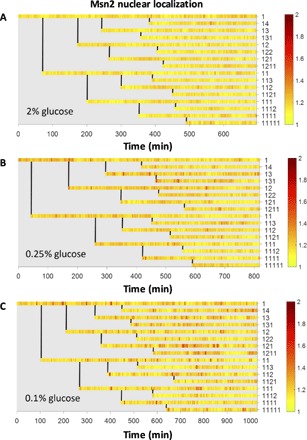
(A to C) Lineage maps of Msn2 localization from one experiment each in (A) 2% glucose, (B) 0.25% glucose, and (C) 0.1% glucose. Each row represents Msn2 localization of a single cell. Genealogical position of that cell in the family tree is labeled to the right of a row. Vertical lines denote the time at which a mother cell divides to form a daughter cell. Color bar shows the intensity of Msn2 localization signal.

Modulation of Msn2 nuclear localization across different stress levels

To understand how glucose limitation stress modulates the localization dynamics of Msn2, we first quantified the three dynamical features of Msn2 localization (amplitude, duration, and frequency; Fig. 3A) in each single cell in a movie and then averaged the results across cell populations grown in each stress condition. The amplitude of Msn2 localization was quantified by measuring the single-cell Msn2 localization signals that were above the threshold. The duration of Msn2 localization was quantified by measuring the average of all time intervals during which the single-cell Msn2 localization was above the threshold. Finally, to quantify the frequency of Msn2 nuclear localization in a cell, the total number of Msn2 nuclear localization events above the threshold was divided by the total time interval for which localization was measured for that cell.

Fig. 3. Modulation of Msn2 burst dynamics in population of cells.

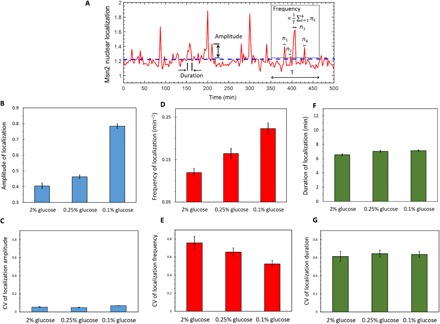
(A) Localization trajectory of a cell, showing how amplitude, frequency, and duration of Msn2 nuclear localization are quantified. Amplitude of Msn2 nuclear localization in a single cell is unitless. The dashed horizontal line denotes the threshold level above which there would be an Msn2 nuclear localization event. n_i denotes the number of above-the-threshold localization events. T denotes the length of time interval used here for the calculation of frequency. (B and C) Mean (B) and CV (C) of Msn2 burst amplitude in different glucose concentrations. (D and E) Mean (D) and CV (E) of Msn2 burst frequency in different glucose concentrations. (F and G) Mean (F) and CV (G) of Msn2 burst duration in different glucose concentrations. Error bars in (B), (D), and (F) represent SEM. Error bars in (C), (E), and (G) were obtained from bootstrapping.

Both amplitude and frequency of Msn2 nuclear localization were found to increase with increasing intensity of the glucose limitation stress (Fig. 3, B and D). On the other hand, the localization duration showed no significant change with stress (Fig. 3F). Throughout the experiments, individual cells grown in the same growth conditions exhibited significant variability in their Msn2 nuclear localization responses. To examine the influence of the glucose stress intensity on the extent of cell-to-cell variability, we analyzed the coefficient of variation (CV) of localization dynamics for each stress conditions (Fig. 3, C, E, and G). Localization amplitude variations were low (CV of ~5.4%) not only across the cells of each environment but also across the three environments. In contrast, localization frequency and duration displayed relatively higher variations. Moreover, localization frequency variations were found to display stress sensitivity, with the CV decreasing from ~75% in the 2% glucose condition to ~52% in the 0.1% glucose condition. We did not observe stress sensitivity for the CVs of localization duration across the three growth conditions.

Modulation of Msn2 nuclear localization dynamics in single cells over multiple generations

To elucidate how glucose limitation stress modulates Msn2 localization dynamics with respect to the number of generations, we measured the amplitude, frequency, and duration of Msn2 nuclear localization in single cells as a function of specific cell generations (Fig. 4). To avoid phototoxicity that would be caused by the visualization of a cytokinesis marker, we defined cell generation as the time interval between two consecutive S phases of a single cell, which was detectable as bud initiation from the bright-field images. We found that the average amplitude, frequency, or duration of localization did not change in a consistent way as a function of the generation numbers (Fig. 4, A to C, and table S5). The localization amplitude and frequency were the highest at the 0.1% glucose environment (Fig. 4, A and B, orange), while the localization duration was not as sensitive to the stress intensity (Fig. 4C). Therefore, we concluded that the stress-dependent amplitude and frequency modulation of Msn2 localization shown in Fig. 3 were present across multiple cell generations.

Fig. 4. Msn2 burst dynamics as a function of cell generation.

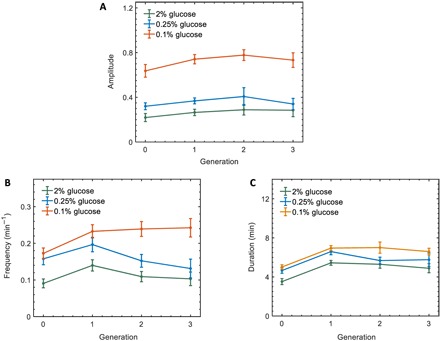
(A to C) Msn2 burst amplitude (A), frequency (B), and duration (C) as a function of cell generations in different glucose concentrations. Error bars represent SEM. One cell generation is defined as the time interval between the onset of two consecutive buds of a cell. Generation 0 refers to the time interval between the birth of a cell to the emergence of its first bud. Table S5 lists the P values resulting from comparing amplitude, frequency, and duration between 2 and 0.25% glucose concentrations as well as between 2 and 0.1% glucose concentrations across different cell generations.

Separately for each of the two localization features (amplitude and frequency), we next calculated correlation coefficients for each feature between their values measured in the first and second generation of a single cell. The frequency of Msn2 nuclear localization was found to be correlated between the generations in the same cell, with the level of correlation being the highest for the highest stress environment (Fig. 5). Unlike frequency, the amplitude of Msn2 localization was only weakly correlated across the generations, reflecting a low level of inheritance (fig. S13).

Fig. 5. Single-cell level correlations in Msn2 nuclear localization frequency between the first and second generations of a cell.

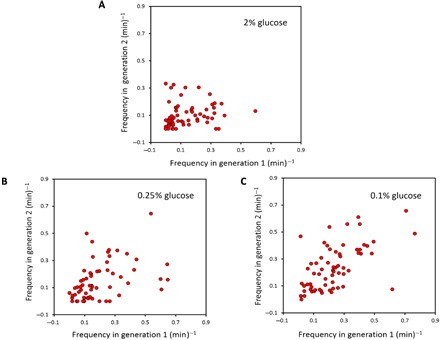
(A to C) Correlations emerge as stress intensity is increased, with the correlation coefficients equal to 0.43 (P = 4.2 × 10⁻⁴) and 0.59 (P = 2.25 × 10⁻⁷) in 0.25 and 0.1% glucose, respectively. No significant correlation was observed in the case of 2% glucose (P = 0.13). One generation duration for a cell was defined as the time interval between the start of two consecutive S phases in a cell.

Integrating the Msn2 signal over time in different stress conditions

We analyzed the Msn2 nuclear localization data by integrating the thresholded Msn2 signal in each cell over time. For each glucose concentration and at each time point, the integral of each cell’s Msn2 localization value was calculated since the cell’s birth. The integrated values were then averaged over all cells present at each time point. We saw that the average above-the-threshold signal followed an approximately linear increase as a function of time (fig. S14), indicating that the overall signaling dynamics does not change over time at the population level. Further, the slope of the linear increase behavior was dependent on the stress level. We interpreted this result as a reflection of some of our previous results (Figs. 3 and 4), which had shown that the average localization frequency and amplitude were the highest at the highest stress level.

Heritability of the Msn2 nuclear localization features

To further understand the variations in the Msn2 localization dynamics, we investigated whether the observed changes in stress response heterogeneity were influenced by potential heritability. To explore whether temporal characteristics of Msn2 nuclear localization patterns were inherited from ancestor cells to their descendants, we first focused on a subset of cell pairs defined by mother-daughter (M-D) relationships. Since cells were born at different times throughout the 15- to 18-hour experiments, we first aligned single cells in silico with respect to the time each cell was born. For each localization trajectory of each cell, we quantified the three dynamical features of Msn2 localization (amplitude, frequency, and duration) and computed a measure of normalized dissimilarity index for each feature between mother and daughter pairs. For a given localization feature f, the dissimilarity index between a mother cell (with f_M) and her daughter (with f_D) was quantified by d(f_M, f_D) = $\frac{|{\mathit{f}}_{\mathrm{M}}-{\mathit{f}}_{\mathrm{D}}|}{{\mathit{f}}_{\mathrm{M}}}$. The dissimilarity indexes for feature f were then averaged over all M-D pairs in the entire experiment, and the resulting value was then compared to the average dissimilarity index of a reference set of cell pairs (Fig. 6 and table S6). The reference set was defined as all pairs of cells in the lineage that were not linked by mother-daughter relationship or grandmother-granddaughter relationship. Similarity in the feature f between mother and daughter cells was calculated by differencing the average dissimilarity indexes of M-D pairs and reference pairs. For all tested glucose concentrations, neither burst amplitude nor duration showed any response similarity between M-D pairs. In contrast, mother and daughter cells showed more similar behavior in localization frequency compared to reference cell pairs, with the extent of similarity increasing as the stress intensity was increased.

Fig. 6. Heritability of localization features of Msn2.

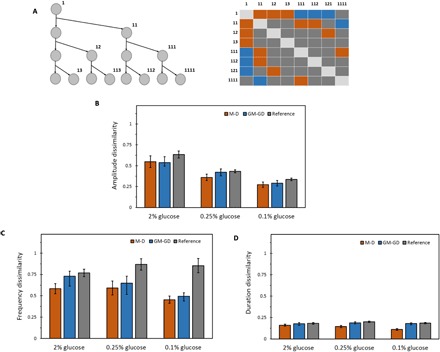
(A) Left: Example of a lineage tree to the third generation. Three generations down, starting from the ancestor cell, give rise to eight cells in different genealogical positions of the tree. Right: All the M-D cell pairs (orange boxes), GM-GD cell pairs (blue boxes), and reference cell pairs (gray boxes) that can be obtained from the lineage tree of three generations. Boxes arranged diagonally do not correspond to pairs with unique cell labels, and hence do not belong to either of the three categories. (B) Normalized dissimilarity index of Msn2 burst amplitude between M-D, GM-GD, and reference cell pairs for each glucose concentration. (C) Normalized dissimilarity index of Msn2 burst frequency between M-D, GM-GD, and reference cell pairs for each glucose concentration. (D) Normalized dissimilarity index of Msn2 burst duration between M-D, GM-GD, and reference cell pairs for each glucose concentration. Error bars represent SEM. Table S6A gives a list of all the P values obtained by comparing amplitude, frequency, and duration of Msn2 localization between M-D pairs, GM-GD pairs, and reference pairs for each glucose concentration.

Next, we addressed how long similarities in localization features persisted and hence assessed the time scale of inheritance. We quantified the similarities in localization amplitude, frequency, and duration between grandmother and granddaughter (GM-GD) cell pairs using an approach similar to the one described above: The dissimilarity index for feature f between a grandmother cell (with f_GM) and a granddaughter cell (with f_GD) pair was quantified by d(f_GM, f_GD) = $\frac{|{\mathit{f}}_{\text{GM}}-{\mathit{f}}_{\text{GD}}|}{{\mathit{f}}_{\text{GM}}}$. The similarity in Msn2 localization frequency still stably persisted in the granddaughter cells, though with a decreased magnitude. Therefore, measuring Msn2 localization dynamics in single cells with regard to genealogy and the subsequent analyses revealed that the apparently random localization events in ancestor cells could be epigenetically inherited by their descendants.

To eliminate the possibility of measured localization features being influenced by spatial distance between cell pairs, we compared the localization features of reference cell pairs that are located far from each other with those of reference cell pairs that are located near each other and found no significant difference in localization features (fig. S15 and table S7).

Inheritance of dynamical patterns of Msn2 nuclear localization

In the previous section, we evaluated the inheritance of localization features between M-D and GM-GD pairs, where comparisons between cell pairs were performed using each response feature averaged across the entire trajectory of an individual cell. However, it is possible that a daughter cell initially correlated in its stress response with its mother for a period of time may become de-correlated over time due to, for example, stochastic nature of reactions involving low copy number of signaling molecules. In such a scenario, instead of using an average dissimilarity index value representing the entire trajectory of a cell, it would be more informative to perform a time-dependent analysis of the dissimilarity index that can capture the entire time dynamic pattern of dissimilarity between related cell pairs as a function of the chronological lifetime of cells. Therefore, to ensure that averaging the localization amplitudes over time in a cell (Fig. 6B) did not mask any potential amplitude similarity between M-D pairs, we compared Msn2 localization amplitudes between M-D pairs time dynamically (fig. S16). For this, we first ranked all the cells from the one carrying the lowest Msn2 amplitude localization to the highest, and then normalized the ranked values to the [0–1] range (lowest amplitude equal to 0 and the highest equal to 1). Next, we compared the absolute difference in rank between mother and daughter cell pairs to that of random cell pairs and still observed no difference in response between the two cases (29). Thus, this analysis further validated the lack of inheritance of Msn2 localization amplitude in lineages of cells.

Next, to quantify the degree of similarity in the time dynamic patterns of Msn2 localization events between related cell pairs, we performed a similarity analysis on the feature of Msn2 localization. Having already shown that glucose limitation stress increased the similarity of localization frequency between genealogically related cell pairs compared to the unrelated pairs, we next wanted to understand how likely they were to also burst or exhibit Msn2 localization spikes in a more synchronous manner. For this, we quantified the similarity in spike pattern of Msn2 localization between related cell pairs using a conceptual framework based on information theory (30). We used mutual information as a metric representing a similarity index for spike patterns between the three categories of cell pairs: M-D, GM-GD, and GGM-GGD.

Specifically, for a given M-D cell pair z, we defined X_z as a random variable representing the occurrence of spike for the daughter cell at any given time. The entropy H(X_z) is then a measure of uncertainty associated with the daughter spike train. Analogously, Y_z was defined as a random variable representing the spike occurrence for the mother cell at any time. The conditional entropy H(X_z|Y_z) then represented the residual uncertainty in the daughter spike train X_z given the knowledge of the mother spike train Y_z. In other words, the conditional entropy H(X_z|Y_z) between a mother and its daughter is a measure of the likelihood of the daughter to spike in a small time window around the instant its mother also exhibited a localization spike. As the small time window, we chose the smallest possible window marked by ±1 time points (Materials and Methods). Finally, the similarity index between the mother-daughter pair was defined as the mutual information I_z = H(X_z) − H(X_z|Y_z). The mutual information metric provided a quantitative estimate for how much information about the spike pattern of a daughter cell can be inferred from the observation of its mother’s spike pattern.

In a probability distribution framework, ${\mathit{I}}_{\mathit{z}}={\sum }_{\mathit{x}}{\sum }_{\mathit{y}}\mathit{p}(\mathit{x},\mathit{y}) \text{log}\left(\frac{\mathit{p}(\mathit{x},\mathit{y})}{\mathit{p}(\mathit{x})\mathit{p}(\mathit{y})}\right)$, where p(y) and p(x) are the marginal probability distributions of Msn2 spikes for mother and daughter cell, respectively, and p(x, y) is their joint probability distribution. Thus, for any given M-D pair, the mutual information metric quantifies the Kullback-Leibler (K-L) distance, which is a measure of the probability that the mother and daughter cell spike simultaneously, compared to the probability that the mother and daughter cell spike independent of each other. Therefore, we computed the mutual information or similarity I_z between all M-D pairs as I = ∑_zp(z) I_z, where p(z) denotes the probability of spike occurrence for an M-D pair z. Since mutual information lies in the range of 0 to maximum of the individual entropies [that is, max(H(X_z), H(Y_z))] (30), we normalized the similarity index I by max(H(X_z), H(Y_z)) to bring it to the range of [0,1]. This analysis revealed that, when related cell pairs exhibited Msn2 nuclear localization spikes, they did so in a synchronous manner (Fig. 7, fig. S17, and table S8). Higher stress levels induced stronger similarities between mother and daughter pairs. For the GM-GD and GGM-GGD (great grandmother–great granddaughter) pairs, although the strength of spike pattern similarity was low in the 0.25% glucose environment, the localization spike patterns were found to be inherited from mother to great-granddaughter cells in the 0.1% glucose environment.

Fig. 7. Inheritance of dynamical patterns of Msn2 localization.

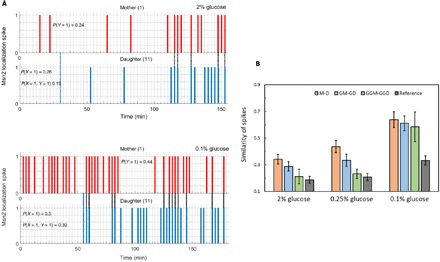
(A) Pattern of Msn2 localization spikes between a mother and daughter cell in 2% glucose (top) and 0.1% glucose (bottom). Dashed blue lines denote the time at which the mother cell divides. Dashed black lines denote simultaneous localization spike events between the mother and daughter. P(Y) and P(X) quantifies the probability of exhibiting an Msn2 localization spike, following the birth of the daughter, in a mother cell and daughter cell, respectively. P(X,Y) quantifies the probability that the mother and daughter cell pair shows Msn2 localization spikes simultaneously. (B) Similarity in pattern of Msn2 localization spikes in M-D, GM-GD, GGM-GGD, and reference cell pairs for different glucose concentrations. Here, reference cell pairs are all pairs of cells that are not linked by mother-daughter, mother-granddaughter, or mother–great granddaughter relationships. The metric used to compute the abovementioned similarity provides a quantitative measure of how often mother and daughter exhibit synchronous occurrence of spikes. Error bars were obtained from bootstrapping. Table S8A gives a list of all P values obtained by comparing similarity of Msn2 spikes between M-D, GM-GD, GGM-GGD, and reference pairs for each glucose concentration.

Using a rolling time-windows approach, we also looked into how the similarity of spikes (Fig. 7B) changed as a function of time for the mother-daughter pairs (fig. S17). As expected, we saw a decreasing trend of spike similarity and the dynamic trend was the most obvious for the highest stress condition (0.1% glucose). We also saw fluctuations due to noise; however, when the absolute value of the similarity level was high enough (as in the case of 0.1% glucose), the decreasing trend was detectable despite the counteracting effects of noise.

Thus, our results indicate that glucose limitation stress increases not only the magnitude of similarity in spike patterns but also the extent to which they persist in progenies of ancestor cells. We note that our findings about how individual cells modulate their localization spike pattern in a partially synchronous fashion (Fig. 7) may provide an explanation for why an overall reduction was observed in the CV of the localization frequencies with increasing stress intensity (Fig. 3E).

What might be the mechanism behind the spike pattern similarity across the progenies of ancestor cells? Inheritance of cellular phenotypes has previously been observed in different biological contexts (31, 32). Specific signaling network topologies can facilitate mechanisms through which phenotypic variations are altered with effects on propagation of phenotypes over multiple cell divisions. For instance, removal of phosphatase Msg5, which is involved in a negative feedback loop in the MAPK cascade, caused increased population variability and decreased mother-daughter correlations (31). As another example, in an engineered galactose utilization network where cells switch between OFF and ON expression states, pairs of closely related cells were found to switch in near synchrony even after several generations since the cells’ physical separation (32). Using a model, these results were explainable by burst-like fluctuations in the levels of a regulatory protein of the galactose network. In our system, Msn2 localizes to the cytoplasm through phosphorylation by upstream PKA. The similarity of spike patterns in progenies is attributable to the PKA activity transferred between mother and daughter cells and/or chromatin configurations being passed on to progenies during cell division. Future studies will demonstrate whether or not nongenetic inheritance of network activity levels is a common phenomenon and will elucidate the specific mechanism(s) through which the inheritance could be facilitated in various networks.

Correlation analysis between Msn2 localization features and cellular growth rate

We next measured the degree of correlation between the frequency or amplitude of Msn2 nuclear localization and the single-cell growth rate. Growth rate of each single cell was calculated based on its doubling times across the movie. Similarly, the Msn2 localization frequency and amplitude for the same cell were separately calculated and averaged across the movie. Next, cells were binned with respect to their growth rates, and correlations between growth rates and frequency or amplitude for each bin were calculated (fig. S18). We saw that the Msn2 localization frequency was correlated with growth rate in stressful environments [with the correlation coefficients equal to 0.829 (P < 0.05) and 0.861 (P < 0.05), in 0.25 and 0.1% glucose, respectively], while no significant correlation was observed between localization amplitude and growth rate. Despite seeing a high degree of correlation between the Msn2 localization frequency and growth rate, we did not observe a strong linear relationship between the two, as reflected by non-steep slopes of the linear relationships shown in fig. S18A.

Measuring Msn2-regulated promoter activity in single yeast cells

To understand the physiological consequences of the Msn2 nuclear localization dynamics at the gene expression level, we measured the activity of an Msn2-regulated synthetic promoter driving CFP every 60 min together with the YFP and bright-field images captured in the same cells every 2.5 min. Cells exhibited heterogeneous CFP expression over time, with the overall magnitude of the expression increasing with increased glucose limitation stress (Fig. 8A). Next, we wanted to assess how the three different dynamical features of the Msn2 nuclear localization contributed to the resulting gene expression behavior. For this, we first sectioned each cell’s Msn2 localization trajectory into windows of 60 min (as the frequency of CFP snapshots was every 60 min) and calculated the average Msn2 localization amplitude, duration, and frequency for each window. Using these measured values, we then applied a regression analysis method called Lasso (least absolute shrinkage and selection operator) to obtain a quantitative estimate of the contribution (1 corresponding to 100% contribution) of each dynamical feature of the Msn2 localization signal on the measured CFP levels (Supplementary Materials). Results from this analysis (Fig. 8B and fig. S19) supported our previous conclusions in terms of the relative “importance” of the three Msn2 nuclear localization features. The amplitude and frequency of the Msn2 localization signal were the main contributors to gene expression activation in the presence of stress (0.1 and 0.25% glucose). This result was robust to the choice of threshold used for quantifying Msn2 localization events (fig. S20). Regarding the analysis of data obtained from the 2% glucose environment, the low signal levels and the noise prevented a faithful Lasso analysis on the data; therefore, we excluded the 2% glucose environment from this analysis.

Fig. 8. Genealogical gene expression dynamics in single cells and a quantitative model linking Msn2 nuclear localization to downstream gene expression.

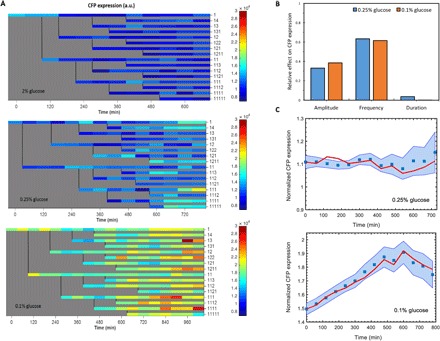
(A)Heat map of CFP expression in single cells collected in a lineage-dependent manner from one experiment in 2% glucose (top), 0.25% glucose (middle), and 0.1% glucose (bottom). Each row represents CFP expression of a single cell. Genealogical position of a cell in the family tree is labeled to the right of a row. Color bar shows the intensity of CFP signal (a.u.). (B) Quantification of relative contribution of the three different Msn2 localization features on CFP expression using Lasso. Amplitude and frequency of Msn2 nuclear localization were found to be the major features affecting CFP expression. (C) Prediction results for CFP expression for 0.25% (top) and 0.1% (bottom) glucose conditions using a linear state-space model. CFP levels were measured in single cells at every 60 min and normalized by the average CFP expression obtained from all cells grown in the 2% glucose condition. Blue square at a given time point represents the average CFP expression across all cells at that time point. Blue shaded area denotes the SEM (n = 8 to 67) calculated from all cells at each time point and extended between 60-min intervals as guide to the eye. The red points denote the CFP expression predicted by the model (at each 60 min) and averaged for all cells at that time point (red lines connecting red points during the 60-min intervals are guide to the eye). Model identification and prediction is discussed in more detail in the Supplementary Materials.

To assess if the experimental measurements of Msn2 nuclear localization amplitude and frequency can predict the transcriptional activity measured from the P_STRE-CFP construct, we used a linear state-space model, which represents the dynamics of CFP expression using a first-order linear system (Supplementary Materials). Training the model with our data and using it for predictions, we showed that the experimental CFP expression trajectories can be explained by a linear relationship between Msn2 nuclear localization amplitude, localization frequency, and a noise term representing noise in gene expression (Fig. 8C, figs. S21 to S24, and table S9). In the high stress environment we set up (0.1% glucose), the phenotypic consequence of Msn2 nuclear localization was an approximately linear increase in the average CFP expression followed by a saturation regime (Fig. 8C, bottom panel), while in the 0.25% glucose environment we observed an approximately flat CFP trend followed by a slight increase in CFP at later time points (Fig. 8C, top panel). The relatively higher CFP expression observed in the 0.1% glucose environment is a reflection of the higher Msn2 nuclear localization frequency and amplitude measured in this environment (Figs. 3 and 4). While the frequency and amplitude of Msn2 nuclear localization events observed in the 0.25% glucose environment (Figs. 2 to 4) were not as high as the ones observed in the 0.1% glucose environment, the events still were more frequent than the ones observed in the 2% glucose environment. The relatively flat CFP expression trend we measured in the 0.25% glucose environment (Fig. 8C) indicates that the effect of the PKA signaling on downstream gene expression is operating near the basal regime, if not truly in the basal regime due to the presence of the increasing CFP levels at later time points (Fig. 8C, top panel). We interpret the sporadic Msn2 nuclear localization measured even in the 2% glucose environment as a reflection of the stochasticity inherent in the cascade of molecular interactions in the PKA system.

DISCUSSION

Performing extended measurements on dynamical systems, as opposed to observing them for shorter time periods, often provides more comprehensive understanding of system behavior. For example, following Msn2 nuclear localization dynamics over a shorter time period of approximately one cell generation, a previous study (9) has found that yeast cells responded to glucose limitation stress by displaying frequency modulation followed by a transient duration modulation. Here, by following longer-term dynamics of Msn2 localization in response to glucose limitation stress, we found that cells modulate both the frequency and amplitude of the Msn2 nuclear localization. We also showed that Msn2 localization frequency was epigenetically inherited in progenies, while localization amplitude and duration did not display inheritance. Between our work and the previous study (9), in addition to the differences in time periods and the number of cell generations followed, our using a new localization metric to determine Msn2 nuclear localization events might also have contributed to the differences in results related to the Msn2 localization amplitude and duration.

Despite the simple nature of the previous localization metrics [for example, averaging the top 10 or 15 brightest pixel intensities in a cell (8, 28)] commonly used to estimate Msn2 nuclear localization intensity without using a nuclear marker, our results show that such metrics can give rise to large errors in estimating the true Msn2 nuclear localization intensity in a cell. A new nuclear marker–free method we introduced and validated in this study significantly increased the accuracy of localization estimations compared to a previously used metric (even for weak nuclear localization signals).

Here, the need to take frequent YFP images (every 2.5 min) and CFP images (every 60 min) throughout the entire durations of the experiments led to increases in cell doubling times. For each of the three glucose conditions, microscopically measured doubling times were roughly 40 min longer compared to the doubling times measured from batch culture experiments performed in a shaker-incubator (tables S1 and S2). While it is hard to estimate the level of phototoxicity based on doubling time extensions alone, we acknowledge that the cells likely experienced phototoxicity under the microscope, the level of which was possibly the same across the three glucose conditions due to the observed similarity in the extent of doubling time increase.

When information from external stimuli is transmitted through a regulatory cascade, genetic noise can cause information loss. Unless cells use strategies to surmount such challenges, the loss of information could lead to suboptimal decision-making by the cell (33–36). Potentially reflecting an evolutionary optimization strategy, we found that the Msn2 nuclear localization frequency (the only epigenetically inherited phenotype) displayed stress-dependent variability. In other words, the CV decreased with increasing stress levels. This can be considered as a beneficial strategy as more cells, and their descendants, would show high-fidelity localization-frequency response in harsh environments. Further, stressful environments are also known to invoke large-scale changes in transcriptional responses as well as in the activity of chromatin remodeling proteins in cells (37, 38). Our work showed that mother and daughter cells exhibit similar pattern of Msn2 localization spikes. If these spikes are propagated downstream to activate gene expression, it may be possible that the target promoters of mother and daughter cells could also be activated in a synchronous manner. Inheritance of the stress-responsive phenotypes may allow cells to adapt faster compared to the responses orchestrated by genetic changes. Investigation of stress response dynamics in single cells and their progenies over long time scales thus provides a rich spectrum of information, helping us understand cross-generational response strategies cells implement to better cope with environmental uncertainties.

MATERIALS AND METHODS

Strain construction

All experiments in this study were performed using a yeast strain (which we named MC01) constructed for a previous study (9) and provided to us by the O’Shea Laboratory. The strain was constructed from an ADE⁺ strain in W303 genetic background (MAT a trp1 leu2 ura3 his3 can1 GAL⁺ psi⁺), using standard methods for growth, transformation, and DNA manipulation of yeast. Msn2 was tagged with yECitrine (39) by polymerase chain reaction amplifying yECitrine::HIS3MX fragment integrated in the C terminus of Msn2 by homologous recombination at the native locus. As a reporter for gene expression, a synthetic promoter containing six tandem STREs (CAAGGGG) and 218 base pairs of CYC1 controlled expression of yECFP (39). Msn4, the partially redundant homolog of Msn2, was deleted from the strain. The C terminus of Nh6pa, a nuclear protein, was tagged with mRFP (monomeric red fluorescent protein) (40) to mark the nucleus. We did not image the nuclear marker in the strain MC01 for any lineage-based time-lapse experiment. The nuclear marker in this strain was used only in figs. S5 to S8 and S10, for the purpose of validating the accuracy of our algorithm in estimating nuclear localization of Msn2 from whole cell.

Time-lapse microscopy experiments using a microfluidic platform

All single-cell measurements were made by combining microfluidics with time-lapse fluorescence microscopy movies on strain MC01. A customized microfluidic chip of height 4 μm was made using standard techniques of plasma etching followed by replica molding with polydimethylsiloxane (PDMS). Yeast cells were grown overnight in a shaking incubator at 30°C for 18 hours in either 2, 0.25, or 0.1% glucose, depending on the magnitude of stress to be applied, to a final OD_600nm (optical density at 600 nm) of 0.1. Exponentially growing cells were loaded into the microfluidic chip, already pretreated with a solution of concanavalin A, CaCl₂, and MnCl₂. Constant media flow was maintained throughout the length of an experiment. The microfluidic chip was mounted on the stage of a Nikon inverted microscope, with bright-field and YFP images being acquired every 2.5 min using a 60× oil immersion objective. Full details of experimental protocol followed to perform a time-lapse movie using the microfluidic chip are given in the Supplementary Materials.

Image analysis

The boundary of each cell was first traced, and assigned with a unique ID, using Nikon Elements software. For measurement of Msn2 localization, a three-image z-stack of ±1.4 μm around the focal plane in the YFP channel was combined using maximum intensity projection (Max IP) of the three z planes. The Max IP images were then fed to a custom-written image analysis algorithm using MATLAB, which estimated the average nuclear intensity of Msn2 from the whole cell. Msn2 localization in a cell was defined as the average intensity of YFP pixels in the estimated nucleus divided by the average intensity of YFP pixels in the whole cell. CFP images were acquired every 60 min only at the focal plane (a single z plane), and the average CFP pixel intensity across the whole cell area was quantified. Full details of image analysis are given in the Supplementary Materials. Msn2 localization time series for every cell was thresholded at 1 SD of the mean of the localization traces obtained for cells induced with 2% glucose. Five replicates of 2% glucose experiments were used for determination of this threshold. Except for fig. S2, all figures throughout this study included analysis from data pooled from five independent experiments for each glucose concentration. For fig. S2, we first analyzed each of the five experiments’ data separately and calculated the associated growth rate, followed by averaging the resulting growth rates across five experiments.

The birth of the daughter cell is defined as the time when the mother-daughter separation occurs. The separation of a daughter from its mother was determined based on the narrowing of the bud neck and formation of a dark line between mother and daughter in a bright-field image (41). While bud-to-bud intervals were used as a representative of the cell cycle in the absence of a cytokinesis marker, we opted to start the first generation of each newborn cell from their birth. We used the approach described above to find the time point at which a daughter cell is called an independent cell (separated from its mother). Despite the relatively lower accuracy of this approach compared to the visible cue provided by bud initiation, it was still preferable compared to the alternative in which the first G₁ phase of a newborn cell would be omitted.

Time-dependent analysis of inheritance of Msn2 amplitude

Analysis of similarity in amplitude of Msn2 localization between M-D and GM-GD cell-pairs was adopted with modifications from Geva-Zatorsky et al. (29). In case of M-D pairs, analysis between any mother and daughter cell pair was performed relative to the birth of the daughter cell. This means that for the mother cell’s trajectory, we focused only on the time interval between the time at which the daughter cell septated from its mother cell and the end of the experiment. Let this be denoted by t_M. For the corresponding daughter cell, the time interval of interest is the entire time trajectory that is simply the time interval between its birth and end of experiment, and denoted by t_D. In the case of GM-GD pairs, we focus only on an interval of time between the birth of the granddaughter and the time at which the experiment ends (t_GM). For the granddaughter cell, it is the entire time trajectory beginning from its birth to end (t_GD). For a given M-D (or a given GM-GD) cell pair p, both cell’s time series, t_M (or t_GM) and t_D (or t_GD), were first ranked in ascending order of Msn2 localization and then normalized by the highest value of Msn2 localization to bring each ranked time series data in a range of [0,1]. At each time point, the absolute difference in normalized rank value between the mother (or grandmother) and daughter (or granddaughter) was calculated to generate another time series [D_p(t)] representing a measure of dissimilarity between that M-D pair p over time. D_p(t), obtained from every M-D (or GM-GD) pair, was then averaged over all such pairs. This quantified how dissimilar M-D (or GM-GD) pairs were on average over time. The analysis method when applied to random pair of cells, chosen without any regard to lineage relationships, on average and at any time gave an absolute difference in normalized rank approximately equal to 0.35.

Time-dependent analysis of inheritance of Msn2 frequency

Briefly, mutual information between two random variables measures the amount of information that one random variable contains about the other. The concept of this is intricately tied to the notion of entropy that measures the amount of uncertainty of a probability distribution, as well as to the concept of relative entropy that measures the distance between two probability distributions. The entropy H(X) of a discrete random variable X with probability mass function p(x) is defined by H(X) = −∑_xp(x)log(p(x)). The relative entropy or the K-L distance between two probability mass functions p(x) and q(x) is defined as $\mathit{D}(\mathit{p}||\mathit{q})={\sum }_{\mathit{x}}\mathit{p}(\mathit{x}) \text{log}\frac{\mathit{p}(\mathit{x})}{\mathit{q}(\mathit{x})}$. The mutual information I (X; Y) between two random variables X and Y is then defined as the amount of reduction in entropy of X (or Y), if Y (or X) is known. Mathematically, it is the K-L distance between the joint probability distribution p(x, y) and the product of the marginal distributions p(x) and p(y) and given as $\mathit{I}(\mathit{X};\mathit{Y})={\sum }_{\mathit{x}}{\sum }_{\mathit{y}}\mathit{p}(\mathit{x},\mathit{y}) \text{log}\left(\frac{\mathit{p}(\mathit{x},\mathit{y})}{\mathit{p}(\mathit{x})\mathit{p}(\mathit{y})}\right)$. From the above equation, it is possible to deduce that mutual information I (X; Y) is the difference between entropy of X and the entropy of X conditioned on Y: I (X; Y) = H(X) – H(X|Y). Thus, by measuring the reduction in uncertainty of a random variable X due to the knowledge of another random variable Y, mutual information allows quantification of mutual dependence and hence the similarity between two random variables (30).

Specifically in this context, let Z be a random variable denoting an M-D pair, that is, $\mathit{Z}\in \{1,2, ..,\mathit{n}\};\mathit{p}(\mathit{z})=\frac{1}{\mathit{n}}$, where n is the number of M-D pairs. When Z = z, let X_z be a random variable denoting the occurrence of a spike at any time point in the daughter, that is, X_z ∈ {0,1}. Similarly, let Y_z be a random variable denoting the occurrence of a spike at any time point in the mother, that is, Y_z ∈ {0,1}. p(x) or p(y) was calculated by counting the number of times the localization value of the daughter or mother cell was above the threshold and then dividing by the total number of time points for which that cell was observed. Similarity I_z for cell pair z was then calculated as ${\mathit{I}}_{\mathit{z}}={\sum }_{\mathit{x}}{\sum }_{\mathit{y}}\mathit{p}(\mathit{x},\mathit{y}) \text{log}\left(\frac{\mathit{p}(\mathit{x},\mathit{y})}{\mathit{p}(\mathit{x})\mathit{p}(\mathit{y})}\right)$. p(x, y) was quantified by calculating the probability that a mother and daughter cell spike simultaneously within a very small time window spanning three time points. Similarity I was then calculated as the expected value of the similarity for all M-D pairs I = ∑_zp(z) I_z. Similarity I was then normalized by its upper bound (30) calculated from max(H(X_z), H(Y_z)). All analyses on M-D time traces were performed by focusing on the time interval following cell division to until the end of the experiment. The same analysis method was applied to obtain the similarity in spike patterns between GM-GD and GGM-GGD cell pairs.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/4/e1701775/DC1

Supplementary Materials and Methods

fig. S1. Design of a microfluidic platform and a typical experimental setup.

fig. S2. Growth of cell populations for cells grown in 2, 0.25, and 0.1% glucose.

fig. S3. Cumulative distribution function of budding intervals measured from individual cells grown in 2, 0.25, and 0.1% glucose.

fig. S4. Budding interval durations of spatially separate cells grown in 2, 0.25, and 0.1% glucose.

fig. S5. Example of erroneous approximation of Msn2 nuclear localization intensity.

fig. S6. Ratio of nuclear to cellular area as a function of the cell area.

fig. S7. Performance of algorithm in estimation of nuclear localization of Msn2 from whole cell, in the absence of a nuclear marker.

fig. S8. Estimation of nuclear localization of Msn2 using the algorithm is not sensitive to the variability in ratio of nuclear to cellular area at the single-cell level.

fig. S9. No photobleaching or significant drop in Msn2 signal was observed over the course of an experiment.

fig. S10. Proportion of cells having localization values below a given threshold k as a function of different thresholds k.

fig. S11. Quantification of Msn2 localization dynamics is robust to the choice of threshold used for localization quantification.

fig. S12. Heritability analysis of different localization features of Msn2 and analysis of inheritance of dynamical patterns of Msn2 localization is not sensitive to the choice of threshold used for Msn2 localization quantification.

fig. S13. Lack of correlation in localization amplitude between the first and second generation of the same cell.

fig. S14. Integral of Msn2 nuclear localization in different stress conditions.

fig. S15. Dissimilarity analysis of different localization features of Msn2 is not affected by spatial proximity between cell pairs.

fig. S16. Time dependent analysis of inheritance of Msn2 amplitude.

fig. S17. Similarity of Msn2 localization spikes as a function of time for M-D cell pairs in different glucose concentrations (related to Fig. 7B).

fig. S18. Correlation analysis between Msn2 localization features and cellular growth rate.

fig. S19. Mean squared error for Lasso solution as a function of different values of regularization or shrinkage parameter.

fig. S20. Lasso analysis is not sensitive to the choice of threshold used for Msn2 nuclear localization quantification.

fig. S21. System and measurement noise for different stress environments.

fig. S22. Block diagram of system identification and prediction steps.

fig. S23. Predicting CFP expression levels using cross-validation.

fig. S24. Sample polynomial fits for single-cell CFP trajectories.

table S1. Population doubling times of cells in different glucose concentrations obtained from fig. S2 (A to C).

table S2. Population doubling times calculated from OD₆₀₀ measurements of cells grown in batch, using a shaker-incubator.

table S3. Values of parameters obtained from fitting data in fig. S6 to a sigmoidal function.

table S4. The P values comparing duration of Msn2 nuclear localization between 2 and 0.25% glucose, as well as 2 and 0.1% glucose across all threshold levels.

table S5. The P values comparing amplitude (A), frequency (B), and duration (C) of Msn2 nuclear localization between 2 and 0.25% glucose, as well as 2 and 0.1% glucose across different cell generations.

table S6. The P values obtained from Mann-Whitney U test.

table S7. The P values obtained from Mann-Whitney U test.

table S8. The P values obtained from Mann-Whitney U test.

table S9. Parameter values extracted from the linear state-space model’s application to the data obtained from 0.25 and 0.1% glucose experiments.

References (42–53)