Skip to main content
PMC home page
Plant Physiology logoLink to Plant Physiology
. 2000 Jul;123(3):1021–1028. doi: 10.1104/pp.123.3.1021

Increases in Water Potential Gradient Reduce Xylem Conductivity in Whole Plants. Evidence from a Low-Pressure Conductivity Method1

Tim J Brodribb 1,*, Robert S Hill 1
PMCID: PMC59065  PMID: 10889251

Abstract

A new method using hydrostatic suctions (less than 0.02 MPa) was used to measure whole-root conductivity (Kr) in saplings of two angiosperm pioneer trees (Eucalyptus regnans and Toona australis) and two rainforest conifers (Dacrycarpus dacrydioides and Nageia fleurii). The resultant Kr was combined with measurements of stem and leaf hydraulic conductivity to calculate whole-plant conductivity and to predict leaf water potential (Ψl) during transpiration. At normal soil temperatures there was good agreement between measured and predicted Ψl during transpiration in all species. Changes in the soil-to-leaf water potential gradient were produced by root chilling, and in three of the four species, changes in Ψl corresponded to those expected by the effect of increased water viscosity on Kr. In one species, however, root chilling produced severe plant wilting and a decline in Ψl significantly below the predicted value. In this species Ψl decreased to a value close to, or below, the Ψl at 50% xylem cavitation. It is concluded that decreased whole-plant conductivity in T. australis resulted from a decrease in xylem conductivity due to stress-induced cavitation.

At least one-half of the resistance to hydraulic flow through plant vascular systems occurs in the root. The largest of these resistances occurs in the radial pathway through the root as water crosses from the root surface, through the cortex, to the vascular tissue (Steudle and Peterson, 1998). Under non-stressed conditions the resistance of the axial pathway from root xylem to the leaves represents only a small fraction of the total resistance of the plant (Kramer, 1938; Frensch and Steudle, 1989; Tsuda and Tyree, 1997). However, studies of axial hydraulic flow through roots and stems have shown that the conductivity of the xylem is dynamic and that embolisms caused by cavitations in xylem conduits can result in very large reductions in axial conductivity, particularly under conditions of water stress (for review, see Tyree and Ewers, 1991).

Xylem embolism increases as a sigmoidal function of xylem water potential (or applied air pressure) (Pammenter and Vander Willigen, 1998), resulting in a rapid loss of conductivity as water potential decreases below a critical level. Although typically associated with water stress, varying degrees of xylem embolism have been observed in virtually all studies of field-grown plants, regardless of stress exposure (Hargrave et al., 1994; Kolb and Davis, 1994; Alder et al., 1996), suggesting that in the field plants frequently operate at water potentials low enough to initiate xylem cavitation. Clearly, cavitation of a large proportion of the functional xylem between the roots and leaves has the potential to shift the major hydraulic resistance in the plant from the radial pathway in the root to axial pathways in the root, stem, and leaves. This leads to an interaction between the vulnerability of the xylem to cavitation, the conductivity of the root, and the evaporative demand of the leaves. In seedling and sapling plants this interaction is particularly important, because competition for light and space often leads to increased carbon allocation to shoots and leaves at the expense of root tissue.

Two of the best correlates with seedling and sapling growth rates are leaf area ratio and leaf mass ratio (Walters and Reich, 1999), illustrating that root investment is commonly sacrificed to enhance growth rate during regeneration. As a result of this relative reduction in root investment, fast-growing pioneer species are often susceptible to water supply deficit. This is commonly observed in nature as wilting of pioneer species when exposed to high-light conditions or vapor-pressure deficit even when soil water is plentiful (Schultz and Matthews, 1997). Thus, there is a significant trade-off between the gains in carbon balance achieved by reducing root investment and the costs associated with either producing xylem and leaf tissue capable of resisting low water potential or suffering tissue damage during periods of high evaporative demand.

In this study we examined water flow through two fast-growing early pioneer species expected to be vulnerable to xylem cavitation and two rainforest conifers expected to be more resistant, under conditions of high evaporative demand, to determine the relative importance of xylem cavitation in vivo. This was achieved by measuring whole-plant hydraulic conductivity during imposed changes in the root-leaf water potential gradient. Rapid changes in the water potential gradients through experimental plants were made by chilling the roots of potted plants while transpiration rates were at a maximum. Hydraulic flow through roots has been shown to respond to temperature as an approximately linear function of the viscosity of water (Kramer, 1940; Hertel and Steudle, 1997), and these changes are large enough to have a profound effect on the hydraulic flux through tissues, e.g. changes in the viscosity of water between 25°C and 5°C will result in root conductance being reduced by about 40%. This enabled root conductance and root-stem water potential difference to be manipulated without the complicated effects of changing soil water potential.

Two methods were used to measure the hydraulic resistance of plant tissues, the evaporative flux (EF) technique and a hydrostatic pressure technique. The EF method involves measuring leaf water potential (Ψl) during periods of steady-state EF to calculate the hydraulic conductivity of the whole plant, whereas the hydrostatic pressure technique determines conductivity by measuring flow through excised tissue when a hydrostatic pressure differential (ΔP) is applied (Brouwer, 1954; Sperry et al., 1988).

The hydraulic conductivity of roots was measured using a modification of traditional pressure-induced flow techniques. With this method a low-pressure hydrostatic suction was applied to the stump of a plant that had been detopped under water. The kinetic response of hydraulic fluxes to two different suction pressures (−0.009 and −0.0175 MPa) were measured as was the hydraulic flux produced when ΔP = 0. Root conductivity was calculated from the difference between flow during suction and passive flow at ΔP = 0 (root pressure). We have assumed that Equation 1 is a good representation of water flow through the root:

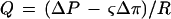graphic file with name M1.gif 1

where Q is the hydraulic flux through the root, ΔP is the hydrostatic driving force, ς is the effective reflection coefficient of the whole root, Δπ is the change in osmotic pressure across the root, and R is the whole-root resistance.

Under hydrostatic tension the hydraulic flux through the root can be expressed by Equation 2:

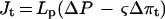graphic file with name M2.gif 2

where Jt is the hydraulic flux under the tension ΔP (kilograms per second), Lp is whole-root conductivity (kilograms per second per megapascal), and Δπt is the change in osmotic pressure across the root under the tension ΔP.

Hence, when ΔP = 0, the hydraulic flux will be expressed by Equation 3:

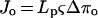graphic file with name M3.gif 3

where Jo is the hydraulic flux when ΔP = 0, and Δπo is the change in osmotic pressure across the root when ΔP = 0.

During rapid measurements of hydraulic flux under tension followed by hydraulic flux when ΔP = 0, ςΔπ should change in proportion to the hydraulic flux, if it is assumed that the active transfer of solutes into the vascular stele remains unchanged between rapid measurements of exudation and hydrostatic flow and the effects of solvent drag are minimized by maintaining a low soil osmotic potential. Under these conditions the ratio of ςΔπo to ςΔπt will be equal to Jt/Jo. This enables ςΔπ to be eliminated from Equations 2 and 3, allowing the expression of Lp solely in terms of Jo, Jt, and P (Eq. 4).

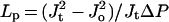graphic file with name M4.gif 4

This is based on the assumption that root transport can be considered a composite process of distinct apoplastic and symplastic pathways for water movement (Steudle and Peterson, 1998). We have also assumed that, during measurements of EF, the osmotic component of Equation 1 would have been minimal, by ensuring that roots remained moist, and that transpiration rates were high (Fiscus, 1975). Under such conditions Q should be primarily responsive to ΔP and changes in root conductance produced by root chilling.

Low-pressure suction has been used to investigate root resistance (Mees and Weatherley, 1957), although the variable resistances reported in their study and by subsequent higher pressure techniques led to a number of papers probing the causes and effects of this feature of root behavior (Fiscus, 1975; Passioura, 1984; Steudle and Peterson, 1998). The issue of variable root conductivity remains unresolved, and according to the large body of data from experiments in which root pressurization was used to measure conductance, the low pressures used here should produce erroneously low conductances because of non-linearity in the response of root tissue to hydrostatic pressure gradients. This was not the case, however, and the root and shoot conductivities measured corresponded well with whole-plant conductivity determined by the EF technique over a range of sizes and of species.

Changes in the xylem resistance of plants were quantified by comparing observed water potential gradients across the plant with those expected from conductivity measurements from the same individuals. Manipulation of root conductance by chilling enabled whole-plant conductivity to be determined at a range of root to Ψl gradients and the effects of xylem cavitation to be assessed.

RESULTS

Root Conductivity

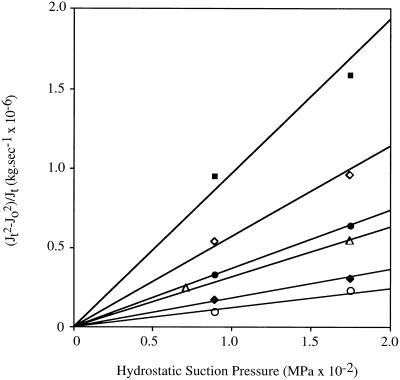
Root conductivity of individuals remained constant over the small range of tensions applied (Fig. 1). There was more than 1 order of magnitude range in the values of absolute root conductance and leaf area specific root conductivity (Table I); however, there was only a relatively small amount of variation in Kr within species. Kr in the two conifer species were within the range of the two angiosperms, both on a leaf area and root dry-weight basis.

Figure 1.

Figure 1

Open in a new tab

Hydrostatic suction applied to the root stump versus hydraulic flux minus osmotic flux (see Eq. 4) in six specimens of E. regnans with leaf areas ranging from 0.17 to 0.95 m2. Regressions have been forced through zero. There is no evidence of non-linearity in the response of flux to applied pressure.

Table I.

Root and shoot conductance parameters for two angiosperm and two conifer species

Species Kr × 10−5 Krdw × 10−7 Ks × 10−5 Kleaf × 10−5 Ψcav50%
kg m−2 MPa−1 s−1 kg MPa−1 s−1 g−1 kg m−1 MPa−1 s−1 kg MPa−1 m−2 s−1 MPa
E. regnans 12.7 ± 2.5 19.2 ± 4.3 26.5 ± 2.1 21.31 ± 4.2 2.7 ± 0.17
T. australis 2.51 ± 0.28 4.40 ± 0.9 17.8 ± 1.7 16.28 ± 0.7 1.4 ± 0.20
N. fleurii 2.01 ± 0.24 1.53 ± 0.5 5.90 ± 0.61 5.56 ± 0.8 3.7 ± 0.20
D. dacrydioides 1.86 ± 0.26 3.90 ± 0.7 7.24 ± 0.76 7.46 ± 0.7 2.3 ± 0.20
Open in a new tab

Mean root conductance ± se (n = 3) is expressed in terms of leaf area (Kr) and whole root dry weight (Krdw); stem conductivity (Ks) in terms of leaf area; and leaf hydraulic conductance (Kleaf). The mean ± se (n = 3) Ψcav50% can be considered the negative of stem water potential resulting in 50% cavitation.

Root Chilling and Whole-Plant Conductivity

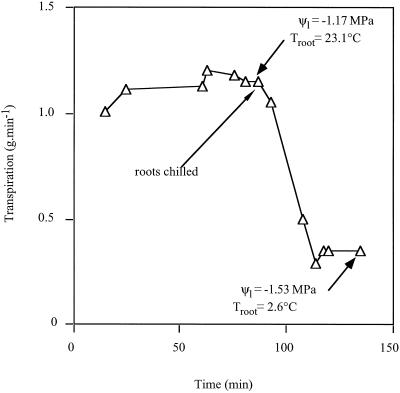
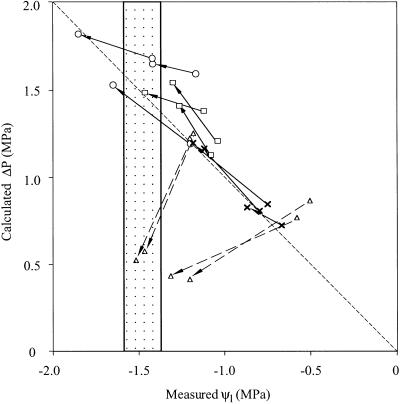
Root chilling caused an immediate decrease in Ψl and transpiration, which stabilized usually within 30 min. The largest decreases were observed in Toona australis plants, which always wilted severely during root chilling (Fig. 2). Neither the angiosperm Eucalyptus regnans nor the conifers Dacrycarpus dacrydioides and Nageia fleurii were observed to wilt, although Ψl did decline by 0.2 to 0.4 MPa in these species. In all species except T. australis, the effect of root chilling on Ψl was close to the predicted value, assuming that root conductance was reduced by only the increased viscosity of water during chilling (Fig. 3). During root chilling in T. australis, however, measured Ψl was substantially lower than the expected value (Fig. 3), indicating increased resistance somewhere in the hydraulic pathway. Rewarming of roots reversed this deviation from expected Ψl in T. australis within 2 h (Fig. 4).

Figure 2.

Figure 2

Open in a new tab

Changes in transpiration and Ψ1 in response to root chilling in T. australis. Air temperature and humidity were maintained constant during the measurement period, indicating that changes in transpiration were largely due to decreases in stomatal conductance. Note that readings of root temperature, transpiration, and Ψ1 were made after 20 min of steady-state EF.

Figure 3.

Figure 3

Open in a new tab

Calculated ΔP versus measured Ψ1 in E. regnans (×), T. australis (▵), D. dacrydioides (□), and N. fleurii (○). Arrows indicate the change in Ψ1 before and during root chilling in the various individuals. The stippled region of the graph indicates the mean Ψcav50% ± se for T. australis. Ψcav50% in other species was less than −2 MPa. Note that only in T. australis does predicted ΔP deviate strongly from measured Ψ1 after root chilling.

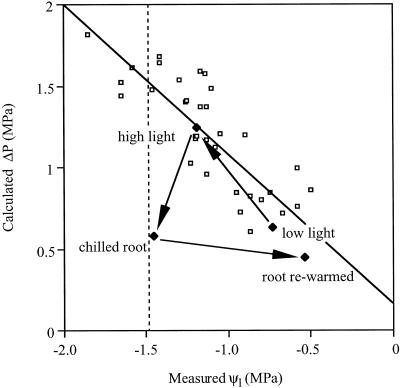
Figure 4.

Figure 4

Open in a new tab

There was a highly significant (P < 0.001) correlation between measured Ψ1 and calculated ΔP in pooled data from un-chilled T. australis and all measurements from E. regnans, D. dacrydioides, and N. fleurii (□). The slope of this regression is not significantly different from −1. Also shown is the change in measured and calculated ΔP in a single specimen of T. australis (⧫) starting at low light (50 μE m−2 s−1), then chilled roots (5.8°C), and finally low light with roots rewarmed. Root chilling in T. australis caused Ψ1 to approach Ψcav50% (marked with a dashed line).

Stem vulnerability to cavitation was found to vary substantially between species. T. australis was extremely sensitive to pressure-induced cavitation, with a 50% loss of stem conductivity occurring at −1.45 MPa, which was within the measured values of Ψl during root chilling. All other species showed little cavitation within the water potential range produced by root chilling (Table I).

DISCUSSION

Low-pressure suction proved to be an easy and effective means of quantifying root conductivity in four woody tree species including two conifers. There was a good correlation between observed and expected Ψl in all species under non-cavitating xylem tensions, although whole-plant conductivities calculated from Ψl were generally slightly higher than those calculated from root, stem, and leaf conductivities (Figs. 3 and 4). One possible reason for this is that root conductivity may decline in response to the release of water tension after detopping (Steudle and Peterson, 1998), and it was noted that conductivity did decrease significantly in the 1st h after shoots were detached. Rapid measurements were made during this 1st h to calculate maximum root conductivity, although there was still up to 35% difference between the observed and expected Ψl. Another possibility is that Ψl measured by the pressure bomb was not accurate in transpiring leaves (Melcher et al., 1998), although this suggestion has recently been strongly challenged (Wei et al., 1999).

Problems associated with non-linearity in the response of hydraulic flux to applied pressure were overcome by assuming that the Δπ at 0 hydrostatic pressure was effectively diluted in proportion to the increase in J resulting from applied pressures (Eq. 4). Root conductivities calculated by this method remained constant over the small range of tensions used here (Fig. 1). These assumptions should have been valid under the experimental conditions used, i.e. low soil π and high water potential during root conductivity and EF measurements and continual referencing of passive hydraulic flux when ΔP = 0.

Values of whole-root conductivity determined here ranged from a maximum in E. regnans of 12.7 × 10−5 to a minimum of 1.86 × 10−5 kg s−1 m−2 MPa−1 in the conifer D. dacrydioides. These values are consistent with data using the high-pressure flow meter technique for tropical tree seedlings (Tyree et al., 1998b) and fall within the large range of Kr produced by root pressure chamber measurements (Lo Gullo et al., 1998; Huxman et al., 1999). Considering the large difference between the maximum tension applied here (0.0175 MPa) and the positive pressures of generally between 0.1 and 0.5 MPa used in other whole-root methods, the agreement in these data adds confidence in the validity of both low- and high-pressure techniques.

In the two conifer species and E. regnans, chilling roots caused a decrease in Kr due to increased fluid viscosity. This in turn caused Ψl to decrease and stomatal conductance to decrease in response (Figs. 2 and 3). The observed decline in Ψl corresponded very closely to that expected if Kr was affected by changing viscosity alone. In these species, decreases in root conductance during chilling caused transpiration and Ψl to decrease, but Ψl did not approach a water potential resulting in 50% loss of stem conductance (Ψcav50%, measured in megapascals). In T. australis, however, the increased water potential gradient produced by root chilling was much higher than that expected by viscosity changes alone. This substantial decrease in plant conductivity was probably due to large decreases in xylem conductivity due to cavitation. Support for this hypothesis comes in fact that stem xylem vulnerability to cavitation by water tension was extremely high in T. australis (Table I) and Ψl was always near or below Ψcav50% during root chilling.

If the observed decrease in whole-plant conductance in this species was due to a combination of viscosity effects and cavitation in the stem xylem, then it would represent approximately a 95% loss of stem conductivity. This is possible given the very rapid decrease in stem conductivity typically observed once Ψcav50% is exceeded (Pammenter and Vander Willigen, 1998), although measurements of embolism by flushing (Sperry et al., 1988) in T. australis indicated only a 50% to 65% loss in stem conductivity after chilling (T.J. Brodribb, unpublished data). Another possibility is that cavitation in root and petiole xylem may have contributed to the loss in conductivity as it is likely that either of these could be more susceptible to cavitation than stem tissue. According to the vulnerability segmentation theory (Tsuda and Tyree, 1997) roots are the least vulnerable and petioles the most vulnerable to cavitation, although there is evidence to the contrary (Sperry and Saliendra, 1994; Hacke and Sauter, 1996). Other observations that covering leaves had no significant effect on Ψl during root chilling (T.J. Brodribb, unpublished data) suggest that the major loss of conductivity occurred in the stem or root xylem.

These results provide evidence that xylem cavitation can exert a strong influence over Ψl and whole-plant conductivity in vivo. Previously the only evidence of cavitation in living plants has been the detection of acoustic emissions (corresponding to cavitation events) from stems (Jackson et al., 1995). The rapid reduction in stomatal conductance by T. australis in response to root chilling was not rapid enough to prevent significant xylem cavitation, indicating that this species operates with a narrow safety margin before catastrophic xylem dysfunction (Tyree and Sperry, 1988). This is consistent with the ecological niche of T. australis as a fast growing rainforest pioneer (Herwitz, 1993), and in agreement with other studies that have detected cavitation in similar pioneer species when exposed to relatively small water potential deficits (Schultz and Matthews, 1997).

Root conductivity of the two conifer species here were within the range of the two angiosperms both on a leaf-area and dry-mass basis. This has been shown in other studies, although the data are limited (Sands et al., 1982; Rudinger et al., 1994; Becker et al., 1999). The absence of vessels in conifer roots probably does not produce a significant impedance to water flow in young plants at least, because the radial resistance in small root systems is substantially higher than axial resistance, and vessels only affect higher axial hydraulic conductivity. The fact that no evidence of cavitation was observed in E. regnans or either of the two conifer species indicates that a more substantial safety margin exists between operating Ψl and Ψcav50% in these taxa (Table I). In conifers this may be due to the fact that low root pressures make embolism repair inefficient and, hence, the xylem is more resistant to water stress-induced cavitation than associated angiosperm taxa (Sperry and Tyree, 1990; Tyree et al., 1998a). E. regnans, on the other hand, produces a high conductivity and root pressure, and relatively cavitation-resistant xylem, giving it the capacity for extremely high growth rates, but these characters probably contribute to its low shade tolerance (Van Der Meer et al., 1999).

In summary it was found that low-pressure suction was a simple and effective means of quantifying root hydraulic conductivity, yielding values of Kr that agreed with whole-plant measurements using the EF technique. Root chilling in T. australis caused Ψl to approach or exceed Ψcav50% resulting in a substantial decrease in whole-plant conductivity, presumably by xylem cavitation. Quantification of the change in whole-plant conductivity during root chilling may provide a useful technique for measuring the relative safety margins within which plant species operate.

MATERIALS AND METHODS

Plant Material

Seeds from angiosperm wet-forest pioneers, Eucalyptus regnans and Toona australis, and the rainforest conifers, Nageia fleurii and Dacrycarpus dacrydioides, were germinated in sand and transferred to a pine-bark/sand potting medium in 5-L pots. Three plants of each species were grown under natural light conditions in a heated greenhouse until they reached a size of between 1 and 1.5 m tall.

Whole-Plant Conductance and Manipulation of Root Conductance

EF was measured in individually potted plants, in the greenhouse under conditions of full-sun or under metal halide lamps producing a photosynthetic photon flux of 500 to 600 μE m−2 s−1 and approximately 25°C and 35% to 45% relative humidity. Prior to measurement, plants were soaked with water, and pots were covered with plastic bags to eliminate water loss. Transpiration was measured gravimetrically, with average rates calculated every 10 to 15 min depending on rates of evaporation. When the EF had stabilized for at least 30 min, three leaves (or leaflets) were detached for Ψl measurements. Pots were then removed from the balance and iced water flowed through them until root temperature had decreased to between 2°C and 5°C. Soil temperature was recorded by four thermocouples inserted among the roots. Temperature measurements on the stems of plants during chilling indicated that the chilling effect was largely confined to the roots, with stem temperatures increasing to 20°C at a height of approximately 10 cm above the soil. After the plants had cooled, they were placed in an insulated container on the balance, and EF was monitored for 2 h, or until a new steady state had been reached. After the chilled-root steady state was reached, an additional three leaves were removed for Ψl measurement and soil temperature recorded. In one individual of each species, four leaves were wrapped in laboratory film (Parafilm, American National Can, Greenwich, CT) and foil during the early morning, and Ψl was measured on these wrapped leaves during maximum transpiration at mid-day. Ψl of these leaves were compared with Ψl in uncovered leaves to calculate a mean leaf hydraulic conductivity for each species. All Ψl data were collected using a Scholander-type pressure bomb with a dissecting microscope attached for precise determination of the end point.

Plants were allowed to recover from root chilling for 5 to 10 d before they were harvested for measurement of shoot and root conductivity.

Shoot Conductivity and Vulnerability

To measure conductivity across the bulk of the shoot, stem segments were cut as long as possible, running from the base of the shoot to the tip of a terminal branch. Side shoots were all removed and plugged with Teflon tape and petroleum jelly. Conductivity was measured by applying a hydrostatic pressure of 6 kPa to the base of the segment and measuring the efflux of water on an electronic balance. Conductivity was expressed as the hydraulic flux (kilograms per second) divided by the pressure gradient across the stem (megapascals per meter) and also as the leaf-area specific conductivity by dividing by the leaf area supplied by the stem segment.

After conductivity was measured, stems were placed into a 15-cm-long double-ended pressure bomb (Sperry and Saliendra, 1994) and flushed with filtered water at 0.175 MPa until conductivity remained at a maximum stem hydraulic conductance prior to air injection (Km, kilograms per second per megapascal per meter). Following this, chamber pressure was gradually increased to 0.50 MPa for 20 min and released, and conductivity was remeasured. This process was continued at 0.50-MPa increments until conductivity declined to 5% of Km. Applied pressure was then plotted against the percentage loss of conductivity relative to Km at each pressure, and a regression was fitted assuming a loss of conductivity by a cumulative normal curve shape (Brodribb and Hill, 1999). From these curves the Ψcav50% was interpolated.

Root Conductivity

Plants were detopped under water during mid-morning. Stumps were quickly shaved with a razor and attached to a length of tubing filled with degassed water. Tubing led to a pipette whose tip was submerged in a reservoir of water placed on a computer-interfaced balance. Air temperature in the laboratory was controlled to 22°C, and root temperature was monitored by four thermocouples placed around the root. Roots remained in soil, but were continually bathed by a slow flow of water, ensuring that the soil remained fully saturated and the osmotic potential of the soil was a minimum. Initially a hydrostatic pressure of −0.0175 MPa was applied by placing the surface of the water reservoir 1.78 m below the center of gravity of the pot. Balance readings of the mass of water exuded were made every 2 min, and as soon as the hydraulic flux stabilized (usually 10 min) the pot and balance were leveled and the hydraulic flux was remeasured. A second tension of 0.009 MPa was then applied and the flux was remeasured. Several measurements were made at each of the two tensions while passive flow from the roots was regularly referenced. Immediately after a pressure change, hydraulic flux was unstable, decaying to a steady state within 5 to 10 min; hence, measurements of hydraulic flux were made at these steady states. Usually it was the case that both root pressure and conductivity decreased slowly after detopping, and hence only the initial two to three measurements were averaged to produce a value for whole-root conductivity. Tensions of more than −0.0175 MPa resulted in air being drawn through the root, and hence this was the maximum suction applied to the root.

It was assumed that the flux of solutes into the root vascular stele responsible for passive flow when ΔP = 0 remained constant between passive flow measurements and small applied tensions, and hence, Equation 2 was used to calculate whole-root conductivity. Conductivities were all normalized to the water viscosity at 20°C. No attempt was made to quantify root area; thus, root conductivities were either expressed as kilograms per second per megapascal and matched to EF data expressed on a leaf-area basis (Kr) or root dry-weight basis for comparisons between individuals (Tyree et al., 1998b).

EF versus Hydraulic Conductivity Data

Comparison of EF and hydrostatic conductivity measurements were made by using the whole-plant conductivity (combined Kr, leaf hydraulic conductivity, and stem hydraulic conductivity) for each individual to calculate the expected soil-leaf ΔP (equal to Ψl under the saturated soil conditions used here) at each observed EF. This expected ΔP was compared with the average Ψl determined from the pressure bomb. It was assumed that, during rapid transpiration while the pot was soaked with water, the osmotic gradient across the root was low and that soil water potential was approximately zero.

ACKNOWLEDGMENT

The authors thank Dr. Greg Jordan for comments.

Footnotes

1

Financial support was provided by an Australian Research Council grant.

LITERATURE CITED

  1. Alder MN, Sperry JS, Pockman WT. Root and stem xylem embolism, stomatal conductance, and leaf turgor in Acer grandidentatum populations along a soil moisture gradient. Oecologia. 1996;105:293–301. doi: 10.1007/BF00328731. [DOI] [PubMed] [Google Scholar]
  2. Becker P, Tyree MT, Tsuda M. Hydraulic conductances of angiosperms versus conifers: similar transport sufficiency at the whole-plant level. Tree Physiol. 1999;19:445–452. doi: 10.1093/treephys/19.7.445. [DOI] [PubMed] [Google Scholar]
  3. Brodribb T, Hill RS. The importance of xylem constraints on the distribution of conifer species. New Phytol. 1999;143:356–372. [Google Scholar]
  4. Brouwer R. The regulating influence of transpiration and suction tension on the water and salt uptake by the roots of intact Vica faba plants. Acta Bot Neerl. 1954;3:264–312. [Google Scholar]
  5. Fiscus E. The interaction between osmotic- and pressure-induced flow in plant roots. Plant Physiol. 1975;55:917–922. doi: 10.1104/pp.55.5.917. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Frensch J, Stuedle E. Axial and radial hydraulic resistance to roots of maize (Zea mays L.) Plant Physiol. 1989;91:719–726. doi: 10.1104/pp.91.2.719. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Hacke U, Sauter JJ. Drought-induced xylem dysfunction in petioles, branches, and roots of Poplus balsamifera L. and Alnus glutinosa (L.) Gaertn. Plant Physiol. 1996;111:413–417. doi: 10.1104/pp.111.2.413. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Hargrave KR, Kolb KJ, Ewers FW, Davis SD. Conduit diameter and drought-induced embolism in Salvia mellifera Greene (Labiatae) New Phytol. 1994;126:695–705. [Google Scholar]
  9. Hertel A, Steudle E. The function of water channels in Chara: the temperature dependence of water and solute flows provides evidence for composite membrane transport and for slippage of small organic solutes across water channels. Planta. 1997;202:324–335. [Google Scholar]
  10. Herwitz SR. Growth rates of selected Australian tropical rainforest tree species under controlled conditions. Oecologia. 1993;96:232–238. doi: 10.1007/BF00317736. [DOI] [PubMed] [Google Scholar]
  11. Huxman KA, Smith SD, Neuman DS. Root conductivity of Larrea tridentata and Helianthus annuus under elevated CO2. Plant Cell Environ. 1999;22:325–330. [Google Scholar]
  12. Jackson GE, Irvine J, Grace J. Xylem cavitation in Scots pine and Sitka spruce saplings during water stress. Tree Physiol. 1995;15:783–790. [Google Scholar]
  13. Kolb K, Davis SD. Drought tolerance and xylem embolism in co-occurring species of coastal sage and chaparral. Ecology. 1994;75:648–659. [Google Scholar]
  14. Kramer PJ. Root resistance as a cause of the absorption lag. Am J Bot. 1938;25:110–113. [Google Scholar]
  15. Kramer PJ. Root resistance as a cause of decreased water absorption by plants at low temperatures. Plant Physiol. 1940;15:63–79. doi: 10.1104/pp.15.1.63. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Lo Gullo MA, Nardini A, Salleo S, Tyree MT. Changes in root hydraulic conductance (Kr) of Olea oleaster seedlings following drought stress and irrigation. New Phytol. 1998;140:25–31. [Google Scholar]
  17. Mees GC, Weatherley PE. The mechanism of water absorption by roots: II. The role of hydrostatic pressure gradients across the cortex. Proc R Soc London Ser B. 1957;147:381–391. doi: 10.1098/rspb.1957.0057. [DOI] [PubMed] [Google Scholar]
  18. Melcher PJ, Meinzer FC, Yount DE, Goldstein G, Zimmermann U. Comparative measurements of xylem pressure in transpiring and non-transpiring leaves by means of the pressure chamber and the xylem pressure probe. J Exp Bot. 1998;49:1757–1760. [Google Scholar]
  19. Pammenter NW, Vander Willigen C. A mathematical and statistical analysis of the curves illustrating vulnerability of xylem to cavitation. Tree Physiol. 1998;18:589–593. doi: 10.1093/treephys/18.8-9.589. [DOI] [PubMed] [Google Scholar]
  20. Passioura JB. Hydraulic resistance of plants: I. Constant or variable? Aust J Plant Physiol. 1984;11:333–339. [Google Scholar]
  21. Rudinger M, Hallgren SW, Stuedle E, Schulze ED. Hydraulic and osmotic properties of spruce roots. J Exp Bot. 1994;45:1413–1425. [Google Scholar]
  22. Sands R, Fiscus E, Reid CPP. Hydraulic properties of bean and pine roots with varying degrees of suberisation, vascular differentiation and mycorrhizal infection. Aust J Plant Physiol. 1982;9:559–569. [Google Scholar]
  23. Schultz HR, Matthews MA. High vapour pressure deficit exacerbates xylem cavitation and photoinhibition in shade-gown Piper auritum during prolonged sunflecks: I. Dynamics of plant water relations. Oecologia. 1997;110:312–319. doi: 10.1007/s004420050164. [DOI] [PubMed] [Google Scholar]
  24. Sperry JS, Donnelly JR, Tyree MT. A method for measuring hydraulic conductivity and embolism in xylem. Plant Cell Environ. 1988;11:35–40. [Google Scholar]
  25. Sperry JS, Saliendra NZ. Intra- and inter-plant variation in xylem cavitation in Betula occidentalis. Plant Cell Environ. 1994;17:1233–1241. [Google Scholar]
  26. Sperry JS, Tyree MT. Water-stress-induced xylem embolism in three species of conifers. Plant Cell Environ. 1990;13:427–436. [Google Scholar]
  27. Steudle E, Peterson CA. How does water get through roots? J Exp Bot. 1998;49:775–788. [Google Scholar]
  28. Tsuda M, Tyree MT. Whole-plant hydraulic and vulnerability segmentation in Acer saccharinum. Tree Physiol. 1997;17:351–357. doi: 10.1093/treephys/17.6.351. [DOI] [PubMed] [Google Scholar]
  29. Tyree MT, Ewers FW. The hydraulic architecture of trees and other woody plants. New Phytol. 1991;119:345–360. [Google Scholar]
  30. Tyree MT, Patino S, Becker P. Variability to drought-induced embolism of Bornean heath and dipterocarp forest trees. Tree Physiol. 1998a;18:583–588. doi: 10.1093/treephys/18.8-9.583. [DOI] [PubMed] [Google Scholar]
  31. Tyree MT, Sperry JS. Do woody plants operate near the point of catastrophic xylem dysfunction caused by dynamic water stress? Answers from a model. Plant Physiol. 1988;88:574–580. doi: 10.1104/pp.88.3.574. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Tyree MT, Velez V, Dalling JW. Growth dynamics of root and shoot hydraulic conductance in seedlings of five neotropical tree species: scaling to show possible adaptation to differing light regimes. Oecologia. 1998b;114:293–298. doi: 10.1007/s004420050450. [DOI] [PubMed] [Google Scholar]
  33. Van Der Meer PJ, Dignan P, Saveneh AG. Effect of gap size on seedling establishment, growth and survival at three years in mountain ash (Eucalyptus regnans F. Muell.) forest in Victoria, Australia. For Ecol Manag. 1999;117:33–42. [Google Scholar]
  34. Walters MB, Reich PB. Low-light carbon balance and shade tolerance in the seedlings of woody plants: do winter deciduous and broad-leaved evergreen species differ? New Phytol. 1999;143:143–154. [Google Scholar]
  35. Wei C, Steudle E, Tyree MT. Water ascent in plants: do ongoing controversies have a sound basis? Trends Plant Sci. 1999;4:335–380. doi: 10.1016/s1360-1385(99)01466-1. [DOI] [PubMed] [Google Scholar]

Articles from Plant Physiology are provided here courtesy of Oxford University Press

RESOURCES