Review and perspective on mathematical modeling of microbial ecosystems

Abstract

Understanding microbial ecosystems means unlocking the path toward a deeper knowledge of the fundamental mechanisms of life. Engineered microbial communities are also extremely relevant to tackling some of today's grand societal challenges. Advanced meta-omics experimental techniques provide crucial insights into microbial communities, but have been so far mostly used for descriptive, exploratory approaches to answer the initial ‘who is there?’ question. An ecosystem is a complex network of dynamic spatio-temporal interactions among organisms as well as between organisms and the environment. Mathematical models with their abstraction capability are essential to capture the underlying phenomena and connect the different scales at which these systems act. Differential equation models and constraint-based stoichiometric models are deterministic approaches that can successfully provide a macroscopic description of the outcome from microscopic behaviors. In this mini-review, we present classical and recent applications of these modeling methods and illustrate the potential of their integration. Indeed, approaches that can capture multiple scales are needed in order to understand emergent patterns in ecosystems and their dynamics regulated by different spatio-temporal phenomena. We finally discuss promising examples of methods proposing the integration of differential equations with constraint-based stoichiometric models and argue that more work is needed in this direction.

Introduction

The relevance of bacteria and microbes for life as we know it cannot be exaggerated: they were the first forms of life that drastically shaped Earth's environment, and animal life evolved in a microbe-dominated landscape. After being considered for decades mostly as pathogens, they are now receiving full credit for the fundamental positive role they often play in ecosystems [1]. Many different biological complexes can fall under the term ‘ecosystem’, and similar techniques can be employed to study a microbial mat in the Yellowstone National Park and the gut microbiome of the authors of this manuscript. In general terms, an ecosystem consists of an ensemble of organisms, their shared environment and the complex network of resulting interactions, either among the organisms or between organisms and environment. Depending on the particular interest of the observer, different questions can be addressed with different empirical and theoretical methods.

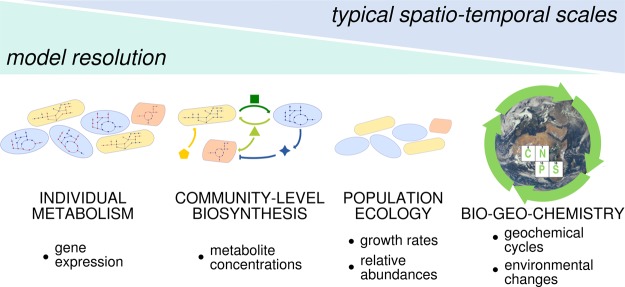
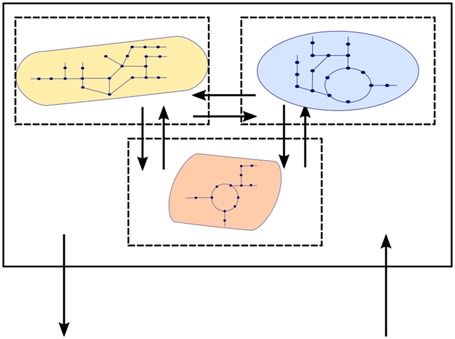
Meta-omics technologies have been so far mostly used for descriptive, exploratory approaches to answer the initial ‘who is there?’ question. Obtaining this sort of ‘stamp collection’ [2] is a necessary but not sufficient condition to build a comprehensive model of how microbial communities assemble, maintain themselves, evolve and function. Once we realize that macroscopic features are the emerging observables of microscopic interactions [3], the need to obtain a mechanistic understanding of the ecosystem dynamics becomes evident. At the same time, it is clear that the same ecosystem is regulated by phenomena acting at very different scales, both in space and time (Figure 1). Observables like growth rates might be typically associated to one specific scale (say, population-level ecology), but are not independent from others (say, individual metabolic states). Mathematical models with their abstraction capability become an essential tool to capture specific phenomena and connect different scales [4].

Figure 1. Examples of different levels of complexity acting at different scales.

Ecosystems span very different levels of complexity and of temporal and spatial scales. The biological question sets the importance of each aspect and defines the abstraction needed for a mathematical representation. Experimental observables also strongly influence the design of input and output of a theoretical model.

This mini-review focuses on two major classes of mathematical methods (differential equation models and constraint-based stoichiometric models) and their recent applications to the study of microbial communities. After highlighting the individual strengths and weaknesses of these methods, attention is given to integrative approaches proposed or desirable in view of obtaining a more comprehensive representation of biological systems. For a broader overview of mathematical modeling of microbial communities, the reader is referred to [5,6]. As a general note, it is worth to point out that this mini-review is describing two deterministic modeling techniques. For the sake of brevity and of uniformity of the manuscript, stochastic models are not considered here, but the reader should be aware that stochasticity is an intrinsic property of Nature. However, as previously mentioned, depending on the biological system under study and the question addressed, different methods can be chosen. Deterministic models can be considered as the macroscopic description of the outcome from microscopic behaviors.

Ecology and differential equation models

The study of emergent patterns in ecosystems and their dynamics on multiple spatio-temporal scales is a central focus in the well-established field of theoretical ecology [7]. Microbial ecological systems biology allows investigating in silico, in vivo and in vitro most of the temporal scales, including evolutionary dynamics. In their recent review, Friedman and Gore [8] highlight how models implementing simple qualitative interactions (competition, cooperation and exploitation) can still have high predictive power.

Almost two centuries ago, Verhulst defined a single deterministic equation to describe population growth which is also capturing population-level behavior of bacterial cultures [9]. Since Lotka [10] and Volterra [11] independently proposed a mathematical model of population dynamics based on ordinary differential equations (ODEs), Lotka–Volterra (LV) models have been widely used to describe the time evolution of ecosystems (Figure 2). In the classical predator–prey LV model, two competing populations directly affect each other's growth, either positively or negatively. The model parameters, including the initial conditions, quantify such direct interactions and will determine the stability of the system. Indeed, these mathematical systems of equations can be numerically solved and the qualitative properties of the steady-state solutions, from periodic oscillations to chaotic attractors, can be evaluated.

Figure 2. Modeling microbial communities with ODE systems.

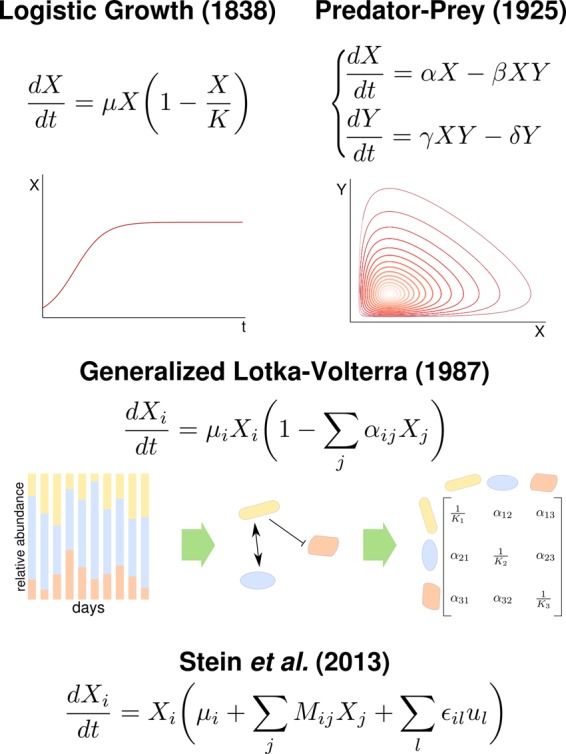
Microbial growth over time follows the logistic rule defined by Verhulst in 1838. Predator–prey systems show an oscillatory dynamic. gLV models are used today in combination with time series of metagenomics data. Stein et al. [16] proposed an extension of the gLV model to include susceptibility to an external time-dependent perturbation.

In 1987, Hofbauer et al. [12] extended the LV equations to an arbitrary number of coexisting populations and studied the mathematical properties of these generalized LV (gLV) models. Figure 2 shows schematically that today a gLV model can be obtained from a time series of metagenomics survey used to infer a co-occurrence network in a rather straightforward way [13]. Owing to the technological advances in sequencing techniques, gLV models have been successfully used over the past few years to study the temporal dynamics of various bacterial communities [14,15]. Their predictive power is, however, still to be demonstrated, especially considering the reductive assumption that the community dynamics is driven by only pairwise interactions and that the environmental conditions are not taken into account.

A promising step forward in gLV model development is the approach by Stein et al. [16]. In a study on colonization of mice gut microbiome by the pathogen Clostridium difficile, they added to the standard gLV formulation (individual growth rates and an interaction matrix) a third term that models individual susceptibility to an environmental perturbation, antibiotic administering, in their case study (Figure 2). Time series of in vivo metagenomics data followed the community composition of the intestinal microbiome of mice under three conditions: unperturbed and infected with C. difficile; perturbed by antibiotic; perturbed and then infected. After discretizing the gLV equations, they could use regularized linear regression to fit the parameters over a training set of data. The obtained gLV model was then used to predict the community behavior in the conditions left out of the training set. Steady-state analysis correctly predicted the infection outcomes in terms of community profiles and composition and allowed for exploration of alternative stable configurations.

To capture spatial effects like diffusion of nutrients and cell motility [17], partial differential equations (PDEs) are commonly applied. In wastewater treatment, the activated sludge system is a process where the microbial biomass is employed to perform specific biological tasks, like removal of N and P from sewage. In this context, models based on differential equations have been developed since the 1980s aimed at aiding the design of industrial plants [18]. An early example of an ODE and PDE model is from Benefield and Molz [19], which described the ecosystem composed by an aggregated microbial suspension (floc particles) and soluble metabolites with a system of five PDEs and four ODEs. Under the assumption that organic C, O, N and P are growth-limiting nutrients and that their transfer within a floc particle is controlled by molecular diffusion, they provide a model that can be tested under different operating conditions, such as oxygenation levels, and which allows assessing, e.g. the influence of including a nitrifying microbe on nutrient limitation.

In conclusion of this section, building on time series of metagenomics data, gLV models can potentially address the question ‘who will be there?’, but their power is generally limited to a data-driven inference of pairwise organism interactions in a certain environment. The reality is far more complex and it is hard to imagine that we will ever answer questions like ‘who does what?’, or ‘what will happen if…?’, without sound mathematical models offering mechanistic insights into the various aspects regulating and characterizing the metabolic state of a microbial community. ODE and PDE models can successfully capture biochemical activity and spatial heterogeneity, but rely on a priori assumptions on the mechanisms and on known parameters. Metabolism is well known to be a key driver of community interactions [20], and differential equation models of large metabolic pathways have been proposed [21]. While technically not impossible, a genome-scale differential equation model of an organism's full metabolism is not practical. Such a model would consist of a system of thousands of equations, each of which requiring empirical knowledge, or inference, of several parameters. This approach cannot keep up with the speed at which new genomes are published and will not help toward a thorough exploration of emerging metabolic properties of ecosystems. As of today, the most convenient method to model genome-scale metabolism is through metabolic network reconstruction and constraint-based stoichiometric models.

Metabolism and constraint-based models

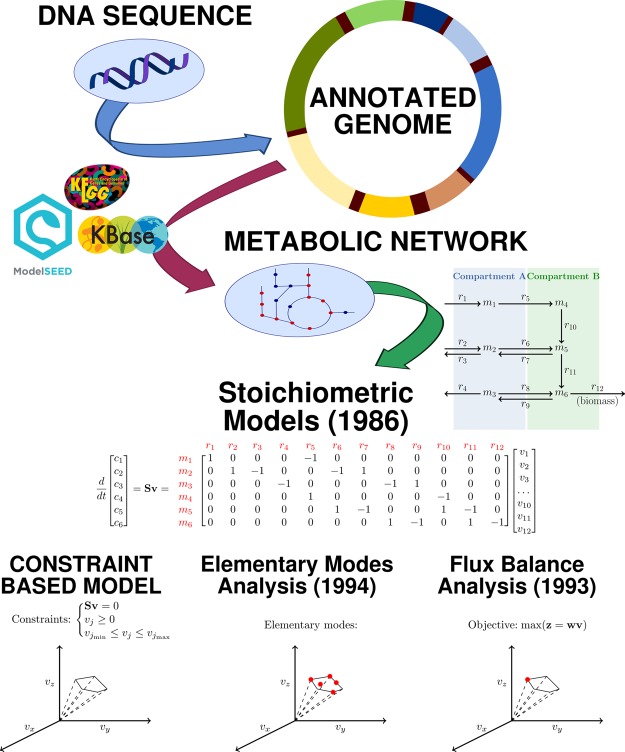
Genome sequencing technology has opened the door for understanding the building blocks of life. There is still, however, a significant gap between what we are able to observe in the genome and what genes can be related to known functions. Our current knowledge of enzymatic activity associated to amino acid sequences is far from complete, but also at the same time is constantly expanding and collected into searchable databases, making it easily accessible to automated computational pipelines. The recent years have seen large improvements in the process of reconstructing operational genome-scale metabolic models [22], also owing to platforms like KBase [23]. An example workflow for the generation and analysis of a genome-scale metabolic model is described in Figure 3. It is important to point out that consensus on a unified standard is highly needed to ensure the reproducibility and reusability of published genome-scale networks [24].

Figure 3. Example workflow for genome-scale metabolic network reconstruction and analysis with FBA.

The process of reconstructing and analyzing a genome-scale metabolic network model starts with a sequenced genome. Functional annotation of the genome [50] links genes to enzymatic activity and allows the reconstruction of a draft network of metabolic reactions. Further steps include compartmentalization, the addition of exchange and transport reactions, the definition of a biomass equation and the gap filling procedure. Gap filling is needed to complement pathways where enzymes are missing, usually because of incomplete annotation knowledge [22]. Today automated workflows like the Model SEED [51] and KBase [23] allow quick reconstruction of genome-scale metabolic network models, but do not solve yet the eventual need for manual curation. The network of reactions can then be represented mathematically as a stoichiometric matrix and analyzed with CBMs under the steady-state assumption and imposing boundaries on the reaction fluxes. Elementary modes [29] and FBA [31] are widely used methods to study the metabolic flux distributions.

Once a network of biochemical reactions is known, it can be mathematically represented as a stoichiometric matrix S of dimension (m, r), where m is the number of metabolites and r is the number of reactions in the model, and the elements of the matrix s_ij are the stoichiometric coefficients of metabolite i in reaction j [25]. The mass balance of intracellular metabolites translates into the set of differential equations resulting from the product of S and the vector of reaction fluxes v (Figure 3). Constrained-based models (CBMs) assume a steady state and impose constraints on reaction flux values based on thermodynamic considerations (e.g. irreversibility of some reactions) and eventually biological or experimental information [26,27]. Since the dimension m is in general lower than the dimension r, the resulting space of solutions for the vector of reaction fluxes v is a convex polyhedral cone, also called flux cone. The metabolic flux distribution reflects a certain cellular state, possibly observable as a phenotype under the defined boundary conditions. The constraints on the reaction flux of import reactions (i.e. reactions transporting metabolites in the system, r₁ and r₂ in Figure 3) typically represent nutrient availability.

Different methods have been developed to study the structure and functionality of genome-scale metabolic networks (Figure 3). Elementary mode analysis (EMA) solves the CBM equations to identify the set of all possible unique and minimal pathways that allow steady-state metabolic fluxes in the network [28,29]. EMA performs a computationally expensive calculation, especially on large genome-scale metabolic networks, but brings rigorous insights into the structure of a network. Pathways can then be accurately and systematically compared and their efficiency, e.g. in terms of molar yields of a product, can be easily assessed. It is important to highlight that EMA does not rely on a priori assumptions on the network except for thermodynamics constraints. Since the computed solutions are scalable, environmental conditions like nutrient availability can be subsequently used, e.g. to define an intake flux and normalize the overall flux distribution. A cellular physiological state is then a weighted linear combination of elementary modes.

Flux balance analysis (FBA) is a convenient method to obtain a single flux distribution in fast computation time [30,31]. FBA assumes the previously described CBM constraints and adds the declaration of an objective function which, if linear in the metabolic fluxes, sets the definition of an optimization problem solvable with linear programming (LP). Typical objective functions are, e.g. maximization of growth rate, maximization or minimization of ATP production, minimization of overall fluxes. As a consequence, however, the resulting flux distribution depends on the modeler's subjective choice of the objective function [32]. Furthermore, alternative optima can exist for the same problem, but FBA will return a unique solution. A plethora of extensions to FBA have been proposed in the past decades and ongoing efforts are particularly focused on integrating information from large meta-omics datasets to further constrain the models with biological data. FBA and its variants have been successfully applied to predict phenotypes of biological systems, e.g. resulting from gene knock-outs and product yield optimization, but most of them rely on strict assumptions and often trade the computational lightness typical of FBA for more accurate solutions [33]. A critical review of the underlying assumptions in FBA and related methods is presented, e.g. in [34].

The so far described approaches have been initially applied, obviously, to single organisms. Scientists are still working on understanding the secrets encoded in an individual genome, but nevertheless it is possible to use metabolic network modeling also to explore the properties of natural and synthetic microbial communities. The first step to take is the definition of the community-level metabolic network model itself, and Henry et al. [35] recently proposed an effective strategy for a data-driven network reconstruction. In Table 1, we show three commonly chosen configurations: lumped or supra-organism network; compartmentalized network; independent multispecies networks. These approaches build on different assumptions and have specific advantages and disadvantages. It is hence up to the modelers to choose the method most suitable for the biological problem at hand. For example, Khandelwal et al. [36] proposed an extension of FBA that with the single assumption of balanced growth (biologically justified in controlled environments where cultures are stabilized at logarithmic growth phases) could predict metabolic fluxes, community growth rate and individual biomass abundances of a compartmentalized community metabolic network model. Other approaches introduce additional assumptions, like a community-level objective or specific functional roles for each community member, thus reducing the range of biological systems that can be modeled to those that can be characterized at the required level. This, however, does not imply that such models are not useful; only that there is a need for new approaches based on ideally universal principles. Since, in general, CBMs of communities have been extensively reviewed (see, e.g. [37–39]), we only highlight some properties and examples of the possible model configurations in Table 1.

Table 1. Examples of community metabolic network analysis strategies.

A community-level metabolic network model can be defined in different ways. Three main approaches are shown here: lumped, compartmentalized and independent networks.

	Lumped	Compartmentalized	Independent
Properties	Supra-organism objective; unresolved community abundance	Community-level objective; scaling for individual abundances	Individual or multilevel objectives; individual abundances
Example references	[47]	[36,48]	[47,49]
Well suited for	Exploration of community metabolic potential with no need of individual resolution	Study, design and prediction of communities at steady state (controlled environments)	Study, design and prediction of dynamic communities and metabolic interaction with the environment

Recently, Beck et al. [40] studied the ecological acclimation to stresses from high irradiance, O₂/CO₂ competition and nutrient limitation in the thermophilic cyanobacterium Thermosynechococcus elongatus BP-1 with EMA and resource allocation theory. T. elongatus is often found in nature in association with heterotrophs in bacterial mats and the authors could assess the impact of stress acclimation on the cyanobacterium's community interactions. Indeed, the analysis of the phenotypic space revealed that reduced carbon byproducts are secreted under environmental stress, creating a favorable ecological niche for heterotrophs. Cross-feeding is a possible strategy for stress relief, as aerobic heterotrophs like Meiothermus ruber would consume O₂, thus lowering O₂/CO₂ competition, and organic acids, thus preventing inhibitory effects. The predicted heterotroph–photoautotroph ratio as a function of stress acclimation was found to be in accordance with measured data.

The previous example showed how EMA on a single organism can reveal ecosystem configurations favorable for natural community establishment. Another approach to study microbial consortia is to assemble a multi-organism stoichiometric model (see Table 1) and investigate the interdependencies of the community members with FBA. Koch et al. [41] used the compartmentalized method to model a bacterial community of three species of industrial interest for biogas production: Desulfovibrio vulgaris, Methanococcus maripaludis and Methanosarcina barkeri. After assessing the performance of single organism metabolic network models, the authors built a community model with a hierarchical objective for FBA: maximal community growth rate and maximal individual biomass yield. By quantifying the degree of optimality as the ratio between the community growth rate and its expected value when all species use substrates optimally for biomass production, they could investigate different community behaviors. Simulations under different substrate utilizations predicted optimal community compositions and related it to methane yield. This information, to be validated experimentally, is an example of how CBMs can be of interest for industrial microbial community design.

Besides the limitations caused by necessary biological assumptions mentioned earlier, in the context of mathematical modeling of ecosystems the main disadvantage of CBMs is the loss, by construction, of dynamic information. To a certain extent, re-integration of dynamic interaction with external (environmental) nutrient availability is straightforward in the dynamic FBA (dFBA) approach [42]. Exchange reactions are included in the metabolic network and their flux values as determined by FBA represent either import or export of a metabolite. By discretizing time in intervals and assuming quasi-steady-state conditions (i.e. metabolism adjusts quickly to external perturbations), it is possible to update at each time step the metabolite levels based on how much has been consumed or secreted. In the next iteration, the flux boundaries for the subsequent FBA problem are accordingly updated and the process continues. In the next section, we discuss approaches expanding this concept and the need for integration of dynamic and structural models to model ecosystems.

Integration approaches

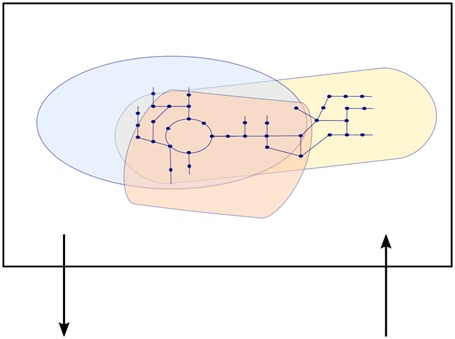
Figure 4 shows a schematic representation of how CBMs and dynamic equations can be integrated. Over the last years, promising approaches to extend dFBA to multi-organism and environmental temporal dynamics have been proposed. The early fundamental works have been previously reviewed, e.g. in [37–39]. We will therefore only briefly highlight some important publications in which a considerable methodological advance was presented. First, Zhuang et al. [43] developed a Dynamic Multi-species Metabolic Modeling framework to couple the CBMs of a Geobacter and a Rhodoferax with a groundwater environment and simulate bacterial competition; then Zomorrodi et al. [44] proposed a multi-objective framework, d-OptCom, that introduced individual- and community-level fitness principles as inner and outer optimization problems, respectively; going a step further, Harcombe et al. [45] added spatial dynamics to the temporal evolution of communities by simulating dFBA on a lattice. More recently, Phalak et al. [46] obtained a temporal and spatial representation with genome-scale resolution of a community of bacteria found in chronic wound biofilm, Pseudomonas aeruginosa and Staphylococcus aureus. The FBA problem is formulated as a series of LP problems with different objectives (maximizing growth, minimizing byproduct secretion and maximizing consumption of key nutrients) to match biological observations or assumptions. By implementing PDEs to describe the convective and diffusional processes in the biofilm layer, the authors could predict the spatial partitioning of the two species. The model also allowed assessing the impact of nutrient competition, cross-feeding and inhibition of S. aureus by a small molecule secreted by P. aeruginosa.

Figure 4. Example integration of CBMs and dynamic equations.

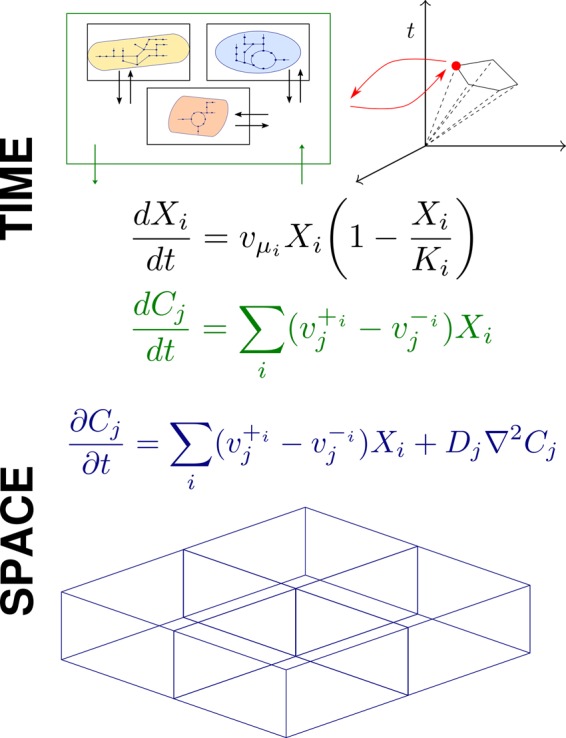
Methods like FBA provide a metabolic flux distribution at steady state. Assuming a quasi-steady state, it is possible to interface FBA with ODEs to capture temporal environmental changes (typically, nutrient availability) and growth dynamics. The spatial component, in particular in terms of particle diffusion, can be obtained by integrating FBA with PDEs. Space can be discretized to reduce the computational cost of the simulation.

All the examples cited so far, relying on more or less stringent biological assumptions, are able to capture certain aspects of ecosystem dynamics directly driven by metabolic interactions like cross-feeding or competition. Assuming that automated reconstruction of functional genome-scale CBMs will substantially improve in the near future, major critical points are still to be addressed. Relevant mechanisms of community behavior are lost because of intrinsic limitations of CBMs (e.g. cofactor dependence of enzymatic activities is modeled by hardcoding cofactors in the biomass function). The implementation of bi-level objective functions still forces the microbes to act following subjective assumptions that might be specific for only certain experimental conditions. The phenomena modeled are in general relative to only organism-level scales, and little abstraction is used to simplify the problem under study, which is one of the strengths of mathematical models.

Perspectives

The technical capability to sequence natural microbial communities including strains that are not culturable in the laboratory opens up a fascinating scenario of possible novel discoveries. Furthermore, a deeper understanding of the mechanisms that regulate and stabilize ecosystems is becoming crucial today to address grand societal challenges like food security and bioremediation.

Theoretical ecology has developed sound mathematical methods to understand emergent dynamics of ecosystems. Dynamic models have the advantage of being easily applied to different spatio-temporal scales, but they often require educated guesses on the fundamental processes to be examined. They are therefore not suitable for systematic surveys of the metabolic capabilities of microbial communities. Multi-organism genome-scale metabolic modeling is today still challenging and heavily based on a priori assumptions, but it is also a rapidly developing field. While still in its infancy, it already now offers insights into the structural properties of metabolism and allows to study pathway optimization and strain engineering, and it is becoming a major investigation tool, owing also to the significant efforts from the systems biology community to integrate it with experimental data. However, genome-scale metabolic modeling alone ignores a fundamental aspect of ecosystems: the cellular response to dynamic environmental changes. These include processes with similar local effects but acting at diverse spatio-temporal scales [4], like changes in nutrient availability caused by global geochemical cycles (e.g. the nitrogen cycle) or man-made perturbations (e.g. artificial fertilizers).

Recently, there has been rising interest in modeling approaches that integrate different methods, and in this manuscript we focused on two of them. We believe that current theoretical tools can achieve a much higher predictive power by following two principles: simplicity and scalability. By recognizing key strengths of specific methods and integrating them to represent multi-scale phenomena, it will be possible to disentangle the complex web of interactions in microbial ecosystem and engineer synthetic communities.

Abbreviations

CBM

constraint-based model

dFBA

dynamic flux balance analysis

EMA

elementary mode analysis

FBA

flux balance analysis

gLV

generalized Lotka–Volterra

LP

linear programming

LV

Lotka–Volterra

ODEs

ordinary differential equations

PDEs

partial differential equations

Author Contribution

A.S. conceived and wrote the first manuscript version. A.S. and O.E. wrote and approved the final version.

Funding

The authors are supported by funding from the Deutsche Forschungsgemeinschaft (EXC-1028-CEPLAS).

Competing Interests

The Authors declare that there are no competing interests associated with the manuscript.