Abstract
Research on spatial non-stationarity of land-cover classification accuracy has been ongoing for over two decades with most of the work focusing on single date maps. We extend the understanding of thematic map accuracy spatial patterns by: (1) quantifying spatial patterns of map-reference agreement for class-specific land-cover change rather than class-specific land cover for both omission and commission expressions of map error; (2) reporting goodness-of-fit estimates for the empirical models, which have been lacking in previous assessments, and; (3) using the empirical model results to map the locations of the relative likelihoods of map-reference agreement for specific land-cover change classes. We evaluated 10 map-based explanatory variables in single and multivariable logistic regression models to predict the likelihood of agreement between map and reference land-cover change (2001–2011) labels using the National Land Cover Database (NLCD) 2011 land cover and accuracy data. Logistic models for omission error had better goodness-of-fit estimates than models for commission error. For the omission error models, the explanatory variable, density of the mapped class-specific change in the immediate neighbourhood surrounding the sample pixel, produced the best model fit results (Tjur coefficient of discrimination, D, ranged from 0.59 to 0.98) compared to multivariable models and all other single explanatory variable models. Maps of the predicted likelihood of map-reference agreement produced from the best fitting omission error models provide a spatially explicit description of spatial variation of classification uncertainty at both local and regional scales. Application of the models indicated higher likelihoods of agreement (>50%) comprised a greater proportion of the land-cover change class area than the proportion of the land-cover change class with lower likelihoods of agreement. NLCD users can apply reported equations to map land-cover change uncertainty.
1. Introduction
Comparison of mapped land-cover labels from a remotely sensed product to reference land-cover labels acquired from higher resolution media is a standard of practice for assessment of land-cover thematic map accuracy (Olofsson et al. 2014; Stehman 2009; Stehman and Czaplewski 1998). The map and reference land-cover labels are compared using a c-x-c cross-tabulation matrix, which shows agreement and disagreement on a class-specific basis for the c mapped classes in a remotely sensed land-cover product. The cross-tabulation matrix is the basis for several statistics that are used to describe map accuracy, including overall agreement and class-specific errors of omission and commission.
Research on the spatial pattern of land-cover accuracy has been a consistent theme for 25 years. The research has been motivated by the realization that the cross-tabulation matrix (hereafter, error matrix) does not provide information on spatial patterns of error and therefore cannot account for changes in error rates that might arise from changing landscape patterns across a map. Several approaches have been used to articulate the influence of spatial pattern on land-cover accuracy. McGwire and Fisher (2001) and Foody (2005) proposed construction of multiple error matrices (up to allowable precision limits) for a single map to uncover how error patterns change spatially. Spatial patterns of land-cover uncertainty have been developed from: (1) the class membership probabilities that often accompany classification algorithms (Bogaert, Waldner, and Defourny 2016; Brown, Foody, and Atkinson 2009; Loosvelt et al. 2012; Löw, Knöfel, and Conrad 2015); (2) spatial statistics including spatial interpolation (Comber et al. 2012; Congalton 1988; Khatami, Mountrakis, and Stehman 2017; Steele, Winne, and Redmond 1998); (3) and regression of map-reference agreement against landscape factors such as topography, roads, and land-cover spatial patterns (Castilla et al. 2014; Moisen, Cutler, and Edwards 1999; Smith et al. 2002; Smith et al. 2003; van Oort 2004; Yu et al. 2008). Each of these research efforts has shown that rates of land-cover misclassification are not constant across a map.
Past research on spatial patterns of land-cover misclassification has been constrained to single date maps. Research efforts to extend spatial patterns of land-cover misclassification to land-cover change are only now beginning to emerge (e.g. Yao, Zhang, and Zhang 2014; Mei and Zhang 2014). This emergence is not unanticipated because land cover is the principle measurement of the capital stock of natural resources from which society derives both necessities (e.g. clean water) and benefits (e.g. recreation), and therefore change in that capital stock intuitively affects provision of those necessities and benefits (Foley et al. 2005). Because of the importance of land-cover change to environmental sustainability and society writ large, the measurement, monitoring, and driving forces of land cover has become its own discipline (Aspinall 2006; Rindfuss et al. 2004; Turner, Lambin, and Reenberg 2007). Understanding spatial patterns of land-cover change misclassification is an important component of the measurement and monitoring of land-cover change.
The U.S. National Land Cover Database (NLCD), a product of the MultiResolution Land Characteristics Consortium (MRLC) (U.S. EPA, 2017), is a monitoring programme that has produced land-cover products for ca. 2001, 2006, and 2011 (Homer et al. 2007; Homer et al. 2015; Fry et al. 2011). Accuracy assessments have been produced for each product (NLCD 2001, NLCD 2006, NLCD 2011) (Wickham et al. 2010; Wickham et al. 2013; Wickham et al. 2017) following well-established standards for land-cover accuracy assessment (Stehman and Czaplewski 1998; Stehman 2001; Stehman et al. 2003). However, no attempt has been made to explore spatial non-stationarity of accuracy patterns for NLCD land-cover change data. The objectives of this research are twofold: (1) extend the error matrix based accuracy results for the NLCD 2011 product (Wickham et al. 2017) by examining spatial patterns of land-cover change accuracy, and; (2) use the empirical models of land-cover change accuracy to map the uncertainty of agreement for specific land-cover change themes. Spatial characterization of uncertainty is likely to be valuable to data users.
2. Methods
The NLCD 2011 product includes land cover and land-cover change for the nominal dates of 2001, 2006, and 2011 (Homer et al. 2015). The products were aligned temporally by identifying areas of spectral change followed by assignment of new land-cover labels for those pixels using a suite of modelling tools and ancillary data (Jin et al. 2013). An accuracy assessment (Wickham et al. 2017) was undertaken following completion of NLCD 2011, using design principles established at the outset of NLCD mapping (Stehman et al. 2003). The NLCD 2011 accuracy assessment used 8000 sample pixels (Stehman and Wickham 2011) to report accuracy for land cover and land-cover change. The reference data were collected from the Google Earth™ historical image archive by a team of four photointerpreters, using the image date that most closely matched the Landsat TM acquisition to determine the reference label. We used the land-cover change data for the terminal NLCD dates (2001 and 2011) organized into 20 reporting themes for this analysis. The 20 reporting themes were loss, gain, and no change for the seven NLCD Level I classes (Table S1) – water, urban, forest, shrubland, grassland, agriculture, and wetland, with the exception that there was no urban loss reporting theme.
Consistent with studies by Castilla et al. (2014), Moisen, Cutler, and Edwards (1999), Smith et al. (2002, 2003), van Oort (2004), and Yu et al. (2008), logistic regression modelling was used to assess the spatial pattern of land-cover change uncertainty. The binary response variable of agreement or disagreement was regressed against land-cover spatial patterns metrics and other landscape factors. Unlike the previous studies cited, we applied separate logistic models to omission error and commission error for each of the 20 reporting themes. The logistic regression modelling approach used here also could have been applied to overall accuracy. We did not include overall accuracy as one of the themes because we anticipated that modelling accuracy of class-specific changes (i.e. reporting themes) would be more relevant to users of NLCD data.
The omission and commission error data were constructed through a series of three database queries. Omission error data were based on the requirement that the map labels matched the reference labels, whereas the commission error data were based on the requirement that the reference labels matched the map labels. The initial query was used distinguish between omission and commission error. For the omission error tables, the initial query was based on the reference data. An example would be selection of all reference data that equalled urban gain (not urban in 2001 and urban in 2011). The second query was selection, from only those sample pixels identified from the first query, all pixels where the map labels also equalled urban gain. This subset of data represented all sample pixels where map and reference labels matched. The binary response variable, Agree, was set to 1 for these pixels. The third query added back all the reference labels that equalled urban gain (i.e. the initial query), and Agree was set to 0 for all the sample pixels that were added back from executing the third query. To create the commission error data, the initial query was based on the map (i.e. map labels that identified urban gain), the second query selected the reference labels that matched the map, and the third query added back all the map labels that equalled urban gain.
Logistic regression modelling (SAS Institute Inc. 2009) was implemented using the following steps: (1) 10 candidate explanatory variables (Table 1) were evaluated to determine the best single variable logistic models (based on the explanatory variable that yielded the smallest p-value for the test of the parameter coefficient of that variable); (2) multivariable models were evaluated by adding remaining candidate explanatory variables and non-target variables (explained below) to the best single variable models; and (3) evaluation of the regional variable (Table 1) in the best models realized from implementing steps 1 and 2. Nine of the 10 candidate explanatory variables (Table 1) were dominated by measures of land-cover spatial pattern because they have been shown to be informative in previous research (Castilla et al. 2014; Moisen, Cutler, and Edwards 1999; Smith et al. 2002, 2003; van Oort 2004; Yu et al. 2008). The regional classification variable was included because the NLCD 2011 accuracy assessment was stratified into east and west regions (Wickham et al. 2017). Significance of the regional classification variable in the logistic models would indicate that there was a broad-scale geographic pattern to agreement between map and reference labels in addition to any local-scale patterns identified by the other explanatory variables.
Table 1.
Spatial pattern explanatory variables.
| Variable (abbreviation) | Description |
|---|---|
| Feature density (fdx) | The abundance (number of pixels) of a change class in square window, where X is the side length surrounding a sample pixel. Window side lengths were 3, 5, 7, 15, and 21 pixels, which equates to 0.81, 2.25, 4.41, 20.25, and 36.69 ha, respectively. Abundance was specific to the change class represented by the sample pixel. For urban gain, for example, fdx was the number of pixels in a window of size X2 surrounding the sample pixel where the NLCD 2001 label was not equal to urban and the NLCD 2011 label was equal to urban |
| Heterogeneity (fv) | The number of change classes in a 3-x-3 pixel window around the sample pixel (fv = focal variety). Values can range between 1 and 9, and a value of one (1) indicates homogeneity in the 0.81 ha neighbourhood surrounding the sample pixel. The change class was defined as the number of different class combinations from conflation of the NLCD 2001 and NLCD 2011 maps (e.g. urban–urban, forest–grassland, forest–urban) |
| Patch size (ps) | The area of like-classified adjacent pixels in which the sample pixel was embedded. Adjacency was defined using the ‘queen’s’ rule: like-classified pixels sharing edges and corners. Like-classification was based on the combined NLCD 2001 and 2011 land cover labels. PS was based on the combined labels, not the reporting themes (e.g. forest loss). For example, if NLCD land cover labels were water (2001) and urban (2011), ps was the number of adjacent (queen’s rule) water–urban pixels |
| Aspect (Ia) | Aspect was derived from a slope map developed from the 30m-x-30m pixel National Elevation Dataset (NED) (Gesch et al. 2002). The 0°–360° aspect map was converted to a 0–1 range (Ia = integrated aspect), where 135° (southeast) was set to 1 and 315° (northwest) was set to 0. Aspect increased linearly in both directions from the minimum value at 315° to the maximum value at 135°. True southeast (135°) was set to 1 because the local Landsat TM acquisition time is 10:30AM and thus southeastern aspects should be the most illuminated. We assumed that classification accuracy would decline as illumination declined. |
| Distance to nearest road (D2Rd) | Euclidean distance (metres) from the sample pixel to the nearest road. NAVTEQ was used as the roads data. Distances were not log transformed, and log transformation did not influence results. |
| Region (R) | A classification variable (east = 1; west = 2) was used to stratify the NLCD 2011 accuracy assessment (Wickham et al. 2017). The east-west boundary was at approximately 100° 0′ 00″W using a boundary line based on the mapping zones (Homer and Gallant 2001) developed for the original NLCD 2001 project (Homer et al. 2004). |
Steps 1, 2, and 3 were implemented sequentially. In step 1, each explanatory variable was used in a single variable logistic regression model to evaluate its performance with respect to patterns of map-reference agreement. Multivariable models (i.e. greater than one explanatory variable) were then evaluated against the best single variable models (step 2) using the remaining variables listed in Table 1 (excluding the regional classification variable) and the non-target variables to determine if the inclusion of additional variables improved model performance. Multivariable models were evaluated using stepwise selection with p ≤ 0.05 used as the significance level for entry into and remaining in the model, and were informed by prior examination of bivariate correlations among the explanatory variables and estimation of tolerance and variance inflation factors (VIF) from ordinary least squares regression (OLS). In step 3, the regional classification variable was then evaluated to determine if it should be added to the best model realized from steps 1 and 2 for each reporting theme and each expression of error (omission, commission). The regional classification variable was used to evaluate whether separate slopes and separate intercepts were required for east and west regions (i.e. a region by explanatory variable interaction). All final models were also tested for spatial autocorrelation of the residuals using Moran’s I, and the resulting p-values indicated that the spatial patterns of residuals were not significantly different from random (Table S2). Statistical models that accounted for spatial correlation would have been used if Moran’s I values had not indicated a random distribution of residuals.
Non-target explanatory variables were evaluated for inclusion in the logistic models because the single date error matrices from the NLCD 2011 accuracy assessment showed high classification error along the forest-shrubland-grassland gradient and among the different classes that included a significant herbaceous component, such as pasture, grassland, and open urban (see Table S1) (Wickham et al. 2017). Non-target variables were defined as feature density (fdx) for the six NLCD level I classes other than the class of the response variable being evaluated in the class-specific (i.e. reporting theme) model. For the model for agriculture loss, for example, the non-target variables included fdx for loss, gain, and no change for the urban, forest, shrubland, and grassland NLCD Level I classes. The water and wetland NLCD Level I classes were not included because of their small sample sizes. To limit the number of possible non-target variables, only the non-target fdx variable matching the best target fdx variable realized in step 1 was included. If the best step 1, single variable model for urban gain, for example, included fd5 as the explanatory variable, then only the fd5 variable for non-target NLCD Level I classes would have been evaluated in step 2.
The logistic models included Firth (1993) adjustments where appropriate. The stratified random sampling used for the NLCD 2011 accuracy assessment (Wickham et al. 2017) focused on changes among forest, shrubland, grassland, and urban, and therefore there were fewer sample pixels for analysis of land-cover changes involving wetland and water, and for the omission error dataset for agriculture gain. When sample sizes are small, it is more common for complete or nearly complete separation of observations by response level (agree = 0; agree = 1) to occur (Figure 1). Maximum likelihood estimates of the logistic function are not estimable when there is complete or nearly complete separation. Therefore, we included Firth (1993) adjustments to reduce bias in parameter estimation by penalized maximum likelihood estimation. Firth adjustments were used for wetland gain (omission), water loss (omission), water gain (omission), and agriculture gain (omission).
Figure 1.
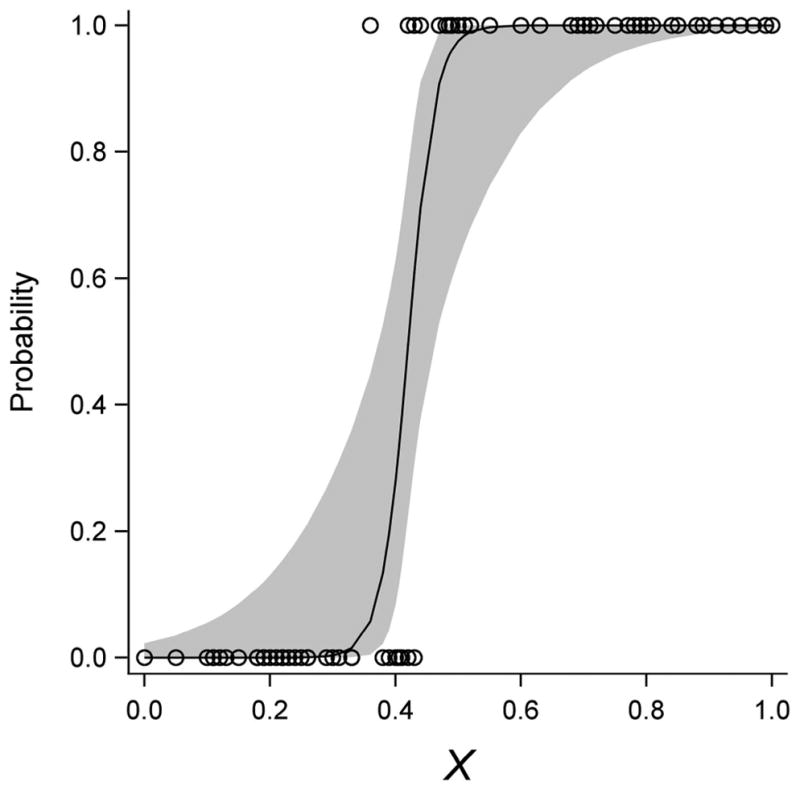
Hypothetical logistic regression model of y = agreement with an explanatory variable x. The open circles represent observed values of x for y = 1 (agreement) and y = 0 (disagreement). The line represents the modelled relationship, and the shaded band is 95% confidence interval. Complete (or nearly so) separation would occur if the observations at y = 0, x > 0.375 (outside confidence interval band) were removed, requiring Firth (1993) adjustments to derive reliable parameter estimates.
We assessed model fit using percentage concordance and the Tjur (2009) coefficient of discrimination (D). Concordance is the comparison of the logistic model predicted outcomes for all possible pairs of sample pixels for which one pixel had disagreement and the other pixel had agreement. The pair is concordant if the agreement observation has a higher predicted value than its paired counterpart for which disagreement was observed. The percentage of concordant 0–1 (disagreement-agreement) pairs is based on the total number of 0–1 pairs; sample pixel pairs that are both agreement (1–1) and both disagreement (0–0) are not included. D (Tjur 2009) is derived by grouping the observations by their observed binary values (i.e. 0, 1) and calculating the absolute value of the difference of the group means from the model-estimated probabilities. D is easy to calculate (Allison 2014) and, like the coefficient of determination (R2) for OLS, ranges between 0 and 1 (SAS 2017).
The explanatory variables from the logistic regression models that produced the best results for each theme were then used to produce maps of the spatial pattern of the likelihood of map-reference agreement (accuracy) for that theme. The slopes and intercepts from the logistic models were applied to every pixel for a given change theme to produce a map of the likelihood of map-reference agreement. The spatial pattern maps provide NLCD data users with pixel-by-pixel geographic information on the likelihood of map-reference agreement for each theme (e.g. shrubland loss).
3. Results
Several patterns emerged from the logistic regression modelling (Table 2). Single variable models (agreement versus a single explanatory variable) provided the best goodness-of-fit results. None of the multivariable models improved model performance relative to the best single variable models. Tjur (2009) coefficients of discrimination (D) were very high for the omission error models, but were much lower and more variable for commission error models. The percentage concordance statistics followed the same pattern. For the omission error models, D exceeded 0.8 for 16 of the 20 models, and concordance values exceeded 95% in all but one case. Conversely, the commission error models had low goodness-of-fit measures, with D ranging from 0.04 to 0.46 and concordance ranging from 58.5% to 90.5%. For all omission error models except wetland loss, the variable fd3, density (proportion) of class-specific change in a 3-x-3 pixel window surrounding the sample pixel, was the most significant explanatory variable (Table 3). In the case of wetland loss, nearly identical D values occurred for the single variable models using fd3, fd5, and fd7. The most important explanatory variables for the single variable commission error models were an assortment of the different feature density variables (fd3, fd5, fd7, fd15, and fd21).
Table 2.
Logistic regression results for agreement versus fdx.
| Change theme | Omission | Commission | ||||||
|---|---|---|---|---|---|---|---|---|
|
|
|
|||||||
| # Obs | Var | D | Concordance | # Obs | Var | D | Concordance | |
| Forest loss | 912 | fd3 | 0.73 | 96.4 | 852 | fd7 | 0.17 | 74.7 |
| Forest gain | 439 | fd3 | 0.89 | 99.2 | 352 | fd21 | 0.08 | 67.1 |
| Forest, no change | 2246 | fd3 | 0.83 | 98.2 | 1360 | fd5 | 0.07 | 71.3 |
| Shrub loss | 616 | fd3 | 0.84 | 98.6 | 749 | fd7 | 0.06 | 64.0 |
| Shrub gain | 674 | fd3 | 0.87 | 99.0 | 608 | fd7 | 0.11 | 67.9 |
| Shrub, no change | 1409 | fd3 | 0.84 | 98.6 | 616 | fd21 | 0.38 | 88.0 |
| Grassland loss | 568 | fd3 | 0.92 | 99.5 | 735 | fd7 | 0.06 | 64.4 |
| Grassland gain | 441 | fd3 | 0.91 | 99.4 | 529 | fd5 | 0.04 | 58.5 |
| Grassland, no change | 1437 | fd3 | 0.83 | 98.8 | 493 | fd21 | 0.21 | 78.6 |
| Urban gain | 1573 | fd3 | 0.92 | 98.7 | 923 | fd5 | 0.12 | 68.1 |
| Urban, no change | 1330 | fd3 | 0.75 | 96.5 | 835 | fd15 | 0.14 | 81.6 |
| Agriculture loss | 303 | fd3 | 0.84 | 98.5 | 270 | fd15 | 0.15 | 71.9 |
| Agriculture gain | 95 | fd3 | 0.98 | 100.0 | 185 | fd7 | 0.09 | 68.1 |
| Agriculture, no change | 1711 | fd3 | 0.84 | 98.5 | 1152 | fd7 | 0.08 | 69.8 |
| Wetland loss | 40 | fd7 | 0.59 | 97.7 | 26 | fd15 | 0.46 | 90.5 |
| Wetland gain | 17 | fd3 | 0.83 | 100.0 | 27 | |||
| Wetland, no change | 603 | fd3 | 0.81 | 97.9 | 462 | fd15 | 0.15 | 74.1 |
| Water loss | 24 | fd3 | 0.85 | 100.0 | 20 | fd3 | 0.29 | 72.0 |
| Water gain | 42 | fd3 | 0.85 | 99.3 | 18 | |||
| Water, no change | 257 | fd3 | 0.92 | 99.6 | 196 | fd3 | 0.30 | 76.7 |
The regional classification variable was significant (p < 0.05) for cases in bold typeface. Blank entries denote that none of the explanatory variables was significant. Underlined entries denote use of Firth adjustments.
Table 3.
Estimated probabilities for a match between map and reference labels for omission error logistic models (a) and slopes and intercepts for logistic model Agree = fd3 (b).
| (a) | fd3 = 1 | fd3 = 2 | fd3 = 3 | fd3 = 4 | fd3 = 5 | fd3 = 6 | fd3 = 7 | fd3 = 8 | fd3 = 9 |
|---|---|---|---|---|---|---|---|---|---|
| Class | (0.11) | (0.22) | (0.33) | (0.44) | (0.55) | (0.67) | (0.78) | (0.89) | (1.00) |
| Urban gain | 0.12 | 0.43 | 0.81 | 0.96 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 |
| Urban no change | 0.04 | 0.10 | 0.24 | 0.48 | 0.73 | 0.89 | 0.96 | 0.99 | 1.00 |
| Forest loss | 0.05 | 0.14 | 0.32 | 0.59 | 0.81 | 0.92 | 0.97 | 0.99 | 1.00 |
| Forest gain | 0.05 | 0.21 | 0.60 | 0.89 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 |
| Forest no change | 0.01 | 0.02 | 0.08 | 0.25 | 0.55 | 0.81 | 0.94 | 0.98 | 1.00 |
| Shrub loss | 0.07 | 0.25 | 0.59 | 0.87 | 0.97 | 0.99 | 1.00 | 1.00 | 1.00 |
| Shrub gain | 0.03 | 0.12 | 0.35 | 0.68 | 0.89 | 0.97 | 0.99 | 1.00 | 1.00 |
| Shrub no change | 0.01 | 0.02 | 0.06 | 0.17 | 0.41 | 0.70 | 0.88 | 0.96 | 0.99 |
| Grass loss | 0.03 | 0.17 | 0.53 | 0.86 | 0.97 | 0.99 | 1.00 | 1.00 | 1.00 |
| Grass gain | 0.01 | 0.08 | 0.38 | 0.81 | 0.97 | 1.00 | 1.00 | 1.00 | 1.00 |
| Grass no change | 0.01 | 0.03 | 0.09 | 0.23 | 0.48 | 0.74 | 0.90 | 0.96 | 0.99 |
| Agric. loss | 0.05 | 0.14 | 0.32 | 0.58 | 0.80 | 0.92 | 0.97 | 0.99 | 1.00 |
| Agric. gain | 0.04 | 0.18 | 0.50 | 0.83 | 0.96 | 0.99 | 1.00 | 1.00 | 1.00 |
| Agric. no change | 0.00 | 0.02 | 0.06 | 0.20 | 0.50 | 0.80 | 0.94 | 0.98 | 1.00 |
|
| |||||||||
| (b) | |||||||||
| Class | Slope (b1) | Intercept (b0) | |||||||
|
| |||||||||
| Urban gain | 15.616 | −3.719 | |||||||
| Urban no change | 9.685 | −4.370 | |||||||
| Forest loss | 9.757 | −3.992 | |||||||
| Forest gain | 15.311 | −4.711 | |||||||
| Forest no change | 11.615 | −6.269 | |||||||
| Shrub loss | 13.553 | −4.134 | |||||||
| Shrub gain | 12.498 | −4.803 | |||||||
| Shrub no change | 10.770 | −6.349 | |||||||
| Grass loss | 15.546 | −5.054 | |||||||
| Grass gain | 17.471 | −6.404 | |||||||
| Grass no change | 10.038 | −5.656 | |||||||
| Agric. loss | 9.568 | −3.934 | |||||||
| Agric. gain | 14.028 | −4.660 | |||||||
| Agric. no change | 12.417 | −6.909 | |||||||
Values in 3a are calculated using the equation p = exp((fd3*b1) – b0)/(1 + (exp(fd3*b1) – b0)), where b1: slope; b0: intercept; exp: ex; and fd3 is expressed as a proportion. Wetland and water results are not reported due to small sample sizes. Values <0.005 in 3a are reported as 0.00.
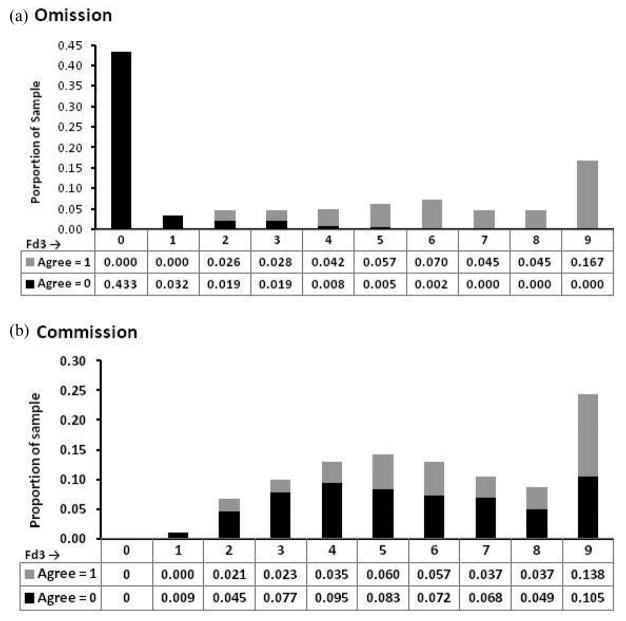
The distinct differences in goodness-of-fit between the omission error and commission error logistic regression models were evident in histograms that are useful for conceptualizing calculation and interpretation of D (Figure 2). The histograms for omission error had stark differences in the distributions of agreement as a function of the value of fd3 (Figure 2(a)), whereas the histograms for commission error did not (Figure 2(b)). The difference in the distributions can be traced back to the construction of the respective datasets. For the omission error sample data, the third query (see Methods) added map locations where the reference labels did not match the change identified in the map, and therefore fd3 tended to be zero (0). D tended to be high for omission-error models because the likelihood of disagreement increased as fd3 decreased and the likelihood of agreement increased as fd3 increased, creating a large difference in the estimated mean probabilities of agreement between the two groups (agree = 0, agree = 1). Large differences in the mean probabilities produced high values of D.
Figure 2.
Stacked bar charts of shrubland loss organized by fd3 and agreement (agree = 1 if map and reference labels match) for (a) omission and (b) commission. Values are the proportion of the total sample size (omission = 616; commission = 749).
The estimated probabilities from the best, single variable omission error models indicated that accuracy of the no change theme was less sensitive to its context than the loss and gain themes (Table 3). In other words, a higher density of no change than change (loss or gain) was required to produce an equivalent likelihood of map-reference agreement. These results were consistent with the 2001–2011 loss, gain, and no change producer’s accuracies reported by Wickham et al. (2017) in that producer’s accuracies for the no change themes were much higher than those for the loss and gain themes. Spatial pattern was expected to be less influential for the no change theme because the aspatial error matrix results suggested there was much less improvement in accuracy that could be realized with changes in spatial pattern metrics.
The other explanatory variables (fv, ps, Ia, D2Rd) were either not statistically significant or their explanatory value was much lower than fd3 (Table S3). Heterogeneity (fv) and patch size (ps) tended to yield lower values of D for single variable models and did not contribute to improved model performance for multivariable models. Aspect (Ia) and distance between the sample pixel and the nearest road (D2Rd) were rarely statistically significant. The regional variable was significant for 5 of the 20 omission-error logistic models (Table 2). In all five cases, intercepts were significantly different but slopes were not statistically different. The estimated likelihood of agreement tended to be higher in the western region than the eastern region for a given value of fd3, but the rate of change in the estimated likelihood of agreement as fd3 varied was not significantly different across regions.
There was a scale dependency between goodness-of-fit and the size of the square pixel window for the omission-based, single variable logistic models that had fdx as the lone explanatory variable (Table 4). D values decreased, often sharply, as the area of the square pixel window surrounding the sample pixel increased. Median differences in D for the first three spatial scales was 0.09 for fd3 versus fd5 and 0.07 for fd5 versus fd7, ultimately resulting in an overall (fd3 versus fd21) median difference of 0.40. The main exceptions to this pattern occurred when Firth adjustments to the logistic model were required. Models requiring Firth adjustments tended to have smaller changes in D as a function of the spatial scale over which feature density (fdx) was measured.
Table 4.
Coefficients of discrimination (D) as a function of pixel window size (side length in pixels) for single variable omission error logistic regression models.
| Land-cover change class | Coefficient of discrimination, D | ||||
|---|---|---|---|---|---|
|
| |||||
| fd3 | fd5 | fd7 | fd15 | fd21 | |
| Forest loss | 0.73 | 0.60 | 0.50 | 0.34 | 0.28 |
| Forest gain | 0.89 | 0.79 | 0.70 | 0.49 | 0.41 |
| Forest no change | 0.83 | 0.71 | 0.62 | 0.45 | 0.39 |
| Shrubland loss | 0.84 | 0.73 | 0.65 | 0.48 | 0.43 |
| Shrubland gain | 0.87 | 0.77 | 0.70 | 0.52 | 0.73 |
| Shrubland no change | 0.89 | 0.82 | 0.78 | 0.70 | 0.58 |
| Grassland loss | 0.92 | 0.86 | 0.80 | 0.63 | 0.55 |
| Grassland gain | 0.91 | 0.83 | 0.74 | 0.53 | 0.43 |
| Grassland no change | 0.68 | 0.66 | 0.64 | 0.55 | 0.50 |
| Urban gain | 0.92 | 0.89 | 0.85 | 0.64 | 0.55 |
| Urban no change | 0.75 | 0.61 | 0.52 | 0.38 | 0.29 |
| Agriculture loss | 0.84 | 0.79 | 0.73 | 0.60 | 0.54 |
| Agriculture gain | 0.98 | 0.98 | 0.98 | 0.96 | 0.93 |
| Agriculture no change | 0.84 | 0.74 | 0.67 | 0.51 | 0.44 |
| Wetland loss | 0.55 | 0.55 | 0.59 | 0.36 | 0.33 |
| Wetland gain | 0.83 | 0.81 | 0.71 | NS | NS |
| Wetland no change | 0.81 | 0.68 | 0.61 | 0.44 | 0.38 |
| Water loss H | 0.85 | 0.81 | 0.73 | 0.62 | 0.51 |
| Water gain | 0.85 | 0.68 | 0.61 | 0.43 | 0.36 |
| Water no change | 0.92 | 0.78 | 0.70 | 0.54 | 0.49 |
Italicized and underlined cell entries in are based on Firth adjustments to the logistic models.
Addition of fdx variables for non-target themes to the best single variable models for commission error yielded improvements in D of 0.00–0.16 (Table S3). Across all change themes, improvements in D tended to be small and did not result in substantially improved model fit. For shrubland gain, for example, addition of non-target themes yielded a D = 0.27, which was an improvement when compared to a D = 0.11 for the best single variable model (Table 2). In other words, despite the confusion between forest, shrubland, and grassland in the single date NLCD data, presence of forest or grassland was not strongly related to the error pattern of shrubland gain for commission error. Overall, the confusion among forest, shrubland, grassland, agriculture and urban in the 2001 and 2011 eras of the single date NLCD data (Wickham et al. 2017) was not useful in explaining spatial patterns of error among their associated land-cover change classes. Addition of non-target themes to target themes for omission-based models was not evaluated because goodness-of-fit estimates were already high and therefore substantial improvements in model fit were unlikely.
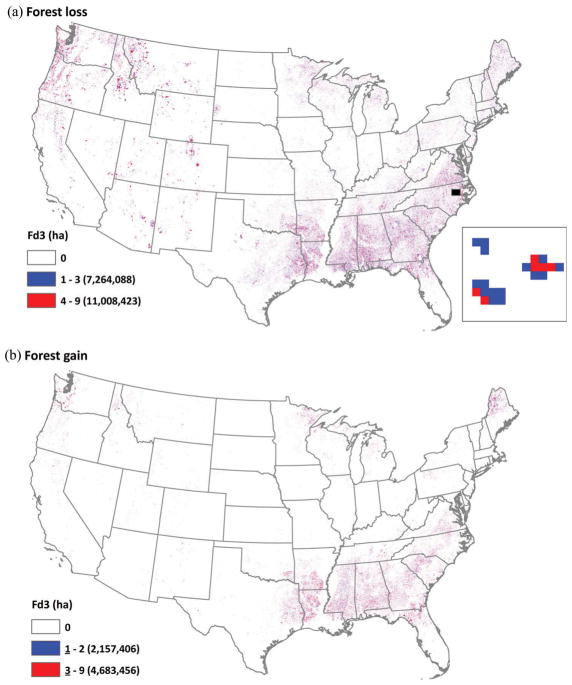
Application of the best omission error logistic regression models (agree = fd3) results to the land-cover change maps revealed local- and regional-scale geographic variation in the spatial pattern of the likelihood of map-reference agreement for loss and gain of forest (Figure 3), shrubland (Figure S1), grassland (Figure S2), agriculture (Figure S3), and urban gain (Figure S4). In general, pixels with lower likelihoods of map-reference agreement (fd3 < 50%) formed ‘halos’ around pixels with higher likelihoods of map-reference agreement (fd3 > 50%). Interspersion of low (fd3 < 50%) and high (fd3 > 50%) likelihoods of map-reference agreement across all loss and gain themes reflect the influence of edge pixels in the formation of ‘halos’ of low likelihoods surrounding areas of higher likelihoods, and regional changes in the preponderance of low and high likelihoods reflect broader scale differences in the patch characteristics of a particular change theme (Figure 3, Figures S1–S4). For example, forest loss accuracy may be higher overall along the Texas-Louisiana border than further west in Texas (Figure 3(a)). Across all change themes (Figure 3, Figures S1–S4), the percentage area representing higher likelihoods (>50%) of map-reference agreement was greater than the percentage area representing lower likelihoods (<50%) of map-reference agreement. The range of ratios across all loss and gain themes was 1.12 (agriculture loss) to 2.85 (urban gain). The range of ratios may reflect differences in patch and edge characteristics across the land-cover change themes. The high ratio for urban gain may indicate that conversions to urban tend to have less edginess and occur in larger patches that have a higher proportion of interior pixels than other land-cover change themes. The ratios also indicate that most change pixels have a higher (>50%) likelihood of correctly capturing change.
Figure 3.
Spatial pattern of fd3 for forest (a) loss and (b) gain. The fd3 thresholds are the values that most closely corresponded to ±50% likelihood of map-reference agreement (Table 3). Values of fd3 were grown by two pixels and re-sampled to 150 m for display. The black box (exaggerated for display) is the location of the cut-out in panel a. Pixels in the cut-out are displayed at their native 30 m resolution.
4. Discussion
We found that local-scale map spatial pattern, expressed as the density of class-specific land-cover change (e.g. urban gain) in the 3-x-3 pixel neighbourhood surrounding a sample pixel, was a significant predictor of omission error for land-cover change. Conversely, the map spatial pattern variables were statistically significant but rather weak predictors of commission error for land-cover change. These results suggest that the density of mapped change has a substantial influence on reference label assignment, but the presence of densely mapped change itself does not guarantee that the assigned reference label will agree with the map label. Relatively small increases in the density of mapped land-cover change over a small area increased the likelihood of map-reference agreement but did not fully explain spatial patterns of agreement because commission error was much less sensitive to density of mapped land-cover change.
The results reported here are not fully consistent with previous results where map-based variables were used in logistic regression models to estimate their influence on the likelihood of map-reference agreement for static land-cover maps. We found that heterogeneity (i.e. fv) and patch size (ps) were poor predictors of the likelihood of agreement between map and reference labels for land-cover change classes, whereas van Oort et al. (2004) and Smith et al. (2002), (2003)) found that these variables were significant predictors of the likelihood of matches between map and reference land-cover class labels for single date land-cover maps. Furthermore, van Oort et al. (2004) found that fd3 was a poor predictor of agreement between map and reference labels. It is possible that contextual information is used differently for collection of reference labels for land-cover change than for land cover. Land-cover accuracy assessment is based on the question ‘which land cover label, among the available set of land cover labels, is the correct or most correct label?’ For land-cover change accuracy assessment, the question changes to ‘has land cover changed, and, if so, what are the correct or most correct before and after labels?’ The shift in the emphasis of the fundamental assessment question may constitute a shift in how contextual information is used in land-cover change accuracy assessments, but well-designed studies would be needed to test this conjecture.
The relationship between density of mapped change and map-reference agreement should be useful for scientists and practitioners that rely on NLCD land-cover change data. At a local spatial scale, the pattern of ‘halos’ of low likelihood surrounding areas of high likelihood is consistent with results from spectral-based models of higher error rates at edges between land-cover classes (Loosvelt et al. 2012). At a regional spatial scale, the spatial pattern of high and low likelihoods (e.g. ±50%) of map-reference agreement is consistent with the concept that error matrices vary regionally within a map (Foody 2005; McGwire and Fisher 2001). Accuracy of NLCD 2001–2011 land-cover change varies both regionally and locally, and the variability appears to be attributable to spatially varying characteristics of land-cover dynamics.
The estimated likelihoods of map-reference agreement provide easy-to-use information to meet NLCD user needs for spatially referenced accuracy information. NLCD users only need to extract the class-specific themes reported here, use GIS neighbourhood functions to construct feature density maps, and apply the reported equations. User’s should recognize that application of the equations provide a guide to locations where change occurred with higher certainty. The low goodness-of-fit for the commission error models suggests that factors we were unable to model also contributed to the likelihood of map-reference agreement for NLCD Level I loss and gain themes.
Supplementary Material
Acknowledgments
The United States Environmental Protection Agency, through its Office of Research and Development, partly funded and managed the research described here. The article has been reviewed by the US EPA’s Office of Research and Development and approved for publication. We appreciate the insights of M. Nash (US EPA) and anonymous reviewers on previous versions of the article. Approval does not signify that the contents reflect the views of the US EPA. S. Stehman’s participation was underwritten by contract G12AC20221 between SUNY-ESF and USGS.
Footnotes
Disclosure statement
No potential conflict of interest was reported by the authors.
Supplemental data for this article can be accessed here.
References
- Allison PD. Measures of Fit for Logistic Regression. SAS Global Forum: Washington, DC; 2014. Paper. 1485–2014. https://support.sas.com/resources/papers/proceedings14/1485-2014.pdf. [Google Scholar]
- Aspinall R. Editorial. Journal of Land Use Science. 2006;1:1–4. doi: 10.1080/17474230600743987. [DOI] [Google Scholar]
- Bogaert P, Waldner F, Defourny P. An Information-Based Criterion to Measure Pixel-Level Thematic Uncertainty in Land Cover Classifications. Stochastic Environmental Research and Risk Assessment. 2016 doi: 10.1007/s00477-016-1310-y. [DOI] [Google Scholar]
- Brown KM, Foody GM, Atkinson PM. Estimating Per-Pixel Thematic Uncertainty in Remote Sensing Classifications. International Journal of Remote Sensing. 2009;30:209–229. doi: 10.1080/01431160802290568. [DOI] [Google Scholar]
- Castilla G, Hernando A, Zhang C, McDermid GJ. The Impact of Object-Size on the Thematic Accuracy of Landcover Maps. International Journal of Remote Sensing. 2014;35:1029–1037. doi: 10.1080/01431161.2013.875630. [DOI] [Google Scholar]
- Comber A, Fisher P, Brunsdon C, Khmag A. Spatial Analysis of Remote Sensing Image Classification Accuracy. Remote Sensing of Environment. 2012;127:237–246. doi: 10.1016/j.rse.2012.09.005. [DOI] [Google Scholar]
- Congalton RG. Using Spatial Autocorrelation Analysis to Explore the Errors in Maps Generated from Remotely Sensed Data. Photogrammetric Engineering and Remote Sensing. 1988;54:587–592. [Google Scholar]
- EPA, U. S. (Environmental Protection Agency) [Accessed 3 October 2017]; [Accessed 3 OCT 2017];2017 https://www.epa.gov/eco-research/multiresolution-land-characteristics-mrlc-consortium.
- Firth D. Bias Reduction of Maximum Likelihood Estimates. Biometrika. 1993;80:27–38. doi: 10.1093/biomet/80.1.27. [DOI] [Google Scholar]
- Foley JA, DeFries R, Asner GP, Barford C, Bonan G, Carpenter SR, Chapin FS, et al. Global Consequences of Land Use. Science. 2005;309:570–574. doi: 10.1126/science.1111772. [DOI] [PubMed] [Google Scholar]
- Foody GM. Local Characterization of Thematic Classification Accuracy through Spatially Constrained Confusion Matrices. International Journal of Remote Sensing. 2005;26:1217–1228. doi: 10.1080/01431160512331326521. [DOI] [Google Scholar]
- Fry JA, Xian G, Jin S, Dewitz JA, Homer CG, Yang L, Barnes LCA, Herold ND, Wickham J. Completion of the 2006 National Land Cover Database for the Conterminous United States. Photogrammetric Engineering and Remote Sensing. 2011;77:858–864. [Google Scholar]
- Gesch D, Oimen M, Greenlee M, Nelson C, Steuck M, Tyler D. The National Elevation Data Set. Photogrammetric Engineering and Remote Sensing. 2002;68:5–32. [Google Scholar]
- Homer C, Dewitz J, Fry J, Coan M, Hossain N, Larson C, Herold N, McKerrow A, VanDriel AN, Wickham J. Completion of the 2001 National Land Cover Database for the Conterminous United States. Photogrammetric Engineering and Remote Sensing. 2007;73:337–341. [Google Scholar]
- Homer C, Gallant A. Partitioning the Conterminous United States in Mapping Zones for Landsat TM Land Cover Mapping. [Last accessed3 February 2017];USGS White Paper. 2001 http://landcover.usgs.gov/pdf/homer.pdf.
- Homer C, Huang C, Yang L, Wylie B, Coan M. Development of a 2001 National Land Cover Database for the United States. Photogrammetric Engineering and Remote Sensing. 2004;70:829–840. doi: 10.14358/PERS.70.7.829. [DOI] [Google Scholar]
- Homer CG, Dewitz JA, Yang L, Jin S, Danielson P, Xian G, Coulston J, Herold ND, Wickham J, Megown K. Completion of the National Land Cover Database for the Conterminous United States – Representing a Decade of Land Cover Change Information. Photogrammetric Engineering and Remote Sensing. 2015;81:345–354. [Google Scholar]
- Jin S, Yang L, Danielson P, Homer C, Fry J, Xian G. A Comprehensive Change Detection Method for Updating the National Land Cover Database to Circa 2011. Remote Sensing of Environment. 2013;132:159–175. doi: 10.1016/j.rse.2013.01.012. [DOI] [Google Scholar]
- Khatami R, Mountrakis G, Stehman SV. Mapping Per-Pixel Predicted Accuracy of Classified Remote Sensing Images. Remote Sensing of Environment. 2017;191:156–167. doi: 10.1016/j.rse.2017.01.025. [DOI] [Google Scholar]
- Loosvelt L, Peters J, Skriver H, LIevens H, Van Coillie FMB, De Baets B, Verhoest NEC. Random Forests as a Tool for Estimating Uncertainty at Pixel-Level in SAR Image Classification. International Journal of Applied Earth Observation and Geoinformation. 2012;19:173–184. doi: 10.1016/j.jag.2012.05.011. [DOI] [Google Scholar]
- Löw F, Knöfel P, Conrad C. Analysis of Uncertainty in Multi-Temporal Object-Based Classification. ISPRS Journal of Photogrammetry and Remote Sensing. 2015;105:91–106. doi: 10.1016/j.isprsjprs.2015.03.004. [DOI] [Google Scholar]
- McGwire KC, Fisher P. Spatially Variable Thematic Accuracy: Beyond the Confusion Matrix. In: Hunsaker CT, Goodchild MF, Friedl MA, Case TJ, editors. Spatial Uncertainty in Ecology: Implications for Remote Sensing and GIS Applications. New York: Springer-Verlag; 2001. pp. 308–329. [Google Scholar]
- Mei Y, Zhang J. Effects of Landscape Characteristics on Accuracy of Land Cover Change Detection. International Spatial Accuracy Research Association (ISARA). Proceedings of Spatial Accuracy; July 7–11, 2014; East Lansing, Michigan, USA. 2014. [last accessed 3 February 2017]. http://www.spatial-accuracy.org/system/files/Paper_13_Mei_Zhang.pdf. [Google Scholar]
- Moisen GG, Cutler DR, Edwards TC., Jr . Generalized Linear Mixed Models for Analyzing Error in a Satellite-Based Vegetation Map of Utah. In: Mowrer HT, Congalton RG, editors. Quantifying Spatial Uncertainty in Natural Resources. Theory and Applications for GIS and Remote Sensing. Chelsea, MI, USA: Ann Arbor Press; 1999. pp. 37–44. [Google Scholar]
- Olofsson P, Foody GM, Herold M, Stehman SV, Woodcock CE, Wulder MA. Good Practices for Estimating Area and Assessing Accuracy of Land Change. Remote Sensing of Environment. 2014;148:42–57. doi: 10.1016/j.rse.2014.02.015. [DOI] [Google Scholar]
- Rindfuss RR, Walsh SJ, Turner BL, II, Fox J, Mishra V. Developing a Science of Land Change: Challenges and Methodological Issues. Proceedings of the National Academy of Sciences, USA. 2004;101:13976–13981. doi: 10.1073/pnas.0401545101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SAS. [Accessed 3 October 2017];Usage Note 39109: Measures and Tests of the Discriminatory Power of a Binary Logistic Model. 2017 http://support.sas.com/kb/39/109.html.
- SAS Institute Inc. SAS/STATR 9.2 User’s Guide. 2. Cary, NC: SAS Institute; 2009. [Google Scholar]
- Smith JH, Stehman SV, Wickham J, Yang L. Effects of Landscape Characteristics on Land-Cover Class Accuracy. Remote Sensing of Environment. 2003;84:342–349. doi: 10.1016/S0034-4257(02)00126-8. [DOI] [Google Scholar]
- Smith JH, Wickham J, Stehman SV, Yang L. Impacts of Patch Size and Land Cover Heterogeneity on Thematic Image Classification Accuracy. Photogrammetric Engineering and Remote Sensing. 2002;68:65–70. [Google Scholar]
- Steele BM, Winne JC, Redmond RL. Estimation and Mapping Misclassification Probabilities for Thematic Land Cover Maps. Remote Sensing of Environment. 1998;66:192–202. doi: 10.1016/S0034-4257(98)00061-3. [DOI] [Google Scholar]
- Stehman SV. Statistical Rigor and Practical Utility in Thematic Map Accuracy Assessment. Photogrammetric Engineering and Remote Sensing. 2001;67:727–734. [Google Scholar]
- Stehman SV. Sampling Designs for Accuracy Assessment of Land Cover Data. International Journal of Remote Sensing. 2009;30:5243–5272. doi: 10.1080/01431160903131000. [DOI] [Google Scholar]
- Stehman SV, Czaplewski RL. Design and Analysis for Thematic Map Accuracy Assessment. Remote Sensing of Environment. 1998;64:331–344. doi: 10.1016/S0034-4257(98)00010-8. [DOI] [Google Scholar]
- Stehman SV, Wickham J. Pixels, Blocks of Pixels, and Polygons: Choosing a Spatial Unit for Thematic Accuracy Assessment. Remote Sensing of Environment. 2011;115:3044–3055. doi: 10.1016/j.rse.2011.06.007. [DOI] [Google Scholar]
- Stehman SV, Wickham J, Smith JH, Yang L. Thematic Accuracy of the 1992 National Land-Cover Data (NLCD) for the Eastern United States: Statistical Methodology and Regional Results. Remote Sensing of Environment. 2003;86:500–516. doi: 10.1016/S0034-4257(03)00128-7. [DOI] [Google Scholar]
- Tjur T. Coefficients of Determination in Logistic Regression Models - A New Proposal: The Coefficient of Discrimination. The American Statistician. 2009;63:366–372. doi: 10.1198/tast.2009.08210. [DOI] [Google Scholar]
- Turner BL, II, Lambin EF, Reenberg A. The Emergence of Land Change Science for Global Environmental Change and Sustainability. Proceedings of the National Academy of Sciences, USA. 2007;104:20666–20671. doi: 10.1073/pnas.0704119104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Oort PAJ, Bregt AK, De Bruin S, De Wit AJW, Stein A. Spatial Variability in Classification Accuracy of Agricultural Crops in the Dutch National Land-Cover Database. International Journal of Geographical Information Science. 2004;18:611–626. doi: 10.1080/13658810410001701969. [DOI] [Google Scholar]
- Wickham J, Stehman SV, Fry JA, Smith JH, Homer CG. Thematic Accuracy of the NLCD 2001 Land Cover for the Conterminous United States. Remote Sensing of Environment. 2010;114:1286–1296. doi: 10.1016/j.rse.2010.01.018. [DOI] [Google Scholar]
- Wickham J, Stehman SV, Gass L, Dewitz J, Fry JA, Wade TG. Accuracy Assessment of NLCD 2006 Land Cover and Impervious Surface. Remote Sensing of Environment. 2013;130:294–304. doi: 10.1016/j.rse.2012.12.001. [DOI] [Google Scholar]
- Wickham J, Stehman SV, Gass L, Dewitz J, Sorenson DG, Granneman BJ, Poss RV, Baer LA. Thematic Accuracy Assessment of 2011 National Land Cover Database (NLCD) Remote Sensing of Environment. 2017;191:328–341. doi: 10.1016/j.rse.2016.12.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao N, Zhang J, Zhang W. Estimation of Probabilistic Accuracy Measures in Remotely Sensed Land Cover Change Information. International Spatial Accuracy Research Association (ISARA). Proceedings of Spatial Accuracy; July 7–11, 2014; East Lansing, Michigan, USA. 2014. [last accessed 3 February 2017]. http://www.spatial-accuracy.org/system/files/Paper_23_Yao.pdf. [Google Scholar]
- Yu Q, Gong P, Tian YQ, Pu R, Yang J. Factors Affecting Spatial Variation of Classification Uncertainty in an Image Object-Based Vegetation Mapping. Photogrammetric Engineering and Remote Sensing. 2008;74:1007–1018. doi: 10.14358/PERS.74.8.1007. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.