The Limiting Pool Mechanism Fails to Control the Size of Multiple Organelles

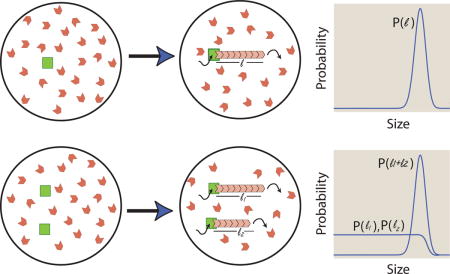
Summary

How the size of micron-scale cellular structures like the mitotic spindle, cytoskeletal filaments, the nucleus, the nucleolus and other non-membrane bound organelles is controlled despite a constant turnover of their constituent parts is a central problem in biology. Experiments have implicated the limiting-pool mechanism: structures grow by stochastic addition of molecular subunits from a finite pool until the rates of subunit addition and removal are balanced, producing a structure of well-defined size. Here, we consider these dynamics when multiple filamentous structures are assembled stochastically from a shared pool of subunits. Using analytical calculations and computer simulations, we show that robust size control can be achieved when only one filament is assembled at a time. When multiple filaments compete for monomers, filament lengths exhibit large fluctuations. These results extend to three-dimensional structures and reveal the physical limitations of the limiting pool mechanism of size-control when multiple organelles are assembled from a shared pool of subunits.

Graphical abstract

Introduction

Cells consist of organelles and other large structures whose size is often matched to the size of the cell. A classic example of this is the scaling of the size of the mitotic spindle with the size of the cell in a developing embryo (Goehring and Hyman, 2012). How organelles and other micron-sized structures within the cell are assembled and maintained to have a specific size is still not well understood.

A simple idea, which seems to provide the answer in several cases, is that the cell maintains a limiting pool of a diffusible molecular component that is required for assembling the structure. In such a case, size control is simply achieved by the structure growing until the limiting pool is depleted to the point when the rates of assembly and disassembly of the structure are matched.

The idea that a limiting pool plays a major role in size control was the subject of a recent review that summarized the experimental evidence for this mechanism in the assembly of diverse structures such as centrosomes, flagella, and the nucleus (Goehring and Hyman, 2012). In addition, a recent in vitro study used a microfluidic system to encapsulate cytoplasm from Xenopus egg extracts in small droplets and showed that spindle size is proportional to the droplet volume, thereby suggesting that the amount of cytoplasmic material controls the size (Good et al., 2013). Furthermore, another study showed inverse scaling of the size of nucleoli with nuclear size in a developing C. elegans embryo in conditions when the number of nucleoli components in the nucleoplasm was fixed, also consistent with the limiting pool mechanism (Weber and Brangwynne, 2015).

The key idea of the limiting pool mechanism of size control is that assembly slows down as the free subunit pool is depleted and the size of the assembling structure increases. When the rate of assembly of the structure matches disassembly, the cytoplasmic (“free”) pool of the limiting component reaches the so-called critical concentration, which is equal to the dissociation constant of the assembly reaction. At this point the structure being assembled reaches a well-defined size. This is the expected assembly dynamics for a single structure, however, what happens to these dynamics when multiple structures are assembled from a shared limiting pool? In this case, once the critical concentration is established, the molecular component that is limiting could stochastically transfer from one to another structure with no change to the free concentration of this component, therefore incurring no free-energy penalty. Notably, additional size control mechanisms can impose a free energy penalty for such an exchange. In this paper, we study the implications of limiting pool mechanism on the size-control of multiples structures growing from a shared pool of diffusing components, when such additional size control mechanisms are absent.

Although the key ideas of our theoretical study can be extended to three dimensional structures like nucleoli (Weber and Brangwynne, 2015), we focus here on the filamentous structures that comprise the cytoskeleton. Filamentous structures are a particularly good model system for investigating questions relating to size control because “size” can be simply defined by the length of the filament. Most cytoskeletal structures are composed of actin filaments and microtubules, which in turn are composed of actin monomers and tubulin dimers. These subunits undergo constant turnover as they are stochastically added and removed from the structure, yet the structures themselves can be maintained at a precise size. This is important since large changes in structure size can produce significant deviations from its normal physiological functions. For example, in yeast cells intracellular transport is disrupted if actin cables overgrow and buckle (Chesarone-Cataldo et al., 2011). In addition, experiments have shown that when filamentous structures are cut to a smaller size, they often grow back to their physiological length suggesting that the length is under tight control (Marshall et al., 2005).

In some instances, multiple filamentous structures, made from a shared pool of actin monomers or tubulin dimers, coexist within the cell’s cytoplasm. For example, actin cables and actin patches in yeast are made up of actin monomers. They have different size, shape, and function, yet they coexist in the same cytoplasm while exchanging actin monomers from an apparently common pool (Michelot and Drubin, 2011). This observation raises the question, how are such diverse structures assembled and maintained from a common pool of subunits?

Here, we consider the stochastic assembly of multiple filamentous structures from a common and limited pool of subunits with a specific focus on the length fluctuations of these assembled structures. We assumed the simple scenario when the limiting components are the building blocks of the filamentous structures being assembled and have no other effect on the length of the filaments. From this simple, analytically tractable model of stochastic assembly we derive general conclusions about the limiting pool mechanism, and describe its limitations in controlling the sizes of multiple structures within the cell.

Notably, this approach purposefully considers the limiting monomer pool to be the only mechanism by which filament length is controlled. Cognizant of the fact that in cells multiple size-regulating mechanisms might be at play, we contend that the simple, limiting pool mechanism discussed here is a useful “null hypothesis” against which experimental data can be analyzed (Marshall, 2016). To the extent that the detailed quantitative predictions of the limiting pool mechanism are not borne out by experiments (that is, the null hypothesis can be rejected based on quantitative measurements), one can be confident that other size control mechanisms are at play.

Results

We consider the limiting pool mechanism of size control in the context of a simple model where filaments grow from a fixed number of nucleating centers within the cell by stochastic addition of diffusing monomers. Monomers, whose number in the cell is fixed, also stochastically dissociate from the filament. The number of filaments is fixed by the number of nucleating centers, which can be a single protein or a protein complex, and which aid in the formation of the filament. An example is provided by formins which help assemble filamentous actin structures. Formins bind to the barbed end of an actin filament and capture (profilin bound) actin monomers from solution, which are then incorporated into the growing filament (see Figure 1A). Note that the model we consider is a significant departure from textbook examples of stochastic filament assembly where every monomer in solution can serve as the site of new filament assembly. In our case filament assembly occurs only from nucleating centers.

Figure 1. Growth of a filament from a single nucleating center and two nucleating centers in the presence of a limiting pool of monomers.

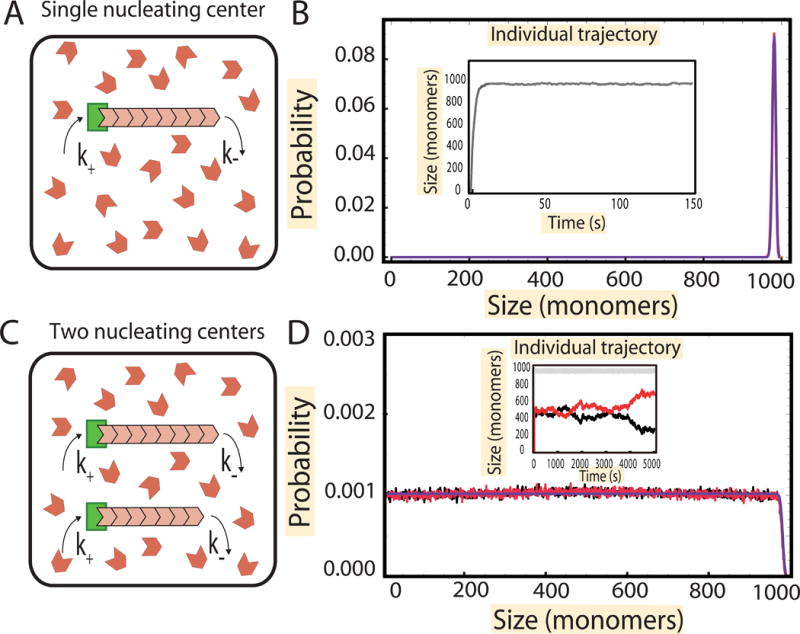
(A) Schematic showing the growth of a single filament (pink) from a single nucleating center (green) in a pool of monomers (in red). (B) (Inset) Numerical simulation of the growth trajectory of a single filament from the nucleating center (gray). After a fast growth phase, the size attains a steady state. By considering several such trajectories, we compute the probability distribution of filament lengths numerically, and a peaked distribution of size is obtained (in red). The parameters used for simulations are $k_{+}^{\prime }=0.5N_{\mathit{free}}^{-1}{s}^{-1}$, k₋ = 10 s⁻¹ and N = 1000, where N_free is the number of free monomers in solution and is equal to N − l where l is the length of the filament in monomers. The simulation results are compared with the analytical results (blue) obtained in STAR Methods, section “Exact solutions of filament distributions”. (C) Schematic showing the growth of filaments (pink) from two nucleating centers (green) in a pool of monomers (in red). (D) (Inset) Numerical simulation of the growth trajectory of the two individual filaments (red and black) and the sum of their lengths (gray). After an initial growth phase where the two filaments grow roughly in unison and the total length of the two filaments reaches steady state, we observe anti-correlated fluctuations in the individual lengths. These fluctuations lead to individual filaments having a uniform distribution of lengths (red and black) in simulations; we compare these to results obtained analytically (blue) in STAR Methods, section “Gamma function representation of two filaments”. The parameters used for simulations are $k_{1,+}^{\prime }=k_{2,+}^{\prime }=k_{+}^{\prime }=0.5N_{\mathit{free}}^{-1}{s}^{-1},$ k₋ = 10 s⁻¹ and N = 1000, where N_free is the number of free monomers in solution and is equal to N − l₁ − l₂, where l₁ and l₂ are the lengths of the two filaments.

We consider three different scenarios, one when there is a single nucleating center in a cell which contains a fixed number of monomers, the case of two identical nucleating centers, and of two distinct nucleating centers, which differ in the rates at which they incorporate monomers. An example of inequivalent nucleators is provided by the two different formins Bni1 and Bnr1 in budding yeast, which assemble actin filaments at different rates (Buttery et al., 2007). Later in this section, we turn our attention to the case of many filaments and also discuss how our results carry over to the case when three dimensional structures are assembled from a limiting pool.

A limiting-pool of monomers assembles into a single filament of a well-defined length

First we consider the case of a single nucleating center, where a single filament is assembled by the addition and dissociation of monomers. The total number of monomers in the cell, N, is fixed, and each monomer can associate to a filament with assembly rate k₊, which is proportional to the number of free monomers in the cell. Hence, for a single filament, its assembly rate starts off as $k_{+}={k^{\prime }}_{+}N$ but as the filament grows, it decreases to k′₊(N − l), ${k^{\prime }}_{+}(N-l)$ where l is the length of the filament in units of monomers. Note that the rate constant k′₊ is obtained by taking the second order rate constant for monomer addition, which has units M⁻¹s⁻¹, and multiplying it by the volume of the cytoplasm within which the free monomers diffuse. The rate of assembly is thus length dependent, and assuming a constant monomer dissociation rate, k₋, it leads to a peaked distribution of filament lengths (Figure 1B).

To describe the dynamics of an individual filament, we model the growth and decay of the filament using the master equation formalism. The key quantity to compute is the probability, p(l, t), that the filament has a length l (measured here in units of monomers) at time t. The master equation describes the evolution of p(l, t) in time, by taking into account all the possible changes of the state (length) of filament that can occur in a small time interval Δt. The master equation for a single filament is (for l > 0)

$$\frac{dp(l,t)}{dt}={k^{\prime }}_{+}(N-l+1)p(l-1,t)+k\_p(l+1,t)-{k^{\prime }}_{+}(N-l)p(l,t)-k\_p(l,t).$$ (1)

We compute the steady-state distribution of filament lengths by setting the left-hand side of the equation to zero and omit the time variable in p(l) to indicate the steady state nature of the distribution. We use detailed balance equations $p(l)k_{+}^{\prime }(N-l)=p(l+1)k_{-}$, to obtain $p(l)=\frac{{\kappa }_d^{N-l}{e}^{-{\kappa }_d}}{(N-l)!}$ (See section “Exact solutions of filament distributions” in STAR Methods), where ${\kappa }_d(\equiv k_{-}/k_{+}^{\prime })$ is a dimensionless dissociation constant for the chemical reaction of a monomer binding to filament (equal to the dissociation constant multiplied with the cell volume). For example, for actin cables in yeast cells we estimate κ_d ~ 10⁴ and N ~ 2 × 10⁵, using the measured concentration of actin in yeast (~ 10μM) (Johnston et al., 2015), the typical volume of a yeast cell (~ 40μm3) (Philips and Milo, 2015) and the measured rates of association (11.6 μM⁻¹ s⁻¹) and dissociation (1.4 s⁻¹) for binding of actin monomers to actin filaments (Pollard, 1986) (See section “Estimates for actin cables in yeast” in STAR Methods for the calculations). The mean and standard deviation of the distribution are given by N − κ_d and $\sqrt{{\kappa }_d}$, respectively. This distribution is very peaked, and the same is true for the distribution of free monomers, which in fact is very close to Poisson (See STAR Methods, “Main inferences and estimates” section). Notably, the typical length of the filament is essentially given by the number of available monomers unless k′₊ and k_ are fine-tuned to be close in value (See STAR Methods, section “Fraction of monomers in filaments”).

We used stochastic simulations to analyze the time evolution of the length distribution. We start with a filament of zero length growing from a single nucleating center and then follow the growth trajectory of the length of the filament in time as monomers attach and fall off. After some time, we observe the filament reaching a steady state (see Figure 1B inset), when the length distribution of the filaments no longer changes with time. The distribution extracted from these simulations matches the analytic results. The time scale over which the steady state is reached is of order 1/k′₊, which can be understood as the time it takes N monomers to be taken up from the pool at a rate k′₊ N (see Box 1 and STAR Methods, section “Growth time scale τ_g” for a more precise calculation).

Box 1. Experimental tests of the limiting-pool mechanism.

Our study makes several predictions that can be used to test the limiting pool mechanism. In case of a single filamentous structure assembled from a pool of monomers, the steady state distribution of filament length (STAR Methods, Section “Main inferences and estimates”) can be tested in experiments in which the total number of monomers is tuned. This can be achieved, for example, by using the microfluidic approach described in (Good et al., 2013). We observe that the mean length (N − κ_d) of the filament depends on the total number of monomers whereas the variance (κ_d) does not. This result can be used as a stringent test of the limiting-pool mechanism of size control.

Furthermore, if there are multiple identical structures being made from a common pool of monomers, we predict the existence of anti-correlated fluctuations of individual filament lengths over time. For the two filament case, we predicted that these fluctuations will be observed at time scales of order N²/k₋, which can also be tuned by controlling the total number of monomers. An experiment with two inequivalent filaments assembling from a common monomer pool should also reveal the time scale of order N, during which the slower assembling filament loses the monomers it quickly accumulated in the initial growth phase.

One example where in vivo experiments can be used to test our predictions for the case of filaments is provided by fission yeast cells. These cells have two different types of actin structures, namely cables and patches which are assembled by different nucleating factors (formins and the Arp2/3 complex, respectively) (Rotty et al., 2015; Suarez et al., 2015). Recently it was shown that it is possible reduce the number of patches in yeast cells by over-expressing profilin, which is an actin-binding protein that has two specific effects on assembly: it significantly favors the formation of cables by increasing the assembly rates of formin-nucleated filaments and it inhibits Arp 2/3 mediated branching and hence represses the formation of patches (Rotty et al., 2015; Suarez et al., 2015). Thus, by regulating the level of profilin either formin or Arp 2/3 generated structures will take up most of the available pool of actin monomers. This observation is consistent with our calculations since we find that when two structures are competing for the same subunit pool the one that assembles faster takes up practically all subunits. Still, further experiments need to be performed in which size distributions of different structures are measured to quantitatively test predictions of the limiting monomer pool model.

Predictions of the limiting pool mechanism for the case of assembly of three-dimensional structures could be tested in C.elegans early embryo cells, where two nucleoli are assembled from a shared pool of nucleoli particles. These nucleoli grow equally in size up until cell division (~ about 20 minutes) (Weber and Brangwynne, 2015). Measurements of the nucleoli size and how they scale with the size of the nucleus are consistent with predictions of the limiting pool mechanism (Weber and Brangwynne, 2015). Experiments have also revealed that during the assembly phase the size (volume) of the nucleolus grows with time to the fourth power (Berry et al., 2015). This measurement is inconsistent with the assumption of size-independent rates k′₊ and k₋, and also with the assumption that the rates grow in proportion to the radius of the nucleolus, presumably due to the active role played by transcription of rRNA. Regardless, in steady state we still expect the assembly and disassembly rates to be balanced, and therefore we predict the same diffusive dynamics and large fluctuations of the sizes of individual nucleoli, as long as the limiting pool mechanism alone is responsible for their size control. Specifically, we predict that in cells engineered to have longer cell cycles one should observe the predicted large, anti-correlated fluctuations in individual nucleoli sizes.

Time scales of assembly

In the Results section, we discussed different time scales associated with growth of filaments from identical nucleating centers, i.e., growth and diffusion timescales and their dependence on the number of monomers in the pool. One can use those calculations to estimate timescales in the case where multiple actin cables are made from a common pool of actin monomers in the mother compartment of a budding yeast cell. Using previously published numbers for cell volume (Philips) and rates of association and dissociation of monomers to actin filaments (Pollard, 1986), we estimate k^′₊ = 5 × 10⁻³ 1/s. Given that the observed number of actin cables is about ten we predict that the growth phase lasts for less than a minute, assuming that there are no additional length control mechanisms at play. (See STAR Methods, sections “Growth time scale τ_g” and “Estimates for actin cables in yeast” for details.)

In contrast, we estimate the diffusion time scale to span several days (STAR Methods, Section “Diffusion time scale τ_d”). In other words, we should never observe order-N² fluctuations in cable lengths on the time scale of live-cell experiments, given a division time of about 90 minutes. Note that for this estimate, we assume that all the actin in the mother compartment of the budding yeast cells are used to make cables. This is a reasonable assumption as these cells have very few or no patches in their mother compartment. A substantially smaller number of actin monomers in cables could bring down the estimate of the diffusion time scale considerably due to the N² dependence of this time scale.

Of course, there could be other reasons why large length fluctuations of cables are not observed in live cell experiments: other length-control mechanisms could be at play, which may reduce length fluctuations, and even lead the system to an altogether different steady state. Indeed, several actin and formin binding proteins have been shown to play an important role in controlling cable length (Chesarone-Cataldo et al., 2011; Mohapatra et al., 2015, 2016).

Two equivalent filaments assembling from a common limiting pool of monomers leads to large, anti-correlated fluctuations in their lengths

Next we turn to the case of assembly of multiple filamentous structures competing for a common, limited pool of monomers. We begin by considering the simplest case of two identical nucleating centers that are growing one filament each (Figure 1C). The results obtained in this simple case are also found in the more general many-filament case, which is described in detail in the STAR Methods.

In the case of two identical nucleating centers, each of the two filaments adds a monomer to it at the same rate k′₊. Therefore, the assembly rate of filaments starts off as k′₊N, however as the two filaments grow, it decreases to k′₊(N − l₁ − l₂), where l₁ and l₂ are the lengths of the two filaments in units of monomers. The rate of dissociation (k₋) of monomers is assumed to be identical for both filaments.

Since there are now two filaments in the cell, we characterize the state of the system with a joint probability distribution p(l₁, l₂, t), which satisfies the master equation

$$\frac{dp(l_1,l_2,t)}{dt}={k^{\prime }}_{+}(N-l_1-l_2+1)(p(l_1-1,l_2,t)+p(l_1,l_2-1,t))+k\_p(l_1+1,l_2,t)+k\_p(l_1,l_2+1,t)-2({k^{\prime }}_{+}(N-l_1-l_2)+k_{\_})p(l_1,l_2,t).$$ (2)

At steady state, $\frac{dp(l_1,l_2,t)}{dt}=0$ and the joint probability distribution takes on the product form $p(l_1,l_2)=p(0,0)\frac{{{\kappa }_d}^{-(l_1+l_2)}}{(N-l_1-l_2)!}$, which is a textbook result from queueing theory (Kelly, 1979) (see “Exact solutions of filament distributions” section in STAR Methods). Here ${\kappa }_d=k_{-}/k_{+}^{\prime }$ is once again the dimensionless dissociation constant. The distribution of lengths for a single filament, i.e., p₁(l₁) and p₂(l₂), can be obtained from the joint distribution by summing over all possible lengths of the other filament (l₂ and l₁, respectively); we perform these calculations explicitly in sections “Equal nucleating centers” and “Gamma function representation of two filaments” of the STAR Methods.

An approximate formula for the distribution of lengths for a single filament in steady state can be derived from a simple argument, which also sheds light on the physics of the problem. In steady state the average number of free monomers left in solution is κ_d, and the distribution of free monomers is very close to Poisson with standard deviation $\sqrt{{\kappa }_d}$, implying that it is very narrowly concentrated around its mean κ_d. (The Poisson approximation to the free monomer pool was previously derived (Hu and Othmer, 2011) by assuming that the probability of a filament having zero length is zero; we rigorously justify this approximation in STAR Methods, section “Equal nucleating centers”.) Hence, the total number of assembled monomers, i.e., the sum of the lengths of the two filaments, is to an excellent approximation a constant N − κ_d. Furthermore, monomers diffuse from one filament to another with equal rates (k₋/2; see STAR Methods, section “Diffusion time scale τ_d”, for the derivation) independent of the lengths of individual filaments. Therefore, every possible configuration of filament lengths that satisfies l₁ + l₂ = N − κd is equally likely. The number of such configurations is N − κ_d + 1, implying that the probability distribution for a single filament is

$$p_1(l_1)\approx \frac{1}{N-{\kappa }_d},$$ (3)

i.e., it is uniform on the interval (0, N − κ_d). This approximation is very accurate except in a very narrow interval of lengths of order $\sqrt{{\kappa }_d}$ when l₁ is close to N − κ_d, where it decays rapidly to zero. This effect is due to the Gaussian fluctuations of the free monomer pool around its mean. This simple argument can be further extended to an arbitrary number of filaments and is validated by our exact calculations (see STAR Methods, section “Equal nucleating centers”).

We also used stochastic simulations to investigate individual growth trajectories for the two filaments and compared the results to our analytical steady-state distributions p₁(l₁) and p₂(l₂) (Figure 1D). Once again, we follow the stochastic trajectory in time of the length of each individual filament. Initially, both filaments grow in unison (subject to small fluctuations) until their combined length reaches the steady state total length N − κ_d. After this rapid growth period the individual trajectories of the filaments diverge, as one grows the other shrinks (Figure 1D inset). These anti-correlated fluctuations in length persist indefinitely and eventually become of order N − κ_d. At the same time the length distributions for each filament, p₁(l₁) and p₂(l₂), settle into their steady state values, Equation 3.

These dynamics are illustrated in Figure 2, where we plot p₁(l₁, t) obtained from stochastic simulations. At first the mean filament length increases until the free monomer pool (or equivalently the total filament length) reaches its steady state (black curves). The time scale for this is of order 1/(2k′₊), same as in the case of a single filament. After that, we observe the widening of the distribution at constant mean (blue curve) which eventually becomes uniform (red curve) at the longest times, of order N²/k₋ (STAR Methods, section “Diffusion time scale τ_d”). Thus, we reach the somewhat surprising conclusion that the limiting-pool mechanism does not control length in the case of two structures competing for the same monomers. In fact, this remains true even when the additional processes of catastrophe and rescues (to simulate microtubules undergoing dynamic instability) were included in our simulation analysis (Figure S1).

Figure 2. Evolution of probability for individual filament lengths in the case of identical nucleating centers.

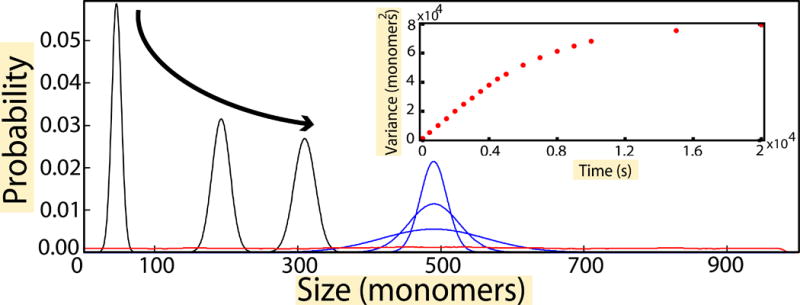
In the initial growth phase (black), the distribution of individual filament lengths starts off as a peaked distribution whose mean increases, until the total length reaches a steady state. The growth phase is followed by the slow phase of monomers swapping which leads to anti-correlated fluctuations are seen in the individual trajectories, which is translated into the increase in the width of the filament length distributions while the mean stays unchanged (blue). The final, steady state distribution (red) is flat. (Inset) Plot of variance of the distribution (σ²) vs. time of simulation. The variance initially increases linearly with time, but later saturates. Time was varied from 0 – 20000 s in steps of 100 s. From the slope of the linear part plot of, we find a diffusion constant D = 5 monomer²/s using the relation σ²= 2Dt. The parameters used for simulations were $k_{+}^{\prime }=0.5N_{\mathit{free}}^{-1}{s}^{-1}$, k₋ = 10 s⁻¹, N = 1000 and N_free = N − l₁ − l₂, is the number of free monomers in solution and l₁ and l₂ are the lengths of the two filaments.

Once the total length of the two filaments has reached a steady state, any monomer that comes off a filament is rapidly taken up by one or the other filament. This is a consequence of the fact that in steady state the total number of monomers in the two filaments is narrowly distributed around its mean value. We therefore expect individual filament lengths to exhibit diffusive dynamics. We demonstrate this explicitly in the inset to Figure 2 where the variance, σ², of the length distribution of an individual filament is seen to increase linearly with time until it eventually saturates. Given the diffusional law σ² = 2Dt the initial slope of the σ² curve in Figure 2 inset gives the diffusion constant D. The diffusion constant can be computed by taking into account that when the total length reaches steady state monomers exchange between the two filaments with the rate k₋. A detailed analysis of all possible exchange processes while accounting for their probabilities leads to the exact result D = k₋/2 (STAR Methods, section “Diffusion time scale τ_d”), which we also checked with stochastic simulations.

Two inequivalent filaments assembling from a common limiting pool of monomers results in only one filament having a well-defined length

Next, we consider the case of two nucleating centers with different assembly rates for filaments in a common pool of monomers (see Figure 3A). As in the example of two different formins in yeast, monomers are stochastically added to the two filaments at different rates: k′_1,+ and k′_2,+. These rates start as k′_1,+N and k′_2,+N but as the two filaments grow they decrease to k′_1,+(N − (l₁ + l₂)) and k′_2,+(N − (l₁ + l₂)) respectively, where l₁ and l₂ are the individual lengths of the two filaments in units of monomers. The rate of dissociation, k₋, of monomers is assumed identical for both filaments.

Figure 3. Growth of filaments from two inequivalent nucleating centers in a limiting pool of monomers.

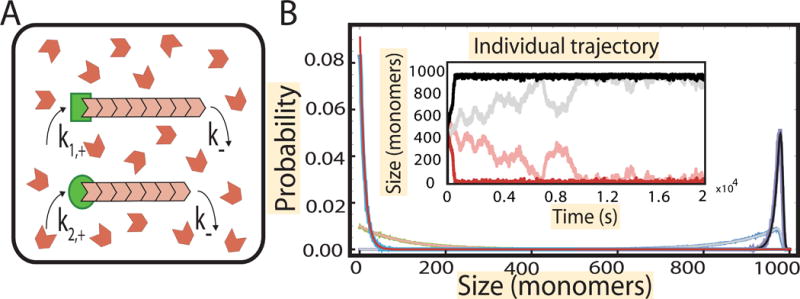
(A) Schematic showing the growth of filaments (pink) from two distinct nucleating centers (green) in a pool of monomers (in red). (B) (Inset) Numerical simulation of the growth trajectory of the filaments from the nucleating centers. Shown are trajectories for 10% difference in assembly rate (dark) and 1% difference (light). After a growth phase, where both filaments accrue monomers, the faster growing filaments attains a steady state by taking up most of the free monomers, while the slower filament shrinks. The faster growing filament attains a peaked distribution of size (black) and the slower one attains a geometric distribution (red). The parameters used are ${k_{1,+}^{\prime }}^{10\%}=0.55N_{\mathit{free}}^{-1}{s}^{-1}$, ${k_{1,+}^{\prime }}^{1\%}=0.505N_{\mathit{free}}^{-1}{s}^{-1}$, ${k_{2,+}^{\prime }}^{1\%}=0.5N_{\mathit{free}}^{-1}{s}^{-1}$, k₋ = 10 s⁻¹, N = 1000 and N_free = N − l₁ − l₂, is the number of free monomers in solution and l₁ and l₂ are the lengths of the two filaments. The simulations are overlaid on the results obtained analytically (blue and green) in STAR Methods, section “Gamma function representation of two filaments”.

As before, the joint probability distribution p(l₁, l₁, t), satisfies a master equation, but now with different assembly rates for the two filaments, namely

$$\frac{dp(l_1,l_2,t)}{dt}=k_{1,+}^{\prime }(N-l_1-l_2+1)p(l_1-1,l_2,t)+k_{2,+}^{\prime }(N-l_1-l_2+1)p(l_1{l}_2-1,t)+k\_p(l_1+1,l_2,t)+k\_p(l_1,l_2+1,t)-(k_{1,+}^{\prime }(N-l_1-l_2)+k_{2,+}^{\prime }(N-l_1-l_2)+2k_{-})p(l_1,l_2,t).$$ (4)

The steady state joint distribution of filament lengths is again given by a product form, from which the distribution of lengths of each individual filament can be computed. The exact calculation is in the STAR Methods (section “Unequal nucleating centers”) and here we provide a simple intuitive argument.

For concreteness, let us assume that the assembly rate of first filament is larger than the second, i.e., k′_1,+ > k′_2,+ (or equivalently, ${\kappa }_{d_2}>{\kappa }_{d_1}$, using ${\kappa }_{d_i}=k_{-}/k_{i,+}$ for the dimensionless dissociation constants). Then over a long period of time, a larger number of monomers will join the first, fast assembling filament. Since the detachments rates are the same, the first filament will accumulate most of the monomers. Hence, p₁(0) ≈ 0, implying that average rate of monomers leaving the first filament is k₋(1 − p₁(0)) ≈ k_. Next, by equating this rate to the rate at which monomers attach to the first filament, i.e., k′_1,+ × (average number of free monomers), we find that the average number of free monomers is ${\kappa }_{d_1}$, and, as in the case of equivalent filaments, we expect the steady-state distribution of the number of free monomers to be Poisson. From this result, we can derive the distribution of lengths for the second, slower growing filament from the detailed balance equations $p_2(l){\kappa }_{d_1}{k^{\prime }}_{2,+}\approx p_2(l+1)k_{-}$, which leads to the conclusion that the lengths for the second filament are distributed geometrically, i.e., $p_2(l)=\left(1-\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right){\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right)}^l$. Then the first filament is virtually unaffected by the presence of the second and the distribution of its lengths is peaked, as in the case of a single filament. The approximate average length of the first and the second filament are given by $N-{\kappa }_{d_1}-\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}-{\kappa }_{d_1}}$ and $\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}-{\kappa }_{d_1}}$, respectively (STAR Methods, section “Unequal nucleating centers”).

Once again, to develop intuition about the assembly dynamics we used stochastic simulations to follow the growth of the two filaments from the two nucleating centers each starting from zero length (Figure 3B, inset). Just like in the case of equal nucleating centers, we observe that there is an initial, fast growth phase which occurs over a time of the order $\left(\frac{1}{{k^{\prime }}_{1,+}+{k^{\prime }}_{2,+}}\right)$. After the growth phase, we observe that filament with a higher assembly rate grows to a steady state characterized by a large length, whereas the other filament shrinks to zero. When the two assembly rates are close in magnitude then we find anti-correlated fluctuations of lengths similar to what we observed in the case of identical nucleating centers. These fluctuations happen over a time scale $\frac{N}{{\kappa }_{d_2}({k^{\prime }}_{1,+}-{k^{\prime }}_{2,+})}$, i.e., over a time that is of order N, and eventually subside as the system settles into a steady state with practically all monomers taken up by the faster growing filament. This is illustrated in the plots of steady-state length distributions for the two filaments, where for the fast-assembling filament we observe a distribution sharply peaked around the mean while the slower assembling filament is characterized by a geometric distribution of filament lengths peaked at zero; see Figure 3B. We find wider distributions when the assembly rates are numerically close to each other, which results from the increased fluctuations of the filament lengths. Comparison of the analytical solution of Equation 4 for p₁(l₁) and p₂(l₂) (see STAR Methods, section “Unequal nucleating centers”) to the simulation data serves as a stringent test of the simulation procedure (Figure 3B).

To summarize, when considering two nucleating centers with different rates of filament assembly, the one with the higher rate wins and assembles a filament of well-defined length, while the other filament does not stably form.

Assembly of many filaments

Thus far we have only considered two filamentous structures competing for the same pool of monomers. In cells, though, it is common to observe multiple structures made from the same pool of monomers. For example, the number of actin cables in budding yeast is about ten or so, while the number of actin patches is of order ten to a hundred.

The key results described for two filamentous structures readily carry over to the case of multiple filaments. More specifically, for any finite number of filaments starting at zero length, growth of all filaments is strongly favored in the initial phase of assembly, and all the filaments quickly reach lengths of order N (the total number of monomers) over a time scale which is independent of N. Then, in case of inequivalent assembly rates, the slower growing filaments gradually lose monomers and diminish in length to a small, geometrically distributed length. The duration of this phase is of order N. Furthermore, at the end of this phase practically all the monomers are taken up by the fast-growing filaments, and the number of free monomers approaches a Poisson distribution with a mean equal to the smallest (dimensionless) dissociation constant among all the filaments. This then implies that the total number of monomers assembled into the fast-growing filaments will have a well-defined size characterized by a peaked distribution. The lengths of individual fast-growing filaments then undergo protracted diffusive dynamics on time scales of the order N². These dynamics are generated by the stochastic swapping of monomers between individual filaments, and eventually lead to a broad, power-law distribution of filament lengths in steady state. Notably, we find that if the number of fast growing filaments is of the order of N, then in the limit of large N the resulting length distribution is geometric (see STAR Methods, section “Equal nucleating centers” for a detailed calculation for this case). This theoretical result might provide a link between two recent experiments on mitotic spindles, one which showed that the spindle size is controlled by a limiting pool mechanism (Good et al., 2013) and the other that found that individual microtubule lengths within the spindle are geometrically distributed (Brugués et al., 2012).

To illustrate our general results regarding assembly of many filaments from a common pool of monomers we show in Figure 4 the different phases of assembly using an example of six filaments with three growing at the same, fast rate and three taking up monomers more slowly. (See section “Aggregate distribution of multiple filaments” in STAR Methods for detailed calculations pertaining to the multi-filament case.)

Figure 4. Growth dynamics of multiple filaments from two types of inequivalent nucleating centers.

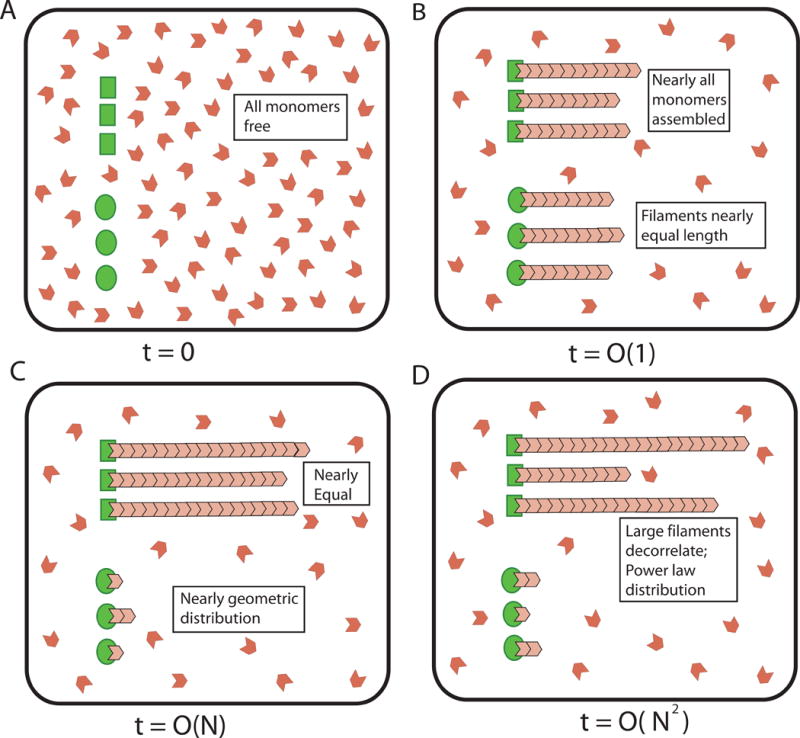
(A) Schematic showing six nucleating centers in a pool of monomers where the first three nucleate filaments that grow at a high association rate k′_h,₊ and the remaining three at a slower rate k′_s,₊ (k′_h,₊ > k′_s,₊); all filaments disassemble with the same rate k₋. (B) After a rapid assembly phase lasting approximately 1/(3(k′_h,₊ + k′_s,₊)), the fast and slow growing filaments reach the average length of Nk′_h,₊/(3(k′_h,₊ + k′_s,₊)), and Nk′_s,₊/(3(k′_h,₊ + k′_s,₊)), respectively. (C) After this rapid assembly phase, the slower growing filaments slowly decrease to nearly zero length over a period of time of order $N/(3{\kappa }_{d_s}({k^{\prime }}_{h,+}-{k^{\prime }}_{s,+}))$, where ${\kappa }_{d_s}=k_{-}/{k^{\prime }}_{s,+}$ is the (dimensionless) dissociation constant for the slow growing filaments. At the end of this phase, the three slow growing filaments are geometrically distributed with parameter ${\kappa }_{d_h}/{\kappa }_{d_s}$, the free monomer pool approaches a Poisson distribution with mean ${\kappa }_{d_h}$, and nearly all the monomers, $N-{\kappa }_{d_h}-3{\kappa }_{d_h}/({\kappa }_{d_s}-{\kappa }_{d_h})$, are taken by the fast growing filaments, and are equally distributed among them. (D) Finally, the sizes of the three largest filaments decorrelate on a slow, diffusion time scale which is of order N², during which the monomers randomly exchange between these large filaments.

Assembly of three dimensional structures

From the preceding analysis, we see that assembling multiple filamentous structures from a shared, limiting pool of monomers does not lead to precise size control of individual structures without additional control mechanisms. This stems from the inherent reversibility of the assembly process once steady state is reached. At steady state exchange of subunits between different structures results in structures with either very small, exponentially distributed sizes, or large sizes whose variability is described by a power-law distribution. Since the key ingredient for this result to hold, namely the reversibility of stochastic assembly, is not limited to one-dimensional filamentous structures, equivalent phenomena are expected to occur for three-dimensional structures assembled from a common and limiting pool of subunits.

In the case of multiple three-dimensional structures being assembled from a shared pool of subunits, the total mass (or equivalently, the total number of assembled subunits) of the structures will reach a well-defined value once the assembly rate and the disassembly rates are balanced, and the pool of free subunits reaches the critical concentration. As in the case of filamentous structures, the masses of individual structures will be broadly distributed.

To demonstrate this explicitly we have done stochastic simulations of assembly of two identical three-dimensional structure from a finite pool of subunits. The three-dimensional nature of the structures is reflected in our choice of assembly and disassembly rates, which are both proportional to the radius of the growing structures (Berg and Purcell, 1977). As in the case of assembling filaments, the assembly rate diminishes as the structures grow and the free monomer pool is depleted. As before we find that after an initial, fast growth phase the system tends to a steady state in which individual masses undergo diffusive dynamics and leading to a mass distribution which is broad (Figure S2).

Discussion

The limiting pool mechanism of size control has been implicated in the assembly of a number of different cellular structures in different cell types (Goehring and Hyman, 2012). In order to understand the quantitative features of this general size-control mechanism we considered a simple model of stochastic growth of filamentous structures from a limiting pool of diffusing monomers, where the number of filaments is determined by the number of nucleating centers at which they assemble. While we found that the limiting-pool mechanism is able to precisely control the length of a single filament, it is unable to control individual filament lengths when multiple filaments are assembled from the same monomer pool, even when additional processes of catastrophe and rescues were included (Figure S1). At steady state exchange of monomers between different filaments results in structures with either very small, exponentially distributed lengths, or large lengths whose variability is described by a power-law distribution. Since the key ingredient for this result to hold, namely the reversibility of stochastic assembly, is not limited to one-dimensional filamentous structures, equivalent phenomena are expected to occur for three-dimensional structures assembled from a common and limiting pool of subunits (Figure S2). We suggest that when in vivo observations demonstrate that size control of multiple structures is precise, mechanisms beyond the limiting pool must contribute to this precision (See Box 1).

One of the consequences of our study is that a limiting pool mechanism by itself is unable to make steady-state structures of different and well defined sizes. Our analysis describes the limitations associated with the limiting-pool mechanism and underlines the necessity for the cell to invest in additional mechanisms to control size. In fact, there are other length-sensing mechanisms that have been reported in the filament literature (Andrianantoandro and Pollard, 2006; Chesarone-Cataldo et al., 2011; Gardner et al., 2011; Marshall et al., 2005; Mohapatra et al., 2015, 2016; Varga et al., 2006). In these studies specific proteins have been identified as being critical to length-control, and found to either modulate the assembly or the disassembly rate of cytoskeletal filaments in a length dependent fashion (Mohapatra et al., 2016). Such size sensing mechanisms might play a role in assembling three dimensional structures as well. For example, an autocatalytic reaction at the core was recently proposed to play a critical role in controlling the sizes of centrosomes (Zwicker et al., 2014), which could provide an additional feedback of centrosome size to the assembly rate. An interesting question is whether such size sensing mechanism exist in other three dimensional structures like the nucleoli, where only the limiting pool has been implicated as the only size control mechanism thus far (Weber and Brangwynne, 2015) (See Box 1).

In summary, the limiting-pool mechanism of size control can produce a single structure of a well-defined size. On the other hand, this mechanism is unable to maintain multiple structures that have a well-defined size, which assemble from a common pool of subunits. Cells can get around this problem by using additional size-regulatory mechanisms (Mohapatra et al., 2016). Quantitative experiments that measure the size and assembly dynamics of intracellular structures, and how they vary with different parameters, like the total amount of the limiting subunit or the size of the chamber within which they are assembled, are needed to quantitatively define the role of the limiting-pool mechanism in regulating size. Such experiments can also help uncover general design principles of how cells regulate the sizes of their organelles.

STAR Methods

In the STAR Methods, we provide the computation and rigorous justification of several results from the manuscript. First, in section “Heuristic derivation of filament distributions”, we present an intuitive derivation of the approximate filament distributions for a general number of equal and unequal nucleating centers; see sections “Equal nucleating centers”, “Unequal nucleating centers” and “General case”. Even though our derivation is heuristic, it leads to explicit and accurate approximations for the range of parameters that are relevant in biology. The accuracy of these approximate solutions in this section is further rigorously validated in section “Exact solutions of filament distributions”. For a general number of filaments with inequivalent assembly rates, our results show that in steady state there can be at most one filament with well-defined length of order N, while all the other filaments are very small O(1); we use O(x) to denote a quantity that is of the order of x. Furthermore, any scenarios that grow multiple filaments of order N yield highly variable lengths whose standard deviation is about the same as the mean.

Section “Time dynamics” describes the time dynamics of our system. We show that filaments undergo three phases, namely the growth, linear adjustment and diffusion ones. The growth phase is relatively quick of the order τ_g = O(1), and at the end of this phase all filaments have length of the order O(N). After this phase, in the case of unequal assembly rates, the system will undergo a linear adjustment phase τ_a = O(N), during which the filaments with smaller assembly rates will decrease to nearly zero and will have geometric distributions. Next, if at the end of this phase there are multiple filaments with the highest assembly rate, they will converge to steady state through a slower diffusion time scale τ_d = O(N²). During this phase, the dissociated monomers will randomly transfer between the longest filaments, which will result in their steady state distribution being a power law. In order to estimate the diffusion time scale, we also compute the diffusion constant.

In the section “Main inferences and estimates”, we briefly summarize our results and make a number of additional inferences that are relevant for biology. We discuss the fraction of monomers in filamentous form, as well as provide explicit expressions for the filament mean and variance under different growth conditions. In addition, we briefly outline our results on time dynamics of the finite monomer pool mechanism.

In section “Exact solutions of filament distributions”, using Queueing Theory arguments (Anselmi et al., 2013), we show that the exact solution to our model admits an explicit representation up to a multiplicative normalization constant. However, the computation of the normalization constant in this solution requires a prohibitively large summation of the order O(N^f), where N is the number of monomers and f is the number of filaments. In addition, even if one were capable of computing the sums, they provide little, if any, insight into the problem. To alleviate these issues, we develop intuitive and explicit representations of the filament distributions in terms of auxiliary random variables in section “Equal nucleating centers”. In addition to being computationally efficient, these explicit representations readily provide a rigorous justification for our heuristic approximations from section “Heuristic derivation of filament distributions”. Furthermore, for 2 nucleating centers, we present computationally suitable representation for the solutions in the section “Gamma function representations of 2 filaments”, which are used in Figure 1D and Figure 3 as comparison to the stochastic simulations.

Finally, in section “Aggregate distribution of multiple filaments”, we derive the aggregate distributions, both for the case of equivalent and inequivalent nucleating centers.

Heuristic derivation of filament distributions

Here, we provide an intuitive derivation of the filament distributions. The accuracy of the derived distributions will be validated through the exact calculations in the following section.

Let N be the total number of monomers and f ≥ 1 be the number of filaments. Next, we use l₁, l₂, …, l_f, to denote the number of assembled monomers in filaments 1, 2, …, f, respectively. Each monomer has a rate k′_i,₊, 1 ≤ i ≤ f to assemble to filament i, and can disassemble one monomer at a time with disassembly rates k_j,₋, 1 ≤ j ≤ f. In addition, we assume that k_j,₋ = k₋, i.e., all filaments disassemble at the same rate. Furthermore, let ${\kappa }_{d_i}=k_{-}/{k^{\prime }}_{i,+}$, 1 ≤ i ≤ f, be the corresponding dissociation constants, and since they are chemical constants, they do not scale with N. Let p(l₁, l₂, …, l_f) be the steady state probability that lengths of filaments 1, 2, …, f, are equal to l₁, l₂, …, l_f, respectively.

Equal nucleating centers: ${\kappa }_{d_i}={\kappa }_d$

We assume that κ_d ≪ N, i.e., the dissociation constant is not too large, otherwise most monomers would be free in steady state. Hence, when N is large and f ≪ N, the probability of a filament having zero length is negligible. Therefore, the rate at which monomers join the free monomer pool is approximately fk_. Let M be the number of free monomers in steady state. Now, when the number of free monomers is M = m, the rate at which monomers leave the monomer pool is mfk′₊. By equating the rates in and out of state M = m, we obtain that the distribution of free monomers satisfies approximately

$$P[M=m]m{k^{\prime }}_{+}\approx P[M=m-1]k_{-}.$$ (1)

This balance equation readily yields a Poisson distribution, i.e., $P[M=m]\approx \frac{e^{-{\kappa }_d}{{\kappa }_d}^m}{m!}$. Note that the preceding derivation is exact for the case of f =1, i.e., in this case the number of free monomers is truncated Poisson; see section “Exact solutions of filament distributions”. Otherwise, the Poisson distribution is an approximation, albeit a good one, since the rate at which monomers join the pool can be smaller than fk₋ at the boundary when some filaments have zero length. The rest of the derivation assumes f ≥ 2.

Next, when κ_d is relatively large, but still κ_d ≪ N, due to the Central Limit Theorem¹, M is very concentrated around its mean, 〈M〉 ≈ κ_d, i.e., M ≈ κ_d. Therefore the total number of assembled monomers is approximately constant, i.e., l₁ + ⋯+ l_f ≈ N − κ_d. Furthermore, monomers diffuse from one filament to others with equal rates (k₋/f, see section “Diffusion time scale τ_d”) independent of the lengths of individual filaments, and therefore, all states l₁ + ⋯+ l_f ≈ N − κ_d are equally likely; the number of configurations satisfying the preceding equation is $\left(\genfrac{}{}{0ex}{}{N-{\kappa }_d+f-1}{f-1}\right)$. Now, if we are interested in the filament distribution, say filament 1, then the remaining filaments satisfy l₂ + ⋯+ l_f ≈ N − κ_d − l₁, and the number of these configurations is $\left(\genfrac{}{}{0ex}{}{N-l_1-{\kappa }_d+f-2}{f-2}\right)$. Therefore, when f ≪ N − κ_d, and l₁ < N − κ_d,

$$p(l_1)\approx \frac{\left(\frac{N-l_1-{\kappa }_d+f-2}{f-2}\right)}{\left(\frac{N-{\kappa }_d+f-1}{f-1}\right)}\approx \frac{(f-1)}{N-{\kappa }_d}{\left(1-\frac{l_1}{N-{\kappa }_d}\right)}^{f-2},$$ (2)

and p(l₁) ≈ 0, for l₁ > N − κ_d. For f = 2, this expression is uniform, i.e., $p(l_1)\approx \frac{1}{N-{\kappa }_d}$ in interval (0, N − κ_d), and p(l₁) ≈ 0 outside of it.

The preceding derivation assumes that f is a fixed constant, which does not scale with N. Now, we consider the case when the number of filaments f is of the same order as N, i.e., when in the limit as N grows to infinity, the ratio (N − κ_d)/(N − κ_d + f) ≈ N/(N + f) → ϕ, 0 < ϕ < 1. Interestingly, in this case, the preceding power law distribution becomes geometric with parameter ϕ. Namely, for any constant l₁, after canceling the common terms in the fraction of two binomial coefficients in Equation 2, we obtain

$$p(l_1)\approx (f-1)\frac{(N-{\kappa }_d)\cdots (N-{\kappa }_d-l_1+1)}{(N-{\kappa }_d+f-1)\cdots (N-{\kappa }_d+f-1-l_1)}.$$

Next, since l₁ is fixed, i.e. l₁ ≪ f, l₁ ≪ N, and κ_d is a chemical constant that doesn’t scale with N the preceding fraction further simplifies to

$$p(l_1)\approx (f-1)\frac{{(N-{\kappa }_d)}^{l_1}}{{(N-{\kappa }_d+f)}^{l_1+1}}\approx f\frac{N^{l_1}}{{(N+f)}^{l_1+1}}\approx (1-\varphi ){\varphi }^{l_1},$$

and hence the distribution of lengths is geometric.

Unequal nucleating centers: ${\kappa }_{d_1}<\underset{2\le i\le f}{\mathit{min}}{\kappa }_{d_i}$

Let us assume that all k_i,₋ = k_, ${k^{\prime }}_{1,+}>\underset{i\ge 2}{\max }{k^{\prime }}_{i,+}$, and that f is finite, i.e., it doesn’t scale with N. Then, over a long period of time, a considerably larger number of monomers will join the first filament than any other filament. Hence, since the detachment rates are all the same, the first filament tends to accumulate most of the monomers, i.e., it gets considerably larger than other filaments. Therefore, in steady state p₁(0) ≈ 0. This implies that the rate at which monomers leave the first filament is k−(1 − p₁(0)) ≈ k_, and the average rate at which monomers are attaching to the first filament is 〈M〉k′_1,+. Then, due to rate conservation, 〈M〉k′_1,+ ≈ k_, yielding $\langle M\rangle \approx k_{-}/{k^{\prime }}_{1,+}={\kappa }_{d_1}$. Now that we know the average number of monomers 〈M〉, we can compute p_i(0), i ≥ 2, from 〈M〉k′_i,₊ = k_(1 − p_i(0)), which gives $p_i(0)\approx 1-\langle M\rangle ({k^{\prime }}_{i,+}/k_{-})=1-{\kappa }_{d_1}/{\kappa }_{d_i}$. Furthermore, the distribution of filament i ≥ 2 satisfies, for l > 1, p_i(l)k_ ≈ 〈M〉k′_i,₊ p_i(l − 1), implying that p_i(l) is geometric, i.e.,

$$p_i(l)\approx p_i(0){\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_i}}\right)}^l=\left(1-\frac{{\kappa }_{d_1}}{{\kappa }_{d_i}}\right){\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_i}}\right)}^l.$$ (3)

For the free monomer pool, the rate at which the monomers are arriving to the pool is

$$\begin{gathered} k_{-}(1-p_1(0))+k_{-}(1-p_2(0))+\cdots +k_{-}(1-p_f(0))\approx k_{-}\left(1+\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}+\cdots +\frac{{\kappa }_{d_1}}{{\kappa }_{d_f}}\right) \\ =\frac{k_{-}}{{k^{\prime }}_{1,+}}({k^{\prime }}_{1,+}+{k^{\prime }}_{2,+}+\dots +{k^{\prime }}_{f,+}) \end{gathered}$$ (4)

and, when M = m, the rate at which monomers are leaving the pool is m(k′_1,+ + k′_2,+ + … + k′_f,₊). Therefore, by equating these rates, we derive an approximate balance equation

$$P[M=m]m\approx \frac{k_{-}}{{k^{\prime }}_{1,+}}P[M=m-1],$$ (5)

resulting in M being approximately Poisson with a mean ${\kappa }_{d_1}$. Finally, L₁ can be computed from N − M − L₂ − …− L_f. From this we can see that, L₁ = O(N), i.e., the first filament takes most of the monomers.

For f = 2, the distribution of first filament is peaked and second filament is geometric, i.e., $p_2(l)\approx \left(1-\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right){\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right)}^l.$

General case: ${\kappa }_{d_1}=\cdots ={\kappa }_{d_{f_1}}<\underset{f_1<i\le f}{\mathit{min}}{\kappa }_{d_i}$

Here, we consider a general scenario where f₁ filaments are growing at a fast rate with dissociation constant ${\kappa }_{d_1}$, and the remaining f₂ = f − f₁ are growing at slower rates; the total number of filaments f is finite, as in the preceding subsection. Again, we show that the limiting-pool mechanism can grow at most one filament of the cell size, O(N), with a well-defined length, i.e., peaked filament distribution.

The same arguments as in the preceding section can show that each of the f₂ filaments will have geometrically distributed and independent lengths. Hence, the total sum of filaments, S₂, in the slower growing group will have a peaked distribution since the sum of independent geometric variables is peaked. In fact, as f₂ increases, the distribution of S₂ will approach the Gaussian, and it will be highly centered around its mean. Therefore, the aggregate distribution of all the fast growing filaments will be highly concentrated around its mean $N-{\kappa }_{d_1}-\langle S_2\rangle$; note that ${\kappa }_{d_1}$ accounts for the average number of free monomers in steady state. Thus, the total number of assembled monomers in the fast growing group will be approximately constant in steady state $N-{\kappa }_{d_1}-\langle S_2\rangle$; note that this group of filaments will grab nearly all monomers. Hence, if f₁ = 1, the first filament will have a well-defined length, i.e., peaked distribution, of order O(N).

However, if f₁ ≥ 2, the monomers in the first group will, similarly as in the derivation of Equation 2, assume any of the equally likely configurations that satisfy $l_1+\cdots +l_{f_1}\approx N-{\kappa }_{d_1}-\langle S_2\rangle$, whose number is $\left(\genfrac{}{}{0ex}{}{N-{\kappa }_{d_1}-\langle S_2\rangle +f_1-1}{f_1-1}\right)$. Hence, if we are interested in a single filament distribution from this group, say filament 1, then the remaining filaments satisfy $l_2+\cdots +l_{f_1}\approx N-{\kappa }_{d_1}-\langle S_2\rangle -l_1$ and the number of these configurations is $\left(\genfrac{}{}{0ex}{}{N-l_1-{\kappa }_{d_1}-\langle S_2\rangle +f_1-2}{f_1-2}\right)$. Therefore, by dividing the preceding binomial expressions, when $f_1\ll N-{\kappa }_{d_1}-\langle S_2\rangle$, and $l_1<N-{\kappa }_{d_1}-\langle S_2\rangle$, one derives that the distribution of a single fast growing filament is a power law

$$p(l_1)\approx \frac{(f_1-1)}{N-{\kappa }_{d_1}-\langle S_2\rangle }{\left(1-\frac{l_1}{N-{\kappa }_{d_1}-\langle S_2\rangle }\right)}^{f_1-2}.$$ (6)

Note that for f₁ = f (f₂ = 〈S₂〉 = 0), the preceding distribution coincides with the previously derived in Equation 2 for of section “Equal nucleating centers”.

Overall, regardless of the number of filaments, there can be at most one filament of order N with well-defined size, i.e., peaked distribution.

Time dynamics

In this section we show that the filament time dynamics occurs on three times scales of the order O(1), O(N) and O(N₂), respectively. First, they go through a quick growth phase where all filaments reach size O(N) in time ${\tau }_g=O(1/{\displaystyle \sum {k^{\prime }}_{i+}})$; see section “Growth time scale τ_g” in STAR methods. Then, in case of inequivalent filaments, they undergo a linear adjustment phase of the order τ_g = O(N), as described in section “Adjustment time scale τ_a for inequivalent filaments”. In this phase filament dynamics can be thought of as diffusion with drift. Finally, in case of two or more fastest growing filaments, they will start performing a random walk until they reach steady state, which will occur at a slower diffusion time scale τ_d ≈N²/(2D), where D is the diffusion constant; see section “Diffusion time scale τ_d”. We provide an expression for the diffusion constant D in section “Calculation of diffusion constant D”.

Growth time scale τ_g

Initially when the filaments start to assemble, there is a strong tendency for them to grow. In this section, we will estimate this growth time scale. To this end, assume f filaments that are growing in a pool of N monomers with possible different association rates $k_{i,+}^{\prime }$ and equal dissociation constant k₋. Now, let us consider a continuous limit, where monomers are treated as fluid. Hence, during the initial phase while all l_i(t) > 0, the continuous (fluid) amount of free monomers m(t) satisfies

$$\frac{dm}{dt}=f{k}_{-}-({k^{\prime }}_{1,+}+\cdots +{k^{\prime }}_{f,+})m,$$ (7)

from which one easily computes, using the initial value m(0) = N,

$$m(t)=\frac{f{k}_{-}}{{k^{\prime }}_{1,+}+\cdots +{k^{\prime }}_{f,+}}+\left(N-\frac{f{k}_{-}}{{k^{\prime }}_{1,+}+\cdots +{k^{\prime }}_{f,+}}\right)e^{-({k^{\prime }}_{1,+}+\cdots +{k^{\prime }}_{f,+})t}.$$ (8)

From this equation we see that the monomer pool is quickly reduced to a small fraction of N in time

$${\tau }_g=O\left(\frac{1}{{k^{\prime }}_{1,+}+\cdots +{k^{\prime }}_{f,+}}\right).$$ (9)

Next, when all filaments grow at the same rate $k_{i,+}^{\prime }=k_{+}^{\prime }$, we immediately obtain by symmetry the continuum approximation for the individual filament lengths

$$l_i(t)=\frac{1}{f}\left(N-\frac{k_{-}}{k_{+}^{\prime }}\right)(1-e^{-f{k}_{+}^{\prime }t}).$$ (10)

Hence, in the case of equal assembly rates, all filaments will quickly grow to length (N − κ_d)/f in time ${\tau }_g=O(1/(f{k}_{+}^{\prime }))$. More specifically, the time required for a filament to get very close to (N − κ_d)/f, say 90%(N − κ_d)/f is given by log (10)/ $(f{k}_{+}^{\prime })$, i.e., ${\tau }_g=O(1/f{k}_{+}^{\prime }))$.

Using $k_{+}^{\prime }\approx 5\times {10}^{-3}{s}^{-1}$, for actin cables in budding yeast cells (see “Estimates for actin cables in yeast” section in STAR Methods for more details), and typical number of cables, i.e. f = 10, we find ${\tau }_g=1/f{k}_{+}^{\prime }=20s$, i.e. less than a minute.

After this initial growth phase, in case that all assembly rates are equal, the filaments will undergo a random diffusion, which is described in section “Diffusion time scale τ_d” in STAR Methods. On the other hand, if some of the association rates are different, there will be a linear adjustment period that we describe in the next section.

Adjustment time scale τ_a for inequivalent filaments

In this section, we study the filament time dynamics when some of the assembly rates are different. It is convenient to denote the sum of all the association rates as ${\overline{k}}_{+}^{\prime }=k_{1,+}^{\prime }+\cdots +k_{f,+}^{\prime }$. Then, the individual filament lengths satisfy

$$\frac{d{l}_i}{dt}=m(t)k_{i,+}^{\prime }-k_{-},$$ (11)

which by replacing Equation 8 from the preceding section and using integration, yields

$$l_i(t)=k\_\left(\frac{f{k}_{i,+}^{\prime }}{{\overline{k}}_{+}^{\prime }}-1\right)t+\frac{k_{i,+}^{\prime }}{{\overline{k}}_{+}^{\prime }}\left(N-\frac{f{k}_{-}}{{\overline{k}}_{+}^{\prime }}\right)(1-e^{-{\overline{k}}_{+}^{\prime }t}).$$ (12)

The preceding equation remains true initially while all filament lengths l_i(t) > 0. From this equation we see that, after a quick growth phase of the order $1/{\overline{k}}_{+}^{\prime }$, the individual filaments will reach approximately lengths $N{k}_{i+}^{\prime }/{\overline{k}}_{+}^{\prime }$, and then, those with assembly rates smaller than the average assembly rate, i.e. $k_{i+}^{\prime }<{\overline{k}}_{+}^{\prime }/f$, will linearly decrease until one of them reaches zero. At that time, say ${\tau }_{a_1}$, we exclude the filaments whose length is zero, and repeat the preceding calculations with the remaining filaments and initial values equal to $m({\tau }_{a_1})$, $l_i({\tau }_{a_1})$. We repeat these calculations for as long as there are filaments that linearly decrease to zero. There can be at most f − 1 such linear adjustment times, and since each time is of the order N, the entire adjustment time in the general case will be τ_a = O(N).

Now, in the case of two inequivalent filaments with $k_{1,+}^{\prime }>k_{2,+}^{\prime }$, the preceding analysis, for all t such that l₂(t) > 0, specializes to

$$m(t)=\frac{2k_{-}}{k_{1,+}^{\prime }+k_{2,+}^{\prime }}+\left(N-\frac{2k_{-}}{k_{1,+}^{\prime }+k_{2,+}^{\prime }}\right)e^{-(k_{1,+}^{\prime }+k_{2,+}^{\prime })t}$$ (13)

and

$$l_2(t)=-k_{-}\frac{k_{1,+}^{\prime }-k_{2,+}^{\prime }}{k_{1,+}^{\prime }+k_{2,+}^{\prime }}t+\frac{k_{2,+}^{\prime }}{k_{1,+}^{\prime }+k_{2,+}^{\prime }}\left(N-\frac{2k_{-}}{k_{1,+}^{\prime }+k_{2,+}^{\prime }}\right)(1-e^{-(k_{1,+}^{\prime }+k_{2,+}^{\prime })t}),$$ (14)

$$l_1(t)=k_{-}\frac{k_{1,+}^{\prime }-k_{2,+}^{\prime }}{k_{1,+}^{\prime }+k_{2,+}^{\prime }}t+\frac{k_{1,+}^{\prime }}{k_{1,+}^{\prime }+k_{2,+}^{\prime }}\left(N-\frac{2k_{-}}{k_{1,+}^{\prime }+k_{2,+}^{\prime }}\right)(1-e^{-(k_{1,+}^{\prime }+k_{2,+}^{\prime })t}).$$ (15)

As in the preceding general case, after the initial growth ${\tau }_g=O\left(\frac{1}{k_{1,+}^{\prime }+k_{2,+}^{\prime }}\right)$, the filaments will reach the respective lengths $\frac{k_{1,+}^{\prime }}{k_{1,+}^{\prime }+k_{2,+}^{\prime }}N$ and $\frac{k_{2,+}^{\prime }}{k_{1,+}^{\prime }+k_{2,+}^{\prime }}N$, i.e., both filaments will be of order N. After that, they will go through an adjustment phase τ_a, during which the second filament will linearly decrease to zero and the first will grow to include nearly all N. We can compute τ_a, by using Equation 14 and setting l₂(τ_a) = 0; hence, by ignoring the small exponential term in Equation 14, τ_a results from solving the linear equation, which produces

$${\tau }_a=\frac{k_{2,+}^{\prime }}{k_{-}(k_{1,+}^{\prime }-k_{2,+}^{\prime })}\left(N-\frac{2k_{-}}{k_{1,+}^{\prime }+k_{2,+}^{\prime }}\right)\approx \frac{N}{{\kappa }_{d_2}(k_{1,+}^{\prime }-k_{2,+}^{\prime })}.$$ (16)

When $k_{1,+}^{\prime }$ and $k_{2,+}^{\prime }$ are close, this adjustment time will be very large, but will still scale linearly in N; one could think of this phase as diffusion with a small drift $k_{1,+}^{\prime }-k_{2,+}^{\prime }$.

Therefore, at the end of this adjustment phase, we have

$$l_2({\tau }_a)=0,l_1({\tau }_a)=\left(N-\frac{2k}{k_{1,+}^{\prime }+k_{2,+}^{\prime }}\right),m({\tau }_a)=\frac{2k_{-}}{k_{1,+}^{\prime }+k_{2,+}^{\prime }}.$$ (17)

Finally, for t > τ_a, there will be a very small correction in size, such that $m(t)\downarrow {\kappa }_{d_1}$ and $l_1(t)\uparrow N-{\kappa }_{d_1}$.while l₂(t) = 0. This will occur very quickly in time $O(1/k_{1+}^{\prime })$.

Diffusion time scale τ_d

In case of two or more fast growing filaments, after the preceding growth and linear adjustment phases are completed, these large filaments will perform a random diffusion until they reach the steady state in diffusion time τ_d. The diffusion constant for this random walk is D = (f − 1)k₋/f, which will be computed in the following section. In order to reach the steady state, the filaments need to cover at least the total average filament length (N − κ_d), which will happen in time of the order τ_d ≈ N²/(2D) = N²/k_.

If we take into account the estimated in vivo rate of disassembly $k_{-}\approx 60\frac{1}{s}$ (see “Estimates for actin cables in yeast” section in STAR Methods), τ_d ~ several days. In other words, it is impossible to see fluctuations in the time scale of experiments. The fraction of F-actin to G-actin in cells and the fraction of F-actin in patches are not well characterized and could contribute to an error to the estimate. But, at the same time, the fact that we do not see the fluctuations in minutes could hint that there are additional length control mechanisms at play and the cables are not determined just by the limited pool of actin monomers.

Calculation of diffusion constant D

As noted earlier, in this section we will provide further arguments that the filament lengths perform a random walk in steady state for the case of equal nucleating centers, and compute its diffusion constant D. Consider the steady state time dynamics of L_i(t), where L_i(t) is the length of filament i at time t, and let all assembly and disassembly rates be equal k′_i,₊ = k′₊ and k′_i,₋ = k′₋, respectively.

Using the analysis from the preceding sections (for finite f), we know that the number of free monomers M in steady state is approximately Poisson with mean κ_d and standard deviation $\sqrt{{\kappa }_d}$, implying when κ_d ≫ 1, that $P[|M-{\kappa }_d|<2\sqrt{{\kappa }_d}]\approx 1$. This and L₁ + ⋯ + L_f = N − M yield for 1 ≪ κ_d ≪ N,

$$P[|L_1+\cdots +L_f-(N-{\kappa }_d)|<2\sqrt{{\kappa }_d}]\approx 1.$$ (18)

Thus, the filaments perform a random walk in steady state in a close proximity of the hyperplane

$$L_1(t)+\dots +L_f(t)\approx N-{\kappa }_d,$$ (19)

and the number of free monomers is very close to

$$M(t)\approx {\kappa }_d=\frac{k_{-}}{{k^{\prime }}_{+}}.$$ (20)

Next, let us pick an interval of time T, such that 1/(fk′₊) ≪ T ≪ N². Now, consider the first filament L₁. Then, in interval (0, T), a Poisson number of monomers with mean Tk_ leaves L₁. Each of these monomers is delayed in the free monomer pool an exponential amount of time with mean 1/(fk′₊), and then it rejoins one of the filaments. Note that the randomly delayed Poisson process is again Poisson with the same rate k₋. After passing through the free monomer pool, each of the monomers will rejoin one of the filaments with probability 1/f. Hence, Tk_/f of these monomers will return to the first filament. Therefore, the net number of monomers that leaves the first filament is approximately Poisson with equal mean and variance given by $\frac{f-1}{f}T{k}_{-}$.

On the other hand, the f − 1 filaments L_i, 2 ≤ i ≤ f, will contribute an independent Poisson number of monomers of mean $\frac{T{k}_{-}}{f}$. Since these contributions are independent and Poisson, their total sum is Poisson with mean and variance equal to $\frac{f-1}{f}T{k}_{-}$.

Thus, by summing the preceding variances for the total number of monomers that leave and arrive, we obtain, for 1 ≪ T ≪ N₂, that

$$\text{Var}(L_1(T)-L_1(0))\approx 2\frac{f-1}{f}T{k}_{-}.$$ (21)

As we can see, the net average number of monomers that leave and arrive to a filament is zero. Hence, the only mechanism with which the filaments change their lengths and approach the steady state is by performing a random walk/diffusion in the proximity of L₁ + L₂ + ⋯ L_f ≈ N − κ_d hyper-plane. This will happen very slowly, in time τ_d = O(N²); see the preceding section. After the system reaches the steady state, this random walk will continue indefinitely.

For f = 2, the variance is Tk_ and consequently the diffusion constant D is k_/2.

Main inferences and estimates

In this section, we briefly summarize our results and make a number of additional inferences that are relevant for biology.

Fraction of monomers in filaments

From section “Heuristic derivation of filament distributions” we see that the number of free monomers M for finite f is closely approximated by the Poisson distribution with mean $\langle M\rangle \approx {\kappa }_d=k_{-}/k_{+}^{\prime }$ (recall k′₊ is the assembly rate per monomer and k₋ is the rate of removal of monomers); note that, in the case of unequal nucleating centers, κ_d is the smallest disassociation constant. Hence, the mean number of assembled monomers in all filaments is given by N − κ_d, where N is the total number of monomers. The fraction of monomers in filamentous form relative to the total pool of monomers is given by $g=(N-{\kappa }_d)/N=1-k_{-}/(N{k}_{+}^{\prime })$. Typically the initial rate of assembly, Nk′₊ is much faster than the rate of disassembly k₋ (Example: In actin, k′₊ = 11.6 μM⁻¹s⁻¹ and k₋ = 1.4 s⁻¹ (Pollard, 1986) at the barbed end of the filament); then this ratio determines the ratio of free monomers at steady state, which will be very small.

From limiting pool mechanism, most of the monomers are going to be in the filaments. In order to obtain a different fraction of monomers in the filamentous form, k′₊ and k₋ will have to be fine-tuned. Such fine-tuning is not seen very often in biology, and cells probably get by this situation by having additional length control mechanisms.

Steady state properties in case of equal nucleating centers

From the approximate expression (Equation 2) for the distribution, or by symmetry, one easily computes an intuitively expected mean filament length $\langle L\rangle \approx \frac{N-{\kappa }_d}{f}$, i.e., the average filament lengths are equal. However, the filament distribution is flat with a very high variance/standard deviation. To compute the variance/standard deviation, we obtain 〈L〉² ≈ (N − κ_d)²/(f(f + 1)) using (Equation 2), and combine it with the preceding expression for the mean

$${\sigma }_L\approx \frac{N-{\kappa }_d}{f}\sqrt{\frac{f-1}{f+1}}\approx \langle L\rangle \sqrt{\frac{f-1}{f+1}}.$$ (22)

We see, maybe somewhat surprisingly, that the standard deviation is of the same order as N and the mean. In the case of f = 2, the distribution is entirely flat, i.e., uniform in interval (0, N − κ_d)

$$p(l)\approx \frac{1}{N-{\kappa }_d},$$ (23)

and p(l) ≈ 0 outside of it. The mean of this distribution is (N − κ_d)/2 and the standard deviation is $(N-{\kappa }_d)/(2\sqrt{3})$.

Interestingly, when the number of filaments scale with N, i.e., N/(N + f) → ϕ, 0 < ϕ < 1, the preceding power law distribution turns into geometric with parameter ϕ.

Steady state properties in case of unequal nucleating centers

Let us first consider f = 2 that are growing in two unequal nucleating centers. The distribution of first filament $(k_{1,+}^{\prime }>k_{2,+}^{\prime };{\kappa }_{d_1}<{\kappa }_{d_2})$ is peaked and second filament is geometric, i.e., $p_2(l)\approx \left(1-\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right){\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right)}^l$. The approximate average lengths of the first and second filament are respectively given by

$$\langle L_1\rangle \approx N-{\kappa }_{d_1}-\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}-{\kappa }_{d_1}},\langle L_2\rangle \approx \frac{{\kappa }_{d_1}}{{\kappa }_{d_2}-{\kappa }_{d_1}}.$$ (24)

The one with higher assembly rates always takes up most of the monomers, leaving not much for the other one. In addition, the average length of the first filament increases with N, while the second one remains constant. Furthermore, their variances are given by

$$\text{Var}(L_1)\approx {\kappa }_{d_1}+\frac{{\kappa }_{d_1}{\kappa }_{d_2}}{{\left({\kappa }_{d_2}-{\kappa }_{d_1}\right)}^2},\text{Var}(L_2)\approx \frac{{\kappa }_{d_1}{\kappa }_{d_2}}{{\left({\kappa }_{d_2}-{\kappa }_{d_1}\right)}^2}.$$ (25)

Here, both variances remain constant as N increases. In either case, it is impossible to obtain multiple peaked distributions of individual filaments with just finite monomer pool. We need additional size-control mechanisms to achieve that.

Finally, if two groups of finitely many filaments f₁, f₂ are growing, where the first group has higher assembly rate $k_{h,+}^{\prime }$, and the second group slower rate $k_{s,+}^{\prime }$, $k_{h,+}^{\prime }>k_{s,+}^{\prime }$, then the second group will have f₂ geometrically distributed filaments. Hence, the expected total number of monomers in the second group will be $f_2{\kappa }_{d_h}/({\kappa }_{d_s}-{\kappa }_{d_h})$, and the first group will have $N-{\kappa }_{d_h}-f_2{\kappa }_{d_h}/({\kappa }_{d_s}-{\kappa }_{d_h})$. Similarly as in the case of two filaments, the variance of each group remains constant as N increases. The first group will grab almost all the monomers, and in the case of a single filament, f₁ = 1, its length will be well defined.

However, in case of multiple large filaments, f₁ ≥ 2, they will have a power law distribution given in Equation 6, with the standard deviation of the same order as the mean, similarly as in Equation 22.

Overall, we show that in general there can be at most one large filament with well-defined size, and thus, additional size-control mechanisms may be needed to achieve multiple filaments of order N.

Time dynamics of the finite monomer pool mechanism

Here, we briefly summarize the main results on the time dynamics of the free monomer pool. As shown in section 2, the filaments undergo three phases, namely the growth, linear adjustment and diffusion ones.

Initially, the environment strongly favors assembly which quickly reduces the monomer pool to a small fraction of N i.e., the filament lengths become (N), in time

$${\tau }_g=O\left(\frac{1}{k_{1,+}^{\prime }+\cdots +k_{f,+}^{\prime }}\right).$$ (26)

At the end of this phase, each filament will grow to the order N size

$$\langle L_i\rangle \approx \frac{k_{i,+}^{\prime }N}{k_{1,+}^{\prime }+\cdots +k_{f,+}^{\prime }}.$$ (27)

After that, in the case of unequal assembly rates, the system will undergo a linear adjustment phase for a period of time τ_a = O(N), during which the filaments with smaller assembly rates will reduce to nearly zero, and their dissociated monomers will be taken up by the fastest growing filaments. The filaments will follow the dynamics given by Equation 12 until one of them reaches the boundary value of zero length. This will happen in time (N). After this time, we exclude the filament of zero length, and study the dynamics of the remaining filaments until all of those with lower assembly rates reach zero.

For example, if there are six filaments, out of which three are assembled at a higher rate $k_{h,+}^{\prime }$, and the other three at a slower rate $k_{s,+}^{\prime }$, $k_{h,+}^{\prime }>k_{s,+}^{\prime }$. Then, the slower growing filaments will be reduced to zero at time

$${\tau }_a=\frac{k_{s,+}^{\prime }}{3k_{-}(k_{h,+}^{\prime }-k_{s,+}^{\prime })}\left(N-\frac{2k_{-}}{k_{h,+}^{\prime }+k_{s,+}^{\prime }}\right)\approx \frac{N}{3{\kappa }_{d_s}(k_{h,+}^{\prime }-k_{s,+}^{\prime })},$$ (28)

which can be computed by setting Equation 12 to zero for the slowest growing filament(s).

Following the linear adjustment period, in case of more than one fastest growing filament, e.g., 3 in the preceding example, the largest filaments will approach the steady state through a slow diffusion time scale of the order τ_d = O(N²). During this phase, the dissociated monomers will randomly diffuse between the fast growing filaments, leading to the flat, power law, distribution in steady state.

Estimates for actin cables in yeast

Now, we will use previously known experimental numbers to estimate the total amount of actin proteins N and the dissociation constant κ_d for actin cables in budding yeast.

Cables consist of a few actin filaments bundled together. These cables are polymerized by a few formins, and hence the assembly rate of cables are about 10 times more than that of single filaments, i.e. $k_{+,\mathit{cables}}^{\prime }\approx 10\times 10\mu M^{-1}{s}^{-1}$ (Pollard, 1986; Yu et al., 2011). Dividing this rate by, 40 μm³, the average volume of an yeast cell (Philips), we get $k_{+,\mathit{cables}}^{\prime }\approx 5\times {10}^{-3}{s}^{-1}$.

Also cables are degraded in about a minute (Goode et al., 2015) so considering a few (~3) filaments per cross section, 4 microns per filament, and 400 monomers per micron of a cable, we estimate a k₋ ≈ 60 s⁻¹. Hence κ_d,_cables≈ 10⁴. Also, budding yeast contains about 10μM free actin (Johnston et al., 2015), which translates to N ≈ 2 × 10⁵ actin proteins.

Exact solutions of filament distributions

In this section we derive the exact expressions for the filament distributions. In addition, at the end of each subsection, we demonstrate how these exact expressions yield the explicit approximations from section “Heuristic derivation of filament distributions”.

Let N be the total number of monomers and f ≥ 1 be the number of filaments. Recall, we use l₁, l₂, …, l_f, to denote the number of assembled monomers in filaments 1,2, …, f, respectively. Each monomer has a rate $k_{i,+}^{\prime }$, 1 ≤ i ≤ f, of assembly to filament i. Here, we consider that each filament disassembles one monomer at a time with disassembly rates k_j,₋, 1 ≤ j ≤ f. Furthermore, let ${\kappa }_{d_i}:=\frac{k_{i,-}}{{k^{\prime }}_{i,+}}$, 1 ≤ i ≤ f, be the corresponding dissociation constants, and let p(l₁, l₂, …, l_f) be the steady state probability that lengths of filaments 1,2, …, f are equal to l₁, l₂, …, l_f, respectively. This model falls into the framework of Queueing Theory presented in (Kelly, 1979), and thus, admits a solution given by

$$p(l_1,l_2,\dots ,l_f)=p(\mathbf{0})\frac{{\kappa }_{d_1}^{-l_1}{\kappa }_{d_2}^{-l_2}\cdots {\kappa }_{d_f}^{-l_f}}{(N-l_1-l_2-\dots -l_f)!},$$ (29)

where 0 = (0,0,…,0) and p(0) is the normalization constant obtained from Σp(·) = 1. One can also check that Equation 29 is a solution by simply substituting it in the detailed balance equations. In addition, this is the unique solution since this Markov chain is aperiodic, irreducible and finite.

For f = 1, one can easily compute the normalization constant, and derive the filament distribution

$$p(l)=\frac{1}{Q(N+1,{\kappa }_d)}\frac{{\kappa }_d^{N-1}{e}^{-{\kappa }_d}}{(N-l)!},$$ (30)

where $Q(N+1,{\kappa }_d)=\Gamma (N+1,{\kappa }_d)/N!={\displaystyle {\int }_{{\kappa }_d}^{\infty }{t}^N{e}^{-t}dt/N!}$ is the regularized Gamma function. Note that the steady state distribution of filament lengths can be computed exactly by using the detailed balance equations $p(l)k_{+}^{\prime }(N-l)=p(l+1)k_{-}$, to obtain $p(l)=p(0){\kappa }_d^{N-l}/(N-l)!$, where ${\kappa }_d\equiv k_{-}/k_{+}^{\prime }$. Typically in cells N ≫ κ_d, and the normalization constant p(0) is numerically indistingushable from e^−κd, yielding the following simple formula for filament distribution $p(l)=\frac{{\kappa }_d^{N-l}{e}^{-{\kappa }_d}}{(N-l)!}$, which is reported in the main text and plotted in Figure 1B for specific parameters. However, the derivation for single filament does not scale for general f since the number of summands grows as O(N^f). To alleviate this problem, in the following two subsections we derive a more intuitive representation for the filament distributions using the auxiliary random variable. To illustrate the idea for f = 1, we can define an auxiliary Poisson random variable M(κ_d) with mean κ_d. Then the preceding solution can be represented as

$$p(l)=\frac{P[M({\kappa }_d)=N-l]}{P[M({\kappa }_d)\le N]},$$ (31)

and the number of free monomers can be shown to be truncated Poisson

$$P[M=m]=\frac{P[M({\kappa }_d)=m]}{P[M({\kappa }_d)\le N]}.$$ (32)

Here, it can be readily seen that P[M(κ_d) ≤ N] is numerically indistinguishable from 1 when κ_d ≪ N, implying that the number of free monomers is effectively Poisson, and the filament length is N − M. This probabilistic representation is essential for the derivations for general f ≥ 2 in the following subsections, as well as the rigorous justifications of our heuristic derivations from section “Heuristic derivation of filament distributions”. Due to the inherent complexity of computing Equation 29, which requires O(N^f) operations, a number of approximate techniques have been developed in prior studies for this and related models. These prior techniques relied on integral/transform methods, as well as the algebraic computation with special type of scaling; see (Anselmi et al., 2013) and the references therein. In contrast to the prior techniques, our probabilistic approach appears to be new, and it readily yields explicit approximations for the quantities and range of parameters that are relevant in biology.

Equal nucleating centers: ${\kappa }_{d_i}={\kappa }_d$

We start with a few probabilistic identities that will be used in our derivations. Let X be an integer valued random variable taking random values in {0,1,2..} and define an indicator/step function 1[x ≤ n] = 1 is x ≤ n, and 1[x ≤ n] = 0, otherwise. With this notation, for any function f(x), we can be conveniently represent the truncated expected value as

$${\displaystyle \sum _{m=0}^{N}P[X=m]f(m)=\langle f(X)1[X\le N]\rangle }.$$ (33)

Also, it will be convenient to write the number of combinations by defining (n)_k = n(n − 1)(n − 2)…(n − k + 1), k ≥ 1 with (n)₀ = 1. With this notation,

$$\left(\genfrac{}{}{0ex}{}{n}{k}\right)=\frac{n(n-1)(n-2)\dots (n-k+1)}{k!}=\frac{{(n)}_k}{k!}.$$ (34)

Normalization constant

Starting with Equation 29 and Σp(n) = 1, or κ_d^N e^−κd Σ p(n) = κ_d^N e^−κd, we derive

$$\begin{gathered} p{(\mathbf{0})}^{-1}{{\kappa }_d}^N{e}^{-{\kappa }_d}={{\kappa }_d}^N{e}^{-{\kappa }_d}{\displaystyle \sum _{0\le l_1+l_2\dots +l_f\le N}\frac{{{\kappa }_d}^{-(l_1+l_2\mathrm{..}f)}}{(N-l_1-l_2\dots l_f)!}} \\ ={\displaystyle \sum _{j=0}^N{\displaystyle \sum _{l_1+l_2\dots +l_f=j}\frac{{{\kappa }_d}^{(N-l_1-l_2-\cdots -l_f)}{e}^{-{\kappa }_d}}{(N-l_1-l_2-\cdots -l_f)!}}} \\ ={\displaystyle \sum _{j=0}^N\left(\genfrac{}{}{0ex}{}{j+f-1}{f-1}\right)\frac{{{\kappa }_d}^{(N-j)}{e}^{-{\kappa }_d}}{(N-j)!}} \\ ={\displaystyle \sum _{j=0}^N\left(\genfrac{}{}{0ex}{}{N+f-1-m}{f-1}\right)\frac{{{\kappa }_d}^m{e}^{-{\kappa }_d}}{m!}} \\ =\frac{1}{(f-1)!}\langle {\left(N+f-1-M({\kappa }_d)\right)}_{f-1}1[M({\kappa }_d)\le N]\rangle , \end{gathered}$$ (35)

where in the last equality, we have used Equations 33 and 34. Note that M(κ_d) is a Poisson random variable with mean κ_d. We introduced the notation M(κ_d) to differentiate it from the free monomer pool M, which is only approximately Poisson. In addition, in the third equality, we have used that the number of nonnegative solutions to $l_1+l_2+\cdots +l_f=j$ is $\left(\begin{array}{c}j+f-1\\ f-1\end{array}\right)$.

Filament distributions

Next, let 0_i denote a vector with i zeros, and let p(0_f, N) denotes explicitly the normalization constant for a problem with f filaments and N monomers. Then it is easy to see that the length distribution for one filament is given by

$$p(l)={{\kappa }_d}^{-1}\frac{p(0_f,N)}{p(0_{f-1},N-l)}.$$ (36)

Hence, by combining the preceding expression with Equation 29, we obtain

$$p(l)=(f-1)\frac{\langle {(N-l+f-2-M({\kappa }_d))}_{f-2}1[M({\kappa }_d)\le N-l]\rangle }{\langle {(N+f-1-M({\kappa }_d))}_{f-1}1[M({\kappa }_d)\le N]\rangle }.$$ (37)

Free monomer distribution

Similarly, we can easily derive the distribution of free monomers

$$\begin{gathered} P[M=m]=P[L_1+\cdots +L_f=N-m] \\ =p(\mathbf{0}){\displaystyle \sum _{l_1+l_2\dots +l_f=N-m}\frac{{{\kappa }_d}^{-(N-m)}}{m!}} \\ =p(\mathbf{0}){\kappa }_d^{-N}{e}^{{\kappa }_d}\left(\genfrac{}{}{0ex}{}{N+f-1-m}{f-1}\right)\frac{{{\kappa }_d}^m{e}^{-{\kappa }_d}}{m!} \\ =\frac{{(N+f-1-m)}_{f-1}P[M({\kappa }_d)=m]}{\langle {(N+f-1-M({\kappa }_d))}_{f-1}1[M({\kappa }_d)\le N]\rangle }. \end{gathered}$$ (38)

Now, we can show how the heuristic approximations from the preceding section follow from these exact results.

Approximation

Assume first that the number of filaments f is finite, i.e., it doesn’t scale with N. Since M(κ_d) is Poisson, its mean and standard deviation are κ_d and $\sqrt{{\kappa }_d}$, respectively. Hence, when κ_d ≫ 1, M(κ_d) is very close to its mean, i.e., it is unlikely to deviate from it more than two standard deviations $P[|M({\kappa }_d)-{\kappa }_d|\le 2\sqrt{{\kappa }_d}]\approx 1$. Therefore, when 1 ≪ κ_d ≪ N, we can approximate M(κ_d) ≈ κ_d, P[M(κ_d) ≤ N] ≈ 1 and P[M(κ_d) ≤ N − l] ≈ 1[l ≤ N − κ_d], to obtain

$$\begin{gathered} p(l)\approx \frac{(f-1){(N-l+f-2-{\kappa }_d)}_{f-2}1[1\le N-{\kappa }_d]}{{(N+f-1-{\kappa }_d)}_{f-1}} \\ p(l)\approx (f-1)\frac{{(N-l-{\kappa }_d)}^{f-2}1[l\le N-{\kappa }_d]}{{(N-{\kappa }_d)}^{f-1}} \\ p(l)\approx \frac{(f-1)}{N-{\kappa }_d}{\left(1-\frac{1}{N-{\kappa }_d}\right)}^{f-2}1[l\le N-{\kappa }_d], \end{gathered}$$ (39)

,i.e., p(l) has approximately polynomial shape in interval (0, N − κ_d), and p(l) ≈ 0 outside of it. On the other hand, when f is large, i.e., of the order of N, similar reasoning leads to a rigorous justification of the geometric approximation from the end of section “Equal nucleating centers”. Here, one has to be more careful in unwinding the numerator and denominator in Equation 37 since they will consist of a large number of products. However, when l is finite, the numerator and denominator in Equation 37 differ only in a finite number of l terms, and we only need to limit these. To this end, we use the fact that κ_d is a finite constant, i.e., κ_d/N → 0 as N grows, implying P[M(κ_d) ≤ εN] ≈ 1 for any small ε > 0 and N sufficiently large. Hence, for ε small and N large enough, Equation 37 simplifies to

$$\begin{gathered} p(l)\approx (f-1)\frac{\langle {(N-l+f-2-M({\kappa }_d))}_{f-2}1[M({\kappa }_d)\le \epsilon N]\rangle }{\langle {(N+f-1-M({\kappa }_d))}_{f-1}1[M({\kappa }_d)\le \epsilon N]\rangle } \\ \approx f\frac{{(N\pm \epsilon )}^l}{{(N\pm \epsilon +f)}^{l+1}}\frac{\langle {(N-l+f-2-M({\kappa }_d))}_{f-2-l}1[M({\kappa }_d)\le \epsilon N]\rangle }{\langle {(N-l+f-2-M({\kappa }_d))}_{f-2-l}1[M({\kappa }_d)\le \epsilon N]\rangle } \\ =f\frac{{(N\pm \epsilon )}^l}{{(N\pm \epsilon +f)}^{l+1}}\approx f\frac{N^l}{{(N+f)}^{l+1}}. \end{gathered}$$

Regarding the free monomer pool, when f is finite, and m ≪ N, then N + f − 1 − m ≈ N, and Equation 38 simplifies to

$$P[M=m]\approx P[M({\kappa }_d)=m].$$ (40)

This also provides a rigorous justification for the previously derived Poisson approximation in Equation 3.

Unequal nucleating centers: ${\kappa }_{d_1}<\underset{2\le i\le f}{\mathit{min}}{\kappa }_{d_i}$

Before proceeding with the derivations, let us observe that the following analysis can be easily extended to include the case when a group of filaments grow at the fastest assembly rate, i.e., ${\kappa }_{d_1}=\cdots ={\kappa }_{d_{f_1}}<\underset{f_1<i\le f}{\mathit{min}}{\kappa }_{d_i}$. However, we omit this extension since it further complicates the notation, and just discuss it heuristically in sections “General case” and “Aggregate distribution of multiple filaments”.

If X₁, X₂, …, are independent random variables taking values in non negative integers, then

$$P[X_1+X_2\dots +X_k=n]={\displaystyle \sum _{n_1+n_2+\cdots +n_k=l}P[X_1=n_1]P[X_2=n_2]\cdots P[X_k=n_k]},$$ (41)

$$P[X_1+X_2\le N]={\displaystyle \sum _{n=0}^{N}P[X_1=n]P[X_2\le N-n].}$$ (42)

Normalization constant

As before, let $M({\kappa }_{d_1})$ be a Poisson random variable with mean ${\kappa }_{d_1}$ and $L_i^{\circ }$, 2 ≤ i ≤ f, geometric random variables with parameters ${\kappa }_{d_1}/{\kappa }_{d_i}$. Note that we introduce the notation $L_i^{\circ }$ to denote a true geometric variable, and differentiate it from the filament length L_i, which will only be approximately geometric. Furthermore, we assume that $M({\kappa }_{d_1})$ and $L_i^{\circ }$ are independent. Next,

$$\begin{gathered} p{(0)}^{-1}{{\kappa }_{d_1}}^N{e}^{-{\kappa }_{d_1}}{\displaystyle {\prod }_{i=2}^f\left(1-\frac{{\kappa }_{d_1}}{{\kappa }_{d_i}}\right)} \\ ={{\kappa }_{d_1}}^N{e}^{{\kappa }_{d_1}}{\displaystyle {\prod }_{i=2}^f\left(1-\frac{{\kappa }_{d_1}}{{\kappa }_{d_i}}\right){\displaystyle \sum _{0\le l_1+l_2\dots l_f\le N}\frac{{{\kappa }_{d_1}}^{-l_1}\cdots {{\kappa }_{d_f}}^{-l_f}}{(N-l_1-l_2\dots l_f)!}}} \\ ={\displaystyle \sum _{j=0}^N{\displaystyle \sum _{l_2\dots +l_f=j}{\displaystyle \sum _{l_1=0}^{N-j}{{\displaystyle {\prod }_{i=2}^f\left(1-\frac{{\kappa }_{d_1}}{{\kappa }_{d_i}}\right)\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_i}}\right)}}^{l_i}\frac{{{\kappa }_{d_1}}^{(N-j-l_1)}{e}^{-{\kappa }_{d_1}}}{(N-j-l_1)!}}}} \\ ={\displaystyle \sum _{j=0}^{N}P[L_2^{\circ }+\cdots +L_f^{\circ }=j]P[M({\kappa }_{d_1})\le N-j]} \\ =P[M({\kappa }_{d_1})+L_2^{\circ }+\cdots +L_f^{\circ }\le N], \end{gathered}$$ (43)

where in last two inequalities, we used Equations 41 and 42; this gives a compact representation for p(0), namely,

$$p(\mathbf{0})=\left(\frac{1}{P[M({\kappa }_{d_1})+L_2^{\circ }+\cdots +L_f^{\circ }\le N]}\right){{\kappa }_{d_1}}^N{e}^{-{\kappa }_{d_1}}{\displaystyle {\prod }_{i=2}^f\left(1-\frac{{\kappa }_{d_1}}{{\kappa }_{d_i}}\right)},$$ (44)

Length distribution for the first filament

Using the above expression, we can evaluate the length distribution for the first filament

$$\begin{gathered} p_1(l)=p(\mathbf{0}){\displaystyle \sum _{j=0}^{N-l}{\displaystyle \sum _{l_2\dots +l_f=j}\frac{{{\kappa }_{d_1}}^{-l_1}\dots {{\kappa }_{d_f}}^{-l_f}}{(N-l_1-l_2\dots l_f)!}}} \\ =\frac{1}{P[M({\kappa }_{d_1})+L_2^{\circ }+\cdots +L_f^{\circ }\le N]}{\displaystyle \sum _{j=0}^{N-l}{\displaystyle \sum _{l_2\dots +l_f=j}{\displaystyle {\prod }_{i=2}^f(1}}}-\frac{{\kappa }_{d_1}}{{\kappa }_{d_i}}){\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_i}}\right)}^{l_i}\frac{{{\kappa }_{d_1}}^{(N-j-l_1)}{e}^{-{\kappa }_{d_1}}}{(N-l_1-l_2\dots l_f)!} \\ =\frac{1}{P[M({\kappa }_{d_1})+L_2^{\circ }+\cdots +L_f^{\circ }\le N]}{\displaystyle \sum _{j=0}^{N-l}P[L_2^{\circ }+\cdots +L_f^{\circ }=j]P[M({\kappa }_{d_1})=N-l-j]} \\ =\frac{P[M({\kappa }_{d_1})+L_2^{\circ }+\cdots +L_f^{\circ }=N-l]}{P[M({\kappa }_{d_1})+L_2^{\circ }+\cdots +L_f^{\circ }\le N]}. \end{gathered}$$ (45)

For the length distribution of the other filaments, 2 ≤ i ≤f we compute

$$\begin{gathered} p_i(l)=p(\mathbf{0}){\displaystyle \sum _{0\le {\displaystyle {\sum }_{j\ne i}{n}_j\le N-l}}\frac{{{\kappa }_{d_i}}^{-l}{\displaystyle {\prod }_{j\ne i}{{\kappa }_{d_j}}^{-l_j}}}{(N-l_1-l_2\dots l_f)!}} \\ =\frac{1}{P[M({\kappa }_{d_1})+L_2^{\circ }+\cdots +L_f^{\circ }\le N]}\left(1-\frac{{\kappa }_{d_1}}{{\kappa }_{d_i}}\right){\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_i}}\right)}^l \\ \times {\displaystyle {\sum }_{j=0}^{N-l}{\displaystyle \sum _{{\displaystyle {\sum }_{h\ge 2,h\ne i}{l}_h=j}}{{\displaystyle {\prod }_{h\ge 2,h\ne i}^f\left(1-\frac{{\kappa }_{d_1}}{{\kappa }_{d_h}}\right)\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_h}}\right)}}^{l_h}{\displaystyle \sum _{l_1=0}^{N-l-j}\frac{{{\kappa }_{d_1}}^{(N-l-j-l_1)}{e}^{-{\kappa }_{d_1}}}{(N-l-j-l_1)!}}}} \\ =\frac{P[L_i^{\circ }=l]}{P[M({\kappa }_{d_1})+L_2^{\circ }+\cdots +L_f^{\circ }\le N]}{\displaystyle \sum _{j=0}^{N-l}P\left[{\displaystyle \sum _{h\ge 2,h\ne i}{L}_h^{\circ }=j]}\right]P[M({\kappa }_{d_1})\le N-l-j]} \\ =\frac{P[L_i^{\circ }=l]P[M({\kappa }_{d_1})+{\displaystyle {\sum }_{j\ge 2,j\ne i}{L}_j^{\circ }\le N-l}]}{P[M({\kappa }_{d_1})+L_2^{\circ }+\cdots +L_f^{\circ }\le N]}. \end{gathered}$$ (46)

Free monomer distribution

By following exactly the same steps one can easily derive the exact distribution for the free monomer pool

$$P[M=m]=\frac{P[M({\kappa }_{d_1})=m]P[L_2^{\circ }+\cdots +L_f^{\circ }\le N-m]}{P[M({\kappa }_{d_1})+L_2^{\circ }+\cdots +L_f^{\circ }\le N]}.$$ (47)

Approximations

Again, we will show how these exact results lead to the justification for the heuristic derivation in the preceding section. Assume that f is finite, ${\kappa }_{d_1}\ll N$, and $E[L_i^{\circ }]\le C$ with (f−1)C ≪ N, then for N large and $l\ll N-{\kappa }_{d_1}-(f-1)C$,

$$P[M({\kappa }_d)+L_2^{\circ }+\cdots +L_f^{\circ }\le N]\approx 1.$$ (48)

The numerator in Equation 46 can be also written as

$$p\left[M({\kappa }_{d_1})+{\displaystyle \sum _{j\ge 2,j\ne t}{L}_j^{\circ }\le N-l}\right]\approx 1.$$ (49)

Hence, we can simplify Equation 45 to

$$p_1(l)\approx P[N-M({\kappa }_{d_1})-L_2^{\circ }-\cdots L_f^{\circ }=l],$$ (50)

i.e., the length of the first filament is approximately equal in distribution

$$L_1\approx N-M({\kappa }_d)-L_2^{\circ }-\cdots -L_f^{\circ }.$$ (51)

Furthermore, when $l\ll N-{\kappa }_{d_1}-(f-1)C$, Equations 46, 48 and 49, yield for i ≥ 2

$$p_i(l)\approx P[L_i^{\circ }=l],$$ (52)

i.e., $L_i\approx L_i^{\circ }$. Hence, the other filaments are approximately geometric. Finally, the equation for the free monomer distribution, when in addition m ≪ N − (f − 1)C, is approximately Poisson

$$P[M=m]\approx P[M({\kappa }_{d_1})=m].$$ (53)

Thus the average filament lengths and average number of free monomers are given by $\langle L_1\rangle \approx N-{\kappa }_{d_1}-{\displaystyle {\sum }_{i=2}^f\frac{{\kappa }_{d_1}}{{\kappa }_{d_i}-{\kappa }_{d_1}}}$, $\langle L_i\rangle \approx \frac{{\kappa }_{d_1}}{{\kappa }_{d_i}-{\kappa }_{d_1}}$ and $\langle M\rangle \approx {\kappa }_{d_1}$. As noted earlier, in this scenario, 〈L₁〉 = O(N) and 〈L_i〉 = O(1), i ≥ 2, i.e., the first filament takes approximately all the monomers.

Gamma function representation of two filaments

In this section, we represent our analytical results in terms of the regularized Gamma function, Q(n, κ_d), that is more suitable for numerical evaluation. Note that Q(n, κ_d), for integer n is equivalent to the cumulative Poisson distribution function, i.e.,

$$P[M({\kappa }_d\le n]=Q(n+1,{\kappa }_d)=\frac{\mathrm{\Gamma }(n+1,{\kappa }_d)}{n!},$$ (54)

where $\mathrm{\Gamma }(n+1,{\kappa }_d)={\displaystyle {\int }_{{\kappa }_d}^{\infty }{t}^n{e}^{-t}dt}$ is the incomplete Gamma function. Now, we will represent the distributions from Equations 37, 45, and 46 in terms of for Q(m, κ_d) for f = 2.

Equal nucleating centers: ${\kappa }_{d_i}={\kappa }_d$

Observe that for f = 2, the Expression 37 reduces to

$$p(l)=\frac{\langle 1[M({\kappa }_d)\le N-l]\rangle }{\langle (N+1-M({\kappa }_d))1[M({\kappa }_d)\le N]\rangle }$$ (55)

Next, by using 〈1[M(κ_d) ≤ N]〉 = P[M(κ_d) ≤ n] = Q(n + 1, κ_d) and

$$\langle M({\kappa }_d)1[M({\kappa }_d)\le N]\rangle ={\displaystyle \sum _{m=1}^{N}m\frac{{\kappa }_d^m{e}^{-{\kappa }_d}}{m!}}={\kappa }_{d}P[M({\kappa }_d)\le N-1]={\kappa }_{d}Q(N,{\kappa }_d)$$ (56)

in the preceding expression for p(l), we obtain

$$p(l)=\frac{Q(N-l+1,{\kappa }_d)}{(N+1)Q(N+1,{\kappa }_d)-{\kappa }_{d}Q(N,{\kappa }_d)}.$$ (57)

Unequal nucleating centers: ${\kappa }_{d_1}<{\kappa }_{d_2}$

Now for f = 2, the expressions in Equations 45 and 46 reduce to

$$p_1(l)=\frac{P[M({\kappa }_{d_1})+L_2^{\circ }=N-l]}{P[M({\kappa }_{d_1})+L_2^{\circ }\le N]},$$ (58)

and

$$p_2(l)=\frac{P[L_2^{\circ }=l]P[M({\kappa }_{d_1})\le N-l]}{P[M({\kappa }_{d_1})+L_2^{\circ }\le N]}.$$ (59)

First, we derive a regularized gamma function representation for the denominator

$$\begin{gathered} P[M({\kappa }_{d_1})+L_2^{\circ }\le N]={\displaystyle \sum _{i=0}^{N}P[M({\kappa }_{d_1})=i]P[L_2^{\circ }\le N-i]} \\ ={\displaystyle \sum _{i=0}^{N}P[M({\kappa }_{d_1})=i](1-P[L_2^{\circ }>N-i])} \\ =P[M({\kappa }_{d_1})\le N]-{\displaystyle \sum _{i=0}^N\frac{{\kappa }_{d_1}^i{e}^{-{\kappa }_{d_1}}}{i!}}{\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right)}^{N-i+1} \\ =P[M({\kappa }_{d_1})\le N]-{\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right)}^{N+1}{e}^{-{\kappa }_{d_1}+{\kappa }_{d_2}}{\displaystyle \sum _{i=0}^N\frac{{\kappa }_{d_2}^i{e}^{-{\kappa }_{d_2}}}{i!}} \\ =Q(N+1,{\kappa }_{d_1})-{\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right)}^{N+1}{e}^{-{\kappa }_{d_1}+{\kappa }_{d_2}}Q(N+1,{\kappa }_{d_2}). \end{gathered}$$ (60)

Next, the numerator in can be represented as

$$\begin{gathered} P[L_2^{\circ }=l]P[M({\kappa }_{d_1})\le N-l]={\displaystyle \sum _{i=0}^{N-l}P[M({\kappa }_{d_1})=i]P[L_2^{\circ }\le N-i]} \\ ={{\displaystyle \sum _{i=0}^N\frac{{\kappa }_{d_1}^i{e}^{-{\kappa }_{d_1}}}{i!}\left(1-\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right)\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right)}}^{N-l-i} \\ =\left(1-\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right){\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right)}^{N-l}{e}^{-{\kappa }_{d_1}+{\kappa }_{d2}}{\displaystyle \sum _{i=0}^{N-l}\frac{{\kappa }_{d_2}^i{e}^{-{\kappa }_{d2}}}{i!}} \\ =\left(1-\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right){\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right)}^{N-l}{e}^{-{\kappa }_{d_1}+{\kappa }_{d2}}Q(N-l+1,{\kappa }_{d_2}). \end{gathered}$$ (61)

Hence, by replacing the preceding expressions in the formula for p₁(l) and rearranging the terms, we obtain

$$p_1(l)=\frac{({\kappa }_{d_2}-{\kappa }_{d_1}){\kappa }_{d_1}^{-(l+1)}{\kappa }_{d_2}^{-(N-l+1)}{e}^{{\kappa }_{d_2}}Q(N-l+1,{\kappa }_{d_2})}{{\kappa }_{d_1}^{-(N+1)}{e}^{{\kappa }_{d_1}}Q(N+1,{\kappa }_{d_1})-{\kappa }_{d_2}^{-(N+1)}{e}^{{\kappa }_{d_2}}Q(N+1,{\kappa }_{d_2})}$$ (62)

and similarly, using

$$P[L_2^{\circ }=l]P[M({\kappa }_{d_1})\le N-l]=\left(1-\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right){\left(\frac{{\kappa }_{d_1}}{{\kappa }_{d_2}}\right)}^{l}Q(N-l+1,{\kappa }_{d_1}),$$ (63)

we obtain

$$p_2(l)=\frac{({\kappa }_{d_2}-{\kappa }_{d_1}){\kappa }_{d_2}^{-(l+1)}{\kappa }_{d_1}^{-(N-l+1)}{e}^{{\kappa }_{d_1}}Q(N-l+1,{\kappa }_{d_1})}{{\kappa }_{d_1}^{-(N+1)}{e}^{{\kappa }_{d_1}}Q(N+1,{\kappa }_{d_1})-{\kappa }_{d_2}^{-(N+1)}{e}^{{\kappa }_{d_2}}Q(N+1,{\kappa }_{d_2})}.$$ (64)

Note that we used Equations 57, 62 and 64 to verify our simulation results in Figure 1D and Figure 3.

Aggregate distribution of multiple filaments

While in this paper, we primarily focus on the individual filament distributions, it may be of some interest to compute the aggregate distribution for all assembled monomers in a group of filaments. To this end, consider a similar situation as in Section “General case”, where two groups of finitely many filaments f₁ ≥ 2 and f₂ ≥ 2 are growing with dissociation constants ${\kappa }_{d_h}$ and ${\kappa }_{d_s}$, respectively; f₁ + f₂ = f. Let filaments L₁, ⋯, $L_{f_1}$, be part of the first nucleating center, and $L_{f_1+1}$, ⋯, L_f, part of the second. Then the total number of assembled monomers in each nucleating center is respectively given by $S_1=L_1+\cdots +L_{f_1}$ and $S_2=L_{f_1+1}+\cdots +L_f$, respectively. Here, we provide a heuristic derivation for the aggregate distribution. This can be validated using the same type of exact calculations as in section “Exact solutions of filament distributions”. To avoid repetitions, we avoid these calculations.

Equal assembly rates: ${\kappa }_d={\kappa }_{d_h}={\kappa }_{d_s}$

By using the same heuristic arguments as in section “Equal nucleating centers”, we can easily compute, for 1 ≤ s ≤ N − κ_d

$$\begin{gathered} P[S_1=s]\approx \frac{\left(\frac{s+f_1-1}{f_1-1}\right)\left(\frac{N-s-{\kappa }_d+f_2-1}{f_2-1}\right)}{\left(\frac{N-{\kappa }_d+f-1}{f-1}\right)}\approx \\ \frac{(f-1)}{N-{\kappa }_d}\left(\frac{f-2}{f_1-1}\right){\left(\frac{s}{N-{\kappa }_d}\right)}^{f_1-1}{\left(1-\frac{s}{N-{\kappa }_d}\right)}^{f_2-1}, \end{gathered}$$ (65)

i.e., S₁ has Beta distribution on interval (0, N − κ_d) with parameters (f₁, f₂), which can be somewhat pointy. The mean and standard deviation are given by

$$\langle s_1\rangle \approx \frac{f_1}{f}(N-{\kappa }_d),{\sigma }_{s_1}\approx \frac{f_1}{f}(N-{\kappa }_d)\sqrt{\frac{f_2}{f_1(f+1)}}=\langle s_1\rangle \sqrt{\frac{f_2}{f_1(f+1)}}.$$ (66)

We can see that the standard deviation is relatively smaller as compared to the single filament case, e.g., when f₁ = f₂, ${\sigma }_{s_1}=\langle s_1\rangle \sqrt{\frac{1}{(f+1)}}$, which comes from averaging. However, it is still very large and of the same order as the mean.

Unequal assembly rates: ${\kappa }_{d_h}<{\kappa }_{d_s}$

Recall from section “General case” that all filaments in the second group are independent and geometrically distributed with parameter ${\kappa }_{d_h}/{\kappa }_{d_s}$, which easily implies that the means and variances are given by

$$\langle S_1\rangle \approx N-{\kappa }_{d_h}-f_2\frac{{\kappa }_{d_h}}{{\kappa }_{d_s}-{\kappa }_{d_h}},\langle S_2\rangle \approx f_2\frac{{\kappa }_{d_h}}{{\kappa }_{d_s}-{\kappa }_{d_h}},$$ (67)

$$\text{Var}(S_1)\approx {\kappa }_{d_h}+f_2\frac{{\kappa }_{d_h}{\kappa }_{d_s}}{{({\kappa }_{d_s}-{\kappa }_{d_h})}^2},\text{Var}(S_2)\approx f_2\frac{{\kappa }_{d_h}{\kappa }_{d_s}}{{({\kappa }_{d_s}-{\kappa }_{d_h})}^2}.$$ (68)

Note that only the first structure can grow with N, while the second remains constant. Furthermore, the distribution of S₂ is given by a negative Binomial

$$P[S_2=s]\approx {\left(1-\frac{{\kappa }_{d_h}}{{\kappa }_{d_s}}\right)}^{f_2}\left(\frac{s+f_2-1}{f_2-1}\right){\left(\frac{{\kappa }_{d_h}}{{\kappa }_{d_s}}\right)}^s,$$ (69)

which is a pointy distribution that approaches the Gaussian as f₂ increases.

Simulation protocol

We used stochastic simulations to solve the master equations in Equations 1, 2 and 4 in the main text. We start with a filament of zero length and then follow the stochastic trajectory of the filament. In the simulation, the state of the system is characterized by the filament length. In one step of the simulation we choose one of the set of all possible transitions from the current state of the system to the next. The transitions are chosen at random according to their relative weight, which is proportional to the rate of the transition. Once a particular transition is chosen the system is updated to a new state, which becomes the new current state. The time elapsed between two consecutive transitions is drawn from an exponential distribution, the rate parameter of which equals the sum of all the rates of allowed transitions. This process is repeated for a long enough time such that the length of the cable reaches steady state. We obtain many such trajectories of a single filament and then compute the steady state distributions of filament lengths.