Modelling interaction dynamics between two foliar pathogens in wheat: a multi-scale approach

Abstract

Background and Aims

Disease models can improve our understanding of dynamic interactions in pathosystems and thus support the design of innovative and sustainable strategies of crop protections. However, most epidemiological models focus on a single type of pathogen, ignoring the interactions between different parasites competing on the same host and how they are impacted by properties of the canopy. This study presents a new model of a disease complex coupling two wheat fungal diseases, caused by Zymoseptoria tritici (septoria) and Puccinia triticina (brown rust), respectively, combined with a functional–structural plant model of wheat.

Methods

At the leaf scale, our model is a combination of two sub-models of the infection cycles for the two fungal pathogens with a sub-model of competition between lesions. We assume that the leaf area is the resource available for both fungi. Due to the necrotic period of septoria, it has a competitive advantage on biotrophic lesions of rust. Assumptions on lesion competition are first tested developing a geometrically explicit model on a simplified rectangular shape, representing a leaf on which lesions grow and interact according to a set of rules derived from the literature. Then a descriptive statistical model at the leaf scale was designed by upscaling the previous mechanistic model, and both models were compared. Finally, the simplified statistical model has been used in a 3-D epidemiological canopy growth model to simulate the diseases dynamics and the interactions at the canopy scale.

Key Results

At the leaf scale, the statistical model was a satisfactory metamodel of the complex geometrical model. At the canopy scale, the disease dynamics for each fungus alone and together were explored in different weather scenarios. Rust and septoria epidemics showed different behaviours. Simulated epidemics of brown rust were greatly affected by the presence of septoria for almost all the tested scenarios, but the reverse was not the case. However, shortening the rust latent period or advancing the rust inoculum shifted the competition more in favour of rust, and epidemics became more balanced.

Conclusions

This study is a first step towards the integration of several diseases within virtual plant models and should prompt new research to understand the interactions between canopy properties and competing pathogens.

INTRODUCTION

In order to optimize crop management in innovative agricultural production systems, it is crucial to better understand how epidemics develop and what factors influence them. Epidemiological models have been used for this purpose to test new hypotheses and to explore the behaviour of biological systems under varied conditions by simulation. However, most epidemiological models focus on interactions between a single pathogen and its host plants. In the field, plants are often co-infected by several parasitic species that compete for the resources of the host (Mitchell et al., 2002; Fitt et al., 2006; Willocquet et al., 2008). The interactions between species in such complexes can be of different nature depending on the pathogens, which make them challenging to model (Jesus Junior et al., 2014). The aim of this study was to develop an epidemiological model for a complex of two foliar fungi that have contrasting traits in terms of colonization of leaf tissues and of spore dispersal. We first used the model to find realistic competition rules between the two species at the leaf level, and secondly to explore the consequences of such interactions on epidemics at the canopy level under varied environmental conditions.

Wheat leaves are frequently infected by both Zymoseptoria tritici that causes septoria tritici blotch (STB) and Puccinia triticina that causes brown rust disease (Robert et al., 2004a, b; Willocquet et al., 2008; El Jarroudi et al., 2013). Zymoseptoria tritici is a hemi-biotrophic fungus that first develops on living tissues during the incubation period, but then kills leaf cells and sporulates on necrotic tissues (Orton et al., 2011; Steinberg, 2015). Puccinia triticina is a strict biotrophic fungus that grows and sporulates only on living tissues (Bolton et al., 2008). Lesions of both fungi develop side by side, competing for leaf area and resource.

Experimental studies at the cellular scale have shown that during biotrophic incubation of Z. tritici, mycelial growth is very slow (Kema, 1996; Keon et al., 2007; Steinberg, 2015; Palma-Guerrero et al., 2016) and it has minor effects on leaf physiology (Robert et al., 2005), suggesting a small effect of septoria lesions on rust development during incubation. During the necrotrophic phase, however, septoria lesions can overgrow living leaf tissues, whereas it is never the case for brown rust lesions, giving a strong advantage to older septoria lesions.

Indeed, experimental studies at the leaf scale have shown strong antagonistic interactions between rust and septoria. Rust colonizes leaf area less efficiently when septoria is present (Madariaga and Scharen, 1986), and the development of rust sporulating tissues is negatively affected by the presence of septoria (Robert et al., 2004a, b). In wheat leaves inoculated with both fungi, the number of sporulating rust lesions strongly decreased because rust lesions cannot develop on necrotic tissues already colonized by STB and also because they are gradually overgrown by new necroses due to STB (Robert et al., 2004a, b). Both fungi impact leaf functioning locally, with a negligible effect on the functioning of the non-infected part of the leaves (Robert et al., 2004a, 2005). This suggests that direct competition for space in the contact zones between lesions of the two fungi is the main mechanism involved in the co-infection dynamics.

Also, the rectangular geometry of septoria symptoms is different from that of circular rust lesions. Puccinia tritici lesions develop preferentially along leaf veins and produce rectangular and lengthened geometry (Keon et al., 2007). Brown rust lesions are smaller and circular (Robert et al., 2005). This difference in shape could influence the interaction between the two types of lesion by affecting the contact probabilities and the patterning of competition at the leaf surface.

All these interactions at the leaf scale reverberate throughout the canopy. Robert et al. (2004a) showed that brown rust symptoms that had appeared on the upper leaves of wheat stands before the STB lesions stopped developing and even regressed after STB lesions killed them. Similar observations were recorded in field experiments in Luxembourg where leaf rust symptoms were dominant in the canopy only when STB showed weak intensity (El Jarroudi et al., 2013). The disease dynamics and the competition in the fields are also affected by the contrasting mode of dispersal of the two fungi. During the growing season, STB is mainly dispersed by rain splash (Saint-Jean et al., 2004) and brown rust by wind (Frezal et al., 2009). Moreover, the life cycle of P. triticina is shorter than that of Z. tritici (Lovell et al., 2004; Lehman and Shaner, 2007). The brevity of the infection cycle associated with frequent wind dispersal ensures that rust can produce new generations more frequently than septoria (Roelfs, 1992). Indeed, the upward progress of septoria from rosette leaves to flag leaves strongly depends on the frequency of rain events (Lovell et al., 2002), and its reproduction is also intrinsically slower than that of rust because of its longer latency period. The timing and intensity of contamination by the primary inoculum could also play a role in the resulting competition between the two pathogens. Finally, the responses to climatic variables are different between the two fungi and can therefore influence the development of epidemics differently in varied climates.

Fungal complex epidemics are thus the results of competition at the leaf scale combined with different types of dispersal, which both influence the opportunity for each pathogen population to reach the healthy leaves of the canopy in varied environmental conditions.

Such multiple interactions make co-infection dynamics difficult to predict. The aim of this study is to develop an epidemiological model that can tackle such multiple interactions at different scales, and simulate the co-epidemics of wheat septoria and brown rust. We first developed a model of competition between lesions at the leaf scale to test rules of competition and to investigate the impact of lesion geometry on the diseases simulation. Secondly, we used a combined disease–three-dimensional (3-D) structural plant model to upscale these results at the canopy level. The combined ‘disease–SPM’ model simulates the interactions between pathogens and plants on individual leaves of the canopy, and also spore dispersal through the canopy in a spatially explicit approach (Room et al., 1998; Calonnec et al., 2008; Robert et al., 2008; Costes et al., 2013; Garin et al., 2014). In this model, the pathogen population develops in response to weather conditions and plant architecture that grows dynamically (Baldazzi et al., 2017; Bucksch et al., 2017). With this useful tool, the aim is to compare the effects of changing environments and plant architectures on single (one fungus) or complex (two fungi) epidemics.

MATERIALS AND METHODS

Overview

Three nested models were developed to study the foliar fungal complex composed of Z. tritici and P. triticina on wheat. The models operate at different spatial scales and simulate the interactions between pathogens with different levels of detail. Competition between lesions is addressed through space occupation on a leaf and, thus, the leaf surface represents a proxy for the resource available for the pathogen. The underlying simplification is that assimilates are uniformly available over the leaf and equally accessible for both fungi.

Model 1 is a geometrically explicit model of lesion growth and interaction on a leaf. It simulates the development of individual lesions considering interactions at the millimetre scale according to a set of rules defining the competition. Model 2 is designed for upscaling model 1. It uses lesion growth equations of model 1, with a simpler, statistical approach for modelling the interactions between lesions. Model 3 is a broader assembly of sub-models including model 2 and it is used to simulate epidemics at the 3-D canopy scale. Spore dispersal between leaves and weather-related dispersal events are only considered in model 3. In models 1 and 2, within-leaf dispersal events occur at constant time intervals, with a higher frequency for rust than for septoria. In all three models, new incoming spores on a leaf are distributed randomly using a uniform distribution. Below we describe the three models. Then we present how they were used to explore interactions between septoria and brown rust.

Presentation of the three models

Model 1: geometric model of lesion growth and interactions at the leaf scale.

This model simulates explicitly the geometrical patterning of symptom development on a leaf. Various assumptions of interaction between lesions of the two species can be specified as input rules. It returns visual outputs comparable with observable symptoms that allow assessment of the consistency of competition rules between lesions of different ages and types.

The wheat leaf is represented as a rectangular grid of pixels oriented along the leaf length. Two parameters, the domain length L, and domain width W, control grid size, and two parameters, pixel length dL and pixel width dW, control grid resolution.

Each lesion is associated with a set of pixels on the grid that represent the geometry of the lesion and the different state of the tissues within it. Each pixel is either empty or occupied by one tissue type of a single lesion. At initiation, the leaf grid is empty apart from pixels designated as infection points for individual lesions. The pixels surrounding a lesion are colonized iteratively, following geometric growth rules representative of a fungus species.

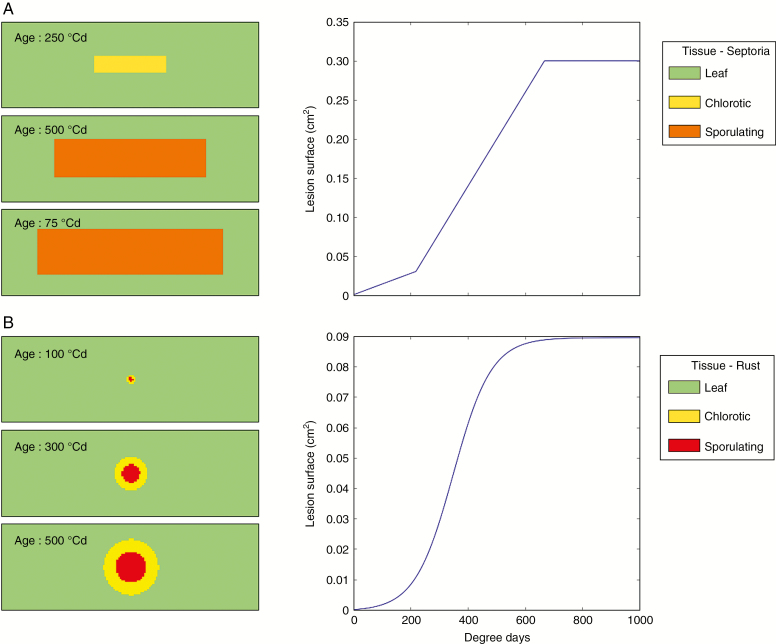
A septoria lesion is represented by a rectangle that grows by colonizing the pixels at its perimeter until it reaches a maximum surface, S_max [Fig. 1A; Table 1; Eqn (1)]. An anisotropic shape factor r is used to simulate a faster growth in the longitudinal direction of the rectangle and mimic the typical development of symptoms parallel to leaf veins (C. Robert, pers. commun.). Each pixel colonized by the fungus undergoes, as a function of its age, A, a number of transformations associated with changes in visible symptoms. It starts in the incubating state, corresponding to infected tissue without visible symptoms. At age A_chlo, it becomes chlorotic, and at age A_spo sporulating. At age A_max, it reaches its maximum size S_max and stops growing. Two constant growth rates, R₀ and R₁ [Eqn (2)] are used to represent the abrupt acceleration of growth in the chlorotic phase (Duncan and Howard, 2000; Palma-Guerrero et al., 2016). Each sporulating pixel produces dE daughter lesions only once. This rule is consistent with observation that spore production is proportional to sporulating surface (Robert et al., 2004a, b), and that the majority of spores of sporulating lesions are emitted after a single rain dispersal event (Eyal, 1971). The daughter lesions are randomly distributed on the leaf. The parameters values are given in Table 1 and come from Robert et al. (2008) and Garin et al. (2014).

Fig. 1.

Growth of a single lesion of Z. tritici (A) and P. triticina (B) simulated with model 1. Left: pixels colonized by the lesion after different times. Right: growth dynamic of the lesion over time (expressed in degree days: °Cd).

Table 1.

Parameters of the lesion models of septoria (values are from Robert et al., 2008 and Garin et al., 2014) and rust (values are from Garin, 2015)

	Name	Value	Unit
Septoria
Growth rate in incubation	R 0	1.9 × 10–4	cm2 °Cd–1
Growth rate after incubation	R 1	6 × 10–4	cm2 °Cd–1
Length–width ratio for growth	r	4	–
Maximal size	S max	0.3	cm2
Age of onset of chlorosis	A chlo	220	°Cd
Age of onset of sporulation	A spo	330	°Cd
Age of end of growth	A max	670	°Cd
Emission rate of daughter lesions	dE	1.7	No. of daughter lesions per cm2 of mother lesion
Brown rust
Maximal size	S max	0.09	cm2
Slope of growth curve at 50 % of Smax	k	0.015	cm2 °Cd–1
Age of the lesion at 50 % of Smax	A 50	350	°Cd
Ratio of surface in sporulation	r spo	0.3	–
Age of onset of sporulation	A spo	180	°Cd
Age of end of sporulation	A endspo	800	°Cd
Emission rate of daughter lesions	dE	20	No. of daughter lesions per cm2 of mother lesion

For septoria, we use a discrete time growth model leading to piecewise linear growth of lesion surface S at time t:

$$S\left(t+\text{ d}t\right)=S\left(t\right)+R\left[A\left(t\right)\right]\times \text{d}t$$ (1)

with the age-dependent growth rate R defined as:

$$R[A\left(t\right)]= \{\begin{array}{cc}{R}_0& \text{if} A\left(t\right)<A_{chlo}\\ R_1& \text{if} A_{chlo}<A\left(t\right)<A_{\text{max}}\\ 0& \text{otherwise}\end{array}$$ (2)

Then, we compute the values of lesion width w(t) and length l(t) using the relationships between length, width and surface of a rectangle with an aspect ratio of:

$$w\left(t\right)= \sqrt{\frac{S(t)}{r}}$$ (3)

$$l\left(t\right)=r \sqrt{\frac{S(t)}{r}}$$ (4)

After A_spo for each lesion, we calculate the sporulating surface S_spo(t). During a dispersal event at time t, the number of emissions of new daughter lesions E(t + dt) is proportional to the sporulating area:

$$E\left(t+\text{ d}t\right)=\text{d}E\times S_{\text{spo}}\left(t\right)\text{if}{A}_{\text{spo}}\le A_{\text{t}}$$ (5)

The actual number of new daughter lesions will depend on the availability of unoccupied leaf surface.

A lesion of P. triticina is represented as a disk that grows by colonizing the pixels at its perimeter until it reaches a maximum surface (Fig.e 1B). Its surface is composed of colonizing tissues in the periphery and sporulating tissues in the centre that represent a constant fraction of lesion area, r_spo. Sporulation starts after the latency period. In order to simulate daily dispersal events caused by wind (Roelfs, 1992), rust lesions produce daughter lesions repeatedly until the end of sporulation in the model. The parameters and state variables that define how a lesion of brown rust grows, ages and sporulates are given in Table 1. The values chosen for the model parameters are from Garin (2015) and were obtained by analysing the laboratory and field observations of Robert et al. (2004a, b, 2005).

We model the growth of the surface area of a rust lesion using a logistic equation:

$$S\left(t\right)=S_{\text{max}}/(\text{1}+\text{exp}\left\{–k\times \left[A\left(t\right)–A_{\text{5}0}\right]\right\}$$ (6)

where S_max is the maximum size, k is a rate parameter and A₅₀ is the age at reaching 50 % of the maximum size. The sporulating surface area S_spo(t) is a fraction of the surface:

$$S_{\text{spo}}\left(t\right)=r_{\text{spo}}\times S\left(t\right)$$ (7)

but note that a lesion starts sporulating only upon reaching the age A_spo and until reaching a maximum age for sporulation A_endspo. During a dispersal event, at time t, the number of emissions of daughter lesions is calculated from the sporulating area:

$$E\left(t+\text{ d}t\right)=\text{d}E\times S_{\text{spo}}\left(t\right)\text{if}{A}_{\text{spo}}\le A_{\text{t}}\le A_{\text{endspo}}$$ (8)

We define competition rules between lesions to assign the fate of pixels in contact zones where different lesions attempt to colonize the same unoccupied pixels or already occupied pixels. These competition rules are inspired from biological knowledge presented in the Introduction. For septoria lesions, the values of w(t) and l(t) define the width and length of the area the lesion would occupy in the absence of competition. We refer to the difference between this area and the currently realized area of the lesion as the ‘potential growth zone’. The pixels in this zone become occupied by the lesion only if they are available for growth, which depends on the presence of competing lesions in these pixels, their current trophic state and the priority rules for competition. It reads: (1) two lesions cannot share the same pixel; (2) each infection stage has either a low or high priority level, depending on its trophic phase: biotrophic phases have low priority; chlorotic and necrotrophic phases have high priority; (3) in the case of lesions with the same priority level attempting to colonize the same empty pixel, the winner is chosen randomly; and (4) a lesion cannot grow on pixels already occupied by a lesion with the same priority level.

The above rules imply that chlorotic and necrotic lesions of septoria (age > incubation period) are given a competitive advantage, i.e. they can overgrow incubating septoria lesions and rust lesions of any age. This is consistent with empirical observations. The leaf colonization dynamics can be depicted visually, and the severity of the disease (in terms of lesion density or covered area) can be calculated.

Model 2: model of lesion growth with global interactions at leaf scale.

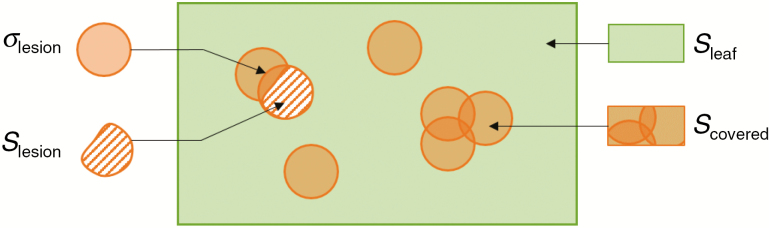
Model 1 is impractical for integration into our 3-D canopy model for computational reasons. We therefore attempted to find a simple approximation, ignoring the position and the geometry of lesions. Following the work of Ma et al. (2008), a Poisson function can be used to estimate the surface area occupied by a randomly distributed population of lesions with given size (i.e. surface area) on a leaf surface. To do so, the model calculates both the potential size of each lesion as if it was not affected by competition (referred to as ‘virtual’ lesion size σ_lesion), and the actual size of this lesion S_lesion once affected by competition with the Poisson model, by estimating the amount of overlap of virtual lesions at time t. The covered surface area S_covered on a leaf surface S_leaf is therefore estimated as a function of the number of lesions n and of the average ‘virtual’ size $\overline{\sigma }$_lesions of these lesions (see also Fig. 2):

Fig. 2.

Diagram showing how a leaf is covered by randomly distributed circular lesions. S_leaf, leaf surface; S_covered, leaf surface covered by lesions; σ_lesion, potential size of a lesion without competition; S_lesion, actual size of a lesion with competition.

$$S_{\text{covered}}=S_{\text{leaf}}\times [\text{1 }–\text{ exp}(–n\times {\overline{\sigma }}_{\text{lesions}}/S_{\text{leaf}})]$$ (9)

The actual surface of each lesion, S_lesion, is then estimated by sharing between lesions the increase of S_covered since the previous time step. In order to simulate the higher priority of chlorotic and necrotic lesions of septoria, we operate in two steps. In the first step, the increase of coverage by high priority lesions is estimated with Eqn (9), and shared among this sub-population only. In the second step, the global increase of coverage is re-estimated for the entire population and shared between all individuals.

Model 3: epidemiological model with interactions at canopy scale.

The epidemiological model simulates combined epidemics of septoria and brown rust in a wheat canopy. It is an assembly of model 2 with other, previously developed models of 3-D wheat canopy, infectious cycles and dispersal of each disease (Garin et al., 2014). In this model, unlike models 1 and 2, pathogen populations interact with the wheat canopy. At the leaf level, the progress of natural senescence influences the green area dynamics, and thus the space available for settlement of new lesions. At the canopy level, the developing 3-D structure influences the dispersal processes, i.e. its ability to access new healthy leaves.

In practice, the following model assembly was set up using the framework developed by Garin et al. (2014): (1) a 3-D wheat model: ADELWheat (Fournier et al., 2003); (2) an epidemiological model of Z. tritici (Robert et al., 2008; Garin et al., 2014); and (3) an epidemiological model of P. triticina (Garin, 2015)

This framework uses a modular modelling strategy developed by Pradal et al. (2008, 2015). The wheat canopy is simulated as a multi-scale tree graph (Godin and Caraglio, 1998) that is used as a shared data structure between models. As described in Garin et al. (2014), it allows for the specification of several populations of lesion (here septoria and rust). The interactions and scheduling of models are specified using a Dataflow management system (Pradal et al., 2015).

The simulation of dispersal is done independently for the two fungi. For septoria, dispersal occurs during rain events (Robert et al., 2008; Garin et al., 2014). At each event, the exposure of individual leaves to rain is computed on the 3-D structure (Garin et al., 2014). The quantity of spores emitted by exposed sporulating leaf tissues is then computed as a function of rain intensity and rain duration (Robert et al., 2008), until exhaustion of a pre-defined stock of spores produced per unit of sporulating area (Garin et al., 2014). Spores are spread vertically through the canopy, using a 1-D multi-layered interception model (Robert et al., 2008) that mimics the upward movement of spores above each emission layer due to splash, and the downward, gravity-based, falling flux of infectious droplets throughout the canopy. For rust, dispersal occurs daily at a fixed time as long as lesions sporulate. The quantity of spores emitted by the sporulating area is defined as a function of wind speed (Willocquet et al., 1998; Garin et al., 2014). Spores are spread vertically upward and downward through the canopy using a 1-D multi-layered interception model (Garin, 2015) that mimics the transport of spores by wind around each emission layer. The probability of interception of a target layer is considered inversely proportional to the exponent of the vertical distance to the source layer (Frezal et al., 2009).

The competition for leaf surface area is the only direct interaction modelled between rust and septoria. Model 2 is used in this context as it affects lesion development.

Simulations with the three models

Definition of disease severity and normalized AUDPC.

In this study, the main output of simulations is disease severity, defined as the percentage of a leaf surface covered by fungal tissues at a given time. Severity curves follow the evolution of severity over time. To summarisz disease severity at the leaf level, we use the normalized area under the disease progress curve (AUDPC) which is derived from the classical variable AUDPC (Madden et al., 2007). The AUDPC is sensitive to the earliness, the rate and the maximal disease severity. It is calculated as the area below the severity curve. The normalized AUDPC is obtained by dividing the AUDPC by a theoretical maximum value corresponding to the situation where the leaf is infected fully just after its emergence.

Model 1: simulations of the patterning of the contact area between two lesions.

In a first scenario, two lesions are positioned close to each other at varied relative positions and left to grow and compete during 1000 °Cd with a 1 °Cd time step. This scenario was repeated for three situations: two septoria lesions, two rust lesions and one lesion of each species. The outputs were analysed visually to see how the lesions had grown relatively to each other and had competed in contact areas. This scenario helps in describing the functioning of model 1 for further simulations.

Model 1: simulations of the patterning of colonization of a leaf section by the complex.

In this second scenario, the model was used to test the competition for leaf surface between populations of lesions of Z. tritici and P. triticina. Leaf colonization was compared when a fungus was alone with when the two fungi were present and inoculated at different dates. The conditions of simulation were the following: (1) leaf dimensions: L = 10 cm × W = 3 cm, dL = 0.01 cm and dW = 0.01 cm; (2) duration of simulation: 1000 °Cd with a 1 °Cd time step; (3) inoculation of the leaf with N₀ = 150 lesions distributed randomly at time t₀ (first both at t₀ = 0 °Cd, then septoria at 0 °Cd and brown rust at 400 °Cd, and then the opposite); (4) computation of lesion growth and interactions; and (5) triggering of dispersal events with a frequency ν characteristic of the fungus dispersal mode. The frequency of the rust dispersal events is greater than that of the septoria [ν_rust = 0.05 (°Cd)^–1 > ν_septoria = 0.01 (°Cd)^–1].

Model 2: comparisons of simulations of models 1 and 2.

The aim is to analyse whether model 2 is an adequate meta-model of model 1. Simulations of model 2 were compared with simulations of model 1 in which the geometry of lesions is explicit. The aims were 3-fold: to test (1) if the synthetic formalism of Eqn (9) can simulate the leaf coverage by isotropic lesions of rust as predicted by model 1; (2) if model 2 can be applied to anisotropic lesions of septoria; and (3) how the synthetic model 2 simulates the interactions between septoria and rust on the same leaf compared with model 1.

For this, 30 simulations were run with model 1, for which the results may vary with the random initial positioning of lesions. The simulations followed the growth of one strong initial inoculum of Z. tritici (N₀ = 200 lesions) or P. triticina (N₀ = 500 lesions), randomly distributed and capable of covering the leaf sector in one infectious cycle. The mean severity and the confidence interval of these simulations with model 1 were compared with the result of model 2 in the same conditions. The difference between the two models was quantified by calculating the root mean square error (RMSE) between them. Simulations of model 2 were also compared with simulations of model 1 with both fungi inoculated at the same time on the leaf (N₀ = 200 lesions of Z. tritici and N₀ = 500 lesions of P. triticina simultaneously).

Model 3: epidemic simulations to reveal key factors in the development of the two diseases in complex.

Multiple conditions of simulation and several parameters were changed to test their influence on the behaviour of the pathosystem and on the development of one disease relative to the other. Among all the conditions tested, four are presented here to illustrate the interest of model 3. In these examples, we show the effects of (1) climate, (2) the rust latency period, (3) the rules of priority between different lesions and (4) the amount of rust initial inoculum. For this, epidemics of septoria alone, rust alone and both fungi in complex were simulated for the following.

• (1) Three varied climatic sequences: 2003, 2012 and 2013 of Grignon (France, 48°32ʹN, 2°37ʹE). The growing season of 2003 was recorded as very dry and unfavourable for both diseases (weekly regional reports: Bulletin de Santé de Végétal, Ile de France). In contrast, 2012 was favourable to both diseases, and 2013 was very favourable to septoria (weekly regional reports: Bulletin de Santé de Végétal, Ile de France; Robert et al., 2017).

• (2) Two latency periods of rust: 180 °Cd (as it was set in the reference model) compared with 130 °Cd (simulating more aggressive strain behaviour).

• (3) Two sets of competition rules between the two fungi: one set with the simple rules defined above against one set with the following new rule added: the sporulating capacity of septoria on a leaf was proportionally reduced as the severity in rust of this leaf increased in order to mimic the competition for a depleting resource.

• (4) Two primary inoculations of rust: strong aerial inoculum, limited in time (peak of inoculum after full deployment of leaf 4), against low and continuous aerial inoculum.

The disease severity curves on the upper leaf ranks and the normalized AUDPCs were compared to analyse the progress of epidemics in each situation.

RESULTS

Model 1: simulations of two lesions

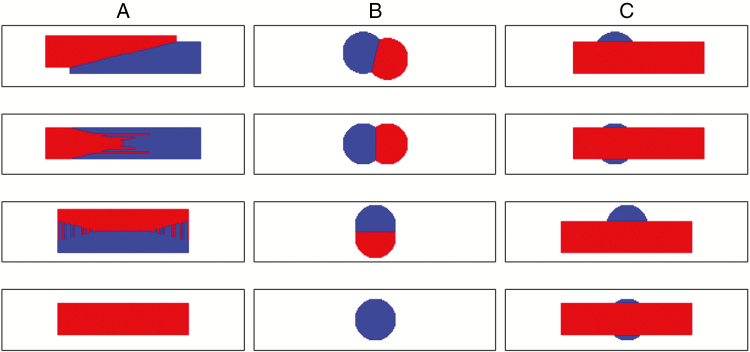
Figure 3 provides growth patterns of two lesions growing close to each other. During growth, the lesions of the same fungus mutually inhibited themselves at their contact zone (Fig. 3A, B). As a result, in most cases, it created a sharp competition front between the two lesions. In the case of septoria, the random order of calculation sometimes gave priority to the red lesion and other times to the blue lesion (Fig. 3A).

Fig. 3.

Output of model 1 for two competing lesions starting at the same infection date from varied relative positions. Columns: A, two septoria lesions; B, two brown rust lesions; C, one septoria lesion and one rust lesion. Lines: varying the position of the infection point.

Figure 3C shows that when a septoria lesion grew near a rust lesion, it overgrew it. In these scenarios, the rust lesion grew faster than the septoria lesion to reach its maximum surface. However. when the septoria lesion reached its necrotrophic stage, it took the advantage and covered the rust lesion.

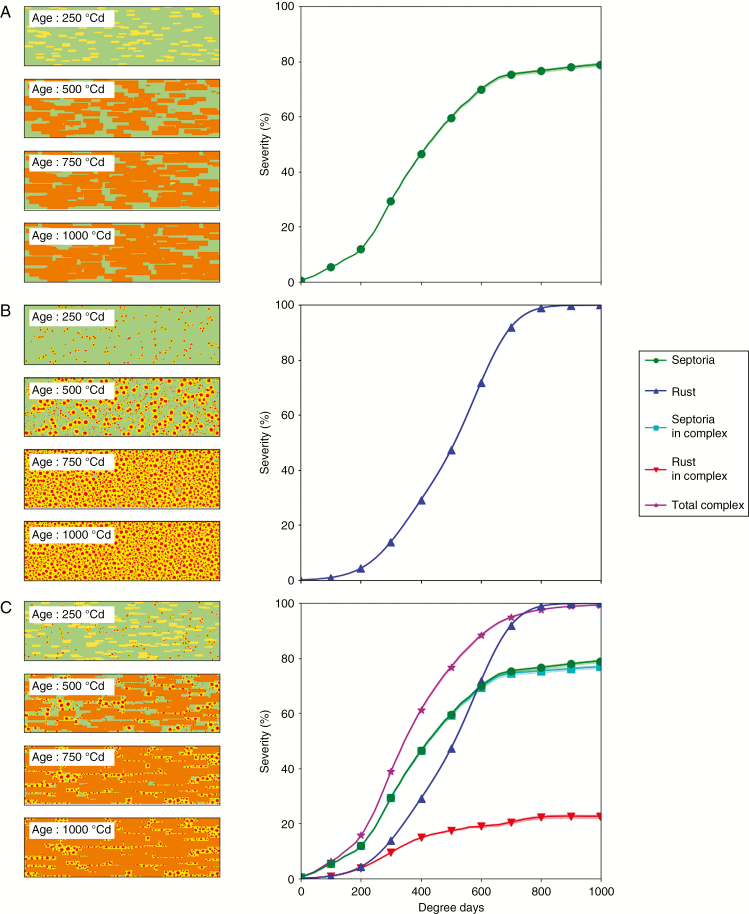
Model 1: simulations on a leaf section

Figure 4A shows the results of simulations when septoria was alone on the leaf. During incubation and until approx. 400 °Cd, the severity curve followed the same profile as the growth of an individual lesion, with a similar slope. This means that lesion growth was sparsely limited at this stage. After this, leaf colonization slowed down despite new contaminations (new spots in chlorosis at 750 °Cd). This is primarily due to the well-established lesions that interfered with each other. Then, the severity level was already high and reduced the likelihood of new infections in the green areas of the leaf.

Fig. 4.

Growth of lesions of Z. tritici and P. triticina simulated with model 1. Left: pixels occupied by lesions. Right: severity curves over time expressed in degree-days (°Cd). Lines with symbols indicate the mean of 30 repetitions; lighter shades indicate the 95 % confidence interval. (A) Z. tritici alone. (B) P. triticina alone. (C) Z. tritici and P. triticina together.

Figure 4B shows the results of simulations when brown rust was alone on the leaf. Again, in this case, lesion disease growth was sparsely limited until 500 °Cd. Many rust lesions reached their maximum size. Then the disease severity on the leaf increased rapidly because of the large number of new lesions on the leaf. However, the final size of each new lesion was reduced as space became limited.

Figure 4C shows the results of simulations when septoria and brown rust were inoculated at the same time on a leaf. The total disease severity of the complex was slightly superior to that of septoria alone. The disease severity of septoria was only slightly reduced when it was in complex compared with when it was alone (Fig. 4A). However, the severity of brown rust was strongly reduced compared with when it was alone. This shows an antagonistic relationship between the two fungi. In short, the competition at leaf scale was favourable to septoria when the two pathogens were inoculated at the same time according to the rules of the model.

Figure 5 shows the simulation results when rust and septoria were inoculated at different times on the same leaf. When septoria was inoculated before rust, its progress was not reduced compared with when it was alone (Fig. 5A: curves with squares and circles). This is explained by the symptoms of septoria that limited the infection sites for rust after 400 °Cd. The first septoria lesions had already completed the incubation phase and could overgrow new rust lesions.

Fig. 5.

Evolution of severity of Z. tritici and P. triticina simulated with model 1 when the inoculation of both diseases is delayed in time. (A) Septoria inoculated 400 °Cd before brown rust. (B) Septoria inoculated 400 °Cd after brown rust. Lines with symbols indicate the mean of 30 repetitions; lighter shade indicate the 95 % confidence interval.

Septoria was more affected by brown rust when rust was already established (Fig. 5B). Again, the number of potential infection sites was reduced for the fungus that came second. Septoria inoculum was reduced compared with when it was alone. After 400 °Cd, the septoria lesions in incubation were competing for space with rust lesions. The rate of increase of septoria severity was reduced. However, after the incubation stage (after 600 °Cd), septoria lesions started to overgrow rust lesions and their growth rate was comparable with when alone.

Model 2: comparison with model 1 for each fungus alone

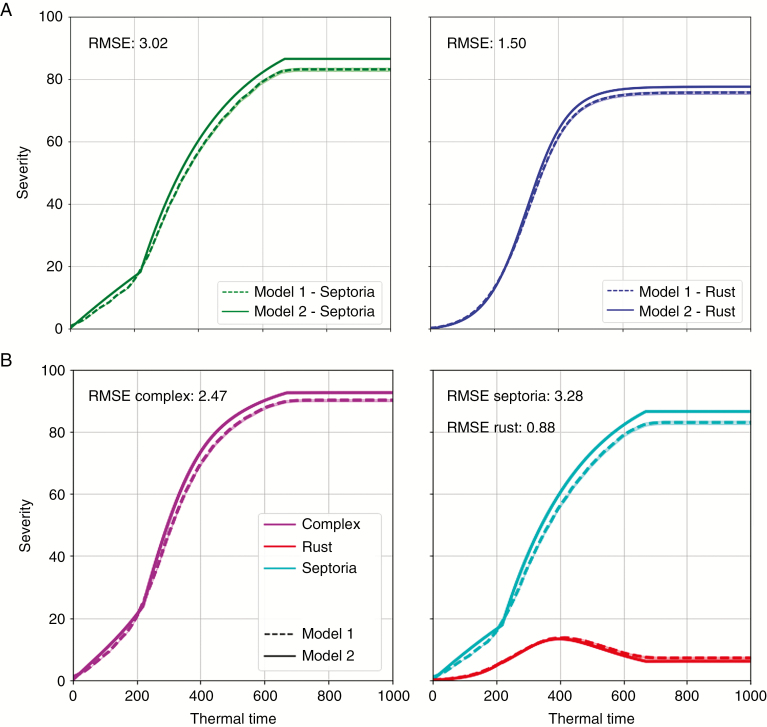
The results of simulation of models 1 and 2 are presented on Fig. 6A for each fungus alone. For both species, the simulations of model 1 showed that lesions interfered with each other so that their spatial arrangement prevented them from occupying the entire leaf surface. The more their surface increased, the more intense became the competition and their growth rate decreased. This behaviour was simulated by both models 1 and 2 for both species. However, the confidence intervals indicate that model 2 tended to overestimate the disease severity compared with the geometrically explicit simulations of model 1, especially for high levels of severity. Thus, the predictions by model 2 of the lesion growth phase were very close to model 1, whereas model 2 overestimated the final lesion size compared with model 1. The low values of RMSE (3.02 % for septoria and 1.50 % for rust) confirmed that model 2 was an interesting synthetic meta-model of model 1 for simulating the competition between lesions on a leaf. It should also be noted that similar results were obtained for different leaf shapes and dimensions (results not shown).

Fig. 6.

Dynamics of leaf colonization by lesions of P. triticina and Z. tritici alone (A), and in complex (B) simulated with model 1 (dashed lines indicate the mean of 30 repetitions; lighter shade indicate the 95 % confidence interval) and with model 2 (solid lines).

Model 2: comparison with model 1 for both fungi in complex

The results of model 2 were compared with those of model 1 in Fig. 6B for both fungi in complex. Model 1 calculated a continuously increasing severity for septoria lesions, which had a competitive advantage after 220 °Cd. After 400 °Cd, rust lesions were overgrown by septoria lesions faster than they grew themselves. The rust severity decreased as a result. Model 2 reproduced this phenomenon in accurate proportions. The overall severity of the fungal complex was similarly simulated. It is worth mentioning that if model 2 slightly overestimated the severity of rust alone, this was not the case in complex with septoria. This was because of the interactions between the two diseases and the fact that model 2 overestimated the severity of septoria alone a bit more than that of rust (as shown by the values of RMSE). This shifted the balance in favour of septoria when the two fungi were present together, which resulted in a slight underestimation of rust. In conclusion, model 2 is an adequate meta-model of model 1 when diseases are in competition (all RMSEs were <3.5 %).

Model 3: epidemic simulations with different weather scenarios

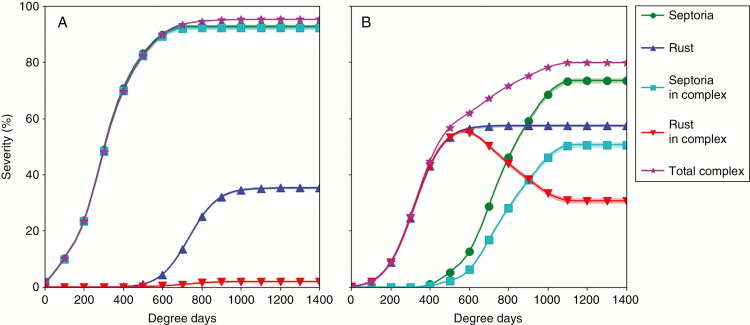
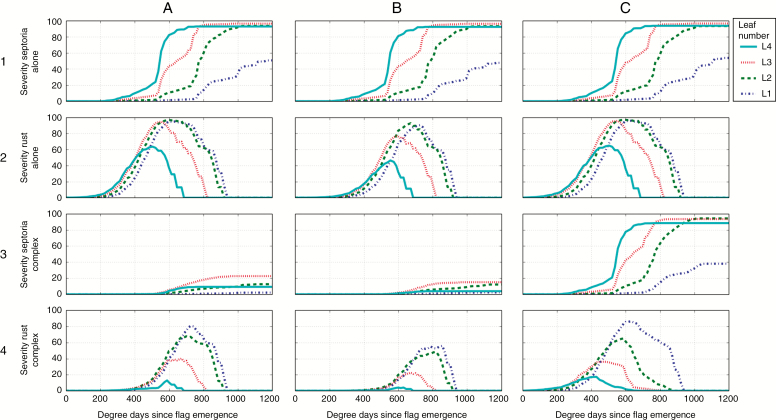
The results obtained with model 2 were satisfying enough to integrate it in model 3 and run simulations at the scale of the canopy. Figure 7 shows the severity curves of septoria and brown rust when they were alone and in complex in the same canopy for three weather scenarios (data from 2003, 2012 and 2013).

Fig. 7.

Severity curves of Z. tritici and P. triticina on successive wheat leaf ranks simulated with model 3 in varied conditions (lines indicate the mean of 30 repetitions). Columns: three seasons with contrasting weather conditions in Grignon (France) in (A) season 2002/2003; (B) season 2011/2012; (C) season 2012/2013. Lines: 1, septoria alone; 2, brown rust alone; 3, septoria in complex; 4, brown rust in complex.

The epidemics of septoria and rust alone showed different behaviours. For septoria, the symptoms progressed from the lower to top leaves. The temporal delay between disease curves and the maximal severity for separate leaves varied with the scenarios. Quantitatively, this was also shown by the normalized AUDPC (Fig. 8). For 2003, very few symptoms were simulated. For 2012 and 2013, the simulated disease was higher while the epidemic was earlier in 2013 than in 2012, resulting in significantly higher AUDPC levels in 2013. This is concordant with field observations reported in these seasons (weekly regional reports: Bulletin de Santé de Végétal, Ile de France; Garin et al., 2017). For brown rust, the simulated disease on the four upper leaf ranks emerged at the same time, in contrast to septoria. This behaviour is consistent with field observations of Robert et al. (2004). The start of the disease was simulated around 300 °Cd after the emergence of leaves 1 (flag leaf). The highest severity level was simulated on the highest leaves. Leaves above rank 4 (numbering from the top of the canopy) were not affected. Less difference than for septoria was predicted between the three weather scenarios for brown rust; 2012 was the most favourable climate and 2003 the least favourable (Figs 7 and 8), which is also concordant with field observations of these growing seasons (weekly regional reports: Bulletin de Santé de Végétal, Ile de France).

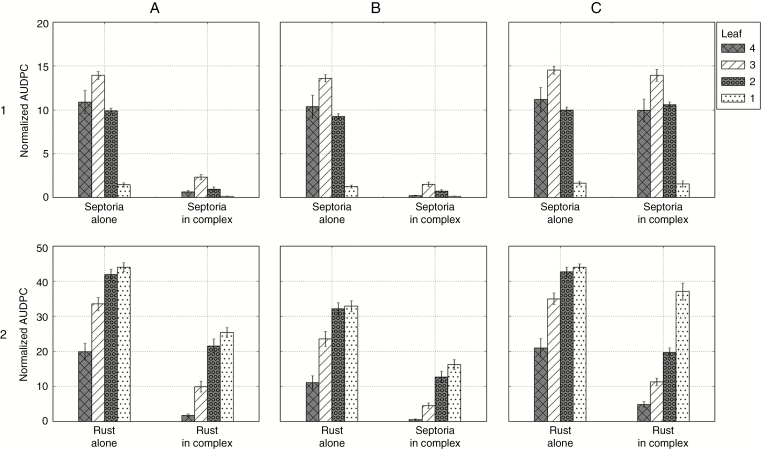
Fig. 8.

Normalized AUDPC of Z. tritici and P. triticina on successive wheat leaf ranks simulated with model 3 in varied conditions (textured bars indicate the mean of 30 repetitions and error bars indicate the 95 % confidence interval). Columns: three seasons with contrasting weather conditions in Grignon (France) in (A) season 2002/2003; (B) season 2011/2012; (C) season 2012/2013. Lines: 1, septoria alone and in complex; 2, brown rust alone and in complex.

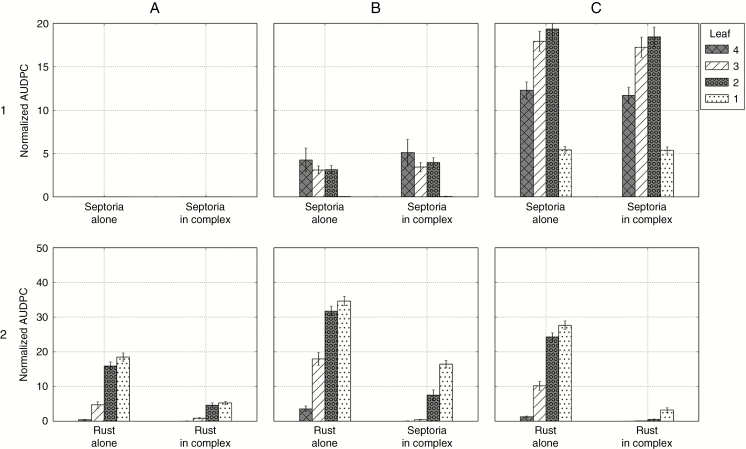
When both fungi were simulated together in the same canopy, several results emerged. First, for the three weather scenarios, the epidemics of septoria were almost not affected by the presence of brown rust. Secondly, the epidemics of brown rust were reduced by the presence of septoria, but the reduction depended on the weather scenario. This was particularly noticeable on Fig. 8, with normalized rust AUDPC levels of leaves 1 passing from 18.5 to 5 in 2003, from 34.6 to 16.2 in 2012, and from 27.5 to 3.1 in 2013. In 2003, despite quite low septoria levels, brown rust developed less than when it was alone on the four upper leaves (Figs 7 and 8). In 2012, brown rust was reduced on all leaves compared with when it was alone. However, rust severity still reached 70 % on leaves 1 (Fig. 7), and reached higher levels of normalized AUDPC than the other years (Fig. 8).

In the model, the reduction of rust severity due to septoria was partly caused by a reduced probability of infection and growth on leaves that were already colonized by septoria. The other part of this reduction was due to necrotic septoria lesions overgrowing brown rust lesions. These effects depended on the timing of emergence of both types of lesions on leaves. In 2013, a very favourable year for septoria, septoria lesions emerged shortly after leaf emergence, and not enough room was left for brown rust lesions. In 2012, on leaves 2, some brown rust lesions emerged before being overgrown by septoria lesions. Septoria barely attacked leaves 1, thus leaving more time and space for brown rust development. The reduction of brown rust levels on top leaves can also be explained by the presence of septoria on intermediate leaves, which hindered the first cycles of production of brown rust inoculum. This was the case in 2003 (Fig. 8) (data not shown). Therefore, the effects of septoria on rust at the leaf scale reverberates strongly at the epidemic scale in the model.

Model 3: key factors affecting epidemic simulation

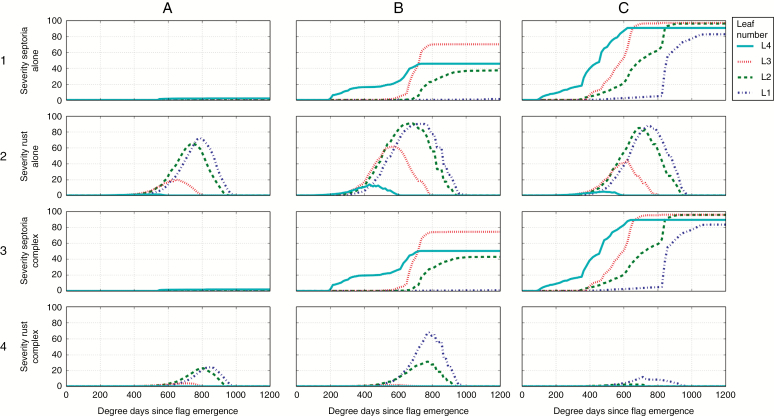
First the model was run with a shorter latent period for brown rust (Figs 9A and 10A). In these conditions, the epidemic of brown rust alone started earlier (cf. Fig. 7B2) and reached higher disease severity and AUDPC levels (cf. Fig. 8B2) on all top leaves. When rust and septoria were simulated together, the level of brown rust was again reduced compared with when it was alone, but less than for a longer latent period (cf. Fig. 8B2). Therefore, with a shorter latent period, brown rust had more chance to develop in the presence of septoria, and the epidemic of septoria was reduced (e.g. normalized AUDPC on leaves 3 passing from 19.9 in average alone to 2.2 in complex).

Fig. 9.

Severity curves of Z. tritici and P. triticina on successive wheat leaf ranks simulated with model 3 in 2011/2012 in Grignon (lines indicate the mean of 30 repetitions). Columns: three varied conditions of simulation: (A) reduced latency period of brown rust; (B) enriched rules of competition between the two fungi; (C) modified conditions of primary inoculation of brown rust. Lines: 1, septoria alone; 2, brown rust alone; 3, septoria in complex; 4, brown rust in complex.

Fig. 10.

Normalized AUDPC of Z. tritici and P. triticina on successive wheat leaf ranks simulated with model 3 in 2011/2012 in Grignon (textured bars indicate the mean of 30 repetitions and error bars indicate the 95 % confidence interval). Columns: three varied conditions of simulation: (A) reduced latency period of brown rust; (B) enriched rules of competition between the two fungi; (C) modified conditions of primary inoculation of brown rust. Lines: 1, septoria alone and in complex; 2, brown rust alone and in complex.

Secondly, the model was run with a different rule of competition between the lesions: the sporulation of septoria was proportionally reduced to the severity of brown rust in order to mimic the competition for a depleting resource in the leaf (Figs 9B and 10B). Changing this rule of competition strongly influenced the simulations of both septoria and rust in complex: (1) the severity of septoria and the corresponding AUDPC on the four top leaves were strongly reduced by the presence of brown rust and (2) the severity and normalized AUDPC of brown rust were much less reduced in complex (cf. Fig. 8B2). Therefore, in this scenario, brown rust had more chance to develop in the presence of septoria. This new rule of competition shifted the competition more in favour of rust and the competition became more balanced.

Thirdly, the model was run with an earlier inoculum for brown rust: a strong rust inoculum was simulated after the fourth leaf emerged (Figs 9C and 10C). This resulted in a stronger epidemic of brown rust alone (Fig. 8B2). It also had a positive effect on rust in the presence of septoria: when simulated in complex, rust could develop strongly on top leaves, before the growth of septoria (75 % severity and normalized AUDPC of 19.9 on leaves 2, and 90 % severity and normalized AUDPC of 37 on leaves 1). Therefore, the asymmetry between the two fungi was weaker in this scenario since the epidemic of brown rust was less affected by the presence of septoria on low and intermediate leaves.

DISCUSSION

This study presented a novel approach to model fungal foliar complexes. We first developed two models at leaf scale. These models are based on the following hypothesis: at every discrete step of simulation, calculating the colonization of the leaf by growing lesions amounts to calculating the overlaying of spots on a given surface. The first model is more detailed with explicit lesion geometry, and served as development support for the second model that is more synthetic [Eqn (9)]. The simpler model and the mechanistic model gave quite similar results. They would still require to be compared with observed data, but the simulated dynamics seem consistent. In addition, model 2 adapts to both lesions with an isotropic shape (rust type) and anisotropic lesions (septoria type).

Concerning the rules of competition between lesions, we assumed, based on the knowledge available, that lesions of rust and septoria constrain each other’s growth when they are incubating. However, the behaviour of septoria lesions changes with age (Kema, 1996; Keon et al., 2007; Steinberg, 2015; Palma-Guerrero et al., 2016). In our models, as septoria lesions become chlorotic, they are able to invade biotrophic lesions. These assumptions allowed testing of a simple implementation that was consistent with experimental observations (Robert et al., 2004a, b). They allowed reproducing by simulation an antagonistic relationship between the two pathogens, as had previously been demonstrated experimentally (Madariaga and Scharen, 1986; Robert et al., 2004a, b). However, these competition rules could be too favourable to septoria for two reasons. First, it is not entirely realistic that chlorotic tissues of septoria constantly overgrow rust lesions. Current simulations seem to overestimate the mortality of rust lesions. Secondly, we made the assumption that septoria lesions keep growing as normal after covering old rust lesions. However, if the rust has used a lot the leaf resources, it is likely that septoria development is decreased thereafter.

More generally, other phenomena have been simplified or ignored when modelling. First, in our models, lesions in contact exclude each other completely when they are in the same trophic stage. This seems reasonable for old lesions in sporulation whose mycelium is highly concentrated. However, this is probably a simplification for young incubating lesions. For those, the colonizing hyphae can probably intertwine in the apoplasm. We do not take into account opportunities for joint colonization during incubation. In addition, we calculate a competition between lesions for the occupation of the leaf surface and not directly for nutrients. The validity of our models is limited to the leaves on which it is acceptable to consider that the nutrient resource is evenly distributed throughout their green surface, and that it does not depend on their rank or age, which is quite unrealistic. This also implies that the presence of fungi does not alter the plant physiology close to symptoms, but also in other part of the leaves. Our approach is nevertheless a first step to take into account the modulation of epidemics by the amount of resources available on the host.

It is interesting to note how epidemics were impacted when simulated in complex compared with when simulated alone. The model simulated a reduction in brown rust epidemics in the presence of septoria. This is consistent with previous experimental results (Robert et al., 2004a). Simulations done with different climates showed that the decrease in rust development was stronger when the septoria epidemic was severe and early. In the model, the rust inoculum usually settled quickly on leaves after leaf emergence because its dispersal is regular and because favourable conditions of infection are often encountered. The establishment of septoria inoculum was more dependent on the occurrence of rainfall events. If these events were infrequent, it gave the rust inoculum time to settle before the arrival of septoria. In addition, rust cycles were shorter (latency <200 °Cd compared with 350 °Cd). This allowed it to grow and reproduce before septoria. This is why in climates 2003 and 2012, the symptoms of rust were highly developed on the flag leaves (Fig. 7). This behaviour was more remarkably noted in Fig. 9A when the latency period of brown rust was reduced. However, in most situations tested, septoria quickly took over rust lesions. The sooner the contamination occurred after leaf emergence, the less time was available for rust to develop on the same leaf. Also, if rust development was hindered on the intermediate leaves of the canopy, then the production of secondary inoculum was reduced and this affected epidemics on the upper leaves. The effects on the uppermost leaves should therefore be analysed in light of the history of the epidemic on the lower leaves.

In the simulations, the colonization of leaves by septoria was often unaffected by rust development. This occurred regardless of the climate sequence. The severity of septoria was, however, significantly reduced by the presence of brown rust when the rules of competition were changed to reduce the sporulation of septoria proportionally to the severity of brown rust (Fig. 9B). Taking into account the competition for a depleting resource in the leaf thus influenced simulated septoria epidemics. In addition, the model initiation strategy (i.e. the amount of initial inoculum of each species, primary contamination dates) had a lot of influence on the rust development in complex (Fig. 9C). They show that a strong peak of rust inoculum in spring can give more priority to rust epidemics.

The competition rules we have defined in this study correspond to what is called interference competition in ecology, meaning competition through direct interaction between individuals, as opposed to exploitative competition (Vance, 1984; Le Bourlot et al., 2014). Interference competition, and the special case of overgrowth in particular, is important and common in the dynamics of sessile organisms: plants, corals and bivalve molluscs (Chadwick and Morrow, 2011; Horwitz et al., 2017). A simple model of overgrowth interference competition shows that the resulting long-term dynamics are one of four cases: species 1 wins, species 2 wins, they coexist, or one excludes the other depending on initial conditions (Crowley, 2005). The relevant case depends on the parameters defining the competitive asymmetry between the species. Interestingly, for the situation of one dominant species that overgrows the other, they find that two cases are possible: either the dominant species outcompetes the other or they coexist. Our model shows that with the basic priority rules, septoria tends to outcompete rust (Fig. 7A, C), whereas with the adjusted rules that are more favourable for rust (Fig. 9A–C) both species coexist.

Conclusion

This study demonstrates that it is possible to simulate several fungal populations with virtual plant models in our modelling framework (Garin et al., 2014). This opens up avenues of research to study interaction between pathogens and their host in varied environmental conditions on virtual plant canopies. In this sense, this approach is also in line with recent studies using virtual plant models to better understand competition between crops and weeds both above- and below-ground (Renton and Chauhan, 2017). Models are becoming increasingly advanced, and we hope recent developments in functional–structural plant modelling such as distribution of nutrient contents in leaves (Barillot et al., 2016) and trade-offs between plant morphology and defence (Ballaré and Pierik, 2017) will allow us to simulate more finely the processes involved in plant–pathogen interactions.