Abstract
Background and Aims
Individual-based models (IBMs) are promising tools to disentangle plant interactions in multi-species grasslands and foster innovative species mixtures. This study describes an IBM dealing with the morphogenesis, growth and C–N acquisition of forage legumes that integrates plastic responses from functional–structural plant models.
Methods
A generic model was developed to account for herbaceous legume species with contrasting above- and below-ground morphogenetic syndromes and to integrate the responses of plants to light, water and N. Through coupling with a radiative transfer model and a three-dimensional virtual soil, the model allows dynamic resolution of competition for multiple resources at individual plant level within a plant community. The behaviour of the model was assessed on a range of monospecific stands grown along gradients of light, water and N availability.
Key Results
The model proved able to capture the diversity of morphologies encountered among the forage legumes. The main density-dependent features known about even-age plant populations were correctly anticipated. The model predicted (1) the ‘reciprocal yield’ law relating average plant mass to density, (2) a self-thinning pattern close to that measured for herbaceous species and (3) consistent changes in the size structure of plant populations with time and pedo-climatic conditions. In addition, plastic changes in the partitioning of dry matter, the N acquisition mode and in the architecture of shoots and roots emerged from the integration of plant responses to their local environment. This resulted in taller plants and thinner roots when competition was dominated by light, and shorter plants with relatively more developed root systems when competition was dominated by soil resources.
Conclusions
A population dynamic model considering growth and morphogenesis responses to multiple resources heterogeneously distributed in the environment was presented. It should allow scaling plant–plant interactions from individual to community levels without the inconvenience of average plant models.
Keywords: Individual-based model, architecture, legume, grasslands, population dynamics, competition, plasticity, nitrogen fixation
INTRODUCTION
Legume-based grasslands are key components of agroecosystems, which supply high-quality protein-rich feed for ruminants, while reducing the need for nitrogen fertilizers, preserving water quality and mitigating greenhouse gas emissions (Jensen et al., 2012; Suter et al., 2015). However, these cultivated plant communities reportedly lack stability and long-term persistence of the legume species and are acknowledged as less predictable than mono-specific grasslands (Beuselinck et al., 1994; Schwinning and Parsons, 1996). The effects of competition for resources and crop management in particular have been shown to be of considerable importance for the dynamics of legumes and to ensure a good balance between species (Sheaffer, 1989; Beuselinck et al., 1994). To date, however, this knowledge has not been integrated in grassland models, most of which consider the whole community through typical ‘big leaf’ approaches, ignoring plant–plant interactions and changes in grassland composition over time (Riedo et al., 1998; Brisson et al., 2008).
Individual-based models (IBMs) of plant communities have long been used in ecology and are important both for theory and for hypothesis testing (Huston et al., 1988; Judson, 1994; Berger et al., 2008). They describe populations made up of individuals that may differ from one another, and take local interactions and resource dynamics explicitly into account (Uchmański and Grimm, 1996). IBMs have also been used in the fields of forestry and agronomy to predict the dynamics and use-value of cultivated plant communities (Liu and Ashton, 1995; Huston, 1999; Rademacher et al., 2004; Soussana et al., 2012). For grasslands in particular, exploring the connection between individual plant traits and ecosystem functioning with such models helped to better understand the determinants of plant performance in grasses (Verdenal et al., 2008; Mony et al., 2011) and proved able to predict the emergence of different plant communities along fertilization gradients (Maire et al., 2013). However, the presence of forage legumes, which are able to fix atmospheric nitrogen and to improve soil fertility, was not considered in these previous approaches.
Grassland plant populations are highly size-structured (i.e. present skewed distributions of individual plant masses, Harper, 1977; Baldissera et al., 2014) and undergo regular changes in their density as a result of competition-induced mortality (Matthew et al., 1995). Inter-individual variability and self-thinning are believed to be tightly linked (Dewar, 1993) and play dramatic roles in the shifts of dominance between species (Schwinning and Weiner, 1998). Both aspects are expected to emerge from the integration of local plant-to-plant interactions for resources as considered in IBMs (Berger et al., 2008). However, because grasslands are frequently located on marginal lands and because of their low input usage, competition in these communities usually occurs for multiple resources (mostly light, water and nitrogen). Such situations are rarely considered in IBMs (Uchmański and Grimm, 1996; Grimm and Railsback, 2005). Interestingly, recent advances in functional–structural plant modelling now enable us to envision biophysical models of plants, rooted in energetic and ecological theories, in order to decipher integration of plant traits and plastic responses above- (Cournède et al., 2008; Barillot et al., 2014; Zhu et al., 2015) and below-ground (Dunbabin et al., 2013; Pagès et al., 2014). In line with this proposal, the ‘Virtual Grassland’ initiative was launched to merge both approaches and propose an individual-based model of grassland communities, considering grass and legume components, and dealing with fluctuating light, water and nitrogen (N) availabilities (Louarn et al., 2014).
In this paper, we present and assess qualitatively the model of forage legumes used in ‘Virtual Grassland’. This model deals with the three dimensional (3-D) shoot and root morphogenesis of contrasting legumes, as well as C, water and N exchanges with the environment. Acquisition and allocation of C and N are represented for each individual by distinguishing four plant compartments (i.e. leaves, stems, taproot, fine roots). The paper describes the equations and formalisms used in the model and tests their behaviour on contrasting legume morphotypes. Model assessments were performed for population dynamics, plant plasticity and C–N acquisition along gradients of competition for light, water and N.
MATERIALS AND METHODS
Overview of the model
The IBM presented hereafter describes the functioning of individual plants based on the L-system formalism (Prusinkiewicz and Lindenmayer, 1990). It operates at the population scale and can simulate isolated plants (i.e. plants at a low density without interactions) as well as dense mono-specific populations or multi-specific communities of legume plants interacting through their effects on environmental resources (i.e. light, water and soil N). The model focuses on the vegetative development of individuals, both above- and below-ground. It does not yet account for the germination and the reproductive periods of development. The model operates for a wide range of legume growth forms and can accommodate contrasting pedo-climatic conditions (including effects of climatic variables, soil types, and soil water and N balances).
Basically, the model computes on a daily time step the potential morphogenesis of shoots and roots as a result of the functioning of plant meristems and growing tissues. Potential plant dry matter production is determined from light interception by shoots, which in turns defines water and N requirements to sustain maximal plant growth. A total of four compartments per plant (i.e. leaves, stems, taproot, fine roots) are considered for the partitioning of dry matter and N. Two major feedback loops are implemented in the model to account for plant plasticity and for the regulation of growth and morphogenesis by light and edaphic resources (Supplementary Data, Fig. S1). The main inputs required to run the model include regular weather data, a description of grassland management (sowing pattern, emergence date, timing and height of defoliation, N fertilization rates, etc.), and a set of plant parameters specifying the potential morphogenesis and responses to water and N stresses for each genotype (Fig. S1, Appendix 1). The main outputs of the model concern architecture, biomass and N content for each individual plant at the plant compartment level (namely leaves, petioles, stems, taproot and fine roots), as well as the main impact of plants on their local environment (water and mineral N uptakes, C and N residues released into the environment through senescent plant tissues).
The model operates on a daily time step, with thermal time (TT) increment calculated as the integral of a non-linear beta function of meristem temperature (T, equal to air and soil temperatures for shoots and roots, respectively; Zaka et al., 2017; eqns 1 and 2). Coupling of the plant model with its environment for the acquisition of light, water and mineral N is currently realized using two spatially explicit environment models accounting for (1) light transfer into the canopy (Sinoquet et al., 2001) and (2) water and N balance of the soil (Louarn et al., 2016). The description of these two models is beyond the scope of the present paper, but the coupling principles are further detailed in the section on model coupling. The following describes the production rules of the L-system capturing the potential morphogenesis of shoots and roots and the responses of growth, development and C–N metabolism to the environment currently integrated in the legume model.
Potential morphogenesis
A. Shoot morphogenesis.
The definitions and units of model parameters and variables are detailed in Appendices 1 and 2, respectively. Production rules (hereafter referred as PR) and symbols used to describe the organogenesis of plant modules in the L-system are summarized in Appendix 3, whereas the main model equations are described in Appendix 4. Each plant is initialized as a seed embryo containing an active bud at the origin of the main axis (B1), a root apex (RA), a collar (CO) connecting plant parts above- and below-ground (PR1), and an initial mass and N content of the seed. At each time step, the potential morphogeneses of shoots and roots are calculated in response to TT increment.
For shoots, the potential development of the different axes is based on a model initially developed for alfalfa (Baldissera et al., 2014) and then extended to contrasting legume species in their vegetative phase (Faverjon et al., 2017). Three main types of shoot axes can generally be distinguished with respect to their developmental properties: the main, primary and secondary axes. For the sake of simplicity, only two are considered in the model (the main and primary axes sharing the same parameters, except for node elongation, Fig. 1A). The model assumes that primary axes arise from collar buds (PR2) and that the production rate of new phytomers by the shoot apical meristem (dNipot/dTT) is constant in the absence of stress [i.e. constant phyllochron, eqn (3); PR3 and PR5 for primary and secondary axes, respectively]. Secondary branching is systematic and occurs from axillary buds of primary axes with a constant delay after phytomer emission (Deldeb, PR4). The production of new active buds at the plant collar increases up to a maximal value (nshmax), following a non-rectangular hyperbola function (PR2, eqn 4; Thornley and Johnson, 1990) and respecting a minimum lag after plant emergence (Deltil). When this maximum value is reached, shoots are renewed from dormant buds of the crown if the apical meristem from their parent shoot is removed during a defoliation event (PR6).
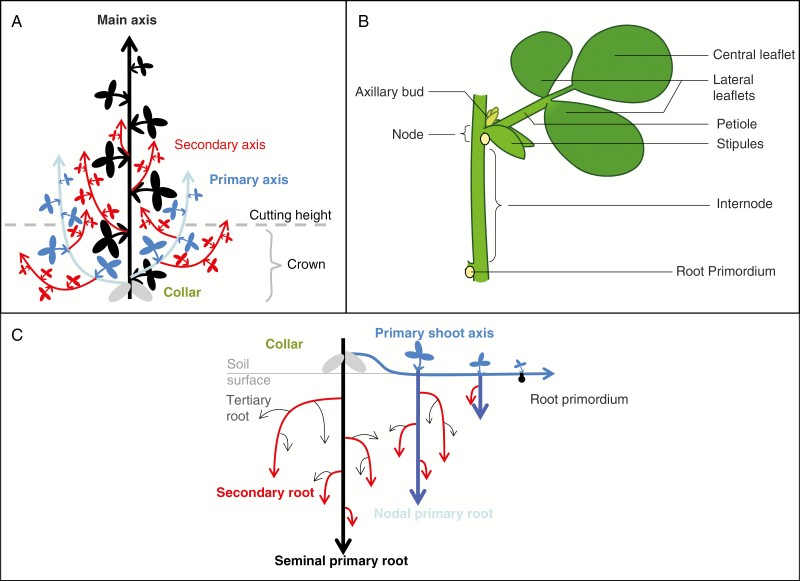
Fig. 1.
Generalized classification of axes and terminology used to describe forage legume shoots (A) and roots (C) as well as the organization of organs within a phytomer (B). In the model the main and primary shoot axes are assumed to share identical developmental properties, except for the elongation of internodes.
Phytomers are all made of the same elements (Fig. 1B): an internode (In), a stipule (S), a petiole (P) and a compound leaf blade (L). Additionally, phytomers from primary axes present axillary buds (B2) and a root primordium (Nr). Growth dynamics of the different organs are scheduled from leaf emergence according to a fixed developmental calendar identical in all the phytomers (Faverjon et al., 2017; PR10). These growth dynamics are assumed to follow a logistic function (eqn 5) expressed in phyllochronic time (tp), making it possible to consider axes with different developmental rates within the same plant using a single equation. For each organ type, the potential organ dimensions in the absence of stress are determined according to their topological position on the axis and follow a regular profile of relative dimensions (Ross, 1981; Faverjon et al., 2017). A bilinear function is used to account for the effect of phytomer rank on potential organ length (Campbell and Norman, 1989; eqns 6 and 7).
In some species, rhizomatous shoots can be developed (Forde et al., 1989). In such cases, a transition from crown buds to aerial shoots very often takes the form of rhizomes spreading below-ground. In the model this is taken into account through the formation of a series of leafless phytomers by the shoot apical meristem before shoot emergence above-ground. The number of rhizomatous phytomers to initiate is determined using a binomial distribution law with two parameters (nrhizo, prhizo). The rate of development of rhizomatous shoots is assumed to be identical to regular primary shoots (Faverjon et al., 2017).
B. Root morphogenesis.
For each root system emerging from the collar, potential root length increments (dRLpot/dTT) are calculated using an average root representation for each branching order. Root elongation and root branching are simulated with an approach adapted from the Archisimple root model (Pagès et al., 2014). Only the primary root and its first two branching orders are considered in the model (eqn 8). The potential elongation rate (ELrootpot) and growth duration (GD) of a root are assumed to be determined by its root tip diameter (D, eqns 9 and 10). Branching occurs from lateral root primordia after a maturation period and a minimal distance from root tip has been reached (DistRA, PR7 and 8). Each new lateral root emerges with a diameter related to that of its parent root (eqn 11). For a given branching order, all the lateral roots are assumed to have the same average diameter determined from the DlDm parameter. Hence, for each root, a length with lateral roots actively growing (ABL, eqn 12) and a number of active lateral roots (nbRA, eqn 13) can be determined and integrated into the calculation of the total potential root length increment.
In addition to the seminal root, nodal roots can eventually be produced from root primordia on phytomers in contact with the soil surface (PR9). This can occur after a maturation delay DelNodal and if the humidity of the soil surface has been above a minimum threshold FTSWNodal during this period (Stevenson and Laidlaw, 1985). Nodal roots then develop with the same properties as the seminal root.
C. Geometrical representations.
3-D representations of plant structures above- and below-ground are used for the interactions of plants with their environment, which require specific parameters (Appendix 1). For shoots, the geometry is generated explicitly using 3-D primitives from the plantGL python library (i.e. cylinders for internodes and petioles; spheres for buds and meristems; polygons for leaves and stipules; Pradal et al., 2009) and simple assumptions regarding leaf angle distributions (regular phyllotaxy, normal distribution of elevation angles) and shoot-bearing (random azimuth and initial elevation, stem curvature driven by a vertical tropism parameter gstem; Prusinkiewicz and Lindenmayer, 1990).
For roots, geometry is not made explicit for the whole 3-D root systems. A density-based approach is used, derived from the principles proposed for leaf area density distribution by Louarn et al. (2008a). For each primary root, a prospection envelope of the root system is generated from the trajectories of a sub-sample of first-order lateral roots, assuming each lateral is ascribed within a cylinder (PR11). The sampling distance along the primary root is defined by the RSL parameter, whereas the trajectory of each lateral root results from the elevation (ElviniR) and gravitropism (groot) parameters of the Archisimple model (Pagès et al., 2014). Total root length corresponding to each cylinder is then assumed to be distributed homogeneously within this volume. The overlap of different envelopes then generates the spatial variations of root length density.
Potential growth, C, N and water demands
A. Dry matter production and partitioning.
For each plant, the potential biomass production (dMSpottot/dt, eqn 14) is computed daily from the photosynthetically active radiation intercepted by its shoots (PARa(t), computed from the light transfer model and meteorological data) using an approach based on the radiation use efficiency (RUE; Monteith, 1977; Louarn et al., 2012a).
The partitioning of dry matter between shoots and roots is assumed to follow an allometric relationship depending on the biomass production cumulated above-ground since plant emergence (Migault, 2015; eqn 15). Dry matter allocation to roots is further split between fine roots and perennial taproots using a proportional approach (eqn 16). A constant proportion of C in plant tissues is assumed is the model. The offer of carbon for fine root growth is compared to the total demand necessary to support potential root elongation, thus defining an offer to demand ratio for these C-heterotrophic organs (QDroot, eqn 17). In the case of insufficient offer (i.e. QDroot < 1), the actual root elongation is scaled in order to balance offer and demand, thus reducing the elongation rates of the different roots proportionally to their relative demands (Pagès et al., 2014). In the case of multiple sub-root systems resulting from the development of nodal roots, carbon partitioning between the different sub-systems (each developing a taproot and fine roots) is realized proportionally to light interception by the axes bearing each nodal root (topological proximity hypothesis, Ryle et al., 1981) and QDroot is in this case calculated at the axis scale.
By contrast, shoots are assumed to be autotrophic for C, resulting in a shoot morphogenesis independent of C balance and being only regulated by edaphic stresses and light signals (Körner, 2015). However, a minimum C requirement is computed for each shoot organ type in order to ensure that minimum structural costs for organ expansions are covered (eqn 18). These organ demands are used to compute dry matter partitioning between shoot compartments, the distribution of new dry matter being determined according to the relative rates of tissue expansion and proportionally to structural C demands (eqn 19). In the case of insufficient C offer (i.e. total of the demands > dMSpotshoot/dt, which usually occurs just after defoliation), the expansion of shoot organs is realized at the expense of C consumption from the perennial taproot (Durand et al., 1989).
B. N demand, N acquisition and partitioning.
The demands of individual plants for N are derived from a critical N concentration defined at the canopy level (Gastal et al., 2015; eqn 20) and from the assumption that light interception and relative shoot biomass accumulation are driving the relative N demands, as proposed by Soussana and Arregui (1995) for multi-species canopies (eqn 21). Similarly, the N demands for roots are upscaled from whole plant biomass and root biomass allocation, assuming a constant root N concentration under optimal N nutrition (Strullu et al., 2014; eqn 21). These N demands can be met first by mineral N uptake in the soil, and second by biological N fixation in root nodules (Voisin and Gastal, 2015). Potential N uptake by fine roots is assumed to be an active process driven by HATS or LATS (high-affinity or low-affinity transport system) transporters and by root length distribution into the soil (Devienne-Barret et al., 2000). The specific absorption capacity (VABS) is computed as a sum of two Michaëlis–Menten functions depending on local soil N concentration (Nsol, eqn 22), whereas the total potential uptake of a plant results from the spatial integration of root length and mineral N distributions (eqn 23).
Regarding N fixation capacity, two periods are distinguished in the plant cycle of perennial legumes (Voisin and Gastal, 2015): an initial period following plant emergence during which the potential rate of fixation is limited by the development of nodules, and a second period starting when the maximum fixation capacity is achieved, corresponding to the start of nodule turnover and an ability of the plant to adjust fixation with fluctuations of N availability into the soil (Naudin et al., 2011). During the first period, the potential fixation rate of a plant is assumed to follow the vegetative development of shoots and to increase linearly with phyllochronic time up to FIXmax (eqn 24). Then, after the DelFIX stage, the potential fixation rate is assumed to reach a steady state and remains constant. The actual N fixation by roots is placed under the trophic dependence of shoots, so that defoliated plants with limited capacity of dry matter production also show reduced fixation capacity (Vance et al., 1979; eqn 26). Furthermore, N-fixation comes at a C cost for the plant, mainly associated with nodule formation and turnover (Voisin et al., 2003). The formation and renewal of nodules is not explicitly simulated by the model, but its cost is taken into account through a feedback effect of fixation (i.e. through the NDFA, the proportion of N derived from fixation) on potential RUE (Gosse et al., 1986; Voisin et al., 2013; eqn 25). Finally, allocation of fixed and absorbed N is realized proportionally to the relative demands of plant compartments. As for C, a remobilization of N from the taproot when there is insufficient uptake to cover shoot demand is implemented up to the limit of a minimum structural N content (%NminT; Volenec et al., 1996).
C. Water demand.
Light interception also drives the energy balance of the crop and plant water requirements. The potential transpiration of the whole canopy (Epotcanopy) is computed from daily reference evapotranspiration (Penman-–Monteith ET0, Allen et al., 1998) using a ‘crop coefficient’ defined from the leaf area index (LAI) of the canopy (Brisson et al., 1992, 2008; eqn 27). The distribution of available energy between the soil and the different plants of the canopy is based on the fractions of intercepted PAR (PARa) computed with the radiative transfer model for each plant, assuming that the partitioning of net radiations follows the same proportions (Brisson et al., 2008). This allows us to define a potential water demand (Epot) for each individual of the canopy (eqn 28). Finally, water uptake is simulated as a passive process and potential water uptake is determined for each plant according to its spatial root length distribution and to the distribution of available soil water (ASW, eqn 29).
Regulation of plant morphogenesis and growth by light, water and N availability
A. Photomorphogenesis.
The light environment of each plant can alter its potential morphogenesis through photo-morphogenetic responses (Ballaré, 1999). Three types of responses to light signals are considered in the model in order to anticipate the trophic effects of competition for light. First, the growth of spacing organs (i.e. internodes and petioles) is modulated by two response functions considering the effects of local transmitted PAR and red/far red ratio (ζ) on the relative elongation rate of shoot organs (eqns 30 and 31). The two functions are adapted from the model proposed by Gautier et al. (2000) for clover, and applied multiplicatively to modulate the potential elongation rate established on isolated plants (eqn 32). Any decrease of the red/far red ratio is assumed to have a proportional positive effect on organ elongation, whereas changes in the average transmitted PAR affect elongation rate through a bilinear function defining a maximal elongation rate at an intermediate value at the intersection of the two linear functions (PARopt).
Second, the deployment of plant leaf area is regulated in the shade by shutting down the development of shoot meristems and active buds exposed to unfavourable light conditions (PR2–6; Baldissera et al., 2014). A parameter ZETAthresh defines the minimum threshold of local red/far red ratio below which axis development will cease.
Finally, the geometry of shoots is known to be affected by light availability. Under shade, shoot bearing in particular can be affected, resulting in more erect stems (Gibson et al., 1992). In the model, this was accounted for by restricting the drawing of initial elevation angles of new shoots to a proportion of the isolated plant distribution when local light conditions fall below ZETAtresh. Given the extreme ability of legume leaflets to track sunlight even in dense stands (Travis and Reed, 1983), it was assumed that the leaf angle distribution remained unchanged.
B. Nitrogen stress.
A plant nitrogen status (NNI) was defined to quantify the overall satisfaction of plant N demand (Soussana and Arregui, 1995). This index relies on the ratio between actual and critical shoot N concentrations (eqn 33). When NNI falls below 1 (i.e. plant N demand is no longer met by N absorption and fixation), the growth rate of shoot organs, developmental rate of shoot axes and net C assimilation rate can be severely reduced (Bélanger et al., 1992; Gastal et al., 2015). For this, a normalized reduction function of each of these processes is used in the model (fNNINi,L,RUE, eqn 34; Supplementary Data Table S1). It is assumed to apply identically to the growth of different shoot organs or the development of different shoot axes. For the morphogenesis and growth of roots, no specific response to N availability is implemented. The effect on the growth rate of roots is purely mediated as a feedback effect of C assimilation by shoots and C allocation to roots (Brun et al., 2010).
C. Water stress.
A plant water status (FTSW) was defined from the fraction of total transpirable water available in the soil volume prospected by its root system (eqn 35). This index depends on soil hydrodynamic properties that determine a total soil available water content (TASW) from soil water content at field capacity and at wilting point (Brisson et al., 2008). When FTSW declines, the growth rate of shoot organs, the developmental rate of shoot axes, plant transpiration and net C assimilation can be severely reduced (Belaygue et al., 1996; Lebon et al., 2006). A normalized reduction function is used for each of these processes in the model (fFTSWNi,L,RUE,gs, eqn 36; Table S1).
As for N, water stress effects on root growth and development are mainly mediated through a systemic response involving the feedback effect of C assimilation by shoots and C allocation to roots. In addition, a direct effect of local soil humidity is considered on the elongation rate of lateral root envelopes in order to limit the exploration of roots in dry soil horizons. To do so, each envelope of lateral roots (Rlap, PR11) responds to the average FTSW in the soil voxels it explored and reduces its elongation rate accordingly using the fFTSWL function.
The different stress functions are applied independently of one another (i.e. multiplicative effects) to determine the actual growth and morphogenesis of the plant from the potential situation (eqns 37–41).
D. Senescence.
Shoot organs and roots are subject to the senescence of tissues even in the absence of stress (Thomas and Stoddart,1980). In vegetative shoots, a potential lifespan is thus defined for leaves and petioles (SPANL, PR12). The internodes of a stem and their axillary buds have an indeterminate lifespan. They enter senescence after all the leaves supported by the stem have died (PR13). For roots, decay occurs as soon as root age computed after growth cessation becomes greater than root lifespan. This root lifespan (Delsenroot) is calculated according to the root apical diameter (eqn 42; Pagès et al., 2014) and enables us to calculate the rate of root length senescence for lateral roots of each order after their respective delay (eqn 43).
The turnover of organs can be hastened by stresses. In the shade, the lifespan of leaves is usually shortened (Dong et al., 2008). The Delsenleaf parameter is used to induce leaf senescence after a prolonged period below the photosynthetic compensation point (defined here by an average transmitted PAR of 25 µmol m−2 s−1, Louarn et al., 2015). The same senescence pattern is applied to the meristems for which development has been stopped due to unfavourable light conditions (PR14). For roots, reduced diameters occur under stress (either shade-, water- or N-induced) as a result of a lower QDroot, which also leads to a faster decay. At the whole plant level, mortality occurs when all the leaves, stems and buds have senesced (i.e. death of all its organs). This decay of all shoot organs entails the senescence for the whole remaining root system (PR15).
Model implementation and coupling with the environment
The model was implemented in python on the OpenAlea platform (Pradal et al., 2008) using the L-py software (Boudon et al., 2012). Above-ground architecture interacts with a radiative transfer model to solve light partitioning and compute PAR interception by the different canopy components (Fig. S1). The RiRi model from RATP is currently used (Sinoquet et al., 2001). Briefly, this turbid medium model requires daily meteorological data, and a discretized representation of leaf area density distribution and leaf angle distribution into a 3-D grid for each plant to be run. A voxel size of 4 × 4 × 2 cm and a sky discretization following a Den-Dulk’s TURTLE with six directions (Den Dulk, 1989) are defined by default. Leaf area is assumed to be homogeneously distributed within each voxel (no clumping considered). Intercepted PAR is computed daily for each plant and for the soil. In addition, the transmitted PAR calculated by the light transfer model is used for local light signalling within each voxel. A local red/far red ratio (ζ) is computed from the daily fraction of transmitted PAR into each voxel. ζ is assumed to follow a non-linear saturating function of transmitted PAR as proposed by Escobar-Guttiérez et al. (2009).
Below-ground, plant root length distributions are coupled to a 3-D soil model to compute water and mineral N uptakes (Fig. S1). A version of the multi-layer STICS soil module (Brisson et al., 2008) generalized to 3-D grids is used (Louarn et al., 2016). As for light, a toricity of the 3-D grid is assumed below-ground to avoid border effects. Daily meteorological data, a description of the spatial distribution of soil properties (texture, hydrological properties, organic C and N contents), a discretized representation of root length density distribution into a 3-D grid and an expression of individual plant demands for water and N are required to run the soil model. A simple assumption of competition being proportional to root size or activity is made to solve within-voxel competition between different root systems. Resource partitioning between different root systems is thus assumed to be proportional to the local root length densities for water, and to the local absorption capacities (VABS(vox,t), eqn 22) for mineral N. Soil parameters are defined at the voxel scale, but the default initialization implies that voxels in a given soil layer share the same initial properties and parameters. In addition, senescing shoot and root tissues enter into a series of residue pools defined by the C/N ratio of senescent organs (Nicolardot et al., 2001). Five pools are either located in a mulch at the soil surface (leaves, petioles, internodes) or distributed into the soil voxels (fine roots and taproots of dead plants).
Qualitative assessment of model behaviour
The impacts of competition for light, water and mineral N on the main model outputs were assessed through a series of virtual experiments. A default parameterization based on parameter values found in the literature was used to simulate four contrasting morphotypes belonging to the four major groups of forage legumes (Supplementary Data Table S2). As a first approximation, parameters driving potential morphogenesis of shoots and roots were used to differentiate plant morphotypes, whereas those defining potential growth, N and water demands, as well as the plant responses to their environment were assumed identical between morphotypes.
The virtual experiments consisted in simulating competition within monocultures of plants from the different morphotypes grown at a wide range of planting densities (4–1600 plants m−2). For each situation, three edaphic conditions were considered: either potential (NW+, irrigation matching potential evapotranspiration; fractionated application of 100 kg N ha−1 during each regrowth), N-limiting (N−, irrigation as for NW+; no fertilization) or rainfed (NW−, no irrigation; no N fertilization). Simulations were performed at one location typical of Western Europe temperate grasslands (Lusignan, 46.26°N, 0.11°E) using 30-year average weather data (1986–2016). The soil at this site is a Dystric Cambisol (IUSS Working Group WRB, 2006) with silty-loamy texture in the surface and clay in the subsoil horizons (Chabbi et al., 2009). A STICS soil calibration available for this site was used, which corresponded to a 1.5-m-deep soil with 268 mm available water at field capacity, and 1.1 g organic N kg−1 in the upper soil layer. Simulated plot areas ranged from 1 m2 (at 1600 plants m−2) to 5 m2 (4 plants m−2) and were replicated five times. These plot sizes encompassed enough individuals to characterize changes in the size structure of the plant population according to the competition gradients studied. The date of emergence was assumed to occur on 1 March [day of the year (DOY) 61] and the management of plant stand consisted in four harvests carried out at fixed dates and defoliation height (4 cm), irrespective of treatments and species. A summary of the initialization conditions and of the different inputs provided to run each simulation is presented in Table S3.
The rationale for such a design was to assess whether the population dynamics and plant plasticity predicted by the model for intra-specific competition complied with the large background knowledge available for even-age plant populations detailed in classical ecology (e.g. Harper, 1977) and agronomy textbooks (e.g. Loomis and Connor, 1992). The main output variables assessed concerned plant dry matter production, dry matter and N partitioning, N fixation, and the size structure and self-thinning of a population in response to competition gradients (NW+, N−, NW−). The size structure and the degree of asymmetry of plant populations were quantified using the Gini coefficient (G), which is a measure of the relative mean difference (i.e. the arithmetic average of differences between all pairs of surviving individuals; Weiner and Solbrig, 1984) often used to qualify the degree of inequality of resource partitioning among individuals in a population:
where n is the number of individuals in the population, and xi and xj refer to the above-ground plant biomasses of any given plant pair. The G values range from 0 (all individuals sharing resources equally) to 1 (all resources captured by a single individual).
RESULTS AND DISCUSSION
Range of plant morphologies
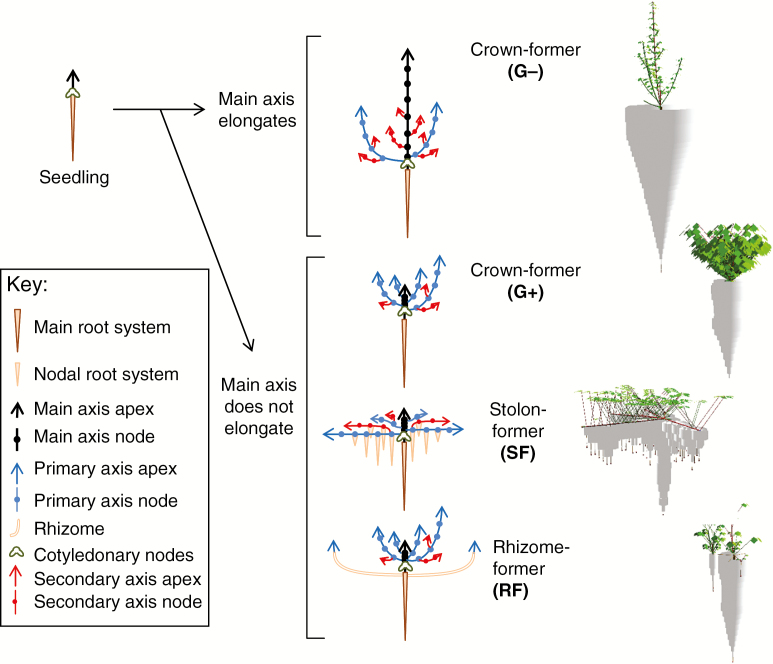
The set of production rules used in the L-system to drive shoot and root morphogenesis proved able to capture plant morphotypes as diverse as erect species typical of crown-formers intolerant to grazing (G−), prostate species perennating either by spreading rhizomes (RF) or stolons (SF), or semi-erect species representative of crown-formers tolerant to grazing (G+, Fig. 2). Concerning roots, a wide range of morphologies can also be simulated in terms of root depth, prospected root volumes, root length density and relative investment in a perennial taproot. These general features cover the range of architectures usually reported in forage legumes (Forde et al., 1989; Matches, 1989; Thomas, 2003) and a wide range of adaptations to grassland management and pedo-climatic conditions (Beuselinck et al., 1994). Based on a literature survey (Table S2), the main parameters discriminating between the tested plant morphologies principally involved differences in branching ability (Phyllo1, Tilr, Dmin), maximal organ growth (Lmax, Dmax), shoot bearing (gstem) and rooting ability (prhizo, DelNodal). G+ and G− differed mainly as a result of different leaf sizes, shoot branching and shoot bearing. RF and SF had shoot developmental patterns closer to G+, but presented differences in shoot bearing and rooting ability.
Fig. 2.
Diagrammatic representation of the vegetative development of forage legumes from the four main morphogenetic groups (left) and images of corresponding model outputs (right, NW+ at 4 plants m−2). G+: crown-formers tolerant to defoliation; G−: crown-formers intolerant to defoliation; SF: stolon-formers; RF: rhizome-formers (see Table S2 for the respective sets of parameter values).
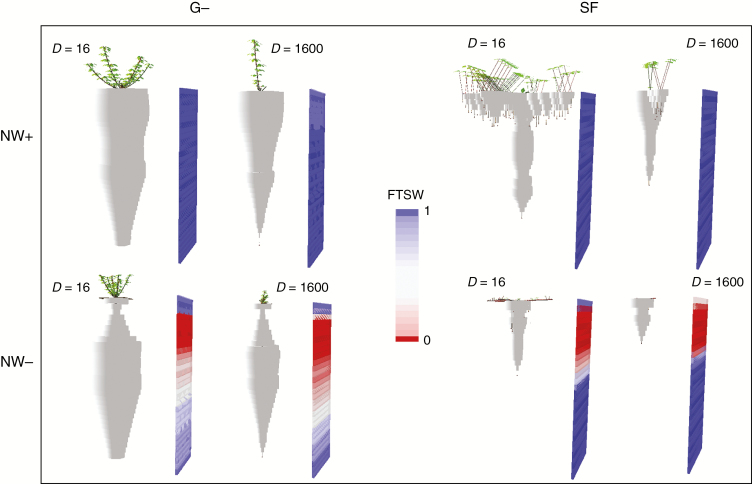
The functional coupling of morphogenesis above- and below-ground largely determines the plasticity of plant architectures in the model. Above- and below-ground parts were each assumed autotrophic for the resource they acquire and heterotrophic for the resources supplied by the other part. The feedback controls they exert upon each other modulated an ontogeny-driven C allocation pattern (eqn 15). By construction, this makes shoot and root growth tightly related (Caradus, 1977), but responsive with different degrees to different resource limitations. Ontogenic tradeoffs emerge from such interactions between above- and below-ground plant parts. As an example, the ability to develop nodal roots deeply affected the whole root system morphology in SF. Indeed, an increased competition for C between sub-root systems limits the development of the main taproot (Fig. S2). The greater number of root apices produced by multiple sub-root systems each receive a lower proportion of the amount of C allocated to roots, resulting in reduced root elongation rates. This behaviour produced plant phenotypes globally consistent with root mutants reported for white clover: larger and deeper seminal taproot in nodal mutants as compared to wild types (White et al., 1998; Thomas, 2003), and preferential development of nodal roots from phytomers connected with vigorous axillary branches in wild types (Thomas et al., 2002).
Overall, although based on a relatively simple geometry and a limited number of geometric parameters (Appendix 1), the model allowed us to integrate at the phytomer level the major morphological traits involved in resource acquisition and partitioning under dense canopy conditions (namely, plant height and vertical distribution of leaf area density for light above-ground; spatial distribution of root length for water and N below-ground; Louarn et al., 2012b; Dunbabin et al., 2013). From this perspective, it could thus provide a legume counterpart to the existing grassland IBMs based on grass morphology only (Verdenal et al., 2008; Soussana et al., 2012).
Stand production and average plant biomass
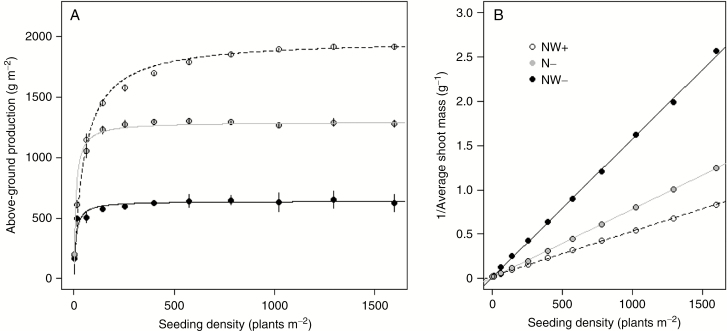
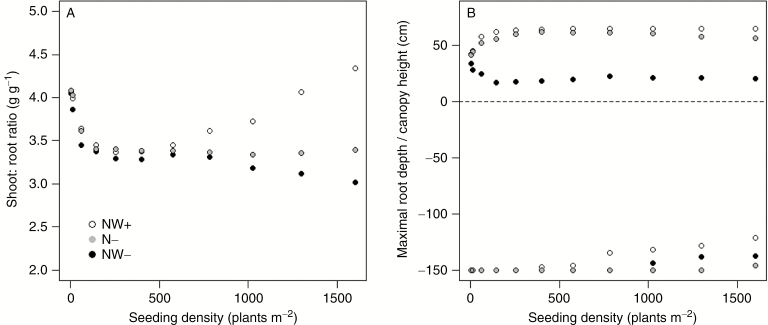
The influence of planting density on dry matter production per unit land area has been extensively studied in many wild and cultivated plant species (Donald, 1951; Willey and Heath, 1969). As described in these studies, the forage production predicted by the model followed a typical saturating function of density, irrespective of species and pedo-climatic conditions (Fig. 3A). This so-called ‘constant final yield’ increased under high water and N availability, the difference between treatments being highest in crowded canopies (Harper, 1977). In our simulations, the ceiling yields resulted from the permanent closure of canopy under NW+ (i.e. full sunlight interception) and from a canopy development limited by soil resource availability in N- and NW−. At low density (4 plants m−2), competition was minimal and each plant secured a large enough soil volume to meet its soil resource requirements, leading to reduced but similar stand productions in all the treatments. At the same time, the response of average plant biomass to planting density showed a typical ‘reciprocal yield response’ (Fig. 3B; Shinozaki and Kira, 1956). Irrespective of pedo-climatic conditions, the plastic responses of plants to the competition with their conspecific neighbours lead to an asymptotic reduction of plant biomass accumulation. This was observed in all four morphotypes, even if the ceiling yield achieved by each species, or the sensitivity of their dry matter production to soil water and N availabilities, may differ (Table 1). The pattern was also predicted independently of the N acquisition mode, with plants lacking the ability to fix atmospheric N (Fig. S3). In all morphotypes, the model also correctly anticipated an increased response of mean shoot biomass to density under favourable growing conditions (Harper, 1977).
Fig. 3.
Response of canopy (A) and average plant dry matter production (B) to seeding density as predicted by the model under different resource scenarios. The data shown are for the G− plant parameterization. Fitted lines correspond to the Shinozaki and Kira (1956) model relating average plant weight (W) to the number of individuals (N) per square meres: W−1 = a+b*N. NW+: irrigation and N fertilization; N−: irrigation, no N fertilization; NW−: no irrigation, no N fertilization.
Table 1.
Comparison of the four morphotypes regarding above-ground annual dry-matter production simulated at high density, population size structure and slope of the self-thinning line
| Morphotypes | |||||
|---|---|---|---|---|---|
| G− | G+ | SF | RF | ||
| Ceiling yield (g m–2) | NW+ | 1852 ± 12 | 1977 ± 9 | 1409 ± 28 | 1504 ± 11 |
| N− | 1268 ± 17 | 1567 ± 10 | 844 ± 38 | 810 ± 25 | |
| NW− | 660 ± 48 | 819 ± 12 | 119 ± 3 | 88 ± 2 | |
| Gini coefficient (DOY 334) | NW+ | 0.393 | 0.254 | 0.321 | 0.204 |
| N− | 0.755 | 0.496 | 0.582 | 0.571 | |
| NW− | 0.779 | 0.771 | 0.204 | 0.124 | |
| Slope | NW+ | −1.08 | −0.95 | −1.02 | −1.01 |
| N− | −1.09 | −0.95 | −* | −* | |
| NW− | −* | −* | −* | −* | |
NW+: irrigation and N fertilization; N−: irrigation, no N fertilization; NW−: no irrigation, no N fertilization. DOY, day of the year.
* The self-thinning slope was not calculated in these simulations: plants all persisted, at least through dormant buds.
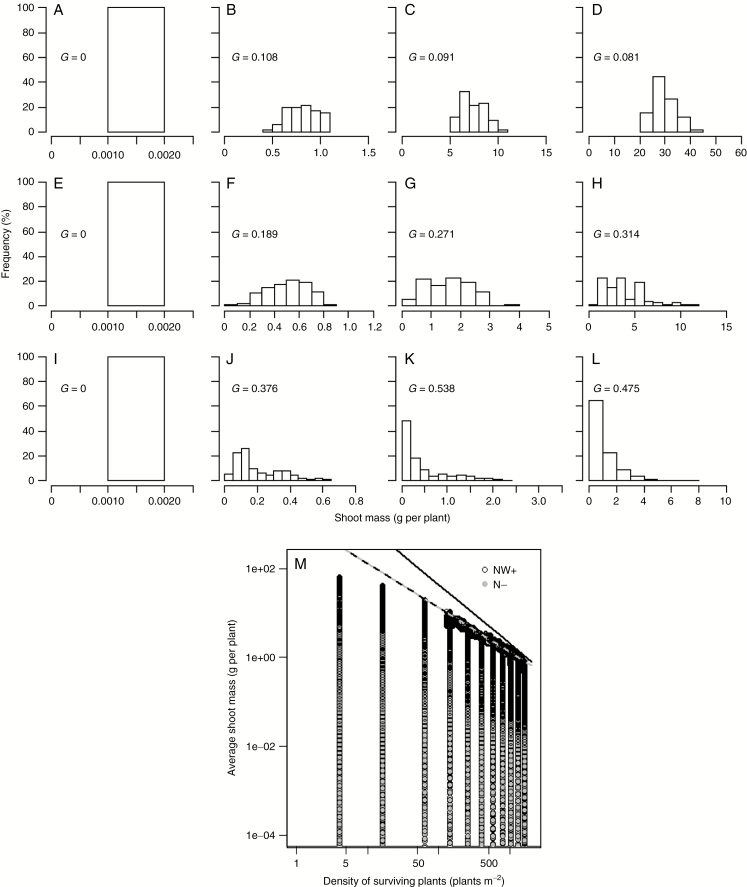
Inter-individual variability, size structure and plant mortality
Individual variations of production within a population are shaped by competition and result from differences in the growth rate of individuals in relation to their ability to capture and use the limiting resources efficiently (Uchmański, 1985; Lomnicki, 1988). The response of even-age plant populations to density generally involves (1) a symmetric normal distribution of plant biomasses at early stages of development and in situations of low competition, (2) positively skewed distributions of plant biomasses when competition increases, ultimately reaching a log-normal distribution, and (3) an increase of mortality accompanying high positive skewness (Harper, 1977). The inter-individual variability predicted by the models met all these propositions under favourable growth conditions (Fig. 4). At low density (e.g. 4 and 16 plants m−2), the size distribution of individuals remained symmetric and G values were low and close to zero (about 0.1 irrespective of species and treatments, Fig. S4), indicating an even contribution of individuals to canopy biomass production all along the simulations. Increasing the plant density systematically resulted in higher G values in WN+ and N− treatments. These dense stands resulted in skewed distributions of plant biomasses (G > 0.25, irrespective of morphotypes; Table 1). As density increased, temporal changes in the size structure occurred earlier in the plant cycle (Fig. 4A; Obeid et al., 1967). At the highest densities (e.g. >400 plants m−2 in G−, WN+), plant growth trajectories approached a self-thinning line that represented a density-dependent mortality and along which any further growth could only be achieved at the expense of a reduction in the population density (Fig. 4B). The slope of the self-thinning line generated by intra-specific competition was found to be between −0.95 and −1.1 on average (Table 1), which is close to slope values reported in many empirical studies (e.g. median value for herbaceous dicots, Weller, 1987). In fact, a slope of −1 appears closer to real plant populations than the −4/3 slope predicted by simpler models derived from metabolic theory (Deng et al., 2006) or the −3/2 slope reported in early theoretical studies (Yoda et al., 1963;Westoby, 1984).
Fig. 4.
Responses of the size distribution of individuals (A–L) and of the density of surviving plants (M) to plant growth at different seeding densities. The data shown are for the G− plant parameterization. Cumulated shoot biomass distributions are shown at DOYs 109 (A, E, I), 165 (B, F, J), 199 (C, G, K) and 260 (D, H, L) for NW+ at 16 plants m−2 (A–D), 400 plants m−2 (E–H) and 1600 plants m−2 (I–L). The plain line in the biomass–density diagram represents the –3/2 self-thinning line, whereas the dashed lines represent the self-thinning line actually predicted by the model for NW+ (black) and N− (grey) treatments. NW+: irrigation and N fertilization; N−: irrigation, no N fertilization; NW−: no irrigation, no N fertilization; G: Gini coefficient.
As competition for soil resources increased, the model generally anticipated an increase in the size class segregation of simulated populations (Fig. S4, Table 1). Under N−, the N-limiting period corresponded to the initial establishment of the nodulation system during which plants with a larger root length had an advantage at assimilating mineral N. This advantage was observed in all the morphotypes and resulted from an initial success in the competition for light shortly after emergence. Similarly, for NW−, the heterogeneity in the distribution of available soil water put deep-rooted plants at an advantage in our simulations. This advantage of some individuals also resulted from their initial success in the competition for light during the establishment phase in spring (water not yet limiting) and a higher C allocation to roots. In the G− and G+ morphotypes, which were able to develop deep rooting systems, this uneven access to a limiting resource deep into the soil led to an increase of the size-asymmetry under water stress. Such a pattern is in agreement with previous predictions (Chu et al., 2010) and with some experimental observations (Deng et al., 2006). However, the same pattern was not observed in SF and RF morphotypes, in which shallow rooting systems never allowed larger plants to overcome soil drying. In these latter cases, all plants experienced severe water stress and displayed limited growth and reduced size-asymmetry, as expected from the common assumption that competition is less size-asymmetric under restricted soil resource availability (Schwinning and Weiner, 1998). Our simulation results demonstrate the possible impact of an uneven access to a limiting soil resource, heterogeneously distributed in space and time, to either amplify or reduce the differences caused by light competition. As local plant resources differed, individual plant growth rates differed, leading to different levels of inter-plant variability. However, unequivocal patterns regarding the mode of competition under limiting soil resources were not apparent.
Plant plasticity in response to resource limitations
The partitioning of dry matter and the morphology of simulated plants were deeply affected by the limiting resource driving competition and its spatial distribution (Figs 5 and 6). The main morphological features of the shade avoidance syndrome (Smith and Whitelam, 1997) arose from competition under ample water and N in all the morphotypes. Indeed, under WN+, increasing densities produced taller plants, with reduced shoot branching, reduced C allocation to roots and shallower root systems. By contrast, increasing competition for water and N resulted in plants with shorter shoots, reduced branching, increased shoot/root mass ratio and altered root length distribution into the soil. The shoot/root ratio followed a general decreasing trend according to density, driven by ontogeny and the decrease in average plant mass (eqn 15). However, as previously reported (e.g. Gedroc et al., 1996; McConnaughay and Coleman, 1999), this ontogenic drift was either accentuated (WN−) or attenuated (WN+) depending on the relative limitation of plant growth by soil resources or solar radiation (e.g. Fig. 5 in G−). A switch between above-ground and below-ground biomass allocation with light versus nutrient/water limitation had already been modelled using IBMs (May et al., 2009; Lin et al., 2014), but only by forcing a predefined function that ignored the drift. In our model, a plastic allocation emerged in addition to the drift from the integration of local morphogenetic responses considered at the organ level and from their differential effects on C and N demands above- and below-ground. Furthermore, owing to the inter-plant variability in biomass accumulation, average, subordinate and dominant plant responses could differ substantially. Regarding the depth of the root systems for instance, the average depth was reduced but the maximal depth was increased in WN− as compared to WN+ in the morphotypes able to develop deep roots (G− and G+). The same occurred for maximal plant height when comparing high- and low-density stands.
Fig. 5.
Responses to seeding density predicted by the model for the shoot/root ratio (A) and for plant morphology as represented by maximal shoot height and maximal rooting depth (B) under different resource scenarios. The data shown are for the G− plant parameterization. NW+: irrigation and N fertilization; N−: irrigation, no N fertilization; NW−: no irrigation, no N fertilization.
Fig. 6.
Visualization of the architectural model outputs for dominant plants of the NW+ and NW− treatments at the end of the summer regrowth (DOY 282). The data shown are for the G− and SF plant parameterizations at two densities (16 and 1600 plants m−2).
Shifts in the mode of N acquisition
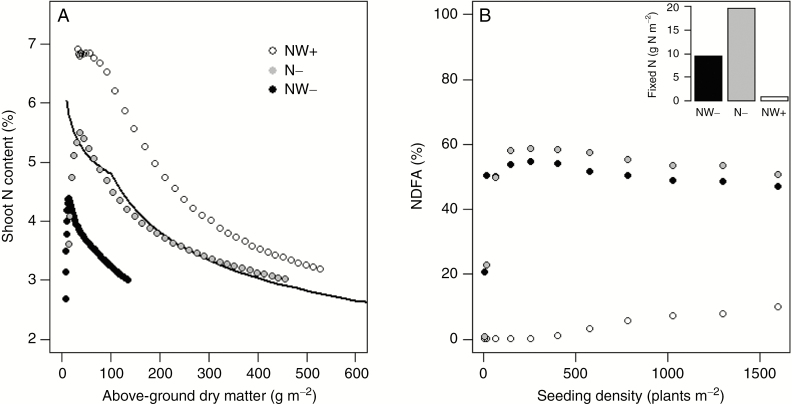
The different managements of water and N in our tests yielded very contrasting results regarding N acquisition and plant N status (Fig. 7). As expected, ample water and N provision led to a mode of N acquisition dominated by soil mineral N absorption (annual NDFA < 8 %) and to plant N status that were non-limiting (i.e. plant and canopy N concentrations above the critical dilution curve), irrespective of plant density and morphotypes. By contrast, N− and NW− treatments quickly required a significant contribution of atmospheric N fixation to sustain plant N nutrition (annual NDFA > 50 % for densities above 100 plants m−2). After the nodule establishment phase, nitrogen fixation was enough to meet crop N requirements in N− but not in NW−. Overall, the rates of nitrogen fixation were close between irrigated and non-irrigated treatments, but the amounts of nitrogen fixed and the plant N-status were much lower under dry conditions. This physiological plasticity was consistent with previous reports made on various legume crops (Danso et al., 1987; Gastal et al., 2015). Although N response parameters were assumed to be identical, different sensitivities to N availability were found between the morphotypes tested, which differentially affected their relative reduction of dry matter production under N- (Table 1). These differences were related to the ability of morphotypes to establish quickly in spring (G+ > G− > SF-RF) in order to take advantage of mineral N mineralization on a longer period and to limit mineral N losses by leaching. At the individual plant level, evidence of a relationship between plant dominance in biomass production and its nitrogen status was found (Fig. S5). The relationship tended to be positive under N-limiting conditions (i.e. larger plants had improved N status), but negative in non-limiting conditions (i.e. larger plants more prone to be N-limited than smaller shaded plants).
Fig. 7.
Relationship between canopy shoot N concentration and dry matter accumulation during the second regrowth (A) and response of annual nitrogen fixation to seeding density as predicted by the model under different resource scenarios (B). The data shown are for the G− plant parameterization. The inset figure represents the annual amounts of nitrogen fixed at 400 plants m−2. NW+: irrigation and N fertilization; N−: irrigation, no N fertilization; NW−: no irrigation, no N fertilization.
Bringing advantages of functional–structural models into IBMs
Overall, the model proved able to bring together interesting properties from both IBMs and functional structural plant models (FSPMs, DeJong et al., 2011). Concerning population dynamics, the model yielded consistent predictions regarding some well-established effects of competition in even-age plant populations. It accounted for the acknowledged effects of plant density on average plant size and its intra-population variation. It could also anticipate a decrease in population size that preferentially affected subordinate plants (Dewar, 1993), mortality in the model resulting from the competition-induced senescence of shoot organs. These patterns were already explained by much simpler phenomenological IBMs able to make competition for idealized resources explicit (Lomnicki, 1988; May et al., 2009, Lin et al., 2014). Most quantitative models, however, ignore plant-to-plant interactions and consider inter-individual variability and population dynamics out of their domain of validity. In FSPMs integrating detailed plant structure and plastic responses to the environment, neighbour effects are often simply mediated through the average population density (e.g. Dong et al., 2008; Feng, 2011), local plant density (Cournède et al., 2008; Verdenal et al., 2008) or an average response of all the plants (Evers et al., 2007; Louarn et al., 2008b). Under these ‘average plant’ assumptions, models lack the possibility to account for population dynamics (Uchmański and Grimm, 1996). By solving competition for multiple resources in an explicit 3-D environment and by considering inter-individual variability, our approach could overcome this current limitation of many FSPMs.
In addition, we demonstrated the model’s ability to account for some emerging properties not usually considered by IBMs. As an integrative model of plant C–N functioning, it showed consistent simulated patterns regarding N accumulation, N dilution with plant growth or shifts in the dominant mode of N acquisition (fixation versus mineral N). Furthermore, as it accounted explicitly for the uptake of distinct pools of resources (PAR, water, NO3–, NH4+, atmospheric N2) heterogeneously distributed in time and space, the model handled interactions between above- and below-ground competition without making a priori assumptions on the degree of size-asymmetry in the partitioning of resources between individuals (Schwinning and Weiner, 1998). This feature opens new possibilities to analyse the determinants of size-asymmetry in real plant populations using IBMs, as illustrated from the different behaviours of deep and shallow rooting morphotypes under water stress. Finally, our model brings from FSPMs a capacity to describe shoot and root morphogenesis with generic approaches, as well as plastic responses to the environment at the boundaries of each individual. Consistent syndromes of response were identified for shade avoidance and soil resource limitations regarding critical aspects of plant morphology involved in resource competition (i.e. plant height, plant leaf area, rooting depth, shoot/root ratio). However, all these features remain to be quantitatively assessed against actual plant observations.
From individual plants to plant communities: towards quantitative models for agro-ecology
Only a partial evaluation of the model could be achieved in this study. Nevertheless, some emerging properties of legume populations, such as the slope of the self-thinning line or the size class segregation, actually met values reported from the literature. For instance, Baldissera et al. (2014) reported G values of about 0.2 and 0.5 for first-year alfalfa stands at 50 and 400 plants m−2 under WN+, close to the predicted values reported in Fig. S4. The ceiling values reached for annual dry matter production in dense stands also conformed to the potential of production generally observed on the simulation site for the different morphotypes. In WN+ treatments, alfalfa usually yields a potential 1800–2000 g m−2 in four harvests (Lemaire et al., 1992), whereas WN− ranges between 400 and 1800 g m−2 depending on the year (Durand et al., 1989). The differences of production between morphotypes (G+ > G− > SF, Table 1) also followed a pecking order well established in this area concerning the legume species used for the calibration (red clover > alfalfa > white clover during the establishment year).
These results were obtained from a calibration based simply on the gathering of data from the literature (Table S2), and would require specific determination for each species or cultivar. Given the high number of parameters (about 120), this will be a challenging task. However, not all parameters present the same degree of sensitivity in the model, or the same genetic variability within and between species. In this study, we proposed that morphogenetic parameters were the most determinant in discriminating between different morphogenetic groups of legumes, and assumed similar rates of exchange and similar resource use efficiencies. Although these traits undoubtedly vary, large amounts of experimental evidence suggest that the traits controlling morphogenesis and resource capture present the largest variations (e.g. Enquist et al., 1998), making it a valid initial assumption. Moreover, most of the morphogenetic parameters are accessible to direct measurements on isolated plants (e.g. Pagès et al., 2014 for root morphogenesis; Faverjon et al., 2017 for shoot morphogenesis), some of which are even potentially determined through phenomic approaches (Cabrera-Bosquet et al., 2016; Jeudy et al., 2016). Significant work remains to be done, but the proposed model structure, derived from a potential morphogenesis approach (Lemaire and Millard, 1999), offers the possibility to build up robust parameterizations by gradually integrating the effects of stresses.
An important feature of IBMs is to make plant-to-plant interactions for resources explicit. As a result, no difference is made between conspecifics and neighbours from a different species in the Virtual Grassland IBM. Only their resultant effects on the availability of resources and light signals in space and time matter. This conveys and integrates competition and facilitation effects for multiple resources irrespective of the identity of individuals in the community. One can expect from such a model (1) that the parameters established for a given species or cultivar will not be dependent on the structure of the community and the identity of neighbours, (2) that the complementarity (e.g. use of different N pools) and facilitation effects (e.g. N transfer, Fustec et al., 2010) can be integrated with the same framework as competition, and (3) that ultimately the scaling from individuals to community will be greatly eased. This is especially interesting for grasslands and other legume-based communities that are pivotal in agro-ecology and for which predictive models integrating positive plant–plant interactions have yet to be developed (Gaba et al., 2015). The present contribution represents a first attempt to a generic approach to link the various traits of legumes with their quantitative effects on the functioning of cultivated plant communities.
CONCLUSION
We have presented a comprehensive individual-based model of legume population functioning in response to light, water and N. The proposed approach merges classical IBMs with FSPM and contributes to the development of a quantitative model of grassland communities. The originality of the approach stems from both modelling fields and enables us (1) to introduce robust formalisms of morphological and physiological plasticity in response to a heterogeneous environment in IBMs and (2) to scale up plant models to population and community by considering inter-plant variability, changes in population size and interactions for multiple resources. To achieve this goal, relatively simple geometric representations and C–N allocation formalisms were used that remain to be assessed. This will be done in a follow-up paper where the model will be assessed on a range of experimental grassland communities. We believe this model will be useful in several domains of plant science, and more particularly in agro-ecology to understand the assembly rules of sown grasslands and to identify key traits and management practices favourable to legume persistence and sustainable forage production.
SUPPLEMENTARY DATA
Supplementary data are available at https://academic.oup.com/aob and consist of the following. Table S1: Main adaptive responses to environmental variables included in the model and their schematic representation. Table S2: List of parameter values used and their corresponding references. Table S3: Initial conditions and summary of the input variables used to run the different combinations of pedoclimate and morphotype. Fig. S1: Diagrammatic representation of the plant model functioning in response to model inputs (blue boxes) and environmental models of radiative transfer (yellow box) and soil functioning (brown box). Fig. S2: Visualization of the architectural model outputs for the SF plant parametrization without production of nodal roots. Fig. S3: Response of canopy (A) and average plant dry matter production (B) to seeding density as predicted by the model under different resource scenarios assuming plants were unable to fix atmospheric N. Fig. S4: Effects of different resource scenarios and seeding densities on the size structure of simulated plant populations. Fig. S5: Example of the relationship between plant hierarchical position in the canopy and plant N status during a summer regrowth.
Supplementary Material
ACKNOWLEDGMENTS
This study was supported by the Poitou Charentes Regional Council (Expoleg-AV project; PhD fellowship for L.F.), the Agence Nationale de la Recherche (PRAISE project, ANR-13-BIOADAPT-0015), and INRA’s Environment and Agronomy Division (PhD fellowship for L.F.). The authors would like to thank A. Escobar-Gutiérrez, D. Combes and R. Barillot for their helpful comments on the manuscript.
APPENDIX 1
Description and units of model parameters. Subscripts In, S, P, L, T, FR refer to parameters related to internode, stipule, petiole, leaf blade, taproot and fine root organs, respectively.
| Parameter | Description | Unit |
|---|---|---|
| Plant development and potential morphogenesis of shoots | ||
| Del50 In,S,P,L | Delay for the onset of organ growth after phytomer emergence | phyllochron |
| Del Deb | Delay of axillary bud budburst | phyllochron |
| Del Til | Delay for the start of primary axes production | phyllochron |
| Elmax In,S,P,L | Maximum relative elongation rate for a given organ type | phyllochron−1 |
| L max In,S,P,L | Maximum organ length at the peak of the length profile | m |
| nsh max | Ceiling number of primary shoots for an isolated plant | − |
| nrhizo | n parameter of the binomial law controlling rhizomatous development | − |
| Peak In,S,P,L | Phytomer rank for the peak of organ length | − |
| Phyllo 1 | Phyllochron for the main and primary axes | °Cd |
| Phyllo 2 | Phyllochron for the secondary axes | °Cd |
| prhizo | p parameter of the binomial law controlling rhizomatous development | − |
| q | Shape parameter of the beta function | − |
| R0 In,S,P,L | Phytomer rank for the minimum organ length | − |
| Rini In,S,P,L | Relative organ length at the basis of the length profile | − |
| T base | Thermal time accumulation at the reference temperature | °Cd |
| T min | Minimum temperature at which development occurs | °C |
| T max | Maximum temperature at which development occurs | °C |
| T ref | Fixed reference temperature (20 °C) | °C |
| Tilr | Relative rate of production of new primary axes | per phyllochron |
| Potential root morphogenesis | ||
| αR | Exponent of the allometric relationship between roots and shoots | − |
| βR | Constant of the allometric relationship between roots and shoots | − |
| Alloc FR | Partitioning coefficient between fine roots and perennial taproot | g g−1 |
| D min | Minimum root apex diameter | m |
| D max | Maximum root apex diameter | m |
| Del Nodal | Maturation delay of the nodal root primordia | phyllochron |
| DlDm | Slope of the relationship between parent and lateral root diameters | m m−1 |
| DistRA | Average length from root apex without branching | m |
| Elmax R | Elongation rate of roots at the maximal apex diameter | m °Cd−1 |
| FTSW Nodal | FTSW threshold allowing nodal root emergence | − |
| GDs | Growth duration parameter for roots | °Cd m−2 |
| IBD | Average inter-branch distance | m |
| RTD | Root tissue density | g m−3 |
| Potential growth, water demand and C, N allocation | ||
| ADIL | Critical N concentration of the shoots for a 1 T ha−1 canopy | % |
| BDIL 1,2 | Exponent of the critical dilution curves for isolated and dense plants | − |
| Del FIX | Delay of root system nodulation | phyllochron |
| FIX max | Maximum plant fixation rate | g N g−1 |
| Km 1,2 | Michaelis constants for the HATS and LATS systems | mol m−1 |
| KMAX | Maximum crop coefficient | − |
| LC min In,P | Minimum specific length of the organ | m g−1 |
| LN min In,P | Minimum specific nitrogen length of the organ | m g N−1 |
| %NoptFR, T | Optimal N concentration of root organs | g g−1 |
| %NminT | Minimal N concentration of root organs | g g−1 |
| NODcost | Relative reduction of the RUE for a 100 % fixing plant | − |
| RUE | Whole plant radiation use efficiency for unstressed non fixing plants | g J PAR−1 |
| SLA min | Minimum specific leaf area | m2 g−1 |
| SLN min | Minimum specific leaf nitrogen | m2 g N−1 |
| VMAX 1,2 | Maximum rates of absorption achieved by the HATS and LATS systems | mol m−1 °Cj−1 |
| Responses to light, water and N availability | ||
| FTSW50 process | FTSW value at which a 50 % reduction of a given process occurs | − |
| NNI50 process | NNI value at which a 50 % reduction of a given process occurs | − |
| PAR thresh In,P | Average PAR threshold inducing the minimum organ growth response | mol m−2 s−1 |
| R0 PAR In,P | Intercept of the response of relative organ elongation to daily average PAR | − |
| R0 r:fr In,P | Relative organ elongation rate for a null red/far red ratio | − |
| SENSI r:fr In,P | Slope of the response of relative organ elongation to red/far red ratio | − |
| SENSI1 PAR In,P | Slope of the response of relative organ elongation to daily average PAR | mol−1 m2.s |
| SENSI2 PAR In,P | Slope of the response of relative organ elongation to daily average PAR | mol−1 m2.s |
| SENSI N process | Maximum relative response of a given process to NNI | − |
| SENSI W process | Maximum relative response of a given process to FTSW | − |
| ZETA tresh | ζ threshold inducing a cessation of axis development | − |
| Senescence | ||
| Del sen | Delay for the onset of leaf senescence in the shade | °Cd |
| LDs | Root lifespan parameter | °Cd m−2 g−1 |
| SPAN L | Leaf lifespan for isolated plants | phyllochron |
| Plant geometry | ||
| Elv S,L | Average elevation angle of the organ | ° |
| Elv ini R | Average initial elevation angle of the lateral roots | ° |
| g stem | Tropism parameter for the stem | − |
| g root | Tropism parameter for the roots | − |
| phyllotaxy | Angle of phyllotaxy | ° |
| RSL | Root segment length for lateral root sampling | m |
| SHAPE L | Allometric leaf shape coefficient | − |
APPENDIX 2
Description and units of the main model variables
| Name | Description | Unit |
|---|---|---|
| ABL | Root length with actively growing lateral roots | m |
| ASW | Locally available soil water (within a voxel) | m3 |
| D | Root tip diameter | m |
| Dem | Minimum C demand to achieve potential organ expansion | g |
| DOY | Day of the year | - |
| E | Daily plant transpiration | m3 |
| E canopy | Daily transpiration of the canopy | m3 |
| EL root | Root elongation rate | m °Cd−1 |
| ET 0 | Daily potential evapotranspiration | m3 |
| FTSW | Fraction of transpirable soil water | – |
| fFTSW | Relative response of a process to the plant FTSW | – |
| fNNI | Relative response of a process to the plant NNI | – |
| fPAR | Relative response of a process to the local PAR | – |
| fzeta | Relative response of a process to the local red to far red ratio | – |
| GD | Root growth duration | °Cd |
| gs | Relative transpiration rate | – |
| L | Organ length | m |
| LA | Total plant leaf area | m2 |
| LAI | Canopy leaf area index | m2 m−2 |
| LD | Root lifespan | °Cd |
| MS root | Total plant root dry biomass | g |
| MS shoot | Total plant shoot dry biomass | g |
| MS tot | Total plant dry biomass | g |
| %Ncanopy | Actual nitrogen concentration of the canopy | % |
| %Ncanopycrit | Critical nitrogen concentration of the canopy | % |
| n | Order of a root axis | – |
| N i | Number of phytomers on axis i | – |
| N root | Total plant root N content | g |
| N shoot | Total plant shoot N content | g |
| N tot | Total plant N content | g |
| nbRA | Number of active lateral roots | – |
| NDFA | Proportion of plant nitrogen derived from the atmosphere | – |
| NNI | Plant nitrogen nutrition index | – |
| nsh | Number of primary shoots | Per plant |
| Nsol | Soil mineral N concentration | g N g−1 |
| Nuptake | Plant mineral N uptake | g |
| Nfixation | Plant atmospheric N fixation | g |
| PAR | Photosynthetically active radiation | mol m−2 |
| PAR a | Plant intercepted PAR | J PAR |
| PARsol a | PAR intercepted by soil surface | J PAR |
| QD root | Carbon offer to demand ratio for roots | – |
| rank | Phytomer position from the base of the axis | – |
| RL | Root length | m |
| RUE | Radiation use efficiency | g J PAR−1 |
| T | Meristem temperature | °C |
| TASW | Locally available soil water at field capacity (within a voxel) | m |
| t p | Phyllochronic time | phyllochron |
| TT | Thermal time cumulated from emergence | °Cd |
| VABS | Specific mineral N absorption capacity of roots | mol m−1 |
| Wuptake pot | Soil water available to the plant root system | m3 |
| ζ | Red to far red ratio | – |
APPENDIX 3
Description of the production rules (PR) and symbols used to describe the organogenesis, growth and senescence of plant modules in the L-system. The parameters controlling the application of production rules are indicated in brackets
| Left member | Right member | Condition | Equation | ||
|---|---|---|---|---|---|
| Axiom | : | [RA]CO[B1] | PR1 | ||
| Shoot organogenesis | |||||
| B1 | → | [D][B1] A | Delay of primary branching (DelTil) & Light (ZETAtresh) | PR2 | |
| A | → | In[Nr][B2][S P L]A | Phyllochron (Phyllo1) & Light (ZETAtresh) | PR3 | |
| B2 | → | a | Delay of sylleptic branching (Deldeb) & Light (ZETAtresh) | PR4 | |
| a | → | In[S P L]a | Phyllochron (Phyllo2) & Light (ZETAtresh) | PR5 | |
| D | → | [D]A | Apical dominance removed (cut) | PR6 | |
| Root development | |||||
| RA | → | Rs[Rlb]RA | Root elongation (ElmaxR, Dmax) | PR7 | |
| Rlb | → | Rlap | Distance from apex (DistRA) | PR8 | |
| Nr | → | [RA]CO | Delay (DelNodal) & Favourable rooting zone (FTSWNodal) | PR9 | |
| Organ growth | |||||
| In, S, F, L (t,rank) | → | In, S, F, L (t+1, rank) | Coordination (Del50) & position (R0, Rini) | PR10 | |
| Rlap(t) | → | Rlap(t+1) | Growth duration (GDs) | PR11 | |
| Senescence | |||||
| L, S, P | → | * | Age (SPANL) or prolonged shading (Delsen) | PR12 | |
| In | → | * | All supporting leaves and meristems dead | PR13 | |
| A, a | → | * | Prolonged shading (Delsen) | PR14 | |
| RA, Rs, Rlap | → | * | All supporting shoots dead | PR15 | |
[]: branching symbol; *: deletion of the module; A: apical meristem of a primary shoot axes; a: apical meristem of secondary shoot axes; B1: active bud of the crown; B2: active axillary bud; CO: collar; D: dormant bud of the crown; In: internode; L: leaf blades; Nr: nodal root primordium; P: petiole; RA: primary root apical meristem; Rlap: lateral root; Rlb: lateral root primordium; Rs: root segment; S: stipules.
APPENDIX 4
Description of model equations; units and descriptions of model parameters are detailed in Appendix 1.
| Equation | Number | |
|---|---|---|
| Plant development and potential morphogenesis of shoots | ||
| [1] | ||
| [2] | ||
| [3] | ||
|
|
[4] | |
| [5] | ||
|
if rank ≤ Peako if rank >Peako |
[6] | |
| [7] | ||
| Potential root morphogenesis | ||
| [8] | ||
|
if D ≥ Dmin and root age < GD if D < Dmin or root age ≥ GD |
[9] | |
| [10] | ||
| [11] | ||
|
if RL > DistRA+ if RL > DistRA and RL < DistRA+ if RL ≤ DistRA |
[12] | |
| [13] | ||
| Dry matter production and C allocation | ||
| [14] | ||
| with | [15] | |
| [16] | ||
| [17] | ||
|
|
[18] | |
|
|
[19] | |
| N demand, acquisition and allocation | ||
|
if ≤1 T ha−1 if >1 T ha−1 |
[20] | |
|
|
[21] | |
| [22] | ||
| [23] | ||
|
if tp ≤ DelFix if tp > DelFix |
[24] | |
| [25] | ||
| [26] | ||
| Water demand and acquisition | ||
| [27] | ||
| [28] | ||
| [29] | ||
| Responses to light, water and N availability | ||
| [30] | ||
|
if transmitted PAR > PARtresh if transmitted PAR ≤ PARopt if PARopt > transmitted PAR ≤ PARtresh |
[31] | |
| [32] | ||
| [33] | ||
| [34] | ||
| [35] | ||
| [36] | ||
| [37] | ||
|
|
[38] | |
| [39] | ||
| [40] | ||
| [41] | ||
| Senescence | ||
| [42] | ||
| with Delsenroot(n)=GD(D(n))+LD(D(n)) for a root of order n | [43] | |
LITERATURE CITED
- Allen RG, Pereira LS, Raes D, Smith M. 1998. Crop evapotranspiration – Guidelines for computing crop water requirements. FAO Irrigation and drainage paper 56. Rome: FAO, 300(9), D05109. [Google Scholar]
- Baldissera TC, Frak E, de Faccio Carvalho PC, Louarn G. 2014. Plant development controls leaf area expansion in alfalfa plants competing for light. Annals of Botany 113: 145–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ballaré CL. 1999. Keeping up with the neighbours: phytochrome sensing and other signalling mechanisms. Trends in Plant Science 4: 97–102. [DOI] [PubMed] [Google Scholar]
- Barillot R, Escobar-Gutiérrez AJ, Fournier C, Huynh P, Combes D. 2014. Assessing the effects of architectural variations on light partitioning within virtual wheat–pea mixtures. Annals of Botany 114: 725–737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bélanger G, Gastal F, Lemaire G. 1992. Growth analysis of a tall fescue sward fertilized with different rates of nitrogen. Crop Science 32: 1371–1376. [Google Scholar]
- Belaygue C, Wery J, Cowan A, Tardieu F. 1996. Contribution of leaf expansion, rate of leaf appearance, and stolon branching to growth of plant leaf area under water deficit in white clover. Crop Science 36: 1240–1246. [Google Scholar]
- Berger U, Piou C, Schiffers K, Grimm V. 2008. Competition among plants: concepts, individual-based modelling approaches, and a proposal for a future research strategy. Perspectives in Plant Ecology, Evolution and Systematics 9: 121–135. [Google Scholar]
- Beuselinck PR, Bouton JH, Lamp WO et al. . 1994. Improving legume persistence in forage crop systems. Journal of Production Agriculture 7: 311–322. [Google Scholar]
- Boudon F, Pradal C, Cokelaer T, Prusinkiewicz P, Godin C. 2012. L-Py: an L-System simulation framework for modeling plant development based on a dynamic language. Frontiers in Plant Science 3: 76, doi: 10.3389/fpls.2012.00076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brisson N, Seguin B, Bertuzzi P. 1992. Agrometeorological soil water balance for crop simulation models. Agricultural and Forest Meteorology 59: 267–287. [Google Scholar]
- Brisson N, Launay M, Mary B, Beaudoin N. 2008. Conceptual basis, formalisations and parameterization of the STICS crop model. Versailles: Quae Ed. [Google Scholar]
- Brun F, Richard-Molard C, Pagès L, Chelle M, Ney B. 2010. To what extent may changes in the root system architecture of Arabidopsis thaliana grown under contrasted homogenous nitrogen regimes be explained by changes in carbon supply? A modelling approach. Journal of Experimental Botany 61: 2157–2169. [DOI] [PubMed] [Google Scholar]
- Cabrera-Bosquet L, Fournier C, Brichet N, Welcker C, Suard B, Tardieu F. 2016. High-throughput estimation of incident light, light interception and radiation‐use efficiency of thousands of plants in a phenotyping platform. New Phytologist 212: 269–281. [DOI] [PubMed] [Google Scholar]
- Campbell GS, Norman JM. 1989. The description and measurement of plant canopy structure. In: Russell G, Marshall B, Jarvis PG, eds. Plant canopies: their growth, form and function. Cambridge: Cambridge University Press, 1–19. [Google Scholar]
- Caradus JR. 1977. Structural variation of white clover root systems. New Zealand Journal of Agricultural Research 20: 213–219. [Google Scholar]
- Chabbi A, Kögel-Knabner I, Rumpel C. 2009. Stabilised carbon in subsoil horizons is located in spatially distinct parts of the soil profile. Soil Biology and Biochemistry 41: 256–261. [Google Scholar]
- Chu CJ, Weiner J, Maestre FT, Wang YS, Morris C, Xiao S, ... &Wang G.. 2010. Effects of positive interactions, size symmetry of competition and abiotic stress on self-thinning in simulated plant populations. Annals of Botany 106(4): 647–652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cournède PH, Mathieu A, Houllier F, Barthélémy D, De Reffye P. 2008. Computing competition for light in the GREENLAB model of plant growth: a contribution to the study of the effects of density on resource acquisition and architectural development. Annals of Botany 101: 1207–1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danso SKA, Zapata F, Hardarson G, Fried M. 1987. Nitrogen fixation in fababeans as affected by plant population density in sole or intercropped systems with barley. Soil Biology and Biochemistry 19: 411–415. [Google Scholar]
- DeJong TM, Da Silva D, Vos J, Escobar-Gutiérrez AJ. 2011. Using functional–structural plant models to study, understand and integrate plant development and ecophysiology. Annals of Botany 108: 987–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Den Dulk JA. 1989. The interpretation of remote sensing, a feasibility study. Thesis, University of Wageningen, The Netherlands. [Google Scholar]
- Deng JM, Wang GX, Morris EC et al. . 2006. Plant mass-density relationship along a moisture gradient in north-west China. Journal of Ecology 94: 953–958. [Google Scholar]
- Devienne-Barret F, Justes E, Machet JM, Mary B. 2000. Integrated control of nitrate uptake by crop growth rate and soil nitrate availability under field conditions. Annals of Botany 86: 995–1005. [Google Scholar]
- Dewar RC. 1993. A mechanistic analysis of self-thinning in terms of the carbon balance of trees. Annals of Botany 71: 147–159. [Google Scholar]
- Donald CM. 1951. Competition among pasture plants. I. Intraspecific competition among annual pasture plants. Crop and Pasture Science 2: 355–376. [Google Scholar]
- Dong Q, Louarn G, Wang Y, Barczi JF, De Reffye P. 2008. Does the structure–function model GREENLAB deal with crop phenotypic plasticity induced by plant spacing? A case study on tomato. Annals of Botany 101: 1195–1206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunbabin VM, Postma JA, Schnepf A et al. . 2013. Modelling root–soil interactions using three–dimensional models of root growth, architecture and function. Plant and Soil 372: 93–124. [Google Scholar]
- Durand JL, Lemaire G, Gosse G, Chartier M. 1989. Analyse de la conversion de l’énergie solaire en maitère sèche par un peuplement de luzene (Medicago sativa L.) soumis à un déficit hydrique. Agronomie 9: 599–607. [Google Scholar]
- Enquist BJ, Brown JH, West GB. 1998. Allometric scaling of plant energetics and population density. Nature 395: 163. [Google Scholar]
- Escobar-Gutiérrez AJ, Combes D, Rakocevic M et al. . 2009. Functional relationships to estimate morphogenetically active radiation (MAR) from PAR and solar broadband irradiance measurements: the case of a sorghum crop. Agricultural and Forest Meteorology 149: 1244–1253. [Google Scholar]
- Evers J, Vos J, Fournier C, Andrieu B, Chelle M, Struik PC. 2007. An architectural model of spring wheat: evaluation of the effects of population density and shading on model parameterization and performance. Ecological Modelling 200: 308–320. [Google Scholar]
- Faverjon L, Escobar-Gutiérrez AJ, Litrico I, Louarn G. 2017. A conserved potential development framework applies to shoots of legume species with contrasting morphogenetic strategies. Frontiers in Plant Science 8: 405. doi: 10.3389/fpls.2017.00405 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng L. 2011. Connection between plant community dynamics models and architectural-functional plant models-the GreenLab case. PhD Thesis, University of Montpellier. [Google Scholar]
- Forde MB, Hay MJM, Brock JL. 1989. Development and growth characteristics of temperate perennial legumes. In: Persistence of Forage Legumes. Madison, WI: American Society of Agronomy, 91–110. [Google Scholar]
- Fustec J, Lesuffleur F, Mahieu S, Cliquet JB. 2010. Nitrogen rhizodeposition of legumes. A review. Agronomy for Sustainable Development 30: 57–66. [Google Scholar]
- Gaba S, Lescourret F, Boudsocq S et al. . 2015. Multiple cropping systems as drivers for providing multiple ecosystem services: from concepts to design. Agronomy for Sustainable Development 35: 607–23. [Google Scholar]
- Gastal F, Lemaire G, Durand JL, Louarn G. 2015. Quantifying crop responses to nitrogen and avenues to improve nitrogen-use efficiency. In: Crop physiology–Applications for genetic improvement and agronomy, 2nd edn Academic Press, Elsevier, 161–206. [Google Scholar]
- Gautier H, Měch R, Prusinkiewicz P, Varlet-Grancher C. 2000. 3-D architectural modelling of aerial photomorphogenesis in white clover (Trifolium repens L.) using L-systems. Annals of Botany 85: 359–370. [Google Scholar]
- Gedroc JJ, McConnaughay KDM., Coleman JS. 1996. Plasticity in root/shoot partitioning: optimal, ontogenetic, or both?. Functional Ecology 10: 44–50. [Google Scholar]
- Gibson D, Casal JJ, Deregibus VA. 1992. The effects of plant density on shoot and leaf lamina angles in Lolium multiflorum and Paspalum dilatatum. Annals of Botany 70: 69–73. [Google Scholar]
- Gosse G, Varlet-Grancher C, Bonhomme R, Chartier M, Allirand JM, Lemaire G. 1986. Maximum dry matter production and solar radiation intercepted by a canopy. Agronomie 6: 47–56. [Google Scholar]
- Grimm V, Railsback SF. 2005. Individual-based modeling and ecology. Princeton: Princeton University Press. [Google Scholar]
- Harper JL. 1977. Population biology of Plants. London: Academic Press. [Google Scholar]
- Huston M. 1999. Forest productivity and diversity: using ecological theory and landscape models to guide sustainable forest management. USDA Forest Service Proc. RMRS-P 12: 329–334. [Google Scholar]
- Huston M, DeAngelis D, Post W. 1988. New computer models unify ecological theory. BioScience 38: 682–691. [Google Scholar]
- IUSS Working Group WRB 2006. World reference base for soil resources, 2006. World Soil Resources Report No. 103. Rome: FAO. [Google Scholar]
- Jensen ES, Peoples MB, Boddey RM et al. . 2012. Legumes for mitigation of climate change and the provision of feedstock for biofuels and biorefineries. A review. Agronomy for Sustainable Development 32: 329–64. [Google Scholar]
- Jeudy C, Adrian M, Baussard C et al. . 2016. RhizoTubes as a new tool for high throughput imaging of plant root development and architecture: test, comparison with pot grown plants and validation. Plant Methods 12: 31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Judson OP. 1994. The rise of the individual-based model in ecology. Trends in Ecology & Evolution 9: 9–14. [DOI] [PubMed] [Google Scholar]
- Körner C. 2015. Paradigm shift in plant growth control. Current Opinion in Plant Biology 25: 107–114. [DOI] [PubMed] [Google Scholar]
- Lebon E, Pellegrino A, Louarn G, Lecoeur J. 2006. Branch development controls leaf area dynamics in grapevine (Vitis vinifera) growing in drying soil. Annals of Botany 98: 175–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemaire G, Millard P. 1999. An ecophysiological approach to modelling resource fluxes in competing plants. Journal of Experimental Botany 50: 15–28. [Google Scholar]
- Lemaire G, Khaiti M, Onillon B, Allirand JM, Chartier M, Gosse G. 1992. Dynamics of accumulation and partitioning of N in leaves, stems and roots of lucerne (Medicago sativa L.) in a dense canopy. Annals of Botany 70: 429–435. [Google Scholar]
- Lin Y, Huth F, Berger U, Grimm V. 2014. The role of belowground competition and plastic biomass allocation in altering plant mass–density relationships. Oikos 123: 248–256. [Google Scholar]
- Liu J, Ashton PS. 1995. Individual-based simulation models for forest succession and management. Forest Ecology and Management 73: 157–175. [Google Scholar]
- Loomis RS, Connor DJ. 1992. Crop ecology: productivity and management in agricultural systems. Cambridge: Cambridge University Press. [Google Scholar]
- Lomnicki A. 1988. Population ecology of individuals, Vol. 25 Princeton: Princeton University Press. [Google Scholar]
- Louarn G, Lecoeur J, Lebon E. 2008a. A three-dimensional statistical reconstruction model of grapevine (Vitis vinifera) simulating canopy structure variability within and between cultivar/training system pairs. Annals of Botany 101: 1167–1184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Louarn G, Chenu K, Fournier C, Andrieu B, Giauffret C. 2008b. Relative contributions of light interception and radiation use efficiency to the reduction of maize productivity under cold temperatures. Functional Plant Biology 35: 885–899. [DOI] [PubMed] [Google Scholar]
- Louarn G, Frak E, Combes D, Escobar-Gutiérrez AJ. 2012a. Modelling variations in individual plant productivity within a stand: comparison of top-down and bottom-up approaches in an alfalfa crop. In: Kang M, Dumont Y, Guo Y. eds. IEEE International Conference on Plant Growth Modeling, Simulation, Visualization and Applications (PMA). Shanghai, China: IEEE. pp. 254–261. [Google Scholar]
- Louarn G, Da Silva D, Godin C, Combes D. 2012b. Simple envelope-based reconstruction methods can infer light partitioning among individual plants in sparse and dense herbaceous canopies. Agricultural and Forest Meteorology 166: 98–112. [Google Scholar]
- Louarn G, Escobar-Gutiérrez A, Migault V, Faverjon L, Combes D. 2014. ‘Virtual grassland’: an individual-based model to deal with grassland community dynamics under fluctuating water and nitrogen availability. In: Hopkins A, Collins RP, Fraser MD, King VR, Lloyd DC. The future of european grasslands, Grassland Sci. Eur, Vol. 19, 242–244. [Google Scholar]
- Louarn G, Frak E, Zaka S, Prieto J, Lebon E. 2015. An empirical model that uses light attenuation and plant nitrogen status to predict within-canopy nitrogen distribution and upscale photosynthesis from leaf to whole canopy. AoB Plants 7: plv116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Louarn G, Faverjon L, Migault V, Escobar-Gutiérrez A, Combes D. 2016. Assessment of ‘3-DS’, a soil module for individual-based models of plant communities. In: IEEE International Conference on Functional-Structural Plant Growth Modeling, Simulation, Visualization and Applications (FSPMA), 125–132. doi: 10.1109/FSPMA.2016.7818298 [Google Scholar]
- Maire V, Gross N, Hill D et al. . 2013. Disentangling coordination among functional traits using an individual-centred model: impact on plant performance at intra-and inter-specific levels. PLoS One 8: e77372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matches AG. 1989. Rooting characteristics of legumes. In: Persistence of forage legumes. Madison, WI: American Society of Agronomy, 159–172. [Google Scholar]
- Matthew C, Lemaire G, Hamilton NS, Hernandez-Garay A. 1995. A modified self-thinning equation to describe size/density relationships for defoliated swards. Annals of Botany 76: 579–587. [Google Scholar]
- May F, Grimm V, Jeltsch F. 2009. Reversed effects of grazing on plant diversity: the role of below-ground competition and size symmetry. Oikos 118: 1830–1843. [Google Scholar]
- McConnaughay KDM, Coleman JS. 1999. Biomass allocation in plants: ontogeny or optimality? A test along three resource gradients. Ecology 80: 2581–2593. [Google Scholar]
- Migault V. 2015. Insertion de la morphogenèse racinaire dans L-grass, un modèle structure-fonction de graminées fourragères. PhD Thesis, Université de Poitiers, France. [Google Scholar]
- Monteith J. 1977. Climate and the efficiency of crop production in Britain. Philosophical Transactions of the Royal Society of London 281: 277–294. [Google Scholar]
- Mony C, Garbey M, Smaoui M, Benot ML. 2011. Large scale parameter study of an individual-based model of clonal plant with volunteer computing. Ecological Modelling 222: 935–946. [Google Scholar]
- Naudin C, Corre-Hellou G, Voisin AS et al. . 2011. Inhibition and recovery of symbiotic N2 fixation by peas (Pisum sativum L.) in response to short-term nitrate exposure. Plant and Soil 346: 275–287. [Google Scholar]
- Nicolardot B, Recous S, Mary B. 2001. Simulation of C and N mineralisation during crop residue decomposition: a simple dynamic model based on the C: N ratio of the residues. Plant and Soil 228: 83–103. [Google Scholar]
- Obeid M, Machin D, Harper JL. 1967. Influence of density on plant variation in fiber flax, Linum usitatissimum L. Crop Science 7: 471–473. [Google Scholar]
- Pagès L, Bécel C, Boukcim H, Moreau D, Nguyen C, Voisin AS. 2014. Calibration and evaluation of ArchiSimple, a simple model of root system architecture. Ecological Modeling 290: 76–84. [Google Scholar]
- Pradal C, Dufour-Kowalski S, Boudon F, Fournier C, Godin C. 2008. OpenAlea: a visual programming and component-based software platform for plant modelling. Functional Plant Biology 35: 751–760. [DOI] [PubMed] [Google Scholar]
- Pradal C, Boudon F, Nouguier C, Chopard J, Godin C. 2009. PlantGL: a Python-based geometric library for 3-D plant modelling at different scales. Graphical Models 71: 1–21. [Google Scholar]
- Prusinkiewicz P, Lindenmayer A. 1990. The algorithmic beauty of plants. New York: Springer. [Google Scholar]
- Rademacher C, Neuert C, Grundmann V, Wissel C, Grimm V. 2004. Reconstructing spatiotemporal dynamics of Central European natural beech forests: the rule-based forest model BEFORE. Forest Ecology and Management 194: 349–368. [Google Scholar]
- Riedo M, Grub A, Rosset M, Fuhrer J. 1998. A pasture simulation model for dry matter production and fluxes of carbon, nitrogen, water and energy. Ecological Modeling 105: 41–183. [Google Scholar]
- Ross JK. 1981. The radiation regime and architecture of plant stands. The Hague: Dr. W. Junk Publisher. [Google Scholar]
- Ryle GJA, Powell CE, Gordon AJ. 1981. Patterns of 14C-labelled assimilate partitioning in red and white clover during vegetative growth. Annals of Botany 47: 505–514. [Google Scholar]
- Schwinning S, Parsons AJ. 1996. Interactions between grasses and legumes: understanding variability in species composition. In: Younie D, ed. Legumes in sustainable farming systems, Occasional Symposium - British Grassland Society no. 30. Reading, UK: British Grassland Society, 153–63. [Google Scholar]
- Schwinning S, Weiner J. 1998. Mechanisms determining the degree of size asymmetry in competition among plants. Oecologia 113: 447–455. [DOI] [PubMed] [Google Scholar]
- Sheaffer CC. 1989. Effect of competition on legume persistence. In: Marten GC, Matches AG, Barnes RF, Brougham RW, Clements RJ, Sheath GW, eds. Persistence of forage legume. Madison, WI: American Society of Agronomy, 327–333. [Google Scholar]
- Shinozaki K, Kira T. 1956. Intraspecific competition among higher plants. VII. Logistic theory of the CD effect. Journal of the Institute of Polytechnics of Osaka City University Series D 7: 35–72. [Google Scholar]
- Sinoquet H, Le Roux X, Adam B, Ameglio T, Daudet FA. 2001. RATP: a model for simulating the spatial distribution of radiation absorption, transpiration and photosynthesis within canopies: application to an isolated tree crown. Plant, Cell and Environment 24: 395–406. [Google Scholar]
- Smith H, Whitelam GC. 1997. The shade avoidance syndrome: multiple responses mediated by multiple phytochromes. Plant, Cell and Environment 20: 840–844. [Google Scholar]
- Soussana J, Arregui M. 1995. Impact de l’association sur le niveau de nutrition azotée et la croissance du ray-grass anglais et du trèfle blanc. Agronomie 15: 81–96. [Google Scholar]
- Soussana JF, Maire V, Gross N et al. . 2012. Gemini: A grassland model simulating the role of plant traits for community dynamics and ecosystem functioning. Parameterization and evaluation. Ecological Modelling 231: 134–145. [Google Scholar]
- Stevenson CA, Laidlaw AS. 1985. The effect of moisture stress on stolon and adventitious root development in white clover (Trifolium repens L.). Plant and Soil 85: 249–257. [Google Scholar]
- Strullu L, Beaudoin N, de Cortàzar Atauri IG, Mary B. 2014. Simulation of biomass and nitrogen dynamics in perennial organs and shoots of Miscanthus × giganteus using the STICS model. BioEnergy Research 7: 1253–1269. [Google Scholar]
- Suter M, Connolly J, Finn JA et al. . 2015. Nitrogen yield advantage from grass–legume mixtures is robust over a wide range of legume proportions and environmental conditions. Global Change Biology 21: 2424–2438. [DOI] [PubMed] [Google Scholar]
- Thomas H, Stoddart JL. 1980. Leaf senescence. Annual Review of Plant Physiology 31: 83–111. [Google Scholar]
- Thomas RG. 2003. Comparative growth forms of dryland forage legumes. In: Legumes for dryland pastures. Proceedings of a New Zealand Grassland Association symposium, Lincoln University, 18–19. [Google Scholar]
- Thomas RG, Hay MJM, Newton PCD. 2002. A developmentally based categorization of branching in Trifolium repens L.: influence of nodal roots. Annals of Botany 90: 379–389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Travis RL, Reed R. 1983. The solar tracking pattern in a closed alfalfa canopy. Crop Science 23: 664–668. [Google Scholar]
- Thornley JH, Johnson IR. 1990. Plant and crop modeling: A mathematical approach to plant and crop physiology. New York: Oxford University Press. [Google Scholar]
- Uchmański J. 1985. Differentiation and frequency distributions of body weights in plants and animals. Philosophical Transactions of the Royal Society of London B: Biological Sciences 310: 1–75. [DOI] [PubMed] [Google Scholar]
- Uchmański J, Grimm V. 1996. Individual-based modelling in ecology: what makes the difference?. Trends in Ecology & Evolution 11: 437–441. [DOI] [PubMed] [Google Scholar]
- Vance CP, Heichel GH, Barnes DK, Bryan JW, Johnson LE. 1979. Nitrogen fixation, nodule development, and vegetative regrowth of alfalfa (Medicago sativa L.) following harvest. Plant Physiology 64: 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verdenal A, Combes D, Escobar-Gutiérrez AJ. 2008. A study of ryegrass architecture as a self-regulated system, using functional–structural plant modelling. Functional Plant Biology 35: 911–924. [DOI] [PubMed] [Google Scholar]
- Voisin AS, Gastal F. 2015. Nutrition azotée et fonctionnement agrophysiologique spécifique des légumineuses. In: Scheider A, Huyghe C, eds. Les Légumineuses pour des systèmes agricoles et alimentaires durables. Versailles: Quae, 79–138. [Google Scholar]
- Voisin AS, Salon C, Jeudy C, Warembourg FR. 2003. Symbiotic N2 fixation activity in relation to C economy of Pisum sativum L. as a function of plant phenology. Journal of Experimental Botany 54: 2733–2744. [DOI] [PubMed] [Google Scholar]
- Voisin AS, Cazenave AB, Duc G, Salon C. 2013. Pea nodule gradients explain C nutrition and depressed growth phenotype of hypernodulating mutants. Agronomy for Sustainable Development 33: 829–838. [Google Scholar]
- Volenec JJ, Ourry A, Joern BC. 1996. A role for nitrogen reserves in forage regrowth and stress tolerance. Physiologia Plantarum 97: 185–193. [Google Scholar]
- Weiner J, Solbrig OT. 1984. The meaning and measurement of size hierarchies in plant populations. Oecologia 61: 334–336. [DOI] [PubMed] [Google Scholar]
- Weller DE. 1987. Self-thinning exponent correlated with allometric measures of plant geometry. Ecology 68: 813–821. [Google Scholar]
- Westoby M. 1984. The self-thinning rule. Advances in Ecological Research 14: 167–225. [Google Scholar]
- Willey RW, Heath SB. 1969. The quantitative relationships between plant population and crop yield. Advances in Agronomy 21: 281–321. [Google Scholar]
- White DW, Woodfield DR, Caradus JR. 1998. Mortal: a mutant of white clover defective in nodal root development. Plant Physiology 116: 913–921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoda K. 1963. Self-thinning in overcrowded pure stands under cultivated and natural conditions (Intraspecific competition among higher plants. XI). Journal of Biology, Osaka City University 14: 107–129. [Google Scholar]
- Zaka S, Ahmed LQ, Escobar-Gutiérrez AJ, Gastal F, Julier B, Louarn G. 2017. How variable are non-linear developmental responses to temperature in two perennial forage species?. Agricultural and Forest Meteorology 232: 433–442. [Google Scholar]
- Zhu J, Werf W, Anten NP, Vos J, Evers JB. 2015. The contribution of phenotypic plasticity to complementary light capture in plant mixtures. New Phytologist 207: 1213–1222. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.