Designing oil palm architectural ideotypes for optimal light interception and carbon assimilation through a sensitivity analysis of leaf traits

Abstract

Background and Aims

Enhancement of light harvesting in annual crops has successfully led to yield increases since the green revolution. Such an improvement has mainly been achieved by selecting plants with optimal canopy architecture for specific agronomic practices. For perennials such as oil palm, breeding programmes were focused more on fruit yield, but now aim at exploring more complex traits. The aim of the present study is to investigate potential improvements in light interception and carbon assimilation in the study case of oil palm, by manipulating leaf traits and proposing architectural ideotypes.

Methods

Sensitivity analyses (Morris method and metamodel) were performed on a functional–structural plant model recently developed for oil palm which takes into account genetic variability, in order to virtually assess the impact of plant architecture on light interception efficiency and potential carbon acquisition.

Key Results

The most sensitive parameters found over plant development were those related to leaf area (rachis length, number of leaflets, leaflet morphology), although fine attributes related to leaf geometry showed increasing influence when the canopy became closed. In adult stands, optimized carbon assimilation was estimated on plants with a leaf area index between 3.2 and 5.5 m² m⁻² (corresponding to usual agronomic conditions), with erect leaves, short rachis and petiole, and high number of leaflets on the rachis. Four architectural ideotypes for carbon assimilation are proposed based on specific combinations of organ dimensions and arrangement that limit mutual shading and optimize light distribution within the plant crown.

Conclusions

A rapid set-up of leaf area is critical at young age to optimize light interception and subsequently carbon acquisition. At the adult stage, optimization of carbon assimilation could be achieved through specific combinations of architectural traits. The proposition of multiple morphotypes with comparable level of carbon assimilation opens the way to further investigate ideotypes carrying an optimal trade-off between carbon assimilation, plant transpiration and biomass partitioning.

INTRODUCTION

Great improvement in cereal yield has been achieved since the green revolution by selecting plants adapted to specific agronomic practices (Khush, 2001). This was particularly the case in annual crops for which breeding programmes were designed to select key traits (morphological or physiological) defined through ideotypes (Thurling, 1991; Koester et al., 2014; Dingkuhn et al., 2015). The concept of ideotype (Donald, 1968) relies on the ability to combine traits of interest into an ideal plant to reach a specific purpose (yield potential, product quality) in a given environment. Seeking ideotypes thus relies on investigating how physiological and morphological characteristics affect plant production on the one hand, and the ability to combine the phenotypic traits associated with these characteristics by breeding strategies on the other. Improving the resource use efficiency of plants by changing canopy architecture was one of the most successful strategies used to enhance yield, notably for rice and wheat (Khush, 2001). Plant architecture has thus been a criterion in the definition of ideotype for both annual (Peng et al., 2008) and perennial species (Lauri and Costes, 2005; Cilas et al., 2006).

Light interception efficiency (LIE) has widely been studied since light is the source of energy that plants use to produce biomass (for a review, see Niinemets, 2010). LIE can be defined at the plot scale by estimating the fraction of incident photosynthetically active radiation (PAR) that is intercepted by the canopy (Jørgensen et al., 2003; Rey et al., 2008). The quantity of light intercepted by a plant depends on both the leaf area exposed and plant architecture, i.e. the geometrical and topological organization of plant components (Godin et al., 1999). Several studies have focused on detecting the major architectural attributes that influence light interception at the plant scale based on average leaf irradiance or the silhouette to total area ratio (STAR) (Pearcy et al., 2004; Da Silva et al., 2014). Individual leaf area and leaf angles change light distribution within the plant and, consequently, greatly influence self-shading within the canopy (Falster and Westoby, 2003; Sarlikioti et al., 2011; Chen et al., 2014). The efficiency with which a plant intercepts solar radiation also depends on other architectural characteristics involved in the three-dimensional (3-D) arrangement of leaves, such as internode length (Dauzat et al., 2008; Da Silva et al., 2014; Chen et al., 2014), petiole length (Takenaka, 1994; Chenu et al., 2005) and branching patterns (Niinemets, 2007; Da Silva et al., 2014). Plant architecture subsequently impacts carbon assimilation by altering radiative and thermal conditions within the canopy (Niinemets, 2007). Indeed, light intensity and temperature regulate stomatal conductance, which affects CO₂ uptake and water loss as well as the photosynthesis process (Damour et al., 2010). As a result, a specific spatial distribution of leaves within the canopy that optimizes carbon acquisition is likely to exist (Song et al., 2013; Chen et al., 2014). Modelling approaches have typically been used to estimate light interception (Cerasuolo et al., 2013; Da Silva et al., 2013) and canopy carbon assimilation (Sinoquet et al., 2001; Buck-Sorlin et al., 2011; Sarlikioti et al., 2011; Chen et al., 2014) because these variables are hardly accessible through field measurements.

The development of plant modelling opens new paths to explore plant performances and to assist breeding strategies (Martre et al., 2015). Functional–structural plant models (FSPMs) allow us to investigate the relationships between plant structure and physiological responses by explicitly representing plant architecture (Vos et al., 2010). The development of a FSPM relies on the combination of an architectural model, which virtually describes the 3-D architecture of the plant, with biophysical and physiological models (light interception, photosynthesis, transpiration, C or N allocation). FSPMs are thus valuable tools for dissecting biophysical and architectural traits into their constitutive components (Kang et al., 2014). Sensitivity analyses performed on FSPMs furthermore allow the evaluation of the relative contribution of architectural traits to LIE, either at a given developmental stage (Sarlikioti et al., 2011; Song et al., 2013) or over plant development (Chen et al., 2014; Da Silva et al., 2014). As changes of plant architecture over development affect light interception (Da Silva et al., 2014), particular attention must be paid to the effects of architectural parameters at different developmental stages. Different methods can be applied depending on the precision required to characterize parameter effects, from screening methods (global sorting among a large number of parameters) to quantitative measures of the influences of various parameters (Iooss, 2011; Faivre et al., 2013). Screening methods enable us to qualitatively explore models with large number of parameters while metamodelling approaches allow assessment of model behaviour in response to parameter variations (Saltelli et al., 2004; Storlie and Helton, 2008). The exploration of FSPMs with sensitivity analysis thus constitutes a step forward towards the virtual design of architectural ideotypes.

In this study, we used a FSPM of oil palm (Perez et al., 2016) to explore the impact of plant architecture on LIE (defined as the fraction of incident PAR intercepted by the canopy) and potential carbon acquisition. Oil palm production has continuously increased over the past 50 years through breeding programmes based on fruit yield improvement (bunch production and oil extraction rate) (Corley and Tinker, 2016). In recent years, the genomic resources available for the oil palm (sequencing, resequencing and chip development) have consistently increased, making it now possible to explore the genetic basis of other complex traits (Rival, 2017). Thus far, however, little attention has been paid to the relationships between oil palm architecture and the physiological processes underlying oil palm productivity. The present study proposes to explore alternative ways to improve oil palm performances through the enhancement of LIE for a conventional planting pattern and density. Assuming that oil palm architecture-related traits are heritable, which has already been shown for some architectural characteristics (Billotte et al., 2010; Barcelos et al., 2015; Perez et al., 2016), this study aimed at defining architectural ideotypes based on variables related to light interception and carbon assimilation at the plant scale. Based on a previous study that made it possible to virtually generate 3-D oil palms with a detailed description at the leaf scale (Perez et al., 2016), we tested the impact of different combinations of organ geometry on target integrated traits at the tree scale, light interception and carbon acquisition. Numerical simulations reproduced the light environment in an industrial production system, i.e. accounting for planting pattern and density, and under clear sky conditions. Using variations of palm traits observed on five different oil palm progenies, sensitivity analyses were performed that allowed us to detect the major traits that could be taken into consideration to initiate breeding strategies based on architectural ideotypes.

MATERIAL AND METHODS

Overall strategy

The methodological approach developed in the present study is divided into two consecutive sensitivity analyses. Both analyses explore the behaviour of a FSPM that integrates an architectural model, a light interception model and a photosynthesis model (Supplementary Data Fig. S1). The first sensitivity analysis was a screening method, namely the Morris method (Morris, 1991; Saltelli et al., 2004), which aimed at identifying and hierarchizing the influence of a large number of parameters. This first method enabled us to integrate the dynamics of plant growth and development from field planting to canopy closure. Since progenies may differ slightly in their leaf appearance rate, we performed the analyses over the number of emitted leaves (i.e. an ontogenic stage) instead of plant age. Hence it was possible to analyse the constancy of parameter influence over plant development and to detect the parameters with negligible effect. In the second step, the insensitive parameters were fixed to their mean value and a metamodelling approach was performed at the adult stage for the most influential architectural parameters. The metamodel allowed us to explore model behaviour, i.e with a fine assessment of model responses to changes in each architectural parameter and their interactions. The overall methodological process combined (1) computer programs written in Java for building and visualizing 3-D mock-ups in the AMAPstudio platform (Griffon and de Coligny, 2014) and for simulating light interception on the generated virtual plants on the Archimed platform (http://amapstudio.cirad.fr/soft/archimed/start) with (2) R software scripts (R Core Team, 2015) for sensitivity analyses of model outputs (Fig. S1). Simulations for both sensitivity analyses were run and achieved thanks to the Montpellier Bioinformatics Biodiversity platform (http://mbb.univ-montp2.fr/MBB/index.php).

Architectural model

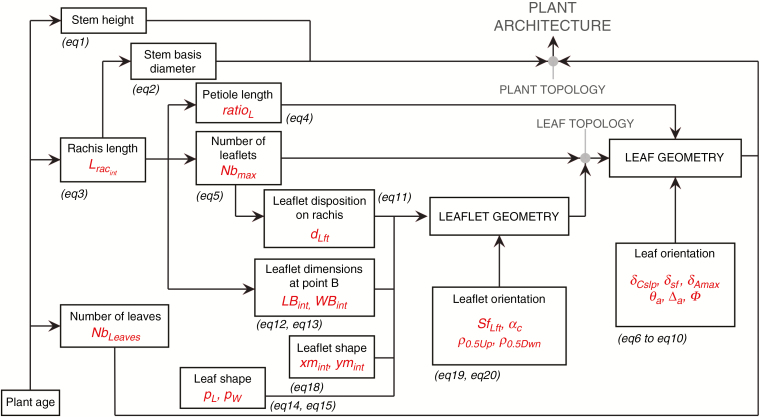
The present study relies on the VPalm model for generating a detailed 3-D architecture of palm trees (Perez et al., 2016; see Supplementary Data Fig. S2). The modelling approach was based on allometric relationships that enabled us to model the geometry of plant components (stem, leaves and leaflets) from spatial and temporal variables (Fig. 1; for detail see the equations in Perez et al., 2016). The model was developed from architectural measurements collected in South Sumatra on five different progenies. One feature of the model is the possibility of modelling inter- and intra-progeny variability through genetically dependent parameters. In the present study we gave attention to the architectural traits that significantly varied between progenies, such as leaf geometry (petiole length, density of leaflets, rachis curvature) and leaflet morphology (gradients of leaflet length and width along the rachis). To limit the number of parameters considered in our study, a unique parameter per allometric relationship was selected when the associated function was composed of several parameters. For each function, the parameter selected was the most variable (most of the time the scaling factor when this existed). Additionally, the ease of interpreting parameter variations was considered. For instance, in a logistic function, the parameter associated with the maximal value of the curve was varying, the two other parameters being fixed to their mean values estimated among all the progenies. Additionally, parameters were selected according to their biological meaning and the feasibility of interpreting their variations (Table 1; see Perez et al. 2016, Table 2, for the complete list of model parameters). Twenty-one parameters were finally selected among which nine were related to leaf and leaflet morphology (Fig. S3), 11 linked to leaves and leaflet orientations (Fig. S2) and a final one associated with the number of expanded leaves composing the crown (Nb_Leaves).

Fig. 1.

Allometry-based approach of the VPalm model with relationships between architectural variables (in black, see Supplementary Data Fig. S2) and the associated parameters (in red) used in sensitivity analysis (see Table 1 for abbreviations). Equation number (eq) refers to the equations presented Table 2 in Perez et al. (2016).

Table 1.

List of architectural parameters. See Fig. S2 for the associated architectural variables.

Parameter	Units	Definition
Crown scale
Nb Leaves	–	Number of green leaves within the crown
δCslp	Degrees rank−1	Evolution of rachis declination angle at point C* along the stem
Φ	degrees	Phyllotaxis
Leaf scale
Lrac int	cm	Rachis length
ratio L	cm cm−1	Ratio of petiole length to rachis length
Nb max	–	Number of leaflets per leaf
δsf	–	Evolution of rachis curvature along the rachis
δAmax	degrees	Declination angle at rachis tip
θa	degrees	Leaf twist at rachis tip
∆a	degrees	Leaf deviation at rachis tip
d Lft	–	Evolution of inter-leaflet distance along the rachis
Leaflet scale
LB int	cm	Leaflets length at point B†
WB int	cm	Leaflet maximum width at point B
p L	–	Relative position of the longest leaflet on rachis
p W	–	Relative position of the largest leaflet on rachis
αC	degrees	Leaflet axial insertion angle at point C
xm int	–	Relative position of maximum width on leaflet
ym int	–	Leaflet shape factor
SfLft	–	Leaflet stiffness
ρ0.5Up	degrees	Leaflet radial insertion angle of upper type leaflets
ρ0.5Dwn	degrees	Leaflet radial insertion angle of lower type leaflets

* Point C represents the transition point on the leaf between the petiole and the rachis.

^† Point B represents the transition point on the rachis where the cross section becomes circular.

Table 2.

Range of values and relative mean deviation (RMD) of model parameters

Parameter	Stage (Σleaves)	min	mean	max	RMD
Crown scale
Nb Leaves	All	35	40	45	0.12
δCslp (degrees rank−1)	All	0.92	1.59	2.64	0.48
Φ (degrees)	All	136	137	139	0.01
Leaf scale
Lrac int (cm)	50	67	91	108	0.23
	100	87	118	141	0.23
	150	114	154	185	0.23
	250	351	472	567	0.23
	350	460	619	743	0.23
	450	486	662	784	0.23
ratio L (cm cm−1)	All*	0.10	0.23	0.39	0.59
Nb max	All*	165	214	255	0.21
δsf	All	–0.17	2.3	7.92	1.04
δAmax (degrees)	All	101	139	177	0.27
θa (degrees)	All	0	17	66	1
∆a (degrees)	All	0	5	33	1
d Lft	All*	1.29	2.32	4.18	0.53
Leaflet scale
LB int (cm)	All*	4.42	30.93	47.28	0.83
WB int (cm)	All*	1.32	2.37	3.84	0.49
p L	All	0.25	0.49	0.85	0.55
p W	All	0.35	0.61	0.85	0.42
αC (degrees)	All	59	87	116	0.33
xm int	All	0.14	0.24	0.40	0.47
ym int	All	0.41	0.59	0.81	0.33
SfLft †	All	1000	5000	10000	0.82
ρ0.5Up (degrees)	All	5	31	67	0.86
ρ0.5Dwn (degrees)	All	–36	–7	–5	0.76

* Parameters used in allometries related to rachis length and subsequently plant stage.

^† Low stiffness (SfLft = 1000) simulates bent leaflets while high stiffness (SfLft = 10 000) simulates erect leaflets.

Estimation of architectural variations over plant development

Measurements of the architectural traits performed in the field (Supplementary Data Fig. S2) were first used to reconstruct 100 mock-ups (20 per progeny), hereafter referred to as ‘representative mock-ups’, to compare them to those generated at an equivalent stage [between 100 and 150 emitted leaves from planting date (Σ_leaves)] in the sensitivity analysis (Morris method). Since those representative mock-ups were directly generated from field measurements, they accounted for the specific correlation between architectural traits of the five studied progenies.

The minimal and maximal values observed for each parameter, independently on progenies, were then estimated to define the range of parameter variations for the sensitivity analyses. Rachis length, number of leaflets, and leaflet length and width were collected on five progenies (25 plants per progeny) at young stages and two other progenies at adult stage. For time-consuming measurements such as leaflet orientation and shape, a unique campaign of measurements was carried out (at plant stage approximately equivalent to 110 emitted leaves) on four plants for the five progenies. The relative range of parameter variations associated with these detailed geometric variables was then used for all the developmental stages studied (Table 2).

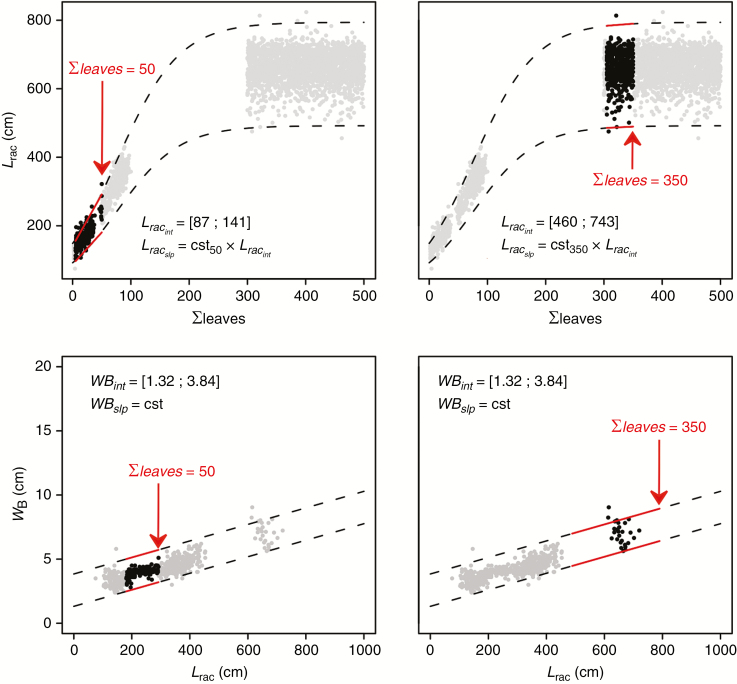
The allometry-based formalism of the VPalm model implies strong dependencies between parameters (Fig. 1). As a result, changes in the range of variation of some parameters constrained the range of variations of others. This was the case for all the parameters involved in the allometric relationships based on rachis length. At each developmental stage, the rachis length of the youngest leaf displaying fully unfolded leaflets at stem top (leaf rank 1; Corley and Tinker, 2016) was estimated from a logistic function of the number of leaves emitted from planting date (Σ_leaves) (Fig. 2). The rachis length of older leaves (rank 2 to Nbleaves) was then modelled as a linear function (parameters Lracint and Lrac_slp; Fig. 2) of leaf rank to keep the linear formalism developed by Perez et al. (2016). At a given stage, the ratio between Lrac_slp and Lrac_int was a constant (cst_Σleaves, Fig. 2) independent of the maximum value of the logistic curve (Lrac_int at 450 emitted leaves), which enabled us to only account for variation of Lrac_int to design different gradients of rachis length within the crown.

Fig. 2.

Parameter range variations (dotted lines) and observations (points) over plant development. Rachis length (Lrac) follows a logistic curve and was modelled as a succession of linear relationships with plant development. Parameters of these linear relationships are the intercept (Lrac_int) and the slope (Lrac_slp), the latter being expressed as a product of Lrac_int and a constant that depends on the stage considered (cst₅₀, cst₁₅₀, …). Leaflet maximum width at point B (W_B) was expressed as a linear function of rachis length (W_B = WBint + Lrac×cst, cst being the average slope fitted against field observations). Solid lines delimit the range for a given age and black points represent the observations carried out at the corresponding age.

For the Morris method, the range of parameter variations was estimated for six stages of development (Σ_leaves = 50, 100, 150, 250, 350, 450, corresponding approximately to 2–15 years after planting) chosen to represent different levels of canopy closure. For the metamodelling analysis, a unique analysis was performed at adult stage (Σ_leaves = 450). Although the model enables the generation of intra-progeny variations, simulations were performed on virtual plots including repetitions of similar 3-D mock-ups in order to better decipher the sensitivity of parameters without dealing with model randomness linked to inter-individual variations.

Radiative balance model

Virtual plants were placed in a plot according to the planting pattern and density used in the experimental site (136 palms ha^–1 spaced one from another by 9.2 m in a quincunx design). To reduce computational time, each simulated plot comprising two replicates of the same plant was virtually duplicated to generate a homogeneous endless plot without border effects. Hence, calculations were performed on the two plants while considering the effect of neighbouring plants on light interception.

Virtual plots were generated in the Archimed platform and the light intercepted by plants in the PAR band was estimated with the MIR model (Dauzat and Eroy, 1997; Dauzat et al., 2008; Rey et al., 2008). Calculations of the irradiance of plant components were performed considering the first order of incident light interception, which represents 90 % of light absorption in oil palm (Corley and Tinker, 2016). Multiple scattering within the palm stand was not considered in our study because it would have drastically slowed the computations. A daily average clearness index (Kt), defined as the ratio of the measured global irradiance to the corresponding irradiance above the atmosphere, was used to simulate radiative conditions (Bristow and Campbell, 1984). Kt was calibrated from daily radiative data collected from 2011 to 2016 in the meteorological station of the studied site (Palembang, Sumatra, 2.99°S), and was fixed to its estimated upper limit (Kt = 0.5) to perform simulation under local optimal conditions (i.e. close to clear sky). Regarding sun positioning and day length, simulations were done for a given day (1 November, 2014; Supplementary Data Table S1), included in the period when detailed architectural measurements were performed. Light interception was simulated every 30 min on every organ of the 3-D mock-ups, each organ being represented by a 3-D mesh. It was thus possible to estimate the distribution of light within the plant canopy, from organ scale to stand scale.

Carbon assimilation model

Irradiance (or photon flux density, PFD), defined as the amount of light intercepted per unit leaf area, was determined for every organ composing the 3-D mock-ups. Irradiance estimated on each leaflet was then combined with a photosynthesis model of C₃ leaves to estimate the carbon assimilation every 30 min, assuming that assimilation from components other than leaflets was negligible. Photosynthesis was modelled using the non-rectangular hyperbola (NRH) curve described as followed (Marshall and Biscoe, 1980; Thornley, 1998):

$$A=\frac{\alpha PFD+A_{max}-\sqrt{{\left(\alpha PFD+A_{max}\right)}^2-4\theta \alpha PFD{A}_{max}}}{2\theta }-Rd$$ (1)

where: A = assimilation (μmol CO₂ m⁻² s⁻¹), PFD = photon flux density or irradiance (μmol photons m⁻² s⁻¹), A_max = maximum assimilation (μmol CO₂ m⁻² s⁻¹), α = photosynthetic efficiency (μmol CO₂ µmol photon⁻¹), θ = flux resistance of CO₂ from the outside of the leaf to the chloroplasts, and Rd = mitochondrial respiration (μmol CO₂ m⁻² s⁻¹)

This model accounts for the non-linearity of photosynthetic response to light conditions. It was parameterized from field gas exchange measurements (GFS 3000 Gas Exchange System, Walz, Germany) conducted in April 2014, on one to two leaves between rank 9 and 17 on eight individuals, under optimal conditions (clear sky and non-limiting water and nutrient supply). Constant conditions (considered as non-limiting for stomatal conductance) were controlled in the gas analyser chamber (temperature: 28 °C, CO₂ concentration: 400 ppm; relative humidity: 70 %) while the intensity of light was progressively changed (PFD from 1600 to 0 µmol photons m⁻² s⁻¹) to draw the response curve of carbon assimilation to light. Since not enough data were available to estimate genetic and leaf rank effects on assimilation, the experimental response curves were pooled together to fit an average NRH curve for all leaves (Supplementary Data Fig. S4). It is noteworthy that the carbon assimilation computed with the NRH function must be considered as a mean potential assimilation since no limiting factors other than light were taken into account in this approach. For all simulations performed in this study, each photosynthetic parameter was fixed to its mean value calibrated with the average NRH curve.

Sensitivity analyses

Model outputs.

LIE was determined as the fraction of incident light intercepted by the canopy over a day (f_PAR) and a light extinction coefficient (k) (Monsi and Saeki, 2005) was derived subsequently (Table 3). Plant mutual shading (MS) was estimated as the difference between the amounts of light intercepted by a single plant in a stand and the amounts intercepted by the same plant in isolated conditions, under similar incident radiation. Daily carbon assimilation (A_d) was finally estimated by integrating the amount of carbon fixed by all leaflets of the plant along the day.

Table 3.

Model outputs

Output	Equation	Variables
Fraction of incident light intercepted	f PAR = PARc/PARi	PARi: Incident PAR above the canopy (MJ day−1 m−2) PARc; PARc intercepted by the canopy (MJ d−1 m−2)
Light extinction coefficient	k = –ln(1–fPAR)/LAI	LAI: leaf area index (m2 m−2)
Mutual shading	MS = (PARisol–PARstand)/PARisol	PARisol: PAR intercepted by the isolated plant (MJ d−1 m−2); PARstand: PAR intercepted by the plant in stand (MJ d−1 m−2)
Daily carbon assimilation	$A_d=\sum _{t = 0}^{24h}\sum _{l = 0}^n$ NRH(PFDt,l)	PFDt,l: irradiance of leaflet l at time t (μmol photons m−2 s−1)
Cumulative light intercepted by the canopy over development	PARcumul = PARc(50leaves)+…+PARc(450leaves)	PARc(Σleaves): PAR intercepted by a plant (MJ d−1 plant−1) at a given developmental stage
Cumulative carbon assimilation over plant development	A cumul = Ad (50leaves)+…+Ad (450leaves)	A d (Σleaves): Daily carbon assimilation of a plant (mol CO2 d−1 plant−1) at a given developmental stage

Morris method.

Replicating a unique individual in a virtual scene rather than dealing with inter-individual variability offered the possibility to run the model in a deterministic way. The factorial screening method of Morris (1991) was used to optimize the number of simulations for integrating the analysis over plant development. The Morris sensitivity analysis is a One at A Time (OAT) method, using discrete parameter values selected in a sampling design (grid) that decomposed each parameter in defined ranges of possible values between a minimal and a maximal value, normalized thereafter between 0 and 1 to make parameter ranges comparable (in our case, each parameter variation was discretized into five normalized values: 0.25, 0.5, 0.75 and 1). To sample this grid, trajectories corresponding to sequences of (n + 1) model runs were chosen at random, n being the number of parameters. The starting point of a trajectory was chosen randomly on the grid. The second point corresponded to a grid jump along one parameter chosen randomly. The next point on the trajectory corresponded to another grid jump (of the same length) along another parameter and so on. As a result a trajectory was composed of successive simulations differing by a unique parameter value, each parameter varying once in a trajectory. A total of 40 trajectories using the same numerical sampling design were explored for each stage of development with the sensitivity package of R software (Pujol et al., 2016). In this way 880 virtual plants (40 trajectories × 22 simulations) with contrasted architecture were followed over six stages of plant development (Supplementary Data Fig. S5), representing a total number of 5280 simulations. Analyses of model outputs (PAR and A_d) were then performed for each date separately and for the whole period, i.e. from 50 to 450 emitted leaves (PAR_cumul and A_cumul, Table 3).

The Morris method enabled us to estimate sensitivity indices for each X_p parameter (p = 1, ..., 21) by evaluating elementary effects due to local changes on the grid. For each trajectory, the difference in output values between two successive simulations, differing from one another by the value of the parameter X_p, allowed us to compute the elementary effect of X_p. The mean value of the 40 elementary effects of the parameter X_p was then calculated to obtain a mean sensitive index μ_p, which represents the mean influence of the parameter X_p on model output. The mean of absolute values of the elementary effects μ*_p (Campolongo et al., 2007) was also used to avoid summing effects of opposite signs. The standard deviation of the elementary effect of the parameter X_p, noted σ_p, indicates if the parameter presents interactions with other parameters and/or if the response of model outputs to changes in X_p is non-linear. Normalized indices (μ_rel, μ*_rel, σ_rel), relative to the most sensitive parameter, were also calculated:

$${\mu }_p{,}_{\text{rel}}={\mu }_p/\text{max}\left(\mu {*}_p\right);\mu {*}_p{,}_{\text{rel}}=\mu {*}_p/\text{max}\left(\mu {*}_p\right);{\sigma }_p{,}_{\text{rel}}={\sigma }_p/\text{max}\left({\sigma }_p\right)$$

Metamodel.

Beyond the global sorting of parameter effects obtained with the Morris method, a second set of simulations was performed to quantify the main effects of parameters and interactions on adult plants (∑_leaves = 450). We decided to focus on the adult stage when crown dimension (length of leaves) is steady over a long period of time (around 15 years) and plants reach their maximal fruit production (Corley and Tinker, 2016). Here, nine parameters were selected based on (1) their impact on model outputs estimated by the Morris method, (2) the ease of calibrating them from field measurements and (3) the previously estimated heritability of the associated architectural traits (Perez et al., 2016). All the other parameters were fixed to their mean value (Table 2). The experimental design was based on orthogonal array-based Latin hypercube (OA-LHS) (Tang, 1993), which enabled us to better explore the space of input parameter values and allowed to estimate parameter interactions. The experimental design was generated from an array of discretized parameter values on which a Latin hypercube sampling (LHS) was applied to generate randomness around the discretized parameter values. The array was designed to allow the estimation of 3^rd order interactions between the nine parameters, with four discretized values per parameter. These chosen criteria required a minimum number of simulations (multiple of 4^{(3 + 1)} = 256). The final design was chosen to be restricted to the available computational time and carried out using the lhs (Carnell, 2016) and planor (Kobilinsky et al., 2016) packages of R, from which 8192 (32 × 256) different combinations of the nine parameters were used to generate 3-D mock-ups.

The metamodelling approach consisted of establishing a simple model (metamodel) linking the 8192 simulation outputs (A_d) and the input parameter values. The choice of designing the metamodel on A_d rather than f_PAR aimed at integrating the saturating nature of the light–photosynthesis relationship. Among metamodelling approaches (Storlie and Helton, 2008), we selected a quadratic polynomial model:

$$A_{d_i}={\theta }_0+\sum _{p=1}^9\sum _{p\text{'}\ne p}\left({\theta }_p{X}_{p,i}+{\alpha }_p{X}_{p,i}^2+{\beta }_{p\text{'}p}{X}_{p^{\text{'}},i}{X}_{p,i}\right)+{\epsilon }_i$$ (2)

where θ₀ represents model intercept, X_p,i the value of the architectural parameter p (p=1, …,9) for plant i, θ_p and α_p model coefficients associated with the parameter p, β_p’p coefficients associated with the interaction between parameters p and p′ (p≠p′) and ε_i the residual error term. Sensitivity indices were computed with the package mtk (J. Wang et al., 2014) according to the coefficient of determination (r²), which indicated the proportion of variance in A_d explained by each of the nine studied parameters, including their interaction. Briefly for each parameter, three polynomial metamodels were estimated: a first one containing all the parameters, a second one with only the parameter of interest and a last one taking into account all the parameters except the former one. Differences in the percentages of explained variations between theses three models permitted to estimate first-order and total sensitivity indices of each parameter.

Identification of ideotypes

From the 8192 simulations used in the second sensitivity analysis, we compared four groups of plants which were discriminated by their capacity to maximize (respectively minimize) light interception (f_PAR) and carbon assimilation (A_d). First, we considered the 30 mock-ups with the highest value of A_d. Since the leaf area index (LAI) greatly influenced f_PAR and A_d, the three other groups of 30 mock-ups, respectively with the lowest values of A_d, the lowest value of f_PAR and the highest value of f_PAR, were selected within the range of LAI observed in the first group. One-way ANOVAs, followed by Tukey’s tests for pairwise comparisons, were conducted to assess which parameters and model outputs were significantly different among the four groups. Some architectural traits at the leaf scale, such as leaf length, average leaf and leaflet area, frequency of leaflets on rachis (FrqLft) and average ratio of leaflet length to leaflet maximal width (LW_ratio) were also compared among groups.

A principal components analysis (PCA) was then performed on values of the nine parameters of the 30 mock-ups with the highest A_d to explore the existence of specific parameter combinations optimizing A_d. The K-means clustering procedure of the R software was processed on the projection values of the PCA to identify distinct groups among the 30 virtual plants. ANOVA and Tukey’s tests were performed to determine which traits were significantly different among the identified groups.

RESULTS

Screening of architectural parameter effects over plant age

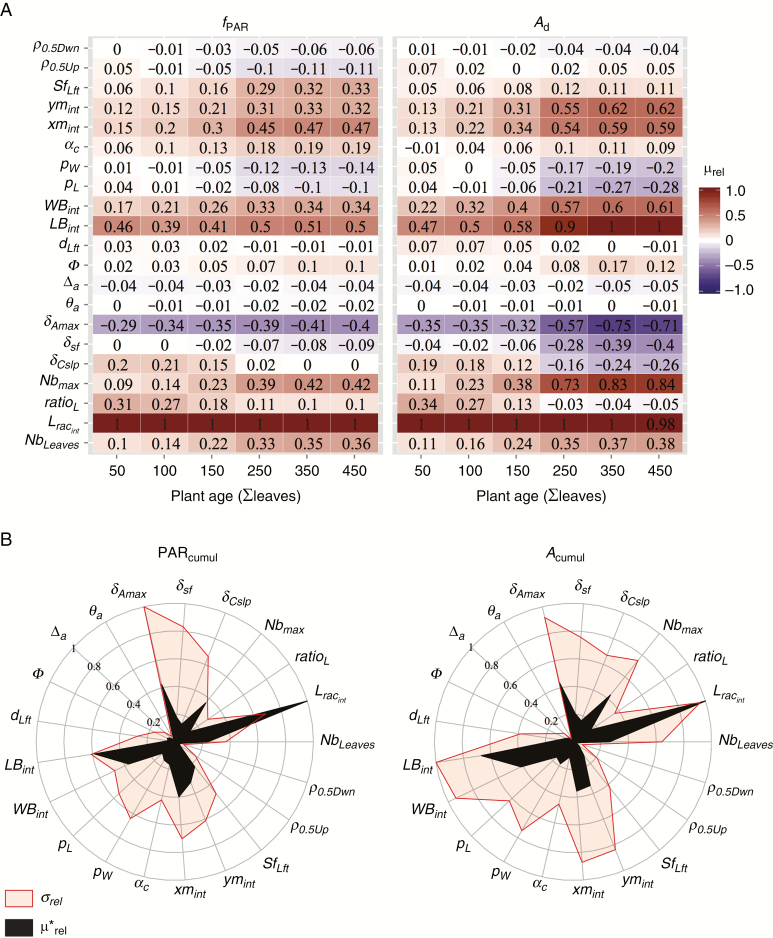
Results of the Morris screening method showed similarities in the ranking of parameter effects over plant development (Fig. 3A and Supplementary Data Fig. S6). The 21 model parameters presented similar effects on both f_PAR and A_d. An increase in leaf and leaflet size-related parameters (Lrac_int, Nb_max, LB_int, WB_int) improved f_PAR and A_d (μ_rel > 0) whereas bent leaves (related to the leaf and leaflet orientation parameters δ_Amax, δ_sf, δ_Cslp, ρ) presented negative effects on the studied variables. The most sensible parameter (μ_rel = 1) over plant development was rachis length (Lrac_int) for both outputs, except for A_d at 450 leaves for which leaflet length (LB_int) had the greatest impact. For f_PAR the elementary effect of Lrac_int was at least twice as strong as any other parameter whereas for A_d, six parameters presented μ_rel > 0.5 (LB_int, WB_int, Nb_max, δ_Amax, xm_int and ym_int). In contrast, rachis twist (θa) and deviation (Δa) had the lowest influence on model outputs at any given developmental stage of the plant. Generally, the relative influence of all parameters increased with plant development stage, particularly for leaflet shape parameters (xm_int and ym_int) and leaf curvature at rachis tip (δ_Amax). Those geometrical attributes affected A_d more than f_PAR (μ_rel > 0.5 for A_d and μ_rel < 0.5 for f_PAR at advanced stages).

Fig. 3.

(A) Heat map of relative mean values of elementary effects (μ_rel) for six stages of plant development, calculated for the fraction of PAR intercepted by the canopy (f_PAR) and carbon assimilation (A_d). Values are given relative to the most sensitive parameter at a given stage. (B) Morris sensitivity indices for cumulated PAR intercepted (PAR_cumul) and cumulated carbon assimilated (A_cumul). Index values are relative to the most sensitive parameter; μ*_rel is the relative absolute mean value of elementary effects.

The ranking for elementary effects was conserved between PAR_cumul and A_cumul, and confirmed that the parameters related to leaf area (Lrac_int, LB_int, WB_int and Nb_max) were the most influential (Fig. 3B). Variations in δ_Amax generated strong variations in output variables, indicating the significant impact of erect leaves to maximize f_PAR and A_d. The highest interactions (σ) were noted for the parameters involved in leaflet morphology (LB_int, WB_int, p_L, p_W, xm_int and ym_int) and leaf geometry (δ_Amax, δ_sf and δ_Cslp) (Fig. 1).

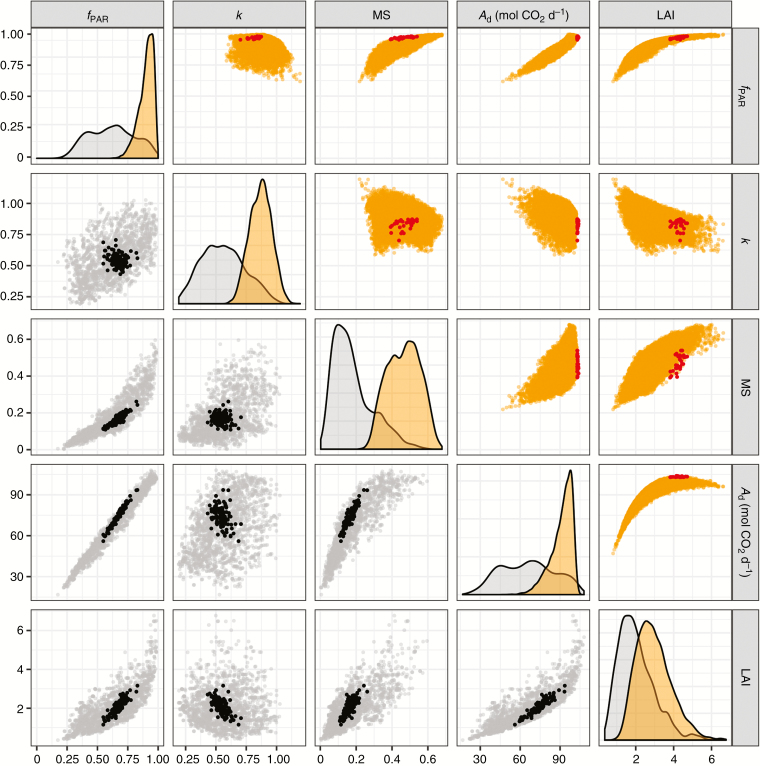
Variations of model outputs for simulated mock-ups and field representative mock-ups

Figure 4 (bottom left plots) presents the dispersion of output variables, estimated either on the mock-ups used for the Morris sensitivity analysis (thereafter called simulated mock-ups) or on the 100 representative mock-ups (100 ≤ Σ_leaves ≤ 150). The simulated mock-ups exhibited a greater range of variation than the representative mock-ups for all the variables studied. All output variables estimated for the representative mock-ups exhibited roughly linear relationships with LAI, suggesting that the traits related to LAI largely affected these variables, at least at these developmental stages. Simulated mock-ups did not highlight a clear threshold value with increasing LAI for MS, contrary to f_PAR and A_d. The relationship between f_PAR and A_d for the representative mock-ups revealed a clear linear pattern, which indicated a constant light use efficiency (LUE, estimated through the slope of this linear relationship) at different levels of interception. Interestingly, LUE tended to be higher for the representative mock-ups than the average LUE estimated for the simulated mock-ups. High correlations were observed between MS, f_PAR and A_d for the representative mock-ups while simulated mock-ups exhibited a plateau in f_PAR and A_d with increasing MS (and LAI), showing the impact of neighbourhood plants on LIE and assimilation.

Fig. 4.

Scatter plots of model output variables estimated from the simulations generated in the Morris method (bottom left plots; grey points) and the metamodelling approach (top right plots; orange points). Plots on the diagonal represent the density plot of output variables (grey: Morris simulations; orange: metamodel simulations). Black points represent the outputs estimated for the 100 representative mock-ups and red points represent the outputs estimated for the 30 mock-ups with the highest values of A_d.

Sensitivity analysis of adult stands

The 8192 mock-ups were generated by varying the eight most influential parameters identified using the Morris method (Lrac_int, Nb_leaves, LB_int, WB_int, Nb_max, ym_int, xm_int and δ_Amax) plus the ratio of petiole length to rachis length (ratio_L), which was identified as the most heritable trait among the five progenies (Perez et al., 2016). The outputs f_PAR, k, MS and A_d were significantly higher than those obtained for the Morris analysis since mock-ups were generated at a later development stage (Fig. 4). Similar patterns in the relationships between output variables were observed in comparisons with the simulation performed for the Morris method, with stronger limitations on f_PAR and A_d due to higher LAI and MS.

A _d increased with LAI until reaching a maximum value of 103 mol CO₂ day⁻¹ per plant and slightly decreased when LAI reached extreme values. Interestingly, the mock-ups with the highest values of A_d (quantile > 95 %) only differed from each other on a maximum of 3.3 mol CO₂ d^–1 whilst they presented variations in LAI between 3.2 and 5.5 m² m⁻².

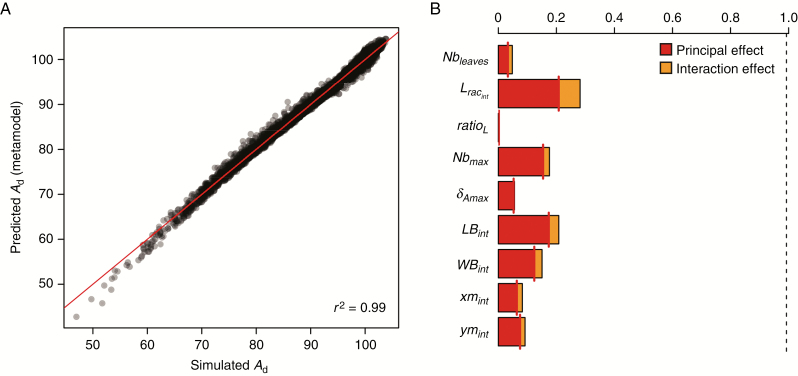
Predictions in A_d from the metamodel were consistent with A_d estimated from the mock-ups, as 99 % of its variability was explained by the metamodel (Fig. 5A and Supplementary Data Table S2). A low bias was observed for values of A_d lower than 65 mol CO₂ d⁻¹, which nevertheless represented less than 1 % of the simulated mock-ups. Variance decomposition allowed ranking the effect of each parameter according to its influence on A_d. The most influential parameters were Lrac_int, which represents 20.7 % of the total variance, followed by LB_int (17.3 %), Nb_max (15.4 %) and WB_int (12.4 %). Interaction effects represented less than 10 % of the variations for each parameter, Lrac_int being the parameter that interacted the most with the others (7 %). These results were consistent with the results of the Morris method at Σ_leaves = 450, but some discrepancies in the ranking of parameters were observed, mainly for the relative effect of δ_Amax, which was lower with the metamodel. In contrast to the Morris approach, the low contribution of δ_Amax to the total variance could be explained by high-order interactions with other parameters related to leaf curvature (δ_Cslp and δ_sf) that were not considered in the metamodelling approach.

Fig. 5.

(A) Quality of metamodel predictions of A_d (red line is the 1: 1 line). (B) Relative contribution of the nine architectural parameters to variation of A_d based on the polynomial metamodel (degree 2). The dotted line indicates the total variation explained by the metamodel.

Ideotyping architectural traits with regard to carbon assimilation

Within LAI values ranging from 3.8 to 4.7 m² m⁻², contrasted leaf geometries were observed between plants selected for their highest A_d, their highest f_PAR, their lowest A_d or their lowest f_PAR (Table 4). Plants maximizing f_PAR and plants maximizing A_d were both characterized by their low values of ratio_L and δ_Amax, i.e. erect leaves with small petiole. A focus on the 30 mock-ups having the highest f_PAR highlighted the importance of leaf area, since the highest values of LAI, individual leaf and leaflet area were found for this group. For these mock-ups, the parameter xm_int, used for modelling leaflet shape, was also high in comparison with the three other groups.

Table 4.

Comparison of parameters, response variables and composite traits for the 30 mock-ups with the highest and the 30 mock-ups with the lowest values of f_PAR and A_d for LAI varying between 3.8 and 4.7 m² m⁻²

Variable	Lowest fPAR	Highest fPAR	Lowest Ad	Highest Ad
Parameters
Nb Leaves	41 ± 3b	42 ± 2ab	43 ± 2a	41 ± 2b
Lrac int (cm)	641 ± 87b	739 ± 33a	755 ± 27a	585 ± 69c
ratio L	0.29 ± 0.07a	0.23 ± 0.08b	0.29 ± 0.06a	0.18 ± 0.06b
Nb max	228 ± 25b	216 ± 24bc	208 ± 25c	244 ± 7a
δAmax (°)	172 ± 3a	114 ± 9b	169 ± 5a	117 ± 13b
LB int (cm)	36 ± 7ab	32 ± 10bc	28 ± 11c	41 ± 6a
WB int (cm)	3.19 ± 0.64a	3.06 ± 0.50ab	2.72 ± 0.64b	3.41 ± 0.30a
xm int	0.26 ± 0.08b	0.32 ± 0.05a	0.28 ± 0.06b	0.27 ± 0.07b
ym int	0.67 ± 0.11ab	0.63 ± 0.10ab	0.61 ± 0.11b	0.68 ± 0.08a
Model outputs
LAI	3.94 ± 0.09c	4.59 ± 0.08a	4.03 ± 0.19c	4.27 ± 0.22b
f PAR	0.93 ± 0.01 d	0.98 ± 0.00a	0.95 ± 0.01c	0.97 ± 0.01b
MS	0.50 ± 0.05b	0.61 ± 0.02a	0.59 ± 0.03a	0.47 ± 0.04c
k	0.68 ± 0.03d	0.89 ± 0.02a	0.74 ± 0.03c	0.83 ±^0.04b
A d (mol CO2 d−1)	97 ± 2.5c	100 ± 0.9b	94 ± 0.5d	103 ± 0.3a
Composite traits
Petiole length (cm)	181 ± 42b	166 ± 61b	221 ± 47a	102 ± 26c
Leaf length (cm)	822 ± 100c	904 ± 67b	976 ± 54a	687 ± 57d
Individual leaf area (m2)	7.11 ± 0.61b	8.03 ± 0.54a	6.96 ± 0.50b	7.70 ± 0.53a
FreqLft (leaflets cm−1)	0.36 ± 0.07b	0.29 ± 0.04c	0.28 ± 0.03c	0.42 ± 0.05a
Individual leaflet area (cm2)	316 ± 44b	376 ± 43a	338 ± 41b	316 ± 20b
LW ratio (cm cm−1)	12.0 ± 4.4a	10.9 ± 4.3a	11.3 ± 6.0a	12.0 ± 2.1a

Superscript letters correspond to significant differences between the four groups (Tukey’s test, P < 0.05).

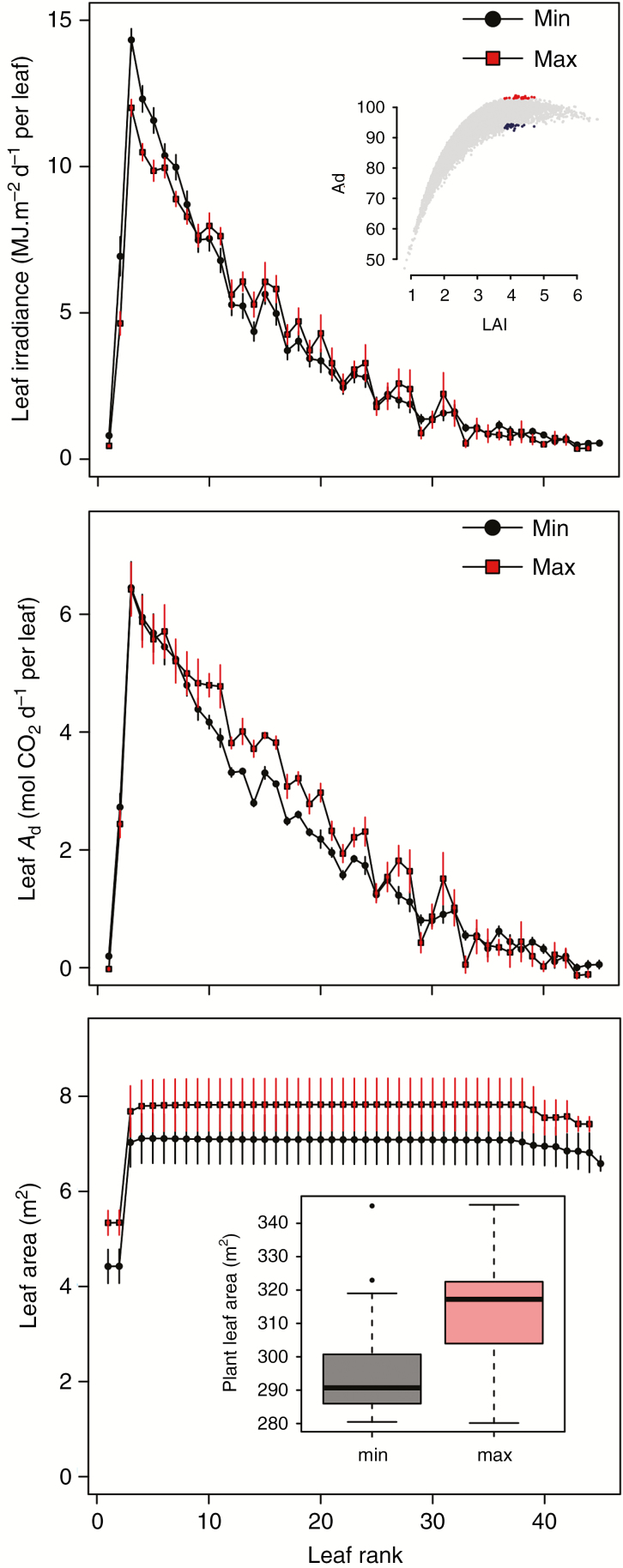
Plants maximizing A_d exhibited the lowest values of mutual shading, mainly due to short rachis and petiole leading to low values of leaf length (= 687 cm). Even if those plants presented the shortest leaves, they also exhibited the highest number of leaflets along the rachis (Nb_max = 244 leaflets and FrqLft = 0.42 leaflets per cm of rachis) and the longest leaflets (LB = 41 cm), contributing to important leaf area. All architectural parameters were significantly different between the groups of mock-ups with the highest values of A_d and the group with the lowest values of A_d, mainly declination angle at rachis tip (i.e. more erect leaves), which was lower for mock-ups having a high A_d (δ_Amax = 117°) than for mock-ups having a low A_d (δ_Amax = 169°). At the leaflet scale, plants that maximized A_d presented longer and narrower leaflets (L = 41, LW_ratio = 12.1) than plants with low A_d (L = 28, LW_ratio = 11.3). A contrasted distribution of light interception and assimilation within the crown was also observed between the two groups (Fig. 6). In both cases, leaf irradiance and assimilation decreased sharply with leaf rank (except for the unfolded leaves; leaf rank < 2). The increase in A_d for the plants with the highest A_d mainly resulted from higher leaf area with higher irradiance from rank 9 to 30. Although plants with the lowest A_d presented less leaf area on the top of the crown, irradiance on the lower leaves was not higher than for plants with the highest A_d. Conversely, plants maximizing A_d presented higher leaf area in the upper leaves without limiting irradiance in the lower leaves, hence leading to a more uniform distribution of irradiance within the crown and an enhanced total assimilation.

Fig. 6.

Daily leaf irradiance (top), daily assimilation (middle) and leaf area (bottom) for the 30 mock-ups with the highest and the lowest values of A_d for a given LAI range varying from 3.8 to 4.7 m² m⁻².

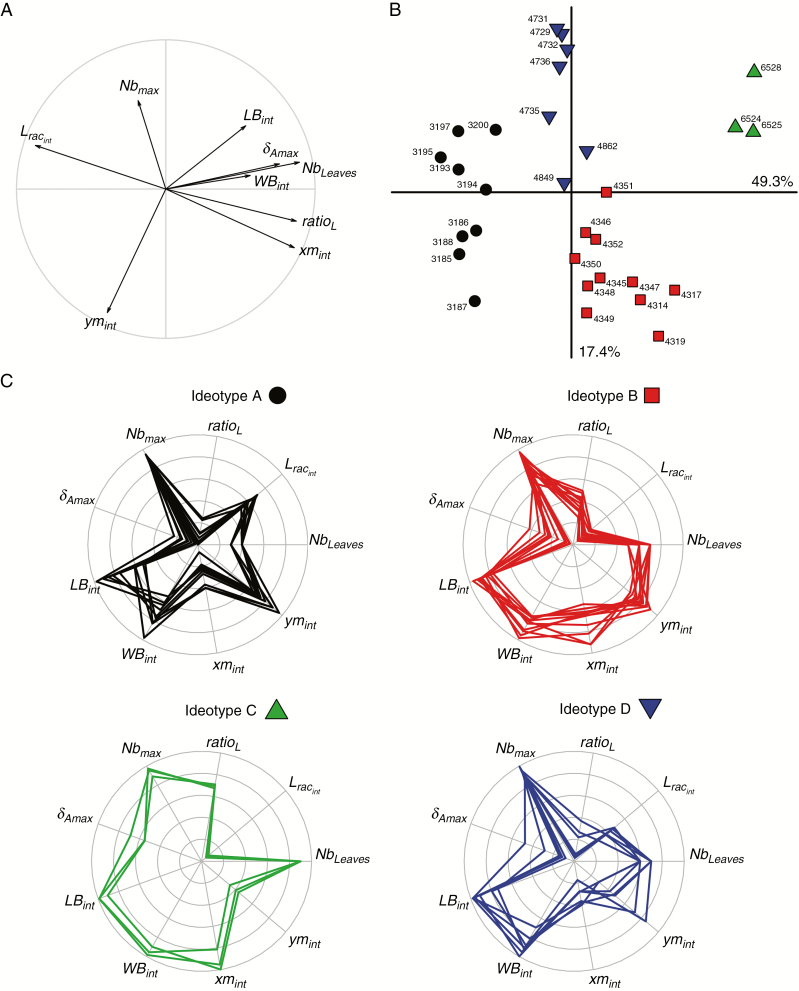
The first two principal components of the PCA performed on the values of the nine studied parameters explained 67 % of the total variance observed on the 30 mock-ups having the highest A_d. The first component was positively correlated to Nb_leaves, ratio_L, xm_int and δ_Amax and negatively correlated to Lrac_int. The second component explained 17 % of the variance and was negatively correlated to ym_int and positively correlated to Nb_max (Fig. 7A). The projection of the 30 mock-ups on the first two components of the PCA and the clustering analysis discriminated four groups of virtual plants, hereafter designed as ideotypes (Fig. 7B, C).

Fig. 7.

Principal components analysis (PCA) of the nine architectural parameters of the 30 mock-ups with the highest value of A_d. (A) Projection of the nine parameters on the two first axes of the PCA. (B) Projection of the 30 mock-ups on the two first axes of the PCA. Cluster analysis based on the two first components of the PCA revealed four contrasted ideotypes. (C) Radial plots of the relative parameter values of the 30 mock-ups classified in the four ideotypes identified from the cluster analysis.

The first group (ideotype A) was characterized by a significantly lower number of leaves, a longer rachis and leaves with shorter petiole (Table 5 and Fig. 8). Ideotype A also exhibited the shortest and the narrowest leaflets but, interestingly, significantly higher leaflet area than other ideotypes, probably due to the combination of high values of ym_int and low values of xm_int. Ideotype B displayed significantly shorter leaves than the other ideotypes. Ideotype C was characterized by the highest number of leaves with long petiole and the shortest rachis. Ideotype C also presented bent leaves at rachis tip (highest value of δ_Amax) and a high density of leaflets on the rachis (highest value of FrqLft). The last ideotype (ideotype D) had intermediate rachis length with short petiole, and narrow leaflet (low values for both xm_int and ym_int).

Table 5.

Comparison of parameters, response variables and composite traits of the four indentified ideotypes

Variable	Ideotype
	A	B	C	D
Parameters
Nb Leaves	39 ± 1c	41 ± 1b	44 ± 0a	41 ± 1b
Lrac int (cm)	670 ± 20a	523 ± 17c	505 ± 5c	608 ± 20b
ratio L	0.13 ± 0.02c	0.21 ± 0.02b	0.30 ± 0.01a	0.14 ± 0.04c
Nb max	246 ± 4a	239 ± 9a	250 ± 4a	247 ± 4a
δAmax (°)	110 ± 5b	115 ± 10b	146 ± 6a	116 ± 11b
LB int (cm)	36 ± 7b	42 ± 3a	46 ± 2a	43 ± 4a
WB int (cm)	3.2 ± 0.3b	3.4 ± 0.2ab	3.7 ± 0.1a	3.5 ± 0.3a
xm int	0.21 ± 0.03c	0.32 ± 0.03b	0.38 ± 0.02a	0.22 ± 0.02c
ym int	0.72 ± 0.04a	0.73 ± 0.03a	0.57 ± 0.02b	0.61 ± 0.08b
Model outputs
LAI	4.36 ± 0.19a	4.08 ± 0.18b	4.40 ± 0.09a	4.40 ± 0.15a
f PAR	0.976 ± 0.00a	0.966 ± 0.01b	0.961 ± 0.01b	0.974 ± 0.01a
MS	0.52 ± 0.01a	0.43 ± 0.03c	0.45 ± 0.01bc	0.49 ± 0.02ab
k	0.85 ± 0.02a	0.83 ± 0.03a	0.74 ± 0.03b	0.83 ± 0.04a
A d (mol CO2 d−1)	103 ± 0.2a	103 ± 0.4a	103 ± 0.0a	103 ± 0.2a
Composite traits
Petiole length (cm)	86 ± 16c	110 ± 13b	152 ± 4a	87 ± 23c
Leaf length (cm)	757 ± 24a	633 ± 27c	657 ± 8bc	695 ± 25b
Individual leaf area (m2)	8.30 ± 0.36a	7.24 ± 0.29c	7.33 ± 0.15bc	7.79 ± 0.20b
FreqLft (leaflets cm−1)	0.37 ± 0.01d	0.46 ± 0.03b	0.49 ± 0.01a	0.41 ± 0.02c
Individual leaflet area (cm2)	338 ± 15a	303 ± 14b	294 ± 11b	315 ± 7b
LW ratio (cm cm−1)	11.6 ± 3.5a	12.2 ± 1.0a	12.3 ± 0.2a	12.3 ± 1.8a

Superscript letters correspond to significant differences between ideotypes (Tukey’s test, P < 0.05).

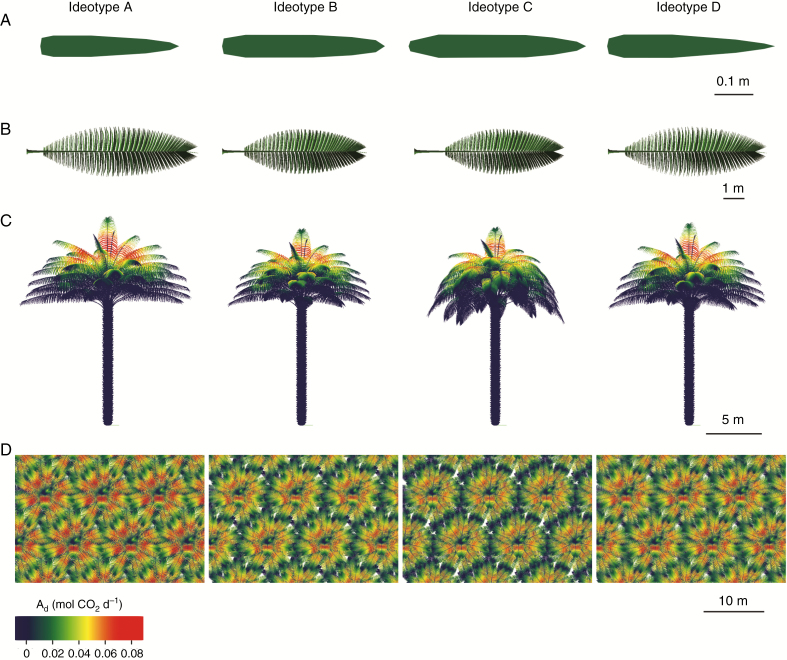
Fig. 8.

Virtual representation of architectural characteristics of the four defined ideotypes at the leaflet, leaf, plant and plot scale. Each 3-D mock-up was generated from the mean values of the parameters associated with the mock-ups classified per ideotype (Fig. 7C). (A) Top view of a leaflet at point B (flattened for better visualization). (B) Top view of a leaf (flattened for better visualization). (C) Lateral view of plants with daily assimilation per plant component. (D) Top view of plant crowns in homogeneous stands with daily assimilation per plant component.

Although the four ideotypes were comparable in terms of potential A_d, dissimilarity in LAI, f_PAR, MS and k was observed (Fig. 4 and Table 5). For ideotypes A and D, leaves strongly inter-penetrate between neighbouring plants due to rather high crown diameters (resulting from the combination of the three parameters ratio_L, Lrac_int and δ_Amax) (Fig. 8D). This led to shaded rachis tips and overall higher values of mutual shading than for the two other ideotypes. Ideotype B showed the lowest value of LAI, f_PAR and MS whereas ideotype C presented a significantly lower value of k than the other ideotypes, as a consequence of a relatively important LAI (4.40 m² m⁻²) with a relatively low f_PAR (0.96).

When focusing on the profile of light distribution and assimilation for the four ideotypes maximizing assimilation (Supplementary Data Fig. S7), different strategies to optimize assimilation were highlighted. Ideotype A improved assimilation by exposing more leaf area and subsequently intercepting more light in the upper leaves, while ideotypes B and C clearly improved total assimilation with higher irradiance on the lower leaves. As a result, even if ideotypes B and C exposed less leaf area, a better distribution of light within the crown enabled them to reach a total assimilation equivalent to ideotype A. Finally, ideotype D represented an intermediate strategy with intermediate values of leaf area and irradiance.

DISCUSSION

Designing an architectural ideotype for oil palm

Our study illustrates the interest in using FSPMs in combination with sensitivity analysis to discriminate the influence of explicit architectural traits on processes involved in plant performance (Da Silva et al., 2014; Streit et al., 2016). The originality of the proposed approach was to perform simulations at different developmental stages and under agronomic conditions with particular planting density and pattern, hence considering the effect of neighbouring plants on the radiative environment.

Globally, the ranking of parameter sensitivity was constant over plant development, suggesting that the most interesting architecture at young age should be the most interesting at the adult stage. Nevertheless, leaflet shape parameters (LB_int, WB_int, xm_int and ym_int), and the parameter associated with leaf structure (Nb_max) and curvature at the rachis tip (δ_Amax) had a greater effect (relative to the most sensitive parameter) over plant development (Fig. 3A). This suggests that a rapid establishment of leaf area is critical at the young stage to increase light interception (Richter et al., 2010), while under high LAI, when the canopy becomes closed, other attributes related to leaf and leaflet arrangement within the crown have a greater influence on light capture by changing light distribution within the crown. The combination of all these traits participated in limiting foliage aggregation (clumping), which has been shown to decrease LIE in stands (Parveau et al., 2008; Cerasuolo et al., 2013; N. Wang et al., 2014).

In this study we considered assimilation rather than light interception as a criterion for designing ideotypes since it accounted for the saturating effect of light on photosynthesis (Song et al., 2013). The comparison between plants with the highest and the lowest assimilation (Fig. 6 and Table 4) reflects the compromise plants must achieve to increase their carbon acquisition: expanding the area of photosynthetic surfaces increases mutual and self-shading; alternatively, decreasing leaf area can lead to a large proportion of the leaf surface being exposed to full sun at saturating values. Interestingly, plants that maximized assimilation maintained a large individual leaf area while neither increasing mutual shading nor decreasing irradiance on the lower leaves. This finding reflects that the best compromise is obtained when light is more evenly distributed within the crown.

The four ideotypes presented LAI varying between 3.8 and 4.7 m² m⁻², which was consistent with LAI estimated in cultivated stands (Barcelos et al., 2015; Corley and Tinker, 2016), but these discrepancies in LAI values did not imply different values of A_d. This emphasized two different strategies to enhance assimilation at the plant scale, either by maximizing leaf area exposed to non-saturating light for photosynthesis or by limiting leaf area while enhancing the distribution of light within the crown and thus limit self-shading (Supplementary Data Fig. S7). Our simulations consistently illustrated that erect leaves (low δ_Amax) are used to avoid light-saturated photosynthesis in the upper leaves and allow light penetration toward lower leaves, thereby reducing the proportion of leaf area with low irradiance (Falster and Westoby, 2003; Zhu et al., 2010; Reynolds et al., 2012). Similarly, long and narrow leaflets (high LW_ratio) enhanced carbon assimilation with a better distribution of light within the plant, which was consistent with results obtained in other species (tomato: Sarlikioti et al., 2011; Chen et al., 2014, pine: Streit et al., 2016).

Viability, benefits and limitations of the modelling approach

The close interactions between parameter effects pointed out by the Morris method (σ) and by the metamodel (Figs 3 and 5) were probably associated with the allometric-based formalism of the model (Fig. 1). The estimated interaction indices were higher for assimilation than for light interception, probably due to the non-linear response of carbon assimilation to leaf irradiance (NRH model), which was confirmed by the low interaction effects estimated by the metamodel approach. A crucial point of the analysis was the study of the effect of architectural parameters over plant development. However, the dynamics of plant growth (modelled through rachis length evolution over plant development) was only tested in a homothetic way (i.e. the plants with highest rachis length in the young stage were those with the highest rachis length at the adult stage; Fig. 2). In fact, too many simulations would have been required to integrate additional developmental trajectories.

Although the allometrically based formalism of VPalm imposed specific ranges on parameter variations, correlations between traits were not taken into account in the sensitivity analyses. As a result, we explored wider architectural possibilities but the extreme values of LAI (<2 and >7 m² m⁻²) obtained in our virtual experiment are probably unrealistic. Further numerical experiments are needed to include constraints between parameter values in order to better ensure potential phenotypes (Picheny et al., 2017).

The NRH carbon assimilation model was chosen in this study because its relative simplicity offered the possibility to reduce computational time. Since simulations were done under optimal field conditions for carbon assimilation, estimated A_d in the present paper must be considered as potential assimilation. Among the various processes that can reduce carbon assimilation, the most important is the stomatal conductance (g_s), which is very sensitive to vapour pressure deficit (VPD) in oil palm (Dufrêne and Saugier, 1993). Moreover, potential photosynthetic capacity is likely to depend on genetic origin (Lamade and Setiyo, 1996), as well as the behaviour of genotype to water deficit. Other studies have also reported that photosynthetic capacity depends on the topological position and the age of the leaf within the crown (Corley, 1983; Dufrêne and Saugier, 1993), presumably in relation to nitrogen content as observed in many plants (e.g. Prieto et al., 2012, for grapevine). Our simulation study highlighted important mutual shading in adult stands (around 50 %) so that improving the photosynthesis of the most shaded leaves could be an option to increase canopy assimilation (Reynolds et al., 2000; Song et al., 2013).

The assumption of a fixed respiration rate (independent of LAI) could be a limit of our study since it imposed a decrease in A_d with increasing LAI (Hirose, 2004). However, the impact of this presumed artefact was low, since only a slight decrease in A_d was observed for high values of LAI (Fig. 4). Finally, light scattering was not considered in the simulations, which limited the study of potential influence of light quality and leaf optical properties, which are likely to slightly change the distribution of light within the crown (Dauzat et al., 2008; Bongers et al., 2014; Kahlen and Chen, 2015; Sadras and Denison, 2016).

Perspectives for oil palm breeding and management

Ideotypes can be defined as ‘cultural’ when they are designed through management practices (shoot pruning in orchards for instance; Willaume et al., 2004; Tang et al., 2015) or as ‘varietal’ when their conception relies on breeding programmes (Martre et al., 2015). Conversely to plants with fluctuating branching patterns depending on ontogenetic stages and environment, the absence of axillary buds in oil palm gives a unique stem, i.e. monopodial habit (Henderson, 2002), which limits its architectural plasticity to variation in leaf morphology. As a result, architectural manipulation based on management practices appears limited for oil palm and consequently leads to consideration of varietal ideotype rather than cultural ideotype.

In cereals, enhancement of production was partly achieved by selecting plants with reduced tillering capacity (Sakamoto and Matsuoka, 2004), thus demonstrating the benefit of the inability to adjust shoot branching to increase performance under a specific planting density (Kumar et al., 2017). By analogy with the ideotype designed in cereal crops to improve light harvest, the four ideotypes presented in this study had relatively short and erect leaves (Khush, 2001; Dingkuhn et al., 2015).

Another strategy for improving productivity via LIE was extension of the vegetative phase for annual plants (Reynolds et al., 2000; Koester et al., 2014). Such a strategy would probably be less efficient for perennial plants such as oil palm, as the time from planting to canopy closure represents a relatively short period of plant lifespan. However, the vegetative growing period before production is likely to be crucial for proper establishment of plant productivity over the years. As a result the kinetics of canopy closure could be a determining criterion for future breeding strategies.

With the four ideotypes selected in this study, we demonstrated that different balances between leaf dimensions, leaf structure and crown geometry could lead to comparable carbon assimilation rates. Different targets for breeding could thus be considered from these various ideotypes since the genetic resources, heritability of architectural traits and correlations between traits would probably limit the selection of some of these theoretical ideotypes. The ideotypes were defined here for a targeted environment under current agronomic practices (density of 136 plants ha⁻¹). Further in silico experiments could be performed to investigate other ideotypes under innovative management practices (Mao et al., 2016). Testing new planting densities has raised interest from oil palm agronomists (Breure, 1988; Bonneau et al., 2014) and illustrated that leaf length is a critical trait in determining planting density (Barcelos et al., 2015). Since such experiments require substantial time and cost inputs, a modelling approach could dramatically reduce them. However, such a perspective emphasizes the need to integrate plant architectural plasticity in the modelling approach, as proposed for rice (Zhu et al., 2015; Kumar et al., 2017).

Other ideotypes would be expected under different planting patterns, density or in association with other crops, but we can suppose that the variations obtained in comparison with the ideotypes proposed in the present study would rely mainly on an adjustment of crown dimensions. Conversely, with a reverse approach, an interesting study would be to investigate optimized management practices for given genotypes, considering production requirements under different socio-economic and environmental conditions (Rival, 2017).

Ideotype definition could be different if a multi-objective approach is followed (Martre et al., 2015; Sadras and Denison, 2016). Although genetic and environmental effects on carbon assimilation were not considered here, our study has provided an interesting perspective in oil palm breeding, notably regarding water deficit. Our simulation outputs revealed that an architecture with relatively low LAI values (close to 4 m² m⁻²) gave a level of potential assimilation comparable to ones with higher LAI (over 5 m² m⁻²). Breeding strategies to limit water stress could thus rely on selecting architectures that confer LAI with an interesting trade-off between assimilation and transpiration. Similarly, a trade-off between carbon assimilation and biomass investment in vegetative parts to establish leaf area (Takenaka et al., 2001) at the expense of reproductive parts would probably lead to different ideotypes. Interestingly, our simulation study revealed an important range of LAI for comparable levels of assimilation, which opens the path for defining new ideotypes by integrating further functional processes already developed in oil palm, such as carbon partitioning and retroactions between functioning and growth (Pallas et al., 2013a, b). Indeed, studies exploring several functioning processes have highlighted the importance of biomass partitioning in yield variability (Lecoeur et al., 2011; Cerasuolo et al., 2016; Koester et al., 2014).

SUPPLEMENTARY INFORMATION

Supplementary data are available at https://academic.oup.com/aob and consist of the following: Fig. S1: Schema of the overall approach with the different steps executed to perform the Morris method and metamodelling. Fig. S2: Geometric variables for assessing and generating 3-D oil palm architecture. Fig. S3: Leaf morphology depending on variation of architectural parameters. Fig. S4: Calibration of non-rectangular hyperbola (NRH) curve for simulating leaf photosynthesis. Fig. S5: Sample of virtual plants generated during the Morris method with the associated relative values of architectural parameters. Fig. S6: Heat map of elementary effects (μ) and interaction effects (σ) for LAI and the four studied outputs over plant age. Fig. S7: Daily leaf irradiance, assimilation and leaf area of the four ideotypes. Table S1: Climate data used for simulating photosynthesis. Table S2: Summary of metamodel adjustments to predict A_d with estimated values of the coefficients associated with the parameters.