Introducing turgor-driven growth dynamics into functional–structural plant models

Abstract

Background and Aims

In many scenarios the availability of assimilated carbon is not the constraining factor of plant growth. Rather, organ growth appears driven by sink activity in which water availability plays a determinant role. Current functional–structural plant models (FSPMs) mainly focus on plant-carbon relations and largely disregard the importance of plant water status in organogenesis. Consequently, incorporating a turgor-driven growth concept, coupling carbon and water dynamics in an FSPM, presents a significant improvement towards capturing plant development in a more mechanistic manner.

Methods

An existing process-based water flow and storage model served as a basis for implementing water control in FSPMs. Its concepts were adjusted to the scale of individual plant organs and interwoven with the basic principles of modelling carbon dynamics to allow evaluation of turgor pressure across the entire plant. This was then linked to plant organ growth by applying the principles of the widely used Lockhart equation.

Key results

This model successfully integrates a mechanistic understanding of plant water transport dynamics coupled with simple carbon dynamics within a dynamically developing plant architecture. It allows evaluation of turgor pressure on the scale of plant organs, resulting in clear diel and long-term patterns, directly linked to plant organ growth.

Conclusions

A conceptual sap flow and turgor-driven growth model was introduced for functional–structural plant modelling. It is applicable to any plant architecture and allows visual exploration of the diel patterns of organ water content and growth. Integrated in existing FSPMs, this new concept fosters an array of possibilities for FSPMs, as it presents a different formulation of growth in terms of local processes, influenced by local and external conditions.

INTRODUCTION

Functional–structural plant models (FSPMs) are state-of-the-art tools to study plant growth and development in response to their environment (Vos et al., 2010). This feat is achieved by their inherent combination of plant architecture with a mechanistic modelling approach to plant development on the scale of individual plant organs. Currently, FSPMs mostly describe growth from a photosynthesis-based carbon (C) availability perspective. However, whereas photosynthesis is the main source of biomass and energy for the plant, photosynthesis rates (i.e. source activity) and plant growth (i.e. sink activity) are not always correlated (Muller et al., 2011). In this context, limited availability of water plays a major role as it affects both source and sink activities, but not in an equally fast or intense way.

Source activity is affected by the closure of stomata as a result of water deficit, lowering the photosynthetic uptake of CO₂, but some evidence suggests that plant growth is inhibited at far lower levels of drought stress than photosynthesis (Muller et al., 2011; Tardieu et al., 2011). In these cases, organ expansion is affected earlier and more intensely than photosynthesis, which leads to the accumulation of non-structural carbohydrates (NSCs) in various plant organs (Woodruff and Meinzer, 2011). These elevated C concentrations in the form of NSCs conflict with the idea of drought-stress-induced C starvation as the cause of constrained growth and plant mortality (Muller et al., 2011). While the physiological mechanisms of drought response in terms of C starvation and hydraulic failure are still under intense debate (McDowell et al., 2008; McDowell and Sevanto, 2010; Sevanto et al., 2014; Rodríguez-Calcerrada et al., 2017), these observations demonstrate that plant hydraulics play a fundamental role in plant growth and a sink-driven modelling approach is essential (Muller et al., 2011; Körner and Basel, 2013; Fatichi et al., 2014; Steppe et al., 2016).

Some FSPMs include water-limitation effects on growth as empirically derived terms of ‘drought stress’ influencing carbon supply and demand (e.g. Allen et al., 2005; Pallas et al., 2013; Kang et al., 2014), but none has integrated a sink-driven approach to water transport with a direct mechanistic link to organ growth. Da Silva et al. (2011) took a first step towards integrating a xylem pathway for water transport on the plant organ level. However, their link to plant organ growth was based on a linear function in terms of water potential and growth rate, rather than a full mechanistic approach. Nikinmaa et al. (2014) managed to mechanistically implement xylem transport, phloem transport, water potential and carbohydrate concentration in a 3-D tree crown. However, the concepts were applied to a static tree architecture (i.e. no new organs are formed in the model) and the link to organ growth was not made.

Turgor pressure within a plant cell, and by extension within a plant organ, is the prime candidate for describing growth from a sink perspective, as it is the critical component in quantifying growth and links organ expansion to plant water status (Lockhart, 1965; Génard et al., 2001; Steppe et al., 2006). Accordingly, Steppe et al. (2006) developed a mathematical sink-driven flow and storage model that describes radial tree stem growth from a plant water relations perspective. Using continuous measurements of sap flow and stem diameter variations (De Swaef et al., 2015; Steppe et al., 2015), this model simulates plant water relations in terms of stem water potential and stem turgor pressure. Furthermore, using biomechanical parameters like tissue elasticity and extensibility, the model quantifies turgor-driven dimensional changes, where tissue elasticity refers to reversible changes (Ortega, 1985) and extensibility to irreversible growth via the Lockhart (1965) equation.

In this paper, we present a conceptual model that provides a general framework to combine the advantages of a sink-based growth model with the FSPM modelling paradigms: turgor-driven growth at the individual organ scale and a dynamically developing 3-D architecture and organogenesis. This provides an important step towards the implementation of sink-driven growth within FSPMs and towards applicability of FSPMs under conditions of drought. Furthermore, it will allow evaluation and visualization of water potential gradients and turgor profiles within the plant with a direct link to organ growth. For this paper, the structural part of the model was intentionally kept simple to provide an easy stepping-stone towards integration in more complex models.

MATERIALS AND METHODS

Basic structural plant model

In our model, the 3-D development of the plant is based on the general concepts of functional–structural plant modelling. Plant structure is represented by a set of interconnected elementary units or phytomers (Vos et al., 2010), and for conceptual simplicity the structure of these phytomers was set as an internode with a single leaf and a flower bud that developed into a fruit after a set time. Internodes were modelled as perfect cylinders, leaves as rectangles (for simplicity, the model is applicable to any leaf shape) with variable leaf thickness and fruits as perfect spheres. The flower buds serve solely as a placeholder for the development of fruits and have no structural purpose. Emergence of new phytomers is based on thermal time [i.e. growing degree days (GDDs) $\left[°\text{Cd}\right]],$ with consecutive phytomers emerging after a fixed time (i.e. phyllochron) (Evers et al., 2005; Watanabe et al., 2005).

$$GDD\left(t\right)=\max \left(0,T_m\left(d\right)-T_b\right)$$ (1)

where $GDD(t)$ is the thermal time $\left[°\text{Cd}\right]$ on day $t,$$T_{\text{m}}\left(\text{d}\right)$ the daily mean air temperature $\left[°\text{C}\right]$ and $T_b$ the plant base temperature $\left[°\text{C}\right],$ which is the minimum temperature required for the metabolic processes involved in plant growth. To illustrate the possibility and effect of dynamically adding growing plant organs across the entire architecture during model development, the hypothetical concept plant used to introduce the turgor-driven model was assumed to have a fixed moment of generative (i.e. fruit) development across the entire plant. After a set amount of degree days ($GE{N}_{induc}[GDD]$), all flower buds simultaneously develop into fruits.

Assumptions for the water transport sub-model

Soil water potential was set as a constant, and equal to the water potential of the root xylem (${\psi }_{roots}^x={\psi }_{soil} \left[\text{MPa}\right]$). We assumed equal hydraulic resistance in all organ types, depending only on organ dimensions. The relations were set directly proportional to the length and inversely proportional to the area of an organ cross-section (i.e. radius squared for the internodes, width times thickness for the leaves), as we assumed this to be a good representation of the amount of transport vessels available in the tissue. Transport resistance within the fruit was considered negligible.

$$\begin{array}{l}{R}_{int\left(i\right)\to int(i+1)}^x=\frac{1}{2}{R}_{flow}^x\left(\frac{l_{int\left(i\right)}}{r_{int\left(i\right)}^2}+\frac{l_{int\left(i+1\right)}}{r_{int\left(i+1\right)}^2}\right)\\ R_{int\left(i\right)\to leaf(i)}^x=\frac{1}{2}{R}_{flow}^x\left(\frac{l_{int\left(i\right)}}{r_{int\left(i\right)}^2}+\frac{l_{leaf\left(i\right)}}{w_{leaf(i)}th{k}_{leaf\left(i\right)}}\right)\\ R_{int\left(i\right)\to fruit(i)}^x=\frac{1}{2}{R}_{flow}^x\left(\frac{l_{int\left(i\right)}}{r_{int\left(i\right)}^2}\right)\end{array}$$ (2)

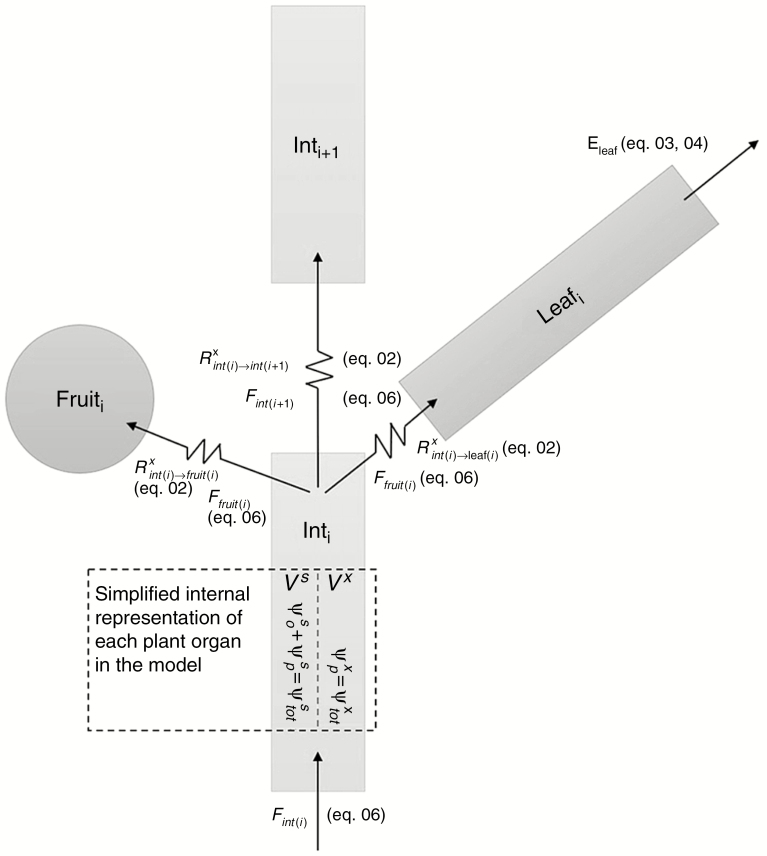
where $R_{int(i)\to int(i+1)}^x\text{},$$R_{int\left(i\right)\to leaf(i)}^x$ and $R_{int\left(i\right)\to fruit(i)}^x$ represent the total xylem flow resistances between two consecutive internodes, between an internode and its leaf, and between an internode and its fruit, respectively ${\text{[MPa h g}}^{-\text{1}}].$$R_{flow}^x$ is a constant representing the elemental xylem flow resistivity $[{\text{MPa m h g}}^{-\text{1}}].$$l_{organ}$ represents the organ length and $r_{organ},w_{leaf},th{k}_{leaf}$ represent the organ radius (internode or fruit), leaf width and leaf thickness, respectively $\left[\text{m}\right].$ All plant organs consist of xylem and ‘living tissue’, the latter including the phloem and being the part of the organ that contributes to water storage. We assumed here that the proportion of xylem and storage tissue is constant across all organs ($V_{storage}^{\%}=80\text{\%}$). We also assumed no radial flow between the xylem and storage tissue, meaning that the water potential of the xylem is assumed equal to the water potential of the storage tissue in each plant organ (Fig. 1). This radial transfer is present in the flow and storage model of Steppe et al. (2006), but is here omitted to substantially reduce model complexity.

Fig. 1.

Schematic illustration of the inward and outward flows in a single phytomer (i). Contrasting with the inward flow of a plant organ, the total outward flow depends on the number of distal plant organs in the plant architecture. Each plant organ is represented as an internally homogeneous object consisting of a xylem portion (V^x) and a storage portion (V^s). The assumption was made that radial water flow is negligible, which implies equal water potentials in the xylem and storage portion of the plant organs $\left({\psi }_{tot}^x={\psi }_{tot}^s\right).$

Plant water flow is driven by transpiration of the individual leaves and is the main input in this model. While leaf transpiration is strongly linked to the intercepted radiation of a leaf, it was intentionally chosen to keep the transpiration model as simple as possible for demonstrative purposes, as it is not the focus of this paper to model transpiration with high accuracy. This approach still allows a straightforward integration of a more complex, light-dependent transpiration model for future FSPM applications. A simple approximation of leaf transpiration $(E_{leaf}\text{[g}{\text{h}}^{-1}])$ was modelled as a diurnal, strictly positive sine function, multiplied by the leaf’s area:

$$E_{leaf}=E_{plant}^{scale}\left(t_{plant}\right)\max \left(0,sin\left(\frac{\left(H-6\right)\pi }{12}\right)\right)l_{leaf}{w}_{leaf}$$ (3)

where $E_{plant}^{scale}$ is a scale factor for transpiration [dimensionless] in terms of plant age $\left(t_{plant}\right)$ [°Cd] and $H$is the time of the day $\left[\text{h}\right]$. The scale factor is used to create values of a realistic magnitude, but also to account for a decrease in plant transpiration towards the end of the growing season at plant maturity. To be able to simulate a conclusive growing season, we assumed full leaf senescence at maturity in our hypothetical plant, resulting in zero transpiration at the end of the growing season. Therefore, the scale factor is modelled as a strictly decreasing sigmoid function (Yin et al., 2003):

$$E_{plant}^{scale}\left(t_{plant}\right)=100\left(1-\left(1+\frac{t_{plant}^e-t_{plant}}{t_{plant}^e-t_{plant}^m}\right){\left(\frac{t_{plant}}{t_{plant}^e}\right)}^{\frac{t_{plant}^e}{t_{plant}^e-t_{plant}^m}}\right)$$ (4)

where $t_{plant}^e$ is the final plant age [°Cd] at maturity (and transpiration = 0) and $t_{plant}^m$ the plant age [°Cd] at which the transpiration has been reduced by 50%. A list of all model variables, parameters and constants is given in Table 1.

Table 1.

Summary of all state variables and parameters in the model with their descriptions and initial conditions (when applicable)

State variables
Symbol	Unit	Initial condition	Description
$C_{plant}^{net}$	g	–	Total plant assimilate pool
$E_{leaf}$	g h−1	–	Leaf transpiration rate
$F_{organ(i)}$	g h−1	–	Sap flow into plant organ
$GDD$	°Cd	0	Thermal time for plant development
$l_{organ}$	m	0.001	Plant organ length
$m_{organ}$	g	0.1$V_{organ}$	Total sugar mass in plant organ
$P_{organ}$	Unitless	–	Sink strength of plant organ
$R_{int\left(i\right)\to int(i+1)}^x$	MPa h g−1	–	Xylem flow resistance between two consecutive internodes
$R_{int\left(i\right)\to leaf(i)}^x$	MPa h g−1	–	Xylem flow resistance between an internode and its attached leaf
$R_{int\left(i\right)\to fruit(i)}^x$	MPa h g−1	–	Xylem flow resistance between an internode and its attached fruit
$r_{organ}$	m	0.001	Internode and fruit radius
$t_{organ}$	°Cd	–	Age of plant organ
$th{k}_{leaf}$	m	0.001	Leaf thickness
$V_{organ}$	m3	–	Volume of plant organ
$w_{organ}$	m	0.001	Leaf width
$W_{organ}$	g	–	Total water content of plant organ
$WU{E}^{\text{a}}$	$\left[{\text{g}}_{\text{sucrose}}{\text{ g}}_{{\text{H}}_2\text{O}}^{\text{-1}}\right]$	–	Actual plant water use efficiency
${\varphi }_x,{\varphi }_y,{\varphi }_z$	MPa h−1	–	Actual dimension-specific cell wall extensibility in relation to non-reversible dimensional changes (tissue growth)
${\psi }_{organ}$	MPa	–	Total water potential of plant organ
${\psi }_{organ}^x$	MPa	–	Xylem water potential of plant organ
${\psi }_{o,organ}$	MPa	–	Osmotic water potential of plant organ
${\psi }_{p,organ}$	MPa	–	Turgor water potential of plant organ
Model parameters
Symbol	Unit	Value	Description
$GE{N}_{induc}$	°Cd	200	Thermal plant age for fruit development
$M_{sucrose}$	g mol−1	343	Molar mass of sucrose
$PHYLLO$	°Cd	50	Phyllochron, denoting the thermal time between the development of two consecutive phytomers
$R$	J mol−1 K−1	8.31	Global gas constant
$R_{flow}^x$	MPa h g−1 m	1 × 10–5	Elemental xylem flow resistance
Model parameters
Symbol	Unit	Value	Description
$t_{organ}^e$	°Cd	200	Organ age at the end of the growth period (i.e. organ age when extensibility reaches 0)
$t_{organ}^m$	°Cd	100	Organ age when organ extensibility is reduced by half of the initial value
$t_{plant}^e$	°Cd	350	Plant age at the end of the growth period (i.e. plant age when WUEa reaches 0)
$t_{plant}^m$	°Cd	231	Plant age when WUEa reduced by half of the initial value
$T$	K	293	Temperature of plant organ
$T_b$	°C	10	Plant base temperature
$T_m$	°C	20	Mean air temperature
$V_{storage}^{\text{\%}}$	Unitless	0.8	Proportion of plant organ contributing to water storage
$WU{E}^{init}$	$\left[{\text{g}}_{\text{sucrose}}{\text{ g}}_{{\text{H}}_2\text{O}}^{\text{-1}}\right]$	0.05	Initial plant water use efficiency
${\epsilon }_x,{\epsilon }_y,{\epsilon }_z$	MPa	0.2, –, 0.2 (internode) 0.5, 0.5, 1 (leaf) –, –, 0.5 (fruit)	Dimension-specific bulk elastic modulus of living tissue in relation to reversible dimensional changes (water storage)
${\varphi }_x^{init},{\varphi }_y^{init},{\varphi }_z^{init}$	MPa h−1	0.25, –, 0.45 (internode) 0.40, 0.01, 0.45 (leaf) –, –, 0.2 (fruit)	Initial dimension-specific cell wall extensibility in relation to non-reversible dimensional changes (tissue growth)
${\rho }_w$	kg m−3	1000	Density of water
$\Gamma$	MPa	0.3	Critical value for the pressure component which must be exceeded for irreversible volume changes (plant growth)
${\psi }_{roots}^x$	MPa	–0.1	Root compartment xylem water potential
${\psi }_{soil}$	MPa	–0.1	Soil water potential

^aWUE stands for water use efficiency and is defined in our model as the ratio of carbon assimilated by a leaf to the amount of water transpired.

Equations of the conceptual water transport model

The mathematical description of water transport in the plant xylem can be derived from the electric analogue approach (Ohm’s law) or expressed by the hydraulic system approach (Darcy’s law) (Steppe et al., 2006):

$$F_{organ(i)}=\frac{{\psi }_{organ\left(i-1\right)}^x-{\psi }_{organ\left(i\right)}^x}{R_{int\left(i-1\right)\to organ}^x}$$ (5)

This indicates that sap flow into an organ of an index $i$($F_{organ\left(i\right)}\left[{\text{g h}}^{-1}\right]$) depends solely on the difference in xylem water potential ${\psi }^x \left[\text{MPa}\right]$ between itself and the underlying organ, and the hydraulic xylem resistance between the two consecutive plant organs. The use of this formula to model total water transport between organs assumes a negligible contribution of phloem transport to the water flow. With the assumption made earlier that the xylem water potential is equal to the water potential of the storage compartment (${\psi }^x={\psi }^s=\psi \left[\text{MPa}\right]$) (Fig. 1), eqn (5) can be rewritten as the difference in total water potential of the plant organ (${\psi }_{organ}\left[\text{MPa}\right]$):

$$F_{organ(i)}=\frac{{\psi }_{organ\left(i-1\right)}-{\psi }_{organ\left(i\right)}}{R_{int\left(i-1\right)\to organ}^x}$$ (6)

This leads to a change in internally stored water ($W \left[\text{g}\right]$) in each plant organ, which can be calculated using the mass balance, as the difference between the water inflow and outflow of a plant organ. Water outflow for a leaf is equal to the transpiration of the leaf, but for internodes the flow to each neighbouring, subsequent plant organ must be evaluated, as each internode is an element in a networking plant structure:

$$\frac{d{W}_{int\left(i\right)}}{dt}=F_{int\left(i\right)}-{\sum }^{\text{}}{F}_{int\left(i+1\right)}-{\sum }^{\text{}}{F}_{leaf\left(i\right)}-{\sum }^{\text{}}{F}_{fruit\left(i\right)}$$

$$\frac{d{W}_{leaf}}{dt}=F_{leaf}-E_{leaf}$$

$$\frac{d{W}_{fruit}}{dt}=F_{fruit}$$

The mass flow of water to and from each plant organ causes a change in organ volume ($V_{organ} [{\text{m}}^3]$). Assuming a constant water density (${\rho }_w$) of 1000 kg m⁻³:

$$\frac{d{W}_{organ}}{dt}={\rho }_w\left(\frac{d{V}_{organ}}{dt}\right)$$ (8)

This change in water content can be directly linked to the organ’s turgor pressure potential (${\psi }_{p,organ}[\text{MPa}$]), resulting in either only elastic (el) expansion and contraction (if ${\psi }_{p,organ}\le \Gamma$) or additional plastic (pl) growth (if ${\psi }_{p,organ}>\Gamma$) (Lockhart, 1965; Ortega, 1985, 1990). While these concepts were originally designed on the cell level, they have been successfully applied to plant organ level (Génard et al., 2001; Steppe et al., 2006):

$$\frac{1}{V_{organ}}{\left(\frac{d{V}_{organ}}{dt}\right)}_{el}=\frac{1}{\epsilon }\frac{d{\psi }_{p,organ}}{dt}for{\psi }_{p,organ}\le \Gamma$$

$$\begin{array}{l}\frac{1}{V_{organ}}{\left(\frac{d{V}_{organ}}{dt}\right)}_{el+pl}=\frac{1}{\epsilon }\frac{d{\psi }_{p,organ}}{dt}+\varphi ({\psi }_{p,organ}-\Gamma )\\ for{\psi }_{p,organ}>\Gamma \end{array}$$ (9)

where $\epsilon$is the bulk elastic modulus of living tissue in relation to reversible dimensional changes $\left[\text{MPa}\right]$, $\varphi$ is the extensibility of the cell walls in relation to non-reversible dimensional changes $\left[{\text{MPa}}^{-\text{1}}{\text{h}}^{-\text{1}}\right]$ and $\Gamma$ represents the threshold value $\left[\text{MPa}\right]$of turgor pressure required to produce irreversible growth in a plant organ.

Evaluating plant volume changes in 3-D requires further decomposition of these equations into dimension-specific equations. Because of our simplified representation of internodes as perfect cylinders, leaves as rectangles with variable thickness and fruits as perfect spheres, their volumes can be calculated as:

$$V_{int}=l_{int}\pi r_{int}^2$$

$$V_{leaf}=l_{leaf}{w}_{leaf}th{k}_{leaf}$$

$$V_{fruit}=\frac{4}{3}\pi r_{fruit}^3$$ (10)

which allows decomposition into dimension-specific components:

$$\frac{1}{V_{int}}\left(\frac{d{V}_{int}}{dt}\right)=\frac{1}{l_{int}}\left(\frac{d{l}_{int}}{dt}\right)+\frac{2}{r_{int}}\left(\frac{d{r}_{int}}{dt}\right)$$

$$\frac{1}{V_{leaf}}\left(\frac{d{V}_{leaf}}{dt}\right)=\frac{1}{l_{leaf}}\left(\frac{d{l}_{leaf}}{dt}\right)+\frac{1}{w_{leaf}}\left(\frac{d{w}_{leaf}}{dt}\right)+\frac{1}{th{k}_{leaf}}\left(\frac{dth{k}_{leaf}}{dt}\right)$$

$$\frac{1}{V_{fruit}}\left(\frac{d{V}_{fruit}}{dt}\right)=\frac{3}{r_{fruit}}\left(\frac{d{r}_{fruit}}{dt}\right)$$ (11)

and the introduction of dimension-specific elastic moduli (${\epsilon }_{z,organ},{\epsilon }_{y,organ},{\epsilon }_{x,organ}$) and extensibility coefficients (${\varphi }_{z,organ},{\varphi }_{y,organ},{\varphi }_{x,organ}$). As internodes were represented as perfect cylinders, the elastic modulus and extensibility coefficient in the y direction can be set equal to those in the x direction. Similarly, the representation of fruits as perfect spheres results in equality in all directions. This leads to:

$$\begin{array}{l}\frac{1}{l_{organ}}{\left(\frac{d{l}_{organ}}{dt}\right)}_{el+pl}=\frac{1}{{\epsilon }_{z,organ}}\frac{d{\psi }_{p,organ}}{\text{dt}}\\ +{\varphi }_{z,organ}(max({\psi }_{p,organ},\Gamma )-\Gamma )\end{array}$$

$$\begin{array}{l}\frac{1}{r_{organ}}{\left(\frac{d{r}_{organ}}{dt}\right)}_{el+pl}=\frac{1}{{\epsilon }_{x,organ}}\frac{d{\psi }_{p,organ}}{\text{dt}}\\ +{\varphi }_{x,organ}(max({\psi }_{p,organ},\Gamma )-\Gamma )\end{array}$$

$$\begin{array}{l}\frac{1}{w_{leaf}}{\left(\frac{d{w}_{leaf}}{dt}\right)}_{el+pl}=\frac{1}{{\epsilon }_{x,leaf}}\frac{d{\psi }_{p,leaf}}{dt}\\ +{\varphi }_{x,leaf}(max({\psi }_{p,leaf},\Gamma )-\Gamma )\end{array}$$ (12)

$$\begin{array}{l}\frac{1}{th{k}_{leaf}}{\left(\frac{dth{k}_{leaf}}{dt}\right)}_{el+pl}=\frac{1}{{\epsilon }_{y,leaf}}\frac{d{\psi }_{p,leaf}}{dt}\\ +{\varphi }_{y,lea\text{f}}(max({\psi }_{p,leaf},\Gamma )-\Gamma )\end{array}$$

where ${\epsilon }_{z,organ}$ and ${\varphi }_{z,organ}$ represent the elastic modulus $[\text{MPa}]$ and extensibility coefficient $[{\text{MPa}}^{-1}{\text{h}}^{-\text{1}}]$ of the plant organ in the longitudinal direction. Similarly, ${\epsilon }_{x,organ}$ and ${\varphi }_{x,organ}$ are valid for the radial direction of the internodes, fruits and the transverse direction of the leaves. ${\epsilon }_{y,organ}$ and ${\varphi }_{y,organ}$ relate to thickness of the leaves. The representation of the plastic component of these equations as a maximum function allows the validity of these equations for each value of ${\psi }_{p,organ}$, as it will be equal to zero in conditions of strictly elastic volume changes.

Combining eqns (8), (10), (11) and (12) allows evaluation of the total change in turgor pressure within the plant organs in terms of the increase or decrease in water content in the plant organs:

$$\frac{d{\psi }_{p,int}}{dt}=\left[\begin{array}{l}\frac{1}{{\rho }_w\pi r_{int}^2{l}_{int}}\frac{d{W}_{int}}{dt}\\ -\left({\varphi }_{z,int}+2{\varphi }_{x,int}\right)\left(max({\psi }_{p,int},\Gamma )-\Gamma \right)\end{array}\right]\left(\frac{{\epsilon }_{z,int}{\epsilon }_{x,int}}{2{\epsilon }_{z,int}+{\epsilon }_{x,int}}\right)$$

$$\begin{array}{lll}\frac{d{\psi }_{p,leaf}}{dt}\hfill & =\hfill & \left[\begin{array}{l}\frac{1}{{\rho }_w{l}_{leaf}{w}_{leaf}th{k}_{leaf}}\frac{d{W}_{leaf}}{dt}\\ -\left({\varphi }_{z,leaf}+{\varphi }_{x,leaf}+{\varphi }_{y,leaf}\right)\left(max({\psi }_{p,leaf},\Gamma )-\Gamma \right)\end{array}\right]\hfill \\ \hfill & \times \hfill & \left(\frac{{\epsilon }_{z,leaf}{\epsilon }_{x,leaf}{\epsilon }_{y,leaf}}{{\epsilon }_{z,leaf}{\epsilon }_{x,leaf}+{\epsilon }_{z,leaf}{\epsilon }_{y,leaf}+{\epsilon }_{x,leaf}{\epsilon }_{y,leaf}}\right)\hfill \end{array}$$ (13)

$$\frac{d{\psi }_{p,fruit}}{dt}=\left[\begin{array}{l}\frac{3}{{\rho }_{w}4\pi r_{fruit}^3}\frac{d{W}_{fruit}}{dt}\\ -\left(3{\varphi }_{x,fruit}\right)\left(max({\psi }_{p,fruit},\Gamma )-\Gamma \right)\end{array}\right]\left(\frac{{\epsilon }_{x,fruit}}{3}\right)$$

Consequently, eqn (12) can now be calculated to evaluate the changes in organ dimensions.

To take the maturing of plant organs into account, the extensibility coefficients were made dependent on organ age $\left[°\text{Cd}\right]$ by using a sigmoid function similar to the scale factor for transpiration (eqn 4):

$${\varphi }_{x,y,z}=\left(1-\left(1+\frac{t_{organ}^e-t_{organ}}{t_{organ}^e-t_{organ}^m}\right){\left(\frac{t_{organ}}{t_{organ}^e}\right)}^{\frac{t_{organ}^e}{t_{organ}^e-t_{organ}^m}}\right){\varphi }_{x,y,z}^{init}$$ (14)

where ${\varphi }_{x,y,z}$ and ${\varphi }_{x,y,z}^{init}$ are the actual and initial extensibility coefficients. $t_{organ}^e$ and $t_{organ}^m$ are the times $\left[°\text{Cd}\right]$ when organ growth reaches its endpoint and halfway point, respectively, and $t_{organ}$ is the organ age $\left[°\text{Cd}\right]$.

Lastly, a term was added to introduce net assimilate production into the plant organs. This provides the link between carbon and water relations, and will impact the osmotic potential of the growing plant organs. As a result, the contribution of carbohydrates is indispensable for simulating the dynamics of turgor pressure. Although very simplified due to the focus of this paper, this framework allows the introduction of more detailed carbohydrate dynamics. Currently, it was included with a very basic implementation of a common assimilate pool with source–sink concept without considering the contributions of respiration or the creation of starch. As we consider a single year of plant development in this model, we assumed the size of the assimilate pool to depend solely on the production during the plant’s development, with no reserve pool, as is the case in trees or other perennials. Consequently, the change in size of the assimilate pool ($C_{plant}^{net} \left[{\text{g}}_{\text{sucrose}}\right]$) at time t was calculated in each step as:

$$\frac{d{C}_{plant}^{net}\left(t\right)}{dt}=WUE*{\sum }^{\text{}}{E}_{leaf}(t)$$ (15)

where $WUE$ is the plant water use efficiency $\left[{\text{g}}_{\text{sucrose}}{\text{ g}}_{{\text{H}}_2\text{O}}^{\text{-1}}\right]$ set at a constant value. ${\sum }^{\text{}}{E}_{leaf}(t)$ represents the sum of transpiration ${\text{[g}}_{{\text{H}}_2\text{O}}]$ across all leaves. The relative sink strength of each organ ($P_{organ(i)}[unitless]$) was set to be proportional to the relative sum of the dimensional extensibility coefficients as an indication of organ growth potential:

$$P_{organ\left(i\right)}=\frac{\left({\varphi }_{z,organ\left(i\right)}+{\varphi }_{y,organ\left(i\right)}+{\varphi }_{x,organ\left(i\right)}\right)}{{\sum }_{i=1}^n\left({\varphi }_{z,organ\left(i\right)}+{\varphi }_{y,organ\left(i\right)}+{\varphi }_{x,organ\left(i\right)}\right)}$$ (16)

where n is the total amount of plant organs in the plant. This allows calculation of the net increase in assimilates in each plant organ by distributing the assimilate pool based on relative sink strength:

$$\frac{d{m}_{organ}}{dt}=C_{plant}^{net}{P}_{organ}$$ (17)

where $m_{organ}$ is the total sugar mass in the plant organ $\left[{\text{g}}_{\text{sucrose}}\right]$. This increase in sugar content will contribute to the size of the osmotic potential (${\psi }_{o,organ}$) of the storage compartment of the plant organ. With the earlier assumption of a constant 80 % of the plant organ volume contributing to storage:

$${\psi }_{o,organ}=-RT\frac{m_{organ}}{V_{organ}^s{M}_{sucrose}}=-RT\frac{m_{organ}}{0.8V_{organ}{M}_{sucrose}}$$ (18)

where $R$ is the global gas constant $[{\text{J mol}}^{\text{-1}}{\text{ K}}^{\text{-1}}]$, $T$ is the temperature [$\text{K}]$ and $M_{sucrose}$ the molar mass of sucrose ${\text{[g}}_{\text{sucrose}}{\text{ mol}}^{\text{-1}}]$. Consequently, we can calculate the total water potential in each plant organ as:

$${\psi }_{organ}={\psi }_{p,organ}+{\psi }_{o,organ}$$ (19)

Model implementation

The model described above is a combination of algebraic equations and ordinary differential equations (ODEs) and while most are straightforward, eqns (2), (5), (6) and (7) depend on the context of the plant organ. Equation (2) requires knowledge of the dimensions of the neighbouring plant organ, eqns (5) and (6) require information on the water potential of the underlying plant organ, and eqn (7) requires knowledge of the number of neighbouring, subsequent plant organs and their sap flow. This imposes no limitations when dealing with a static, known plant architecture as the model can be explicitly implemented with the references to the neighbouring object variables manually implemented. However, such an approach requires a separate set of equations for each plant organ in the plant, leading to a very lengthy implementation. Furthermore, the resulting model will only be applicable for a predefined plant architecture, rendering it useless for dynamically developing structures.

Therefore, the model was implemented in the GroIMP modelling platform (Kniemeyer et al., 2007) for functional–structural plant modelling. GroIMP combines the standard graph structure of FSPMs with XL (an extension of Java to include L systems), as well as a framework for solving ODEs (Hemmerling, 2012; Hemmerling et al., 2013). This allows an object-oriented implementation (i.e. the equations for each organ type are defined only once) combined with queries, which can search the graph (i.e. the plant architecture) to find the neighbouring objects, so the correct variables are found and assigned to the correct equations in the model.

The plant organs were implemented by defining a module, ‘PlantOrgan’, which contains all common variables for the plant organs in the model (e.g. plant organ water potential components, organ sap flow). The modules ‘Internode’, ‘Leaf’ and ‘Fruit’ were then implemented as subtypes of the supertype ‘PlantOrgan’ and contain the organ specific variables and equations (e.g. leaf transpiration, change in turgor pressure). To gain access to GroIMP’s differential equation solver, the model was implemented in a single getRate() function (Hemmerling et al., 2013). This function is required for the internal integrator function to find, collect and execute all equations. Within this function, the model equations are assigned to each organ and grouped to ensure the correct order of execution in the solver.

Our model requires solving the algebraic equations and ODEs on an hourly scale to retain the diel dynamics. The speed of solving such a set of equations is directly proportional to the complexity of the plant structure (i.e. the number of plant organs in the scene, which also changes the number of equations in the system), the numerical solver chosen and the accuracy set in the solver. GroIMP provides immediate access to all the commonly used numerical ODE solvers in Java from the package apache.commons.math. However, the solvers provided in this package are all non-stiff solvers and, due to the stiff nature of this model, they become practically unusable due to numerical instabilities. However, GroIMP also provides a wrapper function that allows access to the native CVODE library written in C (Cohen and Hindmarsh, 1996; Hindmarsh et al., 2005) for solving stiff ODE systems (Hemmerling, 2012), which leads to an immense reduction in computation time. After the CVODE library had been locally installed, it was loaded in GroIMP and set as the active solver by calling the following code in the initialization function of the model:

CVodeAdapter CVODE = new CVodeAdapter(); //Create new instance of solver

CVODE.setAbsTolDefault(1e-12); //set absolute tolerance of solver

CVODE.setRelTolDefault(1e-12); //set relative tolerance of solver

setSolver(CVODE); //set solver to CVODE

This code snippet also demonstrates the functions ‘setAbsTolDefault’ and ‘setRelTolDefault’, which allow the user the set the absolute and relative tolerances of the solver. Both tolerances were set to 10⁻¹². The ‘setSolver’ function supports both the Java solver libraries and the CVODE library and provides access to the model equations within the getRate() function described above.

RESULTS

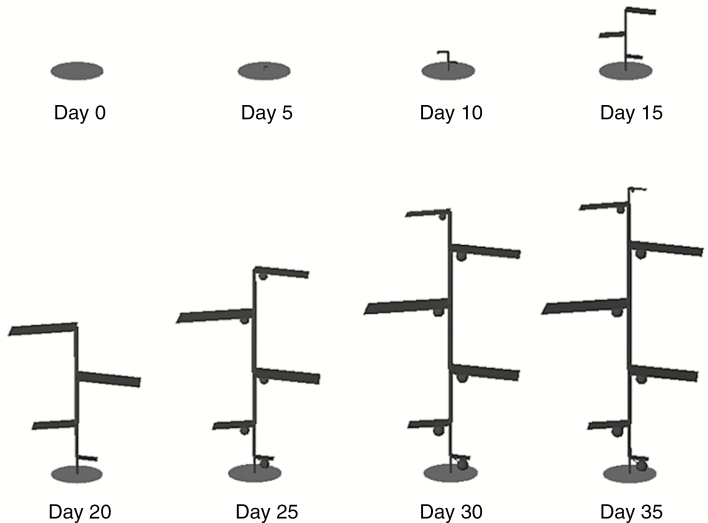
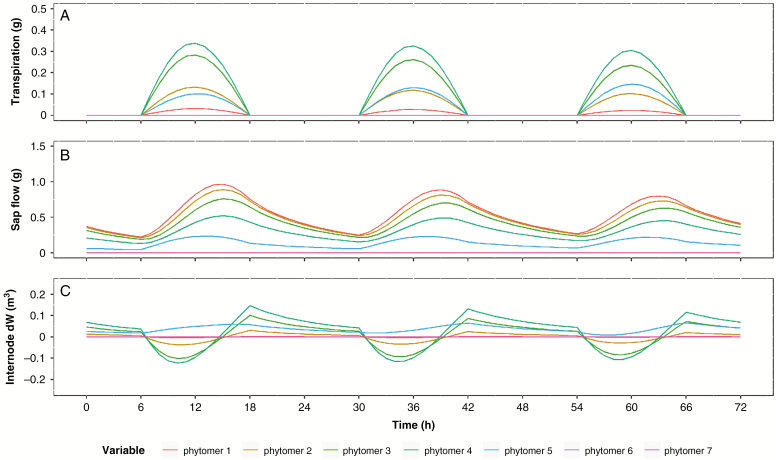
The model with initial conditions as given in Table 1 was run to simulate a period of 35 d. The calculation time for this 35-d simulation period was ~2.5 min on a laptop with an Intel Core i7-6700HQ processor and 16 GB of RAM. The simulation resulted in a simple plant architecture consisting of seven phytomers along the main stem (Fig. 2). The dynamics of turgor pressure in the model are the result of a combination of water availability (i.e. soil water potential, xylem transport resistance and transpiration) and carbohydrate availability (i.e. total carbohydrate production and source–sink distribution), which results in clearly distinguishable diel (Figs 3 and 4) and long-term (Fig. 3) dynamics. The diel patterns in the sap flow model are triggered by transpiration and simultaneous organ sugar load. As soon as transpiration starts, water is lost from the leaves, resulting in a lower water potential and elastic shrinkage of the leaves. The lower water potential of the leaves draws water from neighbouring organs, resulting in a lowering of water potential across the plant, which allows the plant to take up water from the soil to refill the lost storage. As the plant’s dimensions increase, the flow resistance from soil to leaves simultaneously increases, resulting in a time delay between peak transpiration and peak sap flow (Figs 3 and 4). During this time period, transpirational water loss results in a net loss of leaf water content and consequently internode water content. The increase in flow resistance also increases the time required for a night-time equilibrium of zero sap flow, resulting in positive night-time flow at larger plant dimensions.

Fig. 2.

Dimensions of a basic plant architecture in 5-d intervals, resulting from running the model to simulate 35 d with the initial conditions described in Table 1, clearly displaying an exponential pattern of the final organ dimensions.

Fig. 3.

Patterns of transpiration, sap flow and change in internode water content (dW) per phytomer over the course of the entire simulation time. The transpiration pattern shows the exact solution of eqn (3) in terms of the phytomer leaf area. The differences between phytomer sap flow illustrate the distribution of water within the plant. The total plant sap flow corresponds to the sap flow in phytomer 1 as all water entering the plant must pass the first internode. The pattern of internode dW is the result of the time delay between sap flow and transpiration. As transport resistance increases, more internal water is remobilized at the start of the day, resulting in a negative dW, which is compensated when sap flow catches up with transpiration water loss. The net increase in organ water content is an indication of plant growth. The highlighted sections of the graphs are illustrated in more detail in Fig. 4.

Fig. 4.

Patterns of transpiration, sap flow and change in internode water content per phytomer over the course of three selected days (i.e. days 23, 24 and 25) within the simulation time. This illustrates the time delay between sap flow and transpiration. At the start of transpiration, sap flow starts to increase but is unable to fully compensate for the water loss due to flow resistances. As a result, internal water reserves are depleted and dW becomes negative.

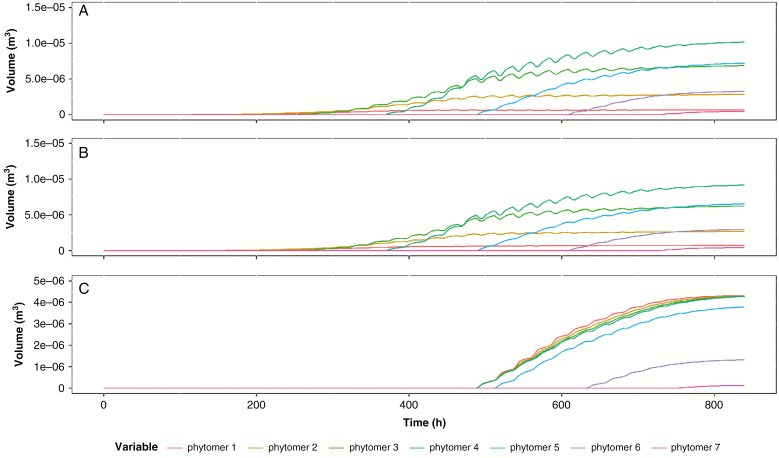
The volume changes in each plant organ show distinct patterns as a result of turgor changes, which are translated to volumetric changes using the elasticity and extensibility parameters (Fig. 5). As sugar load in each organ is volumetrically homogeneous, the final dimensional proportions of each plant organ are the result of differences in relative values of dimension-specific extensibility coefficients (Fig. 6). The development of the elongated shape of an internode is the outcome of ${\varphi }_{\text{z}}>{\varphi }_{\text{x}},{\varphi }_{\text{y}}$ with${\varphi }_{\text{x}}={\varphi }_{\text{y}}$, while the planar shape of the leaves results from ${\varphi }_{\text{z}},{\varphi }_{\text{x}}\gg {\varphi }_{\text{y}}$. Changing the relative proportions of the extensibility coefficients directly changes the dimensional proportions of the growing plant organs, which in turn influences plant hydraulics. Table 2 illustrates the effect of shifting the dimensional extensibility coefficients 10 % in favour of the longitudinal component and the radial component, respectively (in such a way that the volumetric response to turgor pressure (eqn 13) and the sink strength (eqn 16) remained unchanged). The result is the creation of thin and long internodes when the longitudinal component is increased as opposed to thick and short internodes when the radial component is favoured. Thin and long internodes cause a heavy increase in xylem flow resistance due to eqn (2), which lowers the turgor pressure, and consequently the growth potential, in plant organs higher up. This results in an overall decrease in growth, with smaller leaves and less sugar load leading to an overall less voluminous plant.

Fig. 5.

Changes in plant organ dimensions over time for each phytomer in the model simulation. (A) Internodes. (B) Leaves. (C) Fruits. The contractions and expansions illustrate the diel response of plant organ volume to changes in turgor pressure due to tissue elasticity and extensibility.

Fig. 6.

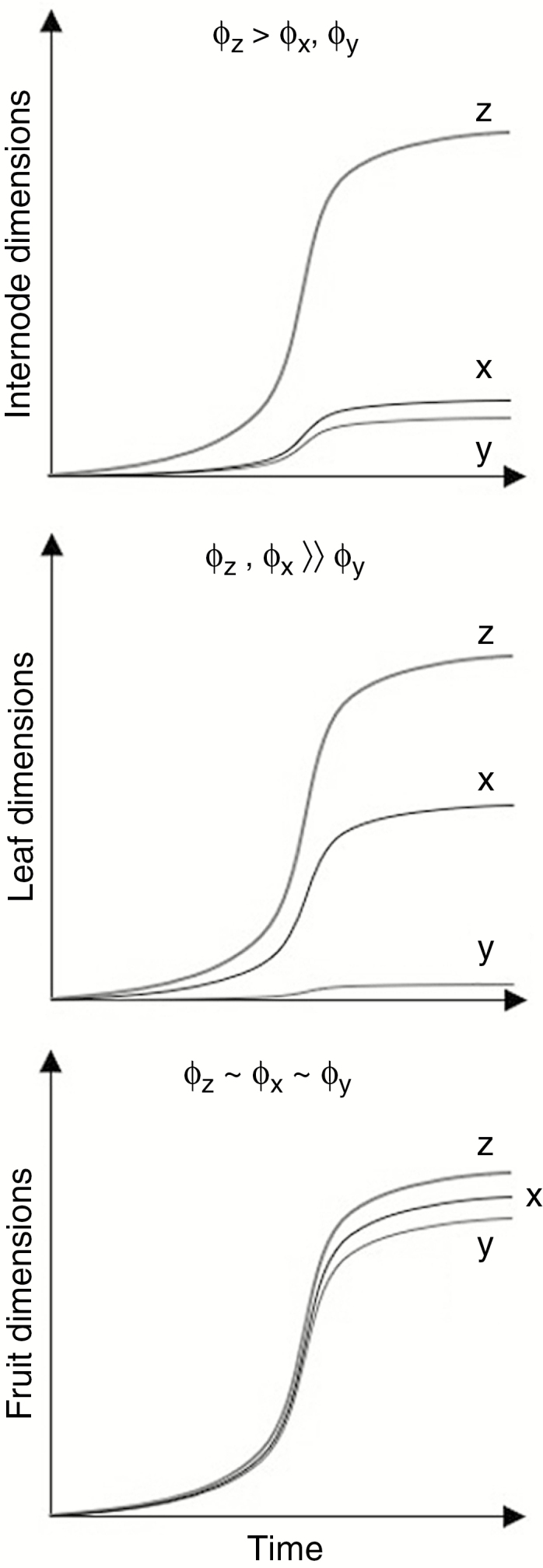
Final organ dimensions of individual plant organs as explained by differences in dimension-specific extensibility coefficients (${\varphi }_x,{\varphi }_y,{\varphi }_z$), which represent the ability of the organs to expand irreversibly (i.e. to grow) under sufficiently high values of turgor pressure. Their relative values result in an elongated shape for the internodes, a planar shape for the leaves and a round shape for the fruits.

Table 2.

Influence of a shift in dimensional extensibility coefficients in the internodes in terms of final plant height, plant volume, leaf volume and fruit volume. The elongated shift represents simulation results from a 10 % shift in extensibility in favour of the longitudinal dimension as opposed to the standard simulation. The widened shift results from a 10 % shift in extensibility towards the radial dimension. The resulting internode dimensions greatly affect plant flow resistance, with elongated and thinner internodes, greatly increasing xylem flow resistance and vice versa. Higher flow resistance results in a lower turgor pressure in plant organs higher up in the plant, lowering their growth potential and finally total plant volume

Simulation	Final plant length	Final plant volume	Final leaf volume	Final fruit volume
Normal	0.54	8.26 × 10−05	2.88 × 10−05	2.23 × 10−05
Elongated	0.90 (+66%)	5.82 × 10−05 (−30%)	2.05 × 10−05 (−29%)	1.49 × 10−05 (−33%)
Widened	0.30 (−44%)	9.73 × 10−05 (+18%)	3.36 × 10−05 (+17%)	2.70 × 10−05 (+21%)

DISCUSSION

The turgor-driven growth FSPM presented in this paper was intentionally kept simple to highlight the core concepts and reasoning behind our approach. Even so, it reveals some interesting diel and long-term dynamics underlying plant organ size. The diel dynamics in plant organ turgor pressure are the drivers of organ growth, resulting in patterns of elastic compression and expansion (Fig. 5) alongside irreversible growth. These are diagnostic patterns consistent with patterns of expansion and compression measured in stem diameter variations (e.g. De Swaef et al., 2015; Steppe et al., 2015). The magnitudes of elastic and plastic volume changes in a plant organ are driven by the magnitudes of their elasticity and extensibility, respectively. In the long term an exponential growth pattern is shown until the development of the fruits (Figs 2 and 5). Smaller phytomer size at the bottom of the plant results from lower transpiration in the early stages of development. As transpiration and carbohydrate production are dependent on leaf area, turgor dynamics during these early stages of development are far less distinct. Simultaneous development of fruits across the plant occurs when phytomer 5 is created, resulting in a large increase in sinks. This translates into a smaller amount of carbohydrates available for the growing organs, resulting in a smaller decrease in osmotic potential, lower turgor and consequently smaller organ sizes. This effect is amplified further by the reduced leaf transpiration with time, decreasing transpiration and carbohydrate production to zero on day 35.

In terms of final organ size, plant organs with different dimensions are created (Figs 2 and 5) despite the inherently identical parameters. This results from the interaction between the mechanisms underlying growth. The relative final dimensions depend on the conditions during their development. Water availability, transpiration and carbohydrate availability all play a role in establishing turgor pressure in the plant organs, which is required for growth. Therefore, there is no need to determine the ‘potential growth’ of each individual organ, a parameter often used in models of plant growth (Vos et al., 2007; Fourcaud et al., 2008). Potential growth is defined as the maximal growth of a plant organ in non-limiting conditions. It is determined by conducting experiments under low-limiting conditions for nutrients, light, water and internal competition (Drouet and Pagès, 2007). However, optimal growth conditions are hard to achieve and within-plant sink competition is difficult to neutralize (Marcelis, 1996). Furthermore, growth potential is not a static parameter, and depends on factors such as developmental stage or temperature (Marcelis, 1996).

Whereas our turgor-driven growth FSPM adds significant complexity to the current carbon-based approach in FSP modelling, it expresses this complexity in terms of quantifiable tissue properties (e.g. tissue elasticity and extensibility) and plant state variables (e.g. plant sap flow, stem diameter variations, plant organ turgor pressure). This not only allows valuable insights into plant functioning on a spatio-temporal scale, but also provides an opportunity to assess the validity of underlying growth dynamics by incorporating measurements of plant state variables regarding plant water status.

One of the primary reasons why current plant models retain a focus on C metabolism originates from the historic availability and ease of use of measurement tools for source-related processes such as photosynthesis, whereas sink-related processes such as cell expansion or phloem transport are much harder to quantify (Körner and Basel, 2013; Hubeau and Steppe, 2015). In recent years there has been increased interest in monitoring plant water status with direct (i.e. plant water potential) and indirect methods. Direct, non-invasive and continuous monitoring of plant water potential is still not straightforward, and indirect methods such as sap flow or stem diameter variations are more widespread. Firstly, measurements of sap flow can aid in estimating plant water status as it responds to soil water availability and atmospheric water demand (Jones, 2004). Secondly, automated monitoring of stem diameter variations allows insight into the radial water flow between xylem and surrounding storage tissue (Steppe and Lemeur, 2004; Steppe et al., 2006; De Swaef and Steppe, 2010; De Swaef et al., 2015). The continuous nature of data on these two variables provides a wealth of information regarding the diel dynamics of plant hydraulics. When combined with a process-based model, they allow insight into the dynamics of direct plant water status, such as stem water potential and turgor pressure (Génard et al., 2001; Steppe et al., 2006, 2008, 2016; Saveyn et al., 2007; De Schepper and Steppe, 2010; De Swaef and Steppe, 2010).

Furthermore, since this approach includes recordings of reversible and irreversible changes in stem diameter, biomechanical parameters like cell wall elasticity and extensibility are taken into account (De Swaef et al., 2015; Steppe et al., 2015). Elasticity and extensibility are parameters describing the plant cell’s volumetric response to changes in turgor pressure. Elasticity indicates the potential of a plant cell for reversible expansion and shrinkage, whereas extensibility quantifies irreversible cell growth, because of cell wall yielding. These relations between water status and plant growth have been described in the mathematical flow and storage model of Steppe et al. (2006). As extensibility and elasticity are parameters under genetic control specific to the plant tissue/organ (Mirabet et al., 2011), quantifying them alongside knowledge of plant organ turgor pressure gained through modelling essentially allows a quantification of growth potential from a sink perspective.

Our conceptual model focuses on the mechanistic aspects of plant water status, providing direct links to transpiration, carbon assimilation and source–sink behaviour, which are now incorporated in a very simplified manner. As these are the most commonly integrated mechanistic processes in C-based FSPMs, they provide anchor points for integration in more complex FSPMs. For instance, combination of our model with a mechanistic coupled transpiration and photosynthesis model (e.g. Kim and Lieth, 2003; Müller et al., 2007) would allow a mechanistic response to both water and light availability.

Another simplification was made in eqn (5), which is built on the assumptions of a negligible osmotic water potential in the xylem as well as a negligible contribution of the phloem to the total sap flow. While the former assumption is a generally accepted simplification, the contribution of phloem sap flow is variable and can contribute significantly in situations such as fruit filling [e.g. in tomato the phloem contribution to water influx is ~80–90 % (Liu et al., 2007; Hanssens et al., 2015)]. However, this assumption, together with that of no radial water transport, allows a large reduction in model complexity and, consequently, computation time. As we aimed to provide a relatively simple concept, which allows the exploration of the interaction between plant water status, turgor pressure, and organ growth, these simplifications were made after thorough consideration. Depending on the envisaged application of the turgor-driven FSPM, the model can be increased in complexity according to the current state of the art in water and sugar transport [e.g. De Schepper and Steppe (2010)] for which this model will provide a convenient stepping-stone. An example would be the integration of desorption curves, which describe tissue water content in relation to tissue water potential, and/or vulnerability curves, which describe the decrease in hydraulic conductivity in relation to the plant water potential (Baert et al., 2015; Vergeynst et al., 2015; Epila et al., 2017; Salomón et al., 2017). These can further improve the realism of the model’s growth response to water availability using variables already integrated in the model.

In this paper a conceptual sap flow and turgor-driven growth model is introduced for functional–structural plant modelling. It provides immediate links to the most prominently used ecophysiological submodels in FSP modelling, namely photosynthesis, transpiration and source–sink relations. Integration of this model into an FSPM allows translation of the water limitations on growth in terms of turgor pressure, but also evaluates growth in terms of quantifiable tissue properties in 3-D. As a result, the growth rate of an organ strongly depends on the conditions in which it develops. This leads to the development of plant organs from a sink perspective with significantly different dimensions originating from the same intrinsic parameters.