Plant architecture and foliar senescence impact the race between wheat growth and Zymoseptoria tritici epidemics

Abstract

Background and Aims

In order to optimize crop management in innovative agricultural production systems, it is crucial to better understand how plant disease epidemics develop and what factors influence them. This study explores how canopy growth, its spatial organization and leaf senescence impact Zymoseptoria tritici epidemics.

Methods

We used the Septo3D model, an epidemic model of Septoria tritici blotch (STB) coupled with a 3-D virtual wheat structural plant model (SPM). The model was calibrated and evaluated against field experimental data. Sensitivity analyses were performed on the model to explore how wheat plant traits impact the interaction between wheat growth and Z. tritici epidemics.

Key Results

The model reproduces consistently the effects of crop architecture and weather on STB progress on the upper leaves. Model sensitivity analyses show that the effects of plant traits on epidemics depended on weather conditions. The simulations confirm the known effect of increased stem height and stem elongation rate on limiting STB progress on upper leaves. Strikingly, the timing of leaf senescence is one of the most influential traits on simulated STB epidemics. When the green life span duration of leaves is reduced by early senescence, epidemics are strongly reduced.

Conclusions

We introduce the notion of a ‘race’ for the colonization of emerging healthy host tissue between the growing canopy and the developing epidemics. This race is 2-fold: (1) an upward race at the canopy scale where STB must catch the newly emerging leaves before they grow away from the spore sources; and (2) a local race at the leaf scale where STB must use the resources of its host before it is caught by leaf apical senescence. The results shed new light on the importance of dynamic interactions between host and pathogen.

INTRODUCTION

Septoria tritici blotch (STB) caused by Zymoseptoria tritici is one of the most loss-causing diseases on wheat. With the development of resistance to fungicides (Leroux and Walker, 2011; Fraaije et al., 2012) and tighter regulation, innovative strategies of control are needed. Properties of the crop canopy could be used to dampen the pathogen pressure (Lovell et al., 1997, 2004; Ando et al., 2007; Calonnec et al., 2012; Costes et al., 2013). For this, a thorough understanding of the fungal biology and its interactions with the host and the environment is required. Epidemics of STB are initiated in autumn often by wind-dispersed ascospores infecting the first leaves of the plant (Sanderson and Hampton, 1978; Shaw and Royle, 1989; Suffert et al., 2011). Zymoseptoria tritici then causes polycyclic epidemics that result from the repeated successions of infection cycles and spore dispersal. The interactions between the plants and the pathogen occur both at the leaf scale where foliar tissues influence the infection cycle and at the canopy scale where canopy architecture influences spore dispersal.

Wheat plant architecture modulates the epidemics of Z. tritici. In the 1980s, Eyal and Ziv (1974) noticed that the introduction of dwarf wheat varieties was correlated with an explosion in STB severity. Several authors reported that tall plants were attacked less by Z. tritici, independently of intrinsic resistance (Tavella, 1978; Danon et al., 1982; Camacho-Casas et al., 1995; Simón et al., 2005, Arriano et al., 2009). Pycnidiospores are dispersed by rain splash from the lower infected leaves to the upper leaves during the cropping season. The closer leaves are, the more easily spores are transported up the plant (Bahat et al., 1980; Lovell et al., 1997, 2004). Indeed, the number of splashed droplets declines exponentially with height from the source (Shaw, 1987). The distance between infected and healthy tissues is therefore critical, and newly emerged upper leaves may escape disease according to plant architecture and weather conditions. The distances between leaves change throughout the season due to multiple processes: leaf and stem growth, leaf curvature and tillering dynamics. Each of these architectural traits could influence STB progress. We introduce the notion of a ‘race’ between the growing host and the developing pathogen population, to describe host colonization dynamics resulting from differences in the speed of disease progress and plant development. After infection, there is an upward race between plant growth and epidemic progress that depends on wheat architecture.

At the leaf scale, another type of race between pathogens and the plant may occur, namely a race for the use of green leaf tissue. For wheat, leaf apical senescence enables the recycling of nitrogen from shaded locations towards unshaded ones and thus optimizing plant photosynthesis (Bertheloot et al., 2008). Depending on the progress in the infection cycle, the impact of senescence on the hemibiotrophic fungus Z. tritici should vary. The penetration into the leaf and the growth of primary mycelium occur in living foliar tissue. This is followed by the emergence of chlorotic symptoms, which then develop into necrotic and sporulating lesions. The latest stages of the infection cycle are achieved on necrotic tissue (Palmer and Skinner, 2002; Keon et al., 2007; Robert et al., 2008; Sánchez-Vallet et al., 2015). In our model, we thus assume that germinating spores and young hyphae are trapped if apical leaf senescence reaches them, but that older lesions are not impacted.

Based on the above, we argue that two different types of race occur: an upward race to infect new healthy leaves before they reach a critical distance; and a local race to colonize the infected leaf before natural senescence. Our study aims to quantify the effect of plant structure on STB epidemics in the light of these two types of race. As proposed by Room et al. (1996) and Wilson and Chakraborty (1998), we use functional–structural plant models (FSPMs) to disentangle, understand and quantify the multiple and dynamic effects of plant architecture on epidemics (Lovell et al., 2004; Robert et al., 2008). We use Septo3D (Robert et al., 2008; Garin et al., 2014), an STB epidemic model combined with a structural plant model (SPM) of wheat (Fournier et al., 2003; Abichou et al., 2013). The latter simulates how 3-D plant architecture develops dynamically, as well as the progress of senescence at the level of individual leaves (Vos et al., 2007; Balduzzi et al., 2017). In this way, the size, location and distance of source and target leaves can be taken into account, as well as their size during spore dispersal, and also how leaf senescence impacts the infection cycle of Z. tritici (Robert et al., 2008). A previous sensitivity analysis of Septo3D has shown a potentially important role for several architectural traits on epidemics (Robert et al., 2008). Septo3D has also been used to show the impact of wheat density during winter on STB epidemics (Baccar et al., 2012). In the work of Garin et al. (2014), the model has been updated and modularized under the OpenAlea modelling platform (Pradal et al., 2008, 2015) to facilitate its extension to other pathosystems.

In the present study, we first reveal the effects of plant properties on epidemics by means of Septo3D sensitivity analysis and supported by field experimental work. Next, we use Septo3D to study the impact of certain plant properties on the race between plant growth and pathogen epidemics, in relation to disease escape. In particular, we aim to disentangle the influence of plant structure on the upward and the local race between host tissue growth and its colonization by Z. tritici.

MATERIALS AND METHODS

Study overview

Our work consists of three parts: (1) a 3 year field experiment was performed to observe in detail the upward disease progress in varied wheat canopies and under varied weather conditions; (2) these experimental data were used to test the capacity of the model to reproduce such disease dynamics on the upper leaves of the canopy; and (3) the model was used to explore the ‘weather × wheat architecture × STB’ interactions with the aim of revealing the most influential plant traits on STB epidemics and how plant architecture influences the race for green leaves by STB.

Field experiment

Overview.

A field experiment was performed over three growing seasons. Plant architecture, weather and disease measurements were performed throughout each growing season.

Experimental design.

The field experiment was carried out in 2010–2011, 2011–2012 and 2012–2013 (referred to as seasons 1, 2 and 3) at the research station of Arvalis – Institut du Végétal at Boigneville (France, 48°32ʹN, 2°37ʹE). Two wheat isogenic lines with contrasting architecture were sown in season 1: Mercia and Mercia-Rht3 (referring to Triticum aestivum Mercia with an Rht3 allele, from the John Innes Centre, UK). A third architecture was tested using the cultivar Tremie that was sown in season 2 and 3. All three wheat lines used are susceptible to STB. Air temperature at a height of 2 m, amount of rainfall in millimetres, relative humidity and radiation were monitored hourly over the three seasons. More details on the experimental design are given in Supplementary Data Information 1.

Wheat plant assessments.

The dynamics of leaf appearance, tillering and the organ dimensions were measured on main stems in season 1, 2 and 3 (Supplementary Data Information 1). In parallel to these measurements, two destructive samples on 0.6 × 0.6 m micro-plots were used to measure the leaf area index (LAI) in seasons 2 and 3.

Disease and senescence assessments.

The dynamics of apical senescence and sporulating lesions of Z. tritici were monitored at the individual leaf level on the main stem of tagged plants. The percentage of leaf area covered by apical senescence was assessed in the three seasons. In season 1, the percentage of STB sporulating lesions in the green part of the leaf was assessed, which is a good estimate of the total leaf area covered by necrotic sporulating lesions as long as leaf area covered by senescence is <50 %. Assessments on the four top leaves were carried out on 30 plants per block (total 90 plants) at two dates: flowering stage (25–26 May) and 10 d later (8 June). In seasons 2 and 3, the percentage of leaf area covered by necrotic lesions of STB was assessed on nine dates between 3 April and 12 June, and between 22 May and 15 July in season 2 and 3, respectively. For this, ten and 15 plants per block (total 30 and 45 plants) were marked with rings to identify leaf ranks in season 2 and 3, respectively. At each measurement date, the five upper leaves were assessed. Additional measurements on the four top leaves were carried out on an increased number of plants (90 plants) on two occasions: 31 April–8 June and 13 June–26 June in season 2 and 3, respectively. They were used to assess whether the marked plants were a good representation of the whole population.

Calculation of thermal time.

Within the temperature range encountered during the experiment (<25 °C), the thermal time (Γ, degree days denoted °Cd) was calculated by assuming a linear response to temperature above a base temperature T_b (taken as 0 °C):

$$\Gamma =\frac{1}{24}{\displaystyle \sum _i\max (0,T_{air}-T_b)}$$ (1)

where i is the number of hours elapsed after seedling emergence and T_air is the hourly averaged air temperature at 2 m height.

Analyses of disease measurements.

Disease data were grouped by date and by leaf rank. Leaf numbers were counted from the top of the canopy, starting with 1 for the flag leaf. The variability in the data sample was estimated using the 95 % confidence interval, except for samples with <20 replicates where bootstrapped 95 % confidence intervals were used. For each data set, the observed epidemic progress was analysed in comparison with an optimal epidemic development. In optimal climates for Z. tritici (periodic rain events and high humidity levels), wheat leaves can be infected successively shortly after leaf emergence. In this case, they display the first sporulating symptoms one latency period (approx. 350 °Cd) after leaf emergence, which occurs sequentially every new phyllochron (approx. 100 °Cd). We thus expect an optimal infection sequence to produce parallel disease curves, with strong slopes, every phyllochron. In summary, the observed data were analysed for: (1) the date of emergence of the first sporulating symptoms on each leaf relative to leaf emergence (in comparison with one latency period); (2) the difference in time of infection between successive leaf ranks (in comparison with one phyllochron); and (3) the speed of leaf colonization after first symptoms (in comparison with an exponential growth). In this perspective, the epidemic data for each leaf rank were plotted in thermal time since sowing and also in thermal time since host leaf emergence. For seasons 2 and 3, disease progress was also compared between plants with different final numbers of leaves within the same canopy.

SEPTO3D model overview

Septo3D (Robert et al., 2008; Garin et al., 2014) is an FSPM combining a wheat architectural plant model (ADELWheat, https://github.com/openalea-incubator/adel) with an STB epidemic model. The model is distributed as open source software and is available on github for reproducibility (https://github.com/openalea-incubator/alep). Wheat growth, leaf infection, lesion development and spore dispersal are handled by separate sub-models that operate at different spatial and temporal scales. A simulation covers a full growing season and uses climatic and architectural input data. A brief overview is given in this section. Parameters are given in Table 1.

Table 1.

List of parameters in the model of septoria leaf blotch

Parameter (unit)	Symbol	Value	Source
Lesion
Incubation period (°Cd)	TTincubation	220	Robert et al. (2008)
Chlorosis period (°Cd)	TTchlorosis	60	Robert et al. (2008)
Non-sporulating necrosis period (°Cd)	TTnecrosis	50	Robert et al. (2008)
Vulnerable period to senescence (°Cd)	TTsenescence	100	C. Robert pers. com.
Lesion growth rate (cm2 °Cd–1)	r	6e-4	Robert et al. (2008)
Lesion surface after incubation (cm2)	Smin	0.03	Robert et al. (2008)
Maximal lesion surface (cm2)	Smax	0.3	Robert et al. (2008)
Minimum relative humidity for lesion growth (%)	RHmin_les	35	Calibrated with Tremie 2012
Dispersal unit
Maximal irradiance (micromole PAR m–2)	PARmax	644	Robert et al. (2008)
Minimum relative humidity for infection (%)	RHmin_inf	85	Robert et al. (2008)
Cumulative hourly loss rate		8e-4	Robert et al. (2008)
Dispersal process
Number of rain events before empty	n	10	Calibrated with Tremie 2013
Maximum height reached by dispersal (cm)	H	55	Calibrated with Tremie 2013

The wheat model simulates a growing 3-D canopy (Fournier et al., 2003; Abichou et al., 2013). The model simulates dynamically the architectural development as a function of thermal time. We assume that epidemics do not influence plant architecture, which is a reasonable assumption for Northern Europe. The canopy is a population of individual plants. Each plant is described by its axes (main stem and tillers) and leaves characterized by their age, size, shape, curvature, and green and senesced area. Axes may have different total leaf numbers. We use a dynamic model of leaf shape curvature during leaf expansion (Fournier and Pradal, 2012; Robert et al., 2015). Using the methods of Fournier et al. (2003) and Abichou et al. (2013), organ growth and dynamics of tillering are reconstructed. We obtain a wheat model that describes in detail the dynamics of the canopy architecture for which the boundaries are determined according to a parameter calibration against field data (see the calibration model). The model allows us to compute the LAI throughout the season, which is used as a verification of the accuracy of our canopy model. Leaves in the wheat model are divided into transverse sections (of a few square centimetres) that define the resolution of the plant model with regards to the disease model.

The STB model simulates a polycyclic epidemic driven by climatic conditions (temperature, rain, light and humidity) and plant development. The equations for the following epidemic stages are given in both Robert et al. (2008) and Garin et al. (2014). First, the primary inoculum is simulated in winter by considering a fraction of ground area being a source of spores. This assumption was also used in Baccar et al. (2012) and in Audsley et al. (2005). The dispersal model, described below, is applied to the soil as if it was a large uniform source of spores. The infection cycle model describes lesion development in terms of infection, incubation, latency and sporulation. Lesions of the same age present on the same leaf section are grouped in cohorts for greater computing performance. Infection can occur on green tissue only if the temperature is within a favourable range and if the leaves stay wet long enough (Table 1). After incubation, a lesion consists of young chlorotic tissues that colonize surrounding green areas, while the oldest, inner tissues become necrotic and sporulating. Each stage has a fixed thermal time duration (Table 1), except that ageing of incubating lesions is paused when the relative humidity (RH) is too low (<RH_{min_les} in Table 1) (Shaw et al., 1990, 1991). The parameter RH_{min_les} was included after observations of season 2 that revealed a long pause of disease progress during an exceptionally dry event. Simulations for seasons 1 and 3 were found to be identical with or without the introduction of this new parameter. Once leaf senescence progresses over the lesion, lesion growth stops. Young incubating tissues (age <TT_senescence in Table 1) are killed by senescence. Older tissues keep ageing. The position of lesions on the leaf determines the space available for growth and the timing at which the lesion encounters senescence. The higher the number of leaf sections simulated in the wheat model, the more precise is the location of lesions and hence the influence of senescence, but the costlier the computation.

The model of spore dispersal operates at the canopy scale. In our model, seasonal epidemic development is the result of splash dispersal of pycnidiospores. We do not consider the possible role of wind-dispersed ascospores. Emission of dispersal units is a function of the exposure of sporulating lesions to rain, of the re-emission of droplets by splashing at lesion sites and of the availability of spores at these lesion sites. The exposure of lesions to rain is computed at the scale of individual leaf sections with a 3-D direct light interception model (the Caribu model; Chelle et al., 1998) considering that rain drop flux is analogous to a vertical light photon flux. The emission of droplets from leaf sections exposed to rain is computed by multiplying a rain-dependent droplet emission flux density (droplets m^–2 h^–1) by the duration of the rain (hours) and by the exposed sporulating area of the section (square meters). The droplet emission flux density is obtained from a bivariate look-up table relating rain intensity (mm h^–1) and rain duration (hours) to droplets emission flux density. This table was constructed using the statistical approach by Saint-Jean et al. (2004) to estimate rain drop flux, rain drop diameter distribution and rain drop velocity distribution from rain intensity and rain duration, and physical empirical laws from Saint-Jean et al. (2004) for estimating droplet emissions per drop as a function of drop diameter and velocity. Compared with the study of Robert et al. (2008), that considered a constant proportionality between rain intensity and droplet emission density, this new approach takes into account both rain intensity and rain duration: on average this results in a 55 % smaller droplet flux density than those of the original model. This increased level of realism has only a minor computational cost. The model of transport simulates the vertical repartition of emitted dispersal units in the canopy. Dispersal units travel a limited distance upward (Table 1). The density of emitted droplets decreases exponentially with distance. Droplets then fall vertically with gravity. During both movements, droplets are intercepted or not by the vegetation. As a result, a flux of dispersal units is assigned to individual leaf sections. Following the model of Ma et al. (2008), a Poisson function was used to take into account droplets overlaying on leaf surface. Then a new infectious cycle may start for each deposited dispersal unit.

In the model, plant structure influences epidemics through the foliar green tissue available for infection and lesion growth, the density of vegetation that affects rain penetration and the distribution of infectious droplets by rain splash, and the position of leaves that determines distances between infected and healthy tissue. We have selected eight key plant traits for the analyses of their effects on STB dynamics (Table 2). For the plant organs’ dimensions we analyse the effects of leaf length (Length_leaf), leaf width (Width_leaf) and internode length (Length_stem). These are the parameter values for the flag leaf. They also determine the size of all the other leaves as the model is based on fixed allometric laws that relate organ position to organ dimension. The five other parameters modify the dynamics of plant growth. Phyllochron sets the delay between the emergences of two successive leaves, and between the elongation of two successive internodes. Elongation_leaf and Elongation_stem set the rate of leaf elongation and stem elongation, respectively. Curvature_leaf controls the dynamics of leaf bending with leaf age (higher value accelerates leaf bending). Senescence_leaf determines the onset of apical senescence. These plant traits are likely to have different effects on epidemics. The parameters affecting the stem dimension (Length_stem) and elongation rate (Elongation_stem) modify the distance between infected and healthy emerging tissue and thus impact the upward race. The effect of leaf dimensions on epidemics is potentially multiple. Leaf area influences the interception of rain and of infectious droplets. It also determines the amount of available tissue for the fungus. Leaf curvature dynamics could also have multiple effects by influencing both rain interception and distance between the leaves. Senescence timing determines the temporal window for fungal development on the leaves and therefore the local race at the leaf scale.

Table 2.

List of plant parameters controlling plant architecture used in the sensitivity analysis of the model

Parameter (unit)	Symbol	Reference value	Unit
Earliness of leaf/internode emergence	Phyllochron	91.2	°Cd
Rate of leaf elongation	Elongation leaf	0.86	mm °Cd–1
Rate of leaf curvature (inverse of bending duration)	Curvature leaf	0.002	°Cd–1
Length of flag leaf	Length leaf	15.72	cm
Width of flag leaf	Width leaf	1.9	cm
Earliness of leaf senescence	Senescence leaf	895.7	°Cd
Height of flag leaf	Length stem	65,18	cm
Rate of internode elongation	Elongation stem	1.3	mm °Cd–1

The third column indicates the reference values chosen as observed in season 3.

Model calibration and evaluation

The aim of this part of the study was to assess the capacity of the epidemic model to simulate STB progress in a given wheat stand, under given climatic conditions, on the upper leaves of the canopy. The following paragraphs explain the methods of calibration and model evaluation.

Conditions of simulation.

There is an intrinsic stochasticity in the model that causes variation in the outputs between runs. This stochasticity comes from random plant parameters controlling the intra-canopy variability in dates of plant emergence, in final leaf number, in probability of tiller emission and mortality, and from the random orientation of plants and its impact on spore dispersal. In this study, simulations were run on toric canopies (i.e. without border effects) obtained by a virtual infinite duplication of a microplot of 15 different individual plants whose leaves are divided into seven sections. The sampling of plant parameters was constrained so that all parameter distributions in the virtual canopy are the same as the observed distributions. This choice was the result of a compromise between computation time and result stability (data not shown). For each season, the severity curve on each leaf layer was the mean of ten repetitions of the simulation. Overall, the time of simulation for one season was approximately one night (Intel Core i7-3770CPU@3.40GHz, RAM 8Gb, Python 2.7.8).

Model calibration.

The model ADELWheat simulating the wheat canopies was calibrated using mock-ups of wheat stands with all available data from the field experiment for each isogenic line and each season, i.e. (1) at the organ level on main stems, the number, size, emergence, senescence and geometry of leaves and stem; and (2) at the canopy level, the axis density and the probability of axis emission were all fitted to field measurements (Supplementary Data Information 2). The canopy was corrected for incidental damage during winter, insects in season 1 and frost damage in season 2. Sub-modules of ADELWheat were used for simulating the dynamics and co-ordination of elongation of the different organs (Fournier et al., 2003) and the organ dimensions on tillers (Abichou et al., 2013).

For the STB disease model, we used the same parameters for the three seasons (Table 1). Most of the parameters values were identical to those of Robert et al. (2008). The value for TT_senescence was taken from new experimental results (C. Robert, pers. comm.). Two independent parameters n and H have been calibrated on the data set of season 3, which was the most complete (Table 1).

The primary inoculum is the initial condition for the epidemic model. In the field it varies each year and it cannot be predicted with our model. It was hence calibrated for each year to fit the disease severity on the lowest assessed leaves. In practice, the root mean square error (RMSE) between simulation and observation was minimized on leaves 3 of Mercia in season 1, on leaves 5 in season 2, and on leaves 5 and 6 on average for season 3. As a result, we used values of 1.5 × 10^–5, 4 × 10^–3 and 1.5 × 10^–3 sporulating m² m^–2 of ground for seasons 1, 2 and 3, respectively, (RMSE of 3, 12.1 and 6.4 %, respectively). For season 1, the value for the primary inoculum was identical for both wheat lines.

Model evaluation.

The model was evaluated on the quality of its simulation of the detailed dynamics of disease progress at the individual leaf level on upper leaves, given a fitted inoculum each year that controlled the disease severity on the lower leaves. The simulated severity curve was compared with disease measurements on each upper leaf layer. We tested how the model ranked the severity of the epidemics among architectures. The average RMSE was calculated for seasons 2 and 3, which had enough data. This assessed how close the simulated curves were to the observed data points. We also checked how the model simulated the detailed features of epidemics such as: the onset of symptoms, the time to reach maximum severity and the temporal succession on leaf layers. The model was also tested for plants with different final numbers of leaves within the same canopy.

Sensitivity analysis of the model

Three types of sensitivity analysis (SA) were done: (1) a global SA; (2) a single plant trait SA; and (3) a detailed SA focusing on the two types of race. These three analyses are complementary and correspond to a sequential increase in detail of the analysis. The first SA allows for a global sweep of a large parameter space. The second SA zooms in on the importance of eight selected plant traits, comparing three values for each trait (–20 %, 0 and +20 % change). The third SA is a fine analysis of the three selected plant traits thought to be critical in the plant–pathogen race, comparing 11 values of each trait (from –30 %, –25 %, …, +30 % change). Due to differences in computational demands, the first was done for only two different weather scenarios whereas the latter two SAs were run for eight different weather scenarios. The output variables used were the maximal STB severity or the area under the disease progress curve (AUDPC). The AUDPC is sensitive to the earliness, the rate and the maximal STB severity (Madden et al., 2007). We tested eight key plant traits listed in Table 2. The reference plant architecture was the wheat of season 3 (Tremie). An intermediary level of initial inoculum was used (1.5^e–3 m² of sporulating tissue m^–2 of ground).

Global sensitivity analysis.

We used the Morris method that is suited for models that require significant computation times (Morris, 1991; Campolongo et al., 2007). The Morris method is an iterative process in which two successive evaluations of the model differ by only one input factor. For each input factor x_i (with i = 1, …, k), a range of variation is defined, standardized as a [0, 1] interval and divided into p equidistant values or levels. In this way, the region of experimentation Ω is a k-dimensional p-level grid. In this study, k = 8 wheat parameters and p were fixed to 5. A relative range of variation of ±20 % was considered for the eight plant parameters (Table 2). Then, the sampling strategy provides n random trajectories in Ω so that the space is explored from more than one reference point (Campolongo et al., 2007). Consequently, the total number of model evaluations is n × (k + 1). An elementary effect E_i is calculated for each trajectory as follows:

$$E_i=[Y(x_1,\dots ,x_i+\Delta ,x_k)–Y\left(x_i\right)]/\Delta$$ (2)

where Y(x_i) is the value of model output at input x_i, i = 1, …, k, and Δ is the distance, in the range [1/(p – 1), …, 1–1/(p – 1)], between two consecutive levels (Morris, 1991; see Campolongo et al., 2007 for more details). In the end, two sensitivity indicators are measured for each factor: the absolute value of the mean of elementary effects μ* (overall influence) and their standard deviation σ (higher order effects, i.e. non-linearity or interactions with other parameters). The influence of parameters is usually discriminated with a graphical representation of σ vs. μ*: the most influential parameters will have high values of μ* and σ (Campolongo et al., 2007).

This analysis was run for two different seasons with contrasted weather conditions: Grignon, France, 2011 and 2013. For each season, three repetitions of the same analysis were made. We used the Morris functions of the open-source Python library (SALib-0.4-py2.7) (Usher et al., 2015).

Single plant trait sensitivity analysis.

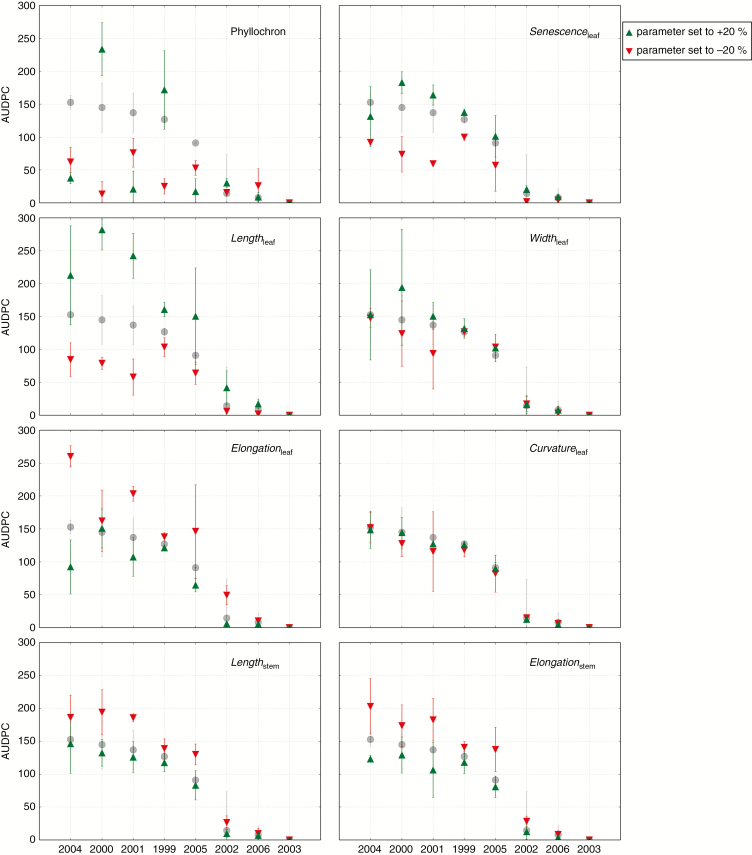
This analysis quantified one-by-one the effects of the eight plant traits (Table 2) in eight seasons with contrasted weather conditions (Grignon, France, 1999 to 2006) (Supplementary Data Information 3). The simulation results on flag leaves were compared for three values of each plant trait: –20 %, Reference and +20 %. For each parameter value and each season, three repetitions were run.

Sensitivity analysis focusing on the two types of race.

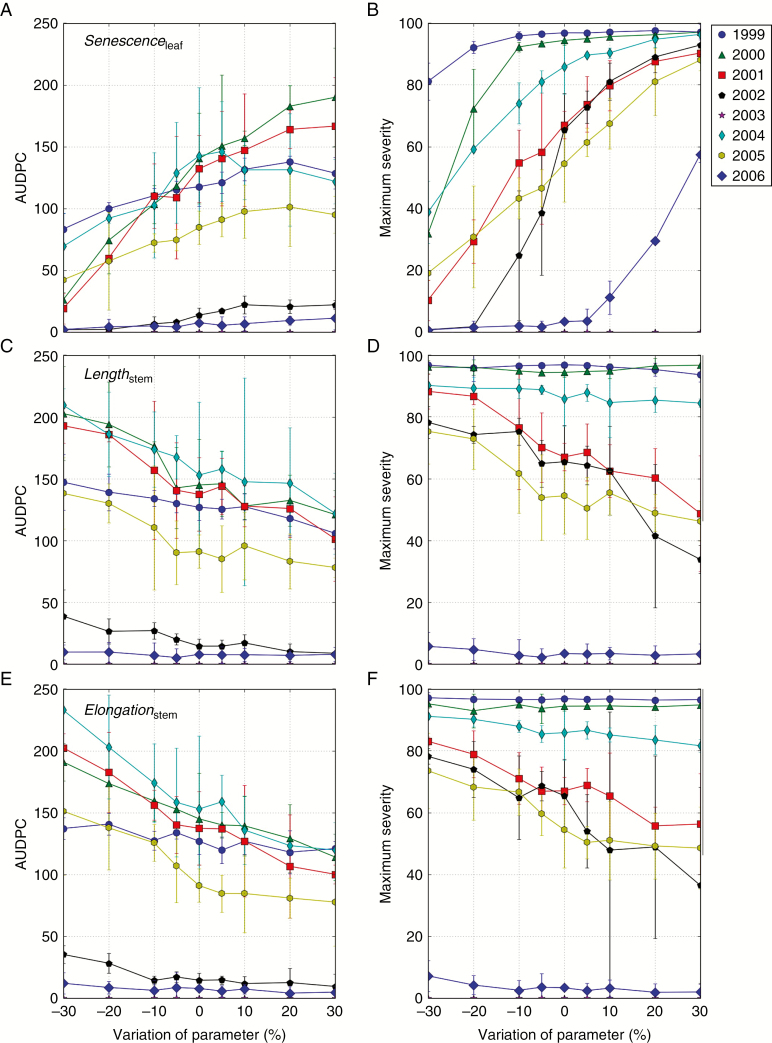
Among the eight plant traits tested, three were selected because of their direct influence on STB. Length_stem and Elongation_stem determine stem height and thus impact the upward race. Senescence_leaf controls the onset of senescence and thus impacts the local foliar race. Each parameter was varied from –30 % to +30 % of its reference value with a 5 % step, in eight seasons with varied weather conditions (Grignon, France, 1999–2006). For each parameter value and each season, three repetitions were run.

RESULTS

Field experiment

Weather conditions.

Weather conditions were different for the 3 years of the experiment (Supplementary Data Information 3). In all three winters (0–700 °Cd post-sowing), the RH stayed high, the temperatures were often not limiting for infection and rain events were frequent. A frost period was recorded in season 2. Pronounced differences between seasons appeared in spring (between 700 and 1700 °Cd post-sowing). The spring of season 1 was the driest, with frequent drops in relative humidity and few rain events. In season 2, two periods of drought occurred (1000–1200 °Cd and 1500–1700 °Cd post-sowing). However, many rain events occurred between 1200 and 1500 °Cd under mild temperatures. In season 3, the humidity was maintained at a high level and rain events occurred at a steady rate.

Wheat development and architecture.

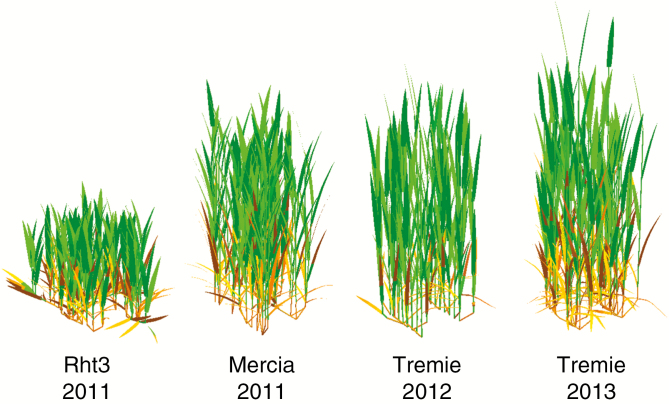
The wheat plants of all growing seasons and lines displayed contrasting architectural features. At the population level, the axis density reached a maximal density of around 1000 axis m^–2 in every season, but then tillering dynamics differed. These differences were partly explained by axis loss due to insect attacks in season 1 and to frost damage in season 2. The final number of leaves on main stems varied from 11 to 13 between seasons and varieties (Table 3). A modal number of leaves was observed for two-thirds of the plants, and a secondary mode for one-third of the plants. The dates of plant emergence followed a normal distribution with an s.d. of 50 °Cd. The rate of leaf appearance was 20 % higher on Tremie than on Mercia. This resulted in a significantly shorter vegetative phase on Tremie regardless of the final number of leaves. For Tremie, the rate of leaf appearance was almost identical between axes bearing different leaf numbers, whereas for Mercia the rate decreased with final leaf number. For Mercia, numbering leaves from the top thus resulted in an almost synchronous date of leaf appearance at a given leaf position for the plants with different final leaf number. For Tremie, however, this resulted in delayed leaf appearance at a given leaf position for plants with a higher final leaf number. For the flag leaf, this delay is approx. 50 °Cd in season 2 and 20 °Cd in season 3. On all varieties, the delay between ligulation and the start of leaf senescence increased strongly for upper leaves. Tremie had shorter green leaf life spans than Mercia. The dimensions of organs on main stems were similar in Mercia and Tremie, but Mercia-Rht3 displayed much shorter internodes, sheaths and blades. Mercia-Rht3 also had wider leaves, but still had the smallest leaf areas. These differences led to a halving of the canopy height for Mercia-Rht3 (Table 3), and to almost identical individual heights in the other canopies. Leaves were erectophilic for all varieties (Fig. 1). At the canopy level, contrasted dynamics of green LAI were observed and simulated with the model. Much of the variation in maximal LAI was explained by differences in axis density, with an additional reduction of leaf size for Mercia-Rht3.

Table 3.

Axis number, canopy heights and total leaf number on the main axis for the different experiments

	Mercia season 1	Mercia-Rht3 season 1	Tremie season 2	Tremie season 3
Plant density	211 ± 8.5	215 ± 4.5	281 ± 22.3	235 ± 34.0
Axis density at harvest	444 ± 55	384 ± 31	491 ± 56	675 ± 65
Canopy height (cm)	66.1 ± 4.6	29.3 ± 4.1	69.6 ± 6.0	n.a.
Leaf number on main stems	12 (11)	11 (12)	13 (12)	11 (12)

For measured densities and heights, we indicate the s.d. For leaf numbers, we indicate the dominant (regular) and the minor (italics) modes.

Fig. 1.

Plant architecture simulated by the model ADELWheat for the four experimental treatments (canopies of 15 plants at 1500 °Cd since sowing).

Epidemic development.

The disease development was spatially homogeneous in the three untreated experimental plots in the three seasons, as shown by the narrow distribution of severity (Fig. 2). In seasons 2 and 3, the two disease measurements from larger samples did not differ significantly from weekly measurements, indicating high consistency in observations and no influence of handling on disease progression.

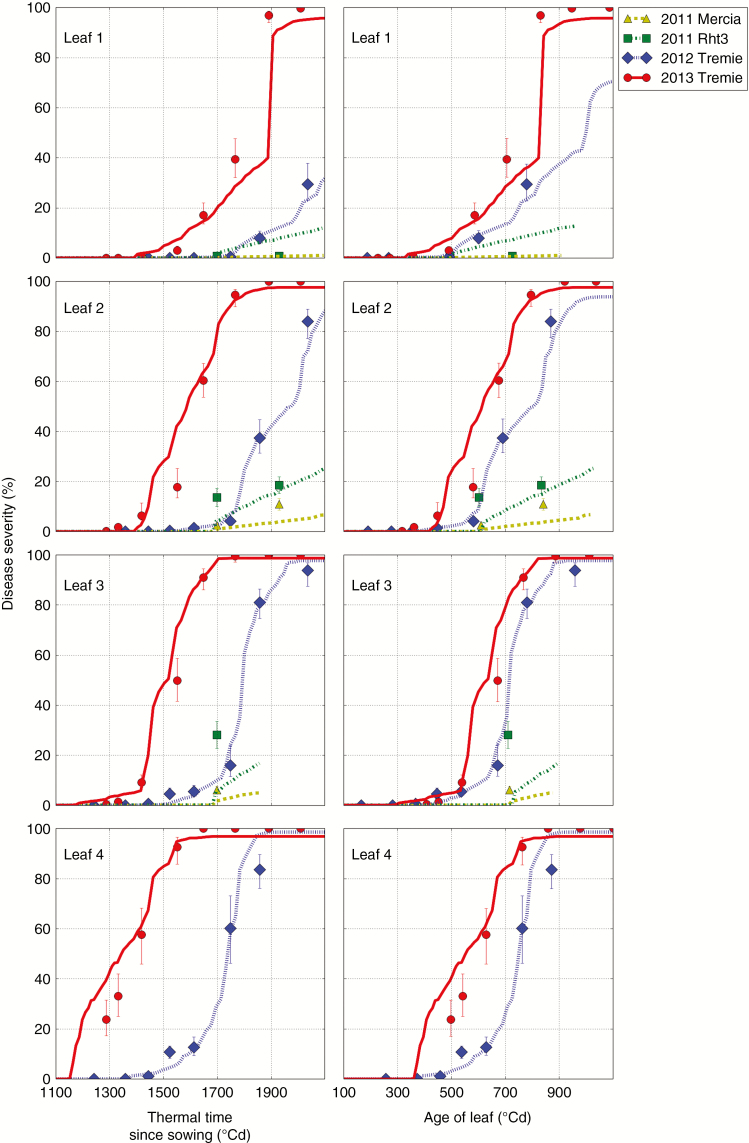
Fig. 2.

Observations and simulations of STB severity plotted against thermal time since sowing (A) and against the age of leaves (B) on leaf ranks 1–4. Dots: means and 95 % confidence interval of observations. Lines: results of the simulation.

The data show contrasting STB development in the three seasons. In season 1, the level of disease was low on both wheat lines (Mercia and Mercia-Rht3). It was much lower than in seasons 2 and 3 (Table 4). The data also show a significant effect of the Rht3 locus substitution, with almost no disease on Mercia and a moderate severity on Mercia-Rht3 (Table 4). In seasons 2 and 3, the level of disease was high. The maximal severity was >80 % for leaves 2–5. Disease progress was regular and fast in season 3: the severity progress followed a steep and regular increase and the STB progress on successive leaf ranks was almost parallel and separated by a delay of 100 °Cd approximately (Fig. 2). In season 2, the severity progress was more irregular (Fig. 2): the delays separating two successive leaf layers were variable. Two periods of low disease development were noted (1200–1400 °Cd, and 1500–1600 °Cd after sowing). However, after 1600 °Cd, the severity increased rapidly on the leaves, with a similar slope to that in season 3. When disease severity was plotted in thermal time since sowing (Fig. 2A), it increased much earlier in season 3 than in season 2: up to 300–400 °Cd earlier depending on the leaf rank. These differences were, however, strongly reduced when severity was plotted for each rank against the thermal time since leaf emergence (Fig. 2B). The ages of leaves at the time of appearance of the first symptoms were nearly the same in seasons 2 and 3 (around one latency period after leaf emergence approx. 350 °Cd) (Fig. 2B).

Table 4.

Mean severity (and 95 % confidence intervals) observed on leaves 1, 2 and 3 of Mercia and Mercia-Rht3 wheats in season 1, and of Tremie in seasons 2 and 3 at the same plant age

Variety	Date	Degree days	1	2	3
Mercia	25 May 2011	1690	0.18 ± 0.10	2.52 ± 0.58*	6.07 ± 1.44*
	8 June 2011	1921	0.31 ± 0.30	10.92 ± 2.36*	–
Mercia-Rht3	25 May 2011	1690	0.84 ± 0.77	13.64 ± 3.65*	28.17 ± 5.41*
	8 June 2011	1921	0.81 ± 0.43	18.56 ± 3.35*	–
Tremie season 2	25 May 2012	1749	0.40 ± 0.21	4.12 ± 0.82	15.88 ± 4.3
	31 May 2012	1858	7.9 ± 2.13	37.49 ± 6.09	81.05 ± 6.67
Tremie season 3	17 June 2012	1648	17.09 ± 3.39	60.35 ± 6.81	91.05 ± 4.88
	2 July 2012	1892	96.92 ± 2.88	100 ± 0.00	100.0 ± 0.00

Pairwise significant differences between the plants in season 1 are indicated with an asterisk (Mann–Whitney–Wilcoxon RankSum non-parametric test: P < 0.05).

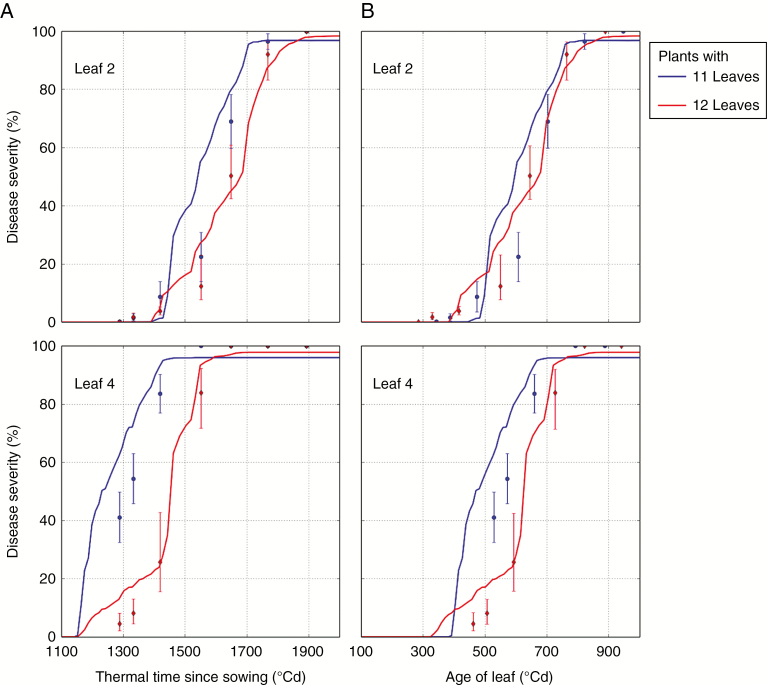
In seasons 2 and 3, the wheat plants with the lowest final number of leaves displayed an earlier STB development than those with the highest final number of leaves when STB severity was plotted in thermal time since sowing (30–50 °Cd earlier depending on the leaf rank) (Fig. 3). For leaves 1, 2 and 3, no more difference was observed between the two groups of final numbers of leaves when STB severity was plotted in thermal time since leaf emergence. A difference (20 °Cd) remained for leaves 4 in season 3 and leaves 5 in season 2.

Fig. 3.

Comparison of STB severity on plants with different final number of leaves: 11 and 12 observations and simulations, plotted against thermal time since sowing (A) and against the age of leaves (B) on leaf ranks 2 and 4 of Tremie wheat in season 3. Dots: means and 95 % confidence interval of observations. Lines: results of simulation.

Disease-model simulation

Overall, the model reproduced quite well the effect of weather on disease progress on the upper leaves (Fig. 2): simulations suggest that the low epidemic of season 1 was due to very dry spring conditions. For season 1, the STB model predicted lower disease levels in the Mercia than in the Mercia-Rht3 wheat line. Quantitatively, the simulations were more accurate for Mercia than for Mercia-Rht3. In seasons 2 and 3, the simulations quite consistently followed the data and mostly fell within the confidence intervals. The average RMSE was 5 and 11 % in season 2 and 3, respectively. The shapes of simulated disease progress curves were regular and fast in season 3 but irregular in season 2, as observed in the data. The former was caused by weather conditions inducing regular dispersal and infection events, and the latter by successive dry periods. In season 2, the model simulated the observed gentler beginning of the curves on leaves 4 and 3 correctly. This was caused by low humidity levels, while this effect was underestimated on leaf 5. The model predicted the subsequent steep increase due to favourable climatic conditions. Simulations also suggest that the lower slope of disease severity on leaf 1 in season 2 was a result of less sporulating area on lower leaves at the time of flag leaf emergence. Simulations were consistent with the data when plotted both in thermal time post-sowing (Fig. 2A) and in thermal time since leaf emergence (Fig. 2B). The model predicted well the age at which leaves showed their first symptoms, suggesting that the model captured well the dispersal events triggering the contamination of each leaf layer.

The difference in STB dynamics due to the final number of leaves was also captured by the model, even if the prediction is a little ahead of the observations for plants with 11 leaves (Fig. 3). In simulations, these differences resulted mainly from delays in leaf emergence dates. For example, in season 2, for plants with 12 leaves, a dispersal event occurred after the emergence of leaf 4 (resulting in infection), but for plants with 13 leaves, it occurred just before the emergence of leaf 4 (resulting in no infection). In simulations in season 3, for both groups, the leaves 4 were infected after the same dispersal event, but because of the difference in emergence date, the leaves of plants with the lower final number of leaves were more developed at the date of infection and more spores could reach them.

Sensitivity analysis of the model

Global sensitivity analysis.

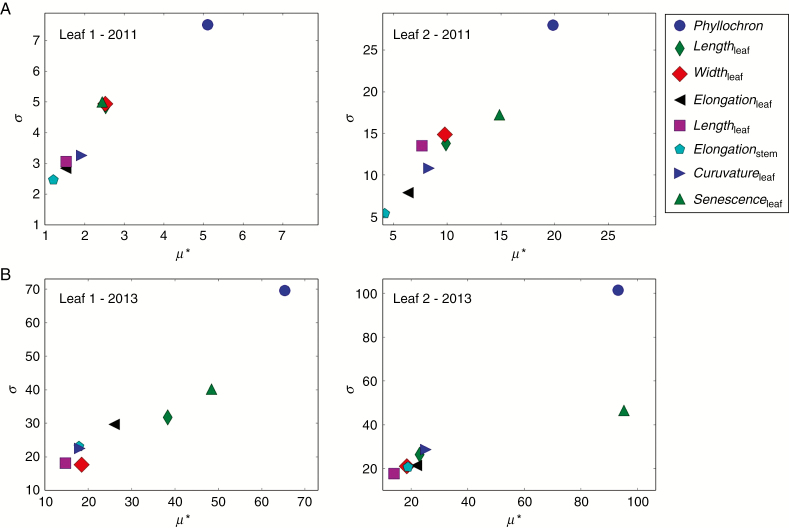
Whereas the AUDPC is sensitive to all parameters, the two most influential parameters (i.e. highest values of μ* and σ by leaf in Fig. 4) are Phyllochron and Senescence_leaf. The same results were obtained for both years with different weather conditions. Quantitatively, however, sensitivities were lower for the less favourable weather conditions. Sensitivity analysis with respect to maximum disease severity gave similar results (data not shown).

Fig. 4.

Results of model sensitivity analysis with the Morris method on leaf ranks 1 and 2, weather conditions of season 1 (A) and season 3 (B). Two sensitivity indicators are measured for each factor: the absolute value of the mean of elementary effects μ* (overall influence) and their standard deviation σ (higher order effects, i.e. non-linearity or interactions with other factors). Eight plant traits are tested (Table 2). Note: the factors in the top right of each graph will be considered as the most influential.

Single plant trait sensitivity analysis under varied weather conditions.

Weather conditions had a strong effect in simulations on the flag leaf AUDPC (varying from 0 to 150; Fig. 5) and on the maximum disease severity (from 0 to 100 %). This emphasizes the strong effect of climatic conditions on epidemics. For example, 2003 was a remarkably dry year in France for which the model simulated no disease on flag leaves for any tested plant architecture (Fig. 5).

Fig. 5.

AUDPC on flag leaves simulated by the model for different seasons varying in weather conditions and values of plant parameters. Eight plant traits are tested (Table 2). Circles show the reference values of parameters. Years are sorted in decreasing order in terms of disease level in the reference simulation. Lines indicate 95 % confidence intervals.

Figure 5 presents the results for AUDPC. Decreasing Phyllochron (i.e. increasing the rate of plant development) reduced the simulated disease. Increasing Phyllochron had both favourable (2000 and 1999) and unfavourable effects (2001, 2004 and 2005) on the disease. Simulated disease was always negatively correlated with stem height and stem growth rate. This confirmed the previously negative effect of stem height and elongation rate on disease progress. However, the results suggest that these parameters are not as influential as other tested parameters, such as onset of senescence for instance. The five parameters affecting leaf characteristics had contrasted effects. Increasing leaf length (Length_leaf) increased the AUDPC. The effect of leaf width (Width_leaf) was much weaker. The AUDPC always correlated negatively with the leaf elongation rate, but the sensitivity depended on weather conditions (Elongation_leaf). The effect of the leaf curvature rate (Curvature_leaf) was always small. Finally, the onset of leaf senescence (Senescence_leaf) had a strong effect on the AUDPC: earlier senescence lowered the simulated disease. The sensitivities depended on weather conditions: (1) in unfavorable seasons, the AUDPC was insensitive to any plant traits (Fig. 5, years 2002, 2003 and 2006); (2) for Phyllochron, Width_leaf and Elongation_leaf, weather conditions could reverse or cancel the effect of the plant trait; and (3) for the other plant traits, weather only influenced the degree of the sensitivity. The sensitivity analysis gave qualitatively similar results for simulated maximum disease severity, except that the latter was also insensitive to any plant traits under very favourable weather conditions.

Detailed sensitivity analysis of ‘the race’.

The parameters Senescence_leaf, Elongation_stem and Length_stem strongly influenced the simulated disease on flag leaves (Fig. 6). For the AUDPC (Fig. 6A, C, E) the sensitivity was very low for the two seasons with unfavourable weather conditions (2003 and 2006). The AUDPC increased almost linearly with decreasing stem height (Fig. 6C) or stem elongation rate (Fig. 6E), with a small interaction with weather.

Fig. 6.

AUDPC (left) and maximum severity (right) on flag leaves simulated by the model for different seasons varying in weather conditions and values of wheat parameters selected for their influence of STB progress in the range of variation –30 % to +30 % of their reference value. (A) and (B) Senescence_leaf. (C) and (D) Length_stem. (E) and (F) Elongation_stem. Symbols and colours designate the season. Lines indicate 95 % confidence intervals.

The effect of senescence was more non-linear and depended more strongly on weather: the simulated AUDPC was very sensitive to early senescence but tended to level off at late senescence (e.g. 1999, 2004 and 2005). Reducing the starting date of senescence by 30 % resulted in the strongest AUDPC decrease on flag leaves.

The simulated maximum disease severity (Fig. 6B, D, F) exhibited a more non-linear response than the AUDPC, due to a saturation effect (100 % at full coverage). As a consequence, sensitivity was the highest at intermediate disease severity levels. Sensitivity was the highest for Senescence_leaf in all the seasons. In the most favorable years (1999, 2000 and 2004), the simulated maximum severity decreased only with this parameter.

We found that the effect of the three parameters (Senescence_leaf, Elongation_stem and Length_stem) were of similar quantitative importance in influencing disease on the flag leaf in our simulations. Therefore, both the upward and the local foliar races impacted disease progress. Overall, varying the parameter Senescence_leaf induced slightly more variation than parameters Elongation_stem and Length_stem. The effect was noticeable on the AUDPC (Fig. 6A) in years 2000 and 2001, passing from almost no disease to strong epidemics with increasing Senescence_leaf. Moreover, while maximal disease severity on flag leaves was unaffected by the variation of Elongation_stem and Length_stem in 2000 and 2006 (Fig. 6D, F), it was affected by the variation of Senescence_leaf (Fig. 6B). The maximum severity passed from 90 to 30 %, and from 55 to 5 % when leaf life span was reduced by 30 % in 2000 and 2006, respectively.

DISCUSSION

The race between host and pathogen

Our mixed modelling–experimental study exploited the realistic features of the FSPM framework, that offer a great potential for model–data comparison, in order to explore the effects of plant traits on epidemics. Our results offer a new perspective on the race between the host and its pathogen. An upward race occurs at the canopy scale where Z. tritici must catch the leaves that emerge one after another (Lovell et al., 1997, 2004; Robert et al., 2008). We argue that there is an additional race at the leaf scale where Z. tritici must use the resources of its host before it is caught by natural senescence. In order to evaluate the importance of the upward against the local race, we have computed the sensitivity of stem height and elongation rate (that impact the upward race only) and of the onset of senescence (that impacts the local race only). We found that both the upward and local races strongly influenced STB progress. One main difference was that the upward race only influenced disease on upper leaves, while senescence influenced all the leaf layers. In our tested parameter range, the senescence timing was the trait that allowed the strongest disease reduction, a result that is of interest for disease escape.

Model evaluation and complexity

The three seasons differed in spring weather. This resulted in different epidemics. The dwarf wheats (with allele Rht3) were attacked more than the taller Mercia wheats. The model reproduced the effects of architecture between the lines Mercia and Mercia-Rht3, and correctly ranked the three seasons with different weather conditions in terms of disease severity. The STB simulations on the upper leaves were consistent with the data on most of the leaf layers. The date of appearance of the first symptoms on each leaf layer was consistently simulated. Our model also reproduced coherently the differences in disease severity observed on plants with different final leaf numbers. For the very dry season 1, the simulations were the least accurate. More data on varied wheat architectures and weather conditions are, however, needed for a sound model validation.

We think there is room for improvement in the simulation of epidemic slowdowns during dry periods (Shaw et al., 1990, 1991), and also by taking into account the role of airborne ascospores. In addition to the well-established role of pycnidiospores, ascospores may contribute to epidemic development in particular environmental conditions (Hunter et al., 1999; Sameh et al., 2011; Suffert et al., 2011; Duvivier et al., 2013; McDonald and Mundt, 2016; Morais et al., 2016; Suffert et al., 2016). For instance, ‘escaped upper leaves’ could receive ascospores by wind from other crops, which then allowed a second round of conidial multiplication. This question is an interesting perspective for future work.

Our model represents in detail the epidemic development in a structured canopy. The fine resolution of the model in terms of plant structure and spatial dynamics of the epidemics has enabled us to compare in detail model dynamics and the field observations. The explicit description of plant architecture and growth allowed investigation of the importance of several plant traits in epidemics. However, our model is complex and requires many parameters and input data. It must also be noted that, in the light of the results of Ben Slimane et al. (2012) that suggest that leaf senescence is not accelerated by Z. tritici, no retroaction of the fungus on the plant, such as induced resistance, was added in the model. Model formulation, parameterization, validation and analysis are very time-consuming processes limiting the range of questions that can pragmatically be addressed. We argue that an important role for this type of model is to identify processes or traits that are potentially influential and could be of interest in integrating in simpler models. In particular, it would be interesting to compare our modelling results with simpler modelling studies in order to find results that are robust to the level of model complexity, and to be able to explore a larger range of conditions.

Rate of plant development and STB progress

One striking result of our field experiment is how disease progress was affected by the rate of plant development: the dates of leaf emergence had a strong effect on the timing of epidemics. The simulations showed that the start of symptoms was dependent on the coincidence between the dates of leaf emergence, the occurrence of dispersal events and the presence of inoculum on the lower leaves (Shaw and Royle, 1993; Moreau and Maraite, 1999, 2000). Between-season differences in disease progress can be partly attributed to differences in the timing of rain events and plant development. Within the same canopy, plants with different final leaf numbers had different STB progress. Our analysis showed that this difference in severity was due to the fact that leaves appeared slightly later on plants with the lowest final number of leaves (Baccar et al., 2011). Even slight differences could induce delays in the progress of STB (Shaw and Royle, 1993). Between-plant developmental variability could therefore influence epidemics.

Influence of plant traits

Our work confirmed the negative effects of the internode length (Eyal and Ziv, 1974; Bahat et al., 1980; Shaw, 1987; Simón et al., 2005; Arraiano et al., 2009) and of the stem elongation rate (Lovell et al., 1997; Robert et al., 2008). Both traits impacted disease progress on the upper leaves by influencing distances between spore sources and susceptible leaf tissue. We found that increasing leaf dimensions increased the severity on flag leaves for most of the weather conditions tested. Interestingly, the length of leaves was much more influential than their width. These findings suggest that the sheltering effect of greater leaf area was weaker than the positive effects of having more green tissue for pathogen growth and of reducing distances for dispersal with longer leaves. We also found that the timing of plant development was one of the most influential traits on simulated epidemics, but it was also one of the least predictable because the effect was reversed in certain weather conditions. This variability was explained by the importance of the timing of rain events relative to the date of leaf emergence for dispersal. One of our main predictions was that the timing of leaf senescence strongly influences STB epidemics. When the green life span duration was reduced by early senescence, epidemics were reduced. This suggests that the time available for infection and lesion growth is a limiting factor in fungal development. This is consistent with field works of Shaw and Royle (1993) and Armour et al. (2003) that pointed out that upper leaves need to be infected early after their emergence in order to be strongly affected. This result thus provides an alternative explanation for the observed correlation between resistance for foliar pathogens and senescence (Krattinger et al., 2009). It must be noted that the influence of plant traits on STB depended on weather. A low influence of architecture was found for unfavourable weather conditions (as in Bahat et al., 1980; Shaw and Royle, 1993; Robert et al., 2008). The effect of senescence timing, stem parameters and leaf length were robust and only changed qualitatively depending on the weather.

Disease escape

Our work has revealed plant traits that enable regulation of STB. These influential traits are potential targets for breeders and agronomists for control strategies. In order to be of interest, traits should fulfil several criteria: (1) sufficiently strong effect on the disease and (2) sufficiently robust to climatic variability. Based on (1) and (2), our study highlights classical regulation traits such as stem height or earliness, and less known traits such as the stem elongation rate or leaf length. In addition, we propose green leaf life span as a potentially influential trait. Yet candidate traits should also be (3) feasible and (4) not in contradiction to other agronomic criteria. For instance, a high stem height poses problems of lodging which is not the case for a fast stem elongation. Green leaf life span is crucial for the production of biomass and yield. Our results suggest the idea to develop wheat with more leaves of shorter life span. The main idea is to minimize STB development by shortening the time for the infection cycle on each leaf, while at the same time producing more leaves, to keep the same total amount of photosynthetic area for the plant. Using cultivars that would be more efficient for mobilizing nutrients with early senescence is an interesting perspective. However, the cost of rapidly remobilizing nutrients from more leaves should be balanced with the benefit. Further experimental studies, but also modelling studies computing the potential of light interception by such ideotypes, are needed in collaboration with geneticists and breeders. Our model can be used to compare in silico the epidemics on different ideotypes of wheat (Rebetzke et al., 2011). Combining FSPM with disease models and fungicide models could be helpful for coupling both disease escape and optimal timing of fungicide sprays for keeping the pathogen lower in the canopy (Robert et al., 2015; Fournier et al., 2016). However, the Z. tritici population is highly diverse and associated with potential rapid fungal adaptation (MacDonald et al., 2016). This raises the question of the sustainability of escaping traits for slowing down the disease (Précigout et al. 2017).

So far we have focused on the impact of individual plant traits on epidemics. The next step is to take into account known correlations between traits to assess the scope for disease escape more realistically (Arraiano et al., 2009). Furthermore, knowing the influential plant traits should help to disentangle the effects of resistance from architectural effects, and hence improve the quantification of cultivar resistance to STB (Arraiano et al., 2009; Miedaner et al., 2013; Brown et al., 2015). In this study, we only considered cultivars sensitive to STB, focusing on disease escape. It would be an interesting perspective to study interactions between resistance and plant architecture. In the model, differences in resistance could be taken into account via the infection cycle parameters such as infection probability, lesion growth rate or sporulation.

SUPPLEMENTARY DATA

Supplementary data are available at https://academic.oup.com/aob and consist of the following. Supplementary Information 1: field experimental set-up. Supplementary Information 2: wheat model calibration. Figure S1: axis density at canopy level. Figure S2: the dimensions of organs of main stems as a function of their position. Figure S3: the phenology of the appearance and senescence of leaves on main stems. Supplementary Information 3: weather conditions for tested seasons. Figure S4: displays the conditions for the experimental study. Figure S5: displays the conditions for the sensitivity analyses.