Abstract
Background and Aims
Predicting both plant water status and leaf gas exchange under various environmental conditions is essential for anticipating the effects of climate change on plant growth and productivity. This study developed a functional–structural grapevine model which combines a mechanistic understanding of stomatal function and photosynthesis at the leaf level (i.e. extended Farqhuhar–von Caemmerer–Berry model) and the dynamics of water transport from soil to individual leaves (i.e. Tardieu–Davies model).
Methods
The model included novel features that account for the effects of xylem embolism (fPLC) on leaf hydraulic conductance and residual stomatal conductance (g0), variable root and leaf hydraulic conductance, and the microclimate of individual organs. The model was calibrated with detailed datasets of leaf photosynthesis, leaf water potential, xylem sap abscisic acid (ABA) concentration and hourly whole-plant transpiration observed within a soil drying period, and validated with independent datasets of whole-plant transpiration under both well-watered and water-stressed conditions.
Key Results
The model well captured the effects of radiation, temperature, CO2 and vapour pressure deficit on leaf photosynthesis, transpiration, stomatal conductance and leaf water potential, and correctly reproduced the diurnal pattern and decline of water flux within the soil drying period. In silico analyses revealed that decreases in g0 with increasing fPLC were essential to avoid unrealistic drops in leaf water potential under severe water stress. Additionally, by varying the hydraulic conductance along the pathway (e.g. root and leaves) and changing the sensitivity of stomatal conductance to ABA and leaf water potential, the model can produce different water use behaviours (i.e. iso- and anisohydric).
Conclusions
The robust performance of this model allows for modelling climate effects from individual plants to fields, and for modelling plants with complex, non-homogenous canopies. In addition, the model provides a basis for future modelling efforts aimed at describing the physiology and growth of individual organs in relation to water status.
Keywords: Vitis vinifera, functional–structural plant model, photosynthesis, water transport, hydraulic conductance, leaf water potential, plant water status, stomatal conductance, water stress
INTRODUCTION
A comprehensive understanding of plant–water relations is fundamental in characterizing the impact of water status on fruit composition and organoleptic quality, e.g. concentrations of primary and secondary metabolites in grapevine (Vitis vinifera L.). Ecophysiological process-based models are increasingly used in perennial fruit crop research (Génard et al., 2010; Baldazzi et al., 2013), and are interesting heuristic tools for integrating and exploring the effects of environmental factors on plant and fruit growth (Damour et al., 2010). An ecophysiological model that can predict both plant water status and leaf gas exchange under various environmental conditions is essential for anticipating the effects of climate change on fruit yield and composition (Sadras and Soar, 2009; Chew et al., 2014; Tardieu and Parent, 2016).
Considerable hydro-mechanical modelling efforts have been made to integrate plant water status and leaf gas exchange using stomatal conductance as a key variable (Dewar, 2002; Gao et al., 2002; Tuzet et al., 2003; Buckley et al., 2003). The model of Dewar (2002) combined the essential features of the Ball–Berry–Leuning stomatal model (Ball et al., 1987; Leuning, 1995) and the Tardieu–Davies stomatal model (Tardieu and Davies, 1993). In the model of Ball–Berry–Leuning, stomatal conductance (gs) was calculated based on net photosynthesis (Anet), CO2 partial pressure and vapour pressure deficit (VPD) at the leaf surface without accounting the effects of water status. By contrast, in the model of Tardieu–Davies, gs was calculated based on leaf water potential (ψleaf) and xylem sap abscisic acid concentration ([ABA]xyl) derived from water stress experiments. Another model proposed by Tuzet et al. (2003) coupled the calculation of stomatal conductance, photosynthesis, leaf energy balance and transport of water through the soil–plant–atmosphere continuum. In this model, photosynthesis was calculated using the biochemical photosynthesis model of Farquhar, von Caemmerer and Berry (FvCB module; Farquhar et al., 1980). To date, Buckley et al. (2003) provides one of the most advanced hydro-mechanical models of stomatal conductance which integrates the hydropassive (purely physical or hydraulic feedbacks) and hydroactive (guard cell osmotic pressure is actively regulated in proportion to leaf turgor) feedback loops, and a simplified version of this model has been validated against experimental data in various species (Buckley et al., 2012; Rodriguez-Dominguez et al., 2016). Despite these advances in modelling stomatal conductance, it remains challenging to simultaneously integrate detail gas exchange and water status at the leaf level while scaling to the whole plant, and even field, level.
A functional–structural plant model (FSPM) is a model that describes the 3-D architecture of individual organs, plants and/or populations, the impact of this architecture on physiological processes at the organ level, and its feedback on the evolution of the 3-D architecture itself (e.g. see Fig. 1; Vos et al., 2010). Models described previously, namely Dewar (2002), Tuzet et al. (2003) and Buckley et al. (2003), consider the whole canopy as one big leaf. This assumption is reliable when the canopy is homogenous, e.g. a dense wheat field, but may prove inaccurate for heterogeneous canopies, e.g. a vineyard with a row-structured discontinuous canopy, an orchard or a potted greenhouse plant. FSPMs that integrate plant water status and leaf gas exchange while accounting for the microclimate at the individual organ level and for the heterogeneous radiation conditions within the canopy will help in addressing this limitation.
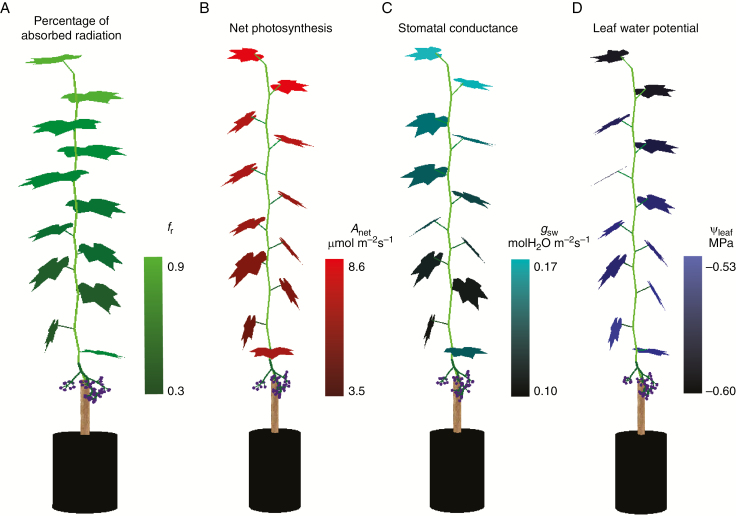
Fig. 1.
Illustration of the simulated percentage of absorbed radiation (A), net photosynthesis (B), stomatal conductance (C) and leaf water potential of each leaf (D). The environmental conditions for the simulation were set as: Ta 25 °C, CO2 400 ppm, −0.3 MPa, Ra 2000 µmol m−2 s−1 (PAR 1100 µmol m−2s−1), VPD 1 kPa. The comparison between simulated canopy leaf temperature and canopy thermal picture (FLIR T450sc, FLIR Systems AB, Frankfurt am Main, Germany) is presented in Fig. S1. A movie showing the diurnal dynamics of leaf transpiration within a soil drying cycle is presented in Video S1.
Several attempts have been made in integrating either an FvCB module (Evers et al., 2010; Prieto et al., 2012) or water status (Da Silva et al., 2011; Baldazzi et al., 2013) into FSPMs. However, these studies treated the plant as a series of static resistances when many studies have demonstrated that resistances along the water transport pathways vary both in time and with development. For example, Vandeleur et al. (2009) showed that root conductance changes diurnally. Further studies confirmed that root and leaf conductance increased with water flux rates (Gambetta et al., 2012; Simonin et al., 2015; Vandeleur et al., 2014) and decreased with the percentage of xylem embolism (Zufferey et al., 2011; Hochberg et al., 2016; Charrier et al., 2016). Baert et al. (2015) further showed that a variable soil-to-stem hydraulic resistance was crucial to describe the responses of gs and transpiration to drought.
The objectives of this study were: (1) to develop an FSPM, using grapevine as a model plant, that couples the dynamics of water transport with leaf gas exchange; (2) to analyse the responses of stomatal conductance, net photosynthesis, transpiration, and leaf and xylem water potentials under various environmental conditions, e.g. total radiation (Ra), VPD, CO2 and Ta and soil water content; and (3) to simulate the effect of plant hydraulic conductance and stomata sensitivity to water potential and [ABA]xyl on plant water use behaviours.
MATERIALS AND METHODS
Model description
A functional–structural grapevine model (hereafter GrapevineXL) was developed under the 3-D plant modelling platform GroIMP (Hemmerling et al., 2008; Kniemeyer, 2008). GrapevineXL used greenhouse grapevine fruiting cuttings trained to only one primary shoot axis with a single cluster per plant (Mullins and Rajasekaran, 1981) as model plants (Fig. 1). The structure of individual leaves, petioles, internodes and berry bunches were described in detail (Fig. 1). Root and soil were both treated as one compartment. All objects were connected based on their morphological positions. GrapevineXL simulated hourly leaf photosynthesis, transpiration, stomatal conductance, whole plant root conductance (Lr), individual leaf conductance (kleaf), xylem water potential (ψxyl) and individual leaf water potential, [ABA]xyl, based on environmental conditions, such as CO2, radiation, temperature, relative humidity, soil water content and water potential (Fig. 1, Supplementary Data, Fig. S1).
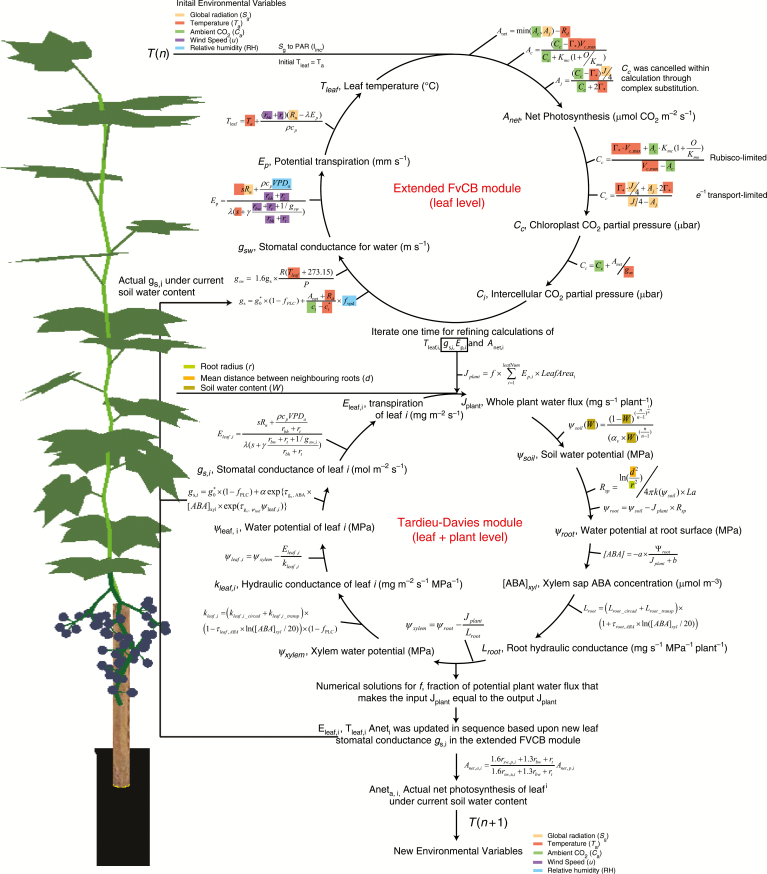
GrapevineXL included three main parts: (1) an extended-FvCB module which calculated the potential photosynthesis, transpiration, leaf temperature and stomatal conductance at a given atmospheric condition, and updated these variables under water stress with a given stomatal conductance (Yin and Struik, 2009); (2) a Tardieu–Davies module which calculated water transport from soil to root surface to xylem and to leaf with an electrical resistance analogy and with variable hydraulic conductance (Tardieu et al., 2015) – the Tardieu–Davies module calculated the water potential of each organ and actual stomatal conductance under the given ambient and soil condition; and (3) a radiation module that simulated light capture by each organ within a heterogeneous environment using a ray tracing method (Evers et al., 2010; Zhu et al., 2015). The extended-FvCB module and Tardieu–Davies module were coupled by allowing the former to feed the potential leaf stomatal conductance without the effect of VPD to the Tardieu–Davies module and by allowing the Tardieu–Davies module to pass the actual leaf stomatal conductance and transpiration back to the extended-FvCB module. The effect of VPD on the potential leaf stomatal conductance was removed as it was included in leaf water potential and [ABA]xyl via transpiration in the calculation of the Tardieu–Davies module. Detail summaries of the model algorithms and calculating sequence are presented in Fig. 2 and in the following paragraphs.
Fig. 2.
Schematic representation of the coupling of the extended-FvCB module with the Tardieu–Davies module. Plant water status and leaf gas exchange were coupled in three steps. In the first, potential values of leaf photosynthesis, stomatal conductance, transpiration and leaf temperature were calculated in sequence by the extended-FvCB module based on current ambient conditions without accounting for plant water status. One iteration was used as follows: leaf photosynthesis was first calculated using air temperature instead of leaf temperature; the calculated leaf photosynthesis was then used to find stomatal conductance, which is subsequently used to calculate transpiration and leaf temperature; leaf temperature was then input for the second round of calculation of photosynthesis. In the second step, the potential values of leaf and leaf transpiration were input into the Tardieu–Davies module to numerically solve the actual leaf transpiration and actual under the given ambient and soil conditions. This numerical method tries to find a plant water flux () that makes the summed leaf transpiration determined by and [ABA]xyl, which was influenced by (see eqn 3), equal to itself (eqns S11–S24). Finally, the actual leaf transpiration was fed back to the extended-FvCB module to recalculate the leaf temperature and the potential leaf net photosynthesis under the newly calculated leaf temperature. The effect of actual gs on actual net photosynthesis was taken into account by eqn (5). Intermediate variables influenced by certain environmental factors are marked with the same colour that represents that environmental variable. Note that as the water potential was calculated in sequence, all water potentials are influenced by soil water content and root properties [mean distance between neighbouring roots (d), root radius (r), root length per plant per surface area (La, m m−2)].
Extended-FvCB module: leaf photosynthesis, transpiration and temperature
Hourly leaf photosynthesis, transpiration and temperature during daytime were calculated using the extended-FvCB module (Figs 1 and 2). The extended-FvCB module developed by Yin and Struik (2009) provided several advanced features: (1) an analytical approach for simultaneously solving Anet under various environmental conditions that significantly reduced calculation time; (2) introduction of mesophyll conductance (gm) for calculating CO2 partial pressure around the chloroplast (CC), which was in principle required by the FvCB module and was often assumed to be equal to intercellular CO2 partial pressure (Ci); and (3) a refined calculation of leaf temperature based on leaf level energy balance. Detailed descriptions of the methodology and all equations have been provided in the supplementary data of Evers et al. (2010). All parameters used in this paper with their values and units are listed in Table S1. Essential equations for calculating net photosynthesis, transpiration and leaf temperature are presented in Fig. 2 and in the Supplementary Data, Method S1 eqns (S1)–(S11).
A modification, comparing to the extended-FvCB module, was made in the calculation of the residual stomatal conductance at the light compensation point of net photosynthesis (Anet = 0), also known as minimal stomatal conductance (). As stomatal conductance decreased with the decline of leaf water potential and with the percentage loss of leaf and stem hydraulic conductivity (Zufferey et al., 2011; Nolf et al., 2015; Charrier et al., 2016), it was assumed that decreased in proportion to (eqn 1). increased exponentially with the decrease in leaf water potential (eqn 2; Hochberg et al., 2016). A quantitative relationship between and leaf water potential were derived from Hochberg et al. (2016), where measurements were obtained in vivo on grapevine through magnetic resonance imaging, a non-invasive method. This assumption does not exclude other plausible relationships between residual stomatal conductance, water potential and abscisic acid (ABA):
| (1) |
| (2) |
where is the stomatal conductance for CO2 (µmol m−2 s−1 µbar−1, equivalent to mol m−2 s−1) calculated by the extended-FvCB module without accounting for the water status; is residual or minimal stomatal conductance under well-watered conditions when equals zero (mol m−2 s−1); is the minimal stomatal conductance under current plant water status conditions when is greater than zero; is partial pressure of intercellular CO2 (µbar, 10−1 Pa); is the intercellular CO2 compensation point (µbar, 10−1 Pa); Rd is daytime respiration, respiratory CO2 release other than by photorespiration (µmol CO2 m−2 s−1); and is a dimensionless lumped parameter representing the vapour pressure deficit (VPD) effect on stomatal conductance (Yin and Struik, 2009). is the leaf water potential when 50 % of the leaf conductivity is lost (MPa); is a coefficient that decribes the rate of the loss of conductivity (MPa−1); is the leaf water potential of the previous step. is updated with at each step. The refilling of embolism was not considered in this model.
Water transport from soil to leaf (Tardieu–Davies module)
The Tardieu–Davies module used an electrical resistance analogy for the transport of water from soil to the root surface to xylem and to leaf, and described variable leaf and root hydraulic conductance as a function of transpiration, circadian rhythms and [ABA]xyl (Tardieu and Davies, 1993; Tardieu et al., 2015). The Tardieu–Davies module was able to simulate five essential physiological variables related to plant water relations: plant water flux () and [ABA]xyl. Essential equations are presented in Fig. 2 and in the Supplementary Data, Method S2 eqns (S11)–(S24) and Fig. S2.
In addition to eqn (1), which calculated stomatal conductance based on photosynthesis rate and VPD in the extended-FvCB module, stomatal conductance was calculated via eqn (3) in the Tardieu–Davies module.
| (3) |
| (4) |
where + is maximal gs of leaf i under the current ambient conditions as determined by the extended-FvCB module without the effect of VPD. is the stomatal sensitivity to xylem [ABA]xyl (µmol m−3) and is stomatal sensitivity to (MPa–1). The stomatal conductance for H2O in crossing the stomata () was 1.6 times that for CO2 () due to the faster diffusion of H2O than CO2. was used in the calculation of transpiration, with its units converted to physical resistance units (m s−1, eqn S7).
The Tardieu–Davies module (Tardieu et al., 2015), which considers the whole canopy as a single large leaf, was used to calculate leaf conductance, leaf water potential and percentage loss of conductivity on each individual leaf (eqns S21–S24). Leaf conductance ( mg m−2 s−1 MPa−1) was defined as the conductance from stem to leaf i. In this paper, the hydraulic conductivity of petiole and leaf blade was treated as a whole.
Coupling of water transport and leaf gas exchange
Water transport and leaf gas exchange variables were coupled in three steps. In the first, potential values of leaf photosynthesis, transpiration, temperature and were calculated by the extended-FvCB module without taking into account plant water status. In the second step, the potential without the effect of VPD and current soil water content were input into the Tardieu–Davies module to numerically solve for actual leaf transpiration and actual under the given ambient and soil conditions. The numerical method tried to find an input plant water flux () that makes the summed leaf transpiration determined by and [ABA]xyl (see eqn 3), which were updated based on equal to the input (Fig. 2, eqns S11–S24). Finally, the actual stomatal conductance of each individual leaf was fed back to the extended-FvCB module to recalculate leaf temperature. Potential leaf net photosynthesis and stomatal conductance were recalculated under the newly calculated leaf temperature as well. The actual stomatal conductance calculated by the Tardieu–Davies module and newly determined potential stomatal conductance and leaf net photosynthesis were then used to recalculate the actual net photosynthesis with eqn (5) (Yin and van Laar, 2005):
| (5) |
where is the actual net photosynthesis of leaf i, is the potential stomatal conductance for water of leaf i (m s−1), is the actual stomatal conductance for water of leaf i (m s−1), is the boundary layer resistance for water (s m−1) and is the turbulence resistance (s m−1); represents the total resistance for CO2 from ambient air to intercellular air space. The value 1.37 is a factor accounting for the faster diffusion of water vapour compared to CO2 in crossing the boundary layers.
Experimental setups
The data for model calibration were derived from a soil drying cycle experiment conducted in a semi-controlled greenhouse (Peccoux et al., 2018). Briefly, homografted plants of ‘Cabernet Sauvignon’ were grown in 7-litre pots and placed on balances (CH15R11 CHAMPII, Obaus GmbH, Nänikon, Switzerland) with automatic recording of pot weight. The pots were filled with 1 kg of gravel for drainage and 4.6 kg of dry soil, and were covered with a black plastic film to avoid water evaporation from the soil surface. All lateral shoots were removed throughout the experiment. Maximal leaf length and maximal leaf width, leaf area and leaf plastochron index were determined during the experiment. Leaf plastochron index was calculated using the scheme of Schultz and Matthews (1988), which accounted for the total number of leaves longer than 30 mm, leaf rank counting acropetally, and the length of the leaf in question. Root length density, root length area and mean root diameter were determined on five well-watered plants before the experiment following the procedure of Bouma et al. (2000). Detail descriptions of the experimental setups and measurements were provided in Peccoux et al., 2018. Environmental conditions over the entire experimental period are shown in Supplementary Data Fig. S4.
Plant responses during a drying cycle
One week before the beginning of the drying cycle, the plants were irrigated to 100 % of soil water-holding capacity every day. The irrigation was then stopped for 6 d (soil water content decreased to 0.012 ± 0.005 kg H2O kg soil–1). Twenty-five plants were selected. Whole plant transpiration was determined from the pot water loss (Marguerit et al., 2012).
Leaf gas exchange, leaf water potential and [ABA]xyl were measured daily over the course of the drying cycle (Fig. S5). Leaf gas exchange was measured daily between 10:00 and 13:00 H during the drying cycle with a portable open-system infra-red gas exchange apparatus (GFS-3000, Heinz Walz GmbH, Effeltrich, Germany; see equipment settings in Method S3). was measured with a pressure chamber (SAM Précis 2000, Gradignan, France; Turner, 1988). An overpressure of 0.4 MPa was applied to the leaf after recording of to collect xylem sap. The abundance of ABA in xylem sap was assessed by liquid chromatography/mass spectrometry (Agilent 6410 Triple Quadrupole LC-MS/MS, Agilent Technologies Inc., Santa Clara, CA, USA) using a stable isotope dilution assay (Speirs et al., 2013).
Photosynthetic light response curves were established on three well-watered plants using leaves with similar physiological age (leaf plastochron index 10 ± 2). Additional CO2 response curves were obtained from Quereix et al. (2001), where measurements were conducted on the same cultivar within a similar experimental setup.
Representation of plant architecture and radiation absorption by each leaf
The shape of an individual leaf blade was represented by a set of triangles adapted from a leaf shape function developed for cotton leaves (Gu et al., 2014). Parameters for the leaf shape function were updated based on observed leaf length to width ratio, and the relationship between leaf area and leaf length on ‘Cabernet Sauvignon’. Petioles, internodes and wood were represented by cylinders. Leaf length, width, petiole length and internode length along the stem were determined on fruiting cuttings of ‘Cabernet Sauvignon’ through destructive samples in 2015. The relative sizes of leaves, petioles and internodes along ranks were assumed to be the same in different experiments. The size of each leaf was multiplied by a factor to give the observed leaf area per vine recorded in different experiments. The declination angle between the petiole and internode, and the declination angle between leaf blade and petiole were measured by a protractor on intake plants before destructive sampling. The azimuth angle between consecutive leaves was set to 180° plus a random value between −20° and 20°.
Radiation absorption by each leaf was calculated through a ray tracer method provided by the GroIMP platform (Hemmerling et al., 2008). For simplicity, only diffuse radiation was used to represent the light environment in the greenhouse. Diffuse radiation was approximated using an array of 72 directional surface light sources positioned regularly in a hemisphere in six circles with 12 light sources each (Supplementary Data Fig. S3, Evers et al., 2010; Zhu et al., 2015). The intensity of the total radiation was input based on hourly records measured within the greenhouse (Campbell 21X, Campbell Scientific Inc., Loughborough, UK).
Model calibration and validation
The model was calibrated and verified in three steps. In the first, photosynthesis under well-watered conditions was calibrated based on the CO2 response curve and light response curve. Vc, max, Jmax and Rd were first obtained from the CO2 response curve by using the genetic algorithm of Su et al. (2009). Vc, max, Jmax and Rd were linearly related to leaf nitrogen content (Prieto et al., 2012). The slope of Vc, max, Jmax and Rd to leaf nitrogen content was calculated based on measured leaf nitrogen concentration, and was input into the following optimization for the light response curve. The conversion efficiency of incident photosynthetically active radiation (PAR) into electron transport at limiting light level (, mol electrons mol−1 photons), convexity factor of the light response curve ( dimensionless) and leaf nitrogen content (Nleaf, g m−2, not determined in this experiment) were subsequently optimized using the light response curve. The criterion for this optimization was to maximize the sum of the log-likelihood of the simulated net photosynthesis given the observed photosynthesis. The optimization was done by using the Metropolis–Hastings algorithm in the random walk Markov chain Monte Carlo (MCMC) methods in R (Plummer et al., 2006; R Development Core Team, 2016). This algorithm accepts a new parameter set only when the log-likelihood calculated based on the new parameter set is larger than the previous one. The value of each new parameter is randomly sampled around the value of the previous parameter based on a normal distribution with a given variation. The parameters that control the photosynthetic responses to temperature (activation and deactivation energy of both Vc, max and Jmax, Table S1) were obtained from data on Vitis vinifera L. ‘Semillon’ reported by Greer and Weedon (2012). A constant mesophyll conductance (gm, Table S1) obtained from data on ‘Cabernet Sauvignon’ (Tomás et al., 2014) was used in the extended-FvCB module. The slope of Vc, max, Jmax and Rd to leaf nitrogen content, and leaf nitrogen contents were kept the same for leaves at different positions of the canopy.
In the second step, the effect of soil water deficiency on photosynthesis was implemented. First, the sensitivity of stomatal conductance to [ABA]xyl () and to ( eqn 3) was estimated based on the observed stomatal conductance, leaf water potential and [ABA]xyl during the soil drying cycle. The estimation was done by maximizing the sum of the log-likelihood of the simulated stomatal conductance (eqn 3) given the observed values. Second, to evaluate the performance of the extended-FvCB module under water stress, the observed stomatal conductance as well as the estimated stomatal conductance calculated via eqn (3) were input into eqn (5) to calculate the actual net photosynthesis. The potential and potential net photosynthesis in eqn (5) were determined by the extended-FvCB module with chamber climate condition during the photosynthesis measurements as input.
In the third step, ABA synthesis rate (eqn S16 parameter a) and the sensitivity of root conductance to whole plant water flux (eqn S18, ) were optimized using the whole plant transpiration data recorded during the drying cycle. The criterion for the optimization was to maximize the sum of the log-likelihood of the simulated whole plant water flux given the observed values. Optimization for the whole plant water flux was done at the computing facilities MCIA (Mésocentre de Calcul Intensif Aquitain, on the cluster AVAKAS) of the University of Bordeaux due to the large computation time required for running the whole plant model and the Metropolis–Hastings optimization algorithm.
The model was validated under both well-watered and water-stressed conditions with a separate data set which contains leaf area, whole plant water flux, soil water content, radiation, VPD and temperature. The experiment was done in 2012 in the same greenhouse with similar experimental setups. Within this experiment, soil water content was maintained within a certain range for both well-watered (around 0.28 kg H2O kg soil–1) and water-stressed (around 0.16 kg H2O kg soil–1) conditions. Environmental conditions of the validation data are shown in Supplementary Data Fig. S6.
Sensitivity analysis
A sensitivity analysis was conducted to assess the changes in plant water flux, midday leaf water potential, photosynthesis and stomatal conductance at different soil water potentials in relation to changes in (by changing the sensitivity of to plant water flux rate, ), and This sensitivity analysis was done to allow comparison with a new theoretical framework that describes plant responses to drying soil based on the quasi-linear relationship between midday and predawn leaf water potentials as described by Martinez-Vilalta et al. (2014). The intercept of the relationship (Λ) characterizes the maximal transpiration rate per unit of hydraulic transport capacity, whereas the slope (σ) measures the relative sensitivity of plant transpiration rate and hydraulic conductance to declining soil water availability. A value of σ between 0 and 1 implies that the reduction of transpiration is more rapid than that of hydraulic conductance, whereas σ > 1 implies that the reduction of transpiration is slower than that of hydraulic conductance. The derivation of this relationship and interpretation of the intercept and slope are provided in eqns (S25)–(S28), adapted from Martinez-Vilalta et al. (2014). Simulation scenarios were created by varying the values of these three parameters ( and Table S1) from 10 to 210 % of the default values with an interval of 20 %. One additional value, ten times the default value, was added for both and Moreover, for all the scenarios, simulations were conducted at two contrasting evaporative demands (Ra = 1000 μmol m−2 s−1, Ta = 20 °C, VPD = 1 kPa, CO2 = 400 ppm vs Ra = 2000 μmol m−2 s−1, Ta = 30 °C, VPD = 2 kPa, CO2 = 400 ppm).
A further sensitivity analysis was conducted to test the responses of stomatal conductance, net photosynthesis and plant water flux to Ta, CO2, soil water potential () and their interactions (Supplementary Data Method S5 and Figs S7–S10).
All simulations were made with an infinite canopy, which removes the border effects, although only nine plants were described in a scene. The nine plants were configured in three rows with three plants in each row. Row distance was set to 0.8 m, and plant distance was set to 0.3 m based on the row settings in the greenhouse. The mean summed leaf area of a single plant in the soil drying cycle experiment was 0.12 m2 (18 leaves per plant). The mean of the nine plants was used in the calculation and optimization.
An infinite canopy was formed by virtually replicating a periodic canopy from a finite set of plants – the initial/base scene – multiple times in the plain (Chelle et al., 1998). When a light ray exits the base scene at one side it will enter a copy of the same scene on the other side. In this way a scene was shading a copy of itself. Detail simulation setups are provided in Method S6.
RESULTS
Calibration and verification of the extended-FvCB module
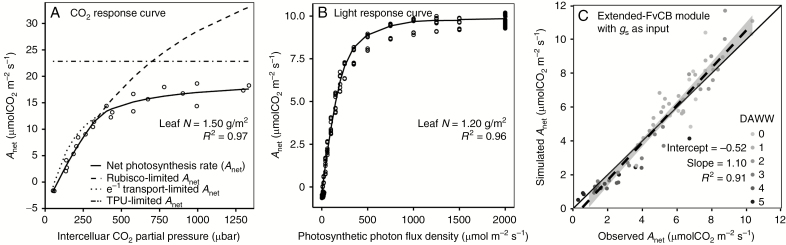
The extended-FvCB module well reproduced the net photosynthesis rate at different levels of CO2 and light intensity on well-watered plants after calibration (Fig. 3A, B). The calibrated extended-FvCB module was further tested for its performance under water stress with gsw as an input (eqn 5 and Fig. 3C). With the observed gsw as an input, eqn (5) captured the variations in the observed net photosynthesis (slope = 1.10, R2 = 0.91), demonstrating that the extened-FvCB module was able to correctly simulate net photosynthesis even under water stress.
Fig. 3.
Calibration of the extended-FvCB module to CO2 response curve (A) and to light response curve (B), and verification of the performance of the extended-FvCB module under water stress with observed stomatal conductance as input (C). Points are observed values determined on individual leaves and lines are fitted values. The shaded areas around the dashed lines in C are the 95 % confidence interval of the fitted values. DAWW in C represents days after withholding water. Experimental data in A were derived from Quereix et al. (2001), while those in B and C were from the present study (see Materials and Methods for details).
Calibration and verification of the coupled extended-FvCB module and Tardieu–Davies module
The coupling of the extended-FvCB module and Tardieu–Davies module was first verified by inputting the stomatal conductance calculated by the Tardieu–Davies module based on observed and [ABA]xyl (eqn 3) into the extended-FvCB module. The extended-FvCB module satisfactorily reproduced the observed net photosynthesis with the simulated gsw as input (Supplementary Data Fig. S11, slope = 0.87, R2 = 0.69).
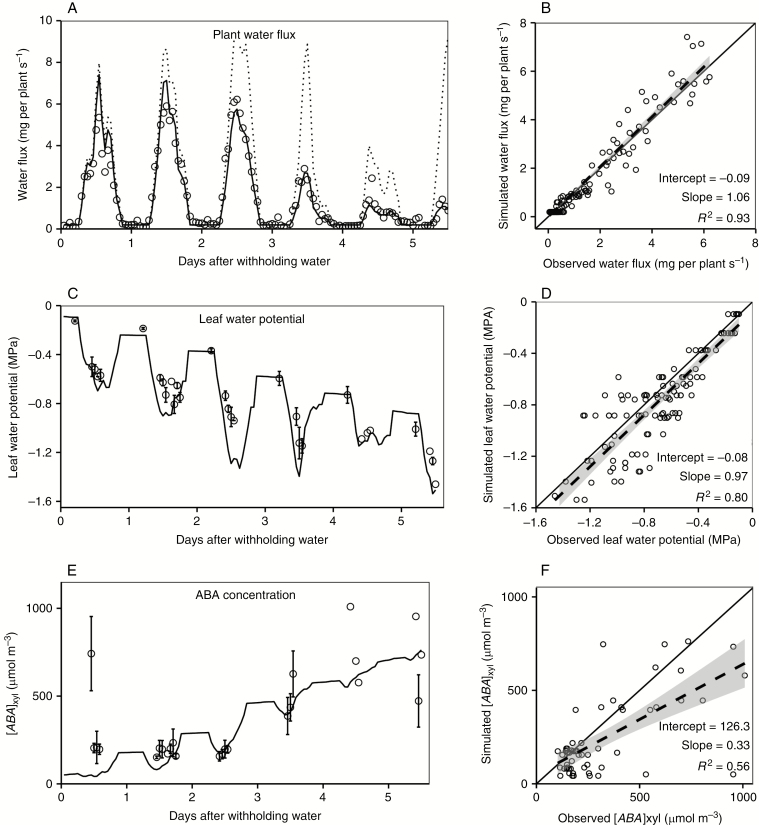
The coupled model was further verified by comparing the simulated water flux, and [ABA]xyl with the observed values with only ambient conditions and soil water content as inputs. The simulated hourly water flux reproduced the diurnal pattern and instantaneous drops of observed water flux, as well as the decline of water flux during the soil drying period (slope = 1.06, R2 = 0.93, Fig. 4A, B). Soil water supply started to limit plant water flux approximately after 48 h of water withholding, and the gap between potential and observed water flux gradually increased during the soil drying period (Fig. 4A). The model captured the commonly observed diurnal changes in leaf water potential and the steady decline of midday leaf water potential within the soil drying period (Fig. 4C). The model slightly underestimated leaf water potential (slope = 0.93, Fig. 4D). The simulated [ABA]xyl increased steadily as the soil gradually dried (Fig. 4E). The simulated [ABA]xyl under dry conditions was lower than the mean of the observed values, but there was a large variation in the observed [ABA]xyl. The simulated root conductance tightly followed the pattern of plant transpiration (Fig. S12).
Fig. 4.
Verification of the simulated hourly plant water flux (A, B), leaf water potential (C, D) and xylem sap ABA concentration (E, F) within a soil drying cycle. Left panels (A, C, E) are comparisons between observed values and simulated values over time, and right panels (B, D, F) are direct comparisons. Points in the left panels are hourly mean of observed values, and solid lines are simulated values. Dashed lines in A are potential water flux rates calculated by the extended-FvCB module based on the ambient condition without accounting for plant water status. The gap between dashed lines and solid lines represents the effects of water stress. Solid lines in right panels are the 1: 1 lines between observed and simulated values, and dashed lines are linear regression lines. The shaded areas around the dashed lines are the 95 % confidence interval of the fitted values. Error bars represents one standard error (mean ± s.e.).
Spatial and temporal variability of leaf-level simulations within the drying cycle
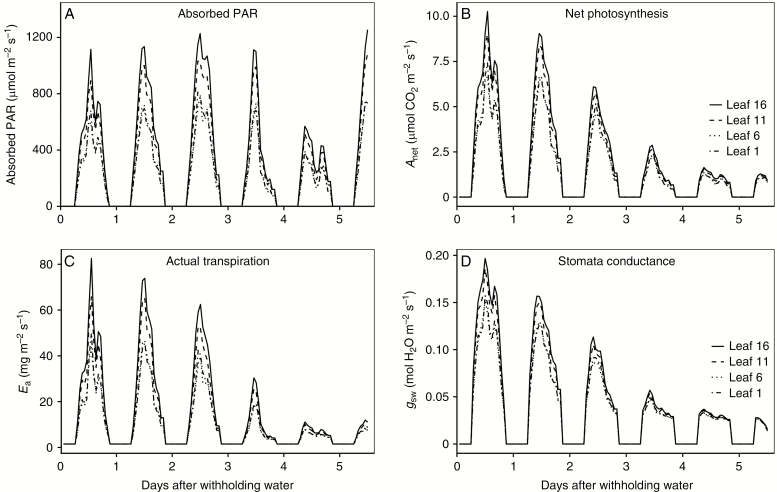
The calibrated coupled model was used to verify its performance for the within-canopy variations during the drying cycle (Fig. 5, Fig. S1). A gradient in absorbed PAR within the canopy was reflected by the model simulation, with the top leaves (leaves 16 and 11) showing higher values than the bottom leaves (leaves 6 and 1, Fig. 1A and 5A) under our experimental conditions. Net photosynthesis, actual transpiration and stomatal conductance showed a similar gradient across different leaf positions to the absorbed PAR (Figs 1B, C and 5B–D). The model resulted in a steady decline in (from ~10 to ~1 μmol CO2 m−2 s−1), Ea (from ~80 to ~8 mg m−2 s−1) and (from ~0.20 to ~0.02 mol m−2 s−1) as the soil gradually dried, although the absorbed PAR did not show large differences during the first 4 d of the dying cycle (Fig. 5).
Fig. 5.
Diurnal changes of absorbed radiation (A), net photosynthesis (B), actual transpiration (C), stomatal conductance for water (D) of leaf 16 (solid lines), leaf 11 (dashed lines), leaf 6 (dotted lines) and leaf 1 (dot-dashed lines) within a soil drying cycle.
Model validation
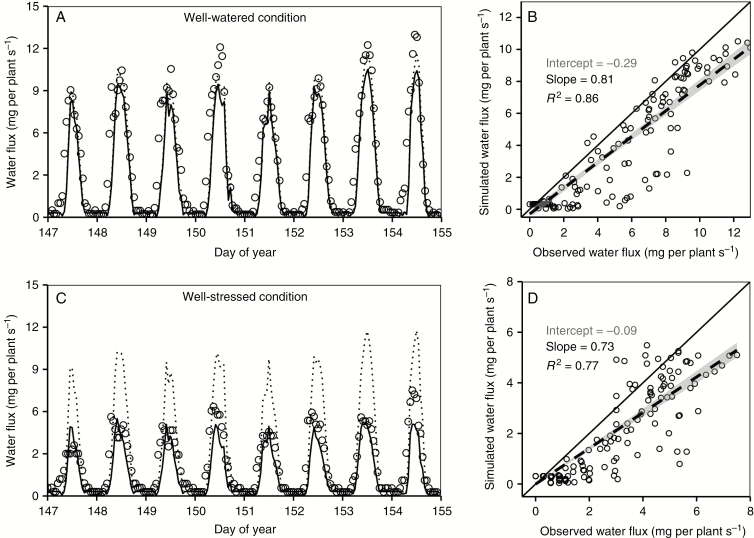
The model was validated with a separate data set by comparing the hourly water flux rate under both well-watered and water-stressed conditions. By inputting the environmental conditions and leaf nitrogen content of the validation data set, the model captured 86 % of the variation in observed transpiration under the well-watered condition and 77 % of the variation under water stress (Fig. 6). The model correctly predicted the diurnal transpiration pattern and the time of the peak under both well-watered and water-stressed conditions, although with some under-estimation for plant transpiration.
Fig. 6.
Validation of the simulated hourly plant water flux under well-watered (A, B) and water-stressed conditions (C, D). Left panels (A, C, E) are comparisons between observed values and simulated values over time, and right panels (B, D, F) are direct comparisons. Points in left panels are hourly means of observed water flux, and solid lines are simulated values. Dashed lines in A and C are potential water flux rates calculated by the extended-FvCB module based on the ambient condition without accounting for plant water status. Solid lines in right panels are the 1: 1 lines between observed and simulated values, and dashed lines are linear regression lines. The shaded areas around the dashed lines are the 95 % confidence interval of the fitted values.
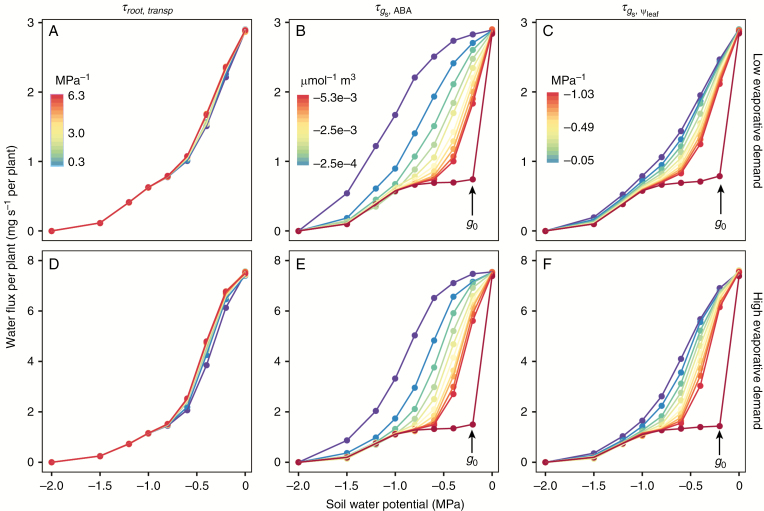
Response of water flux and midday to changes in hydraulic conductance and stomata sensitivity to [ABA]xyl () and to
Plant water flux decreased rapidly as the soil gradually dried and slowed down when was more negative than −1.0 MPa (Fig. 7). Plant water flux was insensitive to changes in the sensitivity of root conductance to the rate of water flux () at both low (2.4 mg s–1, Fig. 7A) and high (6.0 mg s–1Fig. 7D) evaporative demand, although moderate differences in plant water flux were found when was between −0.3 and −0.8 MPa. Similar trends were also found when changing the sensitivity of leaf conductance to the rate of leaf transpiration (Supplementary Data Fig. S13). The simulated plant water flux with different values of and first diverged as decreased, and then converged when decreased further (Fig. 7B, C, E, F). High sensitivity of stomatal conductance to [ABA]xyl and (dark red points and lines in Fig. 7) resulted in a rapid reduction in water flux as the soil gradually dried, and reached a stage when water flux was largely controlled by residual stomatal conductance much earlier than when the sensitivity of stomatal conductance to [ABA]xyl and were low (purple points and lines). Similar trends were also confirmed on photosynthesis and stomatal conductance (Figs S14 and S15).
Fig. 7.
Response of plant water flux at different soil water potentials to changes in (A, D), (B, E) and (C, F). Row 1 represents low evaporative conditions (2.4 mg per plant s−1), and row 2 represents high evaporative conditions (6 mg per plant s−1). The colour gradient from purple to red represents increasing absolute value of the tested parameters, 10–210 % of the default value (median value in the legend). One extra simulation (dark red points and lines), 10 times the default value was added for both and
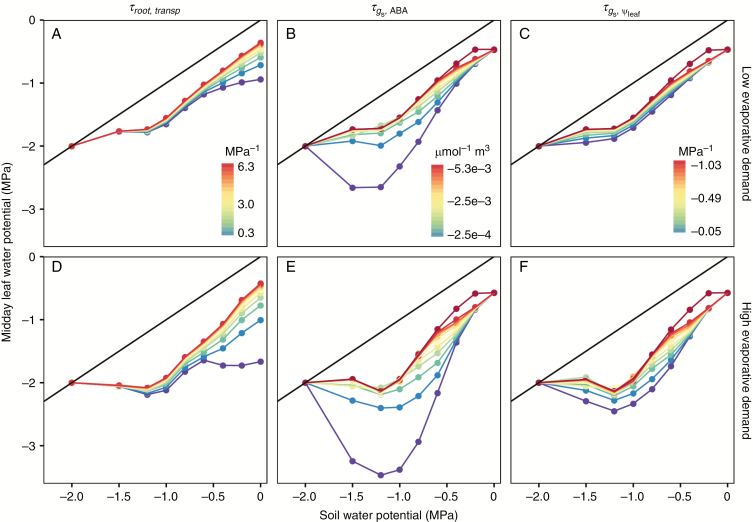
Simulated midday was linearly related to when MPa for a large range of tested parameter values (Fig. 8). For the default parameter set, the intercept (midday when ) was ~−0.42 MPa and the slope was ~1.11 under low evaporative demand, and the intercept was ~−0.57 MPa and the slope was ~1.33 under high evaporative demand (only for the range ≥ −1.2 MPa). The decrease in root conductance, induced by resulted in more negative intercepts and smaller slopes under both low and high evaporative demands (Fig. 8A, D). A nearly constant midday phase (0 ≤ ≤ −0.6 MPa) resulted when was reduced to 10 % of the default value under high evaporative demand (purple points and line in Fig. 8D). Differences in midday induced by varying gradually diminished as the soil progressively dried and crossed the 1:1 line (Fig. 8) when the water flux became zero (Fig. 7).
Fig. 8.
Response of midday leaf water potential at different soil water potentials to changes in and Row 1 represents low evaporative conditions (2.4 mg per plant s−1), and row 2 represents high evaporative conditions (6 mg per plant s−1). The colour gradient from purple to red represents increasing absolute value of the tested parameter, 10–210 % of the default value. One extra simulation (dark red points and lines), 10 times the default value was added for both and Black lines represent the 1: 1 lines.
In contrast to the effects of changes in root hydraulic conductance on midday (namely larger effects at well-watered conditions and diminished effects as the soil dried), an opposite effect was found for changes in and (Fig. 8B, C, E, F). The simulated midday values were initially the same for different values of and and then diverged as the soil dried, and converged again. High sensitivity of stomatal conductance to [ABA]xyl and (red points and lines in Fig. 8) were able to maintain a constant within only a small range of (−0 to −0.3 MPa). Low sensitivity of stomatal conductance to [ABA]xyl resulted in a decrease of to −3.5 MPa under high evaporative demand when equalled −1.2 MPa.
DISCUSSION
Response of residual stomatal conductance to plant water status
GrapevineXL incorporated the percentage loss of hydraulic conductivity () in both the calculation of leaf conductance () and residual stomatal conductance (). The value of was assumed to be constant in both the calculation of the extended-FvCB module (eqn 1) and the Tardieu–Davies module (eqn 3). The model simulations here revealed that a constant resulted in large, artefactual drops in under severe water stress even when stomata aperture was largely closed (Supplementary Data Figs S16 and S17). For example, when using a constant midday decreased to −7 MPa when was −2.0 MPa under high evaporative demand (Figs S16 and S17). Thus, to avoid unrealistic it is essential to include the effect of water status on
Increasing efforts have been made to investigating the nocturnal stomatal conductance measured in the night where Anet ≤ 0 (Zeppel et al., 2012), similar to residual stomatal conductance defined as the stomatal conductance at the light compensation point when Anet = 0. Coupel-Ledru et al. (2016) suggested that nocturnal stomatal conductance may be important in breeding for high water-use efficiency grapevine genotypes. They found night-time transpiration can be reduced without altering growth on some genotypes obtained from a cross between Vitis vinifera ‘Syrah’ and ‘Grenache’. In addition, nocturnal stomatal conductance varied significantly between species and under different VPD and soil water potential (Cavender-Bares et al., 2007; Zeppel et al., 2012; Ogle et al., 2012), and contributed significantly to the low in Vitis vinifera ‘Semillon’ during warm and dry nights (Rogiers et al., 2009).
The definition of nocturnal stomatal conductance and residual stomatal conductance may differ in the literature, although both were related to the period when Anet ≤ 0. Residual stomata conductance has normally been defined in one of two ways: (1) as a ‘fitted’ parameter – an extrapolated intercept between gs and Anet (Ball et al., 1987; Barnard and Bauerle, 2013); and (2) as the value of gs at light compensation point Anet ≤ 0 (Barbour and Buckley, 2007; Evers et al., 2010; Prieto et al., 2012). Barnard and Bauerle (2013) found that the observed stomatal conductance when Anet ≤ 0, measured under dark conditions ~1 h after nightfall, was always larger than the extrapolated intercept between gs and Anet, probably because the relationship between gs and Anet becomes non-linear or asymptotic at low light levels.
To date, our understanding of the physiological mechanisms regulating and nocturnal stomatal conductance is incomplete (Dawson et al., 2007; Ogle et al., 2012). The regulation of and nocturnal stomatal conductance probably involves genetic differences, circadian rhythm, nutrient avaliability, stomatal density and (Caird et al., 2007; Dawson et al., 2007). The function between and that we applied was emperical and represented as a function of leaf water potential (Hochberg et al., 2016). The result was that GrapevineXL generated a reduction in stomatal conductance with decreasing in line with experimental observations (Ogle et al., 2012). To our knowledge, the relationship between and implemented in the model represents the first attempt in incorporating the effects of water status on in a stomatal conductance model. Nevertheless, further efforts are needed to quantify the evolution of with decreasing
Model robustness
GrapevineXL provided good predictions of the effects of simultaneous changes in Ra, Ta, CO2, VPD and soil water content on leaf gas exchange and on plant water status (Figs 4–8, Supporting Data Figs S7–S10). Consequently, the model was able to dissect the relative contributions of atmospheric factors and soil water status on water fluxes. For instance, the model discriminated that the reduction in water flux at the third day after withholding water was essentially due to a decrease in soil water content, while the reduction at the fourth day after withholding water was due mutually to the decreases of transpiration demand and soil water content (Fig. 4). The simulated temperature response curve of photosynthesis (Fig. S8) was consistent with observations on grapevine and other C3 species, where maximum photosynthesis rates were observed at leaf temperatures of 27–32 °C and the optimum temperature increased with increasing CO2 concentration at saturated light conditions (Zufferey et al., 2000; Wise et al., 2004; Greer and Weedon, 2012). The emerging relationship between stomatal conductance and soil water potential (exponential decay, Fig. S7) agreed with field observations (Williams and Araujo, 2002; Zufferey et al., 2011; Williams et al., 2012; Pagay et al., 2015), and empirical functions (e.g. negative exponential or linear) implemented in stomata models (Jarvis, 1976; Macfarlane et al., 2004; Misson et al., 2004). The emerging relationship between root conductance per unit of root dry mass (mg s−1 MPa−1 g−1root, root conductance divided by root biomass ~15 g in our experiment) and mean leaf transpiration rate (mmol m−2 s−1, plant water flux times leaf area 0.12 m2 divided by molar mass of water 18) was comparable to those of Vandeleur et al. (2009, 2014) for grapevine root conductance. The slope of this relationship was 0.439 in our simulation for the soil drying cycle (Fig. 4 and Supplementary Data Fig. S12), including all the effects of transpiration, circadian rhythm and [ABA]xyl, which was similar to the value (0.48) in Vandeleur et al. (2009) but slightly smaller than the value (0.715) in Vandeleur et al. (2014).
Exploring plant water use strategies via modelling
Plant water use strategies are generally divided into two groups: isohydric and anisohydric (Bates and Hall, 1981). Isohydric species adjust their stomatal conductance tightly in order to maintain a relatively stable midday as environmental conditions change. By contrast, anisohydric species have a less sensitive stomatal control, maintaining higher stomatal conductance even with significant decreases in Although these contrasting types of regulation have been observed in various species, the underlying mechanisms are still poorly understood (Buckley, 2005, 2016; Maurel et al., 2016) and the delimitation between an isohydric and anisohydric species can be difficult to discern (e.g. Chaves et al., 2010; Collins et al., 2010; Rogiers et al., 2012; Zhang et al., 2012; Bota et al., 2016).
Recently, Martinez-Vilalta et al. (2014) developed a framework for dissecting isohydric and anisohydric strategies, based on the relationship between midday and predawn leaf water potentials (assumed as a linear relationship). The slope of the relationship (σ) measures the relative sensitivity of the transpiration rate and plant hydraulic conductance to declining water availability (see ‘Sensitivity analysis’). A strict isohydric behaviour would be represented by σ = 0 and increasingly anisohydric behaviour as σ moves closer to 1.
Based on this framework, an in silico analysis using GrapevineXL was conducted. The model was able to reproduce the two different water use strategies through changes in hydraulic conductance and stomata sensitivity to [ABA]xyl and (Fig. 8). Reduction in hydraulic conductance decreased σ by inducing a more negative intercept, while reduction in stomata sensitivity to [ABA]xyl and (small absolute value) increased σ with the intercept remaining the same. Interestingly, the model simulations were not able to reproduce more extreme isohydric behaviours with high stomata sensitivity to [ABA]xyl and alone. These would need to be paired with a relatively low hydraulic conductance, which was associated with a more negative intercept (Fig. 8), or a higher vulnerability to embolism, which reduced and helped in closing stomata completely (Figs 7 and 8). This suggested that hydraulic conductance was a critical parameter when considering the mechanisms driving these contrasting behaviours. This was consistent with Schultz (2003), who hypothesized that differences in hydraulic conductance contributed to the different behaviours of ‘Grenache’ (isohydric) and ‘Syrah’ (anisohydric) under water deficit. Equally, Vandeleur et al. (2009, 2014) showed that plant anisohydric behaviour was related to enhanced aquaporin expression and activity in roots and shoots, which increased whole plant hydraulic conductance, thereby buffering water potential and favouring open stomata.
Potential limitations of this study
The simulated plant water flux and stomatal conductance were insensitive to changes in the hydraulic conductance of roots and leaves under well-watered conditions although responds correspondingly (Figs 7 and 8). This was probably due to the interaction between [ABA]xyl and presented in eqn (3). Mathematically in eqn (3), when [ABA]xyl remains at a low concentration under well-water conditions even large water potential drops can induce only a small reduction in stomatal conductance. This was consistent with the findings that stomata can stay open under high temperature (Greer and Weedon, 2012) and VPD conditions in irrigated field grown grapevine, even when leaf water potential was below −1.0 MPa (Soar et al., 2006).
Recent studies found that can induce ABA synthesis within the leaf and cause stomatal closure (McAdam and Brodribb, 2015; McAdam et al., 2016; Buckley, 2016). This was supported by Rodriguez-Dominguez et al. (2016), who found that leaf turgor (positively related to ) can explain most stomatal responses under moderate drought in three woody species. However, Speirs et al. (2013) provided evidence that ABA synthesized in the roots played a key role in linking stomatal response to soil moisture status. It is plausible that the sources of ABA that causes stomatal closure and the effects of ABA on stomatal conductance may differ between species. A simulation trial was conducted by removing the effect of ABA in the calculation of (eqn 3) and determining with alone. The result showed that simulated plant water flux and stomatal conductance became sensitive to changes in root hydraulic conductance (Supplementary Data Fig. S18). The linear relationship between midday and was preserved in this simulation trial, and water flux reduced correspondingly with decreases in However, this simulation trial was not able to capture isohydric behaviour (i.e. decreasing with a constant ) as is determined by alone. Further investigations are needed to understand the sources of ABA in the leaf and how it interacts with in closing stomata (Buckley, 2005, 2017; Lovisolo et al., 2010).
Plant water capacitance was not included in this model due to its small contribution to transpiration in grapevine (2–6.5 % of transpiration at midday, Schultz, 2003) and in order to keep the algorithm simple and robust. Including plant water capacitance, which was dynamically changing over the day, would make the water influx into the roots different from the water outflow from the leaves, and thus increased the difficulty for estimating water flux under dynamic environmental conditions. Similarly in Tardieu et al. (2015), water flux into the roots was assumed to be equal to water outflow from the leaves although the equations describing the effect of plant water capacitance on leaf water potential were included in the model.
Potential applications and perspectives
Quantifying the response of plant water status to the environment and its effects on carbon acquisition are essential in understanding plant performance under drought conditions. Such quantification can provide insights into the interaction among carbon metabolism, plant hydraulics and the regulation of plant water status, which are critical for cell function and avoiding hydraulic failure (Nardini et al., 2001; Franks, 2006). Our quantitative model provides a foundation for simultaneously integrating various mechanisms that regulate photosynthesis and water status at the organ and even cell levels while scaling up to the plant or field level.
Furthermore, as water deficits uncouple growth from photosynthesis and modify the relationships between carbon and growth in sink organs (Muller et al., 2011), a plant model that includes water status in simulating growth will perform better than carbon-based plant growth models in identifying the traits that limit plant performance under drought (Parent and Tardieu, 2014). For example, one can potentially leverage parameters that quantify the effects of plant hydraulic properties and stomatal responses to [ABA]xyl and on water fluxes under various environmental conditions, in revealing differences within genetic populations (Tardieu, 2003, 2012). This information can be further used by breeders for selecting specific plant traits that are well adapted for particular environments.
Including water status in plant models is also essential for simulating fruit quality, which is largely dependent on sugar and water transport (Fishman and Génard, 1998). Several attempts have been made in tomato and peach to simulate the effects of crop load, temperature, VPD and radiation intensity on fruit growth with xylem water potential being estimated from continuous stem diameter measurements (De Swaef et al., 2014; Hannssens et al., 2015). Our model provides a basis for future modelling of the physiology, growth and ripening of individual fruits. In the future, GrapevineXL can be linked with leaf and fruit growth modules, which incorporate the effects of water status on growth, to simulate carbon and water influx to individual leaves and fruits under various environmental conditions. Such a model can provide insights into canopy management and irrigation strategies to optimize fruit yield and quality.
SUPPLEMENTARY DATA
Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Table S1. List of the main parameters used in the model, their values and units. Video S1. Diurnal dynamics of leaf transpiration during a soil drying cycle. Method S1. Equations for the extended-FvCB module. Method S2. Equations for the Tardieu–Davies module. Method S3. Leaf gas exchange determination. Method S4. Equations for the theorectial framework for descriping the plant responses to drying soil as developed by Martinez-Vilalta et al. (2014). Method S5. Sensitivity of model performance to Ta, CO2, and their interactions. Method S6. Setup of the model simulation. Fig. S1. Comparison of the simulated canopy leaf temperature and canopy thermal picture. Fig. S2. Relationships between soil water potential, soil water content, and soil hydraulic conductivity and the resistance from soil to root surface. Fig. S3. Illustration of the arrangement of diffuse radiation in a virtual hemisphere. Fig. S4. Environmental conditions during the drying cycle. Fig. S5. Observations during the drying cycle. Fig. S6. The environmental conditions of the experiment used for model validation. Fig. S7. Response of stomata conductance to temperature, CO2, soil water potential and their interactions. Fig. S8. Response of net photosynthesis to temperature, CO2, soil water potential and their interactions. Fig. S9. Response of plant water flux to temperature, CO2, soil water potential and their interactions. Fig. S10. Effect of vapour pressure deficit on leaf gas exchange under two different temperatures and radiations. Fig. S11. Verification of the stomata conductance calculated from [ABA]xyl and Fig. S12. The simulated diurnal changes of root conductance and xylem water potential within a soil drying cycle. Fig. S13. The response of plant water flux at different soil water potentials to changes in leaf conductance as induced by Fig. S14. Response of mean leaf net photosynthesis at different soil water potentials to changes in and Fig. S15. Response of mean leaf stomatal conductance at different soil water potentials to changes in and Fig. S16. Response of midday leaf water potential at different soil water potentials to changes in and when removing the effect of on Fig. S17. Response of plant water flux at different soil water potentials to changes in and when removing the effect of on Fig. S18. Response of midday leaf water potential and plant water flux at different soil water potentials to changes in without the effect of ABA.
ACKNOWLEDGEMENTS
We thank Drs Jochem B. Evers, Xinyou Yin and Francois Tardieu for sharing their model codes, Drs Gilles Vercambre, Michel Génard, Valsesia Pierre, Eric Lebon and Vivian Zufferery for helpful discussions, Dr Guillaume Charrier for sharing data on leaf water potential, Nabil Girollet for assisting in running the model on Avakas, Dr Philippe Pieri for assisting in taking the thermal picture, Dr Bryan Loveys for analysing the ABA concentrations, and anonymous reviewers for helpful comments on the manuscript. We greatly acknowledge the financial support from the European Community’s Seventh Framework Program (FP7/2007-2013) under grant agreement no. FP7-311775, Project INNOVINE and the financial support from the French National Research Agency (ANR) in the frame of the Investments for the future Programme, within the Cluster of Excellence COTE (ANR-10-LABX-45), and the computing facilities MCIA (Mésocentre de Calcul Intensif Aquitain, on the cluster AVAKAS) of the University of Bordeaux.
LITERATURE CITED
- Baert A, De Schepper V, Steppe K, Mencuccini M. 2015. Variable hydraulic resistances and their impact on plant drought response modelling. Tree Physiology 35: 439–449. [DOI] [PubMed] [Google Scholar]
- Baldazzi V, Pinet A, Vercambre G, Benard C, Biais B, Genard M. 2013. In-silico analysis of water and carbon relations under stress conditions. A multi-scale perspective centered on fruit. Frontiers in Plant Science 6: 495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ball JT, Woodrow IE, Berry JA. 1987. A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions. In: Biggins J, ed. Progress in Photosynthesis Research: Volume 4Proceedings of the VIIth International Congress on Photosynthesis Providence, Rhode Island, USA, August 10–15, 1986 Dordrecht: Springer Netherlands, 221–224. [Google Scholar]
- Barbour MM, Buckley TN. 2007. The stomatal response to evaporative demand persists at night in Ricinus communis plants with high nocturnal conductance. Plant, Cell & Environment 30: 711–721. [DOI] [PubMed] [Google Scholar]
- Barnard DM, Bauerle WL. 2013. The implications of minimum stomatal conductance on modeling water flux in forest canopies. Journal of Geophysical Research: Biogeosciences 118: 1322–1333. [Google Scholar]
- Bates LM, Hall AE. 1981. Stomatal closure with soil water depletion not associated with changes in Bulk leaf water status. Oecologia 50: 62–65. [DOI] [PubMed] [Google Scholar]
- Bota J, Tomás M, Flexas J, Medrano H, Escalona JM. 2016. Differences among grapevine cultivars in their stomatal behavior and water use efficiency under progressive water stress. Agricultural Water Management 164: 91–99. [Google Scholar]
- Bouma TJ, Nielsen KL, Koutstaal B. 2000. Sample preparation and scanning protocol for computerised analysis of root length and diameter. Plant and Soil 218: 185–196. [Google Scholar]
- Buckley TN. 2005. The control of stomata by water balance. New Phytologist 168: 275–292. [DOI] [PubMed] [Google Scholar]
- Buckley TN. 2016. Stomatal responses to humidity: has the ‘black box’ finally been opened?Plant, Cell and Environment 39: 482–484. [DOI] [PubMed] [Google Scholar]
- Buckley TN. 2017. Modeling stomatal conductance. Plant Physiology 174: 572–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckley TN, Mott KA, Farquhar GD. 2003. A hydromechanical and biochemical model of stomatal conductance. Plant, Cell and Environment 26: 1767–1785. [Google Scholar]
- Buckley TN, Turnbull TL, Adams MA. 2012. Simple models for stomatal conductance derived from a process model: cross‐validation against sap flux data. Plant, Cell and Environment 35: 1647–1662. [DOI] [PubMed] [Google Scholar]
- Caird M, Richards JH, Donovan L. 2007. Nighttime stomatal conductance and transpiration in C3 and C4 plants. Plant Physiology 143: 4–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavender-Bares J, Sack L, Savage J. 2007. Atmospheric and soil drought reduce nocturnal conductance in live oaks. Tree Physiology 27: 611–620. [DOI] [PubMed] [Google Scholar]
- Charrier G, Torres-Ruiz JM, Badel E et al. . 2016. Evidence for hydraulic vulnerability segmentation and lack of xylem refilling under tension. Plant Physiology 172: 1657–1668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaves MM, Zarrouk O, Francisco R et al. . 2010. Grapevine under deficit irrigation: hints from physiological and molecular data. Annals of Botany 105: 661–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chew YH, Wenden B, Flis A et al. . 2014. Multiscale digital Arabidopsis predicts individual organ and whole-organism growth. Proceedings of the National Academy of Sciences 111: E4127–E4136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chelle M, Andrieu B, Bouatouch K. 1998. Nested radiosity for plant canopies. The Visual Computer 14: 109–125. [Google Scholar]
- Collins MJ, Fuentes S, Barlow EWR. 2010. Partial rootzone drying and deficit irrigation increase stomatal sensitivity to vapour pressure deficit in anisohydric grapevines. Functional Plant Biology 37: 128–138. [Google Scholar]
- Coupel-Ledru A, Lebon E, Christophe A et al. . 2016. Reduced night-time transpiration is a relevant breeding target for high water-use efficiency in grapevine. Proceedings of the National Academy of Sciences 113: 8963–8968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damour G, Simonneau T, Cochard H, Urban L. 2010. An overview of models of stomatal conductance at the leaf level. Plant, Cell and Environment 33: 1419–1438. [DOI] [PubMed] [Google Scholar]
- Dawson TE, Burgess SSO, Tu KP et al. . 2007. Nighttime transpiration in woody plants from contrasting ecosystems. Tree Physiology 27: 561–575. [DOI] [PubMed] [Google Scholar]
- Dewar RC. 2002. The Ball–Berry–Leuning and Tardieu–Davies stomatal models: synthesis and extension within a spatially aggregated picture of guard cell function. Plant, Cell and Environment 25: 1383–1398. [Google Scholar]
- Evers JB, Vos J, Yin X, Romero P, van der Putten PEL, Struik PC. 2010. Simulation of wheat growth and development based on organ-level photosynthesis and assimilate allocation. Journal of Experimental Botany 61: 2203–2216. [DOI] [PubMed] [Google Scholar]
- Farquhar GD, Caemmerer S, Berry JA. 1980. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149: 78–90. [DOI] [PubMed] [Google Scholar]
- Fishman S, Génard M. 1998. A biophysical model of fruit growth: simulation of seasonal and dirunal dynamics of mass. Plant, Cell and Environment 21: 739–752. [Google Scholar]
- Franks PJ. 2006. Higher rates of leaf gas exchange are associated with higher leaf hydrodynamic pressure gradients. Plant, Cell and Environment 29: 584–592. [DOI] [PubMed] [Google Scholar]
- Gambetta GA, Manuck CM, Drucker ST et al. . 2012. The relationship between root hydraulics and scion vigour across Vitis rootstocks: What role do root aquaporins play?Journal of Experimental Botany 63: 6445–6455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao Q, Zhao P, Zeng X, Cai X, Shen W. 2002. A model of stomatal conductance to quantify the relationship between leaf transpiration, microclimate and soil water stress. Plant, Cell and Environment 25: 1373–1381. [Google Scholar]
- Génard M, Bertin N, Gautier H, Lescourret F, Quilot B. 2010. Virtual profiling: a new way to analyse phenotypes. Plant Journal 62: 344–355. [DOI] [PubMed] [Google Scholar]
- Greer DH, Weedon MM. 2012. Modelling photosynthetic responses to temperature of grapevine (Vitis vinifera cv. Semillon) leaves on vines grown in a hot climate. Plant, Cell and Environment 35: 1050–1064. [DOI] [PubMed] [Google Scholar]
- Gu S, Evers JB, Zhang L et al. . 2014. Modelling the structural response of cotton plants to mepiquat chloride and population density. Annals of Botany 114: 877–887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hannssens J, De Swaef T, Steppe K. 2015. High light decreases xylem contribution to fruit growth in tomato. Plant, Cell and Environment 38: 487–498. [DOI] [PubMed] [Google Scholar]
- Hemmerling R, Kniemeyer O, Lanwert D, Kurth W, Buck-Sorlin GH. 2008. The rule-based language XL and the modelling environment GroIMP illustrated with simulated tree competition. Functional Plant Biology 35: 739–750. [DOI] [PubMed] [Google Scholar]
- Hochberg U, Albuquerque C, Rachmilevitch S et al. . 2016. Grapevine petioles are more sensitive to drought induced embolism than stems: evidence from in vivo MRI and microCT observations of hydraulic vulnerability segmentation. Plant, Cell and Environment 39: 1886–1894. [DOI] [PubMed] [Google Scholar]
- Jarvis PG. 1976. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 273: 593–610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kniemeyer O. 2008. Design and implementation of a graph grammar based language for functional–structural plant modelling. PhD thesis, Brandenburg University of Technology, Germany. [Google Scholar]
- Leuning R. 1995. A critical appraisal of a combined stomatal-photosynthesis model for C3 plants. Plant, Cell and Environment 18: 339–355. [Google Scholar]
- Lovisolo C, Perrone I, Carra A et al. . 2010. Drought-induced changes in development and function of grapevine (Vitis spp.) organs and in their hydraulic and non hydraulic interactions at the whole plant level: a physiological and molecular update. Functional Plant Biology 37: 98–116. [Google Scholar]
- Macfarlane C, White DA, Adams MA. 2004. The apparent feed-forward response to vapour pressure deficit of stomata in droughted, field-grown Eucalyptus globulus Labill. Plant, Cell and Environment 27: 1268–1280. [Google Scholar]
- Marguerit E, Brendel O, Lebon E, Van Leeuwen C, Ollat N. 2012. Rootstock control of scion transpiration and its acclimation to water deficit are controlled by different genes. New Phytologist 194: 416–429. [DOI] [PubMed] [Google Scholar]
- Maurel C, Verdoucq L, Rodrigues O. 2016. Aquaporins and plant transpiration. Plant, Cell & Environment 39: 2580–2587. [DOI] [PubMed] [Google Scholar]
- Martinez-Vilalta J, Poyatos R, Aguadé D, Retana J, Mencuccini M. 2014. A new look at water transport regulation in plants. New Phytologist 204: 105–115. [DOI] [PubMed] [Google Scholar]
- McAdam SAM, Brodribb TJ. 2015. The evolution of mechanisms driving the stomatal response to vapour pressure deficit. Plant Physiology 167: 833–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAdam SAM, Sussmilch FC, Brodribb TJ. 2016. Stomatal responses to vapour pressure deficit are regulated by high speed gene expression in angiosperms. Plant, Cell and Environment 39: 485–491. [DOI] [PubMed] [Google Scholar]
- Misson L, Panek JA, Goldstein AH. 2004. A comparison of three approaches to modeling leaf gas exchange in annually drought-stressed ponderosa pine forests. Tree Physiology 24: 529–541. [DOI] [PubMed] [Google Scholar]
- Muller B, Pantin F, Génard M et al. . 2011. Water deficits uncouple growth from photosynthesis, increase C content, and modify the relationships between C and growth in sink organs. Journal of Experimental Botany 62: 1715–1729. [DOI] [PubMed] [Google Scholar]
- Mullins MG, Rajasekaran K. 1981. Fruiting cuttings: revised method for producing test plants of grapevine cultivars. American Journal of Enology and Viticulture 32: 35–40. [Google Scholar]
- Nardini A, Tyree MT, Salleo S. 2001. Xylem cavitation in the leaf of Prunus laurocerasus and its impact on leaf hydraulics. Plant Physiology 125: 1700–1709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nolf M, Creek D, Duursma R, Holtum J, Mayr S, Choat B. 2015. Stem and leaf hydraulic properties are finely coordinated in three tropical rain forest tree species. Plant, Cell and Environment 38: 2652–2661. [DOI] [PubMed] [Google Scholar]
- Ogle K, Lucas RW, Bentley LP et al. . 2012. Differential daytime and night-time stomatal behavior in plants from North American deserts. New Phytologist 194: 464–476. [DOI] [PubMed] [Google Scholar]
- Pagay V, Zufferey V, Lakso Alan N. 2015. The influence of water stress on grapevine (Vitis vinifera L.) shoots in a cool, humid climate: growth, gas exchange and hydraulics. Functional Plant Biology 43: 827–837. [DOI] [PubMed] [Google Scholar]
- Parent B, Tardieu F. 2014. Can current crop models be used in the phenotyping era for predicting the genetic variability of yield of plants subjected to drought or high temperature?Journal of Experimental Botany 65: 6179–6189. [DOI] [PubMed] [Google Scholar]
- Peccoux A, Loveys B, Zhu J, Gambetta GA, Delrot S, Vivin P, Schultz HR, Ollat N, Dai Z. 2018. Dissecting the rootstock control of scion transpiration using model-assisted analyses in grapevine. Tree Physiol: in press. doi:10.1093/treephys/tpx1153. [DOI] [PubMed] [Google Scholar]
- Plummer M, Best N, Cowles K, Vines K. 2006. CODA: convergence diagnosis and output analysis for MCMC. R News 6: 7–11. [Google Scholar]
- Prieto JA, Louarn G, Perez Peña J, Ojeda H, Simonneau T, Lebon E. 2012. A leaf gas exchange model that accounts for intra-canopy variability by considering leaf nitrogen content and local acclimation to radiation in grapevine (Vitis vinifera L.). Plant, Cell and Environment 35: 1313–1328. [DOI] [PubMed] [Google Scholar]
- Quereix A, Dewar RC, Gaudillere JP, Dayau S, Valancogne C. 2001. Sink feedback regulation of photosynthesis in vines: measurements and a model. Journal of Experimental Botany 52: 2313–2322. [DOI] [PubMed] [Google Scholar]
- R Development Core Team R 2016. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Rodriguez-Dominguez CM, Buckley TN, Egea G et al. . 2016. Most stomatal closure in woody species under moderate drought can be explained by stomatal responses to leaf turgor. Plant, Cell and Environment 39: 2014–2026. [DOI] [PubMed] [Google Scholar]
- Rogiers SY, Greer DH, Hutton RJ, Landsberg JJ. 2009. Does night-time transpiration contribute to anisohydric behaviour in a Vitis vinifera cultivar?Journal of Experimental Botany 60: 3751–3763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogiers SY, Greer DH, Hatfield JM et al. . 2012. Stomatal response of an anisohydric grapevine cultivar to evaporative demand, available soil moisture and abscisic acid. Tree Physiology 32: 249–261. [DOI] [PubMed] [Google Scholar]
- Sadras VO, Soar CJ. 2009. Shiraz vines maintain yield in response to a 2–4 °C increase in maximum temperature using an open-top heating system at key phenostages. European Journal of Agronomy 31: 250–258. [Google Scholar]
- Schultz HR. 2003. Differences in hydraulic architecture account for near-isohydric and anisohydric behaviour of two field-grown Vitis vinifera L. cultivars during drought. Plant, Cell and Environment 26: 1393–1405. [Google Scholar]
- Schultz HR, Matthews MA. 1988. Vegetative growth distribution during water deficits in Vitis vinifera L. Functional Plant Biology 15: 641–656. [Google Scholar]
- Da Silva D, Favreau R, Auzmendi I, Dejong TM. 2011. Linking water stress effects on carbon partitioning by introducing a xylem circuit into L-PEACH. Annals of Botany 108: 1135–1145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simonin KA, Burns E, Choat B, Barbour MM, Dawson TE, Franks PJ. 2015. Increasing leaf hydraulic conductance with transpiration rate minimizes the water potential drawdown from stem to leaf. Journal of Experimental Botany 66: 1303–1315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soar CJ, Speirs J, Maffei SM, Penrose AB, McCarthy MG, Loveys BR. 2006. Grape vine varieties Shiraz and Grenache differ in their stomatal response to VPD: apparent links with ABA physiology and gene expression in leaf tissue. Australian Journal of Grape and Wine Research 12: 2–12. [Google Scholar]
- Speirs J, Binney A, Collins M, Edwards E, Loveys B. 2013. Expression of ABA synthesis and metabolism genes under different irrigation strategies and atmospheric VPDs is associated with stomatal conductance in grapevine (Vitis vinifera L. cv Cabernet Sauvignon). Journal of Experimental Botany 64: 1907–1916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su Y, Zhu G, Miao Z, Feng QI, Chang Z. 2009. Estimation of parameters of a biochemically based model of photosynthesis using a genetic algorithm. Plant, Cell and Environment 32: 1710–1723. [DOI] [PubMed] [Google Scholar]
- De Swaef T, Mellisho CD, Baert A et al. . 2014. Model-assisted evaluation of crop load effects on stem diameter variations and fruit growth in peach. Trees 28: 1607–1622. [Google Scholar]
- Tardieu F. 2003. Virtual plants: modelling as a tool for the genomics of tolerance to water deficit. Trends in Plant Science 8: 9–14. [DOI] [PubMed] [Google Scholar]
- Tardieu F. 2012. Any trait or trait-related allele can confer drought tolerance: just design the right drought scenario. Journal of Experimental Botany 63: 25–31. [DOI] [PubMed] [Google Scholar]
- Tardieu F, Davies WJ. 1993. Integration of hydraulic and chemical signalling in the control of stomatal conductance and water status of droughted plants. Plant, Cell and Environment 16: 341–349. [Google Scholar]
- Tardieu F, Parent B. 2016. Predictable 'meta-mechanisms' emerge from feedbacks between transpiration and plant growth and cannot be simply deduced from short-term mechanisms. Plant, Cell and Environment 40: 846–857. [DOI] [PubMed] [Google Scholar]
- Tardieu F, Simonneau T, Parent B. 2015. Modelling the coordination of the controls of stomatal aperture, transpiration, leaf growth, and abscisic acid: update and extension of the Tardieu–Davies model. Journal of Experimental Botany 66: 2227–2237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomás M, Medrano H, Brugnoli E et al. . 2014. Variability of mesophyll conductance in grapevine cultivars under water stress conditions in relation to leaf anatomy and water use efficiency. Australian Journal of Grape and Wine Research 20: 272–280. [Google Scholar]
- Turner NC. 1988. Measurement of plant water status by the pressure chamber technique. Irrigation Science 9: 289–308. [Google Scholar]
- Tuzet A, Perrier A, Leuning R. 2003. A coupled model of stomatal conductance, photosynthesis and transpiration. Plant, Cell and Environment 26: 1097–1116. [Google Scholar]
- Vandeleur RK, Mayo G, Shelden MC, Gilliham M, Kaiser BN, Tyerman SD. 2009. The role of plasma membrane intrinsic protein aquaporins in water transport through roots: diurnal and drought stress responses reveal different strategies between isohydric and anisohydric cultivars of grapevine. Plant Physiology 149: 445–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandeleur RK, Sullivan W, Athman A et al. . 2014. Rapid shoot-to-root signalling regulates root hydraulic conductance via aquaporins. Plant, Cell and Environment 37: 520–538. [DOI] [PubMed] [Google Scholar]
- Vos J, Evers JB, Buck-Sorlin GH, Andrieu B, Chelle M, de Visser PHB. 2010. Functional–structural plant modelling: a new versatile tool in crop science. Journal of Experimental Botany 61: 2101–2115. [DOI] [PubMed] [Google Scholar]
- Williams LE, Araujo FJ. 2002. Correlations among predawn leaf, midday leaf, and midday stem water potential and their correlations with other measures of soil and plant water status in Vitis vinifera. Journal of the American Society for Horticultural Science 127: 448–454. [Google Scholar]
- Williams LE, Baeza P, Vaughn P. 2012. Midday measurements of leaf water potential and stomatal conductance are highly correlated with daily water use of Thompson Seedless grapevines. Irrigation Science 30: 201–212. [Google Scholar]
- Wise RR, Olson AJ, Schrader SM, Sharkey TD. 2004. Electron transport is the functional limitation of photosynthesis in field-grown Pima cotton plants at high temperature. Plant, Cell and Environment 27: 717–724. [Google Scholar]
- Yin X, van Laar HH. 2005. Crop systems dynamics: an ecophysiological simulation model for genotype-by-environment interactions. Wageningen: Wageningen Academic. [Google Scholar]
- Yin X, Struik PC. 2009. C3 and C4 photosynthesis models: an overview from the perspective of crop modelling. NJAS - Wageningen Journal of Life Sciences 57: 27–38. [Google Scholar]
- Zeppel MJ, Lewis JD, Chaszar B et al. . 2012. Nocturnal stomatal conductance responses to rising [CO2], temperature and drought. New Phytologist 193: 929–938. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Oren R, Kang S. 2012. Spatiotemporal variation of crown-scale stomatal conductance in an arid Vitis vinifera L. cv. Merlot vineyard: direct effects of hydraulic properties and indirect effects of canopy leaf area. Tree Physiology 32: 262–279. [DOI] [PubMed] [Google Scholar]
- Zhu J, van der Werf W, Anten NPR, Vos J, Evers JB. 2015. The contribution of phenotypic plasticity to complementary light capture in plant mixtures. New Phytologist 207: 1213–1222. [DOI] [PubMed] [Google Scholar]
- Zufferey V, Murisier F, Schultz HR. 2000. A model analysis of the photosynthetic response of Vitis vinifera L. cvs Riesling and Chasselas leaves in the field: I. Interaction of age, light and temperature. Vitis 39: 19–26. [Google Scholar]
- Zufferey V, Cochard H, Ameglio T, Spring JL, Viret O. 2011. Diurnal cycles of embolism formation and repair in petioles of grapevine (Vitis vinifera cv. Chasselas). Journal of Experimental Botany 62: 3885–3894. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.