A Template and Probabilistic Atlas of the Human Sensorimotor Tracts using Diffusion MRI

Abstract

The purpose of this study was to develop a high-resolution sensorimotor area tract template (SMATT) which segments corticofugal tracts based on 6 cortical regions in primary motor cortex, dorsal premotor cortex, ventral premotor cortex, supplementary motor area (SMA), pre-supplementary motor area (preSMA), and primary somatosensory cortex using diffusion tensor imaging. Individual probabilistic tractography analyses were conducted in 100 subjects using the highest resolution data currently available. Tractography results were refined using a novel algorithm to objectively determine slice level thresholds that best minimized overlap between tracts while preserving tract volume. Consistent with tracing studies in monkey and rodent, our observations show that cortical topography is generally preserved through the internal capsule, with the preSMA tract remaining most anterior and the primary somatosensory tract remaining most posterior. We combine our results into a freely available white matter template named the SMATT. We also provide a probabilistic SMATT that quantifies the extent of overlap between tracts. Finally, we assess how the SMATT operates at the individual subject level in another independent data set, and in an individual after stroke. The SMATT and probabilistic SMATT provide new tools that segment and label sensorimotor tracts at a spatial resolution not previously available.

Introduction

The corticospinal tract and the corticobulbar tract are crucial for the performance of dexterous motor execution (Heffner and Masterton 1983; Nudo and Masterton 1990a, 1990b; Lemon and Griffiths 2005; Jang 2009). Structural neuroimaging experiments in humans converge with lesion studies in nonhuman primates to show that damage to the descending motor tracts lead to profound deficits in fine and gross motor function (Travis 1955; Rouiller et al. 1998; Schaechter et al. 2008, 2009; Schulz et al. 2012; Groisser et al. 2014; Morecraft et al. 2015). The extent of damage to these tracts predicts deficits in function as well as recovery potential after injuries such as stroke (Stinear et al. 2007, 2012; Lindenberg et al. 2012; Schulz et al. 2012). Precise measurement of descending motor tract microstructure is also fundamental to our understanding of diseases and disorders that impact motor function such as upper motor neuron syndrome (Sach et al. 2004), multiple sclerosis (Tovar-Moll et al. 2015), traumatic brain injury (Caeyenberghs et al. 2010; Jang and Kim 2016), spinal cord injury (Hou et al. 2016), and cerebral palsy (Jaspers et al. 2015). Current approaches to studying the microstructure of the descending motor tracts in humans focus on the corticospinal tract descending from the primary motor cortex (M1) (Schaechter et al. 2008, 2009; Lindenberg et al. 2012; Groisser et al. 2014). However, corticospinal and corticobulbar tracts originate in areas beyond the M1. Tracing studies in monkey estimate that 50% of corticospinal projections originate from M1, with the remainder made up of projections that originate in the premotor areas and parietal lobe (Dum and Strick 1991; Galea and Darian-Smith 1994). Functional imaging data show that premotor and higher motor areas are important for motor planning and motor execution (Mayka et al. 2006; Coombes et al. 2010, 2011, 2012; Plow et al. 2015) and have the capacity to influence motor function based on their distinct connections to subcortical areas (Lehericy et al. 2004a, 2004b) and their direct projections to the spinal cord (Dum and Strick 1991). Tracing studies in rodents and nonhuman primates show that projections from different cortical regions are topographically organized through the internal capsule and begin to overlap in the cerebral peduncle (CP) (Barnard and Woolsey 1956; Fries et al. 1993; Coleman et al. 1997). Together these findings suggest that the segregation between tracts associated with different regions in sensorimotor cortex may be preserved in humans. However, there is currently no tract template or probabilistic atlas available to identify different segments of these tracts based on their topographical organization in sensorimotor cortex.

The only noninvasive in vivo method to study the 3D architecture of the sensorimotor tracts in humans is diffusion-weighted imaging (Johansen-Berg and Rushworth 2009; Jones et al. 2013). Probabilistic tractography is one approach that has gained traction because it uses diffusion-weighted images to generate a likelihood map of connectivity between different brain regions which are termed seeds and waypoints (Behrens et al. 2003a, 2003b; Jbabdi et al. 2015; Archer et al. 2016; van Baarsen et al. 2016). Each voxel in the likelihood map is assigned a value based on the number of streamlines that traverse that particular voxel. Voxels in which the number of streamlines is near zero have a low probability of being part of the tract, whereas voxels with a high number of streamlines have a higher probability of being part of the tract. Three important methodological decisions can shape how a tract is identified: (1) seed location and seed size from which the tracking algorithm will begin, (2) location and size of waypoints through which the tract must pass, and (3) the probability threshold level that determines which voxels are included in the tract.

Studies that focus on the corticospinal tract typically identify a seed region in M1, waypoints in the posterior limb of the internal capsule (PLIC) and CP, and a single threshold value based on a percentage of the maximum probability value of all voxels identified in the tract (Newton et al. 2006; Lindenberg et al. 2012; Park et al. 2013; Archer et al. 2016). Probability values are high in the PLIC where more streamlines follow the same trajectory through fewer voxels. Probability values are relatively lower in cortical areas where fewer streamlines follow the same trajectory through each voxel. Conventional approaches use a single threshold level for the entire tract. This threshold value has to be kept low to avoid false negatives that occur when eliminating voxels in the cortex (Newton et al. 2006; Schaechter et al. 2009; Lindenberg et al. 2012; Park et al. 2013; Archer et al. 2016; Potter-Baker et al. 2016). However, the low threshold increases the probability of false positives in the PLIC where fewer voxels are eliminated. As a result, much of the PLIC is included in the tract, despite evidence that tracts from different cortical regions are topographically organized through the internal capsule (Barnard and Woolsey 1956; Fries et al. 1993; Coleman et al. 1997). A low threshold value can work well when tracking a single pathway from the cortex as long as tract segmentation in subcortical regions is not essential. However, segmenting tracts into multiple compartments through the internal capsule based on different regions of the sensorimotor cortex requires a new approach that minimizes false negatives in the cortex to maintain tract volume, while also minimizing false positives in the internal capsule to maintain tract segmentation.

The purpose of this study is to create a high-resolution template that segments the sensorimotor tracts into multiple compartments based on 6 cortical seeds extracted from the human motor area template (HMAT: M1; dorsal premotor cortex (PMd); ventral premotor cortex (PMv); supplementary motor area (SMA) proper; pre-supplementary motor area (preSMA); and primary somatosensory cortex (S1)) (Mayka et al. 2006). First, for each seed in each hemisphere, we conducted probabilistic tractography analyses at the individual level in 100 subjects using high-resolution Human Connectome Project data (Van Essen et al. 2013; Sotiropoulos et al. 2013a). Planar waypoints were positioned in the PLIC and the CP. Second, we implemented a novel thresholding approach such that each slice was thresholded independently at 9 different thresholds (10–50% in increments of 5%). Third, tract overlap, tract volume, and coefficient of variation of fractional anisotropy (CV_FA) within each tract were calculated at each threshold percentile for each slice. Segmented regression analyses were then used to minimize tract overlap while preserving tract volume. Individually determined threshold percentiles were then applied to each slice and the slices were merged together to form the sensorimotor area tract template (SMATT). Finally, we quantified the amount of overlap between the tracts in each hemisphere to determine the probability that a single voxel is unique to a specific tract. Probability values for all voxels included in the template are provided in the sensorimotor area tract probabilistic atlas.

Materials and Methods

Human Connectome Subjects

Diffusion-weighted imaging of 100 healthy individuals was obtained from the Human Connectome Project website (http://www.humanconnectomeproject.org) (Feinberg et al. 2010; Moeller et al. 2010; Setsompop et al. 2012; Van Essen et al. 2013; Sotiropoulos et al. 2013b). All subjects (54 females, 46 males) were within the age range of 21–35. Diffusion images (resolution: 1.25 mm × 1.25 mm × 1.25 mm isotropic; slices: 111; field of view: 210 × 180; flip angle: 78°; b-values: 1000, 2000, and 3000 s/mm²) were collected using a customized Siemens 3 T scanner (Connectome Skyra). Each individual's diffusion magnetic resonance imaging (MRI) session consisted of 6 separate scans, each lasting approximately 10 min (Van Essen et al. 2013; Sotiropoulos et al. 2013a). The Human Connectome Project data were preprocessed, which included eddy current distortion correction and head motion correction (Andersson and Sotiropoulos 2015, 2016). Following download, fiber orientations were estimated with BEDPOSTX, in which 3 fibers were modeled per voxel (Jbabdi et al. 2012). The FA map for each individual's data was created via DTIFIT (Jenkinson et al. 2012). To obtain a standardized space representation of the FA map, the original FA map for each individual was registered to the FMRIB FA template in standard space (1 × 1 × 1 mm) by an affine transformation with 12 degrees of freedom and trilinear interpolation using FLIRT (Jenkinson and Smith 2001; Jenkinson et al. 2002). This resulted in a linear transformed FA map and its corresponding transformation matrix. The linear transformation was followed by a nonlinear transformation (Smith et al. 2004; Woolrich et al. 2009; Jenkinson et al. 2012), in which the input was the original FA map and the FLIRT transformation matrix. The output of this step was the standardized space representation of the FA map and the corresponding nonlinear coefficient file. All 100 subjects were used to create the tractography template.

University of Florida Subjects

Diffusion-weighted imaging of 20 healthy individuals was collected at the University of Florida (11 males, 9 females; age and handedness are shown in Table 1). Each subject provided informed consent before testing. Scanning was approved by the local Institutional Review Board and was in accord with the Declaration of Helsinki. MRIs were collected using a 32 channel head coil inside a 3 Tesla magnetic resonance scanner (Achieva, Best, the Netherlands). Diffusion MRI images (resolution: 2 mm isotropic, 64 noncollinear diffusion directions, b-value of 1000 s/mm² and one with a b-value of 0 s/mm², 75 axial slices covered the cortex and brainstem) were collected from each subject. FA images were obtained for each subject and normalized to standard space, using the protocol identical to the Human Connectome Project subjects outlined above.

Table 1.

Age, sex, and hand dominance for University of Florida subjects used in the slice-by-slice profile analysis in Figure 7

Subject	Human connectome project			University of Florida
	Age	Gender	Handedness	Age	Gender	Handedness
1	22	M	R	22	M	R
2	32	M	R	32	M	R
3	36	M	R	37	M	R
4	34	M	R	34	M	R
5	34	M	R	34	M	R
6	30	M	R	30	M	R
7	23	M	R	25	M	R
8	23	M	R	21	M	R
9	23	M	R	21	M	R
10	30	M	R	30	M	R
11	24	M	R	23	M	R
12	26	F	R	26	F	R
13	31	F	R	31	F	R
14	22	F	R	22	F	R
15	26	F	R	26	F	R
16	22	F	R	22	F	R
17	25	F	R	25	F	R
18	23	F	R	21	F	R
19	22	F	R	20	F	R
20	24	F	R	21	F	R

Probabilistic Tractography

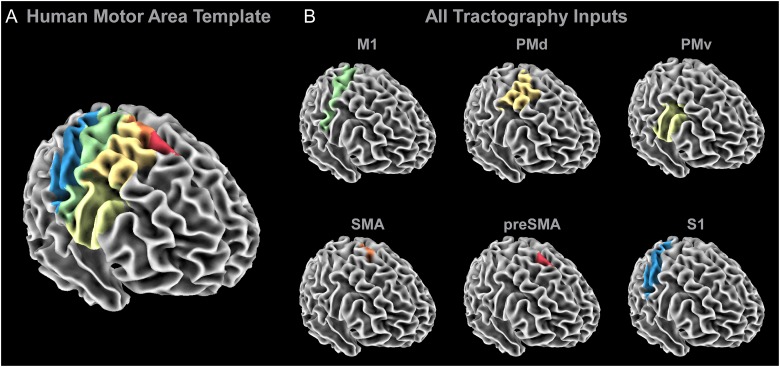
Probabilistic tractography was conducted using the probtrackx2 program in FSL (default setting—curvature threshold of 80°, 5000 streamlines per voxel, step length of 0.5 mm) (Behrens et al. 2003b, 2007). The HMAT regions were used as seeds (Fig. 1A) to generate tracts from specific sensorimotor regions (Mayka et al. 2006). The HMAT contains 6 separate sensorimotor areas: M1, PMd, PMv, SMA, preSMA, and S1 (Fig. 1B). Additional regions of interest in the tractography analysis were planar waypoints at the level of the PLIC (z = 7 to 9) and CP (z = −31 to −29). A planar point was placed at the midline (x = −1 to 1) to exclude transcallosal fibers. Tracking was completed at the individual subject level in native subject space. Seeds from the HMAT were transformed to each subject's native space using the inverse of the nonlinear coefficient file from the spatial normalization procedure outlined above. Tracking was conducted separately for each hemisphere. The output of this step resulted in 6 sensorimotor tracts in the left hemisphere (M1, PMd, PMv, SMA, preSMA, and S1) and 6 sensorimotor tracts in the right hemisphere (M1, PMd, PMv, SMA, preSMA, and S1) for each individual subject. Each voxel in each tract was assigned a probability value corresponding to the number of streamlines that traversed that voxel in that individual. Each subject's tracts were warped to standardized space using the nonlinear coefficient file from the FA map normalization procedure outlined above.

Figure 1.

Probabilistic tractography inputs. (A) The regions within the HMAT were used as seed regions in the probabilistic tractography analyses. (B) A separate probabilistic tractography analysis was conducted for M1 (green), PMd (dark yellow), PMv (light yellow), SMA (orange), preSMA (red), and S1 (blue), in which a planar waypoint was placed at the level of the PLIC (z = 7 to 9) and the CP (z = −31 to −29). Additionally, transcallosal streamlines were excluded by including a planar exclusion mask at the midline (x = −1 to 1).

Tract Level Thresholding Versus Slice Level Thresholding in the M1 Tract

Thresholding is conducted at the individual level. Conventional probabilistic tractography studies implement a threshold approach that takes the maximum probability value (based on the number of streamlines) in any voxel in the identified tract and sets a threshold value based on a percentage of this maximum probability value. A single value is, therefore, used to threshold the entire tract. This conventional thresholding approach is sensitive to differences in the number of streamlines throughout the tract which can be driven by differences in fiber proximity in different regions of the brain. In the current study, we implemented a novel approach for thresholding probabilistic tractography data. Instead of identifying and calculating a single value for the whole tract based on a percentage of the voxel with the maximum number of streamlines, we used a segmented approach. First, we split the tract into individual slices using fslsplit. When using fslsplit in the z-direction, the image was split into 181 axial 1 mm slices. When using fslsplit in the x-direction, the image was split into 181 sagittal 1 mm slices. Next, the maximum value within any voxel of each slice was identified and threshold levels were calculated based on that maximum value for that slice independently. We first assess volume of the M1 tract in a single subject using a conventional approach and our slice level thresholding approach. For the conventional approach, the entire M1 sensorimotor tract was thresholded based on values equal to 10%, 25%, and 50% of the maximum probability value found in the entire tract. For our proposed approach, each slice was thresholded based on values equal to 10%, 25%, and 50% of the maximum probability value within each slice. Following thresholding, tracts were binarized and the volume of the tract at each threshold level was compared between approaches.

Slice Level Thresholding Including all Sensorimotor Tracts

The proposed experimental approach will characterize 6 tracts in each hemisphere (M1, PMd, PMv, SMA, preSMA, and S1) using 9 percentile thresholds (10–50% in increments of 5%) in 100 subjects. The majority of the sensorimotor tracts can be split into axial slices because their primary direction of travel is along the z-axis. However, the PMv sensorimotor tract moves medially from the PMv toward the PLIC, and then travels inferior to the CP. Slice level thresholds for PMv were, therefore, calculated for axial and sagittal slices. PMv was included with all other tracts in axial slices from z = −35 to 20. Lateral regions of the PMv tract in the right hemisphere were identified using the slice level threshold approach in sagittal slices from x > 30. Portions of the tract between z > 20 and x < 30 were identified using a conjunction analysis of the axial and sagittal PMv sensorimotor tracts, in which voxels common to both tracts were included in the final PMv tract. The same logic was used for the left hemisphere using negative values in the x-direction. Individual tracts were thresholded at the 9 threshold levels, and then binarized for each subject. Binarized tracts were then submitted to a group level conjunction analysis such that within each tract, voxels were retained if the voxel was common to at least 10 individuals. We used a liberal threshold here, so that tracts could be refined objectively as described below. The output of this stage of the analysis was 9 binarized tracts (one at each percentile threshold) for each of the 6 cortical seed regions (M1, PMd, PMv, SMA, preSMA, and S1), for the left and the right hemisphere.

Overlap

Binarized conjunction maps for each tract were used to determine the extent of overlap between tracts at each threshold level. We counted the number of voxels within each slice, within each tract, that were also common to other tracts. For example, voxels in the M1 tract with no overlap with any other tracts were assigned a value of 0. Voxels in the M1 tract that were common to one or more other tracts were assigned a value of 1. Every voxel in the M1 tract was assigned a value of 0 or 1 following this logic. Overlap values were then summed to create a single overlap value for the M1 tract for a single slice. The same procedure was completed for each tract, in each slice, at each threshold, in each hemisphere.

Coefficient of Variation of FA

To constrain tracts primarily to white matter, we calculated a normalized variability measure using FA. The CV_FA was calculated for each tract at each slice for each threshold percentile for each individual. The binarized tracts from the group level conjunction analysis were used as masks at the individual level to calculate CV_FA (SD of mean FA/mean FA). CV_FA values were averaged across individuals for each tract, at each slice, for each threshold percentile. At lower thresholds, we expected relatively higher CV_FA values because greater tract volume should increase the chances that voxels containing gray matter or cerebrospinal fluid will be included in the tract.

Volume

To determine the extent to which threshold levels influence the number of voxels retained within each tract, we calculated tract volume. Tract volume was calculated at the group level for each of the binarized tracts identified in the conjunction analysis. Volume was calculated by summing the number of voxels included in each tract at each threshold percentile at each slice.

Threshold Selection

After overlap, CV_FA, and volume were calculated, the 3 values were multiplied together for each tract, for each threshold, and for each slice. Note that when overlap was equal to zero, it was eliminated from the calculation. We expected this summary score to have high values at low percentiles and relatively lower values at higher percentiles for all tracts. A single summary score was then calculated for each slice at each percentile by summing values across tracts. As a result, 9 values were associated with each slice; one at each threshold percentile. Segmented regression analyses were then conducted (segmented package in R version 3.2.1) at each slice to fit 2 simple regression models to the 9 data points. The breakpoint analysis was used to identify the point of intersection of the 2 linear functions of different slopes. The goal was to identify the point at which increases in threshold no longer led to large decreases in overlap or volume. Hence, we wanted to identify the point at which overlap is best minimized while volume is maximized. CV was included as a control variable to ensure that the tract is restricted to white matter. The segmented regression analysis method fits 2 different linear regression models to the data, in which the models are separated where the linear relationship changes (called the breakpoint) (Muggeo 2003). The threshold closest to this breakpoint was then used for its corresponding slice. Threshold levels were held constant across tracts for the same slice, but were able to vary across slices based on slice level breakpoint analyses. The resulting tracts identified in each of the 181 slices were then merged with the results from all other slices to create a group level whole-brain template for each sensorimotor tract.

Sensorimotor Area Tract Probabilistic Atlas

Once the sensorimotor tract template was compiled, we next determined the probability that each voxel within the template was unique to a specific tract. For example, if a voxel was common to the M1 and the S1 tracts, there was a 50% chance that the voxel was unique to the M1 tract and a 50% chance that the voxel was unique to the S1 tract. Since there are 6 tracts in each hemisphere, each voxel could be assigned a value ranging from one-sixth (i.e.,16% chance that the voxel is unique to one specific tract) to 1 (i.e., 100% probable that the voxel is unique to one tract). We expected voxels in the most inferior portions of the tracts to have low probabilities due to an increase in fiber density in subcortical brain regions, and probabilities to increase in cortical regions as fiber density decreased.

Evaluation of the SMATT in an Independent Data Set

To evaluate how the SMATT operates in an independent data set, we overlaid the template on diffusion scans of 20 individual subjects from an independent data set collected at the University Florida. We overlaid the template onto the scans of 20 individual subjects from the Human Connectome Project (HCP) data set. These 20 subjects were a subset of the 100 subjects used to create the template and were selected to match the University of Florida data set for age (HCP: 26.15 ± 5.31 years; UF: 26.6 ± 4.72 years), sex, and handedness (see Table 1 for subject details). We also calculated FA values for each slice of each tract for each individual. As the 2 data sets were collected on different scanners using different pulse sequences, we first normalized each individuals FA map by calculating their mean whole-brain FA and dividing their FA map by this value.

Evaluation of the SMATT in an Individual after Stroke

Diffusion-weighted imaging of one chronic stroke individual was obtained at the University of Florida. This subject provided informed consent and scanning was approved by the local Institutional Review Board and was in accord with the Declaration of Helsinki. Diffusion parameters were identical to the parameters for the other University of Florida subjects noted above. The subject was a 65-year-old male with a single subcortical ischemic stroke in the left hemisphere, who was impaired on the right hand (right-hand grip strength: 30.8 N; left-hand grip strength: 70.4 N). Time since stroke was 5.59 year, the Upper Extremity Fugl-Meyer Assessment score was 30, and the Mini Mental State Examination score was 29. The SMATT was used to characterize tract microstructure and stroke location.

Results

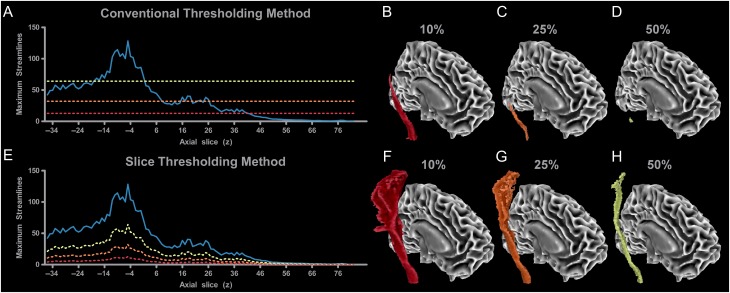
Figure 2 shows probabilistic tractography data from one subject for the M1 sensorimotor tract in the right hemisphere using a conventional thresholding approach (Fig. 2A–D) and our proposed slice level thresholding approach (Fig. 2E–H). The solid blue line in Figure 2A shows the maximum number of streamlines from any single voxel within each axial slice along the M1 tract between the CP (z = −36) and M1 (z = 80). The maximum number of streamlines is 120 which is located at z = −5 within the inferior PLIC. Conventional thresholding approaches take this value and then multiply it by an arbitrary percentage. For example, a 10% threshold level would correspond with a streamline value of 12, a 25% threshold level would lead to a value of 30, and a 50% threshold level would lead to a value of 60. Slices in which all voxels have streamline values below this value are then eliminated from the tract. For instance, the red dotted horizontal line in Figure 2A shows that at 10%, the most superior cortical slices would be eliminated (z > 40), and the resulting 3D tract is shown in Figure 2B. At 25%, more of the tract is eliminated (z > 8) as shown by the orange horizontal dotted line in Figure 2A and the decrease in tract volume in the 3D representation of the tract in Figure 2C. At 50% (yellow horizontal line in Fig. 2A), most of the tract is eliminated (z < −16 and z > 0) as shown in Figure 2D, with only slices adjacent with the slice with the maximum voxel being retained in the final output. When tracking the entire sensorimotor tracts using this conventional approach, low threshold levels must, therefore, be used to retain volume in cortical regions of the tract.

Figure 2.

Tract level thresholding versus slice level thresholding in the M1 tract. (A) When performing probabilistic tractography from M1 to the CP, the number of streamlines per slice varies (blue line), in which there is a peak number of streamlines at z = −5. Conventional tract level thresholding calculates the maximum number of streamlines within the profile and bases the threshold on a percentage of this value. Thresholds can be arbitrarily set at 10% (red line), 25% (orange line), or 50% (yellow line) of the peak value. Higher thresholds lead to a reduction in tract volume (B–D). Blue lines that fall below the threshold line would be excluded from the final results. Therefore, a threshold of 10% results in some loss of cortical volume (z > 40 eliminated), while a 25% threshold results in additional loss of volume in the cortex (z > 8 eliminated). At 50%, the only slices which remain are within the PLIC (z = −16 to 0 remain). (E) By splitting the tract into individual slices, each slice can be thresholded independently. A benefit of this method is that it does not result in any excluded slices within the tract. At 10%, tract volume is high. At 25% and 50% the volume of the tract decreases but volume is maintained in every slice of the tract (F–H).

Figure 2E shows the data analyzed using our novel approach, based on the same blue streamline profile shown in Figure 2A. Using the same threshold percentages, but applying them independently to each slice leads to clear differences in tract volume. The dashed lines in Figure 2E show that at the 10% level the threshold changes along the trajectory of the tract. The corresponding red 3D tract in Figure 2F shows that tract volume is retained in every slice, and overall volume is greater than the corresponding conventional approach shown in Figure 2B. As the threshold increases to 25% (orange dashed line in Fig. 2E and orange 3D tract in Fig. 2G) and 50% (yellow dashed line in Fig. 2E and yellow 3D tract in Fig. 2H) it is important to note that the overall volume of the tract is reduced without eliminating entire slices from the tract. Previous studies that use a conventional approach often decide on an arbitrary threshold level that ensures that volume is retained across the whole sensorimotor tract. Although implementing a slice level thresholding approach addresses the volume issue, threshold levels are still arbitrary and are not based on an objective data-driven metric. To address this issue, we propose a novel approach which identifies a threshold at each individual slice based on a combined measure that includes tract overlap, CV_FA, and tract volume.

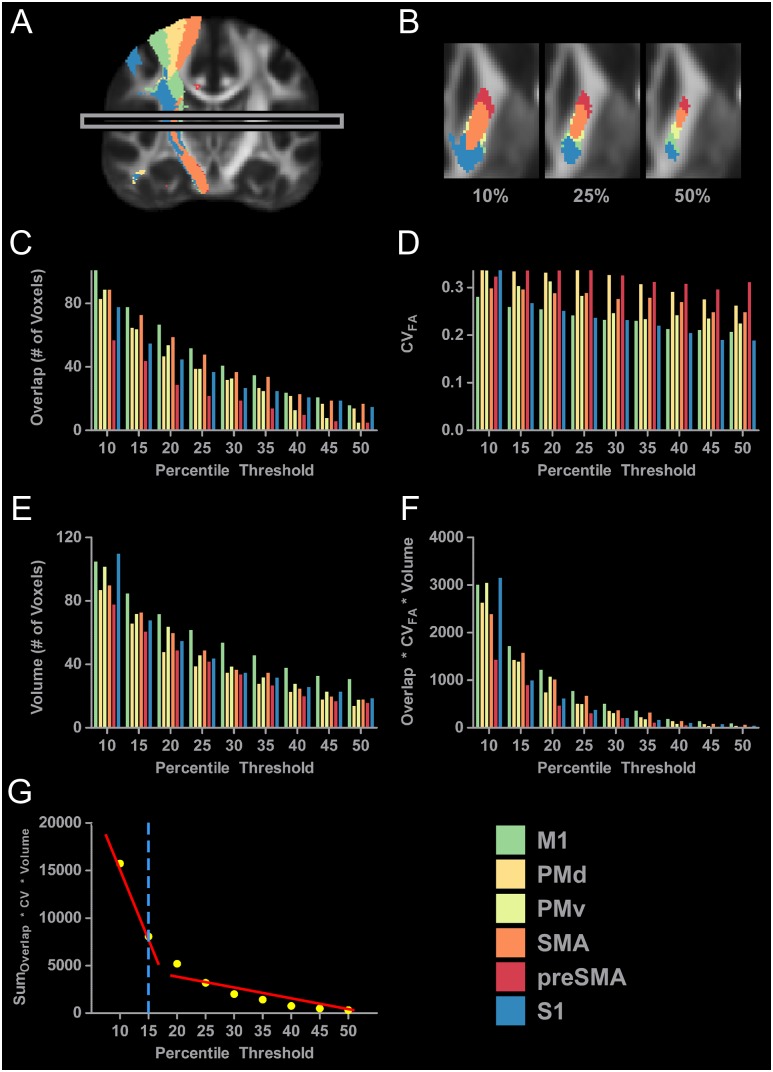
Figure 3A shows the 6 binarized tracts in the right hemisphere derived from individual probabilistic tractography results thresholded at 10%. The box in Figure 3A highlights one slice positioned at z = 10. All remaining panels (Fig. 3B–G) show data calculated for this slice. Figure 3B shows an axial view of the 6 tracts within the right PLIC thresholded at 10%, 25%, and 50%. The tracts descending from M1 (green), PMd (dark yellow), PMv (light yellow), SMA (orange), preSMA (red), and S1 (blue) are shown. At 10%, there is high volume for each tract and high overlap between tracts making tract segregation difficult. As thresholding increases to 25% and then 50%, both volume and overlap decrease making tract segregation more viable. Figure 3C shows overlap values for each tract for each threshold from 10% to 50% in 5% increments. At 10%, 102 voxels within the M1 sensorimotor tract were also common to one or more other tracts. At the same 10% threshold level, overlap in preSMA was 57 voxels. As thresholding increases there is a decrease in overlap, with thresholds set at 50% leading to overlap values of 16 for the M1 tract and 5 for the preSMA tract. Figure 3D shows CV_FA at each threshold. The CV_FA for M1 was 0.281 at 10%, and decreased to 0.208 at 50%. Figure 3E shows tract volume at each threshold. At 10%, the M1 tract has a volume of 105 voxels, whereas preSMA has a volume of 78 voxels. As thresholding increases to 50%, we see a reduction in volume in all tracts, with voxel count in the M1 tract decreasing to 31 voxels and voxel count in the preSMA tract decreasing to 16 voxels. Measures of overlap, CV_FA, and volume were then multiplied together and these data are shown in Figure 3F. At 10%, the value is high for all tracts, and this value approaches zero as thresholding increases to 50%. Values across tracts were then summed to create one overall score for each threshold and these scores are represented by the yellow dots shown in Figure 3G. Summed values were then used as dependent variables in a segmented regression analysis. Two lines were fit to the data (red lines in Fig. 3G), and the breakpoint was calculated to be at 17.24%. Threshold levels were rounded to the nearest multiple of 5 within the 10–50% range. Therefore, the threshold for this slice was selected as 15% (blue dashed line in Fig. 3G). The same procedure was conducted independently for each slice in each hemisphere.

Figure 3.

Slice level thresholding of sensorimotor tract data. (A) The probabilistic tractography results for all 6 sensorimotor tracts in the right hemisphere at the 10% threshold level. At this low threshold, aberrant voxels are still present. For instance, red voxels that are associated with the preSMA tract can be seen above the corpus callosum, and blue and yellow voxels can be been in the ventral temporal lobe. The presence of these aberrant voxels support our position that thresholding the entire tract at one relatively low percentile can lead to the inclusion of lowly probably voxels. The gray box identifies the individual slice (z = 10) that is analyzed in Figure 3B–G. (B) Axial slices of the PLIC in the right hemisphere with the sensorimotor tracts thresholded at 10%, 25%, and 50%. Increases in threshold lead to a decrease in volume and a decrease in overlap between the tracts. (C) Overlap of each sensorimotor tract with every other sensorimotor tract was calculated at each percentile. The 6 sensorimotor tracts were thresholded at 9 percentiles. (D) The CV_FA of each sensorimotor tract was calculated for each percentile threshold. (E) The volume of each sensorimotor tract was calculated for each percentile threshold. (F) The overlap, CV_FA, and volume were incorporated into one variable and calculated for each tract at each percentile threshold. (G) Values shown in 3F were summed across tracts for each percentile (yellow dots) and a segmented regression analysis was conducted. Two lines were fit to the data (red lines), and the breakpoint was calculated to be at 17.24%. Threshold levels were rounded to the nearest multiple of 5 within the 10–50% range. The threshold for this slice was selected as 15% (blue dashed line).

Sensorimotor Area Tract Template

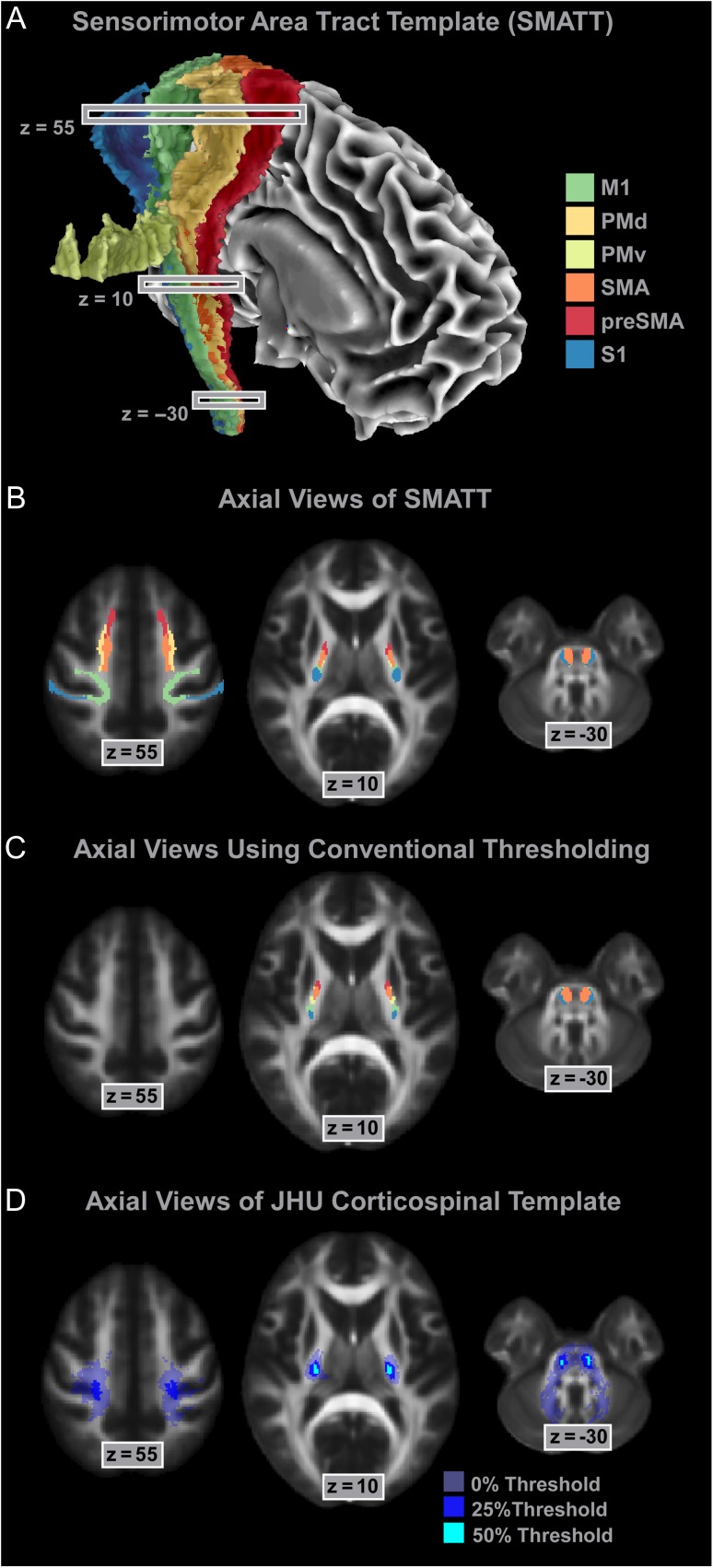
The mean threshold for the left hemisphere was 16.43% (SD = 2.45, range: 10–25). The mean threshold for the right hemisphere was 19.83% (SD = 3.11, range: 15–25). We also averaged across slices to calculate regional thresholds. For cortical regions between z = 84 and z= 19 the average threshold across the left and the right hemisphere was 17.6%. For the PLIC between z = 18 and z = −4 the average threshold was 20.0%. Below the internal capsule from z = −5 to −35 the average threshold was 17.9%. The important point here is that although the threshold percentages are relatively similar, the maximum probability value that they are applied to is different between regions (see Fig. 2). To control for tract-specific differences in volume between hemispheres, we used a conjunction analysis by overlaying tracts from the left hemisphere onto the tracts in the right hemisphere. Only voxels that were common to both tracts were included in the final template. Figure 4A shows the assembled SMATT in the right hemisphere. Volume was retained in all slices of each tract. Figure 4B shows an axial view of the SMATT overlaid on an anatomical image at slice z = 55, z = 10, and z = −30. At z = 55, Figure 4B shows that cortical topography was relatively well maintained in the SMATT, and that the SMATT is constrained to white matter. Overlap is increased at z = 10, as compared to the cortex, but this is to be expected given the increase in fiber proximity in the PLIC. Cortical topography was generally well maintained in PLIC, with the preSMA tract most anterior and the S1 tract most posterior with no overlap between these 2 tracts. Highest overlap was found between tracts in the most inferior portions of the descending tracts, such as in the CP which is shown at z = −30. To show the utility of slice level thresholding, we took the average slice level thresholding value (18%), and used this percentage to perform a tract-wide threshold (Fig. 4C). Figure 4C shows that with a tract-wide threshold of 18%, cortical volume is abolished in all tracts. Figure 4D shows the Johns–Hopkins template of the corticospinal tract thresholded at 3 different levels (Hua et al. 2008). When using the Johns–Hopkins template with a 0% threshold, it is clear that white and gray matter will be included in the template. At the 25% threshold, the template is restricted to a small area in the medial portion of M1, and at the 50% threshold there is no volume in cortical areas of the tract. Similar patterns are shown at z = 10 and z = −30. The SMATT overcomes each of these issues while also identifying tracts that are specific to distinct cortical regions.

Figure 4.

The SMATT. (A) The assembled SMATT (M1—green; PMd—dark yellow; PMv—light yellow; SMA—orange; preSMA—red; S1—blue). Note that nonuniformity in the lateral portion of the PMv tract is driven by the tract traveling around gray matter. (B) Axial slices of the SMATT in the cortex (z = 55), PLIC (z = 10), and CP (z = −30). (C) To compare independent slice level thresholding and tract level thresholding, we used the average slice level threshold (18%) to threshold each entire tract. At z = 55 there is no volume in any cortical tracts. At z = 10 and z = −30 tract location follows a similar pattern as the SMATT. (D) Axial slices of the Johns–Hopkins corticospinal template thresholded at 0%, 25%, and 50% in the cortex (z = 55), PLIC (z = 10), and CP (z = −30).

Probabilistic SMATT

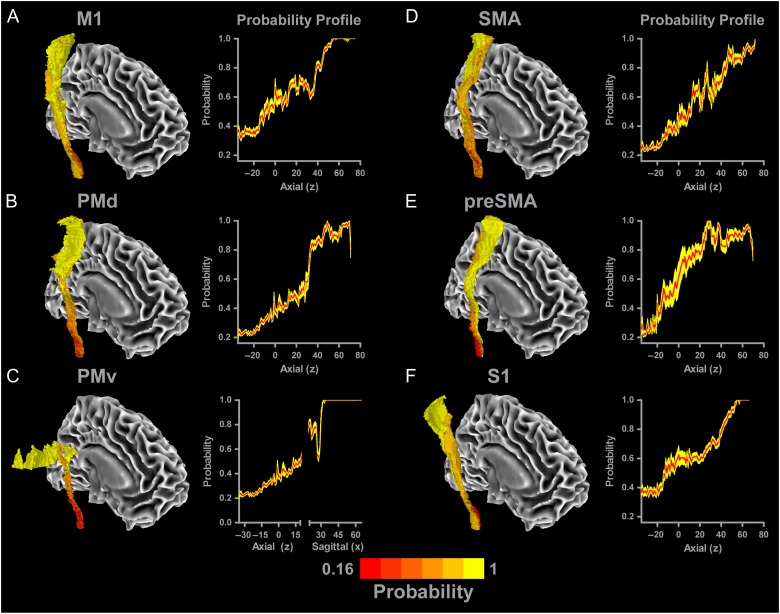
The overlap of each tract in the SMATT was quantified by summing the number of tracts that were common to each voxel in the SMATT. Each voxel in the probabilistic SMATT can be represented by a value ranging from one-sixth (or 0.167) to 1, in which higher values indicate more certainty that a particular voxel is unique to a particular sensorimotor tract. Figure 5A shows the probabilistic M1 tract atlas in the right hemisphere. Red colors represent voxels that have a low probability of residing in a single tract. As the colors get brighter voxels have a higher probability of being unique to the M1 tract, as shown by the increase in number of yellow voxels starting at the level of the PLIC. A probability profile for the M1 tract is shown on the right side of Figure 5A. The red line represents the mean probability value for each axial slice in the M1 tract. The yellow shading represents the corresponding ± SEM. At the more inferior portions of the tract, probability is approximately 0.35. As the tract travels through the PLIC (z = 10), probability of being unique to the M1 tract increases to approximately 0.6. Superior to the PLIC, there is a progressive increase in the probability of voxels being within M1 tract until z = 40. At z = 40, there is a sharp increase in probability, which reaches 1 at z = 55. 3D images and probability profiles for the remaining tracts in the right hemisphere are shown in Figures 5B–F. All tracts show similar probability profiles to the M1 tract, with probability generally increasing in more superior regions of the tract. Based on the conjunction analyses performed on the SMATT, probability values in the left hemisphere are the same as in the right hemisphere. The probabilistic SMATT includes values for both hemispheres for all tracts.

Figure 5.

Probabilistic SMATT. Each tract was overlaid with one another to quantify the amount of overlap between tracts so that a probabilistic value could be calculated for each voxel in the template. The mean probability of each slice is shown with a red line, with the yellow shading representing the mean ± SEM. A view of each tract (A—M1; B—PMd; C—PMv; D—SMA; E—preSMA; F—S1) is shown, in which darker red colors indicate higher overlap with other tracts (i.e., low probability voxel is only part of one tract), whereas brighter yellow colors identify voxels with low overlap with other tracts (i.e., high probability voxel is only part of one tract). Probability profiles are shown for each tract. As the tracts reach more superior regions, the probability of voxels being unique to a particular sensorimotor tract increases.

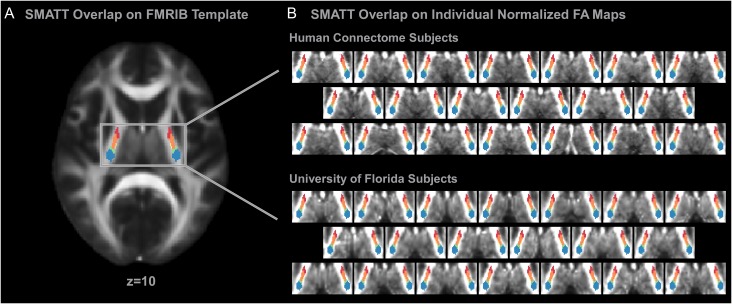
Evaluation of SMATT in an Independent Data Set

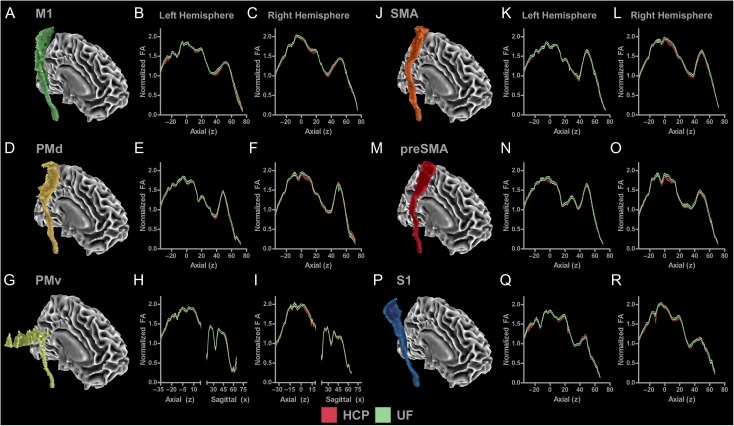
To assess how the SMATT operates in individual subjects, we first visually inspected alignment of the SMATT within the PLIC at the individual level using a subset of 20 subjects from the Human Connectome Project data set as well as individual subjects collected at the University of Florida. Figure 6A shows the SMATT overlaid on an axial slice of the FMRIB anatomical template at the level of the PLIC (z = 10). Figure 6B shows the SMATT overlaid on individual subject anatomical images in standard space. Individual data from 20 subjects collected as part of the Human Connectome Project and individual data from 20 subjects collected at the University of Florida are shown. The SMATT is well aligned in both groups for all tracts, even though the data from the University of Florida has a lower resolution than the Human Connectome Project. Next, we created mean normalized FA profiles (average SMATT FA within each slice divided by whole brain mean FA) for each tract for each data set. Figure 7A shows the M1 tract in the right hemisphere. Figure 7B,C show the slice-by-slice profiles of normalized FA values for the left and right hemisphere. HCP data are represented with black lines and red shading (mean ± SEM), and University of Florida data are represented with black lines and green shading (mean ± SEM). Figure 7B shows that the M1 tract begins at z = −35 at the level of the CP and terminates in M1 at z = 75. HCP and University of Florida profiles show a similar pattern. Normalized FA was approximately 1.1 within the CP and increased to approximately 1.6 within the PLIC (z = −20 to 20). From z = 20 to 40, there is a reduction in normalized FA, which is consistent with the associated crossing fibers within the centrum semiovale. At z = 40, there is a steady increase in normalized FA which peaks at z = 55, followed by a slow decrease in normalized FA in cortical regions of the M1 tract. Figure 7C shows that a similar pattern was evidenced in the right hemisphere. Profiles were created for each of the 5 remaining tracts in both hemispheres and are shown in Figure 7D–R.

Figure 6.

SMATT overlaid on individual subject data. (A) SMATT overlaid on an axial slice of the FMRIB anatomical template at the level of the PLIC (z = 10). (B) The SMATT overlaid on individual subject anatomical images in standard space. Individual data from 20 subjects collected as part of the Human Connectome Project and individual data from 20 subjects collected at the University of Florida are shown. The SMATT is well aligned in both groups for all tracts. Axial slices are shown at z = 10 which is within the PLIC. M1—green; PMd—dark yellow; PMv—light yellow; SMA—orange; preSMA—red; S1—blue.

Figure 7.

Mean normalized FA profiles for each tract for each hemisphere for data collected as part of the Human Connectome Project and data collected at the University of Florida (UF). (A) M1 tract in the right hemisphere. (B) Slice-by-slice profile of normalized FA values in M1 tract in the left hemisphere. (C) Slice-by-slice profile of normalized FA values in M1 tract in the right hemisphere. HCP data are represented with black lines and red shading (mean ± SEM). UF data are represented with black lines and green shading (mean ± SEM). HCP and UF profiles show a similar pattern in the M1 tract across group and hemisphere. Profiles were created for each of the 5 remaining sensorimotor tracts in both hemispheres and are shown in Figures (D–R).

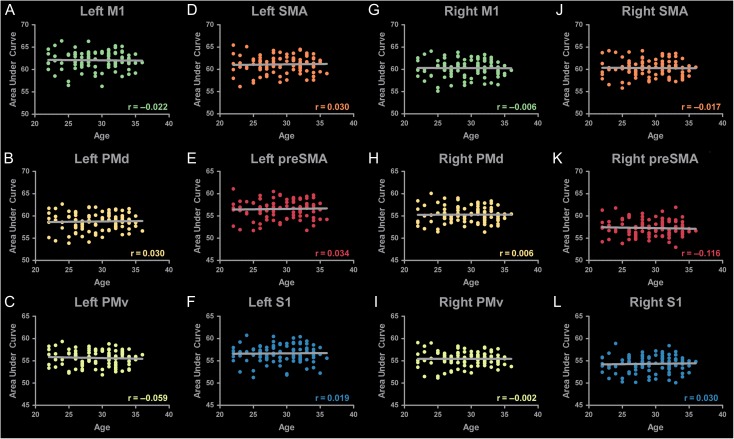
To determine whether subject age influenced the development of the template, we calculated area under the curve (AUC) for each individuals FA profile for each tract. Figure 8 shows correlations between age and AUC in all tracts in the left hemisphere (A–F) and the right hemisphere (G–L). No significant correlations were found between FA and age in any tract.

Figure 8.

Correlations of SMATT FA with Age. FA profiles were created for each individual. FA values for each tract were summed to create an area under the curve measure. This measure was correlated with age for all tracts in the left (A–F) and the right (G–L) hemisphere. No significant correlations were found between FA and age.

Evaluation of SMATT in a Stroke Subject

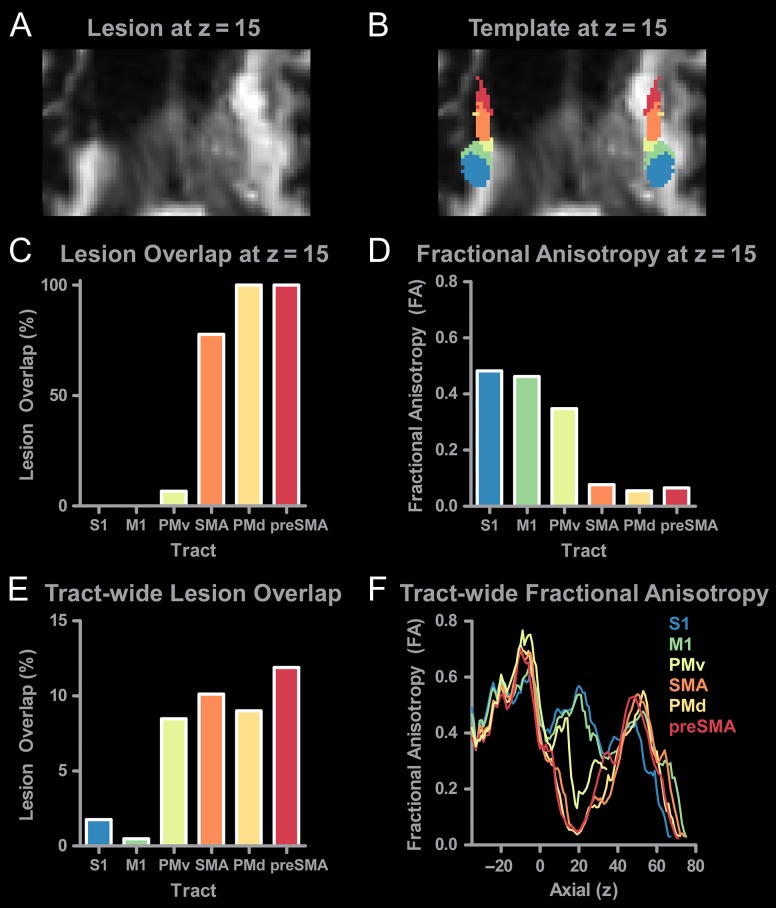
An axial view of the chronic stroke subject's FA map is shown in Figure 9A at z = 15 at the level of the PLIC. The lesion merges with the ventricle in the left hemisphere. Anterior regions of the PLIC show extensive damage. Figure 9B shows the SMATT overlaid on top of the same structural scan shown in Figure 9A. Here, we show successful normalization of the lesioned brain to MNI space, which allows the SMATT to overlay well. Anterior regions of the template in the left hemisphere overlap the lesion. Lesion overlap in the template was calculated within each tract at z = 15 for the left hemisphere, and is shown in Figure 9C. The x-axis is sorted from posterior to anterior, and shows that S1 and M1 have 0% lesion overlap whereas lesion overlap for PMd and preSMA is 100%. FA was quantified for each tract at z = 15 (Fig. 9D), and shows an inverse relationship with lesion overlap. Regions with high lesion overlap have lower FA. We also quantified lesion overlap in the entire tract (Fig. 9E), and show that the more posterior tracts have low lesion overlap (<2.5%), while the more anterior tracts had higher lesion overlap (>7.5%). Lesion overlap provides an overall assessment of lesion impact, but it does not provide information on lesion location. We next calculated FA profiles for each tract in the z-direction (Fig. 9F). Profiles for S1 and M1 tracts follow a similar pattern to the profiles of healthy controls which are shown in Figure 7B. Anterior tracts including PMv, PMd, SMA, and preSMA which had higher lesion overlap show large reductions in FA from z = 5 to 40. Our observations suggest that the SMATT can be useful to locate and characterize lesions that impact the sensorimotor tracts.

Figure 9.

Using the SMATT to assess tract-specific damage after stroke. (A) Diffusion-weighted image at z = 15 showing lesion damage to the internal capsule. (B) SMATT overlaid on the diffusion-weighted image. (C) Lesion overlap was calculated for each tract in the left hemisphere at z = 15. No lesion overlap was found for S1 or M1. Extensive overlap was found for SMA, preSMA, PMv, and PMd. (D) FA was calculated for each tract at z = 15. FA was greatest in more posterior regions of the tract (S1, M1) as compared to anterior regions (SMA, preSMA, PMd, and PMv). (E) Tract-wide lesion overlap in all left hemisphere tracts. (F) Tract-specific FA profiles were calculated for each slice for each sensorimotor tract. Profiles directly impacted by the stroke (SMA, preSMA, PMd, and PMd) can be identified based on the distinct reductions in FA between z = 5 and z = 40.

Discussion

The purpose of this study was to develop a high-resolution template of the sensorimotor tracts which segmented the tracts based on 6 cortical regions in M1, PMd, PMv, SMA, preSMA, and S1. Individual probabilistic tractography analyses were conducted in 100 subjects using the highest resolution data currently available. Tractography results were refined using a novel algorithm to objectively determine slice level thresholds that best minimized overlap between tracts while simultaneously preserving tract volume. Our observations are consistent with tracing studies in monkey and show that cortical topography is generally preserved as the tracts descend through the brain, with the preSMA tract remaining most anterior and the S1 tract remaining most posterior through the internal capsule. We have combined the 6 individual tracts into a white matter template named the SMATT. We also provide a probabilistic SMATT that quantifies the extent of overlap at the voxel level between tracts. The probabilistic SMATT showed that overlap between adjacent tracts increased as tract proximity increased through the internal capsule and CP. We also show that the SMATT operates well in an independent data set based on slice-by-slice normalized FA profiles. Finally, we infer tract-specific and slice-specific damage to the sensorimotor tracts in a stroke patient by using the template to extract FA profiles. The SMATT and probabilistic SMATT provide new tools that segment and label sensorimotor tracts at a spatial resolution not previously available.

Sophisticated tracing techniques have been used in rodents and monkeys to identify the axons that link the motor cortex with the reticular formation and spinal cord (Barnard and Woolsey 1956; Dum and Strick 1991; Fries et al. 1993; He et al. 1993, 1995; Coleman et al. 1997; Maier et al. 2002). Over the last several decades important advances in structural neuroimaging have allowed us to start characterizing the sensorimotor pathways in vivo in humans. However, as compared with tracing studies in animal models, when using diffusion MRI and probabilistic tractography to identify these pathways, tract volume and tract overlap are more variable and can be influenced by factors that include seed masks, waypoint and exclusion masks, and threshold values.

The selection of seed masks is a large source of variability between probabilistic tractography studies. One approach is to generate seed masks by extracting regions from templates such as the Johns–Hopkins DTI-based white matter atlas (Wakana et al. 2007; Hua et al. 2008). A second approach is to hand draw seeds in the precentral gyrus (Schaechter et al. 2008; Lindenberg et al. 2010, 2012), and the hand bump region in particular (Stinear et al. 2007; Schaechter et al. 2009), based on anatomical landmarks in structural scans and fiber direction in FA maps (Newton et al. 2006; Schaechter et al. 2008; Lindenberg et al. 2012). However, the landmarks used to identify seeds are different between studies, and hand drawing regions for large data sets can be time consuming. A third approach is to generate seed masks based on clusters of voxels identified in task-based functional MRI experiments or tract-based spatial statistics (TBSS) analyses that identify correlations between microstructure and behavior (Stinear et al. 2007; Schaechter et al. 2008, 2009; Lindenberg et al. 2010, 2012; Schulz et al. 2012; Leunissen et al. 2013; Archer et al. 2016). Identifying seeds based on individual task-based studies means that the seed locations are constrained by the specific task used and by the specific subjects tested in the study. In addition, the volume of each seed region is variable across studies. In the current study, we overcame these issues by using seed regions derived from the HMAT (Mayka et al. 2006). The template identifies the borders of 6 sensorimotor areas (M1, PMd, PMv, SMA, preSMA, and S1) based on activation-likelihood estimation from 126 functional neuroimaging studies that manipulated upper and lower limb motor control. Generating seeds from the HMAT ensured that the SMATT is based on segregated brain function in the cortex, and is generalizable to the upper and lower limbs.

Following seed generation, the use of waypoint masks and exclusion masks can have a profound impact on probabilistic tractography results. Tract volume generally decreases when using small waypoint masks and when the total number of waypoint masks and exclusion masks increases. In the case of the tract descending from M1, the PLIC and the CP are often used as waypoints (Schaechter et al. 2008, 2009; Lindenberg et al. 2010, 2012; Archer et al. 2016; Potter-Baker et al. 2016) and a planar sagittal slice at the midline can be used as an exclusion mask to eliminate transcallosal fibers. As with seed generation, waypoint masks can be hand drawn, extracted from white matter templates, or obtained from TBSS analyses (Stinear et al. 2007; Schaechter et al. 2008, 2009; Lindenberg et al. 2010, 2012; Archer et al. 2016; Potter-Baker et al. 2016). However, there is currently no established way of identifying segregated subcortical waypoints that map to our 6 cortical regions. As a result, we used an unconstrained approach by placing axial planar waypoints at the level of the PLIC (z = 7–9) and at the level of the CP (z = −31 to −29). Additionally, we placed an exclusion mask at the midline (x = −1 to 1) to exclude transcallosal fibers. Minimally constrained tractography results were then refined using a novel thresholding approach.

Determining the appropriate threshold to use when refining tractography results has received little attention and is often arbitrary and unjustified (Clatworthy et al. 2010). The most common method is to threshold based on a percentage of the maximum probability value within the tractography results (Schaechter et al. 2009; Lindenberg et al. 2012; Schulz et al. 2012). This approach is sensitive to peaks in probability values within the tract, and these values vary according to tract length and tract location. For instance, a recently developed white matter tract template for the cerebellum successfully used a threshold of 50th percentile (van Baarsen et al. 2016), whereas tractography studies focused on the sensorimotor tract from M1 have used lower thresholds that range from 0% to 2% of the maximum to preserve volume across the whole tract and minimize false negatives in the cortex (Newton et al. 2006; Schaechter et al. 2009; Lindenberg et al. 2012; Park et al. 2013). Here, we aimed to circumvent this issue by developing a method that independently thresholded each slice at 9 different levels (10–50% in increments of 5%) and then objectively identified the threshold to use for each slice using a data-driven approach. Our slice level approach was designed to minimize false negatives in cortical regions and minimize false positives in subcortical regions.

A single threshold level was independently determined for each slice based on 3 factors: overlap between the different tracts, the CV_FA, and the volume of each different tract. Overlap was incorporated into the analysis to quantify tract segregation. Although segregation between cortical regions is well established based on anatomy and function (Dum and Strick 2005; Behrens et al. 2006; Mayka et al. 2006), segmentation of sensorimotor tracts in vivo in humans is not as well developed. Tracing studies in rodents show that axons from spatially distinct cortical areas occupy different regions of the cross-sectional area of the internal capsule (Coleman et al. 1997). Similar topography has been demonstrated in monkey (Barnard and Woolsey 1956; Fries et al. 1993) and human (Newton et al. 2006), where axons of M1 pass through the middle third of the PLIC, and axons from SMA course through more anterior regions of the PLIC. More caudally within the rodent brain, axons in the CP and the longitudinal pontine fasciculus from distant cortical areas remain largely separate, but those from adjacent cortical areas begin to overlap. Our observations in the CP are consistent with these findings and show that tract separation is most pronounced for cortical regions that are furthest from each other. By the medullary pyramid, the pyramidal decussation, and the dorsal column of the spinal cord, the representations of all the cortical regions overlap as axons become intermingled (Coleman et al. 1997). Similar conclusions have been drawn from studies in monkey which show that different cortical regions project onto the same motoneurons in the cervical spinal cord (Barnard and Woolsey 1956; Maier et al. 2002). These findings suggest that topographically organized corticospinal tracts in the cortex converge at some level of the neuroaxis (Dum and Strick 1991; He et al. 1993, 1995).

In monkeys, we know that the preSMA projects weakly, if at all, to the spinal cord (Dum and Strick 1991; Luppino et al. 1994). In addition to the striatum and prefrontal cortex, preSMA projects to the reticular formation (Keizer and Kuypers 1989) by way of the CP. Here, we map this descending tract, and show that the preSMA tract is most anterior in PLIC and most medial in the CP. In contrast, the S1 tract coursed through posterior regions of PLIC and was located more laterally in the CP. These findings are in good agreement with other human tractography studies (Newton et al. 2006; Park et al. 2008; Schulz et al. 2012; Archer et al. 2016), and suggest good preservation of cortical topography at the level of the internal capsule in humans.

Probabilistic tractography has previously been used to identify descending tracts from multiple cortical areas, but overlap between tracts has not been reported, sample sizes are generally small, and thresholding has been set at a single value for the entire tract (Newton et al. 2006; Schulz et al. 2012; Jang and Seo 2015; Archer et al. 2016; Potter-Baker et al. 2016). Our findings suggest that the low threshold values used in previous studies (0–2%) likely lead to high volume and high overlap between tracts, which further diminishes one's ability to track topography through the internal capsule and CP. Without knowing the extent of overlap between tracts, it is difficult to make a firm conclusion about the characteristics of different tracts.

The probabilistic SMATT advances the current literature by offering greater spatial localization in the sensorimotor tracts. White matter atlases such as the Johns–Hopkins white matter template (Wakana et al. 2007; Hua et al. 2008) and the Harvard–Oxford cortical and subcortical structural atlas (Frazier et al. 2005; Desikan et al. 2006; Makris et al. 2006; Goldstein et al. 2007) can be used to generate masks of entire tracts and their corresponding regions (i.e., PLIC and CP), but specific information within these regions corresponding to distinct cortical targets is not currently available. The probabilistic SMATT extends the literature by providing probability values that a voxel is contained within a specific sensorimotor tract, and has the potential to localize lesions with greater precision. For instance, we used the template to extract the FA measure for one stroke subject and showed that lesion overlap was greatest and FA values were lowest for the SMA, preSMA, PMd, and PMv tracts. Slice level FA profiles revealed tract-specific and slice-specific decreases in FA within these same tracts (Fig. 9). The use of the template in future studies will provide greater specificity when examining the association between brain structure and behavior (Lindenberg et al. 2010, 2012; Zhu et al. 2010; Stinear et al. 2012). To evaluate whether the SMATT worked in an independent data set, we overlaid the template onto individual FA maps from 20 healthy adults in standard space. Alignment of the SMATT to white matter was good for all individual subjects (Fig. 7), suggesting that the SMATT translates well to independent data sets. Consistency across individuals was also demonstrated by similar normalized FA profiles across the HCP group data and the independent data set (Fig. 7). One advantage of using the SMATT in future studies is that probabilistic tractography and slice level threshold analyses will not have to be completed. For instance, in the clinical setting, any structural scan can be collected, normalized, and then the SMATT can be used to extract tract-specific profiles from the data. In principle, any lesion or tumor that directly impacts an SMATT tract should be evident within the corresponding profiles. This procedure takes approximately 5 min to complete on a standard desktop computer with a single core. In instances where tractography analyses do need to be completed, our observations suggest that region specific, rather than slice specific, thresholds may be a viable approach that is computationally less intensive.

A well known limitation of tractography is its ability to track through areas of the brain which contain crossing fibers (Wedeen et al. 2008). This limitation is mitigated to some extent by the increased spatial resolution of the Human Connectome Project data, and advanced tractography algorithms that allow for the tracking of 3 fibers per voxel (Jbabdi et al. 2012), rather than conventional approaches which allow for the tracking of 1 or 2 fibers per voxel. Diffusion MRI images are susceptible to partial volume effects and noise. Partial volume effects are smaller; however, when fiber bundles are larger and curvature is lower, as is the case for the sensorimotor tracts (Vos et al. 2011). We have avoided using “corticospinal tract” and “corticobulbar tract” when labeling the template. Without collecting data from the cortex to the cervical spinal cord and then placing a waypoint in the cervical spinal cord, it is impossible to differentiate the corticospinal tract from the corticobulbar tract. It is, therefore, probable that many of the individual tracts in the SMATT include both corticospinal and corticobulbar fibers (Dum and Strick 1991; Galea and Darian-Smith 1994).

The SMATT was created using diffusion MRI data from healthy adults ranging in age from 21 to 35. Correlation analyses did not reveal any association between tract microstructure and age, and we show that the template can be useful in identifying tract- and slice-specific changes in FA after stroke in an individual who is 65 years old. Nevertheless, caution should be exercised when using this template to study older individuals and disease states that are associated with known changes in brain anatomy. Although we have demonstrated that the SMATT works well at the individual subject level, by necessity this requires that the data to be assayed is accurately warped to standard space. The SMATT was created using data from 87 right handers and 13 left handers. Future studies will be necessary to determine whether tract volume and tract orientation varies as a function of handedness and hemisphere. Although the thresholds used to create the SMATT were objectively determined, the measures that contributed to the calculation were subjectively determined. As the field progresses, new variables may be identified that help contribute to the optimal slice level threshold value. It is also important to note that the current template in no way provides a quantitative estimate of the actual strength of direct anatomical connectivity between the cortex and CP, a measure that cannot be derived from any form of structural imaging (Jones et al. 2013).

Precise measurements of the tracts that link the sensorimotor cortex with the CP are fundamental to our understanding of diseases and disorders that can impact the human motor system such as stroke (Newton et al. 2006; Schaechter et al. 2008, 2009; Lindenberg et al. 2012; Schulz et al. 2012; Groisser et al. 2014; Archer et al. 2016), upper motor neuron syndrome (Sach et al. 2004), multiple sclerosis (Tovar-Moll et al. 2015), traumatic brain injury (Jang and Kim 2016), spinal cord injury (Hou et al. 2016), pain (Misra and Coombes 2015; Misra et al. 2016), and cerebral palsy (Jaspers et al. 2015). Conventional approaches to studying the microstructural properties of the sensorimotor tracts in humans are focused on the M1 tract and likely include voxels that are also common to the corticospinal and corticobulbar tracts that descend from regions beyond M1 (Schaechter et al. 2008, 2009; Lindenberg et al. 2012; Groisser et al. 2014). The SMATT provides a new tool that can be used to localize tract-specific damage, and to quantify microstructure in specific tracts that are associated with distinct cortical regions. Increases in spatial localization may improve diagnostic and prognostic evaluations across a range of diseases and disorders. The SMATT and probabilistic SMATT are freely available at www.lrnlab.org (Laboratory for Rehabilitation Neuroscience).

Funding

The American Heart Association (contract grant number 15GRNT25700431) and the National Institutes of Health (contract grant number R01 NS058487).