Automated Cell Segmentation for Quantitative Phase Microscopy

Abstract

Automated cell segmentation and tracking is essential for dynamic studies of cellular morphology, movement, and interactions as well as other cellular behaviors. However, accurate, automated, and easy-to-use cell segmentation remains a challenge, especially in cases of high cell densities where discrete boundaries are not easily discernable. Here we present a fully automated segmentation algorithm that iteratively segments cells based on the observed distribution of optical cell volumes measured by quantitative phase microscopy. By fitting these distributions to known probability density functions, we are able to converge on volumetric thresholds that enable valid segmentation cuts. Since each threshold is determined from the observed data itself, virtually no input is needed from the user. We demonstrate the effectiveness of this approach over time using six cell types that display a range of morphologies, and evaluate these cultures over a range of confluencies. Facile dynamic measures of cell mobility and function revealed unique cellular behaviors that relate to tissue origins, state of differentiation and real-time signaling. These will improve our understanding of multicellular communication and organization.

I. Introduction

CELL segmentation and tracking within populations of cultured cells is often used to study two-dimensional migration and morphology as cells are genetically or chemically influenced, enabling the study of cellular communication and movement during differentiation in states of health and disease, and aiding in the optimization of culture conditions to better model development and behavior. Despite being bandwidth limited and prone to error, manual and computer-aided cell segmentation and tracking remains the most accessible way to analyze time-dependent cellular behavior in culture. Thus, the improvement and automation of both these tasks is a goal that promises to fundamentally change how we analyze individual and grouped cell behaviors in response to a variety of stimuli. As the precursor to automatic, long-term, large population tracking systems, cell segmentation plays the vital role of detection, shape analysis, spatiotemporal assignment, and determination of intercellular separation for each cell in a given field-of-view.

Many automated cell segmentation algorithms have been developed, and several of them have been designed to work with ubiquitous phase contrast and differential interference contrast data. The most commonly seen approaches include intensity-based thresholding [1, 2], feature detection and linear filtering [3, 4], morphological and nonlinear filtering [5], region accumulation [3], and deformable model fitting [3, 6–8]. Software packages have also been developed to combine many of these common approaches, including CellProfiler [9, 10] and plugins for ImageJ [11, 12]. But even with packages combining approaches, these efforts are tailored toward specific modalities not well suited for segmentation, primarily because of how widely used these modalities are. Strategies to circumvent these issues are to precondition common modalities into more segmentation-independent modes [13], or to use machine learning algorithms including bag-of-Bayesian classifiers [14] and supervised random forest classifiers [15] that make these approaches more flexible to accommodate various modalities.

Several toolkits have been devised that are easy to use and applicable across multiple cell lines and modalities, including Ilastik [15] and FogBank [16]. In the former case, user defined labels are classified in real-time using generic, nonlinear features that are modality-independent. In the latter case, seed points for geodesic region growing are determined via histograms and user-defined size constraints.

As has been reviewed, none of the existing approaches are perfect [17]. Most segmentation algorithms begin to break down as cell densities approach confluency. Other algorithms cater to specific cell types and their unique morphologies. More general weaknesses can include under- or over-segmentation, involved user-controlled parameters, complications of low signal-to-noise ratios (SNR), and manual detection for initialization. Additionally, many of these techniques focus on detecting smooth, generalized cell shapes and require postprocessing for accurate cell boundary detection. Much of this can be attributed to analyzing data sets that are qualitatively intuitive, but challenging to work with quantitatively.

In terms of analyzing segmented cell image data, several distribution models have been demonstrated in the literature to model or fit data comparable to those obtained here. For example, lognormal distributions have been fitted to blood platelet volumes [18–20] and Gamma distributions have been used with protein levels [21–23], but most studies of this kind are limited to a kernel density estimation (KDE) of the data [24].

In this work, we present the first unique cell segmentation algorithm designed specifically for use with quantitative phase microscopy (QPM), taking advantage of the modality’s ability to both measure optical thickness and clearly detect cell boundaries, offering more useful information for segmentation than just cell area or staining efficiency. Our iterative thresholding and flexible segmentation scheme allows for a wide range of cell types and morphologies to be segmented with high accuracy, requiring virtually no input from the user. We briefly introduce QPM and our specific time-lapse imaging setup in Section II. In Section III, we describe our algorithm in detail, demonstrating our iterative segmentation scheme and search for optimal volumetric thresholds. In Section IV, we show our results from testing on eight data sets and on six different cell types, demonstrating our performance on highly diverse cell morphologies, sizes, and densities; and validate our method by comparing our results to images manually labeled by biologists familiar with QPM. Finally, we conclude with a discussion in Section V emphasizing the benefits of a flexible, automated approach for cell boundary segmentation.

II. Imaging With QPM

Quantitative phase microscopy (QPM) is an interferometric optical modality used to generate contrast intrinsically in optically transparent specimens, generating an optical path length (OPL) map for an entire field of view (FOV) [25]. The physical thickness of the sample h(x,y) is proportional to the measured phase ϕ(x,y), wavelength λ, and difference between the refractive indices of the cells and the medium in which they reside Δn:

$$h\left(x,y\right)=\left(\lambda /2\pi \Delta n\right)\varphi \left(x,y\right).$$ (1)

This enables direct measurement and monitoring of nanoscale membrane fluctuations [26], growth and division cycles [27], overall dry mass [25, 28, 29], and volume [30] in living cells. Automated segmentation was not required for these studies, but an automated segmentation scheme could introduce statistical relevance to any study by enabling the simultaneous study of hundreds or thousands of cells at a time. By integrating phase over the area of a cell, we obtain what we call optical volume. With careful calibration using measured indices of refraction, absolute cell volume measurements are possible, but not necessary for this approach.

For the purposes of segmentation, QPM compares favorably to commonly used modalities such as Zernike phase contrast, differential interference contrast (DIC), and fluorescence microscopy. As demonstrated in Figure 1, QPM is uniquely suited for automated segmentation. Phase contrast microscopy (Fig. 1a) highlights most cell boundaries with its halo artifact, but cell regions without resolvable details fail to differentiate from background, and highly packed cells lack consistent halos. DIC microscopy (simulated, Fig. 1b) provides highlighting of features within cells, but smoothly tapered features and boundaries can be hard to discern. Fluorescence microscopy (Fig. 1c) can provide signals comparable to QPM when cells exhibit uniform fluorescence intensity, but suffers from a range of issues resulting in inconsistent labeling and photobleaching. In addition, transfection and labeling cells to generate fluorescence can alter cell properties and behaviors. In comparison to these modalities, QPM (Fig. 1d) provides consistent and more informative cell signal with low background. Intracellular signal comes in the form of optical thickness, rather than scattering and absorption or integrated fluorescence, which are difficult to standardize. Since QPM signals are proportional to physical thickness, segmentation decisions can be made according to a cell’s optical volume instead of area. Furthermore, QPM’s relatively low light exposure and lack of exogenous labels or dyes makes it well suited for time-lapse experiments and for imaging especially sensitive cell types.

Fig. 1.

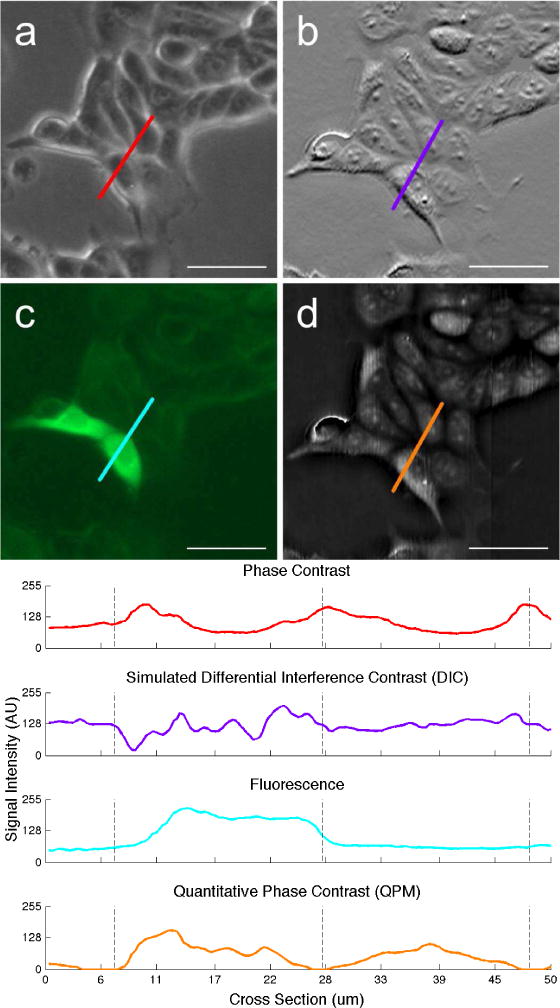
Comparison of common microscopy methods using viable cultured MCF-7 breast cancer cells expressing green fluorescent protein (GFP). Modalities shown: (a) Phase contrast, (b) simulated DIC, (c) fluorescence, and (d) QPM. Corresponding signal intensity plots are shown below. Phase contrast and fluorescence images were taken on an Invitrogen EVOS FL epiillumination microscope 30 minutes after the QPM image was taken. The DIC image (b) was simulated from (d) by calculating the one-dimensional gradient [31]. The bright artifact in the center-left of (d) is a phase wrap caused by residual error during the phase reconstruction process, and is smoothed out prior to segmentation, Scale bars represent 50 μm.

QPM has two major drawbacks. The first is the requirement that each image be extracted digitally from a raw interferogram. Although this is an extra step not needed for other modalities, it is not of great concern in terms of running time, as QPM data can be acquired and processed in real-time, if needed [32, 33]. A bigger problem is that this reconstruction is prone to error in the form of phase wraps, which are caused by an optically thick specimen and abrupt changes in phase.

The second major drawback is sensitivity to optical misalignment. QPM requires some minor adjustments to maintain alignment and a fresh background image at the start of each experiment. Optical misalignments (e.g., angle between the camera’s sensor and the stage) result in a ramp signal, and are a major source of background signal in our experiments. This effect is observed regardless of imaging location on the petri dish. Alignment of our system is simplified by utilizing a partially common-path design, which is highly stable. Some groups avoid this issue entirely by illuminating asymmetrically and computationally calculating comparable phase imaging data [34].

A. Optical Setup

Of the many QPM variants in literature, we implemented a recent method referred to as diffraction phase microscopy (DPM) [35], shown in Figure 2, which enables single shot acquisitions and high temporal stability. In our DPM system, we obtain spatially coherent light from a white light LED (Luxeon Rebel) that is collimated by a 50 mm lens and passed through a band-pass filter centered at 525 nm with a 50 nm bandwidth (Omega Optical 525AF45). Green filtering enables us to sample the interferogram at twice the resolution of red or blue on a Bayer-filtered RGB camera sensor, and limiting the bandwidth mitigates chromatic aberrations from the beam splitter. Our inverted microscope (Olympus IX50) uses a 10X, 0.3 NA, infinity-corrected objective lens to collect the light before directing it through the output port in collimated form.

Fig. 2.

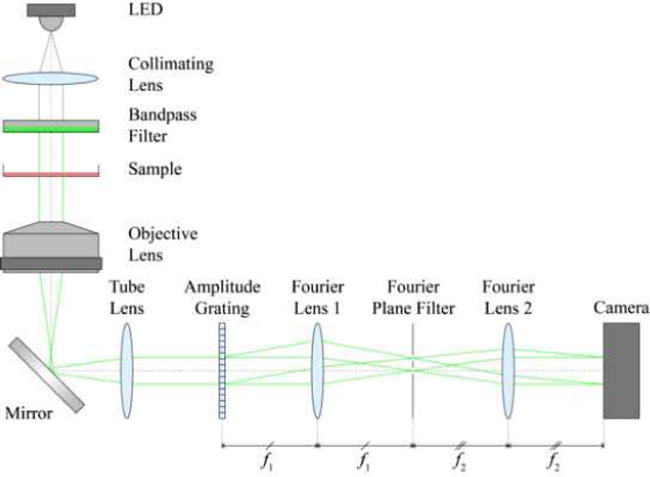
Schematic of QPM optical setup.

Outside the microscope, a transmission grating beam splitter (Edmund Optics, 110 lines/mm) at the image plane generates diffraction orders each containing full spatial and phase information. A 4 f lens system (f₂/f₁ = 75 mm / 75 mm = 1) is used to provide a Fourier filtering plane. At said plane, a micro-machined mask with 350 μm pinhole spatially low-pass filters the 0^th order (reference) beam, passes one of the 1^st order (sample) beams, and blocks all other orders. The two beams then interfere on the camera sensor (Amscope MU1403, 13.5 MP, CMOS). With the camera’s pixel size of 1.4 μm × 1.4 μm, we sample the interferogram with 8–16 pixels per fringe, depending on final magnification [19]. The interferometer is implemented as an additive module to a commercial microscope. The resolution and FOV of our final, reconstructed image is 2.7 μm and 350 μm × 450 μm, respectively. Lateral resolution for our QPM setup is slightly lower than that of the standard microscope platform being used due to a lack of a condenser lens matching illumination NA with the objective’s collection NA.

Time-lapse imaging experiments are controlled through a custom graphical user interface (GUI) and software written in Visual Basic. The GUI allows the user to control, among other parameters, number of wells in the culture plate, number of images per well, frame rate, integration time, lighting power, autofocus settings, and the imaging location within each well. The FOV is translated by an XY stage and DC servomotor (ASI MS-2000). This translation stage is mounted to the microscope’s stage, and includes a custom incubation fixture that holds the sample. The incubator includes top and bottom thermal plates (Tokai Hit) for controlling temperature and preventing condensation on the cover plate, as well as a 5% CO₂ input and water bath for humidity control.

B. Optical Path Length Map Reconstruction

In order to obtain the OPL map from an acquired interferogram image, we employ the Hilbert transform-based reconstruction method proposed by Pham, et al [36]. In this method the raw interferograms from both the sample image and reference image (taken without the sample in place) are each Fourier transformed, circularly shifted such that the peak corresponding to the first order is centered, and inverse transformed. The final OPL map is then calculated as the angle of the quotient of the two transformed images. By taking the arctangent after dividing by a reference image, we cancel out much of the noise to which the tangent operation is highly sensitive.

In comparison to single-shot reconstruction algorithms, this method also eliminates the linear phase ramp introduced by off-axis interferometry by using pixel-wise division during reconstruction, as opposed to after. Without this linear phase ramp in the reconstructed image, two-dimensional unwrapping is no longer needed, saving significant computational cost and preventing unnecessary reconstruction errors [37]. And because the optical setup is nearly common-path, it is robust enough to allow just a single reference image be used in the reconstruction for every image in a time-lapse experiment. Reconstruction takes on the order of a few seconds per image, quick enough not to impede data acquisition during a time-lapse experiment.

III. Iterative Segmentation

A. Image Preparation and Pre-Processing

By concatenating multiple images into one, we obtain two advantages beyond just improving our FOV. First, the use of multiple images provides better sampling of background phase and avoids the need for imaging an empty well as a control. This is because as we mechanically translate between adjacent FOVs, we progressively observe different areas of the common unobstructed background due to different cell layouts. Second, we obtain a larger ratio of cells fully sampled to those lying on the FOV’s boundary, reducing artificial skewedness in optical volume distributions generated later. By combining nine images into a 3×3 montage, we obtain a combined FOV of 1.05 mm × 1.35 mm. Larger montages are of course possible, but can limit temporal resolution in multi-well experiments due to the finite bandwidth of the camera and stage motors.

Errors like stiction and backlash in the stepper motors controlling our sample’s positioning can result in slight misalignments between adjacent FOVs in the montage. These errors are small enough to avoid significant skewing of volumetric data, but contain high frequency artifacts that can interfere with cell boundary detection. Realigning neighboring frames is possible, but takes time, limiting the system’s throughput. We apply a simple averaging scheme to smooth out these up to 3 um-sized artifacts along each frame’s boundary with its neighbor.

After the montage is compiled and misalignments are filtered, we perform a background subtraction to eliminate any minor signals caused by optical aberrations or misalignment. Each frame in the montage is averaged together and low-pass filtered to obtain the background image. This background image is then reduced in magnitude by 20% before subtraction to avoid removing small cell features or low-contrast cell boundaries. If we were to remove too little background during this stage, the absolute volumetric measurements would be affected, skewing the raw distributions left or right. However, because we normalize these distributions to within [0, 1], ending up with relative distributions, this effect is largely mitigated.

To search for phase wraps introduced by physically thick samples and abrupt phase changes we calculate the image gradient and retain the strongest 1% of responses. Areas with large high-frequency spatial variation are then median-filtered. This removes sharp phase responses but retains much of the phase intensity, keeping a rough volumetric estimation of the cell.

The final pre-processing step before segmentation is to apply a median filter with kernel height and width approximately equal to twice our lateral resolution. This helps to mitigate minute fluctuations within the cell that could lead to over-segmentation, and also helps to preserve the naturally convex shape the cells exhibit, smoothing both cell boundaries and cutting lines.

B. Iterative Thresholding

The iterative segmentation process is shown in Algorithm 1 and in Figure 3, where output bw is a binary mask for a single large feature with an apparent single boundary (a.k.a. blob consisting of a single cell or grouping of cells), input grey_blob is a grayscale blob, input volume_thresh is a volumetric threshold corresponding to the minimum expected cell volume (explained in Section III-C), and variable cc is a binary connected component region. The output of this algorithm, bw, shows distinct cell areas as connected components (true), and cutting lines as zeros (false). A blob can be a cell or connected grouping of cells, with either grayscale or binary representation.

Fig. 3.

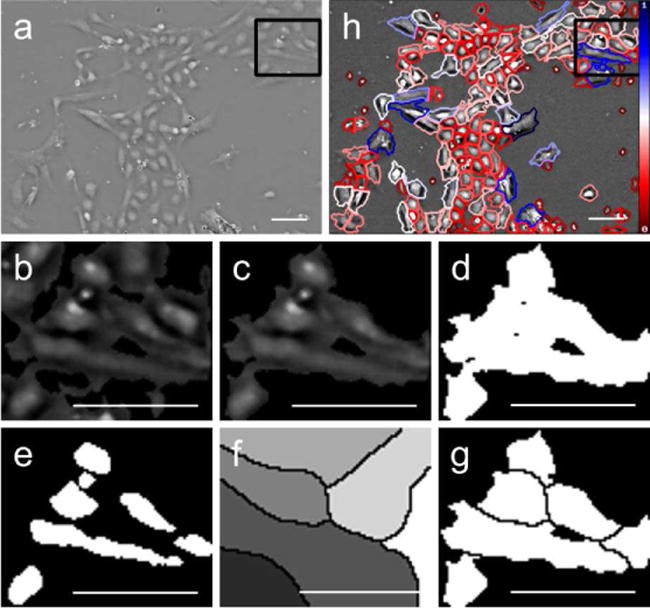
Demonstration of a single iteration of segmentation for a single blob. (a) Original image of H9 hESC cells with QPM. (b-g) Close-up view of region selected in (a) and (h). (b) Contrast enhanced region from (a). (c) Single connected blob passed to the segmenter. (d) Initial binary mask. (e) Threshold results showing first instance of connected component separation. (f) Watershed transform. (g) Cutting mask applied to binary blob. (h) Final segmentation results. Scale bars represent 50 μm. Color bar in (h) indicates relative optical cell volume from the minimum (red) to the maximum (blue).

The iterative segmentation process occurs independently for each grayscale blob grey_blob in the original image. As such, each cut made is based on local observations uninfluenced by other, more distant cells. Thresholding a single grayscale blob begins with the minimum observed signal and increases toward the maximum observed signal. Scaling the image intensity to [0, 1] without saturating preserves relative volumetric readings and offers a consistent range over which to iterate. Each of these iterations produces a binary mask bw_blob of the blob with smaller and smaller area. If at any point during this process the bw_blob contains more than one connected component (cc), we check the optical volumes in the grayscale image corresponding to each binary component. If two or more of these volumes is greater than our predefined volumetric threshold volume_thresh, we immediately break and perform the corresponding watershed cut(s). Connected components corresponding to volumes smaller than our threshold are removed from the mask.

Following a successful pass, we then calculate the Euclidean distance transform [38] of the binary mask bw_blob. The distance transform reassigns each pixel to the distance between the current pixel’s location and the nearest nonzero pixel’s location. In doing so, we treat each connected component as a “catchment basin”, and calculate the watershed transform [39] of the resultant image to find our cutting, or “watershed”, lines.

Once every blob in our image has undergone this iterative thresholding process, we deem one round of cutting complete, generate images and move on to the next round (Figure 4). If after any round no cuts have been made, the segmentation process is finished for a given volumetric threshold. This entire process may be repeated in order to identify the optimum volumetric threshold and corresponding segmentation results.

Fig. 4.

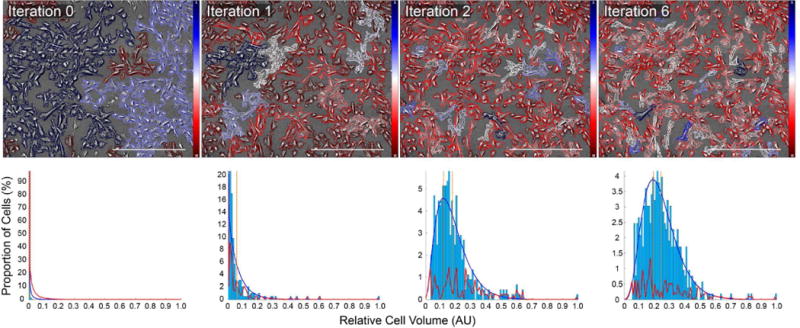
Iterative segmentation results for CD31/CD34 double negative iPSCs. Top row, left to right: Segmentation results after 0, 1, 2, and 6 rounds of iterative segmentation. Cell boundaries are overlaid with a diverging red-blue colormap indicating each cell’s volume relative to all those observed in the current FOV. Bottom row, left to right: Corresponding distribution of volumetric data. With each round of segmentation, the distribution of cell volume data moves away from an exponential-like distribution and toward a Gamma-like one. Per-bin fitting error between histogram data and fitted Gamma curve plotted in red. Each image represents a 3×3 montage of the same FOV. Scale bars represent 500 μm. Color bars in top row indicate relative optical cell volume from the minimum (red) to the maximum (blue).

C. Volumetric Distributions

Our segmentation scheme is highly dependent on a single threshold parameter, which is not known a priori. Instead, we make several passes using different values for volume_thresh, and analyze the resulting distributions of cell volumes to find the optimum value.

We generate a histogram of relative cell volume measurements after each segmentation iteration, normalized to within the interval [0, 1] for data fitting. We then fit a Gamma distribution with probability density function (PDF) of the form

$$f\left(x|\alpha ,\theta \right)=\frac{1}{{\theta }^{\alpha }\Gamma \left(\alpha \right)}{x}^{\alpha -1}\exp \left(-x/\theta \right),$$ (2)

where x is the positive data being fitted and Γ(·) is the Gamma function. Maximum likelihood estimation is used to solve for positive shape parameter α and scale parameter θ. The density of the distribution is then normalized to match the total area of the histogram, and a fitting error is calculated on a per bin basis [40]. The summed fitting error among all bins is used as our quality metric during our search for the optimum volumetric threshold.

Both shape parameter α and scale parameter θ are always larger than zero, but vary based on round of segmentation, cell type, and confluency rate. For example, one 48 hr time-lapse imaging pluripotent cells resulted in shape (α) values between 1.81 and 5.32 and scale (θ) values between 0.155 and 0.195. Alternatively, the image of iPSCs from Figure 4 undergoing multiple rounds of segmentation resulted in shape (α) values between 0.15 and 4.54 and scale (θ) values between 0.03 and 0.07.

We chose to model our volumetric distributions as Gamma-like for three reasons: (1) each image’s data is skewed right with a unimodal distribution, (2) the data is strictly positive, but normalized, and (3) we wanted a model flexible and general enough for fitting data from all stages of segmentation, even the exponential-like distributions from early rounds of segmentation. To quantitatively evaluate our choice, we fitted over 20 different distribution types to volumetric distributions from all stages of segmentation and across all cell types, and measured goodness of fit. Although the Gamma distribution showed the most consistent goodness of fit, other continuous, univariate, semi-infinite interval distributions performed well, including Burr and Weibull distributions. Qualitative assessments using quantile-quantile (Q-Q) plots verified these findings.

Algorithm 1.

Iterative Thresholding

1:	Input: Masked grayscale image of single blob grey_blob and volume threshold volume_thresh
2:	Output: Binary mask bw corresponding to grey_blob, with applicable cuts made
3:	increment = 0.05, thresh = increment, bw = grey_blob > 0
4:	while thresh < 1 do
5:	bw_blob = grey_blob > thresh
6:	for each cc in bw_blob do
7:	volume = cc.* grey_blob
8:	if volume < volume_thresh then
9:	remove cc from bw_blob
10:	end if
11:	end for
12:	num_ccs = number_of_ccs(bw_blob)
13:	if num_ccs > 1 then
14:	break
15:	end if
16:	thresh += increment
17:	end while
18:	if num_blobs > 1 then
19:	dists = distance_transform(bw_blob)
20:	basins = watershed(dists)
21:	cut lines = basins == 0
22:	bw = and(bw, ~cut_lines)
end if

Algorithm 2.

Volumetric Threshold Search

1:	Input: Integer values for upper and lower volumetric threshold bounds, maximum number of iterations max_iterations, if desired
2:	Output: Volumetric threshold volume_thresh corresponding to the global minimum distribution fitting error
3:	min_thresh = lower_bound, max_thresh = upper_bound, current_thresh = min_thresh
4:	for i=l: max_iterations do
5:	if i > 1 do
6:	current_thresh = max_thresh
7:	else do
8:	sorting_indices = sort(errors, ‘ascending’)
9:	current_thresh = round(men(threshes(sorting_indices (1)), threshes(sorting_indices (2))))
10:	end
11:	past_threshes(i) = current_thresh
12:	if past_threshes(i) = past_threshes(i−1) do
13:	break
14:	end
15:	segment image using current_thresh
16:	generate histogram of volumetric data
17:	calculate fitting_error for Gamma distribution
18:	past_errors(i) = sum(fltting_error)
19:	end

D. Automated Threshold Convergence

As described earlier, Algorithm 1 showcases how the optical volumetric threshold parameter volume_thresh controls segmentation decisions. This single value defines the minimum acceptable cell volume and is thus responsible for dictating which blobs are too small to be recognized as cells as well as when to segment. Forcing the user to input values for this parameter would either lead to under- or over-segmentation choices or require a priori knowledge of volumetric data for the specific cell type being studied. Instead, we present a fully automated method for finding the optimal volumetric threshold based on the observed distribution of volumes in a given FOV.

Algorithm 2 describes the search for volume_thresh, in which we attempt to find the volumetric threshold that maximizes the goodness of fit, and minimizes the summed fitting error fitting_error, between our volumetric histogram and a fitted Gamma distribution. We initialize the search with reasonable upper and lower volumetric bounds, acting as our seed thresholds from which to start. These bounds represent the smallest and largest volumetric measurements expected, which can be set by the user manually. These parameters have little effect on the final results, and are included as a way to correct for differences in image magnification and resizing Larger and higher magnification images will require a larger upper bound, for example.

For each iteration, we find the two lowest total fitting_errors for each segmentation result, and the corresponding volumetric thresholds used for those attempts. The next iteration is the mean of those two values, rounded to the nearest integer. If the current volumetric threshold matches that from the last iteration, the search has converged and is ended. If there are multiple threshold solutions that result in comparable fitting errors (<5% difference), the larger threshold is chosen in an attempt to further avoid over-segmentation.

Figure 5 demonstrates this search graphically. The total Gamma distribution fitting error, in number of cells, typically exhibits a roughly convex shape, allowing us to find a global minimum. This shape was too rough for algorithms sensitive to local minima such as gradient descent. However, when plotted as a percentage, the fitting error across the range is nearly linear due the exponential dependence of the total number of cells on volumetric threshold.

Fig. 5.

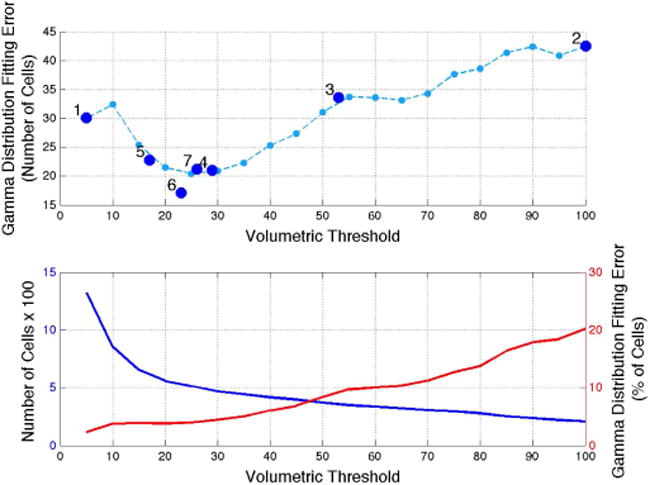
Iterative optimization of volumetric threshold. Top: The search for a global minimum of total Gamma distribution fitting errors, taking 7 iterations. The undersampled line (light blue) was generated using threshold values from 5 to 100 in intervals of 5, and is not known a priori. Bottom: The total number of cells (blue) decreases exponentially with volumetric threshold. Because of this, the percent fitting error (red) lacks a convex region.

The convergence of finding a volumetric threshold is designed to require as little prior knowledge as possible. We make no assumptions about rates of cell growth, proliferation, or migration into or out of the FOV. Each cell population is considered asynchronous (i.e., in different growth stages) and non-steady-state. As we move from frame to frame in a continuous time-lapse, we observe differences in the number of cells, as well as in the distribution of cells pertaining to certain phases. This results in sporadic shifting of the Gamma curves’ shape and scale parameters, as well as to volumetric threshold. The only parameter that seems to have a positive correlation with time is goodness of fit, due to generally increasing numbers for a proliferating population. However, this too, is noisy, and would not be applicable for all studies. Thus, a complete search is required at each time point in a time-lapse data set. The benefit from this is that no changes to the algorithms or parameters therein are required when switching from individual images to time-lapse data sets. This choice to treat each image in a time-lapse as discrete and unrelated reinforces the idea that no preceding knowledge should be required to segment data in a fully automated fashion.

IV. Results

A. Cell Lines

Our segmentation algorithm was tested on six cell types:

• 1)Human bladder-derived smooth muscle cells (BD-SMCs)
• 2)CD31/CD34 double negative induced pluripotent stem cells (iPSCs), verified using fluorescence-activated cell sorting (FACS)
• 3)CD31/CD34 double positive iPSCs, verified using FACS
• 4)H9 human embryonic stem cells (hESCs)
• 5)Huf3 human fibroblasts (FBs)
• 6)Pluripotent stem cells shed from an embryoid body (EB)

Montages were acquired every 10–20 minutes during each 24–72 hour time-lapse. Montages can be single images, 2×2, or 3×3 individual images stitched together. Proliferation was uninhibited during each experiment, resulting in a wide range of confluency rates on which to test. The maximum observed confluency rate was ~70%, based on a 100% confluency rate of 10³ cells/mm². Figure 6 demonstrates segmentation results on cells imaged for 25 hours representing a range of densities. Between the start of imaging and 25 hours later, cell confluency doubled from 37.5% to 66.0%, with no significant drop of in segmentation accuracy.

Fig. 6.

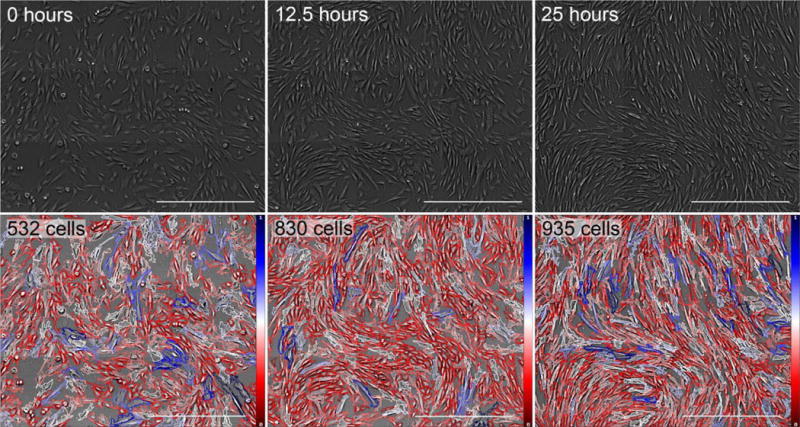
Segmentation results for time-lapse imaging of Huf3 FBs sampled at three different time points. From left to right: images taken at 0, 12.5, and 25 hours (shown left to right). During this time, the total number of cells within our FOV nearly doubles, increasing from 500 cells to just fewer than 1,000 cells. Each image represents a 3×3 montage of the same FOV. Scale bars represent 500 μm. Color bars in bottom row indicate relative optical cell volume from the minimum (red) to the maximum (blue).

B. Run Time

Due to its iterative approach, the algorithm’s run time increases nearly linearly with both number of cells and image size. Downscaling (resizing) the image prior to processing greatly decreases computational cost, but sacrifices cell boundary resolution. For example, it takes ~45 s for each round of segmentation on a 1.4 MP image sampling approximately 500 cells, but only ~20 s per round for the same image scaled down by 50% to 0.7 MP. For an image from that same time-lapse, taken 24 hours later with approximately double the cells, segmentation takes ~93 s for a 1.4 MP version and ~44 s for a 0.7 MP version. As we iterate through the segmentation process, run time for each round increases directly with the number of blobs, thus these numbers represent the average time per round.

If an image takes between five and ten rounds of segmentation for each volumetric threshold, then testing a single threshold takes anywhere between 1.7 min and 15 min for the best and worst cases presented above, respectively. If seven volumetric threshold iterations are required to reach convergence, as was the case in Figure 5, total run times grows to 11.7 min and 108.5 min. When considering throughput and data density, calculating run time on a per cell basis results in 1.4 s to 6.5 s per cell.

All calculations and image processing are implemented on a laptop with a 2.3GHz Intel Core i7 processor and 16GB of memory, running OS X 10.10.5. All scripts are written and executed in MathWorks Matlab R2013a (64-bit).

C. Accuracy

To determine segmentation accuracy, one montage from each data set was randomly chosen for accuracy measurements. Two experts familiar with QPM then independently scrutinized each segmented image on a cell-by-cell basis. We categorized errors into six mutually exclusive classes: (1) false negatives, (2) false positives, (3) poor boundary detection, (4) under-segmented cell clusters, (5) over-segmented cells, and (6) cell clusters segmented into the correct number of cells but at the wrong location. An example of each error type is demonstrated in Figure 7. Total error rates are the sum of these six categories. As shown in Table 1, we obtained an average combined detection and segmentation accuracy rate of 91.5% over the 5,377 observed cells.

Fig. 7.

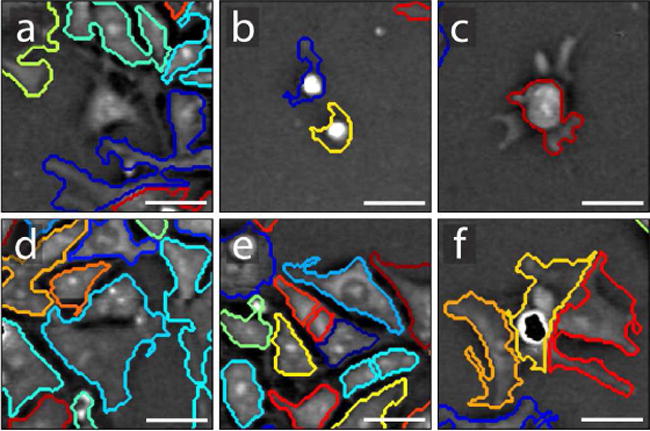
Examples of each error type: (a) false negative, (b) false positive, (c) poor boundary detection, (d) under-segmented cell cluster, (e) over-segmented cells, and (f) poor segmentation location. False negatives are usually caused by poor contrast. False positives are usually caused by dead cell material, dust, or bubbles. Poor boundary detection usually comes in the form of under-sensitive detection of low contrast cell boundaries, especially if there is a dip in signal between branch-like areas and the bulk of the cell, but can also include over-sensitive detection of background regions. Poor segmentation location has little to do with detection sensitivity. It occurs when cells are segmented into the correct number of cells, but at an incorrect location, caused by phase variations within the cell triggering the watershed algorithm. Although subjective, we aimed to count an error for each cell boundary that underestimates or overestimates a cell’s area by about 25%. Under- and over-segmentation errors are most common for tightly packed cells, but drops in signal from a cell’s nucleus can also affect segmentation. Poor segmentation location is most often caused by occlusion and phase wraps. Examples are taken from H9 hESC image data during different (not necessarily final) rounds of iterative segmentation. Each FOV is 50 × 50 μm. Scale bars represent 15 μm.

TABLE I.

Quantitative evaluation of detection and segmentation errors for eight images, one selected randomly from each data set. Units in number of cells, unless otherwise labeled.

Montage	1	2	3	4	5	6	7	8
Total Cells	482	751	121	929	912	773	568	841
False Negatives	0	0	0	0	2	0	2	0
False Positives	0	2	7	1	0	2	2	0
Poor Boundary Detection	16	23	3	14	27	28	4	16
Under-segmented	3	3	2	21	2	6	5	15
Over-segmented	14	28	0	26	19	18	14	29
Poor Segmentation Location	3	6	3	25	4	16	8	17
Total Errors	36	62	15	87	54	70	35	77
Total Error (%)	7.47	8.26	12.40	9.36	5.92	9.06	6.16	9.16

False negatives, or cells left undetected, were rare, only occurring four times. False positives were only slightly more common, occurring 14 times. On the other hand, poor boundary detection was a significant issue, occurring 131 times. Together, these errors represent a detection failure rate of 2.78%. Most of these errors are caused by parts of cells flattening to the point where the cell’s boundary is difficult to observe, and SNR approaches one. Some error is also attributed to overly aggressive background removal. Although most of the cell is detected and segmented correctly, this is still counted as an error.

Over-segmentation occurred about 2.5 times as often as under-segmentation and about 1.8 times as often as poor segmentation location. This mix of under- and over-segmentation errors shows the algorithm is approaching an optimum volumetric threshold and has successfully mitigated watershed’s tendency to over-segment.

Although the number of cells we can check for accuracy is throughput-limited, we observe some cell type-dependent error bias. Pluripotent cells tended to have less than average error rates, with the notable exception being the EB data set, which had the highest error rate in the test (12.4%). This was the only data set comprised of 1×1 montages, limiting how many cells we could image at a time. Additionally, this set also showed the lowest observed contrast and resolution. Error rates for fully differentiated cells did not vary as much as those for pluripotent cells. SMCs had a slightly lower than average error rate of 7.64%, while FBs had a combined error rate of 9.11%. We hypothesize this is due to FBs being more elongated in shape than SMCs, which tends to increase occlusion. Our algorithm makes no attempt to account for cells occluding one another. This results in some dendritic-like extensions of cells being detected as whole, accounting for a large portion of poor segmentation location errors.

D. Flexibility

Figure 8 demonstrates the range and density of morphologies segmented with this approach. In comparing major and minor axis lengths in the left plot, cells along the 1:1 boundary appear round, while those farthest away from that boundary are greatly elongated. Analyzing how far away cells are from the origin on this plot may help in identifying mitosis or apoptosis.

Fig. 8.

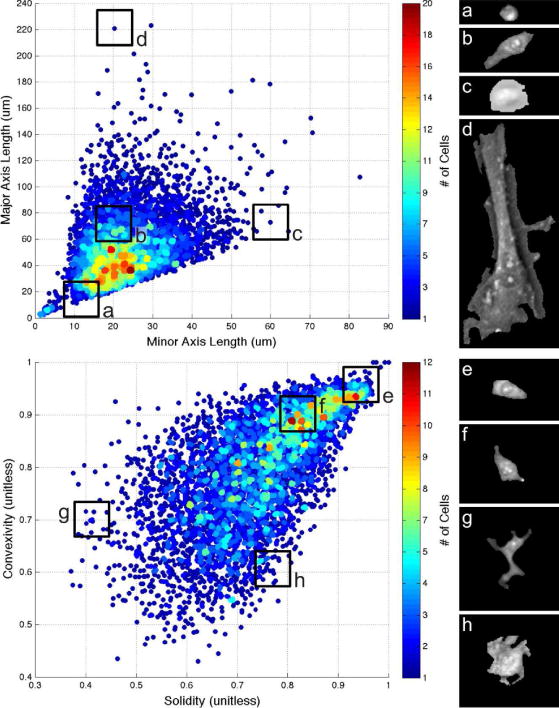
Range and density of segmented cell morphologies. Top heat map plots major vs. minor axis length, quantifying how round or slender cells appear. Bottom heat map plots convexity vs. solidity, quantifying perimeter energy and how spread out each cell is. Each heat map is accompanied by four example cells representing morphologies of different areas of the map. Data shown includes one image from each of our data sets, totaling over 5,000 cells.

From plotting convexity vs. solidity in the second plot, we see a range of dendritic-like features and smooth perimeters. Convexity is calculated as the ratio of the convex hull’s perimeter over the cell’s actual perimeter, and is sensitive to the number and shapes of protrusions and cavities. Solidity is calculated as the ratio of actual area over convex area, and is sensitive to the size of these features relative to overall cell size. In the plot, samples are densely populated all the way up to the 1:1 limit, suggesting that large ratios in either direction could contribute to identifying poor cell boundary detection or segmentation location. No settings or parameters were changed during this testing.

E. Comparison to Other Algorithms

To offer a point of comparison for our approach to segmentation, and to demonstrate how other algorithms might work on QPM data, we evaluated six other established algorithms designed for use on more commonly used modalities such as bright field, phase contrast, and fluorescence. These six algorithms are: (1) k-means++ clustering [41, 42], (2) marker-based watershed segmentation [39], (3) distance regularized level set evolution (DRLSE) [43], (4) level sets using active contours without edges (ACWE) [44], (5) Ilastik [15], and (6) FogBank [16]. These approaches are represented here because of their efficacy outside of QPM and their collective range of approach. K-means++ and watershed are relatively basic, but widely applicable algorithms. DRLSE and ACWE are more state-of-the-art applications of level set algorithms, but with different methods of control over the propagation of different numbers of segmentation contours. Ilastik and FogBank are software packages designed for broad applicability and ease of use. Ilastik is unique in this group, as its random forest classifier requires user defined labels and offers real time classification feedback. FogBank is based on modified morphological watershed principles, making it a comparable but more advanced version of the classic watershed transform. The qualitative results of these algorithms (except DRLSE) and our own applied to different cell types and packing densities are shown in Figure 9.

Fig. 9.

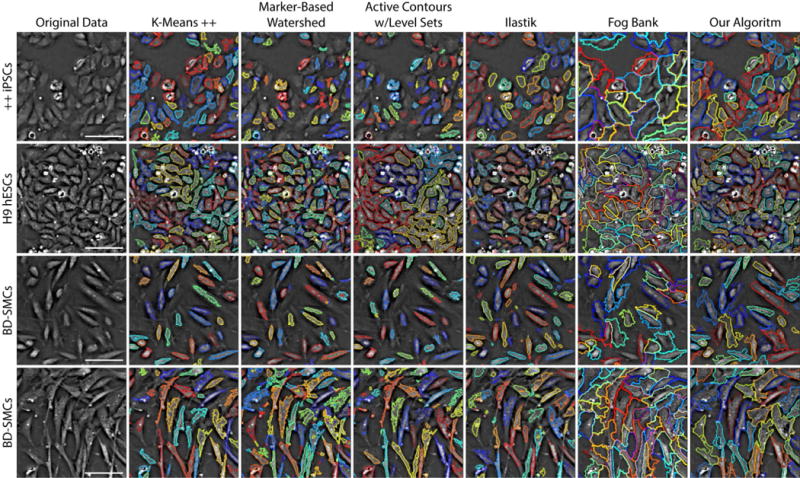
Qualitative comparison of segmentation techniques on QPM data. Different cell lines are presented row-wise, from top to bottom: (1) double positive CD31/CD34 iPSCs, (2) H9 hESCs, and (3 and 4) BD-SMCs from different experiments and time-points. Different segmentation techniques are shown column-wise, from left to right: (a) original data, (b) k-means++, (c) marker-based watershed, (d) active contours with level sets, (e) Ilastik, (f) FogBank, and (g) our iterative algorithm. Although none of these approaches were designed for use with QPM, most show strong potential for utility. Outlines are shown with random color assignments to help visualize boundary separation. Each FOV is 145 × 145 μm. Scale bars represent 50 μm.

As expected, K-means++ clustering and watershed segmentation, although easy to work with, show that they alone are not effective enough for accurate cell detection and segmentation, but can be useful as part of a more intricate solution. K-Means++ detects most cells showing strong contrast, but lacks a solution for segmenting closely packed cells. Conversely, watershed tends to over segment when left unconstrained.

We evaluated two forms of level set-based algorithms. Distance regularized level set evolution (DRLSE) is a somewhat traditional level set algorithm, which depends on the image’s gradient to stop its curve evolution. This introduces a dependence on clear cell boundaries for accurate detection, which is often, but not always, the case with QPM. DRLSE isn’t designed to segment objects placed close together, as it uses a single level set equation. (We omit these results from Figure 9 because of this.) This could be overcome by, for example, detecting and using cell center points as initial conditions for multiple level set equations, but the reliance on clearly defined cell edges would remain. A more applicable algorithm for this modality can be found in active contours without edges. By using a stopping term based on the Mumford-Shah functional [45] rather than on the gradient, the Chan-Vese algorithm can deal with cells that have ambiguously defined boundaries. While we found this algorithm to perform much better than more traditional level set methods, high confluency rates and low contrast still limit it. Modifying this algorithm to include (a) a heuristic for finding initial contours, (b) a volume or area constraint to aid with segmentation, and/or (c) more sensitive detection could greatly improve this approach for use with QPM.

Finally, we compared two processing toolkits designed for ease of use across different cell lines and modalities. Ilastik is a supervised learning model featuring point-and-click labeling, a random forest classifier trained on a set of generic, nonlinear features, and real-time classifier feedback. As such, it is extremely easy to use and can provide accurate results for lower cell densities. We found that with its use of textures and its corresponding need to label image areas, there exists a direct tradeoff between accurate boundary detection and ability to segment closely packed cells. We also found that training and testing must occur on the same cell line under the same conditions for best results. If this technique could detect when cells are closely packed, and replace its area classifier with a drawn boundary, it could prove very useful for densely packed cells. Another easy to use toolkit is FogBank, a morphological watershed-based technique using geodesic region growing and histogram binning for detecting seed points. These two features limit watershed-based over segmentation and preserve and accurate cell boundaries. Because it is designed to segment cells that are physically touching, segmentation on lower packing densities can result in boundaries that are too large and inclusive. Additionally, we found it to be extremely sensitive to its area parameters, which may need adjustment as time-lapse studies elapse. Of all the compared techniques shown here, FogBank shows the most potential applicability for QPM and segmenting densely packed cells, as long as its area-based constraint can eventually be swapped for a volume-based one.

V. Discussion and Conclusions

In this work we evaluated a fully automated algorithm that uses QPM measurements of optical thickness and volumetric distributions to drive decision making for cell segmentation. The algorithm iteratively segments cell clusters and checks for valid cuts according to a minimum acceptable optical volume threshold. This process is repeated for several thresholds, converging when the resulting volumetric distribution best matches a fitted Gamma curve. We evaluate our approach quantitatively on eight data sets with six different cell types and confluency of up to 70%, achieving a combined, average detection and segmentation accuracy rate of 91.5%.

By using a volumetric threshold instead of an area- or amplitude-based one, we gain a more complete picture of when segmentation should or should not occur. Under this scheme, cells undergoing apoptosis or mitosis are shown with no bias over flatter cells with larger areas but lower average thickness. And by using QPM, a modality that inherently transforms physical thickness into signal amplitude, we are able to identify optimum segmentation locations using a modified, but simple, watershed algorithm.

In designing our algorithm, we assumed all cell populations to be monolayer. However, we failed to take into account minor occlusions caused by extreme cell elongation and dense cell packing. Future development might include some method to account for this, perhaps by searching for these dendritic-like extensions and treating them separately, or by allowing cell boundaries to overlap one another.

We anticipate that this algorithm could be applied to cell mixtures, in which a mixture of Gamma distributions could be applied to volumetric distributions for data fitting and finding volumetric thresholds. The segmentation results shown here hold promise as the first step in a whole solution for automated cell tracking using QPM, regardless of a cell population’s purity.

There are three immediate options for run time optimization of this approach. The first and simplest solution is to move from an interpreted language to a compiled one such as C# or C++. The second is to include a low-resolution version of the code that downsamples images greatly prior to calculating volumetric distributions and segmenting locations. The third is to improve on the iterative search for volumetric thresholds when using time-lapses by constraining the search bounds based on data from previous time points.

The advent of automated segmentation, particularly for densely packed cell populations and time-lapse studies, could open the door for studying localized environmental effects on cell growth and division, as well as on localized orientation and neighboring or social phenomena. For example, automated segmentation could enable the study of how densely packed and oriented cardiomyocytes impede localized electrical potentials. Automated segmentation and tracking could also help us understand how local abrasians or temperature fluctuations affect the formation of scar tissue or functional muscle tissue. One recent study used semi-automated cell segmentation and tracking on phase contrast data to understand how pluripotent stem cells, which are inherintely heterogeneous in terms of functional properties and observed dynamics, require neighbors and socialization in order to thrive long-term [46]. Fully automated software could strengthen any of these studies by increasing throughput and allowing for supplementary variables to be tested.